Abstract
The recent pandemic of COVID-19 has brought about tremendous impact on every aspect of human activities all over the world. The main route of transmission is believed to be through coronavirus-bearing respiratory droplets. The respiratory droplets have a wide spectrum in droplet size, ranging from very small droplets (aerosol droplets) to large droplets of tens and even hundreds of μm in size. The large droplets are expected to move like projectiles under the action of gravity force, buoyancy force and air resistance. Droplet motion is complicated by droplet evaporation, which reduces droplet size in its trajectory and affects the force acting on it. The present work attempts to determine the trajectories of the large droplets by using a simplified single-droplet approach. It aims at providing a clear physical picture to elucidate the mechanics involved in single droplet motion and the various factors affecting the range. Assuming an indoor environment with an air temperature of 18 °C and relative humidity of 50%, the horizontal range of large respiratory droplets (diameter 120 μm–200 μm) in common respiratory activities are as follows: Speaking, ≈ 0.16 m–0.68 m, coughing, ≈ 0.58 m–1.09 m, and sneezing, ≈ 1.34 m–2.76 m. For the smaller droplets (diameter < 100 μm), the droplets are reduced to aerosol droplets (≤5 μm) due to evaporation, and will remain suspended in the air instead of falling onto the ground like a projectile.
Keywords: COVID-19, Respiratory droplets, Droplet trajectory, Indoor environment, Social distancing, Numerical
Highlights
-
•
Trajectories of droplets (initial dia. 40–200 μm, vel. 2–50 m/s) are studied.
-
•
Air resistance is the most important factor in affecting droplet motion.
-
•
Relative humidity and evaporation also play a significant role.
-
•
Smaller droplets (diam. ≤ 100 μm) are reduced to aerosol droplets in the air.
-
•
The range is 0.16–0.68, 0.58–1.09, 1.34–2.76 m in speaking, coughing, sneezing.
Nomenclature
drag coefficient (dimensionless)
density of water (kg/m3)
force (N)
- R
droplet radius (m)
- Rs
settling droplet radius (m)
buoyancy force (N)
- Re
Reynolds number (dimensionless)
drag force or air resistance (N)
- RH
relative humidity (%)
gravity force (N)
- ,
displacement along x and y (m)
force acting by air on vapor from droplet evaporation
time (s)
time at which droplet becomes an aerosol droplet (R ≤ 2.5 μm) (s)
time at which droplet is entirely evaporated (s)
acceleration due to gravity (m/s2)
air temperature (0C)
parameter characterizing rate of change of droplet radius (m/s)
initial droplet temperature (0C)
horizontal distance travelled after escape from jet (m)
settling time (s)
mass (kg)
- ,
velocity and components (m/s)
- ,
coordinates at which droplet becomes an aerosol droplet (R ≤ 2.5 μm)
momentum and components (kg.m/s)
ejection angle (0)
density of air (kg/m3)
1. Introduction
The outbreak of COVID-19 in late 2019 has rapidly burst into a pandemic over a short period of a few months. The pandemic, which is caused by a novel coronavirus officially named as SARS-CoV-2, has recorded 18 million of confirmed cases and 0.69 million of deaths globally as of August 5, 2020 according to the situation report by WHO 2020 [1]. In addition to these threatening figures the pandemic has brought about tremendous impact on economic and other human activities all over the world. The impact results from the lockdown of cities, suspension of work and business, shutdown of public facilities, prohibition of public gathering and advice to stay at home or quarantine, in attempts to contain the disease and to slow down the spreading of COVID-19 via social distancing.
While the virus SARS-CoV-2 is thought to be initially transmitted from wild animals, it is now spreading rapidly among humans with an estimated median basic reproduction number of about 2.79 as reported in Liu et al. [2]. Although there is report of suspected cases of infection from aerosol droplets generated in toilet flushing of virus-bearing faeces or urine and transmitted via drainage piping, the main route of transmission among the general public is generally believed to be through coronavirus-bearing respiratory droplets from carriers (WHO 2020 [3]). The virus in these respiratory droplets could reach the susceptible directly or indirectly.
Respiratory droplets are expelled from a person in activities like coughing, sneezing, speaking, or even simply breathing. The respiratory droplet cloud contains droplets having a wide spectrum of droplet size and velocity as mentioned in Xie et al. [4]. The droplet size ranges from <5 μm for very small droplets (commonly known as aerosol droplets) to hundreds of μm for large droplets (Tellier et al. [5] and Yan et al. [6]). As respiratory droplets are the main transmission media of coronavirus, there has been interest in the behavior of the respiratory droplets after leaving the human body. Aerosol droplets will remain suspended in the air for a long time (Liu and Novoselac [7]) and their movement and settling time are largely affected by local airflow as reported by Wang et al. [8]. On the other hand the large droplets are expected to move like projectiles. Both the small and large respiratory droplets, if they are virus-bearing, would cause infection if they reach the susceptible and land on the membrane in the respiratory system, or even on the eyes. These droplets could reach the susceptible in a direct or indirect manner. The aerosol droplets might be inhaled directly, and the large droplets could also be inhaled, or deposited directly on membrane in the nose, mouth, or eyes. Such a direct route of transmission could be effectively interfered or stopped via wearing a surgical mask by the susceptible even if someone nearby is shedding virus-bearing respiratory droplets as mentioned in Leung et al. [9]. On the other, the virus in the large droplets may reach the susceptible in an indirect manner. The large droplets may travel in the air like projectiles and be eventually deposited on some surface nearby, which could a table surface, the wall, the floor, or even clothes. If someone happens to touch these contaminated surfaces with his hands and subsequently touch his nose, mouth, or eyes, the virus may be transmitted to him. It is thus of pragmatic importance to study the trajectories of these large droplets so that one can roughly estimate the range of the droplets after shedding by the carriers (Zhang et al. [10]). The importance of respiratory pathogen emission in transmission of COVID-19 was emphasized by Bourouiba [11]. There are numerous studies on various aspects of respiratory droplets, including droplet size distribution by Tseng and Li [12], Morawska et al. [13], Haslbeck et al. [14], Han et al. [15] and Drossinos and Stilianakis [16] and respiratory clouds in violent expiratory events by Bourouiba et al. [17] and Wei and Li [18]. In particular, Lindsley et al. [19,20] and Zayas et al. [21] reported detailed studies in the aerosol particles generated during coughing while interesting results of the aerosol particles emitted during speech with different loudness were reported by Asadi et al. [22].
Different aspects of respiratory droplets have been studied by Berrouk et al. [23] and He et al. [24] using experimental, numerical and simulation methods. In particular, simulations on the effect of humidity on droplet transport was reported by Wang et al. [25], the effect of ventilation on droplet transport in a room was reported by Sun and Ji [26], the transmission of droplet-mediated respiratory diseases on airline was investigated by Hertzberg et al. [27], the droplet transmission of infection between flats was reported in Gao et al. [28], and Li et al. [29] studied the transmission among occupants in a room. Meanwhile, it is also interesting to understand the various factors that affect the trajectory of an individual droplet via basic physics. This is achieved via using a simple model in the present study with the inclusion of droplet evaporation. Evaporation of droplets has been a topic of interest in various fields since the publication of the classic paper by Wells [30]. In particular, a few years after the outbreak of SARS in 2003, Xie et al. [31] modified Wells’ model and presented a detailed study of exhaled jets. The present study derives and solves the equation of motion of an evaporative droplet under the action of gravity, buoyancy and air resistance, with simplifying assumptions on droplet evaporation rate and drag coefficient, in order to provide a clear physical model of droplet movement. The aim of the present work is thus to employ a simplified approach to highlight the salient features of large respiratory droplet motion and to investigate the effects of various factors affecting droplet range. The results of the present study on the horizontal range of large respiratory droplets are compared with the social distance recommended by public health authorities (WHO 2020 [32] and CDC [33]) and experimental values in the literature.
2. A simplified model and governing equations for droplet motion
The present study aims at building a simplified model to study the trajectories of droplets in indoor environment. The major assumptions used in deriving the equations of motion are listed below. These assumptions are made with the aim of showing the salient features of droplet trajectory without being masked by complicated formulation. These simplifying assumptions are discussed in the following sections and the consequence of these assumptions is also discussed.
2.1. Major assumptions
-
1.
The respiratory droplets are non-deforming spheres.
-
2.
The respiratory droplets are made of pure water.
-
3.
After leaving the exhaled jet the respiratory droplets are moving in static indoor air. In a ventilated room the motion of droplet can be divided into two parts: (i) motion in static air under gravity force, etc., and (ii) motion due to indoor air movement. These two motions can be superposed to give the actual motion of the droplet. An analytical approach is used here to determine the trajectory of droplets in static air. The effect of ventilation on droplet range, which is assumed to be superposable, is discussed in section 3.5.
-
4.
The rate of decrease of droplet size due to evaporation follows a simplified form given in Kukkonen et al. [34].
As a droplet travels through the air and experiences various types of force, including gravity force , buoyancy force and drag force or air resistance . The droplet motion is complicated by evaporation from its surface as it moves through the ambient air. Assume the vapor from evaporation becomes static in mixing with the surrounding air. This means destruction of momentum by the surrounding air, which exerts an additional force opposing the vapor from the droplet. The key equation governing droplet motion is Newton's second law:
| (1) |
where is the momentum, is the droplet mass, is the droplet velocity and is the total force acting on it.
Taking the positive x-direction to be from left to right and the positive y-direction to be the downward direction, the component form of Eq. (1) can be expressed as
| (2a) |
| (2b) |
where p x , p y are the momentum components, are the velocity components, F g , F b and F d = ( ) are the gravity force, buoyancy force and drag force, respectively. ) is the force responsible for the momentum destruction of vapor from evaporation. These forces can be expressed as follows.
| (3a) |
where R is the droplet radius, is the density of droplet, assuming to be water, and g is the acceleration due to gravity.
| (3b) |
where is the density of air.
| (3c) |
where is the drag coefficient, which is dimensionless, and .
The components of F d are given by
Momentum destruction of vapor from evaporation is described by
| (3d) |
Putting Eq. (3a), (3b), (3c), (3d) in Eqs. (2a), (2b),
| (4a) |
| (4b) |
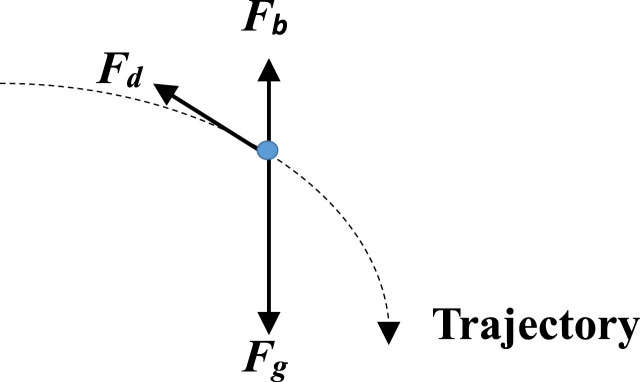
The forces acting on a droplet as it moves through the air are shown in Fig. 1 .
Fig. 1.
Diagram showing gravity force Fg, buoyancy force Fb and drag force Fd acting on a droplet.
Note that the force ) responsible for the momentum destruction of vapor from evaporation is not included for clarity as it is not involved in the residual droplet motion ( , ) according to Eq. (4a), (4b).
As a droplet moves through the air, its size will decrease due to evaporation. The evaporation from a droplet surface is a complicated phenomenon (Kukkonen et al. [34]). In a simplified form the rate of evaporation may be expressed as
| (5a) |
where is approximately a constant at a given temperature and ambient pressure.
Thus or
| (5b) |
where k or is a complicated function of the air temperature, relative humidity, thermodynamic properties of the droplet liquid (assumed to be water), etc. (Kukkonen et al. [34]).
Integrating Eq. (5b) gives
| (6a) |
| (6b) |
The parameter depends on the ambient conditions. In the present study an indoor environment with an air temperature of 18 °C the parameter depends on the relative humidity RH. may be regarded as some kind of decay or shrinking constant for R 2 or droplet surface area.
The time t e for a droplet of initial radius to totally disappear due to evaporation can be obtained from Eq. (6a) by putting .
| (6c) |
The parameter can be estimated from the curves relating and in Xie et al. [31] or from the empirical formula in Ferron and Soderholm [35]. The values of at initial droplet temperature 33 °C and air temperature 18 °C are shown in Table 1 for different values of relative humidity.
Table 1.
Values of (μm)2/s) at initial droplet temperature 33 °C and air temperature 18 °C.
| RH (%) | |||||
|---|---|---|---|---|---|
| RH (%) | 0 | 30 | 50 | 70 | 90 |
| 180 | 115 | 74 | 42 | 13 | |
Table 1 clearly shows that decreases linearly as RH increases. This is an expected result because at higher RH evaporation should be slower.
Putting Eq. (6b) into Eqs. (4a), (4b) yields a system of coupled differential equations in v x and v y.
| (7) |
| (8) |
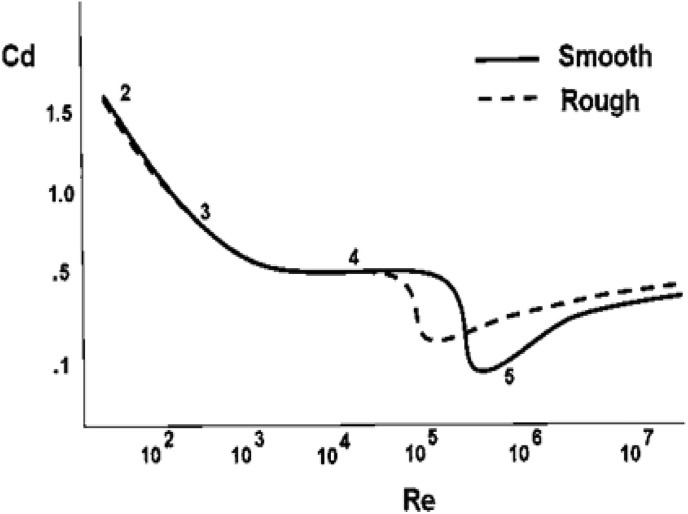
Note that the drag coefficient C d is a complex function of the Reynolds number R e (Fig. 2 ).
Fig. 2.
Drag coefficient Cd for a sphere as a function of the Reynolds number Re, taken from NASA [36]. NASA website: https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html.
Taking the droplet diameter to be 200 μm (maximum droplet size in the present study) and velocity to be 50 m/s (maximum droplet velocity in the present study), and the kinematic viscosity ν of air to be 1.488 × 10−5 m2/s, R e = DV/ν = 672. Thus for the conditions in the present study, R e ≤ 672.
For 0.2 < Re < 2 × 103, Polezhaev and Chircov [37] stated that the drag coefficient for a sphere can be approximately expressed as
| (9) |
The droplet in the present model is assumed to be a non-deforming sphere and this is another simplifying assumption stated at the beginning of this section. In reality, a droplet would deform (flattened a bit) when it moves through the air due to air resistance and hence deviates somewhat from sphericity. Its shape may even oscillate with changing sphericity. This will increase the reference area used in Eq. (3c) for the drag force and the drag coefficient C d. The assumption of a non-deforming sphere will lead to a smaller drag force and hence a longer horizontal range for the droplet.
By using Eq. (9) and the values of in Table 1, the coupled differential equations (Eq. (7a) and 7(b)) with given initial conditions can be numerically solved for , . The displacements and in the x (horizontal) and y (downward) direction are then obtained via numerically solving the following equations.
| (10) |
with initial conditions , .
In numerically solving the equations for velocity (, and displacement (, , the Runge–Kutta method is employed, with a time step depending on the initial velocity. For example, for m/s, the time step selected is 0.01 s, to maintain computational stability. Computation is terminated when the droplet reaches the ground (y = 2 m) or when its size is reduced to 5 μm in diameter or 2.5 μm in radius. For such small droplets, known as aerosol droplets as pointed out by Tellier et al. [5], the motion is not governed by Eq. (7).
The trajectories for various cases relevant to conditions of indoor environments are given in the following sections.
3. Results and discussion
3.1. General features of droplet motion
To obtain the general features of a droplet motion, an example with the following conditions and data is used:
R 0 = 100 μm, 0, initial droplet temperature 33 °C, air temperature 18 °C, RH = 50%, = 0.9986 × 103 kg/m3, 1.2077 kg/m3, = 74 μm)2/s. (Table 1).
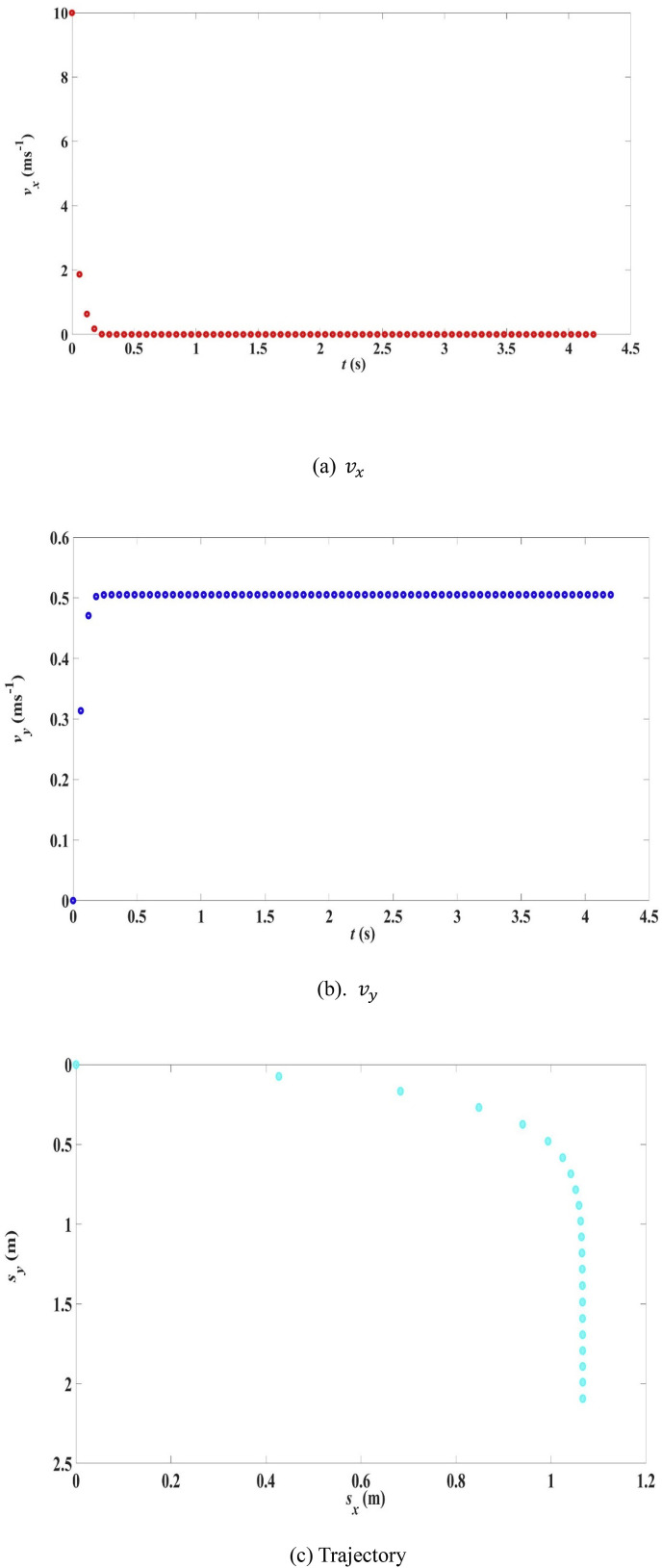
The velocity components as a function of time are shown in Fig. 3 (a) and (b) while the trajectory is shown in Fig. 3(c).
Fig. 3.
Velocity components and trajectory for R0 = 100 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50%.
The curves in Fig. 3 are typical of a respiratory droplet projecting horizontally into the air. The downward velocity asymptotically approaches a terminal value (about 0.5 m/s in this example) and the horizontal velocity asymptotically approaches zero, both occurring at about t = 0.25 s. After this the droplet is almost falling vertically with a constant downward velocity of 0.5 m/s. These asymptotic features arise from air resistance or drag force. In Fig. 3(a), the variation of with time shows that the deceleration is very large at the beginning. This is because the drag force, which opposes the motion, is large when the velocity is large at the beginning. When decreases, the drag force decreases and the deceleration in also decreases, making the change in negligible. For respiratory droplets, the value of at 2 m is commonly taken to be the droplet range in the literature. That is, the range is the horizontal distance travelled when the droplet has fall through a vertical distance of 2 m. For the scenario above, the time to fall through a vertical distance of 2 m (to the ground), known as the settling time , is around 4.02 s, which is much longer than the time in a free fall (about 0.6 s).
3.2. Effect of relative humidity
The relative humidity is one factor affecting the evaporation rate. The trajectories for the case: R 0 = 60 μm or 100 μm, 0, initial droplet temperature 33 °C, air temperature 18 °C, at different values of RH are shown in Fig. 4 .
Fig. 4.
Trajectories for R0 = 60 μm and 100 μm, 0, 33 °C, 18 °C, at different values of RH.
At lower RH, the evaporation rate is higher. Hence for a given droplet, its radius is smaller compared with the case of higher RH at corresponding times. A smaller droplet radius leads to a smaller Reynolds number R e and hence a larger drag coefficient C d and a larger air resistance. Thus the range is smaller at lower RH, as depicted in Fig. 4. The range L x , settling time t s and the settling radius on reaching the ground R s are shown in Table 2 . Note for a droplet of initial radius R 0 = 60 μm at RH = 0%, the droplet radius is reduced to 2.5 μm (becoming an aerosol droplet) before reaching the ground.
Table 2.
Range Lx, settling time ts and settling radius Rs of droplet with initial radius R0 = 60 μm and 100 μm at different RH.
|
R0 = 60 μm | ||||||||
|---|---|---|---|---|---|---|---|---|
| RH | ts (s) | Lx (m) | Rs (μm) | Percentage Decrease in R | ||||
| 0% | – | – | – | – | ||||
| 50% | 7.87 s | 0.75 m | 49.35 μm | 17.75% | ||||
| 90% |
7.94 s |
0.80 m |
58.25 μm |
2.92% |
||||
| R0 = 100 μm | ||||||||
| RH |
ts (s) |
Lx (m) |
Rs (μm) |
Percentage Decrease in R |
||||
| 0% | 4.01 s | 0.98 m | 92.46 μm | 7.54% | ||||
| 50% | 4.02 s | 1.07 m | 96.98 μm | 3.02% | ||||
| 90% | 4.06 s | 1.20 m | 99.47 μm | 0.53% | ||||
The results for droplets in the present study (R 0 = 60 μm–100 μm, or diameter from 120 μm–200 μm) show that RH has important effect on the range or fate.
3.3. Effect of initial droplet size R0
When a respiratory droplet enters the ambient air its size is continuously reduced due to evaporation. If the droplet remains large enough (R ≥ 2.5 μm) in the air, it will eventually reach the ground with a horizontal range L x. If it is reduced to an aerosol droplet (R ≤ 2.5 μm) before reaching the ground, it will remain suspended in the air for a long time. For a given indoor environment, the fate of a respiratory droplet depends on its initial size. For air temperature = 18 °C and RH = 50%, and taking the initial droplet height to be 2 m, it is found that R 0 = 60 μm is the demarcation in droplet size. Droplets with R 0 ≥ 60 μm can reach the ground while those with R 0 ≤ 50 μm are reduced to aerosol droplets in the air.
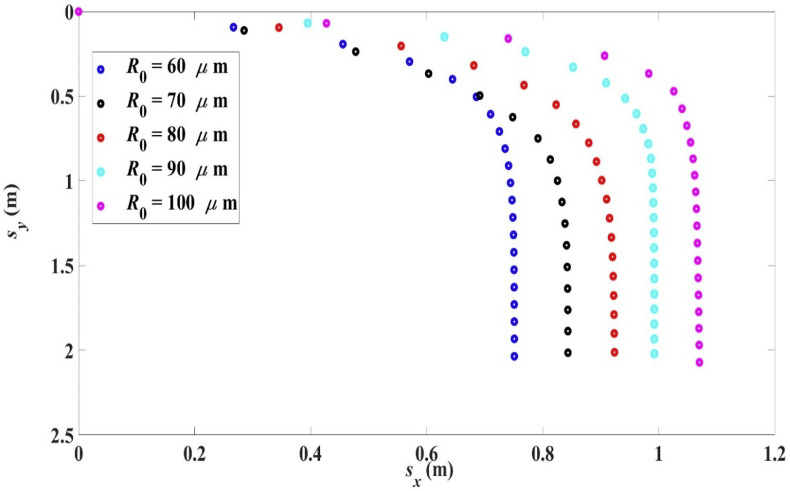
The trajectories of droplets of different initial size (R 0 = 60–100 μm) having the same initial velocity of 10 m/s and under the same environmental conditions are shown in Fig. 5 .
Fig. 5.
Trajectories for droplets with initial radius R0 in the range 60 μm–100 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50%.
The range L x , settling time t s and the settling radius on reaching the ground R s are shown in Table 3 . The trend shows that the range increases with the initial droplet size because of larger initial kinetic energy or momentum and a smaller percentage decrease in size.
Table 3.
Range Lx, settling time ts and settling radius Rs of droplet with initial radius R0 in the range 60 μm–100 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50%.
| R0 (μm) | ts (s) | Lx (m) | R (μm) | Percentage Decrease in R |
|---|---|---|---|---|
| 60 | 7.87 s | 0.75 m | 49.35 μm | 17.75% |
| 70 | 6.35 s | 0.84 m | 62.35 μm | 10.10% |
| 80 90 |
5.37 s 4.56 s |
0.92 m 0.99 m |
74.87 μm 86.17 μm |
6.41% 6.23% |
| 100 | 4.02 s | 1.07 m | 96.98 μm | 3.02% |
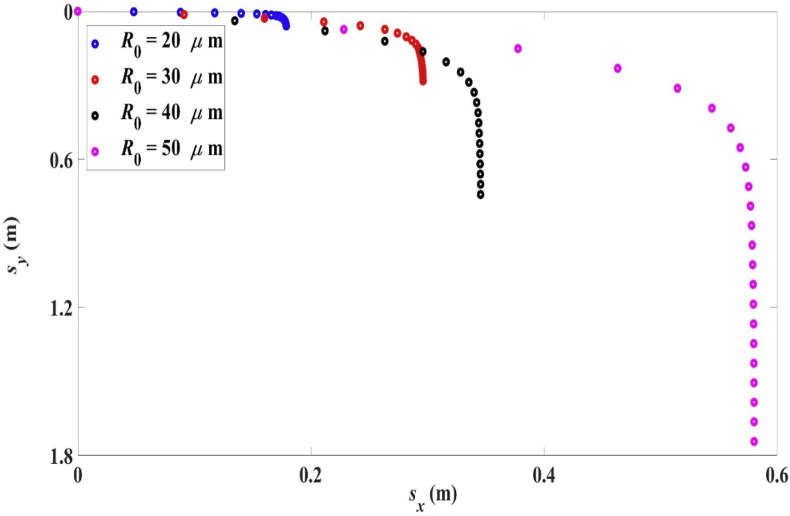
For the smaller droplets (initial radius R 0 ≤ 50 μm), they are reduced to aerosol droplets in the air before reaching ground. Their trajectories before being turned into aerosol droplets are shown in Fig. 6 . The time and position at which this occurs are shown in Table 4 .
Fig. 6.
Trajectories for droplets with initial radius R0 in the range 20 μm–50 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50%.
Table 4.
Fate of the smaller droplets with initial radius R0 in the range 20 μm–50 μm in an environment with air temperature 18 °C and RH = 50%.
| R0 (μm) | 20 | 30 | 40 | 50 |
|---|---|---|---|---|
| ta (s) | 1.33 | 3.02 | 5.38 | 8.43 |
| xa (m) | 0.18 | 0.30 | 0.35 | 0.58 |
| ya (m) | 0.06 | 0.28 | 0.74 | 1.74 |
and (xa, ya): time and position at which droplet becomes an aerosol droplet (R ≤ 2.5 μm).
3.4. Effect of initial droplet velocity
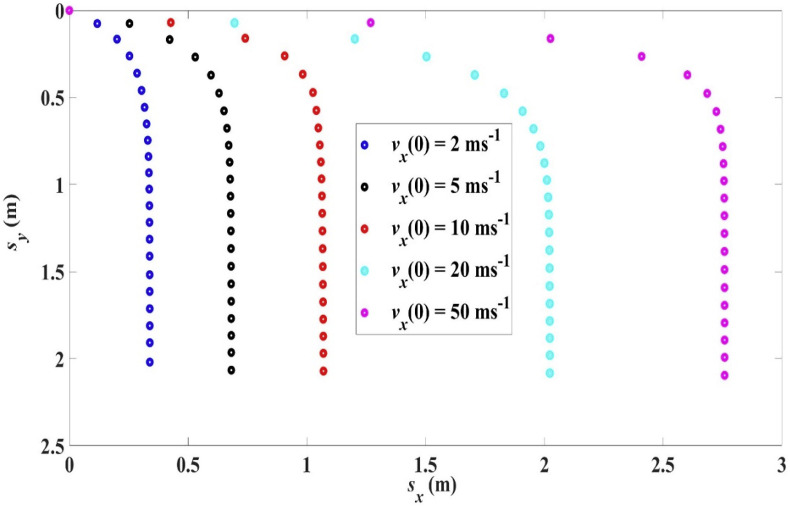
When a droplet is ejected with a higher velocity, it is expected that its range will be longer. This is demonstrated by the trajectories in Fig. 7 for a droplet of initial size R 0 = 100 μm but with different initial velocities. Note that in all the cases the horizontal distance travelled increases only slightly beyond a vertical drop of about 0.75 m, suggesting that the droplet has consumed its initial horizontal momentum after falling through this height. Table 5 shows the range L x and the settling time t s for different initial velocities.
Fig. 7.
Trajectories for R0 = 100 μm, 0, 33 °C, 18 °C, RH = 50%, at different values of .
Table 5.
Range Lx and settling time ts for R0 = 100 μm, 0, 33 °C, 18 °C, RH = 50%, at different values of .
| (ms−1) | ts (s) | Lx (m) |
|---|---|---|
| 2 | 4.01 s | 0.34 m |
| 5 | 4.01 s | 0.68 m |
| 10 | 4.02 s | 1.07 m |
| 20 | 4.04 s | 2.02 m |
| 50 | 4.06 s | 2.76 m |
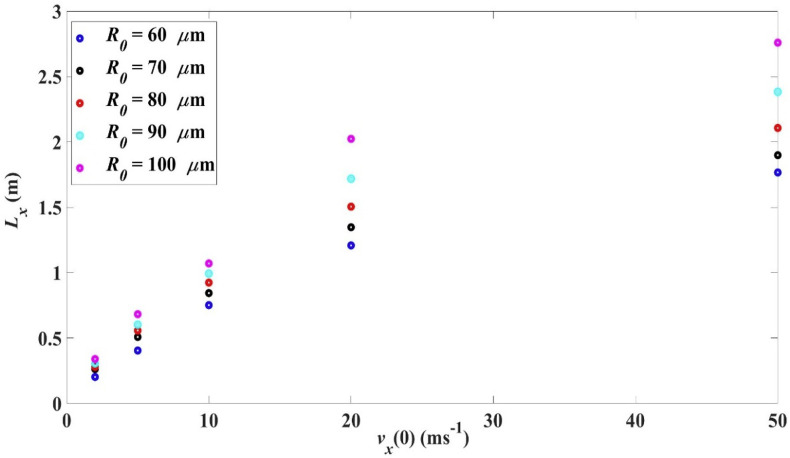
3.5. Effect of initial droplet size R0 and initial velocity on range and settling time
Fig. 8 below compares the range L x for droplets of different values of initial size R 0 and initial velocity . It is obvious that for a given initial size, the range increases with the initial velocity while for a given initial velocity the range increases with the initial droplet size. This again shows that larger initial kinetic energy or momentum results in a longer range, though the dependence is complicated.
Fig. 8.
Effect of initial velocity and initial droplet size on horizontal range for 0, 33 °C, 18 °C, RH = 50%.
Taking droplet initial velocity to be 2–5 m/s in speaking (Chao et al. [38]), the range is within 0.16 m–0.68 m. In coughing, assuming an ejection velocity of 10 m/s (Chao et al. [38]), is within 0.58 m–1.09 m. In sneezing, assuming an ejection velocity of 50 m/s horizontally (Tang et al. [39]), is within 1.34 m–2.76 m. The value for sneezing may be over-estimated as the ejection direction in sneezing is commonly not horizontal, as will be discussed in a later section.
The experimental values of the range of large respiratory droplets have been reported in a number of studies over the past twenty years. Li et al. [40] studied droplet dispersions of respiratory plumes produced by a mannequin and measured the range using water-sensitive paper. For large droplets (larger than 50–100 μm), the range is about 1.5 m for breathing. It should be commented that this value is much larger than common values reported in the literature obtained by other methods. Xie et al. (2007) estimated a range of less than 1 m in breathing using numerical method. Zhu et al. [41] used particle image velocimetry to study expelled during coughing. A maximum velocity of 22 m/s was recorded, and the range is more than 2 m. Bourouiba et al. [17] reported experimental study using high-speed videography of human subject exhalations. Droplets expelled during sneezing and coughing were carried within a turbulent gas cloud and the range could reach 2.5 m. Wei and Li [18] used water tank experiments and found that the large particles (96 μm) could travel a distance up to 1.4 m.
It should be pointed out that the range calculated in the present study refers to the horizontal distance travelled by a droplet after escaping from the exhaled cloud or jet. As the droplet has been carried forward in the cloud or jet for some distance before falling out, the actual range measured from the exhalation point should be larger than that calculated in the present study, as illustrated in the experimental values above. In view of the values of range calculated or experimentally determined, one may comment that the general advice of maintaining a safe social or physical distance of about 2 m from others is adequate except for violent expiratory events like coughing and sneezing ([32,33]).
In the analysis above, the indoor air is assumed to be static. In a room with ventilation airflow is present and this will affect the range. The motion of droplet can be regarded as coming from two origins: (i) motion in static air under gravity force, etc., and (ii) motion due to indoor air movement. These two motions can be superposed to give the actual motion of the droplet. The aim of the present work is to study the motion (i). The influence of indoor air movement on droplet motion is complicated by the variability of air velocity at different locations indoor. To a first approximation the following estimated amendment to the range could be made if the settling time of droplets and the air velocity are known. The settling time t s for droplets of initial sizes and velocities are shown in Table 6 , which shows that t s roughly lies between 4 and 8 s. Assuming an air velocity of 0.33 m/s in a ventilated room (Chen and Zhao [42]) a respiratory droplet would be carried through a distance of 1.32 m–2.64 m simply by the airflow. Thus if the airflow direction is the same as that of the droplet at ejection, both being horizontal, then this distance will add to the horizontal range of the droplet to cause an increase in the range. Under certain conditions a droplet can be reduced to an aerosol droplet (R ≤ 2.5 μm), which will remain suspended in the air. In this case the airflow in a ventilated indoor environment can bring the aerosol droplet to a much greater distance.
Table 6.
Settling time ts for droplets of different initial sizes and velocities.
|
| |||||
|---|---|---|---|---|---|
| \R0 | 60 μm | 70 μm | 80 μm | 90 μm | 100 μm |
| 2 m/s | 6.78 s | 6.15 s | 5.09 s | 4.39 s | 4.01 s |
| 5 m/s | 7.80 s | 6.25 s | 5.25 s | 4.54 s | 4.01 s |
| 10 m/s | 7.87 s | 6.35 s | 5.37 s | 4.56 s | 4.02 s |
| 20 m/s | 7.97 s | 7.10 s | 5.38 s | 4.58 s | 4.04 s |
| 50 m/s | 8.04 s | 7.35 s | 5.40 s | 4.60 s | 4.06 s |
3.6. Effect of air resistance and evaporation on range
In order to illustrate the relative significance of the effect of air resistance and droplet evaporation on the range, the following cases are considered.
R 0 = 100 μm, 0, initial droplet temperature 33 °C, air temperature 18 °C, RH = 50%,
Case A: Motion considering gravity and buoyancy only, without considering air resistance and evaporation. Then Eq. (7) reduces to:
| (11) |
Under the environmental conditions above, the factor that describes buoyancy is very small, being about 0.998. Thus the droplet motion or trajectory is almost the same as a free projectile motion. That is, the effect of buoyancy is negligible. In addition, it can be seen that the motions in the horizontal and vertical direction are independent of each other as the two differential equations in the x-direction and y-direction are uncoupled. On the other hand, the two differential equations in Eq. (7) are coupled by the drag force term.
Case B: Motion considering gravity, buoyancy, air resistance but without evaporation. Since evaporation is assumed to be absent, throughout the trajectory. Then Eq. (7) reduces to:
| (12) |
Case C: Motion considering gravity, buoyancy, air resistance and evaporation. This is the general case governed by Eq. (7a) and Eq. (7b).
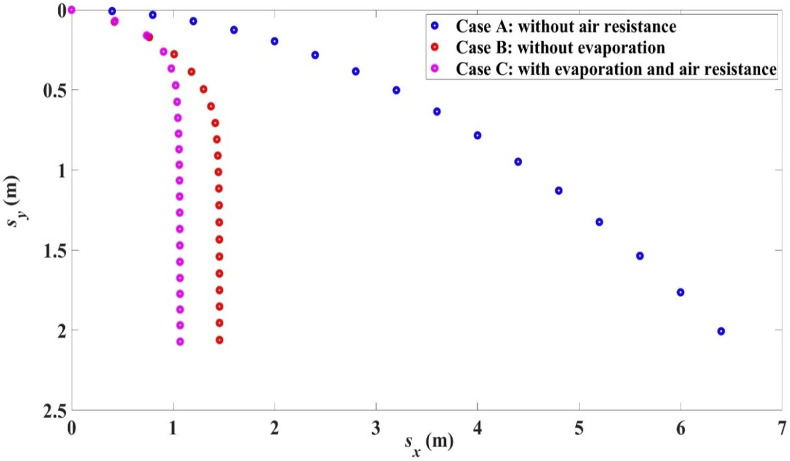
The trajectories of these three cases are shown in Fig. 9 while the settling times and ranges are shown in Table 7 . It can be seen that air resistance or drag force has the largest effect on droplet trajectory and range and on the settling time. Comparing case A and B, the range is reduced by about 77% solely due to the presence of air resistance. For the conditions in the example shown, evaporation also decreases the range (by about 27%) as depicted by the values in Table 7 for case B and case C. Evaporation would reduce the size of the droplet in its course, which in turn would decrease the Reynolds number and increase the drag coefficient or force. This leads to a decrease in the range. It is also interesting to note from Table 7 that air resistance greatly increases the settling time while evaporation mildly increases the settling time.
Fig. 9.
Effect of air resistance and evaporation on trajectory, = 100 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50%.
Table 7.
Settling time ts and range Lx for = 100 μm, 10 m/s, 0, 33 °C, 18 °C, RH = 50% in the three cases.
| Case | ts (s) | Lx (m) |
|---|---|---|
| A | 0.64 s | 6.39 m |
| B | 3.89 s | 1.46 m |
| C | 4.02 s | 1.07 m |
3.7. Effect of ejection angle
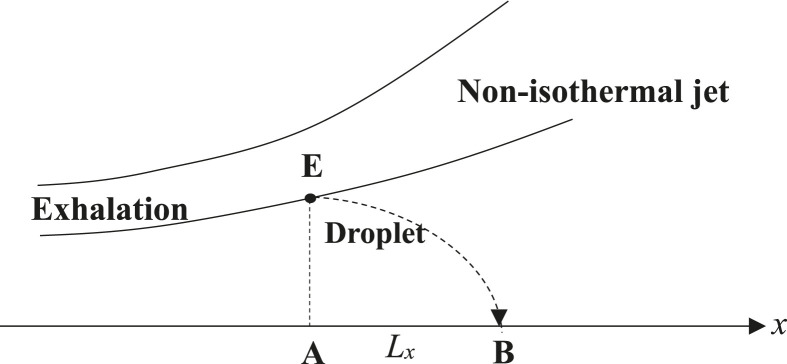
The range of a respiratory droplet depends on the ejection velocity (initial velocity) of the droplet, which in many studies, is taken to be horizontal. However, respiratory droplets are ejected in an exhaled cloud or jet, the centerline of which might not be horizontal. In addition, as the exhaled air jet has a temperature (about 33 °C) different from that of the indoor ambient air (say 18 °C), the jet is a non-isothermal one, which has a centerline curving upward after exhalation even if the initial jet direction is horizontal, as shown in Fig. 10 .
Fig. 10.
Escape of droplets from a non-isothermal jet exhaled by a human subject. The droplet escapes from the jet at E and reaches the ground at B (Bourouiba et al. [17] and Baturin [43]).
Thus the velocity of a droplet at escape (the initial velocity in the present study) might not be horizontal, but might bear an angle to the horizontal. It is interesting to study the effect of the ejection angle (the angle at escape from cloud or jet) on the range. Suppose a droplet is ejected with initial velocity at an angle θ (θ is taken as negative if it is an angle of elevation and as positive if it is an angle of depression) about the horizontal. Then the initial velocity components are given by
| (13a) |
| (13b) |
Using the differential equations Eqs. (7a) and (7b) and the initial conditions given by Eqs. (13a), (13b), the trajectories for droplets ejected at different angles can be determined using numerical method.
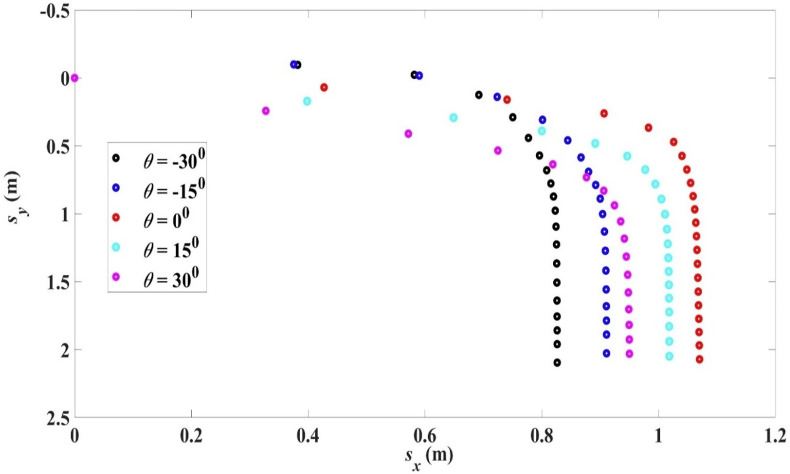
The trajectories for R0 = 100 μm, , initial droplet temperature 33 °C, air temperature 18 °C, RH = 50%, at different ejection angles are shown in Fig. 11 .
Fig. 11.
Trajectories for droplet R0 = 100 μm, with different ejection angles, 33 °C, 18 °C, RH = 50%. The range and settling time for different ejection angles are shown in Table 8.
In a free projectile when a particle is ejected at an elevation angle, both the time in air and the horizontal velocity component depend on the angle. When this angle increases, the time of travel increases but the horizontal velocity component decreases and the range is maximized at an elevation angle of 450. When air resistance and evaporation are present, the case becomes complicated and no simple conclusion can be drawn. As shown in Fig. 11 and Table 8, an elevation angle for droplet ejection would decrease the range, though the settling time is increased.
Table 8.
Range and settling time for droplet R0 = 100 μm, with different ejection angle, 33 °C, 18 °C, RH = 50%.
| Ejection angle θ | Range Lx | Settling time ts |
|---|---|---|
| −300 | 0.83 m | 5.51 s |
| −150 | 0.91 m | 5.36 s |
| 00 | 1.07 m | 4.02 s |
| 150 | 1.02 m | 3.71 s |
| 300 | 0.95 m | 3.16 s |
For speaking or coughing, one may assume that the ejected jet has a centerline which is horizontal. However, this is not the case in sneezing. In sneezing the ejection angle is normally a depression angle θ below the horizontal and this will affect the range and also the settling time .
The trajectories for R 0 = 100 μm, (sneezing), at different ejection angles (depression) are shown in Fig. 12 with the settling time and range given in Table 9 .
Fig. 12.
Trajectories for droplet R0 = 100 μm, ejected with different depression angles, 33 °C, 18 °C, RH = 50%.
Table 9.
Range and settling time for droplet R0 = 100 μm, with different ejection angle, 33 °C, 18 °C, RH = 50%.
| Ejection angle θ | Range Lx | Settling time ts |
|---|---|---|
| 00 | 2.76 m | 4.06 s |
| +300 | 2.18 m | 3.45 s |
| +450 | 1.87 m | 2.62 s |
| +600 | 1.54 m | 2.17 s |
When a droplet is ejected at a depression angle, both the settling time and the initial horizontal velocity component are decreased. Thus the range is decreased compared with a horizontally ejected droplet at the same initial velocity, as illustrated in Fig. 12 and Table 9. It can be seen that the greater is the angle of depression, the shorter is the range as both the settling time and horizontal velocity component are decreased.
4. Conclusions
In the present work the motion and trajectories of large respiratory droplets are studied using a simplified single-droplet approach aiming at elucidating the mechanics governing the droplet motion. In addition to gravity force, buoyancy force, and air drag force, evaporation from droplets are included in the formulation. Droplets with initial radius R 0 in the range 20 μm–100 μm (diameter 40 μm–200 μm) and ejection velocity in the range 2 m/s – 50 m/s are studied with the trajectories determined using numerical methods. The following concluding remarks on the effect of various factors like initial droplet size and velocity, ejection angle, and relative humidity can be made:
-
1.
For the respiratory droplets studied, air resistance has the most important effect on droplet motion.
-
2.
Relative humidity and hence droplet evaporation also affects the droplet range and fate. For small droplets at low RH, the evaporation rate may be high enough to reduce the droplet to an aerosol droplet, which will remain suspended in the air for a long time instead of falling onto the ground as a projectile.
-
3.
Under the same environmental conditions, initial droplet ejection velocity and droplet size are the important parameters in determining the droplet range. Higher initial velocity and large initial droplet size result in a longer range.
-
4.
Assume an indoor environment with air temperature at 18 °C and relative humidity at 50%. Taking droplet velocity to be 2 5 m/s in speaking, the range is within 0.16 m–0.68 m. In coughing, assuming an ejection velocity of 10 m/s, is within 0.58 m–1.09 m. In sneezing, assuming an ejection velocity of 50 m/s horizontally, is within 1.34 m–2.76 m. The value for sneezing may be over-estimated as the ejection direction in sneezing is normally not horizontal, but downward at an angle. In addition, the calculated values of range are slightly smaller than the experimental values because the former refer to the distance travelled by droplets after leaving the expelled cloud or jet.
The values of range for respiratory droplets obtained in the present study suggest that the general advice from authorities of maintaining a safe social or physical distance of about 2 m is adequate except for violent expiratory events like coughing and sneezing.
-
5.
It has to be pointed out that these values of droplet range have been obtained without considering ambient airflow. For indoor environment with standard ventilation, airflow at a velocity of 0.33 m/s is present. By superposition and assuming a settling time of 4–8 s for droplets with initial diameter in the range 120 μm–200 μm, the airflow may result in an additional 1.32 m–2.64 m in range in the most favorable case. For droplets which are reduced to aerosol droplets, they may be carried to a much greater distance due to their long life in suspension.
Funding
The work described in this paper was supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China for the project “A study on powder explosion hazards and control schemes when clouds of coloured powder are sprayed in partially confined areas” (Project No. PolyU 15252816) with account number B-Q53X.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.WHO (World Health Organization) Coronavirus disease 2019 (COVID-19) situation report – 198, 5 August 2020. 2020. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200805-covid-19-sitrep-198.pdf?sfvrsn=f99d1754_2 accessed 6 August 2020.
- 2.Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Trav. Med. 2020;27:1–4. doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.WHO (World Health Organization) Coronavirus disease (COVID-19) Scientific brief: modes of transmission of virus causing COVID-19: implications for IPC precaution recommendations. 2020. https://www.who.int/news-room/commentaries/detail/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations 29 March 2020.
- 4.Xie X., Li Y., Sun H., Liu L. Exhaled droplets due to talking and coughing. J. R. Soc. Interface. 2009;6:S703–S714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tellier R., Li Y., Cowling B.J., Tang J.W. Recognition of aerosol transmission of infectious agents: a commentary. BMC Infect. Dis. 2019;19:101–109. doi: 10.1186/s12879-019-3707-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yan Y.H., Li X.D., Tu J.Y. Thermal effect of human body on cough droplets evaporation and dispersion in an enclosed space. Build. Environ. 2019;148:96–106. doi: 10.1016/j.buildenv.2018.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu S., Novoselac A. Transport of airborne particles from an unobstructed cough jet. Aerosol Sci. Technol. 2014;48:1183–1194. [Google Scholar]
- 8.Wang Y., Wu S.H., Yang Y., Yang X.N., Song H., Cao Z.X., Huang Y.Q. Evaporation and movement of fine droplets in non-uniform temperature and humidity field. Build. Environ. 2019;150:75–87. [Google Scholar]
- 9.Leung N.H.L., Chu D.K.W., Shiu E.Y.C., Chan K.H., McDevitt J.J., Hau B.J.P., Yen H.L., Li Y., Ip D.M.K., Peiris J.S.M., Seto W.H., Leung G.M., Milton D.K., Cowling B.J. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 2020;26:676–680. doi: 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang H., Li D., Xie L., Xiao Y. Documentary Research of human respiratory droplet characteristics. Procedia Eng. 2015;121:1365–1374. doi: 10.1016/j.proeng.2015.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: potential implications for reducing transmission of COVID-19. J. Am. Med. Assoc. 2020;323:1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- 12.Tseng C.C., Li C.S. Collection efficiencies of aerosol samplers for virus-containing aerosols. J. Aerosol Sci. 2005;36:593–607. doi: 10.1016/j.jaerosci.2004.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Morawska L., Johnson G.R., Ristovski Z.D., Hagreaves M., Mengersen K., Corbett S., Chao C.Y.H., Li Y., Katoshevski D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009;40:256–269. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haslbeck K., Schwarz K., Hohlfeld J.M., Suemem J.R., Koch W. Submicron droplet formation in the human lung. J. Aerosol Sci. 2010;41:429–438. [Google Scholar]
- 15.Han Z.Y., Weng W.G., Huang Q.Y. Characterizations of particle size distribution of the droplets exhaled by sneeze. J. R. Soc. Interface. 2013;10:20130560. doi: 10.1098/rsif.2013.0560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Drossinos Y., Stilianakis N.I. What aerosol physics tells us about airborne pathogen transmission. Aerosol Sci. Technol. 2020;54:639–643. [Google Scholar]
- 17.Bourouiba L., Dehandschoewercker E., Bush J.W.M. Violent expiratory events: on coughing and Sneezing. J. Fluid Mech. 2014;745:537–563. [Google Scholar]
- 18.Wei J.J., Li Y.G. Enhanced spread of expiratory droplets by turbulence in a cough jet. Build. Environ. 2015;93:86–96. [Google Scholar]
- 19.Lindsley W.G., Pearce T.A., Hudnall J.B., Davis K.A., Davis S.M., Fisher M.A., Khakoo R., Palmer J.E., Clark K.E., Celik I., Coffey C.C., Blachere F.M., Beezhold D.H. Quantity and size distribution of cough-generated aerosol particles produced by influenza patients during and after illness. J. Occup. Environ. Hyg. 2012;9:443–449. doi: 10.1080/15459624.2012.684582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lindsley W.G., Reynolds J.S., Szalajda J.V., Noti J.D., Beezhold D.H. A cough aerosol simulator for the study of disease transmission by human cough-generated aerosols. Aerosol Sci. Technol. 2013;47:937–944. doi: 10.1080/02786826.2013.803019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zayas G., Chiang M.C., Wong E., MacDonald F., Lange C.F., Senthilselvan A., King M. Cough aerosol in healthy participants: fundamental knowledge to optimize droplet-spread infectious respiratory disease management. BMC Pulm. Med. 2012;12:11. doi: 10.1186/1471-2466-12-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Asadi S., Wexler A.S., Cappa C.D., Barreda S., Bouvier N.M., Ristenpart W.D. Aerosol emission and superemission during human speech increase with voice loudness. NHRI Sci. Rep. 2019;9:2348. doi: 10.1038/s41598-019-38808-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Berrouk A.S., Lai A.C.K., Cheung A.C.T., Wong S.L. Experimental measurements and large eddy simulation of expiratory droplet dispersion in a mechanically ventilated enclosure with thermal effects. Build. Environ. 2010;45:371–379. doi: 10.1016/j.buildenv.2009.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.He Q., Niu J.L., Gao N., Zhu T., Wu J.Z. CFD study of exhaled droplet transmission between occupants under different ventilation strategies in a typical office room Build. Environ. Times. 2011;46:397–408. doi: 10.1016/j.buildenv.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang B., Zhang A., Sun J.L., Liu H., Hu J., Xu L.X. Study of SARS transmission via liquid droplets in air. J. Biomech. Eng. 2005;127:32–38. doi: 10.1115/1.1835350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sun W., Ji J. Transport of droplets expelled by coughing in ventilated rooms. Indoor Built Environ. 2007;16:493–504. [Google Scholar]
- 27.Hertzberg V.S., Weiss H., Elon L.K., Si W.P., Norris S.L. Behaviors, movements, and transmission of droplet-mediated respiratory diseases during transcontinental airline flights. Proc. Natl. Acad. Sci. Unit. States Am. 2018;115:3623–3627. doi: 10.1073/pnas.1711611115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gao N.P., Niu J.L., Perino M., Heiselberg P. The airborne transmission of infection between flats in high-rise residential buildings: particle simulation. Build. Environ. 2008;43:1805–1817. doi: 10.1016/j.buildenv.2007.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li X.P., Niu J.L., Gao N.P. Spatial distribution of human respiratory droplet residuals and exposure risk for the co-occupant under different ventilation methods. HVAC R Res. 2011;17:432–445. Indoor Air Quality, Ventilation and Energy Conservation in Buildings: Innovation and Integration (Part 1) [Google Scholar]
- 30.Wells W.F. On air-borne infection. Study II. Droplets and droplet nuclei. Am. J. Hyg. 1934;20:611–668. [Google Scholar]
- 31.Xie X., Li Y., Chwang A.T.Y., Ho P.L., Seto W.H. How far droplets can move in indoor environments – revisiting the Wells evaporation–falling curve. Indoor Air. 2007;17:211–225. doi: 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
- 32.WHO (World Health Organization) Coronavirus disease (COVID-19) advice for the public. 2020. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/advice-for-public/ accessed 20 July 2020.
- 33.CDC (Centers for Disease Control and Prevention), USA Coronavirus disease 2019 (COVID-19), social distancing. 2020. https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/social-distancing.html/ accessed 20 July 2020.
- 34.Kukkonen J., Vesala T., Kulmala M. The interdependence of evaporation and settling for airborne freely falling droplets. J. Aerosol Sci. 1989;20:749–763. [Google Scholar]
- 35.Ferron G.A., Soderholm S.C. Estimation on the times for evaporation of pure water droplets and for stabilization of salt solution particles. J. Aerosol Sci. 1990;21:415–429. [Google Scholar]
- 36.NASA (National Aeronautics and Space Administration) Open source, drag of a sphere. 2015. https://www.grc.nasa.gov/www/k-12/airplane/dragsphere.html/ accessed 20 July 2020.
- 37.Polezhaev Y.V., Chircov I.V. Drag coefficient. Thermopedia. 2020. http://www.thermopedia.com/content/707/
- 38.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tang J.W., Nicolle A.D., Klettner C.A., Pantelic J., Wang L., Suhaimi A.B., Tan, Tan Y.L.A., Ong W.X.G., Su R., Sekhar C., Cheong D.W., Tham K.W. Airflow dynamics of human jets: sneezing and breathing - potential sources of infectious aerosols. PLoS One. 2013;8 doi: 10.1371/journal.pone.0059970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Li Y.G., Chwang A.T.Y., Seto W.H., Ho P.L., Yuen P.L. Understanding droplets produced by nebulisers and respiratory activities. Hong Kong Med. J. 2008;14:29–32. [Google Scholar]
- 41.Zhu S.W., Kato S., Yang J.H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006;41:1691–1702. [Google Scholar]
- 42.Chen C., Zhao B. Some questions on dispersion of human exhaled droplets in ventilation room: answers from numerical investigation. Indoor Air. 2010;20:95–111. doi: 10.1111/j.1600-0668.2009.00626.x. [DOI] [PubMed] [Google Scholar]
- 43.Baturin V.V. third ed. Pergamon Press; 1972. Fundamentals of Industrial Ventilations; pp. 79–119. [Google Scholar]