COVID-19, flattening the curve, and Benford’s law

Abstract

For many countries attempting to control the fast-rising number of coronavirus cases and deaths, the race is on to “flatten the curve,” since the spread of coronavirus disease 2019 (COVID-19) has taken on pandemic proportions. In the absence of significant control interventions, the curve could be steep, with the number of COVID-19 cases growing exponentially. In fact, this level of proliferation may already be happening, since the number of patients infected in Italy closely follows an exponential trend. Thus, we propose a test. When the numbers are taken from an exponential distribution, it has been demonstrated that they automatically follow Benford’s Law (BL). As a result, if the current control interventions are successful and we flatten the curve (i.e., we slow the rate below an exponential growth rate), then the number of infections or deaths will not obey BL. For this reason, BL may be useful for assessing the effects of the current control interventions and may be able to answer the question, “How flat is flat enough?” In this study, we used an epidemic growth model in the presence of interventions to describe the potential for a flattened curve, and then investigated whether the epidemic growth model followed BL for ten selected countries with a relatively high mortality rate. Among these countries, South Korea showed a particularly high degree of control intervention. Although all of the countries have aggressively fought the epidemic, our analysis shows that all countries except for Japan satisfied BL, indicating the growth rates of COVID-19 were close to an exponential trend. Based on the simulation table in this study, BL test shows that the data from Japan is incorrect.

1. Introduction

Coronavirus disease 2019 (COVID-19) was first identified in December 2019 and has since spread globally, resulting in the ongoing 2020 coronavirus pandemic. For many countries attempting to control the fast-rising number of coronavirus cases and deaths, the race is on to “flatten the curve,” with the “curve” being the projected number of people who will contract COVID-19 over a period of time. This “curve” can vary based on the growth (infection) rate and degree of intervention. Thus, “flattening the curve” requires intervention efforts, such as social distancing, to slow the growth rate of COVID-19 infections and give more time to hospitals and health systems to cope with the large number of infected patients.

In the absence of significant control interventions, the curve could be steep, with the number of COVID-19 cases growing exponentially. In fact, this level of proliferation may already be happening, since the number of patients infected in Italy closely follows an exponential trend according to Remuzzi and Remuzzi [1]. Thus, we propose a test. When the numbers are taken from an exponential distribution, it is demonstrated that they automatically follow Benford’s Law (BL) [2], [3]. As a result, we can infer that when the epidemic growth curve follows exponential distribution, the number of infections and deaths will obey BL. To state it differently, if the current control interventions are successful and we flatten the curve (i.e., we slow the rate below an exponential growth rate), then the number of infections or deaths will not obey BL. Therefore, BL may be useful for assessing the effects of the current control interventions and may be able to answer the question, “How flat is flat enough?”

BL was an empirically discovered pattern for the frequency distribution of first digits in many real-life datasets [4], [5].1 It states that in many naturally occurring collections of numbers, the leading digit is non-uniformly distributed in a predictable manner. In addition, the leading significant digit is likely to be small. For example, the number 1 occurs as the first digit about 30.1% of the time, while 9 occurs as the first digit about 4.5% of the time. In this situation, the number 1 appears more than six times more frequently than 9. Checking for the validity of BL in this dataset would be the best approach in a forensic analysis looking at potential manipulations of the number of cases [7], [8], since a distribution of first digits that deviates from the expected distribution may indicate fraud. Prior studies have shown that BL is also applicable to genome data [9], the half-lives of unstable nuclei [3], self-reported toxic emissions data [10], tax auditing [11], accounting [12], election data [13], [14], stock markets and final data [15], [16], [17], [18], [19], [20], regression coefficients [21], inflation data [7], World Wide Web [22], religions [23], [24], [25], birth data [26], river data [27], first letter words [28], elementary particle decay rates ([29], astrophysical measurements [30], and more.

In this study, our goal was to use an epidemic growth model in the presence of interventions to describe the potential for a flattened curve, to investigate whether the epidemic growth model followed BL, to test the model against empirical COVID-19 data on the number of deaths in multiple countries, and to discuss whether or not the model could be used to detect fraud in the reported number of deaths that have occurred in the presence of interventions.

This paper is organized as follow: Section 2 briefly introduce the BL; Section 3 describes the theoretical relationship between BL and epidemic growth model in the absence (and presence) of control intervention; Section 4 describes simulation for testing the theoretical development from Section 3; Section 5 applies BL and the epidemic growth model in the presence of intervention to COVID-19 data, and finally Section 6 concludes.

2. Benford’s law

BL is the observation that in many collections of numbers from real-life data or mathematical tables, the significant digits are not uniformly distributed; they are heavily skewed toward the smaller digits. More precisely, the significant digits in many data sets obey a very particular logarithmic distribution. The special case of the first significant digit is

$$P\left(D_1=d_1\right)={log}_{10}\left(1+d_1^{-1}\right)\text{for all }{d}_1=1,2,\dots ,9,$$

where $D_1$ denotes the first significant digit. From a statistical standpoint, a Borel probability measure $P$ on $\mathbb{R}$ is Benford if $P\left(\left\{x\in \mathbb{R}:S\left(x\right)\le u\right\}\right)=logu$ for all $u\in [1,10)$, where $S$ is the significant of a real number is its coefficient when it is expressed as a floating point. That is, the significant function $S:\mathbb{R}\to [1,10)$ is defined as follows: if $x$ is a non-zero real number, then $S\left(x\right)=u$, where $u$ is the unique number in $[1,10)$ with $\left|x\right|=10^{k}u$ for some $k\in \mathbb{Z}$. Then, a random variable $X$ is Benford if its distribution $P_X$ on $\mathbb{R}$ is Benford, i.e., if $P_X\left(\left\{x\in \mathbb{R}:S\left(x\right)\le u\right\}\right)=logu$ for all $u\in [1,10)$.

The useful result for this study is that if $U$ is a random variable uniformly distributed on $[0,1)$, then the random variable $X=10^U$ is Benford. To show this, let us say the cumulative distribution function of a Benford random variable $X$ is $F_X\left(x\right)={log}_{10}\left(x\right)$ for all $x\in [1,10)$. Then, by rewriting the cumulative distribution function as $10^{F_X\left(x\right)}=10^{{log}_{10}\left(x\right)}$, we have $10^{F_X\left(x\right)}=x$, where $F_X\left(x\right)\sim U(0,1)$. Thus, a Benford variable $X$ can be generated by $10^U$, where $U\sim U(0,1)$.

To evaluate the degree of deviation between the observed and expected first digit distribution from BL, we considered the chi-squared test. For the corresponding ${\chi }^2$, the statistic can be estimated as

$${\chi }_{stat}^2\left(8\right)=\sum _{i=0}^9\frac{{\left(e_i-b_i\right)}^2}{b_i},$$

where $e_i$ is the observed frequency in each bin in the observed data, and $b_i$ is the expected frequency based on Benford’s distribution. The chi-square statistic works as a measure of the gap between the realization observed in the data and that implied by the Benford distribution; the larger the chi-square statistic is, the stronger the deviation from the Benford distribution will be. In this case, with a 95% confidence level, ${\chi }^2\left(8\right)=15.507$ is the critical value for the rejection of the null hypothesis; if the value of the ${\chi }_{stat}^2$ is less than the critical value, then we accept the null hypothesis and conclude that the data fits the Benford distribution. Then, the null hypothesis ($H_0$) is that the observed distribution of the first significant digit in the case of interest is the same as expected on the basis of BL; the alternative hypothesis ($H_A$) is that the observed distribution of the first significant digit in the case of interest is not the same as expected on the basis of BL. Particularly in forensic analysis, if the null hypothesis can be rejected, the observed series does not satisfy BL and thus infers a possible manipulation of data.

3. A generalized epidemic growth model and benford’s law

The growth pattern of infectious disease outbreak assumes exponential growth dynamics based on the differential equation:

$$\frac{dP}{dt}=\alpha P^r,$$

where $P$ is the cumulative number of cases, $t$ is time, and $\alpha$ is a positive constant (growth rate), which varies as the exponent $r$ changes.

3.1. Growth model in the absence of control intervention: $\mathit{r}=1$

When $r=1$, we can solve with the separation of variables:

$$\frac{1}{P}dP=\alpha dt$$

$$P\left(t\right)=e^c{e}^{\alpha t},$$

where $c>0$. $P\left(t\right)$ is considered the classical epidemic growth model; the cumulative number of cases, $P\left(t\right)$, grows according to the equation, where $\alpha$ is the growth rate per unit of time, $t$ is time, and $e^c$ ($=P_0\left(t\right)$) is the number of cases at the start of the outbreak. The growth rate, $\alpha$, is related to $R_0=1+\alpha ∕\gamma$, as derived from SIR (susceptible–infected–removed) models, where $\gamma$ is the mean infectious period.

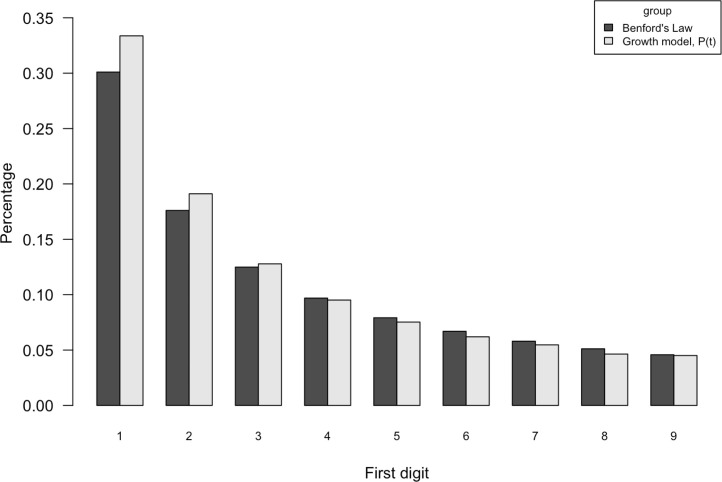
The function $P\left(t\right)$ is Benford. The proof relies on Weyl’s equidistribution theorem, which states that if $i$ is irrational, then for large $T$, the fractional parts of $it$ for $1\le t\le T$ are uniformly scattered over the unit interval ([31], [32]). More specifically, the function $e^c{e}^{\alpha t}$, can be written as $10^{\left(c+\alpha t\right){log}_{10}e}$, where ${log}_{10}e$ is irrational. Thus, for the large range of $t$ the fractional parts of $\left(c+\alpha t\right){log}_{10}e$ become uniformly distributed over the interval $[0,1)$. As we mentioned in Section 2, if $U$ is a random variable uniformly distributed on $[0,1)$, then the random variable $X=10^U$ is Benford. Therefore, the numbers taken from the function $P\left(t\right)=e^c{e}^{\alpha t}$ naturally follow BL. To visualize the relationship between $P\left(t\right)$ and Benford. We generated 1000 observations from $P\left(t\right)=e^c{e}^{\alpha t}$, where $e^c\sim N(1.1,0.01)$, $\alpha \sim N\left(0.1,0.03\right)$, and $T=50$. In Fig. 1, the simulated first-digit distribution of the growth model in the absence of control intervention is represented (gray) along with the corresponding probability mass for Benford’s distribution (black). Although digit 1 and digit 2 exhibit slightly higher proportion than BL, the simulated data from the growth model are quite close to following Benford distribution. We discuss the validity of BL in more detail with different simulation scenarios in Section 4.

Fig. 1.

Frequency of first digit in growth model in the absence of control intervention. Note: $P\left(t\right)=e^c{e}^{\alpha t}$, where $e^c\sim N(1.1,0.01)$, $\alpha \sim N\left(0.1,0.03\right)$, and $T=50$; Simulated first-digit distribution of the growth model in the absence of control intervention is represented (gray) along with the corresponding probability mass for Benford’s distribution (black).

3.2. Growth model in the presence of control intervention: $0<\mathit{r}<1$

When $0<r<1$, we have a function that does not grow as fast as exponential functions. Let us define $r=1-1∕n$, where $n$ is a positive integer. As we mentioned before, the larger the number we choose as $n$, the closer we are to exponential growth, and therefore, the function naturally follows BL. Now, we have

$$P^{1∕n-1}dP=\alpha dt$$

$$P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n,$$

which is a polynomial of degree $n$. In terms of the epidemic growth model, $P\left(t\right)$ describes the cumulative number of cases at time $t$, $\alpha$ is a positive growth rate, and $r\in (0,1)$ is a deceleration of the growth parameter.

Similarly, in Section 3.1, the function can be written as $10^{n{log}_{10}\left(\frac{\alpha }{n}t+c\right)}$, where ${log}_{10}\left(\frac{\alpha }{n}t+c\right)$ is irrational. However, Weyl’s equidistribution theorem requires large $n$ in order to achieve the state (or aspect) of the fractional parts that are uniformly scattered over the unit interval, and thus, the function is Benford. If $r=0$ (i.e., $n=1$), this function describes the cumulative number increases linearly, and thus, $P\left(t\right)$ is not Benford; however, if $r=1$ (i.e., $n=\infty$), this function describes the exponential growth, and thus, $P\left(t\right)$ is Benford. In observational study, given the small value of $\alpha$, the growth may be not as great as exponential growth because no matter how large $n$ is, $r$ is still less than 1.

When $r$ is intermediate, values that lie between 0 and 1, the function describes polynomial growth patterns. For example, if $r=1∕2$ (i.e., $n=2$), the function describes constant incidence over time, while the cumulative number of cases follows a quadratic polynomial; if $r=2∕3$ (i.e., $n=3$), the function describes incidence grows quadratically, while the cumulative number of cases fits a cubic polynomial.

Thus, we believe that when $r$ is small we may able to “flatten the curve”. But, how small is small enough not to obey BL? To better understand the association between $r$ and Benford, we run simulations in the next section.

4. Simulation

In the previous section, we show that when the epidemic growth model can satisfy BL, epidemic growth in the presence (absence) of control intervention may dissatisfy (satisfy) Benford distribution. Nevertheless, we want to check this claim with more generality under uncertainty (e.g., randomly generated parameters, randomly generated initial values, and relatively small fixed samples). Thus, we run simulations of the growth model in order to evaluate the satisfaction of BL.

Simulation 1: The growth model in the absence of control intervention, $P\left(t\right)=e^c{e}^{\alpha t}$. We generate a random variable $X$ from the growth model with $r=1$, such as $P\left(t\right)=e^c{e}^{\alpha t}$, where $t=1,2,\dots ,30,e^c\sim N(1.1,0.01)$, $\alpha \sim N\left({\alpha }_0,0.03\right)$, and ${\alpha }_0\in \left\{0.1,0.2,0.3\right\}$. As mentioned before, after the calculation of the first-digit occurrence, we conduct the ${\chi }^2$ test to detect deviations from BL. Table 1 presents the results of generating 10,000 series of simulated data representing the epidemic growth in each different value of the growth rate. The length of each series is fixed at $T=30$. We found that in each scenario, the number of detected Benford cases (i.e., ${\chi }_{stat}^2<15.507$) are consistently greater than 95%, regardless of the growth rate (${\alpha }_0$). To state it differently, under the uncertainty created when the deceleration of growth ($r$) is 1, most of the epidemic growth will follow BL. Notably, in the absence of control intervention, the growth model will likely satisfy BL, regardless of whether the growth rate was high or low; even a low growth rate may cause exponential growth in the absence of intervention.

Table 1.

Growth model in the absence of control intervention ($r=1$): $P\left(t\right)=e^c{e}^{\alpha t}$, where $t=1,2,\dots ,30,e^c\sim N(1.1,0.01)$, $\alpha \sim N\left({\alpha }_0,0.03\right)$, and ${\alpha }_0\in \left\{0.1,0.2,0.3\right\}$.

Growth rate, ${\alpha }_0$	Deceleration of growth parameter, $r$	Number of Benford cases
0.1	1	9,681 (96.81%)
0.2	1	10,000 (100.00%)
0.3	1	9,890 (98.90%)

Simulation 2: The growth model in the presence of control intervention, $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$. We generate a random variable $X$ from the growth model, such as $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$, where $t=1,2,\dots ,30,c\sim N\left(1.1,0.01\right)$, $r\sim N\left(r_0,0.03\right),r_0\in \left\{0.1,0.2,\dots ,0.9\right\}$, $\alpha \sim N\left({\alpha }_0,0.03\right)$, and ${\alpha }_0\in \left\{0.1,0.2,0.3\right\}$. Table 2 presents the results of generating 10,000 series of simulated data representing the epidemic growth in each different value of the growth rate (${\alpha }_0$) and the deceleration of the growth parameter ($r_0$). The length of each series is also fixed at $T=30$. We found that when the epidemic growth rate is around 0.1, the number of cases in BL was hinged on the deceleration of growth parameter ($r$). For example, when ${\alpha }_0=0.1$ and $r_0=0.1$, we found that only 752 cases out of 10,000 (7.52%) satisfied BL. In contrast, when ${\alpha }_0=0.1$ and $r_0=0.9$, we found that 9,281 cases out of 10,000 (92.81%) satisfied BL. Notably, only moderately strong intervention ($r_0\le 0.3$) may effectively decrease the growth when the growth rate is around 0.1, and therefore, the model will likely dissatisfy BL (e.g., when ${\alpha }_0=0.1$ and $r_0=0.3$, we found less than half of simulated cases (45.41%) satisfied BL). To state it differently, in this setting, we may able to “flatten the curve” if ${\alpha }_0=0.1$ and $r_0\le 0.3$.

Furthermore, when ${\alpha }_0\ge 0.2$, in all of the scenarios, the number of detected Benford cases (i.e., ${\chi }_{stat}^2<15.507$) is greater than 89%, regardless of the deceleration of the growth parameter $r$.

Table 2.

Growth model in the presence of control intervention ($0<r<1$): $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$, where $t=1,2,\dots ,30,c\sim N\left(1.1,0.01\right),$$r\sim N\left(r_0,0.03\right),r_0\in \left\{0.1,0.2,\dots ,0.9\right\},$$\alpha \sim N\left({\alpha }_0,0.03\right),$ and ${\alpha }_0\in \left\{0.1,0.2,0.3\right\}$.

Growth rate, ${\alpha }_0$	Deceleration of growth parameter, $r_0$	Number of Benford cases
0.1	0.1	752 (7.52%)
	0.2	2,455 (24.55%)
	0.3	4,541 (45.41%)
	0.4	6,472 (64.72%)
	0.5	7,873 (78.73%)
	0.6	8,514 (85.14%)
	0.7	9,015 (90.15%)
	0.8	9,105 (91.05%)
	0.9	9,281 (92.81%)
0.2	0.1	8,927 (89.27%)
	0.2	9,848 (98.48%)
	0.3	9,984 (99.84%)
	0.4	9,999 (99.99%)
	0.5	10,000 (100.00%)
	0.6	10,000 (100.00%)
	0.7	10,000 (100.00%)
	0.8	10,000 (100.00%)
	0.9	10,000 (100.00%)
0.3	0.1	9,997 (99.97%)
	0.2	10,000 (100.00%)
	0.3	10,000 (100.00%)
	0.4	10,000 (100.00%)
	0.5	10,000 (100.00%)
	0.6	10,000 (100.00%)
	0.7	10,000 (100.00%)
	0.8	10,000 (100.00%)
	0.9	10,000 (100.00%)

5. COVID-19 application

5.1. Data

In this section, we apply the epidemic growth model to the number of deaths attributed to COVID-19. The World Health Organization declared the coronavirus outbreak to be a pandemic in early March 2020. Most countries affected by COVID-19 have tried to stop the spread of the virus through various means, such as social distancing and quarantines. We collected the number of deaths from the 2019 Novel Coronavirus Visual Dashboard operated by the Johns Hopkins University Center for Systems Science and Engineering (JHU CSSE; https://coronavirus.jhu.edu/). The 2019 Novel Coronavirus Visual Dashboard provides daily data on the cumulative number of deaths since January 22, 2020. We selected 10 countries that showed a relatively high mortality rate. To apply the epidemic growth model to the growth patterns of the number of deaths, we followed the methodology used in other epidemiological studies. In particular, we focus on the analysis of the early ascending phase of COVID-19; we used the day when coronavirus-related deaths were first observed to the day when the number of deaths peaked in each country as the early ascending phase for this study [33], [34], [35], [36]. For example, in the case of the US, the first deaths were observed on February 29, which is 39 days after January 22. The peak in the number of deaths was observed on April 6, which is 76 days after January 22.

5.2. Estimation and confidence intervals

To jointly estimate the parameters $\alpha$ and $r$, we used the least-square curve fitting, as in prior studies [36], [37]. In particular, we fit the cumulative number of deaths to the equation $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$. We then implemented a least-square fitting procedure in R using the built-in function lsqcurvefit in the pracma package. In order to increase the accuracy of the estimation, the parameters were updated with the mean square errors and prior knowledge of the parameters (i.e., the estimated parameters in the previous iteration). Our estimation method differs from existing studies in two respects. First, our proposed estimation approach sequentially updates the parameters by using the estimated parameters from the previous iteration; after setting the initial value of $c$, the parameters $\alpha$ (growth rate parameter) and $r$ (deceleration of growth parameter) were jointly estimated after 100 times iteration. Second, the proposed method incorporates the overall mean squared error (MSE) into the estimation procedure; once the iteration has ended, we can choose the estimated $\alpha$ and $r$, which gives the minimum value among 100 MSEs. In contrast to our proposed approach, which is based on many estimations (i.e., 100 iterations), to the best of our knowledge, existing studies rely on only one estimation (i.e., one iteration).

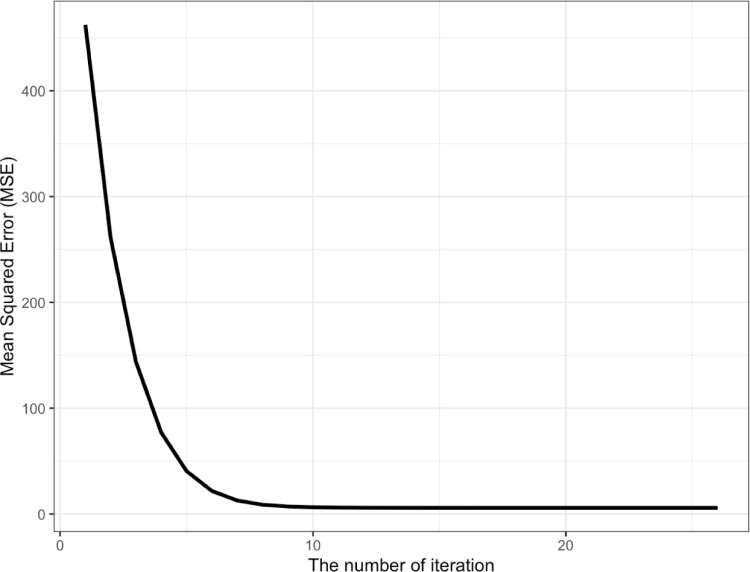
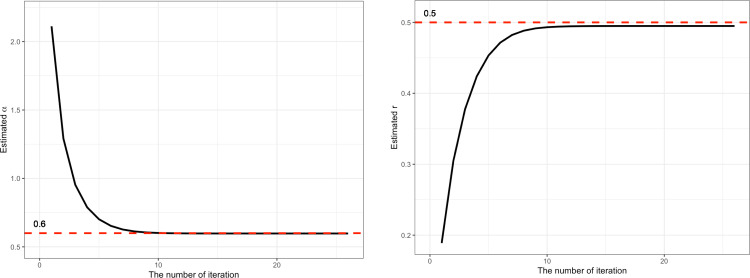
To illustrate how the proposed approach will work with COVID-19 data, we generated values from $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$ with $T=50$, $c=3$, $\alpha =0.6$, and $r=0.5$ (i.e., $n=2$). The initial values for $\alpha$ and $r$ were given as 0. The initial value of c was given as the first observation of the generated sample. Fig. 2 shows the mean squared errors (MSEs) against the iteration number. The plot indicates that the proposed approach rapidly reaches a stationary distribution. When the number of iterations ($m$) exceeded 13, the MSE was about 3.86; when there was no sequential updating ($m=1$), the MSE was 462.29. Thus, the MSE of the proposed approach was approximately 120 ($\approx 462.29∕3.86$) times lower than the MSE of the approach that did not update the estimates (i.e., estimating the parameters based on $m=1$). Fig. 3 shows the estimated parameters when we employed our proposed approach. As the iteration proceeded, the estimated parameters became closer to the true parameters. The dashed line indicates the true parameters. For example, after iteration 10, we obtained estimated parameters of 0.59 and 0.49 for $\alpha$ and $r$, respectively. When $m=1$, the estimated parameters for $\alpha$ and $r$ were 2.11 and 0.18, respectively. Through this analysis, it was found that the method of the least-squares fitting of the curve was highly affected by the initial value of $c$. Thus, we believe that the proposed approach is always desirable when $c$ is not known. For additional clarity, we have provided the source code that was used to test the proposed approach (in the R statistical environment) as an Appendix A alongside the full text of the manuscript. We hope to spark a discipline-wide discussion of the merits of advanced and flexible matching methods in a contemporary organizational setting.

Fig. 2.

Mean squared error for simulated data against the iteration.

Fig. 3.

Values of the estimated parameters against iterations ($\alpha =0.6$ and $r=0.5$).

Before estimating the parameters, we set the initial value for $\alpha$, $r$, and c. The initial values for $\alpha$ and $r$ were given as 0. For the US, the UK, and Japan, the initial value of c was given as 2. For China, Spain, Germany, and the Netherlands, the initial value of c was given as 3. For South Korea and Italy, the initial value of c was given as 4.2 After setting the initial value, the parameters $\alpha$ and $r$ were jointly estimated after 100 times iteration. Once $\alpha$ and $r$ were jointly estimated, the value of c was updated as the initial value of $c^{1∕\mathrm{r}}$. Given the estimated $\alpha$, $r$, and c, the mean squared error was calculated using the fitted growth model and the original data. After we obtained the mean squared error, the next iteration started, and $\alpha$ and $r$ were updated as those from the previous iteration were. Once the iteration ended, we chose the estimated $\alpha$ and $r$, which could minimize the mean squared error.

We constructed a 95% confidence interval for the $\alpha$ and $r$ estimates using the parametric bootstrapping method [36], [37], [38], [39]; based on the 1000 estimates (by fitting the least-squares method 1000 times), we calculated the variance (standard errors) of the estimated parameters, as prior studies have [36], [37], [38]. More precisely, the bootstrapping error was estimated by simulating 1000 realizations of the best-fit curve using the parametric bootstrap with a negative binomial error structure. Using the bootstrapping error, we then obtained the nominal 95% confidence intervals. In particular, we generated $M$ (in this study, $M=1000$) sets of boosted cumulative numbers of cases ($B_m\left(t\right)$, where $m=1,2,\dots ,M$) based on the observed data ($P\left(t\right)$, where $t=1,2,\dots ,T$) in the following manner. For $t=1$, simply let $b_m\left(1\right)=P\left(1\right)$. For $t\ge 2$, $b_m\left(t\right)$ was sampled from a negative binomial (NB) distribution with mean $P\left(t\right)-P(t-1)$, which is the daily change in observed samples between day $t$ and $t-1$. In each $M$, the total number of bootstrapped values is $T$. In this study, $T$ indicates the length of the data points. For example, if $t=2$, $P\left(1\right)=1$, and $p\left(2\right)=5$, we generated $M$ samples from the NB distribution with mean $4$. In this study, we used a NB instead of a Poisson distribution because of the overdispersion problem and chose the dispersion parameter range 0.001–0.9.3 Overdispersion refers to the presence of a greater variance of observed data than would be expected in a given parametric model. Notably, an overdispersion problem often occurred when fitting a Poisson distribution to the data. The Poisson distribution had only one parameter. Thus, the variance of the distribution was equal to the mean. The corresponding realization of the cumulative number of deaths due to COVID-19 was given by $B_m\left(t\right)={\sum }_{j=1}^t{b}_m\left(j\right)$. The $\alpha$ and $r$ were then estimated from each of the 1000 simulated epidemic growths. The empirical distribution of the estimated parameters was used to construct 95% confidence intervals. The estimated parameters and confidence intervals are reported in Table 3.

Table 3.

COVID-19, growth model in the presence of control intervention, and BL test.

Johns Hopkins Coronavirus Resource Centera					Growth model in the presence of control intervention			BL test
Country	The early ascending phase (Dates in 2020)	T	$c$		Growth rate, $\alpha$ (95% C.I)	Deceleration of growth parameter, $r$ (95% C.I)		${\chi }_{stat}^2$	$p$-value
US	02/29 $\sim$04/06	38	1		0.364 (0.355, 0.371)	0.921 (0.917, 0.924)		1.388	0.990
China	01/22 $\sim$02/11	21	17		1.485 (1.453, 1.515)	0.612 (0.609, 0.614)		2.691	0.952
South Korea	02/20 $\sim$03/02	12	1		0.590 (0.521, 0.657)	0.549 (0.535, 0.562)		8.698	0.368
Japan	02/13 $\sim$04/04	52	1		0.140 (0.136, 0.144)	0.773 (0.761, 0.783)		25.166	0.001
UK	03/05 $\sim$04/04	30	1		0.369 (0.363, 0.374)	0.929 (0.926, 0.931)		5.674	0.684
Spain	03/03 $\sim$04/02	31	1		1.021 (1.005, 1.036)	0.774 (0.772, 0.776)		7.101	0.526
Italy	02/21 $\sim$03/26	35	1		0.722 (0.704, 0.739)	0.802 (0.799, 0.805)		3.499	0.899
Germany	03/09 $\sim$04/08	31	2		0.525 (0.515, 0.534)	0.819 (0.815, 0.822)		4.594	0.800
Netherlands	03/06 $\sim$04/07	33	1		0.672 (0.660, 0.682)	0.761 (0.757, 0.764)		5.288	0.726
Sweden	03/11 $\sim$03/27	17	1		0.271 (0.257, 0.286)	0.999 (0.982, 1.018)		7.375	0.497

Note: The early ascending phase is the period between the day when the first death was observed after January 22, 2020 and the day when the number of deaths peaked after January 22, 2020; we used the number of deaths observed in these periods to estimate $\alpha$ and $r$ and conduct the BL test. T denotes the length of the data points. ${\chi }_{stat}^2$ is reduced a chi-squared statistic.

^aData source: https://coronavirus.jhu.edu/.

5.3. Results

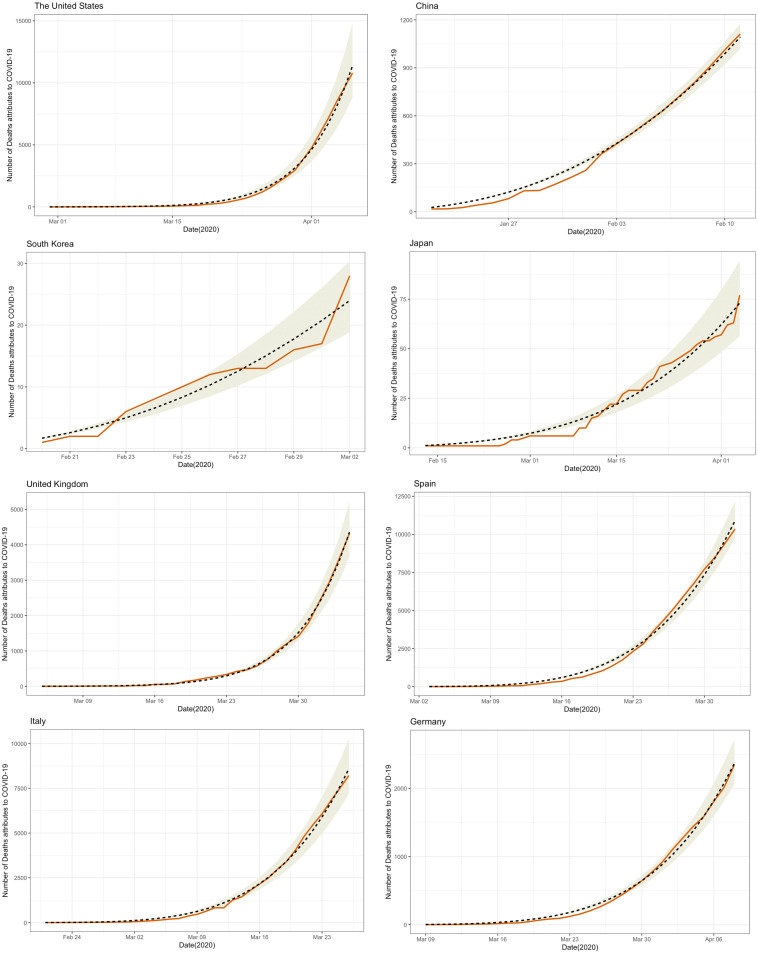
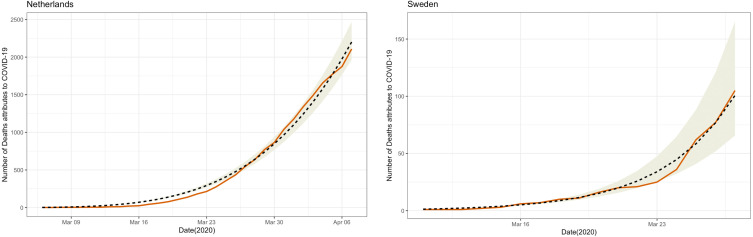
It is possible to fit the data for the number of coronavirus deaths into the growth model in the presence of control interventions, as reported in Fig. 4. The predicted value of the number of deaths can be computed based on the estimated parameters ($\hat{\alpha }$ and $\hat{r}$) and is consistent with the observed number of deaths attributed to COVID-19 that were reported by the JHU CSSE. The consistency between the model prediction and the reported data is very close in all 10 countries.

Fig. 4.

Tracking COVID-19 deaths across countries using epidemic growth model in the presence of control intervention ($0<r<1$): $P\left(t\right)={\left(\frac{\alpha }{n}t+c\right)}^n$. Note: The red solid lines indicate the observed number of deaths attributes to COVID-19 reported by the JHU CSSE; the black dashed lines indicate the predicted value of the number of deaths based on the estimated parameters ($\hat{\alpha }$ and $\hat{r}$); the shaded area indicates the 95% confidence interval of the predicted number of deaths attributes to COVID-19.

Overall, our analysis revealed a diversity of profiles across the countries. Estimates of the deceleration of growth parameter $\hat{r}$ ranged from 0.549 in South Korea, reflecting a high degree of intervention, to 0.999 in Sweden. Nevertheless, the epidemic growth in all countries satisfied BL with the exception of Japan.4 These findings are consistent with the simulation. Based on the simulation, we showed that when ${\alpha }_0\ge 0.2$ in all of the scenarios, the number of detected Benford cases was greater than 89%, regardless of $r_0$. For example, the estimated deceleration of growth in South Korea was the lowest ($\hat{r}=0.549$) among the 10 countries, but the estimated growth rate was $\hat{\alpha }=0.590$, which was greater than 0.2. Thus, it followed BL.

The estimated growth rate and deceleration of growth in Japan were 0.140 and 0.773, respectively. Based on the simulation, this profile’s number of detected Benford cases was between 90.15% (${\alpha }_0=0.1$ and $r_0=0.7$) and 91.05% (${\alpha }_0=0.1$ and $r_0=0.8$), as shown in Table 2. However, the calculated ${\chi }^2$ statistic was 25.166 ($p$<0.001), indicating the values from Japan were significantly different from the theoretical values of BL.

As a robustness check, we performed BL test on the data sets for the dates after the COVID-19 peak. Thus, the data set in each country contains from the date when the first death was observed after January 22, 2020, to the (fixed) date of June 18, 2020. Not surprisingly, the empirical findings from all countries were statistically significant at the 0.05 level, indicating that the epidemic growth in all countries does not satisfy BL (for more in details, see Appendix B).

6. Conclusion

The objective of this study was to (1) introduce an epidemic growth model that could capture the intervention (e.g., flattening the curve) efforts in different countries in order to better understand the growth rate of COVID-19 infections, (2) establish a link between this epidemic growth model and BL, and (3) propose a sequential updating scheme for parameter estimates.

We found that the predicted number of deaths from the model was very close to the observed number of COVID-19 deaths across all 10 countries. Mathematically, we also showed that epidemic growths without intervention are likely to satisfy BL, because epidemic growths naturally follow an exponential family distribution. Thus, BL was applicable to the epidemic growth model.

Furthermore, it is possible that when the degree of intervention is high, the growth of death or infection rates may not obey BL. This theory would mean that “flattening the curve” interventions would not only be able to slow the growth rate of the outbreak, but also change the characteristics of its nature so that the distribution of first digits followed BL. As a result, BL testing alone would not be sufficient to detect potential manipulations of the growth of the death rate. For this reason, it is important to interpret the model’s estimated parameters for the growth rate ($\alpha$) and deceleration of growth ($r$), because they can provide insight into how likely a given case satisfies BL based on the simulation.

Although all of the countries have aggressively fought the epidemic, our analysis shows that 9 out of 10 countries satisfied BL, indicating the growth rates of COVID-19 in these 9 countries were close to an exponential trend. This finding may be due to the fact that the estimated growth parameters for all were greater than 0.2. Notably, Sweden’s strategy for fighting COVID-19 depends on the development of herd immunity [40]. Herd immunity occurs when a large portion of the population becomes immune to the pandemic. Thus, Sweden has not imposed a lockdown [41], [42]. Based on the BL test on the data from Sweden, the calculated ${\chi }^2$ statistic was 7.375 ($p=0.497$), indicating that the growth of the epidemic in Sweden has satisfied BL (see Table 3 in the manuscript). This finding means that all countries that used interventions (except for Japan) satisfied BL, indicating that the growth rates of COVID-19 were similar in countries that did not use significant interventions (e.g., Sweden).

However, Sweden has shown the lowest deceleration of growth among the 10 countries considered in this study. The estimated deceleration of growth in Sweden is 0.999 with a 95% confidence interval (0.982, 1.018). Since the 95% confidence interval contains a deceleration of growth parameter of 1.000 ($r=1$) regardless of the growth rate ($\alpha$), the growth pattern of COVID-19 in Sweden can be better described by the growth model in the absence of control interventions (Section 3.1).

In the case of Japan, we further investigated the inconsistency between the simulation test (where, given $\hat{\alpha }=0.140$ and $\hat{r}=0.773$, the number of detected Benford cases was greater than 90.15%, as shown in Table 2) and BL test (where, given the estimates, the values from Japan did not satisfy the Benford distribution with a $p$-value=0.001, as shown in Table 3). We then conducted a BL test based on each of the boosted samples ($M=\text{10,000}$) that we used for constructing the 95% confidence intervals (see Section 5.2). Given $\hat{\alpha }=0.140$ and $\hat{r}=0.773$, the result from the bootstrapped sample showed that the number of detected Benford cases was 88.33%, which was close to the simulation shown in Table 2, even though the simulation scheme was different from the parametric bootstrapping method. Thus, we believe the data generating process in Japan is distinct from the other 9 countries in this study and does not obey BL. One of the possible reasons of the difference between Japan and the other 9 countries is that although JHU CSSE provides public access to the global cases and trends of COVID-19 and updates their data daily, they must rely on self-reported data from each country [43]. The problem with this type of data is that it is subject to intentional manipulation, thus diminishing its reliability or suitability for data analysis. Benford’s law has already attracted interest in antifraud analysis [44], [45]. For that reason, testing Benford’s law is particularly attractive for the detection of fraudulent self-reported COVID-19 data [44], [45]. Based on the empirical findings and the simulation Table 2, BL test shows that the data from Japan is incorrect. These inconsistent results (between the BL test and the simulation table) are important to note because they can discourage researchers from investigating any other self-reported data by Japan further in detail, such as by checking whether the hospitals are managing to cope with the number of infected patients admitted in critical care.

In this study, we also found that the method of the least-squares fitting of the curve was highly affected by the initial value of $c$. Thus, we believe that the proposed approach in Section 5.2 is always desirable when $c$ is not known.

CRediT authorship contribution statement

Kang-Bok Lee: Conceptualization, Methodology, Software, Visualization, Writing - original draft, Supervision. Sumin Han: Conceptualization, Methodology, Software, Writing - original draft, Writing - review & editing. Yeasung Jeong: Data curation, Formal analysis, Investigation, Resources.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Estimation for $\alpha$ and $r$

Appendix B.

See Table B.1.

Table B.1.

BL test on the entire phase of COVID-19.

Johns Hopkins Coronavirus Resource Centera				BL test
Country	The entire phase (Dates in 2020)	T		${\chi }_{stat}^2$	$p$-value
US	02/29 $\sim$06/18	111		15.364	0.052
China	01/22 $\sim$06/18	149		275.420	< 0.001
South Korea	02/20 $\sim$06/18	120		177.680	< 0.001
Japan	02/13 $\sim$06/18	127		69.904	< 0.001
UK	03/05 $\sim$06/18	106		51.742	< 0.001
Spain	03/03 $\sim$06/18	108		158.54	< 0.001
Italy	02/21 $\sim$06/18	119		97.019	< 0.001
Germany	03/09 $\sim$06/18	102		183.750	< 0.001
Netherlands	03/06 $\sim$06/18	105		135.14	< 0.001
Sweden	03/11 $\sim$06/18	100		46.633	< 0.001

Note: The entire phase is the period from the date when the first death was observed after January 22, 2020, to the date of June 18, 2020. T denotes the length of the data points.

^aData source: https://coronavirus.jhu.edu/.