Abstract
A thermally-activated constitutive model is developed based on dislocation interactions, crystallographic orientations and microstructural evolution to describe the elasto-plastic stress-strain behavior during multi-axial loading. The aim is to contribute to the quantification of complex strain path response in solid solution strengthened alloys. In detail, dislocation/dislocation interactions are incorporated in the model to quantify latent and kinematic hardening phenomena during loading path changes. Dislocation density-based constitutive relations are included to account for dislocation features such as dislocation forests, walls and channels. Moreover specifically, dislocation/solute atom interactions are also considered in order to account for both dynamic and static strain aging as well as static recovery. The model is validated against multiple multi-axial data sets for AA5754-O with changes of loading path and various degrees of pre-strain and time intervals between tests.
Keywords: Dislocation interaction, Strain path dependence, Aging, Recovery, Solid solution
I. Introduction
Metal forming is often a multi-step process along different loading paths. Path changes cause a complex deformation response upon reloading. Polycrystalline materials often exhibit a higher yielding strength and higher hardening rate (i.e., the slope of the plastic deformation region of the stress-strain curve) when reloading along another direction because of latent hardening (also known as “cross-hardening”), except for reverse loading (Franciosi, 1985; Franciosi et al., 1980). Latent hardening results from the fact that activity on one slip system hardens other systems to different degrees because of the specifics of dislocation interactions (Franciosi, 1985; Franciosi et al., 1980). It is observable when changes in loading path result in changes in dislocation slip activities and consequent changes in flow stress. The multiaxial stress state during metal forming induces multiple slip activities, resulting in the formation of a spectrum of dislocation junctions and their associated strengths (Franciosi, 1985; Franciosi et al., 1980; Hirth, 1961; Madec et al., 2003). The junctions act as obstacles to mobile dislocations moving on intersecting slip systems. Strain path changes activate new types of dislocation interactions, resulting in different dislocation junctions and, consequently, changes in hardening behavior (Franciosi, 1985; Franciosi et al., 1980). During plastic strain, dynamic recovery allows dislocation substructures to form (e.g., dislocation walls and channels) (Kocks and Mecking, 1979) that influence the strain hardening when the loading path changes. Thus, preferred crystallographic orientation (i.e., texture), dislocation-dislocation interactions and dislocation structures should be considered in the constitutive laws used to model the strain path dependence of polycrystalline materials (Barlat et al., 2013; Beyerlein and Tome, 2007; Gérard et al., 2013; Kitayama et al., 2013).
Dislocation densities have been extensively incorporated in crystal plasticity-based approaches to accurately capture the stress-strain behavior, although a main interest of this approach is for monotonic loading (Estrin, 1998; Ma and Roters, 2004) and tension/compression (Estrin et al., 1996; Pham, 2013; Pham et al., 2013) without including latent hardening. Recently, several attempts to extend this approach to include latent hardening were made for complex loading path problems (Barlat et al., 2013; Beyerlein and Tome, 2007; Beyerlein and Tomé, 2008; Gérard et al., 2013; Kitayama et al., 2013). However, previous work in our group showed that latent hardening cannot effectively describe the hardening behavior of a solid solution strengthened aluminum alloy during bi-linear strain paths, i.e., balanced biaxial straining up to prescribed strain levels followed by uniaxial straining (Iadicola et al., 2012). One reason is that, in solid solution strengthened alloys, dislocation cores strongly interact with solute atoms. This strong interaction is responsible for a number of microstructural phenomena during plastic straining and during unloading. In particular, it causes dynamic strain aging during plastic deformation even at room temperature (Cottrell and Bilby, 1949; Fressengeas et al., 2005; Pham and Holdsworth, 2012). The strain aging during the first strain step can occur continuously during unloading, and for a short period of time after unloading, i.e., static strain aging. Both dynamic and static strain aging affect material response upon reloading. Static recovery reduces dislocation density and relaxes the strong interaction between dislocations (that were mobile during deformation) and solute atoms. In general, strain aging usually causes the aged material to be harder initially but is also accompanied by lower hardening rate, whereas static recovery decreases yield strength but restores the hardening rate as well as the ductility. Moreover, if the deformed sample remains unloaded for a sufficiently long period of time, static recovery occurs due to (i) the reduction in dislocation density, (ii) the rearrangement of dislocations (polygonization), and (iii) solute atoms diffuse into dense dislocation structures, leading to the relaxation of the interactions between dislocations (that were mobile during deformation) and solute atoms. Static recovery also influences the deformation behavior during reloading (Nes, 1995). Consequently, it is necessary to include both aging and recovery in the constitutive models in order to account for microstructural changes when altering the loading path, and ultimately to capture the material behavior upon reloading.
Testing mechanical response during strain path change often involves unloading. Dislocations often reverse their slip directions during unloading, which affects the dislocation structure. The yield stress in the reverse loading is often lower than at the end of forward loading. This phenomenon is known as the Bauschinger effect (Stout and Rollett, 1990). The variation in the yield strength and hardening response due to a loading path reversal is called kinematic hardening. To deal with the unload step, kinematic hardening is also included in this work by considering the interactions between dislocations in slip systems that share the same slip plane and slip direction, but have a different direction of slip, i.e., opposite sign.
The considerations of latent and kinematic hardening, strain aging and recovery motivate the current work that builds on our previous efforts (Hu et al., 2012; Iadicola et al., 2012; Pham et al., 2014a). Because recovery and interactions between dislocations and solute atoms are dependent on temperature, a thermally-activated constitutive model in this study is developed on the basis of :
the relationships between detailed dislocation/dislocation interactions and dislocation densities to resolved shear stresses in order to account for latent hardening and kinematic hardening (Sects. II.1 and II.2),
the evolutions of dislocation densities and dynamic recovery (Sects. II.3) and
interactions between dislocations and solute atoms to account for strain aging and recovery (Sects. II.4 to II.6).
All these considerations are then implemented in an elasto-plastic self-consistent framework to take account of texture (Sect. II.7). Finally, the model is applied to simulate a large dataset of stress-strain measurements in an aluminum alloy (AA) 5754 that include strain path changes with variable wait times between tests (Sects. III and IV). For this application of the model, a description and discussions of the material behavior during multi-step strainings are presented in Sect. III. Parameter values of the developed model for this specific application are obtained in Sects. IV.1 and IV.2. Application results are given and discussed in Sect. IV.3.
II. Model formulation
In this section, thermally-activated constitutive laws for obstacle-controlled plastic deformation are formulated based on (i) the Orowan kinetic equation of dislocation motion (Orowan, 1940), (ii) dislocation/dislocation interactions and (iii) dislocation substructure development (Sect. II.1). Dynamic recovery is then incorporated into the dislocation density evolution in Sect. II.2. Dynamic and static strain aging is then discussed and incorporated into the thermally-activated constitutive model in Sects. II.3 & 4. As mentioned before, if enough time elapses between tests static recovery can occur and this is described in sub-section II.5. Sect. II.2 gives some details of the dislocation/dislocation interaction model, in particular for face-centered cubic (FCC) materials, while Sect. II.7 presents a brief review of the homogenization procedure of deformation response of polycrystalline aggregates using an elasto-plastic self-consistent approach.
II.1. Constitutive equations for obstacle-controlled plastic deformation
In this section, the resolved shear stress in response to plastic deformation is related to densities and interactions of dislocations. In addition, the role of dislocation structures is accounted in the model based on the similitude relationship (Sauzay and Kubin, 2011) and Mughrabi’s dislocation composite structure hypothesis (Mughrabi, 1983).
A density of mobile dislocations (ρmo) moving through discrete obstacles on slip system i with an average velocity () according to (Orowan, 1940) can result in a strain rate of
| (1) |
| (2) |
Here β is a dimensionless constant, b is the magnitude of Burgers vector, and υ is an attempt frequency. ΔG(τ(i)) is the Gibbs free energy of activation for the cutting or by-passing of an obstacle. For irregularly spaced obstacles (Kocks et al., 1975):
| (3) |
where ΔF is the activation energy required to overcome the obstacles without the aid of external stress, ΔF = ημb3 with μ is the shear modulus and η is a pre-factor and less than 1.
τ(i) is the resolved shear stress on slip system i. is the critical resolved shear stress needed to move dislocations through obstacles without the assistance of thermal energy on slip system i. This stress equals the yield strength of materials at 0 K. evolves during deformation, and is proportional to the dislocation mean free path (L(i)), i.e., where α represents the interaction strength between dislocations and obstacles. For the interaction between dislocations, α reflects the strength of junctions resulting from dislocation/dislocation interactions. The dislocation/dislocation interactions in FCC materials are discussed in detail later in Sect. II.2.
Inserting Eqns. 2, 3 into 1, we have:
| (4) |
| (5) |
where is the reference shear rate ( is the necessary stress to move mobile dislocations in obstacle-free regions). is about 106 s−1 (Frost and Ashby, 1982).
For single phase polycrystals, obstacles to dislocation motion are other dislocations, dislocation substructures (e.g., dislocation walls), precipitates (or secondary particles), and grain boundaries. In other words,
| (6) |
where ρ(i) is dislocation density in slip i; , , and are the inter-spacing of the dislocation substructures (e.g., dislocation walls), of precipitates, and the size of primary grains in slip i.
If the primary grains are coarse and there is no precipitation (i.e., ), and . Therefore, the contributions of grain size can be neglected, i.e., .
arises due to short-range interactions of individual dislocations (i.e., forest hardening). In addition, according to the generalized Taylor relationship proposed by Franciosi et al. (Franciosi et al., 1980), can be calculated by
| (7) |
In this refinement of the scalar model, αij is the strength of the interactions between dislocations in slip i and slip j (the dislocation interactions of FCC materials are discussed in detail in Sect. II.6), and is the density of forest dislocations present on slip system j.
For well-annealed materials where the dislocations are widely spaced and randomly distributed, so is a small fraction of the shear modulus at the beginning of deformation. During deformation, dislocation substructures, such as dislocation walls separated by dislocation channels, form due to dislocation interactions. In general, dislocation substructures evolve from randomly distributed dislocations to weakly-organized structures (e.g., dipole mats or dislocation veins), to cells and finally to subgrains (at large enough strains and/or high enough temperature). Dislocation substructures induce long-range stresses and contribute to an increase in the critical resolved shear stress (CRSS). In addition, the similitude theory (Sauzay and Kubin, 2011) suggests that the increase of the CRSS due to the presence of dislocation substructures is proportional to the increase of the CRSS resulting from the presence of dislocations, i.e.,
| (8) |
with Ksimi is called the similitude factor, Ksimi is estimated to be from 5 to 10 when dislocation cells are well formed.
The dislocation density (ρ(j)) in Eqn. 8 is often believed to be the total density that consists of densities of dislocations within walls and channels. However, Mughrabi (Mughrabi, 1983) found that the long-range internal stress associated with dislocation substructures relates to the plastic deformation incompatibility between high dislocation density regions (such as dislocation bundles or walls) and within low dislocation density regions (such as dislocation channels). This plastic deformation incompatibility requires geometrically necessary dislocations () in the interface between walls and channels. Therefore,
| (9) |
The plastic deformation incompatibility is small for well-annealed materials, increases with strain, and saturates once well-organized dislocation cells form. So the density of geometrically necessary dislocations increases. The similitude factor, Ksimi, also evolves in the same manner (The evolutions of dislocations and the similitude factor are later described in Sect. II.3).
The evolution of the CRSS due to the development of dislocation density is given by
| (10) |
Combining Eqn. 5 with Eqn. 10, we have
| (11) |
The first and second terms in the right-hand side of Eqn. 11 have a mathematically similar form. However, the thermal dependence of obstacle-controlled movement of dislocations when mobile dislocations are stopped by other individual forest dislocations is different than that if they are stopped by dislocation walls. Because dislocation substructures induce long-range internal stresses that are insensitive to the thermal assistance, for the second term in Eqn. 11 (Kocks et al., 1975).
Finally, the resolved shear stress is
| (12) |
II.2. Interactions between dislocations, latent hardening and kinematic hardening
In this section, different types of dislocation/dislocation interactions in FCC materials are presented to account for latent and kinematic hardening by the strengths of dislocation junctions is also given in detail.
In addition to the self-interactions of dislocations in the same slip system, there are five categories of interactions between dislocations moving in different slip systems during plastic deformation. For example, there are twelve {111} < 110 > slip systems for FCC, which are depicted by the Thompson tetrahedron in Fig. 1 (Thompson, 1953) and Table 1. Dislocation interactions between different slip systems form resultant junctions that hinder the movement of dislocations, leading to latent hardening. The most frequent interactions are those that give rise to Lomer-Cottrell (LC) sessile junctions (Cottrell, 1953; Cottrell, 1952; Lomer, 1951). The other dislocation interactions are Hirth (H), coplanar (COP), glissile (GL), and collinear (COL) (B. Devincre et al., 2008; Hirth, 1961; Martinez et al., 2008). These interactions result in the formation of H, COP, GL, COL dislocation junctions, whose strengths are represented by αH, αCOP, αGL, αLC, αCOL, respectively. The interactions between dislocations in different slip systems and corresponding dislocation junction for FCC materials are given in Table 1.
Figure 1:
(a) Thompson tetrahedron (Thompson, 1953) and (b) its expansion to describe slip systems in FCC materials.
Table 1:
Dislocations Interactions in FCC materials (refer to Figure 1 for detailed description of system label)
| Slip | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Self | COP | COP | H | GL | LC | COL | LC | LC | H | LC | GL |
| 2 | COP | Self | COP | LC | COL | LC | GL | H | LC | LC | H | GL |
| 3 | COP | COP | Self | LC | GL | H | GL | LC | H | LC | LC | COL |
| 4 | H | GL | LC | Self | COP | COP | H | LC | GL | COL | LC | LC |
| 5 | LC | COL | LC | COP | Self | COP | LC | H | GL | GL | H | LC |
| 6 | LC | GL | H | COP | COP | Self | LC | LC | COL | GL | LC | H |
| 7 | COL | LC | LC | H | LC | GL | Self | COP | COP | H | GL | LC |
| 8 | GL | H | LC | LC | H | GL | COP | Self | COP | LC | COL | LC |
| 9 | GL | LC | H | LC | LC | COL | COP | COP | Self | LC | GL | H |
| 10 | H | LC | GL | COL | LC | LC | H | GL | LC | Self | COP | COP |
| 11 | LC | H | GL | GL | H | LC | LC | COL | LC | COP | Self | COP |
| 12 | LC | LC | COL | GL | LC | H | LC | GL | H | COP | COP | Self |
Because the strengths of dislocation junctions differ, each type causes different hardening rates. The non-coplanar interactions usually induce higher hardening rates than for self-interaction. Although it is still a matter of debate as to which dislocation junction is strongest, it is quite widely accepted that the LC and COL are the two strongest junctions (Dupuy and Fivel, 2002; Madec et al., 2003; Martinez et al., 2008; Picu and Soare, 2010). Following a recent study that claims in addition to having high strength, the COL type also strongly influences microstructural evolution (Madec et al., 2003), the order of strength of dislocation junctions: self<(H=COP=GL)<LC< COL is assumed. A change in loading path alters dislocation slip activities and dislocation interactions, leading to different hardening behavior. Depending on the degree to which the path change reverses slip on each system, either latent hardening or kinematic hardening or both can occur. For example, if the path change occurs during plastic deformation without unloading, the dominant interactions do not involve slip reversals. Thus latent hardening is predominant compared to kinematic hardening. However, if the loading path change consists of unloading, kinematic hardening is significant because dislocations reverse their direction.
The contributions of the interaction between dislocations in slip i and slip j to the hardening are quantified by αij in Eqns. 7 to 16. αij = αself where i=j represents the self-interaction of dislocations, i.e., self-hardening. While αij (with i≠j and i and j are not a forward and backward pair) can be any of αH, αCOP, αGL, αLC, αCOL for latent hardening, αij = αbackαself (with i≠j and i and j are the forward and backward slipping pair) represents kinematic hardening.
II.3. Dislocation density evolution and dynamic recovery
The evolution of dislocation density during plastic deformation is proportional to the generation rate of dislocations () minus the annihilation rate of dislocations (). While the rate of the generation of dislocations is inversely related to the dislocation mean free path, that of the annihilation of dislocations depends to a first approximation linearly on the dislocation density (Essmann and Mughrabi, 1979; Kocks and Mecking, 1979; Mecking et al., 1976), i.e.,
| (13) |
where: k1 and k2 are coefficients characterizing the storage and annihilation rates, respectively. k1 is an athermal coefficient, and can be considered as constant during plastic deformation. k1 is in the range from 8 to 80 (Kocks, 1966). Whereas, k2 relates to the dynamic recovery process that is increasingly active during plastic straining. Because cross slip and dislocation climb are mainly responsible for dynamic recovery and are thermally activated, k2 is a thermally dependent term. At saturation (i.e. ignoring Stage IV hardening), i.e., d ρ(i) / dγ = 0, and . We assume that the saturation values of dislocation density and drag stress are the same for all slip systems at saturation. Because the collinear interaction is associated with the cross slip (Madec et al., 2003) that is mainly responsible for the dynamic recovery at low temperatures (Puschl, 2002), αij in Eqn. 14 is considered to be equal to the strength of the collinear interaction, i.e., αij = αCOL, giving
| (14) |
Therefore,
| (15) |
Dynamic recovery also results in the re-arrangement of dislocations to form high dislocation density regions (e.g., dislocation walls) and low dislocation density regions (e.g., dislocation channels). The contribution of dislocation rearrangement to the critical resolved shear stress is via Ksimi and ρn_sub. The similitude factor (Ksimi) is related to the degree of organization of dislocation structures (Gómez-García et al., 2006). ρn_sub is the density of geometrically necessary dislocations to accommodate the plastic deformation incompatibility between dislocation high density and low density structures. Ksimi and ρn_sub should evolve in a similar fashion when dislocation structures develop from randomly distributed dislocations to weakly-organized structures (e.g., dipole mats or dislocation veins), to cells and finally to subgrains (at large enough strains and/or high enough temperature). By solving Eqn. 13, the general evolution of dislocation density can be described by . Therefore, the evolution of the similitude factor for slip i can be similarly represented by:
| (16) |
II.4. Dynamic strain aging
Dynamic strain aging (DSA) takes place in the course of straining when solute atoms diffuse into dislocation lines that are temporarily stopped at obstacles to form atmospheres of solute atoms around dislocation cores (Cottrell and Bilby, 1949; Pham and Holdsworth, 2012). The solute atom atmospheres strengthen the locking effect that requires a higher stress to re-mobilize dislocations (or to generate other dislocation sources). Once the external stress reaches a critical value, a large number of dislocations are unlocked and slip, resulting in a stress drop and a consequent reduction in the dislocation speed thus allowing dislocations to once again be anchored by solute atoms. This locking and unlocking process happens repeatedly, resulting in stress serrations (Pham and Holdsworth, 2012). Flow stress serration is one of the most obvious manifestations of DSA and has been extensively studied as the Portevin-LeChatelier effect (Kang et al., 2005). The locking effectiveness of atmospheres of type s (of solute atoms) relates to the square root of the ratio of the solute atom concentration on dislocation cores (Cs) to the nominal concentration of the solute atoms (Cs0) (Cheng et al., 2001). Under the influence of DSA, the activation energy for dislocation movement is increased because of the presence of solute atom atmospheres (Cheng et al., 2001). Therefore, the thermal activation energy (ΔFnon_sub) in Eqn. 12 are scaled by . In addition, the strength of dislocation junctions is also enhanced due to the binding force between solute atom atmospheres and the core of dislocation junctions. In other words, under the influence of DSA, (1). Eqn. 12 becomes,
| (17) |
The way of including the influence of DSA via strengthened junctions of dislocations also accounts for other effects of DSA on dislocation density and hardening rates. It was found that DSA: (1) results in a higher dislocation density and (2) a higher hardening rate compared to conditions outside the DSA regime (Pham and Holdsworth, 2014; Pham and Holdsworth, 2012). Dislocations with strengthened junctions require higher stress to move, causing a higher hardening rate. In addition, the strengthening of dislocation junctions makes (1) them more stable (i.e., more difficult to unzip strengthened junctions), and (2) dislocations are less mobile (i.e., lower annihilation rates). Therefore, when dislocation junctions are strengthened by the strong interaction with solute atoms, it results in a higher hardening rate and requires a higher dislocation density to accommodate the same prescribed plastic strain as without the strong interaction between dislocations and solute atoms. This approach is similar to methods used by Cheng, Nemat-Nasser and Guo (Cheng et al., 2001) which was demonstrated as an effective way to account for the effects of strong interaction between dislocations and solute atoms on microstructural condition (Lindgren et al., 2008; Pham, 2013).
II.5. Static strain aging
Static strain aging (SSA) occurs when deformed materials with solute are completely (or partially) unloaded and held over a short period of time. During the holding time, under the assistance of internal residual stresses, solute atoms diffuse into dislocation lines to form solute atom atmospheres, resulting in a higher initial yield stress upon reloading than the stress just before unloading. The mechanism of SSA is very similar to that of DSA except it happens in the unloaded state. Of course, both DSA and SSA depend on solute diffusion and they both inherently depend on the strain history (Kubin et al., 1992; Van den Beukel and Kocks, 1982) via the dislocation structure. In some cases where the dynamic/static recovery is negligible, the stress increases and reaches a saturation value with increasing pre-strain. Louat (Louat, 1981) modeled the yield stress increase after the aging time of ta as follows,
| (18) |
Here td_s is a characteristic time constant relating to solute atom diffusivity and the dislocation/solute atom binding energy; td_s is typically in the range 1 s to 100 s for AlMg alloys at room temperature (Kubin et al., 1992). is the maximum pinning stress.
During unloading and holding times, solute atoms can diffuse into mobile dislocations when they wait at obstacles. The time to let solute atoms diffuse to dislocation lines to form a solute atmosphere is defined as the “aging time” while the time that mobile dislocations are temporarily arrested at obstacles is defined as the “waiting time”. During static strain aging, the aging time (ta) is normally equal to the average waiting time (tw) of mobile dislocations at obstacles. The travelling time (ttr) of mobile dislocations moving through discrete obstacles is negligible compared to the waiting time. According Orowan’s kinetic equation, we have:
| (19) |
Here L is the total dislocation mean free path, with ρt = ρmo + ρf + ρn_sub
| (20) |
Inserting Eqn. 20 into Eqn. 18, we can describe the yield stress increase due to the static strain aging by
| (21) |
II.6. Static recovery
Static recovery can happen under a zero-load condition and returns strained material after a sufficient period of recovery time towards the annealed state. This recovery process is rather complex, and also involves interactions between dislocations themselves and with dissolved atoms, e.g., Mg in AlMg alloys. Static recovery is controlled by solute drag and by dislocation annihilation. During static recovery, (1) dislocations migrate, annihilate and form more stable configurations, and (2) solute atoms preferably diffuse into dense dislocation substructures to relax their strong interactions with dislocations (that were mobile during deformation). The reduction in dislocation density and the relaxation of interactions between dislocations and solute atoms allow dislocations to move more easily, resulting in a decrease in the yield stress upon reloading. The fraction of residual yield strength (R) is closely related to the annealing out of dislocations under the influence of solute atom Mg during static recovery.
For deformed AlMg alloys at low temperatures, R can be modeled by the following equation (Nes, 1995):
| (22) |
where:
k is Boltzmann’s constant (1.3806503 × 10−23 m2kg/(s2K))
T is temperature (K)
ΔFrec_static = ηrec_staticμb3 with ηrec_static is a positive constant relating to interactions between dislocations and weak obstacles, e.g., lattice in FCC materials, solute atoms etc. ηrec_static should be less than 0.2 according to (Frost and Ashby, 1982)
t is the static recovery time
r is a relaxation parameter relating to the relaxation of the interactions between dislocations and solute atoms during static recovery.
Consequently, the yield stress evolution during static recovery is described by
| (23) |
As mentioned above, in contrast to strain aging that increases the yield stress and lowers hardening rate, recovery reduces the yield stress and restores the hardening rate to the as-received value. It is necessary to take account of the influence of static aging and static recovery on the hardening rate. It is obvious that (i) the reduction in hardening rate is proportional to ΔτSSA and ; (ii) the increase in the hardening due to recovery relates to the reduction in the yield strength during static recovery, (1 − R). The hardening rate during reloading is updated by:
| (24) |
where hage and hre are proportionality factors.
II.7. Grain Interaction
When polycrystals deform, there are various assumptions on how the crystals in the aggregate behave. Taylor assumed that the strain of all grains is equal, which automatically satisfies the compatibility condition across grain boundaries (Taylor, 1938). Sachs assumed that all grains experience the same stress, which automatically satisfies the stress equilibrium condition (Schoeck, 1994). These assumptions lead to over- or under-estimates of the yield stress in relation to the CRSS, which provide upper and lower bounds for material deformation response. Experience shows that the upper bound approach gives better albeit imperfect agreement with experiment (Kocks et al., 1998). To account for the reality that there are strong neighbor effects, the visco-plastic self-consistent (VPSC) approach treats each grain as an elliptical inclusion embedded in a elasto-plastic homogeneous equivalent medium whose response coincides with the average behavior of the polycrystals (Lebensohn and Tomé, 1993). The VPSC approach can satisfy both compatibility and stress equilibrium conditions across grain boundaries in an average sense. The approximation depends on the choice of homogenization methods for linear behavior at the grain level. The tangent approximation is obtained by a first order Taylor expansion of the constitutive equation in the vicinity of overall response. It was shown that, as opposed to the completely stiff body assumed in the Taylor model, the tangent scheme describes a relatively compliant matrix in terms of the grain and matrix interaction (Kocks et al., 1998). Recently, there is an extension of VPSC model to elasto-plastic self-consistent (EPSC) problems. An EPSC code (Turner and Tomé, 1994) was developed based on the same scheme as the VPSC. Neil at el. (Neil et al., 2010) demonstrated that the EPSC is able to fit the experimental stress-strain behavior. It can qualitatively capture the evolution of internal stresses, and the texture evolution and has therefore been used to model lattice strains measured by diffraction experiments. In this study, the constitutive relationships (given in Eqns. 15, 16, 17, 21, 23 and 24) representing the dislocation interactions, strain aging and recovery were implemented in EPSC. The developed model is validated by applying the model to describe and predict the deformation response of a solid solution strengthened alloy during monotonic loading and during multi-step path loading.
III. Strain path dependence of AA5754-O: Experiments
III.1. Material description
The material of interest in this study is a commercially available AA5754-O sheet. The material used in this investigation was industrially processed AA5754-O annealed sheet, nominally 1 mm thick. The grain diameter in the rolling plane is approximately 40 μm. The alloy derives its strength from the solid solution strengthening, with magnesium atoms strongly interacting with dislocations. This interaction results in the dynamic strain aging during plastic straining even at room temperature, leading to serrated uniaxial flow stress and negative strain rate sensitivity (i.e., the material tends to be stronger during plastic deformation with a lower strain rate) (Cottrell, 1953; Iadicola et al., 2012; Picu, 2004). The strong interaction between dislocation lines and Mg solute atoms also delays the dynamic recovery during plastic straining. The crystallographic texture of the as-received (AR) condition was described by Banovic et al. (Banovic et al., 2008) and is used in this study. The initial texture condition combines recrystallization components (mainly Cube with intensity of about 4 times uniform (i.e., random)) and some retained rolling components (Brass and Copper orientations). The volume fractions of Brass and Copper components were almost identical, with intensities about 2 times uniform. Here we review the experimentally measured mechanical response, aging, and recovery, for a specific deformation history.
III.2. Experimental procedure
A three-step deformation/aging path is investigated here: (Step 1) separate sheets of as-received material are strained in a balanced biaxial (BB) deformation to multiple strain levels, followed by (Step 2) an unload and storage, and finally subjected to additional (Step 3) uniaxial (U) plastic straining. Various Step 2 aging conditions were investigated. The experimental data trends were used to determine key model parameters (Sects. IV.1 and IV.2) for all of these types of behavior over a selected range of applicability. The model predictions are then compared to the experimental results (Sect. IV).
Step 1 samples were plastically strained in balanced biaxial deformation similar to (Iadicola et al., 2008). The deformation was applied continuously to selected strain levels ranging from 11 % to 40 % von Mises equivalent strain. During Step 2, the specimens were unloaded and uniaxial samples were cut from each BB strained sample. The unloaded Step 2 samples were held at room temperature for various times between approximately 20 minutes and 6 months. The samples aged for 6 months were uniaxially strained as part of another study (Iadicola et al., 2012). The uniaxial deformation in that study included plastic straining followed by multiple elastic unload/reload cycles with intermediate holds in strain (with stress never less than 80 % of the as-received yield stress). This deformation history was needed for the X-ray diffraction (XRD) calibration (Iadicola et al., 2012). The same uniaxial data is used here with the elastic unload/reload portions removed for clarity. The results are used to assess the initial yield and hardening upon reloading after path change. All of the samples aged less than 6 months at room temperature were carefully monitored for temperature-time from the end of Step 1 deformation. After Step 1, the samples were immediately quenched to about 0 °C in an ice bath and placed in a −20 °C freezer, to prevent recovery. The BB strained specimens were raised to room temperature briefly during machining of the uniaxial samples by water-jet, and then were immediately returned to the ice bath and freezer. The reported recovery times for all of the water-jet cut samples includes the total time that the specimen was at room temperature from the end of Step 1 to the start of Step 3 testing. The samples with shortest recovery times (about 20 minutes) were removed from the freezer and placed in a room temperature water bath, and then tested to failure. Specimen with longer recovery times were removed from the freezer, brought to room temperature, and held there until uniaxial testing to failure. Step 3 deformation for samples aged ≈ 6 months was performed at average strain rates of the same order as the strain rates used between strain steps in the BB deformation. The uniaxial strain rate used for the samples aged 6 months was applied manually with the intent of quasi-static deformation, but the strain rate was not determined quantitatively.
III.3. Experimental results
Multiple sets of experimental data for the same material were used here to develop a more complete picture of the material behavior. Figure 2a and b present the true stress vs. true strain in the sheet rolling direction (RD) and in the transverse direction (TD) during balanced biaxial straining adopted from (Iadicola et al., 2008). The error bars associated with each experimental data point were calculated as the standard deviation of measurement uncertainties described in Iadicola et al. (Iadicola et al., 2008). The BB XRD results in each direction are fit by a Chaboche-type function ( σ = (a/b) × (1-exp(−bε))+c) (Chaboche, 2008). Fig. 2a-b shows the fitted curves, with a=25.3, b=0.073 and c=75 for BB stress in RD and with a=29.4, b=0.109 and c=78 for BB stress in the TD direction. Values interpolated at uniform strain increments from the curve fits were used to calculate von Mises equivalent stress and strain during monotonic BB straining. The same function was used to fit stress and strain for monotonic uniaxial loading along RD with following parameters: a=22.00, b=0.0983 and c=84 (Fig. 2c). The von Mises equivalent stress and strain curve during BB straining is used as a reference in Fig. 3, Fig. 4 and Fig. 5.
Figure 2:
(a) and (b) Experimental flow stresses during monotonic BB straining measured by X-ray diffraction method and with the Chaboche function fit. (a) Stress-strain curve in RD (direction 1 corresponds to RD). (b) Stress-strain curve in TD (direction 2 corresponds to TD). (c) Stress-strain curves during monotonic uniaxial loading along RD (URD).
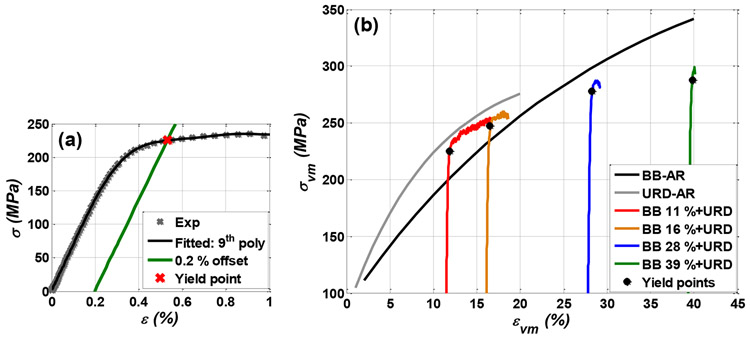
Figure 3:
(a) True stress-strain behavior of a BB strained sample during URD and its yield point corresponding to 0.2 %-strain offset. (b) von Mises equivalent flow stress of as-received (AR) samples during monotonic URD (grey line) and BB (black line) versus the flow stresses (and corresponding yield stresses) upon reloading after Step 1 BB straining up to various strain levels with a Step 2 static recovery time of 20 minutes.
Figure 4:
von Mises equivalent flow stress of as-received (AR) samples during monotonic URD (grey line) and BB (black line) versus the flow stresses (and corresponding yield stresses) upon reloading in Step 3 after Step 1 BB straining to various strain levels with a Step 2 static recovery time of 6 months.
Figure 5:
von Mises equivalent flow stress during monotonic BB straining versus the flow stresses upon reloading after BB straining up to various strain levels (29 % ± 1 %) with different Step 2 static recovery times (e.g., 20 minutes, 3 days, and 6 months).
Changing the strain path from BB (Step 1) to uniaxial tension (Step 3) significantly affects the plastic stress-strain response of the material because dynamic strain aging and dynamic recovery take place during the first step, and both static aging and static recovery occur during unloading in the second step, affecting the material behavior upon reloading in the third step. Here we focus on the material deformation response when changing path from BB to URD since a similar response was also observed when changing path from BB to uniaxial tension in TD. Depending on the degree of BB straining (Step 1) and the interruption time (Step 2), the yield stress of the material during reloading (Step 3) along the second path can be either higher or lower than stresses just before unloading (Figs. 3-6).
Figure 6:
Summary of yielding stresses of the AR material (), and of deformed samples as a function of Step 1 BB strains and of Step 2 static recovery times.
The yield stress is calculated as the stress of 0.2 % strain offset, Fig. 3a. A polynomial of degree 9 (Fig. 3a) was only used here to fit experimental data to help in finding the yield stress, i.e., the intersection between the 0.2 % strain offset and the fit curve. As Fig. 3b shows, with a short interruption time (i.e., the recovery time) of about 20 minutes, the yield stresses during URD reloading after BB straining of εvm ≤ 20 % are higher than they were before unloading (the red and orange curves to the left in Fig. 3b). In addition, the associated hardening rate of the flow stress during the third straining step is lower than in monotonic BB (or uniaxial) straining (Fig. 3b). A more detailed discussion on the influence of dynamic/static strain aging is given in Section III.1.2.
The yield stress of a sample reloaded uniaxially along RD after Step 1 BB straining up to εvm ≈ 16 % and after a Step 2 short interruption time of 20 minutes was only slightly higher than it was during BB straining (Fig. 3b), while samples deformed in Step 1 up to higher strains show lower yield stress than during the first step straining (Fig. 3b). Particularly, the yield stresses of the material upon URD reloading after BB straining to von Mises equivalent strains higher than 25 % are usually lower than those observed before unloading (Fig. 3b).
When pre-deformed samples were left in air at room temperature for sufficient periods of time, e.g., 3 days or 6 months, static recovery happens for all BB strain levels, resulting in lower yield strength and a higher hardening rate (compared to that of a short interruption time of 20 minutes) upon reloading (Figs. 4 and 5). The roles of dynamic recovery and static recovery are discussed in detail in Sect. III.1.3.
III.4. Discussions on the strain path dependence of AA5754-O
III.4.1. Influences of dynamic and static straining aging
The material behavior upon reloading Step 3 along the second path depends on the degree of BB straining in Step 1 and the recovery time in Step 2 because of the competition between aging and recovery during the Step 1 BB deformation and during unloading Step 2. The yield strength of the material can be either higher or lower than the flow stress of the first deformation step, depending on whether aging or recovery is dominant. For example, the yield strength upon URD reloading is higher than the stress just before unloading if the von Mises equivalent BB strain is less than ≈ 20 % for static recovery time of 20 minutes (Fig. 3b). In addition, the strain-hardening rate of the pre-deformed material is lower than that if the material would have been continuously loaded without path change (Fig. 3b). Since the material is strengthened by solid solution, the interaction between dislocation lines and solute atoms causes the DSA during the first strain step. The interaction restricts the cross slip activity of dislocations (leading to delayed dynamic recovery). Consequently, DSA is dominant during BB straining up to εvm of 20 %. The strong interaction between dislocations and solute atoms is further strengthened during unloading over a short period of time (i.e., the deformed material undergoes static aging). DSA during the Step 1, in conjunction with the static strain aging during short unloaded times (Step 2), affects the deformation response upon uniaxial reloading (Step 3). The strong interaction between dislocation lines and solute atoms requires higher stress to keep dislocations moving, resulting in higher yield stress. Strain aging also results in a lower hardening rate, i.e., when the velocity of dislocations increases, the aged materials softens and stress decreases due to the negative strain rate sensitivity associated with DSA (Cottrell, 1953). This explains why there is overshoot in the yield strength followed by a lower strain hardening rate during reloading of deformed material after Step 1 BB strain of εvm < 20 % and Step 2 static recovery time of 20 minutes. For larger Step 1 BB strains, dynamic recovery is increasingly active. Moreover, if the Step 2 static recovery time is sufficiently long, static recovery takes effect to further recover deformed samples. The dynamic (and/or static) recovery first balances out the aging, and then dominates during URD reloading.
III.4.2. Influence of dynamic/static recovery
Dynamic recovery during the BB deformation in Step 1 is increasingly active at larger strains where cross-slip is strongly active and promotes formation of dislocation substructures. Consequently, increasing the Step 1 BB strain levels can compensate for the influence of dynamic and static strain aging, leading to a reduction in the yield strength of deformed specimens upon reloading in Step 3. It explains why the yield stress of the pre-deformed material during URD reloading after BB strains higher than 20 % is usually lower than that before unloading (Figs. 3b).
If a BB strained sample is left at room temperature for a sufficient period of time during Step 2, static recovery occurs, which reduces their yield strength, and restores strain hardening and ductility (Figs. 4-6). During static recovery, (1) dislocations migrate, annihilate and form more stable configurations, and (2) solute atoms preferably diffuse into dense dislocation substructures to relax their strong interactions with individual dislocations (that were mobile during previous deformation). The reduction in dislocation density and the relaxation of interactions between dislocations and solute atoms cause a decrease in yield strength of deformed samples. However, the formation of more stable configurations of dislocations provides an effective means to restrict the movement of dislocations during reloading, resulting in an increase in hardening rates when recovered samples are reloaded (Figs. 4, 5).
The yield stresses of the AR sample and samples deformed in Step 1 to various strains and after undergoing different static recovery times in Step 2 are summarized and shown in Fig. 6. The yield stress during the second straining after a BB strain of ≈16 % and after static recovery of 3 hours is omitted to avoid obscuring the curves for static recovery times of 20 minutes and 3 days. The yield stress of the AR sample does not change with respect to the static recovery time because the AR sample was over-aged.). The experimentally measured yield stresses are fit using a power law function (σy = (a/b)×(1-exp(-b×εpre))+c) (dark green lines in Fig. 6).
IV. Strain path dependence of AA5754-O: Modeling
IV.1. Parameter identification for monotonic loading
The following simulation was done with the same crystallographic texture as Hu et al. used for the AR material in our previous studies (Hu et al., 2012; Iadicola et al., 2012). We fit the true stress-true strain curve in the 1 (RD) direction during the monotonic BB straining by the modified EPSC code. The average dislocation density is typical from 1010 m−2 to 1012 m−2 for well annealed metallic materials (Hull and Bacon, 2001). For annealed FCC materials, the initial value of average dislocation densities in all individual slip systems is low. The initial value of the necessary dislocation density to accommodate the plastic incompatibility between high-density regions and low-density regions in the AR condition is also not high (it can be a small multiple of ) because the plastic deformation incompatibility is small for well-annealed materials. Thus =1.0 x1011 m−2 and =5.0 x1011 m−2 were used for all slip systems in this study. Values of the storage rate (k1) for ρf and ρn_sub are, respectively, 21 and 50 which are in the range of [8, 80] as suggested by Kocks (Kocks, 1966). The evolution of the similitude factor due to dislocation rearrangement is represented by Eqn. 16. The saturation value () of the similitude factor is 10, which is the maximum value in the suggested range when well-organized dislocation cellular structures are present (Sauzay and Kubin, 2011). In addition, because the plastic deformation incompatibility is small for well-annealed materials, we used an initial value of the similitude factor, .
Concerning the strength of dislocation junctions, the square root of the strength of dislocation junctions is from 0.1 to 0.6 (Mughrabi, 1983). The square root of the average strength of dislocation junction is about 0.3 (Sauzay and Kubin, 2011). The strength of collinear junctions (αCOL) is assumed to be highest as suggested by Madec et al. (Madec et al., 2003), followed by the strength of LC junctions. It is widely believed that the H, COP and GL junctions are slightly stronger than the self-interaction junctions, but weaker than for LC (Franciosi et al., 1980). Values for αCOL, αG, αH, αLC, and αself are taken to be 0.25, 0.09, 0.09, 0.16, and 0.03, respectively. The kinematic hardening parameter, αback, that accounts for the relationship between the yield stress during reverse loading and that during forward loading strongly depends on the initial microstructural condition, the degree of prestraining and the type of reverse loading. For example, the difference between yield stresses during forward loading and reverse loading (e.g., the Bauschinger effect) was also observed to be larger for materials having secondary particles than those without particles (Atkinson et al., 1974; Moan and Embury, 1979; Stout and Rollett, 1990). A compilation of a measurement of Bauschinger effect for various non-shearable precipitate FCC alloys during tension/compression cyclic test with the zero mean strain (Table V in (Stoltz and Pelloux, 1976)) shows that a reduction in the yield stress during reverse loading was about from 0.3 to 0.6 of during forward loading. In case of unloading without compression reverse loading, the yield stress reduction could be half of that during the full tension/compression cyclic test, i.e., the reduction in yield stress is approximately of 0.15-0.3. Therefore, a reasonable range for the stress reduction for materials without precipitates is 0.0-0.3, i.e., αback = 0.7 − 1.0. In this present problem, αback = 0.8 was used. The value of to take account for DSA is often found to be close to 2 for FCC interstitial alloys exhibiting DSA (Lindgren et al., 2008; Pham, 2013). Therefore, a value of 2 was used in this model.
The friction stress due to the lattice in FCC is usually negligible. The strong interaction between dislocations and solute atoms mainly contributes to drag stress. Consequently, , the maximum pinning stress due to the dislocation/solute atom interaction. The identification of needs to be tuned to that of . It is shown later in the Sect. IV.2 that and are estimated to be about 30 MPa, which is a typical value for AlMg alloys (Kubin et al., 1988; Kubin et al., 1992). The values m and n in Eqns. 15, 17 that represent the temperature dependence are m=0.37 and n=1.37. These are the same as those used to model the thermal dependence of flow stress in the DSA regime of another interstitial FCC alloy (Pham, 2013). These values are also close to those used in (Lindgren et al., 2008). The modified EPSC code with the parameters given above accurately fits the experimental true stress-strain in the RD (1) direction during BB straining (Fig. 7a). The von Mises equivalent stress-strain is re-calculated by the current model, and given in Fig. 7a. The re-calculation gives the same result as obtained by using the Chaboche model (Fig. 7a). It shows that the model implemented in EPSC can describe very well the deformation behavior of the material during monotonic loading. With the same identified values, it also gives a reasonable prediction of stress-strain behavior during URD (Fig. 7b).
Figure 7:
(a) Stress-strain curves during monotonic BB straining fitted by Chaboche and EPSC. (b) Flow stress during monotonic URD: Experimental and Chaboche fitted data versus predicted data by EPSC with parameters identified from the fitting in figure (a).
IV.2. Parameter identification for multi-step loading
Because the experimental Step 1 BB strain levels are not exactly the same, to calculate the evolution of the fraction residual strain hardening (R), it is necessary to interpolate values of yield stress at same BB strain level after different static recovery times. The fitted curves, Fig. 6, permit interpolation of yield stress at the same BB strains to calculate R (Fig. 9). In addition, static recovery depends on the BB strain. Fitting the measured evolution of the fraction of residual yield strength (R) during static recovery of deformed samples after Step 1 straining by Eqn. 21 gives values (and their average values) for model parameters describing the static recovery response (Table 2).
Figure 9:
Modeling of the increase in the yield strength due to the static aging.
Table 2:
Values of model parameters for static recovery
| Parameters | von Mises equivalent strain in Step 1 | Values | Average |
|---|---|---|---|
| ηrec_static | 11 % | 0.128 | 0.155 |
| 16 % | 0.139 | ||
| 30 % | 0.169 | ||
| 40 % | 0.185 | ||
| r | 11 % | 36339 | 27431 |
| 16 % | 32522 | ||
| 30 % | 22330 | ||
| 40 % | 18531 |
Because the SSA relates to dislocation conditions, the SSA is strain history dependent. The DSA and dislocation evolution during the Step 1 deformation influence the SSA that occurs during a short period of Step 2 interruption time. As mentioned before, the density of mobile dislocations is less than that of the forest dislocations. In this development, the initial density of mobile dislocations used for Eqn. 20 is . However, because of their high mobility, mobile dislocations annihilate faster than forest dislocations. Here we used . The stress amplitude of the stress flow serration, which is about 10 MPa for AA5754-O at room temperature, relates to the maximum pinning stress, . As reported by Kubin et al. (Kubin et al., 1988; Kubin et al., 1992), should be higher than the stress amplitude of the serration.
The constitutive relationships described by Eqns. 21, 23 and 24 are implemented in the modified EPSC to fit the flow stresses of two Step 1 deformed samples. Both samples were prestrained to εvm = 11 %, but one underwent static recovery of 20 minutes (the most far left curve in Fig. 3b), another experienced static recovery of 6 months (the most far left curve in Fig. 4). Parameter values to describe the stress-strain behavior during the BB straining (Step 1) are the same as those identified in Sect. III.2.1. The parameters for Eqn. 22 to simulate the influence of the static recovery are the averages (column 4 in Table 2) of the fitted values for all Step 1 BB strain levels. The fitting gives =30 MPa (which is also a typical value reported for AlMg alloys (Kubin et al., 1988; Kubin et al., 1992)) hage = 5 and hre = 12.
With the parameters identified above, Eqn. 21 is able to describe the BB strain dependence of SSA as shown in Fig. 9. The strain dependence of SSA shown in Fig. 9 is classified as the type I dependence that is often seen in interstitial FCC alloys or in hexagonal-closed-packed Ti+O alloys as discussed by Kubin et al. (Kubin et al., 1992).
The key parameters of the constitutive relationships (used in Eqns. 15, 16, 17, 21, 23 and 24) representing the dislocation interactions, strain aging and recovery identified in Sects. IV.1 and IV.2 for this alloy are given in Table 3 (Note: The detailed information of suggested ranges for important model parameters obtained from literature is given in Appendix).
Table 3:
Summary of identified values of model parameters
| Parameters | Equation(s) | Values (References) |
|---|---|---|
| αCOL, αG, αH, αLC, αself, αback | 15, 17 | 0.25, 0.09, 0.09, 0.16, 0.03, 0.8, respectively (Sects. II.2, IV.1) |
| b | 15, 16, 17, 21 | 2.546x10−10 m |
| ηdyn_rec = ηnon_sub | 15, 17 | 0.5 |
| , | 15, 17, 21 | 106 s−1 (Frost and Ashby, 1982), 10−5 s−1, , respectively |
| 15 | 21 (Sect. IV.1 and (Kocks, 1966)) | |
| 15 | 50 (Sect. IV.1 and (Kocks, 1966)) | |
| μ | 15, 17 | 25.333 GPa |
| m, n | 15, 17 | 0.37, 1.37, respectively (Sect. IV.1 and (Pham, 2013)) |
| T | 15, 17 | 300 K |
| 15 | 30 MPa (Sects. IV.1, IV.2, and (Kubin et al., 1988; Kubin et al., 1992)) | |
| Ksimi_0, Ksimi_sat | 16 | 2.5, 10, respectively (Sect. IV.1 and (Sauzay and Kubin, 2011)) |
| Cs / Cs,0 | 17 | 2 (Sect. IV.1 and (Lindgren et al., 2008; Pham, 2013)) |
| 17, 21 | 1.0 x1011 m−2 for all slip systems | |
| 17, 21 | 5.0 x1011 m−2 for all slip systems | |
| 21 | 5.0 x1010 m−2 for all slip systems | |
| td_s | 21 | 40 s (Sect. IV.2 and (Kubin et al., 1988; Kubin et al., 1992)) |
| 21 | 30 MPa (Sects. IV.1, IV.2 and to (Kubin et al., 1988; Kubin et al., 1992)) | |
| ηrec_static | 23 | 0.155 (Sect. IV.2, Fig. 8 and Table 2) |
| r | 23 | 27431 (Sect. IV.2, Fig. 8 and Table 2) |
| hage | 24 | 5 (Sect. IV.2) |
| hre | 24 | 12 (Sect. IV.2) |
IV.3. Results and Discussion
The developed model with the identified parameters can fit the stress-strain deformation behavior of AA5754-O for monotonic BB straining equally as well as the Chaboche model, Fig. 7a. It also gives a good prediction of the true stress-strain response during URD (i.e., when loading condition varies), Fig. 7b. This demonstrates that the current choice of the strength of dislocation junctions, with COL being the strongest (Table 3), enables the material behavior along another direction to be modeled reasonably well. However, other choices of the strength of dislocation interactions may provide a better prediction of the material behavior during URD. In particular, our recent study (Pham et al., 2014b) shows that incorporation of dislocation multi-junctions in constitutive laws provides substantial improvement in the prediction of stress-strain response when the loading boundary condition varies, based on only a single set of parameter values identified from a fit of the stress-strain curve during BB straining. One possibility to improve the predictive capability of the model is, therefore, to include the higher-order interactions of dislocations in the constitutive laws.
Concerning the plastic deformation behavior of the material during multi-step straining with a short static recovery time of 20 minutes in Step 2, the developed model accurately describes the overshoot in the yield stress (Fig. 10). It also predicts well the decreases in yield stresses of deformed samples during Step 3 URD straining (Fig. 11) after being strained in BB, Step 1, to various strain levels and after long static recovery of 6 months during Step 2. In particular, the model captures not only the elasto-plastic transient but also the hardening behavior during Step 3 URD straining for all considered Step 1 BB strains and Step 2 static recovery times (Figs. 10 and 11). This description of the strain path dependence of AA 5754-O is improved relative to models that omit strain aging and static recovery phenomena (Iadicola et al., 2012). Together with our previous study (Iadicola et al., 2012), it demonstrates that, without considering static aging and static recovery during the interruption between loading paths, constitutive models cannot simulate the strain path dependence of solid solution strengthened materials. As shown in Fig. 11, the model predicts the plastic deformation behavior of samples recovered after 6 months better for BB straining to 20 % and 30 % than for BB straining to 10 % and 40 %. The reason for this difference is that the values of parameters for Eqn. 23 to account for the influence of the static recovery are the averages (column 4 in Table 2) of the fitted values for all BB strain levels.
Figure 10:
(a)-(b) Modeling of flow stresses during monotonic BB straining and during multi-step straining with static recovery time of 20 minutes in Step 2.
Figure 11:
(a)-(c). Modeling of flow stresses during multi-step straining with a Step 2 static recovery of 6 months.
V. CONCLUSIONS
It is shown in our previous work (Iadicola et al., 2012) that most of latent hardening models including the kinematic hardening cannot capture the variation of yield stress and hardening behavior of solid solution strengthened alloys during multi-step strains. The reason is that dislocations not only interact strongly between themselves but also with solute atoms. This strong dislocation/solute atom interaction is responsible for a number of microstructural phenomena (dynamic/static strain aging and dynamic/static recovery) during plastic straining, unloading, holding and reloading. In contrast to the strain aging that increases the yield stress and lowers hardening rate, recovery reduces the yield stress and restores the hardening rate. Consequently, it is necessary to consider dynamic/static strain aging and dynamic/static recovery occurring during previous deformation steps and interruption in order to model accurately the complex behavior of solid solution strengthened alloys after changes in strain path. In this paper, thermally activated constitutive laws (Eqns. 15, 16, 17, 21, 23 and 24) are developed by including both dislocation/dislocation and dislocation/solute atoms interactions in order to account for latent/kinematic hardening, dynamic recovery, dynamic strain aging during plastic deformation, and static strain aging and static recovery during the interruption between different loading paths. The developed model is then applied to simulate the complex behavior of AA5754-O that underwent three loading steps. This application shows that the model not only accurately simulates the variation in the yield stress, but also the hardening behavior during multi-step loading paths that involve balanced biaxial straining, unloading, holding and reloading along other directions.
VI. ACKNOWLEDGEMENTS
Dr. Carlos Tomé is thanked for providing the EPSC program. This work was supported by the NIST Center for Automotive Lightweighting. The financial support of Materials Genome Initiative at National Institute of Standards and Technology is also acknowledged.
VII. APPENDIX
| Parameters | Equation(s) | Suggested ranges obtained from literature |
|---|---|---|
| αCOL, αG, αH, αLC, αself | 15, 17 | 0.1-0.6 (Mughrabi, 1983; Sauzay and Kubin, 2011). References for the order of the strength of dislocation junction types are (Cottrell, 1952; Dupuy and Fivel, 2002; Franciosi et al., 1980; Hirth, 1961; Lomer, 1951; Madec et al., 2003; Martinez et al., 2008; Picu and Soare, 2010) |
| αback | 15, 17 | 0.7-1.0 for FCC materials without precipitates (Atkinson et al., 1974; Moan and Embury, 1979; Stoltz and Pelloux, 1976; Stout and Rollett, 1990), also refer to Sect. IV.1 |
| ηdyn_rec = ηnon_sub | 15, 17 | 0.2-1.0 for forest dislocations; small and weak precipitates (Table 2.1 in (Frost and Ashby, 1982)) |
| 15, 17, 21 | 106 s−1 (Section 2.2 in (Frost and Ashby, 1982)) | |
| , | 15 | from 8 to 80 (Kocks, 1966) |
| m, n | 15, 17 | 0≤m≤1, 1≤n≤2, respectively (Eqn. 2.8 in (Frost and Ashby, 1982)) |
| τsat_drag, | 15, 21 | , and should be higher than the magnitude of stress serration (Kubin et al., 1988; Kubin et al., 1992) (also refer to discussions in Sects. IV.1, IV.2 in this present study) |
| Ksimi_sat | 16 | 5-10 (Sauzay and Kubin, 2011) |
| Cs / Cs,0 | 17 | ≈2 (for interstitial alloys like austenitic stainless steels (Lindgren et al., 2008; Pham, 2013)) |
| , , | 17, 21 | Average total dislocation density is typical from 1010 m−2 to 1012 m−2 for well annealed metallic materials (Hull and Bacon, 2001). As described in Sect. IV.1 and IV. 2, the order of these densities is |
| td_s | 21 | from 1 s to 100 s (Kubin et al., 1988; Kubin et al., 1992) |
| ηrec_static | 23 | < 0.2 for lattice resistance, solution hardening (Table 2.1 in (Frost and Ashby, 1982), also refer to Eqn. 22, Sect. IV.2, Fig. 8 and Table 2 in this present study) |
Figure 8:
Modeling of residual yield strength of deformed materials during static recovery. Note: the yield stress during Step 3 straining after Step 1 BB straining of ≈16 % and Step 2 static recovery of 3 hours is not shown in Fig. 4 or 5 to avoid the overlay with those after 20 minutes and 3 days in the Figures.
Footnotes
It should be noted that αij is generally reported to be rather smaller than 1. Therefore, we set . Nevertheless, still smaller than 1 with common values of Cs / Cs0 for FCC materials in literature.
VIII. REFERENCES
- Atkinson JD, Brown LM, Stobbs WM, 1974. Work-Hardening of Copper-Silica .4. Bauschinger Effect and Plastic Relaxation. Philos Mag 30, 1247–1280. [Google Scholar]
- Devincre B, Hoc T, Kubin L, 2008. Dislocation Mean Free Paths and Strain Hardening of Crystals. Science 320. [DOI] [PubMed] [Google Scholar]
- Banovic SW, Iadicola MA, Foecke T, 2008. Textural development of AA 5754 sheet deformed under in-plane biaxial tension. Metall Mater Trans A 39A, 2246–2258. [Google Scholar]
- Barlat F, Ha JJ, Gracio JJ, Lee MG, Rauch EF, Vincze G, 2013. Extension of homogeneous anisotropic hardening model to cross-loading with latent effects. Int J Plasticity 46, 130–142. [Google Scholar]
- Beyerlein IJ, Tome CN, 2007. Modeling transients in the mechanical response of copper due to strain path changes. Int J Plasticity 23, 640–664. [Google Scholar]
- Beyerlein IJ, Tomé CN, 2008. A dislocation-based constitutive law for pure Zr including temperature effects. Int J Plasticity 24, 867–895. [Google Scholar]
- Chaboche JL, 2008. A review of some plasticity and viscoplasticity constitutive theories. Int J Plasticity 24, 1642–1693. [Google Scholar]
- Cheng JY, Nemat-Nasser S, Guo WG, 2001. A unified constitutive model for strain-rate and temperature dependent behavior of molybdenum. Mechanics of Materials 33, 603–616. [Google Scholar]
- Cottrell A, 1953. Dislocations and plastic flow in crystals. Clarendon Press, Oxford. [Google Scholar]
- Cottrell AH, 1952. The Formation of Immobile Dislocations during Slip. Philos Mag 43, 645–647. [Google Scholar]
- Cottrell AH, Bilby BA, 1949. Dislocation Theory of Yielding and Strain Ageing of Iron. Proceedings of the Physical Society of London Section A 62, 49–62. [Google Scholar]
- Dupuy L, Fivel MC, 2002. A study of dislocation junctions in FCC metals by an orientation dependent line tension model. Acta Mater 50, 4873–4885. [Google Scholar]
- Essmann U, Mughrabi H, 1979. Annihilation of Dislocations during Tensile and Cyclic Deformation and Limits of Dislocation Densities. Philos Mag A 40, 731–756. [Google Scholar]
- Estrin Y, 1998. Dislocation theory based constitutive modelling: foundations and applications. Journal of Materials Processing Technology 80-1, 33–39. [Google Scholar]
- Estrin Y, Braasch H, Brechet Y, 1996. A dislocation density based constitutive model for cyclic deformation. Journal of Engineering Materials and Technology-Transactions of the Asme 118, 441–447. [Google Scholar]
- Franciosi P, 1985. The Concepts of Latent Hardening and Strain-Hardening in Metallic Single-Crystals. Acta Metallurgica 33, 1601–1612. [Google Scholar]
- Franciosi P, Berveiller M, Zaoui A, 1980. Latent Hardening in Copper and Aluminum Single-Crystals. Acta Metallurgica 28, 273–283. [Google Scholar]
- Fressengeas C, Beaudoin AJ, Lebyodkin M, Kubin LP, Estrin Y, 2005. Dynamic strain aging: A coupled dislocation—Solute dynamic model. Materials Science and Engineering: A 400–401, 226–230. [Google Scholar]
- Frost HJ, Ashby MF, 1982. Deformation-mechanism maps the plasticity and creep of metals and ceramics. Pergamon Press, Oxford a.o. [Google Scholar]
- Gérard C, Cailletaud G, Bacroix B, 2013. Modeling of latent hardening produced by complex loading paths in FCC alloys. Int J Plasticity 42, 194–212. [Google Scholar]
- Gómez-García D, Devincre B, Kubin LP, 2006. Dislocation Patterns and the Similitude Principle: 2.5D Mesoscale Simulations. Phys Rev Lett 96, 125503. [DOI] [PubMed] [Google Scholar]
- Hirth JP, 1961. On Dislocation Interactions in Fcc Lattice. Journal of Applied Physics 32, 700–&. [Google Scholar]
- Hu L, Rollett AD, Iadicola M, Foecke T, Banovic S, 2012. Constitutive Relations for AA 5754 Based on Crystal Plasticity. Metall Mater Trans A 43A, 854–869. [Google Scholar]
- Hull D, Bacon DJ, 2001. Introduction to dislocations, 4th ed. Butterworth-Heinemann, Oxford Oxfordshire ; Boston. [Google Scholar]
- Iadicola MA, Foecke T, Banovic SW, 2008. Experimental observations of evolving yield loci in biaxially strained AA5754-O. Int J Plasticity 24, 2084–2101. [Google Scholar]
- Iadicola MA, Hu L, Rollett AD, Foecke T, 2012. Crystal plasticity analysis of constitutive behavior of 5754 aluminum sheet deformed along bi-linear strain paths. Int J Solids Struct 49, 3507–3516. [Google Scholar]
- Kang J, Wilkinson DS, Embury JD, Jain M, Beaudoin AJ, 2005. Effect of type-B Portevin–Le Chatelier bands on the onset of necking in uniaxial tension of strip cast AA5754 sheets. Scripta Mater 53, 499–503. [Google Scholar]
- Kitayama K, Tome CN, Rauch EF, Gracio JJ, Barlat F, 2013. A crystallographic dislocation model for describing hardening of polycrystals during strain path changes. Application to low carbon steels. Int J Plasticity 46, 54–69. [Google Scholar]
- Kocks UF, 1966. A Statistical Theory of Flow Stress and Work-Hardening. Philos Mag 13, 541–&. [Google Scholar]
- Kocks UF, Argon AS, Ashby MF, 1975. Thermodynamics and Kinetics of Slip. Progress in Materials Science 19, 1–281. [Google Scholar]
- Kocks UF, Mecking H, 1979. A Mechanism for Static and Dynamic Recovery, in: Haasen P, Gerold V, Kostorz G (Eds.), Fifth Int. Conf. on the Strength of Metals and Alloys, pp. 345–350. [Google Scholar]
- Kocks UF, Tomé CN, Wenk HR, 1998. Texture and Anisotropy: Preferred Orientations in Polycrystals and their Effect on Materials Properties. Cambridge University Press, Cambridge, U.K. [Google Scholar]
- Kubin LP, Chihab K, Estrin Y, 1988. The rate dependence of the portevin-Le chatelier effect. Acta Metallurgica 36, 2707–2718. [Google Scholar]
- Kubin LP, Estrin Y, Perrier C, 1992. On Static Strain Aging. Acta Metall Mater 40, 1037–1044. [Google Scholar]
- Lebensohn RA, Tomé CN, 1993. A Self-Consistent Anisotropic Approach for the Simulation of Plastic-Deformation and Texture Development of Polycrystals - Application to Zirconium Alloys. Acta Metall Mater 41, 2611–2624. [Google Scholar]
- Lindgren LE, Domkin K, Hansson S, 2008. Dislocations, vacancies and solute diffusion in physical based plasticity model for AISI 316L. Mechanics of Materials 40, 907–919. [Google Scholar]
- Lomer WM, 1951. A Dislocation Reaction in the Face-Centred Cubic Lattice. Philos Mag 42, 1327–1331. [Google Scholar]
- Louat N, 1981. On the Theory of the Portevin-Le Chatelier Effect. Scripta Metall Mater 15, 1167–1170. [Google Scholar]
- Ma A, Roters F, 2004. A constitutive model for fcc single crystals based on dislocation densities and its application to uniaxial compression of aluminium single crystals. Acta Mater 52, 3603–3612. [Google Scholar]
- Madec R, Devincre B, Kubin L, Hoc T, Rodney D, 2003. The role of collinear interaction in dislocation-induced hardening. Science 301, 1879–1882. [DOI] [PubMed] [Google Scholar]
- Martinez E, Marian J, Arsenlis A, Victoria M, Perlado JM, 2008. Atomistically informed dislocation dynamics in fcc crystals. J Mech Phys Solids 56, 869–895. [Google Scholar]
- Mecking H, Kock UF, Fischer H, 1976. Hardening, Recovery, and Creep in FCC Mono- and Polycrystals, Int. Conf. on the Strength of Metals and Alloys, Nancy, France, pp. 334–339. [Google Scholar]
- Moan GD, Embury JD, 1979. Study of the Bauschinger Effect in Al-Cu Alloys. Acta Metallurgica 27, 903–914. [Google Scholar]
- Mughrabi H, 1983. Dislocation wall and cell structures and long-range internal stresses in deformed metal crystals. Acta Metall. 31. [Google Scholar]
- Neil CJ, Wollmershauser JA, Clausen B, Tomé CN, Agnew SR, 2010. Modeling lattice strain evolution at finite strains and experimental verification for copper and stainless steel using in situ neutron diffraction. Int J Plasticity 26, 1772–1791. [Google Scholar]
- Nes E, 1995. Recovery Revisited. Acta Metall Mater 43, 2189–2207. [Google Scholar]
- Orowan E, 1940. Problems of plastic gliding. Proceedings of the Physical Society 52, 8. [Google Scholar]
- Pham M-S, Holdsworth S, 2014. Evolution of Relationships Between Dislocation Microstructures and Internal Stresses of AISI 316L During Cyclic Loading at 293 K and 573 K (20 °C and 300 °C). Metall and Mat Trans A 45, 738–751. [Google Scholar]
- Pham MS, 2013. Fatigue behaviour of steel AISI 316L: Mechanical response, Microstructural evolution, Fatigue crack growth & Physically-based constitutive modelling. Diss. ETH No. 20864, ETH Zurich, Zurich, p. 252. [Google Scholar]
- Pham MS, Holdsworth SR, 2012. Dynamic strain ageing of AISI 316L during cyclic loading at 300°C: Mechanism, evolution, and its effects. Mat. Sci. Eng. A 556, 122–133. [Google Scholar]
- Pham MS, Holdsworth SR, Janssens KGF, Mazza E, 2013. Cyclic deformation response of AISI 316L at room temperature: mechanical behaviour, microstructural evolution, physically-based evolutionary constitutive modelling. Int. J. of Plasticity, 47 (2013), 143–164. [Google Scholar]
- Pham MS, Hu L, Iadicola M, Creuziger A, Rollett AD, 2014a. The strain path dependence of plastic deformation response of AA5754: Experiment and modeling, NUMISHEET 2014. AIP Conference Proceedings, Melbourne, Australia. [Google Scholar]
- Pham MS, Rollett AD, Creuziger A, Iadicola MA, Foecke T, 2014b. Constitutive Modeling Based on Evolutionary Multi-Junctions of Dislocations, Key Engineering Materials, pp. 1771–1776. [Google Scholar]
- Picu RC, 2004. A mechanism for the negative strain-rate sensitivity of dilute solid solutions. Acta Mater 52, 3447–3458. [Google Scholar]
- Picu RC, Soare MA, 2010. Asymmetric dislocation junctions exhibit a broad range of strengths. Scripta Mater 62, 508–511. [Google Scholar]
- Puschl W, 2002. Models for dislocation cross-slip in close-packed crystal structures: a critical review. Progress in Materials Science 47, 415–461. [Google Scholar]
- Sauzay M, Kubin LP, 2011. Scaling laws for dislocation microstructures in monotonic and cyclic deformation of fcc metals. Progress in Materials Science 56, 725–784. [Google Scholar]
- Schoeck G, 1994. The Interaction of Dislocations and Planar Faults in Solids. Phil Mag Lett 69, 131–134. [Google Scholar]
- Stoltz RE, Pelloux RM, 1976. The Bauschinger Effect in Precipitation Strengthened Aluminum Alloys. Metall and Mat Trans A 7A, 1295–1306. [Google Scholar]
- Stout MG, Rollett AD, 1990. Large-strain Bauschinger effects in fcc metals and alloys. MTA 21, 3201–3213. [Google Scholar]
- Taylor GI, 1938. Plastic strain in metals. Journal of the Institute of Metals 62, 307–324. [Google Scholar]
- Thompson N, 1953. Dislocation Nodes in Face-Centred Cubic Lattices. Proceedings of the Physical Society of London Section B 66, 481–492. [Google Scholar]
- Turner PA, Tomé CN, 1994. A study of residual stresses in Zircaloy-2 with rod texture. Acta Metall Mater 42, 4143–4153. [Google Scholar]
- Van den Beukel A, Kocks UF, 1982. The Strain Dependence of Static and Dynamic Strain-Aging. Acta Metallurgica 30, 1027–1034. [Google Scholar]