Resampling and deconvolution of linear time-of-flight records for enhanced protein profiling

Abstract

We have developed a peak deconvolution strategy that is applicable to the full mass range of a time-of-flight (TOF) spectrum. This strategy involves resampling a spectrum to create a time series that has equal peak widths (in time) across the entire spectrum, and then using the deconvolution filters we have previously described. We use this technique to deconvolve the protein mass spectra for blood serum and cell lysates acquired on three separate TOF instruments. Following deconvolution, we resolve spectral structures consistent with expected events such as multiply charged ions, matrix adducts and post-translational protein modifications. The deconvolution procedure produces a 40% improvement in the resolution and enhanced experimental sensitivity over the full length of the linear TOF record, up to m/z 150 000. This approach is particularly appropriate for automated data analysis and peak detection in dense TOF spectra.

Time-of-flight mass spectrometry (TOFMS) is a promising approach for proteomic analysis of complex samples such as bodily fluids or cell assays.^1–3 It currently provides a major data source for many national cancer proteomics initiatives such as the Early Detection Research Network, the Human Proteome Organization and the Cancer Biomedical Informatics Grid. Although there are many up-front strategies to reduce unwanted proteins or to enhance the yield of desired proteins, the spectra are nevertheless very dense, having many overlapping mass spectrum lines.

Ions in survey MS are typically produced by matrix-assisted laser desorption/ionization (MALDI), which imposes limitations on resolution due to the relatively broad distribution of initial velocities.⁴ Delayed ion extraction is usually employed in linear TOF to enhance mass accuracy over a broad mass range by focusing velocity distribution with the optimal time-lag.⁵ With such focusing, mass resolution slowly increases before the optimum, and slowly decays after it. MALDI byproducts, like matrix adducts and neutral losses, may additionally crowd the spectra by the overlap with the precursor ion peaks.

The high spectral density means it is essential to use rapid peak-finding routines when using survey TOFMS for biomarker discovery. Similarly, it is also important that any peak-finding routines to be used in these high-throughput sample analyses do not require that many parameters be optimized. Thus, to use automated peak-finding routines, high density survey studies present two competing needs. First, the data usually requires smoothing to prevent automated peak-finding routines from finding false peaks where the noise significantly deviates from its average value. Second, the data could benefit from deconvolution procedures that can insure the optimum instrument resolution. We previously developed a series of TOF data filters that can simultaneously smooth and deconvolve data.⁶ In related work,⁷ we determined which filter parameters produce an optimal filtered spectrum, minimizing filtered noise with simultaneously maximized peak narrowing. However, those filters could only be applied to the spectral region where all mass peaks had approximately the same number of time points. Fortunately, this region coincides with time-lag optimization range in TOF survey spectra, and is typically large (m/z 2000–10 000) under optimal delayed extraction conditions.⁵

In this paper, we extend these same filtering techniques to enhance the sensitivity and resolution of TOFMS data over the full range, well beyond the time-lag optimization region. We illustrate the generality and wide applicability of these new procedures by smoothing and deconvolving data from three different linear TOF instruments, taken under three different sets of experimental conditions. In each case, we start with a simple characterization of the instrumental function for the experimental linear TOF record over the full mass range. We then employ a spectrum resampling strategy that recovers a constant point density per peak by summing the data from adjacent points. This resampling procedure increases the signal without appreciably increasing the noise, thereby enhancing the sensitivity for the broad peaks of heavy ions. Finally, we apply the deconvolution filtering process to increase the spectrum resolution and further enhance the signal-to-noise ratio, facilitating peak detection. These improvements provide us with spectra that are tailor-made for automated peak finding, and have sufficient precision to discriminate between mass shifts consistent with multiply charged states, chemical adducts and protein post-translational modifications in the deconvolved spectra of epithelial cell lysates and pooled serum. The results demonstrate the feasibility for performing adduct and charge deconvolution for profiled proteins from complex body fluids, ultimately achieving a quantification of the profiling spectra for biologically important species over a range greater than m/z 150 000.

EXPERIMENTAL

Mass spectrometry

Data acquisition

The data was acquired as .XML files from each of the experimental instruments. There were three experimental data sets derived from two laboratories, Eastern Virginia Medical School (EVMS) and the Centers for Disease Control and Prevention (CDC, CAMDA06, ftp.camda.duke.edu/CAMDA06_DATASETS/). Two sets of spectral data were derived from pooled serum samples collected at EVMS and the CDC on IMAC-Cu (immobilized copper) and NP20 (normal phase) affinity capture surfaces, respectively. The third data set for epithelial cell lysates was derived from EVMS with WCX2 (weak cationic exchange) surface. Sample preparation and data acquisition protocols for the three data sets are described in detail elsewhere^8,9 (CDC 2005, protocols.) The XML files contain all experimental parameters in addition to the original, unprocessed data. Each of the three data sets comes from a separate commercial linear TOF spectrometer (PBS II or PBSc; Ciphergen, Inc., Fremont, CA, USA) and have different affinity surface chemistry, different time-lag and different laser power. For the CDC pooled serum spectrum, the mass deflector was set at m/z 4000, and the delayed extraction optimized in the mass range between m/z 7000–50 000. The spectra from the epithelial cell lysates were collected with the highest laser intensity and detector gain and had time-lag focusing optimized between m/z 3000–50 000. The spectra for the pooled serum from EVMS used a laser intensity setting similar to CDC data set, and time-lag focusing optimized between m/z 2000–20 000. Typically, each average spectrum included about 200 laser shots on 12–15 subpositions on one sample spot. The nominal instrumental mass resolution for these TOF spectra was between 350 and 650 with maximum at the optimal time-lag, typically in the middle of the optimization range. The summed spectral intensities after multiple shots were recorded as integers, sampled every 4 ns.

Mass scale calibration

For the EVMS samples, we used an external calibration from a seven-peptide mixture, run on a normal-phase NP20 chip during the same week as the experimental samples. For all samples, we converted to a mass axis with a quadratic equation:

$$m/z=ak{\left(t-t_0\right)}^2+b$$ (1)

for the mass range from m/z 1–150 000, where a, k, t₀, and b are calibration constants. (The manufacturer-supplied k parameters were the eight calibration corrections for each spot on a chip.) The a, t₀, and b calibration constants were optimized by a linear regression for 3–5 peaks in the spectrum of the calibration mixture. Although the heaviest calibration mass was below 7 kDa, we applied the calibration equation globally over the full experimental mass range without further recalibration. For the CDC sample, calibration constants were obtained from .XML data file, and TOF to m/z conversion performed according to Eqn. (1).

Data processing

Peak shape analysis

Peaks in all three sets of experimental TOF data were well represented by an asymmetric line shape with a half-Gaussian rising edge and a half-Lorentzian falling edge, with the same width parameter, τ, as defined in Eqn. (2):

$$\frac{S}{S_0}=\{\begin{array}{ll}{e}^{-\frac{{\left(t-t_0\right)}^2}{{\tau }^2}}\hfill & t<t_0\hfill \\ \frac{1}{1+\frac{{\left(t-t_0\right)}^2}{{\tau }^2}}\hfill & t>t_0\hfill \end{array}$$ (2)

In all cases, the observed minimum-width line shape was at least twice as broad as the expected isotopic broadening (as modeled by the public domain software ProteinProspector¹⁰), and between 8 and 13 points full width at half maximum (FWHM) for the three data sets.

This shape assumes no background signal, so we subtracted the slowly varying baseline from each spectra using the charge accumulation model that we described previously.⁶ Any algorithm for baseline correction should be sufficient, as long as it does not introduce frequencies comparable to those of the true mass peaks or subtract a true signal that results from numerous closely overlapping peaks. For example, a convex hull baseline subtraction¹¹ can remove much of the intensity in the base of overlapping peaks especially for heavy masses. Because some of this subtracted data could actually be small side features, this process could then jeopardize subsequent deconvolution.

The laser intensity for all of this data was sufficiently high to produce detector overload in the low-weight region where the matrix species dominates. In the EVMS data, this produced severe peak clipping and broadening for the masses below m/z 2000 (5000 TOF points), and we therefore discarded data below this threshold from subsequent analysis. For the CDC data, the early time points were not present, because the mass deflector cut off was set at approximately 5500 TOF points.

TOF resampling

Figure 1 shows that the rising-edge τ of the TOF peaks stays nearly constant at 4–7 time samples in the time-lag optimization range,⁶ and then grows approximately quadratically. (Note, Fig. 1 plots $\sqrt{\tau }$, showing a straight line at long times.) Accordingly, the point density per peak increases quadratically above 10 000 TOF points for all three data sets. For low masses (TOF < 10 000), the total number of samples under the peak, 4τ (Fig. 1), was a constant different for each of the three data sets, between 16 and 28 time points. The parameters for the quadratic fit were somewhat different for each of the three sets too, as expected from the different laser intensities and time-lag optimizations. We used these measured curves to determine a prescription for resampling each spectrum to generate a new TOF spectrum that maintained τ at its low mass value by summing intensities from all the points within the resampling interval. The length of the resampling interval is the ratio of measured τ to the optimum (low mass) τ in the time-lag optimization range, rounded to the nearest integer. This integer corresponded to the number of TOF points around a ‘resampled’ point whose intensity was summed and assigned to a new point in the middle of the resampled interval. Unlike the conventional moving average, each original point contributed its intensity only once to a new resampled point. To smooth step-like jumps in the resampled intensities, which occurred near the edges between the intervals of odd and even length, we automatically corrected the step in intensities by linear interpolation between two adjacent points. Since the length of the resampled interval grew quickly with the TOF (Fig. 1), the frequency of step events was very low at high m/z. By visual inspection of the even-odd interval transition, we also ensured that none of the steps occurred on the top of the mass peak in the resampled spectrum. Since the number of TOF points decreases dramatically with resampling, each point contributes its intensity only once to the new, resampled series, and the resampled signal values are much larger than the original. The signal enhancement in the resampled spectrum is proportional to the original peak width and grows with increasing mass.

Figure 1.

Peak line width (t from Eqn. (1)) measured on the rising edge for proteins captured from pooled serum on IMAC-Cu (diamonds), NP20 (circles), and from cells on WCX2 (squares). The stars show the expected line width due to the isotopic distributions.

Resampling the series produces a new density of points along the m/z axis, since an m/z is recalculated for each resampled position. This resampling quadratically increases the distance between new mass points in time; however, the effective resolution, Δm/m, is not changed, since a peak width and position remains unchanged. The only difference is that fewer points span a peak, with larger amplitude signals at each point. This procedure recovers the constant point density per peak required by the deconvolution filter and it integrates several time points to enhance the sensitivity for the heavier ions.

Target filtering

We filtered each spectrum two times using two different filtering techniques: (1) an optimized linear filter that simultaneously smoothes and narrows to produce the largest signal-to-noise ratio (SNR) per unit line width, and (2) a nonlinear filter that further narrows the spectrum, enhancing the SNR per unit bandwidth and suppressing deconvolution artifacts. Analytical and numerical analysis of these correlation filters is presented in greater detail in our other work.⁷ Here we summarize the properties and parameters for the developed filters, which determine precision of the peak detection in the studied data sets. The optimal linear filter produces a 10% width reduction and a 4-fold increase in the SNR for linear MALDI-TOF data. The nonlinear filter procedure reconstructs the spectrum from a geometric mean of three linearly filtered signals. The optimal nonlinear procedure suppresses filter artifacts down to input random noise level, and improves the signal resolution by a factor of 1.7, reducing the width to 60% of its initial value.

Each shaping filter¹² creates a filtered output, by summing over the current and later input values weighted by the M filter coefficients. For a time series of N input signal values of x_k, this filter will produce output signal values,y_k, according to:

$$y_k=\sum _{j=1}^M{a}_j{x}_{k+j},1<k<N-M,$$ (3)

where a_j are the M filter coefficients. In the following, all sums are to be truncated whenever an index falls outside of its allowable range. We determined the filter coefficients by solving the system of M equations:

$$\sum _{k=1}^M{a}_k\left(r_{ki}+v{\lambda }_0{\delta }_{ki}\right)=\sum _{j=1}^M{d}_{j-i}{b}_j,1<i<M,$$ (4)

where b_k is the expected input wave shape and d_k is the desired target shape (both having M points); $r_{ik}={\sum }_{j=1}^M{b}_j{b}_{j+i-k}$ are the elements of a matrix formed from the autocorrelation of the input wave; δ_ik is the Kronecker delta; ν is a parameter that weights the importance of noise smoothing (high ν values) to signal shaping (low ν values), and λ₀ is the sum of any row or column of r_ik. The signal model is described over a bounded domain (usually about M/3, see below), and is close to zero outside it. Although the average value of the signal is always positive in our application, following original terminology introduced by Robinson and Treitel,¹² we will refer to signal models as wavelets in our present work.

We chose the same target shape as the signal wavelet, although with a reduced line width parameter, τ (Eqn. (2)). We truncated both input and target signal wavelets for values less than 1/512 (simulating the 8-bit ADC in the PBS instrument). We chose a filter length between 450 and 850 points, depending on the input wavelet model, and then offset the target wavelet by 200–300 time points to ensure that the cross-correlation function of these wavelets begins and ends with zero values. We similarly shifted the output backwards in time by the same number of points after filtering. We truncated the calculated filter coefficients after the first third (140–270) values to remove numerical artifacts from the model wavelet truncation. Thus, the final filter width was 145, 181, and 267 points for the EVMS pooled serum, the CDC pooled serum, and the EVMS cell lysate spectra, respectively. The longer filters were necessary because the correspondent input wavelets had a larger width.

We constructed target filters, using parameters that automatically achieved an optimal compromise between noise suppression and resolution enhancement. Our merit criterion equally weighted SNR and resolution enhancement (maximizing the product of the two for the filtered spectrum). A spectral analysis of the target filters showed that the weighting parameter, ν, effectively sets a high frequency roll-off. Values of ν < 1 produced narrower output, but at the expense of enhancing the noise. Higher values produced smooth spectra, but caused broadening. In the limit of ν > 100, the target filter became a matched filter, with the maximum possible SNR enhancement of 5 (for an asymmetric input wavelet as used here), at the expense of 40% broadening. We created an optimal linear filter, which suppressed the noise by a factor of 4 and reduced the signal width by 10% so that SNR enhancement per line width was maximal. For each data set it required using ν = 0.01, and a target τ_target = 0.8τ_input. We found that in general the choice of optimal parameters (location of the optimum in the (τ_target, ν) parameter space) depended only on the input wavelet shape. This shape was determined by instrumental parameters and stayed invariant across each resampled experimental TOF spectrum.

We also constructed a nonliner filter output as the geometric mean of the output of three filters, which had ν values of 10⁻², 10⁻³, and 10⁻⁴ and target widths of τ_target = 0.2τ_input, 0.2 τ_input, 0.5τ_input, respectively. Changing filter parameters (τ_target, ν) altered the phase and location of the filtering artifacts, while the signal position and phase remained unchanged. Geometric averaging of the filtered signals with the above described parameters allowed suppression of artifacts down to the input (resampled) noise level with 40% enhanced resolution for all studied data sets. Filters with greater resolution enhancement, although possible with different parameters, were found impractical since they would enhance the artifacts above the input noise level and produce high uncertainties in locations of the filtered peaks. After application of the described filters, the narrow, filtered signals maintained their detected peak centroid position to better than a final (filtered) half- linewidth for all peak signals with an input SNR in excess of 4 for the nonlinear filter, and in excess of 0.9 for the optimal linear filter. For higher input SNR the uncertainties in peak location were proportionally reduced. The filter construction process was the same for each data set, differing only in the determination of the input width parameter, τ, and in the resampling rate. Matlab scripts and implementation details are available for academic users upon request.

RESULTS AND DISCUSSION

In a typical expression profiling experiment, one monitors the relative changes in amounts of a large number of proteins from a large number of patients. These high-throughput experiments thus require automated peak detection procedures, which usually work best when peaks are well resolved and of high SNR. Consequently, a method that enhances resolution and sensitivity without requiring peak locations ab initio can significantly enhance the performance of many peak detectors. Our deconvolution filters are a simple and easy step that is particularly appropriate for linear TOF spectra, where the instrumental broadening ultimately degrades the high mass resolution. However, these deconvolution filters assume an invariant line shape and stationary noise. Resampling simply transforms a TOF spectrum to produce these results. The target filter coefficients are calculated to achieve a desired compromise between deconvolution and artifact suppression in the filtered data.¹² We optimized target filter deconvolution by choosing filter parameters that simultaneously maximized the filtered SNR and minimized the filtered line width.

Previously, we developed a deconvolution technique in the time-lag optimization TOF range, where the peak broadening is constant in time and the noise is nearly stationary.⁶ Here, we extend this method with optimized parameters to cover the entire range of the TOF record of 200 ms or up to m/z 150 000. In the following text, we start by describing the procedure for data resampling to recover constant point density per peak over the full range of a TOF record. Then, we discuss the effects of resampling on signal and noise in a TOF spectrum. This is followed by the introduction of peak detection and centroid precision thresholds, which are adequate for the two deconvolution filters applied. Finally, we illustrate the benefits of this resampling and filtering approach by enhancing the sensitivity and resolution of three spectral data sets. We show how enhanced resolution allows detection of mass shifts consistent with multiply charged ions, matrix adducts and protein modifications outside the time-lag optimization range.

Our resampling and filtering procedure helps to enhance information about the signal and suppress the noise background. This is achieved by separating and concentrating signal intensity, originally spread over a broad interval, on the basis of different correlation properties of signal and noise. Thus, by decreasing the density of the sampling points and making assumptions about the mathematical form of the signal, invariant across the spectrum, the useful information in the linear TOF spectra is made more accessible.

There are a number of factors that lead to broadening of high mass peaks in linear MALDI-TOF spectra.⁵ The most basic is the increasing spread due to the high number of combinations of various isotopes for complex biomolecules.¹⁰ With high enough sampling rates this produces a group of peaks separated by 1 Da, skewed towards heavier masses. For a constant sample time, the total width of these isotope multiplets corresponds to a nearly constant number of samples, as shown in Fig. 1 (stars). However, this broadening is well below the resolution of any of the linear TOF spectra considered here. More importantly, the distribution of initial kinetic energies in the laser-induced plume usually produces significant broadening, even in the region optimized by time-lag focusing.⁵ For masses heavier than those in the optimization region (TOF > 10 000), the combination of the initial kinetic energy spread, and the (now) mismatched time-lag focusing, broaden the heavy TOF peaks approximately quadratically, as shown in Fig. 1. Thus, with a constant sampling rate in the time domain, the point density per peak is much larger for the heavier masses. Integrative resampling of intensity from experimentally oversampled peaks can enhance signal information over random noise per time sample, since we decrease the number of samples while summing the intensities. Subsequent deconvolution into a narrower peak shape can further enhance signal detection, if deconvolution artifacts are not confused with the signal.

To apply our deconvolution filtering,⁶ which assumes that general peak form and noise are invariant across the spectrum, we need to recover constant point density per peak over the full range of the TOF record. This is achieved by resampling the signal with the rate determined by the ratio of measured peak width to the width within the time-lag optimization range (Fig. 1). The filter extrapolation is possible because in the studied spectra the general peak shape appears to be preserved, the only changing parameter being width with easily characterized analytical dependence (Fig. 1). The peak shape for a linear TOF instrument is a function of the instrument tuning and hardware setting conditions; however, these settings do not change during the acquisition of a single spectrum. Before extrapolating the described filtering procedures to other MS techniques (e.g., ESI, ICR), caution should be exercised to insure that instrumental peak shape and its parameters are well characterized over the range of filter application to avoid misshaping artifacts (phony peaks) in the filtered spectra.

Resampling the signal intensities means summing all of the signal intensity at the points within the interval that is being replaced by the lower resampling rate. This resampling enhances intensity of the signal peaks by an amount proportional to their original width to produce a constant point density per peak and peak maxima of comparable amplitudes over the full length of the TOF record. Figure 2 shows the effect of resampling for baseline-subtracted data, outside the time-lag optimization range. The high mass peaks are still broader in Fig. 2, which has an m/z horizontal axis, but the point density of the high mass peaks is noticeably lower, and their apparent SNR is higher than in unprocessed data. The albumin peak (m/z ~67 000) and its plausible doubly charged companion (m/z ~33 000) are enhanced by resampling so that they are clearly above the original noise level. Note that any errors in baseline subtraction can be enhanced by this integrating resampling procedure.

Figure 2.

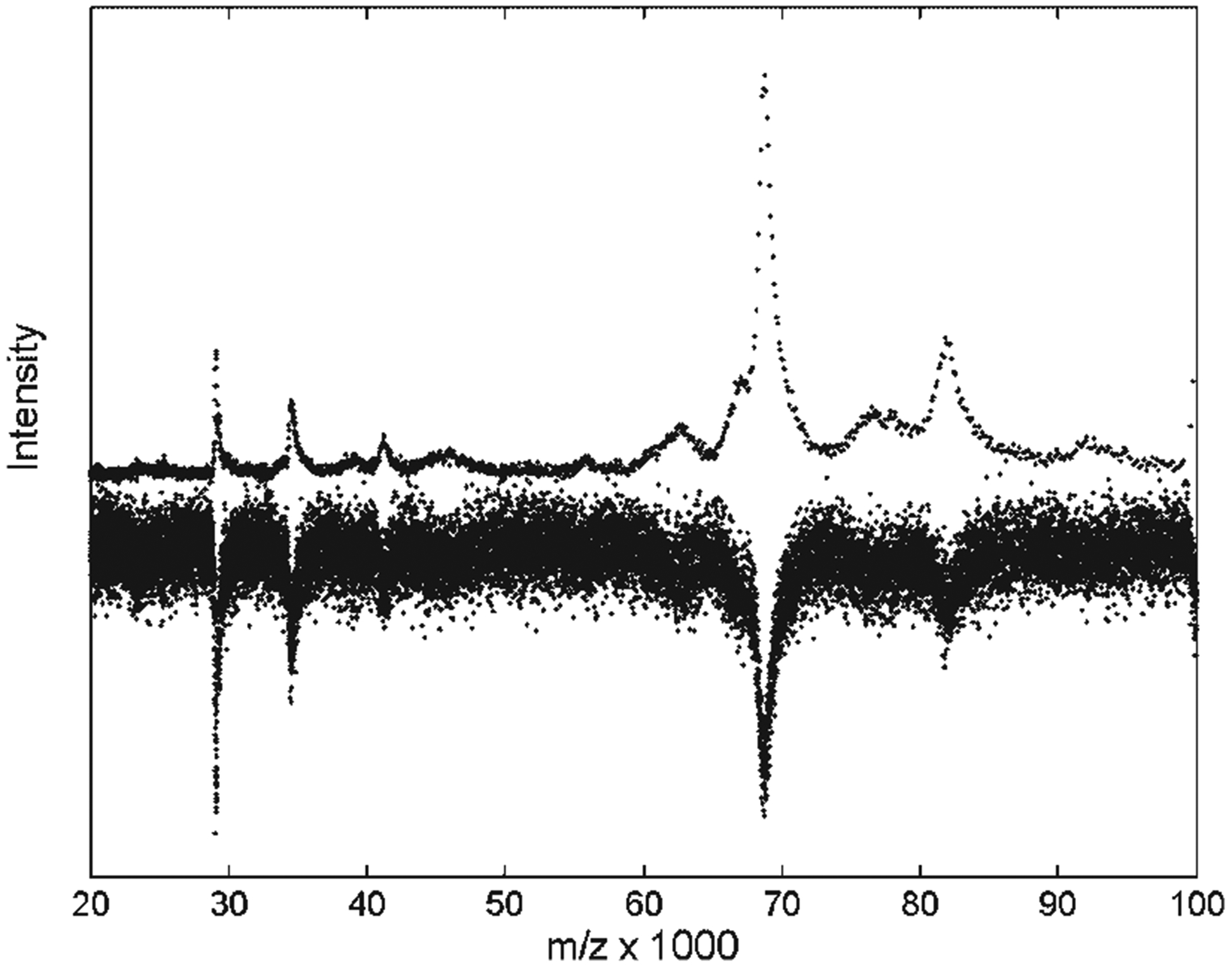
Resampling the spectrum of pooled serum on an IMAC-Cu surface decreases the point density and increases the SNR of the high mass peaks. The original spectrum is shown inverted, and scaled to a similar signal amplitude.

Our deconvolution filters assume a white noise background, and they are easiest to use if the noise level is constant (stationary), since that sets a constant sensitivity threshold for peak detection. In fact, we have observed that the noise in our mass spectrometers appears to be the difference between two white noise signals, as might be expected since the signal is digitized output of a differential amplifier. Such signals have depressed low frequencies compared to pure Gaussian noise, but we found that the depressed low frequency noise did not adversely affect the resampling and deconvolution. Surprisingly, resampling these signals produced no increase in the noise level. The amplitude of a perfectly white, Gaussian noise should increase as the square root of the number of integrated points with resampling, while the signal would grow proportionally to that number. In this case, resampling would enhance SNR proportionally to the square root of the resampling window width. Furthermore, to recover stationary noise amplitude in the resampled data with Gaussian noise, such data would need to be rescaled by the square root of the resampling window before application of the target filters. However, the noise from the difference of two white noise systems will not increase with resampling, as the summing undoes the original difference and leaves only the noise from the end points of the interval. Thus, resampling of experimental signals with noise from a differential amplifier enhanced the SNR for the heavy masses proportionally to their original width. Furthermore, no data rescaling was necessary, since resampling preserved stationary noise.

The time spacing in the resampled signal will grow according to the resampling rate (Fig. 1), which is quadratic with growing time in our studies. When converted from TOF to the m/z domain, the spacing between mass points will grow approximately as m/z^3/2. Resampling ensures that the point density per peak does not change across the spectrum. As with any shaping correlation filter, target filter extrapolation to the broad mass range relies on the assumption of constant point density per peak, and is not sensitive to the changing point spacing. Since the filtered signal is calculated from the correlation between filter coefficients and input (Eq. (3)), resampling the input effectively replaces the need to resample the filter coefficients.

Any filter relying on assumptions about signal shape can benefit from the suggested resampling procedure, before extrapolation to the full range of the MALDI-TOF spectrum. For instance, maximum likelihood maximum entropy (MLME) methods^13,14 that rely on constraints on signal shape cannot be extrapolated over the broad range without accommodation of the changing line width. Resampling can aid such extrapolation. MLME techniques applied over the narrow m/z range^15,16 have shown superior sensitivity to the signal detection in noise, since they usually rely on the well-characterized noise model. In essence, both MLME deconvolution^17,18 and target filters,¹² described here, involve curve fitting and error minimization. However, unlike target filters, MLME methods use multi-parameter fitting for an entire spectrum with iterative optimization, which is not guaranteed to find a global optimum. As nonlinear deconvolution methods, they also are very sensitive to the errors in models for noise, baseline and line shape,^13,15 which may lead to poorly characterized filtering artifacts and altered relative intensities of deconvolved features. Target filters, on the other hand, guarantee an optimal solution in the least-squares sense,¹² and allow straightforward characterization of artifacts and introduction of meaningful thresholds for TOFMS signal detection.

After resampling, we applied deconvolution target filters over the full range of the experimental TOF records. By deconvolving much of the instrumental broadening with the nonlinear filter, we enhanced the resolution almost to the limit of the natural isotopic broadening. Among other factors, further resolution enhancement for survey data is not possible because the initial sampling rate is too low to represent multiple peaks in an isotopic distribution. For each data set, we used an optimal linear filter to suppress the noise without broadening (10% narrowing), and a nonlinear filter to almost double the spectral resolution (40% narrowing) without enhancing the noise (see details in Experimental, Target filtering.) Although target filters can narrow noiseless signals down to a single time point, the presence of the noise in real spectra always enhances artifacts in the filtered signal. Two of the target filters described above achieve the optimal compromise between narrowing and artifact suppression, when both criteria are equally weighed. Such controlled filter construction allows introduction of global peak detection thresholds with associated uncertainties for downstream analysis of detected peak splittings.

With the optimal linear filter, the uncertainty in peak position for the signals above the input (resampled) noise level threshold is less than half-width of the filtered peak in time bins. The same peak location uncertainty for nonlinear filters, whose filtered half-width is 40% smaller, is at the input SNR threshold of 4. For the signals with better SNR, the uncertainty in peak location is proportionally smaller. Note that the peak centroid precision in the m/z domain will grow quadratically with time. The information on peak m/z precision, resolution and SNR enhancement achieved by resampling and deconvolution specific to the three studied data sets is summarized in Table 1. Note that resampling makes the major contribution to SNR enhancement for higher masses, where resampling intervals are longer proportionally to the original peak width.

Table 1.

Effect of resampling and deconvolution on resolution, SNR and precision of peak location in the m/z domain for the three studied data sets (data shown in Figs. 3–5). ‘@Peak’ values correspond to the largest peak in the cluster, and ‘Threshold’ corresponds to the peak intensities at the horizontal line marked on the figures

	SNR enhancement (with resampling)		Resolution enhancement		Peak centroid precision in ±m/z and its (fold-improvement)
					Linear		Nonlinear
Spectra	Linear ±2	Nonlinear ±1	Linear ±0.02	Nonlinear ±0.1	@Peak	Threshold	@Peak	Threshold
Fig. 3	16	4	1.10	1.7	±2 (10)	±15 (10)	±4 (4)	±30 (4)
Fig. 4	32	8	1.10	1.7	±2 (25)	±27 (25)	±6 (10)	±70 (10)
Fig. 5	8	2	1.10	1.7	±2 (3)	±10 (3)	±5 (1.2)	±25 (1.2)

The results summarized in the Table 1 refer to the well-resolved peaks (separated at least by 2 HWFM). For such peaks, the uncertainty in the peak centroid after using the optimal linear filter is always smaller than after using the nonlinear filter. However, in the case of peak overlap, the precision for the linear filter will decrease proportionally, while the nonlinear filter resolves structures almost two times better. Some peaks may be completely missed by the linear filter, especially if an automated peak detection scheme is used after the filtering. For overlapping peaks with high SNR, the nonlinear filter will produce (at least) two-fold smaller peak centroid uncertainties and higher resolution. On the other hand, for well-resolved peaks with low SNR, the optimal linear filter is preferred to enhance peak detection. Both filters improve precision of peak centroids many fold compared to the original data, the fold-improvement larger for higher m/z.

The uncertainties in peak amplitudes after filtering are equal to 1/SNR of input signals, which determine the peak detection threshold. For linear filters applied to all three sets, the threshold of input (resampled) SNR = 1 for filtered peak centroid uncertainty to be within the filtered half-width is always higher than the peak intensity (detection) threshold, since SNR in the filtered spectra is enhanced by a factor of 4. For nonlinear filters, filtering artifacts around peaks are suppressed below the original noise level outside three half-widths of the filtered peak. For these artifacts, the peak centroid (half-width uncertainty) threshold of SNR = 4 is again always higher than the peak detection threshold. However, in the vicinity of the large peaks (within three half-widths from the peak maximum) the amplitude of filtered artifacts for nonlinear filters could be dominated by incomplete suppression of sinc-lobes, which can be at most 5% of peak intensity. For such high intensity peaks (observed in the studied resampled data above m/z 60 000) the peak detection threshold is higher than the one for peak location uncertainty. The highest of the two thresholds for the nonlinear filter is shown in the figures below.

Deconvolution of overlapping peaks helps detect m/z shifts consistent with chemical adducts to parents peaks, as shown in Fig. 3. Figure 3 shows that deconvolution with either an optimal single filter (dashed line), or with the nonlinear filter (solid line), reveals a single cluster with m/z values consistent with the abundant serum protein apolipoprotein A-I (apoAI^19,20) and its sinapinic acid adducts (MALDI matrix, M = 224 Da). After resampling and the use of an optimal linear filter (dashed line in Fig. 3), two adduct peaks are clearly evident. However, the nonlinear filter shows that this structure may extend to three adducts. The small lower mass peak (m/z <29 000) is not likely to be a sinapinic acid loss, but may be a doubly ionized shadow of a higher peak. Although more controlled experiments would be necessary to validate this preliminary assignment, the resampling and deconvolution process clearly enhances detection of the signal splittings compared to the noisy original data.

Figure 3.

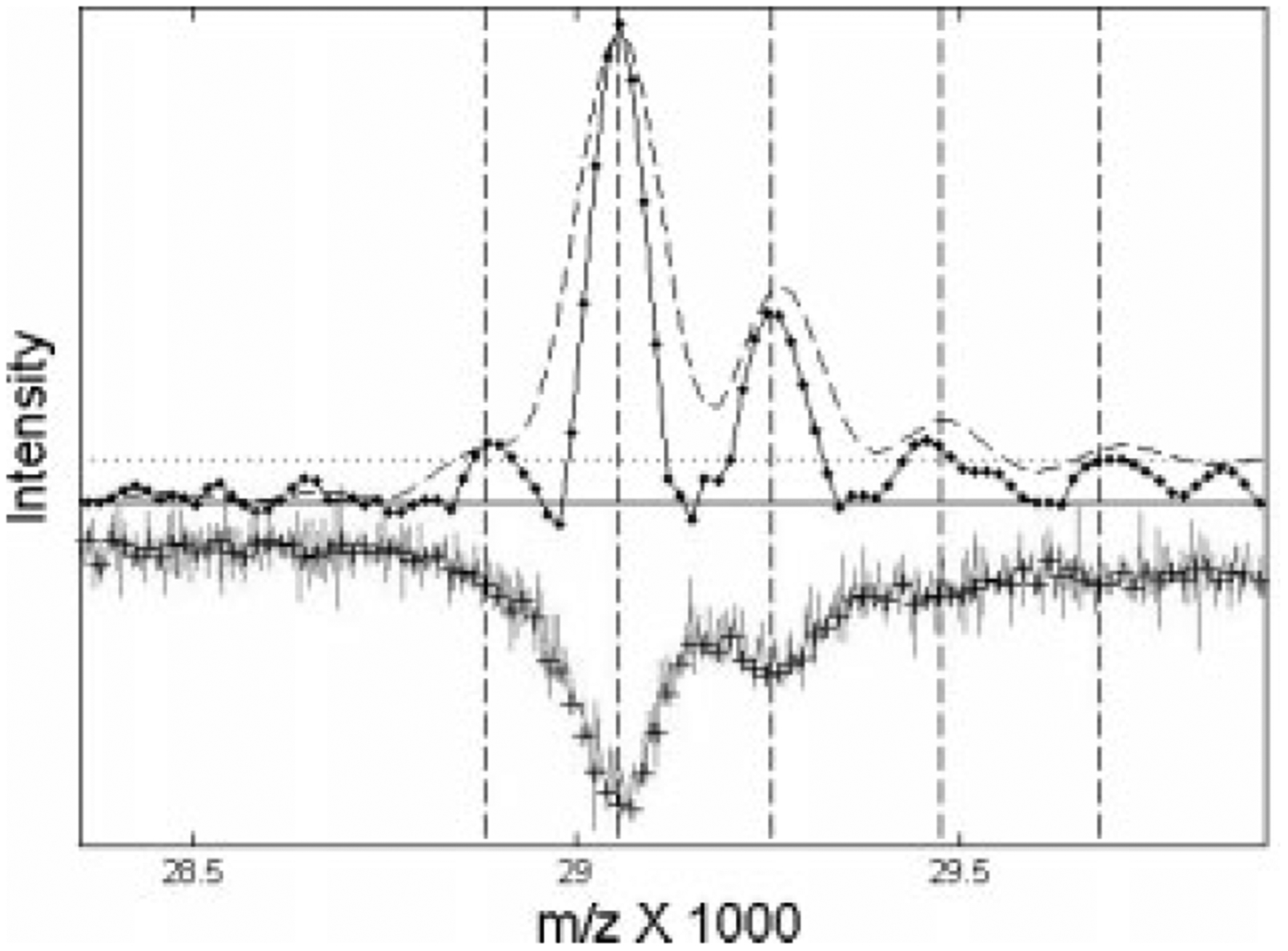
Deconvolved spectrum near the expected m/z value of apoA-I for pooled serum on an IMAC-Cu surface. The original data (inverted line) and resampled points (pluses) has been rescaled to an amplitude comparable to the filtered data. The dashed curve shows the results of an optimal linear filter, while the solid line with actual data points shows the results of the nonlinear filter. The dotted horizontal line shows a peak-detection threshold based on an input SNR > 4.

The distance between resampled signal points (pluses) across the shown cluster is about 16 m/z (compared to 3.2 m/z before resampling). However, due to approximately five times higher point density per peak and proportionally lower SNR in the unprocessed data, peak centroid precision, e.g., for the largest parent peak is about ±20 m/z (HWFM/SNR = ±20·3.2/3.0), while it is better than ±4 m/z after resampling and filtering (Table 1). Note that uncertainty for the same peak before processing was about six original mass intervals, while it is less than a quarter of the mass interval after resampling. The m/z precision is lower at the threshold values due to lower SNR. Figure 3 shows that with resampling the optimal linear filter more efficiently suppresses high frequency noise (16-fold SNR enhancement), while the nonlinear filter almost doubles the resolution (Table 1).

We obtained similar results for the apoA-I m/z range in CDC pooled serum spectrum on NP20, but we did not detect the peak for this serum-specific protein in the cell lysate spectra on WCX2 (as expected). We also observed similar adduct structures in the mixture of five calibration proteins with masses from 6 to 67 kDa on the NP20 surface. For this calibration mixture, the m/z shifts that we detected after resampling and deconvolution for matrix adducts to, e.g., cytochrome C (12 360 Da) and myoglobin (16 950 Da) calibrants were consistent with literature reports.¹⁷ Note that, if one used a baseline subtraction algorithm that fitted the minima of the peaks in the raw spectrum, much of the intensity of these overlapping peaks would have been erroneously removed.

The major advantage of our resampling process is that it enables deconvolution over a very wide range of m/z values. To illustrate this, Fig. 4 shows the results of these deconvolution filters for the average spectrum of the CDC pooled serum on an NP20 chip in the mass range of m/z 70 000–8000. The original data (inverted in Fig. 4) suggests an additional ‘shoulder’ structure to the right of the main peak that is enhanced by the optimal linear filter (dashed curve in Fig. 4) after resampling. However, the nonlinear filter (solid line with data points) clearly separates the shoulder peaks from the main signal. Examination of the mass shift for the resolved doublet at about m/z 74 000 suggested that it might be a doubly charged reflection of the protein peak at about m/z 150 000 (not shown), which fell on the edge of the CDC TOF record. We observed a similar doubly charged reflection for the albumin peak enhanced by resampling in the calibration mixture of five known proteins on NP20. Both of the applied filters were the same filters as used for the low-mass regions below m/z 10 000. The only change from low masses was the higher resampling rate, as shown by the low density of points in the nonlinear filtered spectrum in Fig. 4. The distance between mass points in the resampled spectrum was Δm/ z =90 m/z, compared to approximately 5 m/z before resampling. However, a peak centroid precision of ±6 m/z (Table 1) for the detected doublet after resampling and filtering was much better than Δm/z due to significant enhancement of SNR and peak resolution.

Figure 4.

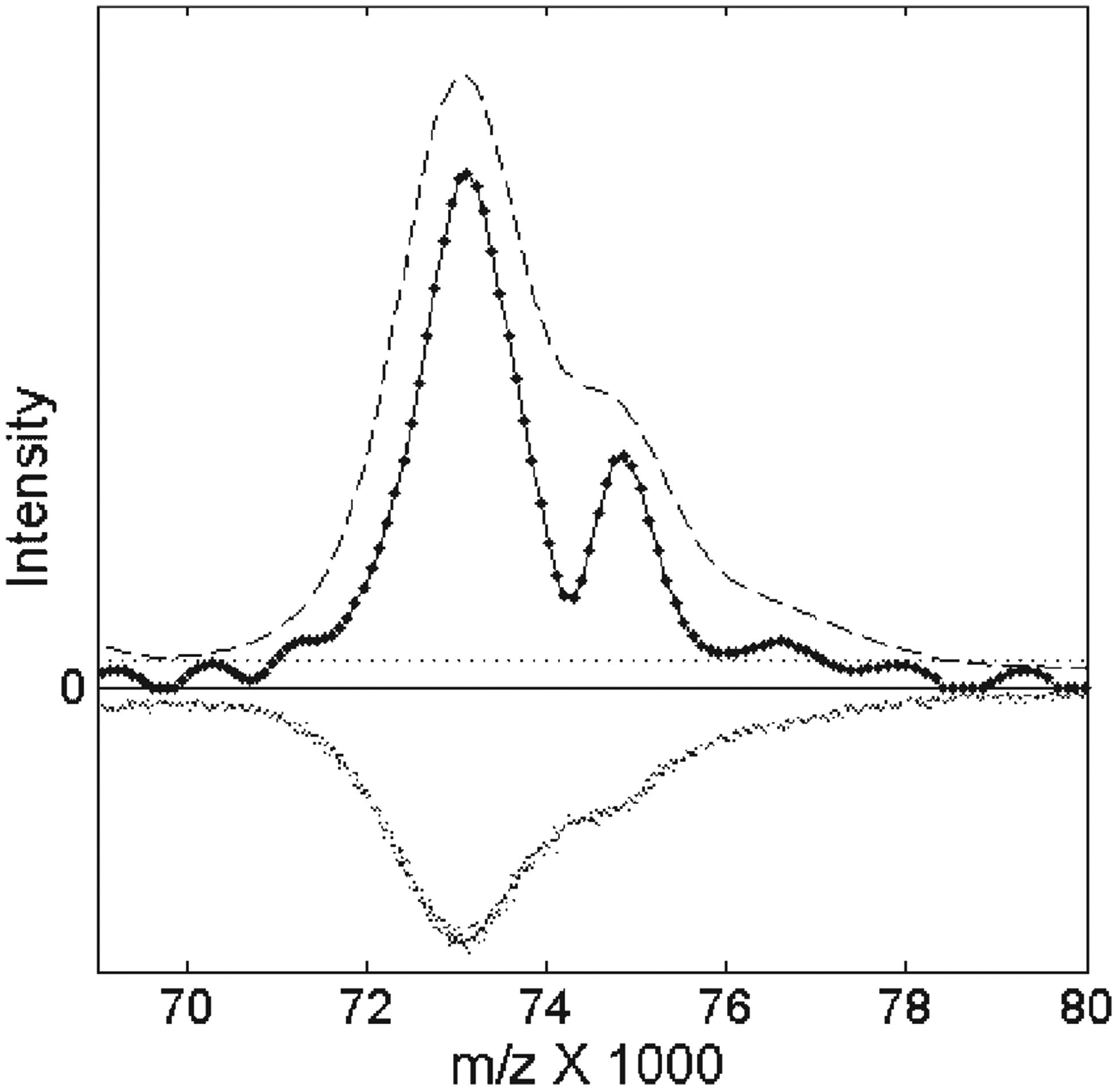
Filtering TOF mass spectra for CDC pooled serum enhances the visibility of the structure near m/z 74 000. The unfiltered data has been rescaled to approximately the same amplitude and inverted for clarity. The optimal linear filter produced the dashed curve, while the nonlinear filter produced the solid curve with data points. The dotted horizontal line shows the peak detection threshold, because the residual artifacts produced by the nonlinear filter should be less than 5% of the maximum signal size within three half-widths of the filtered peak on both sides.

Perhaps the most exciting application of this resampling and filtering procedure is that it enhances the potential to detect functionally important protein modifications over the full range of the survey TOF record. For example, in Fig. 5, we show the deconvolution of an average spectrum from cell lysates on the WCX2 chip. Researchers commonly use an average spectrum of many samples to detect a common set of peaks that represents an important structure, as the averaging process reduces the random noise.²¹ However, if the average is composed of two different types of spectra, this averaging process can lead to overlapping peaks. In Fig. 5(b), we show that this is in fact the case in the region near m/z 11 000 for the spectra of cell lysates from two breast cancer groups. Although the distinct structure has been completely obscured in the average spectrum (Fig. 5(a), inverted curve), our resampling and deconvolution procedure effectively resolves the two peaks near m/z 11 400. As these two peaks are clearly resolved in the average spectra of the two separate groups (Fig. 5(b)), they certainly cannot be an artifact of our filtering process.

Figure 5.

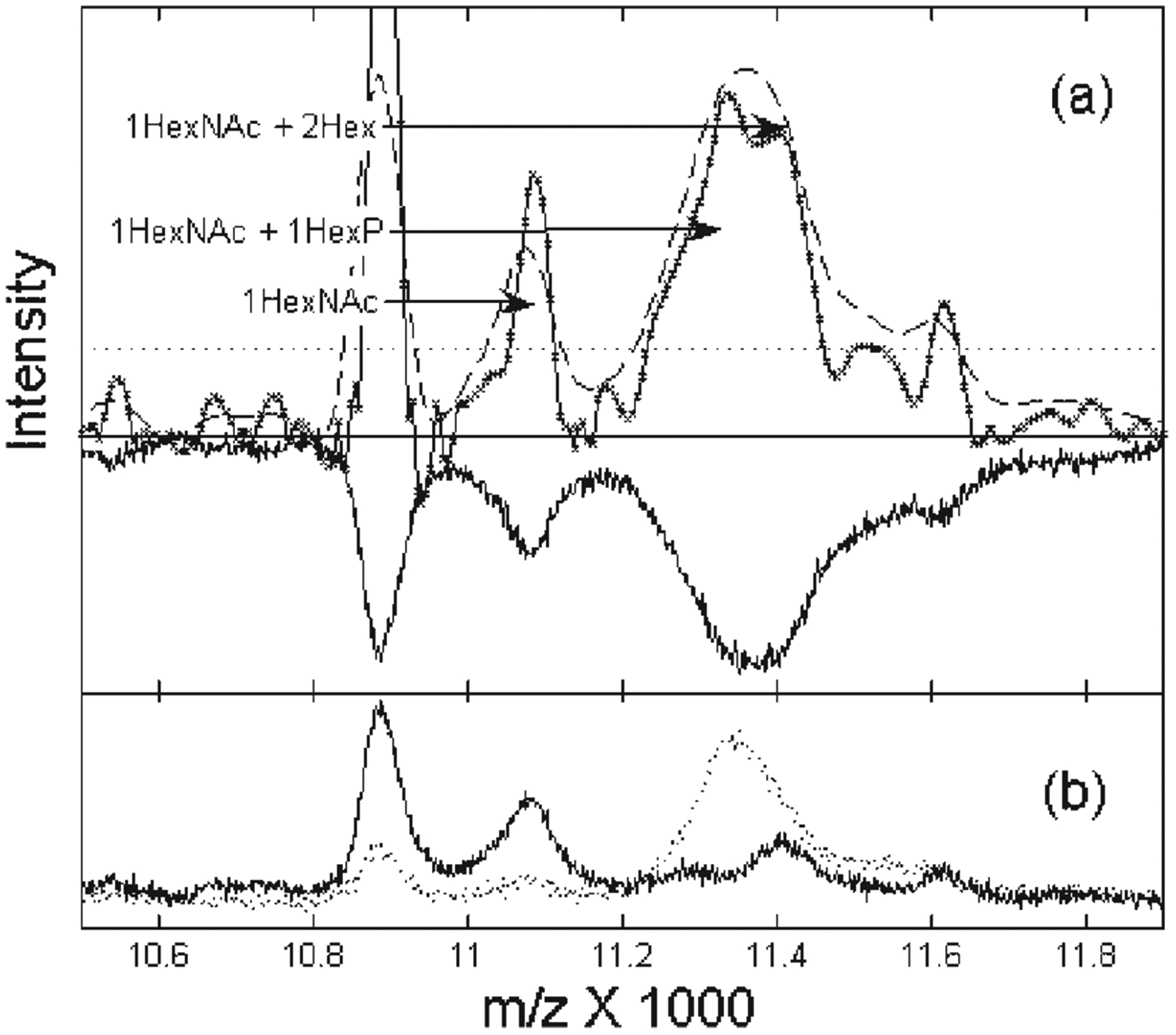
Enhanced resolution resolves mass shifts consistent with different states of the phosphoryl-glycoconjugated protein cluster near m/z 11 000. In (a), the inverted spectrum is the average of the unprocessed spectra from the cell lysates of the two breast cancer groups on WCX2, shown separately in (b). The dashed curve is the results of the optimal linear filter; the solid curve is the result of the nonlinear filter. The arrows mark likely glycosylation states as described in the text. The dotted line shows the peak detection threshold based on the input noise level.

Moreover, by measuring the relative mass shifts of the peaks detected in the 11 000 cluster with peak centroid precision of better than 10 m/z, we have tentatively identified the resolved doublet as two different glycosylation states⁴ of a protein at m/z 10 875. Within m/z uncertainty, each peak has a mass shift consistent with the addition of a monosaccharide,¹⁴N-acetyl-D-hexoseamine (HexNAc, mass of 203 Da), and either a hexose-phosphate molecule (HexP, mass of 242 Da) or two normal hexose molecules (Hex, each of mass 162 Da). Thus, the deconvoluted spectrum suggests that the peak structure near m/z 11 000 corresponds to a phosphoryl-glycoconjugated protein that may be a post-translational modification of a parent protein species. Interestingly, the resolved peak consistent with HexP addition (Fig. 5(a)) is detected only in one of the studied breast cancer groups (Fig. 5(b)), and, therefore, might be indicative of a disease state.

Application of resampling and target filtering over the full range of the TOF survey spectra enhances signal detection. However, this does not replace the necessity to validate and identify the detected features in the independent, more controlled experiments, e.g., with purified, preconcentrated samples. When target filtering is applied to survey spectra before statistical analysis (e.g., discrimination between disease groups), biomarker identification may become more robust, and greater biochemical insights could be possible. In planning additional MS experiments to identify and explore specific morphology and structure of detected biomarker proteins, we can use preliminary mass assignments such as those presented here to define, e.g., a set of endoglycosidases for deglycosylation of the sample.⁴ In our future research, we plan to use this improved sensitivity and increased resolution for charge and adduct deconvolution to further enhance sensitivity to precursor ions, for local recalibration of mass axis²² to enhance mass accuracy, and ultimately, for planning independent experiments to identify modified protein species.

CONCLUSIONS

Deconvolution filtering after integrative resampling enhances the resolution and sensitivity over the full range of linear TOF data up to m/z 150 000. The sensitivity enhancement is proportional to the resampling rate and is higher for heavy masses. This methodology is generally applicable for linear TOF instruments, although the specifics of resampling and sensitivity enhancement depend on the characteristics of an individual apparatus and experimental protocol. The resampling rate will be closely tied to the net increase in instrumental broadening in the time domain, while the sensitivity increase may vary depending on the instrumental noise characteristics. Integrative resampling of the data recovers a constant point density per peak prior to filtering. Filter parameters are chosen to maximize SNR per unit line width in the filtered data. With this merit criterion, the optimal linear filter achieves 10% narrowing with 4-fold SNR increase, when applied to resampled data. The optimal nonlinear filter almost doubles the resolution with artifacts not exceeding the resampled noise level. Application of the filters allows introduction of global thresholds for peak detection with meaningful estimates of uncertainties for peak locations. The precision of peak centroid detection grows many fold for heavy masses after resampling and filtering. For well-resolved peaks with low SNR, the optimal linear filter achieves best precision. The enhanced resolution achieved by deconvolution with the nonlinear filter improves detection of peak splittings for high SNR signals. The m/z shifts detected in the studied linear TOF spectra are consistent with mass shifts for adducts, multiply charged ions, as well as glycosylation modifications. These preliminary assignments facilitate planning further validation and identification experiments.