Curve sprinting in soccer: relationship with linear sprints and vertical jump performance

Abstract

We examined the relationships among linear speed, vertical jumping ability and curve sprint (CS) performance. Moreover, the correlations between linear and curvilinear sprint velocities and CS deficit were tested. Twenty-eight under-20 soccer players performed squat and countermovement jumps, 17-m linear sprint (with split times at 5 and 10 m), and a CS test for both sides. For the first time, the new proposed CS deficit was calculated as the difference between 17-m velocity and CS test velocity. Pearson’s product moment of correlation was performed to determine the relationships among the distinct variables tested. Significance level was set at P < 0.05. Large to very large relationships between linear sprint speed and CS performance were observed, on both the “good” and “weak” sides. In addition, moderate to large correlations between linear and curve sprint abilities and vertical jumps were found. Finally, the CS deficit was negatively associated with the CS good side performance. Linear sprint and CS velocities for both good and weak sides were closely related. The CS deficit was only related to the CS weak side performance, and the vertical jumping ability was significantly associated with both linear and curvilinear sprint velocities. The present results suggest that training methods capable of improving linear sprint and vertical jumping abilities may also improve CS performance.

INTRODUCTION

Sprinting is the most predominant action preceding goal situations in professional soccer [1, 2]. A previous study showed that short sprints, with and without the ball, represent ~ 64% of the powerful actions preceding goal situations in the German National League, revealing the crucial role of sprint performance in soccer [1]. Sprints are commonly performed over distances shorter than 10 m, up to 60 times per game, varying as a function of competitive level and playing position [3–5]. Overall, ~98% of maximum acceleration efforts start from low to moderate velocities (< 4.17 m·s^-1), and ~50% of these tasks do not exceed this velocity threshold [5]. Furthermore, players usually spend ~30% of “purposeful movement periods” (i.e., time executing game-related activities) moving in backward, lateral, diagonal, and arced directions [6]. Fitzpatrick et al. [7] observed that soccer players usually perform arced runs at angles up to ~6.2°; however, in some specific cases, these angles can exceed 30°. The majority of “arc movements” are performed in the forward direction, by midfielders and forwards, suggesting that these curvilinear actions may be important to create spaces or evade opposing players during decisive match situations (e.g., to assist or score goals) [6, 7].

A previous study showed that the “nonlinear sprint performance” differentiates professional from younger soccer players (i.e., under-17, -19, and -23) [8]. According to the authors, this finding indicates that nonlinear sprint ability is a critical skill for elite soccer players. Indeed, in elite soccer, approximately 85% of maximum sprint efforts may be characterized as “curve sprints” (CS) [9]. CS can be defined as “the upright running portion of the sprint completed with the presence of some degree of curvature” [9, 10]. In view of its practical relevance, more recently, Filter et al. [10] created and validated a new CS test for soccer players, which can be easily performed in the arc of the area, within a radius of 9.15 m (official FIFA radius) and a distance of 17 m. In that work, the authors also observed that CS and linear sprints are distinct motor tasks (i.e., shared variance of ~35%) and, hence, should be independently assessed. Nonetheless, to date, there is no consensus about what types of training or exercises are more or less appropriate to effectively improve CS performance. Therefore, there is an emergent need to produce new and more comprehensive studies on this topic.

A first step to identify more clearly the set of abilities that underpin successful performances in a variety of athletic skills is by examining the associations which may exist between different physical performance tests and exercises. For example, Yanci et al. [11] detected a nearly uniform pattern of moderate correlations between a number of vertical and horizontal jump tests and different types of change of direction (COD) assessments in Spanish soccer players. Similarly, Nimphius et al. [12] found consistent strong to very strong relationships between body mass and relative strength with linear speed and COD ability in female softball players evaluated over the course of a competitive season. Nevertheless, although predictable, the associations between different metrics of strength, speed, and power with nonlinear sprint performance should be viewed with caution, since it was recently reported that faster, stronger, and more powerful players tend to be less efficient at changing direction, exhibiting higher magnitudes of “COD deficit” [13, 14] (i.e., a measure that represents the additional time that one directional change requires when compared to a straight sprint over an equal distance [15]). Considering the nonlinear trajectory of curved movements, we can also expect a similar effect on the CS ability. In this regard, besides analysing the relationships between certain performance parameters (e.g., vertical jump height) and CS time, it is essential to test the correlations between “CS deficit” (i.e., the difference between linear sprint and CS times) and linear and curvilinear sprint performance. This is important to guide coaches in their efforts to develop strategies that are more likely to improve the physical performance of soccer players.

As the CS test is a very recent measurement, there are no studies investigating the best predictors of CS performance in professional soccer players. Therefore, the aim of this study was to examine the relationships between linear speed and vertical jumping ability with CS performance. Moreover, we tested the correlations between linear and curvilinear sprint performance and CS deficit. Based on previous results and empirical evidence, we hypothesized that faster players in linear sprints would be less efficient at performing curved movements.

MATERIALS AND METHODS

Participants

Twenty-eight under-20 soccer players (age: 18.5 ± 0.5 years; height: 175.7 ± 8.5 cm; body mass: 70.3 ± 7.4 kg) from the same team participated in this study. The sample was composed of 7 central defenders, 7 forwards, 5 fullbacks, and 9 midfielders. Soccer players were assessed immediately before starting the preseason period. The study was approved by the local Ethics Committee and all participants signed an informed consent form.

Study design

This cross-sectional correlational study was designed to test the relationships between vertical jump, and linear and CS performances in soccer players. On the same day, they performed in the same order: squat jump (SJ), countermovement jump (CMJ), 17-m linear sprint (with split times at 5 and 10 m), and the CS test. All players were familiarized with the testing procedures. Prior to the tests, players performed a standardized warm-up which included general (i.e., running at a moderate pace for 10 min followed by stretching exercises for 3 min) and specific exercises (i.e., submaximal jump and sprint attempts). Between each test, a 10-min interval was provided to explain the procedures, allow adequate recovery, and adjust the equipment.

Procedures Vertical jumping tests

Vertical jump height was assessed using the SJ and CMJ. In the SJ, players were required to remain in a static position with a 90° knee flexion angle for ~2 s before jumping, without any preparatory movement. In the CMJ, players started from a standing position and were instructed to execute a downward movement followed by complete extension of the legs and were free to determine the countermovement amplitude to avoid changes in jumping coordination. All jumps were executed with the hands on the hips and the players were instructed to jump as high as possible. The jumps were performed on a contact platform (Elite Jump, S2 Sports, São Paulo, Brazil) and the jump height was calculated based on the flight time [16]. Players were instructed to land on the same place as the take-off. A total of five attempts were allowed for each jump, interspersed by 15-s intervals. The best attempts for the SJ and CMJ were used for subsequent analyses.

Linear sprint test

Four pairs of photocells (Smart Speed, Fusion Sport, Brisbane, Australia) were positioned at the starting line and at the distances of 5, 10, and 17 m. Soccer players sprinted twice, starting from a standing position 0.5 m behind the starting line. Sprint velocity was calculated as the distance travelled over a measured time interval. A 5-min rest interval was allowed between the two attempts and the fastest time was considered for analysis.

Curve sprint test

The CS test was performed as previously described [10] (Figure 1). The trajectory of the CS was the semi-circle of the goalkeeper area (of an official soccer field), which is standardized as follows: a 9.15-m radius (from the penalty spot); a 14.6-m distance from the initial to the final point in a straight line; an angle of 105.84° of amplitude from the point of the penalty spot; a 17-m total distance (obtained from a trigonometrical analysis). Two pairs of photocells (Smart Speed, Fusion Sport, Brisbane, Australia) were positioned at the beginning and at the end of the curved trajectory. Soccer players sprinted twice for each side (first to the left, then to the right), starting from a standing position 0.5 m behind the starting line. A 5-min rest interval was allowed between the two attempts for each side, and the fastest time was considered for analysis. Sprint velocity was calculated as the distance travelled over a measured time interval. From the best attempt of each side, the “good” (fastest time) and “weak” (slowest time) sides were obtained. To properly assess the efficiency of the players to use their linear speed during a CS, a CS deficit calculation was used for both good and weak sides. Accordingly, the CS deficit was calculated as follows: CS deficit = (17-m velocity-CS test velocity).

FIG. 1.

Schematic presentation of the curve sprint test.

Statistical analysis

Data are presented as mean, standard deviation, and 90% confidence limits. The normality of data was confirmed via the Shapiro-Wilk test. The paired t-test was performed to analyse the differences between 17-m linear and CS tests. The Pearson product moment test was performed to determine the relationships among the distinct variables tested. The correlation coefficients were qualitatively interpreted as follows: < 0.09, trivial; 0.10–0.29, small; 0.30–0.49, moderate; 0.50–0.69, large; 0.70–0.89, very large; > 0.90 nearly perfect [17]. The significance level was set at P < 0.05. All physical tests performed demonstrated high levels of absolute and relative reliability (i.e., intraclass correlation coefficients > 0.90 and coefficients of variation < 5%) [17].

RESULTS

Table 1 shows the descriptive data of the physical tests performed with the soccer players. Significant differences (P < 0.05) were observed between 17-m linear and CS good side (CSGS) and CS weak side (CSWS) velocities. Table 2 presents the correlation coefficients between SJ and CMJ performances and linear and CS velocities, and CS deficit.

TABLE 1.

Descriptive data of the physical tests performed in soccer players.

	Mean ± SD	90% CL
SJ (cm)	39.3 ± 3.9	38.0 – 40.5
CMJ (cm)	42.8 ± 4.3	41.5 – 44.2
VEL 5-m (m·s-1)	5.09 ± 0.26	5.01 – 5.17
VEL 10-m (m·s-1)	5.89 ± 0.22	5.82 – 5.96
VEL 17-m (m·s-1)	6.70 ± 0.20	6.64 – 6.77
CSGS (m·s-1)	6.45 ± 0.20*	6.39 – 6.51
CSWS (m·s-1)	6.27 ± 0.15*	6.22 – 6.32
CSGS deficit (m·s-1)	0.26 ± 0.12	0.22 – 0.29
CSWS deficit (m·s-1)	0.44 ± 0.14	0.39 – 0.48

Note: SD: standard deviation; CL: confidence limits; SJ: squat jump; CMJ: countermovement jump; VEL: velocity; CSGS: curve sprint good side; CSWS: curve sprint weak side.

^*P< 0.05 in relation to VEL 17-m.

TABLE 2.

Correlation coefficients (r) between vertical jumps, linear and curve sprints performances, and curve sprint deficit.

	VEL 5-m	VEL 10-m	VEL 17-m	CSGS	CSWS	CSGS deficit	CSWS deficit
SJ	0.38*	0.42*	0.48*	0.52*	0.55*	0.05	0.03
CMJ	0.41*	0.46*	0.63*	0.57*	0.61*	-0.02	-0.13

Note: SJ: squat jump; CMJ: countermovement jump; VEL: velocity; CSGS: curve sprint good side; CSWS: curve sprint weak side;

^*P < 0.05.

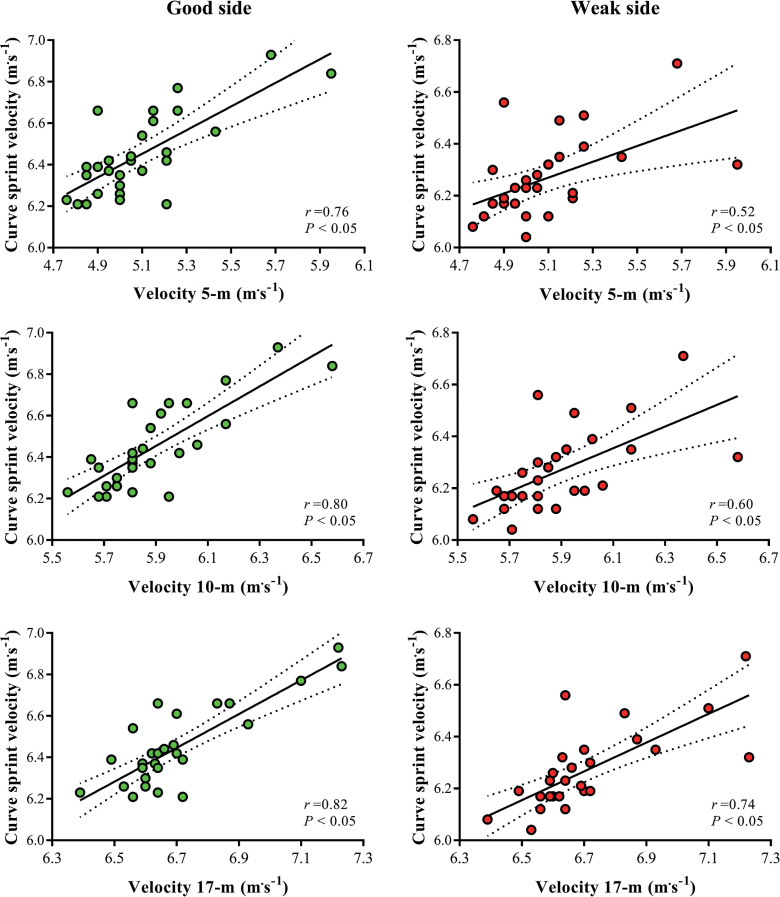
Figure 2 depicts the correlation coefficients between linear sprint velocity in the distinct distances tested and CS performances for both good and weak sides. Large to very large significant (P < 0.05) relationships were observed between linear and CS performances. Finally, Table 3 shows the correlation coefficients between CS deficit and linear and CS performances.

FIG. 2.

Correlation coefficients between linear sprint velocity in the different sprint distances and curve sprint performance for both good and weak sides.

TABLE 3.

Correlation coefficients (r) between curve sprint deficit and linear and curve sprint performances.

	CSGS deficit	CSWS deficit
VEL 5-m	0.10	0.60*
VEL 10-m	0.10	0.55*
VEL 17-m	0.17	0.50*
CSGS	-0.44*	0.10
CSWS	-0.27	-0.23

Note: VEL: velocity; CSGS: curve sprint good side; CSWS: curve sprint weak side;

^*P < 0.05.

DISCUSSION

This is the first study to examine the relationships between different parameters of physical performance and CS ability in under-20 professional soccer players. Overall, we found large to very large correlations between linear sprint speed and CS performance, on both good and weak sides, with a clear trend of increased associations towards CSGS and greater distances. Likewise, in general, we observed moderate to large correlations between linear and curve sprint abilities and vertical jump height. Importantly, the CSGS deficit is negatively associated with the CSGS velocity, which means that players who performed better in CSGS presented lower levels of CSGS deficit. Finally, soccer players faster in 5-, 10-, and 17-m distances displayed greater magnitudes of CSWS deficit. Thus, as expected, faster players in linear trajectories are less efficient at executing curvilinear sprints, but this phenomenon only occurs in CSWS.

The large to very large correlations (i.e., 0.52–0.82) between linear and curvilinear sprints reported here suggest that the CS ability is substantially influenced by the straight sprint performance. Given the standard CS test distance (i.e., 17 m), these relationships tend to naturally increase as distance increases, from 5 to 17 m, for both good and weak sides (Figure 2). Curiously, the associations are stronger for CSGS (~0.8) than for CSWS (~0.6), indicating that during CSGS soccer players are more apt to effectively utilize their linear velocities to sprint over curvilinear trajectories. This is still more evident when observing: 1) the large correlations between linear sprints and CSWS deficit, and 2) the absence of significant associations between linear sprints and CSGS deficit. This implies that, throughout sprinting on good sides, for some mechanical reason, players make better use of their linear velocities to accelerate faster and thus achieve higher velocities. These results differ from those obtained by Filter et al. [10], who reported a correlation of ~0.59 (R² ~35%) between curve and linear sprint performances, for both CSGS and CSWS. The stronger relationships detected here might be explained by the sample characteristics, since we assessed under-20 players from a professional soccer club who played in the first division league, whereas the previous study evaluated semiprofessional players from the second and third divisions. As more qualified athletes, our subjects are probably more efficient at stabilizing the joints in the frontal plane throughout CS, generating an appropriate amount of centripetal force to effectively follow the curved paths during maximum sprints [18, 19]. The larger correlations observed between CSGS and linear sprints may be related to biomechanical variations associated with limb dominance or asymmetry score [20, 21]. However, this question is challenging, as both leg dominance and asymmetry appear to be highly method-dependent [21, 22]. Further research is warranted to better elucidate the mechanisms influencing CS performance in soccer players.

The under-20 soccer players were faster in linear than in curvilinear trajectories (Table 1). This finding is in agreement with previous studies reporting higher velocities during straight sprinting compared to CS in male sprinters [18, 19]. For the authors, asymmetrical changes in force production, in order to stabilize the movement in the frontal and transversal planes and counterbalance joint moments caused by the gradual increases in mediolateral forces, are probably the most important factors affecting running speed during curved paths [18, 19]. These mechanical adjustments may lead to critical alterations in sprinting technique, especially in the “inside leg”, increasing its contact time and reducing the respective step length and frequency (compared to straight sprinting) [19, 23]. Curiously, contrary to our results, Filter et al. [10] observed higher velocities in CSGS than in linear sprints in semi-professional soccer players. As mentioned above, these inconsistences may be related to the differences in sample characteristics (i.e., elite young vs semiprofessional soccer players); nevertheless, due to the lack of studies on this topic (especially evaluating players from distinct age categories) it is currently impossible to draw any conclusions or even to “speculate” on the physiological and neuromuscular mechanisms behind these findings. On the other hand, the fact that our subjects performed better in linear than in curvilinear trajectories allowed us, for the first time, to calculate the “CS deficit” (i.e., CS deficit = 17 m sprint velocity-CS test velocity). This simple approach can help coaches to better estimate the ability of their players to effectively use their linear sprint velocities during curved paths, potentially impacting on the development of more efficient CS training schemes.

The multiple associations among CS deficit with linear and CS velocities varied between CSGS and CSWS. The CS deficit is solely (and largely) related to the CSWS performance. This agrees with the fact that the relationships between linear sprints and CSGS are much stronger than the relationships between linear sprints and CSWS.

Together, these observations have important implications, as they suggest that training strategies should vary between good and weak sides. As previously discussed, for some unknown reason, soccer players may be more effective in coping with the increased centripetal forces when sprinting on good sides, thus altering their sprinting pattern to a lower extent (compared to CSWS). Conversely, during CSWS they probably present meaningful disruptions in sprinting technique, which may strongly impact their performance and hence reduce the resultant velocity. In this context, it has been previously shown that a number of coupled biomechanical constraints placed on the stance leg make the inside leg ineffective for applying the force necessary to achieve higher velocities over curved paths [24]. From these data, it is plausible to speculate that, in the course of weak side performances, the inside leg (recognized to be a performance-limiting factor) [25, 26] encounters more difficulty in dealing with these mechanical alterations, provoking a marked reduction in sprint velocity. Therefore, practitioners are recommended to consider the differences in CSWS and CSGS when designing training programmes to improve the CS ability of soccer players. The execution of a higher number of maximum CS efforts on the weak side in a training session might be a viable alternative to reduce the differences between CSWS and CSGS performance. However, we recognize that this issue is complex and is beyond the scope of the current study.

Close relationships between jumping and sprinting abilities are commonplace in studies involving soccer players [11, 27, 28] and may be easily explained by some mechanical concepts. Vertical jump heights are measures able to express values already normalized to body mass [29]. To jump higher, an athlete has to quickly apply substantial amounts of force against the ground, from the beginning of the movement to the point of projection (i.e., take-off) [29, 30]. As the ground reaction force increases, the vertical velocity at takeoff becomes higher and, hence, the jump height is increased [29]. Correspondingly, it has been shown that the transition from lower to higher sprint velocities results in shorter contact times with a simultaneous and considerable increase in vertical peak force [31, 32]. Therefore, from a mechanical point of view, it can be expected that players able to jump higher will also be more efficient at accelerating their bodies forward and will achieve higher velocities over short distances [2, 29]. The correlations between vertical jump height and linear sprint velocity tended to progressively increase with distance (Table 2), which agrees with previous research revealing the crucial role played by vertical force production at faster running speeds [2, 31, 32]. These associations were also significant for both CSWS and CSGS, which can also be predicted by considering the interrelationships observed between linear and curvilinear sprint velocities. As such, it seems reasonable to consider that improvements in vertical jumping ability may be potentially transferred to these speed-related capacities. This hypothesis should be tested in future studies examining the effects of plyometric training interventions on both linear and CS performance.

This study is intrinsically limited by its cross-sectional design, which precludes definitive conclusions about causality. In addition, as the sample was composed of under-20 players at the end of their development process, the extrapolation of the data to more specialized populations (e.g., senior soccer players) should be made with caution. Nevertheless, this is the first investigation to assess the correlations between different physical parameters of physical performance and CS ability and examine their associations with CS deficit in a sample composed of under-20 soccer players. The present findings open new avenues for future research and may serve as a basis for the development of novel strategies to optimize CS performance. In conclusion, we demonstrated that linear sprint and CS velocities are closely related and that these correlations are stronger for CSGS (in comparison to CSWS). Furthermore, we observed that the CS deficit is solely related to the CSWS performance, and that the vertical jumping ability is significantly associated with both linear and curvilinear sprint velocities.

CONCLUSIONS

The ability to effectively sprint over curved paths is essential for elite soccer players [9]. From our results, it is possible to suggest that, in elite young soccer players, training methods capable of improving linear sprint and vertical jumping abilities are potentially capable of improving CS performance. However, these increases may not be similar between CSWS and CSGS, which might be associated with asymmetry scores or biomechanical issues related to limb dominance. Thus, sport scientists and practitioners are recommended to use the standard CS test for both right and left sides, along with the newly proposed CS deficit calculation, in order to check for differences between CSWS and CSGS. This methodological approach could help soccer coaches to implement more efficient “nonlinear sprint training practices”, according to the individual needs and requirements of their players. Additional studies are needed to verify whether improvements in linear sprint and jump performance can be transferred to positive changes in CS ability.

Disclosure of interest

No potential conflict of interest was reported by the authors.