An adaptive power prior for sequential clinical trials – Application to bridging studies

Abstract

During drug evaluation trials, information from clinical trials previously conducted on another population, indications or schedules may be available. In these cases, it might be desirable to share information by efficiently using the available resources. In this work, we developed an adaptive power prior with a commensurability parameter for using historical or external information. It allows, at each stage, full borrowing when the data are not in conflict, no borrowing when the data are in conflict or “tuned” borrowing when the data are in between. We propose to apply our adaptive power prior method to bridging studies between Caucasians and Asians, and we focus on the sequential adaptive allocation design, although other design settings can be used. We weight the prior information in two steps: the effective sample size approach is used to set the maximum desirable amount of information to be shared from historical data at each step of the trial; then, in a sort of Empirical Bayes approach, a commensurability parameter is chosen using a measure of distribution distance. This approach avoids elicitation and computational issues regarding the usual Empirical Bayes approach. We propose several versions of our method, and we conducted an extensive simulation study evaluating the robustness and sensitivity to prior choices.

1 Introduction

Bayesian inference is increasingly used in clinical trial planning, implementation and analysis. It has the advantage of using external information (historical data from previous clinical data, electronic health records, the medical literature, expert opinion, etc.) into the statistical framework. This property allows the reduction of sample size while increasing the statistical power.^1–3 However, incorporating external sources of data into the prior distribution needs to be done carefully, as these data can either be in conflict with or empower the resulting posterior. In these cases, specific tools for prior distribution calibration are required.

Two efficient approaches have been proposed in recent years to calibrate and tune prior information: the effective sample size (ESS) method and the power prior approach. The ESS method allows us to interpret the calibrated parametric prior in terms of the number of hypothetical patients who were used to develop the prior distribution. The ESS can be viewed as “how informative” a prior distribution is and can quantify it.^4–6 In addition, the power prior was first proposed when incorporating historical data into the analysis of clinical trials.^7–9 In this context, one weights the amount of information that will be used in the posterior computation. For this aim, a weight is introduced as a power parameter and is defined between 0 and 1 (where 0 = non-informative prior and 1 = full borrowing prior). However, this parameter requires subjective elicitation which can lead to prior misspecification if it is not done correctly.¹⁰ Recently, a class of commensurate priors has been proposed, that can be viewed as an attempt to quantify the degree of similarity between the informative prior distribution and the likelihood. Indeed, if the two distributions are superposed, there would be a full borrowing. Therefore, the amount of “borrowing” depends, in this case, on the amount of commensurability between the prior and the likelihood.^1,11 To do that, the authors define a commensurability parameter that is estimated once the trial data (that are resumed in the likelihood) are observed. Other efforts have also been made to set the power prior to control the type I error in the case of data-prior conflict,^12,13 or when historical data are simulated from medical device and their uncertainty is taken into account.¹⁴ Regarding commensurability, a meta-analytic approach was also proposed by Schmidli et al.¹⁵ with the robust meta-analytic predictive (MAP) prior.

However, when designing a sequential adaptive trial, interim analyses are performed regarding dose modification, safety or efficacy estimation depending on the trial design and the clinical trial phase (early or confirmatory). Owing to the sequential aspect of the process, (1) one cannot wait the end of the trial to estimate the commensurability or power prior parameter, (2) one cannot necessarily decisively elicitate the power parameter, as it either has a large weight that is too informative during the initial interim analysis because the trial did not yet reach its full sample size or a small weight that renders it non-informative at the time of the final analysis, and (3) one can propose a small value of the power parameter but all the advantages of information borrowing are lost.

Early phase dose-finding clinical trials aiming at estimating the maximum tolerated dose (MTD) are sequential. In model-based methods, the dose administered to the next cohort of patients depends on all the doses given and the associated toxicities observed so far. Recently, methods were proposed that allow using external information into the dose-finding design, where either external data were used for choosing the skeleton (working model) of the design or for calibrating the prior of the dose-toxicity relationship parameter(s).^16,17 Liu et al. proposed using a Bayesian model averaging (BMA) dose-finding method in which the estimated probabilities of toxicity at the end of the previous trial are used to build three different skeletons, that will be averaged during the present trial.¹⁸ Takeda and Morita defined a “historical-to-current” (H-C) parameter representing the degree of borrowing based on a retrospective analysis of previous trial data.¹⁹ Finally, Petit et al. used external information to calibrate the dose range and the working model.²⁰

1.1 Motivating case study

Bridging studies are designed to bridge the gap of clinical data, such as efficacy, comorbidities, safety and dosing regimens between two populations. According to the International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use E5 (ICH-E5) guidelines, a bridging study of a medicine can be defined as an additional study executed in a new population, for example, in another ethnic group, to “build a bridge” to the new clinical data on safety, efficacy, and dose response.²¹ These studies are important for both pharmacodynamic and pharmacokinetic reasons. Indeed, ethnic diversity in drug response for some drugs with respect to safety, efficacy and the resulting similarities or differences in recommended doses have been well described.²² Some of these differential responses may be related to the pharmacogenomics of a particular drug.²³ In some situations, it might be desirable to share information between populations to look for a more efficient use of resources but in other cases, it should not be done if the populations are very different from each other. For instance, the MTD of lapatinib, a tyrosine kinase inhibitor used in breast cancer, was estimated to be 1800 mg in Japanese patients but was higher in US and European patients. By contrast, the MTD of sunitinib, a multi-targeted receptor tyrosine kinase inhibitor, which is given for renal cell carcinoma, is equal to 50 mg and is similar in all countries. Accordingly, it will be pertinent to achieve “full borrowing” when the populations are similar, “no borrowing” when they are different or “tuned borrowing” when some, but not all, information can be borrowed.²⁴

The aim of our work is to propose a new method which, using the information coming from an existing fixed historical trial, helps the design and dose-allocation of a new prospective clinical trial. In this paper, we propose an adaptive power prior (APP) approach, based on a criterion constructed using the power prior, the ESS and the Hellinger distance. Using the advantages of each approach, the ESS is used for checking the maximum desired amount of information, the power prior is used for adding historical data, and the Hellinger distance is used for tuning the final borrowing. A criterion measures the similarity between distributions and decides how much information should be used in the clinical trial. We used the example of a phase I dose-finding study, because sequential and adaptive dose allocation need to be performed often during the trial.

In Section 2, the proposed method is described in detail along with several variants of the application to phase I bridging studies. Then, the simulation study is shown in Section 3, followed by the results in Section 4. The article ends with a discussion on strengths, weaknesses, and future improvements of the method.

2 Methods

Let θ be the parameter or the vector of parameters of interest. For simplicity, we will write all notations as if we are in one dimension, but everything can be easily generalised to vectors and matrices. Let D₀ denote the historical data, $D_0={\left\{y_j\right\}}_{n_0}$, n₀ the sample size of D₀, and $L(\theta |D_0)$ the likelihood function of θ given the historical data. In a similar manner, define D as the current data, $D={\left\{y_i\right\}}_n$, n as the sample size of D and $L(\theta |D)$ as the likelihood function of θ given the current data. We propose the following adaptive power prior π^APP

$${\pi }^{\mathit{APP}}(\theta )=\frac{L{(\theta |D_0)}^{{\alpha }_0(1-\gamma )}{\pi }_0(\theta )}{\int L{(\theta |D_0)}^{{\alpha }_0(1-\gamma )}{\pi }_0(\theta )\text{d}\theta }$$ (1)

where π₀ represents a non-informative prior distribution for θ and the original power prior parameter, introduced in Ibrahim and Chen,⁸ is split into two parts, $0\le {\alpha }_0\le 1$ and $0\le \gamma \le 1$. Since the two new parameters, α₀ and γ called the “quantity of information” and “commensurability” parameters, respectively, have two separate and specific interpretations, we propose a two-steps approach to set their values.

2.1 Quantity of information parameter value

In the first step, α₀ is chosen to add an upper limit on the quantity of information that is desirable to borrow. γ is temporarily set to 0, and the ESS of equation (1) is computed as $s=\mathit{ESS}[{\pi }^{\mathit{APP}}(\theta |\gamma =0)]={\alpha }_{0}ESS[L(\theta |D_0)]+\mathit{ESS}[{\pi }_0(\theta )]$, where $L(\theta |D_0)$ should be seen as a distribution.⁴ If a very non-informative prior is chosen for π₀, for example an improper uniform distribution when possible, the second term of the summation, $\mathit{ESS}[{\pi }_0(\theta )]=s_0$, tends towards zero. Moreover, since $L(\theta |D_0)$ includes n₀ observations, it is straightforward to think that the ESS can be approximately equal to n₀ (a proof of the convergence is given in the Supplementary Material). The resulting ESS can be written as $s\hspace{0.17em}\approx \hspace{0.17em}{\alpha }_0{n}_0+s_0$, and it is linearly dependent on the parameter α₀. Therefore, after setting a desirable ESS $s^{*}$ for the upcoming analysis, α₀ can be chosen to invert the previous equation, that is ${\alpha }_0=(s^{*}-s_0)/n_0$. α₀ can be viewed as an upper limit on the quantity of information borrowed, because $\mathit{ESS}[{\pi }^{\mathit{APP}}(\theta |\gamma =0)]>\mathit{ESS}[{\pi }^{\mathit{APP}}(\theta |\gamma >0)]$. A desirable $s^{*}$ depends on the application and on the sample size n of the actual data. Except in rare cases, it is usually accepted that $s^{*}<n$ to avoid the situation where the prior distributions overcome the actual data.

2.2 Commensurability parameter value

In the second step, we set the commensurability parameter γ. This parameter takes care of the possible conflict between the historical and current datasets. When the two datasets are very different, a non-informative prior should be preferable; when they are similar, a complete borrowing is preferred. We suggest linking γ to a measure of distance between the two datasets, that is, between D₀ and D. This distance should be a positive number between 0 and 1, and it should tend towards the maximum value when the two datasets are very different, and to zero when D₀ and D are close. Since in some applications, such as dose finding, the data can come from a non-homogeneous population, the approach of Pan and Yuan²⁵ cannot be directly used. For instance, in dose-finding trial data, each dose of the panel will produce a different population outcome. To overcome this issue, we propose, in a sort of Empirical Bayes method, to use the Hellinger distance with the normalised likelihoods, as follows

$$d^2(D_0,D)=\frac{1}{2}{\displaystyle \int {\left(\sqrt{\frac{L(\theta |D)}{\int L(\theta |D)\text{d}\theta }}-\sqrt{\frac{L{(\theta |D_0)}^{\frac{n}{n_0}}}{\int L{(\theta |D_0)}^{\frac{n}{n_0}}\text{d}\theta }}\right)}^2}\text{d}\theta$$ (2)

where d² refers to the square of the Hellinger distance. Each likelihood has a normalisation constant to ensure that it can be viewed as a probability distribution. Moreover, $L(\theta |D_0)$ is raised to a factor $n/n_0$ to allow it to be comparable to $L(\theta |D)$. Since $n_0\ge n$, we expect that the information included in the historical likelihood is more accurate, or in other words, has less variance then the actual data. Therefore, it is not directly comparable to a likelihood with fewer data points. We propose the addition of this factor to avoid this inconvenience. For example, in the Bernoulli case, e.g. y_i follows a Bernoulli distribution, we have that $L(\theta |D_0)=p^{{\displaystyle {\Sigma }_{n_0}{y}_i}}{(1-p)}^{n_0-{\displaystyle {\Sigma }_{n_0}{y}_i}}$, and, when we add the exponent, we obtain $L{(\theta |D_0)}^{n/n_0}=p^{n{\overline{y}}_{n_0}}{(1-p)}^{n-n{\overline{y}}_{n_0}}$, where ${\overline{y}}_{n_0}=({\displaystyle {\Sigma }_{n_0}{y}_i})/n_0$. If we rewrite ${\displaystyle {\Sigma }_{n_0}{y}_i}$ as $n_0{\overline{y}}_{n_0}$ in the likelihood without the exponent, we can easily see that the mean of the data is preserved, and the historical and the actual likelihood can now be compared with regard to their variability. Another example is given by the Gaussian case, where $y_i\hspace{0.17em}\sim \hspace{0.17em}N(\mu ,{\sigma }^2)$. In this situation, $L(\theta |D_0)={(2\pi {\sigma }^2)}^{-n_0/2}\exp \left(-{(2{\sigma }^2)}^{-1}{\displaystyle {\Sigma }_{n_0}{(y_i-\mu )}^2}\right)$ and $L{(\theta |D_0)}^{n/n_0}={(2\pi {\sigma }^2)}^{-n/2}\exp \left(-{(2{\sigma }^2)}^{-1}n\left({\displaystyle {\Sigma }_{n_0}{(y_i-\mu )}^2}\right)/n_0\right)$. Again, writing ${\displaystyle {\Sigma }_{n_0}{(y_i-\mu )}^2}$ as $n_0({\displaystyle {\Sigma }_{n_0}{(y_i-\mu )}^2})/n_0$, we can see that the quantity $({\displaystyle {\Sigma }_{n_0}{(y_i-\mu )}^2})/n_0$ is preserved but its “intensity” is reduced to n. The same reasoning can be done for the variance parameter. To be noted, equation (2) assumes that $n_0\ge n$, but it can be easily generalised as follows

$$d^2(D_0,D)=\frac{1}{2}{\displaystyle \int {\left(\sqrt{\frac{L{(\theta |D)}^{\min \left(1,\frac{n_0}{n}\right)}}{\int L{(\theta |D)}^{\min \left(1,\frac{n_0}{n}\right)}\text{d}\theta }}-\sqrt{\frac{L{(\theta |D_0)}^{\min \left(1,\frac{n}{n_0}\right)}}{\int L{(\theta |D_0)}^{\min \left(1,\frac{n}{n_0}\right)}\text{d}\theta }}\right)}^2}\text{d}\theta$$ (3)

where each time we downgrade the more accurate likelihood.

Finally, we set $\gamma =\sqrt{d^2(D_0,D)}$, considering, of course, the only real root (this reasoning will be applied for now on for all other c-roots). Any other power of d can be used to define the parameter γ, since $\gamma =d^c(D_0,D)\in [0,1]$ $\forall c\in R^{+}$. Values greater than 1 will reduce the computed distance and will lead to more borrowing, while values less than 1 will lead to a more conservative approach and will increase the computed distance.

2.3 Application in phase I bridging studies

The adaptive power prior distribution naturally fits the sequential nature of the phase I bridging study. It is only necessary to set the maximum ESS that a prior can have at each stage of the trial. One can set the maximum ESS as a vector where each number is related to a trial cohort, or set it as a function with the number of patients already accrued as an independent variable. In this article, as an example, we apply the APP on phase I bridging studies where the continual reassessment method (CRM) was used as the design. In particular, we chose the logistic model, that is

$$\text{logit}(p_i)=a+\exp (\beta ){\tilde{d}}_i$$

where p_i refers to the probability of toxicity at dose i, a = 3 is a constant parameter, ${\tilde{d}}_i$ is the “effective” dose, which is defined as the prior estimate of the probability of toxicity associated with dose level i and β is the parameter of interest (to be estimated).²⁶ Usually, a normal distribution with a mean equal to 0 and variance equal to 1.34 is used as prior distribution for β.²⁷ In our setting, we used the same distribution as ${\pi }_0(\beta )$, that is as the non-informative distribution, to build the ${\pi }^{\mathit{APP}}(\beta )$, and we propose several possible versions of it.

The classical CRM, that is when γ = 1 or directly α = 0 for all cohorts to ensure that no historical data is shared, will be called P_NI from now on. P_ESS refers to the model where only the ESS part is specified and constant, and in parentheses, the amount of information desired will be specified. AP_L denotes the model with $\gamma =\sqrt{d^2(D_0,D)}$ and a linear ESS that depends on the number of patients, $s^{*}(n)=n$. Other forms, including the rounded sigmoid form, gave almost the same results; therefore, we opted for the simpler version. The version called AP_S is the same as before but with $\gamma =\sqrt[4]{d^2(D_0,D)}$, that is, to have the square root of the distance equal to γ. To make the prior more robust, we checked the performance of the method using a mixture prior, AP_MIX(ω), built as follows $\pi (\theta |D)=\omega {\pi }^{\mathit{APP}}(\beta )+(1-\omega ){\pi }_0(\beta )$, where ω represents the mixture weight parameter. Then, following the example of Liu et al.,¹⁸ we also propose using the Bayesian model averaging technique, where the two models involved are AP_L, as M₁, and AP_NI, as M₂.²⁸ Details on the BMA methods, called AP_BMA, are given in the Supplementary Material. We have also reshaped the idea of Occam’s windows,²⁹ frequently used in BMA, to set a threshold on $\alpha ={\alpha }_0(1-\gamma )$ or on γ. In this way, $\alpha =\alpha I(\alpha >{\tau }_{\alpha })$, where I is the indicator function. In other words, α is set to zero if its value is less than the pre-specified threshold. In the same manner, we can define $\gamma =\gamma I(\gamma <{\tau }_{\gamma })+I(\gamma \ge {\tau }_{\gamma })$.

3 Simulation studies

To evaluate the performance of the proposed method, we carried out an extensive simulation study, in which 1000 independent phase I trials per scenario were simulated. The aim is to evaluate the performance of the dose-finding methods in different scenarios, when the generating probabilities of the prospective trial are similar to the ones estimated by D₀ and when they are different. In any case, D₀ is considered fixed, since we are not interested in their generated probabilities: the best guesses are, of course, the estimated ones.

First, to compare the dose-finding methods, we simulated subject responses, which follow Bernoulli distributions with parameters defined depending on the scenario, to all doses for each trial. Then, each simulated dataset was stored, and when running a trial, regardless of the method applied, subject responses were read from this stored dataset. In this way, when two methods coincide when proposing the dose allocation to the next patient, the results on the simulated patient are the same.

Regarding the design, each trial had a maximum sample size of 30 patients, six dose levels, a cohort size of one patient. The no-skipping rule was applied; that is, a higher dose was not proposed if all previous ones were not already given. For simplicity, stopping rules were not applied, except for scenario 6. Six scenarios were studied with a target toxicity of 20% and the trial plotted in Figure 1 was assumed as historical data D₀. In particular, D₀ followed a CRM design with six doses, a cohort of one and a maximum sample size of 30, as the main simulation trials. There were five dose-limiting toxicities (DLTs) at dose level 3 and one at dose level 5. The final posterior probability of toxicity was estimated to be $(0.052,0.073,0.205,0.406,0.506,0.555)$, and the MTD was declared to be dose level 3. Scenarios (that is, the choice of the probability of toxicity at each dose level) were generated to have the MTD be in several positions in the dose panel. This attribute allowed us to study cases where the probabilities of toxicity per dose were higher than the historical one, a scenario where these probabilities coincide in the two trials and in others where the probabilities of toxicity per dose in the actual trial were lower than in the historical one. As a skeleton, we adopted probabilities $(0.05,0.07,0.2,0.4,0.5,0.55)$ that reflect the probabilities of the historical data. In order words, we checked the performance of borrowing information when we already had a very good setting.

Figure 1.

Dose allocation and toxicity representation for the historical data. On the x-axis, the number given to the accrued patient is shown, while on the y-axis, it is marked at which dose s/he was allocated. A circle denotes that the patient did not experience any DLT, while a cross indicates that the patient had at least a DLT. The historical trial followed a CRM design with six doses, $d_i,i=1,\dots ,6$, and generating probabilities of toxicity at each dose equals to $p_T(d_1)=0.05,p_T(d_2)=0.07,p_T(d_3)=0.2,p_T(d_4)=0.4,p_T(d_5)=0.5$ and $p_T(d_6)=0.55$. This specific trial was chosen since the estimated probabilities of toxicities were similar to the generating ones.

After preliminary simulations (not shown here), we decided to use all methods that require a distance computation after the 10th patient enrolled in the trial in order to gather some information before starting to compute the commensurability parameter. For comparison, we ran the classic CRM (denoted by P_NI) and the CRM with power prior where the power α, which is denoted by AP_EB, was chosen using the Empirical Bayes method.³⁰ In the latter case, α is chosen to maximise the marginal likelihood

$$m(D,D_0,\alpha )=\frac{{\displaystyle \int L}(\theta |D)L{(\theta |D_0)}^{\alpha }{\pi }_0(\theta )\text{d}\theta }{{\displaystyle \int L}{(\theta |D_0)}^{\alpha }{\pi }_0(\theta )\text{d}\theta }$$

As a third competitor model, we run the bridging CRM (denoted by BCRM) of Liu et al.¹⁸ We utilised the code that was provided online by the authors. However, using D₀, the principal skeleton estimated gave two doses at the same prior probability; therefore, we added 0.01 to the estimation of the higher dose in the couple to distinguish between them and then ran the BCRM.

Computations were carried out in R (version 3.5.0),³¹ running under macOS High Sierra 10.13.6. rstan package (2.17.3)³² was used for Bayesian inference, the ks package (1.11.3)³³ was adopted to approximate the distribution-like likelihoods in equation (2), and Monte Carlo sampling was used to approximate the final integral. R scripts will be available at the GitHub of the corresponding author.

4 Results

Among the models compared, we added the AP_SOC1 that refers to the AP_S with an Occam’s window with ${\tau }_{\alpha }=0.2$, and AP_SOC2, which is the same version of AP_SOC1 with the ESS term replaced with $s^{*}(n)=\min (n,20)$. In the latter case, we reduced the possible amount of ESS to 20 instead of 30, as in the other models.

Table 1 summarized the characteristics of each method compared through simulation study. Table 2 shows the main results: the percentage of correct selection (PCS) and the number of DLTs, each for six different scenarios.

Table 1.

Methods notation summary.

Method	$s^{*}(n)$ (ESS)	γ	Description
P_NI	$s^{*}(n)=0$	–	Classic CRM, without historical information
P_ESS(10)	$s^{*}(n)=10$	γ = 0	Constant ESS
AP_L	$s^{*}(n)=n$	$\gamma =d(D_0,D)$	Linear ESS, commensurability criterion equal to the modified Hellinger distance
AP_S	$s^{*}(n)=n$	$\gamma =\sqrt{d(D_0,D)}$	Linear ESS, commensurability criterion equal to the square root of the modified Hellinger distance
AP_Mix(ω)	$s^{*}(n)=n$	$\gamma =d(D_0,D)$	Mixture prior with $\pi (\theta |D)=\omega {\pi }^{\mathit{APP}}(\theta )+(1-\omega ){\pi }_0(\theta )$, with πAPP denoting the prior distribution obtained with AP_L
AP_SOC1	$s^{*}(n)=n$	$\gamma =\sqrt{d(D_0,D)}$	Linear ESS, commensurability criterion equal to the square root of the modified Hellinger distance, $\alpha =\alpha {\mathbb{I}}_{\alpha >0.2}$
AP_SOC2	$s^{*}(n)=\text{min}(20,n)$	$\gamma =\sqrt{d(D_0,D)}$	Threshold (equals to 20) on the linear ESS, commensurability criterion equal to the square root of the modified Hellinger distance, $\alpha =\alpha {\mathbb{I}}_{\alpha >0.2}$
AP_EB	–	–	Empirical Bayes,30 α is chosen to maximise the marginal likelihood $m(D,D_0,\alpha )=\frac{\int L(\theta |D)L{(\theta |D_0)}^{\alpha }{\pi }_0(\theta )\text{d}\theta }{\int L{(\theta |D_0)}^{\alpha }{\pi }_0(\theta )\text{d}\theta }$
BCRM	–	–	Bridging CRM18

CRM: continual reassessment method; ESS: effective sample size.

Table 2.

Results for each method and each scenario in terms of the percentage of dose selection at the end of the trial, the PCS in bold and median number of DLTs, along with the first and the third quartiles. At the beginning of each scenario section, the true probabilities used for the scenario simulation are displayed. All methods were provided with stopping rules for scenario 6.

	% dose selection						DLTs	% dose selection							DLTs
Method	1	2	3	4	5	6	Median(25q, 75q)	0	1	2	3	4	5	6	Median(25q, 75q)
Scenario 1								Scenario 2
$p_{\text{tox}}$	0.001	0.01	0.05	0.07	0.2	0.4			0.01	0.05	0.07	0.2	0.4	0.5
P_NI	0	0	2	28	54	16	5 (5, 6)		0	1	25	61	12	1	6 (5, 7)
P_ESS(10)	0	0	10	51	32	7	2 (2, 3)		0	0	36	61	3	0	3 (3, 4)
P_ESS(30)	0	0	68	32	0	0	1 (1, 2)		0	0	84	16	0	0	2 (1, 3)
AP_L	0	0	8	37	39	16	4 (4, 5)		0	0	45	48	6	1	5 (4, 6)
AP_S	0	0	6	32	47	15	5 (4, 5)		0	0	37	54	8	0	5 (4, 6)
AP_MIX(0.5)	0	0	6	34	46	14	5 (4, 5)		0	0	39	53	7	1	5 (4, 6)
AP_SOC1	0	0	5	26	52	17	5 (5, 6)		0	0	38	50	11	1	5 (4, 6)
AP_SOC2	0	0	3	28	52	17	5 (5, 6)		0	0	30	58	11	1	5 (5, 6)
AP_EB	0	0	9	34	43	14	5 (4, 5)		0	0	46	47	6	1	5 (4, 6)
BCRM	0	0	16	45	38	1	3 (2, 4)		0	1	51	44	3	0	4 (3, 5)
Scenario 3								Scenario 4
$p_{\text{tox}}$	0.05	0.07	0.2	0.4	0.5	0.55			0.07	0.2	0.4	0.5	0.55	0.65
P_NI	1	18	70	11	0	0	6 (5, 7)		17	68	15	0	0	0	6 (6, 8)
P_ESS(10)	0	12	84	4	0	0	6 (5, 7)		10	73	17	0	0	0	8 (7, 8)
P_ESS(30)	0	4	95	0	0	0	6 (4, 7)		1	64	35	0	0	0	9 (8, 10)
AP_L	0	9	87	4	0	0	6 (5, 7)		11	61	28	0	0	0	7 (6, 8)
AP_S	0	11	84	5	0	0	6 (5, 7)		15	63	22	0	0	0	7 (6, 8)
AP_MIX(0.5)	0	10	85	4	0	0	6 (5, 7)		14	62	24	0	0	0	7 (6, 8)
AP_SOC1	1	10	85	5	0	0	6 (5, 7)		18	58	24	0	0	0	7 (6, 8)
AP_SOC2	1	11	80	8	0	0	6 (5, 7)		18	62	19	0	0	0	7 (6, 8)
AP_EB	0	6	90	4	0	0	6 (5, 7)		12	54	34	0	0	0	8 (7, 9)
BCRM	1	22	73	4	0	0	5 (4, 6)		21	68	10	0	0	0	6 (5, 7)
Scenario 5								Scenario 6
$p_{\text{tox}}$	0.2	0.4	0.5	0.55	0.65	0.7			0.35	0.45	0.5	0.6	0.7	0.8
P_NI	86	14	1	0	0	0	8 (7, 9)	88	10	2	0	0	0	0	9 (8, 10)
P_ESS(10)	76	23	1	0	0	0	9 (8, 10)	54	39	7	0	0	0	0	10 (9, 11)
P_ESS(30)	40	57	3	0	0	0	12 (11, 13)	7	54	37	2	0	0	0	13 (12, 14)
AP_L	77	22	1	0	0	0	8 (7, 9)	86	10	3	1	0	0	0	9 (8, 10.25)
AP_S	79	20	1	0	0	0	8 (7, 9)	86	10	2	1	0	0	0	9 (8, 10)
AP_MIX(0.5)	79	20	1	0	0	0	8 (7, 9)	86	10	3	1	0	0	0	9 (8, 10)
AP_SOC1	86	13	1	0	0	0	8 (7, 9)	88	10	1	1	0	0	0	9 (8, 10)
AP_SOC2	86	13	1	0	0	0	8 (7, 9)	88	10	2	1	0	0	0	9 (8, 10)
AP_EB	76	21	3	0	0	0	8 (7, 9)	85	11	3	2	0	0	0	9 (8, 11)
BCRM	90	10	0	0	0	0	7 (6, 9)	81	18	1	0	0	0	0	9 (8, 9)

DLT: dose-limiting toxicity; PCS: percentage of correct selection.

In scenario 1, where the MTD was placed at dose level 5, that is two ranks higher than the MTD of the historical data, the best PCS (54%) was obtained by P_NI, followed by AP_SOC1 (52%) and AP_SOC2 (52%). These three methods share the same percentage of dose allocation (shown in Supplementary Material) and median number of DLTs. The PCS of the other methods is smaller by 10–22% (in absolute change), except for the full borrowing method P_ESS(30). In the second scenario, the MTD was set one position higher with respect to the historical data. P_NI, P_ESS(10) and AP_SOC2 achieved a similar PCS, approximately 60%, while P_NI had a higher median number of DLTs than the other two methods. The performance of the rest of the methods, except of P_ESS(30), was between 44% and 54%. Scenario 3 represents the situation where both the historical data and the actual data came from the same population. All methods increase the PCS with respect to P_NI, except for the BCRM, which, by contrast, experiences a lower number of DLTs. The maximum PCS (95%) was reached by P_ESS(30), followed by AP_EB (90%). The other methods ranged between 80% and 87%, and the dose allocation table shows that more patients were treated at the MTD. In scenario 4, where the MTD was one rank less than the historical data, P_ESS(10) had the best result, 73%, followed by the other methods whose PCSs ranged between 58% and 68%. The lowest performance was achieved by AP_EB with a PCS of 54% and a higher median number of DLTs. In scenario 5, the MTD was set to two ranks lower than the historical data, and all methods, except for P_ESS(30), had an high PCS, ranging from 76% to 90%. P_ESS(10) and P_ESS(30) tended to assign more patients to toxic doses. Finally, scenario 6 represents the situation where all doses are toxic. We added the same stopping rule to all methods, that it the trial is stopped if the posterior probability that the probability of toxicity of the first dose is higher than the pre-specified toxicity threshold is higher than 0.9. P_ESS methods stopped and/or selected no dose with a lower percentage than the rest of the method, whose PCS ranges from 81% to 88%.

Sensitivity analyses regarding the ESS shape, mixture priors with different weights, BMA and Occam’s window types are given in the Supplementary Material.

Then, we focused on the amount of borrowing, defined as the total power used in the power prior, that is, $\alpha ={\alpha }_0(1-\gamma )$, at the end of trial for three methods: AP_SOC2, AP_S and AP_MIX(05). The results are shown in Figure 2, where the scenarios are resumed in the x-axis through the difference of the probability of toxicity at dose 3 with respect to the historical data (assumed to be 0.20). The median and the first and third quartiles of the final α are represented on the y-axis. Between the three methods, AP_MIX(05) is the one that borrows more information in scenario 3 (denoted by SC3 in the figure), with a median greater than 0.7. However, AP_MIX(05) also adds more bias in the other scenarios, since its median is always greater than 0.1. Going through AP_S to AP_SOC2, the amount of borrowing is decreased in all scenarios, but borrowing information is still permitted in scenario 3 (median greater than 0.3) and does not add too much bias in the other scenarios.

Figure 2.

Evolution of the amount of borrowing value, that is, $\alpha ={\alpha }_0(1-\gamma )$, at the end of the trial, for models AP_SOC2, AP_S and AP_MIX(05) in all five scenarios. On the x-axis, scenarios (SC) are represented by their difference in the probability of toxicity at dose 3 with respect to the historical data (assumed to be 0.20). On the right, more toxic scenarios than SC3 are plotted.

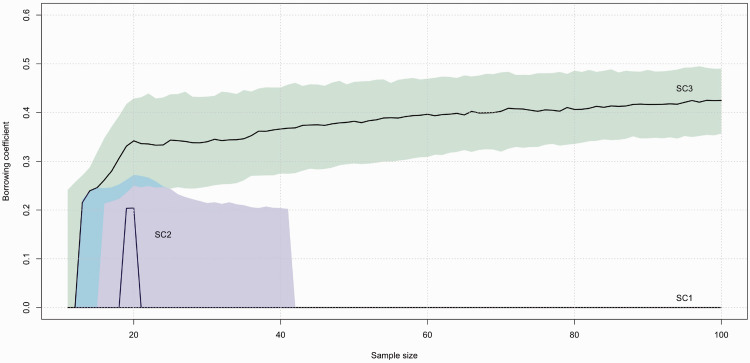
We also examined at the convergence properties of α for AP_SOC2. We increased the sample size of each trial up to 100 and we used equation (3) to compute the distance to be used in γ. The results are plotted. Figure 3 shows the median value of α along with the first and the third quartiles for scenarios 1, 2 and 3. In scenario 3, where full borrowing is desired, the median has an increasing trend, while the range tends to become narrower as the sample size increases. After 70 patients, α starts to be greater than 0.4. In scenario 1, the median and the first and third quartiles coincide and are all equal to zero. In scenario 2, the median goes up to 0.20 when the sample size is approximately 20 patients, but then it decreases quickly to zero. Additionally, the third quartile decreases to zero after 40 patients. Scenarios 4 and 5 give similar results as scenarios 2 and 1, respectively; therefore, we did not plot them.

Figure 3.

Evolution of the α value in model AP_SOC2 for a sample size going up to 100 patients. The median and the first and third quartiles are plotted for scenario 1 (SC1), scenario 2 (SC2), and scenario 3 (SC3).

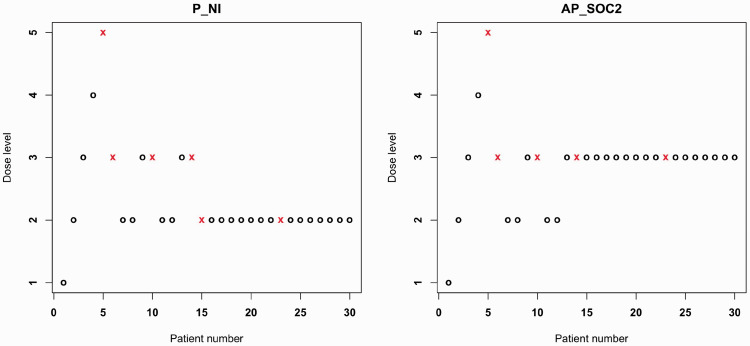
Finally, in Figure 4, we showed the dose-allocation/toxicity of the same trial, simulated under scenario 3, using the non-informative prior (left side) and the AP_SOC2 (right side). Both dose-allocation schemes coincide until the 14th patient. Then, the AP_SOC2 remains at the MTD level, while P_NI is more conservative and decreases the dose level.

Figure 4.

Dose allocation representation for the same trial using P_NI (left) and AP_SOC2 (right). Each point represents a patient, a circle indicates no toxicity, and a cross indicates toxicity.

5 Discussion

The aim of our work was to propose a modification of the power prior by incorporating external fixed data into a sequential adaptive design. Indeed, during sequential clinical trials, several adaptations are possible, including dose or regimen modification which are usually performed in early phase dose-finding studies. As noted in the Introduction, using the data from another population, indication or schedule can empower the trial results when the data are not in conflict. Our method has been shown to be able to detect data conflict during sequential adaptive trials and to add it when there is a strong reliable belief in its usefulness. To note, our method is tailored to check if the prospective trial is similar to a fixed historical dataset, not if both datasets come from the same population, that is, if both trials have the same generating probabilities.

We proposed several ways of using π^APP and the amount of historical information that could be used in the analysis of clinical trials. In our setting, the best method, on average, was AP_SOC2, but in other settings, another choice could be better. Therefore, a sensitivity analysis should always be performed before the study onset. The Occam’s window threshold on α (the total borrowing) was set to 0.2, that is, if the total borrowing is less than 0.2, we set it to zero. Therefore, a great variability in SC2 is shown, since all numbers below 0.2 are set to zero by the method. Otherwise, we have an increasing alpha and then, after approximately 20-22 patients, a slower decrease. The effect of the Occam’s window is a strong cut and we “feel” a greater variability than we expect in SC2. In our point of view, large decrease in PCS, in scenarios where the actual population is different from the previous one, should have more weight in the decision of which method to use. As usual, there is a trade-off between benefit and risk.

From our simulations, the amount of borrowing value was, on average, between 0.3 and 0.5 according to the method when the data were not in conflict. As the sample size of the clinical study was fixed at 30, which represents the additional information of 10 to 15 patients, the overall trial accuracy increased.

We compared our propositions to the Empirical Bayes approach and to the BCRM. It has been shown that the EB approach works best when there are no data conflict. However, in situations where there is major conflict between the data, it fails to detect that no borrowing is necessary. A way of improving its performance would be to incorporate the EB approach in our γ parameter, such as $\gamma =\text{arg}\max (m(D,D_0,\alpha ))$. However, it could experience computational issues in optimisation when moving in multidimensional parameter space. Even if equation (2) involves three possibly multidimensional integrals, where the dimension depends on the length of the vector θ, it can be easily approximated using Monte Carlo approaches. First, to reduce computational time, we suggest an MCMC approach, where the two pseudo distributions, $L(\theta |D)/\int L(\theta |D)\text{d}\theta$ and $L{(\theta |D_0)}^{n/n_0}/\int L{(\theta |D_0)}^{n/n_0}\text{d}\theta$, can be obtained as Bayesian posterior distributions, for example, by setting an improper uniform prior on θ and forcing the likelihoods to be $L(\theta |D)$ and $L{(\theta |D_0)}^{n/n_0}$, respectively. Then, the final integral of the distance in equation (2) can be computed using the Monte Carlo approach and the density kernel estimation from the previous sampling results. To the best of our knowledge, this approach works well in up to six dimensions and is robust. Regarding the BCRM, its aim is to select a proper skeleton for the prospective trial and not to increase the information used in the analysis. Therefore, the comparison is not fair in our setting, since it is made to maintain a constant PCS and to not increase in the case of no data conflict between populations. In our case, we experienced some issue in computing the skeleton. The final proposed skeleton had two couples of doses with the same probability of toxicity. Changing the skeleton and/or adding our method as one of the models inside the BMA procedure in the BCRM could increase the performance.

Our method is based on several parametrisation choices. First, we used the ESS to tune the quantity of information used from the historical data. In this case, we fixed a threshold that reflects the maximum amount of hypothetical patients who are incorporated into the prior with respect to the number of patients who will be included in the present trial. In our case, for the AP_SOC2 method, we simulated a phase I clinical trial with 30 patients and we fixed the maximum ESS threshold to 20. Even if our method is built to add information only when necessary, increasing the threshold can decrease the PCS when data are in conflict, as shown above. However, this threshold is already high, as it already allows the incorporation of 67% (20/30) additional information.

Second, the value of γ is defined between zero and one. We chose to parametrise it using the Hellinger distance $d(.)$ or its square root. As proposed in the methods section, γ can also be parametrised as $d^c(D_0,D)\in [0,1]$ $\forall c\in R^{+}$. If c is higher than 1, it will reduce the computed distance and will lead to more borrowing, while a value less than 1 will lead to a more conservative approach with an increase in the computed distance. Trial statisticians can decide to use other possibilities for γ, but an extensive sensitivity analysis is required.

Third, the method is based on the power prior approach and, therefore, on some notion of exchangeability.³⁴ When the two datasets can be seen as a realisation from the same process, we would assume full exchangeability; that is, the two datasets would have the same parameter, but not otherwise. Many models, such as hierarchical models and the power prior, are based on the assumption of exchangeability. As pointed out by Psioda et al.,³⁵ we prefer to see historical data that give the prior as non-random. In this point of view, the prior simply reflects the previous knowledge, which can be near the truth or not with respect to the new prospective trial. Therefore, even though exchangeability is an intrinsic part of the design, whether the patients in the two trials are actually exchangeable is not important when evaluating the impact of borrowing the prior information on the PCS.

Our approach is not limited to early phase dose-finding clinical trials. It can be generalised to any adaptive sequential method and trial phase. It can adapt the amount of the historical information that could be used in any interim analysis. Of course, some choices need to be fixed before the beginning of the trial, such as the ESS, the Occam’s window threshold and the parametrisation of γ. The generalisation of our method is straightforward because it does not depend on the number of interim analyses or on the type of outcomes. Then, it should be noticed that the term “fixed historical dataset” does not mean necessarily a unique dataset; this can be extended either for the averaging of several datasets or for a meta-analysis of several phase I datasets in order to take into account the inter- and intra-trials’ variability.³⁶

Being able to incorporate external data into small sample trials is an advantage when the data are not in conflict. Proposing a full borrowing when not appropriate will conduct to a wrong choice of the MTD in the majority of cases. Full borrowing should not be considered, unless there is a strong evidence of similarity. Our method was shown to be able to detect conflict and avoid it. This method will help investigators and clinical trial statisticians use historical data without the fear of adding bias to the results when the data are in conflict. We believe that such approaches should be further developed in the future.

Authors' note

Codes which are a part of the supplemental material will be available at the GitHub of the corresponding author.

Declaration of conflicting interests

The author(s) declare no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research of Adrien Ollier and Moreno Ursino was funded by the Institut National Du Cancer, grant numbers INCa_11324 and INCa_9539, respectively.

Supplemental material

Supplemental material for this article is available online.