The Wiring of Intelligence

Abstract

The positive manifold of intelligence has fascinated generations of scholars in human ability. In the past century, various formal explanations have been proposed, including the dominant g factor, the revived sampling theory, and the recent multiplier effect model and mutualism model. In this article, we propose a novel idiographic explanation. We formally conceptualize intelligence as evolving networks in which new facts and procedures are wired together during development. The static model, an extension of the Fortuin–Kasteleyn model, provides a parsimonious explanation of the positive manifold and intelligence’s hierarchical factor structure. We show how it can explain the Matthew effect across developmental stages. Finally, we introduce a method for studying growth dynamics. Our truly idiographic approach offers a new view on a century-old construct and ultimately allows the fields of human ability and human learning to coalesce.

Formal models of intelligence have greatly evolved since Spearman’s (1904) fundamental finding of the positive manifold: the robust pattern of positive correlations between scores on cognitive tests (Carroll, 1993). In explaining this manifold, contemporary models have diverged from the popular reflective latent factor models (e.g., Spearman, 1927) to various proposed mechanisms of emergence (Conway & Kovacs, 2015). Models that have been key in expanding the realm of explanatory mechanisms include sampling models (Bartholomew, Deary, & Lawn, 2009; Kovacs & Conway, 2016; Thomson, 1916; Thorndike, Bregman, Cobb, & Woodyard, 1926), gene–environment interaction models (Ceci, Barnett, & Kanaya, 2003; Dickens, 2007; Dickens & Flynn, 2001, 2002; Sauce & Matzel, 2018), and network models (Jung & Haier, 2007; van der Maas et al., 2006, van der Maas, Savi, Hofman, Kan, & Marsman, 2019). We embrace this trend because exploring alternative mechanisms for the positive manifold may significantly aid us in our understanding of intelligence (Bartholomew, 2004).

The contributions of Dickens and Flynn (2001) and van der Maas et al. (2006) have been serious attempts to encapsulate development into the theory of general intelligence. Here, we combine ideas from both their Gene × Environment and network approaches to conceptualize general intelligence as dynamically growing networks. This approach creates a completely novel conception of the shaping of intelligence—idiographic and developmental in nature—that uncovers some of the complexity thus far obscured. Our proposed formal model not only explains how idiographic networks can capture intelligence’s positive manifold and hierarchical structure but also opens new avenues to study the complex structure and dynamic processes of intelligence at the level of an individual.

The article is divided into two parts. In the first part, we briefly review current formal models of intelligence and discuss the desire to give idiography and development their deserved place within this tradition of formal models. In the second part, we introduce an elaborate developmental model of intelligence. We explain how the model captures various stationary and developmental phenomena and portray an individual’s complex cognitive structure and dynamics. Finally, in the Discussion section, we explore the model’s implications and limitations.

Formal Models of Intelligence

In this first part, we begin with a discussion of the primary modeling traditions in intelligence research. This discussion is followed by an analysis of what we call idiographic and developmental blind spots in formal models of intelligence: the failure of factor models in particular to seriously consider idiography and development. Finally, we discuss a formal mechanism for development, called Pólya’s urn scheme, to elucidate how surprisingly simple growth mechanisms can create phenomena that are key in the development of intelligence.

The positive manifold and its explanations

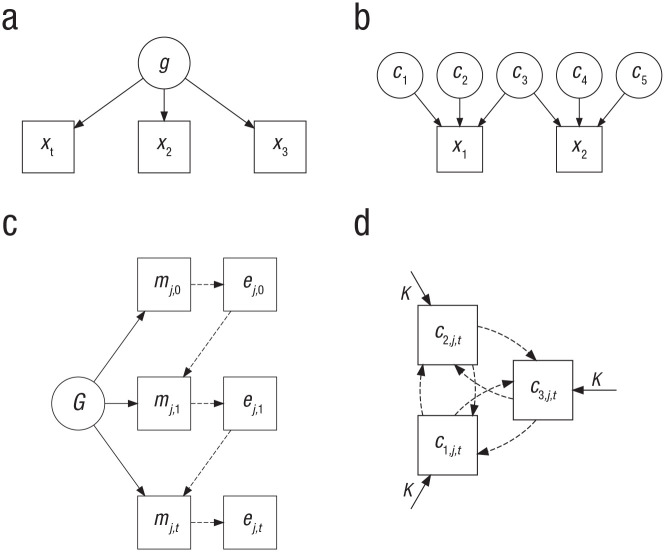
The first challenge for theories of general intelligence is to explain the pattern of positive correlations, the positive manifold, between scores on cognitive tests across individuals. Thus far, the proposed explanations form a colorful palette of diverse conceptions. We summarize four influential explanations—captured in Figure 1—that were formalized in various theories of intelligence. This summary requires two remarks. First, we use the terms model and theory interchangeably. However, whereas models provide a conceptual representation (e.g., the factor model), strictly speaking, they carry no theoretical load. Theories, on the other hand, add theoretical interpretation to a model (e.g., the—rather vague—theory that the factor named g represents mental energy). Here, we consider conceptually different models that have been used for serious theories of intelligence. In the following, we will shortly introduce each of the four models one by one and discuss their differences and similarities.

Fig. 1.

Four explanations of the positive manifold (simplified). Circles represent unobserved entities, whereas boxes represent observed entities. Dashed lines represent relations that have an influence over time. g = general intelligence, x = cognitive test, c = basic cognitive process (of person j at time t), G = genetic endowment, m = measured IQ of person j at time t, e = environment of person j at time t, K = genetic and environmental factors.

Factor models

Spearman (1904) not only discovered the positive manifold but also gave it an elegant explanation. In his two-factor model, Spearman (1927) introduced the general factor, g, assuming the existence of an underlying common source that explains the scores on multiple cognitive tests (see Fig. 1a). Although lacking a formal explanation, Spearman primarily hypothesized it to be some source of mental energy. Note that whereas intelligence generally is viewed as an intraindividual characteristic, g stems from an interindividual observation and must be understood in that context (Borsboom, Kievit, Cervone, & Hood, 2009). Spearman’s factor-analytic approach inspired many scholars to propose models in the same tradition.

Among the most influential contributions is Thurstone’s (1938) theory of primary mental abilities. Thurstone initially argued that Spearman’s unitary trait is a statistical artifact and proposed a multifactor model that also explains the positive manifold and is thus consistent with g but consists of seven distinct latent constructs. Other theorists followed this approach, with Guilford (1967, 1988) pushing the limits by ultimately including 180 factors in his influential structure of intellect model. Thurstone, on the other hand, eventually had to climb down because verifying his model on a new empirical sample compelled him to add a second-order unitary factor to his model. This work set the stage for various hierarchical models of intelligence (Ruzgis, 1994).

The marriage between a multifactor theory and a hierarchical theory has evolved into what is currently the most widely supported factor-analytic model of intelligence: the Cattel–Horn–Carrol theory (McGrew & Flanagan, 1998). The first theory, Cattell and Horn’s g_f-g_c model (Cattell, 1963; Horn & Cattell, 1966), postulated eight or nine factors, including the well-known fluid and crystallized intelligence (derived from Hebb’s intelligence A and B; Brown, 2016; Hebb, 1949). Crystallized intelligence refers to one’s obtained knowledge and skills, whereas fluid intelligence refers to one’s capacity to analyze novel problems independent of past knowledge and skills. The second theory, Carroll’s three-stratum hierarchy (Carroll, 1993), postulated a hierarchy of three levels, or strata, consisting of a general ability, broad abilities, and narrow abilities. In Cattel–Horn–Carrol theory, the broad stratum consists of Cattell and Horn’s primary abilities.

Sampling models

In the past decade, after a century-long dominance of factor theories of general intelligence, three alternative theoretical approaches to explaining the positive manifold have been introduced or reintroduced. The first, the sampling (or bonds) model, was originally advocated by Thomson (1916, 1951) and Thorndike et al. (1926) as an alternative to Spearman’s g theory. Rather than by introducing a general factor that explains cognitive performance, the sampling model suggested that the positive correlations between test scores simply originate from insufficiently specific cognitive tests. Different tests share many of the involved underlying basic cognitive processes (or bonds), and this overlap in processes that the tests tap into will necessarily result in positive correlations between tests (see Fig. 1b).

Bartholomew et al. (2009), Bartholomew, Allerhand, and Deary (2013), and more recently Kovacs and Conway (2016) reintroduced the sampling theory of general intelligence. The former generalized Thomson’s model to account for multiple latent factors, and the latter further extended sampling theory to account for the effects of domain-general executive processes, identified primarily in research on working memory, as well as more domain-specific processes.

Gene–environment interaction models

A decidedly more recent explanatory mechanism for the positive manifold was introduced by Dickens and Flynn (2001, 2002). In aiming to solve the paradox of both high heritability estimates in IQ and large environmental influences on IQ, they hypothesized a gene–environment interaction, in which, through reciprocal causation, IQ influences one’s close environment and that environment in turn influences one’s IQ, creating a multiplier effect (see Fig. 1c). Moreover, rises in the IQ of others may also affect one’s IQ, a so-called social multiplier. Dickens (2007) extended the multiplier model to include multiple abilities. As Dickens and Flynn (2001) noted, their model is similar to Scarr’s (1992) model of intelligence and school achievement. More general theories that relate complex gene–environment interactions to the positive manifold can be traced back to, for instance, the work of Tryon (1935).

Evidence suggests that indeed such gene–environment interactions exist (e.g., Tucker-Drob & Bates, 2015), and social multipliers are hypothesized to be involved with differences in the Flynn effect—generational changes in the IQ test scores of a population—across intelligence domains (Pietschnig & Voracek, 2015). Moreover, in an effort to reconcile genetic and environmental claims on cognitive ability, Ceci et al. (2003) nicely summarized a variety of models that are built on multiplier principles. Among Dickens and Flynn’s (2001) models for intelligence, they distinguished four other areas in which models with similar dynamics have been proposed, such as in dynamical systems theory and bioecological theory. Each of these areas provide a compelling case for multiplier effects in cognitive development.

Network models

The final new explanation of the positive manifold, based on network modeling, was introduced by van der Maas et al. (2006) and has since seen various developments (van der Maas et al., 2019). Inspired by dynamical explanations of ecosystems—such as food webs—the idea of their mutualism model is that the cognitive system consists of many basic processes that are connected in a network with primarily positive interactions (see Fig. 1d). These processes, which the authors define “in a general sense, including such notions as modules, capacities, abilities, or components of the (neuro)cognitive system, . . . have mutual beneficial or facilitating relations” (pp. 844–845). One may recall that, although less formally, Ferguson (1954) too theorized that “differences in ability are the results of the complex interaction of the biological propensities of the organism” (p. 99). However, the mutualism model adds that, during development, the initially uncorrelated basic processes become correlated because of positive reinforcements, as “each process supports the development of other processes” (van der Maas et al., 2006, p. 845). And indeed, these mutual positive reinforcements too exhibit a multiplier effect.

This network approach has particularly resonated in the domain of psychopathology, resulting in a recent surge of research (see Borsboom, 2017, for a comprehensive overview). In intelligence, van der Maas, Kan, Marsman, and Stevenson (2017) extended the mutualism model, allowing for test sampling, mutualistic relations and multiplier effects, and central cognitive abilities. Lastly, an entirely different research tradition—brain modeling—also provides an important class of network models. The parieto-frontal integration theory provides a network model based on various neuroimaging studies and connects parietal and frontal brain regions to explain individual differences in intelligence (Jung & Haier, 2007).

Differences and similarities

What unites these diverse models is that they all explain the positive manifold equally well. Yet a lot sets them apart. In g factor models, the correlations are due to a common source of cognitive performance in many domains. The g factor is understood as a so-called reflective latent variable. That is, in theorizing the nature of intelligence, the general factor is understood as a causal entity. Spearman’s notion of mental energy is an example of that. Note that this notion of a psychological g, reflective and causal in nature, is a hypothesized one and not uncontroversial.

In the mutualism model, there is no such common source. Rather, the positive manifold emerges from the network structure. The nevertheless apparent statistical g factor is interpreted as formative variable because an index variable of the general quality of the cognitive system (Kovacs & Conway, 2019; van der Maas, Kan, & Borsboom, 2014), akin to economical indices such as the Dow Jones Industrial Average. Contrary to psychological g, this psychometric g is well established and noncontroversial (e.g., Carroll, 1993).

In sampling theory, the statistical g factor should also be interpreted as a formative variable. But that is not to say that sampling theory and the mutualism model are very similar. In sampling theory, the positive manifold is essentially a measurement problem. If we would be able to construct very specific tests targeted at the fundamental processes, the overlap in measurement would disappear, and so will the correlations between tests. In the mutualism model, on the other hand, the correlations are real, created during development, and will not disappear when IQ tests become more specific.

In both the multiplier effect model and mutualism model, the positive manifold emerges from positive reciprocal reinforcements. However, the two models differ in several key respects. Most important, the mutualism model proposes an internal developmental process, whereas the multiplier model depicts development through an interaction with the external environment.

Finally, and importantly, as, for instance, Bartholomew et al. (2009) and Kruis and Maris (2016) noted, g theory and sampling theory and factor models and network models cannot be statistically distinguished on the basis of correlation indexes alone, nor do they necessarily contradict one another. Van der Maas et al. (2017) illustrated this in their unified model of general intelligence. However, this is not to say that these models are equivalent with respect to their explanatory power. Each conception might tap into a different granularity of general intelligence, ultimately aiding us in our understanding of the construct. In addition, it is not to say that the models cannot be distinguished. Time-series data and experimental interventions may very well distinguish between the models (e.g., Ferrer & McArdle, 2004; Kievit et al., 2017; McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002). Marsman et al. (2018) described these issues in more detail.

The developmental blind spot

Intelligence cannot be understood in isolation. It is a product of genetic, environmental, and developmental factors and must be considered within this complex context. Nonetheless, particularly the development of intelligence has long been an afterthought in its formal modeling tradition. We briefly provide two possible reasons for this unfortunate fact and in the process aim to convey the importance of exploring formal developmental notions of intelligence.

One dominant model

A first reason for the developmental blind spot is the dominance of g theory. Although g does not necessarily nail down its origin, be it genetic, environmental, or both, it does not naturally capture development. Ackerman and Lohman (2003) concisely summarized this by explaining that

one of the most intractable problems in evaluating the relationship between education and g is the problem of development and age. As near as we can tell, g theories have failed to provide any account of development across the lifespan. (p. 278)

Note that Nisbett et al. (2012) observed that “the high heritability of cognitive ability led many to believe that finding specific genes that are responsible for normal variation would be easy and fruitful” (p. 135). Although arguably a reification fallacy, a better understanding of the—relative—contribution of genes to intelligence is of obvious importance. Nisbett et al.’s conclusion, directly following the previous quote, summarized this obtained understanding: “So far, progress in finding the genetic locus for complex human traits has been limited” (p. 135). After several attempts in the past decade, the generally shared insight is that many genes may be involved with small effects (e.g., Hill et al., 2018; Lee et al., 2018) and that environmental factors require a better understanding. This polygenic view, or possibly even omnigenic view (Boyle, Li, & Pritchard, 2017), supports a both more complex and more realistic theory of intelligence.

The closest factor models have come to providing an account of development across the life span is in Cattell’s (1987) investment theory. In his landmark book, Cattell hypothesized that one develops a pool of crystallized intelligence by the “investment” of fluid intelligence in conjunction with the “combined result of the form of the school curriculum, and of the social, familial, and personal influences which create interest and time for learning simultaneously in any and all forms of intellectual learning” (p. 140). This idea, derived from Hebb’s (1949) two intelligences (intelligence A, “an innate potential, the capacity for development,” and intelligence B, “the functioning of a brain in which development has gone on”; Brown, 2016), was never formalized but is argued to explain the Matthew effect (Schalke-Mandoux, 2016)—a key developmental phenomenon discussed in the next section.

In his investment hypothesis, Cattell (1987) thus explicitly sketched an evident role for the environment in which genes and the environment are united to explain individual differences in intelligence. More recent insights, however, demand a further integration of the two. In discussing the puzzling heritability increase, Plomin and Deary (2015) explained that

Genotype-environment correlation seems the most likely explanation in which small genetic differences are magnified as children select, modify and create environments correlated with their genetic propensities. This active model of selected environments—in contrast to the traditional model of imposed environments—offers a general paradigm for thinking about how genotypes become phenotypes. (p. 98)

This developmental notion of a gene–environment interaction (Tabery, 2007) suggests a causal mechanism between the two that may give rise to the phenotype IQ.

Dickens and Flynn’s (2001) novel formal multiplier model capitalized on such a developmental gene–environment interaction, giving the high heritability of IQ a convincing explanation. According to their model (see Fig. 1c), children not only actively select their environment in accordance with their genetic endowment, but also this environment influences their IQ, creating reciprocal causal relations between the phenotype and the environment. This way, Dickens and Flynn arrived at a truly developmental model of intelligence.

Even more recently, and following a decidedly different track, van der Maas et al. (2006) showed how interactions between cognitive processes are capable of explaining high heritability. Whereas Dickens and Flynn (2001) broke g into genetic and environmental factors, van der Maas et al. (2006) proved that a single underlying factor is no intrinsic requirement for explaining some of the most important phenomena in intelligence.

One dominant phenomenon

A second reason for the developmental blind spot is the primary focus on the positive manifold. Thanks to the work of particularly Spearman (1904) and Carroll (1993), the positive manifold is an undisputed phenomenon. In turn, static factor models have provided an elegant parsimonious explanation of this phenomenon. Yet, the positive manifold lacks a similarly strong developmental companion that can function as a yardstick for the proposed models. Cattell (1987) beautifully stressed the importance of such a phenomenon:

The theorist who wants to proceed to developmental laws about abilities—who wants to be “dynamic” in his explanations of the origin, growth, and nature of intelligence—must be patient to make and record observations first. He can no more focus meaningful movement without this “description of a given moment” than a movie director can get intelligible movement in a film without the individual “static” frames themselves presenting each a clearly focused “still.” (p. 4)

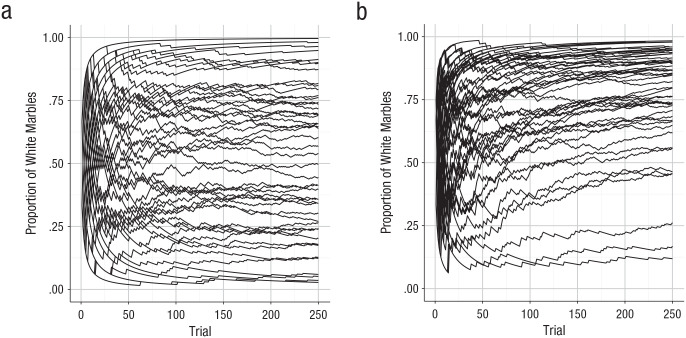
One phenomenon, the Matthew effect, results from exactly those descriptions of given moments: static frames that have been put in chronological order to give a description of the development of cognitive abilities. The Matthew effect is characterized by initially diverging yet increasingly stable patterns of development, as illustrated in Figure 2a, and may serve as a primary candidate for the role of developmental companion to the positive manifold.

Fig. 2.

Pólya urn demonstrations of (a) the Matthew effect and (b) the compensation effect. Starting with an urn that contains a white marble and a black marble, in each trial the drawn marble is replaced with two or three marbles of the same color, depending on the desired effect. The figures show the development of the proportion of marbles for 50 independent urns.

Originally coined by Merton (1968) to describe the widening gap in credit that scientists receive during their career, the term Matthew effect refers to the popular catchphrase “the rich get richer and the poor get poorer” and is named after the biblical figure Matthew. Although the Matthew effect does not necessarily involve the poor getting poorer, it does involve a widening gap between the rich and the poor in which the rich and the poor can be metaphors (e.g., for the skilled and the unskilled).

The Matthew effect is in no way an isolated phenomenon. Although the preferred term varies between (and within) disciplines, including cumulative advantage, preferential attachment, and dynamic complementarity, the intended process is essentially the same. Other related terms, on the other hand, such as the fan-spread effect and power law, may refer to the observed effect rather than the underlying process (Bast & Reitsma, 1998; Perc, 2014). Perc (2014) provided a comprehensive overview of the Matthew effect in empirical data.

Stanovich (1986) was probably the first to link the Matthew effect to education in an attempt to conceptualize the development of individual differences in reading. In this field, he argued, initial difficulties with reading acquisition can steadily propagate through reciprocal relationships with related skills, ultimately creating more generalized deficits.

Yet, the effect is not undisputed. For instance, Shaywitz et al. (1995) found a Matthew effect for IQ but not for reading when controlling for regression to the mean. Moreover, there is also evidence for the opposite developmental trajectory, the so-called compensation effect. This effect, for instance found by Schroeders, Schipolowski, Zettler, Golle, and Wilhelm (2016), describes a closing rather than widening gap.

Complicating things further, it is often hypothesized that both the factors driving and combating the gap influence development. This is, for instance, clearly explained by Schroeders et al. (2016): “It seems that the compensation effect of a formalized learning environment counteracts the effect of cumulative advantages that is present in a non-formalized setting” (p. 92). This idea at least provides an explanation for the more ambiguous status of these two developmental phenomena, especially compared with the positive manifold.

However, and importantly, evidence for a “general factor of cognitive aging” is consistent with the Matthew effect. In an exciting meta-analysis, Tucker-Drob, Brandmaier, and Lindenberger (2019) showed that “individual differences in longitudinal changes in different cognitive abilities are moderately to strongly correlated with one another” (p. 21). Such a developmental notion of a positive manifold strongly supports a Matthew effect because it implies that a future cognitive state positively depends on a past cognitive state. Moreover, the authors were right to warn that the observed general factor of cognitive aging does not necessarily imply a single cause. Rather, “an equally logical possibility is that the common factor of change represents an emergent property of dynamical systems processes that occur more directly between etiological factors and ability domains” (Tucker-Drob et al., 2019).

Summarizing, it should not come as a surprise that Protopapas, Parrila, and Simos (2014) suggested to focus on the reciprocal relations that drive Matthew effects rather than estimating the gap itself. And intriguingly, one deceptively simple mechanism—driven by such reciprocal relations—can actually explain the Matthew and compensation effects. However, before we introduce the mechanism, we first briefly discuss a second blind spot: idiography.

The idiographic blind spot

Confusingly, whereas it is generally understood that intelligence is a property of a single individual, many key phenomena in intelligence—including the positive manifold and Matthew and compensation effects—reflect structural differences between multiple individuals. Jensen (2002) warned us for this confusion, by explaining that

it is important to keep in mind the distinction between intelligence and g. . . . The psychology of intelligence could, at least in theory, be based on the study of one person, just as Ebbinghaus discovered some of the laws of learning and memory in experiments with N = 1. . . . The g factor is something else. It could never have been discovered with N = 1, because it reflects individual differences in performance on tests or tasks that involve any one or more of the kinds of processes just referred to ads intelligence. The g factor emerges from the fact that measurements of all such processes in a representative sample of the general population are positively correlated with each other, although to varying degrees. (p. 39–40)

Jensen’s (2002) warning is far from frivolous and concerns the broader field of psychological science. For instance, Molenaar (2004) and Borsboom et al. (2009) expanded on this cautionary tale by showing that intraindividual (idiographic) interpretations of interindividual (nomothetic) findings lead to erroneous conclusions, only exempting cases in which very strict assumptions are met. Consequently, models of individual differences should be based on models of the individual—a message that is reinforced by Molenaar’s urgent call for an idiographic approach to psychological science: explaining nomothetic phenomena with idiographic models.

One promising approach to idiography are network models, briefly discussed in relation to the mutualism model from van der Maas et al. (2006). Indeed, networks are an ideal (and idealized) tool for modeling the individual. These networks, or graphs, are a general and content-independent method for representing relational information. It graphically represents entities, typically rendered as circles called nodes or vertices, and their relations, typically rendered as lines called edges or links. Because networks are content-independent, few sciences, if any, fail to appreciate their value. Notable applications span from social networks, describing relations between individuals (e.g., Duijn, Kashirin, & Sloot, 2014), to attitude networks, describing relations between attitudes across individuals (e.g., Dalege, Borsboom, van Harreveld, Waldorp, & van der Maas, 2017), and psycho-pathological networks, describing relations between symptoms within individuals (e.g., Kroeze et al., 2017).

In the next section, we discuss a simple yet powerful mechanism that explains idiographic development. Although the mechanism is too simplistic for our ultimate aim—the formal model of intelligence introduced in second part—it convincingly conveys the power of simple developmental mechanisms. We show how it explains the previously discussed Matthew and compensation effects as well as the third source phenomenon. Finally, we use a simple network transformation to illustrate the benefit of networks in idiographic science.

Idiographic development: the case of Pólya’s urn

Before we proceed with the second part—the introduction of the model—we briefly discuss an elegant abstraction of a growth process. The Pólya–Eggenberger urn scheme (Eggenberger & Pólya, 1923), or simply Pólya’s urn, intuitively mimics a system that grows dynamically through preferential attachment and hence gives us a convenient tool to illustrate a basic mechanism of development. Moreover, we use the obtained surface understanding of Pólya’s urn to clarify not only the Matthew and compensation effects but also the third source phenomenon.

A brief example may clarify the mechanism. Imagine a girl receiving a tennis racket for her birthday. Before her first tennis lesson, she practices the backhand twice at home, incorrectly unfortunately. Then, during the first lesson, her trainer demonstrates to her the correct backhand. She now has three experiences, two incorrect and one correct. Now, suppose her backhand development is based on a very simple learning schema. Whenever a backhand return is required, she samples from her earlier experiences, and the sampled backhand is then added to the set of earlier experiences. How will she develop? That is, how will her backhand develop in the long term? And what is the long-term expectation for her equally talented twin sister with the same trainer?

Pólya’s urn gives us an important intuition. It is represented as an urn that contains two different-colored marbles, say black and white. One marble is randomly drawn from the urn and replaced by two marbles of the same color, a procedure that is repeated $n$ trials. The time course of this process is rather counterintuitive. One might expect this process to diverge to extreme values, but it rather progresses toward a random number between 0 and 1.¹ As can be deduced from this process, it ensures dynamical growth through preferential attachment: The urn grows each trial, with a preference toward the most abundant color.

In the example of the girl learning to play tennis, her previous experience thus affects her future experience. With two incorrect experiences and one correct experience, her next experience is most likely incorrect. However, because it is a stochastic process, her next experience might as well be correct, creating a new situation in which she has a 50% chance of hitting the ball correctly on her next try. Of course, this is the case assuming that she practices on her own. A second intervention by her trainer might help her to increase her chances of hitting the ball correctly.

The applicability of Pólya’s urn is endless, and various modifications have been proposed to accommodate a diversity of issues. In Eggenberger and Pólya’s (1923) original work, the number of replaced marbles can be of any positive value, and Mahmoud (2008) described a number of modifications to this basic scheme. Important applications range from the evolution of species (Hoppe, 1984) to unemployment (Heckman, 1981).

Crucially, models of contagion—such as Pólya’s urn—cannot be statistically distinguished from factor models. This situation is analogous to the previously discussed incapacity of statistical models to distinguish between factor models, sampling models, and network models. Greenwood and Yule (1920) provided the probability distributions that result from contagious processes and latent causes, and later it was realized that both distributions can be rewritten into the beta-binomial distribution. The importance of this fact for epidemiology, in which it is well known, can hardly be overlooked: Imagine combating Ebola from an entirely genetic perspective rather than preventing contagion. However, in intelligence research, this realization is just as fundamental: The fit of a statistical model to correlational data cannot illuminate the actual underlying causal processes.

Pólya’s urn and the Matthew effect

Here, we are concerned with the urn’s ability to simulate typical developmental patterns of cognitive ability. We consider the unmodified version of Pólya’s urn that we described previously. Figure 2a shows the proportions of white marbles for 250 trials from 50 independent urns. As you can see, the urn compositions quickly diverge. The earlier trials have the largest effects, with gradually decreasing influence over time. Indeed, this pattern closely resembles the general Matthew effect, in which at the start, within-person variance is high, gradually decreasing over time, and between-person variance is low, gradually increasing over time.

Pólya’s urn might thus be conceived as a model for a developmental process that produces a Matthew effect. The initial configuration of the urn depicts the genetic component, whereas the trials represent the environmental experiences. The white marbles can, for instance, represent skills that reinforce advantageous experiences, whereas the black marbles might represent misconceptions that reinforce disadvantageous experiences. Via a strict random process, the urns’ configurations diverge in a similar vein as the multiplier process of in Dickens and Flynn (2001). In this Pólya process, skills and misconceptions are reinforced, ultimately growing toward a stable state.

However, one significant additional property over the multiplier mechanism must not be overlooked. Because the distribution of color of each independent urn is exactly equal at the start, it is shown that Pólya’s urn does not require initial genetic differences for the multiplier process to do its work. This illuminating effect is not necessarily an artificial property of Pólya’s urn: For example, Freund et al. (2013) showed that individual differences actually can emerge in genetically identical mice. Summarizing, Pólya’s urn shows that neither genetic nor environmental differences are necessarily required for individual differences to arise, although surely, one should not be fooled into thinking that those therefore play no role in intelligence. We briefly expand on this observation in the section following the next.

Pólya’s urn and the compensation effect

Naturally, environmental influences are less random than assumed here. One strong systematic influence is formal education, which is hypothesized to create compensatory effects that counteract the Matthew effect. Figure 2b shows what this effect could look like. To obtain the effect, we slightly adapted Pólya’s urn to allow for one possible effect of education. Rather than reinforcing an advantageous experience with one extra marble, we now reinforce it with two extra marbles, with p = .5, while keeping the rule for reinforcing disadvantageous experiences the same. An adaptation such as this can, for instance, be conceptualized as the beneficial effect of practice and instruction in education. Likewise, remediation of disadvantageous experiences such as errors may too create a compensation effect and can be modeled by not reinforcing such an experience with an extra marble.

Pólya’s urn and the third source

One more connection deserves to be discussed: Pólya’s urn and the third source of developmental differences. The third source refers to phenotypic variability that cannot be attributed to either genetic or environmental factors. To explain the third source phenomenon, two articles (Kan, Ploeger, Raijmakers, Dolan, & van der Maas, 2010; Molenaar, Boomsma, & Dolan, 1993) proposed rather complicated nonlinear models. Conveniently, the third source becomes directly apparent in Pólya’s urn. In the two examples of Pólya processes in Figure 2, both the genetics (the initial urn configurations) and the environment (the rules for drawing and replacing the marbles) are identical. Yet, the developmental trajectories vary greatly.

The third source is also clearly shown when heritability estimates are calculated for Pólya’s urn. If solely genetic and environmental factors would contribute to phenotypic variability, heritability estimates in Pólya’s urn—with identical initial urn configurations and growth mechanisms—would be $1$. In Figure 3, we show the heritability estimates over time based on identical twins with identical environments. Clearly, heritability estimates are not 1 even for twins whose initial urns already contain 10 times as many marbles as the urns used in Figure 2 and are therefore less prone to diverge.

Fig. 3.

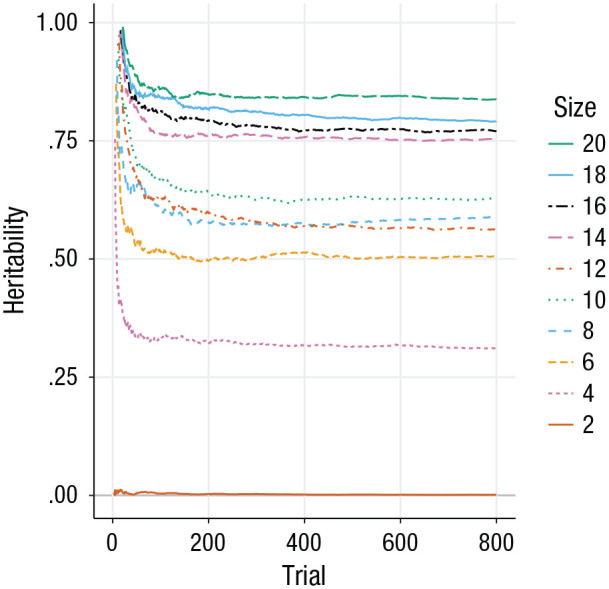
Heritability estimates of 200 identical twins in Pólya’s urn. Initial urn configurations are sampled such that each urn contains black and white marbles. The standard growth mechanism is used for all twins: One marble is randomly drawn from the urn and replaced by two marbles of the same color. This process is repeated until the urn contains 800 marbles. At each developmental step (x-axis), the heritability is calculated (y-axis) as the squared correlation between the proportions of white marbles in current and past developmental steps of a twin pair, averaged over all twin pairs. This process is repeated for different initial urn sizes (line type and line color).

Pólya’s urn as a network

By transforming the example of Pólya’s urn to a network representation, the benefit of networks in an idiographic science is clearly shown. Conveniently, Pólya’s urn permits a simple transformation to such a network representation. Imagine a network with two types of nodes: black nodes that represent some kind of misconception and white nodes that represent some kind of correct conception. Analogous to the urn example, the initial network may consist of a disconnected black and white node. Now, on each trial, one node is randomly attached to one of the existing nodes in the network, copying its color. This simple mechanism ensures that the probability of a new node receiving a certain color is proportional to the number of existing nodes with that color, essentially a preferential attachment mechanism.

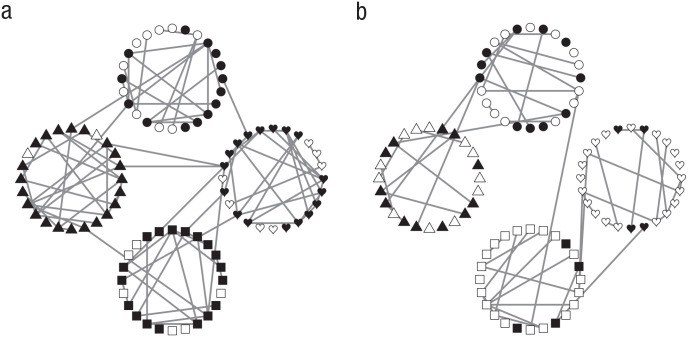
Each of the Pólya’s urn networks in Figure 4—graphs created with the qgraph package (Version 1.6; Epskamp, Cramer, Waldorp, Schmittmann, & Borsboom, 2012) for the R software environment (Version 3.6.1; R Core Team, 2019)—represents a different individual and already illustrate their benefit in an idiographic science: For each individual, the values of the nodes and presence of the links are shown. However, the unidimensional structure of this simple urn example is too simplistic for the ultimate objective to describe a multidimensional intelligence. While preserving the network perspective, in the next part, we introduce a new, formal, and multidimensional model of intelligence—a theory that explains both stationary and developmental phenomena, an abstraction that concretely describes an individual’s skills and knowledge on the level of specific educational items, and an avenue for separating the role of genetics and the environment.

Fig. 4.

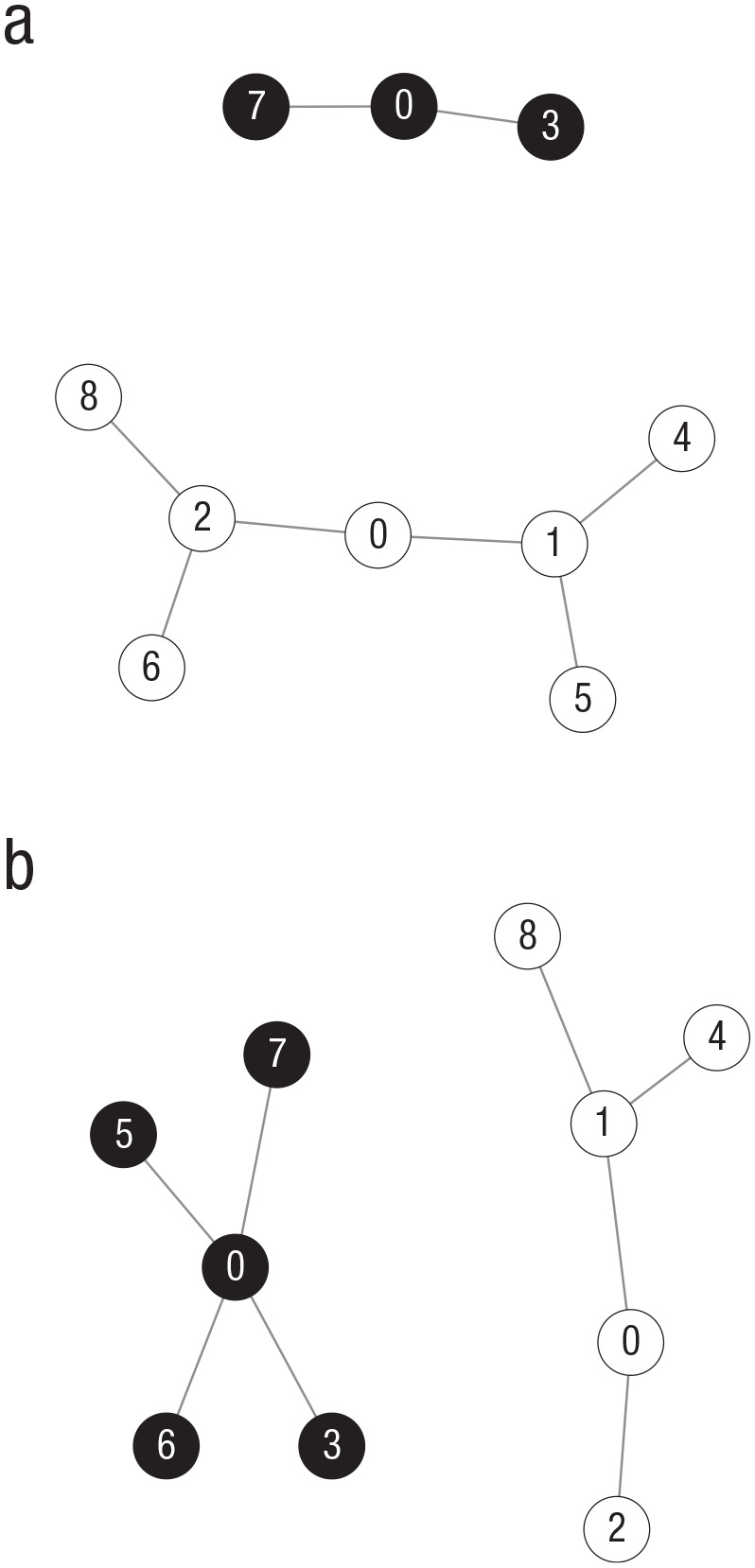
Two instances of a Pólya’s urn network. Both networks started with a single black node and a single white node (t = 0). In addition, the networks share an identical growth mechanism: A new node is randomly connected to one of the existing nodes and copies its color. The numbers show the time points at which the nodes were added.

The Wiring of Intelligence

At the intersection of the issues discussed in the previous part, we propose a novel formal model of intelligence.² We conceptualize intelligence as evolving networks in which new facts and procedures are wired together during development. Take Cornelius, a 6-year-old student who has just started to learn addition. In his—still limited—cognitive network, some first addition nodes can be observed. One obtained node represents the “7 + 7 = 14” fact. He memorized this fact from one of those times his older brother Pete was showing off what he had learned that day at school, and the node is therefore not connected to other facts and procedures. Some other obtained nodes, such as the “2 + 2 = 4” and “2 + 3 = 5” facts, are connected to his counting skill because Cornelius still counts his fingers to obtain the answers to those problems. Another group of interconnected yet unobtained nodes seems to share a common cause: Cornelius’s teacher recently tried to explain how one should add single-digit numbers and two-digit numbers, and Cornelius now systematically—and mistakenly—adds 1 rather than 10 to the sum of the units. Thus, Cornelius’s complete cognitive network can be seen as a collection of his obtained and unobtained facts and procedures that steadily evolves during his development.

In this second part, we first describe a static model, hereafter referred to as wired intelligence, and clarify how it explains two key stationary phenomena: the positive manifold and intelligence’s hierarchical structure. We then describe a dynamic model, hereafter referred to as wiring intelligence, and clarify how it explains developmental phenomena such as the Matthew effect and the age dedifferentiation hypothesis. The model’s composition of a static and dynamic part reflects its twofold aim—explaining stationary and developmental phenomena—and stresses the poor balance in substantiation of the phenomena in both categories. Moreover, it enables the static and dynamic part to be assessed and further developed in relative isolation.

Statics: wired intelligence

We conceptualize intelligence as an individual’s network of interrelated cognitive skills or pieces of knowledge, such as illustrated in Figure 5. In this network, G = (V, E), the set of p distinct cognitive skills or pieces of knowledge (terms used interchangeably in the remainder of the article) are represented as labeled nodes V and their possible relations as edges E. It is assumed that the set E contains all p(p – 1)/2 possible relations between the p nodes of the network. To each node i in the network, we associate a random variable that takes one of two values,

Fig. 5.

Two instances of the Fortuin and Kasteleyn (1972) model. The cognitive networks of (a) Cornelius and (b) Pete consist of 96 nodes, equally distributed across four domains (represented by nodes of different shapes). Cornelius has 25 pieces of obtained knowledge (white nodes), and Pete has 65 pieces of obtained knowledge. Networks were generated with ${\mathrm{\theta }}_W=.07$, ${\mathrm{\theta }}_B=.005$, and µ $=.03$; parameters are introduced in the text of the article.

$$x_i=(\begin{array}{ll}+1\hfill & \mathrm{if}\mathrm{the}\mathrm{skill}\mathrm{or}\mathrm{knowledge}i\mathrm{is}\mathrm{obtained}\hfill \\ -1\hfill & \mathrm{if}\mathrm{the}\mathrm{skill}\mathrm{or}\mathrm{knowledge}i\mathrm{is}\mathrm{unobtained}.\hfill \end{array}$$

Furthermore, we associate to each edge $e=〈i,j〉$ in $E$ a random variable ${\mathrm{\omega }}_e$ that also takes one of two values,

$${\mathrm{\omega }}_e={\mathrm{\omega }}_{〈i,j〉}=(\begin{array}{ll}1\hfill & \begin{array}{l}\mathrm{if}\mathrm{a}\mathrm{direct}\mathrm{connection}\mathrm{between}\mathrm{skills}\\ \mathrm{or}\mathrm{knowledge}i\mathrm{and}j\mathrm{is}\mathrm{present}\end{array}\hfill \\ 0\hfill & \begin{array}{l}\mathrm{if}\mathrm{a}\mathrm{direct}\mathrm{connection}\mathrm{between}\mathrm{skills}\\ \mathrm{or}\mathrm{knowledge}i\mathrm{and}j\mathrm{is}\mathrm{absent}.\end{array}\hfill \end{array}$$

This assembly of dichotomous nodes and edges thus forms our abstraction of idiographic intelligence. In addition, two remarks must be made regarding the nodes. First, the model is ignorant with respect to their exact substance, that is, the cognitive skills or pieces of knowledge they represent. Second, besides the obtained and unobtained knowledge that the nodes represent, it is important to consider that the majority of possible nodes is absent from the cognitive network. To illustrate, in the network conception of 6-year-old Cornelius, nodes that reflect concepts such as integrals are most likely unobserved. Thus, the actual presence of nodes depends on factors such as maturation and education.

Fortuin–Kasteleyn

The definitions of nodes and edges give us a minimal description of the wired intelligence network. Now, the model aims to describe the probabilities with which skills are either obtained or unobtained and how they are related. It is this description of probabilities that enables us to explain the established stationary phenomena.

The following model, proposed by Fortuin and Kasteleyn (1972, hereafter referred to as the Fortuin–Kasteleyn model) in the statistical physics literature, forms the basis of this approach,

$$p(x,\mathrm{\omega })=\frac{1}{{\mathrm{Z}}_F}\prod _{i=1}^{p-1}\prod _{j=i+1}^p\left\{\mathrm{\theta }{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-\mathrm{\theta })(1-{\mathrm{\omega }}_{〈i,j〉})\right\},$$ (1)

in which $\mathrm{\theta }$ is a parameter of the model that describes the probability that any two skills become connected, the factor $(x_i{x}_j+1)/2$ is equal to zero whenever $x_i\ne x_j$ and equal to one whenever $x_i=x_j$, and ${\mathrm{Z}}_F$ is a normalizing constant. To illustrate the model, Table 1 shows the various possible states of a network with two nodes and gives the probabilities for those states given three different values of $\mathrm{\theta }$.

Table 1.

Evaluation of the Fortuin–Kasteleyn Model With Two Nodes

State	$p(x,\mathrm{\omega })\propto$	$p(x,\mathrm{\omega })$	$\mathrm{\theta }=1$	$\mathrm{\theta }=1/2$	$\mathrm{\theta }=0$
$x_1=+1$; $x_2=+1$; $\mathrm{\omega }=1$	$\mathrm{\theta }$	$\mathrm{\theta }/{\mathrm{Z}}_F$	$1/2$	$1/6$	$0$
$x_1=-1$; $x_2=+1$; $\mathrm{\omega }=1$	$0$	$0$	$0$	$0$	$0$
$x_1=+1$; $x_2=-1$; $\mathrm{\omega }=1$	$0$	$0$	$0$	$0$	$0$
$x_1=-1$; $x_2=-1$; $\mathrm{\omega }=1$	$\mathrm{\theta }$	$\mathrm{\theta }/{\mathrm{Z}}_F$	$1/2$	$1/6$	$0$
$x_1=+1$; $x_2=+1$; $\mathrm{\omega }=0$	$1-\mathrm{\theta }$	$(1-\mathrm{\theta })/{\mathrm{Z}}_F$	$0$	$1/6$	$1/4$
$x_1=-1$; $x_2=+1$; $\mathrm{\omega }=0$	$1-\mathrm{\theta }$	$(1-\mathrm{\theta })/{\mathrm{Z}}_F$	$0$	$1/6$	$1/4$
$x_1=+1$; $x_2=-1$; $\mathrm{\omega }=0$	$1-\mathrm{\theta }$	$(1-\mathrm{\theta })/{\mathrm{Z}}_F$	$0$	$1/6$	$1/4$
$x_1=-1$; $x_2=-1$; $\mathrm{\omega }=0$	$1-\mathrm{\theta }$	$(1-\mathrm{\theta })/{\mathrm{Z}}_F$	$0$	$1/6$	$1/4$
	${\mathrm{Z}}_F=4-2\mathrm{\theta }$	$1$	$1$	$1$	$1$

Note: The eight possible states of a network with two nodes (Column 1), evaluated under the Fortuin–Kasteleyn model (Columns 2 and 3), for three different values of $\mathrm{\theta }$ (Columns 4, 5, and 6). States differ with respect to whether the nodes ($x_1$ and $x_2$) are obtained ($+1$) or unobtained ($-1$) and connected ($\mathrm{\omega }=1$) or not connected ($\mathrm{\omega }=0$). The values in the final three columns represent the probabilities of observing a certain state of the network (Column 1) given the value of $\mathrm{\theta }$ (Columns 4, 5, or 6) and are calculated from the model (Column 3, i.e., Column 2 proportional to its sum). The bottom row sums over all states. Fortuin–Kasteleyn = Fortuin and Kasteleyn (1972).

An important property of the model is that whenever two skills are connected to one another, they are necessarily in the same state, that is, they are either both present or both absent. Consequently, whenever two skills are in different states, that is, one skill is present while the other is absent, then these two skills cannot be connected to one another. With this simple rule and the single parameter $\mathrm{\theta }$, the model can describe the joint probability distribution of both the nodes (i.e., skills or knowledge) and their relations.

Idiography

This unaltered Fortuin–Kasteleyn model already has highly beneficial properties for the study of intelligence, making it a convenient point of departure. Figure 5 illustrates a few of the properties thus far discussed. To begin with, we can ensure idiography, the first modeling principle. Because the model is characterized by both random nodes and edges, both skills and their relations may vary across individuals. This is clearly seen in the differences between the individuals in the figure, Cornelius and Pete, which are instances of the exact same model. In Pete’s network, considerably more knowledge is obtained than in Cornelius’s network, while at the same time it is less densely connected (both within domains and between domains). In addition, interesting differences between domains exist; Pete clearly performs differently on two of the four domains. The careful eye spots that the connected nodes form clusters only with either obtained knowledge or unobtained knowledge, a homogeneity that is dictated by the model.

Positive manifold

The next property of this model we turn to is the positive manifold it produces. As discussed in the introduction, the uncontested significance of this phenomenon renders a plausible explanation a burden of proof for any serious theory of intelligence. Intuitively, this property of the Fortuin–Kasteleyn model is shown by the fact that the correlation between any two nodes $x_i$ and $x_j$ in the network is positive. This is the case whenever the probability that the two nodes are in the same state, $p(x_i=x_j)$, is larger than the probability that the two nodes are in a different state, $p(x_i\ne x_j)$. The following equation by Grimmett (2006, p. 11) confirms this,

$$p(x_i=x_j)=\frac{1}{2}+\frac{1}{2}p(i\leftrightarrow j)\ge \frac{1}{2},$$

in which $p(i\leftrightarrow j)$ is the probability that nodes $i$ and $j$ are connected by an open path (i.e., are in the same cluster). Because $p(i\leftrightarrow j)$ is nonzero, $p(x_i=x_j)$ is strictly larger than $0.5$, and the positive manifold emerges.

Figure 6 shows the positive manifold using a heat map. Each of the patches in the figure represents a correlation between two nodes. The positive manifold can be deduced from the fact that all patches indicate a positive correlation. For this figure, we considered 1,000 idiographic networks, construed from the Fortuin–Kasteleyn model, with some important extensions laid out in the following sections.

Fig. 6.

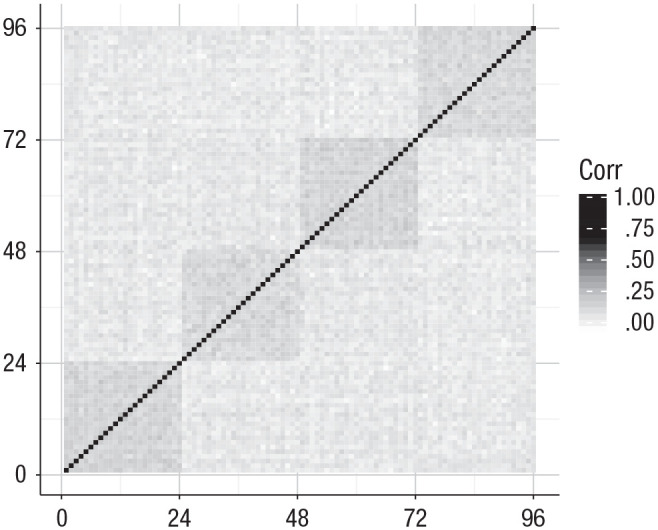
Heat map of the correlational structure of the nodes of the Fortuin and Kasteleyn (1972) model. As analogues to Spearman’s very first observation of the positive manifold in the correlational structure of his cognitive tests, the exclusively positive patches illustrate the positive manifold as a constraining property of the Fortuin–Kasteleyn model. In addition, the hierarchical structure of intelligence is clearly reflected in the block structure. Networks were generated with ${\mathrm{\theta }}_W=.07$, ${\mathrm{\theta }}_B=.005$, and µ $=.03$. Corr = correlation.

Hierarchical structure

Arguably the second most important stationary phenomenon in intelligence is its hierarchical structure. Although the debate on whether g is organized in a bifactor or higher-order structure continues to keep some intelligence researchers occupied, the fact that some cognitive domains form clusters, with higher correlations within clusters than between clusters, is uncontested (e.g., Carroll, 1993; Spearman, 1904). This phenomenon is reflected in the typical block structure seen in correlation matrices of intelligence tests (see Fig. 6).

Crucially, although the block structure clearly is present, the blocks are not fully isolated. Indeed, the small but meaningful correlations outside the blocks indicate interactions between the blocks. Simon (1962) termed this property near decomposability and demonstrated its ubiquitous presence across a multitude of complex hierarchical systems. In his words, “intra-component linkages are generally stronger than intercomponent linkages. This fact has the effect of separating the high-frequency dynamics of a hierarchy—involving the internal structure of the components—from the low frequency dynamics—involving interaction among components” (p. 477). The presence of both a general factor and a hierarchical structure can be seen to reflect this.

The human brain serves as a convenient illustration. The functional specialization of our brain can cause different cognitive tasks to tap into structurally dispersed brain areas (e.g., Fodor, 1983; Johnson, 2011; Spunt & Adolphs, 2017), making within-community connectivity more likely and between-community connectivity less likely. An example is the (increasing) functional specialization of arithmetic (e.g., Dehaene, 1999; Rivera, Reiss, Eckert, & Menon, 2005). Note that the hierarchical structure seems consistent with brain networks of fluid intelligence (Santarnecchi, Emmendorfer, & Pascual-Leone, 2017). Naturally, this does not exclude the possible existence of processes that play a more general, or maybe central, role in cognitive functioning, such as mitochondrial functioning (Geary, 2018).

In network models, the block pattern is generally referred to as a community structure. In the model proposed here, we impose such a structure by creating communities of nodes that have a higher probability of connecting with nodes within their community than with nodes in other communities. Note that the model is ignorant with respect to the exact substance, or content, of a component because for the theoretical purpose of the model, the levels of the hierarchy are irrelevant. Yet, for illustrative purposes, in the specification of the model hereafter, we assume that the communities are known.

Suppose that there are two communities: skills that are related to mathematics and skills that are related to language. We partition the set of nodes V into two groups, V = (V_M, V_L), one associated to each community. Likewise, we partition the set of edges E into three parts, E = (E_M, E_L, E_ML), in which E_M are the relations between different mathematics skills, E_L the relations between different language skills, and E_ML are all the relations between a mathematics-related skill and a language-related skill. In principle, we may associate to each community of skills c a unique probability θ_c to connecting its members and associate to each pair of communities c and d a unique probability π_cd to connect members from the community c to members of the community d. However, for now, it is sufficient to have one probability θ_W to connect the skills within a community and one probability θ_B to connect skills between two different communities. If θ_W > θ_B, it follows that $p(i\leftrightarrow j)$ is larger for any two skills $i$ and $j$ within the same community than for two skills $i$ and $j$ that are not a member of the same community. As a result, a hierarchical pattern of correlations emerges from the model, with higher correlations between skills within a community than between skills from different communities.

Figure 5 shows two networks that arose from our extended model, of which a formal expression is given in the Appendix. The four communities in the networks are denoted by the various node shapes. Note that communities should not be confused with clusters—the nodes, or groups of nodes, that are isolated from the rest of the network. In these networks, the within-community connectivity was set to ${\mathrm{\theta }}_W=.07$ and between-community connectivity to ${\mathrm{\theta }}_B=.005$. Of course, these probabilities can be seen as an empirical estimation problem, which we do not consider here. Figure 6 shows how the community structure is reflected in the correlational structure of 96 nodes across 1,000 extended Fortuin–Kasteleyn models.

General ability

Note that the Fortuin–Kasteleyn model has no preference toward obtained or unobtained pieces of knowledge. However, in the proposed model, we assume that there actually is a preference and indeed toward general ability. Reminded of the previously mentioned 6-year-old named Cornelius, this preference reflects the fact that, for instance, education usually is at the level of the student and aims at attainable goals (i.e., learning generally takes place in the zone of proximal development; Vygotsky, 1978), and interactions with the environment fit the individual to a large extent (i.e., there is a significant degree of reciprocity in people’s intelligence and how they create and select their environments and experiences; Scarr & McCartney, 1983). Moreover, anticipating the growth perspective that is introduced in the next section, it is evident that individuals tend to become more able rather than less able (i.e., if we ignore cognitive decline due to aging and degenerative diseases).

To account for this bias toward aptitude, we impose a so-called external field µ that is minimally positive. External fields are used in physics to represent some outside force that acts on variables in a network, and to understand this idea, magnetism provides a clarifying illustration. In the study of magnetism, variables in the network may represent the electrons in a piece of iron that either have an upward spin (i.e., $x_i=1$) or a downward spin ($x_i=-1$). When the spins align, the iron is magnetic. One way to magnetize a piece of iron is by introducing an external field (i.e., holding a magnet close to the object) that pulls the electrons in a particular direction.

By applying a minimally positive external field, we thus ensure that the nodes in the network have a slight preference toward general ability. Consequently, on average, knowledge is more often obtained than unobtained in the population. For an individual network, this fact implies that it is more likely that the knowledge in a particular cluster is all obtained rather than all unobtained. Our model extension that includes the external field µ is given in the Appendix. In the networks used to create Figures 5 and 6, we set µ $=.03$.

Moreover, as is shown in the Appendix, the probability that a cluster consists of obtained knowledge is proportional to the size of the cluster. This means that the larger the cluster is, the more likely the nodes in the cluster reflect obtained knowledge. This idea ensures—with high probability—that the giant component (the largest cluster) consists of pieces of knowledge that are obtained rather than unobtained. Note that the external field could be negative too, in the rare situation that the environment elicits misconceptions.

Dynamics: wiring intelligence

The static wired intelligence model provides a solid basis for the second aim. We conceptualize intelligence as evolving networks in which new facts and procedures are wired together during development. In this section, we therefore explore the model from such a developmental point of view. We discuss three scenarios.

Scenario 1: development toward equilibrium

Al-though we do not know the exact causal mechanisms that drive development, we can observe the model during development. In the first scenario, we started the network in an undeveloped state, with solely unobtained pieces of knowledge and no edges. We then used a Gibbs sampling procedure to grow the network toward its equilibrium state: the extended Fortuin–Kasteleyn model with its desirable properties. The positive manifold and hierarchical structure displayed in Figure 6, discussed in the previous section, necessarily follow from this approach because they are properties of the Fortuin–Kasteleyn model.

Here, we are concerned with how the model develops over time. As the Gibbs sampler rapidly converge the networks to an equilibrium state, we slowed down the process by updating the nodes and edges in each iteration with $p=.15$. This way, we aimed to get insight into how the model behaves toward its equilibrium state. In Figure 7, we illustrate, for 1,000 networks, the growth in the number of obtained pieces of knowledge across the first 30 iterations of the decelerated Gibbs sampler. We considered 96 nodes across four domains and set the external field to .03, the within-community connectivity to .07, and the between-community connectivity to .005.

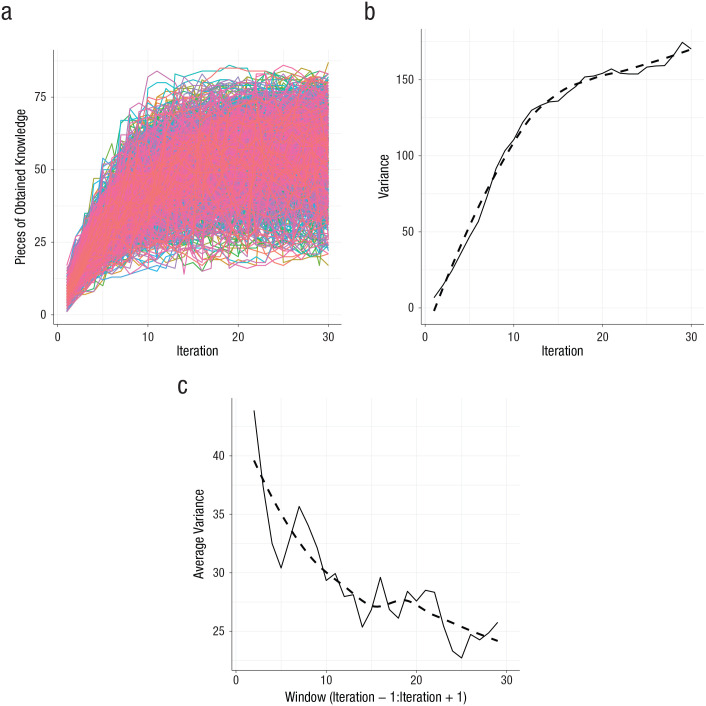
Fig. 7.

The Matthew effect when the Gibbs sampler—used to sample a network from the model—is decelerated. The graph in (a) shows the fan spread that characterizes the Matthew effect. The graph in (b) shows the variance in obtained pieces of knowledge across networks. The graph in (c) shows the average variance in obtained pieces of knowledge across subsequent states of individual networks. The dashed line indicates the smoothed variance; the solid line indicates the actual variance.

Figure 7 provides a clear indication of the Matthew effect. First, Figure 7a shows the fan-spread effect that characterizes the Matthew effect. Although all simulated persons were conceived with the exact same cognitive networks, early differences in the number of obtained pieces of knowledge become more pronounced over time, until they stabilize. Figure 7b shows that the variance in obtained pieces of knowledge across networks indeed increases and ultimately stabilizes.

Moreover, Figure 7c shows that the variance in obtained pieces of knowledge across subsequent states of individual networks decreases over time, an effect that is also observed in the example of Pólya’s urn that is displayed in Figure 2c. However, as opposed to the Matthew effect in the Pólya’s urn example, the positive external field in the wired intelligence model ensures that a general ability arises.

This scenario, in which a cognitive network grows from an undeveloped state into an equilibrium state, was also used by van der Maas et al. (2006) in their description of the mutualism model. A criticism of this approach is that from the onset of development until the moment it reaches its equilibrium state, the exact properties of the network are unknown. In the next scenario, we avoided this issue by inspecting the networks solely in equilibrium but across different sizes.

Scenario 2: development in equilibrium

Rather than observing the model during the sampling dynamics, in the second scenario, we investigated the development of the model across equilibrium states of networks of different sizes like—in the previously cited words of Cattell (1987)—the movie director that inspects the stills. To this end, we sampled networks ranging in size from 20 to 300 nodes, in steps of four nodes. We set the external field to .005, the within-community connectivity to .07, and the between-community connectivity to .01.

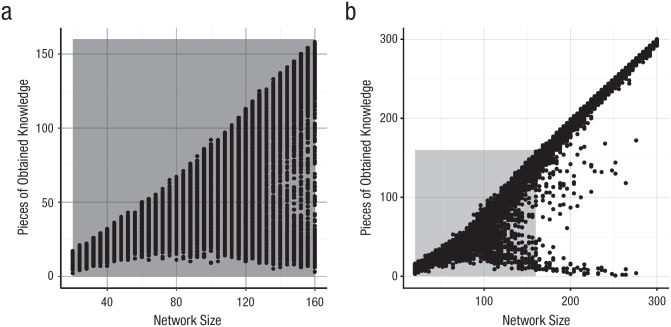
In Figure 8, we illustrate the growth in obtained pieces of knowledge across the increasing number of nodes in the respective networks. Naturally, the number of obtained pieces of knowledge cannot be higher than the total number of nodes in a network, hence the fact that all observations are in the lower right triangle. Figure 8a again shows the Matthew effect. This time, all observations are completely independent from one another, so no lines are shown.

Fig. 8.

The Matthew effect and bifurcation in developing networks. Points represent the number of obtained pieces of knowledge (y-axis) across networks of different sizes (x-axis). Each point represents an independent observation. The gray rectangles show the parts of the figures that overlap.

Note that when the networks continue to develop, they start to bifurcate. In Figure 8b, it is shown that this is the case for networks that contain roughly 100 or more nodes. This pattern bears similarities to the Matthew effect found in science funding (Bol, de Vaan, & van de Rijt, 2018), in which a similar divergence is seen for scholars that are just below and just above the funding threshold. In the case of science funding, the effect is partly attributed to a participation effect: Scholars just below the funding threshold may stop applying for further funding. In education, this participation effect is institutionalized through stratification: Students just below an ability threshold will receive education on a different level.

Here, the bifurcation arises from the preference of the Fortuin–Kasteleyn model to form clusters and from the fact that only nodes that are in the same state can become connected. As soon as all nodes are connected in a giant component, the networks contain either obtained or unobtained pieces of knowledge. In addition, the positive external field ensures that the larger the cluster, the higher the probability that it contains obtained pieces of knowledge, and hence the larger the number of observations near the diagonal. Finally, the low connectivity in the simulated networks creates some observations in between the two forks of the bifurcation.

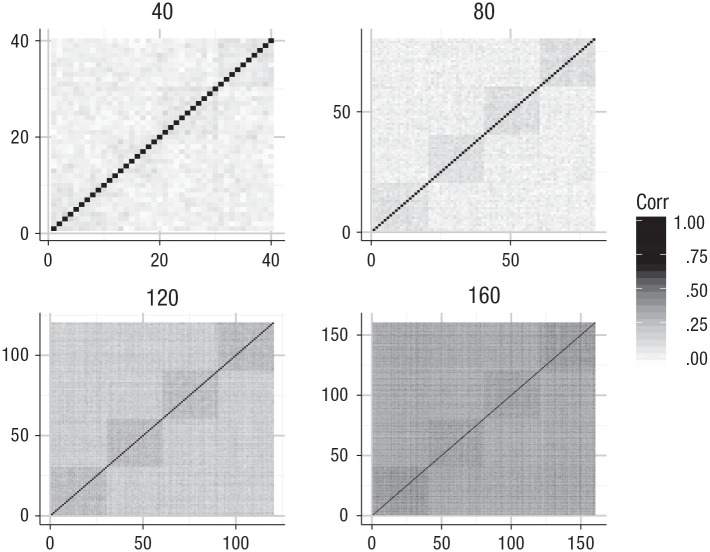
The growth of cognitive networks can also shed a new light on the positive manifold. In Figure 9, the positive manifold is shown again but this time across four different network sizes. We considered networks with 40, 80, 120, and 160 nodes and show that the positive manifold steadily increases with more nodes. This property of the model reflects a much discussed phenomenon in intelligence: the age dedifferentiation hypothesis. Dedifferentiation is the gradual increase of the factor g or, put differently, the increasingly common structure in intelligence across individuals. The hypothesis states that such dedifferentiation takes place from adulthood to old age. Age dedifferentiation’s antagonist, the age-differentiation hypothesis, posits that differentiation takes place from birth to early maturity.

Fig. 9.

Heat maps of the correlational structure of cognitive networks with 40, 80, 120, or 160 nodes (note the scale of each heat map) across four different domains. Each heat map is based on 1,000 networks. The exclusively positive patches illustrate the positive manifold, and the block structures illustrate the hierarchical structure. With networks increasing in size, the positive manifold increases too. Corr = correlation.

Evidence for the age differentiation and dedifferentiation hypotheses is both poor and problematic. Many scholars have tried to summarize the evidence, but all come to the conclusion that the evidence for either of the hypotheses is inconclusive. Methodological problems such as selection effects and measurement bias are commonly mentioned to account for the inconclusive evidence (e.g., van der Maas et al., 2006, which also discusses similar problems with ability differentiation). In the model proposed here, the strength of the positive manifold is primarily determined by the size of the giant component, which increases with the size of the network.

Scenario 3: a growth mechanism

Ultimately, the formulation of a formal developmental theory of intelligence requires the identification of mechanisms of growth and possibly decline. Although we are unaware of growth mechanisms that keep the Fortuin–Kasteleyn structure intact, we nonetheless end this section with a third approach. We first describe a simple growth mechanism, and because it may force the network out of equilibrium, we then briefly discuss an additional method that repairs the network to ensure that the discussed stationary phenomena remain guaranteed during development.

In this scenario, we conceptualize growth as the addition of previously absent nodes and edges to the cognitive network in which those new nodes may represent obtained as well as unobtained pieces of knowledge.³ Effectively, in the growth model, edges are sampled from the finite set of possible edges that constitute the full network. Nodes connected by a sampled edge—if previously absent—are added to the network. Then, the communities of the nodes connected by the edge are determined, and the nodes are actually connected in the cognitive network with a probability respective to the determined communities. We further explicate this growth mechanism below.

Growth mechanism

Let us start with the sampling mechanism for the edges. In our approach, we focus on growing the network topology—the wiring of skills and knowledge in a cognitive network—and let the states of the skills follow this process. To do so, we make use of the following factorization of the model:

$$f(x,w)=f(x|w)f(w),$$

in which $f(w)$ is the model for the topology, known as the random cluster model (Fortuin & Kasteleyn, 1972; Grimmett, 2006), that describes the wiring of the cognitive network.

This idea can be summarized as follows. Suppose that there is a full theoretical network $G=(V,E)$ that includes all potential skills, knowledge, and their relations. At conception, an individual may start with an empty network or a small initial subset of the network that may represent his or her genetic endowment. As time proceeds, skills, knowledge, and their relations are added to the network by sampling edges and their attached skills and knowledge. An edge $e=〈i,j〉$ between skills $i$ and $j$ is included in the individual’s cognitive network, with simply the previously discussed probability ${\mathrm{\theta }}_W$ to connect the nodes of the same community and probability ${\mathrm{\theta }}_B$ to connect the nodes of two different communities.

This very basic growth model allows for substantial variation across individual networks, thus satisfying the idiography principle. Edges may or may not be sampled, and once sampled, the attached nodes may become connected or disconnected, directly or indirectly via paths. The nodes may become obtained or unobtained pieces of knowledge and may end up isolated or connected with nodes of the same or other communities in small or large clusters. All of this process may all vary across development.

Restrained freedom

Two important remarks must be made with regard to this growth process, one on the considerable amount of freedom in this approach and one on a self-imposed restriction. First, and importantly, we do not prescribe a sampling model. That is, we conceptualize the sampling mechanism as an empirical fact, a process that can be simulated by one’s preferred theoretical model. To give some examples, edges may be added following an educational model (curricula determine the [order of the] sampled edges) or using a genetic model (the state of the initial network determines the sampled edges) or, for instance, reflect the multiplier effect model (both the subsequent states of the network and the environment determine the sampled edges). The model proposed in this article thus provides a unique opportunity to study the effects of such diverse sampling models.

Second, and not easily observed, is the fact that the suggested growth mechanism cannot guarantee that the properties of the static model, such as the positive manifold, will continue to hold. Therefore, to keep the model tractable during its growth, we impose a restriction that helps retain those properties. Basically, we repair the network if it is observed to deviate from the static model by re-pairing the most recent set of added nodes. This rewiring is sometimes required when two clusters are joined in the cognitive network. The procedure was described by Fill and Huber (2000).

One way to interpret the rewiring that is part of Fill and Huber’s (2000) approach is that it inspires a change in obtained knowledge of a newly joined cluster. That is, unobtained pieces of knowledge could be relatively static on a cluster over time but might switch states when two clusters are joined, reflecting a new insight. Because the giant component is increasingly likely to represent obtained knowledge, a newly connected component is likely to turn into a component of obtained knowledge. This way, learning occurs gradually in the cognitive network, one skill at a time, but also through phases, growing obtained knowledge on entire clusters at once.

A second consequence of this effort to retain the properties of the static model in a continuously evolving network is the fact that in the growth mechanism we do not determine the states of the nodes during development. This means that although at each point in time the network can be frozen and the states of the nodes determined, subsequent states are independent evaluations of the model. Although from a developmental point of view this idea might be seen as problematic, the justification is twofold. The first is a feature: Small clusters—such as clusters of a single node—represent unconnected knowledge or skills for which instability can be an actual property. Across the independent evaluations, these small clusters may flicker accordingly. On top of that, the positive external field discussed in the static model section ensures that the larger the cluster, the higher the probability that the nodes represent obtained knowledge. This probablity thus ensures that the larger the cluster, the more stable its state.

To conclude, it must be stressed that the discussed restriction—although not necessarily problematic—primarily provides us with a mathematical convenience rather than reflecting an empirical fact. And although we believe it is a welcome convenience for this initial suggestion of a growth mechanism, it may well be abandoned in future suggestions. For now, the growth and repair mechanisms—along with the static model—give us a minimal description of a wiring intelligence network.

Discussion

Since Spearman’s first attempt to explain the positive manifold, it has been the primary aim for formal theorists of intelligence. Although many scholars followed his factor-analytic footsteps, an approach that is dominant as of today, we now also know that it is only one of many possible explanations. Recent contributions to scholarly intelligence, such as the contemporary mutualism model and multiplier effect model, have greatly aided the field by providing novel explanations of a much-debated construct. In this article, we took those new directions two steps further by providing another alternative explanation. First, we introduced a truly idiographic model that captures individual differences in great detail. In doing so, it bridges the two disciplines of psychology by explaining nomothetic phenomena from idiographic network representations. Second, the model provides a formal framework that particularly suits developmental extensions and thus enables the study of both genetic and environmental influences during the development of intelligence.

The static wired intelligence model proposes a parsimonious and unified explanation of two important stationary phenomena: the positive manifold and the hierarchical structure. It does so without a need for mysterious latent entities and with an opportunity to study individual differences. Indeed, many more—yet less robust—phenomena have been identified in the past century. Although in its current form the model does not aim to explain all of these phenomena, it may very well serve as a point of departure for exploring or adding more of intelligence’s complexities. The dynamic wiring intelligence model is a much more modest contribution, a specimen of the potential of developmental mechanisms and an explicit call for increased inquiry into both developmental mechanisms and phenomena. Nevertheless, it may too serve as a point for departure for subsequent theorizing. Importantly and self-evident, both parts can be further built on by subjecting them to empirical facts.

An influential division only touched on in the introduction is that of fluid and crystallized intelligence. Although no formal theories exist that in detail disambiguate the structure or mechanisms underlying both components—thus far, the distinction is primarily descriptive—it is useful to relate both components to the model introduced here. This model clearly reflects the crystallized component of general intelligence: The static part gives structure to the skills and knowledge of the individual, and the dynamic part provides a placeholder for the mechanisms through which those skills and knowledge are acquired. The fluid component, on the other hand, is less easily related to the model. One way to think of fluid intelligence in terms of the model is that the individual, when confronted with novel information or situations, can actively manipulate the cognitive network to accommodate that novel information or situation, for instance by transforming existing—or generating new—edges or nodes. Such adaptivity is a property of many complex systems and primarily modeled by means of evolutionary mechanisms; however, it is not considered in the current model.

In this Discussion section, we first explain three modeling principles and then discuss how the model interprets and explains the positive manifold, hierarchical structure, and developmental effects from an idiographic perspective. Finally, we illustrate how this approach provides a unique opportunity to relate microlevel phenomena to the macrolevel phenomena prominent in intelligence research.

Modeling principles

In building the proposed model, we aimed to follow three important principles. First, a scientific theory should be formal. That is, the theory should be formulated as a mathematical or computational model. The traditional factor models of general intelligence are statistical models of individual differences. They do not specify a (formal) model of intelligence in the individual. In contrast, the multiplier effect model and the mutualism model have been formulated mathematically. The advantages are that these models are precisely defined, predictions can be derived unambiguously, and unexpected and undesirable by-effects of the model can be detected, for instance in simulations.

The second principle is that a theory of intelligence should be idiographic. With the network approach, we intend to bridge two separate research traditions: on the one hand, experimental research on cognitive mechanisms and processes and on the other hand, psychometric research on individual differences in intelligence. Cronbach’s (1957) famous division of scientific psychology into these two disciplines is still very true for the fields of cognition and intelligence. In the words of Ferguson (1954), “this divergence between two fields of psychological endeavour has led to a constriction of thought and an experimental fastidiousness inimical to a bold attack on the problem of understanding human behaviour” (p. 95). The model proposed in this article brings these fields together by enabling explanations of individual differences from hypothesized cognitive mechanisms.

Similarly important as the previous idea, the third idea is that a theory of intelligence should be psychological. This idea is expressed in Box’s (1979) famous argument that “all models are wrong but some are useful” (p. 202). Our aim was a model that is indeed illuminating and useful by carefully weighing mathematical convenience and psychological plausibility and ensuring it creates novel predictions about, for instance, the structure of intelligence and the role of education in the shaping of intelligence. Thus, the model proposed in this article acknowledges the need for explanatory influences of the environment, education, and development.

A new perspective

The introduced model strongly adheres to these principles and introduces a novel conception of intelligence. Other than by a unified factor (e.g., g models), a measurement problem (e.g., sampling models), or positive interactions (e.g., mutualism model and multiplier effect model), we explain the positive manifold by the wiring of knowledge and skills, or facts and procedures, during development.

In addition, in the model, the hierarchical structure of intelligence has an incredibly straightforward explanation: Knowledge and skills that are more related have a higher probability of becoming connected. This idea follows a simple intuition. If student Cornelius is trying to learn a new word, this word will attach with high probability to related words and with low probability to distant words. The richer his vocabulary, the higher the chance that this new word will stick. In cognitive science, this principle is dealt with in the study of schemata (e.g., Bartlett, 1932; van Kesteren, Rijpkema, Ruiter, Morris, & Fernández, 2014).

Finally, developmental phenomena are an unusual suspect in formal models of intelligence. Although decidedly less straightforward than the discussed stationary phenomena, we do believe that developmental trends—such as the Matthew and compensation effects—must play a key role in the study of developmental intelligence. As argued by Protopapas et al. (2014) and Schroeders et al. (2016) and as illustrated in the example of Pólya’s urn, mechanisms that can provide an explanation for both phenomena can turn out to be worthwhile in understanding key drivers of development.

In the proposed model, we show that a Matthew effect may spontaneously appear not only when an undeveloped network is grown toward its equilibrium state but also when cross-sections of networks in development are inspected. This observation of the Matthew effect is in line with Schroeders et al.’s (2016) hypothesis for nonformalized learning environments, as discussed in the introduction. In the model, a nonformalized learning environment can simply be seen as the natural growth that occurs without an educational intervention, whereas formalized learning would comprise small beneficial interventions, such as illustrated with Pólya’s urn.

A second insight from the model is that the continuous differences observed in the Matthew effect can at some point start to bifurcate into clearly discrete groups. This pattern can be compared with the effect of stratification in education. An even deeper insight of this bifurcation process is that growth mechanisms that satisfy the Fortuin–Kasteleyn model must contain a degenerative component, such as a forgetting mechanism. Only then can some networks grow into a less able state. In the next section, we discuss such aspects of a growth mechanism. Besides, a more critical assessment of the bifurcation is also possible: One may wonder whether the strength of the bifurcation in the wired intelligence model represents realistic developmental patterns. It is therefore important to stress that other than the magnetic field that ensures that individuals sample skills and knowledge that are within reach (e.g., that are within their zone of proximal development), in the current parsimonious wired intelligence model, there is no mechanism that repairs errors. Such a mechanism, such as proper education, would reduce the strong observed bifurcation. Nevertheless, it should also be noted that in principle, a cognitive network structure may actually grow into an increasingly unable state: Conspiracy theories could be seen as a practical example of that principle and also in, for instance, the balance-scale task in which some children are seen to develop increasingly complex yet incorrect strategies (Jansen & van der Maas, 2002).

Finally, what is particularly intriguing about the idiographic network perspective is that the discussed phenomena are observed by aggregating specific representations of many individuals. Here, we like to echo Jensen’s (2002) remark that “the psychology of intelligence could, at least in theory, be based on the study of one person” (p. 39). The proposed model overtly distinguishes intelligence from g, and it is exactly this fact that makes the idiographic approach such a powerful one. Although the study of the individual goes beyond the scope of the current research, in the following, we do give some context.

An idiographic approach

In addition to the model’s capacity to explain two of the—mostly nomothetic and macroscopic—phenomena in intelligence, its idiographic nature also enables straightforward interpretations of microscopic phenomena. Thus, rather than the previously discussed aggregated phenomena that are at the forefront of intelligence research, here we mean the phenomena that reside at the level of the individual, the phenomena that originate from the long traditions of experimental and cognitive psychology. Ebbinghaus’s (1913) law of forgetting is one great example that we will first turn to.

In the introduced model, cognitive disability is explained as the result of a stochastic process. However, cognitive networks such as in the proposed model moreover allow for intuitive mechanisms of forgetting and other degenerative processes. Both nodes and edges may be forgotten either randomly or dependent on the time a node resides in the network. Moreover, forgetting mechanisms can easily become more interesting, for instance, by taking the frequency of activation of a node into account or even the degree of a node—the number of edges it is attached to—because it may be viewed to signal robustness. In the proposed model, the external field already creates a naive form of forgetting: The state of a cluster of nodes is evaluated at each iteration, and the probability that the nodes in a cluster represent obtained knowledge is a function of the size of the cluster. The states of poorly connected nodes may therefore vary considerably, whereas well-connected nodes tend to stay in the same state.

Very much related to forgetting are the well-established testing and spacing effects (e.g., Karpicke & Roediger, 2008). Again, the model allows one to consider these effects within a formalized theory of intelligence. In the proposed growth mechanism, testing and spacing are reflected in the sampling of the edges. Intuitively, testing and spacing help increase the density of the edge structure of a network, which leads to both a more resilient network and larger clusters and hence more obtained knowledge. Related is the fact that in actual learning, the sampling frequency may naturally vary from individual to individual. In combination with a forgetting mechanism, testing and spacing effects thus help determine the birth and death processes underlying the development of a network.

The network topology itself also allows for interpretations of the individual. The number and size of clusters, or the degree distribution of a network, may, for instance, resonate the robustness of the cognitive network. Isolated pieces of unobtained knowledge may be viewed as slips, whereas clusters of unobtained knowledge may be viewed as structural misconceptions. Note that the preference for clustering in the model combined with the positive external field creates a very natural dynamic. At first, isolated pieces of unobtained knowledge such as slips are quite probable. The preference for clustering will then cause some of these pieces of unobtained knowledge to evolve into straight misconceptions. Finally, the external field ensures that misconceptions that become too pronounced are repaired.

A developmental approach

In discussing the idiographic approach, we already alluded to developmental mechanisms. Indeed, we believe that to understand intelligence, its development must be understood too. In discussing the model, we used the first two scenarios to get a grip on its developmental predictions. In the second scenario, we followed the development of the networks as they increased in size yet while they remained in an equilibrium state. This scenario allowed us to derive the developmental predictions of the model, such as the Matthew effect and ultimately the bifurcation, without the need to know the growth mechanism.

Note that these predictions hold in case the networks indeed grow within the limits of the equilibrium. Following from this, one evident challenge is to study growth mechanisms that keep the Fortuin–Kasteleyn properties intact. However, the assumption that development takes place in equilibrium may just as well turn out to be too restrictive. Conveniently, the network approach allows one to consider diverse growth mechanisms and study the effect on development. Having said that, it may also give one too many degrees of freedom. We solved this dilemma, which is inherently tied to formal modeling approaches, by suggesting a straightforward growth and repair mechanism.

Most important though, the true restrictions must come from developmental phenomena. This bring us to an important question: What are the key developmental phenomena in intelligence? As we aimed to reflect in the introduction, this is not an unexplored area. Phenomena such as the Matthew and compensation effects or the age differentiation and dedifferentation hypotheses are actively studied. Nevertheless, much confusion still exist about these phenomena. As evidenced in the introduction, contradictory phenomena are being observed, and some argue that the causal mechanisms must be studied to come to grips with it.

This brings us to a second question: What are the important developmental mechanisms? The Pólya’s urn example convincingly illustrates the explanatory power of a seemingly simplistic growth mechanism. In the field of intelligence, the mutualism and multiplier effect models give other examples of such mechanisms. In addition, we sense that approaching the contradictory developmental phenomena with causal mechanisms might indeed turn out to be fruitful. The fact that the same mechanism under different circumstances can explain contradictory phenomena is intriguing and should be further explored.

Clues for developmental mechanisms may be found in the near field of developmental biology. Plants and humans share many important attributes, such as their growth, decline, variation, and genetic and environmental influences. Developmental biologist use, for instance, the cellular Potts model (Graner & Glazier, 1992)—a generalization of the Ising model, which is in its turn related to the Fortuin–Kasteleyn model—to explain a multitude of developmental phenomena. Grieneisen, Xu, Marée, Hogeweg, and Scheres (2007) used it to explain root growth of plants, Li and Lowengrub (2014) used it for the growth of tumor cell clusters and Chen, Glazier, Izaguirre, and Alber (2007) for morphogenesis. The much less mature field of developmental intelligence may greatly benefit from the techniques and mechanisms used in these and other applications (e.g., Prusinkiewicz & Runions, 2012). We believe that the fact that the model proposed here provides a framework to incorporate such developmental mechanisms is one of its major strengths, and studying developmental phenomena and mechanisms should be a primary concern in intelligence research.

Appendix A

The distribution of node states in the Fortuin–Kasteleyn (1972) model

The marginal distribution of the node states p(x)—that is, the probability of observing a particular configuration of skills, knowledge, or abilities—is an integral part of our formal theory. In fact, each of the phenomena that we aim to explain with the proposed model constitutes a particular pattern of observations from this marginal distribution. It is therefore highly convenient that the marginal distribution p(x) of the model for the node states x and their relations ω is of a known form (e.g., Fortuin & Kasteleyn, 1972; Grimmett, 2006). We next show that the marginal distribution of the formal model is an instance of the Ising network model (Ising, 1925). The Ising model is of the form

$$\sum _{\mathrm{\omega }\in \mathrm{\Omega }}p(x,\mathrm{\omega })=p(x)=\frac{1}{{\mathrm{Z}}_I}\exp \left(\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}{x}_i{x}_j+\sum _{i=1}^p{\mathrm{\mu }}_i{x}_i\right),$$

in which ${\mathrm{\mu }}_i$ denotes the main effect of node $i$ and ${\sigma }_{ij}$ denotes the pairwise interaction between nodes $i$ and $j$. According to the model, nodes $i$ and $j$ prefer to be in the same state when ${\sigma }_{ij}>0$ and prefer to be in different states when ${\sigma }_{ij}<0$. In the absence of the influence of other variables in the network, node $i$ prefers to be active ($x_i=+1$) when µi ${\mathrm{\mu }}_i>0$ and prefers to be inactive ($x_i=-1$) when µi ${\mathrm{\mu }}_i<0$. Here, it is assumed that both the pairwise interactions ${\sigma }_{ij}$ and the main effects ${\mathrm{\mu }}_i$ are all positive.

Without loss of generality, here we consider the case in which the edge set $\mathrm{E}$ consists of all $p(p-1)/2$ possible edges between $p$ nodes, with a unique probability ${\mathrm{\theta }}_{ij}$ associated to each pair of nodes $i$ and $j$ and a unique external field ${\mathrm{\mu }}_i$ associated to each node $i$. The Fortuin–Kasteleyn model that is consistent with this specification is (Cioletti & Vila, 2015; Grimmett, 2006)

$$\begin{array}{l}p(x,\mathrm{\omega })=\frac{1}{{\mathrm{Z}}_F}\prod _{i=1}^{p-1}\prod _{j=i+1}^p\left\{{\mathrm{\theta }}_{ij}{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-{\mathrm{\theta }}_{ij})(1-{\mathrm{\omega }}_{〈i,j〉})\right\}\\ \prod _{i=1}^p\exp ({\mathrm{\mu }}_i{x}_i).\end{array}$$

The first step in expressing its marginal distribution $p(x)$ is to sum out the edge states

$$\begin{array}{l}p(x)=\sum _{\mathrm{\omega }\in \mathrm{\Omega }}p(x,\mathrm{\omega })=\frac{1}{{\mathrm{Z}}_F}\prod _{i=1}^{p-1}\prod _{j=i+1}^p\left\{{\mathrm{\theta }}_{ij}\frac{x_i{x}_j+1}{2}+1-{\mathrm{\theta }}_{ij}\right\}\\ \prod _{i=1}^p\exp ({\mathrm{\mu }}_i{x}_i).\end{array}$$

The second step is to rewrite this expression using ${\mathrm{\theta }}_{ij}=1-\exp (-2{\sigma }_{ij})$, making use of the assumption that ${\sigma }_{ij}>0$. Observe that for a pair of nodes $i$ and $j$, this boils down to

$$\begin{array}{l}{\mathrm{\theta }}_{ij}\frac{x_i{x}_j+1}{2}+1-{\mathrm{\theta }}_{ij}\Rightarrow \left\{1-\exp (-2{\sigma }_{ij})\right\}\frac{x_i{x}_j+1}{2}\\ +\exp (-2{\sigma }_{ij})=\exp ({\sigma }_{ij}[x_i{x}_j-1]),\end{array}$$

which leads us to the following equation:

$$\begin{array}{c}p(x)=\frac{1}{{\mathrm{Z}}_F}\prod _{i=1}^{p-1}\prod _{j=i+1}^p\exp \left({\sigma }_{ij}\left[x_i{x}_j-1\right]\right)\prod _{i=1}^p\exp ({\mathrm{\mu }}_i{x}_i)\\ =\frac{1}{{\mathrm{Z}}_F}\exp \left(\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}{x}_i{x}_j-\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}+\sum _{i=1}^p{\mathrm{\mu }}_i{x}_i\right).\end{array}$$

It is now easily seen that

$${\mathrm{Z}}_F\exp \left(\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}\right)={\mathrm{Z}}_I=\sum _x\exp \left(\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}{x}_i{x}_j+\sum _{i=1}^p{\mathrm{\mu }}_i{x}_i\right),$$

in which the sum on the right hand side is taken over all $2^p$ possible realizations of $x$. That is, we have found the marginal distribution

$$p(x)=\frac{1}{{\mathrm{Z}}_I}\exp \left(\sum _{i=1}^{p-1}\sum _{j=i+1}^p{\sigma }_{ij}{x}_i{x}_j+\sum _{i=1}^p{\mathrm{\mu }}_i{x}_i\right),$$

that we set out to do.

Observe that the original Fortuin–Kasteleyn model for the complete edge set E is consistent with an important special case of the Ising model that is known as the Curie-Weiss model (Kac, 1968). This version of the Ising model is obtained whenever all pairwise interactions are constrained to have the same value (i.e., all pair of nodes have the same wiring probability $\mathrm{\theta }$ in the Fortuin–Kasteleyn model and the external fields are all equated to zero), for example,

$$p(x)=\frac{1}{{\mathrm{Z}}_C}\exp \left(\sigma \sum _{i=1}^{p-1}\sum _{j+1}^p{x}_i{x}_j\right)=\frac{1}{{\mathrm{Z}}_C}\exp (\sigma x_{+}),$$

in which $x_{+}={\sum }_i{x}_i$ is the sum over all node states. The model was introduced by Kac as a simple model for magnetism on the basis of the magnetic theories of Curie and Weiss (for a recent review of the model’s theoretical properties, see Kochmański, Paszkiewicz, & Wolski, 2013). The relation between the Curie-Weiss model and contemporary psychometric models is discussed by Marsman et al. (2018), and Marsman, Tanis, Bechger, and Waldorp (in press) studied its statistical properties. Here, the Curie-Weiss model serves as the starting point for our analysis because it is the simplest nontrivial network model that is consistent with the positive manifold.

The positive manifold and the Rasch model

In the previous section, we showed that the marginal distribution of the node states in the Fortuin–Kasteleyn model is an Ising network model. Marsman, Maris, Bechger, and Glas (2015) and Epskamp, Maris, Waldorp, and Borsboom (2018) showed that this Ising network model is statistically equivalent to multidimensional item-response theory (IRT; Reckase, 2009), which is a class of latent variable models for binary response variables that are commonly used in educational measurement. It is important to note that when the pairwise interactions in the Ising model are constrained to have the same value (e.g., the Curie-Weiss model), it is a special case of the marginal Rasch model (Marsman et al., 2018), for example,

$$p(x)={\int }_{ℝ}p(x|\eta )f(\eta )\mathrm{d}\eta ,$$

in which $p(x|\eta )$ is the simplest nontrivial IRT model that is known as the Rasch model and $f(\eta )$ is a probability distribution for the latent variable. The interaction strength $\sigma$ of the Curie-Weiss model functions as an a priori variance in the latent variable distribution $f(\eta )$. One important observation is that the Rasch model, just as the unidimensional factor model, is consistent with the positive manifold (Holland & Rosenbaum, 1986). Because the Curie-Weiss model is a marginal Rasch model, it is also consistent with the positive manifold. Fortuin, Kasteleyn, and Ginibre (1971) showed the same for the Fortuin–Kasteleyn model, which follows from their expression of the two-point correlation

$$p(x_i=x_j)=\frac{1}{2}+\frac{1}{2}p(i\leftrightarrow j)\ge \frac{1}{2},$$

that we discussed earlier (see also, Grimmett, 2006).

The hierarchical structure and multidimensional IRT

To accommodate the hierarchical pattern in observed correlations, we group nodes into communities and introduce a single probability ${\mathrm{\theta }}_W$ for connecting nodes within a community and a single probability ${\mathrm{\theta }}_B$θB—with ${\mathrm{\theta }}_B<{\mathrm{\theta }}_W$θB < θW —to connect nodes from different communities. The extended Fortuin–Kasteleyn model that we propose is then of the form

$$\begin{array}{c}p(x,\mathrm{\omega })=\frac{1}{{\mathrm{Z}}_F}\prod _{i,j\in E_W}\left\{{\mathrm{\theta }}_W{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-{\mathrm{\theta }}_W)(1-{\mathrm{\omega }}_{〈i,j〉})\right\}\\ \times \prod _{i,j\in E_B}\left\{{\mathrm{\theta }}_B{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-{\mathrm{\theta }}_B)(1-{\mathrm{\omega }}_{〈i,j〉})\right\},\end{array}$$

in which $E_W$ denotes the set of edges relating skills within a community and $E_B$ denotes the set of edges relating skills between communities. In the two-community structure that is described in the main text, the within-community edge set $E_W$ is the union of the edges within the mathematics community and the edges within the language community, $E_W=E_M\cup E_L$, and the between edge set is simply $E_{ML}$. The two community-specific probabilities ${\mathrm{\theta }}_W$ and ${\mathrm{\theta }}_B$ in our Fortuin–Kasteleyn model translate to community-specific interaction terms ${\sigma }_W=-\frac{1}{2}\ln (1-{\mathrm{\theta }}_W)$ and ${\sigma }_B=-\frac{1}{2}\ln (1-{\mathrm{\theta }}_B)$ in the associated Ising model.

One way to represent the structure this imposes on the Ising model is to consider it in the form

$$p(x)=\frac{1}{{\mathrm{Z}}_I}=\exp \left(\frac{1}{2}{x}^T\mathrm{\Sigma }x\right),$$

in which $\mathrm{\Sigma }=[{\sigma }_{ij}]$ is a $p\times p$ connectivity matrix that consists of two parts:

$$\mathrm{\Sigma }={\sigma }_B{1}_p+({\sigma }_W-{\sigma }_B)\mathrm{C}={\sigma }_B{1}_p+{\sigma }_C\mathrm{C},$$

in which $1_p$1p is the $p\times p$ matrix of ones, ${\sigma }_C={\sigma }_W-{\sigma }_B>0$, and $\mathrm{C}=[c_{ij}]$ is a $p\times p$ matrix with entry $c_{ij}=1$ when nodes $i$ and $j$ belong to the same community and $c_{ij}=0$ otherwise. When the nodes are ordered with respect to their communities, we find that $\mathrm{C}$—and thus also $\mathrm{\Sigma }$—is a block-diagonal matrix.

Observe that we can decompose the quadratic form $x^T\mathrm{\Sigma }x$ as follows

$$x^T\mathrm{\Sigma }x=x^T\left({\sigma }_B{1}_p+{\sigma }_C\mathrm{C}\right)x={\sigma }_B{\left(\sum _{i=1}^p{x}_i\right)}^2+\sum _{c=1}^n{\sigma }_C{\left(\sum _{i\in {\mathrm{V}}_c}{x}_i\right)}^2,$$

in which the second term on the right consists of a sum over nodes $i$ in a community $c$ for communities $c=1,\dots ,n$. As a result, the marginal distribution of the node states is formulated as

$$p(x)=\frac{1}{{\mathrm{Z}}_i}\exp \left(\frac{1}{2}{\sigma }_B{\left(\sum _{i=1}^p{x}_i\right)}^2+\frac{1}{2}\sum _{c=1}^n{\sigma }_C{\left(\sum _{i\in {\mathrm{V}}_c}{x}_i\right)}^2\right),$$

which can be related to a $(n+1)$-dimensional IRT model using the ideas of Marsman et al. (2015) and Epskamp et al. (2018). For our example with $n=2$ communities, the matrix of discriminations—or factor loadings—of the three-dimensional IRT model is of the form

$$\Lambda =\left(\begin{array}{ccc}\sqrt{2{\sigma }_B}& \sqrt{2{\sigma }_C}& 0\\ ⋮& ⋮& ⋮\\ \sqrt{2{\sigma }_B}& \sqrt{2{\sigma }_C}& 0\\ \sqrt{2{\sigma }_B}& 0& \sqrt{2{\sigma }_C}\\ ⋮& ⋮& ⋮\\ \sqrt{2{\sigma }_B}& 0& \sqrt{2{\sigma }_C}\end{array}\right),$$

which reflects one single overarching dimension that is consistent with the positive manifold and $n$ community-specific dimensions that are consistent with the hierarchical structure.

The external field

In our model, we assume a slight preference toward the acquisition of knowledge, which we incorporate by including a positive external field. By introducing the external field—using the approach of Cioletti and Vila (2015)—the model extends into

$$\begin{array}{c}p(x,\mathrm{\omega })=\frac{1}{{\mathrm{Z}}_F}\prod _{i,j\in E_W}\left\{{\mathrm{\theta }}_W{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-{\mathrm{\theta }}_W)(1-{\mathrm{\omega }}_{〈i,j〉})\right\}\\ \times \prod _{i,j\in E_B}\left\{{\mathrm{\theta }}_B{\mathrm{\omega }}_{〈i,j〉}\frac{x_i{x}_j+1}{2}+(1-{\mathrm{\theta }}_B)(1-{\mathrm{\omega }}_{〈i,j〉})\right\}\\ \times \exp \left(\mathrm{\mu }{x}_{+}\right),\end{array}$$

in which $\mathrm{\mu }$ denotes the external field and $x_{+}$ denotes the sum over all node states.

In the Ising network model, the external field is a main effect that is associated with the nodes; node $i$ tends to $+1$ when ${\mathrm{\mu }}_i>0$µ and to $-1$ when ${\mathrm{\mu }}_i<0$µ . In the IRT model, the external field is an item easiness parameter; item $i$ is correctly answered ($+1$) more often when ${\mathrm{\mu }}_i>0$ and answered incorrectly more often when ${\mathrm{\mu }}_i<0$.⁴ In the Fortuin–Kasteleyn model, the external field has a similar effect; node $i$ tends to $+1$ when ${\mathrm{\mu }}_i>0$ and to $-1$ when ${\mathrm{\mu }}_i<0$µ . However, in the Fortuin–Kasteleyn model, this influence of the external field is a population effect because for individual networks, the external field acts on the clusters and not on the individual nodes.

The effect of the external field for an individual network in the Fortuin–Kasteleyn model is most easily revealed through the conditional distribution $p(x|\mathrm{\omega })$, which factors into the conditional distribution

$$p(x|\mathrm{\omega })=\prod _{k=1}^{\kappa (\mathrm{\omega })}p(x_i|i\in K_k(\mathrm{\omega })),$$

in which $\kappa (\mathrm{\omega })$ denotes the number of open clusters in a network and $K_k(\mathrm{\omega })$ the set of nodes that are in cluster $k$, $k=1,\dots ,\kappa (\mathrm{\omega })$. The probability that the node states in cluster $k$ are equal to $+1$ is (Cioletti & Vila, 2015)

$$\begin{array}{l}p(x_i=+1|i\in K_k(\mathrm{\omega }))\\ =\frac{\exp \left({\sum }_{i\in K_k(\mathrm{\omega })}{\mathrm{\mu }}_i\right)}{\exp \left({\sum }_{i\in K_k(\mathrm{\omega })}{\mathrm{\mu }}_i\right)+\exp \left(-{\sum }_{i\in K_k(\mathrm{\omega })}{\mathrm{\mu }}_i\right).}\end{array}$$

Observe that this probability depends on the sum of the external fields of all nodes in the cluster. In the model, there is a positive external field $\mathrm{\mu }$ that applies to all nodes equally. In this case, the probability that the node states in cluster $k$ are equal to $+1$ is

$$\begin{array}{l}p(x_i=+1|i\in K_k(\mathrm{\omega }))\\ =\frac{\exp \left(|K_k(\mathrm{\omega })|\mathrm{\mu }\right)}{\exp \left(|K_k(\mathrm{\omega })|\mathrm{\mu }\right)+\exp \left(-|K_k(\mathrm{\omega })|\mathrm{\mu }\right)},\end{array}$$

in which $|K_k(\mathrm{\omega })|$ is the size of cluster $k$. With µ $\mathrm{\mu }>0$, this probability is strictly larger than $.5$ for each cluster, and it is an increasing function of cluster size. The original symmetric case is obtained when $\mathrm{\mu }=0$, which reveals the uniform assignment of the values $+1$ and $-1$ across clusters.