Abstract
Understanding the diffusion of gold nanorods (AuNRs) and their composites in dispersion is important at fundamental level and in fields as diverse as material science, nanobiotechnology to drug delivery. The translational and rotational diffusion of AuNRs decorated with thermoresponsive poly(N-isopropylacrylamide) brushes having hydrophilic and hydrophobic end groups was investigated in the dilute regime by dynamic light scattering. The same series of functionalized AuNRs were studied in the isotropic concentrated dispersions by high-resolution NMR diffusometry. The dependence of translational and rotational diffusivity upon molecular weight and polymer end group were measured as a function of temperature in the region of the brush phase transition. The effective hydrodynamic radius of AuNR composites proved to be the most sensitive quantity to the temperature-induced phase transition of brushes, allowing the evaluation of the brush thickness in the swollen and collapsed states.
1. Introduction
Stochastic mass transport of macromolecules, nanoparticles, and composites in dispersions plays an important role in various fields of modern science.1−3 This molecular process not only reflects intrinsic properties of the diffusing species itself but also can emphasize on the morphology and architecture of environment and allows characterization of chemical and biological phenomena.4−7
The mass transport at the molecular level of anisotropic particles such as gold nanorods (AuNRs) was investigated for understanding the use of these nanoobjects in diagnostic and therapeutic purposes.8−10 In many applications ranging from self-assembly to bioengineering, the thermal energy which dictates the self-diffusion of the particles is comparable to the interaction energy at the nanoscale.11 Furthermore, functional gold nanoparticles (AuNPs) modified with thermosensitive brushes recently have been of considerable interest because of their applications for catalysis and photooptic devices.12 Hybrid nanoparticles of core–shell microgels consisting of spherical AuNPs cores and cross-linked poly-N-isopropylacrylamide (PNIPAm) shells were investigated by dynamic light scattering (DLS) and UV–vis spectroscopy.13 The effects of temperature and cross-linking density were studied and the molar mass of the hybrid particles as well as the refractive index of the thermoresponsive shells where measured. Moreover, the optomechanical actuation of AuNRs homogenously coated with a microgel shell of cross-linked PNIPAm was also studied by UV–vis spectroscopy and transmission electron microscopy (TEM).14 Irradiation with a near-infrared (NIR) laser can be sensed by AuNRs inducing reversible size switching of core–shell nanocomposites. The dependence of the effective hydrodynamic diameter of the AuNRs assumed to be spherical as a function of the dispersion temperature was determined by DLS. Nevertheless, the process of temperature-induced phase transition was not characterized by its specific thermodynamic parameters. Furthermore, stimuli-responsive polymers tethered on the AuNPs will open new possibilities for temperature-controlled nanoheater applications induced by NIR irradiation.15,16 To this point, soft microrobots employing nonequilibrium actuation via plasmonic heating were developed.17
Anisometric nanoparticles can be characterized by translational and rotational diffusivity that were measured by normalized intensity autocorrelation function in DLS experiments.18,19 The scattered centers in DLS measurements are represented by nanoparticles with the diffusivity affected by molecular weight, grafting density, and end-group functionalization of polymer brushes. In standard DLS experiments, only light scattered with polarization parallel to the incident beam is measured (vertical–vertical (VV) geometry), whereas with depolarized DLS, the polarization perpendicular to the incident light (horizontal–vertical geometry) is detected. The last technique proved to be efficient for separate measurement of translational (Dt) and rotational (Dr) diffusivity of anisotropic nanoparticles.20−23 The sensitivity of Dt and Dr diffusivity to the nanorods aspect ratio L/d, where L is the length and d is the diameter of the rod can be used for establishing the validity of the hydrodynamic models of diffusivity.24−30 Moreover, the translational and rotational diffusivity of gold colloids are sensitive to nanoparticle aggregation.31,32
High-resolution NMR spectroscopy and relaxometry were recently used for investigation of the temperature-induced phase transition of asymmetrically end-functionalized PNIPAm with hydrophobic benzyl and thiol groups (hereafter Bn-PNIPAm-SH) as well as with a hydrophilic NIPAm-like end group (hereafter NIPAm-PNIPAm-SH) for both free polymer and tethered brushes onto AuNRs in aqueous dispersions.33,34 The NMR observable represented by spectral integral intensity reflects changes in transverse relaxation times as an indicator of the polymer chain conformations and dynamics.33 For this purpose, a two-state statistical model of thermodynamic observables was developed valid in the temperature region of phase transition. A strong dependence of transition temperature, transition entropy, and the width of transition on hydrophilic/hydrophobic end-groups was detected.32,33 The two-state approach was also applied to describe phase transition revealed by self-diffusion coefficients of NIPAm-PNIPAm-SH and Bn-PNIPAm-SH free polymers in aqueous dispersions.35
To the best of our knowledge, there are no reported studies of gold metal by NMR at ambient temperatures. Gold (Au) has a single isotope, 197Au, with 100% natural abundance and the nuclear spin I = 3/2. Because of its quadrupole moment, a fast quadrupole relaxation is present at ambient temperature inducing extremely broad and weak NMR resonances, and therefore, NMR spectra and relaxation were reported in gold metal only in the temperature range 1–4 K.36 Hence, the self-diffusion of AuNPs by NMR diffusometry in conditions relevant for basic studies and applications can be performed only on nanocomposites using the tethered polymer brushes as NMR markers.
The aim of this study is to investigate by DLS and high-resolution NMR diffusometry the self-diffusion of AuNR–PNIPAm composites. The diffusivity of AuNR composites was investigated in the region of temperature-induced phase transition of stimuli-responsive R-PNIPAm-SH polymer brushes onto AuNRs, in aqueous dispersion with hydrophilic (R = NIPAm-like), and hydrophobic (R = Bn) end groups. The measured quantity is the translational diffusivity of AuNR nanocomposites in the isotropic concentrated regime using the proton NMR signals of the polymer brush as a marker. Translational and rotational diffusion coefficients were measured by DLS, in the dilute regime of the same series of AuNR nanocomposites. The temperature dependence of the diffusion coefficients for different brush molecular weights reveals the temperature dependence of the brush thickness.
2. Theory
2.1. Translational and Rotational Diffusivities of AuNRs with Thermoresponsive Brushes in Dilute Dispersion
When rod-like nanoparticles, for example, a AuNR in dilute regime is diffusing in an unbound fluid, its translational diffusion coefficients along (easy direction) and perpendicular (hard directions) to the rod axis are given by24−30
| 1 |
and
| 2 |
where kB is the Boltzmann constant, T is the absolute temperature, and η is the temperature-dependent viscosity of the dispersion medium. The aspect ratio of the nanorod is defined as p = L/d, where L and d are the length and effective diameter of the rod, respectively. In the case of PNIPAm brushes tethered onto nanorods, we can write d = d0 + 2z(T), where d0 is the diameter of bare rod and z(T) is the thickness of the thermoresponsive brush. As will be discussed later for our AuNRs, the inequality L ≫ 2z is fulfilled and hence, L + 2z ≈ L. End-effect coefficients are denoted by e∥ and e⊥.27 The end-effect coefficients are function of aspect ratio p and converge to asymptotic values when p → ∞.
The translational diffusivity tensor in the rod principal axis system representation moving into an isotropic medium is given by
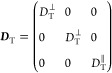 |
3 |
where DT∥ and DT correspond to fast and slow translational diffusivity, respectively.29,30 The nanorods in the dilute, semidilute, or concentrated dispersions do not have preferential orientation and thus, the isotropic component of the diffusivity tensor is measured. The translational diffusivity of the rod center of mass can be written as
| 4 |
From the above equation and eqs 1 and 2, we finally yield
| 5 |
Lang and co-workers21 used for DLS of AuNRs with low aspect ratios the following relation for end-effect correction as second-order polynomials in 1/p
| 6 |
valid for the aspect ratio range 2 < p < 20.26,27 Finally, we can write
| 7 |
where temperature-dependent aspect ratio function is given by
| 8 |
Similar arguments can be applied for rotational diffusivity and we can write21
| 9 |
where
| 10 |
The polymer brush temperature-induced phase transition will affect the above aspect functions by the temperature dependence of the brush thickness z(T). Furthermore, the effect of the hydrophilic or hydrophobic end-groups of the brushes is mainly included in the above relationship of diffusivities by the brush thickness. This effect is related to the hydrodynamic interactions that affect the nanorods diffusion. The motion of one of the brush units accompanies motions of the adjacent solvent molecules. Their effect propagates to another brush monomeric unit to facilitate its motion in the same direction.30 This interaction is affected by the hydrophilic/hydrophobic character of tethered polymer end-groups and it was detected for linear, free PNIPAm with NIPAm-like and benzyl end groups.35 Hence, it is expected to be also present for PNIPAm brushes tethered onto AuNRs. In the following, we will assume the end-groups effect to be the same for both translational and rotational diffusivities.
2.2. Effective Hydrodynamic Radius of AuNRs with Thermoresponsive Brushes in Dilute Dispersion
An effective hydrodynamic radius (RH) of the nanorods in dispersion can be computed from the center-of-mass diffusivity eq 7 and is given by30
| 11 |
The constant e, the
result of the end-rod effect, is around e ≈
0.3, (see eq 8). The
aspect ratio 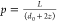 for a thermoresponsive brush depends on
the molecular weight, grafting density, and temperature via the brush
thickness z. In the approximation of the two-state
model,33 we assume that the temperature
dependence of the statistical average of brush thickness z(T) in the process of swollen-collapsed polymer
chains can be described by the relationship
for a thermoresponsive brush depends on
the molecular weight, grafting density, and temperature via the brush
thickness z. In the approximation of the two-state
model,33 we assume that the temperature
dependence of the statistical average of brush thickness z(T) in the process of swollen-collapsed polymer
chains can be described by the relationship
| 12 |
where zswollen and zcollapsed correspond to the brush thickness for swollen and collapsed polymer chains, respectively. The thermodynamic parameters of phase transition are given by Tt and |ΔS|/kB, where Tt is transition temperature and |ΔS|/kB, is the normalized entropy change. More elaborate theories describing the collapse of thermoresponsive brushes were published as for instance that of ref (36).
2.3. Translational Diffusivities of AuNRs with Thermoresponsive Brushes in Isotropic Concentrated Dispersion
We shall discuss in the following the translational diffusion that is accessed by NMR diffusometry for AuNRs composites with polymer brushes, in the regime of isotropic concentrated dispersions. The motion of the AuNRs parallel to the tube axis (“easy” direction) is not hindered by the neighboring rods that define the tube.29 Hence, the parallel translational diffusion component DT∥ will have value close to that of diffusivity tensor component in dilute dispersion. Moreover, the perpendicular components DT related to the “hard” translational directions, are very small (DT⊥ ≈ 0) provided the small-scale rod motion of order of tube diameter. Thus, in the regime of nanorod isotropic concentrated dispersions where entanglement effects are present, we can write for the diffusivity tensor
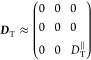 |
13 |
The nanorods in the isotropic concentrated dispersions do not have preferential orientation and thus the relevant isotropic component of the diffusivity tensor is measured, that is,
| 14 |
Using the results for the dilute solution eq 1, we yield
| 15 |
where the polynomial coefficients of the end-effect corrections are A = −0.207, B = 0.980, and C = −0.133.27
3. Materials and Methods
3.1. Synthesis of AuNRs and Functionalization with PNIPAm Brushes
Cetyltrimethylammonium bromide (CTAB)-stabilized AuNRs were synthetized according to the literature.33−35 The surface functionalization with α-ω-heterobifunctional, tiol-bearing PNIPAm having a hydrophobic end group (Bn-PNIPAm-SH) or a hydrophilic NIPAm-like end group (NIPAm-PNIPAm-SH) was done as recently reported.33−35 For more information, see also Supporting Information, Section S1.
3.2. Inductively Coupled Plasma Atom Emission Spectroscopy
The concentration of elemental gold in aqueous AuNR–CTAB dispersion was determined using an inductively coupled plasma atom emission spectroscopy (ICP–AES) Plasma 400 (Fa. PerkinElmer). AuNR–CTAB (100 μL) were vortexed for a couple of minutes. Three milliliters of HCl solution (30%, Suprapur, Fa. Merck) and 1 mL of HNO3 solution (65%, Suprapur, Fa. Merck) were added, and the samples were placed in PTFE vessels (Type XP 1500) and treated in the microwave (Mars 5, Fa. CEM). The clear solutions were finally diluted to 20 mL with deionized water and the gold content was determined using the Wolle 800W software. The effective AuNRs weight concentration (cAuNRs) was determined from three different AuNR–CTAB dispersions.
3.3. UV–Vis Spectrophotometry
UV–vis spectra were recorded on a JASCO V-630 spectrophotometer connected to a Huber Pilot-ONE “Petite Fleur” thermostat using silicone oil (temperature range −40 to 110 °C) as thermofluid. Absorbance (Abs. in arbitrary units, abbreviated as arb. units) was measured in quartz glass cuvettes (d = 10 mm) with a scan speed of 1000 nm/min at fast response (data pitch = 1 nm). Spectrum analyses were evaluated using the JASCO spectrum manager software (version 2).
3.4. Transmission Electron Microscopy
TEM micrographs were taken on a Carl Zeiss Libra 120 microscope equipped with an in-column energy filter. The electron beam accelerating voltage was set at 120 kV. A drop of the sample was trickled on a carbon-coated copper grid. Before being placed into the TEM specimen holder, the copper grid was air-dried under ambient conditions. We estimated the average dimensions of the AuNRs: the length of L = 70 nm and diameter of d = 16 nm that gives an average aspect ratio of 4.4.
3.5. DLS Measurement
Temperature-induced phase transition reflected in translational diffusivity and hence, into effective hydrodynamic radius (RH) was determined by photon correlation spectroscopy (fluorescence correlation spectroscopy) using a Zetasizer Nano ZS (Fa. Malvern) at a laser wavelength λ = 633 nm. We have measured the light scattered at the angle θ = 173° with polarization parallel to the incident beam, that is, in the VV geometry. Purified AuNRs–PNIPAm dispersions with a concentration of 0.1 mg mL–1 have been typically used as stock. The temperature range of 20–50 °C was used determining the diffusion coefficient from the decay of normalized intensity autocorrelation function. The water bath temperature was controlled to a precision of ±0.1 °C. For individual DLS measurements in the heating mode, individual data were collected within temperature steps of 1 °C. At each temperature, an equilibration time of 10 min was allowed. The heating rate was set to 1 °C/min. The dispersions were sufficiently dilute (i.e., 0.1 mg mL–1) to diminish multiple scattering. At each temperature, three data points were taken, and the average from these measurements was presented.
3.6. High-Resolution NMR Spectroscopy and Diffusometry
Proton high-resolution magic-angle sample spinning (HRMAS) NMR on NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes onto AuNRs were recorded on a wide bore AV700 Bruker NMR spectrometer operating at frequency of 700.2378 MHz, equipped with a cross-polarization MAS probe with a 3.2 mm rotor. The rotor frequency was set at 5 kHz. All the 1H HRMAS spectra were externally referenced to tetramethylsilane. For all measurements, the recycle delay was 7 s, the radio-frequency pulse length was 1.9 μs, while the dwell time was 10 μs, and the number of scans was 64. The time domain data were 4k, and the zero filling was done with 16k.
The apparent diffusivity D of PNIPAm brushes onto AuNRs were measured using the AV700 Bruker NMR wide bore spectrometer with a Diff50 Bruker unit by pulsed-field-gradient stimulated echo (PFGSE) sequence of Stejskal–Tanner.38 The experiment is two-dimensional, by recording the dependence of the NMR peak integral intensity upon the applied field gradient strength. The apparent diffusivity was obtained by fitting the normalized stimulated spin echo decay as a function of gradient strength g to the Stejskal–Tanner equation37
| 16 |
where we employ the convention q = γδg, for the diffusion wave vector.2−4 In the above equation, I(g) is the integral intensity of the methyl peak or aliphatic spectral region obtained by the Fourier transform of the half decay of stimulated echo at a given value of magnetic field gradient g, and I0 is the integral intensity for small values of field gradient value compared with the maximum of the gradient strength gmax. Equation 16 can be rewritten as
| 17 |
where the quantity b is defined
as 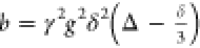 and magnetogyric ratio γ
has the
units of rad s–1 T–1. The duration
of the gradient pulse is denoted by δ, and Δ is the diffusion
time defined as the time interval between the gradient pulses. In
all the 1H high-resolution NMR diffusometry experiments
reported in this study, the delays were set to δ = 2 ms and
Δ = 20 ms. A field gradient g in the z direction was applied, incremented in 16 steps in a linear
ramp from 2 to 95% of maximum field gradient in the range of gmax = (1–10) T/m. The stimulated echo
decay was collected into 16k data points and Fourier transformed by
applying zero filling to 32k data points and an exponential window
function with a line broadening factor of 5 Hz. A relaxation delay
of 7 s was used with a spectral window of 6 kHz. For all NMR measurements
made in deuterated aqueous dispersions, the PNIPAm concentration was
50 mg mL–1. For both CPMAS 3.2 and Diff50 NMR probeheads,
the temperature calibration was made using neat ethylene glycol chemical
shift resonances. The intensity of the NMR free-induction decay and
hence, the detected normalized stimulated echo is proportional to
the Curie factor and therefore, depends on the inverse of temperature.
We will neglect in the following this dependence in the limited range
of temperatures 10–55 °C used in our NMR measurements.
The sample temperature was controlled by gradient cooling system to
avoid convection effects induced by small temperature gradient in
the radio-frequency insert.
and magnetogyric ratio γ
has the
units of rad s–1 T–1. The duration
of the gradient pulse is denoted by δ, and Δ is the diffusion
time defined as the time interval between the gradient pulses. In
all the 1H high-resolution NMR diffusometry experiments
reported in this study, the delays were set to δ = 2 ms and
Δ = 20 ms. A field gradient g in the z direction was applied, incremented in 16 steps in a linear
ramp from 2 to 95% of maximum field gradient in the range of gmax = (1–10) T/m. The stimulated echo
decay was collected into 16k data points and Fourier transformed by
applying zero filling to 32k data points and an exponential window
function with a line broadening factor of 5 Hz. A relaxation delay
of 7 s was used with a spectral window of 6 kHz. For all NMR measurements
made in deuterated aqueous dispersions, the PNIPAm concentration was
50 mg mL–1. For both CPMAS 3.2 and Diff50 NMR probeheads,
the temperature calibration was made using neat ethylene glycol chemical
shift resonances. The intensity of the NMR free-induction decay and
hence, the detected normalized stimulated echo is proportional to
the Curie factor and therefore, depends on the inverse of temperature.
We will neglect in the following this dependence in the limited range
of temperatures 10–55 °C used in our NMR measurements.
The sample temperature was controlled by gradient cooling system to
avoid convection effects induced by small temperature gradient in
the radio-frequency insert.
The use of NMR spectroscopy has the advantage of a small effect of radio-frequency field on gold dispersions functionalized with polymer brushes. The gold has a skin depth of δ = 2.85 μm at the frequency of 700 MHz, and therefore, the induced heat is produced in bulk not only at the surface of AuNRs with d = 16 nm. The induced radio-frequency energy is reduced and dissipated due to short pulses of the order of few microseconds and long recycle delays of the order of several seconds. Hence, in a good approximation the temperature gradient along the polymer brushes can be neglected.
4. Results and Discussion
4.1. Dilute, Semidilute, and Isotropic Concentrated Dispersions of AuNRs
Static and dynamic properties of gold AuNRs in aqueous dispersion depend essentially on the number of AuNRs in unit volume denoted by ν relative to a critic value ν*. The last quantity is of the same order of magnitude as ν2, the inverse of the excluded volume between the nanorods.29 This is defined as ν2 = 1/dL2, where L is the length of the rod and d is its diameter.29
From the TEM micrograph shown in Figure 1a, the AuNR average dimensions are L ≅ 70 nm and d ≅ 16 nm33 that allows estimating the excluded volume to be ν2 ≈ 8.9 × 1023 m–3. The number of AuNRs per volume is given by29
| 18 |
where cAuNRs is the concentration of the AuNR composite, NA is the Avogadro number, and MnAu is the gold molecular weight. Depending on the relative values of ν, ν*, and ν2, different concentration regimes can be reached: (i) dilute, (ii) semidilute, (iii) isotropic concentrated dispersion, and (iv) liquid crystalline dispersion.29 In the above classification for ν ≥ ν2 [case (iii)] or ν ≥ ν*, [case (iv)], the possible aggregation effects were neglected.
Figure 1.
TEM micrograph of AuNR–PNIPAm dispersions in water: (a) single AuNR showing a PNIPAm brush rim, (b) AuNR–PNIPAm with cAuNRs = 0.1 mg mL–1, (c) AuNR–PNIPAm with cAuNRs = 1 mg mL–1, and (d) AuNR–PNIPAm with weight concentration cAuNRs = 50 mg mL–1.
In this study the AuNR weight concentrations of cAuNRs = 0.1, 1, and 50 mg mL–1 were used. The number of AuNRs per unit volume ν estimated using eq 18 is given in Table 1 together with the average number NAuNRs of AuNRs per μm3, measured by ICP–AES.
Table 1. Number of AuNRs per Unit Volume ν Estimated by Eq 18, and Average Number of AuNRs per μm3 Measured by ICP–AES for Different Weight Concentrationa.
The TEM micrograph shown in Figure 1b–d follows qualitatively the ν and NAuNRs trends of the values given in Table 1. Figure 1b,c corresponds to the semidilute AuNRs solution where ν < ν2 and isotropic concentrated solution ν > ν2, respectively. The regime of isotropic concentrated dispersion is shown in Figure 1d at cAuNRs = 50 mg mL–1. In spite of the large number of AuNRs, that is, NAuNRs ≈ 345 nanorods/μm3, (see Table 1), the nanorods aggregation and liquid crystal behavior were not detected. The 1H HRNMR diffusometry measurements made for AuNRs with concentration of cAuNRs = 50 mg mL–1 proves that the rods are not aggregated in the overall temperature range investigated (see below).
The correlation between aggregation of AuNRs, dispersion concentration, temperature, and presence of free PNIPAm was also investigated by UV–vis and sample photographs (Figure 2). Purified AuNR dispersions, free of unbound polymer, show no thermally induced aggregation upon heating above the low critical solution temperature (LCST) of the PNIPAm tethers (see Figure 2a). The UV–vis spectrum at 50 °C shows a slight decrease in the absorbance and a minor hypochromic shift of 6 nm of the longitudinal surface plasmon resonance band. We assign this to polarity changes due to the collapsed, dense PNIPAm shell on the AuNR surface. Moreover, even at high concentration, no AuNRs aggregation could be observed (Figure 2b). We address this effect to the present negative repulsive surface charges as the PNIPAm brush is already collapsed at 50 °C (Figure 2c left-hand side).12 This behavior is consistent with recently reported literature on PNIPAm-modified AuNP, where a free polymer was found to induce nanoparticle association.39,40 Also in the case reported here, the addition of unbound sulfur-free PNIPAm triggers the particle aggregation, independent of the PNIPAm end group (Figure 2c).40 Nevertheless, the association process is reversible by cooling the dispersion back to 20 °C (T < LCST), shown in Figure 2c, right-hand side.40
Figure 2.
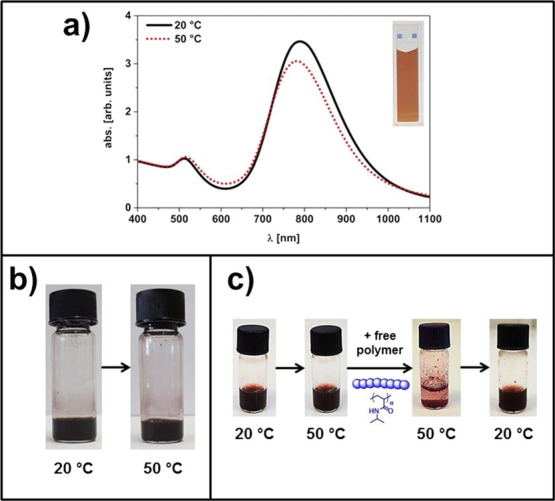
(a) UV–vis absorption spectra of Bn-PNIPAm-SH brushes onto AuNRs in aqueous dispersion with cAuNRs = 1 mg mL–1 at 20 °C (solid line) and 50 °C (dotted line). The polymer molecular weight is Mn = 30 000 g mol–1. The inset shows the photograph of the corresponding aqueous dispersion that is temperature-independent. (b) Photographs of Bn-PNIPAm-SH brushes (Mn = 30 000 g mol–1) onto AuNRs in purified aqueous dispersion with cAuNRs = 50 mg mL–1 at 20 and 50 °C. (c) Photographs of Bn-PNIPAm-SH brushes (Mn = 12 500 g mol–1) onto AuNRs in purified aqueous dispersion with cAuNRs = 1.3 mg mL–1 (V = 500 μL) at 20 and 50 °C (left-hand side) and after addition of 12.5 mg sulphur-free PNIPAm (Mn = 12 500 g mol–1) at 50 °C and after cooling back to 20 °C (right-hand side).
4.2. Grafting Density of PNIPAm Brushes onto AuNRs
The number of bound PNIPAm per unit surface area, that is, grafting density σ, is a critical feature to consider for diffusion of nanoparticles with polymer brushes and colloidal stability of nanoparticles.41 Besides many other analytical methods NMR spectroscopy can be effective in the measurements of surface coverage.42−44 We discuss in the Supporting Information the details of the HRMAS NMR spectroscopy applied to the measurements of the PNIPAm grafting density in the case of AuNRs. The final relation used for grafting density evaluation is given by
| 19 |
where VD2O is the dispersion volume of deuterated
water in mL, mAuNRs is the mass of AuNRs
in mg, and MAu is the molecular weight
of gold in g mol–1. The ratio r is defined as 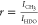 where the NMR peak integrals under
methyl
CH3– of PNIPAm and partially deuterated water (HDO)
are denoted by ICH3 and IHDO, respectively (see Figure S1 of Supporting Information). The internal reference
is given by the HDO NMR peak. The integral peak ratio for a series
of NIPAm-PNIPAm-SH brushes onto AuNRs with different molecular weights
is given in Table S1 of Supporting Information. The grafting density for NIPAm-PNIPAm-SH brushes onto AuNRs measured
by 1H HRMAS NMR spectroscopy is shown in Table 2. High-resolution TEM micrograph
of AuNRs–PNIPAm nanocomposites shown in Figure 1a proves the existence of a uniform grafting.
This represents the validity condition of eq 19 used for evaluation of grafting density
shown in Table 2.
where the NMR peak integrals under
methyl
CH3– of PNIPAm and partially deuterated water (HDO)
are denoted by ICH3 and IHDO, respectively (see Figure S1 of Supporting Information). The internal reference
is given by the HDO NMR peak. The integral peak ratio for a series
of NIPAm-PNIPAm-SH brushes onto AuNRs with different molecular weights
is given in Table S1 of Supporting Information. The grafting density for NIPAm-PNIPAm-SH brushes onto AuNRs measured
by 1H HRMAS NMR spectroscopy is shown in Table 2. High-resolution TEM micrograph
of AuNRs–PNIPAm nanocomposites shown in Figure 1a proves the existence of a uniform grafting.
This represents the validity condition of eq 19 used for evaluation of grafting density
shown in Table 2.
Table 2. Grafting Density vs Mn for NIPAm-PNIPAm-SH Brushes onto AuNRs Measured by 1H HRMAS NMR Spectroscopy.
| Mn [g mol–1] | σa [chains/nm2] |
|---|---|
| 4000 | 0.011 |
| 12 500 | 0.023 |
| 30 000 | 0.0038 |
Estimated errors of the order of 20%.
The grafting density reported in Table 2 can be compared with those obtained by neutron reflection for PNIPAm grafted onto a flat gold substrate.45 For instance, for PNIPAm with a molecular weight of 33 000 g mol–1, the reported grafting density in ref (45) is σ = 0.0063 chains/nm2. Tacking into account the differences in brush architecture onto AuNRs and flat gold surfaces as well as the accuracy in the methods used for σ measurements, we estimate that NMR spectroscopy can obtain reliable results. It can be noted that no significant differences were observed in the PNIPAm grafting density for low molecular weights. The grafting density values for Bn-PNIPAm-SH brushes onto AuNRs are of the same order of magnitude as those of NIPAm-PNIPAm-SH polymers.
4.3. Translational and Rotational Diffusion of AuNRs Composites by DLS. The Effect of End-Group Functionalization
DLS can measure directly the diffusivities of the composite nanoparticles in the dilute regime represented by AuNRs modified with PNIPAm brushes. This technique gives access to the normalized electric field autocorrelation function g1(t) = (g2(t) – 1)1/2, of optically isotropic rods where g2(τ) is the normalized intensity field autocorrelation function.18−20 In DLS experiments with VV geometry, the g1(t) function can be expanded as a weighted sum of exponential decay18−20
| 20 |
where Si(qL), (i = 0,2) are the scattering
amplitudes fulfilling the condition S0 + S2 = 1. In eq 20, q is the magnitude of
the wave scattering vector given by 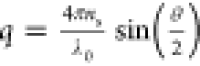 , where ns is
the real part of the refractive index of solvent, λ0 is the vacuum wavelength of radiation, and θ is the scattering
angle. For qL < 2, the scattering amplitudes fulfill
the condition S2(qL)
< S0(qL).46 Nevertheless, as was discussed in ref (22), S0 and S2 can be considered as fit
parameters that will generate effective translational and rotational
diffusivities. The relaxation rates defined by Γ1 = q2DT and
Γ2 = q2DT + 6DR fulfill the condition
Γ2 > Γ1 and gives access to DT and DR diffusivities
of AuNRs. Figure 3 shows
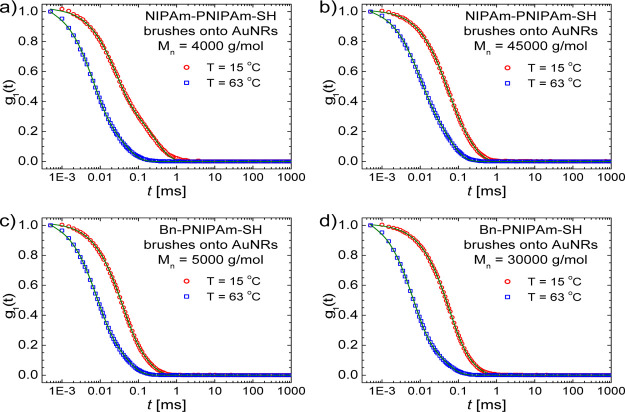
the g1(t) decays for
AuNRs modified with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes at 15
and 63 °C. The samples shown in these figure have the extreme
values of the polymer molecular weight used in this investigation.
Relaxation rates are faster for hydrophobic benzyl end groups compared
with the hydrophilic NIPAm-like end groups. This can be correlated
with the values of hydrodynamic drag coefficients.35 For instance, the drag coefficient ξ measured by
NMR diffusometry have the values of ξ = 12.9 × 10–11 J s m–2 K–2 and ξ = 191.4
× 10–11 J s m–2 K–2 for Bn-PNIPAm-SH (Mn = 30 000
g mol–1) and NIPAm-PNIPAm-SH (Mn = 45 000 g mol–1) brushes,
respectively. The grafting density for both PNIPAm types onto AuNRs
are in the same range and cannot explain the large differences between
the diffusivities of NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes (see
below).
, where ns is
the real part of the refractive index of solvent, λ0 is the vacuum wavelength of radiation, and θ is the scattering
angle. For qL < 2, the scattering amplitudes fulfill
the condition S2(qL)
< S0(qL).46 Nevertheless, as was discussed in ref (22), S0 and S2 can be considered as fit
parameters that will generate effective translational and rotational
diffusivities. The relaxation rates defined by Γ1 = q2DT and
Γ2 = q2DT + 6DR fulfill the condition
Γ2 > Γ1 and gives access to DT and DR diffusivities
of AuNRs. Figure 3 shows
the g1(t) decays for
AuNRs modified with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes at 15
and 63 °C. The samples shown in these figure have the extreme
values of the polymer molecular weight used in this investigation.
Relaxation rates are faster for hydrophobic benzyl end groups compared
with the hydrophilic NIPAm-like end groups. This can be correlated
with the values of hydrodynamic drag coefficients.35 For instance, the drag coefficient ξ measured by
NMR diffusometry have the values of ξ = 12.9 × 10–11 J s m–2 K–2 and ξ = 191.4
× 10–11 J s m–2 K–2 for Bn-PNIPAm-SH (Mn = 30 000
g mol–1) and NIPAm-PNIPAm-SH (Mn = 45 000 g mol–1) brushes,
respectively. The grafting density for both PNIPAm types onto AuNRs
are in the same range and cannot explain the large differences between
the diffusivities of NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes (see
below).
Figure 3.
Electrical field autocorrelation function decays measured by DLS, for AuNRs with NIPAm-PNIPAm-SH brushes at 15 and 63 °C. The brush molecular weights are (a) Mn = 4000 g mol–1 and (b) Mn = 45 000 g mol–1. In (c,d) the same dependences are shown for Bn-PNIPAm-SH brushes onto AuNRs with comparable molecular weights.
The distribution functions of the relaxation rates Γ1,2 and implicitly of the AuNRs diffusivities can be obtained from the g1(t) decays using the inverse Laplace transform (ILT).4,19 These normalized distribution probability as a function of temperature are shown in Figure S2 in Supporting Information. The presence of three intense peaks in the normalized probability as a function of relaxation rate Γ can be explained by the experimental errors present in the tail of the decay function and possible numerical artifacts generated by the ILT procedure.4 Furthermore, the supplementary peak can originate from the presence of free PNIPAm in the AuNRs dispersion. However, we can note that the dispersions were extensively purified by multiple centrifugation and redispersion steps and therefore, free PNIPAm was not detected by 1H HRNMR diffusometry decays (see below).
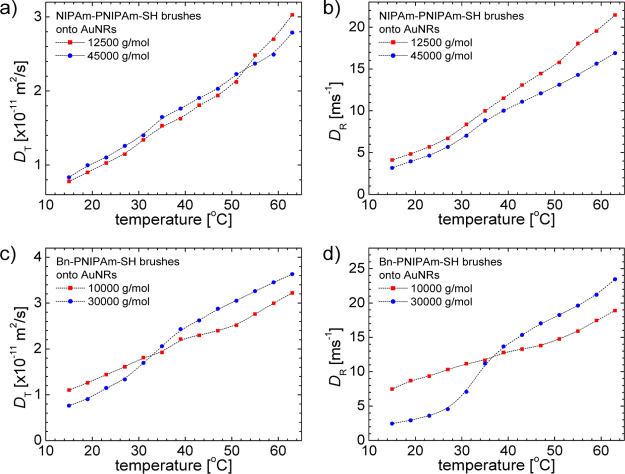
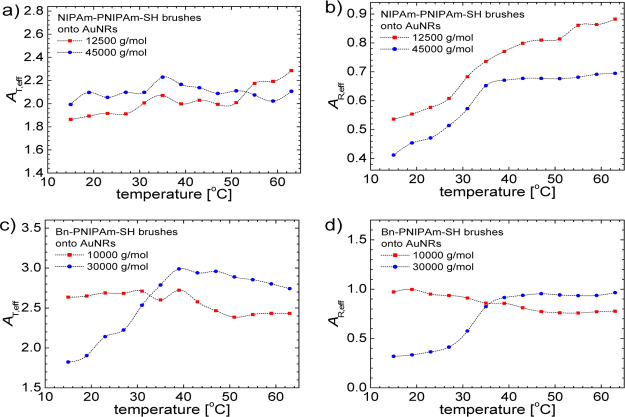
The temperature dependence of translational and rotational diffusivities for nanocomposite AuNRs with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes are shown in Figure 4a,b and 4c,d, respectively. The temperature-dependent factor T/η(T), that occurs in eqs 7 and 9 dominates the temperature dependence of DT and DR. The temperature dependence of viscosity is taken from ref . A weak phase transition can be detected mainly in the temperature dependence of rotational diffusion coefficients (Figure 4b,d). The brush phase transition is encoded into effective aspect functions AT,eff and AR,eff, shown in Figure 5. As revealed by eqs 8 and 10, the aspect functions depend on aspect ratio p = L/d, where d = d0 + 2z(T). Taking into account that the temperature dependence of the rod length L and bare rod-diameter d0, the fact can be neglected that in a good approximation the brush thickness z(T) reflects the process of phase transition.
Figure 4.
Temperature dependence of translational (DT) and rotational (DR) diffusivity of AuNRs measured by DLS. The AuNRs are functionalized with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes with different molecular weights, and DT and DR diffusivity are shown in figures (a,b) and (c,d), respectively. The continuous lines are spline interpolation of the data for the eyes.
Figure 5.
Temperature dependence of effective translational (AT,eff) and rotational (AR,eff) aspect ratio functions of AuNRs measured by DLS for NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes shown in figures (a,b) and (c,d), respectively. The continuous lines are spline interpolation of the data for the eyes.
In the process of brush collapse the aspect ratio increases by the decrease of brush thickness and AT,R,eff functions will increase with temperature as revealed by the results shown in Figure 5. As expected the encoding of brush phase transition will be more intense for larger molecular weight as shown in Figure 5d for Mn = 30 000 g mol–1.
The thermodynamic parameters of brush phase transition are dependent on the hydrophilic or hydrophobic end groups.33−35 Hence, the change in brush thickness and therefore, aspect ratio at a given temperature is different for PNIPAm with benzyl or NIPAm-like end groups. This explains the differences between the temperature dependences shown in Figure 5.
In the dilute regime of AuNRs, the effective hydrodynamic radius RH can be measured in DLS experiment using the Stokes–Einstein approach.19,30 The temperature dependence of RH for AuNRs with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes are shown in Figure 6. The presence of brush temperature-induced phase transition was clearly revealed. This is related to the fact that effective diffusion coefficient depends on the translational and rotational diffusivities and consequently, are more sensitive to the changes in the brush thickness induced by phase transition. Furthermore, for both end-groups, the effective hydrodynamic radius is larger for Mn = 45 000 g mol–1 (NIPAm end group) and Mn = 30 000 g mol–1 (Bn end group) compared with the brushes with lower molecular weight.
Figure 6.
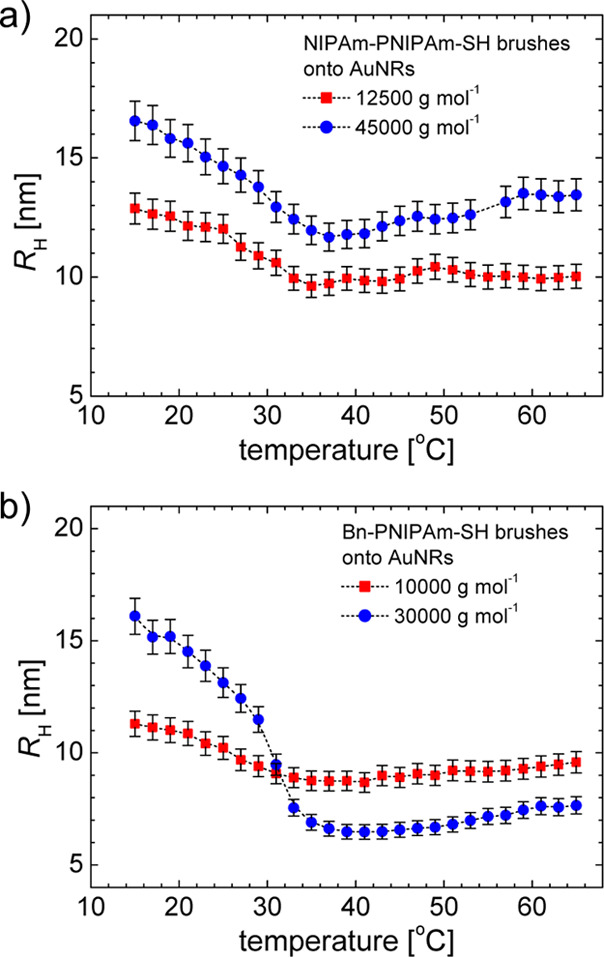
Temperature dependence of the effective hydrodynamic radius obtained from DLS measurements for AuNRs with (a) NIPAm-PNIPAm-SH and (b) Bn-PNIPAm-SH brushes. The molecular weight Mn values are indicated in the figure legends.
The temperature dependence of brush thickness z(T) can be obtained from eq 11 and is shown in Figure 7. The functions z(T) have a sigmoidal shape corresponding to a temperature-induced phase transition. The fit of the data in Figure 7 with a two-state model given by eq 12 allows the estimation of the brush thickness in the swollen and collapsed states. These values are given in Table 3 as a function of molecular weight. The brush thickness increases with the increasing of polymer molecular weight and are also dependent on the hydrophilic or hydrophobic end groups.
Figure 7.
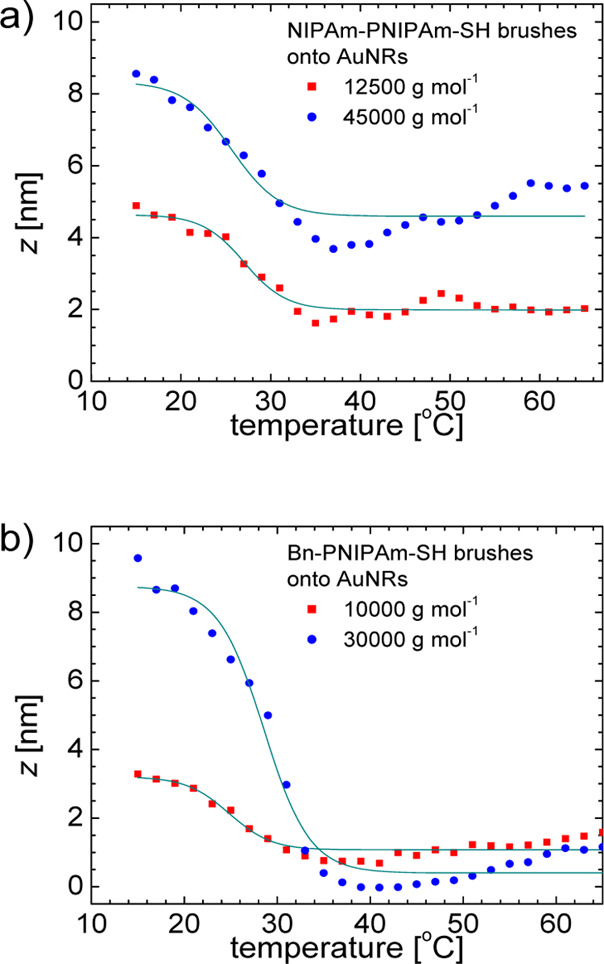
Temperature dependence of brush height obtained from DLS measurements for AuNRs with (a) NIPAm-PNIPAm-SH and (b) Bn-PNIPAm-SH brushes. The molecular weight Mn values are indicated in the figure legends. The continuous lines show the fit with eq 12.
Table 3. Polymer Brush Thickness for Swollen and Collapsed States Obtained by the Fits of z-Temperature Dependences with Eq 12.
| sample | Mn [g mol–1] | zswollen [nm]a | zcollapsed [nm]a |
|---|---|---|---|
| NIPAm-PNIPAm-SH brushes onto AuNRs | 12 500 | 4.6 | 2.0 |
| 45 000 | 8.3 | 4.6 | |
| Bn-PNIPAm-SH brushes onto AuNRs | 10 000 | 3.2 | 1.1 |
| 30 000 | 8.7 | 0.4 |
The estimated errors are of the order of 10%.
The self-consistent field approximation applied at moderately surface coverage gives for the maximum thickness of polymer brush the following dependence on the molecular weight, that is,46
| 21 |
where R is the cylinder radius of curvature and ε = 2 for a cylinder surface with large curvature. The second virial coefficient for the free energy of the system is denoted by ν̅.48 In the case of NIPAm-PNIPAm-SH brushes onto AuNRs from the data of Table 3, we can calculate the ratio zswollen (Mn = 45 000 g mol–1)/zswollen (Mn = 12 500 g mol–1) ≅ 1.80. This ratio evaluated from eq 20 and Table 2 is about 1.35 that is in agreement with that obtained from DLS measurements. Moreover, thermodynamic parameters characterizing the temperature-induced phase transition of polymer brushes onto AuNRs present in the two-state model, that is, transition temperature and normalized change in the entropy (see eq 12) obtained from fits of brush thickness (Figure 7) are reported in Table S4 of the Supporting Information.
4.4. AuNRs Translational Diffusivity in the Isotropic Concentrated Dispersion by High-Resolution NMR Diffusometry
High spectral resolution offered by NMR spectroscopy allows the separate
detection of polymer brush peaks and HDO solvent molecules (see Figure
S1 of the Supporting Information). The
diffusion decays measured by 1H PFGSE high-resolution NMR
method2,38 for NIPAm-PNIPAm-SH and Bn-PNIPAm-SH polymer
brushes used as NMR markers onto AuNRs with concentration of cAuNRs = 50 mg mL–1 in D2O are shown in Figure 8a and b, respectively. From the gradient dependence of detected
NMR signal given by eq 17, we can write 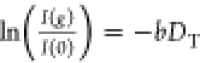 , where the quantity b was
varied by steps in the gradient strength. This magnetic field gradient
encodes in the phase of stimulated echo the center of gravity position
of the nanoparticles, and therefore, the translational diffusivity
is the quantity that is measured. The apparent translational diffusivity DT of AuNRs can be evaluated from Figure 8, and the values of DT for grafted NIPAm-PNIPAm-SH and Bn-PNIPAm-SH
polymer brushes for two polymer molecular weights are compared in
Figure S4 of the Supporting Information. For both PNIPAm brushes with hydrophilic and hydrophobic end groups
the AuNR translational diffusivity decreases with the increase of
molecular weight of the polymer brush. This is related to the increase
in the hydrodynamic drag coefficients of the functionalized AuNRs.
The same trend in the evolution of DT with Mn was detected for linear, free NIPAm-PNIPAm-SH,
and Bn-PNIPAm-SH in the regime of isotropic concentrated solutions.35
, where the quantity b was
varied by steps in the gradient strength. This magnetic field gradient
encodes in the phase of stimulated echo the center of gravity position
of the nanoparticles, and therefore, the translational diffusivity
is the quantity that is measured. The apparent translational diffusivity DT of AuNRs can be evaluated from Figure 8, and the values of DT for grafted NIPAm-PNIPAm-SH and Bn-PNIPAm-SH
polymer brushes for two polymer molecular weights are compared in
Figure S4 of the Supporting Information. For both PNIPAm brushes with hydrophilic and hydrophobic end groups
the AuNR translational diffusivity decreases with the increase of
molecular weight of the polymer brush. This is related to the increase
in the hydrodynamic drag coefficients of the functionalized AuNRs.
The same trend in the evolution of DT with Mn was detected for linear, free NIPAm-PNIPAm-SH,
and Bn-PNIPAm-SH in the regime of isotropic concentrated solutions.35
Figure 8.
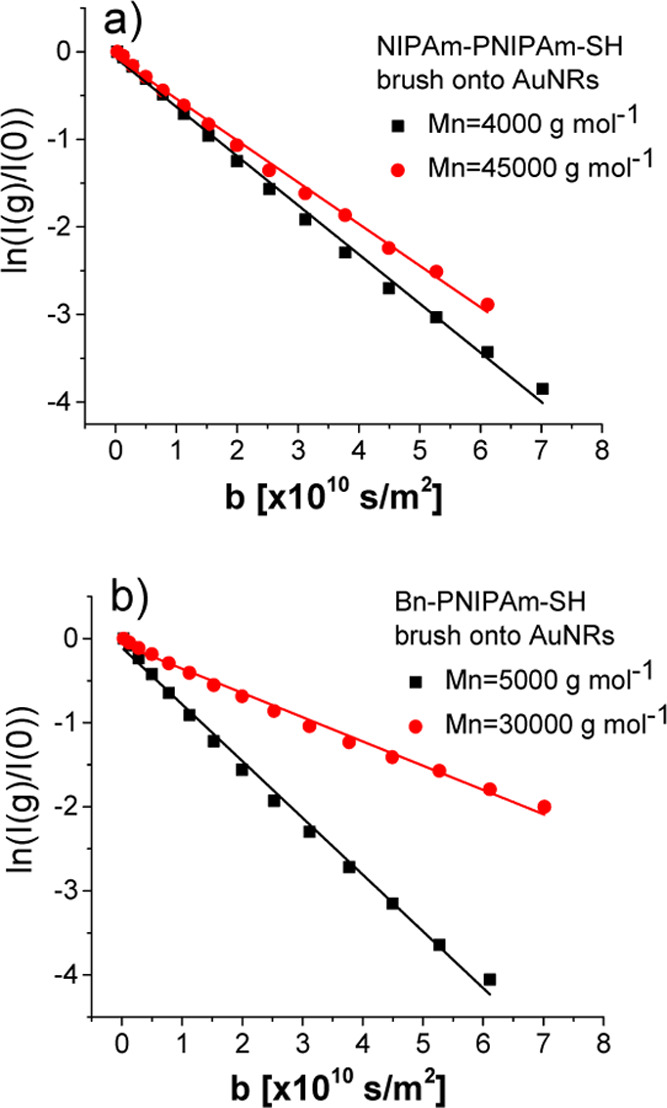
Diffusion decays measured by Stejkal–Tanner method38 using 1H high-resolution NMR spectroscopy of the aliphatic spectral region of NIPAm-PNIPAm-SH (a), and Bn-PNIPAm-SH (b) polymer brushes onto AuNRs. The measurements were made at 20 °C.
High-resolution NMR diffusometry gives access to the normalized translational diffusivity given by eqs 14 and 15 valid for AuNRs in the regime of isotropic concentrated dispersions. In such conditions, the AuNRs stochastic motion is hindered and particles mainly diffuse along the elongated axis of the rods. The temperature dependence of DT/DT0 ratio, where DT0 is the diffusion coefficient measured at 20 °C, is shown in Figure 9. To avoid the adverse effect of AuNRs convection, the diffusivity measurements are limited to the expected region of brushes phase transition temperature.35
Figure 9.
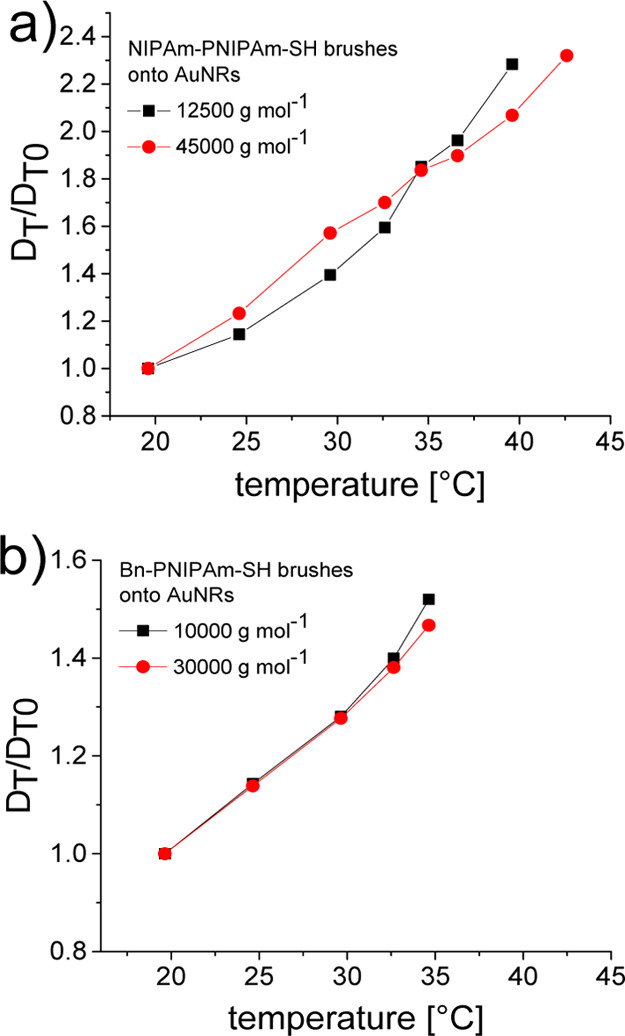
Temperature dependence of the normalized translational diffusivity for (a) NIPAm-PNIPAm-SH and (b) Bn-PNIPAm-SH polymer brushes onto AuNRs measured by HRNMR diffusometry. The functionalized AuNRs–PNIPAm concentration in D2O was cAuNRs = 50 mg mL–1.
The translational diffusivity of AuNRs having NIPAm-PNIPAm-SH polymer brushes shown in Figure 9a is increasing with temperature similar to that reported in Figure 4a using the DLS method. The temperature dependence is dominated by the factor T/η(T) and not by the polymer brush phase transition. The same behavior is shown for AuNRs with Bn-PNIPAm-SH brushes. This can be related to the fact that in isotropic concentrated aqueous dispersions the brush interactions with the other AuNRs in the tube has a big contribution to diffusion compared with the interaction between polymer brushes facing away from the AuNR surface and water molecules.
5. Conclusion
The DLS method directly obtains information about the self-diffusion of noble metallic nanoparticles in our case AuNRs, whereas in the case of NMR diffusometry, a polymer marker grafted onto AuNPs is needed. The temperature dependence of AuNRs diffusion in the presence of tethered thermoresponsive brushes in the regime of dilute water dispersions measured by DLS reveals a weak dependence upon temperature-induced phase transition in the case of translational and rotational diffusivities. We demonstrate that rotation diffusion is more sensitive to brush thickness variation than translational diffusion. The highest sensitivity is obtained from effective hydrodynamic radius due to contribution from both translational and rotational diffusion. The modeling of this quantity by hydrodynamic theory of nanorods with small aspect ratio30 in combination with the two-state approach33 extended to diffusion35 allowed us to estimate the temperature-dependent changes in the brush thickness. This quantity depends on the molecular weight and end group of the polymer brush. Furthermore, the influence of polymer brush fluctuations in the swollen state upon the rotational diffusion was not explicitly taken into account.49
In the case of NMR diffusometry working in the regime of isotropic concentrated solutions the effect of diffusion in a tube have to be taken into account. The strong hydrodynamic interactions between AuNRs orient the rod diffusion along the rod long axis and reduce the diffusivity. Hence, a reduced dependence on the polymer brush phase transition was detected. Nevertheless, the diffusivity of AuNRs with small aspect ratio is depending on the molecular weight of polymer brush and end group functionalization. In general, in the case of NMR methods, the dilute concentration regime is difficult to be investigated due to sensitivity reasons while photon correlation spectroscopy is based on a complex formalism in the presence of nanorods entanglement.19 The results presented in this work will contribute to better understanding of the transport behavior of asymmetrically shaped nanocomposites employed in many applications.
Acknowledgments
One of the authors (M.M.) gratefully acknowledge the support of an Advanced Grant from the European Research Council (ERC), Jellyclock 695716. The funding from DFG-SFB 985 is also gratefully acknowledged. This work was performed in collaboration with the Center for Chemical Polymer Technology CPT, which was supported by the EU and the federal state of North Rhine-Westphalia (grant EFRE 30 00883 02). We thank Dr. Helmut Keul and Dr. Rostislav Vinokur for useful discussions.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b01289.
1H HRMAS spectrum in the aliphatic region of Bn-PNIPAm-SH brushes; ratio VD2O/mAuNRs versus Mn for NIPAm-PNIPAm-SH brushes onto AuNRs; ratio r from 1H HRMAS NMR spectra versus Mn for NIPAm-PNIPAm-SH brushes onto AuNRs; grafting density σ versus Mn for NIPAm-PNIPAm-SH brushes onto AuNRs; normalized probability of relaxation rates Γ obtained by Inverse Laplace transform of autocorrelation functions g1(t); proton HRMAS spectra of NIPAm-PNIPAm-SH brushes onto AuNRs; transition temperature (Tt) and normalized change in entropy; and translational diffusivities of AuNRs with NIPAm-PNIPAm-SH and Bn-PNIPAm-SH brushes for two molecular weights (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Kärger J.; Ruthven D. M. Diffusion in Nanoporous Materials: Fundamental Principles, Insights and Challenges. New J. Chem. 2016, 40, 4027–4048. 10.1039/c5nj02836a. [DOI] [Google Scholar]
- Kimmich R.NMR Tomography, Diffusometry, Relaxometry; Springer-Verlag: Berlin, 1997. [Google Scholar]
- Callaghan P. T.Translational Dynamics and Magnetic Resonance; Oxford University Press: New York, 2011. [Google Scholar]
- Shapiro Y. E. Structure and dynamics of hydrogels and organogels: An NMR spectroscopy approach. Prog. Polym. Sci. 2011, 36, 1184–1253. 10.1016/j.progpolymsci.2011.04.002. [DOI] [Google Scholar]
- Demco D. E.; Filipoi C.; Zhu X.; Fechete R.; Möller M. Morphological Heterogeneity by Diffusional Kurtosis NMR Spectroscopy in Perfluorosulfonic Acid/SiO2Composite Proton-Exchange Membranes. Macromol. Chem. Phys. 2013, 214, 1345–1355. 10.1002/macp.201300039. [DOI] [Google Scholar]
- Ohkubo T.; Ohira A.; Iwadate Y. Deconvolution and Estimation of Water Diffusion in Sulfonated Polyethersulfone Membranes Using Diffusion-Weighted Inversion Recovery. J. Phys. Chem. Lett. 2012, 3, 1030–1034. 10.1021/jz3002458. [DOI] [PubMed] [Google Scholar]
- Rollet A.-L.; Simonin J.-P.; Turq P.; Gebel G.; Kahn R.; Vandais A.; Noël J.-P.; Malveau C.; Canet D. Self-Diffusion of Ions at Different Time Scales in a Porous and Charged Medium: The Nafion Membrane. J. Phys. Chem. B 2001, 105, 4503–4509. 10.1021/jp0023462. [DOI] [Google Scholar]
- Kujawa P.; Winnik F. M. Innovation in Nanomedicine through Materials Nanoarchitectonics. Langmuir 2013, 29, 7354–7361. 10.1021/la4014619. [DOI] [PubMed] [Google Scholar]
- Kuo W.-S.; Chang C.-N.; Chang Y.-T.; Yang M.-H.; Chien Y.-H.; Chen S.-J.; Yeh C.-S. Gold Nanorods in Photodynamic Therapy, as Hyperthermia Agents, and in Near-Infrared Optical Imaging. Angew. Chem. 2010, 122, 2771–2775. 10.1002/ange.200906927. [DOI] [PubMed] [Google Scholar]
- Jain P. K.; Huang X.; El-Sayed I. H.; El-Sayed M. A. Noble Metals on the Nanoscale: Optical and Photothermal Properties and some Applications in Imaging, Sensing, Biology, and Medicine. Acc. Chem. Res. 2008, 41, 1578–1586. 10.1021/ar7002804. [DOI] [PubMed] [Google Scholar]
- Alam S.; Mukhopadhyay A. Translational Anisotropy and Rotational Diffusion of Gold Nanorods in Colloidal Sphere Solutions. Langmuir 2015, 31, 8780–8785. 10.1021/acs.langmuir.5b01682. [DOI] [PubMed] [Google Scholar]
- Yusa S.-i.; Fukuda K.; Yamamoto T.; Iwasaki Y.; Watanabe A.; Akiyoshi K.; Morishima Y. Salt Effect on the Heat-Induced Association Behavior of Gold Nanoparticles Coated with Poly(N-isopropylacrylamide) Prepared via Reversible Addition–Fragmentation Chain Transfer (RAFT) Radical Polymerization. Langmuir 2007, 23, 12842–12848. 10.1021/la702741q. [DOI] [PubMed] [Google Scholar]
- Karg M.; Jaber S.; Hellweg T.; Mulvaney P. Surface Plasmon Spectroscopy of Gold–Poly-N-isopropylacrylamide Core–Shell Particles. Langmuir 2011, 27, 820–827. 10.1021/la1039249. [DOI] [PubMed] [Google Scholar]
- Roddriguez-Fernández J.; Fedoruk M.; Hrelescu C.; Lutich A. A.; Feldmann J. Triggering the Volume Phase Transition of Core–Shell Au Nanorod–microgel Nanocomposites with Light. Nanotechnology 2011, 22, 245708. 10.1088/0957-4484/22/24/245708. [DOI] [PubMed] [Google Scholar]
- Timko B. P.; Arruebo M.; Shankarappa S. A.; McAlvin J. B.; Okonkwo O. S.; Mizrahi B.; Stefanescu C. F.; Gomez L.; Zhu J.; Zhu A.; Santamaria J.; Langer R.; Kohane D. S. Near-infrared-actuated devices for remotely controlled drug delivery. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 1349–1354. 10.1073/pnas.1322651111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitsuishi M.; Koishikawa Y.; Tanaka H.; Sato E.; Mikayama T.; Matsui J.; Miyashita T. Nanoscale Actuation of Thermoreversible Polymer Brushes Coupled with Localized Surface Plasmon Resonance of Gold Nanoparticles. Langmuir 2007, 23, 7472–7474. 10.1021/la701215t. [DOI] [PubMed] [Google Scholar]
- Mourran A.; Zhang H.; Vinokur R.; Möller M. Soft Microrobots Employing Nonequilibrium Actuation via Plasmonic Heating. Adv. Mater. 2017, 29, 1604825. 10.1002/adma.201604825. [DOI] [PubMed] [Google Scholar]
- Pecora R. Spectrum of Light Scattered from Optically Anisotropic Macromolecules. J. Chem. Phys. 1968, 49, 1036–1043. 10.1063/1.1670189. [DOI] [Google Scholar]
- Schmitz K.An Introduction in Dynamic Light Scattering by Macromolecules; Academic Press: Boston, 1990. [Google Scholar]
- Lehner D.; Lindner H.; Glatter O. Determination of the Translational and Rotational Diffusion Coefficients of Rodlike Particles Using Depolarized Dynamic Light Scattering. Langmuir 2000, 16, 1689–1695. 10.1021/la9910273. [DOI] [Google Scholar]
- Rodríguez-Fernández J.; Pérez-Juste J.; Liz-Marzán L. M.; Lang P. R. Dynamic Light Scattering of Short Au Rods with Low Aspect Ratios. J. Phys. Chem. C 2007, 111, 5020–5025. 10.1021/jp067049x. [DOI] [Google Scholar]
- Badaire S.; Poulin P.; Maugey M.; Zakri C. In Situ Measurements of Nanotube Dimensions in Suspensions by Depolarized Dynamic Light Scattering. Langmuir 2004, 20, 10367–10370. 10.1021/la049096r. [DOI] [PubMed] [Google Scholar]
- Shetty A. M.; Wilkins G. M. H.; Nanda J.; Solomon M. J. Multiangle Depolarized Dynamic Light Scattering of Short Functionalized Single-Walled Carbon Nanotubes. J. Phys. Chem. C 2009, 113, 7129–7133. 10.1021/jp900731q. [DOI] [Google Scholar]
- Broersma S. Rotational Diffusion Constant of a Cylindrical Particle. J. Chem. Phys. 1960, 32, 1626–1631. 10.1063/1.1730994. [DOI] [Google Scholar]
- Brenner H. Rheology of a dilute suspension of axisymmetric Brownian particles. Int. J. Multiphase Flow 1974, 1, 195–341. 10.1016/0301-9322(74)90018-4. [DOI] [Google Scholar]
- Ortega A.; García de la Torre J. Hydrodynamic properties of rodlike and disklike particles in dilute solution. J. Chem. Phys. 2003, 119, 9914–9919. 10.1063/1.1615967. [DOI] [Google Scholar]
- Tirado M. M.; Martínez C. L.; de la Torre J. G. Comparison of theories for the translational and rotational diffusion coefficients of rod-like macromolecules. Application to short DNA fragments. J. Chem. Phys. 1984, 81, 2047–2052. 10.1063/1.447827. [DOI] [Google Scholar]
- Tsay J. M.; Doose S.; Weiss S. Rotational and Translational Diffusion of Peptide-Coated CdSe/CdS/ZnS Nanorods Studied by Fluorescence Correlation Spectroscopy. J. Am. Chem. Soc. 2006, 128, 1639–1647. 10.1021/ja056162i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi M.; Edwards S.. The Theory of Polymer Dynamics; Oxford University Press: Oxford, 1986. [Google Scholar]
- Teraoka I.Polymer Solutions; Wiley Interscience: New York, 2002. [Google Scholar]
- Liao J.; Zhang Y.; Yu W.; Xu L.; Ge C.; Liu J.; Gu N. Linear Aggregation of Gold Nanoparticles in Ethanol. Colloids Surf., A 2003, 223, 177–183. 10.1016/s0927-7757(03)00156-0. [DOI] [Google Scholar]
- Zimbone M.; Musumeci P.; Baeri P.; Messina E.; Boninelli S.; Compagnini G.; Calcagno L. Rotational Dynamics of Gold Nanoparticle Chains in Water Solution. J. Nanopart. Res. 2012, 14, 1308–1319. 10.1007/s11051-012-1308-4. [DOI] [Google Scholar]
- Schweizerhof S.; Demco D. E.; Mourran A.; Keul H.; Fechete R.; Möller M. Temperature-Induced Phase Transition Characterization of Responsive Polymer Brushes Grafted onto Nanoparticles. Macromol. Chem. Phys. 2017, 218, 1600495. 10.1002/macp.201600495. [DOI] [PubMed] [Google Scholar]
- Schweizerhof S.; Demco D. E.; Mourran A.; Keul H.; Fechete R.; Möller M. Thermodynamic Parameters of Temperature-Induced Phase Transition for Brushes onto Nanoparticles: Hydrophilic versus Hydrophobic End-Groups Functionalization. Macromol. Rapid Commun. 2017, 38, 1700362. 10.1002/marc.201700362. [DOI] [PubMed] [Google Scholar]
- Schweizerhof S.; Demco D. E.; Mourran A.; Fechete R.; Möller M. Polymers Diffusivity Encoded by Stimuli-Induced Phase Transition: Theory and Application to Poly(N -Isopropylacrylamide) with Hydrophilic and Hydrophobic End Groups. Macromol. Chem. Phys. 2018, 219, 1700587. 10.1002/macp.201700587. [DOI] [Google Scholar]
- Halperin A.; Kröger M. Collapse of Thermoresponsive Brushes and the Tuning of Protein Adsorption. Macromolecules 2011, 44, 6986–7005. 10.1021/ma201006h. [DOI] [Google Scholar]
- Narath A. Nuclear Magnetic Resonance and Relaxation ofAu197in Gold Metal andAg109in Gold-Silver Alloys. Phys. Rev. 1967, 163, 232–237. 10.1103/physrev.163.232. [DOI] [Google Scholar]
- Stejskal E. O.; Tanner J. E. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. J. Chem. Phys. 1965, 42, 288–292. 10.1063/1.1695690. [DOI] [Google Scholar]
- Jones S. T.; Walsh-Korb Z.; Barrow S. J.; Henderson S. L.; del Barrio J.; Scherman O. A. The Importance of Excess Poly(N-isopropylacrylamide) for the Aggregation of Poly(N-isopropylacrylamide)-Coated Gold Nanoparticles. ACS Nano 2016, 10, 3158–3165. 10.1021/acsnano.5b04083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han F.; Soeriyadi A. H.; Vivekchand S. R. C.; Gooding J. J. Simple Method for Tuning the Optical Properties of Thermoresponsive Plasmonic Nanogels. ACS Macro Lett. 2016, 5, 626–630. 10.1021/acsmacrolett.6b00222. [DOI] [PubMed] [Google Scholar]
- Benoit D. N.; Zhu H.; Lilierose M. H.; Verm R. A.; Ali N.; Morrison A. N.; Fortner J. D.; Avendano C.; Colvin V. L. Measuring the Grafting Density of nanoparticles in Solution by Analytical Ultracentrifugation and Total Organic Carbon Analysis. Anal. Chem. 2012, 84, 9238–9245. 10.1021/ac301980a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sofia S. J.; Premnath V.; Merrill E. W. Poly(ethylene oxide) Grafted to Silicon Surfaces: Grafting Density and Protein Adsorption. Macromolecules 1998, 31, 5059–5070. 10.1021/ma971016l. [DOI] [PubMed] [Google Scholar]
- Liu Q.; de Wijn J. R.; de Groot K.; van Blitterswijk C. A. Surface Modification of Nano-Apatite by Grafting Organic Polymer. Biomaterials 1998, 19, 1067–1072. 10.1016/s0142-9612(98)00033-7. [DOI] [PubMed] [Google Scholar]
- Garcia-Fuentes M.; Torres D.; Martín-Pastor M.; Alonso M. J. Application of NMR Spectroscopy to the Characterization of PEG-Stabilized Lipid Nanoparticles. Langmuir 2004, 20, 8839–8845. 10.1021/la049505j. [DOI] [PubMed] [Google Scholar]
- Yim H.; Kent M. S.; Mendez S.; Lopez G. P.; Satija S.; Seo Y. Effects of Grafting Density and Molecular weight on the Temperature-Dependent Conformational Change of Poly(N-isopropylacrylamide) Grafted Chains in Water. Macromolecules 2006, 39, 3420–3426. 10.1021/ma0520949. [DOI] [Google Scholar]
- Dhont J. K. G.An Introduction to Dynamics of Colloids; Studies in Interface Science; Elsevier, 1996; Vol. II. [Google Scholar]
- Hardy R. C.; Cottington R. L. Viscosity of Deuterium Oxide and Water from 5° to 125°C. J. Chem. Phys. 1949, 17, 509–510. 10.1063/1.1747310. [DOI] [Google Scholar]
- Wijmans C. M.; Zhulina E. B. Polymer Brushes at Curved Surfaces. Macromolecules 1993, 26, 7214–7224. 10.1021/ma00078a016. [DOI] [Google Scholar]
- Bolisetty S.; Hoffmann M.; Lekkala S.; Hellweg T.; Ballauff M.; Harnau L. Coupling of Rotational Motion with Shape Fluctuations of Core–Shell Microgels Having Tunable Softness. Macromolecules 2009, 42, 1264–1269. 10.1021/ma8022603. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.