Estimating Contextual Effects from Ego Network Data

Abstract

Network concepts are often used to characterize the features of a social context. For example, past work has asked if individuals in more socially cohesive neighborhoods have better mental health outcomes. Despite the ubiquity of use, it is relatively rare for contextual studies to employ the methods of network analysis. This is the case, in part, because network data are difficult to collect, requiring information on all ties between all actors. This paper asks whether it is possible to avoid such heavy data collection while still retaining the best features of a contextual-network study. The basic idea is to apply network sampling to the problem of contextual models, where one uses sampled ego network data to infer the network features of each context, and then uses the inferred network features as second-level predictors in a hierarchical linear model. We test the validity of this idea in the case of network cohesion. Using two complete datasets as a test, we find that ego network data are sufficient to capture the relationship between cohesion and important outcomes, like attachment and deviance. The hope, going forward, is that researchers will find it easier to incorporate holistic network measures into traditional regression models.

Introduction

How are individuals affected by their social environment? This is a core question in the discipline, motivating hundreds of papers across a diverse set of subfields, from deviance in schools to mental health in neighborhoods (Berkman et al. 2000; Wray, Colen, and Pescosolido 2011; Sharkey and Faber 2014). Many studies in this tradition use network concepts to characterize the features of the social context. For example, past work has asked if individuals in more cohesive neighborhoods have better mental health outcomes, with fewer suicide attempts and lower chances of depression (Maimon and Kuhl 2008; Ivory et al. 2011). Despite the common use of network ideas, it is uncommon for contextual studies to employ the methods and measures of network analysis (even with recent calls to do so, see Pescosolido 2006 and Entwisle 2007).

Contextual-network approaches are uncommon, in part, because network data are difficult to collect (McCormick and Zheng 2015; Krivitsky and Morris 2017). Network data offer a rich means of measuring contextual features, but this comes at a cost, as there are practical challenges to collecting network data in multiple contexts. Traditionally, network measures require census information on the population of interest. This means having information on all of the actors and all of the ties between actors. In an ideal case, a researcher would interview every actor in every context, using the network data (e.g., friendships between students) to measure the global network features of each school, town, etc. in the study (Entwisle et al. 2007; McFarland et al. 2014). Such data can be difficult to collect, however, especially when there are a large number of contexts and/or a large number of actors in each context (Hipp and Perrin 2006; Smith 2015).

A more typical approach is to sample. For example, a researcher may interview a subset of students from each school in the study. This eases the data collection burden, but also makes it difficult to measure global network properties, which are based on the interdependences between actors (Smith and Burow 2018). It is telling that most sampled-based studies use attitudinal data (e.g., do you feel this is a safe neighborhood?), rather than network data, to infer the social features of a context (Hipp and Perrin 2006).

This paper asks a practical, important question: is it possible to accurately estimate a contextual model using network features (like density or transitivity) while avoiding the data burden of traditional network studies? The basic idea is to apply network sampling techniques (Handcock and Gile 2010; Smith 2012) to the estimation of typical regression models, where outcomes like health or mental health serve as the dependent variable (McPherson and Smith 2019). Network sampling offers a bridge between survey methods and network analysis, as a researcher uses sampled data to infer the global features of a network (Frank 1978; Krivitsky, Handcock and Morris 2011; Smith 2015). A researcher could thus collect sampled data across contexts, use the sampled data to infer the network features of each context and then use the inferred network features as second-level predictors in a hierarchical linear model (HLM) (Raudenbush and Bryk 2002). Here, we assume that the data are collected via simple random sampling without replacement.

The potential payoff from network sampling is large, as contextual-network studies would be much easier to undertake. A researcher could avoid collecting census information in every context, while still employing a network measure as a contextual-level predictor. The reduced data burden would also make it easier for contextual-network studies to move beyond institutionally bounded populations. It is an open question, however, if sampled network data can be used to accurately estimate a contextual model. Past work has focused on the network features themselves (e.g., can we use sampled network data to infer network distance?) leaving the more difficult problem of HLM estimation unexplored (Granovetter 1976; Frank 1978; Smith 2012).¹ For example, Smith (2015) mentions HLMs as the ideal application for network sampling, but they do not actually test this idea, suggesting that future research should take up the problem.

Here, we directly apply network sampling techniques to the problem of contextual models. We ask if HLM results based on sampled network data can mimic the results using complete network data. Substantively, we focus on the effect of network cohesion (which we define in the analytical setup section below) on individual-level outcomes, a common topic for contextual studies (e.g., Gottfredson and DiPietro 2010; Legewie and DiPrete 2012). We offer two tests. The first case uses empirical data on adolescents in schools (using Add Health data). We model two individual-level outcomes, school attachment and behavioral problems in school, as a function of network cohesion, measured as a school-level network feature. Do students in more cohesive schools have better outcomes (higher attachment, fewer behavioral problems), net of individual-level characteristics? And can this be answered just using sampled ego network data? The second case uses simulated data as the basis for the test, where the relationship between network cohesion and the outcomes of interest are known from the start.

The larger hope is that any study with multiple contexts will be able to incorporate a holistic network measure into their analysis, thus connecting the strengths of a network approach (a rich depiction of the social features of a context) with the strengths of traditional survey methods (wide coverage of the population and ease of data collection). We begin the paper with discussion of network sampling. We then discuss the analytical test of the approach, before presenting two sets of results.

Background on Network Sampling

Network sampling has a long tradition, stemming from the important early work of Frank (1971; 1978) and Granovetter (1976). The goal is to solve a fundamental problem in network studies: how can a researcher take sampled network data and still undertake a proper analysis of the network structure, which is based on the pattern of relations between all actors? Network samples can take many forms. Most of the early work on network sampling employed subgraph samples, where all of the ties between a randomly selected subset of actors are recorded. Unfortunately, subgraph samples on large networks tend to yield very little information (as few ties between sampled actors are recorded), and recent work has employed alternative sampling schemes, such as ego network sampling, scale-up methods or snowball sampling designs (e.g., Burt 1984; Thompson and Frank 2000; Feehan and Salganick 2016).

With a snowball sample, for example, a set of initial seeds enumerate their social contacts, or alters, who are brought into the study; these recruits then enumerate their alters who are also brought into the study, and the process is repeated until a sufficient sample is collected (see Handcock and Gile 2011 for debates about the usage of snowball sampling). Past work on snowball sampling has generally fallen into two traditions, one employing formula-based estimators and the second using simulation-based approaches to inference (see Verdery et al. 2017 and Illenberger and Flötteröd 2012 for examples of formula-based approaches). Most of the simulation approaches draw on the exponential random graph model (ERGM) framework. The basic idea is to estimate a model predicting the presence/absence of a tie based on the snowball sample (Handcock and Gile 2010; Pattison et al. 2013; Stivala et al. 2016). The estimated parameters of this model are then used to simulate complete networks, thus inferring the rest of the network (Rolls and Robins 2017; Koskinen, Robin, and Pattison 2010).

Snowball sampling is useful in many settings, but it can also be difficult to implement, making it less than ideal for the problem at hand — estimating contextual network models from sampled data. Snowball sampling designs require that a researcher identify, find and interview the people named by the respondent as a social connection (alternatively, the respondents must be tasked with bringing in their associates into the study). This is a difficult undertaking in a single setting, let alone across many settings; which would be necessary in a study of contextual network effects. Additionally, a snowball sampling design is not easily incorporated into existing surveys.

Ego network data, in contrast, are a natural fit for a contextual, network sampling approach and serve as the focus of this paper. Ego network data are based on a random sample of independent cases, where each respondent answers questions about their personal, or local, network. The data collection burden is comparatively low (Marsden 2011). All information comes from the respondents themselves, as the named network alters are not identified and not interviewed. Ego network data are thus easy to collect and easily incorporated into a multi-context study. A researcher would sample within each context of interest, interviewing a subset of people in each school, neighborhood, etc. Importantly, ego network data are easily added to existing surveys, meaning a researcher could turn traditional contextual studies (on schools, for example) into a network study by adding a few questions to the base survey.

Figure 1 plots 3 example ego networks. Ego network surveys begin by asking respondents to list their alters, or those individuals they are socially connected to (Burt 1984; Marsden 1990; Smith, McPherson, & Smith-Lovin 2014). A study may ask about friendship, social support and so on. This offers information on the degree (i.e., number of ties) for each actor. In Figure 1, the first ‘respondent’ names 3 friends, the second names 2, and the third names 0. In a contextual study, a researcher may have respondents list all of their alters; respondents would then be asked which alters reside in the context (school, neighborhood, etc.) of interest.

Figure 1.

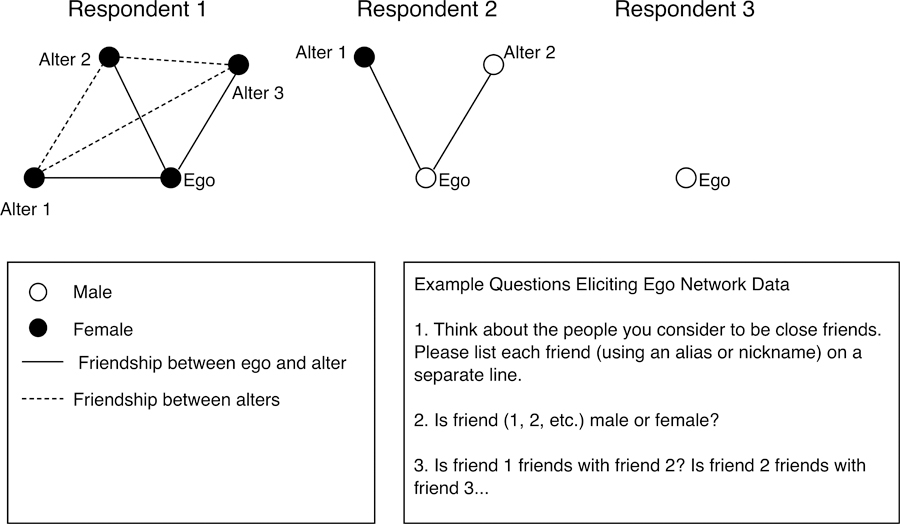
Ego Network Data from Three Hypothetical Respondents

Ego network data will also include demographic information, both about the respondents and the named alters. A researcher may ask the respondent about their age, education and gender, while asking them to report on the age, education and gender of each alter (Burt 1984). Figure 1 demonstrates this in the case of gender. The first respondent is female and reports that all three of the named alters are female, suggesting something about the level of homophily in the network (the tendency for similar actors to interact at high rates).

Finally, ego network surveys will often ask respondents to report on the ties between alters. For example, the first respondent in Figure 1 reports that alter 1 and 2 are friends, that alter 1 and 3 are friends and that alter 2 and 3 are friends. The alter-alter ties capture the tendency for friends to also be friends with each other, or transitive closure. Note that no identifying information on the alters is collected. This means that the alter-alter tie information cannot be used to map particular ties (or edges) in the network.

The vast majority of inferential work on ego network sampling has been at the local level, measuring items like mean degree (how many alters were named on average?) or homophily (how similar are ego and the named alters in terms of gender, race, etc.?) (e.g., McPherson, Smith-Lovin and Brashears 2006). Other, more global, features of the network have been traditionally difficult to capture from ego network data, as there is no way of connecting one sampled ego to another (McPherson and Smith 2019) (i.e., this is more than a simple missing data problem-Smith, Moody and Morgan 2017).

Past work has consequently employed simulation as an analytical approach, in a similar way to the literature on snowball sampling (Morris and Kretzschmar 2000; Morris et al. 2009). The basic idea is to take information from the sampled data, like number of named partners, similarity between ego and alter and generate full networks that are consistent with that local information (Krivistky et al. 2011; Smith 2012). For example, Krivitsky and Morris (2017) simulate complete sexual networks from ego network data based on degree, homophily on race (and sex) and degree differences by race and sex. As is typical with simulations based on ego network data, the model does not include any term for transitive closure (i.e., did their sexual partners share other partners?).

Smith (2012) offers a related, but distinct approach to simulating full networks from ego network data. His approach fully incorporates the alter-alter tie data into the simulation, thus conditioning the generated networks on the pattern of transitive closure found in the ego network data. This is an important development in network inference, as models that do not incorporate transitive closure will tend to yield unrealistic networks in most cases (i.e., excluding sexual networks, where closure is relatively weak), with features that do not approximate the true network well. Empirically, past work has shown that the approach offers better estimates than models just based on degree and homophily (Smith 2012).

Gjoka, Smith and Butts (2014) offer a different approach to a similar problem, offering unbiased estimators for clique size based on independently sampled ego network data. See also Anderson, Butts, and Carley (1999) who discuss the estimation of density from ego network data. Their approach (and similar formula-based approaches) are simple to implement but are limited to a narrow set of statistics where formulas are possible to derive; as opposed to a simulation approach where any statistic can be calculated on the generated networks.

In this paper, we draw on the simulation approach of Smith (2012; 2015) to infer network properties from sampled data across multiple contexts, which are then used as predictors in an HLM. We also consider formula-based estimators where appropriate. We offer a short background section on the simulation approach before describing the test case of interest.

Background on Inferential Approach

The simulation approach described in Smith (2012) has three main steps: first, summarize the key features of the sampled ego networks; second, simulate a full network consistent with the sampled information using ERGM; and third, map out the path structure of the generated network, using that to measure network properties of interest. We offer a brief overview of the approach here but see Smith (2015) for a more detailed discussion (and see Appendix B for a discussion of scope conditions). We begin with a short background on ERGMs.

ERGM

ERGMs are statistical models used to test hypotheses about network structure/formation (Wasserman and Pattison 1996; Hunter et al. 2008). Define y as the observed graph and Y as a random graph on N, where each possible tie, ij, is a random variable. The ERG models the Pr(Y=y). The “independent variables” are counts of local structural features in the network (Robins et al. 2007), such as number of ties. We can write the model as:

$$P\left(\mathit{Y}=\mathit{y}\right)=\frac{exp\left({\theta }^{T}g\left(\mathit{y}\right)\right)}{\kappa \left(\theta \right)}$$ (1)

where g(y) is a vector of network statistics, θ is vector of parameters, and κ(θ) is a normalizing constant.

ERGMS are typically used to test hypothesis about the features of a network, but it is also possible to generate, or simulate, networks from a specified model (e.g., Robins et al. 2005; Morris et al. 2009). The coefficients reflect the effect of different local processes on the probability of a tie existing; those coefficients can then be used to predict the presence/absence of a tie between actors in a synthetic network. This is the manner in which ERGMs are used here.

Key Steps to Simulating Networks using ERGM

The method begins by summarizing the information available from the sampled ego networks. It is crucial to extract as much information as possible as the networks are generated based on the sampled data. The degree distribution is estimated first. This is taken directly from the sampled data: the proportion in the sample with 0, 1, 2, 3, etc. alters is used as the estimate of the degree distribution. We then summarize the information from the alter-alter tie data, showing the tendency towards transitive closure. Smith (2012) proposed a novel characterization of the alter-alter tie data, where the data are used to construct a distribution of ego network configurations. Each respondent is characterized as a distinct structural type, based on the size of the ego network and the pattern of ties between alters. See Figure A1 for an example ego network configuration distribution.

The next main step is to set up the simulation itself. A network of size N (based on the population of interest) is first seeded with the correct degree distribution, estimated from the sample. Each node in the generated network is then seeded with demographic characteristics from the sampled data. Nodes in the generated network are matched with sampled respondents with the same degree; each selected node is assigned all of the demographic characteristics of that respondent, such as gender, age and education. Such a matching process ensures that demographic groups with higher degree in the ego network data will also have higher degree in the generated network, thus constraining the network based on differential degree.

The method then estimates the initial ERGM coefficients. The terms in the ERGM specify which local features are used to construct the full network. The terms in the model will reflect all of the information available from the ego network data, specifically in terms of homophily and the ego network configuration distribution (differential degree and the degree distribution are already used to construct the base network). The model will include homophily terms for every demographic variable available in the ego network survey. For continuous variables, like age or education, this takes the form of an absolute difference coefficient, reflecting the absolute difference between respondents and their alters on that dimension. For categorical variables, like race or gender, the model includes a mixing matrix showing the number of ties going between different demographic groups. These coefficients can be estimated within the ERGM framework or using case control logistic regression (see Smith et al. 2014).

The model will also include a term for the geometrically weighted edgewise shared partner (GWESP) distribution (Snijders et al 2006). GWESP captures the tendency for actors (who are themselves socially connected) to have shared partners, or common associates (so if i and j are friends and both are friends with k and l, that edge would have 2 shard partners). The GWESP statistic is a geometrically weighted mean of the shared partner distribution and is based on two items: the actual distribution of shared partners and a scaling parameter. The scaling parameter captures the relative weight put on the second, third, fourth, etc., shared partner when performing the summation. When the scaling parameter is 0, for example, the term puts all the weight on the initial shared partner, and simply sums up the number of edges where there is at least one shared partner in common.

Substantively, GWESP captures higher order transitivity in the network (i.e., given that actors i and j are friends, do actors i and j have many friends in common?), or the tendency for small groups to emerge. Within the simulation, GWESP is included to capture the ego network configuration distribution. Because it parameterizes ties between alters, GWESP mirrors many of the structural features of the ego networks, making it an appropriate choice to reproduce them. For example, within an ego network, ego’s friends may be friends with each other; this is analogous to seeing many shared partners in the network. Unlike with the homophily coefficient, the coefficient for GWESP cannot be easily set prior to the simulation (as is it not possible to solve for the value on GWESP that will yield a network with the correct ego network configuration distribution). The GWESP coefficient is thus set at an initial value and is updated during the simulation as the method searches for the best fitting network. Note that the degree distribution and differential degree of the initially seeded network are maintained throughout the simulation.

The framework then takes the initial model (coefficients, terms and constraints) and simulates a network. The homophily rates in the simulated network are then compared to the empirical data to ensure that they match. The homophily coefficients are updated if this is not the case. The basic idea is to compare the level of homophily in the generated network to that observed in the ego network data (along each dimension available in the ego network data) and update the model accordingly. Coefficients are increased if there are too few ties between groups and decreased if there are too many. See Smith (2012) for technical details on how to adjust the homophily coefficients.

The next step is to evaluate the simulated network by how well it matches the ego network configuration distribution seen in the sample. Ego networks are first drawn from the simulated network and placed into a structural type. See Figure A1. The distribution of ego network configurations from the simulated network is then compared to the distribution in the sample using a chi square value. The chi-square value is written as:

$${\sum }_{i=1}^n\frac{{\left(O_i-E_i\right)}^2}{E_i}$$ (2)

where O_i is the observed frequency in the simulated network, E_i is the frequency found in the sample, and n is the total number of possible ego network configurations. A large chi-square value indicates a poor fit, as the distribution in the simulated network deviates from the distribution from the sample.

The model is then updated to find a better fitting network, defined as a network that better matches the true ego network configuration distribution (conditioned on the other features found in the ego network data). The ego network configuration distribution is used as a benchmark to judge the simulated networks. The question then becomes what coefficient will yield a network with the lowest chi-square value. The framework finds the best fitting network by: a) simulating networks with different values for GWESP; b) calculating the chi-square value for each network, and c) searching for a ‘better’ fitting GWESP coefficient, given the results. This process is repeated until no better fitting network can be found. See Smith (2012; 2015) for more technical details.

The end result of the search process is a network with the same properties as the sampled ego network data. The simulated network will have the same degree distribution, differential degree, homophily and ego network configuration distribution as in the sample. A researcher can then take the generated network and calculate statistics of interest; in this case to be used as predictors in an HLM.

Analytical Setup: Testing the Method

The main question of this paper is whether it is possible to use sampled network data to estimate traditional HLMs: can a researcher test contextual theories using sample-based estimates of network features? The empirical test of a network sampling approach focuses on network cohesion, although we do consider other contextual-network measures in the appendix (specifically average betweenness, average closeness, transitivity and proportion isolated). We focus on network cohesion as an empirical example because there is a long tradition in the social sciences of using cohesion as a contextual-level predictor (e.g., Sampson, Raudenbaush and Earls 1997; Browning and Cagney 2002). Social cohesion is typically understood as a multidimensional concept, with emotional and relational components that are thought to mutually reinforce each other, leading to lower rates of psychological distress, deviant behavior and the like (Moody and White 2003; Friedkin 2004). Here, we focus on the relational component of cohesion, which can be parameterized naturally using network methods (Bearman 1991).

We utilize two global measures of network cohesion, density and bicomponent size (defined below). Both measures have often been used by past work as network measures of cohesion (e.g., Moody 2004; Tulin, Pollet and Lehman-Willenbrock 2018). Importantly, both are defined at the contextual-level (or network-level), reflecting a feature of the context itself. Thus, the hope is that a researcher could collect sampled data across a number of contexts, use the sampled data to infer density or bicomponent size in each context, and then use the inferred network measures as predictors in an HLM—thus greatly reducing the data collection burden while still retaining the best feature of a network approach.

We test the validity of a sampling approach by comparing the true HLM coefficients to the same coefficients estimated from the sampled ego network data. The baseline estimates serve as the gold standard, where the researcher knows the true values of density and bicomponent size for each context and can use those values within the HLM. In order to make the comparisons equivalent, both the true models and the ego network models are estimated based on the same samples. The only difference is that in the true models, the values for density and bicomponent size are known, while in the ego network models, density and bicomponent size must be inferred from the sample itself. This makes it possible to isolate the bias in the estimates (i.e., only bias that arises from using an inferred measure of cohesion).

We present two tests of the approach, one based on an empirical data set and one based on a simulated data set. The empirical data set has the advantage of representing actual conditions (in terms of networks and outcomes), while the simulated case has the advantage of being full controlled, with known parameters. We focus primarily on the empirical example, describing the test and results in full before moving to the simulated case.

There are seven steps to testing a network sampling approach: 1) select a test data set; 2) specify an HLM to be used in the test; 3) take samples from the complete dataset; 4) estimate the true HLM using known values of density and bicomponent size; 5) estimate the values for density and bicomponent size from the sampled ego network data; 6) estimate an HLM using the inferred values of density and bicomponent size (from Step 5); 7) compare the true HLM coefficients to the ego network-based HLM coefficients.

Select Test Case

In Step 1, we select a dataset for the analytical test. We use Add Health (National Longitudinal Study of Adolescent to Adult Health) for the first case study because it has a nested structure (students within schools), complete network information for each context, and appropriate outcomes of interest. Add Health is a nationally representative survey of public and private schools covering middle schools and high schools (Harris et al. 2009). We utilize the wave I, in-school data. Saturating each school in the survey, all students in the school (or as many as possible) were asked a series of questions about health, behavior and social connections. The network information is based on friendship ties. Students were asked to list up to 5 male and 5 female friends, and these nominations are used to construct the complete, known network for each school. It is necessary to have complete networks so that the true values of density and bicomponent size can be calculated. Each network is assumed to be symmetric. This symmetrizing is done using a ‘weak’ rule, where a tie is exists if either i or j nominates each other. We restrict the analysis to schools that are larger than size 400, which corresponds to the 80 largest schools in the dataset.²

Specify HLMs

In Step 2, we specify the HLMs of interest, used to test a network sampling approach. This entails specifying the dependent variables, the main predictors at the contextual-level, and the control variables at the individual-level. Students are nested within schools, with schools serving as the contextual (or second) level in the models.

Dependent Variables

We conduct two tests of the approach, using two different dependent variables. The first outcome of interest is attachment to school, an individual-level variable capturing the perceived attachment of each student to their school. Attachment is a scale variable, constructed from 3 different questions. Students responded to the following prompts: “I feel close to people at this school.”; “I feel like I am part of this school.”; “I am happy to be at this school.” For each question, students could respond 1–5, with 1=strongly agree and 5= strongly disagree. We take the mean over the 3 answers to form the attachment scale. This variable is then reverse coded, so that higher values correspond to feeling more attached to the school.

The second dependent variable captures behavioral problems. We use three ordinal variables to construct a scale, again, based on the means over the three variables. The three questions of interest are: “Since school started this year, how often have you had trouble: 1) “getting along with your teachers?” 2) “paying attention in school?” 3) “getting your homework done?” The responses range from 0–4 with 0 meaning never and 4 meaning everyday. The values are coded such that higher values equate to having more trouble.

Contextual-level Predictors

The key predictor of interest in the HLM is network cohesion, defined as a contextual-level variable. The two measures are density and bicomponent size. Density is defined as the number of ties (friendship, social support, etc.) relative to the number of possible ties in a network of that size (Wasserman and Faust 1994). Density can be written as:

$$Dens=\frac{\sum \sum \mathit{y}}{N*\left(N-1\right)}$$ (3)

where y is the observed network and N is the total number of people in the network. As a measure of cohesion, lower density suggests lower cohesion in the network. It is important to remember, however, that the number of possible ties increases non-linearly as network size increases, with important implications for understanding density in large networks (Mayhew and Levinger 1976; Anderson et al. 1999).

Bicomponent size is defined as the largest set of actors connected by at least two independent paths, so that removing a single actor leaves the entire set connected (Moody and White 2003). The basic idea is that a network that is difficult to tear apart is socially cohesive, where higher values for bicomponent size suggest a more cohesive network. Figure 2 explores some of the key properties of bicomponent size. The figure consists of two networks with the same density but different proportions in the largest bicomponent (see Moody and White 2003 for a more detailed discussion). It is clear that the network in the top half effectively splits into two groups and is disconnected by removing a single actor. The bottom half tells a different story. The network has the same density but the pattern of ties is different, where our two loosely connected groups are now much more integrated. This would be missed by looking at density alone, but is captured by bicomponent size, which is based on the number (and type) of paths connecting the actors. We can see the proportion in the largest bicomponent goes from .6 to 1, while density is the same in the two plots.

Figure 2.

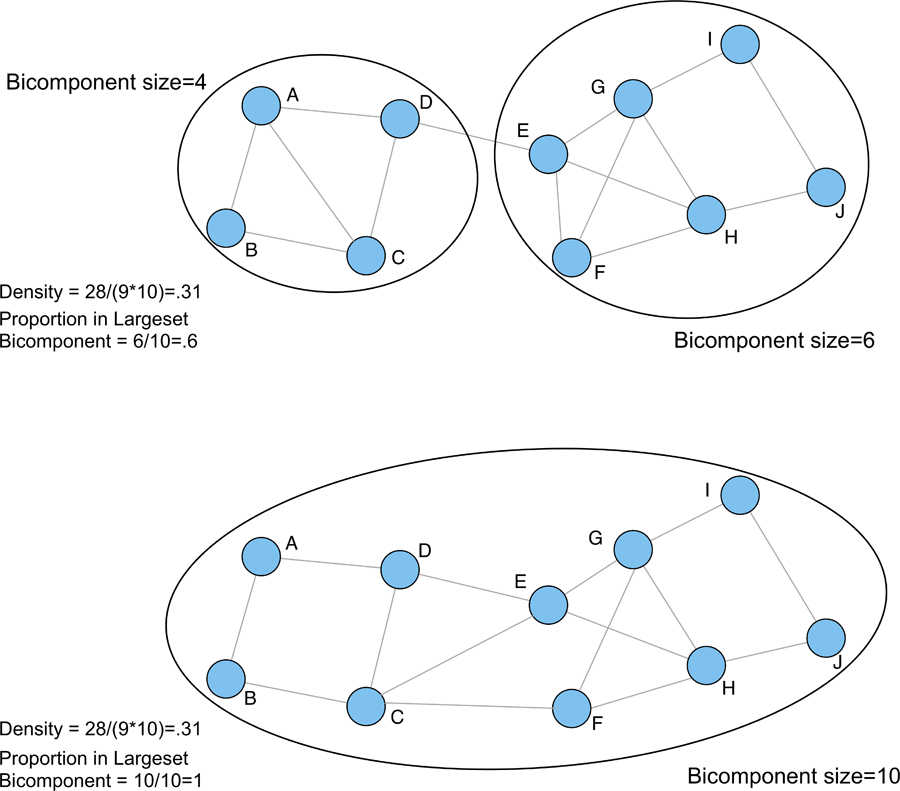
Measuring Cohesion Using Bicomponent Size

Density and bicomponent size (defined as the proportion of people in the largest bicomponent) are measured for each school in the dataset. We run separate models, first with density as the main predictor and then bicomponent size as the main predictor.

Control Variables

We also include a number of individual-level controls in the model. We include control variables to see if the estimates for the cohesion coefficient are robust to different model specifications. We include variables for gender (male or female), race (black, Asian, Hispanic, white or other) and social isolation (1 if the person has 1 or less social ties and 0 otherwise).

Models

We run 4 models. In each case, we predict attachment or behavioral problems as a function of contextual-level network cohesion and a set of control variables. The first model includes only the measure of cohesion, either density or bicomponent size. The second model adds demographic controls to the first model, while the third model adds social isolation to the first model. The final model includes all predictors: cohesion, race, gender and social isolation. For the full model:

$$Y_{ij}=b{0}_j+b1\left(Asian\right)+b2\left(Black\right)+b3\left(Hispanic\right)+b4\left(Other\right)+b5\left(Female\right)+b6\left(Isolated\right)+{\epsilon }_{ij}$$

$$b{0}_j=a00+a01\left(Cohesio{n}_j\right)+u_{0j}$$

where a01 is the coefficient of interest, capturing the fixed-effect interaction of cohesion on the intercept (allowed to vary across schools). These four models are estimated for each dependent variable (attachment and behavioral problems) and measure of cohesion (density and bicomponent size).

Sampling Setup

In Step 3, we take random samples from the complete Add Health dataset. We assume that an independent sample is drawn from each of the 80 Add Health schools in the analysis. We begin by taking a hypothetical survey for each school. It is hypothetical in the sense that we are not actually interviewing any respondents and all information comes from the data itself. We are simply mimicking, as closely as possible, what a survey on this population would have looked like. We assume that the ‘survey’ includes an ego network component, as well as more general questions about attachment, behavioral problems, and demographics.

For the ego network portion, we assume the following information is collected: number of alters (with no cap on number reported); respondent and alter characteristics, including race, grade, sex, and club; and reports on the ties between alters. To mimic a realistic survey, we assume that respondents are only asked to report on the first five alters named (in terms of alter characteristics and alter-alter ties).³ As this is not an actual survey, the five alters are randomly selected amongst the full set of alters for each respondent; this, of course, is only necessary for those respondents with more than 5 friends.

The analysis is repeated for 3 different sample sizes: 15%, 25% and 35%. The sample size refers to the percentage of each school that is sampled. Note that a 15% sample need not yield an absolutely large number of respondents if the school is small. This process is repeated 100 times for each sample size. We take 100 samples in order to capture the variability in the estimates.

Estimate HLMs Using True Values for Density and Bicomponent Size

In Step 4, we estimate the true, baseline HLMs. The models specified in Step 2 are estimated using the samples from Step 3 and the true values of density and bicomponent size. The true models thus represent the results one should have gotten with the sample in question. The true values for density and bicomponent size are calculated using the complete Add Health network data for each school (i.e., not the sampled data). There will be sample-to-sample variation in the cases in the regression but the contextual-level variables are assumed to be known and fixed and thus do not vary sample-to-sample. We estimate separate models predicting attachment and behavioral problems for each sample.

Using Sampled Ego Network Data to Estimate Density and Bicomponent Size

In Step 5, we use the sampled ego network data (from Step 3) to infer density and bicomponent size for each school/sample.

Density is based solely on the volume of ties in the network, which makes the inferential process much easier than with bicomponent size. While a researcher cannot simply apply equation 3 (as one is missing effectively all of the information from the full matrix y), it is possible to directly use sampled ego network data to estimate global network density, without recourse to any complicated computational methods (see Marsden 1990; Anderson et al. 1999). The basic idea is to start with two inputs: first, the list of alters for each respondent; and second, the total size of the network, defined as N (assumed to be known). The first step is to calculate average degree for the sampled respondents, defined as the mean number of alters listed. The second step is to divide that by (N-1), yielding an estimate for density. Formally, define sample average degree as: $\overline{d}=\frac{1}{n}{\sum }_{i=1}^n{d}_i$, where n is number of sampled respondents, and d_i is degree of person i, equal to the number of alters listed. The total volume of ties in the network can then be written as: $v=\overline{d}*N$. The sample-based density is thus estimated by:

$$\frac{v}{\left(N*\left(N-1\right)\right)}=\frac{\overline{d}}{\left(N-1\right)}$$ (4)

Bicomponent size is more difficult to estimate from sampled data, as it captures the pattern of ties between actors more directly (see Figure 2). Ego network data are local, offering pieces of the network that cannot be connected. Ego network data thus cannot be used to directly map out the path structure in the network, yet this is exactly what the measure of bicomponent size is based on. Here we must rely on the full simulation-inferential approach of Smith (2012; 2015). A researcher would take the sampled data in each context, simulate a network consistent with the sampled information, and measure bicomponent size on the generated networks.

Estimate HLMs Using Ego Network-based Estimates of Density and Bicomponent Size

In Step 6, we estimate the HLMs using the ego network-based estimates of cohesion. The analysis is exactly the same as in Step 4, except the values for density and bicomponent size are inferred from the sampled ego network data (estimated in Step 5). Thus, the data used to estimate the HLMs (for each sample) are exactly the same as in the true models, with only the estimates for density or bicomponent size varying.

Compare True Models to Ego Network-Based Models

In Step 7, we compare the coefficients from the ego network models (Step 6) to the coefficients from the true models (Step 4). In both cases, there are 100 X 2 X 2 X 4 X 3 estimates, as there are 100 samples, 2 dependent variables, 2 measures of cohesion, 4 models, and 3 sample rates. The question is how closely the ego network-based coefficients approximate the true coefficients.

Results

Comparing True Network Values to Statistics Inferred from Ego Network Data

We begin the results section by comparing the true values for density and bicomponent size to the estimated values inferred from the ego network samples. The true values are calculated from the complete network data for each school. We begin with the network statistics before moving to the HLMs (in the next section), as the HLMs are dependent on the inferred measures of bicomponent size and density. It is thus important to check the estimation of bicomponent size and density before moving to the harder test, where those estimates are used as predictors in a regression.

The results are presented in Figure 3. The first row presents the results for density while the second row presents the results for bicomponent size. Each subplot captures a different sampling rate, running from 15% to 35%. The results are presented as a series of boxplots, with one boxplot for each network in the study (within a subplot). The boxplots capture the distribution of the estimated values for density or bicomponent size for that school and sample rate. The boxplots are aligned so that each school is placed on the x-axis at the corresponding true value for density or bicomponent size. We have also added a reference line, showing where the boxplots should be centered if the estimator is unbiased.

Figure 3.

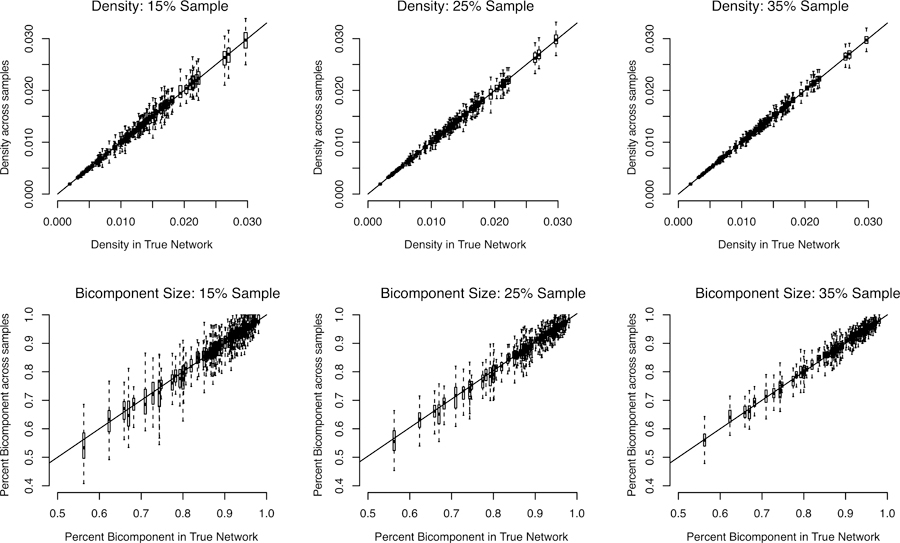
Estimate of Density and Bicomponent Size by True Values for Add Health Networks

Looking at the first row, the results suggest that density can be effectively estimated using sampled network data. The boxplots are centered at the true value for density in every case. The variability of the estimates does increase somewhat in more dense schools (as the range of degree is higher, leading to more variability sample to sample) but is overall relatively modest, with the sample-to-sample estimates clustered tightly around the true value.

The second row presents the results for bicomponent size. The results are again quite good, with the inferred values of bicomponent size centered at the true values. The correlation between the mean estimate (for each school, across samples) and the true value is .998 for all 3 sample rates. Here, however, we can see that the variance of the estimates can be high, especially at the lower sampling rates. For example, for the 15% sample, the average standard error (across all schools) is .029, with some schools having standard errors above .05. Thus, the results show that bicomponent size can, on average, be accurately captured from sampled ego network data, but that any given sample may offer an estimate that deviates substantially from the true value.

The initial results are encouraging. Still, it is an open question if the estimates for density and bicomponent size are good enough to serve as second-level predictors in an HLM. As Figure 3 shows, the estimates for density or bicomponent size may be above/below the true value in any given sample. It is these imperfect measures (due to sampling variability) that a researcher must use as inputs into the HLM. With these results in mind, we now turn to testing a network sampling approach in the context of HLMs.

True HLM Models: Attachment to School

We begin the HLM results section by looking at the true HL models predicting attachment to school. The true models are estimated using the actual, known values for density and bicomponent size. Table 1 reports the HLM coefficients for the 35% sample. There are four models, with varying combinations of control variables. In each case, we focus on the estimate for network cohesion, either density or bicomponent size. We report the mean estimate for density and bicomponent size over the 100 samples, as well as the 95% error bounds (such that 95% of the values fall in that interval). The table reports two sets of results for each model, one for bicomponent size and one for density.

Table 1.

HLM Results for School Attachment, 35% Sample: Using Empirical Measure of Cohesion, Bicomponent Size or Density

Variables	Model 1a	Model 2a	Model 3a	Model 4a	Model 1b	Model 2b	Model 3b	Model 4b
Intercept	2.411*	2.533*	2.487*	2.609*	2.56*	2.669*	2.605*	2.782*
	(2.388, 2.434)	(2.503, 2.565)	(2.465, 2.511)	(2.579, 2.641)	(2.549, 2.572)	(2.650, 2.689)	(2.593, 2.617)	(2.699, 2.739)
Contextual Level Variables
Density	14.976*	13.559*	11.802*	10.681*
	(12.701, 17.002)	(11.222, 15.627)	(9.392, 13.881)	(8.28, 12.861)
Bicomponent					0.654*	0.381*	0.253*	0.007
					(0.510, 0.810)	(0.232, 0.537)	(0.110, 0.409)	(−0.137, 0.162)
Individual Level Variables
Asian		−0.069*		−0.059*		−0.073*		−0.064*
		(−0.115, −0.023)		(−0.104, −0.011)		(−0.117, −0.026)		(−0.109, −0.017)
Black		−0.195*		−0.175*		−0.194*		−0.177*
		(−0.234, −0.155)		(−0.213, −0.134)		(−0.233, −0.154)		(−0.215, −0.136)
Hispanic		−0.101*		−0.085*		−0.104*		−0.091*
		(−0.138, −0.067)		(−0.122, −0.051)		(−0.14, −0.071)		(−0.128, −0.057)
Other		−0.202*		−0.19*		−0.202*		−0.191*
		(−0.243, −0.166)		(−0.230, −0.155)		(−0.243, −0.166)		(−0.231, −0.156)
Female		−0.073*		−0.094*		−0.073*		−0.094*
		(−0.094, −0.053)		(−0.115, −0.073)		(−0.094, −0.053)		(−0.115, −0.073)
Isolated			−0.457*	−0.459*			−0.458*	−0.461*
			(−0.494, −0.416)	(−0.496, −0.418)			(−0.495, −0.417)	(−0.499, −0.42)
N	20458	20458	20458	20458	20458	20458	20458	20458

^*Denotes coefficient where 95% interval does not contain 0.

The results suggest, in general, that individuals in more cohesive schools report higher levels of attachment. This is clearest in Model 1, where no controls are included in the model. Looking at the density results, 95% of the estimates fall between 12.70 and 17.00, with a mean value of 14.98. Even in Model 4, with controls for gender, race and social isolation, we see that density remains a strong predictor of school attachment. The mean coefficient is 10.68, while 95% of the values fall between 8.28 and 12.86. From Model 1 to Model 4, the effect of density only decreases by 28%. This suggests that a dense network facilitates and supports individual attachment to the school. It is difficult to ignore that one is part of a larger group (here the school) if most people are friends with each other.

The results for bicomponent size are very different: here the effect of cohesion is highly dependent on the controls included in the model. In Model 1, 95% of the coefficients for bicomponent size fall between .51 and .81. The effect for bicomponent size clearly decreases, however, when individual level controls are added to the model. Model 2 includes controls for race and gender and the effect of bicomponent size is reduced by roughly 40%, going from .65 to .38; compare this to the 10% drop seen with density. The coefficient for bicomponent size in the full model (Model 4) approaches 0, with a mean coefficient of .007 and 95% of the estimates falling between −.14 and .16. The results for bicomponent size are thus weaker than with density, suggesting that robustness (as opposed to whether everyone knows everyone else) does not uniformly increase attachment for the whole school, net of individual-level controls.

Ego Network Results: Attachment to School

The ego network results for the same models are presented in Figures 4–5 and Tables A1–A2. The question is whether an ego network approach will yield the same estimates and conclusions as in the baseline models. Figure 4 presents the results for the density coefficient, while Figure 5 presents the results for the bicomponent coefficient. The results are presented as boxplots, capturing the distribution of the cohesion coefficient (either density or bicomponent size) across the 100 samples. The figures are organized by model and sampling rate, with Models 1–4 on the columns and the three sampling rates on the rows. There are two boxplots for each subplot: the true coefficients, where bicomponent size and density are known for each school; and the ego network-based coefficients, where bicomponent size and density are inferred from the sampled ego network data. In the ideal case, the boxplots from the ego network approach will be close to the boxplots from the true models. The tables in the appendix present summary statistics.

Figure 4.

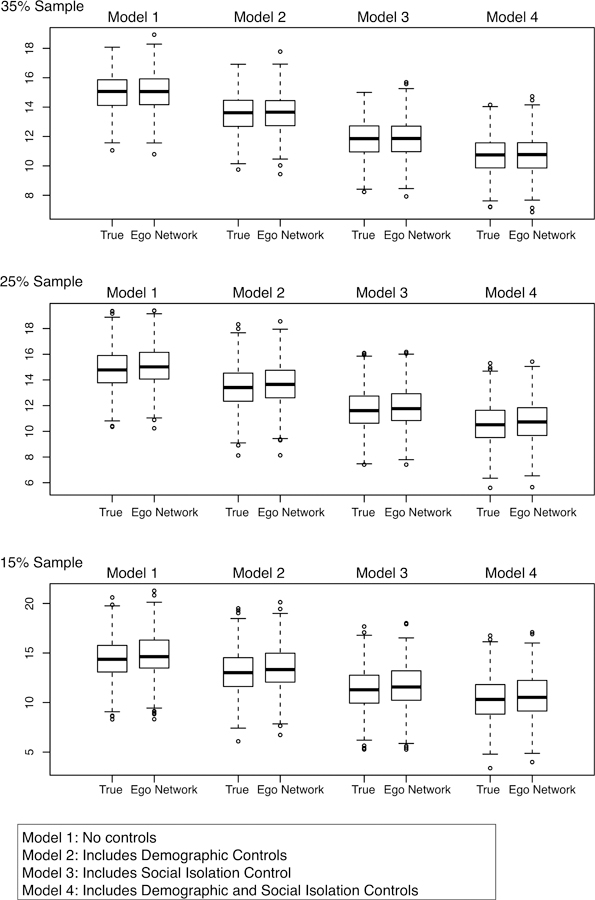
Boxplots of Density Coefficients for Attachment to School Models

Figure 5.

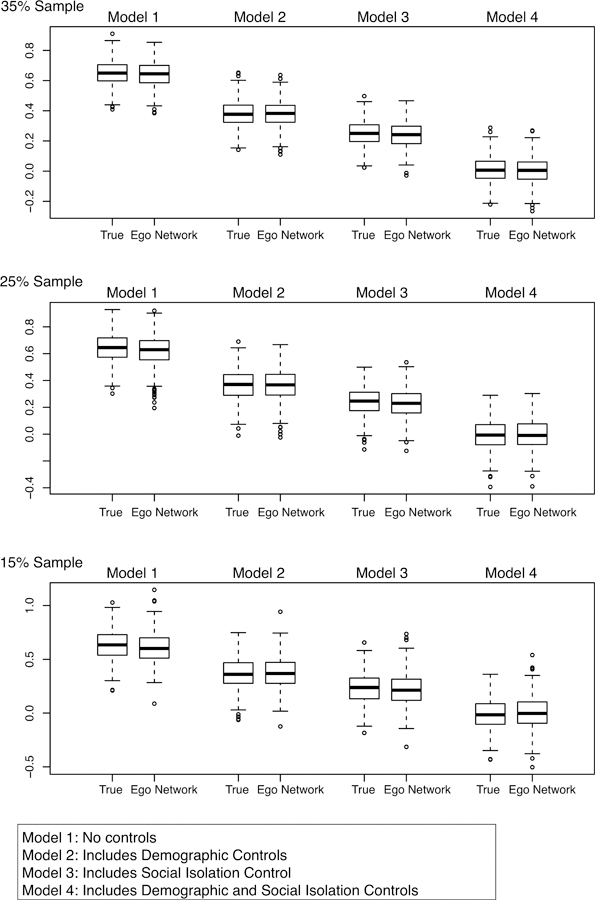
Boxplots of Bicomponent Cofficients for Attachment to School Models

Figure 4 presents the results for density. The ego network results are quite good across models and sampling rates. Looking at Model 1 (no individual-level controls), the ego network-based estimates closely approximate the true coefficients for density, with the ego network boxplots nearly identical to the true boxplots. For example, in the 35% sample, the true mean estimate is 14.976, and 95% of the estimates fall between 12.70 and 17.00. In the ego network analysis, the mean coefficient is 14.99 and 95% of the estimates fall between 12.60 and 17.16. See Table A1. Model 2 controls for gender and race but this does not greatly affect the results. For example, the mean estimate for the 35% sample is 13.56 using the true measure of density. The ego network-based estimate is 13.59, a difference under 1%. Looking at Figure 4, the results for Model 3 (controlling for isolation) and Model 4 (all controls included) are similar, as the estimates using the ego network data are close to the estimates using the true values for density. Overall, moving from Model 1 to Model 4, the density coefficient is reduced by 28% in the ego network models (using the 35% sample: 14.999 to 10.701), the exact same value as in the true HLMs. As in the true models, the ego network-based results suggest that density is a significant predictor of attachment, even controlling for demographics and social isolation (as 95% of the coefficients fall between 8.35 and 12.88 in Model 4). Thus, the ego network models yield the same conclusions as the true models, where density is measured on the complete, known networks. The 15% and 25% results are similar but have higher variance and are (slightly) less accurate.

Figure 5 and Table A2 present the results using bicomponent size as the measure of network cohesion. These models provide a more difficult test, as bicomponent size is harder to estimate from sampled data than density. The results in Figure 5 are quite good, despite the difficulty of the test.⁴ Across all models, the coefficients based on the ego network data are very similar to the estimates using the true values of bicomponent size. This is clear as the ego network boxplots are very close to the true boxplots. For example, in Model 1 the true coefficient for bicomponent size is on average .65 for the 35% sample, with 95% of the coefficients falling between .51 and .81. Using the ego network data, the mean estimate is .64 (1.7% different than the true estimate) with 95% of the estimates falling between .48 and .80. See Table A2. The story is similar for Models 2–4. For example, controlling for isolation in Model 2, the true mean coefficient is .381 (using the 35% sample) while the mean coefficient for the ego network analysis is .379. In the true models, 95% of the estimates fall between .232 and .537; compare this to .199 and .545 in the ego network models. There are similar results for the 15% and 25% samples, although the estimates are predictably more variable as sample size decreases.

The ego network models also capture the reduction in the bicomponent coefficient across models. Looking at the 35% sample, the bicomponent coefficient is reduced by 99% from Model 1 to Model 4 (from .654 to .007) in the true models and 99.5% in the ego network models (from .643 to .003). More generally, the ego network models capture the null results in Model 4, which controls for social isolation, gender and race/ethnicity. For the ego network analysis, 95% of the bicomponent coefficients fall between −0.17 and 0.17 (using the 35% sample). The true interval is −.14 to .16. Thus, the ego network models correctly show that the effect of bicomponent size is largely explained via demographic variables and social isolation (as 0 is contained in the 95% interval).

True HLM Models: Behavioral Problems in School

Table 2 presents the baseline HLM results for behavioral problems in school. The models are estimated as before, using the known, true values for bicomponent size and density. The only difference is that the outcome of interest is now behavioral problems in school, where higher values correspond to worse outcomes.

Table 2.

HLM Results for Behavioral Problems, 35% Sample: Using Empirical Measure of Cohesion, Bicomponent Size or Density

Variables	Model 1a	Model 2a	Model 3a	Model 4a	Model 1b	Model 2b	Model 3b	Model 4b
Intercept	1.623*	1.574*	1.600*	1.558*	1.605*	1.599*	1.593*	1.589*
	(1.594, 1.651)	(1.543, 1.609)	(1.571, 1.63)	(1.527, 1.593)	(1.592, 1.619)	(1.577, 1.619)	(1.579, 1.607)	(1.566, 1.61)
Contextual Level Variables
Density	−1.849	2.023	−0.916	2.65
	(−4.995, 1.023)	(−1.119, 4.847)	(−3.97, 2.063)	(−0.453, 5.436)
Bicomponent					−0.945*	−0.531*	−0.84*	−0.458*
					(−1.131, −0.75)	(−0.73, −0.331)	(−1.021, −0.648)	(−0.652, −0.262)
Individual Level Variables
Asian		0.147*		0.145*		0.138*		0.136*
		(0.079, 0.207)		(0.076, 0.204)		(0.069, 0.199)		(0.067, 0.197)
Black		0.206*		0.201*		0.195*		0.192*
		(0.162, 0.242)		(0.159, 0.238)		(0.152, 0.234)		(0.149, 0.232)
Hispanic		0.222*		0.218*		0.21*		0.208*
		(0.183, 0.262)		(0.179, 0.258)		(0.172, 0.25)		(0.168, 0.248)
Other		0.188*		0.185*		0.184*		0.182*
		(0.146, 0.236)		(0.144, 0.232)		(0.142, 0.231)		(0.14, 0.228)
Female		−0.164*		−0.159*		−0.163*		−0.159*
		(−0.19, −0.14)		(−0.186, −0.136)		(−0.189, −0.139)		(−0.186, −0.136)
Isolated			0.135*	0.101*			0.125*	0.094*
			(0.093, 0.177)	(0.058, 0.141)			(0.083, 0.168)	(0.052, 0.134)
N	20458	20458	20458	20458	20458	20458	20458	20458

^*Denotes coefficient where 95% interval does not contain 0

The results in Table 2 suggest that more cohesive schools have fewer behavioral problems, with (typically) negative coefficients for density and bicomponent size. Thus, while more cohesive schools promote attachment, they reduce the propensity for students to have behavioral problems. The effect for density is, however, quite weak, with no significant coefficient in Models 1–4. The results are more consistent for bicomponent size, where a strong negative relationship holds across all 4 models, even controlling for demographics and social isolation. For example, 95% of the coefficients fall between −.65 and −.26 in Model 4 for the 35% sample. The results reflect the fact that a structurally robust network is conducive to promoting shared norms, and thus reducing behavioral problems in school.

Ego Network Results: Behavioral Problems in School

The ego network-based results are presented in Figures 6–7 and Tables A3–A4. The ego network-based results for density are, as with attachment, quite good. Looking at the boxplots in Figure 6, the ego network-based coefficients are close to the coefficients based on the true values of density. For example, for Model 1 in the 15% sample, the median coefficient is −1.82 in the true model and −1.85 in the ego network model, a difference of 1.6%. Similarly, 95% of the coefficients in the true model fall between −6.42 and 2.82, while 95% of the coefficients in the ego network model fall between −6.60 and 2.93. A researcher would thus arrive at the right conclusion, that density is not a significant predictor of behavioral problems, just using the ego network data. The 25% and 35% samples offer substantively similar results. See Table A3.

Figure 6.

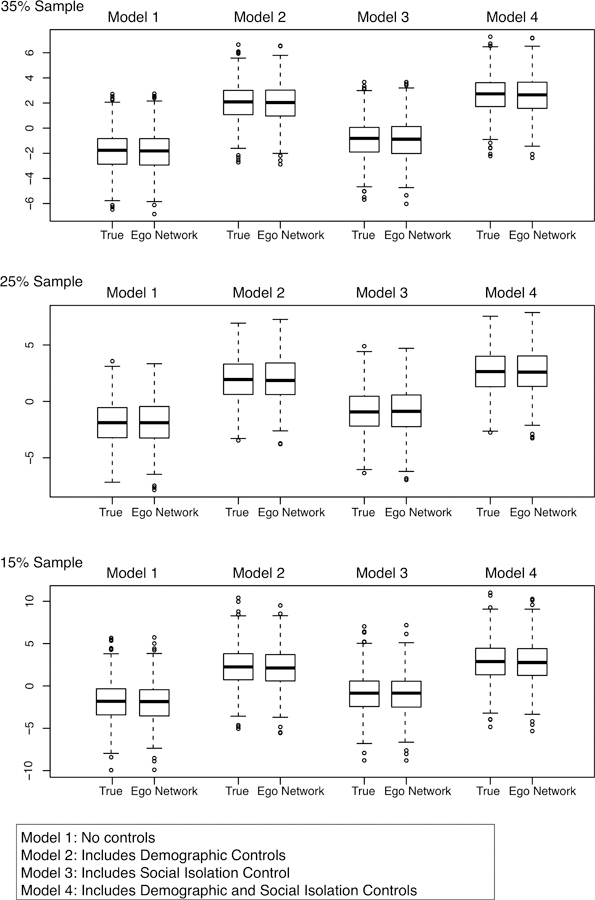
Boxplots of Density Coefficients for Behavioral Problems Models

Figure 7.

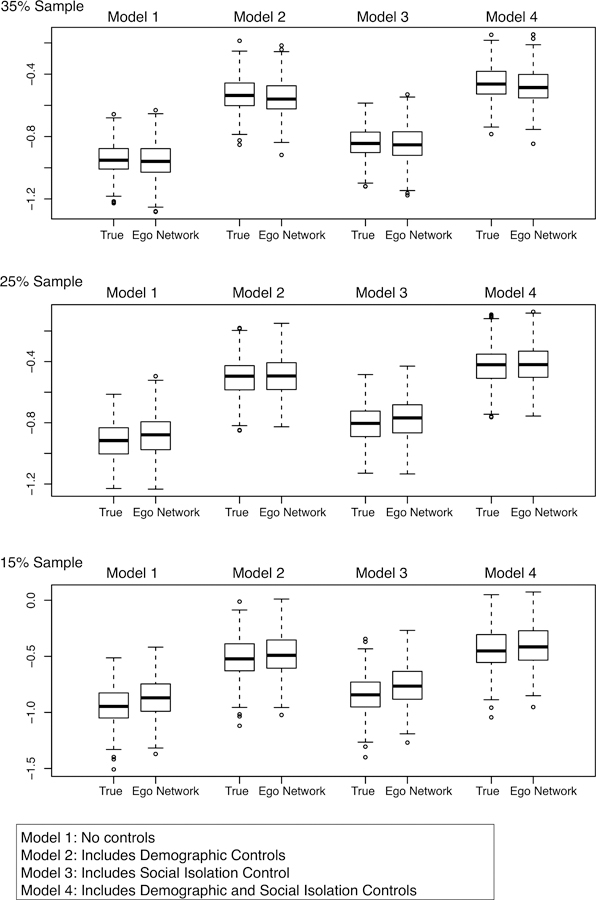
Boxplots of Bicomponent Coefficients for Behavioral Problems Models

The bicomponent results paint a more complicated picture. In Model 1, the ego network-based estimates for the bicomponent coefficient clearly improve as sample size increases. In the 15% sample, the mean coefficient in the true model is −.94, while the mean coefficient in the ego network model is −.87, a difference around 8%. The percent difference (between the true and ego network estimates) decreases to 4% in the 25% sample and 1% in the 35% sample. The results are similar for Model 3, where the ego network coefficients converge with the true coefficients in the 25% and 35% samples. For example, in the 35% sample, the mean coefficient is −.84 in the true model and −.85 in the ego network model, a difference around 1%. Models 2 and 4 provide more consistent results across sampling rates. In Model 2, the mean coefficient for the 15% sample is −.51 in the true model and −.49 in the ego network model. In the 35% sample, the true coefficient is −.531 and the ego network estimate is −.552 (a difference of about 5% in the 15% sample and 4% in the 35% sample).

As with school attachment, the ego network models offer the same substantive conclusions as the true models. For example, consider Model 4 for the 35% sample. Using the ego network data, 95% of the density coefficients fall between −.56 and 5.52, while 95% of the bicomponent coefficients fall between −.69 and −.28. This correctly suggests that bicomponent size, but not density, reduces the propensity for students to have behavioral problems, net of other controls.

In sum, the ego network estimates effectively mirror the true estimates, albeit with some inconsistent results across sampling rates. It is instructive to consider why these results, while generally accurate, are more inconsistent than with school attachment. The difference between the two results lies in the presence/absence of strong outliers in the data. A small number of schools have very high levels of behavioral problems compared to the rest of the Add Health schools (i.e., more than 1.5 times the IQR). These outlier schools have a potentially disproportionate effect on the coefficients for the second-level predictors, in particular bicomponent size. There are no parallel outliers in the school attachment analysis. Thus, with behavioral problems, the estimation is more difficult at low sampling rates. A few outlier schools have the potential to drive the estimation, while bicomponent size for those schools is measured imperfectly (as each sample will yield a different value for bicomponent size). It is telling that the estimation improves as sample size increases, making the measure of bicomponent size more consistent across samples.

Robustness Checks: Testing the Approach under Different Ego Network Conditions

A network sampling approach, while promising, must contend with the practical limitations of ego network data. We have thus far assumed that a researcher could collect information on the number of alters, the characteristics of the alters and the ties between alters. Such data collection may not always be possible, however. For example, the alter-alter tie data can be burdensome to collect. Surveys will thus often restrict the ego network questionnaire, including questions for number of alters and alter characteristics, but not the alter-alter ties. Similarly, we have so far assumed that the ego network data are measured without error, yet this may be an optimistic assumption (Almquist 2012). Ego network surveys ask respondents to report secondhand on the relationships between their alters. Respondents may not always know if their named alters are friends, however, and an uncertain respondent may be forced to guess if a tie exists, creating bias. Thus, even when the alter-alter ties can be collected, there may still be problems with the data.

We explore these issues in Appendix C, where we replicate the analysis under different conditions surrounding the alter-alter tie data. In the first analysis, we assume that no information on the alter-alter ties is collected. The analysis is exactly the same as in the main text, but here the researcher must infer bicomponent size using ego network data that only includes degree and homophily information (as there is only information on number of alters and their characteristics). In the second analysis, we assume that the alter-alter ties are available but that there is measurement error in the data. We take the true ego network data (the data under perfect reporting) and construct scenarios where 15% of the ties are reported with error. This error-filled data become the input to the simulation approach.

The results for the 35% sample are presented in Tables C1 and C2 in Appendix C. We only present the results for bicomponent size as density does not depend on the alter-alter tie data. Looking at Table C1 (attachment is the dependent variable), we can see that the results are good, on the whole, using the limited ego network data, although not as accurate as with the complete ego network data. For example, the true coefficient for bicomponent size in Model 1 is .654; the estimate using the complete ego network data is .643, while it is .684 with no alter-alter data and .634 with the measurement error data. The results are similar for the other models. Overall, the results are largely encouraging, with estimates that suggest that a researcher can ‘get away’ with collecting imperfect ego network data and still correctly estimate an HLM using sampled network data — even if the estimates are not as good as with full information. See Appendix C for the full results.

Robustness Checks: Other Contextual Network Measures

We present another set of supplementary results in Appendix D. Here we run the same basic analysis, estimating HLMs using inferred network features, but use an alternative set of network measures. Instead of focusing on density and bicomponent size, we include results for average betweenness, average closeness, transitivity and proportion isolated. The results are presented in Table D1. In this case we focus just on the results for the 35% sample. We also only include results for Model 1 (no controls) to simplify the discussion. Table D1 includes results for both attachment and behavioral problems.

Overall, the results are quite good for attachment, with the estimates based on the ego-network data approximating the true estimates. For example, for transitivity, the true mean coefficient is .42, while the ego network based estimate is .41. Or, for proportion isolated, 95% of the ego network estimates fall between −1.79 and −1.22; compare this to the true sampling distribution, where 95% of the values fall between −1.75 and −1.26. We see similar results for average betweenness, with a true mean coefficient of −3.77E-5 and an inferred estimate of −3.83E-5. The results are not as strong for average closeness, where the ego-based estimate is −1.19 and the true estimate is −1.04 (a difference of 14%). Closeness is notoriously difficult to measure with incomplete data and thus inference in the HLM context is challenging (Smith et al. 2017). We see similar results for behavioral problems, although the ego network based estimates fare even worse for average closeness, possibly due to outliers in the data (the transitivity coefficient is also estimated poorly here). The mean true coefficient for average closeness is −1.133 while the ego network estimate is −.771 (a difference over 30%). The results thus suggest that an HLM, network sampling approach can, potentially, work beyond measures of cohesion, but that some networks measures (and outcomes) will be more conducive than others.

Robustness Checks: Testing the Approach using Simulated Data

We offer one more test of a contextual network sampling approach. This test uses the same setup as with the Add Health analysis, but utilizes data that are constructed with known properties, rather than being based on empirical data. The basic idea is to test a network sampling approach in a case where the networks and outcomes of interest can be fully controlled. There is thus no measurement error in the data used for the test and the coefficients of interest are known from the start. We can also systematically vary the network features, as well as the relationship between the measures of cohesion and the dependent variables. We only consider measures of cohesion here. The test offers an important robustness check, seeing if a network sampling approach will work on a completely different case, one with different networks, outcomes and models.

We present the methodological details and results in Appendix E, but briefly describe the results here. The test is based on 36 constructed networks with systematically different features (in terms of density and bicomponent size). The test is based on two outcomes, constructed to have known relationships with our measures of cohesion. The first outcome is constructed so that bicomponent size, but not density, is related to the outcome of interest. The second outcome has the inverse pattern, with only density related to the outcome of interest. The rest of the test is analogous to that used above, with three sample rates (15%, 25%, 35%), 100 samples per sample rate, and similar assumptions about the ego network data.

The results are presented in Tables E1 and E2 (in Appendix E) and they offer strong support for a contextual, network sampling approach. A researcher with only ego network data would arrive at the correct estimates for density and bicomponent size. With the first outcome, the positive, strong effect for bicomponent size is approximated quite well, while the null effect for density is also correctly captured. For example, for the 25% sample, the mean estimate is 1.009, while the true coefficient is 1.00. With the second outcome, a network sampling approach correctly picks up the opposite effects, with density, but not bicomponent size, affecting the outcome of interest. For example, the true coefficient for density is 50 and the ego network based estimates have a mean of 49.272 for the 25% sample. One drawback to using the ego network data is that the coefficients have relatively high variance, higher than if we had known the true values of bicomponent size and density. Thus, in cases where the true effect of density or bicomponent size is very strong, measuring those network properties imperfectly (as each sample will yield a slightly different estimate) yields coefficients that are measured uncertainly. Still, even with higher variance, the estimated coefficients from the ego network data offer a viable means of doing contextual network models. See Appendix E for the full set of results.

Conclusion

Network data are a natural fit for contextual models. Global network measures offer a rich picture of a social context, showing how micro-level interactions cohere into a larger whole (Robins et al. 2005; Butts 2008). A researcher could collect network data in each context of interest, measure global network features like cohesion and use the network measures to predict health, mental health, deviance, etc. The drawback of a network approach is that the data collection burden (at least traditionally) is quite high, as one would need to collect census data in every context in the study. This paper considers an alternative approach, one where the researcher estimates contextual-network models but is able to avoid the heavy data collection toll. The basic idea is to combine HLMs with network sampling, where one uses sampled ego network data to infer the network features of each context, and then uses the inferred network features as second-level predictors in an HLM (Raudenbush and Bryk 2002; Smith 2012).

We test the validity of this idea using two complete datasets. The main test uses empirical data from Add Health. We examine the relationship between two measures of network cohesion, density and bicomponent size, and two individual-level outcomes, school attachment and behavioral problems in school. The results are encouraging. Across all models, it is possible to approximate the true coefficients for density and bicomponent size just using the ego network data. Importantly, the substantive conclusions based on the ego network data are exactly the same as in the baseline models, using the true values for density and bicomponent size. Our second test uses simulated data and we find similar results, offering additional supporting evidence.

Overall, the results suggest that contextual-network models can be estimated using sampled data, thus reducing the data burden of the researcher considerably. The implications are clear: any study with sampled individuals can become a network study, where individual outcomes, behaviors and interactions are placed within a larger relational context.

A contextual, network sampling approach is not without limitations, however. For example, some network measures are easier to estimate from sampled data than others. Network measures that capture features of path-based connectivity are generally more difficult to estimate than measures that are independent of the path structure. With our cohesion measures, for example, we found that the estimates around bicomponent size (dependent on the path structure) are more variable than the estimates for density, which does not depend on the path structure. The results for average betweenness and average closeness are also instructive. Both are path-based network measures but the results are better for betweenness than for closeness. This is the case because average betweenness is based on the number of shortest paths between vertices, while average closeness is based on the length of the shortest paths. It is easier to capture general properties about the path structure (e.g., reachability between actors) than more specific properties of those paths (e.g., distance between actors). Overall, the method is most easily applied in cases where the network measure does not depend on the path structure (density, proportion isolated). The next best case is for network measures that depend on the general features of the path structure (bicomponent size, average betweenness). The most difficult case is where the network measure depends on the specific path lengths between actors (average closeness).

The method is also only appropriate for certain types of networks. The networks of interest must be undirected, as ego network do not capture asymmetric relationships very well. Similarly, the networks of interest must capture a strong relationship, where it is difficult to maintain a very large number of ties. This is the case as the inferential approach can have problems when the degree distribution is badly skewed, with one or two actors capturing a disproportionately high number of ties (as a random sample may not always capture these important actors) (Smith 2015). In such cases, a researcher may have to consider alternative sampling schemes, like a two-step snowball sample, where the alters of ego are interviewed (offering more information than the simple ego network data).

Similarly, the method for generating whole networks from ego network samples is based on a simulation approach and is limited by factors that make computation expensive, such as: the number of actors in the network, the number of ties between them, and the transitivity in the network. Large, dense, transitive networks are more difficult to simulate than small, sparse and non-clustered ones. These factors combine in complex ways to determine the practical application of the approach. A large, sparse network (e.g., 50,000 nodes) with low transitivity may be practical to infer while a smaller network (e.g., 10,000 nodes) that is very dense and very transitive may prove prohibitive (in terms of run time). Practical experience suggests that it is possible to infer networks up to around 75,000 nodes, but that the most likely applications will be on much smaller networks — especially in the case of HLMs, where multiple networks must be inferred.

There are fewer limitations when it comes to the dependent variables that are appropriate for the approach. For example, we were able to estimate the HLMs using ego network data even in cases where the relationship between cohesion and the outcome was weak (e.g., the case of bicomponent size and attachment). The main limitation is with outliers, where the models are more difficult to estimate when there are strong outliers on the dependent variable (so that some contexts have very high/low values on the outcome of interest). Additionally, our results are restricted to the case of continuous variables, and the approach may not fare as well with categorical outcomes (like binary variables), where the variance on the dependent variable is constrained.

As a final limitation, measurement error in the ego network data may cause estimation problems (Feld and Carter 2002; Alwin 2007). We considered the case of misreporting in the alter-alter ties, but there are other possible sources of error that may affect the results. For example, past work has found that respondents will sometimes report fewer alters than they actually have (Marin 2004). Such underreporting will distort the number of alters listed per respondent, which is a key input into the density and bicomponent size calculations. Alternatively, respondents may name an alter as more of an aspirational tie than an actual one (i.e. someone they wished were their friend), adding an alter to the list who should not actually be included. The HLM estimates (ultimately the item of interest here) will only be affected, however, if the bias is: a) quite high; b) stronger in some contexts than others; and c) correlated with the outcome of interest. There is no a priori reason to believe that such conditions are likely. Still, it will be important for future work to consider the problem of alter misreporting more closely.

This paper has focused on network cohesion across schools, but an HLM-network sampling approach is general, appropriate for any research setting concerned with the effect of social context on individual outcomes. Methodologically, future work could test the approach using other contextual-level network measures (e.g., centralization or modularity), seeing if the approach can accurately reproduce the effect of these features on important outcomes of interest (see Appendix D for an initial test on betweenness, closeness, transitivity and proportion isolated). More substantively, ego network sampling could be applied to such diverse topics as deviance in neighborhoods, mental health in organizations, or health behaviors in schools. Moving forward, the hope is that researchers will find it easier to blend traditional survey methods with a network approach, thus maintaining the coverage and convenience of a sample without sacrificing the holistic, relational feel of a network study.