A discussion on some simple epidemiological models

Abstract

The present text discusses some basic considerations on the dynamics of the coronavirus pandemic, in particular in France. The goal is not to make accurate predictions, which is probably impossible, but to illustrate some general qualitative behaviors which may be observed. The conclusions of the text only correspond to consequences of the models discussed here, where the parameters are roughly estimated as a function of the evolution of the number of deaths due to COVID-19. They are of course not definitive and are subject to possibly important modifications, due to new information or applications of less simplistic models.

1. Summary of the main points

This first section serves both as an extended introduction and as a global discussion of our results described in more detail below. The reader may wish to look first at this section briefly to get the main ideas, then consult it again later as a summary.

In this article, we first establish a basic model of the number of infected people as a function of time without involving any policies such as lockdown, social distancing, testing, mask protection, etc. We then modify the basic model to include extra parameters associated with implementing policies. The basic models assume that all infected individuals infect the same number of people on average. We further consider a more sophisticated two-category model, where different categories of individuals infect different numbers of people. We apply various measures, such as age and degree of socialization, to differentiate the two categories, and illustrate them with numerical examples. We also discuss herd immunity for both basic and two-category models.

We use the estimated Chinese fatality rate and the fatality rate aboard the Diamond Princess1 by age to estimate the French fatality rate, taking into account that the age distribution of infected people is not the same as the general age distribution. We then estimate the number of infected individuals by the reported number of deaths and the estimated fatality rate. We use the number of deaths instead of the number of confirmed cases since the majority of cases are expected to remain undetected.

We note that the fatality rate is important for the evaluation of the general public’s acceptance of getting a large proportion of the population infected, which is needed for herd immunity. Some kind of testing sample can be helpful to evaluate the total number of infected people, which implies an evaluation of the fatality rate by dividing the number of deaths by the total number of infected individuals. A large decrease of the fatality rate by effective or at least partially effective treatments may increase the general public’s acceptance of herd immunity.

The well-known reproduction number R in epidemiological models is analyzed and estimated for the models introduced in this article. The general strategy for controlling the spread of the epidemic is to reduce the value of R.

The following observations are drawn from our oversimplified models applied to France which may be modified by additional information:

• • The values of R with or without policy implementation. With no action taken to control the epidemic, it grows approximately exponentially until the population quickly reaches herd immunity. The reproduction number in France is likely to be between 2.5 and 4, with an increase in the number of infected people of about 30 percent per day.

  The epidemic is globally controlled under lockdown, with a reproduction number estimated to be between 0.4 and 0.7, and an estimated decrease in the number of infected people of about 6 percent per day.

• • The fatality rate. We estimate the fatality rate to be less than 0.5 percent among people under 60 years old, around 1 percent for people between 60 and 69 years old, and much higher for people 70 years old or older.

  There have been discussions about a partial lockdown for people 70 years old or older. Such a strategy cannot prevent the growth of the epidemic by itself since the lockdown is not perfect, thus a significant proportion of people 70 years old or older may still be infected. However, based on our analysis, this can reduce the proportion of infected people 70 years old or older, which decreases the global fatality rate. The overall fatality rate depends not only on the fatality rate by age, but also on the age distribution of the infected population: it is likely that older people are less infected than younger people because they have less contact with others. In one of the two-category examples presented in this article, we get a possible decrease of the fatality rate by a factor of 2 or 3 in this scenario.

• • Herd immunity. The current level of herd immunity is expected to play a minor role in the control of the epidemic, because only a small (but not negligible) minority of the population has been infected. Herd immunity requires a large fraction of the population to be infected. Controlling the growth of the epidemic until herd immunity is reached reduces the proportion of infected people, but not necessarily by very much. The usual formulas giving the proportion of infected people as a function of the reproduction rate are overestimated when the population is not homogeneous in terms of contagion. However, the order of magnitude is not dramatically changed. A possible situation where herd immunity could be reached earlier would be the case where a significant part of the population is, from the beginning, not susceptible to infection (for example, if there is cross immunity with other viruses).
• • Simulations. At the end of the article, we present some simulations of the epidemic for the coming months, until the summer of 2021, under twelve different scenarios. The simulations give very different results, depending on the values of the parameters chosen. This illustrates the great uncertainty of the current situation, and suggests that there is an important risk of a second peak around the beginning of summer 2020.

According to our analysis, in order to completely suppress the epidemic in France by itself, a lockdown would need to last more than 6 months. The epidemic will be difficult to control after releasing the lockdown; social distancing, protection like masks, tests and contact tracing are expected to be helpful for that. Social distancing restrictions should be widely respected in order to keep the reproduction number at a low level. A minority of the population not respecting the restrictions may significantly increase the reproduction number. When the reproduction number becomes larger than 1, everyone is affected by the growth of the epidemic, even if those with less contagious contacts remain less infected than those with more contacts.

We should be aware of the uncertainty of the development and investigate carefully the evolution of the epidemic so that we are more prepared to adapt to the new situation. It will be interesting to know if the contagion is slower during spring and summer: this would help to control the pandemic in the coming months, so that we have more time to find effective treatments.

2. The basic model

Here, we consider the following model relative to the number of infected people as a function of time:

• •Every day, each infected individual contaminates β new individuals on average.
• •Every day, a proportion γ of infected individuals are either recovered, dead, or isolated, and are therefore no longer contagious.

The assumptions implied by this model are the following:

• •All infected individuals play the same role in terms of contagion.
• •All infected people have the same chance of recovering the next day: we do not distinguish between different stages of the disease.
• •There are sufficiently many infected people to neglect random fluctuations and the fact that the number of infected people is an integer.
• •The proportion of infected people is small enough to neglect herd immunity.

We choose a date of reference denoted as day 0, and we assume that the number of infected people on this day is X ₀. If X_n is the number of infected individuals at day n, we have for this model:

$$X_{n+1}=X_n(1+\beta -\gamma )$$

which implies

$$X_n=X_0{(1+\beta -\gamma )}^n.$$

There are three main cases:

• •If β < γ, then the factor $1+\beta -\gamma$ is smaller than 1, which indicates that the number of infected people decreases exponentially.
• •If $\beta =\gamma ,$ then the number of infected people remains constant.
• •If β > γ, then the number of infected people increases exponentially.

This model is far too simple to describe reality with any accuracy, but we can still try to find the parameters β and γ which fit observations as well as possible. If we consider the case of the coronavirus in France, the initial rate of growth of the epidemic can be roughly approximated by the rate of evolution of the number of deaths around the date of the lockdown. We look at the number of deaths instead of the number of cases, since the majority of cases are expected to be undetected. During the initial lockdown, we assume that its effect on deaths should be small since the probability of sudden death of newly infected individuals is low. The estimation of the number of deaths in France until March 14 (included), given by Wikipedia, is 91, whereas the number of deaths until March 21, is 562 [1], [4]. The date of the lockdown is March 17. This is a growth by a factor 562/91 ≃ 6 in one week. Hence, values of β and γ fitting the data should satisfy

$${(1+\beta -\gamma )}^7\simeq 6$$

which gives

$$\beta -\gamma \simeq 0.3.$$

Before lockdown in France, the number of infected people appears to have grown by about 30 percent per day! Of course, this is a rough estimate since the total number of infected people is unknown. However, this clearly shows that each day of delay in deciding on lockdown has a huge effect on the evolution of the epidemic. Another remark is that the rate of growth of the number of infected people gives $\beta -\gamma ,$ but not β and γ separately. Policies such as lockdown, wearing masks, improving personal hygiene, social distancing, contact tracing, massive testing, vaccines, etc., can decrease the value of β, while treatments, quarantining infected individuals, etc., can increase the value of γ. The overall effects of all scientific policies should be seriously considered to improve the collective values of the two parameters. For example, massive testing can help detect the infected cases earlier so infected individuals can be treated earlier (increasing γ) and isolated earlier (decreasing β as well as increasing γ).

The initial approach implemented by the French government to contain coronavirus was the lockdown policy, therefore, we first focus on analyzing the difference between having or not having lockdown. The goal of the lockdown is to decrease the value of β by decreasing the number of contacts between people. Lockdown has no direct effect on γ a priori. Let us assume that β is replaced by β′ after lockdown, whereas γ remains unchanged. After lockdown, we deduce that the number of infected people is increased by a factor of $1+{\beta }^{\prime }-\gamma$ every day. If day 0 is assumed to be before the lockdown at day ℓ, we have at any day n ≥ ℓ after the lockdown:

$$X_n=X_{\ell }{(1+{\beta }^{\prime }-\gamma )}^{n-\ell }=X_0{(1+\beta -\gamma )}^{\ell }{(1+{\beta }^{\prime }-\gamma )}^{n-\ell },$$

where again X_n denotes the number of infected individuals at day n. If β and γ are fixed, with β > γ, we have three possible situations depending on the value of β′:

• •If β′ > γ, the epidemic continues to grow exponentially, but at a smaller rate, even after the lockdown.
• •If ${\beta }^{\prime }=\gamma ,$ the epidemic stabilizes after the lockdown.
• •If β′ < γ, the epidemic grows exponentially until the lockdown, and then decreases exponentially.

Since the daily number of deaths in France is lower at the end of April than at the beginning, we may assume that we are in the third situation β′ < γ. According to the current basic model, the peak of the number of infected people is then at the day of the lockdown. The peak of the number of deaths is later due to the time between infection and death. The rate of decay of the number of infected people after lockdown can be approximated by the rate of decay of the number of deaths if the fatality rate of the disease is assumed to be constant, which appears to be reasonable in a short period of time. However, we have to take observations at sufficiently late periods of the lockdown in order to have (almost) all deaths coming from people infected after the lockdown, and therefore (almost) no influence of the pre-lockdown situation on the evolution of the number of deaths. During the week between April 13 and April 19 (one month after the lockdown), there were (according to Wikipedia) 5325 deaths; during the week between May 4, and May 10, (three weeks later, still during the lockdown), there were 1485 deaths in France [1], [4]. This is a ratio of about 0.28 in three weeks, and thus

$${(1+{\beta }^{\prime }-\gamma )}^{21}\simeq 0.28$$

which gives

$${\beta }^{\prime }-\gamma \simeq -0.06,$$

i.e. a decrease of 6 percent per day.

With this rate of decay, we can deduce the time of lockdown which would be needed to suppress the epidemic in France. The order of magnitude of the number of infected people at the lockdown is certainly between 10,000 (not much more than the number of detected cases) and 10,000,000 (more than 1/7 of the total population). In order to suppress the epidemic in France, we have to decrease this number to 0, and this situation is expected to occur when the model provides a value far below 1; hence, a decrease from the peak at the lockdown by a factor, say, between 10⁴ and 10⁸. According to the model, the corresponding day n should be such that

$$X_n/X_{\ell }={(1+{\beta }^{\prime }-\gamma )}^{n-\ell }\in [{10}^{-8},{10}^{-4}],$$

i.e.

$$0.{94}^{n-\ell }\in [{10}^{-8},{10}^{-4}]$$

which implies

$$n-\ell \in [148,298].$$

In words, according to the model, the lockdown should have lasted between 5 and 10 months in order to suppress the epidemic in France. Such a time is far longer than what is politically acceptable, and so it is not reasonable to expect that lockdown alone can suppress the epidemic.

3. The parameter R

In basic epidemiological models, the most well-known parameter is R: the average number of new infections arising from each infected individual. In particular, R ₀ is a particular value of R, which is valid only at the beginning of the epidemics when most of the population is susceptible, or more precisely, everybody but one infected individual. In the basic model above, each individual infects on average β individuals per day, until (s)he is isolated, recovered, or dead, i.e. no longer contagious. The average time of contagion can be modeled as follows. If some day, an individual is contagious, the probability to no longer be contagious the next day is γ, and so the probability to still be contagious the next day is $1-\gamma$. The probability to still be contagious after two days is then ${(1-\gamma )}^2,$ the probability to still be contagious after three days is ${(1-\gamma )}^3,$ and so on. Notice that this reasoning means that the chances to remain contagious from one day to another do not depend on the past, which is of course not very realistic; however, it has the advantage of simplicity. The average time of contagion is then obtained by adding the following numbers:

• •1, since all infected individuals are contagious at least the first day.
• • $1-\gamma ,$ since this proportion of infected individuals are contagious at least one extra day.
• • ${(1-\gamma )}^2,$ since this proportion of infected individuals are contagious at least one further extra day.
• • ${(1-\gamma )}^3,$ since this proportion of infected individuals are contagious at least one further extra day, and so on.

The average time of infection is then

$$\tau :=1+(1-\gamma )+{(1-\gamma )}^2+{(1-\gamma )}^3+\cdots .$$

Multiplying τ by $1-\gamma ,$ we have,

$$(1-\gamma )\tau =(1-\gamma )+{(1-\gamma )}^2+{(1-\gamma )}^3+{(1-\gamma )}^4+\cdots ,$$

thus

$$\begin{array}{ccc}\hfill 1+(1-\gamma )\tau & =& 1+(1-\gamma )+{(1-\gamma )}^2+{(1-\gamma )}^3\hfill \\ & & +{(1-\gamma )}^4+\cdots \hfill \end{array}$$

which implies

$$1+(1-\gamma )\tau =\tau ,1-\gamma \tau =0,$$

and so $\tau =1/\gamma$. An infected individual contaminates on average β individuals per day, for an average time of 1/γ days. The average number of infections arising from an infected individual is then modeled by the number

$$R=\frac{\beta }{\gamma }.$$

Since β/γ > 1 is equivalent to β > γ, the discussion above shows that we have:

• •An exponential increase of the number of infected individuals if R > 1.
• •An exponential decrease of the number of infected individuals if R < 1.
• •A constant number of infected individuals if $R=1$.

Notice that R cannot be recovered directly from the rate of increase of infected people. Indeed, $R=\beta /\gamma ,$ whereas the rate of increase is $1+\beta -\gamma ,$ and β/γ is not uniquely determined by $1+\beta -\gamma$. More concretely, the rate of increase of the epidemic depends not only on the number of new infections per infected individual, but also on the time between generations of infected individuals. That is why the AIDS pandemic has a much slower evolution than most other infectious pandemics, because the average time between generations of infected individuals is some number of months or years, whereas the order of magnitude for the coronavirus is days or weeks. In order to know R, we need not only to have $\beta -\gamma ,$ but also β and γ separately. A way to estimate γ is to evaluate the average time τ for which an individual is contagious. Such evaluation is difficult, in particular for asymptomatic infected people. As we have seen before, $\tau =1/\gamma$ in the model, and so $\gamma =1/\tau$. It is reasonable to assume that the duration of the contagion is at least 5 days. In the minimal case where $\tau =5,$ we get $\gamma =0.2,$ and in the pre-lockdown situation where we have estimated that $\beta -\gamma =0.3,$ we deduce that $\beta =0.5,$ and then $R=\beta /\gamma =2.5$. On the other hand, under lockdown, we have seen that the new value β′ of the rate of infection is expected to approximately satisfy ${\beta }^{\prime }-\gamma =-0.06,$ and since β′ ≥ 0, we have γ ≥ 0.06, which means τ ≤ 1/0.06, i.e. τ ≤ 16.7 days. In the case where the average infection time is $\tau =14$ days, we have $\gamma =1/14\simeq 0.07,$ and so β ≃ 0.37, which gives approximately $R=0.37/0.07\simeq 5.3$. It is then reasonable to assume 2.5 < R < 5.3.

Another way to estimate β and γ separately is to evaluate the decrease of β due to the lockdown. We can, for example, assume the following scenario:

• •A proportion of 5 percent of individuals do not respect the lockdown, and therefore their number of contacts remains the same (multiplied by 1).
• •A proportion of 30 percent of individuals have to go out, for example for work, and their number of contacts is reduced by a factor of 2 (multiplied by 0.5).
• •A proportion of 65 percent of individuals can stay home almost all the time and their number of contacts is reduced by a factor of 10 (multiplied by 0.1).

In this situation, the average number of contacts between individuals is multiplied by

$$(0.05\times 1)+(0.30\times 0.5)+(0.65\times 0.1)=0.265$$

i.e approximately divided by 4. If we assume that the number of contacts transmitting infections is divided by 4, it means that the number of individuals infected by a given person is divided by 4, i.e. ${\beta }^{\prime }=\beta /4$. In this scenario, we have the two equations:

$$\beta -\gamma =0.3,$$

$$\frac{\beta }{4}-\gamma =-0.06.$$

Then subtracting the second equation from the first, we get:

$$\frac{3\beta }{4}=0.36,$$

hence $\beta =0.48,\gamma =0.18$ and R ≃ 2.67. For a division by 3 of the number of infectious contacts, we get $R=2.25,$ for a division by 6, we get R ≃ 3.27, for a division by 10, we get $R=4,$ for a perfect lockdown (no new infections), we get $R=6$. Since it does not seem plausible for the number of contacts to be divided by more than 10, it seems reasonable to assume that

$$2.5<R<4,$$

taking into account the lower bound of 2.5 estimated previously (from the fact that the infection time should be more than 5 days).

It is also interesting to investigate the value of R after the lockdown, which will be denoted by R′. We have

$$R^{\prime }=\frac{{\beta }^{\prime }}{\gamma }.$$

Hence,

$$\frac{R^{\prime }-1}{R-1}=\frac{({\beta }^{\prime }/\gamma )-1}{(\beta /\gamma )-1}=\frac{{\beta }^{\prime }-\gamma }{\beta -\gamma }\simeq \frac{-0.06}{0.3}=-0.2.$$

We then get

$$R^{\prime }=1-0.2(R-1).$$

For 2.5 < R < 4, we get

$$0.4<R^{\prime }<0.7.$$

Notice that for these estimates, the largest value of R corresponds to the smallest value of R′. A more precise study by the Institut Pasteur gave the confidence intervals 3.18 < R < 3.43 and 0.5 < R′ < 0.54, which were later revised as 2.8 < R < 2.99 and 0.65 < R′ < 0.68 [5]. These intervals are inside the intervals computed here.

4. The fatality rate

The fatality rate by age among confirmed cases of coronavirus in China has been estimated as follows: 0.2 percent under 40 years of age, 0.4 percent between 40 and 49 years, 1.3 percent between 50 and 59 years, 3.6 percent between 60 and 69 years, 8 percent between 70 and 79 years, 15 percent above 80 years [2]. However, it is likely that these fatality rates are overestimates of the true fatality rate, because many infected people are not tested since they have no or few symptoms. An interesting example is the Diamond Princess, where wide testing has been done. The population in the Diamond Princess on February 5 was approximately distributed as follows: 22 percent under 40 years of age, 9 percent between 40 and 49 years, 11 percent between 50 and 59 years, 25 percent between 60 and 69 years, 27 percent between 70 and 79 years, 6 percent above 80 years [3]. Among infected people as of February 20, the distribution was the following: 11 percent under 40 years of age, 4 percent between 40 and 49 years, 9 percent between 50 and 59 years, 29 percent between 60 and 69 years, 38 percent between 70 and 79 years, 9 percent above 80 years. If we apply the estimated Chinese fatality rates to the Diamond Princess infected distribution by age, then the overall fatality rate we get is

$$\begin{array}{ccc}& & (0.002\times 0.11)+(0.004\times 0.04)+(0.013\times 0.09)\hfill \\ & & +(0.036\times 0.29)+(0.08\times 0.38)+(0.15\times 0.09),\hfill \end{array}$$

i.e. 0.05589, approximately 5.6 percent. The number of deaths from the Diamond Princess is 14, out of 712 infected people, so a true fatality rate of approximately 2 percent. A plausible way to estimate the true fatality rate by age is then to multiply the Chinese rates given above by 2/5.6, i.e. approximately 0.36. We get approximately: 0.07 percent under 40 years of age, 0.14 percent between 40 and 49 years, 0.47 percent between 50 and 59 years, 1.3 percent between 60 and 69 years, 2.88 percent between 70 and 79 years, 5.4 percent above 80 years.

The global French population is distributed approximately as follows: 47 percent under 40 years of age, 13 percent between 40 and 49 years, 13 percent between 50 and 59 years, 12 percent between 60 and 69 years, 8 percent between 70 and 79 years, 7 percent above 80 years. The age distribution of infected people is not the same as the general age distribution. Indeed, for example, people under 40 years old are 22 percent of the population of the Diamond Princess, but only 11 percent of the infected population [3]. Hence, one can estimate that when a person is under 40 years old, his or her probability of being infected is half the corresponding probability for the general population. Similarly, people over 80 years old are 6 percent of the population of the Diamond Princess, but 9 percent of the infected population [3]. Hence, one can estimate that when a person is over 80 years old, his or her probability to be infected is 1.5 times the corresponding probability for the general population. If we apply these ratios to the age distribution of the general French population, we get numbers proportional to

$$47\times \frac{11}{22}=23.5,13\times \frac{4}{9}\simeq 5.7,13\times \frac{9}{11}\simeq 10.6,$$

$$12\times \frac{29}{25}\simeq 13.9,8\times \frac{38}{27}\simeq 11.3,7\times \frac{9}{6}=10.5.$$

If we rescale this last sequence of numbers in order to get a total of 100 percent, we get the following estimate of the age distribution of infected people in France: 31 percent under 40 years of age, 8 percent between 40 and 49 years, 14 percent between 50 and 59 years, 18 percent between 60 and 69 years, 15 percent between 70 and 79 years, 14 percent over 80 years. Applying the fatality rates by age computed above (by multiplying the Chinese numbers by 0.36), we get an estimation of the overall French fatality rate:

$$\begin{array}{ccc}& & (0.0007\times 0.31)+(0.0014\times 0.08)+(0.0047\times 0.14)\hfill \\ & & +(0.013\times 0.18)+(0.0288\times 0.15)+(0.054\times 0.14),\hfill \end{array}$$

i.e. 0.015207, approximately 1.5 percent.

This computation assumed that the age distribution of infected people is biased with respect to the age distribution of the general population, in the same way for the Diamond Princess and for the general French population. This assumption is questionable because the amount of contact between people of different ages is not distributed in the same way in the boat and in France. If we assume instead that in France, the rate of infection does not depend on age, then the age distribution of infected people is the same as the age distribution of the general population. In this case, we estimate a global French fatality rate of

$$\begin{array}{ccc}& & (0.0007\times 0.47)+(0.0014\times 0.13)+(0.0047\times 0.13)\hfill \\ & & +(0.013\times 0.12)+(0.0288\times 0.08)+(0.054\times 0.07),\hfill \end{array}$$

i.e. 0.008766, approximately 0.9 percent.

The study by the Institut Pasteur mentioned above gives the following confidence intervals for the fatality rates, as functions of age: less than 0.02 percent under 40 years of age, between 0.03 and 0.09 percent between 40 and 49 years, between 0.1 and 0.36 percent between 50 and 59 years, between 0.5 and 1.4 percent between 60 and 69 years, between 1.4 and 3.7 percent between 70 and 79 years, between 6 and 15.6 percent above 80 years [5]. Our estimate is above the confidence interval under 60 years old, inside the confidence interval between 60 and 79 years old, and slightly under the confidence interval over 80 years old.

The overall fatality rate found by Institut Pasteur has a confidence interval between 0.4 and 1 percent [5]; our rate is above this interval in our first computation and at the top of the interval in our second computation. This suggests that in the study by Institut Pasteur, the older people are less likely to be infected than in our estimates.

Notice that all these estimates are subject to very large uncertainty. In particular, they use the fact that there were 14 deaths on the Diamond Princess, which is a small number. The most simple probabilistic model for small random integer numbers is given by a Poisson random variable. Any Poisson random variable with mean between 8 and 22 has more than one percent chance to be exactly equal to 14, whereas the probability is around 10 percent for a Poisson variable of mean 14. Hence, it is plausible that the fatality rate for a large population with the same age distribution as the Diamond Process is anything between 8/14 ≃ 0.57 and 22/14 ≃ 1.57 times the rate effectively observed in the Diamond Princess due to the random fluctuations of the Poisson distribution. These possible multiplicative factors may then be applied to our previous estimate of the French fatality rate. If we combine this uncertainty with the two computations we have done, respectively giving 1.5 and 0.9 percent, we get a range between 0.5 percent and 2.4 percent.

5. The number of infected individuals

The number of infected people is equal to the number of deaths divided by the fatality rate. We can now estimate the number of individuals already infected, or who will be infected until the end of the current lockdown on May 11. Since the peak of infections is on the day of the lockdown (March 17) in the basic model described above, the peak of deaths is at the beginning of April (the typical time between infection and death should be around 2–3 weeks). In the computation of the number of infected people on May 11, we should then roughly take into account the number of deaths until the end of May. This number is approximately 29,000 (28,596 by May 27), then the number of infected people is about 29,000 divided by the fatality rate. All the estimates of the fatality rate discussed above are between 0.4 and 2.5 percent.

For a fatality rate of 2.5 percent, we get 29, 000/0.025, i.e. around 1.2 million infected individuals in France until May 11, i.e. 1.8 percent of the population.

For a fatality rate of 1 percent, we get 29, 000/0.01, i.e. 2.9 million infected people, i.e. 4.3 percent of the population.

For a fatality rate of 0.5 percent, we get 5.8 million infected people, i.e. 8.7 percent of the population.

For a fatality rate of 0.4 percent, we get 7.25 million infected people, i.e. 10.9 percent of the population.

The confidence interval given by the Institut Pasteur was between 2.3 and 6.7 million people, i.e between 3.4 and 10 percent of the population, and has been revised to 1.8 to 4.7 million people, i.e. between 2.7 to 7.1 percent of the population [5].

This estimate of the number of cases gives a slightly refined estimate of the lockdown time we would need in order to suppress the epidemic. We need to go from 1 to 10 million infections to below 1 infection, i.e. a decrease by a factor between 10⁶ to 10⁸. Since the estimated rate of decay under lockdown is 6 percent, we would need between 223 and 298 days, i.e. 7 to 10 months. On the other hand, the infected people are still a small minority of the population. Hence, France is in the most uncertain situation where there is neither hope for a direct suppression of the epidemic by a lockdown, nor significant herd immunity.

6. Reducing R

We recall that the parameter R, representing the average number of persons infected by a given individual, is equal to β/γ where β is the average number of persons contaminated each day by a given infected individual, and γ is the proportion of infected individuals who become non-contagious after one day. In the basic model introduced above, the number of infected individuals is multiplied by $1+\beta -\gamma$ every day. The general strategy, in order to reduce the contagion, is to reduce R, which can be done by reducing β and/or increasing γ. In order to reduce β, we have seen that lockdown is effective: other possibilities are social distancing, protection by masks, hygiene improvement, cancellation of events with a large number of participants, and closure of bars and restaurants. In order to increase γ, one needs to isolate infected individuals, and also increase the number of tests. People with higher probability of being infected, and people with a lot of contacts should be prioritized for testing. In the estimates obtained above, if we assume $R=3.3$ (recall that R has been estimated to be between 2.5 and 4), we have β ≃ 0.43, γ ≃ 0.13 before lockdown, and β′ ≃ 0.07 after lockdown, which gives R′ ≃ 0.54. A crucial question concerns the value of R after lockdown, in particular, whether it can be maintained below 1 or not. With the values just above, a scenario for maintaining R at 1 might be the following:

• •Masks, hygiene and social distancing decrease β from 0.43 to 0.2.
• •Massive testing manages to detect and isolate 7 more percent of the current infected population every day, increasing γ from 0.13 to 0.2.

An important question concerns the seasonality of the disease, which might reduce R during spring and summer.

Here is a scenario where we do not manage to maintain R below 1: γ increases to 0.18, β decreases to 0.27, and the new value of R is 1.5. In this case, the number of infected people increases by $27-18=9$ percent per day, i.e. a multiplication by 14 every month. This is a guarantee to reach herd immunity (see below) during the summer, unless more restrictions are introduced again.

7. Herd immunity

Until now, we have neglected herd immunity in the model, which can be justified by the fact that a small proportion of the population has been infected. The most basic model taking herd immunity into account, called SIR, can be described as follows. At day n, a proportion S_n of the population is susceptible, i.e. is not currently infected but may be infected later by other individuals, and a proportion I_n of the population is currently infected. An infected individual contaminates on average βS_n susceptible individuals in one day, and a proportion γ of infected individuals are not contagious anymore the next day and cannot be re-infected later (we assume that being infected provides immunity, which is natural to expect but still not yet proven). The replacement of β by βS_n here is due to the fact that among the β infectious contacts of a given infected individual, a proportion $1-S_n$ of them are already infected, or have already been infected before, so they are supposed to be immune. We get the following equation:

$$I_{n+1}=(1-\gamma +\beta S_n)I_n,$$

which is similar to the equation satisfied by X_n defined previously, with β replaced by βS_n. The model here is close to the basic model above if S_n is close to 1, i.e. most individuals have still not been infected. Moreover, we have

$$S_{n+1}=S_n(1-\beta I_n),$$

the term $-S_n\beta I_n$ meaning that the newly infected people are not susceptible anymore at day $n+1$. Notice that in general, this model is presented in continuous time, which gives a system of differential equations.

Recall that β ≤ γ corresponds to R ≤ 1 in the previous model. The number of infected individuals is decreasing exponentially if R < 1. Hence, the epidemic is under control. If β > γ, the number of infected people is exponentially increasing at the beginning, until the point where the multiplicative factor $1-\gamma +\beta S_n$ becomes smaller than or equal to 1, i.e. βS_n ≤ γ, S_n ≤ γ/β, or S_n ≤ 1/R. This means that the number of infected people is maximal (we reach the peak of the epidemic) when the proportion of susceptible individuals is 1/R, i.e. the proportion of individuals already infected is $1-1/R$. If 2.5 < R < 4, we get $0.6<1-1/R<0.75,$ i.e. we need to have 60 to 75 percent of people already infected in order to control the epidemic. Notice that after the point when $S_n=1/R,$ the number of infected individuals decreases but does not instantly fall to zero, so there are newly infected people. It is not very difficult to approximate the proportion of individuals who are infected some time during the epidemic. Indeed, we observe that the relative variation of I with respect to the variation of S is given by:

$$\frac{I_{n+1}-I_n}{S_{n+1}-S_n}=\frac{(-\gamma +\beta S_n)I_n}{-\beta S_n{I}_n}=\frac{\beta S_n-\gamma }{-\beta S_n}=-1+\frac{\gamma }{\beta S_n}=-1+\frac{1}{R{S}_n}.$$

Hence,

$$I_{n+1}-I_n=(S_{n+1}-S_n)(\frac{1}{R{S}_n}-1).$$

Now, we can add these equations over all integers n, from $-\infty$ (far in the past), to ∞ (far in the future). We get

$$I_{\infty }-I_{-\infty }=\frac{1}{R}\sum _{n\in \mathbb{Z}}(\frac{S_{n+1}}{S_n}-1)-(S_{\infty }-S_{-\infty }).$$

Let us now suppose that the relative variation of S is small from one day to the next one, i.e. a small proportion of the population is infected on a given day. This approximation may be discussed, and can be made automatically true by replacing a discrete time model by a model in continuous time (which is generally done). If the relative variation of S is small, we can approximate $S_{n+1}/S_n-1$ by $\ln (S_{n+1}/S_n)$. In this case, we get

$$I_{\infty }-I_{-\infty }\simeq \frac{1}{R}\sum _{n\in \mathbb{Z}}\ln \left(\frac{S_{n+1}}{S_n}\right)-(S_{\infty }-S_{-\infty })$$

therefore,

$$I_{\infty }-I_{-\infty }\simeq \frac{1}{R}\ln \left(\frac{S_{\infty }}{S_{-\infty }}\right)-(S_{\infty }-S_{-\infty }).$$

Now, $I_{-\infty }$ and I _∞ are equal to zero, because these numbers correspond to the number of infected individuals before the epidemic and when the epidemic is over. Moreover, $S_{-\infty }=1$: before the epidemic, everybody is susceptible, since nobody is immune. The value of S _∞ is the proportion of people who are never infected during the epidemic, and thus are always susceptible. We get

$$\frac{1}{R}\ln \left(S_{\infty }\right)-(S_{\infty }-1)\simeq 0$$

which gives approximately

$$\frac{1}{J}\ln (1/(1-J))=R$$

where $J=1-S_{\infty }$ is the proportion of individuals who are infected some time during the epidemic. The solution of this equation does not have a convenient closed form, but it can easily be solved numerically. We can also write the equation as

$$1+\frac{J}{2}+\frac{J^2}{3}+\frac{J^3}{4}+\cdots =R.$$

This equality confirms that we are in the situation R > 1. For $R=2.5,$ we get J ≃ 0.89; and for $R=4,$ we get J ≃ 0.98. In other words, without any policy to control the epidemic, most of the population is expected to be infected sometime, according to the SIR model. Notice that the value of J found here is larger than the value of $1-1/R$ usually given for herd immunity. In fact, these numbers correspond to two different situations:

• •If we let the epidemic grow naturally, we get a proportion J of infected people.
• •If we control the growth of the epidemic until a proportion larger than $1-1/R$ of the population is infected, then recovers or dies, we can release the restrictions and the epidemic is stopped by herd immunity.

Hence, temporary control of the epidemic until we reach herd immunity can potentially reduce the proportion of infected people from J to $1-1/R$. For $R=2.5,$ $1-1/R=0.6$ and for $R=4,$ $1-1/R=0.75$: we need 60 to 75 percent of infected people for ”controlled herd immunity,” instead of 89 to 98 percent of infected people for ”uncontrolled herd immunity.”

Notice that these numbers are probably an overestimate. Indeed, the model does not distinguish between individuals, and so implicitly assumes that an infected individual contaminates random people in the French population. In reality, contamination is more local (family, friends, colleagues), so ”local herd immunity” (e.g. if all family members are infected) can prevent the epidemic from reaching levels as high as what is predicted by the SIR model. We will later study how the proportion of infected people is reduced when we consider two categories of people, with different rates of infectious contacts. In any case, it is very likely that a large proportion of the population should be infected in order to reach herd immunity, even controlled.

We can also notice that in the current French situation, it is likely that herd immunity plays a minor role. Since less than 10 percent of the population is likely to be immune, the proportion of susceptible people is more than 0.9. We have estimated that $\beta =0.43$ and $\gamma =0.13$; if we assume that $R=3.3,$ then in this case, we have βS ₀ ≃ 0.39 if $S_0=0.9$. In other words, the daily rate of increase of the number of infected people is reduced by at most 4 percent by herd immunity; and without political decisions to control the epidemic, the ”effective R, ” after taking into account herd immunity, is 0.39/0.13, i.e. 3 instead of 3.3.

8. A model with two categories of individuals

In the models discussed earlier, all infected individuals were assumed to infect the same number of individuals on average. It is possible to consider slightly more sophisticated models, where different categories of individuals are infecting different number of people. We can consider two categories of people, where an individual of category 1 infects β _1,1 people per day in category 1 and β _2,1 people per day in category 2, whereas an individual of category 2 infects β _1,2 people per day in category 1 and β _2,2 people per day in category 2. We assume that these four parameters are strictly positive and we neglect herd immunity for the moment. If at day n, X_n denotes the number of infected individuals in category 1 and Y_n is the number of infected individuals in category 2, we have, after taking into account that a proportion γ ∈ (0, 1) of infected individuals is not contagious anymore the next day:

$$X_{n+1}=(1+{\beta }_{1,1}-\gamma )X_n+{\beta }_{1,2}{Y}_n,$$

$$Y_{n+1}={\beta }_{2,1}{X}_n+(1+{\beta }_{2,2}-\gamma )Y_n.$$

If we denote

$$Z_n:=\left(\begin{array}{c}{X}_n\\ Y_n\end{array}\right),$$

we have

$$Z_{n+1}=M{Z}_n$$

where

$$M=\left(\begin{array}{cc}1+{\beta }_{1,1}-\gamma & {\beta }_{1,2}\\ {\beta }_{2,1}& 1+{\beta }_{2,2}-\gamma \end{array}\right).$$

The eigenvalues λ of the matrix M satisfying the equation:

$$\begin{array}{ccc}& & {\lambda }^2-(2+{\beta }_{1,1}+{\beta }_{2,2}-2\gamma )\lambda +(1+{\beta }_{1,1}-\gamma )(1+{\beta }_{2,2}-\gamma )\hfill \\ & & -{\beta }_{1,2}{\beta }_{2,1}=0.\hfill \end{array}$$

The discriminant of this equation is given by

$$\begin{array}{ccc}& & \Delta ={(2+{\beta }_{1,1}+{\beta }_{2,2}-2\gamma )}^2-4(1+{\beta }_{1,1}-\gamma )(1+{\beta }_{2,2}-\gamma )\hfill \\ & & +4{\beta }_{1,2}{\beta }_{2,1}.\hfill \end{array}$$

Since ${(a+b)}^2-4ab={(a-b)}^2$ for all $a,b\in \mathbb{R},$ we have

$$\Delta ={({\beta }_{1,1}-{\beta }_{2,2})}^2+4{\beta }_{1,2}{\beta }_{2,1}>0$$

since we have assumed that β _1,2 and β _2,1 are strictly positive. Hence, we have two distinct real eigenvalues,

$$\begin{array}{ccc}& & {\lambda }_{-}=1+\frac{1}{2}({\beta }_{1,1}+{\beta }_{2,2}-2\gamma -\sqrt{\Delta }),\hfill \\ & & {\lambda }_{+}=1+\frac{1}{2}({\beta }_{1,1}+{\beta }_{2,2}-2\gamma +\sqrt{\Delta }).\hfill \end{array}$$

Since $\Delta >{({\beta }_{1,1}-{\beta }_{2,2})}^2,$ we have

$$\begin{array}{ccc}& & {\lambda }_{-}<1+\frac{1}{2}({\beta }_{1,1}+{\beta }_{2,2}-2\gamma -|{\beta }_{1,1}-{\beta }_{2,2}|)\hfill \\ & & =1+\min ({\beta }_{1,1},{\beta }_{2,2})-\gamma ,\hfill \end{array}$$

and

$${\lambda }_{+}>1+\max ({\beta }_{1,1},{\beta }_{2,2})-\gamma .$$

The eigenvalues have the same mean as the diagonal entries of M, and a larger mutual difference. If x and y are the coordinates of an eigenvector corresponding to the eigenvalue λ, we need

$$(1+{\beta }_{1,1}-\gamma -\lambda )x+{\beta }_{1,2}y={\beta }_{2,1}x+(1+{\beta }_{2,2}-\gamma -\lambda )y=0.$$

For $\lambda ={\lambda }_{\pm },$ we get

$$1+{\beta }_{1,1}-\gamma -\lambda =\frac{{\beta }_{1,1}-{\beta }_{2,2}\mp \sqrt{\Delta }}{2},$$

and

$$1+{\beta }_{2,2}-\gamma -\lambda =\frac{{\beta }_{2,2}-{\beta }_{1,1}\mp \sqrt{\Delta }}{2}.$$

Since Δ is strictly larger than $|{\beta }_{2,2}-{\beta }_{1,1}|,$ all these numbers are strictly positive for $\lambda ={\lambda }_{-}$ and strictly negative for $\lambda ={\lambda }_{+}$. Since β _1,2 and β _2,1 are non-zero, we deduce that the eigenvector should satisfy:

$$\frac{x}{y}=\frac{{\beta }_{1,1}-{\beta }_{2,2}\pm \sqrt{\Delta }}{2{\beta }_{2,1}}=\frac{2{\beta }_{1,2}}{{\beta }_{2,2}-{\beta }_{1,1}\pm \sqrt{\Delta }}.$$

It is not difficult to check that the two last quotients are equal. Moreover, x and y should have the same sign for $\lambda ={\lambda }_{+}$ and opposite signs for $\lambda ={\lambda }_{-}$. Let us fix two eigenvectors $V_{+}$ and $V_{-}$ corresponding to the eigenvalues ${\lambda }_{+}$ and ${\lambda }_{-}$. We know that $V_{+}$ has coordinates with the same sign, by possibly changing $V_{+}$ to its opposite, we can assume that this vector has positive coordinates. Since $V_{-}$ has coordinates of opposite signs, $V_{+}$ and $V_{-}$ are independent, which implies that they span ${\mathbb{R}}^2$. We can then write

$$Z_0=\left(\begin{array}{c}{X}_0\\ Y_0\end{array}\right)={\alpha }_{+}{V}_{+}+{\alpha }_{-}{V}_{-}$$

for some ${\alpha }_{+},{\alpha }_{-}\in \mathbb{R}$. For all integers n ≥ 0, we have $Z_{n+1}=M{Z}_n,$ and so

$$Z_n=M^n{Z}_0={\alpha }_{+}{M}^n{V}_{+}+{\alpha }_{-}{M}^n{V}_{-},$$

which implies

$$Z_n={\alpha }_{+}{\lambda }_{+}^n{V}_{+}+{\alpha }_{-}{\lambda }_{-}^n{V}_{-}.$$

Since Z_n has positive coordinates and ${\alpha }_{-}{\lambda }_{-}^n{V}_{-}$ has coordinates of opposite signs, we necessarily have ${\alpha }_{+}\ne 0$. Moreover, we can write

$$\frac{Z_n}{{\lambda }_{+}^n}={\alpha }_{+}{V}_{+}+{({\lambda }_{-}/{\lambda }_{+})}^n{\alpha }_{-}{V}_{-}.$$

Recall that

$${\lambda }_{+}=\mu +\frac{1}{2}\sqrt{\Delta }$$

and

$${\lambda }_{-}=\mu -\frac{1}{2}\sqrt{\Delta }$$

where

$$\mu =1+\frac{1}{2}({\beta }_{1,1}+{\beta }_{2,2}-2\gamma ).$$

Recall that γ < 1 (the proportion of infected individuals who recover or are isolated the next day), β _1,1, β _2,2 > 0 and hence μ > 0, which implies that ${\lambda }_{+}>\left|{\lambda }_{-}\right|$. The quantity ${({\lambda }_{-}/{\lambda }_{+})}^n$ exponentially decays to zero, which implies that

$$\frac{Z_n}{{\lambda }_{+}^n}⟶{\alpha }_{+}{V}_{+}$$

when n tends to infinity. In more concrete words:

• •If we are sufficiently advanced in the epidemic, the number of infected individuals grows approximately exponentially, with a daily growth factor ${\lambda }_{+}$.
• •The proportion of infected individuals in each category is proportional to the corresponding coordinates of the eigenvector $V_{+}$.
• •However, the rate of growth may be different at the beginning of the epidemic.

In the case where Z ₀ is proportional to $V_{+},$ then the number of infected individuals evolves exactly exponentially with rate ${\lambda }_{+}$. If β denotes, in this situation, the average number of individuals contaminated in one day by a given infected individual, then the number of infected individuals grows by a factor $1+\beta -\gamma$ every day (the term $-\gamma$ comes from people who are not contagious anymore the next day). Hence, we should have $1+\beta -\gamma ={\lambda }_{+},$ which gives

$$\beta ={\lambda }_{+}+\gamma -1=\frac{1}{2}({\beta }_{1,1}+{\beta }_{2,2}+\sqrt{\Delta }).$$

The average number of people contaminated by an infected individual during all the contagion is then R ≔ β/γ, i.e.

$$R=\frac{1}{2\gamma }({\beta }_{1,1}+{\beta }_{2,2}+\sqrt{\Delta })=\frac{1}{2\gamma }({\beta }_{1,1}+{\beta }_{2,2}+\sqrt{{({\beta }_{1,1}-{\beta }_{2,2})}^2+4{\beta }_{1,2}{\beta }_{2,1}}).$$

As in the basic model, the epidemic grows if and only if $1+\beta -\gamma ={\lambda }_{+}$ is larger than 1, i.e. β > γ, or R > 1. The situation is similar to the case of the previous model, but with a more complicated expression for R.

We can now look at a few examples. The first one is when the separation into two categories is irrelevant for the contagion. Let π ₁ and π ₂ be the proportions of individuals in categories 1 and 2 in the population, respectively, and ${\pi }_1+{\pi }_2=1$. If there is no particular preference between the two categories for contamination, then any individual will contaminate β individuals in one day for some value of β: βπ ₁ individuals in category 1 and βπ ₂ in category 2. We then have:

$$\begin{array}{ccc}\hfill M& =& \left(\begin{array}{cc}1+{\beta }_{1,1}-\gamma & {\beta }_{1,2}\\ {\beta }_{2,1}& 1+{\beta }_{2,2}-\gamma \end{array}\right)\hfill \\ & =& \left(\begin{array}{cc}1+\beta {\pi }_1-\gamma & \beta {\pi }_1\\ \beta {\pi }_2& 1+\beta {\pi }_2-\gamma \end{array}\right).\hfill \end{array}$$

Recall that β _1,2 represents the contaminations from category 2 to category 1. We get

$$\Delta ={\beta }^2{({\pi }_1-{\pi }_2)}^2+4{\beta }^2{\pi }_1{\pi }_2={\beta }^2{({\pi }_1+{\pi }_2)}^2={\beta }^2,$$

which gives

$${\lambda }_{+}=1+\frac{1}{2}\left(\beta \right({\pi }_1+{\pi }_2)-2\gamma +\beta )=1+\beta -\gamma ,$$

$${\lambda }_{-}=1+\frac{1}{2}\left(\beta \right({\pi }_1+{\pi }_2)-2\gamma -\beta )=1-\gamma .$$

The asymptotic rate of growth of epidemic is then the same as in the basic model, namely $1+\beta -\gamma$. In fact, a direct computation of the sum of the coordinates of MV for a given vector V shows that the number of infected individuals is exactly multiplied by $1+\beta -\gamma$ each day. Hence, the predictions of the model are the same as the predictions of the basic model, which is not surprising since we have assumed that the separation into two categories is irrelevant for the contagion.

Another example is when we have two categories of the same size (half the population), one more sociable than the other. We might assume that the mutual contamination of the two categories is proportional to the product of their ”degrees of socialization.” If σ_j denotes the ”degree of socialization” of the category j, we may assume ${\beta }_{i,j}={\sigma }_i{\sigma }_j,$ then

$$M=\left(\begin{array}{cc}1+{\sigma }_1^2-\gamma & {\sigma }_1{\sigma }_2\\ {\sigma }_1{\sigma }_2& 1+{\sigma }_2^2-\gamma \end{array}\right).$$

One can compute the eigenvalues, and one gets:

$${\lambda }_{+}=1-\gamma +{\sigma }_1^2+{\sigma }_2^2,{\lambda }_{-}=1-\gamma .$$

One can take for eigenvectors:

$$V_{+}=\left(\begin{array}{c}{\sigma }_1\\ {\sigma }_2\end{array}\right),V_{-}=\left(\begin{array}{c}{\sigma }_2\\ -{\sigma }_1\end{array}\right).$$

The rate of increase of the epidemics is $1-\gamma +{\sigma }_1^2+{\sigma }_2^2,$ and we can check that

$$R=\frac{1}{2\gamma }({\sigma }_1^2+{\sigma }_2^2).$$

The eigenvector $V_{+}$ shows that in the long run, people are infected proportionally to their degree of socialization. However, if one of the categories is very sociable, ${\sigma }_1^2+{\sigma }_2^2$ is large even if the other category has a very low sociability. If category 1 has sufficient sociability to make R > 1 even when category 2 has very low sociability, then category 2 will be infected with exponential growth even though it is less infected than category 1. It is then essential that decisions of social distancing are widely respected by the population.

Let us illustrate this fact by another example. We assume that after an exponentially growing epidemic, social distancing restrictions are implemented, but with 15 percent of the population not respecting them when they are together. We assume that $\gamma =0.13,$ and that before social restriction, $\beta =0.43$ (this corresponds to the coronavirus before lockdown, in the case where $R=3.3$). Let us divide the population into two categories: category 1 with ${\pi }_1=85\%$ of the population respecting social distancing, category 2 with ${\pi }_2=15\%$ of the population not respecting social distancing. Before the decision to social distance, we may assume that the two categories are irrelevant:

$$M=\left(\begin{array}{cc}1+\beta {\pi }_1-\gamma & \beta {\pi }_1\\ \beta {\pi }_2& 1+\beta {\pi }_2-\gamma \end{array}\right)=\left(\begin{array}{cc}1.2355& 0.3655\\ 0.0645& 0.9345\end{array}\right).$$

The largest eigenvalue is 1.3, which gives a growth of 30 percent per day of the epidemic. The corresponding eigenvector has coordinates 0.85 and 0.15, i.e. 85 percent of the infected population is in category 1 and 15 percent is in category 2. Let us now assume that social distancing divides the contacts by 3.5. If everybody respects social distancing, the rate of contamination is divided by 3.5 and thus β goes from 0.43 down to 0.1229 (which is smaller than $\gamma =0.13$), and so the epidemic is under control (R ≃ 0.94). If people in category 2 do not respect social distancing at all when they are together, we get

$$\begin{array}{ccc}& & {\beta }_{1,1}=\beta {\pi }_1/3.5,\hfill \\ & & {\beta }_{1,2}=\beta {\pi }_1/3.5,\hfill \\ & & {\beta }_{2,1}=\beta {\pi }_2/3.5,\hfill \\ & & {\beta }_{2,2}=\beta {\pi }_2,\hfill \end{array}$$

and after social distancing, the matrix M becomes:

$$\begin{array}{ccc}\hfill M^{\prime }& =& \left(\begin{array}{cc}1+\beta {\pi }_1/3.5-\gamma & \beta {\pi }_1/3.5\\ \beta {\pi }_2/3.5& 1+\beta {\pi }_2-\gamma \end{array}\right)\hfill \\ & \simeq & \left(\begin{array}{cc}0.97443& 0.10443\\ 0.01842& 0.9345\end{array}\right).\hfill \end{array}$$

In this case, the largest eigenvalue is 1.0026, R′ ≃ 1.02, and the epidemic grows. Looking at the coordinates of $V_{+},$ we see that in the long run, about 79 percent of infected individuals are in category 1, and 21 percent in category 2. Hence, even if people in category 1 are less infected than people in category 2 (79 percent of infections for 85 percent of the population), they are still widely infected, and are impacted by the consequences of the growing epidemic. Notice that in this example, people in category 2 still respect social distancing when they meet people in category 1. We can look at what happens when people in category 2 only partially respect social distancing when they meet people in category 1, say, dividing the contacts by 2 instead of 3.5. In this case, the matrix becomes:

$$\left(\begin{array}{cc}0.97443& 0.18275\\ 0.03225& 0.9345\end{array}\right).$$

We get a largest eigenvalue of 1.03379, R′ ≃ 1.26, i.e. a rather fast growth of the epidemic (3.4 percent per day). In the long run, 75 percent of infections are in category 1 and 25 percent in category 2.

Another numerical example can be computed in order to model an almost full lockdown of people aged 70 or more, who are approximately 15 percent of the French population. Let us say that people under 70 are in category 1 and people over 70 are in category 2. In the situation before lockdown, if we assume that the categories are irrelevant for contagion (not necessarily very realistic, since people over 70 have in general fewer contacts than people under 70), we get the same matrix

$$M=\left(\begin{array}{cc}1+\beta {\pi }_1-\gamma & \beta {\pi }_1\\ \beta {\pi }_2& 1+\beta {\pi }_2-\gamma \end{array}\right)=\left(\begin{array}{cc}1.2355& 0.3655\\ 0.0645& 0.9345\end{array}\right)$$

as before. Let us assume that the contacts involving category 2 are divided by 10 after selective lockdown. We then get

$$\begin{array}{ccc}& & {\beta }_{1,1}=\beta {\pi }_1,\hfill \\ & & {\beta }_{1,2}=\beta {\pi }_1/10,\hfill \\ & & {\beta }_{2,1}=\beta {\pi }_2/10,\hfill \\ & & {\beta }_{2,2}=\beta {\pi }_2/10.\hfill \end{array}$$

This gives a new matrix

$$M^{\prime }=\left(\begin{array}{cc}1.2355& 0.03655\\ 0.00645& 0.87645\end{array}\right).$$

In this case, ${\lambda }_{+}\simeq 1.236,$ R ≃ 2.8, i.e. a very quick growth of the epidemic (by 23.6 percent per day), not dramatically different from the situation before selective lockdown. In the long run, about 1.8 percent of infected people are in category 2, instead of 15 percent in the situation before lockdown. In other words, in this model, lockdown of people over 70 is inefficient to globally control the epidemic, but it reduces the portion of older people in the infected population by a factor of 8 to 9. If we refer to the previous estimates of the fatality rates by age, we get that the global fatality rate is reduced by a factor of 2 to 3.

Notice that it is likely that people over 70 years old have fewer contacts than people under 70. Then, even without social distancing restrictions, it is natural to expect that they are less infected than younger people. The estimates we have found on the fatality rate by age are not very far from the estimates given in the study by the Institut Pasteur. However, our estimates of the overall fatality rate (0.8 and 1.3 percent) are significantly larger than the estimates of Institut Pasteur (confidence interval between 0.3 and 0.9 percent). This is probably partially due to the fact that our previous estimates do not take into account that older people are likely to be less infected than younger people.

Another remark can be made when we look at the evolution of the total number of infected people just after the selective lockdown. At the time of the lockdown, for each infected individual, we have on average 0.85 individuals in category 1 and 0.15 in category 2. The day after, we get

$$\left(\begin{array}{cc}1.2355& 0.03655\\ 0.00645& 0.87645\end{array}\right)\left(\begin{array}{c}0.85\\ 0.15\end{array}\right)=\left(\begin{array}{c}1.0556575\\ 0.13695\end{array}\right),$$

i.e. 1.0556575 infected individuals in category 1 and 0.13695 in category 2. In one day, the number of infected individuals is then multiplied by 1.1926075, i.e. increased by about 19.3 percent. This is less than the rate of increase of 23.6 percent which occurs in the long run. To summarize, the daily rate of increase of the number of infected people is 30 percent before selective lockdown, goes down to 19.3 percent the day just after the lockdown, and then increases again to 23.6 percent in the long run. Let us now assume that besides the selective lockdown, we do some massive testing which increases the value of γ from 0.13 to 0.33. In this case, everything remains similar, except that the two eigenvalues are shifted by $-0.2$. The rate of increase is now $-0.7$ percent just after the lockdown, then grows to 3.6 percent: the number of infected people is decreasing for some time and then increases again.

Here, we have discussed models with two categories, it is of course possible to generalize the study to models with more than two categories by using larger matrices.

9. Herd immunity with two categories of individuals

In the previous section, we considered two kinds of individuals, but we neglected immunity, as in the basic model. We will now present a model where we take immunity into account. We take the same basic parameters β _1,1, β _1,2, β _2,1, β _2,2 corresponding to the rates of contagion in the case where the proportion of immune individuals is negligible.

We have two categories of individuals, a proportion π ₁ of them being in category 1 and a proportion π ₂ being in category 2, with ${\pi }_1+{\pi }_2=1$. We assume that at day n, a proportion S _1,n of the total population is in category 1 and susceptible, a proportion I _1,n of the population is in category 1 and infected, a proportion S _2,n of the population is in category 2 and susceptible, and a proportion I _2,n of the population is in category 2 and infected. The proportion of susceptible individuals in category 1 is S _1,n/π ₁ and the proportion of susceptible individuals in category 2 is S _2,n/π ₂. Hence, between day n and day $n+1,$ with the notation above, an infected individual in category 1 contaminates β _1,1 S _1,n/π ₁ individuals in category 1 and β _2,1 S _2,n/π ₂ individuals in category 2. Similarly, an infected individual in category 2 contaminates β _1,2 S _1,n/π ₁ individuals in category 1 and β _2,2 S _2,n/π ₂ individuals in category 2. We then get

$$I_{1,n+1}=I_{1,n}(1-\gamma )+(S_{1,n}/{\pi }_1)({\beta }_{1,1}{I}_{1,n}+{\beta }_{1,2}{I}_{2,n}),$$

$$I_{2,n+1}=I_{2,n}(1-\gamma )+(S_{2,n}/{\pi }_2)({\beta }_{2,1}{I}_{1,n}+{\beta }_{2,2}{I}_{2,n}),$$

$$S_{1,n+1}=S_{1,n}-(S_{1,n}/{\pi }_1)({\beta }_{1,1}{I}_{1,n}+{\beta }_{1,2}{I}_{2,n}),$$

$$S_{2,n+1}=S_{2,n}-(S_{2,n}/{\pi }_2)({\beta }_{2,1}{I}_{1,n}+{\beta }_{2,2}{I}_{2,n}).$$

If we denote

$$B=\left(\begin{array}{cc}{\beta }_{1,1}\hfill & {\beta }_{1,2}\hfill \\ {\beta }_{2,1}\hfill & {\beta }_{2,2}\hfill \end{array}\right),$$

$$I_n=\left(\begin{array}{c}{I}_{1,n}\\ I_{2,n}\end{array}\right),$$

$$S_n=\left(\begin{array}{c}{S}_{1,n}\\ S_{2,n}\end{array}\right),$$

$${\Sigma }_n=\left(\begin{array}{cc}{S}_{1,n}/{\pi }_1\hfill & 0\hfill \\ 0\hfill & S_{2,n}/{\pi }_2\hfill \end{array}\right),$$

we get

$$I_{n+1}=((1-\gamma )\mathrm{Id}+{\Sigma }_{n}B)I_n$$

and

$$S_{n+1}=S_n-{\Sigma }_{n}B{I}_n.$$

Hence,

$$I_{n+1}-I_n=-\gamma I_n+{\Sigma }_{n}B{I}_n=\gamma B^{-1}{\Sigma }_n^{-1}(S_{n+1}-S_n)-(S_{n+1}-S_n).$$

We have

$${\Sigma }_n^{-1}(S_{n+1}-S_n)=\left(\begin{array}{c}{\pi }_1\frac{S_{1,n+1}-S_{1,n}}{S_{1,n}}\\ {\pi }_2\frac{S_{2,n+1}-S_{2,n}}{S_{2,n}}\end{array}\right).$$

If we assume that the relative variation of S _1,n and S _2,n is small in one day, we can approximate $(S_{j,n+1}-S_{j,n})/S_{j,n}$ by $\ln \left(S_{j,n+1}\right)-\ln \left(S_{j,n}\right)$ for j equal to 1 or 2. This approximation becomes rigorously true in a continuous time model. Letting

$$L_n:=\left(\begin{array}{c}{\pi }_1\ln S_{1,n}\\ {\pi }_2\ln S_{2,n}\end{array}\right),$$

we get

$$I_{n+1}-I_n=\gamma B^{-1}(L_{n+1}-L_n)-(S_{n+1}-S_n).$$

Summing for all n ≥ 1, we get

$$I_{\infty }-I_{-\infty }=\gamma B^{-1}(L_{\infty }-L_{-\infty })-(S_{\infty }-S_{-\infty }).$$

As in the one-dimensional model, the number of infected people is zero far in the past and the future. Moreover, everybody is susceptible at the beginning, and then, taking into account the proportion of the population in categories 1 and 2,

$$S_{-\infty }=\left(\begin{array}{c}{\pi }_1\\ {\pi }_2\end{array}\right),S_{\infty }=\left(\begin{array}{c}{\pi }_1(1-J_1)\\ {\pi }_2(1-J_2)\end{array}\right),$$

$$\begin{array}{ccc}& & L_{-\infty }=\left(\begin{array}{c}{\pi }_1\ln {\pi }_1\\ {\pi }_2\ln {\pi }_2\end{array}\right),\hfill \\ & & L_{\infty }=\left(\begin{array}{c}{\pi }_1(\ln {\pi }_1+\ln (1-J_1))\\ {\pi }_2(\ln {\pi }_2+\ln (1-J_2))\end{array}\right),\hfill \end{array}$$

where J_j is the proportion of individuals in category j who become infected some time during the epidemic. We deduce

$$\gamma B^{-1}\left(\begin{array}{c}{\pi }_1\ln (1-J_1)\\ {\pi }_2\ln (1-J_2)\end{array}\right)+\left(\begin{array}{c}{\pi }_1{J}_1\\ {\pi }_2{J}_2\end{array}\right)=0,$$

which implies

$$\left(\begin{array}{c}{\pi }_1\ln (1/(1-J_1))\\ {\pi }_2\ln (1/(1-J_2))\end{array}\right)={\gamma }^{-1}B\left(\begin{array}{c}{\pi }_1{J}_1\\ {\pi }_2{J}_2\end{array}\right),$$

and then

$$\left(\begin{array}{c}\ln (1/(1-J_1))\\ \ln (1/(1-J_2))\end{array}\right)=\mathcal{R}\left(\begin{array}{c}{J}_1\\ J_2\end{array}\right)$$

where

$$\begin{array}{ccc}\hfill \mathcal{R}& :=& {\gamma }^{-1}\left(\begin{array}{cc}{\pi }_1^{-1}& 0\\ 0& {\pi }_2^{-1}\end{array}\right)B\left(\begin{array}{cc}{\pi }_1& 0\\ 0& {\pi }_2\end{array}\right)\hfill \\ & =& {\gamma }^{-1}\left(\begin{array}{cc}{\beta }_{1,1}& {\beta }_{1,2}{\pi }_2/{\pi }_1\\ {\beta }_{2,1}{\pi }_1/{\pi }_2& {\beta }_{2,2}\end{array}\right).\hfill \end{array}$$

In the previous section, we computed a reproduction rate R, and we saw that

$$R=\frac{1}{2\gamma }({\beta }_{1,1}+{\beta }_{2,2}+\sqrt{{({\beta }_{1,1}-{\beta }_{2,2})}^2+4{\beta }_{1,2}{\beta }_{2,1}}).$$

In fact, R is the largest eigenvalue of the matrix $\mathcal{R}$.

Let us now discuss the examples considered in the previous section.

In the case of irrelevant categories, we have

$$\mathcal{R}={\gamma }^{-1}\left(\begin{array}{cc}\beta {\pi }_1& \beta {\pi }_2\\ \beta {\pi }_1& \beta {\pi }_2\end{array}\right).$$

Notice that in the previous section, we had an extra term $1-\gamma$ on the diagonal entries which is not in the matrices B or $\mathcal{R}$. In this case,

$$\mathcal{R}\left(\begin{array}{c}{J}_1\\ J_2\end{array}\right)=(\beta /\gamma )({\pi }_1{J}_1+{\pi }_2{J}_2)\left(\begin{array}{c}1\\ 1\end{array}\right).$$

Since this vector has two equal coordinates, we need to have $\ln (1/(1-J_1))=\ln (1/(1-J_2)),$ then $J_1=J_2=J$ for some J ∈ (0, 1), i.e. the proportion of people who get infected some time is the same in the two categories. Now,

$$\mathcal{R}\left(\begin{array}{c}{J}_1\\ J_2\end{array}\right)=(\beta /\gamma )({\pi }_{1}J+{\pi }_{2}J)\left(\begin{array}{c}1\\ 1\end{array}\right)=R\left(\begin{array}{c}J\\ J\end{array}\right),$$

since we have computed $R=\beta /\gamma$ in this example. Hence, J should satisfy $\ln (1-J)=RJ,$ i.e. the same equation as in the model with a single category. This confirms that the categories are irrelevant in the present example.

In the example with two categories of the same size (${\pi }_1={\pi }_2=1/2$) and different degrees of socialization σ ₁ and σ ₂, we have

$$\mathcal{R}={\gamma }^{-1}\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2\\ {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right).$$

The equations we need to solve are

$$\ln (1/(1-J_1))={\gamma }^{-1}{\sigma }_1({\sigma }_1{J}_1+{\sigma }_2{J}_2),$$

$$\ln (1/(1-J_2))={\gamma }^{-1}{\sigma }_2({\sigma }_1{J}_1+{\sigma }_2{J}_2).$$

The right-hand sides of the equations should be proportional to σ ₁ and σ ₂, and it should be the same for the left-hand sides. We then have, for some α > 0,

$$J_1=1-e^{-{\sigma }_1\alpha /\sqrt{\gamma }},J_2=1-e^{-{\sigma }_2\alpha /\sqrt{\gamma }},$$

and

$$\alpha =({\sigma }_1/\sqrt{\gamma })(1-e^{-{\sigma }_1\alpha /\sqrt{\gamma }})+({\sigma }_2/\sqrt{\gamma })(1-e^{-{\sigma }_2\alpha /\sqrt{\gamma }}),$$

i.e.

$$\alpha =s_1(1-e^{-s_1\alpha })+s_2(1-e^{-s_2\alpha })$$

for $s_1={\sigma }_1/\sqrt{\gamma }$ and $s_2={\sigma }_2/\sqrt{\gamma }$. Notice that we have previously computed $R={\gamma }^{-1}({\sigma }_1^2+{\sigma }_2^2)$ and so $s_1^2+s_2^2=R$. Let us assume that $s_1=0.7,$ $s_2=1.4,$ so $R=2.45$. In this example, category 2 is twice as sociable as category 1. We numerically find α ≃ 1.784, and then

$$J_1=1-e^{-s_1\alpha }\simeq 0.713,J_2=1-e^{-s_2\alpha }\simeq 0.918.$$

The global proportion of infected people is then about 81.5 percent. This is less than the proportion of 88.6 percent which we obtain for the model with a single category for the same value $R=2.45$. As in the example in the previous section for social distancing, if not being respected by 15 percent of the individuals when they are together, we have for ${\pi }_1=0.85,$ ${\pi }_2=0.15,$ and $\gamma =0.13$:

$$\begin{array}{ccc}& & {\beta }_{1,1}=0.43{\pi }_1/3.5,\hfill \\ & & {\beta }_{1,2}=0.43{\pi }_1/3.5,\hfill \\ & & {\beta }_{2,1}=0.43{\pi }_2/3.5,\hfill \\ & & {\beta }_{2,2}=0.43{\pi }_2,\hfill \end{array}$$

which gives approximately:

$$\mathcal{R}\simeq \left(\begin{array}{cc}0.80329& 0.14176\\ 0.80329& 0.49615\end{array}\right)$$

and R ≃ 1.0205. We now need to solve

$$\ln (1/(1-J_1))=0.80329J_1+0.14176J_2,$$

$$\ln (1/(1-J_2))=0.80329J_1+0.49615J_2.$$

We find numerically

$$J_1\simeq 0.03465,J_2\simeq 0.05242.$$

The global proportion of infected individuals is

$${\pi }_1{J}_1+{\pi }_2{J}_2\simeq 0.0373,$$

which is slightly less than what we obtain for the model with one category for the same value of R. In the same example with the contacts between 1 and 2 divided by 2 instead of 3.5, we get

$$\mathcal{R}\simeq \left(\begin{array}{cc}0.80329& 0.24808\\ 1.40576& 0.49615\end{array}\right),$$

and R ≃ 1.26. We solve numerically

$$\ln (1/(1-J_1))=0.80329J_1+0.24808J_2,$$

$$\ln (1/(1-J_2))=1.40576J_1+0.49615J_2.$$

We get

$$J_1\simeq 0.3111,J_2\simeq 0.4948$$

and then a global proportion of

$${\pi }_1{J}_1+{\pi }_2{J}_2\simeq 0.3387.$$

This is again smaller than what we get for a single category with $R=1.26,$ i.e. 0.3821.

The partial lockdown of people over 70 years old gives

$$\mathcal{R}=\left(\begin{array}{cc}2.81154& 0.04962\\ 0.28115& 0.04962\end{array}\right),$$

and R ≃ 2.8166. We solve numerically

$$\ln (1/(1-J_1))=2.81154J_1+0.04962J_2,$$

$$\ln (1/(1-J_2))=0.28115J_1+0.04962J_2$$

and we get

$$J_1\simeq 0.9271,J_2\simeq 0.2385,$$

and a global proportion of infected people of 0.8238, instead of 0.9264 for a single category. Notice that the older people are much less infected than the others, but not by a factor of 10.

In all of the examples above, the fact that the contacts are not uniform in the population reduces the total number of infected individuals for a given value of R > 1, but not in a dramatic way.

The proportion of infected individuals we have computed is not the same as the minimum needed in order to get herd immunity. In order to compute this proportion, we assume that we have controlled the epidemic in such a way that there are very few currently infected people, but sufficiently many immune individuals. Since there should be few new infections, we can assume that the proportion of susceptible individuals in each category stabilizes at levels S ₁ and S ₂. In this situation, the evolution of the number of infected individuals can be written as follows:

$$I_{n+1}=((1-\gamma )\mathrm{Id}+\Sigma B)I_n,$$

where

$$\Sigma =\left(\begin{array}{cc}{S}_1/{\pi }_1& 0\\ 0& S_2/{\pi }_2\end{array}\right),$$

i.e. the same equation as before, but with a fixed number of susceptible individuals. We get herd immunity, i.e. the epidemic is under control, if the largest eigenvalue of $(1-\gamma )\mathrm{Id}+\Sigma B$ is strictly smaller than 1. If we want to minimize the number of previously infected individuals, we need to maximize the global proportion of individuals who are still susceptible, i.e. $S_1+S_2$. In order for the eigenvalues of $(1-\gamma )\mathrm{Id}+\Sigma B$ to be smaller than 1, we need the eigenvalues of ΣB to be smaller than γ, i.e. the eigenvalues of ${\gamma }^{-1}\Sigma B$ to be smaller than 1. We have

$$\begin{array}{ccc}\hfill {\gamma }^{-1}\Sigma B& =& \left(\begin{array}{cc}{S}_1& 0\\ 0& S_2\end{array}\right)\mathcal{R}\left(\begin{array}{cc}{\pi }_1^{-1}& 0\\ 0& {\pi }_2^{-1}\end{array}\right)\hfill \\ & =& \left(\begin{array}{cc}{\mathcal{R}}_{1,1}{S}_1/{\pi }_1& {\mathcal{R}}_{1,2}{S}_1/{\pi }_2\\ {\mathcal{R}}_{2,1}{S}_2/{\pi }_1& {\mathcal{R}}_{2,2}{S}_2/{\pi }_2\end{array}\right).\hfill \end{array}$$

If we assume that a proportion 1/R of the individuals in each category is immune, we get $S_1={\pi }_1/R,$ $S_2={\pi }_2/R,$ and

$${\gamma }^{-1}\Sigma B=R^{-1}\left(\begin{array}{cc}{\mathcal{R}}_{1,1}& {\mathcal{R}}_{1,2}{\pi }_1/{\pi }_2\\ {\mathcal{R}}_{2,1}{\pi }_2/{\pi }_1& {\mathcal{R}}_{2,2}\end{array}\right).$$

This matrix is conjugated to $\mathcal{R}/R$ and so its largest eigenvalue is 1. Hence, we can have herd immunity if the proportion of already infected people is larger than $1-1/R,$ as in the case with one category. However, this situation is not optimal since herd immunity can be obtained with less infected individuals in general. In general, we need to maximize $S_1+S_2,$ conditioned on the fact that

$$\begin{array}{ccc}& & \frac{1}{2}({\mathcal{R}}_{1,1}{S}_1/{\pi }_1+{\mathcal{R}}_{2,2}{S}_2/{\pi }_2\hfill \\ & & +\sqrt{{({\mathcal{R}}_{1,1}{S}_1/{\pi }_1-{\mathcal{R}}_{2,2}{S}_2/{\pi }_2)}^2+4{\mathcal{R}}_{1,2}{\mathcal{R}}_{2,1}{S}_1{S}_2/{\pi }_1{\pi }_2})\hfill \end{array}$$

is smaller than 1.

In the case of irrelevant categories, we get

$$\mathcal{R}={\gamma }^{-1}\left(\begin{array}{cc}\beta {\pi }_1& \beta {\pi }_2\\ \beta {\pi }_1& \beta {\pi }_2\end{array}\right),$$

and then we need

$$\frac{1}{2\gamma }(\beta S_1+\beta S_2+\sqrt{{(\beta S_1-\beta S_2)}^2+4{\beta }^2{S}_1{S}_2})$$

to be smaller than 1. This condition gives $(\beta /\gamma )(S_1+S_2)<1,$ i.e. $S_1+S_2<1/R$. This gives a proportion of infected individuals equal to $1-1/R,$ and there is no improvement with respect to the model with one category.

In the case with two different degrees of socialization σ ₁ and σ ₂, and for ${\pi }_1={\pi }_2=1/2,$ we have

$$\mathcal{R}={\gamma }^{-1}\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2\\ {\sigma }_2{\sigma }_1& {\sigma }_2^2\end{array}\right).$$

Since the determinant of the matrix $\mathcal{R}$ is zero, i.e ${\mathcal{R}}_{1,1}{\mathcal{R}}_{2,2}={\mathcal{R}}_{1,2}{\mathcal{R}}_{2,1},$ we deduce that the quantity inside the square root is equal to

$${({\mathcal{R}}_{1,1}{S}_1/{\pi }_1+{\mathcal{R}}_{2,2}{S}_2/{\pi }_2)}^2,$$

and then we need

$${\mathcal{R}}_{1,1}{S}_1/{\pi }_1+{\mathcal{R}}_{2,2}{S}_2/{\pi }_2=2{\gamma }^{-1}({\sigma }_1^2{S}_1+{\sigma }_2^2{S}_2)<1$$

since ${\pi }_1={\pi }_2=1/2$ in this model. Let us assume that category 2 is more sociable than category 1, i.e. σ ₂ > σ ₁. In this case, $S_1+S_2$ is maximal for fixed values of ${\sigma }_1^2{S}_1+{\sigma }_2^2{S}_2$ when S ₂ is as small as possible, i.e. the most sociable category is infected first. Since S ₁ and S ₂ are between 0 and 1/2, the optimal solution is either $S_1=1/2$ and S ₂ ∈ (0, 1/2), or S ₁ ∈ (0, 1/2) and $S_2=0$ (all category 2 is immune). In the first situation, we need

$$2{\gamma }^{-1}({\sigma }_1^2/2+{\sigma }_2^2{S}_2)<1,$$

which gives

$$S_2<(\gamma -{\sigma }_1^2)/2{\sigma }_2^2=(1-s_1^2)/2s_2^2,$$

where $s_1={\sigma }_1/\sqrt{\gamma },$ $s_2={\sigma }_2/\sqrt{\gamma },$ and then $R=s_1^2+s_2^2$. This solution is available when S ₂ remains positive, i.e. s ₁ < 1. In this case the overall proportion of infected individuals is

$$1-S_1-S_2=\frac{1}{2}-\frac{1-s_1^2}{2s_2^2}=\frac{R-1}{2s_2^2}.$$

If s ₁ ≥ 1, we need all category 2 to be infected in order to have optimal herd immunity. In this case, we get the condition

$$2{\gamma }^{-1}{S}_1{\sigma }_1^2<1,$$

i.e.

$$S_1<\frac{\gamma }{2{\sigma }_1^2}=\frac{1}{2s_1^2}$$

which is smaller than 1/2 as needed. The proportion of infected individuals is

$$1-S_1-S_2=1-\frac{1}{2s_1^2}.$$

In the case where $s_1=0.7,$ $s_2=1.4,$ $R=2.45,$ we are in the first situation and we get a proportion of infected individuals given by

$$\frac{2.45-1}{2\times 1.4^2}\simeq 0.37,$$

74 percent of category 2 and 0 percent of category 1. With a single category, the rate of contamination is about 59 percent. The global improvement is not negligible.

In the case of 15 percent of individuals not respecting social distancing when they are together, we have

$$\mathcal{R}\simeq \left(\begin{array}{cc}0.80329& 0.14176\\ 0.80329& 0.49615\end{array}\right)$$

and R ≃ 1.0205. We need to maximize $S_1+S_2$ for

$$\begin{array}{ccc}& & \frac{1}{2}(0.80329S_1/0.85+0.49615S_2/0.15\hfill \\ & & +\sqrt{\begin{array}{c}{(0.80329S_1/0.85-0.49615S_2/0.15)}^2\hfill \\ +4·0.14176·0.80329·S_1{S}_2/(0.15·0.85)\hfill \end{array}})\hfill \end{array}$$

smaller than 1. The optimum occurs when nobody is infected in category 1, which implies $S_1=0.85,$ and S ₂ ≃ 0.1395. The proportion of infected individuals is then 1.05 percent. With one category, we need 2 percent of infected individuals. In the case where the individuals of category 2 do not fully respect social distancing even if they meet people in category 1, we have computed

$$\mathcal{R}\simeq \left(\begin{array}{cc}0.80329& 0.24808\\ 1.40576& 0.49615\end{array}\right),$$

and R ≃ 1.26. We need to maximize $S_1+S_2$ for

$$\begin{array}{ccc}& & \frac{1}{2}(0.80329S_1/0.85+0.49615S_2/0.15\hfill \\ & & +\sqrt{\begin{array}{c}{(0,80329S_1/0.85-0.49615S_2/0.15)}^2\hfill \\ +4·0.24808·1.40576·S_1{S}_2/(0.15·0.85)\hfill \end{array}})\hfill \end{array}$$

smaller than 1. The optimum again gives nobody infected in category 1, with $S_1=0.85$ and S ₂ ≃ 0.0661. In this case, 8.39 percent of the population is infected. The usual formula $1-1/R$ gives 20.6 percent of the population being infected. With lockdown of people over 70 years old, we get

$$\mathcal{R}\simeq \left(\begin{array}{cc}2.81154& 0.04962\\ 0.28115& 0.04962\end{array}\right),$$

and R ≃ 2.8166. In this case, the optimum is when nobody is infected over 70 years old. We get S ₁ ≃ 0.3007 and $S_2=0.15,$ giving 54.93 percent of infected individuals, all under 70 years old. The usual formula gives 65.5 percent.

The examples above show that the minimal proportion of infected individuals needed for herd immunity can be significantly lower than $1-1/R$ if the distribution of the infectious contacts is inhomogeneous. However, it remains a large proportion of the population if R is significantly larger than 1. Moreover, reaching the minimum implies that we control how much each category of the population is infected, which cannot be precisely done in practice. Notice that the numerical examples discussed here are not necessarily very relevant, since they assume that social distancing decisions are applied in the long run, whereas the main interest of herd immunity is that one can release social restrictions. It would be more relevant to consider matrices of infection rates corresponding to the situation where there are no particular social restrictions when we reach herd immunity.

10. Some simulations for the coming months

In this section, we present a few simulations of the rate of saturation of the hospitals, for twelve different scenarios. This is based on the SIR model. The parameters are the following:

• •The parameter β under lockdown, and without lockdown, after May 11.
• •The parameter γ before, and after improvement of the testing capacity.
• •The minimum rate of saturation of the healthcare system for which a further lockdown is decided.
• •The rate of decay of the hospitalizations due to the improvement of treatments.
• •The seasonality of the disease.
• •The true proportion of infected people at the beginning of the lockdown, on March 17.
• •The time needed to improve testing capacity.
• •The rate of saturation of hospitals at the first peak at the beginning of April, arbitrarily taken to be 80 percent.
• •The duration of future lockdowns.

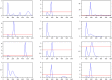
For each of the parameters, different values are considered for each of the twelve scenarios. These values are detailed in the joint scilab program. Each scenario gives a curve representing the evolution of the rate of saturation of hospitals (saturation above the red line), as a function of the date, represented here by the number of days after January 1, 2020. The duration of the simulation is 600 days, i.e. until summer 2021. Summer 2020 is around day 200, and winter 2020–2021 is around day 400. The twelve curves are very different from each other. Seven of them have an important second peak, which can be very big, at the beginning of the summer 2020, one of them (corresponding to a strong seasonality) has a second peak during winter 2020–2021. These curves are not predictions but illustrate the very large uncertainty of the present situation.

CRediT authorship contribution statement

Joseph Najnudel: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing - original draft, Software. Ju-Yi Yen: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.