The Effect of Axial Length on Extraocular Muscle Leverage

Abstract

PURPOSE:

Magnetic resonance imaging (MRI) was used to determine the effect of axial length (AL) on globe rotational axis and horizontal extraocular muscle (EOM) leverage during horizontal duction.

Design:

Prospective observational case series.

METHODS:

At a single academic center, 36 orthophoric adults with a wide range of ALs underwent high-resolution axial orbital MRI in target-controlled adduction and abduction. ALs were measured in planes containing maximum globe cross-sections. Area centroids were calculated to determine globe centers. Rotational axes in orbital coordinates were calculated from displacements of lens centers and globe-optic nerve attachments. Lever arms were calculated as distances between published EOM insertions and rotational axes.

RESULTS:

ALs averaged 26.3±0.3mm (standard error, range 21.5-33.4mm). Rotational axes from adduction to abduction averaged 1.1±0.2mm medial and 1.1±0.2mm anterior to the globe’s geometric center in adduction. Linear regression demonstrated no significant correlation between AL and rotational axis horizontal (R²=0.06) or anteroposterior (R²= 0.07) position. Medial rectus (MR) lever arms averaged 12.0±0.2mm and lateral rectus (LR) lever arms averaged 12.8±0.2mm. Both MR (R²=0.24, p<0.001) and LR (R²=0.32, p<0.001) lever arms significantly increased by about 0.3mm per 1.0mm of increased AL, with a corresponding reduction in predicted per mm effect of surgical repositioning of their insertions.

CONCLUSIONS:

Regardless of AL, the globe rotates about a point nasal and anterior to its geometric center, giving the LR more leverage than the MR. This eccentricity may diminish the effect of tendon repositioning in moderate to highly myopic patients, with reductions in per mm dose/response predicted with longer AL.

Table of Contents Statement

High resolution magnetic resonance imaging in adults having a wide range of axial length shows that regardless of globe length, the eye rotates about a point nasal and anterior to its geometric center, giving the lateral rectus more leverage than the medial rectus muscle. This eccentricity may diminish the effect of tendon repositioning in moderate to highly myopic patients, predicting reductions in per mm dose/response of muscle recession surgery in eyes with greater axial length.

Introduction

The eye is rotated by twisting force, the net torque exerted by the extraocular muscles (EOMs). Torque exerted by any EOM is the product of its force multiplied by its lever arm, the distance between the rotational center of the eye and the location of the force applied in the tangential direction. To simplify biomechanical modeling of the globe’s response to applied EOM forces, consideration of mechanical factors is typically limited to EOM contractile forces, their lever arms,^1,2 their pulling directions as influenced by their pulleys,^3-10 and the tangency of their insertions onto the globe.¹¹ If the eye rotates about the geometric center of a spherical globe, the lever arms of the EOMs are identically equal to the radius of the globe, provided that the EOMs or their tendons wrap over the globe surface. Likewise, while even normal EOM paths at their insertions are not perfectly tangent to the globe,¹¹ the discrepancy is small for the range of normal ductions. Thus, most biomechanical models^{2, 9, 10, 12-15} assume that lever arms and EOM insertional non-tangency can be neglected, leaving rotational eye position solely dependent on the balance of EOM contractile forces and long segment pulling directions.

Magnetic resonance imaging (MRI), however, reveals substantial globe translation – linear motion - within the orbit during horizontal gaze changes (Fig. 1). Eye movements actually consist of combined globe rotation and globe translation, which of course implies that the center of the globe cannot be the axis of rotation.¹⁶ Any eccentricity of the globe’s rotational axis would change relative lever arm lengths for the EOMs and thus their respective torques even at identical contractile tensions, introducing a potentially important biomechanical nuance to the contributions of each EOM to a given duction. Analogous to the larger and smaller gears on a bicycle, an EOM insertion closer to the rotational axis would rotate the globe more degrees per mm of EOM contraction, while an EOM insertion farther from the axis of rotation would rotate the globe fewer degrees per mm of EOM contraction. Continuing this analogy, the effect of this consideration would be expected to depend upon globe size in relation to the amount of translation during eye rotation.

Figure 1:

Axial magnetic resonance images of one representative subject in right and left gaze superimposed at partial transparency. Globe rotation is demonstrated by the change in position of the lens (black arrows) and the globe-optic nerve attachment (white arrows), while globe translation is evident from shifts in position of the sclera (white arrowheads). In both eyes rotating from left to right, the globe translated by almost one mm both posteriorly and horizontally in the direction of gaze.

For this study, we used high-resolution axial orbital MRI to analyze globe translation and rotation during horizontal gaze changes, using differential changes in the positions of anterior and posterior globe landmarks to calculate the location of the rotational axis. We then quantified the effects of both globe axial length (AL) and rotational axis eccentricity on the relative lengths of the horizontal rectus EOM lever arms. We used these relationships to infer mechanical effects of common strabismus surgeries.

Methods

At a single academic institution, 36 adult volunteers (average age 59±13 years, standard deviation, SD, 10 males, 26 females) were recruited through advertising for a prospective observational cohort study. Before participation, each subject consented in writing to a protocol conforming to the tenets of the Declaration of Helsinki that was approved by the Institutional Review Board of the University of California, Los Angeles, and that complied with the Health Insurance Portability and Accountability Act. Comprehensive eye examinations were performed on every subject to verify normal corrected vision, normal binocular alignment, and normal motility.

A 1.5-T General Electric Signa scanner (Milwaukee, WI) augmented with a dual-phased surface coil array (Medical Advances, Milwaukee, WI) was used to acquire high resolution T2 fast spin echo axial MRI¹⁷ in contiguous 2-mm slices over a 11-cm or 10-cm field of view (430- or 390-μm in plane resolution). Imaging was performed while gaze was controlled in large angles of adduction and abduction using a fine, illuminated fiber optic fixation target.

Digital images including both eyes were combined into image stacks. Measurements were performed using the ImageJ program (W. Rasband, National Institutes of Health, Bethesda, Maryland). The following steps were used to register the bony orbital structures for image sets obtained in different gaze positions: 1) the midline structures of the face were rotated into alignment with scanner vertical to control for face turns; and 2) the image stacks were translated to align a fixed extra-orbital anatomic landmark (Fig. 1).

ALs were measured in planes containing the largest globe cross-sections as the length of a line from the corneal apex bisecting the lens and extending to the anterior retinal surface. Clinical duction measurements were approximated by the difference in the angles of these lines between gaze positions. The geometric center of the globe was calculated in scanner coordinates to sub-pixel resolution using ImageJ’s “Area Centroid” function after manually outlining the largest cross-section of the globe, omitting the cornea. Similarly, the area centroids of the largest lens cross-section and the breadth of the globe-ON attachment were calculated after those structures were manually outlined (Fig. 2).

Figure 2:

Axial magnetic resonance image of a left eye in abduction.The change in position of the globe center, lens center, and center of the globe-optic nerve attachment from adduction to abduction were used to calculate the axis of rotation.

Positions of the globe center, lens center, and globe-ON attachment for both gaze positions were defined in a coordinate system with the globe center in the initial gaze position, adduction, defined as the origin. Then, linear algebra was used to calculate the location of the rotational axis with respect to that origin.¹⁶ Finally, assuming normal locations for the EOM tendinous insertions,¹⁸ plane geometry was used to calculate the lengths of the medial rectus (MR) and lateral rectus (LR) lever arms. Because of the geometry, even large offsets (± 2 mm) of the actual EOM insertions from normal have small (< 0.5 mm) effects on the calculated lengths of the lever arms.

Linear regressions were performed between the horizontal and anteroposterior positions of the rotational axes and the EOM lever arm lengths as a function of globe ALs. Statistical significance was set at the 0.01 level to account for multiple comparisons.

Results

Axial lengths ranged from 21.5 to 33.4 mm (average 26.3 ± 0.3 mm, standard error). Clinical ductions averaged 63.2 ± 0.8° from large adduction to large abduction. From classic biomechanical modeling, if eye rotations occurred around the center of the globe, both lens and globe-ON attachment rotations should have been identical to the clinical duction. Instead, using that assumption the lens would have rotated 63.6±0.9° (p = 0.31 compared with clinical duction), but the globe-ON attachment would have rotated much less at 55.2±0.9° (p < 0.001 compared with both clinical duction and lens rotation). The significant difference between these two angles invalidates the assumption and excludes the globe center as the actual rotational axis.

Actual globe rotational axes were computed as described using linear algebra.¹⁶ Figure 3 shows the mediolateral and anteroposterior displacement of the actual rotational axes. The rotational axis averaged over all subjects was 1.1 ± 0.2 mm medial and 1.1 ± 0.2 mm anterior to where the globe’s geometric center was located in the initial position, which was large adduction. Linear regression demonstrated minimal correlation between AL and the rotational axis mediolateral (R² = 0.06, p=0.04) or anteroposterior (R² =0.07, p=0.03) positions (Fig. 3).

Figure 3:

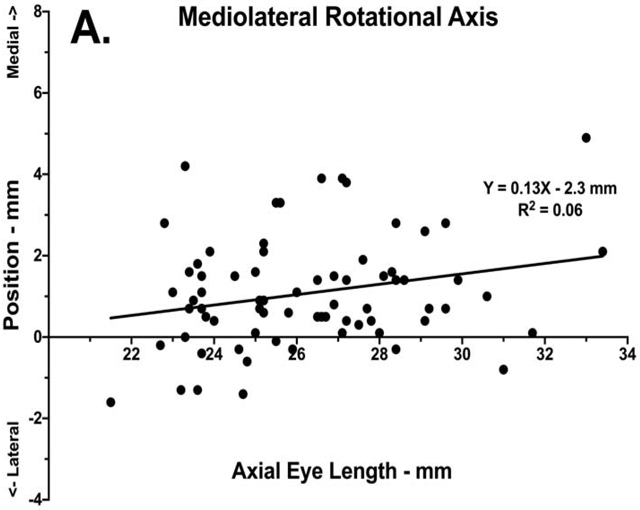
Mediolateral position of the ocular rotational axis during large abduction with respect to globe center in initial adducted position as a function of axial length. Data is plotted for each orbit of each subject, with linear regressions shown as solid lines. A. Mediolateral position. B. Anteroposterior position.

The foregoing eccentricity of globe rotational axis necessarily implies translation during rotation, as graphed for all subjects in Fig. 4. Averaging over all subjects for rotation from large adduction to abduction, the globe translated 0.7 ± 0.1 mm laterally and 0.6 ± 0.1 mm posteriorly. Linear regression demonstrated no significant correlation between AL and globe mediolateral (R² = 0.02, p=0.23) or anteroposterior (R² =0.03, p=0.12) translation. By the conclusion of this translation, the average rotational axis was 1.8 ± 0.2 mm medial and 1.7 ± 0.2 mm anterior to where the globe center had been located in the starting position of adduction. At the start of the rotation in large adduction, the average MR lever arm was 12.0 ± 0.2 mm, 0.8 mm shorter than the 12.8 ± 0.2 mm LR lever arm, giving the LR about 6% more oculorotary leverage than for MR. By the end of the rotation in large abduction, because of globe translation the average MR lever arm shortened to 11.1 ± 0.3 mm as the MR insertion translated nearer to the rotational axis, while the LR lever arm lengthened to 15.1 ± 0.3 mm as the LR insertion translated farther from the rotational axis. The change in lever arm length gave the LR about 26% more leverage than the MR in large abduction.

Figure 4:

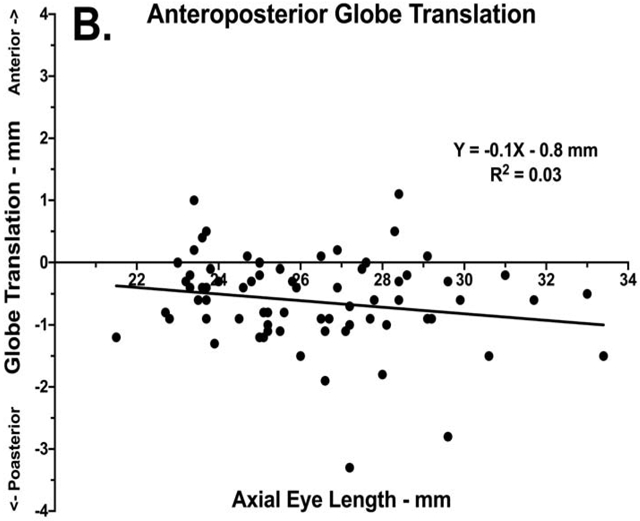
Globe translation with respect to globe center at the start of rotation, in the adducted position, as a function of axial length. Data is plotted for each orbit of each subject, with linear regressions shown as solid lines. A. Mediolateral translation. B. Anteroposterior translation.

The foregoing relationships did not vary significantly with globe AL. Linear regression, however, did demonstrate a significant correlation for MR (R²=0.24, p<0.001) and LR (R²=0.32, p<0.001) initial lever arm lengths with AL (Fig. 5), with the lever arms for both increasing by about 0.6 mm for every 2 mm increase in AL. This change in lever arm length substantially altered the expected globe rotation per mm of horizontal EOM insertional movement along the surface of the globe. For a 12-mm EOM lever arm, 5.0 mm of insertional movement along the globe surface corresponds to rotation of a 24-mm globe 23.2° (42.9 Δ). For a 14-mm lever arm, that same 5.0 mm movement along the globe surface corresponds to rotation of a 24-mm globe only 20.0° (36.3 Δ), a decrease of 3.2° (6.6 Δ) representing reduction of about 15% in rotational effect.

Figure 5:

Initial lever arms of the horizontal rectus muscles during large abduction with respect to globe center in initial adducted position as a function of axial length. Lever arms varied significantly with axial length for both the medial and lateral rectus muscles (p < 0.001 for both).

Discussion

Because eye movements include translation during globe rotation, the center of ocular rotation cannot be located at the geometric center of the globe.¹⁶ For combined rotation and translation in a large group of subjects from large adduction to large abduction, the globe rotated, on average, around an axis more than 1 mm medial and 1 mm anterior to the geometric globe center. This eccentric axis made the MR lever arm shorter and the LR lever arm longer than the globe radius, imparting greater leverage to force applied at the LR insertion compared with the MR insertion. In addition, this mechanical advantage was not static; as the globe translated posteriorly and laterally away from the rotational axis during abduction, LR leverage increased while MR leverage simultaneously diminished. Neither was the asymmetry trivial; the LR leverage advantage over the MR increased from 6% to 26% across the range of a normal horizontal eye movement from large adduction to large abduction.

Although the globe’s kinematic behavior is complex, it appears qualitatively consistent across a wide range of globe sizes. There were no significant differences in either the location of the rotational axis or the magnitude of globe translation as a function of AL. Increasing AL, however, is associated with longer MR and LR lever arms because the larger globe diameter places both EOM insertions geometrically farther from the rotational axis. While a longer lever arm increases the torque created by applied EOM force, it also reduces the predicted degrees of globe rotation per mm of change in EOM insertional position along globe surface, as occurs during normal EOM contraction or caused by surgical recession. This reduction in per mm effect might explain the diminished responses observed after standard surgical repositioning of the EOM insertions in patients with greater AL, leading some authors to advocate augmented surgical dosages to compensate for larger ALs.^19-21

The relationship between globe translation and the location of its rotational axis introduces the possibility of an additional factor that might directly affect EOM leverage: the stiffness of the orbital connective tissue pulley system that surrounds and suspends the globe. Smooth muscle bands have been identified that interconnect the EOM pulleys within the orbit,^22-24 while the pulley tissue itself can rapidly shift anteriorly or posteriorly during relaxation or contraction of the EOM orbital layers.^{9, 25} Since parts of the connective tissue contain innervated smooth muscle and the EOM orbital layer actively and continuously adjusts the positions of the EOM pulleys, it is plausible that active changes in orbital connective tissue tension during eye movements might affect globe translation and thus EOM leverage. Likewise, passive changes in the stiffness of the orbital connective tissue over time, either caused by disease (e.g. dysthyroid orbitopathy²⁶) or senescence (e.g. sagging eye syndrome,^{27, 28}) might also increase or decrease orbital stiffness and thus alter globe translation and EOM leverage during eye movements. Even the ON itself loads the globe in adduction, becoming taut during adduction exceeding about 26°.^29-31 Any factor that directly or indirectly affects the stiffness of the orbital connective tissue could substantially alter the biomechanics of globe rotation and translation and thus might impact EOM leverage.

Preliminary data comparing adduction to convergence suggests that such changes do occur in vivo. In normal subjects, the MR lever arm has been shown to be about a third longer in convergence than in adduction, while the LR lever arm was similar for both eye movements.¹⁶ A change in leverage introduces the possibility of eye movement without any change in EOM tension; the applied torque could increase or decrease through a change in orbital connective tissues without any change in innervation to the EOMs.

This study has limitations. The large gaze change from adduction to abduction was chosen to minimize the effect of any measurement artifacts created by inconsistencies in head position or by head movement during gaze changes.¹⁶ The correspondingly large positional changes of the lens and globe-ON attachment resulted in consistent and reproducible measurements of rotational axes and EOM lever arm lengths, but smaller gaze changes may not be associated with similar magnitudes of globe translation and/or eccentric rotational axes. In addition, there was a trend toward more eccentric rotational axes in longer globes. Since the average axial length of 26.3 mm in study patients was longer than normal, the observed effects might be smaller in subjects with smaller globes. Study of larger numbers of subjects in all ranges of AL might identify subtle differences in EOM mechanical behavior associated with AL. Finally, the study population included more female subjects (72%) and was older (average age 59 years) than the typical population that might undergo strabismus surgery. Future studies with more male subjects and younger subjects would help determine if gender and age affect the stiffness of the orbital connective tissue and thus the mechanics of globe rotation.

In conclusion, irrespective of AL, the globe rotates from adduction to abduction about an axis that is medial and anterior to geometric globe center. This rotational axis location endows the LR with more leverage than the MR, a mechanical advantage that increases during abduction as the globe translates laterally and posteriorly. On average, increasing AL increases lever arm lengths for both the MR and LR, increasing their leverage but simultaneously decreasing the magnitude of predicted globe rotation per mm change in muscle length. This variation in leverage may explain the reduction in the dose-response effect of surgical EOM tendon repositioning in patients who have moderate to high myopia. Future research is required to determine the possible effects of conditions that influence orbital stiffness and globe translation on both rotational axis location and EOM leverage.

Biography

Robert A. Clark MD

Associate Clinical Professor of Ophthalmology,

Stein Eye Institute and Department of Ophthalmology University of California, Los Angeles

Robert A. Clark, MD, has been on the clinical faculty at the UCLA Stein Institute for more than 16 year. He has more than 50 publications, written a book on children’s eyecare for parents, designed new surgical instruments for pediatric surgery, and created new strabismus surgery techniques. He received an Honor Award for his contributions to the American Association for Pediatric Ophthalmology & Strabismus and is a Member of the American Ophthalmological Society.

Joseph L. Demer MD, PhD

Joseph L. Demer received his MD and PhD in Biomedical Engineering from Johns Hopkins in 1983. He is Chief of Pediatric Ophthalmology and Strabismus at UCLA Stein Eye Institute, holds the Rosenbaum Professorship, is Professor of Neurology, and chairs the EyeSTAR residency-PhD program. ARVO awarded Dr. Demer its highest honor, the Friedenwald Award for research on the extraocular muscles and orbital connective tissues. Dr. Demer has published over 280 peer-reviewed scientific papers & 42 book chapters.