Abstract
Objective:
In this study, a 2D index relying on pre-procedural computed tomography (CT) data was developed to evaluate the risk of coronary obstruction during transcatheter aortic valve replacement (TAVR) procedures.
Methods:
Anatomical measurements from pre-TAVR CT scans were collected for 28 patients out of 600 that were flagged as high risk (defined as meeting coronary artery height h < 14 mm and/or sinus of Valsalva diameter SOVd < 30 mm) for coronary obstruction. A geometric model derived from these anatomical measurements was used to predict the post-TAVR native cusp apposition relative to the coronary ostium. The distance from cusp to coronary ostium (DLC2D) was measured from the geometric model and indexed with the coronary artery diameter, d to yield a fractional obstruction measure (DLC2D/d).
Results:
23 out of 28 high risk patients successfully underwent TAVR without coronary obstruction and 1 had coronary obstruction and 4 were deemed non-TAVR candidates. DLC2D/d between the two groups was significantly different (p < 0.0018) while neither h nor SOVd were significantly different (p > 0.32).The optimal sensitivity and specificity for DLC2D/d was 85% and occurred at a cut off of 0.45. The optimal sensitivity and specificity of h and SOVd in this high risk group was only 60% and 40% respectively for a cut off h =10 mm and SOVd of 30.5 mm.
Conclusions:
The derived 2D geometric model in this study shows promising potential to identify patients with low lying coronary ostium and/or small SOVd that may be safely treated with TAVR. DLC2D/d is more predictive of obstruction or poor TAVR candidacy than h and SOVd.
Keywords: TAVR, Coronary Obstruction, Calcification, FEA, Patient-specific
Introduction
Coronary artery obstruction is a rare, yet often fatal, complication that can occur during transcatheter aortic valve (TAV) replacement (TAVR). While TAVR represents a major advancement for the treatment of patients with severe aortic stenosis, complications such as coronary obstruction can determine can candidacy, or mitigate mortality and quality of life benefits ascribed to TAVR[1–4]. As TAVR gains momentum towards Food and Drug Administration Approval (FDA) approval for the treatment of low surgical risk populations, the potential to fundamentally shift the standard of care from surgical valve replacement is becoming realizable[5, 6].
In an effort to avoid coronary obstruction during TAVR, potential TAVR candidates are assessed according to anatomical guidelines which often originate from clinical trials and device instruction for use designed primarily to avoid adverse outcomes [7]. These guidelines typically only consider coronary artery height (h) and sinus of Valsalva diameter (SOVd) (i.e. patients with h < 14 mm and/or SOVd < 30mm), and do not necessarily reflect consensus across devices or institutions[7]. Even with these guidelines however, coronary obstruction still has been reported. Perhaps more importantly, as many as 1/3 of patients that successfully received TAVR might have been excluded had these guidelines been applied [8].
Efforts towards eliminating the occurrence of coronary obstruction and other adverse outcomes during TAVR through procedural pre-planning with experimental studies and computational simulations are not in short supply. An experimental study by Hatoum et al[9] simulated coronary obstruction in a patient who had it occur during the procedure and showed that a different type of TAVs might have permitted avoidance of this event.. Many computational studies have developed finite element simulations modeling the implantation of transcatheter valves into patient specific roots to study potential adverse effects [10–15]. In one such study of 28 potential TAVR candidates, Heitkemper et. al [16] introduced a three-dimensional computational model that was 38% more effective (based on sensitivity and specificity analyses) at predicting coronary obstruction than coronary artery height, and 58% more effective than Sinus of Valsalva diameter. While these studies have identified tools to improve patient selection criteria and finally the outcomes of TAVR, their application within the field is impractical due to large volumes of patients and lengthy set-up and simulation times.
A study by Divir et. al introduced a simplistic model to evaluate the risk of coronary obstruction pre-procedurally in the context of valve-in-valve therapy [17]. The model measures the distance between a virtual transcatheter valve to each coronary ostium, called VTC, and requires only pre-TAVR CT imaging data. VTC was found to be highly predictive of coronary obstruction in a large population, though the measurement relies highly on the ability to identify the bioprosthetic surgical valves, often from their radiopaque stent posts which makes it difficult to clearly identify the limits in the pre-TAVR CT imaging [17].
The objective of this study is to introduce a simple, yet highly accurate mechanistic index that can predict which high risk patients (i.e. patients with h < 14 mm and/or SOVd < 30mm) are not actually at risk for coronary obstruction during TAVR in a native valve annulus. The model proposed allows the derived index to be readily calculated from solely pre-TAVR CT angiographic imaging and to quickly identify patients that are indeed candidates for TAVR, allowing for the highest possible number of patients to safely undergo TAVR without coronary obstruction.
1. Methods
A two-dimensional geometric models that utilizes pre-TAVR CT angiogram imaging is presented in this study – as a part of an institutional review board-approved study - and compared against the conventional guidelines. The model aims to develop a simple mechanistic index that can predict which high risk patients (i.e. patients with h < 14 mm and/or SOVd < 30 mm) are not actually at risk for coronary obstruction and are indeed candidates for TAVR pre-operatively. It should be highlighted that this model is only for patients who already satisfy a conservative risk stratification as previously described.
1.1. Study Population
The study population included all “high-risk” patients, defined by left coronary artery height (h) < 14 mm and/or sinus of Valsalva diameter (SOVd) < 30 mm, flagged from 600 aortic stenosis patients considered for TAVR at The Ohio State University Wexner Medical Center between January 2014 and September 2018. After excluding patients with bicuspid valves, prior valve replacement surgeries, and risk of coronary obstruction due to right coronary artery height or sinus of Valsalva diameter, the 105 remained in the population. Further stratification by risk resulted in 28 patients (labeled A-AB; see Table 1) being flagged as high risk for left coronary artery obstruction during TAVR and included 78.5% women; age, 80± 9 years with symptomatic severe aortic stenosis. In Figure 1, the patient population is divided by risk of coronary obstruction due to h ≤ 12, SOVd ≤ 30, h ≤ 12 and SOVd ≤ 30, or no obstruction with h >12, SOVd > 30 based on Ribeiro et. al’s analysis. We elected to interrogate left coronary obstruction only, as it is more common and consequential than obstruction of the right coronary artery [18–20]. As shown in the figure, left coronary obstruction was expected to occur for 89 % (25/28) of patients, with left SOVd in the range 26 – 36 (mm) and h in the range of 7 – 19 (mm) (Table 1).
Table 1:
List of coronary obstruction predictive parameters including currently used parameters namely coronary ostium height, sinus of Valsalva diameter; and newly proposed predictive parameters based on the 3D computational modeling and 2D geometric modeling for each patient.
| Patient | Sex | Age | Left Coronary Artery Height (mm) | Sinus of Valsava Diameter (mm) | Left Coronary Artery Diameter (mm) | Valve Diameter (mm) | Simulated TAV Expanded Diameter (mm) | DLC2D/d (1) | DLC2D/d (2) | DLC2D/d (3) | TAVR Successful? |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | Male | 88 | 7 | 36 | 5.3 | 26 | 26 | 1.5 | 0.4 | 0.4 | Yes |
| B | Female | 68 | 8 | 26 | 4.6 | 23 | 23 | 1.4 | 1.4 | 1.4 | Yes |
| C | Female | 89 | 9 | 30 | 5.5 | 23 | 23 | 1.2 | 0.4 | 0.3 | Yes |
| D | Female | 81 | 9 | 30 | 4 | 29 | 29 | 0.7 | 0.7 | 0.6 | Yes |
| E | Female | 81 | 9 | 31 | 3.1 | 29 | 29 | 1.3 | 1.3 | 1.3 | Yes |
| F | Female | 77 | 9 | 31 | 3.2 | 23 | 23 | 2.8 | 2.8 | 2.8 | Yes |
| G | Female | 84 | 9 | 31 | 4.2 | 26 | 26 | 2.3 | 2.3 | 2.3 | Yes |
| H | Female | 77 | 9 | 26 | 4.2 | 26 | 26 | 0.8 | 0.8 | 0.8 | Yes |
| I | Male | 61 | 9 | 29 | 2.6 | 26 | 26 | 1.7 | 0.5 | 0.2 | Yes |
| J | Female | 79 | 10 | 30 | 3.3 | 23 | 23 | 2.2 | 1.2 | 0.9 | Yes |
| K | Female | 83 | 10 | 30 | 2.8 | 23 | 23 | 1.5 | 1.0 | 0.7 | Yes |
| L | Female | 82 | 11 | 27 | 3.2 | 23 | 23 | 1.2 | 1.2 | 1.1 | Yes |
| M | Female | 70 | 12 | 27 | 5.4 | 23 | 23 | 0.3 | 0.3 | 0.2 | Yes |
| N | Female | 81 | 12 | 29 | 5.6 | 26 | 26 | 0.9 | 0.8 | 0.2 | Yes |
| O | Female | 74 | 12 | 33 | 4.6 | 23 | 23 | 0.8 | 0.8 | 0.7 | Yes |
| P | Female | 76 | 12 | 33 | 3.4 | 23 | 23 | 1.7 | 1.3 | 0.6 | Yes |
| Q | Male | 86 | 13 | 32 | 3.6 | 25 | 25 | 1.2 | 0.9 | 0.9 | Yes |
| R | Male | 93 | 13 | 30 | 2.8 | 23 | 23 | 1.2 | 0.6 | 0.1 | Yes |
| S | Female | 88 | 13 | 30 | 5 | 29 | 29 | 1.1 | 1.1 | 0.7 | Yes |
| T | Female | 72 | 13 | 29 | 4.9 | 26 | 26 | 1.5 | 1.2 | 0.5 | Yes |
| U | Female | 77 | 13 | 28 | 2.7 | 23 | 23 | 1.7 | 1.4 | 0.7 | Yes |
| V | Female | 91 | 19 | 28 | 3.6 | 29 | 29 | 2.0 | 2.0 | 0.8 | Yes |
| W | Female | 87 | 19 | 27 | 3.2 | 20 | 20 | 1.1 | 1.1 | 0.8 | Yes |
| X | Female | 91 | 8 | 31 | 4.6 | NA | 23 | 0.6 | 0.6 | 0.4 | Not Undertaken |
| Y | Male | 94 | 9 | 32 | 4.6 | NA | 26 | 0.7 | 0.3 | 0.3 | Not Undertaken |
| Z | Female | 75 | 9 | 28 | 5.7 | 23 | 23 | 0.1 | 0.0 | 0.3 | Not Undertaken |
| AA | Female | 62 | 11 | 29 | 4.4 | 23 | 23 | 0.9 | 0.2 | 0.2 | Not Undertaken |
| AB | Male | 80 | 12 | 37 | 5.4 | 29 | 29 | 0.6 | 0.0 | 1.2 | No |
Figure 1.
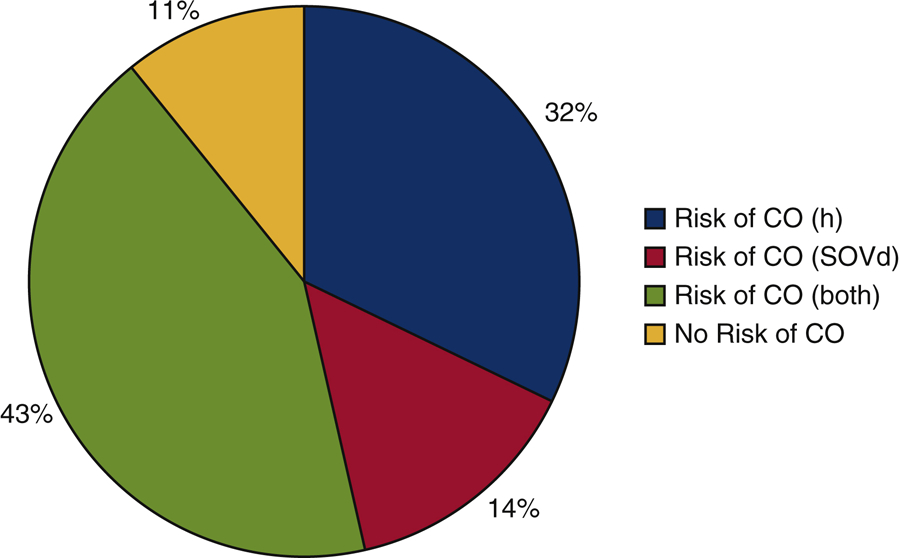
The study population divided by risk of coronary obstruction due to height (h) ≤ 12 (32%), sinus of Valsalva diameter (SOVd) ≤ 30 (14%), height (h) ≤ 12 and sinus of Valsalva diameter (SOVd) ≤ 30 (43%), or height (h) >12 and sinus of Valsalva diameter (SOVd) > 30 (11%).
With respect to the outcomes for these twenty-eight patients, a 3D computational risk assessment was performed prior to TAVR as described in Heitkemper et. al [16]. Based on this risk assessment, it was found that only five of the twenty-eight patients would likely suffer coronary obstruction. The remaining twenty-three patients went on to receive TAVR successfully. Four of the five patients likely to suffer coronary obstruction based on the modeling were not offered TAVR due to risk of obstruction. These four include two females that were referred to surgery with visual confirmation of averted coronary obstruction by the operating surgeon, and one female and one male (patients X and Y who had extremely low lying coronary ostium (8 mm and 9 mm respectively)), that were deemed not candidates for surgical aortic valve replacement due to age and received medical management. The fifth patient that was found to be likely to suffer coronary obstruction, did suffer coronary obstruction, as the risk assessment was not computed prior to TAVR.
1.2. Two-dimensional (2D) Anatomical Models
In order to correctly identify the risk of coronary obstruction within the study population, we aim to elucidate the closest possible distance of the cusp relative to the corresponding coronary ostium, called DLC2D, following a TAV stent deployment. A sketch of the idealized configuration of fully expanded cusps after TAVR is shown in (Figure 2A). Locations of two points in this 2D cross-section are noted; Pc, located on the outer tip of the cusp, and Po, representing the upper edge of the coronary ostium. With this, DLC2D can be calculated using the Pythagorean theorem Equation (1):
| (1) |
Where ∆x and ∆y are the horizontal (x-direction) and vertical distances (y-direction) between Pc and Po respectively. If the cusp is longer than the coronary artery height, ∆y is set to 0. Three different methods of estimating or modeling ∆x and ∆y were explored. In Figure 2A, the first method (DLC2D (1)) does not take into account any calcium that may be present on the cusp and the chord length (L) is the length of a chord connecting the cusp at the annulus to the point at which it intersects another cusp in the closed position. In Figure 2B, the second method (DLC2D (2)), the chord length remains the same as the first, but calcium present on the cusp is included. In Figure 2C the third method is shown, DLC2D (3). In this method, calcium present on the cusp is included and the chord length is a multiple of L, noted (Ltrue), so that Ltrue = αL, to take into account the fact that the true length of the leaflet, Ltrue when the leaflets are pushed open by the TAV stent may not be exactly equal to the chord length L. These models are purely phenomenological as opposed to the 3D model recently published [16], but carry an advantage of the relatively simple calculation without the need for complex finite element analysis.
Figure 2.
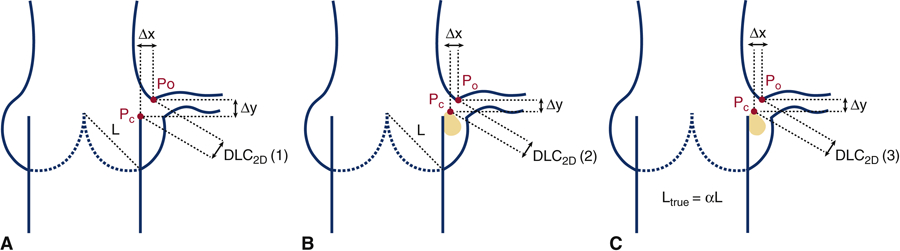
Idealized schematic representing the calculated minimum distance from a point on leaflet calcium (Pc) to a point on the upper ostium of the coronary artery (Po) following a transcatheter aortic valve replacement (TAVR) for the three cases; (A) DLC2D/d (1); (B) DLC2D/d (2); (C) DLC2D/d (3).
Each of the three models require the major anatomical features of a patients aortic root, including aortic chord length denoted L, sinus width at coronary ostium, w, coronary artery diameter, d, calcium nodule thickness on the cusp, denoted t, and coronary artery height from the aortic annulus, h to be measured from the patient’s pre-procedural CT imaging. Calcium nodules (t) were only measured if they were located on the upper half (near cusp tip) of the cusp. All the measurements were taken in the diastolic phase of the cardiac cycle. In Figure 3, an idealized 2D geometric sketch is shown depicting all parameters in one 2D view.
Figure 3.
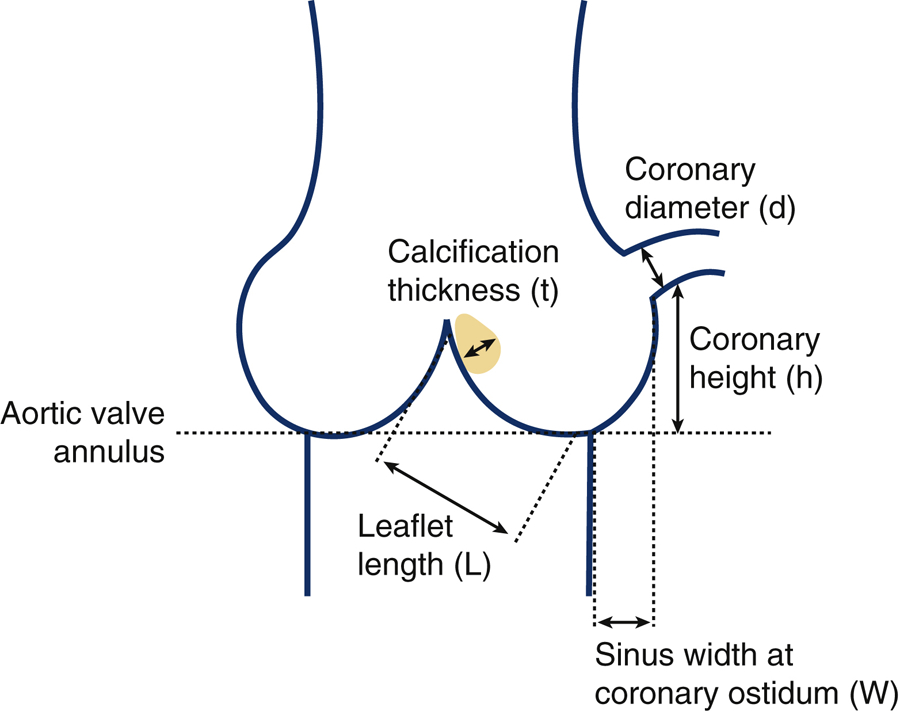
Idealized schematic representing essential aortic root measurements; Aortic left chord length (L), left sinus width at coronary ostium (w), left coronary ostium diameter (d), calcium nodule thickness on left coronary cusp (t), and height of left coronary artery from aortic annulus (h).
The following equations demonstrate how ∆x and ∆y relate to the major anatomical features measured. The first method, DLC2D (1), did not include the presence of calcium on the cusp using Equation (2) and (3), respectively,
| (2) |
| (3) |
Here, if the aortic chord length, L, is greater than the point on the upper ostia (PO), ∆y is set to 0. The second method, DLC2D (2) was identical with the exception of including calcium nodule thickness as shown in Equation (4) and (5),
| (4) |
| (5) |
Here, in addition to the possibility that aortic chord length, L, is greater than the point on the upper ostia (PO) causing ∆y to be set to 0, ∆x is set to 0 if the calcium thickness, t, is greater than the sinus width, w. The third method of relating ∆x and ∆y to the measured parameters, DLC2D (3), aims to identify possible chord lengths by approximating Lnew as some constant (α) multiplied by L. Values of α between 0.9 and 1.4 in increments of 0.1 were explored. The third method of relating ∆x and ∆y to the measured anatomical features is shown in Equation (6) and (7),
| (6) |
| (7) |
Both ∆x and ∆y can be set to 0 in this method as described in the previous methods. DLC2D was calculated for the left coronary ostium by each of the three methods for every patient, as the predicted gap in (mm) available for coronary bound blood flow. DLC2D (in mm) was normalized with respect to the corresponding coronary ostium diameter (d), to obtain DLC2D/d, which represents the dimensionless distance between the aortic cusp and coronary ostium post-TAV deployment. These indices show the available distance for blood flow towards the coronary ostium. A value greater than unity indicates that the gap available for blood flow is greater than the coronary artery diameter. A fractional value approaching zero indicates total occlusion.
1.3. Statistical Analysis
A sensitivity and specificity analysis was performed for each α in DLC2D/d(3) to identify which chord length (αL) resulted in the most accurate sensitive and specific model. The analysis revealed how many patients would identify as true positive, false positive, true negative or false negative for coronary obstruction under a range of cutoff values. The sensitivity was calculated as:
While specificity was calculated as:
as described in Lalkhen and McCluckey (2008) [21]. Following this analysis of DLC2D/d (3) at varying chord lengths (αL), a sensitivity and specificity analysis was also performed for DLC2D/d (1), DLC2D/d (2), h and SOVd. A Mann-Whitney non parametric comparison of means was performed for the most accurate model (DLC2D/d (2) based on sensitivity and specificity analyses), h, and SOVd to compare the mean parameter value between the two groups; the 23 that received TAVR successfully and the 5 patients that did not receive a successful TAVR.
2. Results:
Results that compare the ability of conventional parameters such as h and SOVd to the newly introduced parameter DLC2D/d, to differentiate which high risk patients were not actually at risk and were indeed candidates for TAVR, are presented in this section. Routine anatomical measurements of h and SOVd along with calcuated values from the 2D anatomical models, DLC2D/d (1,2,3), for the high risk study population (28 patients) are presented in Table 1. The individual anatomic measurements used to calculate the DLC2D/d (2) parameter for the two patients (Z and AB) with the most severe prediction of coronary obstruction (ie. DLC2D/d (2)=0.0) are presented in supplementary material Table S1.
Figure 4 shows sensitivity and specificity curves generated for (A) DLC2D/d (1) (Figure 2A) and (B) DLC2D/d (2) (Figure 2B). The first model (which does not include calcium on the cusp) shows the optimal crossover point is slightly above 0.80 with a sensitivity and specificity of 83%. In comparison, the optimal crossover point for the second model DLC2D/d (2) (which does include calcium on the cusp) is at 0.45 and results in a sensitivity and specificity of 85%. Figure 5 shows sensitivity and specificity curves generated for each chord length αL as described in the third model DLC2D/d (3) (Figure 2C). With respect to sensitivity and specificity of the 2D anatomical parameter DLC2D/d (3), the highest sensitivity and specificity is found for α = 1, which is identical to the model DLC2D/d (2). Sensitivity is 29% at a value of 0.0 and increases to 100% at a value of 0.8. The specificity drops from 100% at a value of 0.2 to 57% at a value of 1.0. The optimal crossover point is slightly above 0.60 with a sensitivity and specificity of 85%. In comparison, the optimal crossover point for α = 0.9 results in a sensitivity and specificity of 70% and 65% respectively and for α = 1.1, the sensitivity and specificity at the optimal crossover point of 78%. For α = 1, there is a range of DLC2D/d (3) from 0.40 to 0.60 for which the sensitivity and specificity exceed 80%. For any ratio of DLC2D/d (2) ≥ 0.65, no coronary obstruction is expected to occur during TAVR.
Figure 4.
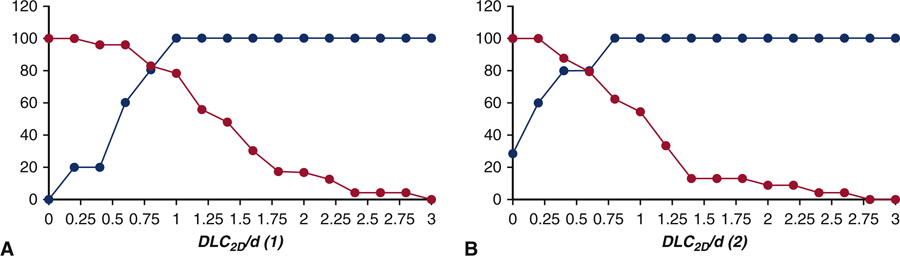
Sensitivity and specificity of (A) DLC2D/d (1) (B) DLC2D/d (2) to predict coronary obstruction for high risk patients with height (h) < 14 mm and/or sinus of Valsalva diameter (SOVd) < 30 mm.
Figure 5.
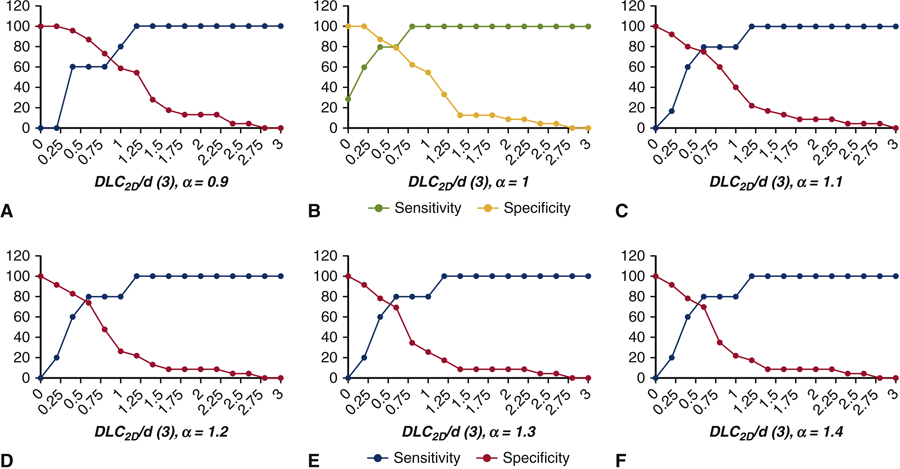
Sensitivity and specificity of DLC2D/d (3) to predict coronary obstruction for high risk patients with height (h) < 14 mm and/or sinus of Valsalva diameter SOVd < 30 mm for varying α; (A) α = 0.9 (B) α = 1 (C) α = 1.1 (D) α = 1.2 (E) α = 1.3 and (F) α = 1.4.
Comparison to current guidelines
Box-and whisker plots of the parameter values for those high risk patients who successfully received TAVR without coronary obstruction are compared to those who did not receive TAVR successfully in Figure 6. The means for these two groups were compared using a Mann-Whitney non-parametric test, and a significant difference between the two groups was found for the DLC2D/d (2) parameter, with p < 0.0018. Neither h nor SOVd was significantly different between the two groups with p = 0.35238 and p = 0.32218 respectively. Figure 6D shows the parameter values computed from the 3D computational model presented in Heitkemper et. al [16], in which a significant difference between the two groups was also reported.
Figure 6.
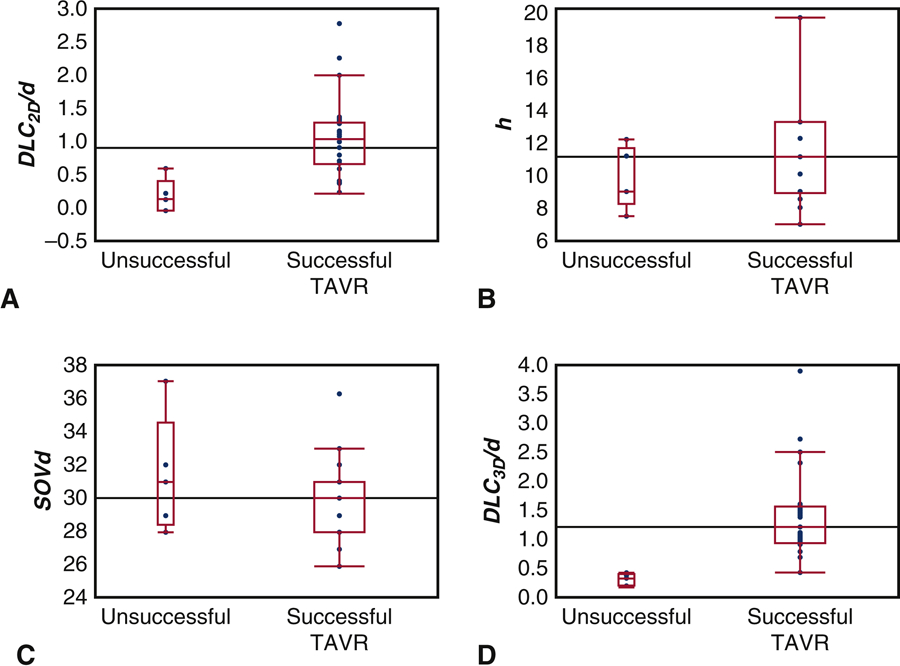
Comparative box and whisker plots for those who successfully received transcatheter aortic valve replacement (TAVR) and those who did not for (A) DLC2D/d (2) (B) height (h) (C) sinus of Valsalva diameter (SOVd) (D) DLC/d. Upper and lower borders of the box represent the upper and lower quartiles, the middle horizontal line represents the median, and the upper and lower whiskers represent the maximum and minimum values of non-outliers. Outliers are represented by single dots.
Figure 7 shows sensitivity and specificity curves generated for (A) DLC2D/d (2) (B) DLC2D/d (2) for the entire population considered for TAVR (C) h (D) SOVd and (E) DLC/d computed from the 3D computational model presented in Heitkemper et. al [16]. The optimal crossover point for the second model in the high risk study population, DLC2D/d (2), is at 0.45 and results in a sensitivity and specificity of 85%. At DLC2D/d (2) = 0.6, the parameter is 100% sensitive which would result in an expectation that 10 of the 28 patients (36%) would have coronary obstruction. In the entire population considered for TAVR, the same model has an optimal sensitivity and specificity of 72% at DLC2D/d (2) equal to 1. The sensitivity of h increases steadily from 0% at an h cutoff of 7 mm to a 100% sensitivity at h cutoff at 12 mm. Specificity of h on the other hand drops steadily from 100% at 7mm to 0% at a cutoff of 19 mm. The crossover point for sensitivity and specificity for h as an optimal predictor of coronary obstruction was at h = 10mm with approximately 60% sensitivity and specificity. At h = 12 mm, the parameter is 100% sensitive which would result in an expectation that 21 of the 28 patients (75%) would have coronary obstruction. The sensitivity and specificity of SOVd as an independent predictor of unsuccessful TAVR is shown in Figure 7C. The sensitivity increases from 0% at SOVd of 28mm to 100% at 38mm. Specificity drops from 100% at 26mm to 0% at 38mm. The optimal crossover point occurs approximately at 30.5 mm with a sensitivity and specificity of 40%. At SOVd = 38 mm, the parameter is 100% sensitive which would result in an expectation that all 28 patients (100%) would have coronary obstruction. With respect to sensitivity and specificity of the 3D computational parameter DLC/d (Figure 7D), the sensitivity is 0% at a value of 0.2 and increases to 100% at a value of 0.45. The specificity drops from 100% at a value of 0.4 to 66% at a value of 1.0. The optimal crossover point is slightly below 0.45 with a sensitivity and specificity of 96% [16]. At DLC = 0.45, the parameter is 100% sensitive which would result in an expectation that only 6 of the 28 patients (21%) would have coronary obstruction.
Figure 7.
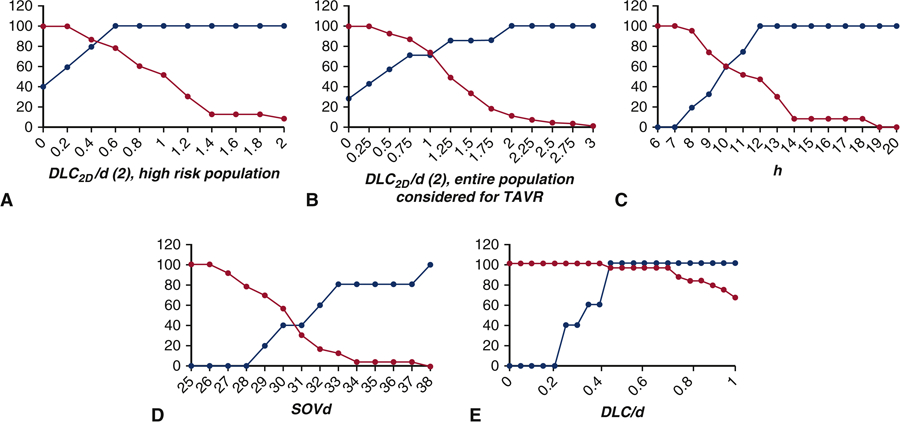
Sensitivity and specificity of (A) DLC2D /d (2) (B) DLC2D/d (2) for the entire population considered for TAVR (C) height(h) (D) sinus of Valsalva diameter (SOVd) and (E) DLC/d to predict coronary obstruction for high risk patients with height (h) < 14 mm and/or sinus of Valsalva diameter (SOVd) < 30 mm.
3. Discussion
Risk of coronary obstruction during TAVR assessed by geometrical factors of patient aortic root geometry, namely h and SOVd, continues to anatomically exclude some patients from receiving the life-saving procedure [8, 22–26]. This study shows that these geometrical factors significantly reduce the number of patients who might have safely undergone TAVR without coronary obstruction and introduces a simple method for the investigation of coronary obstruction risk in patients with severe aortic stenosis prior to TAVR.
The novel method utilizes pre-TAVR CT imaging and coronary obstruction risk can be computed in just minutes. The current guidelines for high risk of coronary obstruction include SOVd less than 30 mm [27] and coronary ostium height (h) less than 12 (mm) [28, 29]. However, these guidelines are not consistently recognized throughout US hospitals. Individual transcatheter aortic valve manufacturers impose their own guidelines, for example, Medtronic suggest that SOVd of ≥ 27 mm and ≥ 29 mm should be included for the 26-mm and 29-mm Evolut R & PRO respectively. Similar to the SOVd guideline, coronary height h ≥14 is recommended by Medtronic. The latter guideline would exclude all but two of the patients in this study population, many of whom safely underwent TAVR without coronary obstruction.
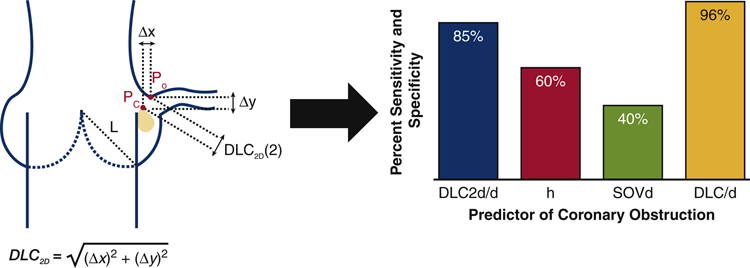
In addition, the patient specific 2D predictive model, DLC2D/d (2), captures a much more accurate representation of the TAVR procedure and would capture the final configuration of TAV stent along with native cusp and aortic wall precisely. Though models were similar, DLC2D/d (1) and DLC2D/d (3) at all α ≠ 1 had lower sensitivity and specificity in the prediction of coronary obstruction. DLC2D/d (1)’s suboptimal prediction of coronary obstruction risk suggests that the evaluation of the presence of calcification on the leaflet is necessary to accurately screen for coronary obstruction risk. Likewise, the suboptimal nature of of DLC2D/d (3) at all α ≠ 1 to be predictive of coronary obstruction risk suggests that an accurate approximation of leaflet length is also necessary. Based on our findings, DLC2D/d (2) (DLC2D/d (3) at α =1) is the only model that can accurately predict risk of coronary obstruction in patients who have been flagged as higher risk for coronary obstruction (h < 14 mm and/or SOVd < 30 mm). Those patients who have DLC2D/d(2) ≥ 0.7 should be considered as patients who are not actually high risk for left coronary obstruction. Patients who have DLC2D/d (2) < 0.7 are at severe risk of coronary obstruction and TAVR should not be attempted in these patients. In patients that have not been flagged as at risk (h < 14 mm and/or SOVd < 30 mm), the sensitivity and specificity of DLC2D/d (2) drops to 72% suggesting a reduced ability to predict obstruction risk alone, without the prior stratification of risk. An idealized schematic representing the simple 2D anatomical model, DLC /d (2) is shown in Figure 8, along with the optimal percent sensitivity and specificity of the 2D model in comparison to the current guidelines, h and SOVd, and a previous computational study DLC/d to predict coronary obstruction for high risk patients with height (h) < 14 mm and/or sinus of Valsalva diameter (SOVd) < 30 mm. The proposed 2D predictive model, in conjunction with the conventional risk stratification, allows for more patients to be accurately screened for coronary obstruction prior to the TAVR procedure and can be computed in a fraction of the time of more complex computational models. However, due to the lower sensitivity and specificity of the 2D model compared to the 3D model, the 2D model should not be used independently and instead could serve as a filter to determine which patients require the more accurate 3D model described in Heitkemper et al [16] to predict risk of coronary obstruction.
Figure 8.
(Graphical abstract) Idealized schematic representing the simple 2D anatomical model used to predict risk of coronary obstruction during transcatheter aortic valve replacement, DLC2D/d, which is the calculated minimum distance from a point on leaflet calcium (Pc) to a point on the upper ostium of the coronary artery (Po). The optimal percent sensitivity and specificity of the 2D model, DLC2D/d, is compared to the current guidelines, height (h) and sinus of Valsalva diameter (SOVd), and a previous computational study DLC/d to predict coronary obstruction for high risk patients with height (h) < 14 mm and/or sinus of Valsalva diameter (SOVd) < 30 mm.
5. Limitations
In this study we did not account for the possibility of coronary obstruction as a consequence of valve mal-positioning (supra-annular). Additionally, right coronary obstruction is not evaluated, since obstruction of right coronary is much less prevalent compared to left coronary [18–20]. However, the 2D model is likely applicable to right coronary artery for pre-operative risk assessment of coronary obstruction. Another limitation of the study is the small number of cases evaluated for coronary obstruction, which is due to its relatively rare occurrence. Although we identified likely coronary obstruction among patients deemed prohibitive risk and referred for SAVR, we did not routinely perform this maneuver among patients at no risk for coronary obstruction. Accordingly, the specificity of this exercise for coronary obstruction has not been established. Finally, the 2D model does not account for potential expansion of the native annulus from the radial force exerted by TAV implantation. This could impact the width, w, in equation (4) by under-estimating the true width available for coronary flow post expansion. Addressing this within a simplified mathematical model is not straight forward and may be better accounted for with 3D modeling.
6. Conclusion
A simple and accurate model to screen patients for possible coronary obstruction during TAVR was successfully derived in this study. The parameters involved in the evaluation of the index are obtained from the anatomical measurements readily calculated from current pre-TAVR CT angiographic imaging. While neither h nor SOVd is predictive of coronary obstruction when considering high risk patients characterized as h < 14 mm and/or SOVd < 30 mm, a new parameter DLC2D/d (2) is capable of predicting coronary obstruction for the same high risk group with a superior sensitivity and specificity. These findings shed light on a rare but significant potential complication during TAVR, and could assist heart teams in decision-making process prior to the TAVR procedure.
Supplementary Material
Table S1. Detailed calculations of DLC2D/d (2) for patients Z and AB, who demonstrate the highest possible predicted risk of coronary obstruction with DLC2D/d (2) = 0.0.
Video 1: Article Summary.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures:
Dr. Dasi and Megan Heitkemper report having two patents filed on novel polymeric heart valves. Dr. Dasi has a patent filed on 3D computational modeling for transcatheter aortic valve replacement, vortex generators and omni/superhydrophobic surfaces. No other conflicts were reported.
References:
- 1.Rodés-Cabau J, Transcatheter aortic valve implantation: current and future approaches. Nature Reviews Cardiology, 2012. 9(1): p. 15. [DOI] [PubMed] [Google Scholar]
- 2.Dasi LP, et al. , On the Mechanics of Transcatheter Aortic Valve Replacement. Annals of Biomedical Engineering, 2016: p. 1–22. [DOI] [PMC free article] [PubMed]
- 3.Dvir D, et al. , Coronary Obstruction in Transcatheter Aortic Valve-in-Valve Implantation. Preprocedural Evaluation, Device Selection, Protection, and Treatment, 2015. 8(1). [DOI] [PubMed] [Google Scholar]
- 4.Gurvitch R, et al. , Transcatheter aortic valve implantation: lessons from the learning curve of the first 270 high-risk patients. Catheterization and cardiovascular interventions: official journal of the Society for Cardiac Angiography & Interventions, 2011. 78(7): p. 977–984. [DOI] [PubMed] [Google Scholar]
- 5.Popma JJ, et al. , Transcatheter Aortic-Valve Replacement with a Self-Expanding Valve in Low-Risk Patients. New England Journal of Medicine. 0(0): p. null. [DOI] [PubMed] [Google Scholar]
- 6.Mack MJ, et al. , Transcatheter Aortic-Valve Replacement with a Balloon-Expandable Valve in Low-Risk Patients. New England Journal of Medicine. 0(0): p. null. [DOI] [PubMed] [Google Scholar]
- 7.Ribeiro HB, et al. , Coronary Obstruction Following Transcatheter Aortic Valve Implantation: A Systematic Review. JACC: Cardiovascular Interventions, 2013. 6(5): p. 452–461. [DOI] [PubMed] [Google Scholar]
- 8.Ribeiro HB, et al. , Predictive factors, management, and clinical outcomes of coronary obstruction following transcatheter aortic valve implantation: insights from a large multicenter registry. J Am Coll Cardiol, 2013. 62(17): p. 1552–62. [DOI] [PubMed] [Google Scholar]
- 9.Hatoum H, et al. , A Case Study on Implantation Strategies to Mitigate Coronary Obstruction in a Patient Receiving Transcatheter Aortic Valve Replacement. Journal of Biomechanics, 2019. [DOI] [PMC free article] [PubMed]
- 10.Finotello A, Morganti S, and Auricchio F, Finite element analysis of TAVI: Impact of native aortic root computational modeling strategies on simulation outcomes. Medical Engineering & Physics, 2017. 47: p. 2–12. [DOI] [PubMed] [Google Scholar]
- 11.Wang Q, Sirois E, and Sun W, Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. Journal of biomechanics, 2012. 45(11): p. 1965–1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang Q, et al. , Simulations of transcatheter aortic valve implantation: implications for aortic root rupture. Biomechanics and Modeling in Mechanobiology, 2015. 14(1): p. 29–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Auricchio F, et al. , Simulation of transcatheter aortic valve implantation: a patient-specific finite element approach. Computer Methods in Biomechanics and Biomedical Engineering, 2014. 17(12): p. 1347–1357. [DOI] [PubMed] [Google Scholar]
- 14.Capelli C, et al. , Patient-specific simulations of transcatheter aortic valve stent implantation. Medical & Biological Engineering & Computing, 2012. 50(2): p. 183–192. [DOI] [PubMed] [Google Scholar]
- 15.Bianchi M, et al. , Effect of Balloon-Expandable Transcatheter Aortic Valve Replacement Positioning: A Patient-Specific Numerical Model. Artificial Organs, 2016. 40(12): p. E292–E304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Heitkemper M, et al. , Modeling Risk of Coronary Obstruction during Transcatheter Aortic Valve Replacement. The Journal of thoracic and cardiovascular surgery, 2019. [DOI] [PMC free article] [PubMed]
- 17.Dvir D, et al. , Coronary obstruction in transcatheter aortic valve-in-valve implantation. Circulation: Cardiovascular Interventions, 2015. 8(1): p. e002079. [DOI] [PubMed] [Google Scholar]
- 18.Dağdelen S, Karabulut H, and Alhan C, Acute left main coronary artery occlusion following TAVI and emergency solution. Anadolu kardiyoloji dergisi: AKD= the Anatolian journal of cardiology, 2011. 11(8): p. 747. [DOI] [PubMed] [Google Scholar]
- 19.Gökdeniz T, et al. , Concomitant complete atrioventricular block and left main coronary artery occlusion during transcatheter aortic valve implantation. Heart, Lung and Circulation, 2013. 22(12): p. 1048–1050. [DOI] [PubMed] [Google Scholar]
- 20.Mizote I, Conradi L, and Schäfer U, A case of anomalous left coronary artery obstruction caused by lotus valve implantation. Catheterization and Cardiovascular Interventions, 2016. [DOI] [PubMed]
- 21.Lalkhen AG and McCluskey A, Clinical tests: sensitivity and specificity. Continuing Education in Anaesthesia Critical Care & Pain, 2008. 8(6): p. 221–223. [Google Scholar]
- 22.Akhtar M, et al. , Aortic root morphology in patients undergoing percutaneous aortic valve replacement: evidence of aortic root remodeling. The Journal of thoracic and cardiovascular surgery, 2009. 137(4): p. 950–956. [DOI] [PubMed] [Google Scholar]
- 23.Apfaltrer P, et al. , Aortoiliac CT angiography for planning transcutaneous aortic valve implantation: aortic root anatomy and frequency of clinically significant incidental findings. American Journal of Roentgenology, 2012. 198(4): p. 939–945. [DOI] [PubMed] [Google Scholar]
- 24.Binder RK, et al. , The impact of integration of a multidetector computed tomography annulus area sizing algorithm on outcomes of transcatheter aortic valve replacement: a prospective, multicenter, controlled trial. Journal of the American College of Cardiology, 2013. 62(5): p. 431–438. [DOI] [PubMed] [Google Scholar]
- 25.Tops LF, et al. , Noninvasive evaluation of the aortic root with multislice computed tomography: implications for transcatheter aortic valve replacement. JACC: Cardiovascular Imaging, 2008. 1(3): p. 321–330. [DOI] [PubMed] [Google Scholar]
- 26.Yamamoto M, et al. , Impact of preparatory coronary protection in patients at high anatomical risk of acute coronary obstruction during transcatheter aortic valve implantation. International journal of cardiology, 2016. 217: p. 58–63. [DOI] [PubMed] [Google Scholar]
- 27.Ribeiro HB, et al. , Predictive factors, management, and clinical outcomes of coronary obstruction following transcatheter aortic valve implantation: insights from a large multicenter registry. Journal of the American College of Cardiology, 2013. 62(17): p. 1552–1562. [DOI] [PubMed] [Google Scholar]
- 28.Achenbach S, et al. , SCCT expert consensus document on computed tomography imaging before transcatheter aortic valve implantation (TAVI)/transcatheter aortic valve replacement (TAVR). Journal of Cardiovascular Computed Tomography, 2012. 6(6): p. 366–380. [DOI] [PubMed] [Google Scholar]
- 29.Holmes DR Jr, et al. , 2012 ACCF/AATS/SCAI/STS Expert Consensus Document on Transcatheter Aortic Valve Replacement. Journal of the American College of Cardiology, 2012. 59(13): p. 1200–1254. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Detailed calculations of DLC2D/d (2) for patients Z and AB, who demonstrate the highest possible predicted risk of coronary obstruction with DLC2D/d (2) = 0.0.
Video 1: Article Summary.