Metals and non-metals in the periodic table

Abstract

The demarcation of the chemical elements into metals and non-metals dates back to the dawn of Dmitri Mendeleev's construction of the periodic table; it still represents the cornerstone of our view of modern chemistry. In this contribution, a particular emphasis will be attached to the question ‘Why do the chemical elements of the periodic table exist either as metals or non-metals under ambient conditions?’ This is perhaps most apparent in the p-block of the periodic table where one sees an almost-diagonal line separating metals and non-metals. The first searching, quantum-mechanical considerations of this question were put forward by Hund in 1934. Interestingly, the very first discussion of the problem—in fact, a pre-quantum-mechanical approach—was made earlier, by Goldhammer in 1913 and Herzfeld in 1927. Their simple rationalization, in terms of atomic properties which confer metallic or non-metallic status to elements across the periodic table, leads to what is commonly called the Goldhammer–Herzfeld criterion for metallization. For a variety of undoubtedly complex reasons, the Goldhammer–Herzfeld theory lay dormant for close to half a century. However, since that time the criterion has been repeatedly applied, with great success, to many systems and materials exhibiting non-metal to metal transitions in order to predict, and understand, the precise conditions for metallization. Here, we review the application of Goldhammer–Herzfeld theory to the question of the metallic versus non-metallic status of chemical elements within the periodic system. A link between that theory and the work of Sir Nevill Mott on the metal-non-metal transition is also highlighted. The application of the ‘simple’, but highly effective Goldhammer–Herzfeld and Mott criteria, reveal when a chemical element of the periodic table will behave as a metal, and when it will behave as a non-metal. The success of these different, but converging approaches, lends weight to the idea of a simple, universal criterion for rationalizing the instantly-recognizable structure of the periodic table where …the metals are here, the non-metals are there … The challenge of the metallic and non-metallic states of oxides is also briefly introduced.

This article is part of the theme issue ‘Mendeleev and the periodic table’.

1. Introduction; ‘…the metals are here, the non-metals are there…’

On 4 June 1889, Dmitri Mendeleev delivered the Faraday Lecture before the Fellows of the Chemical Society of Great Britain; his lecture was entitled The Periodic Law of the Chemical Elements, [1] Mendeleev noted

…While science is pursuing a steady onward movement, it is convenient from time to time to cast a glance back on the route already traversed, and especially to consider the new conceptions which aim at discovering the general meaning of the stock of facts accumulated from day to day in our laboratories.

In that spirit, the present contribution is an attempt to look back and review our understanding of the development of the periodic system of the chemical elements, with a particular emphasis on the question as to why the chemical elements exist either as metals or non-metals under ambient conditions on Earth. In his 1905 treatise, ‘The Principles of Chemistry’ [2] Mendeleev set out one of the early—but recurring—challenges of attempting to define metals and non-metals in the periodic table.

Many elements, although not all of them, have the peculiar lustre, opacity, malleability, and the high thermal and electrical conductivities peculiar to the metals. … But elements are far from all being metals. Those which do not possess the physical properties of metals are called non-metals. These two classes of elements are clearly distinguished in certain definite examples, but in some cases the distinction is not clear, and hence cannot serve as a basis for the exact division of the elements into two groups

This issue of the intermediate nature of certain elements between the two groups—metals and non-metals—raised by Mendeleev where …the distinction is not clear …, of course, relates to the strange status in the p-block elements (p-block elements are unified by the fact that their outermost electrons are in the p orbital; the p-block is on the right side of the periodic table and includes elements from column 13 to column 18. Helium, which is in the top of column 18, is not included in the p-block) as ‘metalloids’, meaning elements with … metal likeness, indicating they resemble metals only somewhat. As with many general terms, the word metal is used in different ways, particularly when trying to understand the issue of elements straddling the demarcation line in (what we now term) the p-block of the periodic table (figure 1).

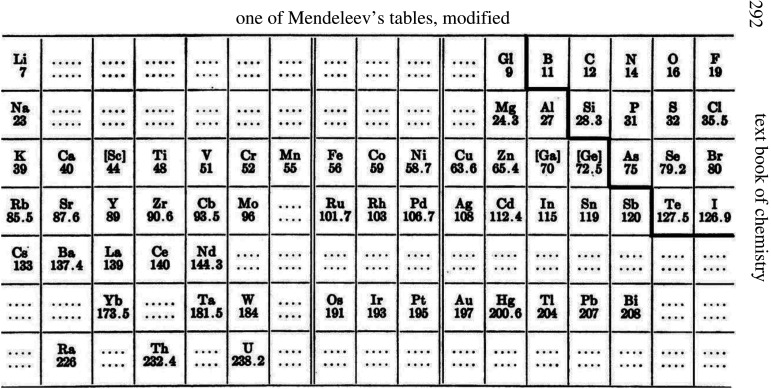
Figure 1.

One of Mendeleev's early periodic tables (modified). Taken from Smith Alexander, Intermediate Text Book of Chemistry. New York, 1919 [3]. Note the (now familiar) diagonal demarcation separating metals from non-metals in what we now term the p-block of the periodic table.

Mendeleev's papers of 1869 [4,5], in addition to his proposed periodic table of the elements, contained suggestions for three other possible representations. It is interesting to note that, in a footnote to this paper, Mendeleev discussed a representation of the periodic system that he said would probably not be a convenient one. The modern form of that very table (figure 1) is particularly popular today! For our present discussion, that form most clearly reflects the metal-non-metal transition as one proceeds across the periodic system. Thus, elemental properties in the p-block change from non-metallic to metallic from top to bottom in vertical groups, and from metallic to non-metallic behaviour from left to right in a horizontal group.

In 1934, Hund [6,7] posed the intriguing question as to why the element Na is metallic, but the element Cl a gas or a non-metallic solid, commenting that, of their characteristic elemental properties, Electrical conductivity as noteworthy . In this early quantum-mechanical description—and a prescient one at that—Hund noted the energy levels of the individual electrons either …form a continuum of states… (thus, metals) or have … a finite energy gap exactly at the place up to which the states are occupied (thus, non-metals) (figure 2).

Figure 2.

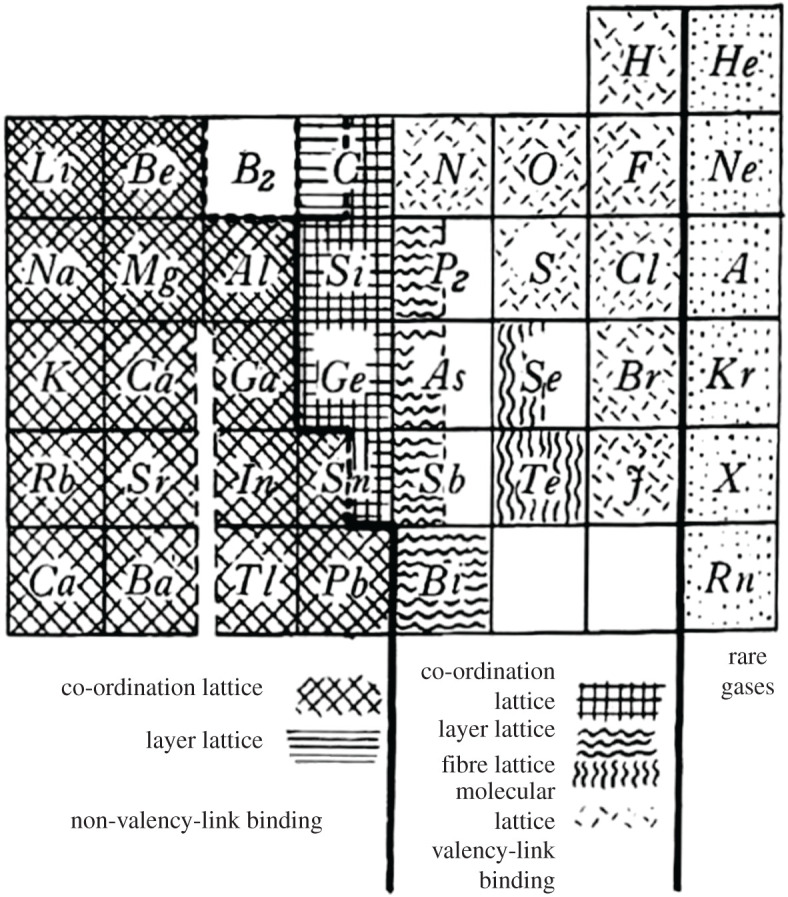
F. Hund's different forms of binding in the periodic table of the chemical elements (taken from [6]).

Although a powerful and important advance using the (developing) quantum-mechanical theory of solids, Hund's approach did not easily provide a ready explanation of the demarcation occurring in the p-block of the periodic table into metals and non-metals and the unique c-status of elements straddling the dividing line between what appeared to be two canonical extremes—the metallic and non-metallic states of the elements.

Landau & Zeldovitch [8] and Mott [9], pointed out that the metallic and non-metallic states of matter can only be distinguished unambiguously at the absolute zero of temperature. Thus, at T = 0 K, electrons in elements and substances are either localized or itinerant; the electrical resistivity of a metal is therefore either finite (as a conducting element), or zero (as in a superconducting element, such as Li, Be, Rh, W, and so on [10]), whereas in non-metals it tends to infinity. Of course, at temperatures above absolute zero, this distinction becomes ambiguous, and challenging.

When searching for a complete definition of a metallic or non-metallic chemical element, we turn to the writing and insights of Sir Nevill Mott. In a letter to one of the authors, and in one revealing sentence, Mott surely established the operational definition of a metal and a non-metal (figure 3).

Figure 3.

Taken from a letter to P. P. Edwards from Sir Nevill Mott, 9 May 1996. In answer to the question, ‘What is a metal?’ Sir Nevill Mott notes at T = 0 … Then a metal conducts, & a non-metal doesn't. [11].

Armed with Mott's perceptive and disarming definition—completely rigorous, but of course derived from a ‘Gedanken’ (Thought) experiment …at T = 0 K—we have sought to identify the chemical elements of the periodic table either as metals or as non-metals to help our discussion of the origins of the differences between these two canonical states of matter.

One can obviously understand why it is somewhat difficult to apply Mott's rigorous and unequivocal definition centred on the electrical conductivities of the chemical elements at T = 0 K! However, even armed with room-temperature conductivity data, one can surely easily identify the broad features of the periodic table for which the appellation of metal or non-metal is appropriate.

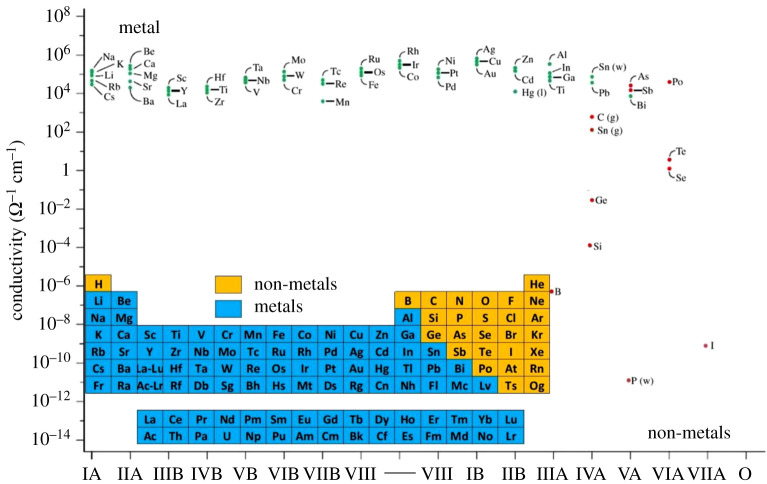
Focussing on ambient conditions of room temperature and room pressure, the differences in conductivities between a metallic element and a non-metallic element of the periodic table are striking. For example, the measured electrical conductivities at room temperature (figure 4) range from values of about 10⁵ (Ω cm)⁻¹ for the ‘simple’ Group IA metals, to approximately 10⁻¹⁸ (Ω cm)⁻¹ for non-metallic elemental sulfur. This range of approximately 10²³ in conductivities has been declared to be the widest range of any known physical property of the elements.

Figure 4.

Room temperature and room pressure electrical conductivities for chemical elements of the periodic table. The inset represents one conventional designation of elements as metals and non-metals based on elemental properties at room temperature and atmospheric pressure, green dots as metals and red dots as non-metals (modified from [11]). (Online version in colour.)

As one can see from figure 4, the chemical elements definitely favour the metallic state: over two-thirds of the elements are metals under ambient conditions.

It is interesting that some materials with different elements crystallize in forms showing different material properties, even if they are composed of the same element. For example, white tin (β-tin) a metal with a body-centred tetragonal crystal structure, density of 7.265 g cm⁻³, showed higher conductivity (around 10⁵ Ω⁻¹ cm⁻¹), however, the gray tin (α-tin) has no metallic properties at all, gray tin with a face-centred diamond-cubic crystal structure, density of 5.769 g cm⁻³, with lower conductivity (around 10² Ω⁻¹cm⁻¹). This is because the gray tin atoms form a covalent structure in which electrons cannot move freely.

And of course, this is where the wonder of the periodic table now catalyses a journey for chemistry teachers around the world, sharing that wonder with their students. As N. Kaiser has so succinctly pronounced:

‘That's why to start with we focus mainly on the gross structure (of the periodic table)—the metals are here, the non-metals are there, and so on …’ [12]

2. On atomic properties which make an element a metal

Sir Alan Cottrell [13] surely penned the complete descriptor of our understanding of a metal in this short, penetrating sentence in his classic text ‘Introduction to the Modern Theory of Metals'; Cottrell noted:

Metals contain free electrons.

The critical question, therefore, as to Why are electrons free in a metal? was raised by Bethe [14] and dates back to the very beginnings of solid-state physics. Remarkably, as noted earlier, the first quantitative attempts to explain this challenging and fundamental scientific enquiry were made in the pre-quantum mechanics era by Goldhammer in 1913 [15] and Herzfeld in 1927 [16]. Their rationalization, in terms of atomic properties which confer metallic or non-metallic status upon a chemical element of the periodic table, has led to what is known as the Goldhammer–Herzfeld criterion for metallization. This criterion sets out the necessary conditions for the occurrence of the metallic and the non-metallic status of the chemical elements.

In Herzfeld's classical approach, the isolated atom is modelled as a Lorentz oscillator. Herzfeld noted that an atom's electron cloud will be polarized by the other 10²³ atoms in an element. He showed that as a result of such mutual polarization effects, the valence electrons of an atom will become dissociated or detached from their parent atom at a particular, critical elemental (atom) density since the associated Hooke's Law force within the individual oscillator vanishes. In other words, at that critical density, the frequency of an individual atom oscillator approaches zero. At, and above, such a critical density of atoms, the valence electrons are, therefore, set free and the element now behaves as a metallic conductor. This allows for some deep insights into Bethe's enquiry.

In a 1927 paper entitled On Atomic Properties Which Make an Element a Metal, Herzfeld predicted that an isolated atom in a dense elemental assembly would become a metallic conductor when the molar volume (V) at a particular elemental density becomes less than, or equal to, that of its gas-phase atomic molar refractivity (R)

$$R\le \frac{4\pi \alpha }{3}{N}_{\text{A}},$$ 2.1

where N_A is the Avogadro number and α is the electronic polarizability of the isolated atom of a particular element.

The Goldhammer–Herzfeld approach is based on what is known as a polarization or dielectric catastrophe. The idea is that the dielectric constant, ϵ, of the condensed phase element will diverge to infinity as the non-metal-to-metal transition density is approached from the non-metallic side.

This can be viewed in the following way. The dielectric behaviour of a non-metallic system is embodied in the Clausius–Mossotti (CM) relation which takes the form;

$$\frac{n^2-1}{n^2+2}=\frac{\epsilon -1}{\epsilon +2}=\frac{4\pi \alpha }{3V}{N}_{\text{A}}=\frac{R}{V},$$ 2.2

where n is the index of refraction, and ϵ is the dielectric constant.

The Herzfeld criterion predicts that an element or material will show metallic behaviour if the molar volume becomes equal to, or reduced below the value of R. In terms of equation (2.2), when R/V = 1, we have (ε − 1) = (ε + 2), a condition which can only be fulfilled when ε is infinite. This represents the situation whereby electrons are no longer bound to individual atoms in the element, and now become free—a metallic conductor of electricity thereby results [15,16].

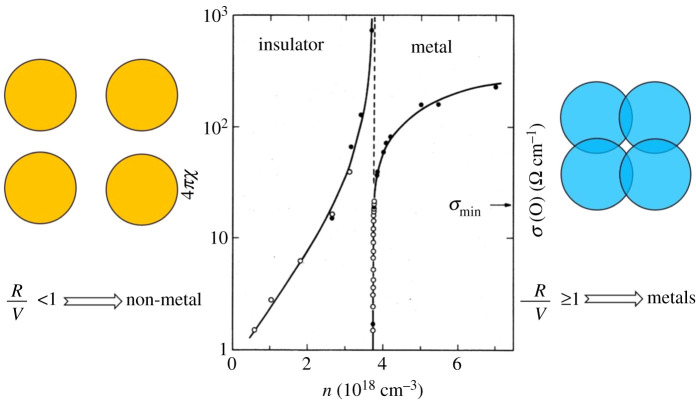
This is the essence of the Goldhammer–Herzfeld metallization/polarization catastrophe criterion. It signals the conditions for the wholesale freeing of valence electrons as the element, system, material or substance undergoes a transition to the metallic state. A spectacular example of this dielectric catastrophe in the transition to the metallic state is given in figure 5 for the case of P doped into the semiconductor Si at, remarkably, millikelvin temperatures—an experimental system attempting to get close to Mott's condition of a T = 0 K for the demarcation between a metal and a non-metal (the latter of course, equivalently, an insulator) [18].

Figure 5.

A representation of the Goldhammer–Herzfeld model and metallization criterion (Edwards PP. Private communication, James S Schilling, 2019) [17] and the experimental dielectric catastrophe (left-hand curve) occurring at the transition to the metallic state in P doped Si single crystals at millikelvin temperatures. The corresponding evolution of the ‘zero-temperature’ electrical conductivity on the same samples across the metal-non-metal (insulator) transition is also shown (right-hand curve) [18]. (Online version in colour.)

A different and hopefully illustrative representation of this engaging theory can be made by considering the model of a classical atom as a point positive charge surrounded by a spherically symmetric, negatively charged electron cloud of constant density extending to a radius r_m. This is the model whereby the atom is represented as a perfectly conducting charged sphere. It can be shown from electrostatics that its molar electronic polarizability is then;

$$\alpha =r_m^3,$$ 2.3

and its corresponding molar refractivity is therefore

$$R=\frac{4\pi r_m^3}{3}{N}_{\text{A}}.$$ 2.4

R/N_A represents the volume occupied by the isolated atom.

Goldhammer and Herzfeld proposed that metallization occurs when the available or molar volume, V, becomes equal to, or less, than R, the volume occupied by the atoms themselves.

At such a critical density when V = R, the system of individual (perfectly) conducting spheres coalesce to become one large, macroscopic electrical conductor (figure 5). An interesting commentary from Linus Pauling, of the Herzfeld view is shown in the letter in figure 6.

Figure 6.

Linus Pauling also offers his visionary insights and remarkable intuition into the success of the Herzfeld criterion in rationalizing the occurrence of metallic character in the periodic table of the chemical elements. Pauling also establishes the direct link with his concept of the metallic orbital. Photograph courtesy of California Institute of Technology [11] (Edwards PP, Sienko MJ. 1983 Private communication, Linus Pauling).

The non-analytic behaviour of the zero-temperature conductivity in the metal and the divergence of the zero-temperature dielectric susceptibility in the insulator (non-metal) probe the nature of the metal-non-metal transition in random system. Figure 5 shows the divergence of the T = 0 K donor dielectric susceptibility 4πx in the insulator (left-hand curve) and the T = 0 K conductivity σ_min in the metal [19] (right-hand curve) as a function of phosphorus donor density n in the P doped Si material. These together characterize the metal-insulator transition in a disordered system and indicate a tendency of 4πx to diverge with a critical exponent assumed to be related to the divergence of the localization length.

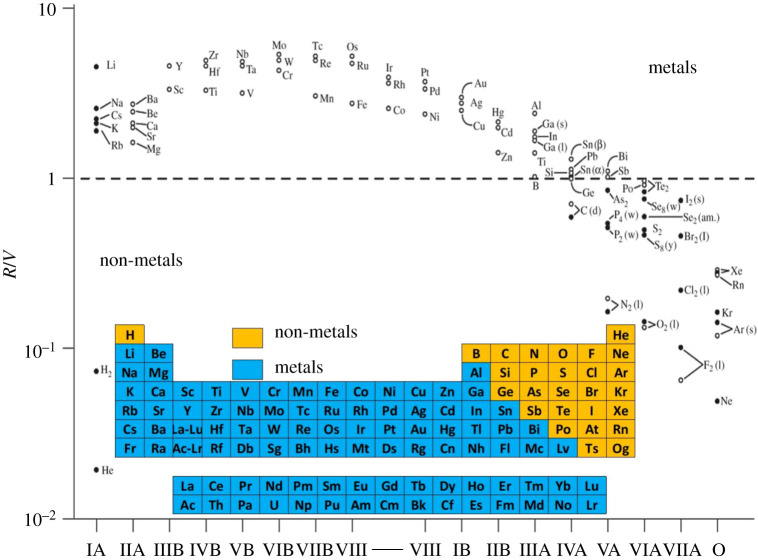
In figure 7, the ratio (R/V) at room pressure/room temperature conditions is plotted for the vast majority of the chemical elements of the periodic table (upper figure). In the same figure, we reproduce the metallic or non-metallic status of those elements based upon their electrical conductivities (figure 4). The simple Goldhammer–Herzfeld criterion is seen to have an amazing power of rationalization in regards to delineating the occurrence of metallic and non-metallic character in the chemical elements.

Figure 7.

The metallization of chemical elements of the periodic table under ambient conditions imposed on this planet. The figure shows the ratio (R/V) for elements of the s, p and d blocks of the periodic table. Here, R is the molar refractivity and V is the molar volume. The shaded circles represent elements for which both R and V are known experimentally. The open circles are for elements in which R is calculated and V is known experimentally [11,20,21]. (Online version in colour.)

Herzfeld used this simple criterion to predict which elements in the periodic table are metallic, which are non-metallic and which are borderline. As discussed by Edwards & Sienko [20,21], the overall features of the periodic classification of the elements conform rather well to this simple criterion. For example, the Group VII elements (the halogens) and the noble gases all have R/V < 1 under ambient conditions and consequently are non-metals. Conversely, the Group I alkali elements all have R/V > 1 and metallic behaviour is predicted, and of course observed for all its members. By contrast, the elements of Groups 14–15 (IIIA-VIA) effectively straddle the demarcation line between metallic and non-metallic behaviour of elements in the p-block of the periodic table.

As representative examples of these concepts, we focus on the alkali and noble gas elements.

As one expects, free atom polarizabilities increase as we descend both of these two groups.

Particularly striking, though, are the relative magnitudes of counterpart atoms in the two groups; thus, the polarizability of an alkali metal atom with atomic number Z + 1 is between one-and two orders of magnitude larger than its noble gas counterpart with atomic number Z. For example, α for Li to Cs is 24 ų to 55 ų, whereas that for He to Xe is 0.205 ų to 4.05 ų [22]. This, surely, is a remarkable manifestation of the periodicity of the chemical elements in terms of the huge differences in all physico-chemical properties—on moving from atomic number Z to atomic number Z + 1.

The relative variation of α as we descend the two groups is illustrated in a schematic 2D representation in figure 8; the resultant R/V values for the two elemental Groups have been shown earlier (figure 7). The molar volumes (under ambient conditions) of the alkali metals are noticeably larger than their noble gas counterparts (as first noted by Meyer [24]), but the ratio R/V is nonetheless always considerably greater than unity for the alkali metals and always substantially less than unity for the noble gases.

Figure 8.

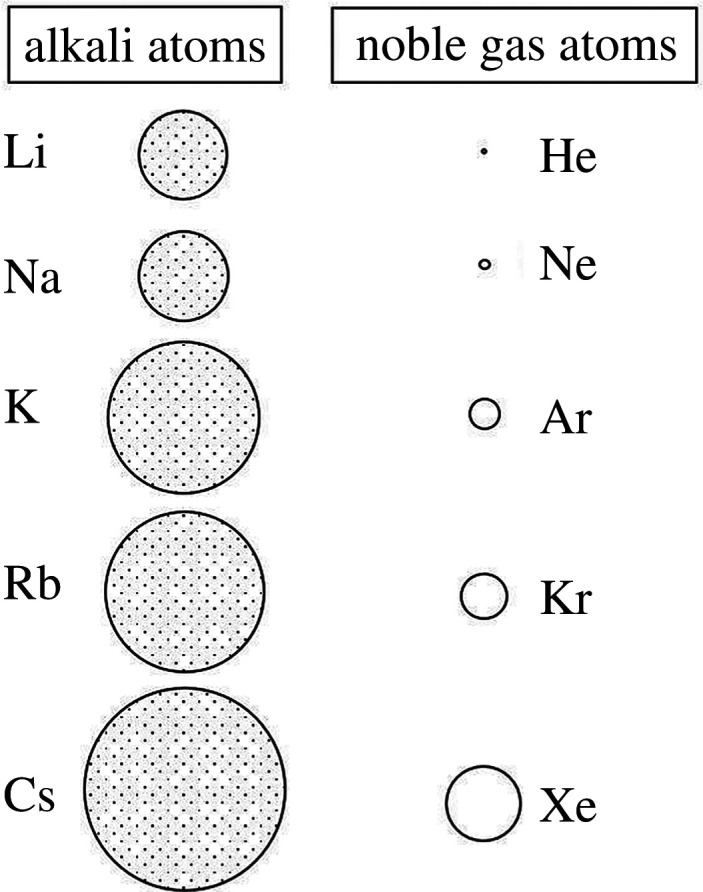
A schematic 2D representation of the free-atom electronic polarizabilities of the alkali and noble gas atoms (the diameter of the circles represents the value of free-atom electronic polarizabilities) (reproduced from [23]).

Groups III (A)-VI (A) of the periodic table are in many ways the most intriguing. These elements effectively straddle the diagonal dividing line between metallic and non-metallic status, as first noted by F. Hund. Two features of the elements from this area of the periodic table are particularly apparent in the approach to the metallization transition region, from the non-metallic side; viz. (R/V) < 1. The first is the marked tendency to form stable diatomic entities or more complicated polymeric entities (e.g. P₄, Se₈, S₈ etc.), as beautifully exemplified by the success of the (8-N) rule for elemental structures. The second aspect concerns the extremely large dielectric constants found, for example, in the Group VA ‘semi-metals’. Both characteristics are symptomatic of the so-called narrow-band transition region that separates the three canonical state of matter, namely; metals, Mott insulators and covalent insulators. [25] Parenthetically, the transition to diatomic and other polymeric states may well be symptomatic of the proximity of these elements under normal conditions to their metallic state achieved at higher temperatures and/or higher elemental densities.

Despite caveats that have been consistently noted in the direct application of the simple criterion, it is clear that the Goldhammer–Herzfeld approach to understanding the metallization of the chemical elements is a valuable one. Indeed, this same criterion continues to be used extensively as a most useful guide for investigating the tendency towards metallization of a range of molecular compounds and materials, including the possibility of metallic nanohydrogen in carbon nanotubes, hydrogen-rich molecular compounds at high pressures and the yet- unexplored science of the heavy halogen element, astatine [26–31].

3. Density and the metallic state: when does a metallic element become a non-metallic element, and vice versa?

The periodic table is a table of elements or atoms, and the elements or atoms themselves are neither metals nor non-metals. Normally, we mention it as metal element or non-metal element means when the element exist as a solid, liquid or gaseous status under ambient temperature and pressure. As well as rationalizing the metallic versus non-metallic status of the chemical elements under ambient conditions, the Goldhammer–Herzfeld model obviously allows one to predict the critical conditions under which a metallic element can become non-metallic or, conversely, a non-metallic element can acquire metallic status. Pioneering studies by Strutt [32] and by Bender [33] in the early part of the last century explored the experimental conditions under which the element mercury was transformed from a metal—surely its recognized, universal status as a magnificent conductor of electricity—to a stubbornly resistive insulator or non-metal. Thus, Strutt noted

It is known that mercury vapour, even at very high temperatures, is a good insulator; a better one in fact than air under similar conditions. Liquid mercury, on the other hand, is of course a good conductor, like other metals. He further noted Since the liquid and saturated vapour are indistinguishable above the critical temperature, one or both of these (states) must undergo a remarkable change of electrical properties as that temperature is approached [32].

Strutt observed a remarkable reduction of close to eight orders of magnitude in the electrical resistance of saturated Hg vapour at high pressures, when compared with its electrical resistance in the vapour under room pressure conditions.

A more recent experimental realization of the remarkable density-driven metal-to-non-metal transition in elemental Hg is given in figure 9. Note its transition from the metallic state to its non-metallic state as the elemental density is reduced. Even though these data are at high temperatures, note the sharpness of this transition to, and from, the metallic state. So here we have a classic example of a prototypical metallic element (from common experience) now transforming into the non-metallic form of that same element; this is a spectacular electronic transition in an element of the periodic table brought about by changes in its density.

Figure 9.

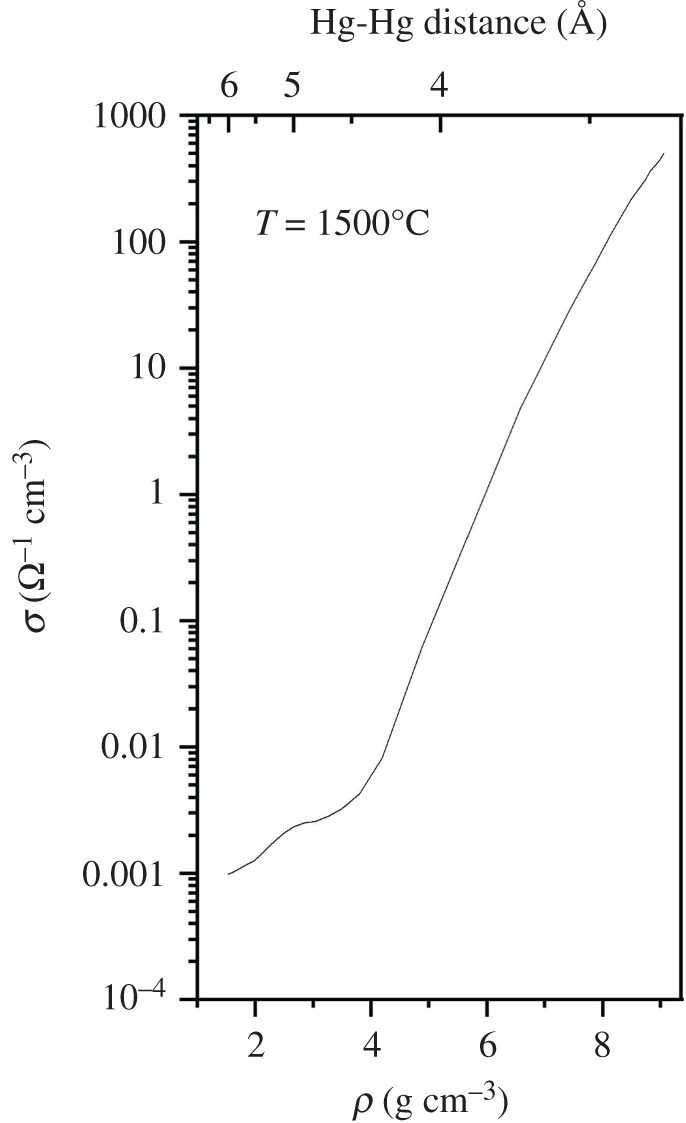
Experimental realisation of the metal-to-non-metal transition in ‘expanded’ elemental mercury showing the density dependence of the d.c electrical conductivity together with the corresponding average Hg-Hg distance (modified from [34]).

Conversely, transitions from the non-metallic to the metallic state have been observed in the (conventionally) non-metallic elements hydrogen, oxygen and nitrogen, when compressed to 100 GPa pressures and temperatures of several 1000 K.

The resulting metallic states in all of these dense fluids are known to be in the strong-scattering electronic regime, close to the so-called minimum metallic conductivity (σ_min) of a metal. Importantly, this characteristic also appears for the fluid elements rubidium and caesium which similarly undergo non-metal-to-metal transitions at comparable temperatures, though at substantially lower pressures of ca 0.01 GPa, but again at values of the corresponding σ_min.

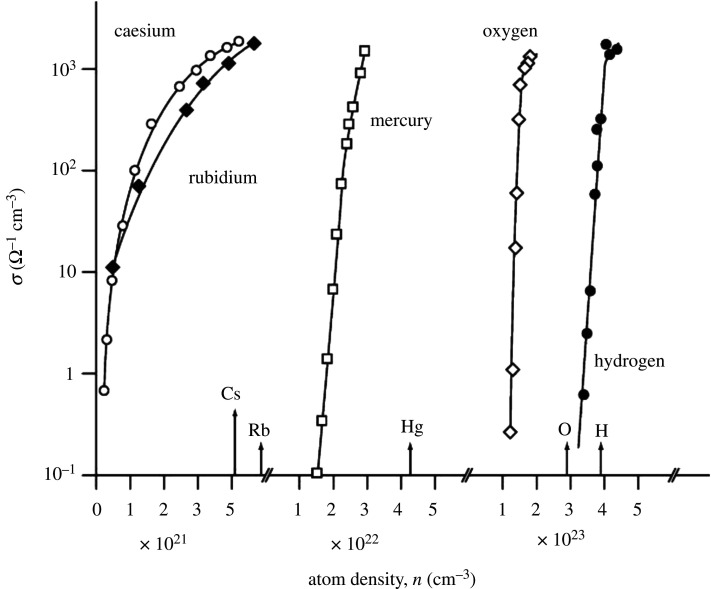
In figure 10, we compare the evolution of the density-driven non-metal-to-metal transition in five widely different chemical elements; caesium, rubidium, mercury, oxygen and finally hydrogen.

Figure 10.

The electrical conductivity of fluid caesium, rubidium, mercury, oxygen and hydrogen versus atom density. The tag lines on the atom density axis denote the predicted metallization densities for each element, based on the Goldhammer–Herzfeld model (see text). Note that the experimented atom densities range from 10²¹ cm⁻³ for caesium and rubidium to over 10²³ cm⁻³ for oxygen and hydrogen (taken from [11]).

Remarkably, all these (superficially) chemically disparate elements from across various groups of metals and non-metals of the periodic table achieve the same electrical conductivities of ca 1000 Ω⁻¹ cm⁻¹ as they transition into their metallic states above a characteristic (and unique) critical density of atoms.

The indicators shown along the atom density (x) axis in figure 10 represent the estimates of the metallization densities obtained from the simple Herzfeld criterion for the location of the metal-to-non-metal transition for each of the chemical elements using values of their respective (and in cases, vastly different) atomic electronic polarizabilities.

Remarkably, the predicted atom densities for metallization from the Herzfeld criterion for each element are in very good agreement with the experimental densities at which one sees a very rapid increase in measured conductivities with increasing atom densities. What we see in figure 10, therefore, represents the density-driven genesis of the highly conducting metallic state in elements as chemically and physically diverse as hydrogen, oxygen, rubidium, caesium and mercury.

4. Systematics of the metal-non-metal transition in chemical elements of the periodic table

In the Goldhammer–Herzfeld picture, increasing the density of atoms through an increase in the elemental density ultimately results in an electronic transition from a non-metallic to a metallic state at the critical condition $(4\pi \alpha /3)N_c=1$, where N_c is the atom density at metallization. This simple criterion, therefore, defines the metallization density—the conditions for the transition to the metallic state—of a chemical element of the periodic table.

Writing the polarizability of a hydrogen-like atom as

$$\alpha =\frac{9}{2}{(a_H^{\ast })}^3.$$ 4.1

The density-driven transition to the metallic state, therefore, occurs at the critical product [35,36];

$$N_c^{1/3}{a}_H^{\ast }=0.38,$$ 4.2

where $a_H^{\ast }$ is taken as the Bohr radius of the isolated atom, conventionally taken as the maximum of the valence electron charge density distribution.

The quantity $N_c^{1/3}{a}_H^{\ast }$ is designated as the Mott criterion for the critical conditions for a metal-non-metal or metal-insulator transition.

Interestingly, this value of the criterion (0.38) derived using the 1927 Herzfeld criterion is not too dissimilar to the value (0.25) prescribed by Mott in 1961 from completely different dielectric screening arguments for the transition to the metallic state as well as the value (0.26 ± 0.05) of the Mott criterion determined empirically by Edwards & Sienko in 1978 from an analysis of experimental data for a wide range of systems and materials exhibiting metal-non-metal transitions [37].

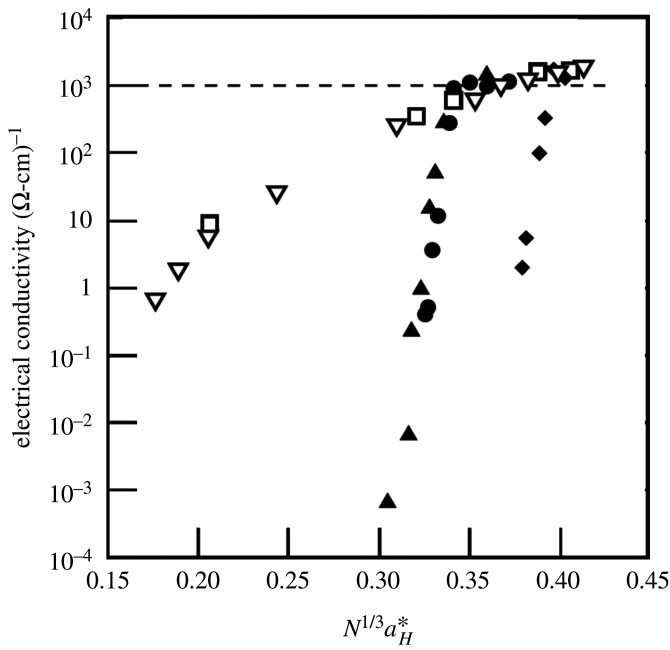
The corresponding density dependence of electrical conductivities for five chemically disparate elements of the periodic table, H, N, O, Rb and Cs, are plotted versus the Mott parameter, $N^{1/3}{a}_H^{\ast },$ in figure 11, where N is the number density of atoms, N^1/3 is the average distance between atoms and $a_H^{\ast }$ is their effective size, usually taken as the effective Bohr radius of the maximum in the outermost (valence) electron probability distribution.

Figure 11.

Electrical conductivities of Cs (open inverted triangles) and Rb (open squares) (Hensel & Edwards [35]), oxygen (solid triangles: Bastea et al. [38]), nitrogen (solid circles: Chau et al. [39]) and hydrogen (solid diamonds: Nellis et al. [40]) plotted versus the Mott parameter, $N^{1/3}{a}_H^{\ast }$, where $a_H^{\ast }$ is the effective Bohr radius of the atomic valence electron distribution and N is the number density of atoms (modified from [39]).

One sees in figure 11, remarkably, across these five chemically diverse chemical elements—ranging from the alkali metals Rb and Cs, to the elements O₂ and N₂, through finally to H₂—a clear, common scaling behaviour for the critical conditions for the transition to the metallic state. [41] Thus, all five of these chemical elements acquire metallic status at a constant, critical value of the scaling or Mott parameter or criterion $N^{1/3}{a}_H^{\ast }=N_c^{1/3}{a}_H^{\ast }=\mathrm{0.38.}$ [42].

On this approach—based primarily on the extent of outer valence electron atomic wave functions—the elements Rb and Cs have the largest radial extents of their charge-density valence electron distributions. Thus for the alkali metal atoms, relatively low density (or pressure compression) is needed to have sufficient overlap of wave functions on nearest neighbours to effect delocalization of the valence electrons and the transition to the metallic state. In stark contrast, of course, H has the smallest radial extent and requires the highest density (and pressure compression—some 140 GPa!) to achieve metallization. [40,43]

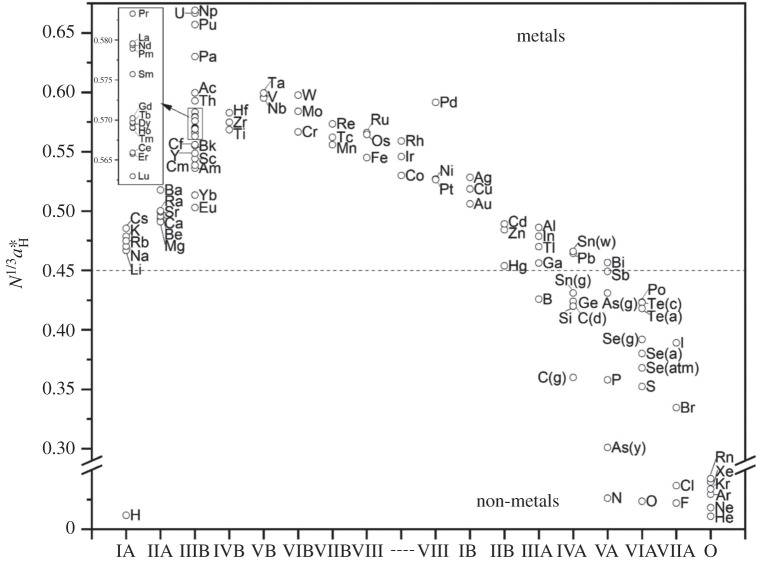
Returning to ‘earthly’ conditions (!), that is for the situation of room temperature/room pressure conditions for the chemical elements, we plot in figure 12 the periodic variation of the Mott parameter, $N^{1/3}{a}_H^{\ast }$.

Figure 12.

The Mott parameter, $N^{1/3}{a}_H^{\ast }$, across the periodic table of the chemical elements. Note the break in the y-axis. The critical value of $N^{1/3}{a}_H^{\ast }$ as 0.45.

The Mott parameter appears to be 0.45 for the dividing line separating metals from non-metals. Future work will undoubtedly lead to a refinement of the basic models, but these criteria in their simplest form are likely to survive, at least for a qualitative source of guidance for understanding how both the atomic and elemental properties make an element either a metal or a non-metal.

The ability of the Mott (and Herzfeld) criteria in rationalizing even the periodic table itself lends weight to the suggestion of a simple, universal criteria for the transition between these canonical states of matter.

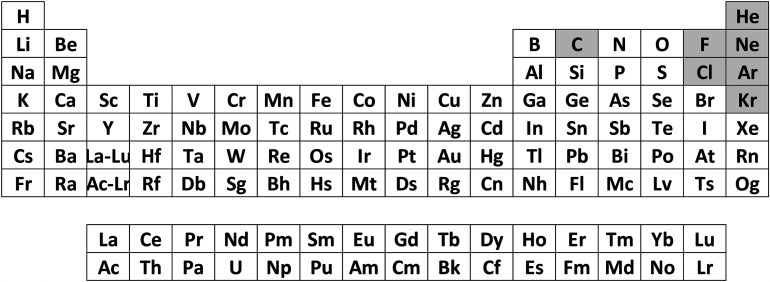
5. The periodic table at three million atmospheres pressure

These developments now force us to reassess our basic perceptions and definitions of metals and non-metals within the periodic classification. The conventional (and accepted) distinction between these two canonical states of matter can now be seen as purely subjective and governed by one's natural experience of the chemical elements under ambient conditions on Earth. Thus, without hesitation, one would instantly classify the elements H₂, N₂ and O₂ as non-metals and the elements Rb and Cs as prototypical metals. However, metallic or non-metallic status is not an inherent and unchanging property for any chemical element. In relation to the periodic table, atomic properties and elemental density are the key parameters governing an element's metallic or non-metallic status.

These data assembled in figure 13 represent a remarkable manifestation of that striking fact.

Figure 13.

A possible form of the periodic table of the elements at a pressure of three million atmospheres. This table is not yet complete—for example, elemental fluorine and a few others are not yet accessible—but note the absence of the traditional diagonal demarcation separating metals from non-metals (grey backgrounds) under normal conditions. The elements C, F, Cl, Ne, Ar, Kr and He have not yet been investigated at sufficiently high pressures to achieve metallization. We show here hydrogen as a metal; this reflects the situation for fluid hydrogen at these high pressures. In stark contrast, solid hydrogen does not attain metallic status, even at three million atmospheres imposed pressure (modified from [44]).

Thus, within the giant planets, our periodic table would appear quite different (one possible form is shown in figure 13) with no evidence of the usual (instantly recognizable) diagonal dividing line within the p-block separating metals and non-metals—the very cornerstone of our classification of the chemical elements on our own planet.

The question we, therefore, should ask of a chemical element of the periodic table is not …

Is this element a metal or non-metal?’ but, rather, ‘When is this element a metal and when it is a non-metal ?

6. The unnaturalness of elemental metals and metallic compounds

One of our reviewers noted the following perceptive, incisive and tantalizing observations.

But as the authors know, chemistry and materials science is about substances that are for the most part not elemental. And perhaps, just perhaps, the elements are… untypical. Would you care to estimate how many molecules and inorganic compounds in their usually solid pure state are metallic, at ambient T? My guess is that it is 0.001% of the 10⁸ molecules made, and around 1% of solid-state inorganics (alloys and intermetallics largely). Why is that so? Using the G-H criterion why do molecules ‘fail’ it?

These observations—and the fascinating challenge—have certainly engaged us and while we do not have a complete response and resolution, we offer certain observations on what we now believe to be a critical central theme for future enquiries—namely, the very unnaturalness of metals and the metallic state. Drawing on our experiences in the natural world, Sir Alan Cottrell made the simple, but potent observation that

Metals and alloys are unnatural [45].

If we think of ‘natural’ metals in the sense that they are found ‘native’ in nature, in the highly conducting state of the elements, some assistance is forthcoming from Wikipedia [46].

A native metal is any metal that is found pure in its metallic form in nature. Only gold, silver, copper and platinum metals occur in nature in large amounts. Over geological time scales, very few metals can resist natural weathering processes like oxidation, which is why generally only the less reactive metals such as gold and platinum are found as native metals. The others usually occur as isolated pockets where a natural chemical process reduces a common compound or ore of the metal, leaving the pure metal behind as small flakes or inclusions.

So, when it comes to actually making metals that we typically view as constituting the majority of chemical elements in the periodic table, the non-metallic constituent ores (typically oxides, sulfides etc.) require an aggressive physico-chemical reduction process through their smelting and melting. The most obvious exceptions of course are gold and silver; ‘natural’ metals in the sense that they are found ‘native’ in nature, in the metallic, highly conducting state. And therefore, following Cottrell, its no wonder that Nature has never used them, as biological parts, even though she has used ions of the metallic elements widely in chemical substances such as haemoglobin to acquire vital biochemical properties. As Cottrell brilliantly concluded,

But lumps of metal, never [45].

Nonetheless, when we do look at the entire ‘Natural and also Unnatural’ metals, the Goldhammer–Herzfeld description highlighting the atomic property (polarizability) and condensed phase density (molar volume) allow us to understand the very make-up of metallic versus non-metallic elements of the periodic table.

Returning to the reviewers prompts ‘What of molecules and compounds in the solid state?’ One must agree with his/her observation that only some 1% (or less) of inorganic compounds are metallic under ambient temperature (and pressure) conditions. The Goldhammer–Herzfeld approach can offer a perspective on designating the conditions for genuine metallicity of inorganic compounds—at room pressure. The metallization of some ‘Simple’ systems, e.g. Xe, Ar, He, I₂ etc. formed the basis of extensive work from the 1980s to the present day but application to more complex inorganic compounds is still in its infancy. [47] One notes, however, that Herzfeld in 1965 rationalized the pressure-induced metallization of TlI using his 1927 model. Of course, what that also meant was he was able to understand the lack of metallicity in TlI at ambient T and P! [48]

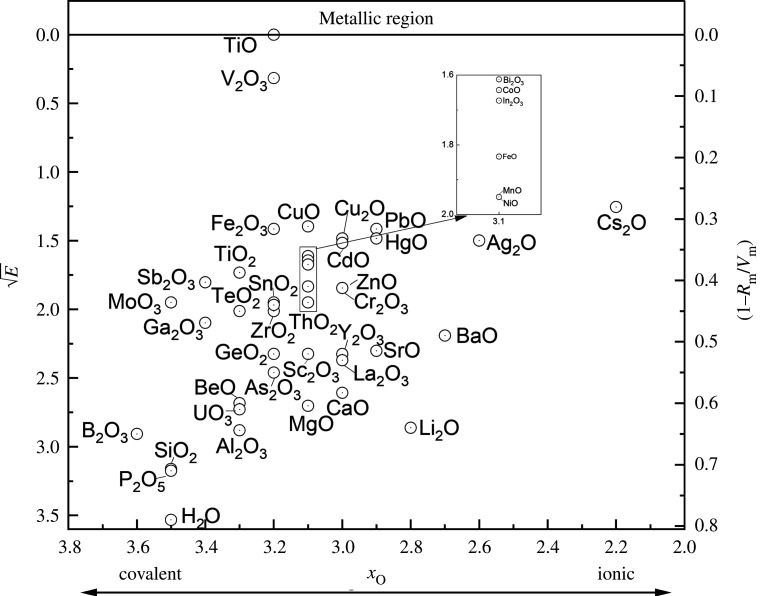
A major advance in appraising the metallic and non-metallic nature in Oxides of the Chemical Elements was the work of Duffy & Binks [49]. They assessed the nature of metallic bonding, and hence metallic status also from the viewpoint of polarization and were most effective in linking experimental parameters of polarization to band theory. Furthermore, this approach used (again as here) the relationship between polarizability and the onset of metallization in oxides as encompassed in Herzfeld's approach. Thus, if the molar volume (V_m) is below a critical value, then a polarization or dielectric catastrophe occurs at which point the valence electrons become itinerant and metallic conduction ensues. Thus (applied to oxides) a material is non-metallic for R_m/V_m less than unity (where R_m is the molar refractivity), but is metallic when R_m/V_m = 1. So this forms the direct link for the metallization condition for oxides and the elements of the periodic table. These authors also linked the metallization condition R_m/V_m = 1 to the electronic energy band gap of oxides, and the transition occurs when the energy, E, and the quantity (1 − R_m/V_m) both approach zero. They found a remarkable correlation between these two quantities and used E (or rather $\sqrt{E}$) and (1 − R_m/V_m) as a measure of the proximity of any oxide to the onset of metallization (shown in figure 14).

Figure 14.

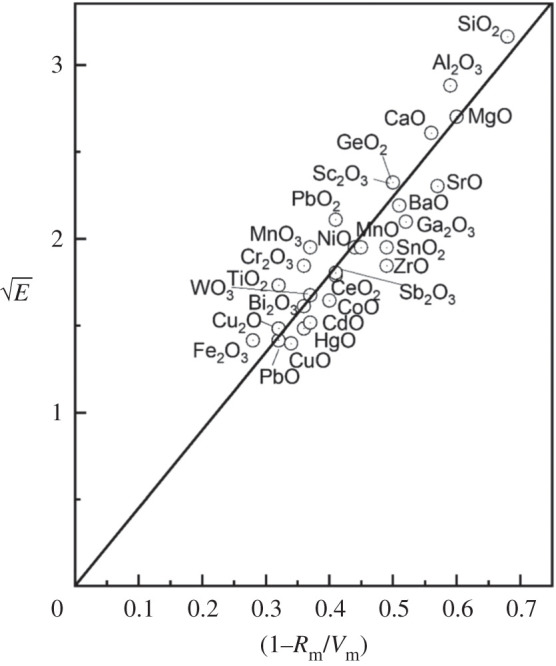
Plot of $\sqrt{E}$ versus (1 − R_m/V_m) for oxides. The straight line is derived from E = 20 (1 − R_m/V_m)². Reproduced with permission from [49].

Oxides can be characterized as to their proximity to the non-metal-to-metal transition whether they are essentially covalent or ionic in nature. In figure 15, Duffy has attempted a Chart or Sorting Map for Binary oxides of the periodic table and produced a horizontal line for a covalent-ionic scale and a vertical scale (using both (1 − R_m/V_m) and $\sqrt{E}$) to represent a growing tendency for the onset of metallization.

Figure 15.

Chart for oxides, M_mO_n,. Covalent oxides are to the left and ionic oxides are to the right-hand side. The height above the covalent-ionic baseline represents the proximity to the non-metal/metal transition. Reproduced from [49].

One notes from figure 15 the scarcity of the metallic state within the binary oxides of the periodic table and, once again, the Herzfeld criterion allows one to reveal the scarcity of genuine metallic binary oxides (as a simple example). Thus, the vast majority of ‘natural or native’ oxides of the periodic table are insulators having almost insignificant metallic character. Those oxides that are closer to the non-metal-metal transition (e.g. as in figure 14) have the ability to be chemically ‘doped’ to induce higher conductivity. A classic and practical example is SnO₂, when doped is used as a transparent—but conducting—oxide. Other techniques (as well as multiple doping and electrochemical approaches) can induce ‘metallic’ character in oxides with little tendency for metallization in their natural form.

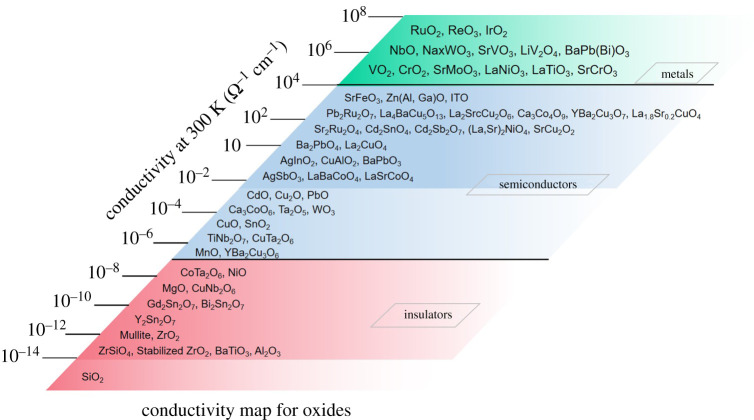
Moving beyond binary oxides of the chemical elements, multinary oxides run the gamut from insulating, to semiconduction through to genuinely metallic properties at room temperature and pressure (in figure 16) [50]. In a major review of the electronic structure of multinary oxides, one of us (C.N.R.Rao) has captured this in the term “Marginally metallic oxides“ [51–53].

Figure 16.

The room-temperature electrical conductivities of oxides; note the enormous range of values for this fundamental property. This allows us to classify the oxides range from metals, through semiconductors to insulators. Taken from [50]. (Online version in colour.)

These generally transition metal oxides at the metal-non-metal boundary, and especially those belonging to the perovskite family, exhibit remarkable phenomena including high temperature superconductivity and giant magnetoresistance. A fascinating aspect to emerge in these phenomena is their proximity to what is known as the ‘Minimum metallic conductivity’—this the experimental signature of a marginally metallic oxide on the very point of electron localization into the non-metallic state! This highlights, once again, the potential power and impact of extending/ adapting the Goldhammer/Herzfeld viewpoint: Here, then, we see the situation where the reviewer's insightful observations could be put to the test to understand the occurrence of the metallic and non-metallic states of oxides.

7. Concluding remarks

We hope to have illustrated that the classification ‘metal or non-metal’—although used universally in terms of the periodic table—is not an inherent and unchanging property of any particular element. For the chemical elements, density represents a critical thermodynamic parameter that plays a major role in dictating either metallic or non-metallic status. So also are the atomic properties which make an element a metal or a non-metal, as first demonstrated by Goldhammer and Herzfeld. This approach—with its roots in how many body (atom) interactions in an element dictate the very nature of the element—also has resonances with the venerable issue of chemical periodicity. Thus in Sanderson's standard text, ‘Chemical Periodicity’ [54], centred as it is on the chemical combinations and relationships among the elements, the author writes

From a thorough knowledge of the structure of an atom, one should be able to predict and understand exactly how that atom would react to any given stimulus of known nature.

Of course, the main focus in chemistry texts, including Sanderson's, understandably centres on how the (electronic) structure of an atom dictates the nature of chemical bonding and chemical combinations. We hope to have illustrated that similar considerations relating to the structure of an atom, and the effects of atom/many-atom interactions in an element, through the Goldhammer–Herzfeld and Mott approaches to metallization, allows one to rationalize when a chemical element of the periodic table behaves as a metal and when it behaves as a non-metal.

As Pauling noted, metals assume a particularly interesting and important position among all the materials with which the chemist deals. For the simplest, and surely most powerful description of a metal or metallic substance, we return to Cottrell's definition, and take the existence of free electrons as the characteristic of a metal. According to Goldhammer and Herzfeld, one can easily understand how the valence electrons in an element experience an instability (instabilen Zustand, as noted by Ehrenreich) at high-enough atomic densities to become dissociated from their parent atoms. This approach allows one to predict which atoms, therefore, assume a metallic character in an element, and which do not. The same applies to the different theory of Mott in terms of screening and localization effects in the multi-atom assemblage that constitutes an element.

In relation to the broader issue of an electronic theory for solids, Wigner & Seitz stated in 1955 [55]

If one had a great calculating machine, one might apply it to the problem of solving the Schrodinger equation for each metal…It is not clear, however, that a great deal would be gained by this. Presumably the results would agree with the experimentally determined quantities…It would be preferable instead to have….a simple description of the essence of the factors …and an understanding of the origins of variations…from metal to metal’.

In that context, it is clear that the Goldhammer–Herzfeld and Mott approaches to metallization are particularly valuable ones which have qualitative—and even quantitative—validity in helping us answer the wonder of the periodic table, where … the metals are here, and the non-metals are there … [12]

Data accessibility

This article does not contain any additional data.

Authors' contributions

P.P.E. and B.Y. worked with all the authors on the conception and design of the article. P.P.E. and B.Y. drafted the article, and all other authors provided further intellectual input into subsequent revisions. P.P.E. was the final approver of the version to be published.

Competing interests

We declare we have no competing interests.

Funding

We gratefully acknowledge the financial support from EPSRC (EP/N009924/1) and KACST, Saudi Arabia.