Summary
Multi‐compartment models have been playing a central role in modelling infectious disease dynamics since the early 20th century. They are a class of mathematical models widely used for describing the mechanism of an evolving epidemic. Integrated with certain sampling schemes, such mechanistic models can be applied to analyse public health surveillance data, such as assessing the effectiveness of preventive measures (e.g. social distancing and quarantine) and forecasting disease spread patterns. This review begins with a nationwide macromechanistic model and related statistical analyses, including model specification, estimation, inference and prediction. Then, it presents a community‐level micromodel that enables high‐resolution analyses of regional surveillance data to provide current and future risk information useful for local government and residents to make decisions on reopenings of local business and personal travels. r software and scripts are provided whenever appropriate to illustrate the numerical detail of algorithms and calculations. The coronavirus disease 2019 pandemic surveillance data from the state of Michigan are used for the illustration throughout this paper.
Keywords: antibody, cellular automaton, COVID‐19, Markov chain Monte Carlo, risk prediction, spatio‐temporal model, state‐space model
1. Introduction
Coronavirus disease 2019 (COVID‐19), an infectious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) (World Health Organization, 2020), has become a global pandemic that has spread swiftly across the world since its original outbreak in Hubei, China, in December 2020. As of 27 June 2020, this pandemic has caused a total of 9 801 572 confirmed cases and 494 181 fatalities in more than 200 countries. Being one of the most lethal communicable infectious diseases in human history, it is expected that the COVID‐19 pandemic will continue spreading in the world population, causing even higher numbers of infections and deaths in the future. With no effective medical treatments or vaccines currently available, public health interventions such as social distancing have been implemented in most of the countries to mitigate the spread of the pandemic. One of the central tasks of statistical modelling is to provide a suitable risk prediction model that enables both government and public health workers to evaluate the effectiveness of public health policies and predict risk of COVID‐19 infection at the national and regional levels. Such information is valuable for governments to assess the preparedness of medical resources (personal protective equipments and intensive care unit beds), to adjust various intervention policies and to enforce the operation of social distancing.
1.1. Building an Infectious Disease Model
Modelling for infectious diseases has a profound role in informing public health policy across the world (Heesterbeek et al., 2015; Siettos & Russo, 2013). The outbreak of the COVID‐19 pandemic in December 2019 has led to a surge of interest in disease projection that ubiquitously relies on mathematical and statistical models. A crucial step in modelling disease evolution is to capture key dynamics of the underlying disease transmission mechanisms from available public health surveillance data, which enables reliable projection of disease infection into the future. A prediction model may help us foresee some possible future epidemic/pandemic scenarios and learn consequent impacts of current economic and personal sacrifices due to various control measures.
Because of both data quality and data limitations from public surveillance data systems, a statistical model should take the following features into account in its design and development. First, a statistical model should be able to make predictions and, more importantly, to quantify prediction uncertainties. Forecasting is known to be a notoriously hard task, which depends heavily on the quality of data at hand and a certain model chosen to summarise the information from observed data and then to reproduce information beyond the observational time period. The chosen model is of critical importance to deliver prediction. This paper concerns a review of the family of classical compartment‐based infectious disease models, which have been the most widely used mechanistic models to capture key features of infection dynamics. We begin with the most basic Susceptible–Infectious–Removed (SIR) model to build up the framework (Section 2), and this three‐compartment model is then generalised to have more compartments to embrace additional features of infection dynamics (Section 3), such as the well‐known four‐compartment model, Susceptible–Exposed–Infectious–Removed (SEIR) model, which takes the incubation period of contagion into account. Given many types of factors potentially influencing the evolution of an epidemic, a single prediction value is insufficient to be trustworthy unless prediction uncertainty is reported as part of forecast analysis. Quantification of prediction uncertainty is of critical importance, especially when a forecast is made at an early phase of an epidemic with limited data. Building sampling variations in infectious disease models makes a statistical modelling approach different from a mathematical modelling approach. A clear advantage of a statistical model is that the model parameters, including those in the mechanistic model, can be estimated, rather than being specified by certain subjectively chosen prior information.
Second, the consideration of building sampling uncertainties in the modelling of infectious disease is a fundamental difference of a statistical modelling approach from a mechanistic modelling approach known in the mathematical literature of dynamic systems. A mechanistic model is typically governed by a system of ordinary differential equations, such as the existing three‐compartment SIR model consisting of three differential equations, which explicitly specifies the underlying mechanisms of an epidemic. This model is assumed to govern an operational system of disease contagion and recovery or death, which, in reality, cannot be directly observed. Most of the time, public surveillance data are accessible, which represent only a few snapshots of the underlying latent mechanistic system of an epidemic. Such gaps may be addressed by a statistical model that incorporates sampling schemes to explain how observed data are collected from the underlying infection dynamics. In turn, prediction uncertainty will reflect forms and procedures of the chosen sampling schemes specified in the statistical model. In this paper (Section 5.1), we will introduce the state‐space model as a natural and effective modelling framework to integrate the mechanistic model and sampling schemes seamlessly.
Third, given the scarcity of the available data in public health surveillance systems, the complexity of a model used for prediction should be aligned with the issue of parameter identifiability. For example, at the beginning of an outbreak, one should consider a simple model, which may be expanded over the course of an epidemic's evolution with increased data availability. To make the specified model useful to answer a certain question of practical importance, a relevant feature should be included in the model building. For example, in the study of control measures to mitigate the COVID‐19 spread, the model specification should incorporate a structure that is sensitive to the influence of a preventive policy. In Section 5.2, we will introduce an expansion of the basic SIR model in that time‐varying control measures are allowed to enter. The flexibility of permitting certain modifications is an important property of a model to be considered in an infectious disease model. In this field, all models need to be tailored with increased data and more knowledge from the literature as a disease evolves over time. From this point of view, compartment‐based models are superior to other models because, for example, it is easy to add other compartments, such as an exposure compartment, a quarantine compartment or a self‐immunisation compartment, to improve the mechanistic model, to answer specific question of practical importance and to capture distinctive data features for better prediction.
Fourth, as the epidemic evolves further, surveillance data become abundant and have higher resolution. For example, in the USA, the numbers of confirmed symptomatic COVID‐19 cases and case fatalities are recorded for each county. The average county population size in the USA is approximately 98 000, so a microinfectious model may be built upon county‐level surveillance data to make high‐resolution prediction and to assess the effectiveness of control measures at a community level. This paper (Section 6) will discuss this important extension of the classical SIR model, essentially a temporal model, to a spatio‐temporal model that enables borrowing of information from different spatially correlated counties in the improvement of risk prediction. This exemplary model generalisation sets up an illustration from a nation‐level macromodel to a county‐level micromodel. The latter is more relevant and useful for local governments to make decisions of business reopenings and for residents to be aware of local infection risk.
Last, to make research findings transparent and to place resulting toolboxes into the hands of practitioners, an open‐source software package must be a deliverable. This is indeed a rather demanding task, as the ease of implementation and numerical stability impact the choice of statistical models and statistical methods for estimation and prediction. Note that not every statistical model permits delivery of a user‐friendly computing package that is general and flexible enough to handle various types of data. In this paper, we focus on the discussion of Markov chain Monte Carlo (MCMC) methods that have been developed in the literature to perform estimation and prediction for state‐space models (Section 5.3).
In this paper, we invite the readers on a journey of surveillance data, modelling, estimation and prediction, implementation and software development. After reading this paper, one should be able to use existing compartment‐based models or to expand them in a study of an infectious disease epidemic, to improve estimation and/or prediction methods, or create one's own software. It is our hope that this paper may pave the path to learning, practising or developing new methodologies that are useful for a broader range of infectious disease modelling problems.
1.2. Mechanistic Modelling Approach
Multi‐compartment models have been the workhorse for modelling infectious diseases since the early 20th century. They are a class of mathematical models used for describing the evolution of masses (in unit of proportions or counts) among the compartments of a varying system, with broad use cases in epidemiology, physics, engineering and information science. This is a dynamic system that is typically represented by a system of ordinary differential equations (ODEs) with respect to time, and, given a starting condition, the mass in each of the components is regulated by a function over time. An ODE is a simple mathematical model to depict a trajectory of a functional trend. One of such examples used extensively in epidemiology is an exponential growth function, f(t)=e t, which may be viewed as a solution to an ODE of the form: , or , where y is a function of time t, which obviously is y=f(t)=e t with an initial condition f(0)=1. It is worth pointing out that this simple ODE explicitly characterises the rate of change (speed or velocity) for function y=f(t), rather than directly specifying a form for the function f(t) itself. Such rate‐based characterisation is termed as ‘dynamics’ in the mathematical literature. Clearly, this ODE is not a statistical model as it does not provide a law of data generation; in other words, there is no randomness in this ODE to reflect sampling uncertainties. A typical multi‐compartment model consists of several ODEs for a vector of rates that are linked each other. This is referred to as a dynamic system. The forms of ODEs are specified according to relevant scientific knowledge about the understanding of the underlying dynamic mechanism related to an infectious disease.
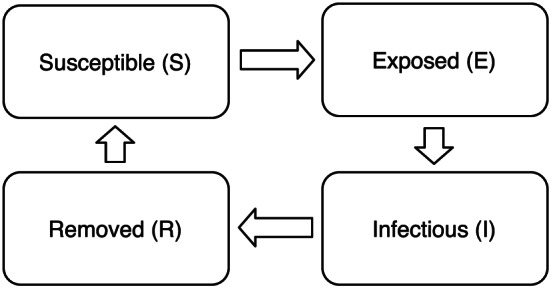
In the context of infectious disease modelling, the SIR model is the most basic three‐compartment dynamic system that describes an epidemiological mechanism of disease evolution over time (see Figure 1). In brief, the model describes the flow of infection states or conditions by (i) moving susceptible individuals to the infectious compartment through a transmission process (the first arrow) and (ii) moving infectious individuals to the removed compartment (either dead or recovered) through a removal process (the second arrow). At a given time, the total population N under a study is partitioned into the three compartments, denoted by S, I and R, and their sizes satisfying S+I+R=N. With a slight abuse of notation, this notation denotes either the type of compartment or the size of compartment, whichever is applicable in a given context. In other words, S, I and R are used to denote the sizes of the mutually exclusive subpopulations of susceptible, infectious and removed individuals, respectively. This compositional constraint, that is, S+I+R=N, may be interpreted in a term of probability (or proportion) as follows: at a given time, an individual in the population is either at risk (susceptible), or under infection by a virus (infectious), or removed from the infectious system due to recovery or death; that is, θ S+θ I+θ R=1, where θ S, θ I and θ R are, respectively, the probabilities of being susceptible, infectious and removed. This presents the primary constraint for a multi‐compartment infectious disease model. More details of the SIR model will be described in Section 2.
Figure 1.

Dynamic system of the basic three‐compartment Susceptible–Infectious–Removed model.
Often times, the interest for such system lies in the function values over time, but the closed‐form analytical solution for such functions may not exist. For example, to answer the question of how many individuals will be infected with the COVID‐19 by the end of the year 2020 (or any future time) requires to know a calculator that computes the cumulative numbers of susceptible, infected and removed cases over time from the past to the future. Unfortunately, in reality, functions relevant to this calculator are usually non‐linear, and their exact forms are difficult to directly specify. In contrast, a set of ODEs helps better understand the disease transmission dynamics (i.e. traits of infectious diseases) and more conveniently captures their key features, where each ODE may correspond to one mode of disease evolution. Such ODEs for disease spread may be regarded as a model for the expected dynamic mechanism, serving as a systematic component in a statistical model. Numerical methods such as the Euler discretisation method or the Runge–Kutta approximation method (Stoer & Bulirsch, 2013; Butcher, 2016) can be used to obtain approximate solutions of such ODEs with given boundary conditions. Regardless of methods used, solutions to a dynamic system are deterministic functions. We illustrate a basic mechanistic model of disease spread in the succeeding text. Additional review from deterministic and mathematical perspectives of multi‐compartment models is given by Anderson et al. (1992) and Hethcote (2000).
Example 1
Consider the SIR model for a hypothetical population with a constant population of N=100 residents and an initial condition of 99 susceptible individuals, 1 infectious individual and 0 individual removed (either died or recovered). Here 100 subjects may be also regarded as 100% if the unit of proportion is used in the interpretation. The transitions between compartments, written in ODEs as in (1), represent population movement from one compartment to another (see Figure 1). We consider an example with β=0.5 (a rate of moving from S to I) and γ=0.2 (a rate of moving from I to R), leading to R 0=β/γ=2.5. Here R 0 is the so‐called basic reproduction number that quantifies an average number of susceptible individuals contracting a virus from one contagious person in an environment of no preventive measures. This is a quite infectious scenario as we will see later. The r script in the succeeding text shows a scenario of obtaining the solution to the system of ODEs by standard ODE solvers (r package deSolve) using the first‐order Euler method (not shown) or the Runge–Kutta fourth‐order (RK4) approximation method (Figure 2). Details about the RK4 method can be found in Appendix A0.1.

Figure 2.
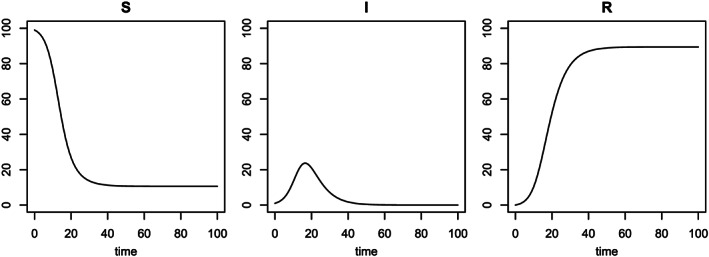
Solution to the ordinary differential equations of the basic Susceptible–Infectious–Removed (SIR) model by Runge–Kutta fourth‐order approximation method.
As shown in Figure 2, on each of these 100 days, the sum of the three values from the three curves is always equal to 100, presenting a time‐varying redistribution of the 100 individuals. With no control measures in this hypothetical infection dynamics, the susceptible compartment quickly drops and reaches an equilibrium state after 35 days of the outbreak, and during the period of first 35 days, the infectious compartment increases to a peak and then decreases to zero (no contagious individuals in the population) as all currently infected individuals move to the removed compartment, which is the exit of the system.
Despite relying on a valid infectious diseases mechanism, deterministic approaches have several drawbacks: (i) the actual population in each compartment at a given time is never accurately measured because we only obtain an observation around the mean; (ii) the nature of disease transmission and recovery is stochastic on the individual level and thus never certain; and (iii) without random component in the model, it is neither possible to learn model parameters (e.g. R 0) from available data nor to assess prediction uncertainty. The latter is of critical importance given many unobserved and uncontrolled factors in surveillance data collection. In an early stage of the current COVID‐19 pandemic, the daily infection and death counts reported by health agencies are highly influenced by the availability of testing kits, reporting delays, reporting and attribution schemes, and under‐ascertainment of mild cases in public health surveillance databases (see discussions in Angelopoulos et al., 2020; Banerjee et al., 2020); both disease transmission rate and time to recovery or death are also highly uncertain and vary by population density, demographic composition, regional contact network structure and non‐uniform mitigation schemes (Ray et al., 2020). Hence, statistical extensions are necessary to incorporate sampling uncertainty in estimation and inference for infectious disease models.
1.3. Organisation
The main focus of this paper will be given to a statistical modelling framework based on a class of state‐space models, in which the systematic component is specified by multi‐compartment infectious disease models while the random component is governed by a certain sampling distribution of surveillance data. Note that multi‐compartment infectious disease models present a class of classical mechanistic models widely used in practice and that incorporating certain sampling distributions allows to make statistical estimation, inference and prediction with quantification of uncertainties. We organise the paper as follows.
In the first part of the paper, we introduce a class of macromodels. We begin with the most basic SIR mechanistic model in details, followed by some important extensions used to address representative scenarios of disease spread and infection evolution. Examples include SEIR model with an additional compartment of exposure accounting for potential incubation period of infection and Susceptible–Antibody–Infectious–Removed (SAIR) model with an additional compartment of antibody accounting for potential self‐immunisation after being infected. Then, we formally introduce the framework of state‐space models, a powerful statistical modelling approach that aims to model available surveillance data from public health databases with the utility of the underlying latent mechanistic model.
In the second part of the paper, we introduce a class of micromodels. When an epidemic continues, data become abundant and of high resolution at community level. For example, the surveillance data of the COVID‐19 pandemic in the USA are collected from individual counties. This allows building county‐level microinfectious models in addition to country‐level or state‐level macromodels. Being a certain subgroup analysis, such micromodelling is appealing to address spatial heterogeneity across the more than 3 000 counties in the USA and consequently improves the prediction accuracy. As far as the spatial modelling of infection dynamics concerns, we review the classical cellular automata (CA) that is extensively used to describe person‐to‐person interacting rules associated with epidemic spreading patterns in a population via relevant interlocation connectivity functions. This CA may vary spatially and temporally, which presents a principled way to extend a state‐level macroinfectious disease model to a stratified microinfectious model. In addition to the case of geographical subgroups, other types of subgroups by, for example, age, race, income, political party and economy, are also of interest.
Our main objective of this paper is to introduce to readers the basics of infectious disease models, underlying modelling assumptions, statistical analyses and possible extensions. Examples will be provided for demonstration purposes. This review targets readers who have had some statistical training but no prior experience in infectious disease modelling.
2. Basic Three‐compartment Models
The first infectious disease model (McKendrick, 1925; Kermack & McKendrick, 1927) is widely known as the Susceptible–Infectious–Removed model, or in short the SIR model (see Figure 1). It is a three‐compartment model for studying how infectious diseases evolve over time on the population level. It defines a mechanism of disease transmission and recovery for a population at risk by a dynamic system of three disjoint states: susceptible, infectious and removed. We note an important distinction between infectious and infected individuals. Infectious individuals are those who are currently infected and not yet recovered or dead (currently infected individuals become infectious immediately in the SIR model, although it may not be true in reality; see the SEIR model in Section 3 where currently infected individuals become infectious with a delay in time), whereas infected individuals could mean only currently infected or both currently and previously infected. For clarity, we will refer to currently infected as infectious so that the three states in the SIR model are mutually exclusive. Individuals in the susceptible state are not immunised and can become infected by coming into contact with infectious cases, so they are at risk at a given time. Individuals in the infectious state contribute to the transmission of the disease until they ultimately recover or die, so they are contagious. Individuals in the removed state include those who either recover or die (without distinction). This is an exit from the infection system, meaning that once an individual leaves this system (recovers or dies), he or she would never return to the system. This is true for people who die from the virus but may not be the case for recovered individuals. Thus, in the SIR model, there is a technical assumption that a recovered individual would become self‐immunised to the virus and no longer impact the disease transmission. A possible way to relax this assumption is to create two separate compartments corresponding to recovery and death states, respectively, leading to a four‐compartment infectious disease model. To make our presentation focused on the basic three‐compartment model, we make this self‐immunisation assumption in this section.
Given what we said earlier, the current version of SIR is only applicable for diseases, where long‐term immunity can be developed, and does not apply to recurring infectious diseases, such as the common cold. This is because the disease transmission rate is set as a constant in SIR. In this section, we introduce the SIR model in its basic deterministic form (Section 2.1), define reproduction numbers (Section 2.2), elaborate its assumptions (Section 2.3) and properties (Section 2.4) and present some technical extensions to the basic SIR model. Mechanistic extensions, such as modifications to the three‐compartment SIR model to account for additional components or disease mechanism, are discussed in Section 3.
2.1. Specification of the Susceptible–Infectious–Removed Model
We use S(t), I(t) and R(t) to denote the time‐course subpopulation sizes (i.e. the number of individuals) distributed into each of the three compartments at a given time t, where t is continuous. Clearly, S(t)+I(t)+R(t)=N,t ≥ 0, where N is the total population size, which is a fixed constant. The starting time is denoted as t=0. The rates of change among these subpopulations are represented by a system of ODEs:
| (1) |
with β ≥ 0 and γ ≥ 0 and initial conditions S(0)>0, I(0)>0, R(0) ≥ 0 and S(0)+I(0)+R(0)=N. Because at a given time t, the constraint S(t)+I(t)+R(t)=N implies dS(t)/dt+dI(t)/dt+dR(t)/dt=0, which is satisfied by the SIR in Equation (1), these three ODEs define a dynamic system of three deterministic functional trajectories over time, including the susceptible trajectory S(t), the infectious trajectory I(t) and the recovered trajectory R(t) for t ≥ 0. This SIR dynamic system is well posed in the sense that non‐negative initial conditions lead to non‐negative solutions of the three functional trajectories. These trajectories collectively demonstrate the evolutionary mechanism of an infectious disease.
The SIR dynamic system in (1) may be interpreted as follows. Let us consider events occurring instantaneously at time t. In the first ODE, the ratio I(t)/N represents the proportion of contagious individuals in the population, which may be thought of as a chance that a person in the at‐risk population may run into a virus carrier. If each individual at risk has an independent chance to meet a contagious person, then, according to the binomial distribution, the expected number of susceptible individuals contracting the virus is S(t)I(t)/N. In reality, a person at risk may run into β (say, 2) contagious individuals, leading to a modified chance βI(t)/N. Thus, instantaneously at time t, the system gains an additional number of infected cases equal to βS(t)I(t)/N, and these cases will leave the susceptible compartment to enter the infectious compartment. Such loss to S(t) is attributed to the negative sign in the first equation. In the second ODE, the first term is the number of new arrivals of contagious individuals and the second term is the loss of contagious individuals at a rate γ who either recover or die and then enter the removed compartment. The third ODE is based on an absorbed compartment that always accumulates with new arrivals with no departure cases. In the literature, the transition rate γ represents the fraction of the infectious population that exits the infectious system per unit time. For example, γ=0.2 means that the infection compartment will decay (or infectious individuals being recovered or dead) at an average rate 20%. In other words, 1/γ describes the expected duration (5 days for γ=0.2) over which an individual stays infectious under the exponential distribution of time for his or her sojourn.
Variations of the form in (1) are often seen in the literature. Among those, the most important SIR specification is given as follows. Because the total population N remains constant over the duration of infection, by dividing both sides of the ordinary differential equations by N, the rates of change in terms of population proportions can be derived, without changing the interpretation of β and γ. That is,
| (2) |
where θ S(t), θ I(t) and θ R(t) are the probabilities (or proportions) of being susceptible, infectious and removed at time t, respectively. Here the probability of being infectious θ I(t) is also known as the prevalence of disease in the epidemiology literature (see, e.g. Osthus et al., 2017; Wang et al., 2020). A clear advantage of this alternative form of the SIR model (2) is that all quantities in the model are adjusted by the population size (which may be allowed to vary in this model formulation), so results obtained from the analyses of data from multiple populations with the SIR model are comparable.
Another formulation of the SIR model is presented as dS(t)/dt=−βS(t)I(t), dI(t)/dt=βS(t)I(t)−γI(t) and dR(t)/dt=γI(t), where the population size N is implicitly absorbed into the parameter of disease transmission rate β, which may be interpreted as a per capita effective contact in proportion to the population (see, e.g. Johnson & McQuarrie, 2009). Despite the differences in notations and presentations, they convey the same infection mechanism, but interpretations need to be given accordingly. Although we use these model specifications exchangeably in this paper, the form given in (2) is recommended to conduct practical studies.
2.2. Reproduction Numbers
Based on the two parameters β and γ in an SIR model, the ratio R 0=β/γ is termed as the basic reproduction number, which captures the expected number of new individuals who directly contract the virus from one contagious individual in an environment with no preventive measures. Intuitively, it is a product of the infection rate β and the infectious duration 1/γ. The basic reproduction number R 0 does not depend on the distribution of people over the three compartments and presents a key appealing disease characteristic for describing and comparing across infectious diseases (see, e.g. Chowell et al., 2004; Ferguson et al., 2006; Khan et al., 2015; Liu et al., 2020). An epidemic is expected to occur when R 0>1, or to disappear when R 0<1. This is because in the SIR model (1), at the condition of S(t)/N≈1, the former is equivalent to β>γ, leading to dI(t)/dt≈(β−γ)I(t)>0, while the latter implies dI(t)/dt<0. The earlier interpretation of R 0 relies on an implicit assumption that all contacts with a contagious individual are susceptible, which contrasts with the effective reproductive number.
The effective reproductive number is defined as . It represents the expected number of newly infected individuals who contract the virus directly from a contagious individual at time t, given that each susceptible individual has a chance of S(t)/N to meet this contagious individual. This is not to be confused with the notation R(t), the removed population. In the early outbreak of an infectious disease in a large population, R e(t)≈R 0 because S(t)/N≈1. In contrast to R 0, which is only descriptive of the disease itself (or the progression of disease near time 0), R e(t) reflects the progression of the infectious disease in a population at any given time because it directs the sign of dI(t)/dt corresponding to acceleration or deceleration of the infection dynamics. This may be seen by the second‐order derivative d 2 I(t)/d t 2; a time, say t ∗, at which d 2 I(t ∗)/d t 2=0 or the rate dI(t ∗)/dt reaches a peak, is referred to as a turning point (see the peak in the middle panel of Figure 2). Hence, R 0 is of most interest during the early phase of an epidemic, whereas R e(t) is of most interest later on during the controlling phases of an epidemic. For example, the so‐called herd immunity is the natural immunity developed when an epidemic reaches R e(t)<1. In other words, without interventions, it requires the proportion of susceptible individuals to be no more than 1/R 0, or the combined proportion of infectious and recovered to be at least 1−1/R 0 in order to contain the spread. As another example, if an effective vaccine becomes available at time , knowing allows us to estimate the remaining proportion of population that needs to be vaccinated in order to control the epidemic (i.e. for achieving R e(t)<1). Figure 3 shows that the effective reproductive number R e(t) for Example 1 decreases as the group of susceptible individuals, S(t), shrinks over time, eventually reaching below the threshold of 1 at time 19. The value at time 0 is R 0=R e(0)=2.5, while R e(19)=1. The time of reaching this threshold also marks a special time of interest—when the number of active contagious individuals starts decreasing at time 19 after reaching its maximum, as shown in the middle panel of Figure 2.
Figure 3.
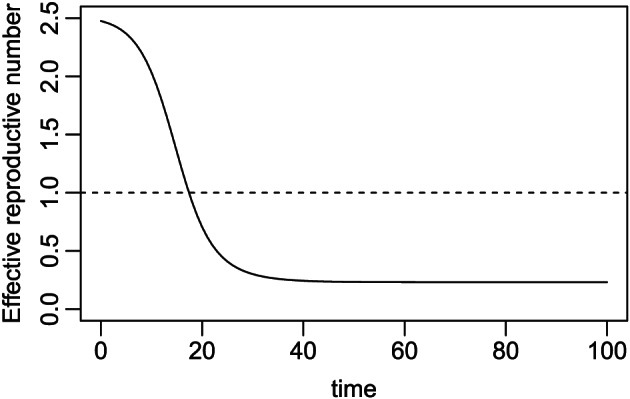
Effective reproductive number over time for Example 1.
2.3. Assumptions and Constraints in the Susceptible–Infectious–Removed Model
Like every mathematical model, there are some assumptions and constraints such as boundary conditions that the SIR model needs to satisfy. These restrictions define the circumstances where the SIR model may be appropriate to use in practice. Although some of them have been mentioned earlier, for the sake of self‐contained summarisation, we list all key assumptions as follows.
- Assumption 1:
- The population involved in the infection is closed with no additions or leakage of individuals, and the size of the population is fixed, say, N. This assumption may be satisfied by an epidemic that is rapid and short lived, during which disease evolution is not affected or is minimally affected by vital changes (e.g. natural births or deaths) and migration (i.e. immigration and emigration). Technically speaking, the three compartments satisfy the condition of the form:
- Assumption 2:
Individuals in the population meet each other randomly in that both probability and degree of interactions with one another remain constant over time, regardless of geographical and demographic factors. This is a strong assumption of homogeneity for the SIR dynamic system that is governed by the same transmission and recovery parameters β and γ. In practice, such a homogeneity assumption may be easily violated. Thus, modelling with heterogeneous dynamics of infection is an important and active research area in the literature on infectious diseases.
- Assumption 3:
One susceptible individual can only develop immunity (or self‐immunisation with antibody against the virus) through infection (i.e. no vaccination). In other words, as shown in Figure 1, the infectious compartment is the only exit of the susceptible compartment, and there is no other state to which an at‐risk individual would move next. Once recovered from infection, one becomes immune to the virus for the remainder of the study period and would not return to be susceptible again. In effect, this is a rigorous definition of recovered case in the SIR model. From a view of the graphic representation in Figure 1, this implies that there is no connection from the removed compartment to the susceptible compartment, or in other words the removed compartment is the terminal state of the infection dynamics. It is worth pointing out that to date the validity of this assumption for the COVID‐19 pandemic remains unknown. In the literature, this condition is assumed for a certain period of time over which risk prediction is considered.
- Assumption 4:
The infection has zero latent period in that one becomes infectious once exposed. This is a key distinction of the SIR model from the SEIR model. Like many infectious diseases, the COVID‐19 has a reported average incubation period of between 4 and 7 days (Li et al., 2020; Pan et al., 2020), which adds some additional complexity in the modelling of infectious disease dynamics. As a matter of fact, this latency of contagion is really the timing of being contagious and not that of being symptomatic. Some studies have found that COVID‐19 carriers are most contagious in the early phase of illness prior to the occurrence of noticeable clinical symptoms (Ip et al., 2017; He et al., 2020). Given these findings, it is tricky to see how the compartment of exposure for incubation would be added to extend the SIR model for the COVID‐19 pandemic.
- Assumption 5:
Because the SIR model has constant transmission and recovery parameters β and γ, which are not time varying, the underlying infection is assumed to evolve in fully neutral environments with no mitigation efforts via external interventions such as a public health policy of social distancing, effective medication or fast testing kits for diagnosis. As far as the COVID‐19 pandemic is concerned, this is the biggest restriction of the SIR model, which is not reflective of the reality—almost all countries with reported COVID‐19 cases have issued various non‐pharmacological control measures. Many researchers have proposed solutions to overcome this unrealistic assumption of the SIR model in the analysis of COVID‐19 data (see, e.g. Wang et al., 2020).
- Assumption 6:
The population size N is large enough to have enough number of incidences, including the number of infections, the number of deaths and the number of recovered cases, so that the SIR model parameters can be stably estimated with high precision. Technically speaking, this is not a model assumption but a condition of sample size for statistical power. Because this mechanistic model will ultimately be used for risk projection, a well‐trained model with reliable data is necessary to not only produce an accurate prediction but also to adequately assess the prediction uncertainty.
Although these six assumptions specifically concern the SIR model, most of these discussions or associated insights are useful to understand the restrictions of SIR model extensions that will be presented in the remaining sections. Knowing possible violations of a certain restriction on a multi‐compartment model in data analyses gives rise to potential new research problems for further investigation.
2.4. Properties of the Susceptible–Infectious–Removed Model
To further understand the mechanism of infection governed by the SIR model, we now give a brief summary of its analytic properties that provide useful guidelines for us to build statistical models and methods to learn the SIR model from available surveillance data from public health databases.
- Property 1:
Strictly speaking, the size of each component population of S(t),I(t) and R(t) is integer valued; however, they are treated as continuous valued. This slight technical drawback vanishes when the probabilities θ S(t), θ I(t) and θ R(t) are used in the SIR model in (2). More importantly, although the dynamic system defined by the SIR model is continuous over time, available surveillance data are reported at discretised measurements over discretised time points. For example, most of the COVID‐19 public databases update data on a daily basis, in which ‘a day’ is the unit of time for measurement. Knowing this discrepancy between the continuous time underlying mechanistic model and the sampling frequency at discrete times for available data is essential to create a statistical framework to link the SIR model with the data at hand.
- Property 2:
The SIR model is deterministic and does not contain any probabilistic components. It is noteworthy that dynamics and stochasticity are two different mathematical properties; a dynamic system (e.g. the SIR model) is not necessarily stochastic, while a stochastic system is not necessarily dynamic. As shown in Figure 2, the compartment sizes S(t),I(t) and R(t) are time‐varying functions with no random fluctuations, which are completely determined by the model parameters and the initial conditions of the SIR model. Obviously, this is a limitation of the SIR model when it is applied for data analysis, where data collection is subject to profuse uncertainties and random errors.
- Property 3:
It is easy to show that the number of individuals at risk (in the entry of the system), S(t), is monotonically non‐increasing and that the number of removed cases (at the exit of the system), R(t), is monotonically non‐decreasing (see Figure 2). Hence, the total number of individuals who have been exposed to a virus is equal to N−S(t)=I(t)+R(t), which is monotonically non‐decreasing. I(t), the number of active contagious cases, or the difference between the two groups of the exposed cases and the recovered cases, can be either increasing or decreasing. The middle panel of Figure 2 nicely conveys such directionality of movements, in which the time of I(t) reaching the peak and the time of I(t) reducing to zero are two important turning points of interest in epidemiology. The former indicates the turning point of disease mitigation, and the latter corresponds to the turning point of disease containment.
- Property 4:
It can be shown that I(∞)=0 (or equivalently, θ I(∞)=0), meaning that the disease will eventually die out. This is because when t→∞, the rate of prevalence θ I(t), given by (βθ S(t)−γ) in (2), will become negative at a certain time and then become more and more negative until converging to zero because θ S(t) is a decreasing function and θ I(t) is bounded in the succeeding text by zero. However, this property of decaying to zero is conditional on the assumptions listed earlier. Violation of Assumptions 1 and 3 are most likely to cause a disease to persist because the monotonicity of S(t) used in the earlier argument is no longer valid. An example of such diseases includes seasonal influenza, where immunity does not last long.
- Property 5:
The SIR model has a recursive property in that at any given time, disease progression (i.e. shapes of the three functions) is only dependent on their current values and not on other information from the past. This property of recursion should not be confused with the Markov property that has exclusively used in the literature of stochastic processes under the conditional probability law. Here there is no probability law involved in the recursive operation, which is indeed a fully deterministic recursion. Such conceptual distinction may help understand the differences between dynamics and stochasticity.
2.5. Extension I: Susceptible–Infectious–Removed Model with Time‐varying Transmission Rate
During an epidemic, various control measures are typically issued by governments to mitigate or contain the spread of the disease. A direct impact of these external interventions is that both the transmission and recovery rates are no longer constant over time. Thus, an important generalisation of the SIR model is to accommodate different degrees of mitigation policies, including social distancing, limiting transportation, mandatory mask wearing and city lockdown. As observed in the ongoing COVID‐19 pandemic, mitigation strategies are changing over time. Limiting mobility of susceptible individuals and medically isolating contagious individuals in the population would reduce the rate of contracting virus, leading to a decreasing disease transmission rate β(t). At the same time, gaining better knowledge on both treatment and self‐management of symptoms and improving medical resources may increase the rate of recovery γ(t) over the course of an epidemic. Incorporating time‐varying parameters into the SIR model leads to an important extension of the basic SIR model (1):
| (3) |
The form of β(t) can be specified mainly in two ways. One is to let β(t) be either a parametric function (e.g. exponential decaying function) or a non‐parametric function (Smirnova et al., 2019; Sun et al., 2020), both of which may be estimated from available data. One useful feature for the use of a parametric function of β(t) is to incorporate seasonality in the transmission rate. It is well known that many infectious diseases spread most quickly in some of the winter months. Especially, respiratory infectious diseases caused by some coronaviruses exhibit seasonal behaviours that are consistent with the trends of temperature and humidity (Barreca & Shimshack, 2012; Sajadi et al., 2020). Accounting for such seasonal periodicity in the model would produce a better long‐term prediction of an epidemic. As the public attention for COVID‐19 pandemic projection gradually shifts from the short term to the long term, it becomes increasingly important to take seasonality into account. Following Dietz (1976), a simple way to introduce seasonality is to assume that the transmission rate β fluctuates over the period of a year:
where β 0 is the average contact rate, σ∈[0,1] is the degree of seasonality with σ=0 reducing the model to the basic SIR model, and ζ∈[0,365) is the offset in time horizon so that peak transmission occurs at t=ζ. Other periodic functions or their combinations can also be used to model seasonality.
As an alternative to a fully non‐parametric function, Wang et al. (2020) assume a form β(t)=βπ(t), 0<π(t) ≤ 1, where π(t) is a known function specified according to given control measures. This specification allows to assess the effectiveness of a target preventive measure, as well as to compare different preventive strategies. Clearly, the model with π(t)≡1 represents disease progression in the absence of any mitigation effort, which sets up the baseline situation in the policy assessment and comparison. The flexibility in specifying π(t) allows easy incorporation of future business reopening events; for example, in the COVID‐19 pandemic, this function may be specified as a U‐shaped curve in that control measures (e.g. social distancing) gradually relax after a certain time point (see more details from Wang et al., 2020, and some numerical results of the COVID‐19 data analysis). More discussions on the time‐varying transmission rate are given in Section 5.5.
2.6. Extension II: Susceptible–Infectious–Removed Model with Vital Dynamics
The assumption of a fixed population size is restrictive, especially when an epidemic remains for a long period of time before it is contained. In this setting, inclusion of natural birth and death dynamics is needed to adequately characterise the time‐varying size of each compartment in the SIR model. First, let μ be the natural birth rate and let ν be the natural death rate. So, the population size will change according to the ODE of the form . In this case, there are three exits for natural deaths, each occurring at one compartment. An extension of the basic SIR model is given as follows:
Noting that S(t)+I(t)+R(t)=N(t), we obtain that as desired. Note that when model (2) is used, N(t) will be automatically absorbed into the proportions and thus no longer appears in the model formulation.
3. Multi‐compartment Mechanistic Models
In this section, we review several four‐compartment mechanistic models as extensions of the basic SIR model introduced in Section 2. Being a simple version of a mechanistic model with three compartments, the SIR model has some limitations in real‐world applications. Thus, extensions of this basic type to account for different disease mechanisms and assumptions have been widely considered in the literature.
3.1. Susceptible–Exposed–Infectious–Removed Model: An Extension with Exposure Compartment
The commonly studied SEIR model takes into account an incubation period by adding an exposed compartment in between susceptible and infectious compartments (see Figure 4). The underlying assumption here is that individuals in this exposure subpopulation have contracted the virus but are not yet contagious and are bound to become contagious. In the current literature, most infectious diseases that are suitable for the SIR model are believed to fit in the SEIR model. The exposed compartment may be regarded as a waiting room for virus carriers who are about to spread the virus in the population. Let δ be the rate for an exposed individual becoming contagious. Then, the basic SIR model can be extended to a four‐compartment model consisting of the following four ODEs:
| (4) |
where E(t) is the size of the exposed compartment at time t. In this case, the compositional constraint becomes S(t)+E(t)+I(t)+R(t)=N, and with N being fixed over time, it implies that . This constraint is clearly satisfied by the SEIR dynamic system defined in (4). Let θ E(t) be the probability (or proportion) of being exposed to the virus. Then, the rates based SIR model (2) can similarly be extended from the model (4) earlier.
Figure 4.

Flow of infection states in the four‐compartment Susceptible–Exposed–Infectious–Removed model.
Technically, the SEIR model often suffers from the issue of parameter identifiability because determining a correct incubation period of an infectious disease and thus the parameter δ is a rather difficult task in practice. First, incubation period varies from one person to another; in the case of COVID‐19, the incubation period ranges from 0 to 15 days, with a median of 5.1 days (Lauer et al., 2020). In another study of COVID‐19 patients in China, Guan et al. (2020) have reported that the estimated incubation period is between 0 to 24 days with a median of 3 days. It is clear that this quantity is very person dependent. Second, ascertainment of contagion may be largely delayed because of shortage of virus testing sources. This length‐biased sampling problem is notoriously challenging for the estimation of the incubation period (Qin et al., 2020). Third, in the literature (e.g. He et al., 2020) researchers found that COVID‐19 carriers tend to be more contagious right after contracting the coronavirus than a week later because they are not self‐quarantined in the absence of clinical symptoms. In other words, in the case of the COVID‐19, the incubation period (or sojourn at exposed state) is too short to play a substantial role in the modelling of the pandemic.
3.2. Susceptible–Exposed–Infectious–Removed–Susceptible Model: An Extension with Reinfection
Not all infectious diseases will develop long‐term immunity. Individuals may develop immunity after recovery only for some time and could lose immunity such that they become susceptible again. Thus, recovered individuals rejoin the susceptible compartment after a certain duration of immunity. This disease evolution is intuitively called the Susceptible–Exposed–Infectious–Removed–Susceptible (SEIRS) model. We assume no death in the removed compartment (see Figure 5 where the recovered branch in the removed compartment is connected to the susceptible compartment). An example of diseases studied using this model includes the common cold. This SEIRS model is defined as follows:
| (5) |
where ξ is the rate of losing immunity and becoming susceptible again after recovery.
Figure 5.
Flow of infection states in the Susceptible–Exposed–Infectious–Removed–Susceptible model.
3.3. Susceptible–Antibody–Infectious–Removed Model: An Extension with Antibody Compartment
Different from the SEIRS model, there are some infectious diseases where long‐term immunity is yielded by individuals who survive from their infection. To build the self‐immunisation into the infection dynamics, Zhou et al. (2020) introduce an antibody (A) compartment to the SIR paradigm, shown in the bottom thread of Figure 6. Because individuals who enter the antibody compartment will no longer be at risk of infection for a certain period of time, this compartment is indeed an exit compartment, at least over a certain time window within which immunity is active, in addition to the removed compartment. In some infectious diseases such as the COVID‐19, the subpopulation of self‐immunised individuals is not directly observed or clinically confirmed by the viral RT‐PCR diagnostic tests because of mild or absent clinical symptoms. They are self‐cured at home with no clinical visits. Adding this compartment in the modelling can help to greatly mitigate the issue of under‐reporting for the actual number of infected cases in the population. This dynamic system consists of four compartments, that is, Susceptible, Self‐immunised, Infectious and Removed, with the following ODEs:
| (6) |
where α is the rate of self‐immunisation, which is not identifiable because of the lack of observed data. An approach to estimating the rate parameter α is to collect data of antibody serological surveys from the population. Refer to Zhou et al. (2020) for more discussions.
Figure 6.

Schematic flow of infection states in the Susceptible–Antibody–Infectious–Removed model.
4. Statistical Methodology: Frequentist Approaches
4.1. Background
This section mainly focuses on an introduction of statistical models to analyse surveillance data of an epidemic. Each statistical model consists of two components: a systematic component and a random component. In the context of infectious disease data analysis, the former may be specified by a dynamic infectious disease model from Sections 2 and 3. The latter is built upon a random sampling scheme that enables a stochastic extension of the mechanistic model (e.g. SIR model) given in the systematic component. Essentially, the notions about disease transmission, recovery or other characteristics are used to define key population attributes or parameters in an infection dynamic system of interest, which will be estimated by available data via a statistical modelling framework, where some covariates may be incorporated to learn some subgroup‐specific risk profiles.
A clear advantage of statistical and stochastic extensions is the ability to quantify uncertainty in both estimation and prediction in connection to sampling variability. This added uncertainty is crucial to policymaking as models not only generate an average estimation or prediction but also present the best and worst possible scenarios for more robust and confident handling of epidemics, given that surveillance data are subject to various issues in the data collection. An example presented in Britton (2010) vividly shows the uncertainty in the progression of an infectious disease. Consider patient zero, who will go on and infect on average R 0 number of other individuals, as defined by a certain disease mechanism. The number of individuals who contract the virus from this patient is in fact stochastic, varying around the expected number of infections R 0, which could be described by a distribution (e.g. Poisson or negative binomial) with mean R 0 on the support of non‐negative integers. With a non‐zero probability of taking the value zero due to the variability in human activities, there is a non‐negligible chance that an epidemic is completely averted. The opposite could be an outbreak with a non‐zero probability that infects tens of thousands of people. Without modelling such uncertainty, we cannot see all these possibilities and associated likelihoods of their occurrences during the course of an epidemic (Roberts et al., 2015). Infectious disease systems governed by the class of multi‐compartment models, though describing the population average, are useful to describe individual‐based stochastic processes if certain random components are introduced into the modelling framework. Thus, the resulting statistical models present more natural approaches to the analysis of surveillance infectious disease data.
Before introducing statistical methodologies that are commonly used for parameter estimation, we distinguish model parameters into two categories. Those that can be determined a priori with no need for estimation, which we term as hyperparameters. Those that cannot be fully determined and need to be estimated using the data at hand, which we term as target parameters. The choices of which parameter should be a target parameter versus a hyperparameter vary widely across methods. Intuitively, the more we know about the biological characteristics of a disease, the more parameters can be held fixed a priori in the analysis. It is however very difficult to determine most of the model parameters early in an outbreak because of the limited amount of knowledge and data about the disease. Indeed, many model parameters are not identifiable because of the lack of relevant data availability. One such example is the rate parameter of immunity α in the SAIR model (6). As relevant knowledge accumulates, literature reveals increasingly precise characterisation of the disease, such as its latency period, recovery rate, death rate, immunity duration and antibody acquirement. Such information is typically obtained from surveys of high‐quality individual‐level data, which may provide much better quantification of these hyperparameters than having to be re‐estimated by epidemic models, which, on the other hand, are largely based on much coarser surveillance data. In the case of the COVID‐19 pandemic, this survey‐based approach may be too costly to carry out in countries with large and heterogeneous populations. In general, target parameters are mostly those that are location specific, for example, transmission rate and fatality rate. They vary largely across regions because of non‐uniform mitigation effort and hospital resources; hence, data‐driven estimations are preferred. In Section 6, we introduce an areal spatial modelling approach to account for spatial heterogeneity in the analysis of infectious disease data.
Because of the issue of parameter identifiability in some mechanistic models, specifying hyperparameters in the model fitting is inevitable. However, holding hyperparameters fixed at certain values according to some external data sources is indeed controversial, and the validity of consequent analyses is highly dependent on the appropriateness of these certain prior values. To relax this technical weakness, later in Section 5, we introduce a Bayesian framework in which such prior information (e.g. hyperparameters) enters the statistical model via certain prior distributions rather fixed values, so that the uncertainty on those hyperparameters is adaptively compensated with the amount and quality of observed surveillance data. Such flexibility has a great advantage in synthesising prior evidence and observed data.
To present this section at a reasonable technical level, most of the discussions in the succeeding text are given in the setting of the basic SIR model, and generalisation to other compartment models should follow with slight modification. In closing, it is noteworthy that the frequentist statistical methods discussed in the succeeding text are based on a fundamental assumption of data collection; that is, the population‐level compartment data S(t), I(t) and R(t), and others if relevant, can be directly collected from the study population. In other words, at given time, every individual in the population can be observed directly for his or her current status of being susceptible, infectious, recovered or died. This is practically impossible. Thus, the interpretation of the estimation results should be carried out with caution.
4.2. Least Squares Estimation
In the SIR model (1), the transmission rate β and recovery rate γ are two target parameters of interest. Estimation of β and γ can be carried out through optimisation in search for a model that best fits to the data. A commonly used minimisation criterion is the least squares loss. Given β and γ, numerical approximations (e.g. Runge–Kutta methods) can be used to solve for the trajectories, S(t),I(t) and R(t). These expected trajectories are then compared with the observed trajectories to compute a discrepancy score, such as the sum (over time) of the squared errors, represented as a loss function of target parameters. Now, it remains to find the estimates of these parameters that give rise to the curve that best fits the data through standard optimisation tools. In this case, the optimisation pertains to a two‐dimensional search, which should be computationally straightforward. Even a greedy search is computationally cheap. We illustrate using both simulated data and real data in Examples 2 and 3, respectively.
Example 2
We first generate an observed sequence of cumulative infectious counts following Example 1, namely, the SIR model with the true parameter values β=0.5 and γ=0.2. For simplicity, we fix γ=0.2 in this example. We then evaluate the sum of squared error (SSE) loss between the expected cumulative infectious count I(t) and its sample counterpart I obs(t), and the value that minimises this loss gives an estimate of β. Figure 7 plots the SSE loss versus β using the simulated data I obs(t), t=1,…,T, with T=10,20,50, respectively. It is found that the SSE loss is minimised at as expected. The longer the observed sequence, the more curved around 0.5 the SSE appears, so the better we can identify the minimum of the SSE curve. The r script shows the example for the case of T=10. Note that the sequence we used to define the fit is I(t), but S(t) and R(t) can also be used in the estimation. Similarly, a two‐dimensional grid search can be used for estimating β and γ jointly when γ is not fixed in which the data of R(t) must be used in the estimation. Here we present only one replicate for illustration.

Figure 7.
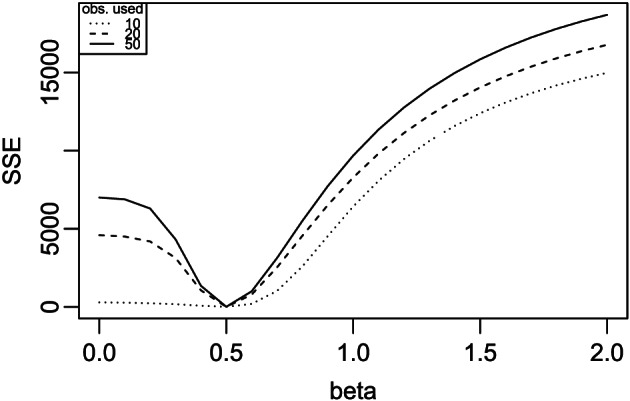
Searching for β in Example 2 using 10, 20 and 50 observations, respectively.
Example 3
We apply the same approach as given in Example 2 for analysing the daily time series of the COVID‐19 cumulative infectious counts in Michigan during 11 March to 1 May 2020. Details of the data are described in Appendix A2, including the I(t) sequence. The already defined SIR function from Example 1 is used as the dynamic model, and the already defined sse function from Example 2 is used as the loss function. By fixing γ=0.2 (i.e. average contagious period of 5 days) the following code computes the solution using the first 10 observations (11 to 20 March). We then increase the number of observations in the estimation; as shown in Figure 8, the value of decreases when more data are used. This is noticeably different from Example 2 where remains constant regardless of the number of observations used. The gradual decrease in our estimate of β indicates a potential reduction in the transmission rate over time in Michigan due to the enforcement of statewide social distancing. In other words, the assumption of a constant transmission rate β is inappropriate for the Michigan data. This result suggests a need for using a more proper modelling technique, which will be demonstrated in Section 5.5.

Figure 8.
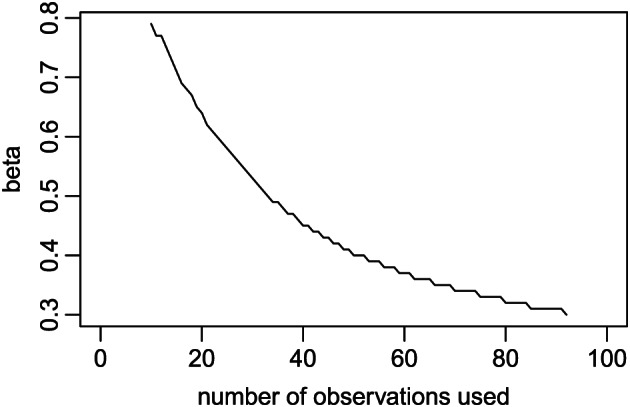
Estimate of β in Example 3 using different lengths of observed I(t) time series.
Being often used as a classic textbook example, this least squares approach is equivalent to the maximum likelihood estimation (MLE) under the assumption that measurement errors are independent and normally distributed with a homogeneous variance. In general, this approach gives consistent estimation and does not require a distributional assumption for the data generation and thus can be applicable to non‐normal data. However, the ordinary least squares loss used in the earlier example assumes that data are independently sampled over time, which is not true because the observations are time series and are thus temporally correlated. Because of this, the least squares estimation is not efficient. Cintrón‐Arias et al. (2009) have discussed the use of a generalised least squares approach to account for more complex error structure, including temporal autocorrelations.
It is not always the best practice to directly use data of I(t) and R(t) in the estimation of the model parameters. The COVID‐19 projection by Gu (https://covid19‐projections.com/) adopts a loss optimisation approach based on the SEIR model using only death counts due to quality concerns with infection counts (e.g. under‐reporting issue). The model uses a discrete state machine with probabilistic transitions to minimise a mixture of loss functions, such as mean squared error, absolute error and ratio error. In the literature, there are many other estimation procedures (e.g. Wallinga & Teunis, 2004; Cori et al., 2013; Thompson et al., 2019). Some of these alternatives do not estimate β and γ, but more directly target the effective reproductive number R e(t) in estimation and inference.
4.3. Method of Moments
Here we present the method of moments, another routine estimation approach in the statistical literature for estimating the model parameters in the SIR model (1). During the early phase of an epidemic, one may assume S(t)/N≈1 and set dt=1 (e.g. a time unit of 1 day for discretisation), so that the second ODE of (1) leads to the approximate exponential function solution:
where without loss of generality I(0)>0 (otherwise time 0 may be redefined in the time series), and T is the last observation time of data collection. Taking the logarithmic transformation, we obtain , which provides a linear mean model with intercept parameter and slope parameter (β−γ) of the covariate time. This slope parameter may be estimated by the least squares method. Likewise, γ may be estimated through another similar approximated linear relationship (without intercept) of the form: ΔR(t)=R(t+1)−R(t)≈γI(t), from the third ODE of the SIR model (1) at discrete times at which data are actually recorded. After estimate is obtained, we obtain immediately. However, the estimation of β is only accurate during the early phase of disease outbreak because the approximation of S(t)/N≈1 is used.
In the literature, other types of moments are also used to derive parameter estimates. For instance, using the approximation from the first ODE of the SIR model (1) at discrete times, one can easily obtain the following expression:
An estimate of β may be obtained by averaging the quantities given in the right‐hand side of the equation earlier. In the case when β(t) varies over time because of changes of a certain mitigation measure, the earlier method of moments estimator may still be applied locally with a possible utility of a kernel weighting function such as the Nadaraya–Watson estimator (Nadaraya, 1964; Watson, 1964). A very similar approach leads to the following approximation:
which may give rise to a non‐parametric estimator of the effective reproductive number. Although R e(t) can be identified at each time point using data solely from t, for numerical stability, the same idea of a kernel weighting (e.g. running‐bin method) smoother is applied to estimate R e(t) at t (see, e.g. Wallinga & Teunis, 2004). Linear approximations are easy to implement; however, the variances produced from such linear fits are typically inadequate in describing the true randomness of an infectious disease to allow valid inference and prediction. Alternatively, it is promising to investigate the local linear fitting method (Cleveland & Devlin, 1988) that produces non‐parametric estimates of the time‐varying model parameters to better reflect temporal dynamics of the infection.
4.4. Probabilistic Transmission and Recovery
In both the least squares estimation and method of moments estimation, there are no explicit assumptions about probability laws for data sampling. Implicitly, both methods are based on the sampling scheme on the entire population; that is, the current status of every individual in the study population is recorded. This is certainly not true in practice. To overcome this, some estimation methods are proposed to account for sampling variability under certain parametric distributions. Distribution assumptions can be made for many quantities in an infectious disease model. Some are fully specified based on given knowledge. For example, the distribution of incubation period of a disease can be represented as a probability mass function by days (Lauer et al., 2020). On the other hand, some distributions are only specified to be from a family of shapes, with the exact form to be estimated. We illustrate the latter using a stochastic SIR model.
Stochastic SIR models typically require the same assumptions as a deterministic SIR model (Section 2.3). To reflect the stochastic nature of disease transmission and recovery, stochastic processes such as a Poisson process are used to model the accumulation of cases. Following the earlier definitions of β and γ, the number of effective contacts in the population is a Poisson process with rate βN. Of these contacts, only those between the contagious and susceptible will lead to new infections. Hence, the counting process defined by the number of exposed (i.e. I(t)+R(t), or equivalently N−S(t)) follows a Poisson process with rate βS(t)I(t)/N. Hence, the number of newly exposed in an instantaneous duration of dt follows a Poisson distribution with mean . On the other hand, the duration of time individuals staying infectious is assumed to be independent and identically distributed according to an exponential distribution with rate γ, and hence, the mean infectious duration is 1/γ. When we jointly consider all I(t) infectious subjects at time t, exit events occur independently with a rate γI(t), and the gap times between two adjacent exits are exponentially distributed with mean 1/{γI(t)}. In summary, the number of removed individuals is a counting process following a Poisson process with rate γI(t). Such stochastic formulation is commonly used, for example, in Bailey (1975) and Andersson and Britton (2000). Through the earlier definitions, S(t),I(t) and R(t) are now random variables that can be directly sampled. In fact, it suffices to assume only two of the three counting processes in order to define a stochastic SIR model due to the constant sample size constraint.
For demonstration, at time t, in an instantaneous time interval [t,t+dt), we may specify a stochastic SIR model as follows:
| (7) |
where I(t)=N−S(t)−R(t). As a result of this probabilistic formulation, the effective reproductive number is now defined as an expectation, that is, R e(t)=E{βS(t)I(t)/N}. The stochastic SIR model (7) is specified in continuous time, and we would hope that dt is very small. In practice, approximation to (7) is used by letting dt=1 or a unit of day, which is typically the smallest time unit used in public surveillance data. As a result, S(t) and R(t) at time t are used to approximate the average in the entire duration of [t,t+1). This approximation turns a continuous time stochastic model into a discrete time scholastic model to proceed with statistical analysis. Other distributions, such as negative binomial or general dispersion family (Song, 2007), may be considered to handle the issue of overdispersion in the counting processes. With distributions in place, we turn the focus to estimation and inference by the maximum likelihood approach.
4.5. Maximum Likelihood Estimation and Inference
Maximum likelihood estimation is often preferred in a parametric model where the underlying probability distribution is properly chosen. For convenience, we take day as the time of unit. By discretising time based on observed sequences, that is, t=0,1,…,T, observed daily increments of counts ΔS(t)=S(t)−S(t+1) in the susceptible compartment and ΔR(t)=R(t+1)−R(t) in the infectious compartment are conditionally independent, given historical accumulated counts S(t) and I(t), according to the definition of model (7). The second model in (7) contains only the removal parameter γ, so the log‐likelihood function of γ with respect to the data of daily increments in the removed compartment, ΔR(t), and daily cumulative counts of infections, I(t), can be written as
where f(k;λ) is the Poisson probability mass function of variable k with mean parameter λ, and ΔR(0)=R(1)−R(0) with R(0)=0 as well as I(0)=1. An estimate of γ can be obtained through the conventional MLE. Likewise, the MLE for β can be obtained from the first Poisson process of model (7). To estimate β and γ jointly, we can write the joint log likelihood of multiple observed sequences of increments. Note that ΔS(t) and ΔR(t) are conditionally independent Poisson random variables, given S(t) and I(t). The log likelihood can be written as
where S(0)=N and I(0)=1. However, one caveat in the simplistic likelihood formulations earlier is that the cumulative time series S(t) and I(t) are assumed to be directly measured without errors. In other words, the earlier likelihood accounts only for the sampling uncertainties in the increments not those in the cumulative counts, so the resulting statistical inference may suffer from underestimated standard errors.
There are two types of statistical inference theory considered in this context, namely, the infill asymptotic theory and the outreach asymptotic theory. The former pertains to the situation where the sampling points increase within a fixed time window (i.e. fixed T), while the latter is a situation of practical relevance where the time window of the data collection tends to infinity (i.e. T→∞). Britton et al. (2019) discuss the infill large‐sample properties under the assumption that the complete epidemic data, that is, continuously observed counting processes (S(t),I(t))t∈[0,T], are available. Under such setting, the asymptotic distribution of the MLE based on continuously observed trajectories is established. Obviously, it is really rare in practice to collect infectious disease data via such infill sampling schemes. Nevertheless, for the sake of theoretical interest, we refer readers to Britton et al.(2019) and references therein.
The outreach large‐sample theory for the MLE with discrete time series data provides a statistical inference relevant to most of infectious disease applications. As an epidemic evolves, the number of equally spaced time points (say, daily) for data collection increases. When sampling errors in both I(t) and S(t) are allowed, the likelihood earlier is indeed a kind of conditional composite likelihood (Varin et al., 2011). Thus, the standard theory of composite likelihood estimation implies that the asymptotic covariance of the estimator is given by the inverse Godambe information matrix (or a sandwich estimator). The sensitivity matrix in the Godambe information is hard to obtain analytically because of the serial dependence in the time series. Instead, one may take a non‐parametric bootstrap approach similar to that considered by Gao and Song (2011) to evaluate the standard errors in order to conduct a valid statistical inference.
Conditional independence is a strong assumption for mathematical convenience in the MLE. Relaxing it has drawn some attention in the literature. For example, Lekone and Finkenstädt (2006) and Allen (2008) construct likelihood‐based approaches using discrete time Markov chain SEIR models; Becker (1977) and Becker and Britton (1999) consider the MLE in the SIR model using martingale methods when all transition events for each individual are observed. It is however unlikely that such individual‐level details are observed in most surveillance data used for modelling of infectious disease mechanisms. Estimators using less detailed data have been proposed (e.g. Becker, 1979; Rida, 1991).
As part of efforts on further relaxing strong conditions in the earlier stochastic SIR model (7), in Section 5.1, we review a state‐space modelling approach that generalises the current likelihood model and estimation framework, where S(t), I(t) and R(t) are not directly measured and rather treated as Markov latent processes. Also, hyperparameters are included via their prior distributions instead of fixed values, and a Bayesian estimation similar to the MLE is established through the MCMC approach. This class of state‐space models is so far one of the most flexible statistical modelling frameworks to analyse infectious disease data.
4.6. Software
We highlight several software packages that are publicly available for estimation of parameters in the multi‐compartment models. Overall, additional efforts in this computational domain are needed. Several packages focus on the estimation and inference for R 0 and R e(t). For example, Obadia et al. (2012), in their r package R0, implements multiple methods, including a method of moments‐type approach (Dietz, 1993), a Bayesian method (Bettencourt & Ribeiro, 2008) and likelihood‐based estimation procedures (Forsberg White & Pagano, 2008; Wallinga & Teunis, 2004; Wallinga & Lipsitch, 2007). Along this line, Cori et al. (2013) and Thompson et al. (2019) develop Bayesian methods to estimate the effective reproductive number and are made available through the r package EpiEstim and Microsoft Excel (https://tools.epidemiology.net/EpiEstim.xls). Their methods use a moving window approach, assuming that the reproduction number R t,τ in this window [t−τ+1,t] is constant. A gamma prior distribution is used to derive the posterior distribution of the R t,τ given new infectious counts.
5. Statistical Methodology: Bayesian Approaches
5.1. State‐space Models
State‐space models refer to a class of linear or non‐linear hierarchical stochastic models with parametric error distributions. The conventional state‐space model is not formulated as a Bayesian model, but later, its Bayesian formulation has gained great popularity because of the availability of MCMC methods for the estimation of the model parameters (Carlin et al., 1992). This class of models primarily attempts to explain the dynamic features of time series of continuous and discrete variables. In particular, it has been used to model the time series of proportions associated with multi‐compartment models given in (2) (see Osthus et al., 2017, for seasonal influenza, and Wang et al., 2020, for the COVID‐19 pandemic, among others).
The state‐space model framework is advantageous over the stochastic compartment models introduced in Section 4.4 in the following aspects of statistical modelling: (i) state‐space model does not assume that the compartment processes S(t), I(t) and R(t) are directly observed, which are treated as latent processes to be estimated from observed data. (ii) State‐space model allows an explicit sampling scheme to be part of the model specification, which enables the quantification of both estimation and prediction uncertainties in the statistical analysis. (iii) State‐space model is built upon the compartment probabilities (or rates or proportions) that automatically adjust for potentially varying population sizes. This conveniently relaxes the condition of a constant population size in the basic SIR model. (iv) State‐space model provides a flexible statistical modelling framework that embraces time‐varying model parameters and integrates prior knowledge of disease mechanisms (e.g. R 0 value from other studies) via prior distributions of the model parameters. (v) Implementation of MCMC methods in state‐space modelling provides a powerful approach to parameter estimation and predictions using conditional distributions given the history. This is different from all estimation methods in Section 4 that are always formulated via marginal distributions under strong assumptions of sampling rules.
A state‐space model consists of two stochastic processes: a d‐dimensional observation process {Y t} and a q‐dimensional state process {θ t} given as follows:
-
•
The state process θ 0,θ 1,… is a Markov chain with initial condition θ 0∼p 0(θ), and transition (conditional) distribution is given by Y t|θ t∼f t(y|θ t).
-
•
The observation process {Y t} is conditionally independent given the state process {θ t,t ≥ 0}, and each Y t is conditionally independent of θ s,s≠t; given θ t, the conditional distribution is Y t|θ t∼f t(y|θ t).
This model can be graphically presented by a comb structure shown in Figure 9. According to Cox et al. (1981), the state‐space model is a parameter‐driven model in that the processes of the compartment proportions are unknown population parameters to be estimated, while the stochastic multi‐compartment model such as the stochastic SIR model in (7) is a data‐driven model where the compartment proportions are directly observed. As pointed out earlier, the validity of the latter is questionable in practice, especially in the analysis of the COVID‐19 pandemic data.
Figure 9.
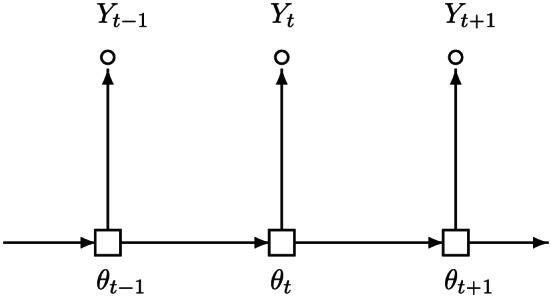
Graphical representation of a state‐space model.
Let Y s be the collection of all observations up to time s, namely, Y s=(Y 1,…,Y s). Let τ be a generic notation for the set of model parameters. Denote the conditional density of θ t, given Y s=y s, by f t|s(θ|y s,τ). Then, the prediction, filter or smoother density is defined, respectively, according to whether t>s, t=s or t<s. This conditional density f t|s(θ|y s,τ) is the key component of statistical inference in state‐space models.
To develop the maximum likelihood inference for model parameters in state‐space models, the one‐step prediction densities f t|t−1 are the key components for the computation of the likelihood function (see Chapter 10 of Song, 2007). Given a time series data {Y t,t=1,…,n}, the likelihood of Y n is
| (8) |
where f 1(Y 1;τ) is expressed as follows:
where by convention, g 1(θ 1;τ)=f 1|0(θ 1|Y 0;τ), conditional on an initial observation Y 0 at time 0.
In the earlier likelihood evaluation, one‐step prediction densities, f t|t−1, and filter densities, f t|t, can be respectively given by the recursions
| (9) |
| (10) |
with the recursion starting with f 0|0(θ)=p 0(θ). In general, exact evaluation of the integrals in (9) and (10) is analytically unavailable, unless in some simple situations, such as both processes being linear and normally distributed. For the linear Gaussian state‐space model, all f t|s are Gaussian, so the first two moments of (9) and (10) can be easily derived from the conventional Kalman filtering procedure, as discussed in Chapter 9 of Song (2007). However, with some computational costs, all integrals in the earlier likelihood and the filter can be evaluated numerically by MCMC methods.
5.2. State‐space Models for Compartment Proportions
Recently, Wang et al. (2020) have developed an extended SIR (eSIR) model that is built upon a state‐space model with two (d=2) observed time series of daily proportions of infectious and removed cases, denoted by and , which are generated from the q‐dimensional underlying infection dynamics {θ t,t ≥ 0} governed by a mechanistic SIR model. In the case of the SIR model, q=3. As shown in Figure 9, the latent process is a time series of the three‐dimensional latent vector of population probabilities that satisfies a three‐dimensional Markov process of the following form:
| (11) |
where parameter κ scales the variance. The function f(·) is a three‐dimensional vector as a solution to the SIR model (2), which determines the mean of the Dirichlet distribution via the RK4 approximation. In comparison with the stochastic SIR model in (7), here the compartment proportions θ t are unobserved and explicitly modelled by a Markov process to account for temporal correlations, so the parameter estimation can be carried out with multivariate likelihood functions. Because the serial dependence is accounted for in the state‐space model, the resulting estimation and prediction are more powerful than those given in Section 4.5.
Two observed time series that are emitted from the underlying latent dynamics of infection θ t are assumed to follow the beta distributions at time t:
| (12) |
| (13) |
where and are the respective probabilities of being infectious and removed at time t, and λ I and λ R are the parameters controlling the respective variances of the observed proportions. It is easy to see that and are conditionally independent given θ t, and and , and τ=(λ I,λ R,κ,β,γ). Because and share a common latent variable θ t, their marginal correlation is modelled. In fact, these two beta distributions define a sampling scheme of observed data, including daily empirical proportions of infectious cases and removed cases, which are a collection of daily signals from the underlying latent SIR infection dynamic system.
5.2.1. Application I—extended Susceptible–Infectious–Removed model
The earlier state‐space model (11), (12) and (13) is useful to assess the effectiveness of control measures (e.g. social distancing) via the projected epidemic evolution in the future time. To process, one can replace the constant transmission rate β by a time‐varying transmission rate βπ(t), where π(t) is a given transmission rate modifier. It is specified as a function in time to reflect different forms and strengths of control measures. This results in an eSIR model proposed by Wang et al. (2020):
where π(t) ≥ 0. Obviously, the basic SIR model is a special case with no intervention in place, π(t)≡1. In general, the π(t) may be specified by a practitioner to reflect a particular control measure. For an example of the COVID‐19 in Hubei Province, China, a possible choice of π(t) given in the following is a step function that reflects government‐initiated macroisolation measures:
When π 0=(π 01,π 02,π 03,π 04) are chosen with different values, as shown in Figure 10(A)–(C), we obtain different types of transmission rate modifiers. Alternatively, π(t) can be a continuous function, say, or , that reflects steadily increased community‐level surveillance and personal protection (wearing face masks and washing hands) as shown in Figure 10(D)–(F). Note that this modifier function does not have to be a monotonic decreasing function and may take a U‐shape to capture the relaxation of control measures. With such a modelling framework, one can carry out comparisons of different preventive protocols via the resulting projected infection risk θ I(t) or other epidemic features such as the time of the effective reproduction number R e(t)<1 and the time of a disease recurrence associated with relaxed control measures.
Figure 10.
Different types of transmission rate modifiers π(t) and the quarantine rate ϕ(t): (A–C) step functions with π 0=(π 01,π 02,π 03,π 04) equal to (1,1,1,1), (1,0.9,0.8,0.5) and (1,0.9,0.5,0.1) at change points (23 January, 4 February and 8 February). (D–F) Exponential functions under difference microquarantine measures over time with λ 0=0.01, λ 0=0.05 and λ 0=0.1. (G–I) Multi‐point instantaneous quarantine rates with ϕ 0=(0,0,0,0), ϕ 0=(0.1,0.4,0.3) and ϕ 0=(0,0.9,0) at change points of (23 January, 4 February and 8 February). [Colour figure can be viewed at wileyonlinelibrary.com]
5.2.2. Application II—Susceptible–Quarantined–Infectious–Removed model
A clear advantage of the state‐space model is that it enjoys the resilience of MCMC being a primary method for statistical estimation and prediction. In other words, the statistical analysis methods can be easily modified to accommodate changes made in the latent multi‐compartment models and/or in the observed time series models. One example of the COVID‐19 pandemic modelling given in Wang et al. (2020) is to extend the three‐compartment eSIR model to a four‐compartment model by incorporating stringent quarantine measures issued by the Hubei government via a new addition of in‐home quarantine compartment. This new model is termed as Susceptible–Quarantined–Infectious–Removed (SQIR) model. This quarantine compartment collects in‐home isolated individuals who would have no chance of meeting any infectious individuals in the infection system. So, it is another exit from the dynamic system in addition to the removed compartment. Let ϕ(t) be the chance of a susceptible person being willing to take in‐home isolation at time t. The basic SIR model in Equation (2) is then extended to include a four‐dimensional latent process :
| (14) |
where . The quarantine rate ϕ(t) may be specified as a Dirac delta function with jumps at times when major quarantine policies are issued by the government. For example, one may specify the time‐dependent quarantine rate function ϕ(t) for Hubei Province as follows:
Note that at each jump, the respective proportion of individuals would leave the susceptible compartment and enter the quarantine compartment. Figure 10(G)–(I) shows three different types of in‐home quarantine rates during the period of the COVID‐19 pandemic in Hubei Province.
5.2.3. Application III—Susceptible–Antibody–Infectious–Removed model
In a similar spirit to the SQIR example of Application II earlier, Zhou et al. (2020) consider an interesting extension of the basic SIR model in the analysis of the US COVID‐19 data to include an antibody compartment to handle the subpopulation of self‐immunised individuals. This four‐compartment model is termed as SAIR model, which has been discussed in detail in Section 3.3. Because the antibody compartment is also a second exit from the infection system, similar to the quarantine compartment, one can turn the SAIR model given in (6) into a similar form of the SQIR model in (14), where ϕ(t) is replaced by α(t), the rate of self‐immunisation. It is known that the population immunity rate cannot be estimated from observed surveillance data, which needs to be figured out by using large‐scale serological surveys in the population. Thus, α(t) may be specified as a Dirac delta function (e.g. Figure 10(G)–(I)) with jumps at times when the surveys are conducted and function values based on the survey results. It is worth pointing out that although the SQIR and SAIR models have very similar model structures, their interpretations are very different. The former is applicable to the case of very stringent self‐isolation control measures in Hubei, while the latter is reflective to the situation of self‐immunisation due to mild control measures in the USA, so that a substantial proportion of individuals who contracted the virus, recovered and became immunised.
5.3. Estimation and Prediction via Markov Chain Monte Carlo
Markov chain Monte Carlo has been extensively used for the estimation and prediction in the state‐space model (see, e.g. Carlin et al., 1992; Chan & Ledolter, 1995; Czado & Song, 2008; De Jong & Shephard, 1995; Zhu et al., 2011, for a vast literature on this topic). Such popularity of MCMC in the state‐space model is rooted in its power to handle the evaluation of high‐dimensional integrals involved in the likelihood function (8). The essential strategy for the calculation of each high‐dimensional integral is to approximate it by a sample mean of the involved integrand. This sample average is obtained from many MCMC sample draws from posterior distributions of the model parameters, including the time series of the latent probability vector θ t.
Let t 0 be the current time up to which we have observed data . Performing M draws of for t∈[0,t 0]∪[t 0+1,T] may produce both the in‐sample draws over [0,t 0] and the out‐sample draws over [t 0+1,T]. The sampling scheme proceeds as follows: for each m=1,…,M,
-
(1)
draw τ (m) from the posterior ;
-
(2)
draw from the posterior of the q‐dimensional latent process, at t=1,…,t 0,t 0+1,…,T;
-
(3)
draw from and according to the observed process, at t=1,…,t 0,t 0+1,…,T, respectively.
Prior distributions are specified for some of the hyperparameters; for example, , R 0=β/γ and γ follow some log‐normal distributions, and λ I, λ R and κ follow some gamma distributions or inverse gamma distributions, respectively.
Convergence diagnostics of the MCMC algorithm may use standard diagnostic tools such as the Gelman–Rubin statistic based on multiple chains with different initial values, monitoring trace plots of the model parameters and so forth. The r package coda provides a comprehensive toolbox of convergence diagnostics (Brooks & Gelman, 1998). Using the MCMC draws collected after the burn‐in, various summary statistics may be obtained to estimate model parameters, conduct inference and make prediction. The summary statistics (e.g. posterior mean and posterior mode) from the in‐sample draws of the model parameters can provide point estimates and 95% credible intervals with the left and right limits set respectively at the 2.5th percentile and 97.5th percentile, and those of the observed processes may be used to check the goodness of fit of a proposed model and to perform model selection via the deviance information criterion (Spiegelhalter et al., 2002; Gelman et al., 2013). More importantly, the summary statistics from the out‐sample draws of the latent process θ t,t>t 0 provide point predictions and their 95% credible prediction intervals. It is interesting to note that the earlier MCMC implementation does not depend much on the form of the Runge–Kutta solution f(θ t−1,β,γ) in the latent process (11). As long as a mechanistic infectious disease model has an approximate analytic solution f(·), the Bayesian estimation and inference can be carried out using MCMC. Such flexibility is appealing to develop software applicable for a broad range of practical studies.
MCMC procedures are well suited for the estimation and inference in the setting of state‐space models because of fast and reliable numerical performances. For the Michigan data analysis example in Section 5.5, using an average personal computer, we spend 1.5 h completing all MCMC calculations of 200 000 draws with thinning bin size of 10 after the burn‐in judged by four separate MCMC chains. This computing speed can be improved by using high‐performance computing facilities and/or some recent posterior sampling methods. As suggested by Zhou and Ji (2020) for a state‐space SIR model, one may set a more efficient sampler over highly correlated posterior spaces by parallel‐tempering MCMC algorithm (Geyer, 1991), which provides rapid mixing in MCMC chains. Also, along the line of online learning, sequential Monte Carlo methods for posterior sampling (Doucet et al., 2001; Dukic et al., 2012) are promising, as they permit efficient updating of existing posteriors with sequentially arrived data, in the hope to avoid refitting the model by running MCMC from scratch using the updated complete data.
5.4. Software
Wang et al. (2020) and Zhou et al. (2020) have developed a series of extended SIR models by introducing time‐varying transmission rate, quarantine process and asymptomatic immunisation process (details in Section 5.2). The proposed methods have been established in an open‐source r package eSIR, available on GitHub (https://github.com/lilywang1988/eSIR). This package calls rjags to generate MCMC chains and retains a few MCMC controllers from rjags. The package is also updated weekly with new summarised US state‐level count data for the COVID‐19 pandemic.
Several robust methods that are developed specifically for the prediction of the COVID‐19 are cited by the Centers for Disease Control and Prevention (https://www.cdc.gov/coronavirus/2019‐ncov/covid‐data/forecasting‐us.html). To name a few, the Bayesian approach (Verity et al., 2020) developed by researchers at Imperial College London (featured in Adam, 2020) and the hybrid modelling approach (IHME COVID‐19 health service utilization forecasting team & Murray, 2020) adopted by the University of Washington Institute for Health Metrics and Evaluation (IHME) (discussed by Jewell et al., 2020) have attracted great public and government attention. We refer to their original work for modelling details. It is difficult to appreciate the original work and followed comments without running real COVID‐19 data using their software, which is lacking for the IHME models, among some others. To increase research transparency, releasing software or computing code used in statistical methods to the public is strongly encouraged.
5.5. Example: Analysis of Michigan State‐level Data
We now illustrate the use of r package eSIR to analyse the COVID‐19 surveillance data during the period of 11 March to 9 June 2020 from Michigan state, USA. The Michigan data used in this analysis are listed in Appendix A2, including both I(t) and R(t). In the data analysis, we demonstrate the use of both the state‐space model described in Application I and the MCMC method, where the transmission rate modifier π(t) is set as exponential functions. From package eSIR, we can extract many useful statistics related to estimation and forecasting. For example, we can obtain both mean and median projections of the prevalence curve θ I(t),t>t 0 as well as their 95% credible prediction intervals. In addition, this package provides the estimated first and second turning points of an epidemic. The former is the time when the daily number of new infectious cases stops increasing, while the latter is the date when the daily number of new infections becomes zero. Mathematically, the first corresponds to the time t at which or the gradient of is zero, and the second is the time t at which the rate of prevalence is zero The following is the r script to perform the data analysis:

In the above program, we consider a time‐dependent declining transmission rate with the modifier value where the parameter λ 0 is chosen so that the modifier equals to 0.6 on 2 May. This value is determined based on the social distancing scoreboard posted by Unacast, Inc. (https://www.unacast.com/covid19/social‐distancing‐scoreboard). One needs to set exponential = TRUE, to activate such setting. Alternatively, as shown in Figure 10(A)–(C), one may use a step function by providing a vector of pi0, values and the corresponding vector of changes dates in change_time. In the main function above, we let the starting date be 11 March and conduct the estimation and projection of 200 days ahead (T_fin = 200) on 10 June and after. We run four separate MCMC chains with different initial values, each with length of 5×105, kept from every 10 draws (thn = 10) (a thinning operation to reduce autocorrelations) after 2×105 draws are dropped. Thus, with a relatively squandering setting, we expect a better performance of convergence and reliable quantification of prediction uncertainty using sample quantiles.
There are two different prior settings for sensitivity analysis. One follows the example code earlier, with the prior mean for the log‐normal distribution of the basic reproduction number to be 3.5, the removal rate 0.1 and thus the mean transmission rate 0.35, and the other with all these values to be 4, 0.2 and 0.8, respectively. The two distinct settings provide similar estimating and forecast results as can be seen in Figure 11. Their estimated reproduction numbers are 3.154 (95% credible interval [2.162, 4.369]) and 3.143 (95% credible interval [2.294, 4.147]), respectively, which are similar considering that their prior settings are quite different. The output Gelman–Rubin statistic developed by Gelman and Rubin (1992) are close to 1 (data not shown). Both pieces of evidence as well as stationary trace plots warrant the convergence of the MCMC chains. One can further check the quality of the MCMC draws through the output by setting save_mcmc = TRUE. The estimation and forecast plots for the rates of infection and removal compartments, diagnostic trace plots and other useful ancillary plots are automatically saved under the directory assigned via file_add by setting save_plot_data = TRUE. Other statistics for the posterior distributions of the parameters and dates of turning points can be saved by setting save_files = TRUE.
Figure 11.

Estimation and forecast from two different prior settings. The cyan areas denote the 95% in‐sample credible intervals of prevalence 9 June, and the salmon areas denote the 95% out‐sample credible intervals of the projected prevalence 10 June, of confirmed infectious cases. The grey and red curves denote the posterior mean and median of the prevalence 10 June, respectively. The vertical lines denote the landmark dates with the maximum increasing rate (green), the maximum prevalence value (purple) and the last observation (blue), respectively. [Colour figure can be viewed at wileyonlinelibrary.com]
The Michigan COVID‐19 data have been preprocessed to smooth away some unnatural gaps caused by the clustered reporting issue as discussed in Appendix A2. Figure 11 shows an adequate model fitting, where all observed numbers of confirmed infections fall in the 95% in‐sample credible intervals of prevalence 9 June. In contrast, the 95% out‐sample credible intervals of the projected proportion ( ) are much wider, reflecting to the significant amount of uncertainty in the prediction. Such uncertainty elevates as the time moves further away from the present time. Despite the large uncertainty, the projected mean and median prevalence curves show a decreasing trend over time, which means that the social distancing works to mitigate the epidemic in Michigan although the rate of improvement is moderate. Also the fact that the two estimated turning points have occurred before 9 June is another piece of evidence for the positive effects of the series of social distancing orders issued by the state governor since 23 March 2020.
Model diagnosis is an important part of a statistical analysis, which is typically conducted using various residual plots. As illustration, in this Michigan data analysis, let be the posterior means over the period of 11 March to 9 June. We consider residuals of the two observed processes, defined by and , noting from (12) and (13) that and . To check the conditional independence between and , we make a scatter plot (the top row of Figure 12) of residuals versus residuals , where two large residuals (not outliers) are excluded in order to display the detailed patterns of their relationship. Clearly, in this plot, all points are randomly distributed with no clear patterns, which confirms the assumption of conditional independence of the two observed processes, as well as approximately constant variances. We also plot partial autocorrelation functions (partial ACF) of the posterior means of the latent processes to check if the first‐order Markov process is appropriate. The bottom row of Figure 12 shows that there are dominant lag‐1 autocorrelation (the three coefficients are about 0.97) and no any additional significant autocorrelations beyond the lag‐1 dependence. This confirms the assumption that the three latent processes are all the first‐order Markov processes.
Figure 12.

Top: a scatter plot of the residuals of the two observed processes and . Bottom: partial autocorrelation functions of the posterior means of the latent processes, , and . [Colour figure can be viewed at wileyonlinelibrary.com]
6. Spatio‐temporal Multi‐compartment Models
6.1. Modelling of Infections Disease with Spatial Heterogeneity
All mechanistic models discussed in the previous sections are useful to analyse the infection dynamics for a large population such as a country or a state in which most of model parameters may be assumed to be homogeneous and representing the entire population. This type of macromodelling approach is particularly valuable at the early phase of disease outbreak when the national public health administration aims to come up with nationwide macrointervention protocols with very limited amounts of relevant data available. Once an epidemic evolves further into its middle phase, with more and more surveillance data collected from local communities, a macromodel is no longer suitable for an in‐depth analysis of microinfection dynamics owing to the existence of substantial heterogeneity across local communities. This section concerns a review of significant extensions of infectious disease models by incorporating spatial heterogeneity across different geographical locations into modelling and analysis. The focus will be on the recent development of integrating the classical spatial cellular automata (CA) (von Neumann & Burks, 1966) with the previously discussed temporal multi‐compartment models, leading to an important class of spatio‐temporal multi‐compartment models. This class of models is useful to predict local infection risk.
Technically speaking, the majority of existing macromechanistic models to study the spread of infectious disease are based on the assumption that the system is homogeneous in space. This means that the spatial characteristics that could potentially play a non‐trivial role in the development and outcome of disease infection are not taken into consideration. This is a valid assumption if the population vulnerable to the infectious disease is mixed well and the human interventions (e.g. vaccination strategies) are homogeneous across different spatial locations. However, in reality, there exists substantial heterogeneity in the urbanisation, ethnic distribution, political views, governance and economic composition across different subgroups of individuals distributed over geographical locations, all of which will influence the spread of infectious disease and make the previous macromechanistic model not appropriate to address the dynamics spatially. One possible extension is to utilise partial differential equations (PDEs) (Murray et al., 1986) in spatial homogeneity, which is relaxed to allow area‐specific spread patterns of epidemics. As noted in the literature, one limitation of PDEs is that this approach ignores the fact that infectious disease is spread through person‐to‐person interactions, rather than by a continuous population. Thus, PDEs may lead to impractical results about the dynamics of an epidemic (Mollison, 1991). A natural strategy is to embrace a micromodel mimicking an interactive particle system, and CA is one of the well‐studied systems with the strength of modelling spatially varying infection dynamics. Originated in the works of von Neumann and Burks (1966) and Ulam (1962), the CA paradigm has been used in many applied fields, including the modelling of infectious diseases.
6.2. Building a General Cellular Automaton
When applied to model spatial variations of epidemic spread, CA has three distinctive features: (i) it treats individuals as discrete entities in order to study person‐level movements in the infection dynamics. This high‐resolution paradigm necessitates the incorporation of individual's heterogeneity such as residential address, age, race, pre‐existing medical conditions and others in the modelling. In surveillance data, geographical information is publicly available (e.g. county that an individual lives), so it is feasible to utilise this variable in the extension of the macromechanistic model. (ii) CA allows to introduce local stochasticity; for example, the CA paradigm may be built upon a person‐to‐person infectious mechanism if individual‐level information is available; otherwise, it may be based on a group‐group infection process. (iii) CA is formulated in a network of particles (e.g. individuals, groups, villages and counties) with certain rules of connectivity and stochastic laws of disease transmission. This network topology is well suited for computations and simulations. Because of these unique advantages, the CA paradigm has been employed by researches as an efficient method to study spread patterns of epidemics (Beauchemin et al., 2005; Ahmed & Agiza, 1998; Boccara et al., 1994; Quan‐Xing & Zhen, 2005; Fuks & Lawniczak, 2001; Willox et al., 2003; Rousseau et al., 1997; Sirakoulis et al., 2000; Fuentes & Kuperman, 1999; Liu et al., 2006; Yakowitz et al., 1990; Sun et al., 2011).
In the modelling of infectious diseases, the basic CA formulation involves three primary components: (i) a two‐way array of cells (e.g. an age group or a county) that contain groups of individuals under study, and each individual belongs to one cell; (ii) a set of discrete states (e.g. susceptible, self‐immunised, contagious, recovered and death) that describe different conditions of individuals during an epidemic; and (iii) some specific rules or updating functions that determine spatially how local interactions with a target cell from its neighbouring cells can influence and change the states of individuals in the target cell; all cells in a CA system achieve a global propagation of infection status updates instantaneously and continuously. In the application of the CA, determining neighbouring cells is tricky, and different types of neighbourhood topology have been proposed in the literature, including von Neumann neighbourhood, Moore neighbourhood, MvonN neighbourhood and extended neighbourhood (Hasani & Tavakkoli, 2007) (see Figure 13 for an example of these four neighbourhood types).
Figure 13.
One‐step forward evolution of the infection prevalence (× 103) for the central cell in the simulation study. Four different neighbourhood types are illustrated, including (A) von Neumann neighbourhood, (B) Moore neighbourhood, (C) MvonN neighbourhood and (D) extended neighbourhood. The numeric value indicates the proportion of infectious people in each cell. The letter indicates target (T) or neighbour (N) cells, respectively. [Colour figure can be viewed at wileyonlinelibrary.com]
In the modelling of influenza A viral infections, Beauchemin et al. (2005) use a simple two‐dimensional CA model to investigate the influence of spatial heterogeneity on viral kinetics. Their study population consists of two types of cell species, the epithelial cells and the immune cells. The epithelial cells are the target of viral infection, and the immune cells are those fighting the infection. The CA model is built upon a two‐dimensional square lattice with the Moore neighbourhood (see Figure 13(B)), where the condition of a certain cell will only be influenced by the eight closest cells around it. The set of states for the epithelial cells include healthy, infected, expressing, infectious or dead, while an immune cell can be in any of two states: virgin or mature. Decision rules of updating the CA system are governed by parameters, such as INFECT_RATE that models the probability of a healthy epithelial cell being infected by contacting each infectious nearest neighbour. Detailed updating functions are discussed in Beauchemin et al. (2005). Simulations show that the proposed CA model is sophisticated enough to reproduce the basic dynamic features of the cell‐to‐cell infection.
Different from the modelling of the influenza A viral infection earlier, Fuks and Lawniczak (2001) propose a lattice gas CA that is closely connected to an SIR framework of an epidemic, where the interacting patterns of individuals are modelled. It is assumed that the status of individuals will change between three types, susceptible, infectious and recovered, denoted as {S,I,R}. The space where the epidemic takes place is set as a group of regular hexagonal cells, in which the individuals are located at the centre of each cell and can move through a channel that is created by connecting two centres of adjacent cells. The evolution of the CA occurs at discrete time steps under the operation of three basic functions, including contact C, randomisation R and propagation P. With the application of function C, an individual who is susceptible can become infected with probability , where β is the transmission rate and N I is the number of infectious individuals within the same cell. Meanwhile, an individual who is infectious can recover with probability γ, where γ is the recovery rate. The function R randomly assigns individuals in each cell to move through the channels, which contributes to modelling the mixing process of individuals. In the final propagation step, individuals simultaneously move to the cells that they are randomly assigned to by R. In addition to the basic epidemic dynamics modelled by the proposed lattice gas CA, Fuks and Lawniczak (2001) also study the effect of heterogeneous spatial distribution of individuals with states S, I and R and the influence of different types of barriers in controlling the spread of an epidemic.
6.3. Building an Susceptible–Infectious–Removed Cellular Automaton
Although the two applications discussed earlier in Section 6.2 give a framework of how CA models the dynamics of epidemic spread, White et al. (2007) provide a more direct incorporation of spatial CA with the temporal SIR compartments at the population level, where each cell stands for a small population (e.g. a county) with different proportions of susceptible, infectious or recovered individuals. The resulting CA‐SIR given in White et al. (2007) is formulated by four parts (C, Q, V and f). First, C={(i,j),1 ≤ i ≤ r,1 ≤ j ≤ c} defines the cellular space, or a collection of r×c cells on a two‐way array, where r×c is referred to the dimension of the cells. Second, Q represents a finite set that contains all the possible states of a cellular space. In the case of the SIR model, Q={S,I,R} corresponding to the susceptible, infectious and removed states. Third, V={(p k,q k),1 ≤ k ≤ n} is the finite set of indices defining the neighbourhood of each cell, and consequently, V ij={(i+p 1,j+q 1),…,(i+p n,j+q n)} denotes the set of neighbouring cells for the central cell (i,j). Specifically, V ∗=V−{(0,0)} represents all the neighbouring cells without the cell at the centre of consideration. Fourth, function f stands for certain updating rules to govern the dynamics of interactions between cells in the a CA‐SIR system. For each cell at a discrete time t (say, today), its current status is described by three cell‐specific compartments , and , where , and represent the cell‐specific probabilities of being susceptible, infectious and recovered, respectively. Clearly, to form a microcell‐level SIR model. The CA‐SIR model is updated based on the following transition functions: for cell (i,j)∈V,
| (15) |
where β is the population macrotransmission rate and γ is the population macrorecovery rate. First, when the set V ∗=∅, that is, an empty set, the CA‐SIR model for cell (i,j) reduces a cell‐level SIR model similar to that given in (2). Second, the numerator is the expected number of infectious cases yesterday (time t−1) in a neighbouring cell (p,q)∈V ∗ whose cell population is N i+p,j+q. So, the ratio is an empirical probability that a person in cell (i,j) randomly runs in a contagious person from its neighbouring cell (p,q). Third, this random chance is weighted by a factor of intercell connectivity, denoted by ; the stronger tie of cell (i,j) with cell (p,q), the higher likelihood of a person from cell (i,j) running in contagious individuals in cell (p,q). Fourth, summing up all such likelihoods gives a total likelihood that an individual from cell (i,j) would run in the virus carriers from all the neighbouring cells. A typical form of the intercell connectivity coefficient is given by , where and are broadly defined as a connection factor and a movement factor, respectively. They are used to characterise the intercell mobility or how easily individuals in the cells can move between the centre cell and its neighbouring cells. This CA‐SIR system, which is integrated with the SIR model, can serve as a basis for the development of useful algorithms to emulate real‐world epidemic infection spatially.
Example 4
We perform a simulation study to illustrate the one‐step ahead evolution of the infection dynamics in a simple CA‐SIR model (15). Assume that there is a 5×5 square array of 25 cells that hold the population under the study of a certain epidemic. Our target cell is the one at the centre (see Figure 13). The prevalence of infection in the central cell is influenced by its neighbouring cells, for which different types are considered, including von Neumann neighbourhood, Moore neighbourhood, MvonN neighbourhood and extended neighbourhood (all cells in the array are neighbouring cells). For simplicity, we assume that all the cells have the same population size. At time t 0, the prevalence of being infectious in each cell c, except for the central one, is simulated from a Uniform U(0,0.01) distribution. We intentionally set I c(t 0)=0 for the central cell to clearly show the change of infection after a one‐step evolution at time t 0+1. It is set that the macrotransmission rate β=0.5 and the recovery rate γ=0.2. For those cells within the neighbourhood of consideration, it is specified that c pq=1 and m pq=0.5 if a cell is a ‘near’ neighbour (i.e. if the cell shares a common edge or vertex with the target cell) and c pq=0.5 and m pq=0.25 for a ‘distant’ neighbour cell. The prevalence of being infectious in the central cell is updated using the second model in Equation (15). The codes for data simulation are listed as follows, and the infection prevalence updates for the central cell and for all its neighbouring cells are shown in Figure 13.


6.4. Spatio‐temporal Models for Infectious Diseases
Based on the basic CA‐SIR model proposed in White et al. (2007), extensions can be easily applied to better model the dynamics of infectious diseases using real data. Zhou et al. (2020) propose a spatio‐temporal epidemiological forecast model that combines CA with an extended SAIR (eSAIR) model to project the county‐level COVID‐19 prevalence over 3 109 counties in the continental United States. This model is termed as CA‐eSAIR model in which a county is treated as a cell. To carry out cell‐level infection prevalence updates, the macroparameters β and γ need to be estimated from the macromodel eSAIR model. In comparison with the eSIR model discussed in Section 5.2, a new antibody compartment (A) is included in the eSAIR model to account for the individuals who are self‐immunised and have developed antibodies to the coronavirus. The inclusion of the antibody compartment can address the under‐reporting issue known for available public databases and to build self‐immunisation into the infection dynamics. In this way, better estimation of the macromodel parameters can be obtained. The eSAIR model can be described using the following ODEs, which govern the law of interactive movements among four compartments or states of susceptible (S), self‐immunised (A), infectious (I) and removed (R):
where α(t) is the self‐immunisation rate, π(t) is a time‐varying transmission rate modifier, β is the basic disease transmission rate and γ is the rate of being removed from the system (either dead or recovered). The earlier eSAIR model is an alternative expression of model (6) based on the compartment probabilities.
In order to apply the CA‐eSAIR system to model the epidemic spread in the USA, Zhou et al. (2020) relax the classical CA‐eSAIR from spatial lattices (or cells) to areal locations of counties. Let be the collection of 3 109 counties. Here we consider the extended neighbourhood type (all counties are neighbouring ones given high mobility in the US population). For a county , N c denotes the county population size, and denotes the set of all the other counties except county c. For county c at time t, the county‐specific probability vector is denoted by . The CA‐eSAIR model at discrete times is expressed by the following form:
where α c(t) is the county‐specific self‐immunisation rate and π c(t) is the county‐specific transmission modifier. Same as the parameter mentioned in the CA‐SIR model (15) earlier, ω cc′(t) is a connectivity coefficient that quantifies the inter‐county movements between counties c and c ′. By applying the proposed CA‐eSAIR model, Zhou et al. (2020) have proposed a t‐day ahead risk forecast of the COVID‐19 as well as a personal risk related to a travel route.
6.5. Example: Analysis of Michigan County‐level Data
We illustrate the predicted risk of infection with the COVID‐19 for all 83 counties in Michigan state using the state‐space model with the mechanistic CA‐eSAIR latent process (Zhou et al., 2020). In the first step, we apply the MCMC method to estimate the model parameters (β and γ) and the vector of four probabilities θ t of being susceptible, self‐immunised, infectious and removed by fitting the eSAIR model with the state‐level surveillance data since 11 March. This can be performed easily using the r package eSIR, which has been illustrated in Section 5.5. Both the antibody rate function α(t) and the transmission rate modifier π(t) are pre‐specified using other data sources with the detail given in the succeeding text. After getting the estimates of the model parameters, we use them as the initial values to make county‐level risk prediction by the CA‐eSAIR model (15). In this example, we consider only a 1‐day ahead infection rate prediction (i.e. 3 May 2020) for all the counties in Michigan, namely, . Given that the COVID‐19 pandemic evolves fast in the state of Michigan in early May 2020, this kind of short‐term forecast or nowcast is of great interest to the Michigan government for timely decision making on either extending an existing governor's ‘Stay‐At‐Home’ order or relaxing this executive order. To perform the prediction, one important task is to specify the inter‐county connectivity coefficient ω cc′(t). As discussed in Zhou et al.(2020), it is challenging to define ω cc′(t) objectively, as it involves many variables. In this illustration, we specify this coefficient as ω cc′(t)=μ cc′exp{−ηr(c,c ′)}, where η is a tuning parameter to be determined. Briefly speaking, the first factor μ c,c′ is the inter‐county mobility factor characterising the decrease of human encounters in terms of their potential movements between counties, which has been given online (https://www.unacast.com/covid19/social‐distancing‐scoreboard). The second factor r(c,c ′) is a certain travel distance between two counties c and c ′ in terms of both geodesic distance (Karney, 2013) and ‘air distance’ based on the accessibility to nearby airports. In addition, the tuning parameter η enables to adjust the scale of the travel distance by minimising the sum of (county‐level) weighted absolute prediction error for the one‐step ahead risk prediction of the infection rate. In addition to the specification of the connectivity coefficient ω cc′(t), the self‐immunisation rate α c(t) is calculated based on the results of the New York statewide antibody test surveys released by the New York governor Andrew Cuomo on 29 April (New York State Report, 2020), and the transmission modifier function π c(t) is specified by the effectiveness score of state‐specific social distancing using cell phone data in the USA from the Transportation Institute at the University of Maryland (https://data.covid.umd.edu/). Additional details of the determination of μ c,c′, r(c,c ′), α c(t) and π c(t) and the tuning of η can be found in Zhou et al. (2020). Figure 14(A) shows the 1‐day ahead projected infectious rate for 83 counties in Michigan on 3 May, and Figure 14(B) plots the corresponding county‐level weighted prediction errors (WPE), which is at the order of 10−7 for the counties. The r package CA‐eSAIR is available on GitHub (https://github.com/leyaozh/CA‐eSAIR).
Figure 14.
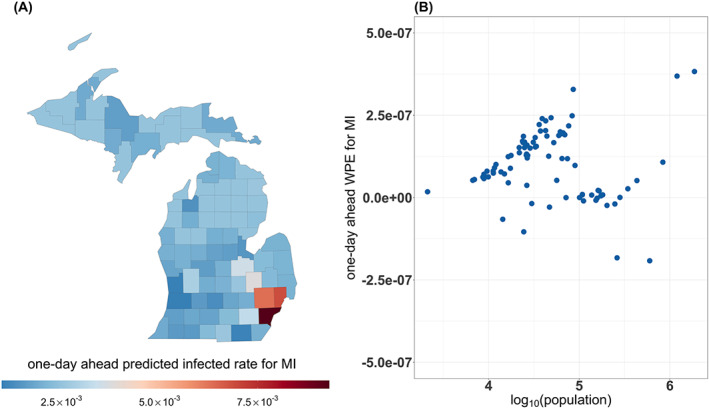
(A) Statewide 1‐day ahead county‐level predicted infectious prevalences and (B) statewide 1‐day ahead weighted (by county population) prediction error (WPE) for all the 83 counties of Michigan, USA, using data up to 2 May. [Colour figure can be viewed at wileyonlinelibrary.com]
7. Future Directions
In this paper, we have presented the basics of multi‐compartment infectious disease models from both deterministic and stochastic perspectives. We emphasise on the probabilistic extension of mechanistic models, which opens the door to a suite of statistical modelling techniques while still preserving the infectious disease dynamics in multi‐compartment models. Within the stochastic modelling framework, both the frequentist and the Bayesian schools of modelling considerations and statistical methods are visited, along with high‐level review and illustrative examples. Epidemic models have played a key role in the past century to provide understanding of past and ongoing infectious diseases, and it is our belief that they will continually be valued and be improved to help us better understand the current COVID‐19 pandemic as well as future infectious diseases. We conclude with several remarks on future directions of stochastic infectious disease modelling.
7.1. Data: Sources, Quality and Sharing
7.1.1. Data quality
Although publicly available surveillance data are useful to build preliminary models for the understanding of spreading patterns of infectious diseases, their data quality in terms of measurement biases and under‐reporting has been known an outstanding issue that significantly impacts the validity of statistical analysis results (Angelopoulos et al., 2020). This is indeed an open problem to date with no appropriate solutions yet. With no insurance of reliable data, statistical methods, regardless of macromodels or micromodels, would fail to produce meaningful results. One potentially promising solution to such a fundamental concern is to build reliable and well‐validated open‐source benchmark databases that include not only traditional surveillance data but also personal clinical data from various sources such as hospital electronic health records, drug trials and vaccine trials. In addition, data from serological surveys and data from mobile devices or as such are also useful to increase information resolution and reliability, to remove major measurement biases and to calibrate data analytics. This task requires also efforts of data integration and international collaborations. Research on the COVID‐19 pandemic certainly gives rise to a new opportunity of developing data integration methods to not only address challenges of data multi‐modality but also overcome many data‐sharing barriers and data confidentiality concerns.
7.1.2. Serological survey
The population of self‐immunised individuals is a significant source of bias in COVID‐19 surveillance data; they have never been captured by public health monitoring systems. According to survey results (New York State Report, 2020), 20% of individuals in the city of New York have been tested antibody positive to the coronavirus. This simply means that a nationwide serological survey is a must in order to come up with an appropriate assessment for the underlying epidemiological features of the COVID‐19 pandemic in the USA. The design of this nationwide serological survey is a challenging statistical problem. Solving it requires some innovative ideas and methods; for example, a cost‐effective design of pooling several serum samples to perform a pooled test (e.g. Gollier & Gossner, 2020), and an efficient design of hierarchical stratified survey sampling schemes. The SAIR model introduced in Section 3.3 presents a basic framework for statistical models incorporating antibody serological surveys into the multi‐compartment dynamics of infectious diseases.
7.1.3. Mobile tracking data
Large‐scale tracking data have played an important role in evaluating the effectiveness of social distancing in communities. The precision of intervention efficacy helps improve both estimation and prediction that directly impact government's decisions on tightening, extending or lifting control measures. One emerging data source pertains to the information of real‐time cell phone locations, which allows better contact tracing so that individual data sequences can be recovered and used for modelling of personal risk and regional hotspots. A research group in the University of Maryland (https://data.covid.umd.edu/) proposes several algorithms to process the cell phone data in the USA to extract key features of personal mobility, including location identification, trip identification, imputation of missing trip information, multilevel data weighting scheme, comprehensive trip data validation, and data integration and aggregation (Zhang et al., 2020; Ghader et al., 2020). However, these types of data are proprietary and subject to the issue of personal privacy (Ienca & Vayena, 2020). Integrating such data type or its summary statistics into infectious disease models should be encouraged, but in a cautious and responsible manner. In this field, statistical learning methods with differential privacy (Dwork, 2008) are of great interest.
7.2. Statistical Models
Statistical methodologies have been greatly challenged in the modelling and analysis of infectious diseases; almost every methodological troubling issue known the statistical literature surfaces, which presents new opportunities to statisticians and data scientists to develop innovative solutions. Among many challenges, we emphasise a few of critical importance, which may be easily ignored in the new methodology development.
7.2.1. Transparency and reproducibility
We strongly advocate for the urgent need to build models that are transparent and reproducible (Peng, 2011). As most methods and models for the COVID‐19 pandemic are fairly recent and many have not yet been carefully peer reviewed, researchers should document the sources of data used, data preprocessing protocols, source computing code and sufficient modelling details to allow external validation from the public. Such details are also necessary to allow others, who may have better quality data but without sufficient statistical expertise, to easily adopt new methodologies to obtain high‐quality results. As mentioned in an original post by Dr Nilanjan Chatterjee (https://link.medium.com/hqUQILEAd6), transparency, reproducibility and validity are three criteria to assess and assure the quality of prediction models. His essay also mentioned the difficulty in reproducing the work given by the IHME to obtain accurate predictions and appropriate confidence intervals. Similar to the IHME method that has no software available, Gu's method for the COVID‐19 prediction (https://covid19‐projections.com/) that has recently received much attention does not provide software, either, unfortunately. Without clear guidance and full reproducibility, even models that currently do well might fail in the future because predictions are relying on certain kinds of extrapolation assumptions that need to be unveiled to the scientific community with full transparency for validation and comparison.
7.2.2. Nowcasting and short‐term projection
Given that model projections for the COVID‐19 pandemic have been changing dramatically from day to day primarily because the underlying models are changing, the primary aim may be set at optimising prediction models for nowcasting or short‐term projections and be aware of the probable worst case scenarios for longer‐term trends. As shown in the data example in Section 6.5, the optimal tuning parameter is determined by the minimal short‐term 1‐day ahead prediction error. As pointed out by Huppert and Katriel (2013), transmission models with different underlying mechanisms may lead to similar outcome in one context (e.g. short term) but fail to do so in another (e.g. long term). The further we project, the more we are uncertain about the validity of model assumptions. Hence, extra caution is needed when reporting and interpreting long‐term projection results. With the available surveillance data, making a nowcast of infection risk in next few hours is difficult; but it may become feasible when certain data sources of local information are accessible, such as electronic health records from local hospitals, viral testing results from local testing centres and mobile tracking data from individual cell phones. This requires a finer‐resolution prediction machinery that may be established by generalising the CA to certain spatial point processes. Despite being challenging, such prediction paradigm would be very useful and worth a serious exploration.
7.2.3. Bias correction
Because of the potential bias in surveillance data, either delayed reporting of infected case or inaccurate ascertainment of death caused by a virus, there are many measurement errors in data. This calls for statistical methods that can directly handle various data collection biases or are robust to such biases. There is little work performed in this important field of statistical modelling and analyses.
7.2.4. Model diagnostics
In the current literature, model diagnostics for infectious disease models are largely lacking. Given that most of the existing mechanistic models are based on certain parametric distributions (e.g. Poisson processes), checking model assumptions is required. For example, for the proposed Poisson process, the assumption of incremental independence and overdispersion should be checked. In addition, procedures of validating prediction accuracy are also important in which the choice of test data is tricky and needs to be guided by some objective criteria.
7.2.5. Adding covariates
A major weakness noted for the existing mechanistic models is the inflexibility of adding individual or subgroup covariates (e.g. age and race). The current strategy of handling these extra variables is via stratification, which would end up with strata with small sample sizes, so that subsequent statistical analyses lose power in both estimation and prediction of infection dynamics. An extension from the CA seems promising as the CA presents a system of particles distributed in different cells (or strata), where individual characterisations on particles may be added via covariates. The resulting model would assess and predict personal risk, as well as identify hotspots of new infection. This is worth serious exploration in the future with appropriate data available (e.g. electronic health records from hospitals).
7.2.6. Meta‐analysis
For a global pandemic such as the COVID‐19 that affects over 200 countries in the world, an integrative analysis is appealing to understand common features of the pandemic so to learn different control measures. Given the fact that a pandemic evolves typically in a certain time lag, experiences from countries with earlier outbreaks may be shared with countries with later outbreaks, where statistical methods may borrow relevant information to set up prior distributions in the model fitting. For example, the estimated reproduction number estimated from the European COVID‐19 data may be a hyperparameter in the statistical analysis of the US COVID‐19 data. There is a clear need of more comprehensive meta‐analysis methods to better integrate data from different countries than using the data to create hyperparameters. Along this line, one of the earliest attempts is to combine COVID‐19 forecasts from various research teams using ensemble learning (see, e.g. https://github.com/reichlab/covid19‐forecast‐hub).
7.3. Impacts on Public Health Policy and Economy
Most investigation efforts made by quantitative researchers have been relatively independent in an academic setting, and it is high time that policymakers and stakeholders are involved and play an active role in such modelling efforts. Long‐term projection of the COVID‐19 is most sensitive to and highly dependent on public health policy. A major source of uncertainty is due to the conflicting demands between public health (disease mitigation) and the need to sustain economic growth (livelihood), and the balance of the two is a moving target. One way to account for the modelling uncertainty is to factor in economic planning as a time‐varying modifier of projection models. Although some efforts have been made to incorporate economical data, most are retrospectively oriented, and we believe more efforts should be spent to prospectively incorporate expert inputs and economic forecasts. This is a research area of great importance worth serious exploration.
7.4. Some Open Questions
We like to close this review paper by casting a few open questions of great interest to the public (at least to ourselves) that statisticians may help deliver answers with existing or new data to be collected by innovative study designs. We also hope that these questions motivate new methodological developments.
- Question 1:
How would researchers assess both timing and strength of the second wave of the COVID‐19 pandemic? Is the second wave worse than the first one? Answers to these questions need a relatively accurate long‐term prediction of the infection dynamics. Among so many different statistical models being able to predict future spreading patterns, we need to identify few ones or their combinations that are particularly useful to make long‐term predictions.
- Question 2:
As many countries and regions started to reopen business, how would government monitor the likelihood of a recurring surge of COVID‐19 caused by business reopenings? Does the social distancing measure help reduce a potentially rising risk? Answers to these questions require adequate data that may not be easily collected by routine approaches. Statisticians may work with practitioners to develop good sampling instruments and schemes for community risk surveillance.
- Question 3:
Is face mask protective? If so, how to assess the compliance of face mask wearing? Questions about the causal effect of face mask wearing on disease progression are very challenging. This is because there is no randomisation in the intervention allocation and many confounding factors are unobserved.
- Question 4:
Is there evidence that the contagion of the coronavirus decays over time because of an increasing recovery rate of virus carriers and a decreasing rate of case fatality? Statisticians ought to work out some thoughtful and convincing answers to the public.
Acknowledgements
The authors are very grateful to the co‐editors for the invitation to contribute a review paper for statistical modelling and analysis of infectious diseases and for their helpful feedback towards improving the manuscript. This research is partially supported by the National Science Foundation grant DMS1811734.
Appendix A.
A.1.
A1 The Runge–Kutta Approximation
The Runge–Kutta method is an efficient and widely used approach to solving ordinary differential equations when analytic closed‐form solutions are unavailable. It is typically applied to derive a numerical functional system of high‐order accuracy with no need of high‐order derivatives of functions. The most well‐known Runge–Kutta approximation is the Runge–Kutta fourth‐order (RK4) method. For example, in the case of the mechanistic SIR model (1), because the three ordinary differential equations of the SIR model are non‐linear, there exist no closed‐form solutions of S(t), I(t) and R(t). These approximate solution can be obtained by the RK4 method.
Assume a general ordinary differential equation problem:
where y is an unknown function in time t, which can be either a scalar or a vector. Then for a preselected (small) step size h>0, a fourth‐order approximate solution of y satisfies at a sequence of equally spaced grid points y n,n=0,1,…, with |y n−y n−1|=h,
where
Because four terms k 1, k 2, k 3 and k 4 are used in the approximation, the earlier method is termed as an RK4 method of the ODE solution to function y. For a general RK approximation, refer to Stoer and Bulirsch (2013).
A2 Michigan Coronavirus Disease 2019 Data
In the succeeding text, we list Michigan data from 11 March to 10 June 2020. The numbers of daily confirmed cases and deaths are obtained from the GitHub repository JHU CSSE (https://github.com/CSSEGISandData/COVID‐19), and the daily recovery data are collected from 1Point3Acres (https://coronavirus.1point3acres.com). The daily cumulative numbers of deaths and recovered cases are then summed as the cumulative number of removed cases. In such surveillance data, there are data reporting gaps shown in Figure A1 that are possibly caused by the so‐called clustered reporting; that is, the recovered cases have not been released on the daily basis. To mitigate this data reporting artefact, we invoked a simple local polynomial regression procedure (LOESS) to smooth such unnatural jumps, resulting in a smooth fitted curve shown in Figure A1. The calibrated cumulative numbers of removed cases from the fitted curve (rounded to the corresponding integers) are available from the corresponding author upon request. The total population in Michigan is set as 9.99 million. The summarised US state‐level count data, which are weekly updated, can be also be found directly from the eSIR package introduced in Section 5.4.
Figure A1.

The prevalence of cumulative removed subjects before (points) and after (red curve) smoothing. [Colour figure can be viewed at wileyonlinelibrary.com]
Tang, L. , Zhou, Y. , Wang, L. , Purkayastha, S. , Zhang, L. , He, J. , Wang, F. , and Song, P. X.‐K. (2020) A Review of Multi‐Compartment Infectious Disease Models. International Statistical Review, 88: 462–513. 10.1111/insr.12402.
References
- Adam, D. (2020). Special report: the simulations driving the world's response to COVID‐19. Nature, 580(7803), 316. [DOI] [PubMed] [Google Scholar]
- Ahmed, E. & Agiza, H.N. (1998). On modeling epidemics including latency, incubation and variable susceptibility. Phys. A Stat. Mech. Appl., 253(1‐4), 347–352. [Google Scholar]
- Allen, L.J. (2008). An introduction to stochastic epidemic models In Mathematical Epidemiology, pp. 81–130. [Google Scholar]
- Anderson, R.M. , Anderson, B. & May, R.M. (1992). Infectious Diseases of Humans: Dynamics and Control. New York, United States:Oxford University Press. [Google Scholar]
- Andersson, H. & Britton, T. (2000). Stochastic Epidemic Models and Their Statistical Analysis. New York, United States:Springer. [Google Scholar]
- Angelopoulos, A.N. , Pathak, R. , Varma, R. & Jordan, M.I. (2020). On identifying and mitigating bias in the estimation of the COVID‐19 case fatality rate. Harvard Data Sci. Rev. Special Issue 1—COVID‐19. https://hdsr.mitpress.mit.edu/pub/y9vc2u36/release/4 [Google Scholar]
- Bailey, N.T. (1975). The Mathematical Theory of Infectious Diseases and Its Applications. Charles Griffin & Company Ltd: 5a Crendon Street, High Wycombe, Bucks HP13 6LE. [Google Scholar]
- Banerjee, A. , Pasea, L. , Harris, S. , Gonzalez‐Izquierdo, A. , Torralbo, A. , Shallcross, L. , Noursadeghi, M. , Pillay, D. , Sebire, N. , Holmes, C. & Pagel, C. (2020). Estimating excess 1‐year mortality associated with the COVID‐19 pandemic according to underlying conditions and age: a population‐based cohort study. The Lancet. [DOI] [PMC free article] [PubMed]
- Barreca, A.I. & Shimshack, J.P. (2012). Absolute humidity, temperature, and influenza mortality: 30 years of county‐level evidence from the United States. Amer. J. Epidemiol., 176(suppl_7), S114–S122. [DOI] [PubMed] [Google Scholar]
- Beauchemin, C. , Samuel, J. & Tuszynski, J. (2005). A simple cellular automaton model for influenza A viral infections. J. Theo. Biol., 232(2), 223–234. [DOI] [PubMed] [Google Scholar]
- Becker, N.G. (1977). On a general stochastic epidemic model. Theo. Popul. Biol., 11(1), 23–36. [DOI] [PubMed] [Google Scholar]
- Becker, N. (1979). An estimation procedure for household disease data. Biometrika, 66(2), 271–277. [Google Scholar]
- Becker, N.G. & Britton, T. (1999). Statistical studies of infectious disease incidence. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 61(2), 287–307. [Google Scholar]
- Bettencourt, L.M.A. & Ribeiro, R.M. (2008). Real time Bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS One, 3(5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccara, N. , Cheong, K. & Oram, M. (1994). A probabilistic automata network epidemic model with births and deaths exhibiting cyclic behaviour. J. Phys. A Math. Gen., 27(5), 1585. [Google Scholar]
- Britton, T. (2010). Stochastic epidemic models: a survey. Math. Biosci., 225(1), 24–35. [DOI] [PubMed] [Google Scholar]
- Britton, T. , Pardoux, E. , Ball, F. , Laredo, C. , Sirl, D. & Tran, V.C. (2019). Stochastic Epidemic Models with Inference. Cham, Switzerland:Springer. [Google Scholar]
- Brooks, S.P. & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat., 7(4), 434–455. [Google Scholar]
- Butcher, J.C. (2016). Numerical Methods for Ordinary Differential Equations. Chichester, United Kingdom:John Wiley & Sons. [Google Scholar]
- Carlin, B.P. , Polson, N.G. & Stoffer, D.S. (1992). A Monte Carlo approach to nonnormal and nonlinear state‐space modeling. J. Am. Stat. Assoc., 87(418), 493–500. [Google Scholar]
- Chan, K.S. & Ledolter, J. (1995). Monte Carlo EM estimation for time series models involving counts. J. Am. Stat. Assoc., 90(429), 242–252. [Google Scholar]
- Chowell, G. , Castillo‐Chavez, C. , Fenimore, P.W. , Kribs‐Zaleta, C.M. , Arriola, L. & Hyman, J.M. (2004). Model parameters and outbreak control for SARS. Emerg. Infect. Dis., 10(7), 1258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cintrón‐Arias, A. , Castillo‐Chávez, C. , Betencourt, L. , Lloyd, A.L. & Banks, H.T. (2009). The estimation of the effective reproductive number from disease outbreak data. Math. Biosci. Eng., 6(2), 261–282. [DOI] [PubMed] [Google Scholar]
- Cleveland, W.S. & Devlin, S.J. (1988). Locally weighted regression: an approach to regression analysis by local fitting. J. Am. Stat. Assoc., 83(403), 596–610. [Google Scholar]
- Cori, A. , Ferguson, N.M. , Fraser, C. & Cauchemez, S. (2013). A new framework and software to estimate time‐varying reproduction numbers during epidemics. Am. J. Epidemiol., 178(9), 1505–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, D.R. , Gudmundsson, G. , Lindgren, G. , Bondesson, L. , Harsaae, E. , Laake, P. , Juselius, K. & Lauritzen, S.L. (1981). Statistical analysis of time series: some recent developments [with discussion and reply]. Scand. J. Stat., 8(2), 93–115. [Google Scholar]
- Czado, C. & Song, P.X.‐K. (2008). State space mixed models for longitudinal observations with binary and binomial responses. Stat. Papers, 49(4), 691–714. [Google Scholar]
- De Jong, P. & Shephard, N. (1995). The simulation smoother for time series models. Biometrika, 82(2), 339–350. [Google Scholar]
- Dietz, K. (1976). The incidence of infectious diseases under the influence of seasonal fluctuations In Mathematical Models in Medicine, pp. 1–15. [Google Scholar]
- Dietz, K. (1993). The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res., 2(1), 23–41. [DOI] [PubMed] [Google Scholar]
- Doucet, A. , de Freitas, N. & Gordon, N. (2001). Sequential Monte Carlo Methods in Practice. New York, United States:Springer. [Google Scholar]
- Dukic, V. , Lopes, H.F. & Polson, N.G. (2012). Tracking epidemics with Google flu trends data and a state‐space SEIR model. J. Am. Stat. Assoc., 107(500), 1410–1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwork, C. (2008). Differential privacy: a survey of results. In International Conference on Theory and Applications of Models of Computation, pp. 1–19, Springer.
- Ferguson, N.M. , Cummings, DerekA.T. , Fraser, C. , Cajka, J.C. , Cooley, P.C. & Burke, D.S. (2006). Strategies for mitigating an influenza pandemic. Nature, 442(7101), 448–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forsberg White, L. & Pagano, M. (2008). A likelihood‐based method for real‐time estimation of the serial interval and reproductive number of an epidemic. Stat. Med., 27(16), 2999–3016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuentes, M.A. & Kuperman, M.N. (1999). Cellular automata and epidemiological models with spatial dependence. Phys. A Stat. Mech. Appl., 267(3‐4), 471–486. [Google Scholar]
- Fuks, H. & Lawniczak, A.T. (2001). Individual‐based lattice model for spatial spread of epidemics. Disc. Dyn. Nat. Soc., 6(3), 191–200. [Google Scholar]
- Gao, X. & Song, P.X.‐K. (2011). Composite likelihood EM algorithm with applications to multivariate hidden Markov model. Stat. Sin., 21(1), 165–185. [Google Scholar]
- Gelman, A. , Carlin, J.B. , Stern, H.S. , Dunson, D.B. , Vehtari, A. & Rubin, D.B. (2013). Bayesian Data Analysis. Boca Raton, United States: CRC Press. [Google Scholar]
- Gelman, A. & Rubin, D.B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci., 7(4), 457–472. [Google Scholar]
- Geyer, C.J. (1991). Markov chain Monte Carlo maximum likelihood. Interface Foundation of North America. Retrieved from the University of Minnesota Digital Conservancy, http://hdl.handle.net/11299/58440
- Ghader, S. , Zhao, J. , Lee, M. , Zhou, W. , Zhao, G. & Zhang, L. (2020). Observed mobility behavior data reveal social distancing inertia. ArXiv.
- Gollier, C. & Gossner, O. (2020). Group testing against Covid‐19. Covid Economics, 1(2), 32–42, Centre for Economic Policy Research CEPR. [Google Scholar]
- Guan, W. , Ni, Z. , Hu, Y. , Liang, W. , Ou, C. , He, J. , Liu, L. , Shan, H. , Lei, C. , Hui, D.S. & Du, B. (2020). Clinical characteristics of 2019 novel coronavirus infection in China. MedRxiv.
- Hasani, B. & Tavakkoli, S.M. (2007). A multi‐objective structural optimization using optimality criteria and cellular automata. Asian J. Civ. Eng. (Buil. Hous.), 8(1), 77–88. [Google Scholar]
- He, X. , Lau, EricH.Y. , Wu, P. , Deng, X. , Wang, J. , Hao, X. , Lau, Y.C. , Wong, J.Y. , Guan, Y. , Tan, X. & Mo, X (2020). Temporal dynamics in viral shedding and transmissibility of COVID‐19. Nat. Med., 26(5), 672–675. [DOI] [PubMed] [Google Scholar]
- Heesterbeek, H. , Anderson, R.M. , Andreasen, V. , Bansal, S. , De Angelis, D. , Dye, C. , Eames, K.T.D. , Edmunds, W.J. , Frost, S.D.W. , Funk, S. & Hollingsworth, T.D. (2015). Modeling infectious disease dynamics in the complex landscape of global health. Science, 347(6227), aaa4339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hethcote, H.W. (2000). The mathematics of infectious diseases. SIAM Rev., 42(4), 599–653. [Google Scholar]
- Huppert, A. & Katriel, G. (2013). Mathematical modelling and prediction in infectious disease epidemiology. Clin. Microbiol. Infect., 19(11), 999–1005. [DOI] [PubMed] [Google Scholar]
- IHME COVID‐19 health service utilization forecasting team & Murray, C.J.L. (2020). Forecasting COVID‐19 impact on hospital bed‐days, ICU‐days, ventilator‐days and deaths by US state in the next 4 months. MedRxiv.
- Ienca, M. & Vayena, E. (2020). On the responsible use of digital data to tackle the COVID‐19 pandemic. Nat. Med., 26(4), 463–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ip, D.K.M. , Lau, L.L.H. , Leung, N.H.L. , Fang, V.J. , Chan, K.‐H. , Chu, D.K.W. , Leung, G.M. , Peiris, J.S.M. , Uyeki, T.M. & Cowling, B.J. (2017). Viral shedding and transmission potential of asymptomatic and paucisymptomatic influenza virus infections in the community. Clin. Infect. Dis., 64(6), 736–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jewell, N.P. , Lewnard, J.A. & Jewell, B.L. (2020). Caution warranted: using the institute for health metrics and evaluation model for predicting the course of the COVID‐19 pandemic. Ann. Intern. Med. to appear, Accessible at 10.7326/M20-1565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, T. & McQuarrie, B. (2009). Mathematical Modeling of Diseases: Susceptible–Infected–Recovered (SIR) Model. Minnesota, United States:University of Minnesota, Morris, Math 4901 Senior Seminar. [Google Scholar]
- Karney, C.F. (2013). Algorithms for geodesics. J. Geodesy, 87(1), 43–55. [Google Scholar]
- Kermack, W.O. & McKendrick, A.G. (1927). A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci., 115(772), 700–721. [Google Scholar]
- Khan, A. , Naveed, M. , Dur‐e Ahmad, M. & Imran, M. (2015). Estimating the basic reproductive ratio for the Ebola outbreak in Liberia and Sierra Leone. Infect Dis Poverty, 4(1), 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer, S.A. , Grantz, K.H. , Bi, Q. , Jones, F.K. , Zheng, Q. , Meredith, H.R. , Azman, A.S. , Reich, N.G. & Lessler, J. (2020). The incubation period of coronavirus disease 2019 (COVID‐19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med., 172(9), 577–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lekone, P.E. & Finkenstädt, B.F. (2006). Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics, 62(4), 1170–1177. [DOI] [PubMed] [Google Scholar]
- Li, Q. , Guan, X. , Wu, P. , Wang, X. , Zhou, L. , Tong, Y. , Ren, R. , Leung, K.S.M. , Lau, E.H.Y. , Wong, J.Y. & Xing, X. (2020). Early transmission dynamics in Wuhan, China, of novel coronavirus‐infected pneumonia. New England J. Med., 382, 1199–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Y. , Gayle, A.A. , Wilder‐Smith, A. & Rocklöv, J. (2020). The reproductive number of COVID‐19 is higher compared to SARS coronavirus. J. Trav. Med., 27(2), taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Q.‐X. , Jin, Z. & Liu, M.‐X. (2006). Spatial organization and evolution period of the epidemic model using cellular automata. Phys. Rev. E, 74(3), 031110. [DOI] [PubMed] [Google Scholar]
- McKendrick, A.G. (1925). Applications of mathematics to medical problems. Proc. Edinb. Math. Soc., 44, 98–130. [Google Scholar]
- Mollison, D. (1991). Dependence of epidemic and population velocities on basic parameters. Math. Biosci., 107(2), 255–287. [DOI] [PubMed] [Google Scholar]
- Murray, J.D. , Stanley, E.A. & Brown, D.L. (1986). On the spatial spread of rabies among foxes. Proc. R. Soc. Lond. Ser. B. Biol. Sci., 229(1255), 111–150. [DOI] [PubMed] [Google Scholar]
- Nadaraya, E.A. (1964). On estimating regression. Theory Probab. Appl., 9(1), 141–142. [Google Scholar]
- New York State Report (2020). Amid ongoing COVID‐19 pandemic, Governor Cuomo announces results of completed antibody testing study of 15,000 people showing 12.3 percent of population has COVID‐19 antibodies. https://www.governor.ny.gov/news/, Released: 2020‐05‐02; Accessed: 2020‐06‐15.
- Obadia, T. , Haneef, R. & Boëlle, P.‐Y. (2012). The R0 package: a toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med. Inf. Dec. Making, 12(1), 147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osthus, D. , Hickmann, K.S. , Caragea, P.C. , Higdon, D. & Del Valle, S.Y. (2017). Forecasting seasonal influenza with a state‐space SIR model. Ann. Appl. Stat., 11(1), 202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan, A. , Liu, L. , Wang, C. , Guo, H. , Hao, X. , Wang, Q. , Huang, J. , He, N. , Yu, H. , Lin, X. , Wei, S. & Wu, T. (2020). Association of public health interventions with the epidemiology of the COVID‐19 outbreak in Wuhan, China. J. Amer. Med. Assoc., 323, 1915–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng, R.D. (2011). Reproducible research in computational science. Science, 334(6060), 1226–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, J. , You, C. , Lin, Q. , Hu, T. , Yu, S. & Zhou, X.‐H. (2020). Estimation of incubation period distribution of COVID‐19 using disease onset forward time: a novel cross‐sectional and forward follow‐up study. MedRxiv. [DOI] [PMC free article] [PubMed]
- Quan‐Xing, L. & Zhen, J. (2005). Cellular automata modelling of SEIRS. Chin. Phys., 14(7), 1370. [Google Scholar]
- Ray, D. , Salvatore, M. , Bhattacharyya, R. , Wang, L. , Mohammed, S. , Purkayastha, S. , Halder, A. , Rix, A. , Barker, D. & Kleinsasser, M. (2020). Predictions, role of interventions and effects of a historic national lockdown in India's response to the COVID‐19 pandemic: data science call to arms. Harvard Data Sci. Rev. Special Issue 1—COVID‐19. https://hdsr.mitpress.mit.edu/pub/r1qq01kw/release/5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rida, W.N. (1991). Asymptotic properties of some estimators for the infection rate in the general stochastic epidemic model. J. R. Stat. Soc. Ser. B (Methodol.), 53(1), 269–283. [Google Scholar]
- Roberts, M. , Andreasen, V. , Lloyd, A. & Pellis, L. (2015). Nine challenges for deterministic epidemic models. Epidemics, 10, 49–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau, G. , Giorgini, B. , Livi, R. & Chaté, H. (1997). Dynamical phases in a cellular automaton model for epidemic propagation. Phys. D: Nonl. Phenom., 103(1‐4), 554–563. [Google Scholar]
- Sajadi, M.M. , Habibzadeh, P. , Vintzileos, A. , Shokouhi, S. , Miralles‐Wilhelm, F. & Amoroso, A. (2020). Temperature and latitude analysis to predict potential spread and seasonality for COVID‐19. Available at SSRN 3550308. [DOI] [PMC free article] [PubMed]
- Siettos, C.I. & Russo, L. (2013). Mathematical modeling of infectious disease dynamics. Virulence, 4(4), 295–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirakoulis, G.C. , Karafyllidis, I. & Thanailakis, A. (2000). A cellular automaton model for the effects of population movement and vaccination on epidemic propagation. Ecol. Mod., 133(3), 209–223. [Google Scholar]
- Smirnova, A. , deCamp, L. & Chowell, G. (2019). Forecasting epidemics through nonparametric estimation of time‐dependent transmission rates using the SEIR model. Bull. Math. Biol., 81(11), 4343–4365. [DOI] [PubMed] [Google Scholar]
- Song, P.X.‐K. (2007). Correlated Data Analysis: Modeling, Analytics, and Applications. New York, United States:Springer. [Google Scholar]
- Spiegelhalter, D.J. , Best, N.G. , Carlin, B.P. & Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 64(4), 583–639. [Google Scholar]
- Stoer, J. & Bulirsch, R. (2013). Introduction to Numerical Analysis. New York, United States:Springer. [Google Scholar]
- Sun, G.‐Q. , Jin, Z. , Song, L.‐P. , Chakraborty, A. & Li, B.‐L. (2011). Phase transition in spatial epidemics using cellular automata with noise. Ecol. Res., 26(2), 333–340. [Google Scholar]
- Sun, H. , Qiu, Y. , Yan, H. , Huang, Y. , Zhu, Y. , Gu, J. & Chen, S.X. (2020). Tracking reproductivity of COVID‐19 epidemic in China with varying coefficient SIR model. J. Data Sci., 18(3), 455–482. [Google Scholar]
- Thompson, R.N. , Stockwin, J.E. , van Gaalen, R.D. , Polonsky, J.A. , Kamvar, Z.N. , Demarsh, P.A. , Dahlqwist, E. , Li, S. , Miguel, E. , Jombart, T. , Lessler, J. , Cauchemez, S. & Cori, A. (2019). Improved inference of time‐varying reproduction numbers during infectious disease outbreaks. Epidemics, 29, 100356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulam, S. (1962). On some mathematical problems connected with patterns of growth of figures. In Proceedings of Symposia in Applied Mathematics, Vol. 14, pp. 215–224. [Google Scholar]
- Varin, C. , Reid, N. & Firth, D. (2011). An overview of composite likelihood methods. Stat. Sin., 21(1), 5–42. [Google Scholar]
- Verity, R. , Okell, L.C. , Dorigatti, I. , Winskill, P. , Whittaker, C. , Imai, N. , Cuomo‐Dannenburg, G. , Thompson, H. , Walker, PatrickG.T. , Fu, H. & Dighe, A. (2020). Estimates of the severity of coronavirus disease 2019: a model‐based analysis. Lancet Infect. Dis., 20(6), 669–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Neumann, J. & Burks, A.W. (1966). Theory of self‐reproducing automata. IEEE Trans. Neural Netw., 5(1), 3–14. [Google Scholar]
- Wallinga, J. & Lipsitch, M. (2007). How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B Biol. Sci., 274(1609), 599–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallinga, J. & Teunis, P. (2004). Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol., 160(6), 509–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, L. , Zhou, Y. , He, J. , Zhu, B. , Wang, F. , Tang, L. , Kleinsasser, M. , Barker, D. , Eisenberg, M. & Song, P.X.K. (2020). An epidemiological forecast model and software assessing interventions on COVID‐19 epidemic in China (with discussion). J. Data Sci., 18(3), 409–454. [Google Scholar]
- Watson, G.S. (1964). Smooth regression analysis. Sankhyā: Indian J. Stat. Ser. A, 26(4), 359–372. [Google Scholar]
- White, S.H. , Del Rey, A.M. & Sánchez, G.R. (2007). Modeling epidemics using cellular automata. Appl. Math. Comput., 186(1), 193–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willox, R. , Grammaticos, B. , Carstea, A.S. & Ramani, A. (2003). Epidemic dynamics: discrete‐time and cellular automaton models. Phys. A: Stat. Mech. Appl., 328(1‐2), 13–22. [Google Scholar]
- World Health Organization (2020). Naming the coronavirus disease (COVID‐19) and the virus that causes it. https://www.who.int/emergencies/diseases/novel‐coronavirus‐2019/te%chnical‐guidance/naming‐the‐ coronavirus‐disease‐(covid‐2019)‐and‐the‐virus‐tha%t‐causes‐it Accessed: 2020‐04‐22.
- Yakowitz, S. , Gani, J. & Hayes, R. (1990). Cellular automaton modeling of epidemics. Appl. Math. Comput., 40(1), 41–54. [Google Scholar]
- Zhang, L. , Ghader, S. , Pack, M.L. , Xiong, C. , Darzi, A. , Yang, M. , Sun, Q. , Kabiri, A. & Hu, S. (2020). An interactive COVID‐19 mobility impact and social distancing analysis platform. MedRxiv. [DOI] [PMC free article] [PubMed]
- Zhou, T. & Ji, Y. (2020). Semiparametric Bayesian inference for the transmission dynamics of COVID‐19 with a state‐space model. ArXiv. [DOI] [PMC free article] [PubMed]
- Zhou, Y. , Wang, L. , Zhang, L. , Shi, L. , Yang, K. , He, J. , Zhao, B. , Overton, W. , Purkayastha, S. & Song, P.X.K. (2020). A spatiotemporal epidemiological prediction model to inform county‐level COVID‐19 risk in the USA. Harvard Data Sci. Rev. Special Issue 1 ‐ COVID‐19, https://hdsr.mitpress.mit.edu/pub/qqg19a0r [Google Scholar]
- Zhu, B. , Taylor, J.M.G. & Song, P.X.‐K. (2011). Semiparametric stochastic modeling of the rate function in longitudinal studies. J. Am. Stat. Assoc., 106(496), 1485–1495. [DOI] [PMC free article] [PubMed] [Google Scholar]


