Childhood Obesity Intervention Studies: A Narrative Review and Guide for Investigators, Authors, Editors, Reviewers, Journalists, and Readers to Guard Against Exaggerated Effectiveness Claims

Abstract

Being able to draw accurate conclusions from childhood obesity trials is important to make advances in reversing the obesity epidemic. However, obesity research sometimes is not conducted or reported to appropriate scientific standards. To constructively draw attention to this issue, we present 10 errors that are commonly committed, illustrate each error with examples from the childhood obesity literature, and follow with suggestions on how to avoid these errors. These errors are: Using self-reported outcomes and teaching to the test; Foregoing control groups and risking regression to the mean creating differences over time; Changing the goal posts; Ignoring clustering in studies that randomize groups of children; Following the forking paths, sub-setting, p-hacking, and data dredging; Basing conclusions on tests for significant differences from baseline; Equating ‘no statistically significant difference’ with ‘equally effective’; Ignoring intervention study results in favor of observational analyses; Using one-sided testing for statistical significance; and, Stating that effects are clinically significant even though they are not statistically significant. We hope that compiling these errors in one article will serve as the beginning of a checklist to support fidelity in conducting, analyzing, and reporting childhood obesity research.

Introduction

“Experimental scientists must have for data a permanent respect that transcends their passing interest in the stories they make up about their data.”¹ Cletus J. Burke, 1954

Childhood obesity is a substantial global public health concern that, despite many efforts, has continued to climb for decades,² and few would argue with the merit of pursuing effective prevention or treatment options. Substantial resources are dedicated to studying childhood obesity.³ However, when prevention or treatment programs use popular or seemingly wholesome practices based on cherished principles, some people might believe that questioning the merits of such programs is inappropriate, or even that doing so subverts or undermines public support for implementing and funding such interventions. Yet, society must increasingly ask whether proposed solutions are evidence-based. Thus, unvarnished presentations of evidence regarding the effectiveness of such programs is vital. Nevertheless, the extent to which studies that assess obesity interventions demonstrate effectiveness of the interventions has been substantially overstated in some cases, leading to concerns about the rigor of childhood nutrition and obesity research in particular.⁴ This observation is not based on a systematic quantification, yet illustrative cases are easy to find when reading the literature from countries around the world. At the very least, such cases demonstrate there is room for improvement.

The scientific community, and those who rely on the community’s work, need accurate information for informed conclusion- and decision-making. Therefore, we delineate 10 errors that exaggerate the apparent extent to which interventions lead to positive improvements in obesity-related outcomes, with a focus on examples from the childhood obesity literature. We use the word ‘intervention’ to include programs, policies, or prescriptions to treat or prevent obesity and obesity-related outcomes. Errors may apply to both controlled and uncontrolled studies; or to randomized and non-randomized experiments. We describe these errors, supported by examples in published studies, and make recommendations to avoid them.

Our use of specific examples is not meant to impugn specific researchers, make judgments of intentionality, or make conclusions about the ultimate effectiveness of interventions. In some examples throughout, the underlying data and interventions appear sound, and analytic or communication errors could explain the discrepancy. One recent case has called into question multiple publications, resulting in multiple obesity-related papers (some related to childhood obesity) being retracted (c.f., six retractions in one notice⁵). Herein, we point out that the published errors exist; any errors in the literature weaken the evidence base regardless of intentionality. We also note these errors are not necessarily limited to the field of childhood obesity; some of these or related errors have been identified in the field of maternal and child nutrition,⁶ in obesity research more generally,⁷ and in science more broadly⁸. Finally, this list is not exhaustive, and the order of presentation herein does not imply ranking, prioritization, or severity among the errors.

We hope this article can serve as a partial checklist of mistakes to be avoided. By highlighting the errors here, authors may be better able to avoid them, and reviewers, editors, journalists, and other readers will be better able to detect the mistakes and adjust their conclusions and actions accordingly.

Inferential Error: Using Self-Reported Outcomes and Teaching to the Test

Error Description

Implement a program that urges the intervention group to change health-related behaviors or conditions, and then give participants a questionnaire that asks about the same health related behaviors and conditions, ignoring the differential bias this practice can induce.⁹

Explanation of the Error and Why the Practice is Wrong

As a simple example, teaching to the test in a childhood obesity intervention could be to encourage children to eat more of a healthy food (the teaching), and considering the children compliant when they report eating more of that food (the test), whether or not they actually do. Stated another way, bias induced by an intervention is a type of social desirability bias (i.e., the tendency for individuals to answer or portray themselves in such a way to avoid criticism, adhere to perceived cultural norms, or garner praise).¹⁰ This can be a particular concern for studies of youth, because school-aged children may be especially prone to “report more socially desirable behavior (or less socially undesirable behavior) when they fear that this information is shared with their parents or other adult authorities.”¹¹ In the context of an intervention, social desirability bias can be stronger or manifest differently in the intervention group because, by the nature of the intervention, those individuals have been coached to change the behaviors that they are subsequently asked about. A few studies have compared the discrepancy between self-reported and objectively measured data in participants in intervention versus control groups. Intervention-induced bias in self-reported diet, physical activity, and body weight outcomes was detected in some^12–15 but not all^16,17 studies. In one study that did not detect bias, the investigators took special care to separate the data collection from the intervention, using three different teams of staff and deceiving the subjects that the goal of the study for which the data were collected was different from the actual goal of the intervention.¹⁶

Examples of the Error

Most weight control interventions use measured rather than self-reported body weight as the primary outcome, but self-report has been used. Self-report measures are used more often to assess intervention effects on physical activity and almost always for diet. Several studies have described differences in self-reported intake^18–20 and/or physical activity^18,21,22 between the intervention and control groups despite no impact of the intervention on measured BMI or body weight. In one illustrative case, investigators implemented an intervention to promote physical activity. Compared to the control, the intervention group self-reported greater physical activity, but the objective accelerometry data did not detect a difference between groups.²³ When the self-reported measures are used, authors often indicate measurement error as a limitation,^18–21 but rarely mention the possibility of intervention-induced bias.¹⁸

Recommendations

Since intervention-induced bias exists in some studies, and because the face validity for its potential is strong, we discourage the use of self-report in trials when feasible objective measures exist, such as body weight and physical activity. For dietary intake (a key component in most weight-related interventions), objective methods are not readily available in most studies. In those circumstances, we advise investigators to forego emphasizing intervention effects on self-reported energy consumption in particular,^24,25 and to remind the reader that bias related to the intervention can occur when diet is measured by self-report. Additionally, we suggest that the term “self-report” be specifically mentioned in the abstract if data are self-reported.

Self-report biases are likely to be found in the same types of individuals who show other types of social desirability bias.²⁶ Research on the efficacy of strategies to reduce the perceived link between the self-reported information and the intervention could result in methods to reduce bias and improve data quality. More research on the attributes of self-report biases in studies that include weight-related interventions is merited.

Inferential Error: Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time

Error Description

Provide an intervention to a sample that consists entirely of individuals greater or less than the average on some characteristic – such as children all with high BMI z-scores – with no control group and assume improvements in the variable result from the intervention, rather than a spontaneous tendency for extreme values to revert toward the population average.

Explanation of the Error and Why the Practice is Wrong

In 1886, when evaluating offspring height relative to tall parents, Sir Francis Galton observed the phenomenon he initially referred to as “regression toward mediocrity.”²⁷ Specifically, and perhaps surprisingly, Galton found offspring were shorter than their parents if they had tall parents. He recognized that by first considering a portion of the population that holds extreme values (e.g., tall individuals), the second measurement (e.g., their offspring’s height) would be closer to the population average and hence the offspring would be shorter. Later, Galton revised the name of this observation to what we today know as regression to the mean (RTM), with much written about examples and methods to avoid or address it over the years (c.f.,^28,29).

Unfortunately, childhood obesity investigators sometimes erroneously conclude positive effects of an intervention that can be attributed to RTM. This typically occurs when a population with extreme baseline values is investigated, such as children with high BMI z-scores (BMIz; a child’s BMI standardized to a reference distribution, such as those proposed by the International Obesity Task Force³⁰). In some cases, investigators exacerbate this phenomenon by analyzing the data by subgroups of baseline levels. When the group is re-measured at the end of the study, the score is lower, with investigators drawing the conclusion that the intervention was effective. However, as observed by Galton, by RTM alone, we expect an extreme group to have lower values at a subsequent point in time. We clarify that RTM does not imply that children with BMIz in the obesity range are expected to spontaneously revert to the normal BMIz range, which would be truly remarkable. Rather, in RTM the subsequent measurements are expected to be lower on average; how much lower depends on many factors related to measurement error, natural variability, and the extremeness of the selected subgroup.

Examples of the Error

A holistic health intervention designed to improve knowledge of and employ healthful behaviors was implemented in 40 participating elementary schools.³¹ BMI-for-Age z scores were recorded at baseline and the authors concluded program effectiveness due to the largest decreases of BMIz at the end of the school year in students who were classified with overweight or obesity at baseline. Using the 1997 National Longitudinal Survey of Youth data as a benchmark strongly supported that these decreases were not a result of the intervention but were attributable to RTM.³² Similarly, when evaluating the impact of nutrition education on African American preschoolers,³³ study authors concluded positive intervention effects when considering only children in the intervention group with overweight or obesity. When the possibility of RTM was suggested to the authors,³⁴ they tested and found a decrease in the control group BMI consistent with RTM, and should be commended for publishing a clear correction that stated, “we cannot make any affirmative statements about the effectiveness of our interventions.”³⁵ Finally, a physical activity intervention program³⁶ that enrolled only children with overweight or obesity found a decrease in BMIz at the post-intervention measurement, again consistent with RTM. More examples exist (e.g.,^37,38).

Recommendations

The best practice to determine a true intervention effect is to include a control group from the same population because RTM will impact the control group as well as the intervention group under standard assumptions (e.g., no bias from differential attrition between the two groups).³⁹ If a control group is not included, the effects of RTM can still be estimated by predicting the expected second measurement from knowledge of the measurement’s reliability and the population mean.⁴⁰ Multiple baseline measurements could also help inform the potential degree of RTM effect. At the very least, authors should clearly, and without reservation, acknowledge the distinct possibility that RTM could explain the improvements after intervention. Watson et al. did just that when communicating their results on a family-based childhood obesity program, albeit without reference to RTM by name: “As with many service evaluations, this study is limited by a lack of control group and a high attrition rate. It is not therefore known what change might have occurred without intervention.”⁴¹

Inferential Error: Changing the Goal Posts

Error Description

When a study to test an intervention’s effect on obesity yields a non-significant result for the primary outcome, use surrogate secondary outcomes to make claims of effectiveness for an intervention.

Explanation of the Error and Why the Practice is Wrong

A meta-analysis reported that 79% of interventions to prevent or reduce childhood obesity were unsuccessful.⁴² Interventions failing to show an effect are therefore the norm. Yet, rather than reporting a non-significant result for the primary outcome of childhood obesity interventions (e.g., BMIz, body weight), some investigators emphasize or only report success based upon secondary outcomes for surrogate obesity measurements or presumed intermediate drivers of obesity such as increased knowledge, improved attitudes, reduced self-reported dietary intake, or increased physical activity. In one version of this error, authors may conclude that success in altering surrogate outcomes support an intervention’s use for improving obesity, despite no improvements in obesity; in another, the authors may ignore the original primary goal of affecting obesity, and instead make conclusions about the surrogate outcomes alone. Often the reader is not informed of the original primary goal. This technique of changing the criteria for success is commonly referred to as changing or moving the goal posts.⁴³

While nutrition-related knowledge or behavior, intake of energy or various nutrients, physical activity, and many other factors may be intermediate drivers of BMI or obesity, it is unreasonable to use them as surrogate markers for obesity itself. A major downside to changing the goal posts is that interventions are reported as effective even though they did not satisfy the pre-specified objective: to prevent or treat childhood obesity. Advocacy for such ineffective interventions as strategies for combating childhood obesity is then added to the literature, giving the false appearance of an increasing body of supporting evidence that yields confidence in efficacy of intervention approaches that, in fact, were not successful.

Examples of the Error

The stated aim of a cluster randomized controlled trial of nutrition education was to use social cognitive theory (SCT) to reduce and prevent obesity among adolescent girls. The study concluded: “Although school-based nutrition education intervention using SCT did not change significantly BMI and WC among the targeted population in this study, dietary habits as well as psychological factors improved significantly in the intervention group.”⁴⁴ Although the study did not affect the stated aim of obesity outcomes, the authors still concluded that a “school-based intervention based on SCT introduces a new approach to health authorities” based on surrogate measures.

Another study using a school-based, cluster-randomized design implemented health-promoting strategies for 3.5 years.⁴⁵ There were no significant differences between the control and intervention group for the majority of the stated primary and secondary outcomes, including BMI, BMIz, and prevalence of overweight and obesity. The authors admitted that “only limited translation of those environmental changes into improved behaviours and weight status were evident at follow up.” Yet, they concluded that, “[t]his 3.5 year intervention demonstrates that it is possible to effect system level change and some improvements in health and wellbeing outcomes from investments that focus on the school environment…” In addition, despite no statistical significance, they declared changes in outcome variables such as vegetable consumption, as a positive outcome.

In the above examples, no effects on obesity were demonstrated and so the outcome focus changed to general statements of health. Sometimes, no effect will be seen on obesity, yet promising results in a surrogate outcome may lead authors to still conclude effects on obesity. As described in a letter to the editor in one such case, the original researchers saw no statistically significant differences in their primary obesity measurement, demonstrated only a single statistically significant difference among a battery of non-registered anthropometric measurements, and still concluded that their intervention may benefit infant adiposity.⁴⁶

Recommendations

Authors of intervention studies to reduce childhood obesity should clearly indicate the results pertinent to the pre-specified primary hypothesis and not obscure those findings by excessive focus on alternative outcomes. We are not discouraging the collection, analysis, or reporting of secondary or surrogate endpoints, but it is important that the primary outcomes are decided in advance and communicated clearly and completely, and alternative endpoints are distinguished appropriately.⁴⁷

A study by Lloyd et al.⁴⁸ offers an exemplary approach for drawing conclusions. This obesity prevention trial of children from 32 schools observed no significant effect on obesity. The authors concluded, “we found no effect of the intervention on preventing overweight or obesity. Although schools are an ideal setting in which to deliver population-based interventions, school-based interventions might not be sufficiently intense to affect both the school and the family environment, and hence the weight status of children”. Importantly, the study did not advocate for the repeat of the same approach. Instead, it recommended that “[f]uture research should focus on more upstream determinants of obesity and use whole-systems approaches.” Similarly, Barkin et al.⁴⁹ noted that their preschool-age intervention did not significantly affect BMI trajectories over 36 months, but did find a significant difference in reported energy intake in favor of the intervention (see “Using Self-Reported Outcomes and Teaching to the Test”]. Nevertheless, the abstract remained focused on the primary outcome: “A 36-month multicomponent behavioral intervention did not change BMI trajectory … compared with a control program. Whether there would be effectiveness for other types of behavioral interventions or implementation in other cities would require further research.”

Journal editors and reviewers should encourage publishing all well-conducted studies, including results from interventional strategies that did not improve childhood obesity. This may ease pressure on authors to provide “spin” ^50,51 on an interventional study with null findings. Where spin exists, it needs to be corrected by reviewers and editors before publication. Finally, readers need to be sure to skeptically read and interpret results.

Inferential Error: Ignoring Clustering in Studies that Randomize Groups of Children

Error Description

Conduct a cluster randomized trial, in which groups of children (e.g., entire classrooms, schools, or pediatric clinics) are randomly assigned to experimental conditions, but analyze the data as though the children were randomized individually.

Explanation of the Error and Why the Practice is Wrong

There are two key aspects to this error, clustering and nesting, and ignoring either can weaken or invalidate statistical inference and thus conclusions. With respect to clustering: children from in-tact social groups, such as classrooms, clinics, or even neighborhoods, tend to be more highly correlated within a cluster than between clusters. In simplest terms, children in one classroom may tend to be more alike than children in another classroom. Reasons for this may include social selection (e.g., educational tracking or impacts of efforts to maintain friendship networks) and common exposures (e.g., teacher A versus teacher B). Statistically, this means that we have less independent information than we would expect from a simple, random, non-clustered sample. Less information means the effective sample size is less than the actual, or nominal, sample size. For example, there may be 100 children in a study but as a result of clustering the study may have information equivalent to only 80 independent children.⁵² Classical regression methods, like ordinary least squares or logistic regression, and classical hypothesis tests, like Student’s t-test or Pearson’s chi-square test, are predicated on the observations being statistically independent. Applying these classical estimation and inference methods to correlated observations from cluster-randomized trials tends to underestimate standard errors, which erroneously makes p-values smaller than they should be, and increases the risk of falsely rejecting a null hypothesis of no intervention effect (i.e., making a type I error).⁷ Simply put, analyses that ignore clustering may yield smaller p-values than proper analyses that incorporate clustering. The Consolidated Standards of Reporting Trials (CONSORT) extension for Cluster Trials, which are best-practice reporting guidelines for cluster trials, include the advice that cluster randomized trials “should not be analysed as if the trial was individually randomized...”⁵³ The issue was further highlighted by the National Institutes of Health in their “Research Methods Resources” website: “Any analysis that ignores the extra variation … or the limited [degrees of freedom] will have a type 1 error rate that is inflated, often badly.”⁵⁴ Thus, ignoring clustering risks type I errors (i.e., concluding there is a difference between groups when a difference does not exist). On the other hand, ignoring the correlated observations in the planning stages of a cluster randomized trial means that cluster randomized trials may be underpowered when analyzed correctly and thus researchers risk making type II errors, as well (i.e., failing to conclude there is a difference between groups when a difference actually exists).⁵⁵

The second issue is nesting, which is to say the randomized clusters (e.g., schools) are nested or wholly located within experimental conditions. As a result, the unique aspects of the clusters themselves (e.g., percentage receiving free and reduced lunch, age of school building, or tax-base supporting the school) may confound intervention effects. To eliminate the threat of such cluster-specific confounding from desired intervention effects, one must have many replicate clusters within experimental conditions. Such cluster-level replicates determine the degrees of freedom (which, roughly speaking, represent the amount of independent information) available for testing intervention effects. Thus, studies cannot have just one cluster per experimental condition: doing so yields zero degrees of freedom for intervention effects. The CONSORT extension for Cluster Trials summarizes the problem by noting “[t]rials with one cluster per arm should be avoided as they cannot give a valid analysis, as the intervention effect is completely confounded with the cluster effect.”⁵³

Though we focus on groups of children, these concerns apply just as much to groups of parents, teachers, or others targeted by an intervention intended to address childhood obesity.

Examples of the Error

Many existing studies randomized clusters of subjects to study groups but subsequently ignored the clustering in the statistical analyses (as reviewed in⁵⁶ and addressed in letters to editors^57,58). In one example,⁴⁴ researchers evaluated anthropometric, nutritional behavior, and social cognitive outcomes among 173 adolescent girls with overweight or obesity assigned to either an intervention or control group. Despite the authors following published guidelines on reporting cluster randomized trials,⁵³ their analyses did not account for the fact that the girls were students belonging to one of 8 schools randomized to the intervention or control groups. Even if the intra-cluster correlation in the observations within these schools were as low as 0.05, the variance inflation⁵⁹ caused by ignoring the clustering would be at least 2.03 under reasonable assumptions, suggesting that their reported outcome variance estimates are likely at most half of the unbiased outcome variance estimates corrected for the clustering. This might have had a profound, invalidating impact on inferences made in that study.

Some examples involve using too few clusters. In one such example, authors included two schools in each of two districts to estimate the effects of a multi-component, school-based intervention.⁶⁰ A letter expressing concerns about this paper⁶¹ noted that despite the authors recognizing the importance of including clustering a priori, the authors failed to include clustering in analyses, and even compared pairs of schools within districts, resulting in tests that would have had zero degrees of freedom if analyzed correctly (i.e., there would be no information to estimate the variability in differences between the groups). In response, the study authors justified their use of incorrect analyses in part by citing others who also used too few clusters,⁶² reinforcing the importance of preventing such misanalysed studies from appearing in the literature to begin with. In response to a subsequent critique of the same study,⁶³ the original authors published a corrigendum that continued to make invalid causal conclusions about their intervention.⁶⁴ In another case, investigators randomized one school each to 4 interventions, plus 4 no-intervention control schools.⁶⁵ A critique of the study noted that “although the number of clusters that are needed in a cluster-randomized trial is not fixed, that number is never 1,” and therefore that the study “could not establish causation and, at best, only had the capacity to create the hypothesis that [the interventions] may have a favorable impact on childhood obesity.”⁶⁶ In one other case, an article making similar mistakes was retracted “because the statistical analysis was not correct given the cluster-randomized design” and the “conclusion that the original paper drew about having demonstrated treatment efficacy was not supported in the corrected analysis.”⁶⁷

Recommendations

The degree to which these issues impact the validity of a cluster randomized trial depends on many things, perhaps most notably the number of clusters randomized, the number of children in each cluster, and how highly correlated the observations are within clusters (i.e., the intra-cluster correlation which can be measured by the ratio of the between-cluster outcome variance to the total outcome variance).⁵⁹ These and other fundamental issues with cluster randomized trials and modern practices for addressing the issues have been described in detail elsewhere⁵⁶ and thorough reviews of design and analysis methodologies for these trials were recently published.^68,69 A rule of thumb is that studies should have at least 10 clusters per experimental condition to have a chance of reasonable power to detect large intervention effects, and such tests must rely on the t-distribution, which adjusts for the limited sample size. Thirty or more clusters per experimental condition are needed for z-tests of intervention effects (i.e., the normal approximation to the t-distribution for large samples). Power analyses and statistical analyses need to include the clustering to appropriately control expected type I and type II errors. In the case of single clusters per group, authors need to be explicit about the downgrading of the study from a cluster-randomized trial to a quasi-experiment because clusters are perfectly confounded with intervention.

Inferential Error: Following the Forking Paths, Sub-Setting, P-Hacking, and Data Dredging

Error Description

If results are not statistically significant with the preplanned primary analysis in the total sample, or if there is no preplanned analysis, keep trying different analyses with different subsets of the sample or various outcomes and base conclusions on whatever is statistically significant.

Explanation of the Error and Why the Practice is Wrong

To report an intervention effect with p < 0.05 generally means that if the null hypothesis were true, appropriately calculated test statistics that are equal or greater in magnitude to that observed would occur in fewer than 5% of samples.⁷⁰ When many possible analyses of the data are performed, and if the null hypothesis is true, the probability of finding at least one statistically significant result by chance increases. Simmons, Nelson, and Simonsohn introduced the phrase “p-hacking” in their demonstration of how flexible stopping rules for recruitment, testing multiple outcomes, and exploring for interaction effects could dramatically raise the chance of a false positive⁷¹; similar approaches have been referred to as “undisclosed flexibility in data collection,” “researcher degrees of freedom,”⁷² “data dredging”,⁷³ and “following the forking paths,”⁷⁴ among other names, with the authors making nuanced distinctions amongst these terms. Generally speaking, if analytical choices are made based on features of the data at hand rather than a priori decisions or pre-specified theory, it is possible that the p-value no longer represents the probability under the null hypothesis, and highlights the importance of preregistering studies and analyses. As a concrete example, consider researchers who decide to pool overweight and obesity into the same category after looking at the data because the number in the obesity category is too small and thus underpowered. Grouping overweight and obesity might be a legitimate decision under some circumstances, but when made after the data are collected and evaluated, it raises the question of whether those categories would have been pooled if the number in the obesity category was larger. It is important to note that the problem arises even when such selection is unintentional, such as many implicit tests for samples that may have been analyzed differently.^75,76

Examples of the Error

It is often difficult to determine whether inappropriate or undisclosed analytic flexibility occurs in any specific case without knowing a priori what authors intended to do. Besides p-curve analyses,⁷² the best evidence may come from comparing randomized trials to their preregistrations. As described with “Changing the Goal Posts,” discordance between registered primary outcomes and the reporting in manuscripts can reveal analytical or reporting decisions. Discordance between registration documents and publications is not uncommon in obesity literature.^51,77 In addition, flexibility in analyses can be detected even through the number of participants included in analyses. In three studies reported from the ACTIVITAL study,⁷⁸ total sample sizes were reported as 1370, 1430, and 1440, and the sample sizes used for analyses included 1046, 1083, and 1224. In addition, one of the papers focused on subgroup analyses.⁷⁹ In some cases, subgroups can be important in evaluating the results of a trial [cf.,⁸⁰], particularly when the subgroups are pre-specified. However, subgrouping can also be associated with researchers wandering through the forking paths of research decisions.⁷⁴ For instance, the authors categorized students into different activity categories based on accelerometer counts, but did not cite or pre-specify the thresholds. It is therefore unclear if the cutpoints were established a priori or based on the data. Conversely, they do cite a priori thresholds for subgrouping households by poverty status, fitness group by established standards, and BMI by International Obesity Task Force criteria. In the latter case, however, the authors chose to pool overweight with obesity. The decisions of sample sizes, cutoffs, and pooling of groups may be perfectly legitimate, but the full process of how the decisions were made is unclear from the reports and the registration, and it is uncertain what effect the flexibility of choices may have had on the final results.

Recommendations

Determining whether p-hacking occurred in a single paper can be difficult even with preregistration. However, approaches called p-curve and p-uniform^72,81,82 were developed to evaluate the distribution of many p-values observed across many studies, such as from a meta-analysis, or multiple analyses within a single study, to test for specific patterns in the p-values. Others have introduced text-mining techniques to investigate p-hacking in scientific literature and test for p-hacking when conducting a meta-analysis.⁸³ Although not perfect, these methods have been used at least once in the childhood obesity and exercise literature.⁸⁴ The results suggested that selective reporting was not obviously present, and the authors suggested that the results were not intensely p-hacked from this small subset of studies.

Researchers can protect against inappropriately capitalizing on chance findings in multiple ways. One familiar approach is to correct for multiple comparisons or attempt to control the false discovery rate. These methods control the type I error rate across multiple comparisons, but in so doing make it harder to reject the null hypothesis (i.e., decrease power), and, hopefully, encourage researchers to make fewer and more focused analyses. Nevertheless, p-value adjustments would depend upon a careful counting of all tests conducted, not just those published, and can fast become unwieldy. In addition, researchers can pre-register their analysis plan and main hypotheses. Pre-registration can protect against any appearances that results were obtained through undisclosed p-hacking, and will likely constrain the number of analyses. In some situations, preregistration is required.⁸⁵ Alternatively, multiple outcomes can be combined into one analysis using hierarchical modeling,⁸⁶ which can mitigate multiple testing concerns. In this way, researchers can present more comparisons of interest and then analyze them together, rather than presenting only fewer or a single pre-chosen comparison (which would limit our ability to learn from data). In any approach, all results should be presented, whether or not the results reach predefined statistical significance thresholds. We do not mean to discourage performing creative or exploratory data analyses. Rather, what is important is openness. Randomized trials should pre-specify primary and secondary outcomes, report the “multiverse” of analyses tried, and describe the analytical paths taken, rather than selecting the subset that achieve some arbitrary threshold of “statistical significance” or desirable results.

Inferential Error: Basing Conclusions on Tests for Significant Differences from Baseline

Error Description

Separately test for significant differences from baseline in the intervention and control groups and if the former is significant and the latter is not, declare the result statistically significant.

Explanation of the Error and Why the Practice is Wrong

Researchers often want to compare the level of a variable between two groups over time. These might be experimental, as in a randomized trial, or observational, as in a cohort study. In both of these designs, we often have an observation of the variable at baseline and follow-up. Some researchers test for changes over time within groups. If one group shows a statistically significant change from baseline, and the other group does not, sometimes authors will conclude that there is a difference between groups. However, no formal between-group test was conducted. This interpretation involves regarding the non-significant difference in one group as showing no difference (i.e., accepting the null), and the significant difference in the other group being interpreted as concluding there is a difference (i.e., rejecting the null). However, “not significant” does not imply “no difference”, only that we do not have sufficient evidence that a difference exists between groups. Testing for differences between groups by separate analyses of within-group changes is also referred to as the Differences in Nominal Significance (DINS) error⁸ or inappropriate testing against baseline values.⁷

It is useful to simulate this method of analysis for the situation in which we know that there is no difference between groups (i.e., the null hypothesis is true). Two of us^87,88 simulated a two group, pre-post design. At the simulated baseline, we generated random observations from the same population, hence having no underlying differences (mean of 0), with a standard deviation of 2.0. We then simulated a random change from baseline to each observation to simulate a follow-up measurement, having the same mean of 0.5 and standard deviation of 1.0. We then carried out paired t tests in each group to test for change from baseline. We found that in 10,000 runs of this simulation, 617 (6.2%) pairs of groups had neither test significant, 5,675 (56.8%) had both tests significant, and 3,708 (37.1%) had one test significant but not the other. Hence, for this particular set-up, where both groups come from the same population and the null hypothesis that the groups come from populations with the same mean is therefore true, the probability of detecting a difference using the separate test strategy is not the 5% we should have, but 37.1%.

If the probability of detecting a statistically significant result for a change over time within each group is P (that is, P is the power to detect a difference over time), the probability that one group will have a significant difference and the other will not is 2P(1-P).⁸⁸ 2P(1–P) has a maximum value of 0.5 when P = 0.50, so that half of all such trials would show a significant difference in one group but not in the other, even if the null hypothesis of no difference between groups is true. If the changes over time also have true null hypotheses, so that there are no differences over time or between groups, the probability of one significant and one not significant comparison of change over time is 2×0.05×(1 – 0.05) = 0.095 – i.e. about twice the nominal 5%. Thus, the separate tests procedure is always misleading.

If the powers for the two tests against baseline are different, P₁ and P₂, the probability of one test being significant and one non-significant becomes P₁(1 – P₂) + P₂(1 – P₁), which can be close to 1 if one power is large and the other small. The differences in P₁ and P₂ can be caused by very different group sizes with identical effect sizes (that is, the null hypothesis is true), or the differences from baseline could vary greatly between groups (that is, the null hypothesis is false). In the latter case, of course, there would be a difference between the groups, but an invalid analysis is still inappropriate, even if it produces the “correct” answer by chance, because in practice we do not know which situation is true.

Statistically significant changes from baseline within a group may be due to the intervention, but there are several other possibilities, including random chance, seasonal variation, systematic changes with age, and regression towards the mean (see “Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time”). We can expect that in a study of obesity, especially in children, the mean height, weight, BMI, or other measurements may change over time and the power of the pre-post test to detect a change may be considerably greater than the 0.05 when, in fact, the null hypothesis is true, thus increasing the probability that one test will be significant and the other not.

Examples of the Error

Many examples of this mistake exist in practice (reviewed generally in ^88,89 and in some letters to editors about childhood obesity specifically^90,91). Two examples specific to childhood obesity are below.

Researchers investigated a health promotion model for children.⁹² The results showed that BMI standard deviations scores (BMI SDS) decreased significantly in the health promotion group (p<0.001), but did not differ significantly in the control group. However, the median change in both groups was −0.1 BMI SDS units, for a between-group difference in medians of 0.⁹³

In another study, researchers compared the effectiveness of family-based interventions for childhood obesity, in which one intervention included parents, the other included both parents and children, and the control was follow-up only.⁹⁴ Although the researchers conducted the appropriate among-group tests that were not statistically significant, the authors nonetheless made conclusions based on the within-group significance of the ‘parents and children’ group.⁹⁵

Recommendations

Authors who compare an outcome measurement with baseline should always be clear that this does not tell them anything about differences between groups for an outcome measure, and does not provide reliable evidence of the effect of the intervention (see “Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time”). The between group comparisons in the case of randomized interventions can be tested several ways, including incorporating the baseline measurement as a covariate, conducting a repeated measures ANOVA, or using follow-up only measurements in the case of randomization (though this would be underpowered compare to including the baseline measurement), among others.

Inferential Error: Equating ‘No Statistically Significant Difference’ with ‘Equally Effective’

Error Description

When an active comparator, instead of a placebo, is used to test a novel intervention’s effectiveness on obesity and there is a null result, conclude that the interventions had ‘equal effectiveness’ rather than ‘were not statistically significantly different.’

Explanation of the Error and Why the Practice is Wrong

The use of placebo or no-attention controls can be controversial, especially when an assumed effective intervention exists. On the one hand, the use of a placebo benchmark for new interventions represents a lower, easier-to-beat efficacy standard than comparing to the existing intervention. On the other hand, because of publication biases⁹⁶ and other forces that distort the evidence in the published literature^97–103 it cannot be taken for granted that the existing intervention is actually effective, or effective in all populations (c.f. ¹⁰³ and ¹⁰⁴ for discussions about placebo controls). For the present discussion, we simply acknowledge that there are principled reasons why a researcher might want to conduct a placebo-less, head-to-head comparison between two interventions, each of which may be conjectured to have some efficacy.

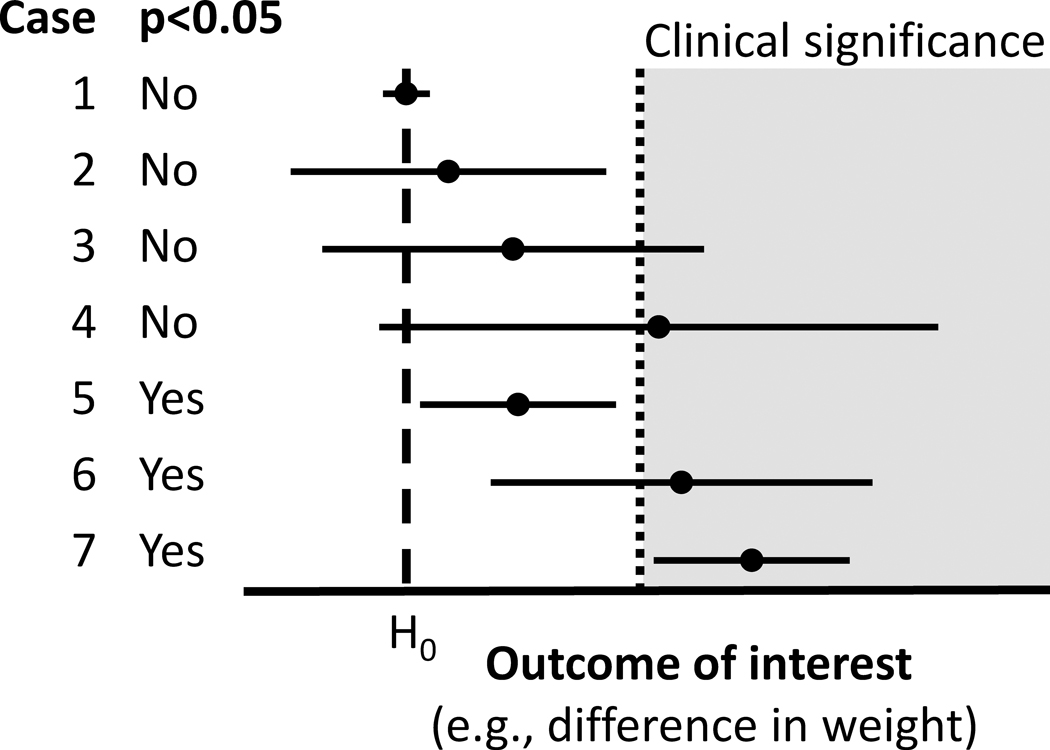
The claims made from such a design, however, are more nuanced. Consider a situation in which two interventions are being compared and the outcome is weight loss. Here, the usual null hypothesis is that the two interventions have the same effectiveness and thus the average weight loss is the same across groups. The complementary alternative hypothesis is that the novel intervention produces either superior or inferior weight loss compared to the existing intervention. This is the setup for a superiority trial.¹⁰⁵ In practice, when the null is rejected, the question of superiority or inferiority is easily settled by the direction of the observed effect; however, the null will only be rejected in sufficiently powered research with either large sample sizes when effect sizes are small, or when there are large effect sizes. On the other hand, if the study has low power and small true effects, one can almost a priori guarantee a non-significant result. When there is no statistically significant difference between groups, and particularly in situations where both groups improved from baseline, researchers may make two mistakes. First, authors may conclude that the change from baseline is evidence that the intervention worked at all; however, without the appropriate placebo control it is always possible that the improvement was coincidental or a statistical artifact like RTM (see “Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time”). Second, because the two groups were not significantly different, authors may incorrectly ‘accept the null’ when discussing non-significant differences between groups and declare ‘equal effectiveness’ between a novel intervention and the existing intervention, when in fact ‘unequal effectiveness’ is also compatible with the data (Figure, Cases 2–4).

Figure.

Seven hypothetical study results, with point estimates and 95% confidence intervals. H₀ represents the null hypothesis (often representing no differences between groups).

Examples of the Error

In a randomized comparison of therapist-led (TLG) and self-help groups (SHG), “[n]o significant between-group differences were detected in the children’s changes in adiposity or dietary intake after 6 and 24 months”; but this does not necessarily mean that “the TLG and SHG intervention groups appear to be equally effective in improving long-term adiposity and dietary intake in obese children.”¹⁰⁶ Similarly, if “[c]hild BMIz outcomes were not statistically different between the two groups (F = 0.023, p = .881)” then one should not necessarily claim that “[b]oth telemedicine and structured physician visit[s] may be feasible and acceptable methods of delivering pediatric obesity intervention to rural children.”¹⁰⁷ Even with a highly significant “reduction in the ZBMI in both groups (P<0.0001), without [a] significant difference between them (P=0.87)” one should not claim that “fixed diet plan[s] and calorie-counting diet[s] led to a similar reduction of ZBMI”¹⁰⁸ because there is no non-treatment or placebo comparator.

Recommendations

If a researcher wants to show that a novel intervention is superior to an existing intervention and furthermore that it is effective in its own right, the way to do this is to conduct a three-arm trial comparing the novel intervention, the existing intervention, and a placebo or non-treatment control. If the two interventions are indeed effective, demonstrating effectiveness versus placebo should not be difficult. However, if both interventions are effective, and the difference in effectiveness between two interventions is small, very large sample sizes may be necessary to detect a difference, which could make the study impractical.

A researcher might a priori decide to investigate whether the novel intervention is ‘equally effective’ or ‘not worse’ than the existing intervention. For either goal, a superiority trial should not be used. Rather, the trial must be set up as an equivalence trial or a non-inferiority trial, respectively.¹⁰⁹ Non-inferiority trials use a different, one-sided null, and as a result a rejected null would be interpreted as “the novel intervention is no worse than Δ% less effective than the existing intervention”, where Δ is small and determined a priori. An equivalence trial is similar, but two-sided: “the novel intervention is no better or worse than Δ% effective than the existing intervention” (Figure, Case 1). However, because of this design choice, a non-inferiority trial cannot be used to show superiority over an existing intervention.¹¹⁰ An extension of the CONSORT guidelines is available for reporting non-inferiority and equivalence trials.¹¹¹

As always, the question to be answered should be determined before the research begins and the corresponding proper design must be implemented. Trying to utilize a superiority trial as a non-inferiority or equivalence trial or vice-versa is unacceptable. Results that are compatible with “equally effective” are also compatible with “equally ineffective.”

Inferential Error: Ignoring Intervention Study Results in Favor of Observational Analyses

Error Description

If the intervention does not produce better results than the control, ignore or underemphasize the original intervention design in favor of observational correlations of intervention-related factors with outcomes.

Explanation of the Error and Why the Practice is Wrong

When differences between the intervention and control groups are not detected, researchers may choose to ignore the original design and instead test for and emphasize associations to support their causal claims. For instance, the control group may be ignored, and regressions between intervention compliance (e.g., number of intervention sessions attended) and outcomes might only be tested within the intervention group. Or, the groups may be pooled, and some aspect of the treatment (e.g., number of fruit and vegetable servings) might be tested for its relation to outcomes across all participants. This vitiates the more sound, between-group inferences and removes intervention assignment, thereby undermining causal inference and forfeiting the strengths of a randomized trial. This becomes even more concerning when comparison groups are formed using characteristics that are measured post-randomization.¹¹² The dropping or pooling of comparator groups to focus on changes over time can be problematic regardless of whether the interventions were randomized (e.g., a randomized trial) or not (e.g., a quasi-experiment), and is therefore related to Errors “Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time” and “Basing Conclusions on Tests for Significant Differences from Baseline”. Secondary or exploratory analyses can lead to important new hypotheses, but selectively ignoring data (e.g., the control group) or study design (e.g., randomization) limits causal inference of the study as designed,¹¹³ and may be misleading if the primary, between-group design is ignored or underemphasized.

Examples of the Error

The Healthy Schools Program (HSP) is a national program that provides schools with tools to design healthy food and physical activity environments. To examine the effectiveness of the program for reducing the prevalence of childhood overweight and obesity, a study was conducted comparing schools with the HSP intervention and propensity-score matched controls.¹¹⁴ Although the study found no differences between the two groups on the prevalence of overweight and obesity, the authors claimed “clear” effectiveness of the HSP based on secondary analyses of the participating schools (excluding the controls), which demonstrated a mild dose-response relationship between years of contact with the program and reduction in prevalence of overweight and obesity. The investigators deemed the intervention as “evidence based” and concluded that it was, “an important means of supporting schools in reducing obesity” despite the lack of evidence from the between-group comparison. A dose response of the intervention is one potential explanation for the within-group results, but, given the non-significant between-groups analysis, a compelling alternative explanation for the association is that the schools that accepted more of the intervention were different from those that accepted less.

Another example investigated the effect of once or twice per week delivery of a family-based intervention.¹¹⁵ Although no differences were seen between the two versions of the program, the authors concluded that “higher attendance, as a proportion of available sessions, leads to better outcomes for children.” This conclusion was based on pooling the two groups and looking for associations among proportion of attendance and outcomes. As in the previous example, it is possible that there is an inherent difference between children who adhere and those who do not. Indeed, in this case, equal adherence to a proportion of sessions meant that the twice-per-week group had to attend twice as many sessions as the once-per-week group, and yet twice the exposure (as randomized) did not result in a difference between groups.

Recommendations

Rigorously conducted and adequately powered studies with non-significant between-group results still provide useful information about the effectiveness – or lack thereof – of the interventions. Ignoring the primary results in favor of testing associations within subgroups or using post-randomization tests is discouraged. These exploratory analyses can be integral to investigating what characteristics of children or the interventions might lead to effectiveness, but the analyses need to be communicated clearly, with appropriate limitations cited, and making it clear to the reader that conclusions are from associations and do not have the strength of trial results.

Inferential Error: Using One-sided Testing for Statistical Significance

Error Description

If statistically significant results are not achieved with a two-sided test at the conventional 0.05 significance level, but the p-value is less than 0.10 and the effect estimate is in the preferred direction, switch to a one-sided test and it will be significant.

Explanation of the Error and Why the Practice is Wrong

Let us take a scenario in which a researcher uses a two-sided t-test at the 5% significance level (α=0.05) to assess the between-group difference in BMI as the primary outcome of a childhood obesity intervention. The researcher expects that the intervention group will have a lower post-intervention mean BMI than the control group, with a formal null hypothesis that the intervention group is equal to the control group. Contrary to the investigator’s hopes, the two-sided p-value turns out to be 0.08 in the favored direction, thus failing to reject the null hypothesis. However, because the researcher is confident that the effect can only be in one direction, the initial analysis plan is abandoned (see “Following the Forking Paths”) in favor of a one-sided test. The null hypothesis for this new test is now that the intervention is worse than or equal to the control, while the alternative hypothesis is that the intervention is better than the control. The one-sided test no longer guards against a mistaken null hypothesis rejection in the opposite direction, so practically speaking for this case the obtained p-value is cut in half when the difference is in the favored direction. The p-value is now 0.04: statistically significant.

When researchers are not formally testing non-inferiority (see “Equating ‘No Statistically Significant Difference’ with ‘Equally Effective’”), the described approach is wrong for at least two reasons.¹ First, unless one is explicitly utilizing Bayesian statistics with subjective priors (not discussed herein), results should be independent of the researcher’s expectations. The results require “a respect that transcends the stories they can tell about how they came to do the experiment, which they call ‘theories.’”^1,116 Although a researcher is not interested in one of the two directions, future readers may come up with another theory that hypothesizes the opposite effect or no effect at all, and reporting and interpreting results in only one direction limits the utility of the results for future scrutiny. Second, the research may result in a large difference in the unexpected direction, yet one-sided tests do not differentiate between no effect and large effects in the undesired direction. Researchers using a one-sided test may then be tempted to offer an explanation for the large effect in the unexpected direction, which violates the assumptions of the one-sided test. One-sided tests only test a single direction, and any attempt to interpret the effect in the unexpected direction essentially has a type I error rate of 10% (5% in each direction) instead of the stated 5%.

Examples of the Error

In some cases, authors justified the use of one-sided tests by stating that their hypotheses are directional to begin with.¹¹⁷ Yin et al.¹¹⁸ specifically argued that their prior study results justified testing new results only in the direction consistent with their prior results. Others reported one-sided tests only for some outcomes.¹¹⁹ Based on the manner in which statistics were reported, it seems likely that one-sided tests utilized in some childhood obesity interventions remain partly disclosed³⁶ or undisclosed¹²⁰ because the authors did not state whether one- or two-sided tests were implemented. For partial disclosure, Siegel et al.³⁶ reported one-sided tests for some analyses, but did not specify for others. In one ambiguous example, change in BMIz was reported with a confidence interval of (−0.09, 0.02) that contained the null value (Figure, Cases 2–4), but also reported a statistically significant p-value, which is impossible if the confidence interval was constructed from the same statistical procedures. However, statistical significance was possible for that example with a one-sided test. Detecting non-disclosure is more difficult. Kilanowski & Gordon¹²⁰ analyzed differences in changes in body weight and BMI between intervention and comparison groups and reported Rank Sum z-values that would provide p-values of 0.107 and 0.121 in two-sided tests, but the authors reported p-values of 0.05 and 0.059 –half of the two-sided (within rounding error), which is consistent with an undisclosed one-sided test.

What is recommended

Long-standing literature on this issue^1,121 emphasizes that a one-sided test in an RCT is not reasonable, except for a non-inferiority trial (see “Equating ‘No Statistically Significant Difference’ with ‘Equally Effective’”). Apart from non-inferiority trials, regardless of justifications, one-sided tests do not seem defensible choices. In all cases, the decision of which tests to use should be stated a priori to guard against post hoc decision-making (see “Following the Forking Paths”).

Inferential Error: Stating that Effects are Clinically Significant Even Though They Are Not Statistically Significant

Error Description

When results are not statistically significant, ignore the statistical tests in favor of making optimistic conclusions about whether the effects are clinically significant (or represent a ‘real-world difference,’ have ‘public health relevance,’ or would create a ‘meaningful impact’).

Explanation of the Error and Why the Practice is Wrong

“Clinical significance may have to be adjudicated by collective groups. This remains in the eye of the beholder, but as a minimum there is no clinical significance without statistical significance.”¹²²

With so much time, energy, and personal commitment invested in an intervention, it may be hard to accept that an intervention was not as unambiguously effective as hoped. This is especially true when statistically non-significant results have a large mean difference, confidence intervals that include impressively large effects, or a p-value close to the threshold of significance, making the results still seem ‘promising.’ The inferential error of ignoring statistical significance in favor of this optimism may reflect at least two misunderstandings of statistical tests.

‘Statistical significance’ here refers to the use of null hypothesis testing as the basis for statistical inference, in which the null hypothesis assumes no difference between groups. There is much discussion about whether¹²³ and how to use null hypothesis significance testing,^123,124 including whether 0.05 is the appropriate cutoff for statistical significance. Herein, we do not debate those issues, but address studies that use null hypothesis significance testing, of which there are many. However, the error described here can be generalized to the practice of ignoring whatever inferential procedures the researchers have initially chosen.

A common misunderstanding is that failing to reject the null hypothesis (often, when p>0.05) means that we conclude that there is no difference – a fallacy known as ‘accepting the null’ (see “Equating ‘No Statistically Significant Difference’ with ‘Equally Effective’”). Rarely are studies conducted in which we try to conclude that there is no difference, which may look like Case 1 in the Figure. Instead, statistically non-significant results could indicate there genuinely is no or minimal effect (i.e., the null is true), or that there is an effect that investigators were unable to observe in the present study. Authors must conclude there is insufficient evidence to reject that the two groups are the same, but instead authors sometimes inappropriately declare such results as ‘clinically meaningful,’ despite failing to meet the pre-specified threshold to conclude the groups are different at all.

A second misunderstanding is of summary statistics. Notably, researchers committing this error often refer to the point estimate (such as the sample mean) to declare clinical significance. We can use confidence intervals – which are directly related to p-values – to illustrate the problem with this logic. Confidence intervals are constructed in a way that a certain percentage (e.g., 95%) of intervals calculated the same way would contain the true effect value under some assumptions. If we take an example where the null hypothesis is ‘zero difference between groups’, then if the interval does not include zero we reject the null hypothesis, which is also consistent with p<0.05 (Figure, cases 5–7). However, if the interval does include zero, the fact that more of the interval is to one side of zero should not be used as evidence to support rejecting the null hypothesis in this statistical framework (Figure, Cases 2–4). Touting the mean difference (Case 4) or upper confidence limit (Case 3) as ‘clinically meaningful’ despite having a null or deleterious lower confidence limit, confuses that we have limited information about the magnitude of the effect (i.e., the effect could be clinically meaningful) with information that the effect is likely to be clinically meaningful, despite the effect potentially being clinically insignificant or even deleterious.

As the introductory quotation for this error makes clear, defining clinical significance is a subjective exercise, just as is defining thresholds for statistical significance. A common convention with statistical significance is p<0.05; but for clinical relevance, it is often unclear just how much an outcome has to change before the effects become meaningful. In public health, a minuscule difference may be declared important when integrated over an entire population; for individual health, results might have to be much more striking before affecting clinical practice. Regardless, for any given application, the threshold should be established a priori. If establishing clinical significance is the goal then researchers have an alternative hypothesis of interest other than just ‘not null.’ This concept is illustrated by the ‘clinical significance’ region in the Figure. Only Case 7 is clearly consistent with rejecting values below clinical significance, and is also statistically significant. For Case 6, we cannot reject values in the clinically non-significant range despite being statistically significantly different from the null with a point estimate above clinical significance.

A corollary is that we must not ignore the clinical triviality of some statistically significant results, such as when the entire 95% confidence interval is below the threshold of clinical significance. That is, we cannot assume clinical significance just because there is statistical significance. Case 5 shows an example where results are statistically significant, and yet fail to include clinical significance in the confidence interval.

We note that comparing confidence intervals to clinical thresholds is related to an approach called magnitude-based inference^125,126 popularized in the field of sports science. It has seen its fair-share of debate on whether it should be implemented^127–130. Therefore, we encourage readers to use caution with that approach.

Examples of the Error

Ignoring statistical tests in favor of clinical significance manifests in several different ways. Sometimes these reports acknowledge that the intervention did not have a statistically significant effect on the primary body composition outcome, but contend that the effect size was none-the-less clinically significant.^131,132 Non-significant interventions have been said to bring “effective results for the prevention of childhood obesity,”¹³³ to be “a promising … strategy for preventing childhood obesity,”¹³⁴ or “can improve … key weight related behaviors.”¹³⁵ Other investigators also recognized the lack of statistical significance at the primary experimental design level, but pointed out that a change in the desired direction was significant in potentially non-pre-specified subgroups (i.e., Errors “Changing the Goal Posts” and “Following the Forking Paths),^136,137 or significant among those who received more exposure to the intervention (i.e., Error “Ignoring Intervention Study Results in Favor of Observational Analyses”).¹³⁸

Recommendations

Defining success in advance is important to prevent this error. Researchers should be discouraged from using ‘clinical significance’ to circumvent statistical significance. Clinical significance should be defined a priori, and built into power analyses and the statistical analysis plan, and success only declared if non-clinically meaningful values are rejected in appropriate statistical tests. If researchers analyze results without using the common approach of statistical significance thresholds (e.g., by using Bayesian analysis instead), it is still important to state the analysis plan and criteria for success a priori. If traditional statistical significance (e.g., evidence the effect is non-zero) is the goal of the research, then the goal of statistical significance should still be defined a priori. These recommendations are facilitated by study registration, which is increasingly becoming required.⁸⁵

Discussion and Conclusions

“[I]n science, three things matter: the data, the methods used to collect the data (which give them their probative value), and the logic connecting the data and methods to conclusions. Everything else is a distraction.”¹³⁹

Reducing childhood obesity is of undeniable importance. So, too, is the need for greater rigor, reproducibility, and transparency in the implementation of much scientific research.^8,139 Our aim here is to be constructive and help the research community interested in this goal to better evaluate, generate, and describe the evidence on strategies to treat or prevent obesity, with an emphasis on childhood obesity interventions. We also hope that this list will lead to elevated – yet healthy – skepticism about claims of effectiveness of childhood obesity interventions. Doubt and skepticism expressed in good faith should be seen as important to advancing science and finding real solutions.¹⁴⁰ White Hat Bias (“bias leading to the distortion of information in the service of what may be perceived to be righteous ends”⁹⁷) risks diverting attention from the important goal, in this case decreasing childhood obesity. Indeed, researchers more readily overlook practices that undermine the validity of research when paired with a justifiable motive,¹⁴¹ reinforcing the importance of focusing on the rigor of the science itself apart from the perceived importance of the topic. Although we have focused on these errors in the childhood obesity intervention literature, we recognize that these same errors can and do occur in obesity intervention studies in general⁷ and in domains other than obesity. As such, this paper may also be useful beyond the focus of childhood obesity.

We make here several recommendations on how to avoid the errors, with full transparency that our recommendations are face-valid, are not necessarily newly proposed by us, and may not yet have been formally proven to improve the practice of science. Some of the errors described herein may be prevented by better statistical and design education, but may also be prevented by substantial inclusion of individuals formally trained in statistics and design as part of an interdisciplinary team. Pre-registration of studies, such as with ClinicalTrials.gov or the Open Science Framework can help researchers plan a priori how they will be conducting and analyzing a study, which decouples data-analysis decisions from data-collection decisions, and gives the authors a predefined roadmap to follow for their primary outcomes. However, in at least one case, having both statistical expertise and pre-registration was not sufficient to avoid some errors (c.f. ⁶¹ about ⁶⁰).

Some more explicit techniques that separate the methods and analysis from the conclusions have been proposed, including: 1) registered reports, in which authors pre-register their design and analysis, and acceptance is dependent on adherence to or justifying deviation from the pre-registered plan. It is important to note here the idea of justified deviation. In one example, the authors report they mistakenly included BMI percentile as opposed to BMIz in their registration, and clarified the distinction well before the final analysis, and still reported both outcomes to remain true to the registration.¹⁴² Journals that require pre-registration implement an informal version of registered reports, but the checking of registrations against the final publications has not been as robust as it should be for this approach to be effective in general,⁴⁷ with sharing of protocols in addition to registration resulting in more clarity in selective outcome reporting.¹⁴³ 2) Separate peer review of methods and conclusions, in which the methods of a study are reviewed prior to seeing results or conclusions, so acceptance decisions are first dependent on the methodology, which give data their meaning. 3) Triple blinded studies, in which the subjects, the evaluators, and the statisticians are blinded. Such blinding can be particularly difficult in obesity interventions, but ethically masking interventions and comparators, the interventionists, the evaluators, and the data analysts as much as possible can better separate expectations from conclusions. And, 4) completely separating the intervention, evaluation teams, and data analysis teams: an extension of our last point. The services of an independent data management and analysis coordinating center may be particularly useful to control inferential errors such as “Changing the Goal Posts” and “Following the Forking Paths”, which are difficult for the reviewer and other readers to detect from the published paper alone. The passion that researchers need to have to overcome the regulatory, community, and interpersonal hurdles of working with children risks biasing the intervention and analysis because we researchers are human and, despite our best efforts, our expectations and desires may influence the research. Putting up firewalls between the components of an intervention may decrease the influence of these expectations and desires.

Finally, as researchers, our commitment should first be to the truth. Authors, reviewers, editors and readers all can play a role in assuring that fidelity is maintained in conducting research and conveying research findings. We hope that our paper may help to recognize flaws that occur in research on interventions aimed at reducing childhood obesity. It may serve as a checklist to complement existing guidelines (e.g., ⁸⁰) and compendia of errors and biases (e.g., ¹⁴⁴) in the spirit of literature showing that simple checklists can be helpful in reducing error rates.¹⁴⁵ It is vital to ensure invalid methodology and interpretations are avoided so that we can identify and support the most promising childhood obesity interventions, while avoiding those that are clearly ineffective.

Table:

10 inferential errors, how they may occur, and recommendations for how to avoid them or how to communicate when they are unavoidable.

Inferential error1	Error description	Recommendations2
Using Self-Reported Outcomes and Teaching to the Test	Urging the intervention group to change health-related behaviors or conditions, then giving participants a questionnaire that asks about the same health related behaviors and conditions, and ignoring the biases this can induce.	Use objective measurements when possible. If self-report is the only measurement tool available, either forego the measurements entirely, do not emphasize the measurements in the conclusions, or at the very least make the reader aware of the potential for biased results.
Foregoing Control Groups and Risking Regression to the Mean Creating Differences Over Time	Providing an intervention only to individuals preferentially sampled to be either higher or lower than the population mean on some variable – such as children all with high BMI z-scores – and assuming improvements over time are caused by the intervention, rather than a spontaneous tendency for extreme values to revert toward the population average.	Include a control group with the same characteristics as the intervention group. If not available, communicate clearly that subgrouping on extreme values risks the follow-up values being closer to the population average because of regression to the mean rather than an actual effect.
Changing the Goal Posts	Using surrogate or secondary outcomes to make claims of effectiveness for an intervention when a study to test an intervention’s effect on obesity yields a non-significant result for the primary outcome.	Focus the report on the pre-registered primary outcome, and communicate intermediate endpoints with great caution.
Ignoring Clustering in Studies that Randomize Groups of Children	Conducting a cluster randomized trial in which groups of children are randomly assigned to experimental conditions, but analyzing the data as though the children were randomized individually.	Always account for clustering in statistical analyses. Have as many clusters as possible, and always more than one cluster per treatment condition.
Following the Forking Paths, Sub-Setting, P-Hacking, and Data Dredging	Trying different analyses with different subsets of the sample or various outcomes and basing conclusions on whatever is statistically significant.	Where appropriate, pre-specify questions and analyses of interest. Be transparent about all analyses conducted, how they were conducted, and whether they were pre-specified. Do not draw definitive conclusions about causal effects from analyses that were not pre-specified or are subsets of many pre-specified analyses uncorrected for multiple testing.
Basing Conclusions on Tests for Significant Differences from Baseline	Separately testing for significant differences from baseline in the intervention and control groups and if the former is significant and the latter is not, declaring the result statistically significant.	Always conduct, report, and emphasize the appropriate between-groups test.
Equating ‘No Statistically Significant Difference’ with ‘Equally Effective’	Concluding that two interventions tested head-to-head had ‘equal effectiveness’ when there is no statistically significant difference between groups.	Include an appropriate non-intervention control group if absolute effectiveness is of interest. When comparing only two interventions head-to-head, do not presume that changes over time reflect effectiveness. Testing equivalence or non-inferiority between two interventions requires special design and analysis considerations.
Ignoring Intervention Study Results in Favor of Observational Analyses	Drawing conclusions from correlations of intervention-related factors with outcomes, rather than testing the actual intervention against a control as designed.	Report primary, between-group analyses from controlled intervention studies. Clearly communicate that observational findings do not carry the same causal evidence.
Using One-sided Testing for Statistical Significance	Switching to one-sided statistical significance tests to make results statistically significant.	Two-sided tests are typically more appropriate. One-sided tests should not be used. In cases where one insists on their use, the testing approach should be pre-specified and justified.
Stating that Effects are Clinically Significant Even Though They Are Not Statistically Significant	Ignoring the statistical tests in favor of making optimistic conclusions about whether the effects are clinically significant.	Pre-specify what counts as statistically or clinically significant, and be faithful to and transparent about the analysis and interpretation plans. If using statistical significance testing, do not claim that effects have been demonstrated if the effect estimates are not statistically significant, regardless of how large the point estimates are.

¹The order of errors as presented does not imply a ranking of importance or severity.

²In most cases, a common recommendation for hypothesis testing is to preregister or predefine as much as possible. The recommendations below are not meant to discourage hypothesis-generating investigations of the data, but rather to encourage making clear distinctions between hypothesis testing, hypothesis generation, and causal inference.