Assessment of Martensitic Transformation Paths Based on Transformation Potential Calculations

Abstract

Transformation potentials for two different martensitic transformation paths are calculated and compared to experimentally measured austenite textures of an SAE 201 stainless steel. The authors conclude that the γ → ε → α′ transformation path is a better match than the γ → α′ transformation path, based on comparison of the texture evolution and transformation potentials. However, significant plastic deformation is also observed in these samples which occurs simultaneously with the transformation. The values of transformation potentials also demonstrate that the transformation path may also be a function of crystal orientation and stress state, in addition to the effect of stacking fault energy (SFE).

Metastable austenitic stainless steels are initially composed of the face centered cubic (FCC) austenite (γ) phase. Upon cooling or deformation, martensitic phase transformations may be observed, transforming the austenite phase to the body centered cubic (BCC) or body centered tetragonal (BCT) α′ martensite phase and/or the hexagonal close packed (HCP) ε martensite phase. For deformation induced martensitic phase transformations in steel, two transformation paths are generally proposed^[1,2]:

$$\gamma \to {\alpha }^{\prime }$$

$$\gamma \to \epsilon \to {\alpha }^{\prime }$$

The γ → α′ transformation is most commonly discussed in the context of low alloy or carbon steels,^[3] while the γ → ε → α′ transformation is mostly discussed in stainless steels,^[1,4–6] twinning induced plasticity (TWIP), or TWIP+transformation induced plasticity (TRIP) steels.^[7] There remains considerable disagreement in the literature in determining which transformation path is active for a given alloy. This paper provides a new method to investigate activity of transformation path, based upon observed crystallographic texture.

Linked to the transformation path are the crystallographic details of the transformation. One technique used to predict austenite transformation that incorporates these details is the method of transformation potentials.^[8,9] This method has also been described in the literature as: potential deformation work^[4]; interaction energy^[10–12]; or driving force^[13] and is one component of the Gibbs free energy of the material. However, this method has typically been applied only as a variant selection criterion for an assumed transformation path. To summarize the method, for each phase transformation there are several crystallographically equivalent directions (variants) determined by the crystallography of the phases present. For a given deformation or stress state, the transformation potential value will vary for each variant depending on the alignment of each variant with the deformation or stress state. The variant that has the largest transformation potential value is the variant expected to appear. Therefore, the maximum transformation potential can be calculated as a function of crystal orientation and stress state^[8,9,13] to determine which variants will occur for a specific orientation. This technique assumes that the martensitic transformation is stress induced, although experimentally stress induced versus strain induced transformations may be difficult to separate.^[14] The relative magnitude of transformation potential for different orientations will also establish the relative order in which selected orientations (or grains) will transform. The influence of orientation on transformation rates is relevant to production of austenitic steels, as it represents an additional mechanism to control the rate of phase transformation. Products using texture engineering to align the majority of grain orientations with transformation potential maxima will result in higher rates of phase transformation. Alternatively, aligning grains with transformation potential minima will delay or prevent transformation.

The majority of the literature on transformation potentials assume a γ → α′ transformation path. Refs. ^{[4,9,11–13,15,16]}, assume the α′ martensite has a body centered cubic (BCC) structure, while references,^[8,10] have used a BCT structure for the α′ martensite. Despite different assumptions on the nature of the transformation, comparison of the calculations shown refs. ^[8,9,13] for a uniaxial stress state and γ → α′ transformation path result in similar transformation potential values for both the BCC and BCT crystallography.

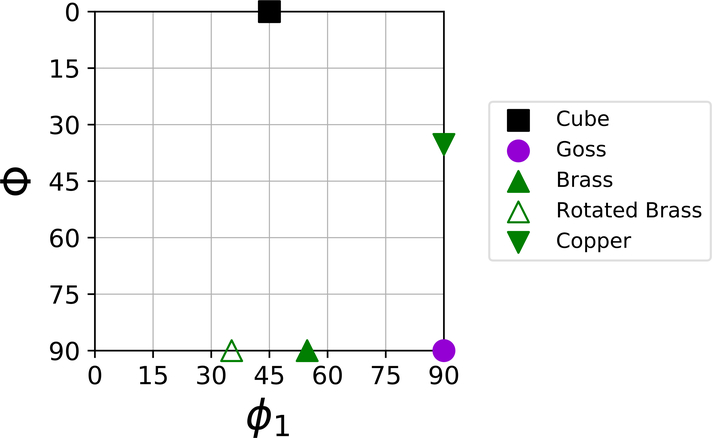
Figure 1 shows the location of selected crystal orientations, plotted using the Bunge angle convention (ϕ₁,Φ, ϕ₂), on a ϕ₂=45° cross section. These orientations are referred to in the text with their shorthand names given in Figure 1. For the deformation state of uniaxial tension along the rolling direction, transformation potential minima are predicted for copper and rotated brass orientations, indicating these orientations will transform last.^[8,9,13] Maxima were calculated for cube and Goss orientations, indicating these orientations would transform first for the same deformation state. Each of these three studies used literature values for the austenite and martensite lattice parameters when calculating the transformation potential, not values specific to the material investigated.

Figure 1.

Key depicting the orientations of cube, Goss, brass, rotated brass, and copper on ϕ₂ =45° cross section. The Bunge angle convention (ϕ₁,Φ,ϕ₂) was used.

However, a series of papers studying an SAE 304 stainless steel with electron backscatter diffraction (EBSD) showed minimal martensite in cube and Goss oriented grains.^[4,17,18] Orientation distribution functions (ODFs) of other austenitic steels have generally shown an increase in cube and Goss oriented grains after uniaxial deformation, also indicating that these orientations were not transforming.^[4,13,15,16] This increase in Goss and cube orientations is in contradiction to expected transformation potential results for a γ → α′ transformation, such as made previously by the authors,^[8] which also predicted that grains with crystal axes aligned with the cube and Goss orientations would transform first.

Comparing the transformation potential values for both transformation paths as a function of crystal orientation represents a novel way to investigate which transformation path is active. The hypothesis tested in this paper is that the transformation potential of a γ → ε transformation path will more accurately describe the texture evolution of the γ phase in an austenitic stainless steel than the transformation potential of a γ → α′ transformation path, as was assumed in prior work. Transformation potentials for both paths were calculated and compared with the experimentally measured texture evolution for the austenite phase of an SAE 201LN austenitic stainless steel.

As noted by De Cooman et al deformation in austenitic steels may occur by ε martensite transformation, ε + α′ transformation, twinning, and/or plasticity.^[7] The stacking fault energy is thought to be a key parameter in determining the activity of these deformation mechanisms. While the SAE 201 family has less Ni with more Mn and N compared to an 304 stainless steel, the stacking fault energies of these materials are similar.^[19] Therefore, the transformation behavior may also be similar for both of these alloys and may be broadly applicable to austenitic steels with similar stacking fault energy.

1. Experimental and Computationals Methods

A series of samples were deformed along the rolling direction in uniaxial tension at room temperature. The strain rate during plastic deformation was approximately 10⁻⁴ s⁻¹ to minimize the effects of adiabatic heating caused by plastic deformation. The deformation was interrupted at selected intervals and texture measurements were performed ex situ. In this paper, analysis was focused on a sample deformed to approximately 27% engineering strain.

Crystallographic texture and phase fraction measurements were performed at the NIST Center for Neutron Research (NCNR) Residual Stress Diffractometer (BT8).^[20] Complete pole figures for the (111), (200), and (220) reflections were measured, and the software package mtex was used to compute orientation distribution functions (ODFs) via pole figure inversion.^[21] Phase fraction calculations were performed using complete pole figure averaging.^[22]

Only the texture of the austenite phase is considered in this paper. The austenite texture evolution is governed by both plastic deformation and phase transformation. In FCC materials, undergoing uniaxial tension, increases in cube, Goss, rotated brass, brass, and copper orientations are observed.^[23–25]

A prior paper by the authors includes details of the transformation potential calculation that was used in this paper.^[8] In summary, the transformation potential W^(k) is calculated for each variant (k) and sample orientation (Q) using the stress state (σ), habit plane (m), and shear direction with magnitude (b) via Equation (1).

$$W^{(k)}=Q_{\mathrm{n}\mathrm{i}}{b}_i^{(k)}{\sigma }_{\mathrm{nm}}{Q}_{\mathrm{mj}}{m}_j^{(k)}$$ (1)

The lattice parameters used in ref. [8], for the γ → α′ transformation assume a BCTstructure and result in habit plane (m) and shear direction with magnitude (b) vectors listed in Equation (2).

$$\begin{gathered} b\text{=}\text{[0.134673,}\text{0.052210,}-\text{0.163034]} \\ m\text{=}\text{[}-\text{0.543031,}-\text{0.210522,}-\text{0.812895]} \end{gathered}$$ (2)

These vectors compare well with those used by other authors^[9,11,15] which use a BCC structure. A list of lattice parameters explored in this work are included in the supporting information as Table S1. Symmetry operators are applied to these vectors to calculate the 24 variants.^[8]

For the γ → ε transformation, habit plane and shear direction with magnitude vectors from the literature were used resulting in values listed in Equation (3).^[4,15]

$$\begin{gathered} b\text{=}\text{[0.144337, 0.144337, }-\text{0.288675]} \\ m\text{= [0.577350, 0.577350, 0.577350]} \end{gathered}$$ (3)

Humbert et al described 12 symmetry operators for these interfaces.^[4] Comparison of the deformation tensors listed by Humbert et al.^[4] with the cubic symmetry operators used previously by the authors^[8] revealed that the cubic symmetry operators reproduce the same deformation tensors, albeit with redundant transformations. This redundancy does not affect the transformation potential calculations, as only the maximum value was retained. As the focus of this paper is the austenite texture, only the γ → ε transformation was considered.

2. Results

The maximum transformation potentials were plotted using the same Euler angle coordinate system used to display an orientation distribution function (ODF). This style of plotting is used to facilitate comparison between the crystallographic textures observed experimentally and the transformation potential value.^[8,9,13] For brevity purposes, only the ϕ₂=45° cross section is shown, and only the uniaxial tension along the rolling direction (“RD-T”) stress state from ref. [8] was used. Scripts and data used in this paper are included in a companion data set.^[26] Uncertainty in the lattice parameters and variation in the local stress environment will have the strongest contributions to uncertainty in the transformation potential value but have not been quantified in this work.

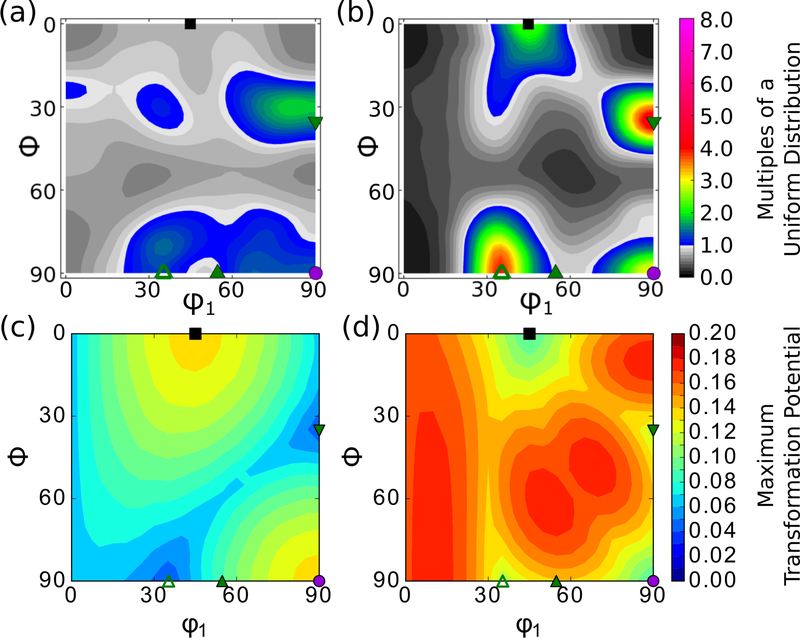
Figure 2a shows the calculated ODF for the as-received material. Prior to deformation, the material was fully austenitic. The ODF was primarily composed of 4 orientations with intensity greater than a uniform distribution (MUD>1.0): copper, rotated brass, brass, and Goss. These orientations are commonly observed for austenitic stainless steel sheet material produced by rolling.^[5,13,27,28] Figure 2b shows the ODF after a uniaxial deformation of 27% engineering strain along the rolling direction. The measured phase fractions are 0.784±0.057 austenite, 0.173±0.023 α′ martensite, and 0.043±0.065 ε martensite for this deformation. These phase fractions were measured via complete pole figure averaging^[22] and assume only these three phases are present. The uncertainties are one standard deviation and are based on the variance of the average normalized intensities, modified to include three phases.^[22] As the phase fraction must be greater than zero, that the uncertainty range extends to values less than zero shows a limitation of this method of calculation of uncertainties, which assume Gaussian distributions. The large uncertainty in the ε martensite is due to the low phase fraction, resulting low diffraction intensity, limited diffraction peaks measured (only 2), and uncertainty in the structure factor calculations for this alloy. Figure 2b shows copper, rotated brass and Goss orientations grow more intense after deformation. The cube orientation also increases in intensity from a MUD < 1.0 to a MUD > 1.0. The brass orientation remains at approximately the same intensity. The austenite phase fraction was not used to rescale the ODF values. Table 1 lists combined ODF volume and phase fraction values.

Figure 2.

a) ODF of the as-received austenite texture. b) ODF of the austenite texture after uniaxial deformation along the rolling direction to 27% engineering strain. c) Maximum transformation potentials for γ → α′ martensite transformation as a function of orientation (reproduced from ref.[8]). d) Maximum transformation potentials as a function of orientation for γ → ε martensite transformation. All plots are on the ϕ₂=45° cross sections and austenite crystal reference frame. The color scale for the ODFs are the same for both ODFs and have values of multiples of a uniform distribution (MUD). The scale for the transformation potential is also shared between (c) and (d), and assumes a stress value of 1 along the rolling direction. The units on the transformation potential are $\frac{J}{m^3}$. Marks for specific orientations are superimposed on each of the plots, as in Figure 1.

Table 1.

Combined ODF volume and phase fraction values (ODF*PF) for each sample.

	As received sample ODF*PF	As received sample ODF*PF uncertainty	27% strain sample ODF*PF	27% strain sample ODF*PF uncertainty
Cube	0.853	0.085	2.28	0.28
Goss	0.962	0.096	1.15	0.14
Brass	1.00	0.10	0.939	0.12
Rotated Brass	1.27	0.13	3.01	0.37
Copper	1.54	0.15	3.03	0.37

The ODF volume fraction (5° tolerance angle) was normazlied by the ODF volume fraction for an uniform distribution and multiplied by the phase fraction of the austenite phase. Uncertainty values come from the phase fraction uncertainty and an assumed 10% uncertainty in the ODF values.^[29]

Figure 2c and d display transformation potential calculations on the same ϕ₂=45° cross section. Assuming the stress is equal among all sample orientations (Reuss bound), orientations that are coincident with transformation potential minima tend to remain untransformed when stress is applied. Figure 2c shows the transformation potential for a γ → α′ path. As shown previously there were only two minima in this cross section, near the copper and rotated brass orientations.^[8,9,13] Cube and Goss orientations were local maxima. Figure 2d shows the transformation potential for a γ → ε path. In this cross section, four minima are visible. There were minima aligned with the cube and Goss orientations, and two other minima were located near the copper and rotated brass orientations. Transformation potential calculations for additional stress states are included in the supporting information document as Figures S1 and S2.

3. Discussion

Orientations aligned with minima of transformation potentials are predicted to remain untransformed. The orientations present in the ODF after deformation (Figure 2b) match the minima present in the γ → ε transformation (Figure 2d). The Goss and cube orientations have high transformation potential values in the γ → α′ transformation, and therefore should be some of the first orientations to transform if this transformation path was active. However, the observation that these orientations increase in intensity after deformation supports the hypothesis that the γ → ε transformation path more accurately describes the austenite texture evolution than the γ → α′ transformation path in this material. The ε martensite subsequently transforms to α′ martensite, as evidenced by the higher α′ martensite fraction than ε martensite fraction. This result may also explain the increases in Goss and cube orientations seen by others.^{[4,13,15,16,18]}

Support for the hypothesis that the γ → ε transformation path more accurately describes the austenite texture evolution is weakened by the observation that the orientations predicted to remain untransformed are also orientations that increase in ODF volume fraction due to plasticity in uniaxial deformation. As indicated, there is an increase in combined ODF volume fraction and phase fraction. Transformation would only account for decreases in this combined value, therefore increases indicate that another mechanism (likely plastic deformation) is adding material to these orientations.

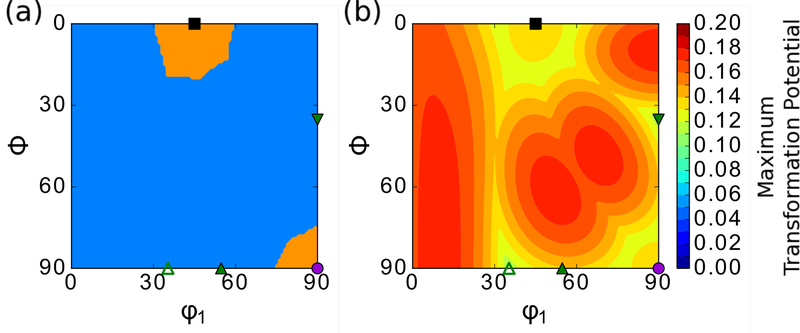
Despite using the same macroscopic stress state, the maximum transformation potential values were also generally larger in the γ → ε transformation than in the γ → α′ transformation. This was due to the larger magnitude of the shear vector (b) in the γ → ε transformation than in the γ → α′ transformation. As the stress state was held constant and the plane is normalized to a unit vector, the authors speculate that the magnitude of the transformation potential values can be compared between the two transformations, as the magnitude would represent the energy to transform a single unit cell. Comparing the same orientation on both transformation potential plots, the γ → ε transformation was generally more favorable, as the maximum transformation potential value is larger. However, this was not the case near the cube and Goss orientations. Here the transformation potentials were larger for the γ → α′ transformation path. The areas where each of the transformation paths were favorable are shown in Figure 3a. The specific location and extent of this boundary will depend on the lattice parameter values used. The maximum transformation potential value for either path is shown in Figure 3b, showing the relative magnitude of transformation potential for either transformation path. Note that the γ → ε transformation minima shown in Figure 2d are less in cube and Goss than copper and rotated brass. However, when both the γ → ε and γ → α′ transformations are considered in Figure 3b, the copper and rotated brass are less than cube and Goss. This behavior is similar to the experimental data shown in Figure 2b, where the cube and Goss texture intensity is less than in copper and rotated brass. The favorability of different transformations based on orientation is an added variable for transformation path selection that has not previously been considered.

Figure 3.

a) Map of the transformation path activity. Regions in blue indicate the maximum transformation potential for the γ → ε transformation is larger than γ → α′. Regions in orange indicate the maximum transformation potential for the γ → α′ transformation is larger than γ → ε. b) Maximum transformation potential values for either the γ → α′ martensite transformation or the γ → εmartensite transformation.

The result that the transformation potential values for the γ → α′ transformation were larger in Goss and cube orientations than the γ → ε transformation may explain why Kundu and Bhadeshia^[11] found γ → α′ sufficient to describe the transformations measured in Gey et al.^[17] as Kundu & Bhadeshia only considered austenite orientations near Goss and cube. Similarly, work by Gey et al.^[17] and Humbert et al.^[4] found better correlation between the variant selection models and experimental results in cube and Goss orientations than the copper and rotated brass orientations.

4. Conclusion

The transformation potential of a γ → ε transformation may more accurately describe the texture evolution of the γ phase than the transformation potential of a γ → α′ transformation for SAE 201LN austenitic stainless steel. The texture evolution, particularly the increases or decreases of cube and Goss orientations, may be used as an indication of which transformation path is active. However, plastic deformation will also affect the textures and is convoluted with these effects. These results also demonstrate an orientation dependence on the transformation path, indicating that the stacking fault energy is not the only factor in determining the transformation path. In materials where the stacking fault energy permits a γ → ε transformation, cube and Goss oriented grains will be slow to transform upon uniaxial deformation and may not transform at all.