Generated time-series prediction data of COVID-19′s daily infections in Brazil by using recurrent neural networks

Abstract

In light of the COVID-19 pandemic that has struck the world since the end of 2019, many endeavors have been carried out to overcome this crisis. Taking into consideration the uncertainty as a feature of forecasting, this data article introduces long-term time-series predictions for the virus's daily infections in Brazil by training forecasting models on limited raw data (30 time-steps and 40 time-steps alternatives). The primary reuse potential of this forecasting data is to enable decision-makers to develop action plans against the pandemic, and to help researchers working in infection prevention and control to: (1) explore limited data usage in predicting infections. (2) develop a reinforcement learning model on top of this data-lake, which can perform an online game between the trained models to generate a new capable model for predicting future true data. The prediction data was generated by training 4200 recurrent neural networks (54 to 84 days validation periods) on raw data from Johns Hopkins University's online repository, to pave the way for generating reliable extended long-term predictions.

Specifications Table

Subject	Infectious Diseases
Specific subject area	Forecasting COVID-19′s daily infections in Brazil by using deep recurrent neural network models with limited pandemic data.
Type of data	- Tables (.csv) - metadata files (.json) - Graphs (.pdf) - Keras saved model files (.h5) - Pickle files (.pkl) - Python notebook files (.ipynb)
How data were acquired	- The data was generated by training 4200 Deep recurrent neural networks RNNs on limited raw data (30 time-steps and 40 time-steps) from COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University at: https://github.com/CSSEGISandData/COVID-19 The models were built using Keras Library with TensorFlow backend version 2.3.0-tf in Python environment and Google Colaboratory: https://keras.io https://colab.research.google.com The prediction tables, graphs, metadata files were generated by writing a code for recursive training and inference functions.
Data format	- Raw: The generated prediction data
Parameters for data collection	- The metadata and training - inference settings for the deterministic setup are located in the settings folder in the data repository.
Description of data collection	The csv file for daily COVID-19 infection numbers from January 22, 2020, to several dates – indicated in the metadata - was downloaded from COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. The csv file was processed, cropped, and divided without scaling into training/testing/evaluation sets in the Python environment. Then the forecasting data in this article was generated by training recurrent neural networks on the aforementioned raw data by using a code that was developed specifically for this task.
Data source location	- City: Cairo - Country: Egypt
Data accessibility	Repository name: Mendeley Direct Mendeley URL to the generated data: http://dx.doi.org/10.17632/t2zk3xnt8y.5 Direct Mendeley URL to the developed and used code: http://dx.doi.org/10.17632/yp4d95pk7n.3

Value of the Data

• •This dataset is useful because it provides researchers with a solid background foundation for predicting COVID-19′s daily infections by depending on very limited data (30 time-steps and 40 time-steps alternatives). This facilitates the prediction process by reducing the crucial need for big data that is required to train deep recurrent neural networks.
• •Government institutions and infection control units can utilize and filter this dataset to estimate and develop the required action plans. As well, researchers can use it in spatial models related to the geographical distribution of the pandemic and the increase in numbers.
• •The generated dataset represents a data-lake that can help researchers to build a reinforcement learning model that can learn how to classify and select the fittest models against upcoming infection rates. More importantly, a reinforcement learning model that adjusts and combines between the best weights in these trained models can be developed to construct a new prediction model for extended long-term prediction purposes.
• •Although real numbers of infected people are higher than reported as there is a worldwide limited capacity to provide more tests to people, therefore, this dataset helps in modeling real numbers more accurately in the studies that perform an estimation of infection prevalence.
• •This dataset can very useful for social scientists who aim at developing analysis frameworks that compare and study the social structure and socioeconomic conditions in different countries and cultures, and the relation of these factors to the prevalence of the pandemic.

1. Data description

In the past five months, many non-medical data articles have focused on critical aspects of transition-related analysis and data of COVID-19′s case, as infections data collection, filtering, geographical mapping of infections [1,2], and forecasting. In that sense, forecasting studies utilized various approaches as exponential smoothing models [3], estimation of the daily reproduction number [4], Susceptible-Infectious-Recovered-Dead (SIRD) models [5], ARIMA models [6,7], and nonlinear autoregressive artificial neural networks - NARANN models [7].  Furthermore, several approaches depended on using more or different data as the SEIRQ model [8], which involved using seven categories of data, one of them is the number of infected people. Similarly, a research study for predicting cases in China depended on extra data from SARS and MERS diseases that are fitted on an exponential growth model [9]. As well, an improved version of Susceptible Exposed Infectious Recovered - SEIR was used with extra data about the intervention and quarantine strategies against the pandemic [10]. On the other hand, this data article focuses on long-term forecasting of the daily infections in Brazil by using limited data of infections numbers only on a recurrent neural network structure that uses Gated Recurrent Unit - GRU mechanism that is similar to Long Short-Term Memory – LSTM mechanism. The choice of 30- and 40-days’ time windows is made experimentally as explained in the methods section. Although there is an accompanying uncertainty in the generated predictions, the evaluation of the models’ performance over various durations (not less than 54 days as shown in the metadata Table 1), shows the possibility of achieving long-term predictions by using limited data. In that sense, the generated predictions show polynomial trendlines between orders two and four for the case of Brazil rather than developing non-stopping exponential or power trends that grow indefinitely. These RNNs are boosted by an online adversarial linear regression evaluation function, which performs a day-by-day correction of the models’ generated data over the whole duration. As the prediction is made till 2020–10–01, this date was selected based on the news of early vaccine release by September 2020 by the British-Swedish pharmaceutical company AstraZeneca [11] among many other pharmaceutical firms such as Moderna that announced manufacturing 100 million doses by the 3rd quarter of 2020 [12]. Similarly, the selection of Brazil is based on the importance of predicting the infection numbers in one of the world's populous countries, which is currently ranked as 2nd in the world regarding the number of total infections with COVID-19 [13] (2020–07–13). Moreover, choosing the second in rank prioritizes having no external factor that can have a substantial influence over the pandemic's behavior, which is possible in the case of the USA (ranked as 1st [13]), where massive demonstrations occurred during June, and July 2020 [14] and this requires different measures to neutralize the influence. In that sense, 4200 Deep recurrent neural networks RNNs were built by Keras Library in Python environment and by using limited data (30 time-steps and 40 time-steps) from COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University [13] that includes infections numbers from January 22, 2020, to several dates – indicated in the metadata in Table 1. These trained models are categorized as follows: 3173 in deterministic mode, 20 in non-deterministic mode, 1001 in a non-deterministic mode for validation, 1 model as a control group for validation by using the data of India, and 5 models for showing performance of different time-steps. The csv file that includes the training data was accessed, processed, cropped, and divided without scaling into training/testing/evaluation sets. Subsequently, the long-term prediction data in this article were generated using the trained models. The deterministic setup aspect is explained in the methods section, as well, the metadata, inference settings, and training settings are located in csv and json files, which can be accessed at the data repository.

Table 1.

Metadata, DM1: Deterministic mode 1, DM2: Deterministic mode 2, NDM: Non-deterministic mode. Source: Author.

ID	Items	DM1	DM2	NDM	Technical validation	Technical validation (control group)
		Values	Values	Values	Values
	Country	Brazil	Brazil	Brazil	Brazil	India
0	Start date for training data	07–04–2020	07–04–2020	07–04–2020	08–03–2020	07–04–2020
1	End date for training data	06–05–2020	06–05–2020	06–05–2020	06–04–2020	06–05–2020
2	Start date for evaluation data	07–05–2020	07–05–2020	07–05–2020	07–04–2020	07–05–2020
3	End date for evaluation data	29–06–2020	29–06–2020	29–06–2020	13–06–2020 29–06–2020	11–07–2020
4	Duration of evaluation data	54 days	54 days	54 days	68 days 84 days	66 days
5	Start date for training process	28–06–2020	28–06–2020	03–07–2020	13–06–2020	12–07–2020
6	End date for training process	30–06–2020	01–07–2020	03–07–2020	13–06–2020	12–07–2020
7	Number of models	1197	1976	20	1001	1
8	Number of predictions	2835	7301	53	3619	1
9	Number of graphs	2835	7301	53	3619	1
10	Number time-steps	30	40	30	30	30
11	Processor	CPU	CPU	GPU	GPU	CPU
12	Crop-point of input data since 22–01–2020: removing data before:	day: 110	day: 110	day: 110	day: 80	days: (110, 115, 125, 135)

Overall, the data in this article consist of models, prediction tables, graphs, settings tables, and a Python notebook. The data are split into two datasets and both are uploaded in two online data repositories. Dataset one includes the model files, predictions, graphs, and metadata, and Dataset two includes the code as one Jupyter Notebook file in Python programming language.  Dataset one is divided into three folders: 1) (Deterministic mode), 2) (Non-deterministic mode), 3) (Technical validation), and one compressed zip file that includes all files and folders in the dataset. Table 1 shows the associated metadata for Dataset 1.

In Dataset one, the deterministic folder contains two folders: 1) 30 time-steps, and 2) 40 time-steps. On the other hand, the Non-deterministic folder and Technical validation folder contain data for 30 time-steps. The generic structure for each time-steps subfolder contains the following four folders:

• 1.(Predictions) folder, including prediction tables (to 2020–10–01) in (.csv) extension. Each csv file includes the predicted daily infections table that was generated by using a trained model. Each table includes three columns: 1) date, 2) model prediction, 3) evaluated prediction. The folder includes an extended evaluation for the best model till 2020–07–11.
• 2.(Graphs) folder, including prediction graphs (to 2020–10–01) in (.pdf) extension. Each graph describes the model's performance against the true data. The graphs mainly include four highlighted trendlines: 1) prediction for the period of the time-steps, 2) prediction for all the validation period, 3) prediction for four steps only, and 4) prediction to the target date. The folder includes an extended evaluation for the best model till 2020–07–11.
• 3.(Settings) folder, including: settings files in (.json) extension. This folder includes all the settings that were used for training the models. The settings folder includes (Metadata) folder, which comprises four tables in (.csv) extension: 1) (dates_info_to_2020–10–01.csv) file includes dates of training and prediction processes. 2) (models_accuracy_settings_to_2020–10–01.csv) file includes models’ settings and accuracy. 3) (gen_data_info_to_2020–10–01.csv) file includes counts of generated data. 4) (best_model_accuracy_settings_to_2020–10–01_.csv) file includes settings and accuracy of the best model.
• 4.(Trained models) folder, including model files in (.h5) extension. These files are the trained models and they can be used in inference by using the predict function in the Python notebook.

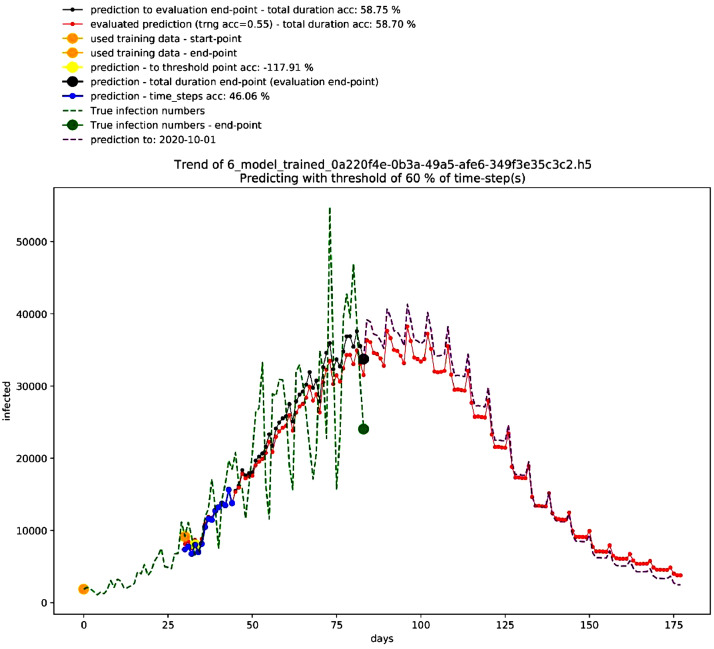
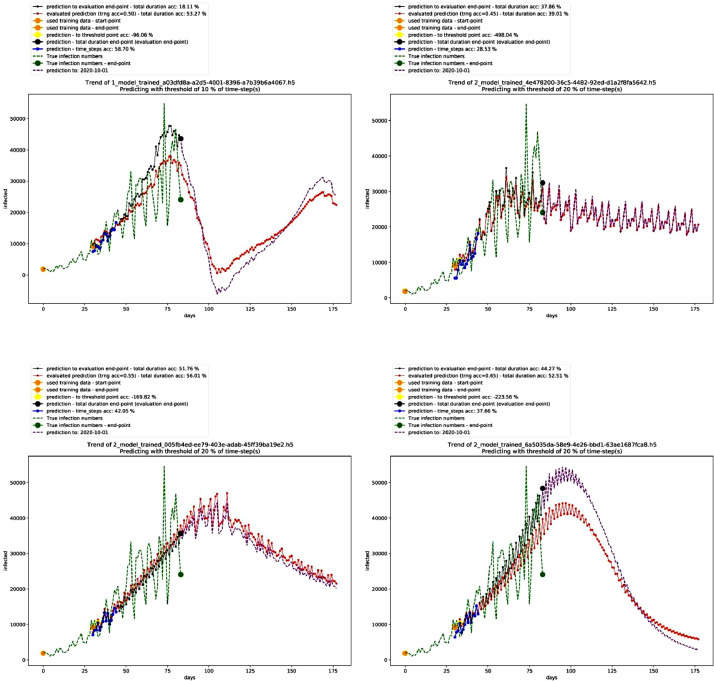
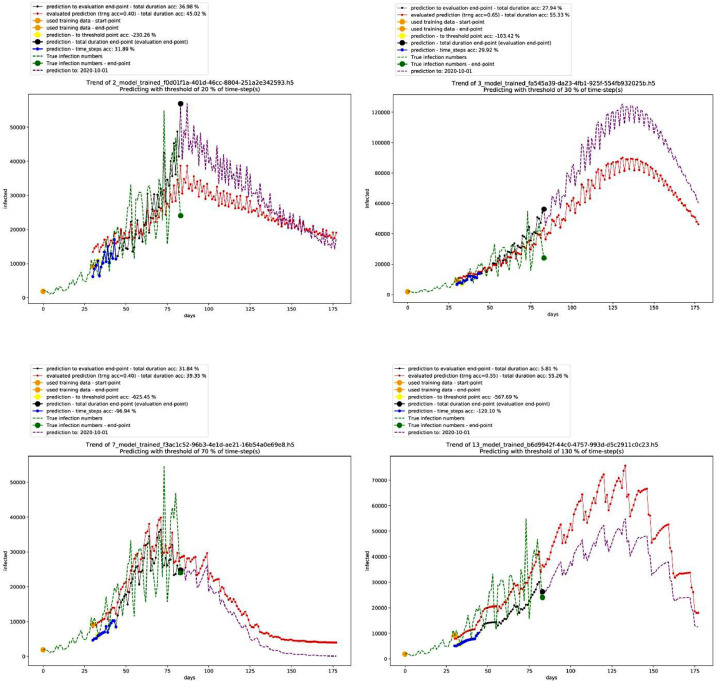
The technical validation folder includes an additional folder named (Control group) for the model of India. As well, there is an additional folder that includes the data for the performance of different time-steps – till 2020–06–29. The following tables and figures show a brief about the results. First, Table 2 shows the best performing 10 models in the deterministic mode 1, Fig. 1 shows the graph for the third-best performing model that is not showing a non-stopping exponential growth, and Table 3 shows the settings of this model. On the other hand, Fig. 2 shows different trends in this mode.

Table 2.

Best 10 performing models in the deterministic mode 1. Source: Author.

ID	Model	r2_all_duration
140	model_trained_d46818b3-b5e8–4aed-b379-d9bb56e5d6a4.h5	0.665547468
2052	model_trained_3664a884–649f-4c54–9b9f-a7450346ba1d.h5	0.589318674
2739	model_trained_0a220f4e-0b3a-49a5-afe6–349f3e35c3c2.h5	0.587505583
590	model_trained_de93114c-7638–4df8-b35d-6b6928edea9f.h5	0.586324501
2827	model_trained_2ddfbf07–8602–4357–9b5f-d41d366dfb61.h5	0.585366432
872	model_trained_45ff443b-8380–46c5-b824-d470d5bf5935.h5	0.583010877
1636	model_trained_bd30a0c6-a93e-441d-b5db-a2a77a18ba90.h5	0.57803346
1374	model_trained_ba60d0a0–64b2–45c8-bf1d-b158686deef1.h5	0.576606486
2166	model_trained_a556979b-a212–49bb-b2be-d24f8ca8c48a.h5	0.57569909
1909	model_trained_cf40d4ca-6cd7–44dc-a1e9-bcb190a5d466.h5	0.574641935

Fig. 1.

Graph of third-best model in the deterministic mode 1. Source: Author.

Table 3.

Settings of third-best model in the deterministic mode 1. Source: Author.

Settings/ID=2739	Value
model	model_trained_0a220f4e-0b3a-49a5-afe6–349f3e35c3c2.h5
r2_all_duration	0.587505583
time-steps	15
epochs	1000
batch-size	1024
validation-split	0.3
rnn	recurrent_v2.GRU
layers	[64, 32, 64]
dropout	0
conv-rnn	TRUE
seed-python	47
seed-tf	8
functional-api	TRUE
t1	6
r2_time_steps	0.460565672

Fig. 2.

Graphs of other models with different trends in the deterministic mode 1. Source: Author.

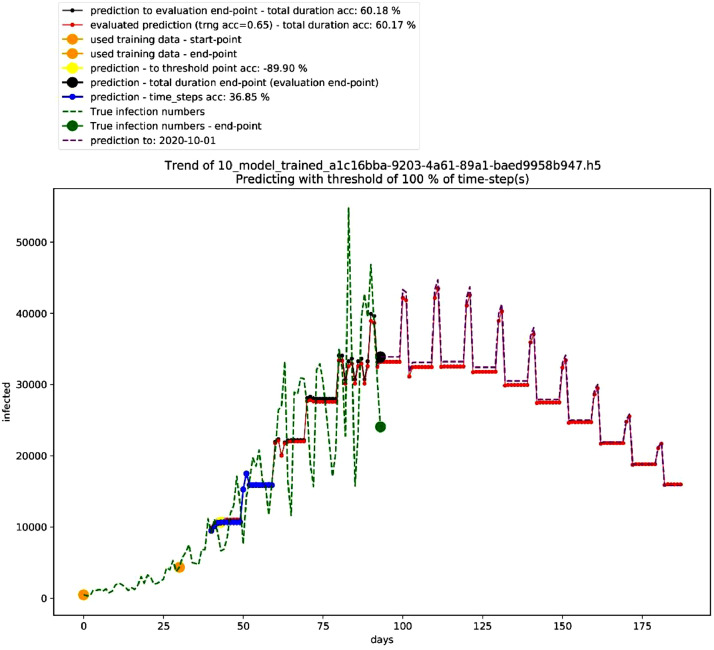
Similarly, Table 4 shows the best performing 10 models in the deterministic mode 2, and Fig. 3 shows the graph for the second-best performing model in this mode showing a polynomial growth (the third in the table as first and second models shown in Table 4 are identical in performance – non-stopping exponential growth – thus, they are ranked together as first). On the other hand, Table 5 shows the settings of this model, and Fig. 4 shows different trends in this mode.

Table 4.

Best 10 performing models in the deterministic mode 2. Source: Author.

ID	Model	r2_all_duration
7221	model_trained_3822084a-e528–4571–9796–43acbd33c9c3.h5	0.602340286
3379	model_trained_8ea50721–243a-4efe-a7a9-cbe0b408cdea.h5	0.602340286
4726	model_trained_a1c16bba-9203–4a61–89a1-baed9958b947.h5	0.60177885
5491	model_trained_b5aa1f4e-281d-4413-a9ed-3842957d936c.h5	0.597394405
4624	model_trained_1671766c-327d-4e18-b4e2-a2619b36bab0.h5	0.59109153
3304	model_trained_c370645c-37d8–429f-b5bb-de572a6297fb.h5	0.590435975
3663	model_trained_019628ca-e614–460b-8445-aefaa667f04f.h5	0.589312596
7095	model_trained_8b5b8f8f-e463–456c-a73e-9b8fc4248cd4.h5	0.58849072
2976	model_trained_d678e1c1–1452–4d5f-9c72–95c97e93ac57.h5	0.587584874
2796	model_trained_5cb9ae23–2f1a-4cbf-9bd1-e429a2250f5e.h5	0.587506132

Fig. 3.

Graph of second-best model in the deterministic mode 2. Source: Author.

Table 5.

Settings of second-best model in the deterministic mode 2. Source: Author.

Settings/ID=4726	Value
model	model_trained_a1c16bba-9203–4a61–89a1-baed9958b947.h5
r2_all_duration	0.60177885
time-steps	20
epochs	1200
batch-size	1024
validation-split	0.3
rnn	recurrent_v2.GRU
layers	[16, 32, 16]
dropout	0
conv-rnn	TRUE
seed-python	46
seed-tf	43
functional-api	TRUE
t1	10
r2_time_steps	0.368462128
r2_sum	0.970240978

Fig. 4.

Graphs of other models with different trends in the deterministic mode 2. Source: Author.

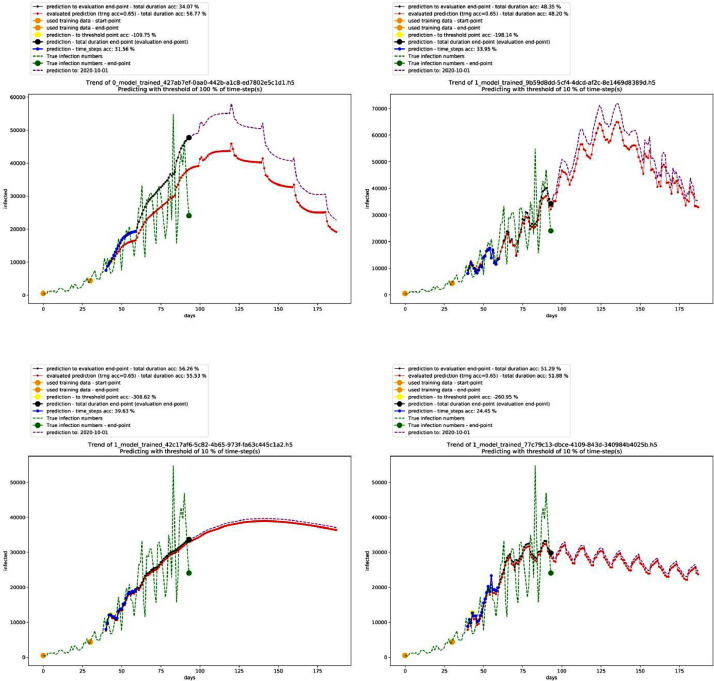
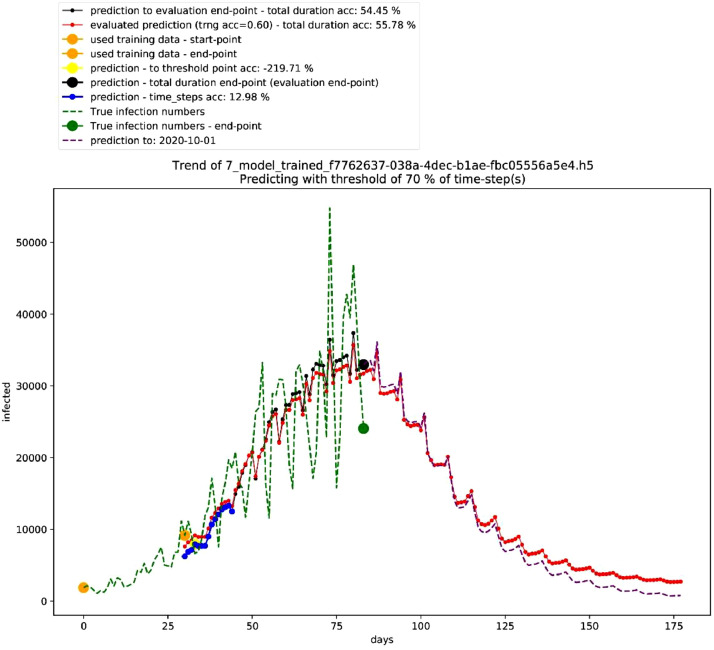
Thirdly, Table 6 shows the best performing 10 models in the non-deterministic mode, Fig. 5 shows the graph for the second-best performing model that shows a polynomial growth, and Table 7 shows the settings of the second-best performing model in the non-deterministic mode. On the other hand, Fig. 6 shows different trends in this mode.

Table 8.

Fast growth pattern in the validation model. Source: Author.

Values	Date
	5/16/2020	5/31/2020	6/14/2020	6/29/2020	10/1/2020
Predicted value	7987	16,651	27,513	44,050	1,565,159
True Value	13,220	16,409	17,110	24,052	NA
Interval - days	−15	0	15	30	110
Increase - predictions	140.86%	108.48%	65.23%	60.11%	3453.14%
Increase - true values	169.91%	24.12%	4.27%	40.57%	NA

Table 6.

Best 10 performing models in the non-deterministic mode. Source: Author.

ID	Model	r2_all_duration
42	model_trained_fe30df8d-1726–4692-a025–3276b035d22d.h5	0.558035054
26	model_trained_f7762637–038a-4dec-b1ae-fbc05556a5e4.h5	0.544462339
11	model_trained_29d990e5-ff1f-485b-9a71–10728826e4ab.h5	0.496746963
12	model_trained_f05990fe-93ab-4634-bb21-eb633bbe8dce.h5	0.493894826
43	model_trained_fe30df8d-1726–4692-a025–3276b035d22d.h5	0.482351598
9	model_trained_c6ef4b9c-b473–493d-a388–2e2223183d19.h5	0.467796218
27	model_trained_f7762637–038a-4dec-b1ae-fbc05556a5e4.h5	0.465112991
5	model_trained_f7e3ec50–0f24–4ab6–9286-fa4e0c3de866.h5	0.458621676
7	model_trained_c6ef4b9c-b473–493d-a388–2e2223183d19.h5	0.437672728
30	model_trained_f3ac1c52–96b3–4e1d-ae21–16b54a0e69e8.h5	0.423220917

Fig. 5.

Graph of second-best model in the non-deterministic mode. Source: Author.

Table 7.

Settings of second-best model in the non-deterministic mode. Source: Author.

Settings/ID=26	Value
model	model_trained_f7762637–038a-4dec-b1ae-fbc05556a5e4.h5
r2_all_duration	0.544462338
time-steps	15
epochs	600
batch-size	1024
validation-split	0.3
rnn	recurrent_v2.GRU
layers	[128, 256, 128]
dropout	0
conv-rnn	TRUE
seed-python	13
seed-tf	4
functional-api	TRUE
t1	7
r2_time_steps	0.129786299
r2_sum	0.674248637

Fig. 6.

Graphs of other models with different trends in the non-deterministic mode. Source: Author.

1.1. Technical validation of the data

To ensure the reliability of the data, technical validation of the data was performed. The csv file for daily COVID-19 infection numbers was accessed from COVID-19 Johns Hopkins University's Data Repository, processed, cropped, and divided into training/testing/evaluation sets.

Predominantly, allowing a relatively large evaluation period (not less than 54 days) reflected a better understanding of the models’ generalizability without new data, this is particularly important in tackling time-sensitive prediction processes with limited data as a basis for decision-making. The evaluation periods are shown in the metadata Table 1.

As well, generating various models within a range of variations of settings serves the exploration of most efficient settings that would benefit future applications and potential reuse of the dataset.

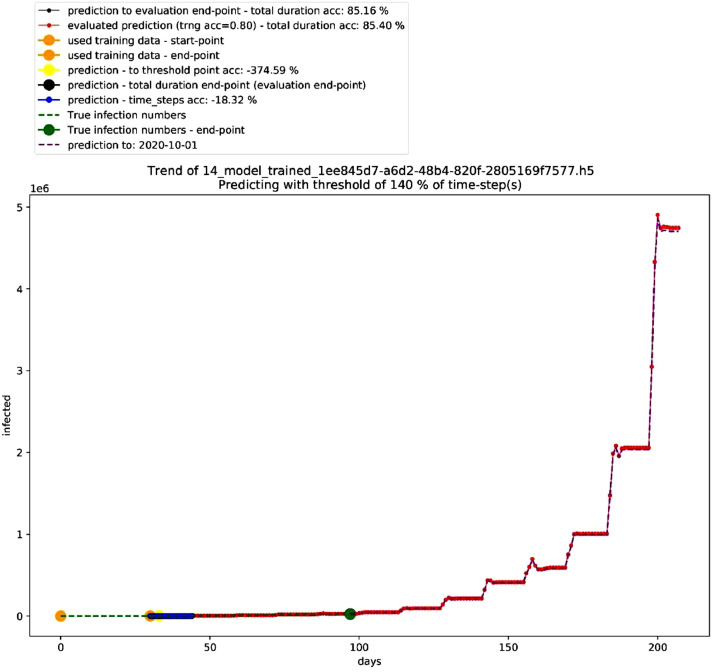
In that sense, after carefully looking at the trendline in the generated graphs, the data shows that a certain degree of uncertainty is reflected in the generated models while maintaining logical forecasting of the future that doesn't involve a non-stopping exponential growth trend regardless of the 85% high accuracy in the validation model. The case of the 85% accurate validation model in Fig. 7 shows a non-stopping exponential growth trend that fits that data – over 68 days till 2020–06–13 – with fast growth in time-series predictions beyond this date. This rapid growth describes a failing long-term prediction of a total infected people to be 108,095,368 over 110 days from 2020–06–14 till 2020–10–01, which is almost half of Brazil's population [15]. On the other hand, the trend that is associated with the true data is approximating a polynomial trendline. Moreover, when testing this accurate model against new true data till 2020–06–29, the accuracy drops to a maximum of 68% (84 days evaluation), while maintaining the same steep exponential growth trendline. The period between 2020–05–31 and 2020–06–29 (30 time-steps) as indicated in Table 8, shows that the model is adopting a fast growth pattern that is cannot maintain logical long-term forecasting.

Fig. 7.

Graph for a validation model. Source: Author.

The fast growth pattern is repeated on dates before 2020–05–31 and after 2020–06–29. This pattern has worked as a guideline for identifying logical models that might be less accurate than 85% as in this validation model, but still more applicable than the validation model. The major difference between this validation model and the other models in the dataset is the cropping date of the data. This cropping point filters the data fed to the validation model to start from 2020–03–08 and end at 2020–04–06. The error – non-stopping exponential growth – can be reproduced when setting the crop-point of the data to day 80 since 2020–01–22. Overall, this validation model provides three main indicators: 1) Around 3 months of validation, indicate that the exponential growth pattern can fit true data on a long-term basis (more than the used time-steps as input to the model, ex. 30 time-steps or 40 time-steps), but it becomes not reliable when it comes to extended long-term predictions. This suggests that a polynomial trendline of order 2 to 4 is more probable to describe the data. 2) Crop-points influence the accuracy and the growth pattern of the trendlines in the models, which is the reason behind testing many crop-points. 3) The exponential growth that is generated by models can be controlled and reduced by adjusting the crop-point to day 110. Fig. 7 shows the prediction graph for one of the validation models.

The complete validation dataset includes 1001 models, by taking 358 models as a sample that shows a 95% confidence level and 4.15% margin of error, the following Table 9 shows that long-term prediction is achievable during 68 days despite exponential growth afterward, as we can be positive that 77%, 81%, 64%, and 1% of the models can achieve more than 50%, 60%, 70% and 80% accuracy, respectively – by using same settings. Nevertheless, using such settings allowed a non-stopping exponential growth pattern.

Table 9.

Analysis for the validation dataset against other datasets, DM1: Deterministic mode 1, DM2: Deterministic mode 2, NDM: Non-deterministic mode. Source: Author.

Item	Value	% of models/ sample size	DM1	DM2	NDM
Confidence level	95%	–	–	–	–
Margin of error	4.15%	–	–	–	–
Number of models	1001	–	1197	1976	20
Sample size	358	–	–	–	–
Number of predictions	5208	–	2835	7301	53
Mean accuracy	48.25%	–	26.51%	30.60%	24.49%
Standard deviation	0.2070	–	0.1506	0.15621	0.1539
Models with accuracy  < 0.4	329	92%	91.73%	91.55%	100.00%
0.5 > Models with accuracy  > 0.4	260	73%	30.83%	51.32%	35.00%
0.6 > Models with accuracy  > 0.5	275	77%	12.61%	26.87%	10.00%
0.7 > Models with accuracy  > 0.6	289	81%	0.08%	0.15%	0%
0.8 > Models with accuracy > 0.7	229	64%	0%	0%	0%
Models with accuracy > 0.8	3	1%	0%	0%	0%
Crop-point	80		110

On the other hand, the deterministic and non-deterministic datasets have fallen into the second and third categories (the models have scored an accuracy of 50% to less than 60%, and 60% to less than 70%). However, two factors have a great influence over the results: the first factor involves the uncontrolled randomness that was eliminated to allow limited reproducibility throughout the training session, as this might have limited the achievement of higher accuracy. As a result, the desired polynomial curve was achievable at the expense of limiting the higher accuracy due to controlled randomness. Consequently, the controlled randomness mostly provides the phases of the logistic function, the initial log phase (slow growth), followed by near-exponential growth, the transitional phase (the slowdown), the saturation phase (transitional phase) then the maturity phase – a plateau or stationary phase – (the growth stops). In that sense, the second factor that influenced the results is the crop-point (a source of randomness itself) of the data, as the “numbers” of the input data – the daily infections numbers – contain inherited randomness that could lead to a pattern that translates into higher accuracy. This particularly means that there is a certain correlation between the numbers that allow better forecasting at a certain crop-point and worse predictions at another crop-point while using the same settings. However, as this validation dataset is non-deterministic, meaning that there is a certain degree of randomness, then the most controlling factor is the crop point as the other three datasets have been tested by using similar settings except for the crop-point (the two deterministic datasets have shown similar results to the non-deterministic dataset in terms of growth). This highlights that the crop-point as a source of randomness exceeds in influence the initial randomness that is created by the neural network to initialize the weights of the network.

Consistently, this certain pattern or correlation can be overcome by allowing a higher level of randomness and much greater variations of settings. This can be computationally impractical and time-consuming. Therefore, the objective of creating a data-lake with many variations in data points and trends, to develop a hybrid leading reinforcement model on top of this data-lake, is more feasible in terms of speed and efficiency as these variations can ease the process of assigning or clustering them to reward and penalty classes in the deep reinforcement learning model. Further validation has been performed over the three best models in the three modes that are reported in the deterministic and non-deterministic modes, Table 10 shows updated performance till 2020–07–11.

Table 10.

Evaluating performance till 2020–07–11. Source: Author.

Mode	Accuracy till 2020–06–29	Accuracy till 2020–07–11
Deterministic (30 time-steps)	0.5875	0.6374
Deterministic (40 time-steps)	0.6018	0.5898
Non-deterministic (30 time-steps)	0.5444	0.5401

The changes in performance are limited, but they reflect the unstable frequency that is inherited in the true data. This unstable frequency can be of natural cause related to the pandemic or a reflection of difficulties due to high numbers of infections and the implications of this on the health care system. Overall, this proves the need for highly varied predictions for the case of Brazil as in this dataset to get a clearer picture of the situation and support future research.

On the other hand, India was chosen as a control group for validation to compare against Brazil in terms of the model's accuracy by using the same RNN's architecture and the same crop-point. In the case of India, a model was capable of achieving 95% accuracy till 2020–07–11 (61 days), the complete report for achieved accuracy by using different settings is shown in Table 11, and the models' files can be found in the data repository.

Table 11.

Evaluating performance of India as a control group till 2020–07–11. Source: Author.

Crop-point	Accuracy till 2020–07–11	Duration of evaluation	Trendline
115	0.9557	61	Exponential
110	0.9404	66	Exponential
115	0.9286	61	Exponential
110	0.9107	66	Exponential
125	0.906	51	Exponential
115	0.8914	61	Exponential
135	0.7992	41	Polynomial
115	0.7251	61	Polynomial

The performance of the models of India's case and the validation of their generated data show that the exponential trendline is reliable in long-term predictions that seek accurate performance for periods that do not exceed two months, which can be very useful to decision-makers. However, it is possibly not credible for longer periods. These accuracy values particularly mean that the inherited randomness in the true input numbers is influencing the results. As well, the unique case and situation related to every country are inherited in the results of the models. However, this also means that extended long-term predictions (more than two months) can become a possibility while using limited data, which contributes to validating the accuracy of the models in Brazil's case.

Lastly, the following options were tested before starting wide-scale training and saving of the models, as they influenced the training:

• 1.Although scaling is a normal procedure in feature engineering for RNN applications, however; it has been found through several validations that it has reduced the accuracy.
• 2.The code can generate overlapping time-series sequences to enlarge the training dataset, however; more accurate models were obtained by using the smaller data.
• 3.It was found that shuffling the data during the training of the models helped the training to generalize the results.
• 4.Filtering raw training data that are fed to the models, proved to be essential to avoid misleading the models by ‘zero’ instances that appeared early since 2020–01–22.
• 5.The non-deterministic mode can – within a certain range – provide a higher accuracy due to randomness, however; the patterns of trendlines are similar between the two modes.

2. Experimental design, materials and methods

The models were built in Python programming language by Keras deep learning library on the Google Colab platform, and they depend only on numerical data of daily infections in each country, no other data has been added to the models except for the time series input.

Mainly, to prepare the data and perform feature engineering, the (gen_rnn_data) function divides the raw dataset in a csv file for the training and evaluation data into training and testing sets, with an option to scale the data and to generate overlapping time-series data to enlarge the data. These two options were found to be not useful during the training of the models, so they were not used. As well, no feature engineering was implemented except for cropping the data to create the validation dataset and to avoid very small numbers as zero, or one, or two, which appeared at the starting point of the data (2020–01–22) till March. The cropping-points are indicated in Table 1.

The architecture of the models is based on predicting 15/20 time-steps (Y) by using 15/20 time-steps for training (X), which is equivalent to using 30/40 time-steps in total for training and testing the models. The choice of these time windows in the case of Brazil was determined experimentally. It was found that smaller time-steps such as 5 (5 for each of X and Y) and 10 (10 for each of X and Y) did produce less generalizability, which can be the same case with higher values as 25. Table 12 below shows different accuracy values for models using the same settings when trained on 50, 40, 30, 20, 10 time-steps. However, these results differ from one country to another.

Table 12.

Comparing performance of different time-steps – till 2020–06–29. Source: Author.

Time-steps (X + Y, ex. 25+25 or 5 + 5)	R2 accuracy
50	−2.770762177
40	0.531547951
30	0.599121699
20	−2.157868562
10	−2.616230335

Generally, the accuracy of all models was calculated using three R squared values (r2 - coefficient of determination): 1) the model's accuracy over the time-steps, 2) the model's accuracy over the whole evaluation period, and 3) the sum of both. The main functions used to train the models are:

• •(train_rnn): A recurrent neural network was chosen as the main architecture of the models as it can handle complex relations in time-series forecasting problems. For that, by using Keras deep learning library, the (train_rnn) function was developed to construct this RNN - by choosing one of these RNNs types: 1) LSTM (Long-Short-Term-Memory) and 2) GRU (Gated Recurrent Unit), along with a convolutional layer within a composite autoencoder's neural network. The choice of the GRU-CNN composite autoencoder is determined based on both, 1) GRU can provide faster convergence and higher performance than LSTM due to the reduced number of parameters in the model and simpler architecture, and 2) the boosted performance when using a hybrid architecture of CNN with RNN, which outperforms RNN alone without CNN. The latter case can be explained by both, CNN's capability of feature learning that identifies the important features in the input sequence as being the first layer, and RNNs capacity to detect temporal dependencies in the input that enables efficient forecasting of multivariate time-sequences. These two architectures were merged without batch normalization that is part of the basic block of CNNs and FCNs in certain applications as computer vision and time-series classification tasks, as it removes – normalizes – the noise in the data, which in return could destroy the dependencies or the relations between the inputs to the GRU autoencoder. The hybrid architecture ends with a dense layer and involves using linear activation function for generating numbers, rather than categorical activation functions such as softmax or sigmoid in traditional CNNs and FCNS when configured for classification tasks.
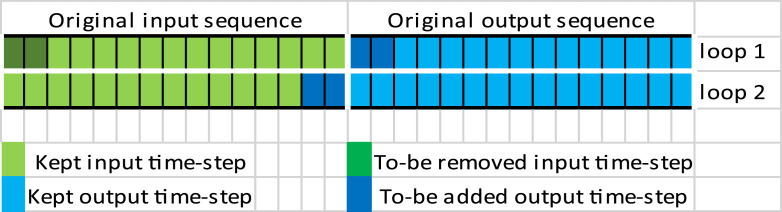
• •Later after training the model, (predict) recursive function can specify a threshold to include several time-steps predictions as shown in Fig. 8, (ex. to keep just the first 2 time-steps predictions out of the 15 time-steps), then it removes the rest and adds the selected ones to the end of the previous input sequence that is used to generate this output, while removing the same number of values at the beginning of the input, to update the input and re-predict the next 15 steps with the newly added values at the end of the input sequence. This loop can be repeated depending on how many time-steps we want to generate. This function allows us to recognize the inherited randomness in the data to explore how the model behaves on every threshold and to which limit it is accurate, so we can later select the best threshold that fits the unseen evaluation data.
• •The (adversarial_evaluation) function was developed to take the output of the model, and train it against daily updated actual numbers to evaluate the predicted numbers as near as possible to the actual numbers to increase the generalizability of the models.
• •The (predict_select_model) function can be used to test the performance of the models against many thresholds and each other, then it returns the best model with the best settings.
• •The (recursive_train_predict) function is the user's interface for the training - prediction process.
• •Helper functions, including 1) (eval_predictions) function that is used to evaluate the performance of the models. 2) (plot_predictions) function that is used to plot the graphs. 3) (train_ml) function that is used within the (adversarial_evaluation) function to perform linear regression operations. 4) (save_tables) function that is used to save the settings and accuracies of the models into tables of different formats and lengths. 5) (get_settings) function that is used to extract and process the settings of the models. 6) (save_data_structure) function that is used to save the folders and files correctly. 7) (select_models_acc) function that is used to filter models based on the accuracy threshold. 8) (select_best_models_acc) function that is used to filter out the best models. And 9) (random_seed_changer) function that is used to change and select a specific random seed across the used libraries in the Python environment to ensure the reproducibility of the results and the weights of the models during the training session.

Fig. 8.

The recursive predict function. Source: Author.

A note on (random_seed_changer) function: Initially, we should not confuse between deterministic settings and replicability, as the first does not necessarily lead to the latter. Generally, there are sources of randomness, since different hardware and software versions of used libraries in deep learning can produce randomness even when deterministic settings are used. For instance, there are four main sources for randomness, ex.: 1) GPU's numerical operations are mostly non-deterministic, so single-threaded CPU was used. 2) The programming environment and the initialization of the neural network can be random; therefore, random values were specified during the training session. 3) Different versions of deep learning libraries can provide different results by using the same settings, this was addressed by using “2.3.0-tf” version. 4) Training on different hardware can introduce randomness, thus, the models were trained on Google's Colab platform at a time-window that is indicated in Table 1. This deterministic setup is useful to serve the procedural objective of the dataset, which is to report settings used to produce all models that were trained in a training session while using the same software and hardware. This can allow future work to evaluate the statistical significance based on no factors influenced the training except for changed settings of the models, which is essential later for uniform training of a reinforcement learning - RL model. This can provide further control over the stochastic process in the neural network, by using the stochastic data that was regulated by deterministic settings during its training process, as training data for an RL model, which is the major objective of the dataset. Table 13 indicates the number of training sessions and models generated in each, and their relevant confidence level, to determine the minimum sample size needed to check the statistical significance in future works.

Table 13.

Number of training sessions. Source: Author.

Mode*	Population	Confidence level	Margin of error	Required sample size per population	Number of training sessions	s1	s2	s3	s4	s5	s6
DM1	1197	95%	4%	400	2	404	793
DM2	1976	95%	4%	461	6	4	355	153	334	600	530
NDM⁎⁎	20	95%	4%	20	1	20
TVM	1001	95%	4%	535	1	1001

^⁎For Non-deterministic modes (NDM and TVM) these values are informative only, as the training sessions are non-deterministic by nature.

^⁎⁎The 20 models in the Non-deterministic mode were all trained in 1 session. The Google Drive File Stream service that syncs files automatically from the training session on Google Colab to Google Drive, has created the designated folder on 3 July and indicated correct created date of 9 files  out of 20 as: 3 July and incorrect modified date as: 25 June for these 9 files that even shows 24 June when downloaded. This error can be noticed in the compressed zip file. However, the code already included a working second layer of protection against these errors, as there is an internal collective settings dictionary file that states exactly all settings used at the beginning of the training process for each model before generating individual settings files, which is created on 3 July. The dictionary clarifies that the actual creation of settings that were used to initialize each training session of the 9 models, occurred on 3 July, as this dictionary creation code is responsible for generating universally unique identifiers as models’ naming convention.

Declaration of Competing Interest

The author declares that he has no known competing financial interests or personal relationships which have, or could be perceived to have, influenced the work reported in this article.