Isotropic MRI Super-Resolution Reconstruction with Multi-scale Gradient Field Prior

Abstract

In this work, we proposed a novel image-based MRI super-resolution reconstruction (SRR) approach based on anisotropic acquisition schemes. We achieved superior reconstruction to state-of-the-art work by introducing a new multi-scale gradient field prior that guides the reconstruction of the high-resolution (HR) image. The prior improves both spatial smoothness and edge preservation. The inverse of the forward model of image formation is used to propagate the gradient guidance from the low-resolution (LR) images to the HR image space. The gradient fields over multiple scales were exploited for more accurate edge localization in the reconstruction. The proposed SRR allows inter-volume motion during the MRI scans and can incorporate with the LR images with arbitrary orientations and displacements in the frequency space, such as orthogonal and origin-shifted scans. The proposed approach was evaluated on the synthetic data as well as the data acquired on a Siemens 3T MRI scanner containing 45 MRI scans from 14 subjects. The evaluation results demonstrate that our proposed prior leads to improved SRR as compared to state-of-the-art priors, and that the proposed SRR obtains better results at lower or the same cost in scan time than direct HR acquisition. In particular, the anatomical structures of hippocampus can be clearly shown in our reconstructed images. This is a significant improvement for the in vivo studies of the hippocampus.

1. Introduction

In magnetic resonance imaging (MRI) practice, a dilemma is inevitably considered in the balance between image resolution, signal-to-noise ratio (SNR), and scan time [1]. High resolution is required for obtaining more image details, correspondingly leading to increased acquisition time. Since SNR is proportional to the slice thickness and square root of acquisition time, long scan time results in reduced SNR, and in high probability introduces artifacts caused by patient motion. Considering MRI resource is limited and costly, thick slices and low scan time have to be leveraged in order to achieve a desired SNR for distinguishing the signal of interest from noise. Many techniques have been developed to handle this dilemma at the acquisition level, including parallel imaging [11] and robust k-space sampling [8]. Recently, it has been shown that super-resolution reconstruction (SRR) achieves better trade-off between image resolution, SNR, and scan time than direct high-resolution (HR) acquisition, for certain image contrasts and sequences, such as T₂-weighted images [9]. As a result, SRR is widely used in MRI to improve the image quality by means of post-processing.

SRR scheme is inspired by the work [17], where multiple low-resolution (LR) natural images are combined into an HR image. The multi-acquisition-based SRR scheme for MRI was introduced in [3]. A milestone work demonstrated that the SRR over multiple anisotropic acquisitions with rotation of the slice selection direction outperforms those with translation [14]. As an extension, the slices with arbitrary orientations and displacements were leveraged in [10]. With these SRR schemes, extensive approaches have been proposed, including frequency-based, image-based, and feature transform-based methods [5].

Image-based SRR has recently been receiving significant interests [4, 12, 13, 16] as it is straightforward to incorporate a forward model with image priors. The forward model describes the image acquisition process. Because the forward model poses an ill-posed problem, images priors are required to embed desired properties into the reconstructed image, e.g., spatial smoothness and edge enhancements. The state-of-the-art priors are Tikhonov cost [9], total variance (TV) [16], and bilateral TV, also known as multi-scale TV (MSTV) [2]. Tikhonov cost is computationally efficient due to the convex relaxation. However, it may result in reduced edge sharpness. TV-based priors are thus leveraged to preserve edges. Edge-directed SRR [15] is emerging as a robust prior to enhance edges in the reconstruction, and shows promising results in obtaining sharper images. However, it focuses on edge preservation only while leaving spatial smoothness unconsidered. Furthermore, that work is data-hungry since it relies on learning the gradient profile prior from a larger collection of natural images.

In this work, we consider the imaged-based MRI SRR based on anisotropic acquisition schemes. Inspired by the success of the edge-directed method [15] for single natural image super-resolution, we proposed a new multi-scale gradient field prior that guides the HR image reconstruction. The prior improves both spatial smoothness and edge preservation. The inverse of the forward model of image formation is used to propagate the gradient guidance from the LR images to the HR image space. The gradient fields over multiple scales are exploited for more accurate edge localization. Our method allows inter-volume motion during the MRI scans and can incorporate with the LR images with arbitrary orientations and displacements in frequency space, such as orthogonal and origin-shifted scans. We evaluate our method on the synthetic data as well as the data acquired on a Siemens 3T MRI scanner containing 45 MRI scans from 14 subjects. The evaluation results demonstrate that our method achieves superior reconstruction over state-of-the-art methods. In particular, the anatomical structures of hippocampus can be clearly shown in the reconstructed images by our method. This is a significant improvement for the in vivo studies on hippocampus.

2. Materials and Methods

We have a set of n LR images, denoted by $\{{\mathbf{y}}_k{\}}_{k=1}^n$, acquired from n scans with arbitrary orientations and displacements in frequency space. The reconstructed HR image x is achieved from the following maximum a posterior estimation

$$\underset{\mathbf{x}}{\max }p(\mathbf{x}|{\left\{{\mathbf{y}}_k\right\}}_{k=1}^n)=\underset{\mathbf{x}}{\max }\prod _{k=1}^{n}p({\mathbf{y}}_k|\mathbf{x})p(\mathbf{x}).$$ (1)

The probability density function $p\left(\right\{{\mathbf{y}}_k{\}}_{k=1}^n\left|\mathbf{x}\right)$ is expanded as the products of p(y_k|x) in Eq. (1) since the LR images are independently acquired. The likelihood p(y_k|x) can be formulated by a forward model that describes the MRI acquisition process. The prior p(x) can be implemented by a regularization term to embed desired properties into the reconstructed HR image.

2.1. Forward Model

Let the images x and y_k be expressed as the column vectors by a lexicographical order of their voxels. The forward model of MRI is thus formulated as

$${\mathbf{y}}_k={\mathbf{D}}_k{\mathbf{H}}_k{\mathbf{T}}_k\mathbf{x}+{\mathit{\mu }}_k,k=1,2,\dots ,n.$$ (2)

T_k is a coordinate transform operator, and implemented as a rigid transform in this work to represent the inter-volume motion during the acquisition. H_k is a spatially invariant blur kernel. It describes the point spread function (PSF) of the MRI acquisition process, and can be decomposed into three kernels in the slice selection, the phase- and the frequency-encoding directions. We consider the PSF in the slice selection direction only and implement it as a truncated Gaussian function. D_k is a downsampling operator. μ_k denotes the noise during the acquisition. Referring to [6], μ_k can be assumed to be additive and Gaussian when the SNR > 3. As a result, the likelihood in Eq. (1) can be found by

$$p({\mathbf{y}}_k|\mathbf{x})=\frac{1}{\sqrt{2\pi }{\sigma }_k}\exp \left(-\frac{\Vert {\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{H}}_k{\mathbf{T}}_k\mathbf{x}{\Vert }_2^2}{2{\sigma }_k^2}\right),$$ (3)

where σ_k denotes the power of the noise μ_k.

2.2. Multi-scale Gradient Field Prior

SRR is an ill-posed problem, and thus, the priors are used to compensate missing information, particularly the loss of high frequencies. Image gradient is usually exploited to preserve edges in the reconstruction, such as Tikhonov and TV priors. Edge-directed methods have recently been emerging as a robust prior [15], where a desired gradient field is imposed on the reconstructed image as a guidance of the edge locations as well as edge strengths. Specifically, the prior is implemented by enforcing $\nabla \mathbf{x}=\widehat{\nabla \mathbf{x}}$, where ∇ computes the gradient of x, and $\widehat{\nabla \mathbf{x}}$ is an input and denotes the desired gradient field. In [15], $\widehat{\nabla \mathbf{x}}$ is learned from a large collection of natural images. However, the learning is designed for edge preservation only while leaving spatial smoothness unconsidered. In this work, we propose a new analytical operator to guide the reconstructed image for both edge preservation and spatial smoothness:

$$g_{\tau }(x)=x{\left(1+{\left(\frac{\tau }{x}\right)}^4\right)}^{-1}.$$ (4)

By inputting an image gradient field ∇x′, g_τ(·) enhances large edges for sharpness and punishes gradient perturbations for smoothness. The parameter τ > 0 balances between the gradient enhancement and punishment. The gradient field prior for the HR image x is therefore obtained from $\widehat{\nabla \mathbf{x}}=g_{\tau }(\nabla {\mathbf{x}}^{\prime })$. To this end, a strategy is required to estimate the image gradient field from the LR images and transform it to the HR image space to form ∇x′.

The difficulty in obtaining ∇x′ is that the blurring in the LR images results in inaccurate edge localization, leading to inaccurate gradient guidance for the reconstructed image. We improve the accuracy of the edge location estimation from two aspects: compute the gradient over multiple scales of the LR images and dynamically update the estimation during the optimization of the reconstruction.

We align up all the LR images and interpolate them by a 3rd-order B-spline method to the images of the same size as x. The mean image of these interpolated images is used as x′. The gradient field in the HR image space at a scale s is then computed from ∇_sx′, and correspondingly $\widehat{{\nabla }_s\mathbf{x}}=g_{\tau }({\nabla }_s{\mathbf{x}}^{\prime })$. In this work, each scale s is related to a unique integer triplet (α, β, γ) that indicates the scales in x, y, and z directions, respectively. We thus define the operator ∇_s as

$${\nabla }_s={\omega }^{\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|}(\mathbf{I}-{\Psi }_{\alpha }^x)(\mathbf{I}-{\Psi }_{\beta }^y)(\mathbf{I}-{\Psi }_{\gamma }^z),$$ (5)

where 0 < ω 1 denotes a weight parameter, I denotes an identity matrix, and the operators ${\Psi }_{\alpha }^x$, ${\Psi }_{\beta }^y$, and ${\Psi }_{\gamma }^z$ shift I by α, β, and γ voxels in x, y, and z directions, respectively. To exclude the repeated scales, we constrain α ∈ [−p, p], β ∈ [0, p], γ ∈ [0, p], and α + β + γ ≥ 0. Since the scale at 0 is trivial, we further exclude the case α = β = γ = 0. We set p = 2 to create 40 gradient fields.

For a robust gradient guidance, ∇_sx is desired to be located at $\widehat{{\nabla }_s\mathbf{x}}$ and yield a heavy-tailed distribution, such as Laplace distribution. As a result, the prior of our SRR approach is formulated as

$$p(\mathbf{x})=\mathbf{\prod }_{s=1}^S\frac{1}{2\sigma }\exp \left(-\frac{\Vert {\nabla }_s\mathbf{x}-g_{\tau }({\nabla }_s{\mathbf{x}}^{\prime }){\Vert }_1}{\sigma }\right),$$ (6)

over S gradient fields, where σ is the variance of the distribution. It is evident that the MSTV prior [2] is a special case of Eq. (6) when $g_{\tau }({\nabla }_x^{\prime })$ is always zero. However, the proposed multi-scale gradient field prior is essentially different from the MSTV prior and its variants. The desired gradient field is exploited in the proposed approach to guide both the spatial smoothness and edge preservation over multiple scales in the SRR.

2.3. Super-Resolution Reconstruction

Referring to Eqs. (1), (3), and (6), the SRR for the HR image x is achieved from

$$\underset{\mathbf{x}}{\min }\sum _{k=1}^n\Vert {\mathbf{y}}_k-{\mathbf{D}}_k{\mathbf{H}}_k{\mathbf{T}}_k\mathbf{x}{\Vert }_2^2+\lambda \sum _{s=1}^S\Vert {\nabla }_s\mathbf{x}-g_{\tau }({\nabla }_s{\mathbf{x}}^{\prime }){\Vert }_1,$$ (7)

where Λ > 0 is a parameter balancing between the likelihood and the prior. We solve Eq. (7) by a gradient descent algorithm, where x is estimated at iteration t by x^t = x^(t−1) + ηΔx^t with the learning rate η and the increment Δx^ί. Meanwhile, to obtain an accurate image gradient guidance, we dynamically update the gradient field over scale-s by g_τ(∇_sx^t) at certain t, e.g., every 50 iterations. τ in Eq. (4) is set to 0.065. According to [2], ω in Eq. (5) is set to 0.6. We suggest λ in Eq. (7) is set in [0.03, 0.1] according to our empirical results.

Our SRR approach can incorporate with various acquisition schemes. We use the orthogonal (axial, coronal, and sagittal) and the origin-shifted acquisitions to demonstrate the efficacy of our method by comparing to those based on state-of-the-art priors, including Tikhonov, TV, MSTV, Huber loss, and Rousseau [12]. We have the synthetic data and the data acquired on a Siemens 3T MRI scanner containing 45 scans from 14 subjects for the demonstrations. All scans were performed in accordance with the local institutional review board protocol.

Synthetic Orthogonal LR Acquisitions.

We simulated a T₁-weighted data set based on the Dryad data package [7]. We downsampled the original image of isotropic resolution of 250 μm to that of 500 μm, and used it as the ground truth. We then downsampled the ground truth image by the factors of {2, 3,4, 5, 6, 8} in the x, y, and z directions, respectively, to obtain an axial, an coronal, and an sagittal LR image at each factor. Simulated motion was added to these downsampled images. We evaluate the reconstructed HR image quality by peak signal-to-noise ratio (PSNR), SSIM [18], and root square mean error (RSME).

Axial and Coronal LR Acquisitions (AC).

We acquired a T₂-weighted turbo spin-echo (T₂W-TSE) data set containing 36 scans from 12 subjects. For each subject, an axial and a coronal LR images were acquired with in-plane resolutions of 0.4 × 0.4 mm² and slice thickness of 2 mm, and correspondingly a T₂-weighted HR image was acquired as the reference. It takes about 2 min in acquiring a T₂W-TSE LR image on a Siemens 3 T scanner. The HR images are reconstructed at the resolution of 0.4 mm³. Instead of RSME, we employ the sharpness metric [4], which is an image gradient-based criteria, to evaluate the edge preservation in the reconstruction. We also qualitatively investigate the edge enhancement.

Axial, Coronal, and Sagittal LR Acquisitions (ACS).

We acquired a T₂-weighted data set containing an axial, a coronal, and a sagittal LR image from a volunteer. The in-plane and through-plan resolutions of the 3 images are 0.4 × 0.4 mm² and 2 mm, respectively. The HR image is reconstructed at isotropic 0.4 mm. We qualitatively compare our reconstruction results to those of baseline methods.

Origin-Shifted Coronal LR Acquisitions (OSC).

We acquired a T₂W-TSE data set containing 3 scans of a coronal LR image of resolution 0.4 × 0.4 × 0.8 mm, and 3 scans of a coronal LR image at the same resolution but with its origin shifted by 0.4 mm. The HR image is reconstructed at isotropic 0.4 mm. We conducted 3 scans for each coronal image for noise suppression in the reconstruction. We aim at clearly showing the hippocampus by our SRR approach.

3. Results and Discussions

Figure 1 shows the evaluation results on the synthetic data set. It is evident that our approach outperforms the 3 baselines that are respectively based on Tikhonov, TV, and MSTV priors. It indicates that the proposed multi-scale gradient field prior improves the SRR on the synthetic data set.

Fig. 1.

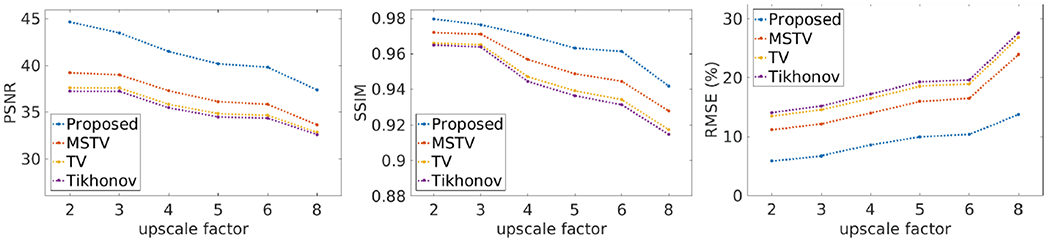
Evaluation results of our and other three methods on the synthetic data set.

Figure 2 shows the evaluation results obtained from our approach and the baselines on the AC data set. The average performance of our method over the 12 sets of reconstructions is: PSNR = 25.96 ± 1.49, SSIM = 0.79 ± 0.047, sharpness = 1.03 ± 0.024, which is better than the 5 baselines in terms of all the 3 metrics. Figure 3 shows a representative reconstructed result on the AC data set. A representative edge is analyzed and the results are shown in Fig. 3(d). It is evident that our proposed prior leads to better edge enhancement than the 3 TV-based baseline priors. The reference image has low contrast due to the long time scan. Therefore, the MSTV, TV and our methods obtain better edges than the reference.

Fig. 2.

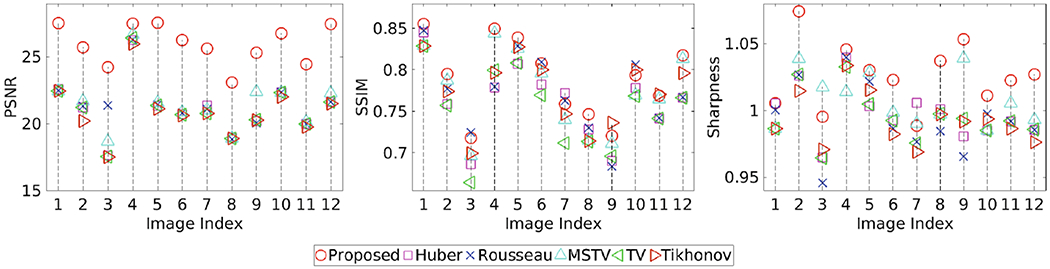
Evaluation results of our and other five methods on the AC data set.

Fig. 3.

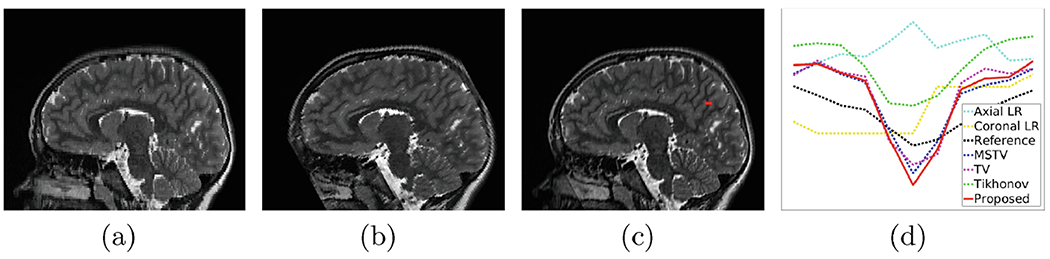
Reconstructed results on the AC data set. (a) A slice from the axial LR image. (b) A slice from the coronal LR image. (c) A slice form the reconstructed HR image by the proposed approach. (d) Edge profile plot over the line marked in red in (c). (Color figure online)

Figure 4 shows the qualitative results on the ACS data set obtained from the Tikhonov, TV, MSTV, and our approach. It can be seen that the SRR over the orthogonal LR scans can achieves good HR images. Our approach performs the best in showing image details and produces sharper edges than the 3 baselines.

Fig. 4.

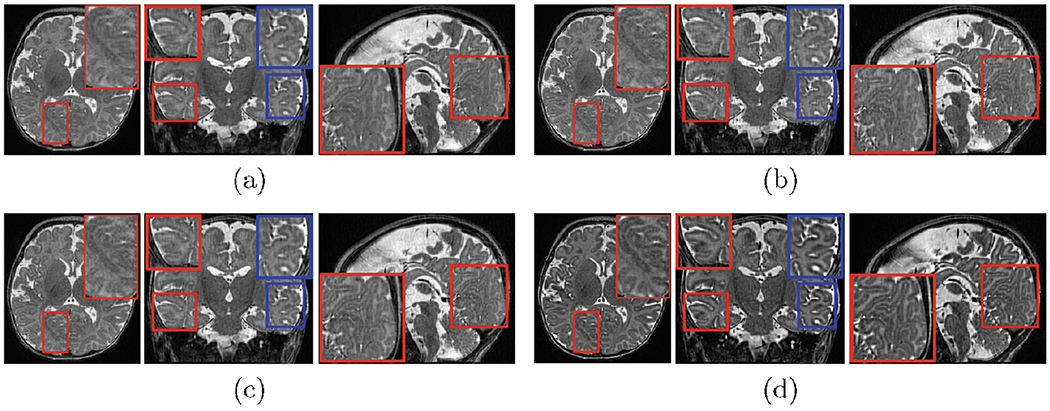
Reconstructed results on the ACS data set, obtained from (a) Tikhonov, (b) TV, (c) MSTV, and (d) the proposed approaches, respectively.

Figure 5 shows the qualitative results on the OSC data set. We can see that our method produces both region-smoothed and edge-sharpened HR image, as compared to the 3 baselines. In particular, the anatomical structures of the hippocampus can be clearly shown in different image planes of our reconstructed image. This is a significant improvement for the in vivo studies on hippocampus.

Fig. 5.

Reconstructed results on the OSC data set. Two coronal slices from (a) an LR image and (b) our reconstruction. The hippocampus in sagittal slices from (c) an LR image, and the images reconstructed via (d) Tikhonov, (e) TV, (f) MSTV, and (g) the proposed approach, respectively.

4. Conclusions

In this work, we have proposed a novel image-based MRI SRR approach based on anisotropic acquisition schemes. We have achieved superior reconstruction to state-of-the-art methods by introducing a new multi-scale gradient field prior that guides the reconstruction of the HR image. The inverse of the forward model of image formation has been used to propagate the gradient guidance from the LR images to the HR image space. The proposed approach has been evaluated on the synthetic data as well as the data acquired on a Siemens 3T MRI scanner containing 45 MRI scans from 14 subjects. The evaluation results have demonstrated that our proposed prior leads to improved SRR as compared to state-of-the-art priors, and that, based on the orthogonal and the origin-shifted LR acquisition schemes, the proposed SRR obtains better results at lower or the same cost in scan time than the direct HR acquisition.