Abstract
This paper presents an individualized Ensemble Model Predictive Control (EnMPC) algorithm for blood glucose (BG) stabilization and hypoglycemia prevention in people with type 1 diabetes (T1D) who exercise regularly. The EnMPC formulation can be regarded as a simplified multi-stage MPC allowing for the consideration of Nen scenarios gathered from the patient’s recent behavior. The patient’s physical activity behavior is characterized by an exercise-specific input signal derived from the deconvolution of the patient’s continuous glucose monitor (CGM), accounting for known inputs such as meal, and insulin pump records. The EnMPC controller was tested in a cohort of in silico patients with representative inter-subject and intra-subject variability from the FDA-accepted UVA/Padova simulation platform. Results show a significant improvement on hypoglycemia prevention after 30 min of mild to moderate exercise in comparison to a similarly tuned baseline controller (rMPC); with a reduction in hypoglycemia occurrences (< 70 mg/dL), from 3.08% ± 3.55 with rMPC to 0.78% ± 2.04 with EnMPC (P < 0.05).
Keywords: Artificial pancreas, Exercise, Hypoglycemia, Type 1 Diabetes
1. Introduction
Type 1 diabetes mellitus (T1D) is an autoimmune condition resulting in absolute insulin deficiency and a life-long need for insulin replacement [1]. Glycemic control in T1D remains a challenge, despite the availability of modern insulin analogs [2], the improving accuracy of glucose monitoring [3, 4], and the widening use of intensive insulin therapy. While new technologies have proven benefits in avoiding diabetes related complications [5] and may reduce excess mortality in some populations [6], excess mortality and complication rates remain significantly higher in T1D when compared to the general population [7, 8].
Monitoring diet and exercise is of paramount importance for blood glucose (BG) control in people with T1D. Exercise has been associated with many health benefits for people with T1D, such as reduced cardiovascular risks, improved psychological well-being, and possible benefits in bone health [9]. However, exercise can also lead to an imbalance between hepatic glucose production and glucose disposal into muscle [10], increased insulin sensitivity related to glucose transporter type 4 translocation upregulation, and impaired counterregulatory hormonal response [11, 12]. In the absence of sufficient insulin reduction and/or carbohydrate supplementation, hypoglycemia often occurs during exercise, as well as during early and late recovery [13, 14]. These metabolic perturbations make participating in sports or exercise particularly challenging for people with T1D [15, 16]. Despite growing awareness of the benefits of exercise, fear of hypoglycemia often results in the avoidance of physical activity [17] or treatment behaviors that overcompensate and lead to worsened metabolic control [18]. Exercise has also been shown to mask hypoglycemic symptoms, thereby facilitating repeated exposure to unrecognized hypoglycemia and potentially causing hypoglycemia-associated autonomic failure [12] with all its negative consequences [1]. For these reasons, many people with T1D engage in less exercise than their nondiabetic counterparts [19]. According to Riddell et al., fear of hypoglycemia, loss of glycemic control, and inadequate knowledge about exercise management are the major barriers for people with T1D to exercise regularly [20]. Additional reasons why people with T1D may not engage in physical activity include insufficient time, limited access to facilities, absence of motivation, issues with body image, and general lack of knowledge around exercising. This is particularly worrisome since it is estimated that from the entire population of people with T1D, 60% are overweight, 40% have hypertension, 60% have dyslipidaemia, and most do not engage in physical activities [20].
For adults with diabetes, 150 min of accumulated physical activity is recommended every week [21]. However, it is still unclear which form of exercise benefits cardiometabolic control in T1D the most [20]. Recent findings indicate that high-intensity interval training has multiple benefits for people with T1D, including less hypoglycemia and better BG control [22].
Artificial pancreas (AP) technology has become a promising solution to diminish the burden of T1D management, offering near optimal BG control and significant reduction in hypoglycemic events. In the past decade, AP studies have advanced from short-term inpatient investigations using algorithm-driven manual control [23], to long-term clinical trials in free-living conditions using wearable, wireless, automated AP systems [24]. Reviews and collections of papers reflecting the progress of the AP field are found elsewhere [25, 26], report a significant reduction of glucose variability (GV), particularly overnight, and lower risk for for hypoglycemia. In September 2016, the FDA approved the first hybrid closed-loop control system, the Medtronic 670G, which is capable of automatically adjusting the pump’s basal rate, but still does not automate insulin boluses [27]. Unannounced meals and exercise bouts are two major challenges that need to be addressed in AP systems [28].
A large volume of AP literature is devoted to the design of MPC-based schemes for automated insulin infusion systems [29, 30, 31, 32, 33, 34, 35]. The success of MPC-based schemes has largely been from the explicit use of a validated patient models for tailored glycemic prediction and the ability to include constraints over the system variables. In this regard, MPC implementation relies mostly on the quality of the model used for prediction [36]. Since MPC refers to a group of strategies rather than a specific scheme, many possible combinations arise. Previous contributions to MPC-based schemes that address unannounced exercise bouts have been documented in [37, 38]. In these contributions, two control schemes were tested both in silico and in vivo, the Zone Model Predictive Control (ZMPC) integrated with the UVA Diabetes Assistant (DiAs) platform and the Enhanced Model Predictive Controller (eMPC), an MPC encompassing three innovations: (i) dynamic tuning system of the controller’s parameters, (ii) an enhanced set-point algorithm, and (iii) a trust index module, which uses prediction accuracy measurements (recent past) to indicate trust in current and future predictions.
Our controller falls into the category of hybrid controllers, because meals must be announced a priori. However, our approach differs from previous contributions since the subject does not need to announce exercise. To this end, our controller utilizes patient-specific exercise-induced signatures (inputs) based on a personalized, physiologically inspired model of glucose homeostasis and the use of regularized deconvolution on historical data (net effect method [39]). The core controller is also able to use the patient’s previous behavior to predict the impact of future exercise bouts. From these predictions a sequence of insulin doses are chosen to avoid hypoglycemia during and after physical exercise. This approach is dependent on a record of the patient’s behavior. Once enough data about the subject is collected (CGM, pump, meal, and activity tracker records), we characterize the subject-specific behavior related to exercise using the net effect method. Then, this information is fed to the controller (the times the subject is most likely to exercise) which assesses the best insulin pattern through a robust control approach. In this regard, our approach does not aim to detect, but rather to anticipate the occurrence of physical activity.
The output-feedback controller is fed by the Unscented Kalman Filter (UKF) algorithm, guaranteeing a reliable estimation of the system’s state at every sampling time. To evaluate the proposed system, we generated a cohort of 50 virtual subjects exhibiting both intra-patient and inter-patient variability by means of our FDA-accepted UVA/Padova simulator. All subjects underwent a two-day trial that included three meals per day and a mild to moderate 30-min exercise bout in the transition from absorptive to postabsorptive state (4:00 4:30 p.m) on the first day with a later dinner at 7:00 p.m.
The manuscript is organized as follows. In Section 2, we describe the prediction model for the controllers and for the generation of the subject’s specific exercise signatures. The method used to characterize the exercise behavior of every subject is presented in Section 3. In Section 4, both the treatment controller (EnMPC) and the baseline controller (MPC) are presented. The UKF used to close the output-feedback loop, is also described in this section. In silico results from the 50 generated virtual patients are presented in Section 5. Finally, discussion and conclusions are provided in Section 6.
2. Control-oriented Model
Physiologically based minimal models have been used for many purposes in diabetes technology [40]. However, black-box or data-driven models have gained attention in past years for automatic control purposes, since they are easier (and cheaper) to obtain than physiological models [29, 30, 41, 42, 43, 44].
The debate of the superiority or inferiority of data-driven models in comparison to physiology-based models is likely to continue for years to come. Currently, it is hard to conclude this argument, because there are no large scale studies directly comparing many different available prediction models in an actual clinical study. Most validations of prediction models are justified with in silico results [44]. Yet, there are some notable differences between the two approaches. Physiology based models, particularly minimal models, have a (relative) small number of model parameters and BG can be predicted for a given subject using population parameters. Thus, eliminating the need for model personalization, but still allowing for it if sufficient amounts of data are available. The quality of a data-driven model, on the other hand, is largely dependent on the assumed model structure and data that is used to train it and it is unclear how much data is necessary to produce accurate prediction values without overfitting. Additionally, an advantage of data-driven models is that they are highly personalized. Data-driven models are also flexible to the addition of other physiological inputs, such as physical activity, whereas most minimal models only consider insulin and meals and need to be enlarged/modified to account for such additional inputs. Data-driven models informed by physical activity signals have garnered success, even in challenging situations where BG is predicted during and after exercise [45]. However, the data-driven approach lacks the inherent descriptive ability and parameter interpretability of its physiological counterpart. For these reasons, we chose to use a physiology-based minimal model that was personalized based on data collected from the subject.
In this section, we describe the physiologic model used for behavioral characterization (exercise), state estimation, and prediction from the controllers (both rMPC and EnMPC). Furthermore, we will discuss how the model can be individualized for each patient.
2.1. The Subcutaneous Oral Glucose Minimal Model
Consider an extended version of the minimal model, known as the Subcutaneous Oral Glucose Minimal Model (SOGMM) [39]
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
| (1f) |
| (1g) |
with
| (2a) |
| (2b) |
where G, X, Q1, Q2, Isc1, Isc1, and Ip denote the plasma glucose concentration [mg/dl], proportion of insulin in the remote compartment [l/min], glucose mass in the stomach [mg], glucose mass in the gut [mg], insulin amount in the first compartment [mU], insulin amount in the second compartment [mU], and plasma insulin [mU], respectively, and ω and Jctrl refer to the rate of mixed-meal carbohydrate absorption [mg/min] and insulin input signal [mU/min], respectively. I and Ra stand for insulin concentration [mU/I] and glucose rate of appearance [mg/min · kg], respectively. The parameters of (1) and (2) are presented in the Appendix in Table A.4 together with population values. Basal glucose, Gb, is found through a transformation of the patient’s most recent glycated hemoglobin, HbA1c, value [39]
| (3) |
Although the meaning of Gb in T1D is not as clear as it is in health, we consider the whole term Sg · Gb as originally conceived. This represents the effects of both glucose disposal and endogenous glucose production (EGP).
2.2. Model individualization
Model individualization was performed using the procedure reported in [46] which is based on the structural and practical identifiability analysis of the model. The SOGMM has 13 parameters, one of which (BW) is easily measured, and another (f) can be fixed based on general human physiology. Of the remaining parameters, the following are found to be locally structural and practically identifiable and hence used for model individualization
| (4) |
Using the last version of the FDA-approved UVA/Padova simulator, we collected 30 days worth of plasma glucose concentration, insulin, meal, and activity records for the considered virtual population. During those days, virtual subjects ate at around 7:00, 13:00, and 19:00 h with a carbohydrate content close to 40g, 60g, and 40g, respectively. The meal times and carbohydrate amounts were assumed to follow uniform distributions on [t − 20min, t + 20min] and [CHO − 20g, CHO + 20g], where t and CHO are the meal time and carbohydrate content for every meal, respectively. Four times a week, the subjects performed a 30-min long moderate-intensity exercise bout at any time from 15:00 to 17:00 h. Bearing the above in mind, model (1) is individualized with (4) using regularized root mean square optimization on patient specific historical data.
3. Exercise-induced net effect
Modeling the glucose-insulin system has been a primary concern in the field diabetes technology over the last 40 years. Numerous investigations have contributed to building up the body of knowledge around the mathematical representation of glucose homeostasis in healthy people and in people with T1D and T2D [47, 48]. However, there are some effects/behaviors that are not fully understood, such as eating and exercise behaviors.
There are mathematical models that represent the oral carbohydrate ingestion and glucose behavior after exercise bouts, but glucose excursions and variability exhibited in CGM records cannot be fully explained from available models. The net effect was conceived and has been used as a way of describing these unmodelled glycemic disturbances [39].
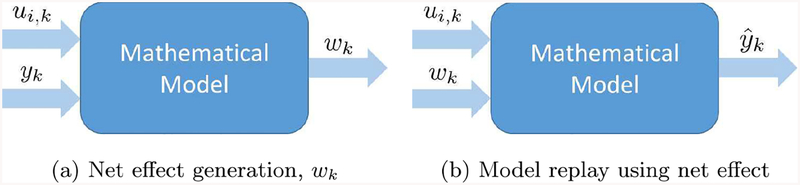
The net effect can be defined as the input that best explains the correlated time series of CGM values and considered input data, accounting for the model used to describe the patient’s physiology. Figure 1 shows the process of estimating the net effect from known inputs (in this case insulin and meal intake) and CGM data by means of a regularized deconvolution method (Fig. 1a); and the process of CGM reconstruction or replay by using the estimated net effect and known inputs (Fig. 1b).
Figure 1:
Net effect: accounting for BG variability, Ui,k, wk, and yk denote insulin, meal, net effect, and measurements at the k − th sampling time, respectively.
The exercise-induced net effect was used this contribution as a way of estimating the effect of a single, moderate-intensity exercise bout on plasma glucose concentration. This estimation characterized the exercise bouts (subject’s behavior) as direct disturbances on the glucose dynamics and was applied in the controller for prediction purposes. The exercise signature informs the controller about the expected glycemic impact of a potential exercise bout. In this case, we used a discrete-time linear time-invariant model of (1), because it allowed the net effect estimation problem to be stated as a convex (quadratic) optimization problem.
Consider the following discrete-time, linear time-invariant model
| (5a) |
| (5b) |
where is the system state at time k, yk refers to the CGM measurements, and UI,k, UM,k, and wk are the insulin, meal intake, and net effect signature, respectively. The matrices A, C and BI, BM, and Bw are the state and measurement matrices and the input matrices exhibiting the effects of insulin, meals, and net effect, respectively. Model (5) is the result of linearizing and discretizing (1) around , with the above coming from the steady-state solution of (1) considering Gss = y1 (the first measurement of the dataset), ωss = 0, and Jctrl,ss = ub. The sampling time used in the discretization was ts = 5min.
The exercise-induced net effect can be computed as the solution of the following quadratic problem
| (6) |
where ycgm is the measured BG from CGM, || · ||1 and || · ||2 represent the 1-norm and 2-norm of (·), respectively, Ne is the length of the dataset (288/day), and are the sequences {e1, e2, …, } and {w1, w2, …,} minimizing the cost function, and λ1 and λ2 are weighing terms, penalizing the sparse values and high variations of the net effect, respectively. By introducing the slack variables Sk the last problem can be reformulated as the following constrained convex quadratic problem
| (7) |
with defined in a similar way as and . The traditional formulation of the net effect has been used to explain disparities between glucose predicted using the SOGMM and observed blood glucose values. The net effect represents the combined effect of disturbances not captured in the known model inputs. These may include physical activity, circadian rhythm, hormonal changes, unreported insulin or meals. In order to inform the controller specifically about exercise, the net effect signal was transformed to highlight the effects of physical activity by means of the following procedure. First, the net effect was calculated using subject-specific SOGMM parameters. Segments of the net effect traces when the patient was exercising plus an additional window of observation (2h) were then selected and normalized by the value of the net effect 15 minutes prior to activity. Following the observation, the net effect value was set to decay exponentially over the next 6 hours. Bearing the above in mind, the new exercise-induced signature is defined by
| (8) |
where and are the times of commencement and ending of exercise and k is the last sampling point during the observation window.
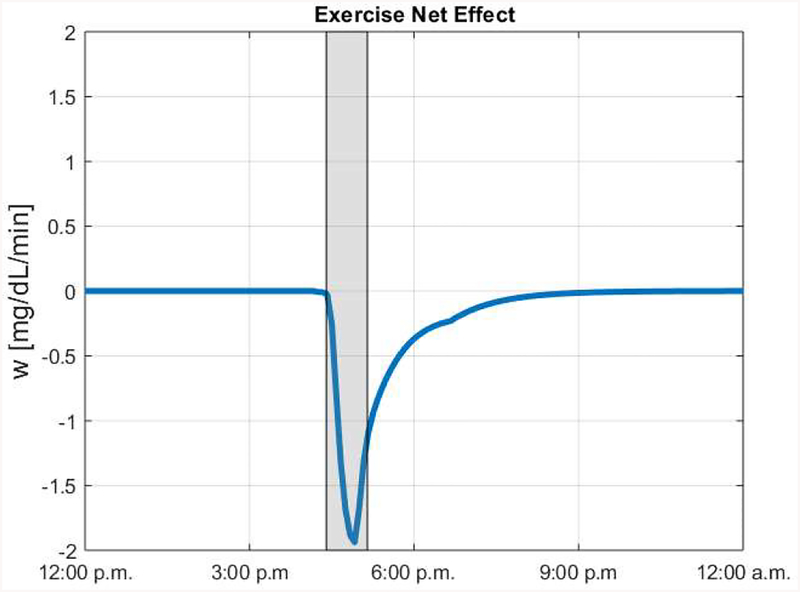
Figure 2 shows an example of an exercise-induced net effect trace for a given in silico subject. It can be seen here that exercise was simulated from 4:30 to 5:15 p.m. As a response to this, the exercise net effect is negative during the exercise bout and in the hours following. This reflects the impact on BG that is expected for the performed exercise.
Figure 2:
Example exercise net effect signal for a representative in silico subject. Moderate exercise was simulated between 4:30 and 5:15 p.m. Gray area indicates when exercise occurred.
The explained procedure can be performed in a clinical setting without major issues. First, CGM, pump, meal (carbohydrate counting), and activity tracker records are collected for every subject for about 30 days. After preprocessing all the gathered data (cleaning, filtering, and gap elimination), the net effect signature can be computed for every day by means of (7). Afterward, the exercise-induced signatures for every day are obtained as presented in (8). Since every signature would hypothetically inform a controller in the ensemble (EnMPC), finding out a trade-off between the number of ensembles and computational burden is key. To do so, we leverage a clustering strategy helping to give a reduced but representative number of signatures.
4. Ensemble Model Predictive Control
In order to account for behavioral disturbances (e.g., unannounced meals and exercise) our group has been working towards a tailored, adapted-to-behavior, advanced controller, known as Ensemble Model Predictive Control (EnMPC) [41]. The EnMPC deals with a control strategy using a set of regular MPCs, each using a specific behavioral signature. The control effort is then computed as a consensus among the MPC’s according to the most likely scenario. In this section, we present both the rMPC and EnMPC which use a linearized version of SOGMM around the operating target for prediction (to reduce the computational burden associated with solving the optimization problem in real time). The state estimation problem is solved using an Unscented Kalman Filter (UKF).
4.1. State Estimation - The Unscented Kalman Filter
The UKF was introduced by Julier et al. in [49] to circumvent precision problems shown by the Extended Kalman Filter without increasing its computational burden [50, 51]. The UKF is based on the principle that it is easier to perform a nonlinear transformation over a single point rather than a complete probability density function (PDF) [50, 51]. In this way, a cloud of so-called sigma points are used to approximate the true PDF of the state vector. In this work, we use a variation of the UKF detailed in [52]. Since SOGMM is not observable (using glucose concentration as the only output), we observe the plasma glucose concentration G and proportion of insulin in the remote compartment X. The remaining states are estimated in open-loop.
| (9) |
4.2. Output-feedback Model Predictive Control
Consider the estimate of xk, computed by the Unscented Kalman Filter (UKF). At each time step k, and using for prediction, the controller must solve the following optimization problem [53
| (10a) |
| (10b) |
| (10c) |
| (10d) |
| (10e) |
| (10f) |
| (10g) |
| (10h) |
| (10i) |
with
the control policy and slack variables to be optimized. The cost function is defined as
| (11) |
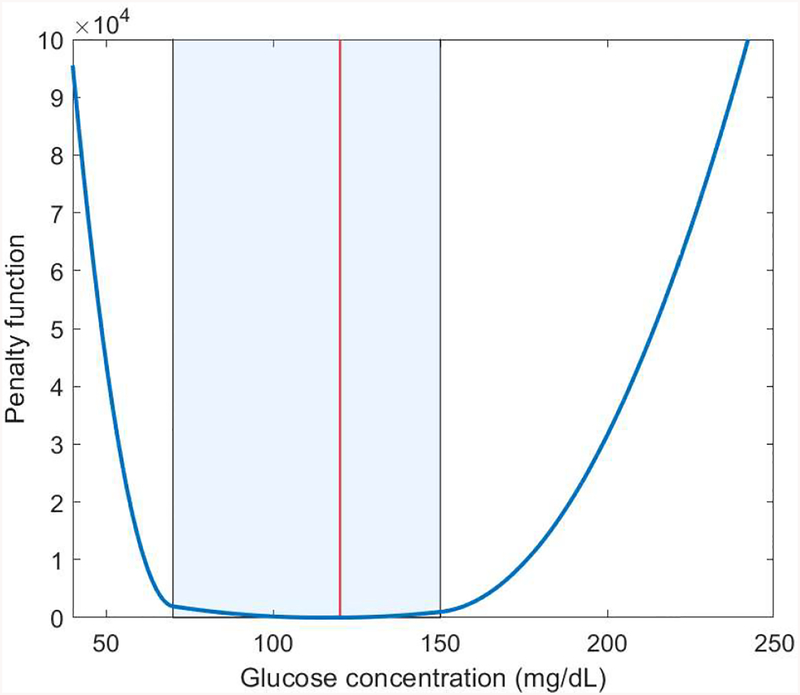
where Np and Nc refer to the prediction horizon and control horizon, respectively, λ1, λ2, κ1, and κ2 are weights for the different costs. In this optimization problem, the control input and the difference Δuk+j|k = uk+j+1|k − uk+j|k must lie in the intervals [umin, umax] and [Δumin, Δumax] ∀j = 1, …, Nc − 1, respectively. The two terms and correspond to penalty costs for hyperglycemia and hypoglycemia, respectively, and are used to soften the hard constraints. The shape of the penalty function is depicted in Figure 3 and is intended to avoid the risk of hypoglycemia and to a lesser extent the risk of hyperglycemia.
Figure 3:
Asymmetric penalty function. The shadowed area corresponds to the safe-to-control area (70–150 mg/dL) and the red line to BG target (120 mg/dL).
To enhance the safety of the algorithm, an asymmetric time-varying exponential reference signal is employed [54]. This reference is used to induce a fast but smooth return to the BG target from a hypoglycemic state. The asymmetric time-varying reference signal is given by
| (12) |
with ysp the glucose target or set point and tk the discrete time.
4.3. Output-feedback Ensemble Model Predictive Control
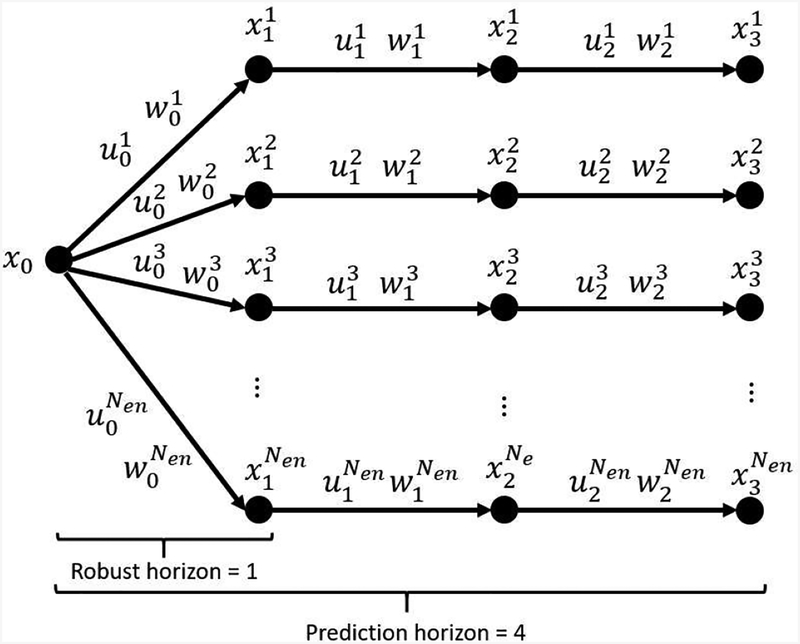
Multi-stage MPC is a type of robust MPC where the model uncertainty is represented by means by a finite number of realizations at every sampling time (discrete scenario tree) [55]. In turn, the Ensemble Model Predictive Control (EnMPC) is a type of multi-stage MPC where the robust horizon is a priori set to 1 and the consistency of the inputs is enforced by means of the so-called non-anticipativity constraint [41, 55, 56]. An example of scenario tree for EnMPC can be seen in Figure 4, where a prediction horizon of 4 is presented for illustrative purposes.
Figure 4:
Scenario Tree representation of the uncertainty evolution in EnMPC. x0 stands for the initial state, , corresponds to variable (·) at time k in scenario j. x, u, and w correspond to the state, input, and net effect signature, respectively. Nen refers to the number of considered ensembles (scenarios).
In order to depict the EnMPC scheme, assume that the specific exercise behavior of a given subject is described by means of Nen exercise signatures computed from retrospective data. At each time step, k, the ensemble model predictive controller (EnMPC) must solve the following optimization problem [41]
| (13a) |
| (13b) |
| (13c) |
| (13d) |
| (13e) |
| (13f) |
| (13g) |
| (13h) |
| (13i) |
| (13j) |
with
the control policy and slack variables to be optimized at the i − th MPC, with i = 1, 2, …, Nen. The cost function is defined as
| (14) |
with the variables defined as before for every MPC. Every model prediction uses the estimate of xk. as the initial condition at every sampling time, computed by the Unscented Kalman Filter (UKF). Eq. (13j) is known as the non-anticipativity constraint and ensures that the first input will be identical for every considered exercise behavior [41, 56].
5. In Silico Study
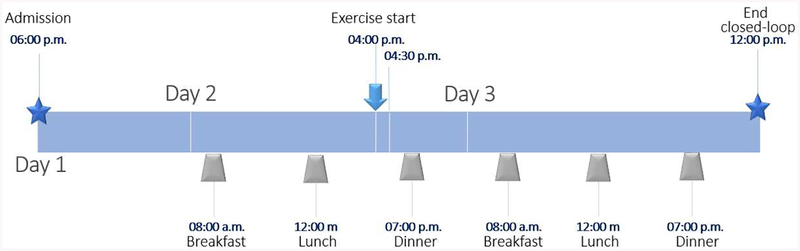
The efficacy of the output-feedback EnMPC is demonstrated via an in silico experiment using of 50 virtual subjects from our in-house FDA-accepted UVA/Padova metabolic simulator. A clinical protocol, similar to ones previously performed by our group, was used as the basis of the in silico tests. In this protocol, data (insulin pump, meals and CGM) was collected from the virtual subjects over 30 days. The experimental setup dictated that subjects perform exercise similar to 30 min of mild to moderate treadmill, static bike, or brisk walking activity, on 15 of the 30 days during the data collection period. For the admission, subjects were placed under closed-loop control at 6:00 p.m. to stabilize CGM values and adjust the AP with the output-feedback EnMPC. During the next two days, patients received three meals at around 7:00 a.m, 1:00 p.m, and 7:00 p.m of 40g, 60g, and 40g of carbohydrates (CHO), respectively. These meals were announced to the controller which used patient-specific carbohydrate ratios to address the meal challenges (Hybrid Closed Loop control). At around 4:00 p.m of the first full day of closed-loop control, subjects underwent a 30 min long mild to moderate exercise challenge (treadmill, static bike, or brisk walk). Subjects were monitored during the following night and next day for possible exercise-induced hypoglycemia. A timeline summarizing this protocol is shown in Figure 5.
Figure 5:
AP session timeline. Subjects start AP mode at 06:00 p.m.
For analysis, the EnMPC controller (the treatment) was compared to a baseline controller, rMPC. The selected parameters for both controllers are shown in Table 1, where stands for the identity matrix of order m. Note that the parameters were held similar in both controllers in order to assess the benefit of the intervention. In the same way, the tuning parameters for UKF are shown in Table 2.
Table 1:
Tuning parameters for rMPC and EnMPC
| Parameter | rMPC | EnMPC | Parameter | rMPC | EnMPC |
|---|---|---|---|---|---|
| Nen | N.A. | 10 | 90 | 90 | |
| Np | 24 | 24 | 20 | 20 | |
| Nc | 15 | 15 | umin | −ub | −ub |
| Qz | Δumin | 0 | 0 | ||
| λ1 | 2 | 2 | Δumax | 50 | 50 |
| λ2 | 0.1 | 1 | ymin | 70 | 70 |
| κ1 | 10 | 10 | ymax | 150 | 150 |
| κ2 | 1 | 1 |
Table 2:
Tuning parameters for UKF
| Parameter | Value |
|---|---|
| Po | 1 × 10−3 |
| Qe | 1 × 10−4 |
| Re | 1 × 102 |
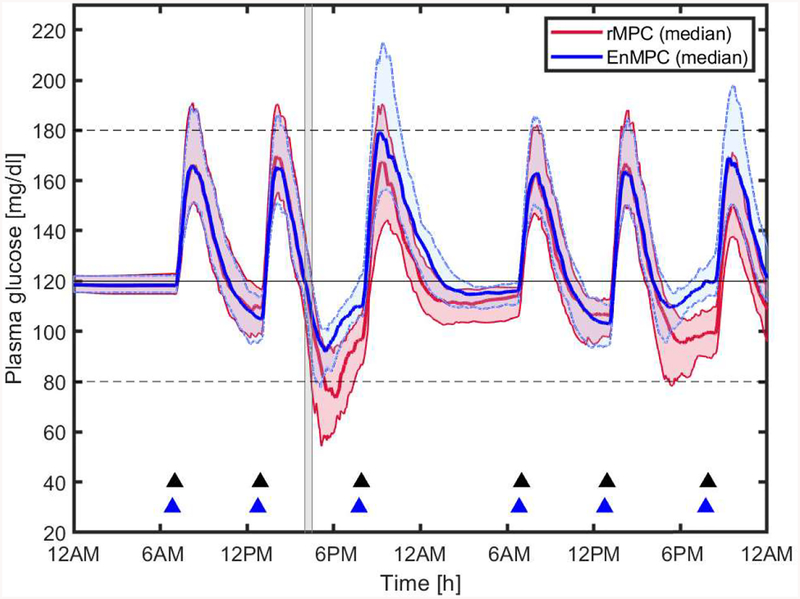
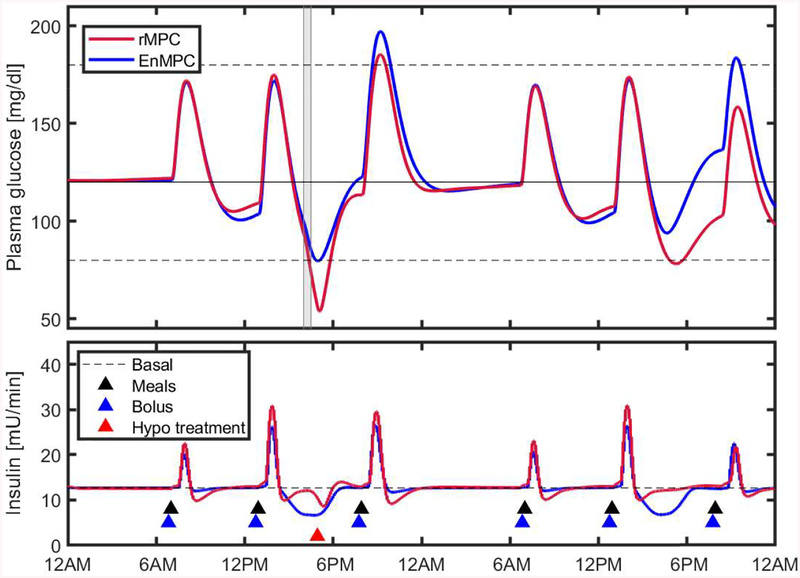
Figure 6 shows the median and interquartile range (25% - 75%) of all virtual subjects for the 48-h AP session. This figure shows the benefit of the control scheme in anticipating the exercise bout according to the behavioral profile of the different subjects. Although not shown in this figure, almost all subjects needed hypoglycemic treatments (15g fast absorption carbohydrates) when using rMPC. Figure 7 shows the time course of BG and insulin traces during the trial for subject # 5. The proposed scheme resulted in a significant improvement of glycemic control even in presence of exercise, maintaining the subjects in the safe zone most of the time.
Figure 6:
Blood Glucose control performance of rMPC (baseline) and EnMPC Median and Interquartile BG plot for 50 virtual subjects from the UVA/Padova Simulator. Solid black line represents the set point (120 mg/dL), dotted black lines the safe glycemic range, gray area the exercise period, and blue and black triangles the bolus insulin and meals, respectively. Blue and red regions show the space between the 25% and 75% quartiles of the BG at every sample for EnMPC and rMPC, respectively.
Figure 7:
Blood Glucose control performance of rMPC (baseline) and EnMPC for a representative subject (patient # 5). Solid black line represents the set point (120 mg/dL), dotted black lines the safe glycemic range (80 – 180 mg/dL), gray area the exercise period, and blue and black triangles the bolus insulin and meals, respectively, sample. Hypo treatment is needed for the subject under rMPC.
The results of the in silico experiment, presented in Table 3, show that there was a significant reduction in hypoglycemia (% Time < 50, 60, 70 mg/dL) under EnMPC control in comparison to the rMPC, without any significant change in time in range (% Time (70, 140) & (70, 180)) and hyperglycemia (% Time > 180, 250, 300 mg/dL).
Table 3:
Time-in-range metrics for the 48-h in silico trial rMPC vs EnMPC.
| rMPC | EnMPC | P | |
|---|---|---|---|
| Time <50 mg/dL (%) | 0.42 ± 0.98 | 0.05 ± 0.18 | 0.0042* |
| Time <60 mg/dL (%) | 1.53 ±2.00 | 0.25 ± 0.59 | 0.0000* |
| Time <70 mg/dL (%) | 3.08 ± 3.55 | 0.78 ± 2.04 | 0.0000* |
| Time in range (70, 140) mg/dL | 74.05 ± 12.36 | 71.78 ± 11.41 | 0.3043 |
| Time in range (70, 180) mg/dL | 92.41 ± 8.28 | 92.81 ± 8.65 | 0.4239 |
| Time >180 mg/dL (%) | 4.51 ± 6.76 | 6.41 ± 8.16 | 0.4670 |
| Time >250 mg/dL (%) | 0.00 ± 0.00 | 0.00 ± 0.00 | - |
| Time >300 mg/dL (%) | 0.00 ± 0.00 | 0.00 ± 0.00 | - |
| Variability (SD) | 25.4984 ± 9.89 | 24.4473 ± 10.27 | 0.5059 |
| Variability (CV) | 0.2083 ± 0.08 | 0.1883 ± 0.08 | 0.1648 |
(P<0.05)
While using the EnMPC subjects experienced less hypoglycemia with an improvement of time < 70 mg/dL from 3.08% to 0.78%. Additionally, time < 60 was reduced from 1.53% to 0.25% and < 50 decreased by 0.37% under EnMPC control.
Mean time in range (70, 180 mg/dL) across all in silico subjects using the EnMPC was 92.81%, which is not significantly different from those using the baseline rMPC controller. Both controllers produced similar time in range values (70, 140 mg/dL), with the EnMPC achieving 71.78% time in the 70 to 140 mg/dL range. Additionally, there was no increase in time > 180, 250, 300 mg/dL. While using the EnMPC on average subjects experienced glucose values > 180 mg/dL 6.41% of the time and no values > 250 mg/dL.
6. Discussion
The novel EnMPC-based strategy offers the possibility of anticipating mar jor glycemic disturbances, in this case physical activity, leading to significant improvements in hypoglycemia protection. Personalization of the underlying model of the EnMPC in combinations with the exercise-induced net effect signatures enhances the controller’s ability to tackle the daily challenges a person with T1D must face, including exercise which is of paramount importance for an optimal long-term glucose control.
The key to the success of the EnMPC approach can be attributed to three main factors, (i) individualized insulin-glucose models, (ii) characterization of exercise as a subject-specific behavioral and physiological pattern, (iii) a robust MPC approach to account for different possible scenarios. Moreover, the EnMPC is equipped with an asymmetric cost function for fast recovery when BG values are below the hypoglycemic threshold (70 mg/dL) and a smooth but efficient scaling for excursions above the safe-to-control range (150 mg/dL). To enhance the safety of the algorithm we employed a time-varying exponential reference signal when BG values are out the target range, giving priority to fast recovery from hypoglycemic events.
The designed in silico protocol allows for a broad assessment of the proposed control strategy and, as such experiments are accepted as replacement for animal trials in pre-clinical demonstration of safety and efficacy by the US regulatory bodies, can directly lead to human subjects experiments. While further experiments testing edge cases and robustness would further our understanding of the strategy’s performances, the validity of the presented results is supported by our FDA-accepted simulation platform which includes a model of the impact of a mild to moderate exercise on subjects with T1D during the transition from the absorptive to the post-absorptive state (> 3–4 h after a meal).
The effectiveness of the proposed scheme was demonstrated both graphically and statistically, where a significant improvement on hypoglycemia prevention without a significant deterioration of the time-in-range was shown in comparison to the baseline controller. It is also worth emphasizing that no hypoglycemic events were recorded while using the EnMPC.
While these results are promising, it is important to acknowledge the limitations of the study its methods. First, although individualized, the mathematical model used is linearized around the set point which may deteriorate the predictive ability of the model. This impacts both the controller’s performance and the characterization of the patient’s behavior through the net effect. Second, we assumed that the patients consistently exercised around the same time (±15 min from the scheduled time), and such limitation in the testing scheme would need to be removed prior to use in vivo. Finally, some conditions were not accounted for in silico such as meal absorption with different macro nutrient compositions, sensor drift, stress, etc. Therefore, additional validations and fine tuning are likely to be necessary before transitioning to in vivo studies.
7. Conclusion
This paper presents a personalized control strategy for hypoglycemia avoidance during and after a mild to moderate 30-min exercise bout for subjects with T1D. The control algorithm was successfully tested in silico using a set of 50 virtual patients with a representative parameter distribution from the UVA/Padova metabolic simulator. The success of the proposed control scheme lies on the identification of the exercise-related behavioral pattern of the individual through the use of the exercise-induced net effect signals and the robustness of the EnMPC to account for multiple possible scenarios.
Numerical simulations demonstrate the ability of the EnMPC to predict the exercise and hence to avoid hypoglycemia during and after exercise when compared to a baseline controller. No significant increase of time in hyperglycemia (> 180 mg/dL) was found in spite of the protective action of the controller. Finally, the controller was able to cope with the long term effect of exercise on insulin sensitivity (~16/h after the exercise bout). Further studies would be required to test greater variability in exercise timing and proportions of days of exercise-no exercise in a week to enlarge the domain of validity of the control scheme and hence give a step forward towards an ambulatory validation.
Highlights.
Subject’s exercise behavior is characterized through the net effect method.
Hypoglycemia prevention during and after a single moderate exercise bout.
Asymmetric objective function to cope with hypoglycemia.
In silico testing through the last version of the FDA-accepted UVa/Padova simulator.
Acknowledgments
This work has been supported by the National Institutes of Health (NIH) under Grant 1DP3DK106826–01.
Appendix A.
Table A.4:
Parameters of SOGMM with population values
| Symbol | Meaning | Value | Units |
|---|---|---|---|
| Sg | fractional glucose effectsiveness | 0.01000 | 1/min |
| Vg | distribution volume of glucose | 1.6000 | kg/dl |
| kabs | rate constant - oral glucose consumption | 0.01193 | 1/min |
| kτ | time constant related with oral glucose absorption | 0.08930 | 1/min |
| p2 | rate constant of the remote insulin compartment | 0.02000 | 1/min |
| f | fraction of intestinal absorption | 0.90000 | - |
| VI | distribution volume of insulin | 0.06005 | 1/kg |
| kcl | rate constant of subcutaneous insulin transport | 0.16000 | 1/min |
| kd | rate constant of subcutaneous insulin transport | 0.02000 | 1/min |
| SI | insulin sensitivity | 6 × 10−4 | 1/min per mU/1 |
| BW | body weight | known | kg |
| Gb | basal glucose concentration | Eq. (3) | mg/dl |
| Ib | Reference value for I(t), associated with the fasting plasma glucose concentration | steady- state |
mU/1 |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Disclosure Statement
MDB consults for Roche Diagnostics, Sanofi-Aventis, and Ascensia Diabetes Care; receives research support from Dexcom, Senseonics, Tandem, Roche Diagnostics, Sanofi-Aventis, and Ascensia Diabetes Care; and holds equity in TypeZero Technologies. JGT and JC report no competing financial interests.
References
- [1].Association AD, et al. , Diagnosis and classification of diabetes mellitus, Diabetes care 37 (Supplement 1) (2014) S81–S90. [DOI] [PubMed] [Google Scholar]
- [2].Hirsch IB, Insulin analogues, New England Journal of Medicine 352 (2) (2005) 174–183. [DOI] [PubMed] [Google Scholar]
- [3].Klonoff DC, Prahalad P, Performance of cleared blood glucose monitors, Journal of diabetes science and technology 9 (4) (2015) 895–910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Castle JR, Jacobs PG, Nonadjunctive use of continuous glucose monitoring for diabetes treatment decisions, Journal of diabetes science and technology 10 (5) (2016) 1169–1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].D. Control, C. T. of Diabetes Interventions, C. D. S. R. Group, Intensive diabetes treatment and cardiovascular disease in patients with type 1 diabetes, New England Journal of Medicine 353 (25) (2005) 2643–2653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Secrest AM, Becker DJ, Kelsey SF, LaPorte RE, Orchard TJ, All-cause mortality trends in a large population-based cohort with longstanding childhood-onset type 1 diabetes: the allegheny county type 1 diabetes registry, Diabetes care 33 (12) (2010) 2573–2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lind M, Svensson A-M, Kosiborod M, Gudbjornsdottir S, Pivodic A, Wedel H, Dahlqvist S, Clements M, Rosengren A, Glycemic control and excess mortality in type 1 diabetes, New England Journal of Medicine 371 (21) (2014) 1972–1982. [DOI] [PubMed] [Google Scholar]
- [8].Nishimura R, LaPorte RE, Dorman JS, Tajima N, Becker D, Orchard TJ, Mortality trends in type 1 diabetes: the allegheny county (Pennsylvania) registry 1965–1999, Diabetes care 24 (5) (2001) 823–827. [DOI] [PubMed] [Google Scholar]
- [9].Brazeau A, Leroux C, Mircescu H, Rabasa-Lhoret R, Physical activity level and body composition among adults with type 1 diabetes, Diabetic Medicine 29 (11) (2012) e402–e408. [DOI] [PubMed] [Google Scholar]
- [10].McMahon SK, Ferreira LD, Ratnam N, Davey RJ, Youngs LM, Davis EA, Fournier PA, Jones TW, Glucose requirements to maintain euglycemia after moderate-intensity afternoon exercise in adolescents with type 1 diabetes are increased in a biphasic manner, The Journal of Clinical Endocrinology & Metabolism 92 (3) (2007) 963–968. [DOI] [PubMed] [Google Scholar]
- [11].Goodyear LJ, Kahn BB, Exercise, glucose transport, and insulin sensitivity, Annual review of medicine 49 (1) (1998) 235–261. [DOI] [PubMed] [Google Scholar]
- [12].Younk LM, Mikeladze M, Tate D, Davis SN, Exercise-related hypoglycemia in diabetes mellitus, Expert review of endocrinology & metabolism 6 (1) (2011) 93–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Davey RJ, Howe W, Paramalingam N, Ferreira LD, Davis EA, Fournier PA, Jones TW, The effect of midday moderate-intensity exercise on postexercise hypoglycemia risk in individuals with type 1 diabetes, The Journal of Clinical Endocrinology & Metabolism 98 (7) (2013) 2908–2914. [DOI] [PubMed] [Google Scholar]
- [14].D. R. in Children Network (DirecNet) Study Group, et al. , Impact of exercise on overnight glycemic control in children with type 1 diabetes mellitus, The Journal of pediatrics 147 (4) (2005) 528–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Lascar N, Kennedy A, Hancock B, Jenkins D, Andrews RC, Greenfield S, Narendran P, Attitudes and barriers to exercise in adults with type 1 diabetes (t1dm) and how best to address them: a qualitative study, PLoS One 9 (9) (2014) e108019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Kennedy A, Narendran P, Andrews RC, Daley A, Greenfield SM, Attitudes and barriers to exercise in adults with a recent diagnosis of type 1 diabetes: a qualitative study of participants in the exercise for type 1 diabetes (extod) study, BMJ open 8 (1) (2018) e017813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Toni S, Reali MF, Barni F, Lenzi L, Festini F, Managing insulin therapy during exercise in type 1 diabetes mellitus, Acta Biomed 77 (Suppl 1) (2006) 34–40. [PubMed] [Google Scholar]
- [18].Riddell MC, Milliken J, Preventing exercise-induced hypoglycemia in type 1 diabetes using real-time continuous glucose monitoring and a new carbohydrate intake algorithm: an observational field study, Diabetes technology & therapeutics 13 (8) (2011) 819–825. [DOI] [PubMed] [Google Scholar]
- [19].Brazeau A-S, RabasarLhoret R, Strychar I, Mircescu H, Barriers to physical activity among patients with type 1 diabetes, Diabetes care 31 (11) (2008) 2108–2109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Riddell MC, Gallen IW, Smart CE, Taplin CE, Adolfsson P, Lumb AN, Kowalski A, RabasarLhoret R, McCrimmon RJ, Hume C, et al. , Exercise management in type 1 diabetes: a consensus statement, The Lancet Diabetes & Endocrinology 5 (5) (2017) 377–390. [DOI] [PubMed] [Google Scholar]
- [21].Colberg SR, Sigal RJ, Yardley JE, Riddell MC, Dunstan DW, Dempsey PC, Horton ES, Castorino K, Tate DF, Physical activity/exercise and diabetes: a position statement of the american diabetes association, Diabetes Care 39 (11) (2016) 2065–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Rooijackers HM, Wiegers EC, Van Der Graaf M, Thijssen DH, Kessels RP, Tack CJ, De Galan BE, A single bout of high-intensity interval training reduces awareness of subsequent hypoglycemia in patients with type 1 diabetes, Diabetes 66 (7) (2017) 1990–1998. doi: 10.2337/db16-1535. [DOI] [PubMed] [Google Scholar]
- [23].Hovorka R, Allen JM, Elleri D, Chassin LJ, Harris J, Xing D, Kollman C, Hovorka T, Larsen AMF, Nodale M, et al. , Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: a phase 2 randomised crossover trial, The Lancet 375 (9716) (2010) 743–751. [DOI] [PubMed] [Google Scholar]
- [24].Anderson SM, Raghinaru D, Pinsker JE, Boscari F, Renard E, Buckingham BA, Nimri R, Doyle FJ, Brown SA, Keith-Hynes P, et al. , Multinational home use of closed-loop control is safe and effective, Diabetes Care 39 (7) (2016) 1143–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Thabit H, Hovorka R, Coming of age: the artificial pancreas for type 1 diabetes, Diabetologia 59 (9) (2016) 1795–1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Kovatchev B, Tamborlane WV, Cefalu WT, Cobelli C, The artificial pancreas in 2016: a digital treatment ecosystem for diabetes, Diabetes Care 39 (7) (2016) 1123–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Bergenstal RM, Garg S, Weinzimer SA, Buckingham BA, Bode BW, Tamborlane WV, Kaufman FR, Safety of a hybrid closed-loop insulin delivery system in patients with type 1 diabetes, Jama 316 (13) (2016) 1407–1408. [DOI] [PubMed] [Google Scholar]
- [28].Schiavon M, Man CD, Kudva YC, Basu A, Cobelli C, In silico optimization of basal insulin infusion rate during exercise: implication for artificial pancreas, Journal of Diabetes Science and Technology 7 (6) (2013) 1461–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Gondhalekar R, Dassau E, Zisser HC, Doyle FJ, Periodic-zone model predictive control for diurnal closed-loop operation of an artificial pancreas, Journal of Diabetes Science and Technology 7 (6) (2013) 1446–1460. doi: 10.1177/193229681300700605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Boiroux D, Duun-Henriksen AK, Schmidt S, Nørgaard K, Poulsen NK, Madsen H, Jørgensen JB, Adaptive control in an artificial pancreas for people with type 1 diabetes, Control Engineering Practice 58 (2016) 2115–2120. doi: 10.1016/j.conengprac.2016.01.003. [DOI] [Google Scholar]
- [31].Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Benedetti M, Orsini Federici M, Pieber TR, Schaller HC, Schaupp L, Vering T, Wilinska ME, Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes., Physiological measurement 25 (4) (2004) 905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
- [32].Magni L, Raimondo DM, Bossi L, Man CD, De Nicolao G, Kovatchev B, Cobelli C, Model predictive control of type 1 diabetes: an in silico trial., Journal of diabetes science and technology 1 (6) (2007) 804–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Clarke WL, Anderson S, Breton M, Patek S, Kashmer L, Kovatchev B, Closed-Loop Artificial Pancreas Using Subcutaneous Glucose Sensing and Insulin Delivery and a Model Predictive Control Algorithm: The Virginia Experience, Journal of Diabetes Science and Technology 3 (5) (2009) 1031–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Bruttomesso D, Farret A, Costa S, Marescotti MC, Vettore M, Avogaro A, Tiengo A, Dalla Man C, Place J, Facchinetti A, Guerra S, Magni L, De Nicolao G, Cobelli C, Renard E, Maran A, Closed-Loop Artificial Pancreas Using Subcutaneous Glucose Sensing and Insulin Delivery and a Model Predictive Control Algorithm: Preliminary Studies in Padova and Montpellier, Journal of Diabetes Science and Technology 3 (5) (2009) 1014–1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Hughes CS, Patek SD, Breton M, Kovatchev BP, Anticipating the next meal using meal behavioral profiles: A hybrid model-based stochastic predictive control algorithm for T1DM, Computer Methods and Programs in Biomedicine 102 (2) (2011) 138–148. arXiv:NIHMS150003, doi: 10.1016/j.cmpb.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Rawlings JB, Mayne DQ, Model Predictive Control: Theory And Design, Nob Hill Pub. Madison, Wisconsin, 2009. [Google Scholar]
- [37].Huyett LM, Ly TT, Forlenza GP, Reuschel-DiVirgilio S, Messer LH, Wadwa RP, Gondhalekar R, Doyle FJ III, Pinsker JE, Maahs DM, et al. , Outpatient closed-loop control with unannounced moderate exercise in adolescents using zone model predictive control, Diabetes technology & therapeutics 19 (6) (2017) 331–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Pinsker JE, Laguna Sanz AJ, Lee JB, Church MM, Andre C, Lindsey LE, Doyle FJ III, Dassau E, Evaluation of an artificial pancreas with enhanced model predictive control and a glucose prediction trust index with unannounced exercise, Diabetes technology & therapeutics 20 (7) (2018) 455–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Patek SD, Lv D, Ortiz EA, Hughes-Karvetski C, Kulkarni S, Zhang Q, Breton MD, Empirical representation of blood glucose variability in a compartmental model, in: Prediction Methods for Blood Glucose Concentration, Springer, 2016, pp. 133–157. [Google Scholar]
- [40].Cobelli C, Man CD, Sparacino G, Magni L, Nicolao GD, Kovatchev BP, Diabetes: Models, signals, and control, IEEE Reviews in Biomedical Engineering 2 (2009) 54–96. doi: 10.1109/RBME.2009.2036073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Boiroux D, Hagdrup M, Mahmoudi Z, Poulsen K, Madsen H, Jørgensen JB, An ensemble nonlinear model predictive control algorithm in an artificial pancreas for people with type 1 diabetes, in: European Control Conference (ECC), IEEE, 2016, pp. 2115–2120. [Google Scholar]
- [42].Forlenza GP, Deshpande S, Ly TT, Howsmon DP, Cameron F, Baysal N, Mauritzen E, Marcal T, Towers L, Bequette BW, et al. , Application of zone model predictive control artificial pancreas during extended use of infusion set and sensor: a randomized crossover-controlled home-use trial, Diabetes Care (2017) dc170500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Laguna Sanz AJ, Doyle FJ III, Dassau E, An enhanced model predictive control for the artificial pancreas using a confidence index based on residual analysis of past predictions, Journal of diabetes science and technology 11 (3) (2017) 537–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Oviedo S, Vehi J, Calm R, Armengol J, A review of personalized blood glucose prediction strategies for t1dm patients, International journal for numerical methods in biomedical engineering 33 (6) (2017) e2833. [DOI] [PubMed] [Google Scholar]
- [45].Zarkogianni K, Mitsis K, Litsa E, Arredondo M-T, Fico G, Fioravanti A, Nikita KS, Comparative assessment of glucose prediction models for patients with type 1 diabetes mellitus applying sensors for glucose and physical activity monitoring, Medical & biological engineering & computing 53 (12) (2015) 1333–1343. [DOI] [PubMed] [Google Scholar]
- [46].Garcia-Tirado J, Zuluaga-Bedoya C, Breton MD, Identifiability analysis of three control-oriented models for use in artificial pancreas systems, J Diabetes Sci Technol 12 (5)(2018) 937–952. doi: 10.1177/1932296818788873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ruan Y, Wilinska ME, Thabit H, Hovorka R, Modeling Day-to-Day Variability of Glucose-Insulin Regulation Over 12-Week Home Use of Closed-Loop Insulin Delivery, IEEE Transactions on Biomedical Engineering 64 (6) (2017) 1412–1419. doi: 10.1109/TBME.2016.2590498. [DOI] [PubMed] [Google Scholar]
- [48].Visentin R, Campos-Náñez E, Schiavon M, Lv D, Vettoretti M, Breton M, Kovatchev BP, Dalla Man C, Cobelli C, The UVA/Padova Type 1 Diabetes Simulator Goes From Single Meal to Single Day, Journal of Diabetes Science and Technology 0 (0) (2018) 1–9. doi: 10.1177/1932296818757747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Julier SJ, Uhlmann JK, Durrant-Whyte HF, A new approach for filtering nonlinear systems, in: American Control Conference, Proceedings of the 1995, Vol. 3, IEEE, 1995, pp. 1628–1632. [Google Scholar]
- [50].Julier SJ, Uhlmann JK, New extension of the kalman filter to nonlinear systems, in: AeroSense’97, International Society for Optics and Photonics, 1997, pp. 182–193. [Google Scholar]
- [51].Julier S, Uhlmann J, Durrant-Whyte HF, A new method for the nonlinear transformation of means and covariances in filters and estimators, IEEE Transactions on automatic control 45 (3) (2000) 477–482. [Google Scholar]
- [52].Simon D, Optimal state estimation: Kalman, H infinity, and nonlinear approaches, John Wiley k, Sons, 2006. [Google Scholar]
- [53].Boiroux D, Finan DA, Jørgensen JB, Poulsen NK, Madsen H, Optimal Insulin Administration for People with Type 1 Diabetes, Vol. 43, IFAC, 2010. doi: 10.3182/20100705-3-BE-2011.00041. [DOI] [Google Scholar]
- [54].Boiroux D, Duun-Henriksen AK, Schmidt S, Nørgaard K, Madsbad S, Poulsen NK, Madsen H, Jørgensen JB, Overnight glucose control in people with type 1 diabetes, Biomedical Signal Processing and Control 39 (2018) 503–512. [Google Scholar]
- [55].Lucia S, Andersson JA, Brandt H, Diehl M, Engell S, Handling uncertainty in economic nonlinear model predictive control: A comparative case study, Journal of Process Control 24 (8) (2014) 1247–1259. [Google Scholar]
- [56].Martí R, Lucia S, Sarabia D, Paulen R, Engell S, de Prada C, Improving scenario decomposition algorithms for robust nonlinear model predictive control, Computers & Chemical Engineering 79 (2015) 30–45. [Google Scholar]