Tumor Growth Dynamic Modeling in Oncology Drug Development and Regulatory Approval: Past, Present, and Future Opportunities

Abstract

Model‐informed drug development (MIDD) approaches have rapidly advanced in drug development in recent years. Additionally, the Prescription Drug User Fee Act (PDUFA) VI has specific commitments to further enhance MIDD. Tumor growth dynamic (TGD) modeling, as one of the commonly utilized MIDD approaches in oncology, fulfills the purposes to accelerate the drug development, to support new drug and biologics license applications, and to guide the market access. Increasing knowledge of TGD modeling methodologies, encouraging applications in clinical setting for patients’ survival, and complementing assessment of regulatory review for submissions, together fueled promising potentials for imminent enhancement of TGD in oncology. This review is to comprehensively summarize the history of TGD, and present case examples of the recent advance of TGD modeling (mixture model and joint model), as well as the TGD impact on regulatory decisions, thus illustrating challenges and opportunities. Additionally, this review presents the future perspectives for TGD approach.

Model‐informed drug development (MIDD) approaches have advanced rapidly in drug development in recent years. Additionally, the Prescription Drug User Fee Act (PDUFA) VI has specific commitments to further enhance MIDD. Tumor growth dynamic (TGD) modeling, as one of the commonly utilized MIDD approaches in oncology, fulfills the purposes to accelerate the drug development, to support new drug and biologics license applications, and to guide the market access. ¹ TGD modeling’s scope includes the assessment of tumor growth inhibition/tumor shrinkage and tumor re‐growth, and their potential as surrogates of predicting the survival probability with the cancer treatment.

The TGD approach has been utilized across various drug development stages. In preclinical and translational stages, it was used to select promising drug candidates, to assist the pharmacological projection of the starting human dose in first‐in‐human trials, and to leverage clinical cancer patient data. ¹ TGD models have also been applied in early and late stages of clinical development. ² , ³ During the phase 1/II stage, TGD can support early clinical decisions (i.e., “Go/No‐go” decisions for moving to phase III), via predicting survival outcomes using the longitudinal tumor size data as the surrogate metrics. ⁴ Additionally, TGD can also address the medical concerns in clinical practice, such as the impact of clinical covariates by quantifying the effects of genotype variations on patient response. ⁵ In addition, TGD models have been applied to identify the sub‐patient populations who would benefit the most for an intended treatment. ⁶ Further, models based on tumor growth data obtained from patients can help in deciding on the optimal dose and dosing algorithms for individual patients during market access.

At the recent American Conference on Pharmacometrics (ACoP) Annual Meeting in 2018, a systematic presentation of TGD, including its history and utilities, ⁷ were discussed in a symposium, thus illustrating challenges and opportunities. Subsequently, several research articles were published, focusing on specific areas of TGD models, such as tumor resistance models, ⁸ and expansion of joint model with new lesions. ⁹ This review is to present the comprehensive view of TGD, from its origin, to advanced mathematical methodologies, to its applications in clinical development, and to regulatory authorization. The presentations and the discussions now are summarized in this review. Additionally, this review presents the future perspectives for the TGD approach, including its innovated applications during the unprecedented coronavirus disease 2019 (COVID‐19) pandemic.

TGD MODEL DEVELOPMENT HISTORY

The history of TGD modeling can be tracked to the early 1930s, when Mayneord ¹⁰ modeled rat sarcomas and found a linear model best fits the data, and Schreck ¹¹ followed up with modeling Walker tumors in rats and confirmed the linear growth rate. After a big quiet gap between the 1930s and 1950s, observed clinical tumor doubling times suggested exponential growth of tumors instead of linear. ¹² , ¹³ Around 1961, Schwartz ¹⁴ had conducted, for the first time, a mathematically rigorous examination of human tumor growth kinetics, and proposed a differential equation model that the rate of tumor growth was proportional to the current tumor size. Based on this first‐order growth model, some flexibilities were added to the model to incorporate both exponential and linear growth by varying the value of exponent on the current tumor size between 0 and 1. ¹⁵ However, this model was yet to explain why the tumor growth rate slowed down as the tumor grows larger. Four years later, Laird ¹⁶ overcame this limitation by using a Gompertz model, which included the maximum size to which the tumor can grow, namely the carrying capacity in the model. The Gompertz model is still an exponential growth model, but its rate of growth is no longer a constant as in the model proposed by Schwartz, and is exponentially decreasing with time as well. The Gompertz model is more biologically sound to describe the profiles of tumor growth than previous models, and its first application for human tumor data was for patients with multiple myeloma by Sullivan and Salmon in 1972. ¹⁷ Besides the Gompertz model, the logistic model and Bertalanffy model were also proposed to explain the slowing‐down phenomenon of tumor growth, whereas the Gompertz model and logistic model used different inflection points. Basically, all these models can be written as a generalized two‐parameter growth model, ¹⁸ dV/dt = aV^α‐bV^β, which incorporates two processes, tumor growth and cell death.

The inhibitory effect of chemotherapy was modeled by Jusko ¹⁹ based on Skipper‐Schabel‐Wilcox model ²⁰ to irreversibly reduce tumor size by a constant fraction. Later, Norton and Simon ²¹ refined the Skipper‐Schabel‐Wilcox model with Gompertz model, and the death rate in response to treatment is considered to be directly proportional to the growth rate at the time of treatment. The drug effect in these models assume that cell killing is directly related to drug concentrations, however, it fails to account for important aspects, including the lag time between drug concentrations and continuous cell death when drug concentrations become zero. Lobo and Balthasar ²² used transit‐compartment model to describe the delay the time course of cell killing, relative to the time course of drug exposure. Other similar models incorporated delay effects, including the model by Simeoni et al. ²³ in 2004, which accounted for delays after cessation of drug therapy, and the model by Bueno et al. ²⁴ in 2008, which used a biomarker delay to account for the drug effect. Kay et al. (2012) applied an upstream and downstream compartment to account for the delays, and Tate et al. ²⁵ used a modified Simeoni model to account for biomarker delays and to split the tumor into growing cells and drug‐resistant cells.

Besides these ordinary differential equation (ODE) or algebraic models, partial differential equation models, such as multiscale models and agent‐based models, have been used in the history of TGD modeling. In contrast to ODE models, which assumed that drug concentration is homogenous within a compartment, partial differential equation models assumed drug concentrations vary in time and space, and could incorporate the compound’s biopharmaceutical characteristics into the models (e.g., diffusion coefficient, vascular and/or cellular permeability, and surface area) to reflect the biological and pharmacological mechanistic. Multiscale models ²⁶ applied quantitative system pharmacology principles to model TGD over time and considered microscale and macroscale time. Gerlee and Anderson ²⁷ associated background oxygen concentration and matrix density to the tumor growth rate and its morphology; Macklin et al. ²⁸ published microscopic‐macroscopic composite models of tumor‐induced angiogenesis and growth response in 2009. Generally, agents in agent‐based models are independent, not centrally governed, heterogeneously active, or adaptive. Agent‐based models are discrete event models and were used to model the complex behavior of individuals, spread of epidemics, population dynamics, and human immune system to provide more details of biology of tumor at individual level. In 2017, Jalalimanesh et al. ²⁹ performed simulation‐based optimization of radiotherapy based on agent‐based modeling and reinforcement learning.

Clinically, modeling human tumor growth is challenging due to between subject variability, responders vs. nonresponders, therapy‐induced resistance, and the difficult to estimate resistance or regrowth parameters in the model because of censoring. Wang et al. ³ modeled tumor growth of 3,398 patients with non‐small cell lung cancer from 4 registration trials (bevacizumab, docetaxel, erlotinib, and pemetrexed), which included 8 active treatments and 1 placebo regimens. The tumor growth was modeled with the combination of exponential shrinkage and linear regrowth. Overall survival (OS) was also modeled as a function of change in tumor size at week 8, however, drug effect was not captured in the model. A similar approach was utilized by Claret et al. ³⁰ in 2009 to model tumor growth inhibition in both phase II (n = 34) and phase III (n = 252) trials of capecitabine, and the relationship between change in tumor size at week 7 and OS in patients with first‐line advanced or metastatic colorectal cancer. Drug exposure was included as an effect on tumor shrinkage in Claret’s model to describe tumor growth inhibition. Although different types of tumor growth models could describe the same tumor growth profile, the selection of biologically appropriate TGD models should address the pertinent question. Currently, most TGD models are ODEs or algebraic function forms, especially within the pharmacokinetic/pharmacodynamic field. The summary of key equations of these models can be found in Supplementary Table S1 . The biggest challenge in TGD modeling is how to translate preclinical models to clinical application, which requires deeper understanding across biological species and efficient implementation mathematically.

MIXTURE OF TUMOR GROWTH DYNAMIC MODELING OF IMMUNO‐ONCOLOGY AND CHEMOTHERAPY AGENTS

The new era of immuno‐oncology therapy warrants new thinking and methodologies to evaluate the TGD of patients with cancer. Unlike chemotherapy, patients with immunotherapy, such as checkpoint inhibitors, demonstrated unique tumor dynamics profiles, in which tumor shrinkage occurs initially and then maintains at the steady‐state tumor burden level for a long time in those patients with stable disease, partial response, or complete response. Many previous published TGD models ³ , ³¹ assumed a uniformed pattern of tumor dynamic, which limited its capability of describing the unique tumor dynamic pattern for immunotherapy. It is important to extend the previous TGD modeling work to better account for the heterogeneity in tumor response of immunotherapy. Mixture of models is an appropriate approach, which enable the description of differentiated TGD patterns as subpopulations.

Ipilimumab phase III CA184169 study ³² was used to demonstrate such an example. Both the characterization of tumor profile using longitudinal tumor size data and its association with OS were evaluated. The flow chart of TGD model development is presented in Figure 1 . Nonmixture model was first developed using previous published TGD models. ³ , ³¹ The uniformed pattern of tumor dynamic modeling structure was used to describe the time‐course of target tumor burden, in which the formula included function of time using a combination of terms for tumor shrinkage and growth. For example, the two components (shrinkage and growth) described in the published Wang ³ model, in which the term describing growth ($\text{TG}\times t$) increases over time, and whereas the term describing shrinkage (${\text{TB}}_0\times e^{‐\text{TS}\times t})$ approaches the value of zero, over time. Therefore, this model is mathematically unable to describe the scenario where the tumor burden only decreases with time and never grows.

Figure 1.

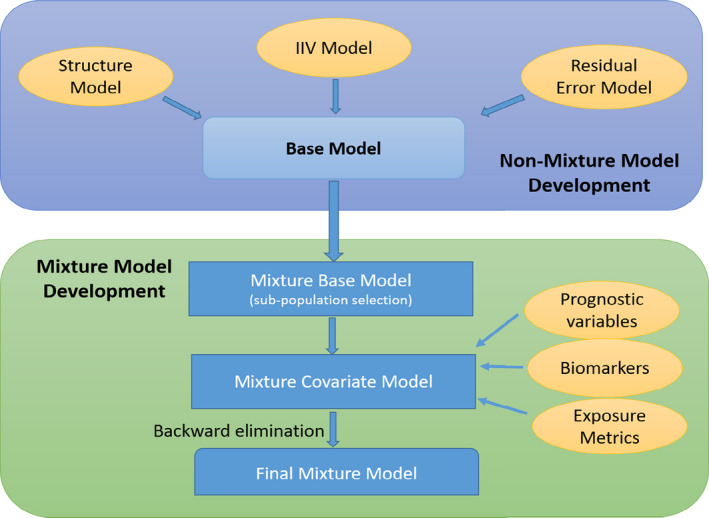
Schematic overview of tumor growth dynamic (TGD) model development. *Note: The flow chart provided schematic overview of TGD model development. The steps could be modified depending on the questions to be addressed by TGD model. Bayesian information criterion (BIC) is used as model selection criteria. Various published function forms are explored in nonmixture model development, together with the assessment of interindividual variability and residual error models. The best nonmixture model (model with lowest BIC) is used to guide the development of mixture base model. Covariates including subjects’ baseline characteristics (e.g., age and body weight), exposure metrics (e.g., minimum concentration (C_min), maximum concentration (C_max)) and laboratory and/or biomarker assessment (e.g., albumin, lactate dehydrogenase) are included in the full model to assess their effect on TGD parameters. Final mixture model might be development using backward elimination approach.

To address this limitation, we implemented a mixture version of the Wang ³ model that allows for differences in parameter distributions in each mixture population, as well as a modified structural model in one of the subpopulations (the “no growth” subpopulation) in which the growth term is replaced by a term describing the steady‐state value of tumor burden. ³³ Bayesian information criterion (BIC) was used as model selection criteria. The improvement in the fit of the data with the mixture TGD model can be clearly illustrated by a comparison of goodness‐of‐fit plots for the mixture and nonmixture TGD models. The mixture model provides a better description of observed data than the nonmixture model, particularly in the “fast” and “no growth” subpopulations. The better model performance of the mixture model is expected, given the substantial decreasing of BIC value (430 points lower) relative to that of the nonmixture model. In addition, the mixture model with three subpopulations (“fast,” “intermediate,” and “no growth”) can further improve the description of tumor dynamics as compared with the other tested models (2‐subpopulation and nonmixture models), which was selected for subsequent covariate model development to predict survival outcome of the study.

Even though ipilimumab exposure (Cavg1) was not a significant covariate on TGD model, the percentage of patients in the “intermediate” and “no growth” subpopulations were higher in the 10 mg/kg dose group than in the 3 mg/kg dose group. These results suggested that more patients might achieve durable responses at a higher dose of ipilimumab, which may also be associated with better OS in the higher ipilimumab (10 mg/kg) dose group. Therefore, in TGD‐OS analysis, various tumor metrics were assessed, including TGD parameters (tumor shrinkage and tumor growth rate), relative change in tumor burden at week 8, and progression rate at week 8 (PRW8). PRW8, derived from the first derivative of Wang model, was identified as the best predictor of OS relative to all the other tested metrics. The model evaluation showed that the OS model using a nonmixture model‐derived tumor metric was not able to provide adequate description of the OS data, which provided further evidence of better TGD‐OS model performance using tumor metrics generated from mixture TGD model. Moreover, sensitivity analysis showed that including mixture subpopulation as a covariate further improved the OS model fitness, as indicated by the lower BIC value. This suggests the prediction of risk of death was improved between subpopulations after accounting for the individual tumor metric effect on OS. In addition, it should also be noted that there is more variability in the derived PRW8 variable in the mixture model compared with the nonmixture model, and the variability tends to shrink to 0 in the nonmixture model. This leads to less differentiation for the TGD effect on OS (as evidenced by the lower BIC (by 33 points) for the OS model when the tumor response measure is derived from the TGD mixture model).

Even though the OS model using PRW8 from the mixture model provided better fit of OS data relative to the model using PRW8 from the nonmixture model, the model appears to underpredict OS at 10 mg/kg dose group. The development of the joint TGD‐OS model might be able to address the issues of lack of sensitivity in the current TGD‐OS model regarding the hazard ratio (HR) between the two treatment arms. In summary, the mixture model allows improved characterization of different patterns of tumor dynamics compared with that of the nonmixture model, especially in subjects who had long durable response with immunotherapy. More importantly, the utilization of tumor response measures from a mixture model improves the OS prediction.

JOINT MODELING OF LONGITUDINAL TUMOR SIZE AND SURVIVAL ANALYSIS IN SOLID TUMORS

The oncology clinical development community has benefited greatly from the increased standardization enabled by the Response Evaluation Criteria in Solid Tumors (RECIST), and RECIST has been used as a basis for drug development strategies and accelerated approvals through the characterization of overall response rate and progression‐free survival (PFS). ³⁴ , ³⁵ However, the same criteria are applied across a wide range of tumor types/sites and treatment modalities, despite reasonable expectations that tumor regression patterns associated with treatment benefits may vary across tumor types and therapeutic treatments. In this context, one idea to overcome the problem would be to develop a generalized statistical model to interrogate different aspects of RECIST criteria as a surrogate for the primary outcome of interest, the OS, and applying the joint model could be helpful for the aim.

The joint modeling methodology ³⁶ brings TGD and time‐to‐event data together and models them simultaneously, so that the dynamic nature of disease progression is incorporated in the modeling of OS, allowing one to assess the relative weights of each criterion in RECIST, depending on their associations with the outcome. It describes tumor size measurements over time via a random effect submodel or a latent class submodel, then links it to the progression or survival time process via a time‐varying covariate hazard submodel of the latent TGD values without measurement error, ³⁷ therefore, the TGD model plays an important role in joint models.

Data from patients treated with gefitinib or carboplatin/paclitaxel doublet chemotherapy in a phase III study (“IPASS,” NCT00322452) were used to develop a joint model using a Hamiltonian Monte Carlo Markov chain (algorithm implemented in Stan software). ⁹ Tumor size dynamics m(t) is given by a nonlinear exponential growth model: $m\left(t\right)=t\beta +{\text{sld}}_0{e}^{‐\alpha t}$, where ${\text{sld}}_0$ is the initial tumor size measured as sum of longest diameter (SLD) and the other parameters $\beta$ and $\alpha$ are empirically introduced to describe the linear growth and exponential shrinkage. Individual variabilities depending on certain covariates, including emergence of new lesion, epidermal growth factor receptor (EGFR), mutation status (positive or negative), and treatments (gefitinib or chemotherapy), were incorporated on the parameter estimates. The longitudinal tumor size $m$, its first derivative $m^{\prime }$ (rate of change), and the appearance of new lesions, were used as covariates for the proportional hazard. Baseline hazard is estimated by using a cubic spline with 6 knots, and a Gauss‐Kronrad quadrature with 13 quadrature points is used to numerically integrate the hazard to estimate patient‐specific survival. The time‐dependent risk of developing a new lesion for a patient can then be derived, given EGFR status and treatment arm. These allowed us to simulate from the distribution of tumor size trajectories, to calculate the individual predicted time‐dependent hazard. Given the predicted time‐dependent hazard, the distribution of individual survival can be estimated, in which both the disease state and the error in the estimated parameters are accounted. Therefore, a patient’s likely change in treatment following progression can be incorporated into the estimate of the hazard (Figure 2 ). This was achieved by predicting progression status, then simulating the incidence of progression as a Bernoulli random event. Following progression, TGD was estimated using a new set of patient‐course‐of‐treatment specific covariates and hyperparameters. The joint model for OS and longitudinal TGDs fits well to the observed data. Both estimated SLD and the rate of change in SLD were measurably associated with OS, whereas new‐lesion association parameters appear to have negatively impacted the OS.

Figure 2.

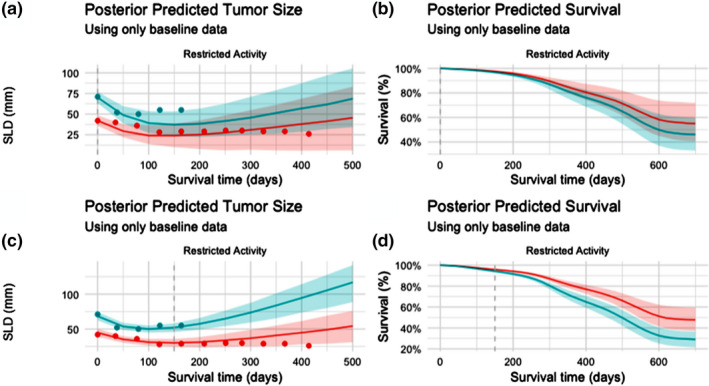
Prospective predicted tumor size and survival probabilities by subject. Prospective (i.e., out of sample) tumor size and survival projections for two subjects in the same Eastern Cooperative Oncology Group (ECOG) status and randomized treatment group (“Restricted Activity” and “Gefitinib”). Results are shown first using only data available at baseline (a‐tumor load, b‐survival), and then updated according to results after the first 150 days of treatment (c‐tumor load, d‐survival). Observed tumor size values are shown in plots a and c using points. Posterior predicted values are summarized as median value, with 50% confidence intervals shaded. SLD, sum of longest diameter.

Tumor size dynamics from a more interpretable perspective, using the same dataset, was also explored. ³⁸ The ODE model was applied, $\frac{\mathrm{d}m\left(t\right)}{\mathrm{d}t}=k_{\text{gr}}m\left(t\right)‐{\mathrm{\Delta }}_{\lambda }{e}^{‐\alpha t}m\left(t\right)$, where $k_{\text{gr}}$ is the net tumor growth rate (after the treatment effect is gone), ${\mathrm{\Delta }}_{\lambda }$ is the intensity of the initial drug efficacy, and $\alpha$ is rate of resistance emergence. The solution for the ODE is expressed as $m\left(t\right)=m_0\exp \left(k_{\text{gr}}t‐\frac{{\mathrm{\Delta }}_{\lambda }}{\alpha }\left(1‐e^{‐\alpha t}\right)\right)$, where $m_0$ is the initial tumor size. Individual variabilities on the parameters are hierarchically assumed by a patient group, which is divided by the treatments and EGFR mutation, and parameters are also estimated in Stan software. The posterior distributions of the parameters for the typical values of each group well capture the difference among groups, characterizing treatment effects, and resistance dynamics. ³⁸ The structure of the model and clearly interpretable parameters are versatile to describe a typical pattern of tumor response (initial size decrease followed by eventual regrowth) will facilitate comparison of drug effects and resistance dynamics among drugs with mechanism of action, and the use of the tumor dynamics model in joint modeling of tumor response and survival events.

This work provides an insight regarding the relative predictive value of RECIST’s components and improvements in trial design that can support bringing the next generation of therapies to market quickly, safely, and with the highest levels of efficacy.

APPLICATIONS OF TGD MODELING IN REGULATORY DECISION MAKING

Tumor growth modeling has been included in some regulatory submissions to support the treatment effectiveness and the dose selection. In oncology trials, dose reduction or interruption is often allowed due to the intolerable drug toxicities. Additionally, quite commonly, only one dosing regimen was investigated in the pivotal trial, as limited by practical issues. Further, it is unethical to study an alternative dosing regimen that may potentially lead to significant loss of efficacy or risks of safety, especially the approved dose that had demonstrated overall positive clinical benefit‐risk profiles. However, the approved dosing regimen is yet optimized. Therefore, for certain regulatory approvals, a postmarketing requirement is issued to optimize the dosing regimen to maximize the benefit‐risk in patients. TGD modeling and simulations can play a critical role in leveraging existing data from various sources, thus determining dosing regimen(s) to be evaluated in the postmarket study. ³⁹ , ⁴⁰

Lenvatinib is such an example. As a tyrosine‐kinase inhibitor, it was originally approved as a first‐line therapy to treat the differentiated thyroid cancer. Subsequently, it was approved for the treatment of advanced or metastatic renal cell carcinoma as a second‐line therapy in combination with everolimus. The approved dose is 18 milligrams lenvatinib plus 5 milligrams everolimus once daily. In the pivotal trial, patients in the lenvatinib‐everolimus combination arm showed significant improvement in PFS as compared with the lenvatinib and everolimus monotherapy. ⁴¹ However, 89% of the patients in the combination arm experienced a dose reduction or interruption due to the drug toxicity, indicating the approved dose may not be optimal for the vast majority of patients. Therefore, the US Food and Drug Administration (FDA) requested a postmarketing study aiming to explore alternative dosing regimens. The FDA reviewers and scientists from industry conducted a complex pharmacokinetic/pharmacodynamic modeling to identify the alternative dose with a better benefit risk profile. Exposure‐response relationship for the time course of tumor size and adverse events leading to dose adjustment was established based on the available data from phase III trials. In the trial simulation step, a dosing history was generated based on exposure‐response model for adverse events at different dosing regimen. Then, the time course of TGD was predicted at different dosing regimen based on the generated exposure profile. The simulation results suggested 14 mg of lenvatinib with option of up titration may provide comparable tumor inhibition to the approved dose; therefore, it was selected as alternative dosing regimens in the postmarket study. ⁴²

The model‐based drug development approach inclusive of biomarkers has been advocated by the FDA, as part of its Critical Path Initiative. ⁴³ Evidently biomarkers at early stage are essential to aid the selection of promising candidates, and to optimize the right dose regimen for confirmatory phase III studies. However, decision making on dose selection and evaluation of antitumor activity during early oncology drug development remain empirical. The FDA embarked on a project aiming to explore the quantitative relationship between clinical outcome (PFS/OS) and tumor dynamics for patients with metastatic breast cancer. A two‐step modeling strategy was implemented, including the development of TGD and survival models, thus linking the tumor size data to the primary clinical end point. A bi‐exponential model was chosen to describe the TGD, after testing several empirical models to fit the individual tumor size profiles in each arm. Cox proportional hazard model was used to select the covariates for the subsequent TGD‐survival modeling. The baseline factors, including demographics, prior treatment, receptor status, metastatic organ status, and baseline tumor size, were initially selected as covariates to establish a semiparametric PFS model. The relative tumor size change at week 6, week 9, or week 12 from baseline, as well as tumor dynamic parameters tumor shrinkage rate, tumor growth rate, or time to growth (TTG), were investigated separately as the tumor size metrics to link with PFS. Several commonly used survival functions, including exponential, Weibull, logistic, log‐logistic, and log‐normal, were tested, along with each of the tumor metrics. As a result, the final model incorporates the relative tumor size change at week 9 and the log‐normal function based on internal evaluation by comparing predicted PFS curves and observed PFS curves (median and 95% confidence interval). Additionally, the Eastern Cooperative Oncology Group or Karnofsky Performance Score, triple negative for estrogen receptor, progesterone receptor, and HER2 receptor, baseline tumor size, TTG, and relative tumor size change at week 9 were the statistically significant factors. Simulations showed the overall comparability of predicted HR vs. observed HR for PFS (Figure 3 ), except for one trial. A high proportion of progression due to nontarget lesion growth or new lesion appearance, and large difference in censoring rate between two arms observed in this particular trial, might contribute to the discrepancy between the observed vs. prediction in PFS.

Figure 3.

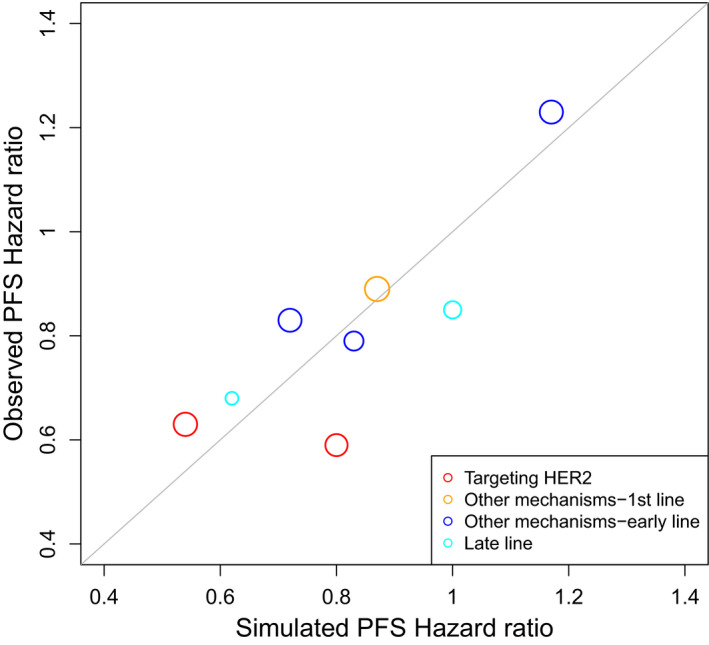
Comparison of predicted hazard ratio and observed hazard ratio of progression‐free survival (PFS).

FUTURE PERSPECTIVES AND CHALLENGES

TGD has made significant progress during the last decade and many more are underway. However, new methodologies and clinical applications can be further advanced by overcoming the challenges and understanding the limitations.

Advancement in modeling methodology for TGD

The mathematical models of TGD have evolved considerably over the years, from the classical analytical functional forms, to the mixture models, and to the complex‐joint model. This prominent trend has been mainly enabled by the increasing availability of computational super‐power, and the motivation of connecting tumor size to OS. With many notable successes in advancing the TGD models, the TGD model may have potentials in two folds. First of all, the current TGD model applies a population estimate approach, and a personalized TGD modeling at the individual level is yet to be developed. Its underdevelopment may be partially limited by large intrasubject variability of the tumor size measurement during the treatment. ⁴⁴ An individualized TGD model would provide prognostic insights and the associated treatment options at the patient level in the clinic. Second, with rapidly expanded broader and deeper understanding in cancer biology, the incorporation of tumor physiology, cellular and molecular heterogeneity, and/or genomic alternations, would provide insights for the interplay between the tumor growth dynamics and these important clinical factors. ⁴⁵ , ⁴⁶

Potential impacts in patient individualization and oncology drug development

TGD modeling has extensive utilities in the oncology drug development, ranging from preclinical efficacy assessment, to the first‐in‐human dose selection, to the late stage drug development. One of the significant impacts of TGD is to identify the clinical benefits of a new drug earlier and provide mechanistic insights.

Concurrent linkage of TGD and PFS (or OS), along with the corresponding baseline characteristics, into a single model, namely the joint model, could provide further potentials at both the patient level as well as the treatment level. For each individual patient, the dynamic dependencies and associations between the longitudinal tumor‐kinetics and the prognosis can be estimated based on the “real time” measurements rather than on the static information at the baseline, which would enable a more accurate assessment of patient progression event. ⁴⁷ In the case of the high likelihood of an event occurring, an alternative treatment option may be intervened to optimize the clinical outcome. At the program level, this simultaneously joint modeling could also inform an earlier decision to either advance or stop an investigational treatment at the early clinical development stage. The same thinking paradigm was previously developed for non‐oncology disease, using the joint‐modeling approach. ⁴⁸ Today, there exist > 69,000 clinical trials registered at clinicaltrials.gov in oncology development (Clinicaltrials.gov). This staggering large amount of clinical trials sheds promising light for the public to access better treatment options, but quite often the investigational drugs may not offer improved benefits compared with the standard of care. It would be of great advantage to the patients if the superior efficacy could be assessed earlier on, so that the patients may switch to the better treatment option and the drug product development would also be accelerated. On the other side, if the treatment is a lack of efficacy, it is unethical to continue the participants in the trials and a decision of termination of the program would reserve the development resources to other more promising assets.

Limitation and future directions

Tumor dynamic analysis has been frequently used for the internal decision making to stop or progress a project, but such analysis and clinical outcome are seldom reported in the literature. The tumor TTG linking with OS model has been applied to analyze a failed phase III study of motesanib in patients with non‐small cell lung cancer, and to predict a probability of success of 81% could be achieved in a combination study with 250 patients per arm. ⁴⁹ Although a phase III study later conducted in Asian patients failed to demonstrate motesanib benefit in combination with carboplatin/paclitaxel with PFS as the primary end point, the model predicted an HR of 0.74, which was very close to the observed value (0.81) in the clinical trial. ⁵⁰

Most reported the TGD model focused on the SLD of all target lesions, therefore, the characterization of tumor dynamic represents the average of all target lesions. However, the dynamic of single lesions could be drastically different, in which some may be more aggressive than others. Utilizing individual lesion dynamics to predict OS could be more sensitive and accurate than using dynamics from the SLD of all target lesions. Unfortunately, the publication and application of individual tumor lesion models in clinical development is very limited. ⁸ , ⁵¹

The COVID‐19 pandemic presents unprecedented challenges to patients, health care providers, and health care systems, including treatment of patients with cancer, due to self‐isolation, significant limitations, or complete restriction to outpatient visit, cross‐contamination during clinical visits, travel restrictions, or other considerations, such as the patient with cancer is also infected with COVID‐19. ⁵² , ⁵³ , ⁵⁴ The American Society of Clinical Oncology (ASCO) provided links for various oncology societies or organizations who developed guidance for treating patients with cancer with priority categories. Along with the patients’ specific characteristics, TGD modeling could predict the prognostic outcome for each individual patient, placing the patient with immediately shorter survival and clinically unstable conditions, as higher priority. This model‐based prediction would be complementary to clinical recommendations. ⁵⁵ , ⁵⁶ , ⁵⁷ Additionally, when the TGD model is jointly developed with the collected time‐varying drug concentrations for participants enrolled in clinical trials, the dynamic relationship between the exposures and tumor size can be established. Subsequently, the dosing regimen may be modified with elongated dosing frequency, as the clinical benefits and risks shift in light of increased COVID‐19 infection in the general clinical setting.

CONCLUSION

In this commentary, we have discussed the history of TGD modeling, the current advancement of TGD methodologies, its utilities in oncology drug development and regulatory review, and future perspectives. With further expansion of computational capacity and clinical patient data, TGD modeling would provide greater accuracy on the individual patient level for appropriate and timely intervention, enhance earlier decisions for new drug development, and further aid the regulatory assessment of benefits and risks.

Conflict of interest

N.H., Y.F., J.Y., Z.L., and J.S. are employees of Regeneron Pharmaceuticals, Bristol‐Myers Squibb, the FDA, and Astellas, respectively. M,N. and D.Z. are employees of AstraZeneca.

Funding

No funding was received for this work.

Disclaimer

The opinions expressed in this article are those of the authors and should not be interpreted as the position of the US Food and Drug Administration.

Supporting information

Table S1