Application of Physiologically‐Based Pharmacokinetic Modeling to Predict Gastric pH‐Dependent Drug–Drug Interactions for Weak Base Drugs

Abstract

Weak‐base drugs are susceptible to drug–drug interactions (DDIs) when coadministered with gastric acid–reducing agents (ARAs). We developed PBPK models to evaluate the potential of such pH‐dependent DDIs for four weak‐base drugs, i.e., tapentadol, darunavir, erlotinib, and saxagliptin. The physiologically‐based pharmacokinetic (PBPK) models of these drugs were first optimized using pharmacokinetic (PK) data following oral administration without ARAs, which were then verified with data from additional PK studies in the presence and absence of food. The models were subsequently used to predict the extent of DDIs with ARA coadministration. Sensitivity analysis was conducted to explore the impact of gastric pH on quantitative prediction of drug exposure in the presence of ARA. The results suggested that the PBPK models developed could adequately describe the lack of the effect of ARA on the PK of tapentadol, darunavir, and saxagliptin and could qualitatively predict the effect of ARA in reducing the absorption of erlotinib. Further studies involving more drugs with positive pH‐dependent DDIs are needed to confirm the findings and broaden our knowledge base to further improve the utilization of PBPK modeling to evaluate pH‐dependent DDI potential.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ There is limited experience in using physiologically‐based pharmacokinetic (PBPK) models to predict pH‐dependent drug–drug interactions (DDIs), especially at the stage of regulatory submission.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ The study explored the utility of PBPK models in predicting gastric pH‐mediated DDI potential for weak‐base drugs and understanding its limitation and knowledge gaps.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ PBPK models, optimized and verified using clinical pharmacokinetic data following oral dosing, appear to adequately predict the lack of pH‐dependent DDIs without false positive prediction. For the drug predicted as positive DDI by the conceptual framework published earlier, a PBPK model can be used to confirm the qualitative prediction results. However, it still merits further research on the quantitative prediction of the magnitude of a positive pH‐dependent DDI.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ It may be possible to use a PBPK model to adequately evaluate pH‐dependent DDI potential qualitatively without a dedicated clinical DDI study.

Many weak base drugs (WBDs) exhibit pH‐dependent solubility. Generally, the solubility of a WBD decreases as pH increases. Thus, when WBDs are administered orally, elevation of gastric pH induced by another drug or disease state may lead to a decrease in WBD absorption and consequently result in reduced systemic exposure to the drug. pH‐dependent drug–drug interactions (DDIs) have been observed for many WBDs, including various anticancer and antiretroviral drugs when they are coadministered with gastric acid–reducing agents (ARAs) such as histamine H₂‐receptor antagonists and proton pump inhibitors. ¹ , ² One example is erlotinib, an epidermal growth factor receptor tyrosine kinase inhibitor. The area under the plasma concentration‐time curve (AUC) and maximum concentration (C_max) of erlotinib were decreased by 46% and 61%, respectively, when the drug was coadministered with omeprazole, a proton pump inhibitor. ³ This may be one reason why patients treated with both erlotinib and ARAs had shorter progression‐free and overall survival time than those without taking any ARAs. ⁴ Current erlotinib labeling recommends that patients avoid concomitant use of erlotinib and proton pump inhibitors if possible. Given the possibility of compromised drug efficacy, the potential for pH‐dependent DDIs should be evaluated for WBDs during drug development. Recently, the US Food and Drug Administration (FDA) solicited public input on best practices in the planning and evaluation of pH‐dependent DDIs (https://www.regulations.gov/document?D=FDA‐2018‐N‐1820‐0001).

Evaluation of pH‐dependent DDI can be achieved through the conduct of a clinical DDI study, which can be costly and time consuming. Methods to determine the need for such a clinical DDI study are highly desirable. Previously, we proposed a preliminary decision framework to predict the potential of pH‐dependent DDI under fasting conditions based on both solubility and clinical dose of the drug, enabling the determination of the need to conduct a clinical study to assess pH‐dependent DDI at the early stage of drug development. ⁵ However, such a simplistic framework does not consider other factors that may also play important roles in drug absorption, such as permeability, supersaturation, and the effect of food, which can limit its utility. In addition, this proposed framework can only qualitatively assess the potential of pH‐dependent DDI.

Physiologically‐based pharmacokinetic (PBPK) modeling has been increasingly used by drug developers to predict DDIs mediated by metabolic enzymes and/or transporters for regulatory submissions. ⁶ , ⁷ However, experience is limited in using PBPK model to predict pH‐dependent DDIs, especially at the stage of regulatory submission. ⁸ , ⁹ , ¹⁰ , ¹¹ The objective of this study was to explore the utility of PBPK modeling in predicting the pH‐dependent DDI potential, specifically gastric pH‐mediated DDI potential, for WBDs and understand the limitation of PBPK models and knowledge gaps with a goal of improving the model prediction performance in the future.

Methods

Development and verification of PBPK models

Figure  1 illustrates the workflow of PBPK model development, verification, and application to predict pH‐dependent DDIs. Briefly, the base model was developed for tapentadol, saxagliptin, darunavir, and erlotinib by incorporating drug physicochemical properties measured in vitro, volume of distribution derived from clinical studies, and drug clearance obtained from either intravenous pharmacokinetic (PK) data or in vitro enzyme kinetics data. The base model used advanced distribution, absorption, and metabolism (ADAM) model as the mechanistic absorption model in Simcyp (version 16, Simcyp Ltd, a Certara company, Sheffield, UK) and employed the advanced compartmental absorption and transit (ACAT) model in Gastroplus (version 9.0, Simulation Plus Inc., Lancaster, CA). The base model was optimized using PK data from one oral dose, except for tapentadol where PK data from two oral doses were used. The model was then verified with data from additional PK studies under fasted or fed conditions. If both the predicted area under the concentration‐time curve from time zero to infinity (AUC_0−∞) and C_max for all the studies used in model development and verification fell within a 1.5‐fold difference compared with the observed data, the model was considered verified.

Figure 1.

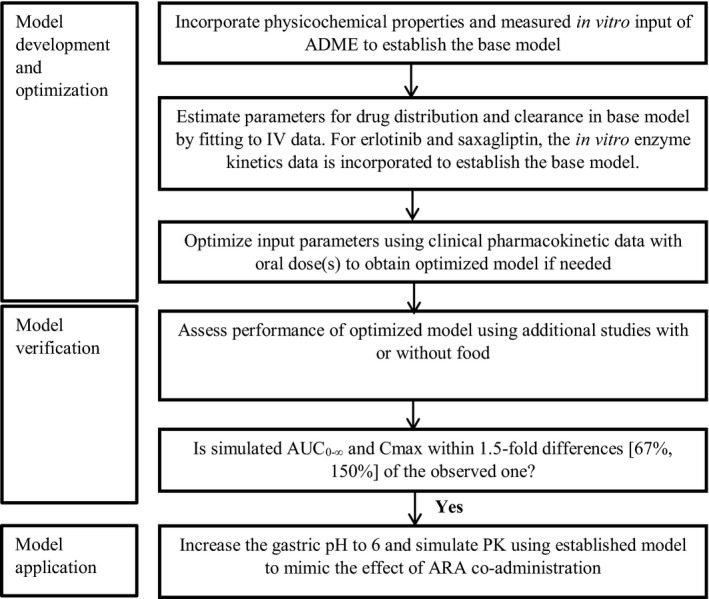
Flow diagram of model development and verification process. ADME, absorption, distribution, metabolism, and excretion; ARA, acid‐reducing agent; AUC_0−∞, area under the concentration‐time curve from time zero to infinity; C_max, maximum concentration; IV, intravenous; PK, pharmacokinetic.

Application of established (final) PBPK model to predict pH‐dependent DDI with an ARA

The established final models were then extended to predict drug exposure in the absence and presence of an ARA using omeprazole as a model ARA. Previously, it was reported that administration of omeprazole at the usual therapeutic dosing regimens could elevate gastric pH to as high as 6. ¹² Thus, simulation of DDI in the presence of omeprazole was conducted by increasing the gastric pH to 6 to represent the worst‐case scenario. As such, the simulation was conducted in a virtual healthy volunteer population by changing the gastric pH from the default values under fasted conditions (Gastroplus, fasted: 1.3; and Simcyp, fasted: 1.5) to 6 for tapentadol, erlotinib, and saxagliptin because the pH‐dependent DDI studies of these drugs were conducted in the absence of food. For darunavir, which has the pH‐dependent DDI study conducted in the presence of food, the simulation was carried out by increasing the gastric pH from the default values under fed conditions (Gastroplus, fed: 4.9; and Simcyp, fed: 5) to 6. The default values for gastric emptying time for both fasted and fed conditions as implemented in the software were used in the analysis. The predicted AUC and C_max ratios in the presence and absence of omeprazole were computed and then compared with the observed clinical data to address the following questions:

• pH‐mediated DDI potential: Can simulations describe the lack of DDI with ARAs (e.g., < 25% decrease in both AUC and C_max) or a positive DDI (e.g., ≥ 25% decrease in AUC or C_max) as observed in dedicated clinical studies?

• Quantitative prediction performance: Can simulations describe the observed AUC and C_max ratios in the presence and absence of an ARA with less than 25% deviation (i.e., is the R value for AUC and C_max between 0.8 and 1.25, where the R value is calculated according to the following equation:

$$R=\frac{{\text{Model Predicted AUC or C}}_{max}\text{ratio in the presence and absence of ARA}}{{\text{Clinically Obseved AUC or C}}_{max}\text{ratio in the presence and absence of ARA}})?$$

Impact of different gastric pH on the model prediction performance

Different doses of omeprazole can increase gastric pH to a different extent. ¹² , ¹³ , ¹⁴ In our study, darunavir was given with 20 mg omeprazole. Daily dosing of omeprazole 20 mg could increase gastric pH to the range of 2.8–4.2. Tapentadol, saxagliptin, and erlotinib were given with 40 mg omeprazole. This could increase gastric pH to the range of 4.4 to 6. Thus, a sensitivity analysis was conducted on gastric pH to evaluate its impact on model prediction performance by changing the gastric pH from 1 to 8.

Results

Development and verification of PBPK models for tapentadol, saxagliptin, darunavir, and erlotinib

Four WBDs in immediate‐release oral dosage forms belonging to Biopharmaceutics Classification System (BCS) classes I–III were selected for PBPK model development based on the availability of aqueous solubility data, i.e., tapentadol (BCS class I), darunavir (BCS class II), erlotinib (BCS class II), and saxagliptin (BCS class III). ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ These drugs were approved between 2003 and 2013 by the U.S. FDA and have the clinical DDI studies conducted with ARAs such as omeprazole (Table  1 ).

Table 1.

Summary of dosing regimen and observed effects on the PK of test drugs in the food effect study and pH‐dependent DDI study

Drug	Dosing regimen or PK parameters	Food effect study a	pH‐dependent DDI study b	Reference
Tapentadol	Dosing regimen	Tapentadol, 100 mg, single dose	Tapentadol, 80 mg, single dose, omeprazole, 40mg, q.d. for 4 days, fasted c	15
	Cmax ratio	1.15	0.91
	AUC ratio	1.25	1.01
Saxagliptin	Dosing regimen	Saxagliptin, 10 mg, single dose	Saxagliptin, 10 mg, single dose, omeprazole, 40 mg, q.d. for 4 days, fasted c	17, 36
	Cmax ratio	1.09	0.98
	AUC ratio	1.27	1.12
Darunavir	Dosing regimen	Darunavir, 400 mg, single dose	Darunavir, 400 mg b.i.d. for 5 days, omeprazole, 20 mg, q.d. for 5 days, fed	19, 37
	Cmax ratio	1.48	1.03
	AUC ratio	1.54	1.05
Erlotinib	Dosing regimen	Erlotinib, 150 mg, single dose	Erlotinib, 150 mg, single dose, omeprazole, 40 mg, q.d. for 5 days, fasted	3, 38
	Cmax ratio	1.57	0.39
	AUC ratio	1.97	0.54

AUC, area under the concentration‐time curve; b.i.d., twice a day; C_max, maximum concentration; DDI, drug–drug interaction; PK, pharmacokinetic; q.d., once a day.

^aThe food effect is expressed as the exposure ratio in the presence and absence of food.

^bThe acid‐reducing agent effect is expressed as the exposure ratio in the presence and absence of omeprazole.

^cAssumed dosing condition when conducting the simulation.

PBPK models for tapentadol, saxagliptin, darunavir, and erlotinib were developed and optimized based on both in vitro and clinical data. The input parameters for the established final models for each drug are listed in Tables S1–S4 . Table  2 , Figure  2 , and Figure  S8 illustrate that the optimized models with both Gastroplus and Simcyp well described the PK profiles following single oral doses. The predicted C_max and AUC values were within 1.5‐fold of the observed values for all drugs. Further external model verification indicated that the models also well described the observed drug exposure for additional oral doses and exposure in the presence of food that were not used for model development (Table  2 ).

Table 2.

Verification results using the established models

Drug	Scenario	IV or Oral dosing	References	Cmax ratio (predicted/observed) a		AUC ratio (predicted/observed) a
				Gastroplus	Simcyp	Gastroplus	Simcyp
Tapentadol	IV dose	34 mg single infusion for 15 min	15	0.92	0.96	1.11	1.13
	Oral dose 1 b	80 mg single dose, IR c tablet	15	0.84	0.95	1.04	0.88
	Oral dose 2 d	129 mg single dose, IR capsule	15	0.72	0.79	0.97	0.82
	Oral dose 3 e	64 mg single dose, IR capsule	15	0.88	1.03	1.14	0.96
	Fed state e	100 mg single dose, IR tablet with food	15	0.68	0.92	0.76	0.75
Saxagliptin	IV dose	0.04 mg, single infusion for 15 mins	39	0.99	0.86	0.92	0.88
	Oral dose 1 b	100 mg single dose, IR tablet	40	0.99	0.98	1.06	1.02
	Oral dose 2 e	5 mg single dose, IR tablet	39	1.08	1.10	1.13	1.18
	Oral dose 3 e	50 mg single dose, solution	41	0.98	1.00	1.16	1.27
	Fed state e	10 mg single dose, IR tablet, with food	36	0.68	0.87	0.97	1.11
Darunavir f	IV dose	150 mg, single infusion for 1 hour	37	1.07	1.20	1.00	1.05
	Dose 1 b	600 mg single dose, IR tablet, with food	37	0.85	0.88	0.88	0.76
	Dose 2 e	400 mg single dose, IR tablet, with food	37	0.71	0.74	0.78	0.74
	Dose 3 e	800 mg single dose, IR, with food	New Drug Submission	0.89	0.89	1.12	0.87
	Fasted state e	400 mg single dose, IR tablet	37	1.01	0.95	1.27	0.93
Erlotinib	IV dose	25 mg, single infusion for 30 mins	42	0.85	1.14	1.15	1.44
	Dose 1 b	150 mg single dose, IR tablet	3	0.81	1.01	1.15	1.06
	Dose 2 e	100 mg single dose, IR tablet	43	0.86	1.19	1.23	1.28
	Dose 3 e	200 mg single dose, IR tablet	16	0.78	0.97	0.96	0.83
	Fed state e	150 mg single dose, IR tablet, with food	38	0.68	1.01	1.09	1.42

^aThe value represents the ratio of predicted and observed C_max or AUC_0‐∞.

^bThe study was used for model refinement when needed. The C_max ratio and AUC_0‐∞ ratio represent the result after model refinement.

^cIR: Immediate‐release.

^dThe study was used for Gastroplus model refinement, but not for Simcyp model refinement.

^eThe study was used for model external verification. It was not used for model refinement.

^fThe model for darunavir was developed with the studies in the presence of 100 mg ritonavir, BID.

Figure 2.

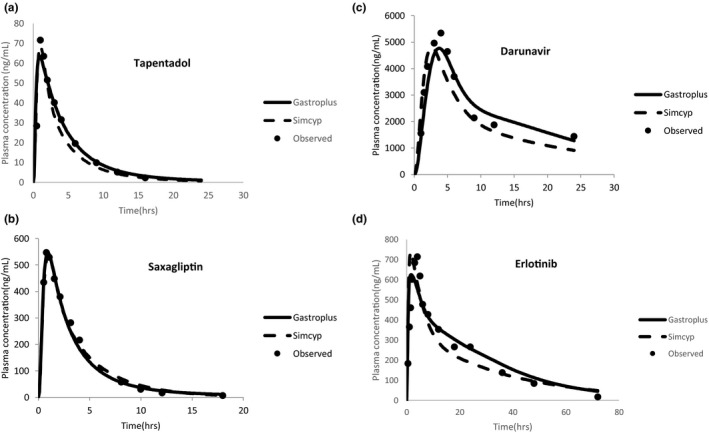
Representative base model verification prediction results. Simulation of plasma concentrations followed by a single oral dose of (a) 80 mg tapentadol, (b) 100 mg saxagliptin, (c) 600 mg darunavir with 100 mg ritonavir under the fed condition, and (d) 150 mg erlotinib using both Gastroplus and Simcyp physiologically‐based pharmacokinetic platforms. Closed circles indicate observed mean plasma concentration. The solid line indicates simulated mean plasma concentration using Gastroplus. The dash line indicates simulated mean plasma concentration using Simcyp.

Prediction of DDI potential with an ARA

The in vivo DDI study with an ARA was conducted by increasing the gastric pH to 6 to represent the worst‐case scenario when omeprazole was coadministered.

For tapentadol, saxagliptin, and darunavir, both the Gastroplus and Simcyp models well described the PK profiles following oral administration of the drug alone and in combination with omeprazole (Table  3 ). In addition, both the Gastroplus and Simcyp models suggested that there was no clinically relevant effect of omeprazole on their PK (i.e., a reduction of < 25% in both C_max and AUC), which was consistent with the clinical data (Table  3 ). ¹⁵ , ¹⁷ , ¹⁹ Moreover, the magnitude of C_max and AUC change were also well predicted (i.e., R values of C_max and AUC were between 0.8 and 1.25 cutoff; Table  3 ).

Table 3.

Prediction performance of the established models on drug exposure (C_max and AUC) and pH‐dependent DDI following a single dose administration with and without concomitant omeprazole

Drug	Platform	Cmax (predicted/observed) a		Predicted Cmax ratio b	Observed Cmax ratio c	R value (Cmax) d	AUC (predicted/observed) a , e		Predicted AUC ratio b , e	Observed AUC ratio c , e	R value (AUC) d , e
		Alone	With omeprazole				Alone	With omeprazole
Tapentadol, 80 mg	Gastroplus	0.81	0.89	1.00	0.91	1.10	1.01	1.00	1.00	1.01	0.99
	Simcyp	0.91	0.96	0.95	0.91	1.05	0.85	0.84	1.00	1.01	0.99
Saxagliptin, 10 mg	Gastroplus	1.00	1.00	0.98	0.98	1.00	1.17	0.99	0.95	1.12	0.85
	Simcyp	1.18	1.20	1.00	0.98	1.02	1.32	1.18	1.00	1.12	0.89
Darunavir, 400 mg	Gastroplus	1.07	1.04	1.00	1.03	0.97	1.15	1.10	1.00	1.05	0.95
	Simcyp	1.05	0.93	0.91	1.03	0.89	1.00	0.90	0.95	1.05	0.90
Erlotinib, 150 mg	Gastroplus	0.85	1.19	0.54	0.39	1.40	1.17	1.70	0.79	0.54	1.45
	Simcyp	0.85	1.19	0.55	0.39	1.40	0.96	1.19	0.67	0.54	1.24

AUC, area under the concentration‐time curve; AUC_0−∞, area under the concentration‐time curve from time zero to infinity; AUC_96−108h, area under the concentration‐time curve from 96 to 108 hour; C_max, maximum concentration; DDI, drug–drug interaction.

^aThe value represents the ratio of predicted and observed C_max or AUC alone or in the presence of omeprazole. Refer to Table 1 for reference information on the pH‐dependent DDI study.

^bThe value represents the model predicted ratio of C_max or AUC in the presence and absence of acid‐reducing agents.

^cThe value represents the observed ratio of C_max or AUC in the presence and absence of acid‐reducing agents. Refer to Table 1 for reference information on the pH‐dependent DDI study.

^d R value is calculated according to Eq. 1 as described in the Methods section, which represents the ratio of predicted C_max or AUC ratio over the observed ratio. Refer to Table 1 for reference information on the pH‐dependent DDI study.

^eAUC_0−∞ for tapentadol, erlotinib, and saxagliptin and AUC_96−108h for darunavir.

For erlotinib, the established drug model in Gastroplus overpredicted the AUC in the presence of omeprazole (i.e., predicted/observed value of 1.7, higher than the 1.5 cutoff value; Table  3 ). Although the model was able to predict the positive DDI with omeprazole, it tended to underpredict the magnitude of DDI for both C_max and AUC (R values of 1.40 and 1.45, respectively, more than 1.25 cutoff; Table  3 ). Prediction using the established erlotinib model in Simcyp reasonably described AUC and C_max of erlotinib in the presence and absence of omeprazole (Table  3 ). Although the model was able to predict positive DDI with omeprazole and described the observed AUC ratio within 1.25‐fold, the model also appeared to underpredict the magnitude for DDI for C_max (i.e., R value of C_max is 1.40; Table  3 ).

Impact of different gastric pH on the model prediction performance

It was reported that different doses of omeprazole can elevate the gastric pH to different levels while we used pH 6 for quantitative predictions. Thus, sensitivity analysis was conducted by changing gastric pH to explore its impact on quantitative prediction of drug exposure in the presence of ARA. As shown in Figure  3 , the AUC and C_max did not dramatically change for tapentadol, saxagliptin, and erlotinib from pH 4.4 to 6. Meanwhile, the AUC and C_max did not significantly change for darunavir from pH 2.8 to 4.2.

Figure 3.

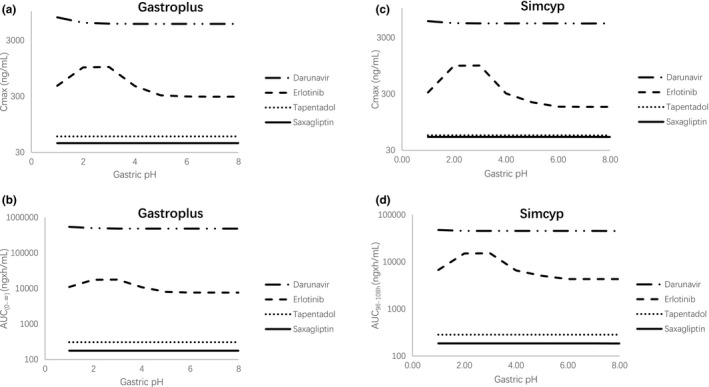
Impact of gastric pH on (a) C_max in Gastroplus, (b) AUC in Gastroplus, (c) C_max in Simcyp, and (d) AUC in Simcyp for darunavir, erlotinib, tapentadol, and saxagliptin using the verified physiologically‐based pharmacokinetic model for each drug. AUC_0−∞, area under the concentration‐time curve from time zero to infinity; AUC_{96 −108h}, area under the concentration‐time curve from 96 to 108 hour; C_max, maximum concentration.

Discussion

In the past decades, PBPK models have been applied to predict first‐in‐human dose, change of drug exposure in specific populations (e.g., renal impairment patients, pediatrics), and DDIs mediated by metabolic enzymes and/or transporters. ²⁰ Recently, a study suggested that the PBPK model that was developed at the preclinical stage could correctly identify pH‐dependent DDI potential for 78% drugs although false negative prediction was observed. ²¹ However, there is still limited application of PBPK modeling to address the questions related to absorption‐related DDIs at the stage of regulatory submissions. ²² , ²³ , ²⁴ , ²⁵ In the years of 2013–2017, PBPK modeling has been used in two New Drug Application submissions to predict the liability of pH‐dependent DDIs to support the labeling recommendations. ²⁶ , ²⁷ In this study, we evaluated the possibility to use PBPK models that were verified with clinical PK data to predict pH‐dependent DDIs. This reflects the scenario at the late stage of drug development.

PBPK models were developed for four WBDs that belong to BCS classes I, II, or III using Gastroplus and Simcyp, two commercially available PBPK platforms. The purpose of using two platforms was to examine the prediction performances generated by different software. Good agreement to the observed data and between different platforms would add to our confidence in the utility of PBPK modeling for predicting pH‐dependent DDIs. Prediction of pH‐dependent DDIs under both fasted and fed conditions were explored. Our analysis suggests that PBPK models, optimized and verified using clinical PK data following oral dosing, appear to adequately predict the lack of pH‐dependent DDIs without false positive prediction. For the drug predicted as positive DDI by the conceptual framework published earlier, a PBPK model can be used to confirm the qualitative prediction results. It is also expected that with appropriate input (clinically relevant solubility or dissolution, etc.) and sufficient verifications for PBPK absorption model using all available clinical study data with ascending doses under fasted/fed conditions, the model may be able to quantitatively predict pH‐dependent DDI.

PBPK model vs. previous decision framework to predict pH‐dependent DDI

Previously, we proposed a preliminary decision framework to predict pH‐dependent DDI potential based on both solubility and clinical dose of the drug. ⁵ Although the framework results in no false negative prediction, it did not consider other critical factors in drug absorption, such as permeability, supersaturation, and the physiological change under fed conditions and thus resulted in false positive prediction on 16% drugs. Thus in this study, we incorporated absorption‐related parameters in the PBPK models and explored its prediction performance on pH‐dependent DDI.

Regarding the prediction performance on the lack of pH‐dependent DDI potential, both PBPK models and the preliminary decision framework achieved the correct prediction on pH‐dependent DDI potential for tapentadol and saxagliptin, which have the pH‐dependent DDI studies conducted under the fasted condition. For darunavir, the DDI study was conducted under the fed condition, which is beyond the scope of the decision framework. However, PBPK model still resulted in correct prediction on the liability of pH‐dependent DDI that took into consideration of the impact of food on various elements in drug absorption, including change in stomach pH and gastric emptying time. Consistent with our findings, the performance of PBPK models to correctly predict the lack of pH‐dependent DDI potential was also demonstrated in a recent study where a Gastroplus model for alectinib, a BCS class IV drug, predicted that there is negligible impact of gastric pH elevation. ²⁸ This was later confirmed by a DDI study with esomeprazole coadministration. ²⁹ By contrast, using our previous preliminary decision framework would incorrectly predict that alectinib may have a positive DDI with ARAs. Overall it seems that PBPK models, with proper verification, could generally provide correct prediction on the lack of pH‐dependent DDI.

Regarding the prediction performance on positive pH‐dependent DDI potential, both the PBPK model and preliminary decision framework for erlotinib could qualitatively predict its positive DDI potential. However, because there is only one example of positive pH‐dependent DDI in our study, it merits further study to confirm our finding.

It should also be noted that beyond the qualitative assessment of the potential of pH‐dependent DDI, PBPK modeling could also target on predicting the extent of AUC and C_max change of a WBD in the presence of ARAs and simulate various scenarios that may not be clinically tested. In addition, sensitivity analysis using the PBPK model can help understand key parameters that may affect drug absorption and DDI, which cannot be achieved based on our preliminary decision framework.

Criteria to evaluate the prediction performance of PBPK models for pH‐dependent DDI

In the current study, we evaluated both qualitative and quantitative prediction performance of PBPK models for pH‐dependent DDI. The qualitative performance was evaluated based on whether the model could achieve a correct prediction on DDI potential (i.e., positive or negative DDI). Here positive DDI was defined as at least 25% reduction in either AUC or C_max, whereas negative DDI was defined as less than 25% AUC or C_max reduction. These are the same criteria as our previous decision framework for the evaluation of pH‐dependent DDI. ⁵

It was reported that about 80% of PBPK models submitted to the FDA from 2008 to 2014 that were used to predict the effect of cytochrome P450 3A (CYP3A) inhibitors and inducers on a substrate drug's PK could yield AUC or C_max ratios within 1.25‐fold of the observed values. ⁶ , ⁷ In our study, we used the same criteria to evaluate the quantitative performance of the model, i.e., based on if the predicted AUC and C_max ratios in the presence and absence of ARA fell within 1.25‐fold of the observed data. It should be noted that a less stricter criteria (i.e., within 1.5‐fold of the observed data) was adopted for model verification because exposure change instead of exposure itself is our interests. Our study suggested that there were gaps for PBPK models to correctly predict change of AUC or C_max in the presence of ARA (see the discussion in the next section).

Performance of the final models in predicting pH‐dependent DDIs

The final models predicted well when there was a lack of interaction as in the cases of tapentadol, saxagliptin, and darunavir. However, the PBPK model for erlotinib underpredicted the decrease in drug exposure (C_max and AUC using Gastroplus and C_max using Simcyp) in the presence of omeprazole under the fasted conditions, as the predicted change was not within 1.25‐fold of the observed value (Table  3 ). In Gastroplus, the default fraction of total colonic fluid volume filled with fluid, which is 10% overpredicted exposure for certain drugs. ³⁰ , ³¹ In our study, when the fraction of total colonic fluid volume filled with fluid was refined to 1% based on the sensitivity analysis for erlotinib, the PBPK model for erlotinib was able to predict the decrease in drug exposure within 1.25‐fold of the observed value (Table  S5 and Figure  S7 ). Consequently, the drug absorbed in the colon was reduced from 15.7% to 4.9%. Our study suggested that there were gaps for PBPK models to accurately predict change of AUC or C_max in the presence/absence of ARAs using less than 1.25‐fold difference from the observed value as prediction performance criteria. This is consistent with the finding from a previous study where exposure change of the compound ARRY‐403 in the presence of famotidine was overestimated by about 2‐fold by the PBPK model. ³² Our study also showed that appropriate model refinement is needed to have a better prediction performance (i.e., within 1.25‐fold of the observed value) for using PBPK to predict pH‐dependent DDI potential, e.g., in the case of erlotinib.

Impact of different gastric pH on prediction of pH‐dependent DDI

Gastric pH can be elevated to different levels with different type, dose, and dosing regimens of an ARA. ¹² , ¹³ , ¹⁴ , ³³ For the four WBDs in our analysis, either 20 or 40 mg omeprazole was administered for 4 days before the WBD was given. It has been shown that the median 24‐hour gastric pH ranges from 2.8 to 4.2 after the administration of 20 mg omeprazole for 5 days, whereas it ranges from 4.4 to 6.1 with 40 mg omeprazole. ¹² , ¹³ , ¹⁴ Thus, to represent a worst scenario for the qualitative prediction of DDI effect in the presence of omeprazole or an ARA, we conducted simulations by increasing the gastric pH to 6 to mimic the maximum ARA effect on gastric pH. In addition, the potential impact of different pH values on model prediction was explored using a sensitivity analysis. This allowed us to examine if applying different gastric pHs other than 6 would result in different AUC or C_max changes in the presence of an ARA. If so, the pH factor may complicate our quantitative prediction of the DDI effect imposed by an ARA. It was shown that for tapentadol, saxagliptin, and erlotinib, which were coadministered with 40 mg omeprazole, AUC and C_max were generally unchanged from pH 4.4 to 6.1 (Figure  3 ). For darunavir, which was coadministered with 20 mg omeprazole in the presence of food, AUC and C_max were also not changed from pH 2.8 to 4.2 (Figure  3 ). These results suggested that prediction results on AUC and C_max change were not likely to be affected for these drugs even though different gastric pH values after the ARA administration were applied.

Limitation of the current study

In our current study, we explored the utility of using PBPK models to predict pH‐dependent DDI for WBDs. Our study showed that although PBPK model could result in a reasonable prediction on pH‐dependent DDI potential, it is still challenging to achieve an accurate quantitative prediction on the extent of AUC or C_max change in the presence of an ARA. Because this was a proof‐of‐concept study to evaluate the possibility of using PBPK to predict pH‐dependent DDI both qualitatively and quantitively for various BCS class drugs, we only included limited WBDs among which only one drug has positive DDI (i.e., erlotinib) in the analysis. Further studies involving more drugs in BCS classes II and IV are needed to confirm the finding.

In terms of model development, four immediate‐release drugs were used in our study. Either the Johnson or Wang‐Flanagan model was used to simulate drug dissolution. However, these dissolution models are generally not applicable to extended‐release formulations as the rate of drug dissolution is controlled by the formulation. Additional factors (e.g., drug release behavior) other than permeability and supersaturation such as biorelevant dissolution methods may deserve to be considered for base model development for extended‐release formulations.

In terms of simulation of the pH effect, the gastric pH was kept constant after an ARA was given in our study. This is a general practice that most PBPK models are taking when predicting pH‐dependent DDIs. ¹¹ , ²⁸ , ³¹ However, numerous studies have shown that gastric pH undergoes a dynamic change after ARA administration and/or food intake. ¹² , ¹³ , ¹⁴ , ³³ Thus, incorporating a dynamic pH change during the simulation may help the model to achieve a better quantitative prediction on pH‐dependent DDI. In addition, in our study, we assume that omeprazole only changed the gastric pH, but not other parameters. However, certain studies suggested that omeprazole could delay gastric emptying, which may also contribute to the change of C_max. ³⁴ , ³⁵ As there is very limited information about gastric emptying time after a repeated dosing of omeprazole, the change of gastric emptying time was not included in the model.

Finally, in this study, we only evaluated the prediction performance of PBPK model on WBDs. For weak‐acid drugs that may have higher rates and extents of absorption in the presence of ARAs, PBPK models may be used to predict their pH‐dependent DDI potential considering that the DDI is also associated with the solubility change of the drug as a result of alteration of gastric pH by the ARA. PBPK model prediction performance on pH‐dependent DDI prediction for weak‐acid drugs warrants further assessment.

Conclusion

Overall, our study suggests that it may be possible to use PBPK modeling to adequately evaluate pH‐dependent DDI potential for WBDs. This initial proof‐of‐concept study evaluated a limited number of drugs, including those that do not show significant pH‐dependent DDIs. The results from our work can serve as catalyst for future studies to systematically examine the qualitative and quantitative prediction performance of PBPK models for additional drugs, in particular BCS class II and IV drugs that show significant pH‐dependent DDIs. This will broaden our knowledge base and further improve the utilization of PBPK modeling to evaluate pH‐dependent DDI potential in lieu of dedicated clinical DDI studies.

Funding

The project was funded by the US Food and Drug Administration's Critical Path research program. Drs. Dong and Li were supported by an appointment to the Oak Ridge Institute for Science and Education (ORISE) Research Participation Program at the Center for Drug Evaluation and Research (CDER) administered by the ORISE through an agreement between the US Department of Energy and CDER.

Conflict of Interest

All authors declared no competing interests for this work. As an Associate Editor for CPT: Pharmacometrics and Systems Pharmacology, Ping Zhao was not involved in the review or decision process for this paper.

Author Contributions

Z.D., J.L., F.W., P.Z., S.‐C.L., L.Z., P.S., and L.Z. wrote the manuscript. F.W., P.Z., S.‐C.L., L.Z., P.S., and L.Z. designed the research. Z.D. and J.L. performed the research. Z.D., J.L., and F.W. analyzed the data.

Disclaimer

The views expressed in this article are those of the authors and should not be construed to represent the US Food and Drug Administration's views or policies. The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the US Food and Drug Administration. Parts of the results were presented at the 2017 American Society for Clinical Pharmacology and Therapeutics Annual Meeting in Washington, DC.

Supporting information

Supplementary Material S1