Accessing new magnetic regimes by tuning the ligand spin-orbit coupling in van der Waals magnets

Previously unknown magnetic regimes and phenomena are revealed by tuning the competition between two types of spin-orbit coupling.

Abstract

Van der Waals (VdW) materials have opened new directions in the study of low dimensional magnetism. A largely unexplored arena is the intrinsic tuning of VdW magnets toward new ground states. Chromium trihalides provided the first such example with a change of interlayer magnetic coupling emerging upon exfoliation. Here, we take a different approach to engineer previously unknown ground states, not by exfoliation, but by tuning the spin-orbit coupling (SOC) of the nonmagnetic ligand atoms (Cl, Br, I). We synthesize a three-halide series, CrCl_{3 − x − y}Br_xI_y, and map their magnetic properties as a function of Cl, Br, and I content. The resulting triangular phase diagrams unveil a frustrated regime near CrCl₃. First-principles calculations confirm that the frustration is driven by a competition between the chromium and halide SOCs. Furthermore, we reveal a field-induced change of interlayer coupling in the bulk of CrCl_{3 − x − y}Br_xI_y crystals at the same field as in the exfoliation experiments.

INTRODUCTION

Spin-orbit coupling (SOC) is an essential ingredient of exotic magnetic phenomena. For example, the Dzyaloshinski-Moriya interaction that leads to the formation of skyrmions originates from a combination of SOC and broken inversion symmetry (1). The Kitaev interaction that leads to long-range entanglement in quantum spin liquids is also rooted in SOC (2, 3). Ferromagnetic (FM) ordering in single atomic layers of two-dimensional (2D) magnets is a result of SOC and magnetic anisotropy according to the Mermin-Wagner theorem (4–8). Despite the fundamental importance of SOC, little has been done to tune this interaction beyond the single-ion level. In this manuscript, we generate the entire magnetic phase diagram of chromium trihalides by tuning the ligand SOC. This is done by varying the ratio of the nonmagnetic ligand atoms (Cl, Br, and I) in CrCl_{3 − x − y}Br_xI_y without affecting the magnetic atom (Cr).

Our experiments were motivated by the following model Hamiltonian recently proposed for chromium trihalides (9–12)

$$\mathcal{H}=-J{\displaystyle \sum _{\langle i,j\rangle }}{\mathrm{S}}_{\mathrm{i}}·{\mathrm{S}}_{\mathrm{j}}-D{\displaystyle \sum _i}{(S_i^z)}^2-\mathrm{\lambda }{\displaystyle \sum _{\langle i,j\rangle }}{S}_i^z{S}_j^z+H_{\text{frust}.}$$ (1)

It describes the Cr³⁺ ions with S = 3/2 and isotropic Heisenberg coupling (J) on a honeycomb lattice (Fig. 1). Magnetic anisotropy is controlled by the single-ion anisotropy (D) and the anisotropic exchange (λ). The main contribution to D is from the SOC of Cr. The main contribution to λ is from the SOC of the heavy ligands (Br and I), and a smaller contribution comes from Cr and Cl. Other interactions that promote magnetic frustration, such as the Kitaev or dipolar interactions, are contained in H_frust.. The in-plane anisotropy in CrCl₃ (13) implies D < 0, and the out-of-plane anisotropy in CrI₃ (14) implies λ > 0. Thus, a competition is built into Eq. 1 that could drive the system into a frustrated regime due to H_frust. when D and λ acquire comparable magnitudes (with opposite signs). The atomic SOC values in Cr, Cl, Br, and I are 90, 40, 220, and 580 meV, respectively (15). From here, we expect to see the effect of H_frust. near CrCl₃ where D and λ could cancel each other, but not in CrBr₃ or CrI₃ where a strong λ leads to a dominant out-of-plane FM order. To search for such a frustrated regime, we grew a series of three-halide crystals CrCl_{3 − x − y}Br_xI_y and mapped their Curie temperature (T_C), Weiss temperature (Θ_W), and frustration index (f = Θ_W/T_C), as a function of Cl, Br, and I content. As expected, our experiments revealed a frustrated regime near CrCl₃ with maximum f in CrCl_2.55Br_0.45.

Fig. 1. Structure of the van der Waals alloys.

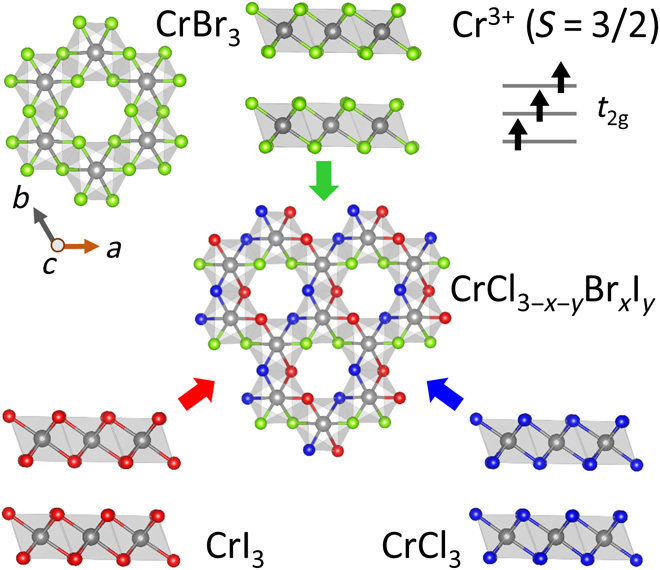
The CrCl_3−x−yBr_xI_y alloys with a honeycomb-layered structure were synthesized by a CVT process from mixtures of CrCl₃, CrBr₃, and CrI₃ in appropriate ratios. The gray, blue, green, and red spheres represent Cr³⁺, Cl⁻, Br⁻, and I⁻, respectively. Cr³⁺ is a spin 3/2 ion with three electrons in the t_2g manifold.

In addition to finding a frustrated regime, we reveal a field-induced change of interlayer coupling from antiferromagnetic (AF) to FM in the bulk CrCl_{3 − x − y}Br_xI_y crystals. So far, such a metamagnetic (MM) transition has been observed only in exfoliation experiments because of the monoclinic stacking of two atomic layers (bilayer) of CrI₃ (4, 5, 16) and CrBr₃ (17). We show that a similar MM transition can be intrinsically engineered in the bulk of CrCl_{3 − x − y}Br_xI_y.

RESULTS

Van der Waals alloys

Single crystals of CrCl_{3 − x − y}Br_xI_y were grown via a chemical vapor transport (CVT) technique from the parent compounds CrCl₃, CrBr₃, and CrI₃ (see Fig. 1 and Materials and Methods). We refer to these single-phase solid solutions as Van der Waals (VdW) alloys. The layered structure of the VdW alloys is illustrated in Fig. 1. Each layer is a 2D honeycomb lattice made of edge-sharing octahedra around the Cr³⁺ ions. There are three electrons in the t_2g levels of Cr³⁺, giving rise to S = 3/2 regardless of the halide ratios in CrCl_{3 − x − y}Br_xI_y (Fig. 1). We point out that mixtures of Cl/Br (CrCl_{3 − x}Br_x) and Br/I (CrBr_yI_{3 − y}) have been reported before (18), but the three-halide series, the frustrated regime, and the bulk MM transition are presented here. We could not grow crystals of CrCl_xI_{3 − x} due to the substantial size difference between Cl and I. A black contour in the phase diagrams of Fig. 2 marks the approximate region of insolubility. Therefore, the intermediate size of Br seems to be crucial in the formation of CrCl_{3 − x − y}Br_xI_y.

Fig. 2. Triangular phase diagrams as a function of Cl, Br, and I content.

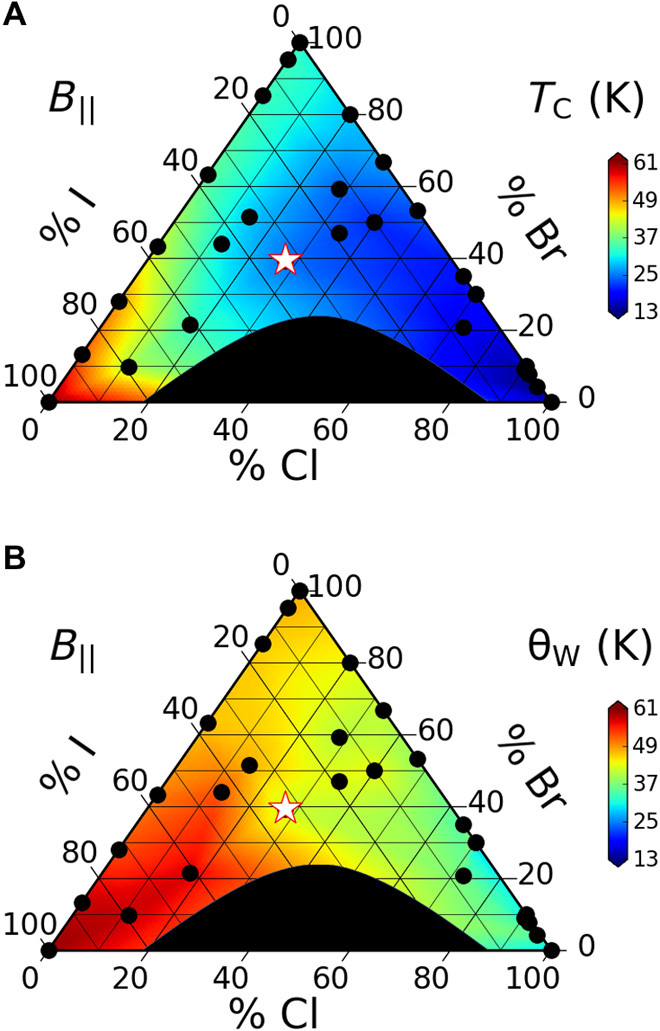
(A) Triangular phase diagram of T_C as a function of composition in CrCl_3−x−yBr_xI_y with field in the plane (B_∥). The star symbol near the center is a composition with 27% Cl (bottom axis), 40% Br (right axis), and 33% I (left axis), corresponding to Cr(Cl_0.27Br_0.40I_0.33)₃ = CrCl_0.8Br_1.2I_1.0. (B) Triangular phase diagram of Θ_W. The color maps are produced by a linear interpolation between the 27 discrete data points, each represented by a black circle. Some of the two-halide samples are the same as in (18).

Triangular phase diagrams

The phase diagrams of Fig. 2 show that both T_C and Θ_W are controlled continuously by tuning the halide composition. This expands the list of available VdW magnets from the parent compounds, CrCl₃, CrBr₃, and CrI₃, to a continuum of compositions CrCl_{3 − x − y}Br_xI_y with tunable magnetic properties. Both T_C and Θ_W acquire minimum values near CrCl₃, intermediate values near CrBr₃, and maximum values near CrI₃. We used a linear interpolation to produce the color maps in Fig. 2 based on the magnetic susceptibility data from 27 samples. For each sample, the data were fitted to a Curie-Weiss (CW) expression, χ = χ₀ + C/(T − Θ_W), where χ₀ is a temperature-independent contribution to susceptibility, C is the Curie constant related to the effective magnetic moment ($\mathrm{\mu }={\mathrm{\mu }}_B\sqrt{8C}$), and Θ_W is the Weiss temperature related to the exchange coupling J = k_BΘ_W/2S(S + 1).

A representative CW analysis is shown in Fig. 3 (A and B) for CrCl_0.8Br_1.2I_1.0, the sample marked as a star near the center of the phase diagrams in Fig. 2. The magnetization of all samples was measured with the magnetic field both parallel (B_∥) and perpendicular (B_⊥) to the honeycomb planes. The effective moment evaluated by the CW analysis in all samples is close to 3.87 μ_B, corresponding to Cr³⁺ (Fig. 2 and fig. S3). The transition temperature for each sample can be determined from the peak in either χ(T) or dχ(T)/dT. Although the results are comparable, we choose the latter criterion because it yields less uncertainty (Supplementary Materials). The triangular phase diagrams of Fig. 2 are constructed from the CW analysis on all samples in the B_∥ configuration. The results for the B_⊥ configuration are similar and presented in the Supplementary Materials.

Fig. 3. Magnetic susceptibility data.

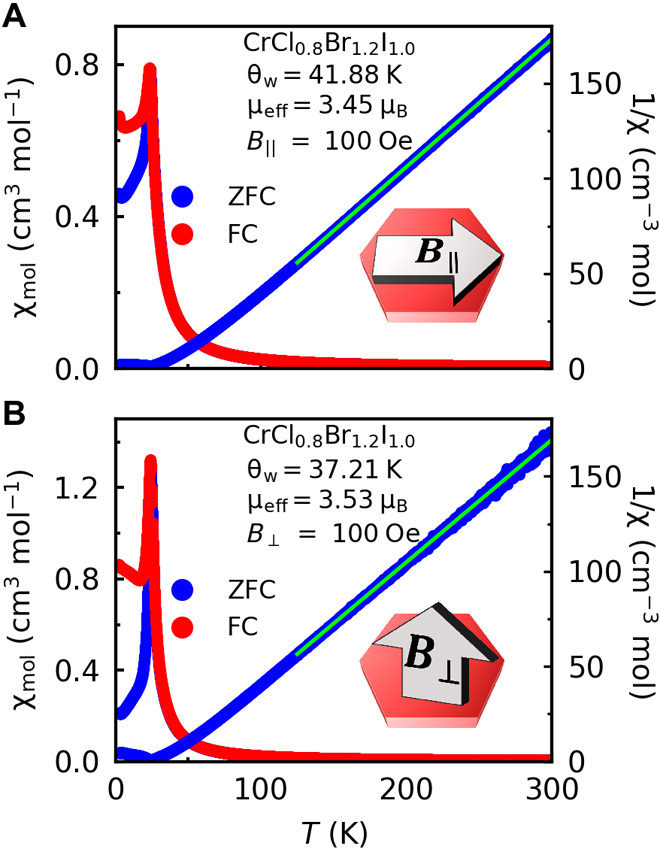
Representative Curie-Weiss analyses on CrCl_0.8Br_1.2I_1.0 measured with field (A) parallel and (B) perpendicular to the honeycomb layers. The observation of a single sharp peak rules out disorder or chemical inhomogeneity (see also fig. S3). Both the zero field–cooled (ZFC; blue) and field-cooled (FC; red) data are presented. Solid green lines show the Curie-Weiss fit to the ZFC data. The Weiss temperature Θ_W and effective moment μ_eff are comparable between the B_∥ and B_⊥ configurations.

Magnetic frustration

A close inspection of the colors in Fig. 2 reveals a subtle point. Whereas the T_C and Θ_W values are nearly identical at the left corner of the phase diagram, they are quite different at the right corner. This observation implies the presence of a moderate magnetic frustration in the compositions near CrCl₃. To clarify, we construct a triangular phase diagram of the frustration index, f = Θ_W/T_C, in Fig. 4. A large frustration index indicates a small T_C relative to the interaction strength J ∝ Θ_W (19). Figure 4 shows that the magnetic frustration is large near CrCl₃, maximizes at the composition CrCl_2.55Br_0.45, and gradually disappears toward either CrBr₃ or CrI₃. Recent theoretical and experimental works have suggested that CrI₃ could be a frustrated VdW material due to the Kitaev interaction (11, 12). However, Fig. 4 suggests that compositions near CrCl₃, specifically CrCl_2.55Br_0.45, are more promising to look for the frustration effects. This is consistent with the competition scenario between the SOC of the transition metal and ligand (or equivalently, between D and λ in Eq. 1), because the atomic SOC in Cr (90 meV) is comparable to Cl (40 meV), but much smaller than Br (220 meV) and I (580 meV).

Fig. 4. Phase diagram of the magnetic frustration.

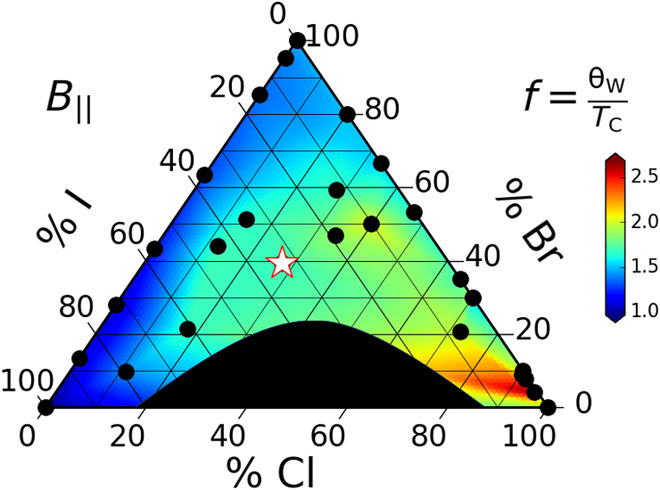
Frustration index (f = Θ_W/T_C) as a function of composition in CrCl_3−x−yBr_xI_y. This map is only a qualitative measure of frustration, especially since the f-index was originally proposed for isotropic (not anisotropic) magnets (19).

Density functional theory

The competition scenario in Eq. 1 and the resulting magnetic frustration in Fig. 4 can be demonstrated from first principles. We performed density functional theory (DFT) calculations for the pure CrCl₃ by controlling the strength of the SOC contributions from Cr and Cl individually.

The DFT Hamiltonian can be written as (9)

$${\mathcal{H}}_{\text{DFT}}={\mathcal{H}}_0+{\mathrm{\alpha }}_{\text{Cr}}{\mathcal{H}}_{\text{SOC}}^{\text{Cr}}+{\mathrm{\alpha }}_{\text{Cl}}{\mathcal{H}}_{\text{SOC}}^{\text{Cl}}$$ (2)

where H₀ is the nonrelativistic Hamiltonian in the absence of any SOC (α_Cr = α_Cl = 0). ${\mathcal{H}}_{\text{SOC}}^{\text{Cr}}$ is the SOC correction in Cr, and ${\mathcal{H}}_{\text{SOC}}^{\text{Cl}}$ is the SOC correction in Cl. By definition, the physical scenario in CrCl₃ corresponds to α_Cr = α_Cl = 1, consistent with the atomic values of the SOC mentioned earlier (15). We can effectively tune the H_DFT from CrCl₃ to CrBr₃ and CrI₃ by increasing α_Cl.

Partitioning the Hamiltonian in Eq. 2 enables us to independently control the contribution from Cr and the halide (Cl, Br, and I) to the magnetic anisotropy and trace the easy-plane versus easy-axis anisotropy. The anisotropy energy of the system is defined as Δ = E_→ − E_↑, where E_→ and E_↑ are the total DFT energies of the in-plane and out-of-plane FM states, respectively. Thus, a negative (positive) Δ corresponds to easy-plane (easy-axis). In the following, we present the analysis in two steps.

First, we show the evolution of the anisotropy energy as a function of the halide SOC in Fig. 5A by fixing the Cr SOC to α_Cr = 1. With increasing α_Cl, Δ gradually approaches zero from negative and turns positive, i.e., the in-plane anisotropy is gradually replaced by out-of-plane anisotropy. In CrCl₃, where α_Cr = α_Cl = 1, the system conserves its easy-plane anisotropy, in agreement with the experimental observation. The alloying process effectively increases the ligand SOC (α_Cl > 1) and leads to Δ > 0, corresponding to the out-of-plane anisotropy found in CrBr₃ and CrI₃.

Fig. 5. Theoretical analysis of the magnetic anisotropy.

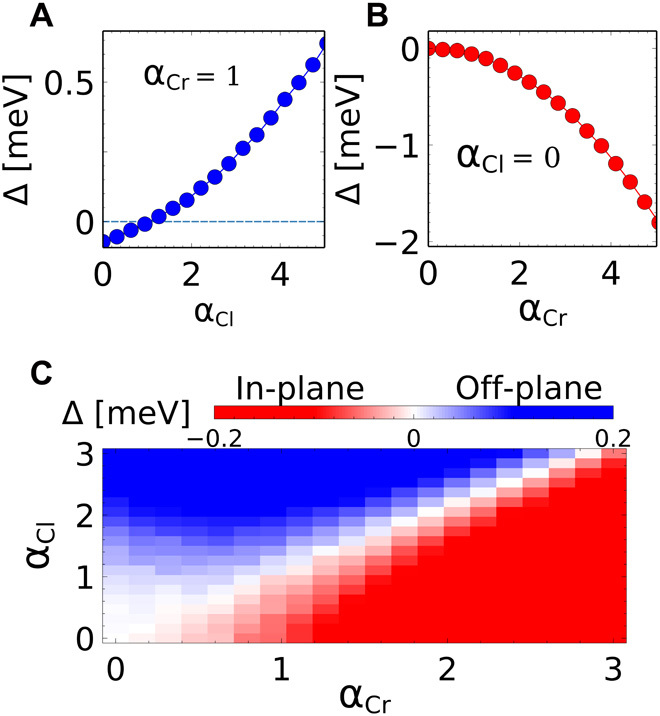
(A) The magnetic anisotropy energy ∆ plotted as a function of Cl SOC (α_Cl) by fixing the SOC of Cr to unity (α_Cr = 1). (B) ∆ plotted as a function of the Cr SOC by switching off the Cl SOC (α_Cl = 0). (C) The anisotropy energy as a function of the SOC in Cr and Cl, showing a competition between in-plane and out-of-plane anisotropies tuned by α_Cr and α_Cl.

Second, we show in Fig. 5B the evolution of the anisotropy as a function of α_Cr by switching off the SOC of Cl (α_Cl = 0). We observe a growing tendency toward in-plane anisotropy (negative Δ) by increasing the Cr SOC. This result confirms that the Cr SOC favors in-plane anisotropy and competes with the halide SOC.

The generic competition between the SOC of the magnetic atom (Cr) and the ligand (Cl) is mapped in Fig. 5C, showing that the anisotropy direction is controlled by the relative strength of the two SOC constants, α_Cr and α_Cl. Notice that CrCl₃ is on the borderline between the in-plane and out-of-plane anisotropy. Thus, the D and λ terms in Eq. 1 nearly cancel each other and drive CrCl₃ toward a frustrated regime (Fig. 4). In contrast, the strong ligand SOC in CrBr₃ and CrI₃ induces a robust out-of-plane FM order and relieves the magnetic frustration. In other words, H_frust. becomes perturbatively irrelevant at low energies in Eq. 1 when the system has a robust easy-axis. We point out that a bare DFT calculation could erroneously predict an easy-axis, instead of easy-plane, in CrCl₃ (20). We had to implement a small (2%) lattice compression to match the DFT results with the experimental in-plane anisotropy in CrCl₃ (details in the Supplementary Materials). We also present DFT results for CrBr₃ in the Supplementary Materials that correctly confirm out-of-plane anisotropy.

MM transition

The first important finding in our experiments was a frustrated regime near CrCl₃ where the effects of D and λ in Eq. 1 nearly cancel out, allowing H_frust. to show its effect. Our second exciting finding is that the interlayer magnetic coupling in the VdW alloys is different from the parent compounds. Recently, an MM transition has been reported at 0.7 T in the bilayers of CrI₃ due to a field-induced change of interlayer coupling from AF to FM (4, 5). The AF-FM switching of the interlayer coupling produces a sharp step in the M(H) curves of CrI₃ bilayers, corresponding to a spin-flip transition. This effect has been used in a spin-filter magnetic tunnel junction where a step-like magnetoresistance has been observed at the MM transition (21, 22). Figure 6A shows a similar MM transition in the bulk crystals of CrCl_0.8Br_1.2I_1.0 as a function of field. Notice that the transition is observed only when the field is perpendicular to the plane (B_⊥). A magnified view of the M(B) curves in Fig. 6B shows that the transition occurs at B_⊥ = 0.7 T, the same field at which CrI₃ bilayers undergo a spin-flip transition (4, 5). However, the MM transition in CrCl_0.8Br_1.2I_1.0 is less sharp than in the bilayers of CrI₃ (4). Hence, we assign this transition to a field-induced spin canting, instead of spin-flop, as illustrated in the inset of Fig. 6B.

Fig. 6. MM transition in the bulk of VdW alloys.

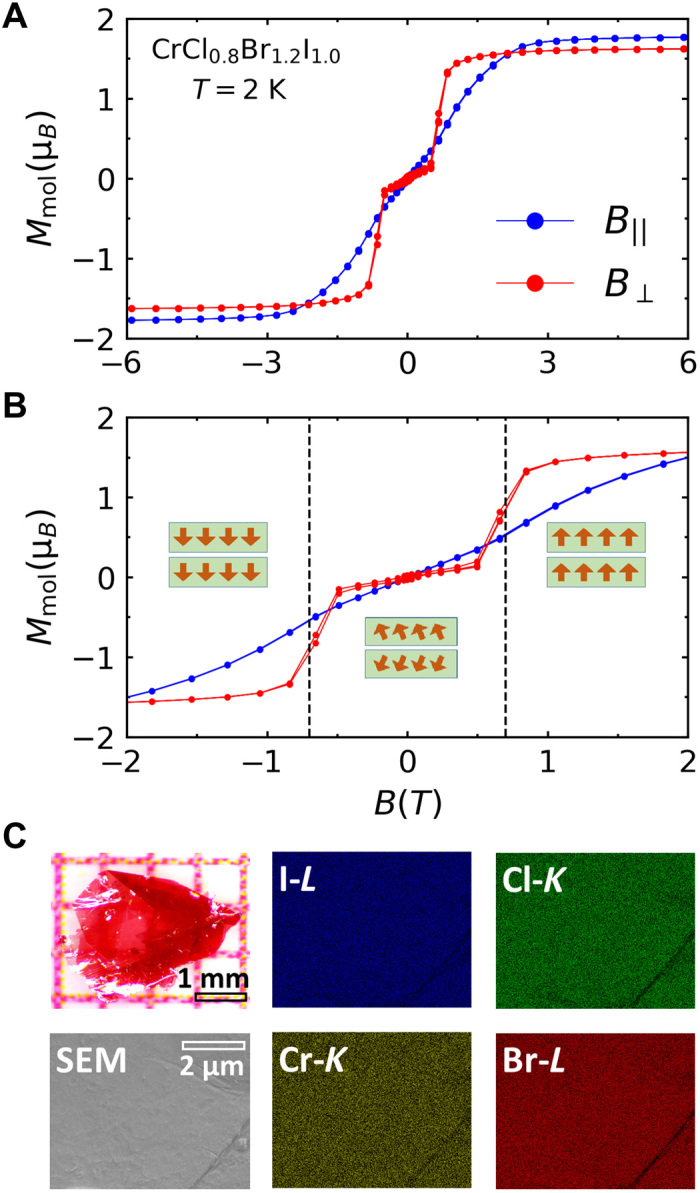
(A) Magnetization plotted as a function of field in CrCl_0.8Br_1.2I_1.0. The red and blue data correspond to the field perpendicular (B_⊥) and parallel (B_∥) to the honeycomb layers, respectively. The saturated moment is consistent with S = 3/2 in Cr³⁺. (B) Magnified view of the spin-canting transition at B_⊥ = 0.7 T. (C) Optical image, scanning electron microscope (SEM) image, and energy-dispersive x-ray spectroscopy (EDX) color maps reveal a uniform distribution of Cr (yellow, K-edge), Cl (green, K-edge), Br (red, L-edge), and I (blue, L-edge) in CrCl_0.8Br_1.2I_1.0. Photo credit: F.T., Boston College.

Chemical inhomogeneity or disorder does not play a role in either the MM transition or magnetic frustration. We performed energy-dispersive x-ray spectroscopy (EDX) on each sample inside a scanning electron microscope (SEM). The SEM-EDX color maps in Fig. 6C confirm a uniform distribution of Cr, Cl, Br, and I atoms in a CrCl_0.8Br_1.2I_1.0 crystal and rule out a phase separation scenario. In materials with impurity phases or inhomogeneous distribution of elements, the color maps reveal regions of dark and light shade (23). A table of EDX results is reported in the Supplementary Materials. Furthermore, all three-halide VdW alloys show a single sharp magnetic transition (Fig. 3 and figs. S2 and S3), similar to the parent compounds (24). If the samples were disordered or chemically inhomogeneous, then we would have expected either a rounded transition or multiple transitions, which is not the case.

DISCUSSION AND OUTLOOK

Despite the conventional wisdom to tune magnetism by doping on the cation site where the magnetic moment resides (25, 26), we highlight the remarkable effect of mixing the anions to synthesize a continuum of VdW magnets with chemical control over the ligand SOC. Note that the change of SOC from Cl to I is enormous (more than one order of magnitude) based on the atomic values of SOC (15), whereas the change of local geometry and bond angle is minimal. For example, the Cr-ligand-Cr bond angles are 93.9° and 93.3° in the low-temperature structure of CrCl₃ and CrI₃, respectively (14, 27). Thus, the dominant tuning parameter in our phase diagrams is the ligand SOC.

The chromium trihalides provided a unique opportunity for our experiments due to their remarkable chemical tunability. Because the SOC of Cl<Cr < Br<I, we were able to tune the SOC of the magnetic ion and the ligands against each other. Without making a solid solution of three halides and mapping the phase diagram of CrCl_{3 − x − y}Br_xI_y, it would have been impossible to find the frustrated regime and the change of interlayer coupling.

We point out that the alloying process inevitably leads to bond randomness. On the basis of the remarkable agreement between our mean-field DFT approach and the experimental results, it appears that the bond randomness at an atomic level does not markedly affect the magnetic anisotropy and magnetic order. However, it would be an interesting future direction to go beyond the mean-field level and explore the role of bond randomness in VdW alloys near the Kitaev limit (28).

The methods presented here can, in principle, be extended to chalcogenides. Examples of chalcogen-based VdW magnets are the itinerant ferromagnet Fe₃GeTe₂ (29, 30), the FM insulator Cr₂Ge₂Te₆ (6), and the AF layered compound FePS₃ (31, 32). One advantage of the chalcogenides is their relatively high transition temperatures. For example, T_C = 220 K in Fe₃GeTe₂ (33), T_C = 60 K in Cr₂Ge₂Te₆ (34), and T_N = 118 K in FePS₃ (31). The magnetic properties of these materials can be controlled by mixing the chalcogens S, Se, and Te. These efforts will not only expand the list of desirable VdW magnets (8, 35), but also lead to new regimes (such as frustration) and new phenomena (such as spin-canting transition).

As mentioned earlier, the magnetic ordering in CrI₃ is known to acquire a layer-dependent structure in the atomically thin limit (single layer, bilayer, and trilayer) (5, 17, 22, 36–38). An important question is whether the MM transition at 0.7 T in the bulk crystals of CrCl_0.8Br_1.2I_1.0 is due to a change of stacking sequence or a structural transition at low temperatures. This question could be answered by low-temperature synchrotron x-ray experiments in the future.

In the Supplementary Materials, we show that the alloyed crystals are as exfoliable as their parent structures. It will be interesting to exfoliate the bulk crystals of CrCl_0.8Br_1.2I_1.0 and isolate bilayers and trilayers to look for a richer pattern of MM transitions by measuring the magneto-optical Kerr effect. These heterostructures will be an invaluable resource for new devices, such as spin-filter tunneling junctions (21, 22, 39, 40) and magnon-assisted tunneling devices (41).

MATERIALS AND METHODS

Crystal growth

The crystals of CrCl_{3 − x − y}Br_xI_y were grown by the CVT method from CrCl₃, CrBr₃, and CrI₃ precursors mixed with appropriate mole ratios (see table S1). In a typical CVT cycle, 400 mg of the starting mixture was placed inside a 15 cm-long fused silica tube and held at 650°C, with a 200°C temperature gradient, for 72 hours. CrCl₃ crystals were grown by vacuum sublimation of polycrystalline CrCl₃ at 650°C for 72 hours. CrBr₃ crystals were grown by annealing a mixture of Cr + 0.75TeBr₄ at 700°C for 72 hours. CrI₃ crystals were grown by annealing a mixture of Cr + 1.5I₂ at 650°C for 72 hours. The starting chemicals, Cr(99.99%), CrCl₃ (99.9%), TeBr₄ (99.9%), and I₂ (99.8%) were purchased from Alfa Aesar. The crystals grew in the form of thin plates, several millimeters across and less than 1 μm thick.

Electron microscopy

The morphology and chemical composition of crystals were studied by SEM and EDX using a JEOL 7900F field-emission SEM equipped with an EDAX detector.

Magnetic measurements

Magnetic measurements were performed using a vibrating sample magnetometer inside a Quantum Design MPMS-3. Thin plate-like crystals were mounted on a low-background quartz or sapphire holder for the B_∥ and B_⊥ measurements, respectively.

Density functional theory

DFT calculations were performed using the all-electron Elk code (42). Lattice relaxations were performed with Quantum Espresso (43), Perdew-Burke-Ernzerhof for solids functional, and PAW pseudopotentials. A 2% lattice compression was imposed to match the DFT results with the experimental observations (see the Supplementary Materials for details) (20, 44). The total energy convergence was set to 0.027 μeV to account for the small energy differences involved in magnetic anisotropies.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/30/eabb9379/DC1