Molding free-space light with guided wave–driven metasurfaces

A guided wave–driven metasurface directly extracts and molds light from a waveguide into arbitrarily complex free-space modes.

Abstract

Metasurfaces with unparalleled controllability of light have shown great potential to revolutionize conventional optics. However, they mainly require external light excitation, which makes it difficult to fully integrate them on-chip. On the other hand, integrated photonics enables packing optical components densely on a chip, but it has limited free-space light controllability. Here, by dressing metasurfaces onto waveguides, we molded guided waves into any desired free-space modes to achieve complex free-space functions, such as out-of-plane beam deflection and focusing. This metasurface also breaks the degeneracy of clockwise- and counterclockwise-propagating whispering gallery modes in an active microring resonator, leading to on-chip direct orbital angular momentum lasing. Our study shows a viable route toward complete control of light across integrated photonics and free-space platforms and paves a way for creating multifunctional photonic integrated devices with agile access to free space, which enables a plethora of applications in communications, remote sensing, displays, etc.

INTRODUCTION

With the fast-growing demands for big data, electronic chips and interconnects with insufficient bandwidth can hardly meet the requirements on data transmission speed and energy efficiency of future computing and storage systems. Wiring light on a chip like electronic circuits, integrated photonics provides a promising long-term solution (1, 2). A photonic integrated circuit (PIC) combines many light-controlling components into a single chip, with the ultimate aim of creating miniature optical circuits similar to CMOS (complementary metal oxide semiconductor) chips that have revolutionized the electronics industry. It offers great advantages in terms of speed, bandwidth, reliability, scalability, power consumption, etc. To fully exploit the benefits of PICs in free-space applications, it is crucial to have an interface that can flexibly control light when it converts between guided and free-space modes. However, two conventional coupling techniques—edge couplers (3) and surface gratings (4)—have limited functionalities and lack complete control over light. Although arrays of gratings can achieve more advanced functions, such as off-chip beam steering (5), focusing (6), and holographic image construction (7), they have large footprints and suffer from loss because of the existence of high-order diffractions. Subwavelength gratings (8) have compact footprints, but they mainly work in controlling the guided waves rather than the manipulation of light across PICs and free space. Recently, optical nanoantennas have been integrated on top of waveguides (9), which provides a new way for interfacing guided and free-space optical modes and adds more functionalities to PICs. Nevertheless, most of them rely on a singular property of nanoantennas to achieve a specific purpose, such as photo detection (10) or modulation (11) based on plasmonic field enhancement and directional routing from spin-orbit coupling (12). A unified approach leveraging the collective free-space functions of nanoantennas on PICs has not been demonstrated.

On the other hand, newly emerging metasurface (13, 14)—an ultrathin artificial surface that manipulates light by locally imposing abrupt changes to optical properties through engineered subwavelength structures also known as meta-atoms—provides unparalleled controllability to the free-space light propagation. However, most of the metasurfaces are driven by free-space light to realize functions, such as beam deflection (13, 14), generating orbital angular momentum (OAM) beams (13), light focusing (15), and holograms (16), which makes it difficult for further on-chip integration (e.g., integrating with light sources on the same chip). Besides, plasmonic metasurfaces have been used to route surface plasmon polariton waves to arbitrary free-space radiation (17–20), and their design principles can be leveraged to bridge the gap between guided waves and free-space waves.

Here, we combined synergically two powerful, complimentary technologies (integrated photonics and metasurfaces) and developed a hybrid architecture where metasurfaces are directly driven by guided waves to realize complex free-space functions. We placed subwavelength-sized meta-atoms on top of photonic integrated components (Fig. 1A). In contrast to existing metasurfaces that operate with both input and output light in free space, our integrated metasurface bridges guided waves inside a waveguide with free-space ones. Through it, the guided light is tapered into free space and molded into desired light fields. The subwavelength spacing of the meta-atoms eliminates diffraction loss and also allows denser on-chip integration. Meanwhile, multiple metasurfaces can be connected via waveguides to achieve different free-space functions simultaneously. Although phase-gradient plasmonic metasurfaces have been used for guided mode conversion (21, 22), their limited phase controllability (~π) makes it inadequate for wavefront shaping. Our design overcomes this limitation by using metal-dielectric-metal nanoantennas to expand the phase tuning range to over 2π. Such guided wave–driven metasurfaces go beyond the existing technology of leaky-wave antennas made of periodic structures (23) and extend the functionalities of microwave waveguide-fed metasurface (24) to new spectral regions.

Fig. 1. Working principle of guided wave–driven metasurfaces.

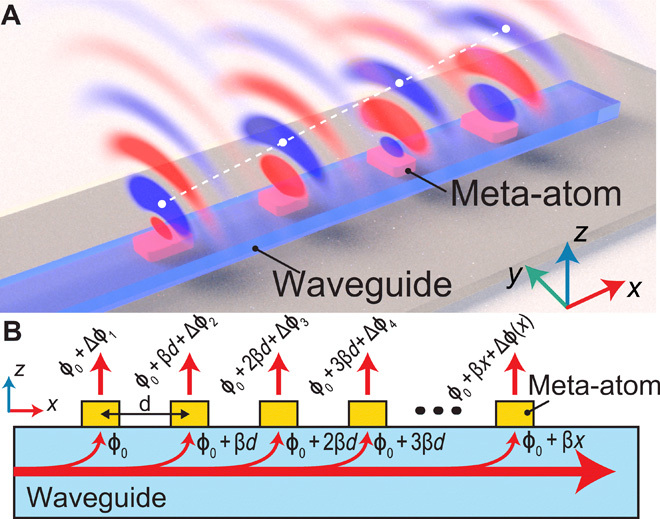
(A) Schematic of a guided wave–driven metasurface. The phase of the extracted light from a guided wave by each meta-atom can be tuned individually. An array of meta-atoms on the waveguide work collaboratively to form certain wavefronts and fulfill different functions, such as beam deflection and focusing. (B) Illustration of the wavefront formation of the extracted wave. The total phase shift of the extracted wave at coordinate x is contributed from two parts: the phase accumulation βx from the guided wave propagation and the abrupt phase change Δϕ(x) induced by the meta-atom. As a result, the phase of the extracted wave can be expressed as ϕ₀ + βx + Δϕ(x), where ϕ₀ is the initial phase of the incidence.

The developed technology will potentially be a huge step toward full control of light across integrated photonics and free-space platforms and will pave exciting ways for building multifunctional PIC devices with flexible access to free space as well as guided wave–driven metasurfaces with full on-chip integration capability. It could enable a plethora of applications in optical communications, optical remote sensing [e.g., light detection and ranging (LiDAR) (25)], free-space optical interconnects (26), and displays (27). In addition, a library of those functional hybrid components can be established for reusing and creating consistency across various devices or systems.

RESULTS

In contrast to the free-space metasurfaces where the spatial phase profile is solely provided by the meta-atoms, the total phase shift of the extracted wave from our guided wave–driven metasurface is contributed from two parts: (i) the phase accumulation from the propagation of the guided wave βx (where β is the propagation constant of the guided mode, and we assumed that the waveguide lays straight along the x direction) and (ii) the abrupt and spatially variant phase shift Δϕ(x) induced by each meta-atom at coordinate x (Fig. 1B). The essence of such metasurfaces is to use subwavelength-sized meta-atoms to form spatially varying optical response, which extracts and molds guided waves into any desired free-space optical modes. This distinguishes such metasurfaces from leaky-wave antennas, which typically do not have spatial-variant electromagnetic responses (23). As a result, the phase distribution of the extracted wave along the x direction can be expressed as

$$\mathrm{\varphi }(x)=\mathrm{\beta }x+\mathrm{\Delta }\mathrm{\varphi }(x)$$ (1)

Although the propagation accumulated phase contributes to the targeted phase function, it only acts as a uniform bias because meta-atoms are uniformly distributed on top of the waveguide. To achieve complete control of the wavefront, at least 2π phase shift range induced by meta-atoms is required. Placing the meta-atoms on the waveguide, it is challenging to use a mirror resonance or a geometrical phase to achieve 2π phase shift (28). Therefore, here, we designed a metal-dielectric-metal sandwiched nanobar antenna (Fig. 2A)—which supports two resonant modes and is evanescently coupled with the guided waves inside the waveguide—as the meta-atom. The fundamental transverse electric mode (TE₀₀) in a dielectric rectangular waveguide (Fig. 2A, left) was used to excite resonant modes of meta-atoms, as its field distribution has a good spatial overlap with the electric dipolar mode in a nanobar antenna. The thickness, width, and length of the sandwiched nanoantennas were carefully chosen so that when the bottom gold cuboid is excited by the evanescent tail of a guided wave and induced an electric dipole, an antiparallel one can be induced in the top cuboids; therefore, an effective magnetic dipolar resonance is excited (fig. S1A). Simultaneously, the electric dipoles induced in the top and bottom gold cuboids do not completely cancel out, resulting in a net electric dipolar resonance. The magnetic resonance combined with the electric one creates a directional radiation that extracts the guided wave to free space, and it also provides an abrupt phase shift range ~2π to the extracted wave (fig. S3). This abrupt phase shift can be tuned by varying the geometrical parameters of the meta-atoms. In addition, by controlling the amount of spatial mode overlap between the antenna mode and the guided mode, we are able to flexibly adjust amplitude of the extracted wave. With the light extraction and control capabilities of meta-atoms, various free-space optical functions can be realized by distributing them strategically along the waveguide.

Fig. 2. Design of meta-atoms for controlling the phase (and amplitude) of free-space waves extracted from guided ones.

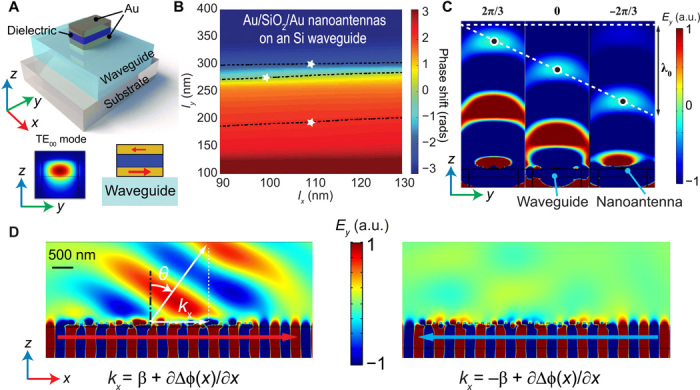
(A) Schematic of a metal/dielectric/metal sandwich-structured meta-atom on top of a photonic integrated waveguide. The bottom left inset shows the simulated electric field distribution of the TE₀₀-guided mode propagating inside the waveguide. The bottom right inset is the simulated magnetic field distribution of the sandwich-structured nanoantenna, which indicates an effective magnetic dipole. (B) Pseudocolor map of the simulated abrupt phase shifts in a parameter space spanned by the meta-atom width (l_x) and length (l_y). A thickness of 30 nm was used for each layer. The meta-atom was placed on top of a silicon ridge waveguide (height, 220 nm). The three white stars indicate the meta-atom designs covering 2π phase range with an even interval. We also ensured that the extracted waves from the chosen meta-atoms have roughly the same amplitude of 1.5 × 10⁵ V/m. (C) Simulated electric field distribution (E_y) of the extracted waves from the three selected meta-atoms, showing abrupt phase shifts of 2π/3, 0, and −2π/3, respectively. (D) Electric field distribution of the extracted light from a phase-gradient metasurface driven by forward-propagating (left) and backward-propagating (right) guided waves. The metasurface consists of an array of meta-atoms that form a phase gradient ∂Δϕ(x)/∂x (which is along the –x direction in this example). The extracted light from a forward-propagating guided wave carries a transverse wave vector k_x = β + ∂Δϕ(x)/∂x, where β is the propagation constant of the guided wave. It is launched into free space with a well-defined angle θ = sin⁻¹(k_x/k₀). In contrast, light extracted from the backward-propagating wave gains a transverse wave vector so large that it exceeds the maximum supportable wave number in free space, and therefore, it bounds to the metasurface and eventually dies out due to ohmic loss from the materials. a.u., arbitrary unit.

To show the capability of the guided wave–driven metasurfaces, we numerically and experimentally demonstrated off-chip beam deflection and light focusing directly from a photonic integrated waveguide. Besides, by spatially arranging meta-atoms on PICs with optical gain materials, we created micrometer-sized photonic integrated microring lasers that directly emit vector optical vortices carrying well-defined, quantized OAM.

Off-chip beam deflection and focusing with an integrated guided wave–driven metasurface

According to Eq. 1, the linear momentum of extracted light along x direction is k_x = β + ∂Δϕ(x)/∂x. If ∂Δϕ(x)/∂x is a constant, the extracted beam has a well-defined angle θ given by θ = sin⁻¹(k_x/k₀), where k₀ is the free-space wave number. In contrast to grating couplers on PICs, our metasurface approach introduces abrupt and large phase shifts with a subwavelength spacing, which eliminates high-order diffractions and offers a much large beam deflection angle range.

We used Au/SiO₂/Au sandwich-structured nanoantennas as the meta-atoms for beam deflection. The meta-atoms are periodically distributed on a silicon waveguide to provide a phase gradient ∂Δϕ(x)/∂x = −2π/Λ, where Λ is the length of a supercell that consists of three meta-atoms with abrupt phase shifts –2π/3, 0, and 2π/3. Therefore, the output angle of the extracted beam is $\mathrm{\theta }={\text{sin}}^{-1}\frac{1}{k_0}(\mathrm{\beta }-\frac{2\mathrm{\pi }}{\mathrm{\Lambda }})$ (Fig. 2D). We simulated the radiation phase shift with respect to the guided wave right underneath the meta-atom using full-wave finite element method (FEM) (fig. S1). We chose meta-atom designs that have uniform amplitude of the extracted wave while having phase shifts that cover the entire 2π phase range, as indicated by the white stars in Fig. 2B. The simulated electrical field distribution for the three selected meta-atoms on the waveguide validates that the extracted waves have uniformly distributed abrupt phase shifts spaced by 2π/3 (Fig. 2C). The asymmetric coupling effect can be observed by reversing the propagation direction of the guided wave. The resulting momentum along the x direction becomes k_x = −β – 2π/Λ, which is too large to be supported in free space (Fig. 2D, left). In this case, the extracted wave bounds to the metasurface and eventually dies out due to ohmic loss from the materials. It is worth noting that reciprocity of the system is preserved as the transmitted power in the waveguide for the forward- and backward-propagating waves is equal.

We fabricated the beam deflection samples using two electron beam lithography steps with precise alignment to define the silicon waveguide and the meta-atoms (Fig. 3A). Different lengths of supercells were chosen to demonstrate flexible control of the beam deflection angles. The propagation constant β was numerically calculated for the fundamental TE modes at different wavelengths. Fourier-space imaging system was used to measure the scattering angles. We experimentally measured the output angles with different wavelengths and supercell periods, respectively, and the results agree well with those from our theoretical calculations (Fig. 3, B and C). The slight discrepancy originates from the fabrication error. The line-shaped intensity profile in Fourier space reveals the in-plane wave vector of the extracted light, where k_x is determined by the metasurface and k_y spans the whole Fourier plane because no phase modulation is applied in the y direction. The divergence of the steering angle, which is depicted by the width of the line, is inversely related to the length of the metasurface region. The bright ends of the lines near the cutoff lines in Fourier-space images limited by the objective’s numerical aperture (NA = 0.95) are originated from the internal reflection in the objective. The Fourier-space images were also validated by theoretical calculations (fig. S6).

Fig. 3. Demonstration of off-chip beam deflection with guided wave–driven metasurfaces.

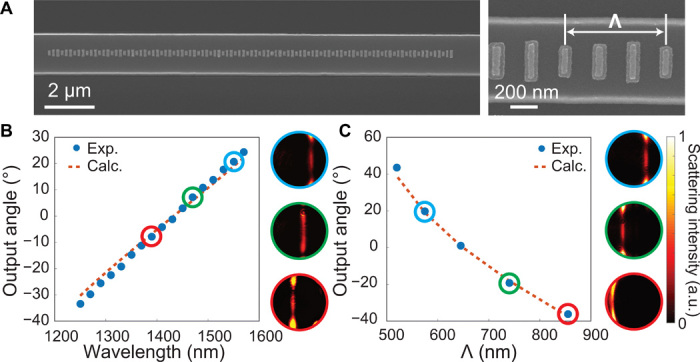
(A) Field emission scanning electron microscope (FESEM) images of a guided wave–driven metasurface on a silicon waveguide (220 nm thick and 600 nm wide). Each supercell consists of three meta-atoms as depicted in Fig. 2B. (B) Output beam angle versus the incident guided wave wavelength with supercell size Λ = 575 nm measured by our Fourier-space imaging system (fig. S4). The blue dots and the red dashed line depict the experimentally measured and the simulated data, respectively. Three typical Fourier-space images of the extracted free-space light corresponding to the circled data points are shown on the right. The horizontal and vertical axes represent k_x and k_y, respectively. An objective with NA of 0.95 was used in the measurements. (C) Output beam angle versus the supercell size at 1550-nm wavelength. The blue dots and the red dashed line depict the experimentally measured and the simulated data, respectively. Similar to (B), three typical Fourier-space images are shown on the right.

The efficiency of the device was estimated using full-wave numerical simulations (fig. S4), which shows a theoretical limitation of 9% because of the existence of large absorption loss from the metallic components. However, this can be alleviated by using pure dielectric SiO₂/Si/SiO₂ sandwiched nanoantennas, which have no material loss in the telecommunication wavelength range. The efficiency can be controlled by the number of supercells integrated on the waveguides, and a maximum value as high as 80% can be expected with enough numbers of supercells. Although our current demonstration used a single set of meta-atoms that were uniformly placed on the waveguide, inspired by the designs of apodized gratings (29–31), we can either vary the meta-atom densities or use multiple sets of meta-atoms with different scattering efficiencies to balance the extraction efficiency everywhere with the propagation/extraction loss of the waveguide mode. In either way, we are able to achieve spatial-variant scattering efficiencies along the waveguide and, hence, to enable uniform-intensity extraction or to construct an arbitrary extraction intensity profile, e.g., a Gaussian beam profile.

In addition, spatially arranging the meta-atoms along a waveguide to fulfill a lens phase function $\mathrm{\varphi }(x)=-k_0\sqrt{x^2+f^2}$, we can focus the wave in free space with a designated focal length f. Therefore, considering Eq. 1, the abrupt phase shifts provided by the meta-atoms should be

$$\mathrm{\Delta }\mathrm{\varphi }(x)=-k_0\sqrt{x^2+f^2}-\mathrm{\beta }x$$ (2)

As a proof of concept, we simulated such a metalens on a silicon waveguide with a focal length f = 5 μm (we chose a short focal length to reduce the demand for computational resources) at 1550 nm (Fig. 4A). Evidently, light is extracted and focused into free space by the metalens. We designed and fabricated a larger guided wave–driven metalens with a focal length of 225 μm. The intensity distribution at different heights above the waveguide was measured and reconstructed in the xz plane (Fig. 4B), which shows clear focusing effect matching our simulation results. In addition, the light focusing effect was also observed at different wavelengths both by simulations and experiments (fig. S5).

Fig. 4. Demonstration of off-chip light focusing with a guided wave–driven metalens.

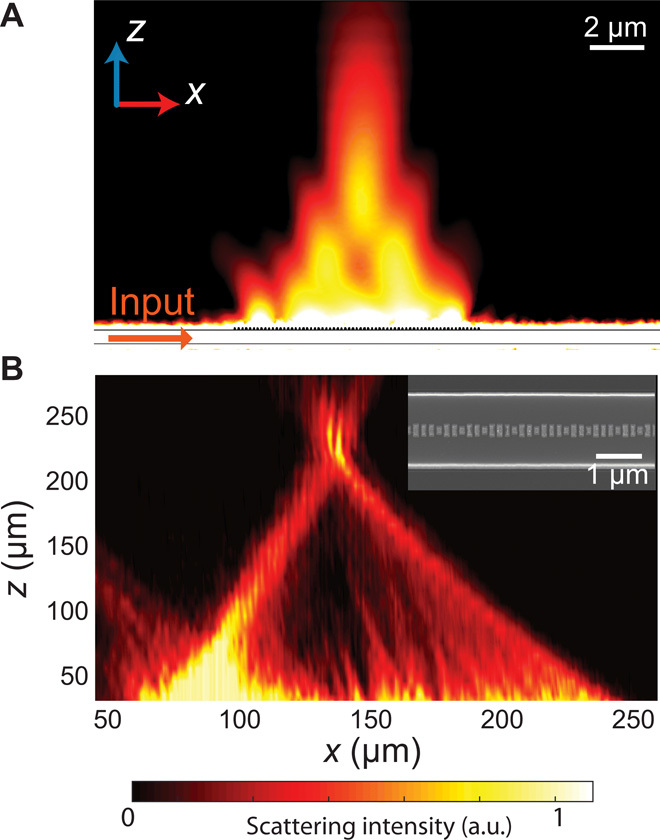
(A) Simulated electric field distribution above a guided wave–driven metalens on a silicon waveguide (500 nm thick and 1.5 μm wide). The extracted light converged at the designed focal point (5 μm above the waveguide) at 1550-nm wavelength. (B) Experimentally measured intensity profile of the focusing effect of a fabricated device. The inset shows an FESEM image of the metasurface region. The designed focal length is 225 μm.

Photonic integrated OAM lasers

Leveraging the asymmetric coupling induced by the guided wave–driven metasurface, we are able to create a photonic integrated microring OAM laser (Fig. 5A). Light beams with an azimuthal phase profile of the form exp.(ilφ) carry an OAM of lℏ (32), where l is an integer known as the topological charge, and φ is the azimuthal angle with respect to the propagation direction. Light can have an infinite number of orthogonal OAM states essentially. This unique property makes it an excellent candidate for encoding information in both classical (33, 34) and quantum (35, 36) optical communications as well as many other applications (37). A conventional system for generating OAM light usually have two separate parts—a light source and an optical component for spatial phase modulation, e.g., spatial light modulator (38), phase plates (39, 40), and metasurfaces (41), which makes it bulky, poor in scalability, and difficult for on-chip integration. A compact, integratable, and scalable source that directly emits OAM light (42, 43) is highly desirable.

Fig. 5. Photonic integrated OAM laser based on the guided wave–driven metasurface incorporated on an InGaAsP/InP micoring resonator.

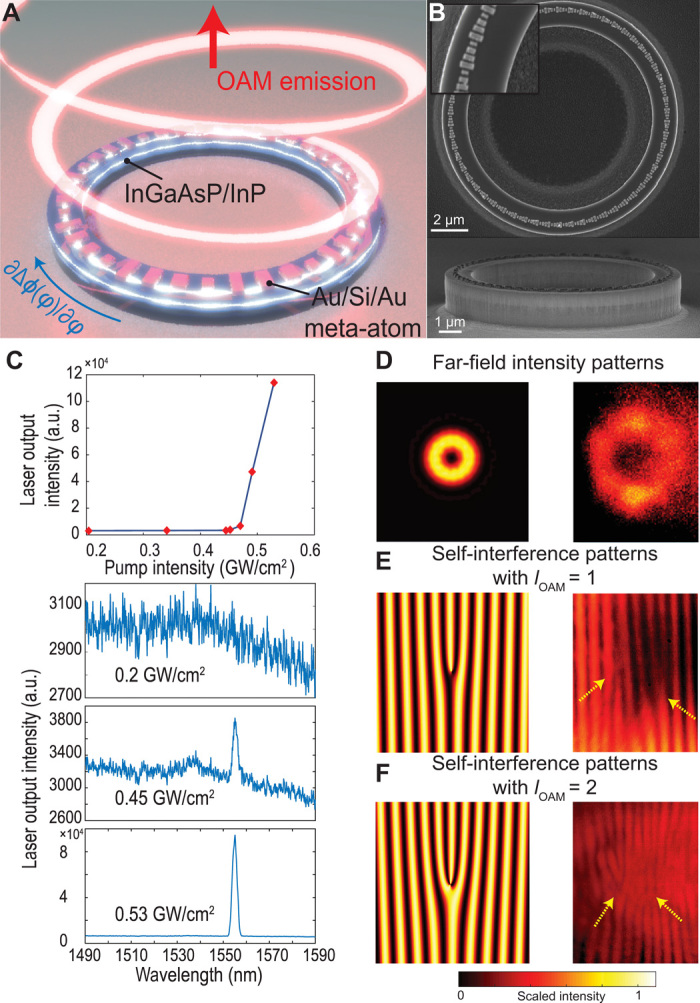
(A) Schematic of a microring OAM laser enabled by the guided wave–driven metasurface. Unidirectional phase modulation provided by the metasurface breaks the degeneracy of the CCW and CW WGMs inside the microring resonator, leading to a selective OAM radiation. (B) FESEM images of a fabricated device. The diameter of the microring is 9 μm and the width is 1.1 μm, and it consists of a 500-nm InGaAsP MQW layer and a 1-μm InP layer. A supercell of the metasurface consists of four Au/Si/Au meta-atoms, which provides the extracted wave with abrupt phase shifts from 0 to 2π. The total number of supercells on the microring is N = 58. (C) Light-light curve of the microring laser (top row), which shows a lasing threshold of about 0.47 GW/cm² at 1555-nm wavelength. Three emission spectra corresponding to different stages—photoluminescence, amplified spontaneous emission, and lasing—of the laser are shown from the second to the last row. (D) Far-field intensity distribution of the OAM laser radiation captured by an infrared camera (right), which matches well with the simulated one (left). Both figures show an annular shape. (E and F) Calculated (left) and measured (right) self-interference patterns of OAM laser radiation. The calculation only took into account the interference between a plane wave and an OAM beam; therefore, it shows one set of fork in the interference pattern. The double fork (E) and triple fork (F) in the fringe patterns confirmed that the resulting OAM emission has a topological charge of +1 (E) and +2 (F), respectively.

The microring resonator intrinsically supports two degenerate whispering gallery modes (WGMs)—a clockwise (CW) and a counterclockwise (CCW) mode. These modes by themselves carry high-order OAM. However, because of the inversion symmetry of the microring, the OAMs of the CW and CCW modes have opposite signs, and the net OAM is zero (43). To obtain controllable OAM emission, our metasurface accomplished three functions: (i) extract light from the microring without destroying the guided modes, (ii) break the degeneracy of the two WGM modes to get nonzero net OAM emission, and (iii) control the topological charge of the OAM.

Because of the asymmetric coupling effect of the guided wave–driven metasurface, only one of the two counterpropagating WGMs can couple to the free-space emission, and therefore, we are able to break the degeneracy of the WGMs and achieve a controllable OAM emission. As the degenerate WGMs interact with the metasurface on a microring that introduces a unidirectional phase gradient ∂ϕ/∂φ (φ is the azimuth angle), the radiated light of CW and CCW mode will gain additional but opposite momenta. One radiation mode will gain too large k to propagate in free space, while the other one can be successfully launched into free space with a well-defined OAM order.

Let us suppose we want the CCW mode to be extracted and form OAM emission in free space. The propagation constant of the M^th-order CCW WGM is given by β_CCW = 2πn_m/λ = M/R, where n_m is the modal index and R is the microring radius. The guided wave–driven metasurface is placed on the microring so that it induces a phase gradient that is equivalent to a wave number k_ms = − 2π/Λ, where the phase shifts provided by the meta-atoms decrease linearly along the CCW direction. The azimuthal phase dependence of the OAM emission can be expressed as ϕ_OAM(φ) = lφ. Because of momentum conservation, the following condition should be satisfied

$$l\mathrm{\phi }={\mathrm{\varphi }}_{\text{OAM}}={\mathrm{\varphi }}_{\text{CCW}}+{\mathrm{\varphi }}_{\text{ms}}={\mathrm{\beta }}_{\text{CCW}}R\mathrm{\phi }-\frac{2\mathrm{\pi }}{\mathrm{\Lambda }}R\mathrm{\phi }$$ (3)

Assuming the total number of metasurface supercells on the microring is N =$\frac{2\mathrm{\pi }R}{\mathrm{\Lambda }}$, we can obtain from Eq. 3 a well-defined topological charge

$$l=M-N$$ (4)

which can be easily engineered either by tuning the order of the WGM mode or by placing different numbers of supercells on the microring.

We designed our OAM laser based on an InGaAsP/InP multi-quantum-well (MQW) microring resonator. Four Au/Si/Au sandwich-structured meta-atoms covering 2π abrupt phase shift range (fig. S7A) were used to construct one metasurface supercell and patterned periodically on top of the microring. These meta-atoms were positioned away from the center of the waveguide by 140 nm to ensure an optimum spatial overlap with the WGM (Fig. 5A). We showed using full-wave FEM eigen-mode simulations that the emitted light is radially polarized and exhibits the characteristics of OAM emission. With M = 59 and N = 58, the electric field E_r forms a spiral pattern, and its phase changes by 2π upon one full circle around the center of the vortex, indicating l = 1 (fig. S7C, left). We also showed the simulation results of l = 2 with M = 59 and N = 57 (fig. S7C, right). The phase profile depicts a 4π winding around the center of the vortex.

We fabricated the microring OAM laser (Fig. 5B) and characterized its lasing properties. The microring was pumped by 900-nm femtosecond pulses (~140 fs) from a Ti:sapphire laser, and the radiation from the microring was collected and analyzed by a spectrometer (fig. S8). The spectra gradually transitioned from spontaneous emission (SE) to amplified SE (ASE) and, finally, to lasing as the pump intensity increased (Fig. 5C). The OAM characteristics were characterized by analyzing both the spatial intensity profile of the emission using a near-infrared camera and its self-interference pattern using Michelson interferometry (fig. S8). We observed the intensity of lasing emission spatially distributed in a doughnut shape with a dark core in the center (Fig. 5D), which is due to the phase singularity at the beam axis where the phase becomes discontinuous. The presence of the OAM was also validated by the self-interference patterns (Fig. 5, E and F). We split equally the beam emitted from the microring into the two arms of a homebuilt Michelson interferometer. Because in an OAM beam, the phase varies drastically (helical) close to the central singularity, whereas it is relatively uniform (quasi-planar) at the outer rim, we intentionally created a horizontal offset between the two split OAM beams at the observation plane, so that the dark center of one beam overlapped with the bright outer rim of the other and vice versa. Because the quasi-planar and the helical phase fronts were reversed at the center of each OAM beam, the interference revealed two inverted forks in the resulting fringes (Fig. 5E). In each fork, a single fringe splits into two, which evidently confirmed that the emission from the laser carries OAM with topological charge l = 1. Similarly, OAM laser emission with topological charge of 2 was also observed experimentally in another design (Fig. 5F), which matches perfectly with our theory.

DISCUSSION

The guided wave–driven metasurface, consisting of subwavelength-spaced meta-atoms, provides a highly versatile and compact platform for bridging the gap between guided waves in PICs and free-space waves. The developed technology not only empowers the photonic integrated devices with agile free-space light controllability in the subwavelength scale but also enables metasurfaces to be directly driven by guided waves, which makes possible a denser and higher level of on-chip integration.

We have experimentally demonstrated off-chip beam deflection and focusing using the guided wave driven metasurfaces on silicon waveguides. In addition, two-dimensional (2D) manipulation of free-space light can be realized by placing a 2D array of meta-atoms on a slab waveguide. This technology can enable a wide spectrum of applications ranging from optical communications to LiDAR, as well as miniaturized display technology for virtual reality and augmented reality devices. Taking advantage of the intrinsic asymmetric coupling that originated from unidirectional phase distribution provided by the metasurface, we also demonstrated an on-chip microring OAM laser that directly emits beam that carries OAM with a designable order. This technique holds great promise for achieving compact on-chip OAM light sources (or detectors) for large-scale photonic integration. In particular, it can be used for free-space optical communications with an additional degree of freedom provided by the OAM states. On the basis of the demonstrated design principles, more complex functionalities can be achieved, such as guided wave–driven holograms, photonic integrated spectrometers, and so on. In addition, because of reciprocity, free-space modes can be selectively coupled into the metasurface-dressed waveguides. The metasurface region can be engineered to couple light with a tilted or even distorted wavefront into a waveguide, which is especially useful for optical sensing and detections. Moreover, dynamic control of the coupling between guided modes and free-space ones can be realized by incorporating tunable elements (44, 45), which further empowers the PICs with the capability of tuning the optical functionalities dynamically.

MATERIALS AND METHODS

Sample fabrication

The samples were fabricated on a commercially available silicon-on-insulator wafer with 220-nm-thick (for beam deflection experiments) and 500-nm-thick (for light focusing experiments) Si device layer and 3-μm buried silicon dioxide. Alignment marker was defined by electron beam lithography followed by evaporation of 50-nm Au with a 5-nm-thick Ti adhesion layer and lift-off process. Then, negative resist FOX-16 (Dow Corning Corp.) was used to define the waveguide pattern and then developed in the CD-26 developer (MicroChem) for 25 min. Chlorine-based inductively coupled reactive ion etching (ICP-RIE) was used to etch crystalline Si with FOX-16 resist as mask. Then, the sample was immersed in buffered oxide etchant for 20 s, followed by water rinse to remove the remaining mask. A second-step electron beam lithography was conducted on ZEP 520A (Zeon) resist to define the metasurface on top of the waveguide with precise alignment. The exposed sample was developed in N-amyl-acetate for 3 min, followed by methyl isobutyl ketone/isopropyl alcohol (1:3) immersion for 1 min. Au/SiO₂/Au films were subsequently deposited using an electron beam evaporation system. The pattern was then lifted off in Remover 1165 (MicroChem) at 85°C in a water bath for 2 hours. The sample was lastly diced along the input port of the waveguide for measurement.

The OAM microring laser was fabricated on an InGaAsP (500-nm, MQW layer)/InP substrate. First, the microring resonator was defined by electron beam lithography with FOX-16 negative resist. The resist acted as an etch mask in the BCl₃-based ICP-RIE process. Then, the sample was immersed in buffered oxide etchant to remove the mask. A second-step electron beam lithography using ZEP 520A resist was performed with precise alignment to define the metasurface on top of the microring resonator. A sequential electron beam evaporation was performed to deposit Au/Si/Au films, followed by a standard lift-off process in Remover 1165 at 85°C in a water bath for 2 hours.

Simulation methods

Numerical simulations were carried out using a commercially available FEM solver package—COMSOL Multiphysics. Third-order finite elements and at least 10 mesh steps per wavelength were used to ensure the accuracy of the calculated results. We simulated individual Au/SiO₂/Au meta-atoms first. We used an eigen-mode solver to find the TE₀₀ mode of the silicon waveguide as well as its modal index at 1550-nm wavelength. Then, this modal index was used in the model to further calculate the phase and amplitude of the extracted light by monitoring the field at a few wavelengths over the waveguide. We swept the geometrical parameters of the meta-atoms to get the phase and amplitude maps/contours (Fig. 2B). The trapezoidal shape of the meta-atoms that resulted from our nanofabrication was also considered in our model to get accurate design parameters.

To simulate the beam deflection, a full device model that consists of an array of meta-atoms placed on top of an Si waveguide was established. The meta-atoms were distributed along the waveguide so that they formed a linear phase gradient (Fig. 2D). In a similar fashion, an array of meta-atoms fulfilling the spatial phase distribution of a lens were placed on top of an Si waveguide to simulate the light focusing effect (Fig. 4A).

We used a similar method to calculate the phase and amplitude of the extracted light from Au/Si/Au meta-atoms on top of an InGaAsP/InP waveguide (fig. S7A). A device-level model of metasurface incorporated microring resonator was constructed to simulate the OAM radiation. Four Au/Si/Au meta-atoms selected from the calculated phase and amplitude maps/contours (fig. S7A) were used to construct a supercell. Fifty-eight supercells (N = 58) were placed on top of the resonator. Using the WGM with M = 59, we achieved OAM radiation with topological charge of +1 according to Eq. 4. Figure S7B illustrates the electric field distribution of the TE₀₀ mode, which shows the typical standing wave pattern formed by the two counterpropagating (CW and CCW) WGMs. The extracted light in free space carries OAM as shown in fig. S7C.

Experimental setups

We characterized our guided wave–driven metasurfaces with beam deflection and focusing functions using the optical setup shown in fig. S4. A free-space laser beam output from a Ti:sapphire laser–pumped optical parametric oscillator (OPO) was coupled into a commercially available tapered lensed single-mode fiber. The focused laser beam from the tapered fiber was coupled into the input port of our fabricated ridge waveguide sample in an end-fire manner by using a 3D translational stage. The coupled-in light propagated through a triangle taper linking the input port and the single-mode waveguide, during which the high-order modes vanished, and only fundamental transverse electrical mode survived. The light scattered into free space by metasurfaces on top of the single-mode waveguide was collected by an objective (NA = 0.95) and then transmitted through a tube lens. Part of the light was reflected by a beamsplitter for real-space imaging. And, the light transmitted through the beamsplitter was focused by a Bertrand lens to form a Fourier-space image. In the off-chip beam-steering measurement, the laser wavelength was tuned using the OPO to acquire wavelength-dependent beam deflection angles. In addition, Fourier-space images were taken by coupling a 1550-nm laser beam into samples with different supercell periods. After that, the scattering angles were extracted from the Fourier-space images calibrated by a ruled reflective grating (grooves density of 600/mm). In off-chip focusing measurement, the samples were mounted on a 3D translational stage with a high-resolution piezo-controlled actuator in the z direction. By moving the z stage, the real-space images were taken at different distances from the waveguide plane, and a 3D intensity distribution was reconstructed.

To observe the lasing spectra and to confirm the OAM properties of the laser radiation, we used the setup shown in fig. S8. In our experiment, a femtosecond pulsed laser (~140 fs, repetition rate 80 MHz) at 900-nm wavelength was reflected by a dichroic mirror and then focused by a Newport 20× objective (NA = 0.40) onto the microring resonator. The pump power was controlled by a circular variable neutral density filter and monitored by a power meter. The lasing emission was collected by the same objective and then transmitted through the dichroic mirror and detected by a spectrometer (Horiba), a far-field imaging system, and a Michelson interferometry setup. With a flip mirror to switch the paths, the laser emission was either sent into the spectrometer/imaging system or the interferometry setup. In the interferometry setup, the laser emission was split into two beams by a pellicle beam splitter and then recombined with an off-center beam overlap to form an interference pattern recorded by an infrared camera. A delay line was used to balance the optical path lengths of the two arms.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/29/eabb4142/DC1