Future precipitation increase from very high resolution ensemble downscaling of extreme atmospheric river storms in California

California’s most intense atmospheric river storms will bring increasingly extreme precipitation in a warming climate.

Abstract

Precipitation extremes will likely intensify under climate change. However, much uncertainty surrounds intensification of high-magnitude events that are often inadequately resolved by global climate models. In this analysis, we develop a framework involving targeted dynamical downscaling of historical and future extreme precipitation events produced by a large ensemble of a global climate model. This framework is applied to extreme “atmospheric river” storms in California. We find a substantial (10 to 40%) increase in total accumulated precipitation, with the largest relative increases in valleys and mountain lee-side areas. We also report even higher and more spatially uniform increases in hourly maximum precipitation intensity, which exceed Clausius-Clapeyron expectations. Up to 85% of this increase arises from thermodynamically driven increases in water vapor, with a smaller contribution by increased zonal wind strength. These findings imply substantial challenges for water and flood management in California, given future increases in intense atmospheric river-induced precipitation extremes.

INTRODUCTION

A large and growing body of evidence suggests that the frequency and intensity of precipitation extremes will increase in a warming climate, even in regions where projected changes in mean precipitation are small and/or uncertain (1, 2). Given the large societal implications of a substantial increase in risk from extreme weather and climate events, understanding the physical processes underlying higher-order state shifts in precipitation and quantifying their magnitude has become urgent. An extensive body of existing literature focuses on the acceleration of the global hydrologic cycle due to increased radiative forcing [e.g., (3–7)], with increased focus on regional processes [e.g., (8)] and impacts, as well as attribution of individual observed extreme events to climate change [e.g., (9)].

However, the emergence of three major impediments to further progress has been recognized: (i) The small sample of observed and/or simulated extreme events (10), (ii) the presence of large internal variability in the coupled ocean-atmosphere system, which complicates isolation of externally forced signals, particularly for rare events (11), and (iii) the relative inability of coarse-resolution general climate models (GCMs) to capture certain fine-scale physical processes that drive extreme precipitation events (12). These challenges have complicated efforts to reach statistically robust conclusions regarding changes in extremes in a warming climate. To bridge these gaps using existing modeling tools, we describe a framework for understanding radiatively forced changes in extreme precipitation using high-resolution, event-based downscaling simulations forced by a large climate model ensemble. We ultimately apply this framework to understand changes in extreme atmospheric river (AR) storms in California’s Sierra Nevada mountains.

ARs are of outsized importance along the U.S. West Coast and particularly in California, where a majority of annual precipitation originates from a few intense AR events each year (13). Recent work points to a spectrum of societal impacts associated with these concentrated filaments of atmospheric water vapor transport—ranging from the beneficial water supply–bolstering effects of weak-to-moderate events to the adverse and damaging effects of extreme events, including flooding, debris flows, and landslides (14–17). In California, both the coastal mountains and taller inland Sierra Nevada mountains are approximately orthogonal to the southwesterly flow associated with cool-season cyclonic storms and associated ARs—an orientation that allows regional topography to play a critical role in triggering extreme orographic precipitation (18). With its complex terrain, extensive coastline and subsequently varied microclimates, California is an ideal case study region for implementing the new modeling framework described in this manuscript.

AR-associated precipitation extremes are likely to intensify in a warming climate, as has been shown in prior studies using coarse-resolution GCMs with grid spacings of ~100 to 200 km (19–21). In general, GCMs have the potential to successfully capture large-scale atmospheric dynamics associated with ARs and offer invaluable insights regarding large-scale variability. However, ARs are long (>2000 km) and narrow (<400 km) filamentary features that interact strongly with the complex terrain along the U.S. West Coast, and topography is critical in simulating AR-induced extreme precipitation. Thus, given the critical importance of representing mesoscale dynamic and thermodynamic processes in simulating AR-induced extreme precipitation (14, 22, 23), coarse resolution GCMs are not appropriate tools to quantify local impacts.

Recent studies using high-resolution atmospheric modeling have increasingly contributed to bridge the gap between spatially coarse GCMs and fine-scale modeling for climatic extremes. Dynamical downscaling using state-of-the-art regional models has yielded promising results over the past decade, including studies specifically targeting U.S. West Coast precipitation extremes (24, 25). These approaches, which typically involve one-way nesting of initial and boundary conditions from a parent large-scale simulation, better capture not only the AR precipitation but also fine-scale variations in horizontal and vertical AR structure over the ocean before landfall (22). In addition, simulations of real-world historical ARs using a state-of-the-art regional model forced by reanalysis boundary conditions have also been extensively validated (23).

Complementary approaches to the regional dynamical downscaling could include mainly sophisticated idealized linear models [e.g., (26)], statistical downscaling [e.g., (27)], and nonhydrostatic variable resolution global model simulations with their different advantages. For example, linear model approach provides an efficient way to investigate the main processes underlying orographic precipitation, such as windward airflow dynamics, condensed water advection, and downslope evaporation [e.g., (26)]. However, the strong underpinning assumptions of linearity, additivity, and time stationarity of atmospheric predictors in linear models may become problematic in extreme, far-from-mean state conditions. In general, dynamical downscaling is better suited to simulating local dynamics and parameterized subgrid scale processes (28). For example, Hughes et al. (29) found that blocking effects are the primary limitation preventing the linear model from accurately representing precipitation climatology when compared to the 6-km regional climate simulation over Southern California. Other missing local dynamics, such as the Sierra barrier jet, could result in biases in the orographic precipitation gradient over the Sierra Nevada in linear and statistical models (30).

Building on previous work, we develop and implement a modeling framework that joins GCM and regional modeling approaches. We perform high-resolution, event-driven dynamical downscaling of extreme ARs forced by a climate model large ensemble with the aim of sampling across a wide range of internal variability. We do so by forcing a high-resolution atmospheric model, the Weather Research and Forecasting Model (WRF V3.8.1) (31), with boundary and initial conditions from the Community Earth System Model Large Ensemble Experiment (CESM-LENS) (32). Leveraging the complementary strengths of a GCM-class climate model ensemble and a high-resolution regional model, we examine changes in extreme AR events affecting California’s Sierra Nevada mountains due to warming induced by increased anthropogenic greenhouse gas forcing. We aim to draw statistically robust conclusions regarding the rarest and most intense subset of landfalling ARs in both present and future climates that would not have been possible using either GCMs or regional models alone. (Further details on the experimental design, as well as the selection procedures for the most intense ARs, can be found in Methods.)

Using the downscaled extreme AR events, we investigate the factors controlling the changes in local precipitation using multiple linear regression (MLR) methods. Factors that could contribute to changes in and uncertainty associated with the local precipitation signal include thermodynamic increases in atmospheric water vapor (33), systematic dynamical changes at the synoptic scale from the driving GCM (e.g., shifts in the position or strength of the Pacific jet stream) (34), and/or local dynamical responses to the altered thermodynamic and dynamic environment imposed by the GCM, such as locally blocked flows or eddies. In this study, we disentangle the large-scale dynamic, thermodynamic, and local dynamical contributions to future changes in extreme precipitation during ARs. We also consider the fine-scale and high-frequency temporal characteristics of the precipitation response and report a spatially inhomogeneous increase in extreme precipitation that is greatest within orographic rain shadows and more broadly at shorter timescales.

RESULTS

Moisture flux and large-scale patterns, present and future

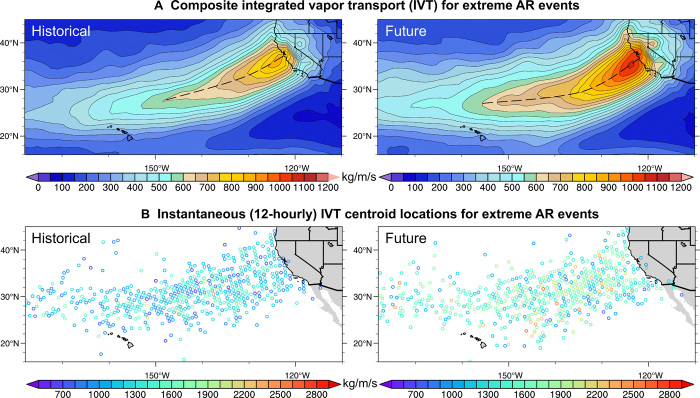
Composite integrated vapor transport (IVT) analysis for all selected extreme AR events depicts a southwest-to-northeast trajectory of AR moisture flux, with an impingement angle nearly orthogonal to the California coast in both present and future [representative concentration pathway (RCP) 8.5] climate scenarios (pattern correlation between present and future events greater than 0.95; Fig. 1A). Composite moisture flux for these extreme events extends initially southwestward and then westward nearly 4000 km over the subtropical Pacific Ocean from central California. This orientation is reminiscent of the so-called Pineapple Express AR subtype, which has historically been associated with some of California’s largest flood events (13).

Fig. 1. Spatial distributions of moisture fluxes from the 60 historical (left) and future (right) AR events (WRF 81 km) under the RCP8.5 forcing scenario.

(A) Composite hourly instantaneous IVT map showing the moisture flux transport pattern averaged over each of the 60 ARs for each period at the time of maximum hourly precipitation over California. (B) Geographical distributions of the AR events, with each open circle denoting the locations at 12-hourly time intervals. The location is defined as the grid box with maximum IVT value; color shading denotes IVT magnitude.

Further analysis of 12-hour IVT “snapshot” values reveals that the majority of the ARs under consideration here would be classified as “Category 5/extraordinary” events using the recently developed AR classification system by (14). These events are defined as having maximum IVT values of >1250 kg/m per second and persisting for more than 48 hours and are considered to be “primarily hazardous,” with societal harm greatly exceeding potential benefits. Thus, the present analysis focuses exclusively on a specific subset of extremely intense landfalling ARs likely to pose substantial societal risks, as opposed to the full spectrum of all ARs (many of which bring net societal benefits).

We report a ~23% increase in AR 12 hourly maximum IVT values (1300 to 1600 kg/m per second) from present to future climate (Fig. 1B). Notably, there is only a single occurrence of maximum IVT of >2500 kg/m per second in simulations from the present climate but more than five such occurrences in a warmer climate under a “high emissions” (RCP8.5) scenario. (Here, we have sampled from 10-year periods across 40 different members, respectively, and therefore, these values correspond to a ~400-year return interval in the historical simulations but a <100-year return interval in the future scenario) (Fig. 1B).

Further, we find that the spatial pattern of present versus future midtropospheric geopotential height at 500 hPa (Z500) anomalies are not statistically distinguishable from one another (P > 0.05), although some subtle shifts are apparent (fig. S1). In both historical and future cases, Z500 is characterized by a distinct region of anomalously low heights over the northeastern Pacific Ocean sandwiched between areas of anomalously high heights the Bering Sea and the Sonoran Desert region of the American Southwest (fig. S1). This large-scale pattern is consistent with the notion that such events are typically associated with well-defined Rossby wave trains extending across much of the North Pacific (35).

While the only statistically significant difference is a region of higher geopotential heights over far northeastern Asia, we also note a broad region slightly increased Z500 over the midlatitude Pacific, as well as a region of modest Z500 decrease over the Aleutian Islands. This result is interesting in light of previous findings by Simpson et al. (8), who report a robust increase in the length scale of intermediate-scale stationary waves over the North Pacific as a response to strengthening zonal winds in the subtropics—a process that is subsequently related to projected mean winter wetting along the U.S. West Coast. We also note that this subtle pattern change is somewhat different from and more muted than the mean state cool-season change in the CESM-LENS ensemble, which depicts a deepening of low pressure and a Z500 decrease in the Gulf of Alaska well to the southeast of the Z500 decrease shown here (2).

In accordance with previous studies of observed extreme ARs of the North Pacific, we find that CESM’s extreme ARs are associated with strong southwesterly flow just west of California throughout the atmospheric column (Fig. 2A) and that the horizontal moisture transport is dominated by zonal rather than meridional winds. Given the presence of a strong low-pressure system in the Z500 composites, it is expected that a strong Pacific jet stream is apparent in the zonal and meridional wind composites around 300 to 250 hPa. Latitude-pressure vertical cross sections show that the strength of both zonal and meridional winds increases substantially around the 300 to 200 hPa level in future relative to historical simulations, with ~20% increase for zonal wind strength and ~10% for meridional wind (Fig. 2B). Within the 700 to 1000 hPa layer in which most of the IVT flux occurs during AR events, we find a consistent increase in the strength of zonal (westerly) winds (1 to 3 m/s or 10 to 15%), with little change in lower tropospheric meridional winds (±<1 m/s). A local maximum of zonal wind increase appears to occur along the central California coast (35° to 40°N) in the 850- to 1000-mb layer (Fig. 2B). This is the elevation band within which the low-level jet and “warm conveyor belt” typically occur—two processes that are critically important to the production of extreme precipitation during AR events (18).

Fig. 2. Mean latitude-height cross section of zonal (left) and meridional (right) wind (near the coast at 130°W) for maximum AR precipitation days over California in CESM-LENS.

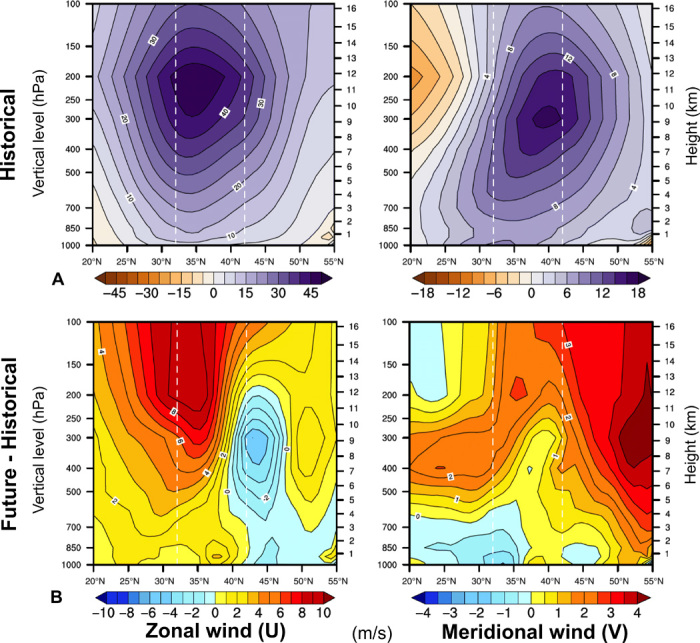
(A) Wind profiles for historical AR events. (B) Changes in wind profiles during future AR cases. The two white vertical dashed lines in each panel denote the lower and upper bounds of the latitude range of California.

We note that previous work has shown that for winter-mean circulation changes near California, the CESM-LENS single model ensemble used in this study appears to be similar to the CMIP5 multimodel mean. For example, Neelin et al. (34) reported a ~15% increase in the ensemble-mean average projected strength of zonal jet stream–level (200 hPa) winds over the Pacific Ocean just west of California during winter (~6 m/s relative to 40 m/s background). We note that these values are similar to those we report here for the CESM-LENS (~8 m/s increase relative to 40 m/s background) (Fig. 2).

Future increase in AR precipitation extremes in 3-km LENS-WRF simulations

A primary goal of this study is to understand and quantify projected changes in future precipitation driven by extreme ARs. As expected from historical climatological patterns, precipitation during extreme AR events is concentrated on the windward (west and south-facing) slopes of the Sierra Nevada. Across all historical AR events, event total precipitation accumulations averaged ~321 mm per event on Sierra Nevada windward watersheds, ~185 mm per event across Sierra Nevada leeside watersheds, and ~130 mm per event over the non-Sierra portion of the domain (Fig. 3A). Event total precipitation reaches as high as 700 to 800 mm across some portions of the Sierra Nevada, with the highest values observed within the Feather River watershed. The simulated extreme AR precipitation accumulations are smaller over adjacent lower elevation regions in California’s Central Valley (varying widely from 50 to 150 mm per event).

Fig. 3. Precipitation and thermodynamic changes in simulated ARs, present versus future (WRF 3 km).

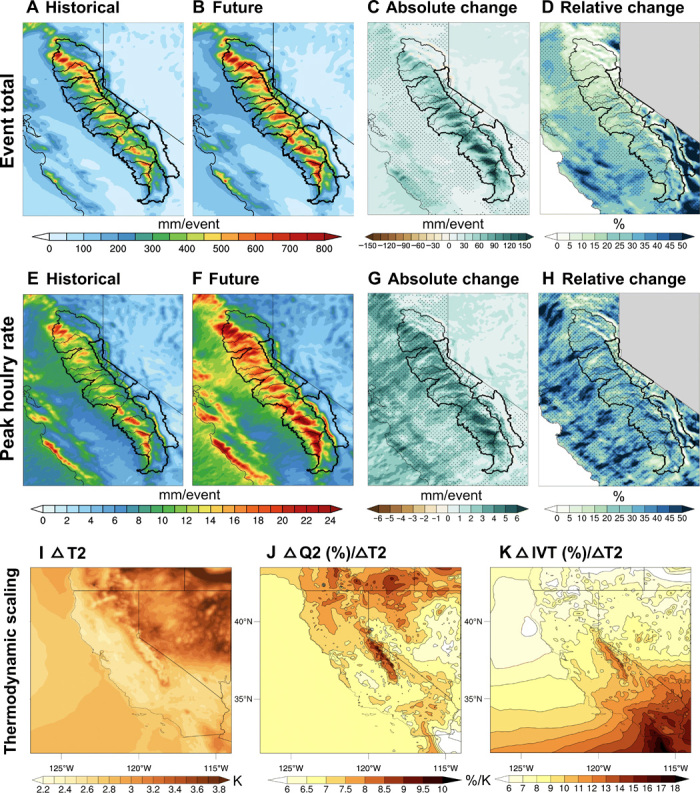
The first two rows show precipitation results zoomed in on the Sierra Nevada region (35.0°N to 41.0°N and −122.5°W to −117.5°W): (A, B, E, and F) for historical and future averaged event total and event maximum hourly precipitation rate from all 60 AR events in each period; (C, D, G, and H) for absolute and relative future changes in event total precipitation and event-maximum hourly precipitation intensity. Stippling in (D) and (H) denotes regions where changes are statistically significant at the P < 0.1 level. Sierra Nevada watershed boundaries are overlaid in all panels, denoted by black outlines. The bottom row illustrates thermodynamic scaling of water vapor in extreme ARs: (I) Near-surface (2 m) warming over California and surrounding region at 9-km resolution; (J and K) relative (%) change in near-surface specific humidity per degree of warming and relative (%) change in IVT per degree of warming. Scaling is calculated using event-averaged quantities.

While we report substantial increases in event total precipitation accumulations across the entire domain under the warmer future (RCP8.5) forcing scenario (~24% increase over the full 3-km domain), these increases are not spatially uniform (~18% over the Sierra Nevada portion of the domain and ~26% over the non-Sierra Nevada portion of the domain) (Fig. 3, B to D). Along the windward western slopes of the southern and central Sierra Nevada, the increases range from 100 to 150 mm per event (representing a 20 to 30% increase and locally as high as 40%). Smaller increases are seen across the northern Sierra (50 to 100 mm per event or a 10 to 25% increase). Across the adjacent low elevation regions, absolute increases in event total precipitation are smaller but relative increases are larger, including an increase of 25 to 50% across the San Joaquin Valley and 25 to 35% across the northern Sacramento Valley. Both subregions are in the rain shadow of California’s coastal mountain ranges. In particular, larger relative increase in event total precipitation occurs over the Sierra Nevada lee-side valleys, with increases greater than 80% in the Owens Valley.

The larger relative increase in event total precipitation on the lee-side of the Sierra Nevada may be due to the weakening of rain shadow effects in a warmer climate. Previous studies have explored this phenomenon, reporting similarly larger relative increases by a factor of up to ~1.5, in extreme precipitation downwind of major topographic barriers compared to (upwind) western slopes (33, 36). The simulated precipitation enhancement on the lee-side slopes could potentially stem from more warming aloft coupled with larger fractional changes in condensation at the lower temperatures characteristic of higher altitudes. As higher altitude hydrometeors are more likely to be advected as far as 30-km downstream as they fall, the distribution of precipitation shifts downwind, favoring the lee side (26). While a comprehensive assessment of the processes underlying this shift is beyond the scope of this manuscript, further analysis would be of considerable value given the potentially substantial implications for flood risk in California’s major urban centers in the Central Valley and the San Francisco Bay Area.

The projected increases in maximum hourly precipitation rates associated with these extreme AR events are even larger than event total precipitation increases, ranging from 10 to 21 mm/hour in historical cases to 12 to 28 mm/hour in future cases over the Sierra Nevada portion of the domain (Fig. 3, E to H). Changes in hourly maximum rates are more spatially uniform than for the event total accumulations, with comparable relative increases over both mountain and valley locations. We report average increases in hourly maxima of 27% over the Sierra Nevada portion of the domain and 32% over the non-Sierra portion of the domain (Fig. 3H). This large increase in maximum hourly precipitation intensity is especially notable because short-duration bursts of intense precipitation pose a much greater risk of flash flooding and other hazards, such as debris flows and mudslides, than do equally large accumulations occurring over a longer period of time (16). The spatial uniformity of these hourly precipitation rate increases may indicate a non-orographic (i.e., frontal and/or convective) origin for these changes.

We note that one potential weakness of the limited-area downscaling done here is that our framework does not conserve energy and cannot communicate its energy anomalies back to the driving GCM. Thackeray et al. (7) found that at the global scale, extreme precipitation increases are compensated by decreases in nonextreme precipitation, due to the atmosphere’s energy conservation requirement. The large increases in extreme precipitation and hence latent heating simulated here suggest that resolving orographic precipitation globally might affect the global atmosphere’s energy budget. This could, in turn, affect changes in the nonextreme parts of the precipitation distribution. Although the upscaling effects of resolving future changes in extreme orographic precipitation is beyond the scope of this study, it is an interesting topic for future work.

Surface warming and moisture increases during extreme ARs

Future extreme AR events are associated with substantially warmer air temperatures than historical events, with near-surface (2 m) warming ranging from 2.2 (near the coast) to 3.8 K (inland) (Fig. 3I) under the RCP8.5 emissions scenario. Warming of this magnitude suggests that streamflow during future extreme precipitation events has the potential to increase beyond what might be expected from the precipitation increase itself, as a substantially greater fraction of precipitation is likely to fall as rain rather than snow (37). We further find that warming conditioned on extreme future AR events is notably weaker (by ~0.4 K over coastal areas and ~0.8 K over inland areas) than the seasonal mean November to March warming during the same period in CESM-LENS (fig. S2). This finding suggests that while future extreme ARs will be likely associated with substantially warmer surface temperatures than their historical counterparts, the magnitude of that warming may be somewhat less than seasonal average background trends might suggest.

We also assess changes in near-surface (2 m) atmospheric moisture during the simulated events. Atmospheric moisture generally increases at a rate close to the exponential relationship expected from the Clausius-Clapeyron (C-C) relation (i.e., ~7%/K) across nearly the entire domain (Fig. 3J). Moisture flux (IVT), however, scales at rates greatly exceeding that which might be expected from the C-C relation (Fig. 3K), ranging from ~7%/K in the far north to ~14%/K in the far south. Given the previously noted increases in zonal wind speed and approximately C-C scaling of surface moisture, this greater-than-C-C scaling of IVT must arise from increases in its horizontal velocity component. The increased moisture fluxes, supporting the simulated increase in extreme precipitation, could be primarily the result of an increase in atmospheric water vapor, with a smaller but non-negligible contribution from an increase in zonal winds, especially across central and southern California.

We find that the WRF-simulated increase in event total precipitation accumulation is slightly higher than that which might be expected from the C-C relation (i.e., a ~7% increase per °C of warming or ~15 to 25% for 2.2° to 3.8°C of simulated warming). However, we report a substantially larger departure from C-C expectations for maximum hourly precipitation rates, with a domain average increase of ~31% (locally exceeding 50%) (Fig. 3H). This “super-C-C” scaling of short–time scale precipitation extremes would be consistent with prior work focused on other geographic regions [e.g., (38, 39)]. However, we also note an important caution regarding the interpretation of super-C-C scaling of subdaily precipitation extremes using daily temperatures. Zhang et al. (40) highlighted the considerable uncertainty that surrounds physical processes underlying subdaily precipitation extremes, as well as the fact that the degree of C-C scaling of such extremes should be expected to vary regionally, seasonally, and as a function of precipitation-generating processes. Thus, we emphasize that our findings in the present analysis demonstrate that this effect specifically exists within primarily nonconvective, cool-season AR regimes.

We report that relative increases in precipitation simulated by LENS-WRF are generally smaller than corresponding increases in IVT at the local scale but exhibit a more complex spatial pattern. Over elevated topography and along the windward slopes of the Sierra Nevada mountains and Coast Ranges, the ratio of precipitation increase to IVT increase (hereafter, PR/IVT) ranges from 0.4 to 0.8—suggesting that the relative “precipitation efficiency,” i.e., the amount of liquid reaching the surface per unit of horizontal moisture flux, decreases by as much as 20 to 60% over mountainous regions (fig. S3). By contrast, the PR/IVT ratio is near 1 over much of the Central Valley, locally as high as 1.6 to 2 in the northern Sacramento Valley and southern San Joaquin Valley and greatly in excess of 2 in the Sierra Nevada leeside valleys and western Nevada—suggestive of a relatively unchanged (or, locally, increased) precipitation efficiency in these regions. We further compare the PR/IVT scaling in LENS-WRF to that in the parent CESM data and note that the spatial patterns in this ratio are quite different between the two. CESM-LENS depicts a large and relatively uniform decrease in precipitation efficiency over most of California and adjacent coastal regions (with PR/IVT broadly between ~0.6 and 0.8 and as low as 0.4 across a broad swath of northern California) and scaling broadly >1 across essentially all of Nevada (fig. S2) and over the adjacent Pacific Ocean. This suggests that these large differences between the CESM and WRF patterns of PR/IVT scaling may result from the markedly smoothed topography at CESM’s native resolution.

Decomposing dynamic versus thermodynamic and large-scale versus local effects

We further diagnose the relative roles of dynamic versus thermodynamic factors, as well as local versus large-scale processes, in driving simulated changes in local extreme AR-associated precipitation using MLR, as described in Methods. First, we examine the contribution of individual predictors to local precipitation (Fig. 4B). From each single-parameter regression, the results show that zonal IVT (IV T_U) explains a large portion of variance across most zones of heavy precipitation, with r² approaching 0.65 over parts of the Sierra Nevada (average across the Sierra Nevada portion of the domain = 0.38). Meridional IVT (IV T_V) alone accounts for a substantial fraction of the variance (20 to 35%) mainly over northern California, including much of the Sacramento River watershed (Fig. 1A). The location parameter (Loc) alone, representing the latitude with maximum IVT among the near-coast grids as in Fig. 5C, contributes only a small amount of explained variance (~10%) in the northern and southern thirds of California and negligibly across the Sierra Nevada (fig. S5).

Fig. 4. Linking large-scale forcing (WRF 81 km) and local vertical motion to dynamically downscaled fine-scale precipitation in 3-km WRF.

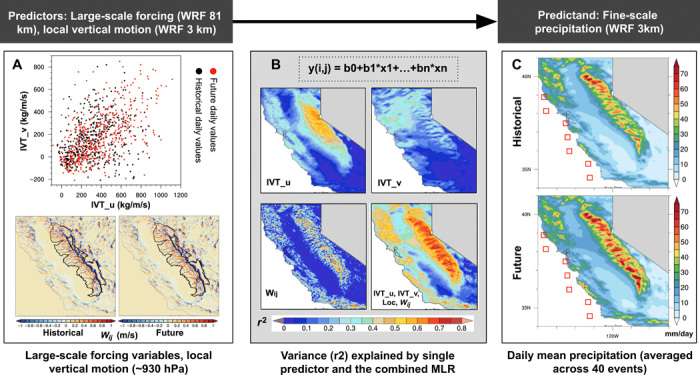
(A) Predictors used are as follows: On top is a scatter plot of the daily mean IVT_u (zonal moisture flux, kg/m per second) and IVT_v (meridional moisture flux, kg/m per second) averaged from the near-coastal grid boxes (see the rightmost column for the grid box locations), and below is the local vertical motion W_ij (m/s) at 3 km from WRF, averaged over all events. Middle column (B): Variance in precipitation explained by single-predictor regression models (see the main text) and by the four-parameter MLR model. (Here, the location factor refers to the grid box location with maximum IVT for each day from the seven coastal grid boxes). (C): Predictand: i.e., daily mean precipitation at fine-scale (3 km) in both periods. Sierra Nevada watersheds are overlaid, as in Fig. 3.

Fig. 5. Statistically predicted precipitation using MLR method and comparison to WRF 3-km precipitation output.

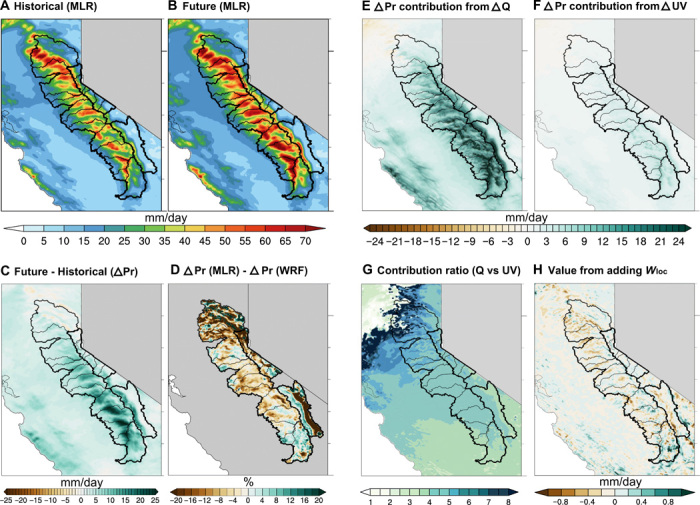
(A) Predicted precipitation using four-parameter MLR for historical and (B) future conditions. (C and D) Predicted precipitation changes from MLR and the relative difference (%) compared to the WRF simulated changes. (E and F) The respective contribution from changes in specific humidity and changes in zonal and meridional winds to future precipitation extremes. (G) Ratio of the contribution to precipitation changes from thermodynamic factors [as in (E)] to that from dynamic factors (U/V winds) [as in (F)]. (H) The precipitation changes added by including W_ij as an additional predictor in the MLR model.

Regional modeling at a sufficiently fine spatial resolution highlights the importance of submesoscale orographic forcing. This is evidenced in the present analysis by the complex spatial details of local vertical motion (W_ij) during AR events (Fig. 4A). In some localized areas, a substantial component of local precipitation variance can be accounted for by local vertical motions alone (Fig. 4B). There are pockets of fraction of variance explained as high as 70% (although the average value across the full Sierra Nevada portion of the domain is ~22%). We also note sharp horizontal contrasts in the fraction of variance explained, i.e., instances where a large fraction of the windward precipitation variance and a small fraction of leeward precipitation variance is explained by local orographic forcing. These heterogeneous small-scale variations in the fraction of variance explained by local vertical motion are in contrast to the more homogeneous spatial structure of fraction of variance explained by IVT, where the dominant spatial scale is approximately that of the entire Sierra Nevada mountain chain. In this way, large-scale predictors (relating to large-scale flow, IV T_U, IV T_V) and local vertical motion predict complementary aspects of the spatial variation in fine-scale precipitation.

On the basis of the single predictor investigation, we find that the combined four-parameter model (i.e., IV T_U, IV T_V, Loc, and W_ij), which includes information regarding both large-scale and local atmospheric motion and moisture fluxes, maximizes variance explained for precipitation extremes over the complex topography of our study regions. Using this model, the fraction of variance explained is ~53% over the full Sierra Nevada portion of the domain (locally up to 78%) and ~63% across a subset of Sierra Nevada grid boxes with event total precipitation above the Sierra Nevada domain average. We then use the four-parameter MLR to reproduce the daily mean historical and future precipitation for the extreme AR cases. We find that the spatial pattern of extreme precipitation from the statistical model closely matches the explicit precipitation output in 3-km WRF, with a spatial correlation r around 0.98 (comparing Fig. 5, A and B, to Fig. 3, A and B). Differences between MLR-predicted precipitation and WRF 3-km precipitation are generally ±10%, although there are regions where the MLR model exhibits higher bias—a key example of which is the statistical model’s underestimate of the future precipitation increase (which slightly exceeds 20% in some areas; Fig. 5D). Regions with largest underestimated changes are generally in rain-shadowed valleys on the leeward side of Sierra Nevada. We acknowledge that the MLR method relies heavily on the assumption that the respective effects of each predictor are additive, as well as that predictors are linearly independent. Nevertheless, we also show that the four-parameter model captures a large fraction of the variation in precipitation—suggesting that it is ultimately a reasonable proxy for the most important underlying physical processes.

With this MLR framework, we are able to partition dynamic and thermodynamic contributions to the precipitation change. We do this by first suppressing the effect of the future thermally driven water vapor increase by setting q to historical values in the MLR prediction of future precipitation change. Likewise, to suppress the effect of the future large-scale wind change, we impose the historical values of large-scale wind when producing future MLR output (see details in Methods). In doing so, we find that the ratio of the thermodynamic to dynamic contributions to the extreme precipitation increase is as high as 8:1 in the northern portion of the domain and as low as 3:1 in the southern portion of the domain (Fig. 5, E to G), with an average of 6.3:1 over the Sierra Nevada portion of the domain. This implies that atmospheric moisture increases are responsible for a large majority of the projected precipitation increase and dominates the overall response. We also note a meridional gradient in the relative importance of Q versus UV. The gradient appears to result from the local maximum in the lower tropospheric (~850 mb) zonal wind increase around 37°N latitude (Fig. 2B), where the role of increased winds is maximized and the Q:UV ratio subsequently decreases. As little change in the zonal wind speed is simulated further north (i.e., around 40°N latitude), nearly all of the precipitation increase at these latitudes is attributable to the increase in Q.

Adding local vertical motion to the MLR model yields more spatially variable fine-scale precipitation patterns. However, it only minimally affects spatially averaged precipitation changes. When W_ij changes are not considered in the MLR model, the Sierra Nevada–wide impact on precipitation is quite small (−0.02 mm/day on average, with a minimum of −1.6 mm/day and a maximum of +2.6 mm/day) (Fig. 5H). We show that small-scale dynamical influences are dwarfed by both the thermodynamic effect of the water vapor increase and background large-scale influences. Previous studies have also emphasized the dominant thermodynamic contribution to increases in precipitation extremes [e.g., (5, 6)]. However, those studies relied on GCM data and hence were unable to explore the factors shaping precipitation extremes in a topographically complex region dominated by orographic precipitation.

DISCUSSION

Summary

In this study, a large ensemble downscaling framework is introduced and applied to explore future changes in high-magnitude hydroclimate events in California’s Sierra Nevada Mountains. This approach targets individual extreme events from ensemble simulations, allowing us to study a large sample (60 in each period) of very high-magnitude and statistically rare AR events in a computationally efficient manner. Coupling a coarse-resolution climate model large ensemble (CESM-LENS, ~110 km) with a very high-resolution nonhydrostatic weather model (WRF, 3 km), we seek to leverage the strengths of both classes of modeling tools. Consistent with historical observations, we find that the majority of extremely intense landfalling California ARs are associated with a strong subtropical moisture connection in both the present and future climate regimes and that horizontal moisture transport (IVT) increases substantially during future events (by ~23%). The spatial similarity of moisture flux patterns (spatial correlation r > 0.95) between historical and future periods suggests that the large-scale characteristics of extreme AR events do not change appreciably even in a much warmer global climate regime.

We report substantial increases in event total precipitation associated with extreme AR events in a warmer future climate (using the high emissions RCP8.5 scenario), with the greatest absolute increases occurring on orographically favored western slopes of the Sierra Nevada (50 to 120 mm per event) and larger relative increases occurring at lower elevations (~18% over the Sierra Nevada portion of the domain versus ~26% across the non-Sierra Nevada portion of the domain). Especially notably, larger relative precipitation increases occur in the climatologically drier Sierra Nevada lee side valleys, where event total precipitation increases by up to 80%. Simulated increases in peak-hourly-rain-rate during extreme AR events are even larger and more spatially uniform than the increase in event total precipitation (~27% over the Sierra Nevada versus ~32% in non-Sierra regions, with local maxima above 50%).

We further investigate the factors controlling the geographical distribution of dynamically downscaled local precipitation by linking large-scale forcings to targeted fine-scale climate extremes using an MLR method. The MLR allows us to separate the relative contributions of different large-scale forcing sources, as well as local dynamics, to fine-scale daily precipitation. Using a variant of the MLR method, we are also able to partition dynamic and thermodynamic contributions to the overall precipitation change. We find that a majority of the simulated increase in precipitation associated with extreme ARs stems from increases in water vapor (~85%, when averaged over the Sierra Nevada watersheds), with a smaller but still positive contribution (~15%) from intensified large-scale wind strength mainly in the zonal direction, although with some spatial variability. Using such a model, local dynamics notably improve the magnitude and spatial details of precipitation distribution but play an almost negligible role in the event mean precipitation changes compared to background thermodynamic and large-scale dynamic factors.

Implications for society and future research

The magnitude of these projected changes in AR-related extreme precipitation has substantial implications for California water and flood management. The projected increase in event total precipitation during extreme AR events implies increased runoff and inflow into California’s mainstem river systems. The projected warming during these events would most likely increase runoff potential even further as precipitation preferentially falls as rain rather than snow, an effect that has already been documented during the recent historical period (37). Of potentially even greater significance is the larger simulated increase in hourly rainfall rates during extreme AR events—which could substantially increase the risk of flash flooding on smaller river systems and in urban areas. The magnitude of the projected increase in extreme Sierra Nevada lee-side precipitation during extreme AR events could also have major implications for southern California’s water supply, given the spatial colocation with critical pieces of water distribution infrastructure. While a comprehensive assessment of these risks is beyond the scope of the present manuscript, these findings motivate additional work to explore potential consequences.

Previous work using coarse-resolution climate models has suggested that the risk of an extreme storm scenario analogous to that which caused California’s “Great Flood of 1862” will rise rapidly in a warming climate, with cumulative odds perhaps rising as high as 50% between 2018 and 2060 (2). Yet, because of poorly resolved topography and other systematic biases in GCM-class models, these studies can only provide relative risk ratios at best rather than spatially explicit estimates of actual precipitation accumulations and rates in specific hydrological basins. Our LENS-WRF framework allows us to provide this information at the spatial and temporal granularity typically associated with operational weather forecasts (23). While formal validation of hypothetical future extreme weather events is not possible, we emphasize that our approach uses a modeling framework that has previously been demonstrated to successfully reproduce observed historical extremes of a comparable magnitude (23). Thus, for present-day natural hazard mitigation and future climate adaptation purposes, this approach may offer a more detailed picture of plausible worst-case hydroclimate scenarios than traditional observational or modeling exercises alone can provide. Last, we point out that a similarly targeted high-resolution ensemble downscaling framework could be applied in other geographic regions and to a wide range of event types, such as tropical cyclones, summertime thunderstorms, severe winter storms, and extreme fire weather.

METHODS

Motivations behind the large ensemble downscaling approach

In this study, we conduct a large number of targeted simulations of extreme AR events in the present (1996 to 2005) and future (2071 to 2080) under the RCP8.5 high emissions forcing scenario climates. We do so by forcing a high-resolution atmospheric model WRF V3.8.1 (31), as detailed in the following modeling section, with 6-hourly forcing output, which is often not archived by large ensemble GCM modeling experiments. This approach builds upon existing work using climate model ensembles to probe the weather-climate interface, such as Phillips et al. (41) (who used short-running climate model simulations to evaluate climate model representation of weather processes), Mahoney et al. (42) (who downscaled individual extreme precipitation events along Colorado’s Front Range present in GCM boundary conditions using the WRF model at 1.3-km resolution), Scinocca et al. (43), Kirchmeier-Young et al. (44), and Fyfe et al. (45) [who used the CanESM2 large ensemble as a basis for dynamical downscaling using two separate regional models (CanRCM4 and CRCM5)]. CESM-LENS has previously been evaluated for its reliability compared to historical observations and its performance relative to other GCM-class models in the CMIP5 ensemble (27). We aim to combine the respective strengths of both a coarse-resolution GCM-class large ensemble and a high-resolution limited-area atmospheric model while optimizing the usage of computational resources as well as storage space (as detailed in the Supplementary Materials).

Large initial condition ensembles offer multiple independent realizations of the same historical or future forcing period (46). Recent work shows that internal variability can induce substantial atmospheric circulation trends in single model members even on multidecadal time scales (11). Thus, our selection of extreme events across all 40 members of the ensemble ensures sampling across a wide range of simulated internal variability. This approach also increases confidence that any differences between historical and future periods are caused by changes under atmospheric conditions and are not spurious products of undersampled internal variability. Ultimately, we aim to obtain a statistically robust sample of only the most intense events of interest (detailed AR selection procedures are described in the next section).

While CESM-LENS provides an extensive set of large-scale boundary conditions that sample across a wide range of internal variability, a high-resolution regional model such as WRF is intrinsically better suited to reproducing the fine-scale physical phenomena and precipitation extrema that occur during extreme AR events in California. Forcing WRF with CESM-LENS boundary conditions (henceforth, “LENS-WRF”), therefore, joins the relative strengths of each modeling tool. We emphasize that these methods differ substantially from the “pseudo global warming” approach used in many other downscaling studies (47), which applies the same mean GCM climate change signals to all individual meteorological events, irrespective of possible differences in those signals from mean-state changes during extreme events.

Extreme AR event selection in CESM-LENS

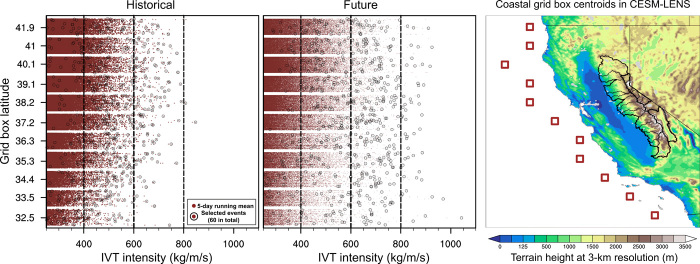
We apply previously established AR detection techniques to the 6-hourly CESM-LENS dataset to calculate 5-day running mean IVT across the North Pacific Basin between 1000 and 200 hPa. We search for ARs during the two time windows across all 40 ensemble members: i.e., 1996–2005 and 2071–2080 as noted above. (See Fig. 6 for the IVT distributions and fig. S6 for the daily frequency distribution.) We then rank these events within the historical and future periods and create an ordered list within three subregions: northern, central, and southern California.

Fig. 6. IVT distributions from 40 CESM-LENS ensemble members for near-coastal grid boxes over California from historical (1996–2005) and future (2071–2080) periods under the RCP8.5 emissions scenario.

Left and middle: Red dots represent the 5-day running mean IVT intensity starting for the entire 10-year historical and future periods. Note that this essentially includes all ARs not just the most extreme events. On the plot, IVT is truncated at the lower bound at 250 km/m per second. Each red horizontal band is a collection of points representing IVT values from each coastal grid box along the California coast. Within each band, values from each of the 40 individual CESM-LENS members are stacked one on top of the other. The corresponding IVT values for each of the 60 extreme AR events selected for downscaling during each period are denoted by black circles. Right: Centroid locations of the corresponding near-coastal grid boxes, with 3-km topography represented by the color contours over land. (Sierra Nevada watershed boundaries are also overlaid with black lines.)

The AR detection algorithm is regionally targeted and informed by specific regional background IVT conditions across the North Pacific basin (48–50). For each 5-day running mean based on 6-hourly increments in boundary conditions, the AR detection algorithm searches for connected sets of grid cells (“objects”) where IVT is 250 kg/m per second greater than the daily climatology. These objects that exceed 2000 km in length and include at least one land grid cell along the U.S. West Coast are classified as landfalling ARs. If there are shared grid cells between a landfalling AR at time step n and another landfalling AR at time step n + 1, then those two ARs are tracked as part of the same event.

Eventually, we select the most intense 20 events from each subregion and period to downscale using the LENS-WRF modeling downscaling framework. By design, the most extreme ARs we selected in the parent CESM-LENS dataset, ranked by the maximum IVT for each defined AR, are evenly distributed from north to south divisions along the California coast, covering the three subregions. Distributions of landfalling AR intensity at each coastal grid box are also shown in Fig. 6. Since we select 60 AR events from a sample of ~400 model years for the historical and future periods, respectively, the mean return interval period of the events in this study is 6 to 7 years for California on average. However, some of the most intense events in the set we selected are considerably more extreme, with higher return intervals up to 400 years regionally.

Targeted dynamical downscaling using WRF

The WRF-ARW (V3.8.1) (nonhydrostatic) (31) configuration used in the present analysis has been used successfully in previous California-based downscaling work. The basic configuration has extensively tested for sensitivity to a wide range of parameterization choices (51, 52). In addition, we conducted a series of test cases to (i) optimize the domain configuration as previously mentioned (see fig. S7) and (ii) determine additional adjustments to model parameterizations to improve the simulation of extreme ARs (described below). The boundary and initial conditions are provided by CESM-LENS with a full suite of atmospheric variables plus sea surface temperatures every 6 hours. To accommodate the transition from relatively coarse CESM boundary conditions to a very high resolution over the U.S. West Coast, we use a series of four nested domains of 81-, 27-, 9-, and 3-km resolution (see fig. S7 for the detailed domain configuration). The outer three domains cover a large portion of the northeastern Pacific Ocean and the entire Western United States.

The model physics parameterizations applied in this study include New Thompson microphysics scheme (53), Dudhia shortwave radiation scheme (54), rapid radiative transfer model longwave radiation scheme (55), Mellor-Yamada and Nakanishi-Niino level-2.5 surface and boundary layer scheme (56), the Kain-Fritsch (new Eta) cumulus scheme (57) (for 81-, 27-, and 9-km domains), and the Noah-MP land surface model (58). In the innermost 3-km domain, the cumulus parameterization was turned off, as, theoretically, it is only valid for parent grid sizes finer than ~10 km (31). This setup uses 44 vertical levels with model top pressure at 50 hPa, with a higher density of vertical levels near the surface to improve the representation of lower-level processes. These processes are especially important in the AR environment given the role of the low-level jet.

Understanding drivers of fine-scale precipitation using MLR

To investigate the factors controlling the geographical distribution of dynamically downscaled local precipitation, an MLR model is developed. We acknowledge that all linear regression approaches rely heavily on the assumption that the modeled effects are additive and that predictors are independent of one another—an assumption that may not strictly hold in all cases. Despite these considerations, however, the MLR allows us to separate the relative contributions of various large-scale forcing sources and local orographic forcing to fine-scale AR-associated precipitation. This method can also be used to partition dynamic and thermodynamic contributions to the precipitation change. We first construct a statistical relationship (Eq. 1) linking large-scale moisture fluxes near coastal California and local circulation (i.e., 3-km grid box–scale vertical motion) to the 3-km grid-scale daily precipitation.

$$y_{\mathit{ijt}}=b_{\mathit{ij}0}+b_{\mathit{ij}1}*x_{t1}+\dots +b_{\mathit{ijn}}*x_{\mathit{tn}}$$ (1)

A series of predictors are selected (i.e., the x variables in Eq. 1) from large-scale forcings at WRF 81 km and local vertical motions at WRF 3 km to predict the daily grid box–scale (3 km) precipitation (i.e., the y_ijt predictand in Eq. 1). Here, i, j, and t represent the 3-km grid indices and timestep index, respectively. Regression coefficients are calculated separately for each 3-km grid box for rainy days, when rainfall is above 1 mm/day during the simulated AR events for the historical AR period (491 total days) and the future period (493 total days). For large-scale predictors, averages are computed over the seven near-coastal grid boxes most relevant for precipitation in the mountainous Sierra Nevada region using a subset (40 of 60 events for each period) that most directly affect the Sierra Nevada.

Our goal in selecting the predictors was to build an MLR model with meaningful explanatory power but which is also parsimonious and avoids overfitting. Guided by physical first principles in initial predictor selection and followed by the systematic elimination of predictors that did not contribute to substantial improvement in model fit (see the Supplementary Materials for details), we found that a four-predictor multiple linear model maximized the variance (R²) in precipitation explained: IV T_U, IV T_V, Loc, and W_ij. Here, $\mathit{IV} T_U(=\frac{1}{\mathrm{\rho }}{\displaystyle \underset{\mathit{sfc}}{\overset{50\text{hPa}}{\int }}}\mathit{qu} \mathit{dp})$ represents the zonal moisture flux, $\mathit{IV} T_V(=\frac{1}{\mathrm{\rho }}{\displaystyle \underset{\mathit{sfc}}{\overset{50\text{hPa}}{\int }}}\mathit{qv} \mathit{dp})$ represents meridional moisture flux, Loc is the location in the 81-km grid with maximum IV T, and W_ij is vertical motion in the 3-km-resolution domain in each local grid box (for all variables and predictors, daily data are used). Among these four variables, the three large-scale predictors (IV T_U, IV T_V, and Loc) are calculated on the basis of the large-scale average over the seven near-coastal grid boxes depicted in Fig. 4C. Thus, atmospheric conditions near the point of AR landfall are used to predict precipitation over the Sierra Nevada.

Using MLR to quantify thermodynamic and dynamic contributions to precipitation change

We partition thermodynamic (q) and dynamic (u and v) contributions to the future precipitation change using the same four-parameter MLR model as described above. We do so by adjusting future IV T_U, and IV T_V in three separate calculations. First, we suppress the effect of the future change in winds (i.e., Fig. 2B) by replacing future u and v with their historical extreme event mean values in the calculation of future IV T_U, and IV T_V. We preserved the future anomalies in u and v, relative to baseline defined by the future mean, so as to preserve the dynamical character of each individual future event, but suppressed future u and v values by multiplying the ratio of historical mean to future mean. This procedure is aimed at isolating the portion of the precipitation change arising from increased atmospheric moisture content rather than changes in the wind (i.e., to keep the mean of u and v the same for both historical and future). The procedure is described mathematically in Eq. 2. Second, we suppress the effect of the future water vapor increase by replacing future q with its historical extreme event mean values in the calculation of future IV T_U and IV T_V as described in Eq. 3. Again, we preserve the anomalies associated with individual events relative to each period’s baseline. Third and last, we suppress both the effects of future changes in winds and water vapor by replacing all future q, u, and v values with their historical event mean values as described in Eq. 4. For all three calculations described above, the regression coefficients from the original MLR are applied to the adjusted future IV T_U and IV T_V to produce the adjusted fine-scale precipitation values. The difference between q or uv adjusted future precipitation and future precipitation with both q and uv adjusted gives the respective contribution from winds or water vapor.

$$\mathit{IV} T_{u_{\mathit{it}}(\widehat{u})}=\frac{1}{\mathrm{\rho }}{\displaystyle \underset{\mathit{sfc}}{\overset{50\text{hPa}}{\int }}}{q}_{\mathit{it}}{\widehat{u}}_{\mathit{it}} \mathit{dp},\text{where} {\widehat{u}}_{\mathit{it}}=( \overline{u_{i(\mathit{hst})}}/\overline{u_{i(\mathit{ftr})}})u_{\mathit{it}}$$ (2)

$$\mathit{IV} T_{u_{\mathit{it}}(\widehat{q})}=\frac{1}{\mathrm{\rho }}{\displaystyle \underset{\mathit{sfc}}{\overset{50\text{hPa}}{\int }}}{\widehat{q}}_{\mathit{it}}{u}_{\mathit{it}} \mathit{dp},\text{where} {\widehat{q}}_{\mathit{it}}=(\overline{q_{i(\mathit{hst})}}/\overline{q_{i(\mathit{ftr})}})q_{\mathit{it}}$$ (3)

$$\mathit{IV} T_{u_{\mathit{it}}(\hat{u}\hat{q})}=\frac{1}{\mathrm{\rho }}\underset{\mathit{sfc}}{\overset{50\text{hPa}}{\int }}{\hat{q}}_{\mathit{it}}{\hat{u}}_{\mathit{it}} \mathit{dp}$$ (4)

Here, i is for the coastal grid index, t is for the daily index, and $\overline{u}$ is for mean over each period. The equations for IV T_V are identical but with v replacing u.

To quantitatively differentiate between projected changes in the elevated topography (Sierra Nevada) portion of the domain and the less complex topography elsewhere, we formally define the following three subregions: the “full domain”, which refers to the subset of the 3-km WRF domain covering a large portion of northern and central California, as plotted in the first two rows of Fig. 3; the “Sierra Nevada portion,” which refers to the mountain watershed boundaries outlined on the map plots depicted in Figs. 3 to 6; and the “non-Sierra Nevada portion,” which refers to the full domain excluding the Sierra Nevada portion. We refer to these three subregions throughout the main text.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/29/eaba1323/DC1