Abstract
Recently, a novel virus called COVID-19 has pervasive worldwide, starting from China and moving to all the world to eliminate a lot of persons. Many attempts have been experimented to identify the infection with COVID-19. The X-ray images were one of the attempts to detect the influence of COVID-19 on the infected persons from involving those experiments. According to the X-ray analysis, bilateral pulmonary parenchymal ground-glass and consolidative pulmonary opacities can be caused by COVID-19 — sometimes with a rounded morphology and a peripheral lung distribution. But unfortunately, the specification or if the person infected with COVID-19 or not is so hard under the X-ray images. X-ray images could be classified using the machine learning techniques to specify if the person infected severely, mild, or not infected. To improve the classification accuracy of the machine learning, the region of interest within the image that contains the features of COVID-19 must be extracted. This problem is called the image segmentation problem (ISP). Many techniques have been proposed to overcome ISP. The most commonly used technique due to its simplicity, speed, and accuracy are threshold-based segmentation. This paper proposes a new hybrid approach based on the thresholding technique to overcome ISP for COVID-19 chest X-ray images by integrating a novel meta-heuristic algorithm known as a slime mold algorithm (SMA) with the whale optimization algorithm to maximize the Kapur’s entropy. The performance of integrated SMA has been evaluated on 12 chest X-ray images with threshold levels up to 30 and compared with five algorithms: Lshade algorithm, whale optimization algorithm (WOA), FireFly algorithm (FFA), Harris-hawks algorithm (HHA), salp swarm algorithms (SSA), and the standard SMA. The experimental results demonstrate that the proposed algorithm outperforms SMA under Kapur’s entropy for all the metrics used and the standard SMA could perform better than the other algorithms in the comparison under all the metrics.
Keywords: Image segmentation problem, Slime mould algorithm (SMA), Whale optimization algorithm, Kapur’s entropy, X-ray images, COVID-19
Highlights
-
•
We proposes a new hybrid approach based on the thresholding technique to overcome the image segmentation problem.
-
•
We developed an integrated slime mold algorithm (SMA) with the whale optimization algorithm to maximize the Kapur’s entropy.
-
•
ISMA has been evaluated on 12 chest X-ray images with threshold levels up to 30 and compared with five algorithms.
-
•
The experimental results demonstrate that our proposed algorithm outperforms SMA under Kapur’s entropy.
-
•
Our algorithm could outperform all other algorithms in the fitness values, SSIM, PSNR, UQI, CPU time and (Std).
1. Introduction
Starting in China and passing to all the worldwide, a novel virus named COVID-19 outbreaks continuously. This virus infects the victim with fever and respiratory symptoms such as cough and sore throat. However, those symptoms do not confirm the infection with COVID-19 [1], so many attempts have been performed to find a tool that confirms if the person infected with COVID-19. After making chest CT imaging for suspects infected with COVID-19, the bilateral pulmonary parenchymal ground-glass and consolidative pulmonary opacities can be used to determine the infection. A rounded morphology and a peripheral lung distribution could sometimes been spotted [2].
Fortunately, since the CT findings are extracted as a normal image, it could be segmented into similar small regions, some of which may contain the features of COVID-19. The process of segmenting an image is commonly known as an image segmentation problem (ISP) and many algorithms have been applied for overcoming ISP. However, those algorithms still suffer from some problems prevent from reaching better-segmented images. As a result, the need for a new robust algorithm to segment the images has significantly been increased those days, especially with appearing chest CT images.
Recently, a novel algorithm known as the slime mold algorithm (SMA) inspired the slime mold behaviors to obtain the optimal track for gathering food. SMA has already been proposed for tackling the continuous optimization problems and could achieve significant success in comparison with the other algorithms. Accordingly, in this paper, SMA is adopted to tackle the chest X-ray image segmentation problem for the first time, as a new addition to separate the similar regions or to extract the region of interest inside an X-ray image. In addition, as an attempt to improve the performance of SMA and proposing a multi-thresholding model has a high ability on tackling ISP, the whale optimization algorithm (WOA) will be integrated with it to borrow its exploration capability within the first half of the iterations and after finishing the predefined first iterations where WOA runs within, the SMA will start to exploit around the best region explored by WOA with disposing of local minima problem under its ability that will re-initialize the solutions within the search space under a certain probability. The proposed model is only observed on X-ray test images infected with COVID-19, so it is proposed for dealing with this type of image. And within our future work, its performance will be validated on a number of test images from The Berkeley Segmentation Dataset and Benchmark to see if its performance is stable on any image or not.
The contribution of this paper is summarized as follows: First, a new integrated approach (HSMA_WOA) is proposed based on the behavior of SMA and WOA for finding the optimal threshold values that overcome the multi-threshold image segmentation problems of chest X-ray images. Second, experiments of HSMA_WOA have been undertaken and outperforming all the compared algorithms in fitness values, PSNR, UQI, SSIM, CPU time, and standard deviation under Kapur’s entropy.
The rest of this paper is structured as follows. In Section 2, some proposed works for ISP has been reviewed. Additionally, Kapur’s entropy is explained in Section 3. Sections 4, 5 give a description of the whale optimization algorithm, and the slime mold algorithm, respectively. Section 6 introduces the proposed work for overcoming the image segmentation problem. Section 7 illustrates the results obtained under both Kapur’s and entropy functions. Finally, Section 8 concludes the paper.
2. Related work
Nowadays, ISP plays a crucial role in image processing [3] and computer vision [4] to focus on an interesting region rather than the whole image until managing to analyze the image with higher accuracy. ISP is present in many fields such as medical diagnosis [5], [6], object recognition [7], satellite image processing [8], remote sensing [9], historical documents [10], and historical newspapers [11], [12].
Several methodologies for tackling ISP, such as region-based [13], edge-based [14], feature selection-based clustering [15], and threshold-based [16], has been suggested to help in separating the similar regions into an image. From involving those methodologies, Threshold-based segmentation is deemed the best one for solving the ISP [3], [17], [18]. Due to its simplicity, speed, and accuracy compared with the others. Thresholding is classified into two types: a bi-level threshold and a multi-level threshold. If the image contains only two similar regions: object and background, then the bi-level threshold is the best candidate for separating those two regions; otherwise, the multi-level threshold is better. Although the multi-level threshold could help in segmenting the image with more than two regions, the time increases exponentially when the number of regions increases.
Some techniques proposed for solving the image segmentation problem are based on an approach that needs to identify some parameters for each class using a probability density function for segmenting the image, those approaches are classified as parametric [19]. Meanwhile, another approach classified as non-parametric [19] maximizes a function (such as Kapur’s entropy [20], fuzzy entropy [21], and Otsu function) without needing to calculate parameters at the outset.
Due to the time complexity problem with the increased threshold levels, traditional techniques failed to be the best tool for solving the ISP. Subsequently, the need for another different technique to overcome the problem of time complexity was significantly increased. Thus, the meta-heuristic algorithms (MHAs) have been more popular among researchers since significant superiorities with less time in several fields were offered by MHAs [22], [23], [24], [25], [26], [27] as the most appropriate tool to solve the ISP and overcome the time complexity. Since the w processing time increases exponentially with increasing thresholds, traditional techniques will use the considerable time to search for the optimal threshold.
Recently, many meta-heuristic algorithms have been suggested for overcoming ISP, such as particle swarm optimization (PSO) [28], [29], [30], ant-colony optimization algorithm [31], bee colony algorithm (BCA) [32], whale optimization algorithm (WOA) [33], genetic algorithm (GA) [34], multi-verse optimizer [35], cuckoo search (CS) [36], symbiotic organisms search (SOS) [37], Harris hawks optimization algorithm (HHA) [38], and firefly optimization algorithm (FFA) [39], flower pollination algorithm (FPA) [40], crow search algorithm [41], gray wolf optimizer [42], honey bee mating (HBM) optimization [43], locust search algorithm (LSA) [44] , moth–flame optimization algorithm (MFA) [33], and firefly optimization algorithm (FFA) [39]. Some of those algorithms are summarized in Table 1.
Table 1.
Some algorithms proposed for solving ISP.
| Reference | Procedure | |
|---|---|---|
| 1 | Singla and Patra [45] | The cluster validity measure was used to investigate the boundaries of the threshold levels to find the bounds that may contain the optimal threshold values. Then, it applied GA on the obtained bounds to search for the optimal threshold values within. |
| 2 | Manikandan et al. [46] | The real coded GA with the simulated binary crossover has been suggested for tackling the ISP of the medical image by maximizing the Kapur’s entropy. This algorithm approved their efficacy compared with the others when solving the ISP of the medical image |
| 3 | Maitra, Chatterjee [47] | PSO improved by cooperative and comprehensive learning has been developed for tackling the ISP. Both cooperative and comprehensive learning used with PSO to alleviate the dimensionality curse and prevent the early convergence |
| 4 | Liu, Y., et al. [48] | The PSO has been modified using adaptive inertia and the adaptive population for tackling the ISP. Adaptive inertia is used to promote the convergence speed of PSO, while the adaptive population is used to prevent stuck into local optima. |
| 5 | Ghamisi et al. [49] | Fractional-order Darwinian PSO has been proposed for overcoming the image segmentation problem based on the Otsu function. The Fractional-derivative was used with PSO to dominate the convergence rate. |
| 6 | El Aziz [33] | WOA and MFA were proposed for tackling the ISP by maximizing otsu method, although just for threshold levels reaching 6 |
| 7 | Chen [50] | In this paper, The Improved FFA (IFFA) has been proposed for solving ISP. IFFA was improved using the Cauchy mutation to avoid local minima and neighborhood strategy to enhance the convergence |
| 8 | Agrawal [36] | In this paper, CS has been proposed to extract the optimal threshold values of an image by maximizing the Tsallis entropy. |
| 9 | Bhandari [51] | In this paper, the satellite image was segmented using ABC based on maximizing a variety of objective functions. ABC was improved using a chaotic search to initialize the population at the outset and the differential evolution to enhance the exploitation capability. |
| 10 | Sanyal [52] | The fuzzy entropy to change between the exploration and exploitation operators was used with The bacterial foraging algorithm (BFA) for getting to the optimal threshold values of an image. |
| 11 | Sathya [53] | In this paper, to accelerate the premature convergence of BFA when solving ISP, the best bacteria among all the chemotactic steps is moved to the subsequent generations. |
| 12 | Tang [53] | This paper integrated the PSO with BFA to provide the global search capability and promote the premature convergence toward the optimal threshold values |
| 13 | Abdel-Basset [54] | A novel equilibrium optimizer (EO) has been proposed for finding the optimal threshold values of an image by maximizing the Kapur’s entropy. |
| 14 | Abdel-Basset [55] | A novel marine predators algorithm (IMPA) improved using the Ranking-based diversity reduction strategy has been suggested to segment the chest X-ray image |
| 15 | Chouksey [56] | In this paper, the antlion optimization (ALO) and the multiverse optimization (MVO) have been developed for tackling the ISP by maximizing the Kapur’s entropy and Otsu method. After investigating the performance of ALO, and MVO, the author notified that MVO is better |
| 16 | Erik Cuevas [44] | In this paper, the locust search algorithm (LSA) was applied for solving the multi-level thresholding image segmentation under a new objective function in a gaussian mixture model. |
All the algorithms listed in the literature were proposed for overcoming the ISP of a normal image and medical image of type X-ray images, but no one of which is experimented on the X-ray images that are considered the most important thing to detect the infection with COVID-19. Currently, there are two ways to be blended for much better performance. First, the high ability of WOA can be used to explore a new region to find a better solution within the first half of iterations. Second, the high capacity of SMA can be used to balance between exploitation and exploration. Thus, authors are motivated to make a hybridization between them to propose a new model to combine those two capabilities for overcoming the ISP for COVID-19 X-ray images. Broadly speaking, the SMA is integrated with WOA to finding a better solution, where the WOA will be run within the first CI iteration to explore various regions within the search space. Afterward, the SMA will take the solutions obtained by WOA to exploit them or explore at the expense of the fitness of each solution as an attempt to use up this capability of SMA. Additionally, SMA increases its exploration capability to escape out of the local minima by re-initializing the current solution randomly within the search space of the problem based on a certain probability. This hybrid approach is abbreviated as HSMA_WOA. SMA and HSMA_WOA are compared with several state-of-the-art algorithms under X-ray test images infected with COVID-19. After comparison, we saw that HSMA_WOA could outperform all the algorithms used to compare most of the test images used in our experiment.
3. Kapur’s entropy
In this section, the mathematical model of Kapur’s entropy method is shown. Kapur’s entropy searches for the optimal threshold values by maximizing the variance between the segmented regions [20]. The mathematical model of this method is described as follows:
supposing that [] refers to the threshold values that subdivide the image into a different similar area, then the Kapur’s entropy can be calculated as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
refer to the entropies obtained by each threshold value, and indicates the count of the pixels having a value , the gray level. And refers to the percent of the pixels in each region to the pixels in the whole image. And indicates the threshold levels.
In order to extract the optimal threshold values, the following equation is maximized:
| (6) |
The proposed algorithm will use Eq. (6) as an objective function to get the optimal threshold values.
4. Standard whale optimization algorithm (WOA)
In WOA [57], the behaviors of the humpback whales are simulated to proposed new optimization algorithms for tackling the continuous optimization problems. These whales move surround the prey in a spiral shape and then move toward prey in a shrinking circle when attacking. This behavior is called bubble-new foraging. This hunting mechanism is mimicked within the WOA by a trade-off between a spiral model and a shrinking encircling prey with a probability of 50%, generating the new solution within the optimization process. The encircling mechanism is athletes described as follows:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where is a vector that expresses the current whale, is the current generation, refers to the values of the best whale in the population, is a numerical vector generated randomly between 0 and 1. refers to the maximum generations, and is a parameter linearly decreased from 2 to 0 and is the distance control factor. The distance between the position of the victim and the whale is used where the helix-shaped movements simulated by a spiral model are done. The spiral model is mathematically modeled as:
| (12) |
| (13) |
where is the difference between the best-so-far solution and th solution, is a number created randomly between [−1, 1], the logarithmic spiral shape is described by as a constant. The best-so-far solution may be a local minima problem, so focusing completely on it within the optimization process may waste the search process within any beneficial mentioned. Therefore, the whale search for another position may contain the prey within the search area by picking a random whale from the population to move the current whale toward finding a better solution. Specifically, if , then the current whale is directed based on a whale picked randomly from the population. The mathematical model of this exploration phase is:
| (14) |
| (15) |
where is a position vector picked randomly from the population. Finally, the steps of the standard WOA are listed in Algorithm 1.
5. Slime mold algorithm (SMA)
Chen [56] has recently been proposed a new optimization algorithm inspired by the behaviors of the slime mold in obtaining the optimal path for connecting food. This algorithm was known as the slime mold algorithm (SMA). The mathematical model of the SMA based on Chen proposition [56] is described in the following.
In the first stage, when SMA searches for the food, it uses its odor in the air as a means of reaching the food. Based on the behavior of the slime mold, it is formulated as follows to simulate the contraction mode [58] :
| (16) |
is randomly generated within as:
| (17) |
| (18) |
And linearly decreases from 1 to 0, indicates the iteration current, indicates the maximum of iteration, is a vector that contains the location with the highest odor concentration found so far. indicates the next position taken by the current slime mold (SM). is the current position of the SM, and and are two vectors containing the location of two randomly selected individuals from the population. The variable is a random number between 0 and 1. describes the slime mold weight and calculated as follows:
| (19) |
| (20) |
where is a random number created within the range of 0 and 1, is the best fitness value within the current iteration, while stands for the worst one, refers to the indices of the sorted fitness values, condition indicates ranks of the first half of the population. In relative to parameter in Eq. (21) is modeled as follows:
| (21) |
where , is the fitness of the current , is the best fitness obtained so far.
In the second phase, the wrapped phase simulates the contraction mode in the venous structure of slime mold, which tunes their positions according to the quality of the food, when the food concentration is high, the weight of this region is bigger. Otherwise, the region’s weight is turned to explore other regions, as shown in Eq. (15). The SM needs to decide when to leave the current area to another one until finding a variety of food sources at the same time rather than the current better one. Generally, the mathematical model of updating the SM position could be re-modeled, as shown in Eq. (18) to simulate the methodology of the SM to find various food sources at the same time when foraging another area.
| (22) |
where and are two numbers generated randomly between 0 and 1, and and are the upper and lower bounds of the problem’s search space. is a probability used to determine it the SMA will search for another food source or search around the best current one. In relative to , , they are used to mimic the venous width variation. Finally, the steps of SMA are presented by Algorithm 2.
6. The proposed work
Within this part, our methodology for overcoming ISP for COVID-19 X-ray images will be illustrated in detail to show our plan for finding the threshold values that will help in extracting the region of interest within the infected images. Specifically, within this section, the following steps that contract the main structure of our proposition will be discussed: Initialization, SMA for ISP, hybrid SMA with WOA.
6.1. Initialization
As an inhabit of all the meta-heuristic algorithms, a set consists of N solutions has been proposed at the start. Each one has a number of dimensions distributed within 0 and 255 randomly using Eq. (23).
| (23) |
Where indicate the boundaries of the gray levels, is a random numerical vector in the range of [0,1], and indicates the th solution.
6.2. SMA for ISP
Last but not least, SMA is adapted for overcoming the ISP of the COVID-19 X-ray images by maximizing Kapur’s entropy. This adaptation will help in extracting similar regions within images that may contain similar features of COVID-19. The main advantages of SMA include a high ability to balance between exploration and exploitation. When the distance between the fitness of the current individual is high, it will try to move toward it in an attempt to exploit it. Meanwhile, if the distance is small, then it will explore another food source to find a better solution. Finally, the steps of SMA for overcoming ISP are listed in Algorithm 3.
6.3. Hybrid SMA_WOA (HSMA_WOA)
In this version, the SMA will be used with the WOA for tackling the ISP, where the SMA is used to pay attention to the best so-far regions obtained by the WOA. At the same time, the WOA is applied at the start of the optimization process until a predefined iteration CI is reached. CI is the end iteration where the WOA will stop and SMA starts. Specifically, WOA is applied at the outset to use up its exploration capability within the first half of the iteration for exploring the search space. After reaching the CI, the WOA will be stopped. SMA then starts to pay attention to searching for a better solution using the high-ability of SMA that will exploit around the best-so-far if the distance between the fitness value of the current solution and the best-so-far solution is higher than a specific value generated randomly. Otherwise, it will work on exploring another region searching for a better food source. In addition to disposing of the local minima using the SMA’s exploration capability that re-initialized the solutions that were within a predefined probability randomly within the search space. This hybridization is aimed to exploit the exploration capability of the WOA at the start. The next step is to enhance the significant balancing capability of SMA and increase their ability to get out of local minima. Therefore, this can achieve full exploration capability when a number generated random SMA is less dependent on the z factor.
The main advantages of this model are as follows:
-
1.
By using the high-ability of the WOA at the start of the optimization process, it can explore most of the regions within the search space to find a better solution.
-
2.
After exploring the search space using the exploration capability of WOA, the SMA is used to exploit around the best-so-far solution if the distance between the fitness of the current one and the best-so-far fitness is higher than a threshold value generated randomly between 0 and 1. Otherwise, the current SM will try to explore another region for another best-so-far solution. Additionally, SMA used another capability to explore another region for a better solution. This capability is based on re-initializing randomly the current mold within the search space of the problem according to a certain probability.
-
3.
This high-ability on exploring at the first half of the optimization process and adjusting that determines if the exploration or exploitation capability will be used within the second half of the optimization process help in proposing a model with high-ability on exploration, exploitation and avoiding dropping into local minima.
-
4.
Having only two parameters, r and CI need to be updated accordingly.
The main drawbacks of this model are as follows:
-
1.
Difficulties in picking the relevant value for CI can lead to using up the ability of this hybridization.
-
2.
It still suffers from the probability of falling into local minima problem if the best-so-far solution obtained by WOA is local minima. The value of z of the SMA used to escape local minima is small, and increasing this value will enhance the probability of randomly re-initializing the current solution within the search space and, subsequently, the convergence toward the best solution significantly reduce.
At the final, the final brief steps for the hybridization of both WOA and SMA are presented by Algorithm 4.
7. Results and discussion
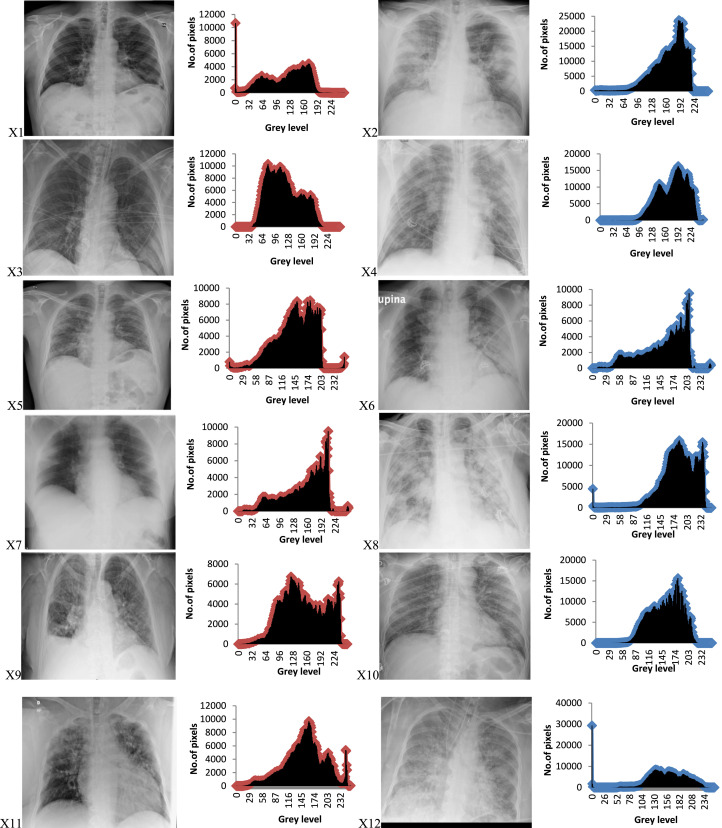
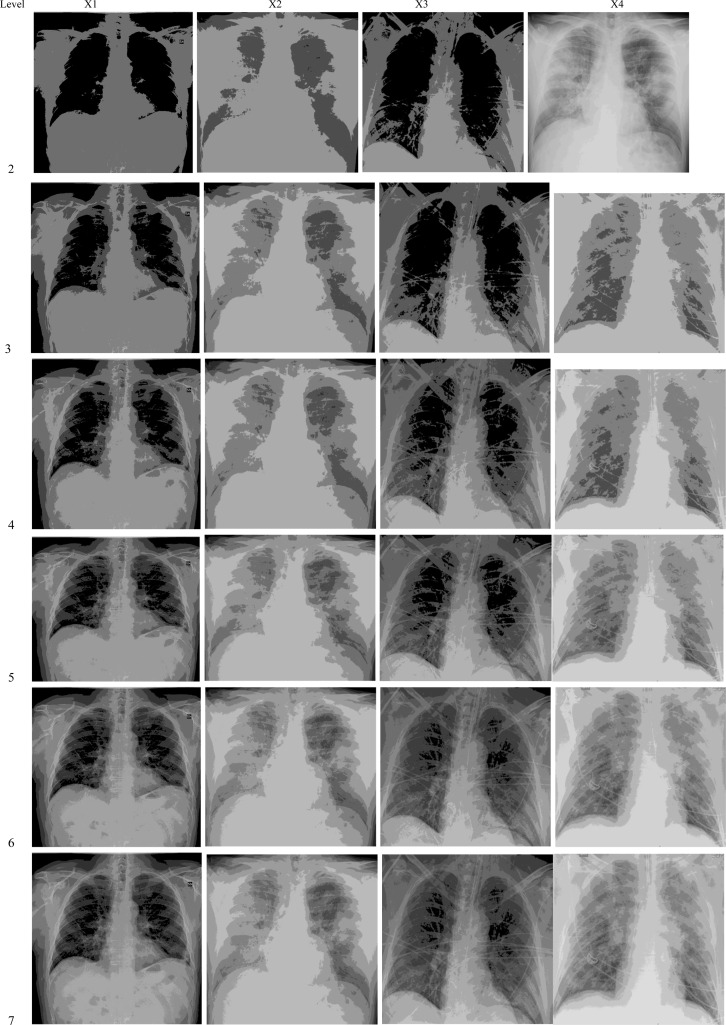
In this section, extensive experiments have been conducted to validate the proposed algorithms’ performance and compare their performance with some of the state-of-the-art algorithms when tackling the ISP. Those experiments were performed on a set of chest X-ray COVID-19 images, namely X1, X 2, X3, X4, X5, X6, X7, X8, X9, X10, X11, and X12 (see Fig. 1).
Fig. 1.
The original COVID-19 images and their histograms.
Additionally, a device equipped with 32-bit windows seven ultimate has been prepared for conducting our experiments. This device has the following capabilities:
-
•
Core i3 processor with speed 2.20 GHz
-
•
1 GB of RAM
In order to check the efficacy of the proposed algorithm, it is compared with several well-known algorithms, such as Lshade [59], FFA [39], WOA [33], SSA [60], and HHA [38]. All those algorithms are further implemented using Java programming language. For the compared algorithms, the parameter values are the same as found in the original paper rather than the maximum iteration and population size that are set to 150, and 30 respectively, for a fair comparison. Additionally, all algorithms run 20 independently times to check the stability and consistency of the results obtained by each one.
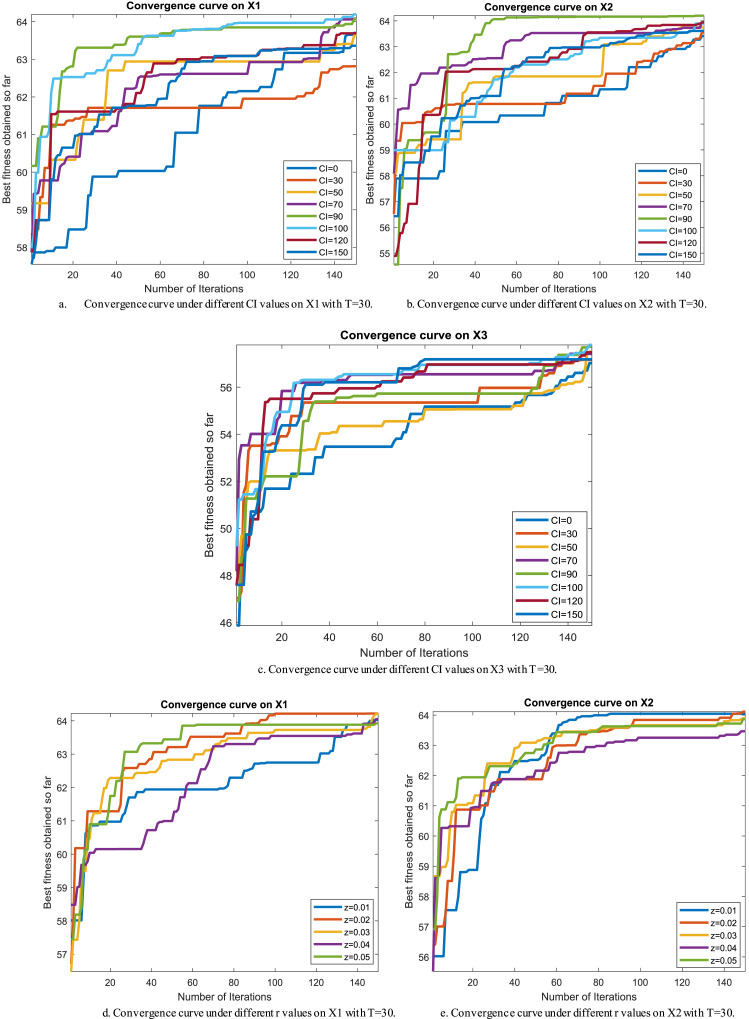
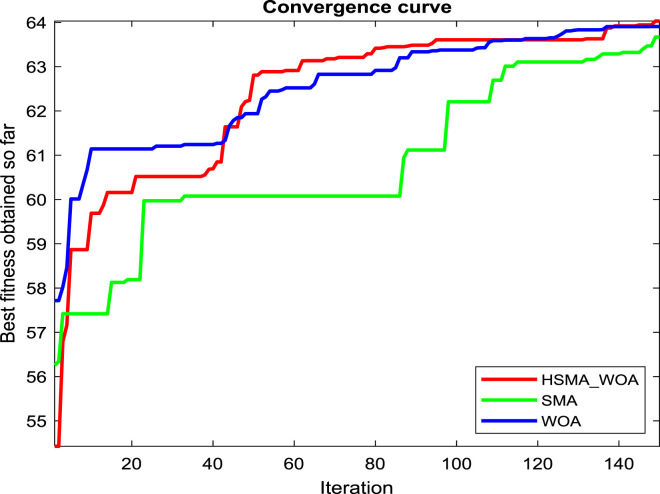
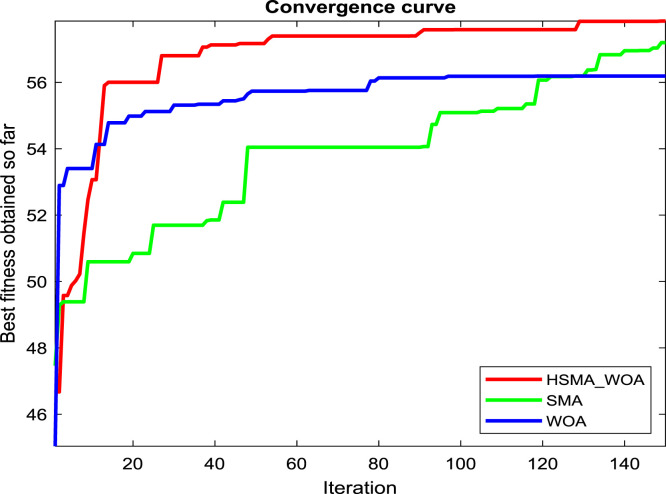
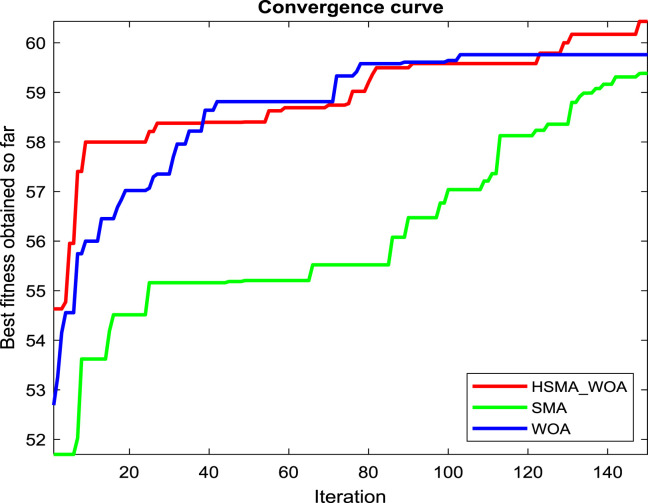
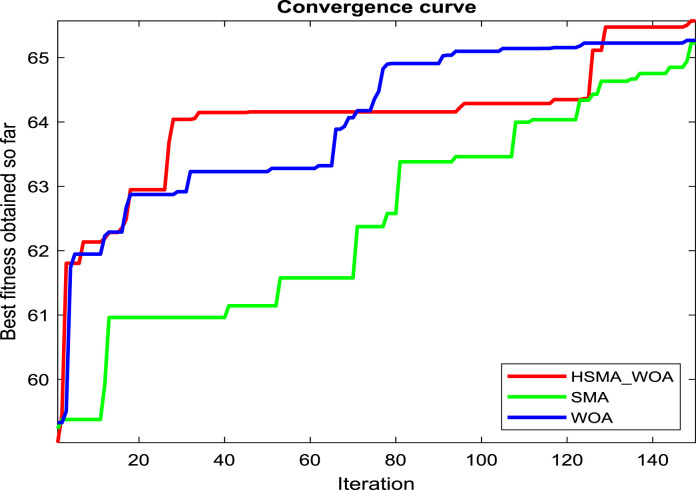
Regarding our proposition, the CI parameter needs to be carefully picked for reaching the best performance for this approach, so several values for it, such as 0, 30, 50, 70, 90, 100, 120, and 150, are checked under test images X1, X2 and X3 to see the best value. And after running the algorithm under each CI value 20 independent runs and drawing the convergence curve of the best run for X1, X2 and X3 in Fig. 2(a), (b), and (c), respectively, we witness that the value 100 is the best for it on X1, and X3. While CI=90 is the best on X2 and its performance is converged with CI=100 on X3. So, the best two candidate values for CI under our experiments are 90 and 100.
Fig. 2.
Adjustment of CI and z parameters.
Regarding the r parameter, five values, such as 0.01, 0.02, 0.03, 0.04, and 0.04, are selected to test the performance of the proposed algorithm under them. After running the algorithm under each r value 20 independent runs, the best run for each value is pictured in Fig. 2(d) and (e) for X1 and X2, respectively. According to those figures, r=0.02 is the best among the others, so it will be used for r within the next extensive experiments. Finally, Table 2 gives the parameter values of the proposed algorithm.
Table 2.
Parameter setting for the proposed.
| Parameter | Value |
|---|---|
| Number of runs | 20 |
| Population size | 30 |
| The maximum number of iteration | 150 |
| Z | 0.02 |
| CI | 100 |
The remainder of this section is listed as follows:
-
1.
Section 7.1: Analyzes the Stability and CPU time.
-
2.
Section 7.2: Discusses the quality of images using Fitness values.
-
3.
Section 7.3: Discusses the quality of images using peak signal to noise ratio.
-
4.
Section 7.4: Discusses the quality of images using a structured similarity index metric.
-
5.
Section 7.5: exposes the outcomes of the universal quality image metric.
-
6.
Section 7.6: Convergence rate among SMA, HSMA_WOA, and WOA.
7.1. Stability and CPU time analysis
In this section, the time taken by each algorithm until finding the threshold levels is observed to see any algorithm could achieve the minimum of time. In addition, some algorithms produce spaced-out results in the different runs, so the stability of the obtained has to be calculated to see which algorithm could achieve converged results in all. This is known using the standard deviation () calculated based on the following formula:
| (24) |
Where indicates the number of times, each algorithm tried. is the fitness value of the th run, and is the average of all the fitness values gotten. SD must be minimized to get to a better result.
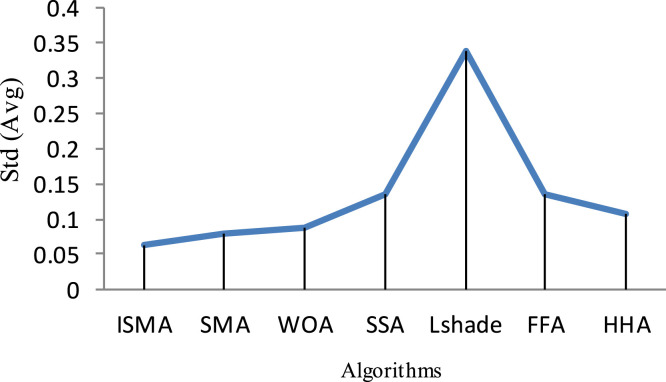
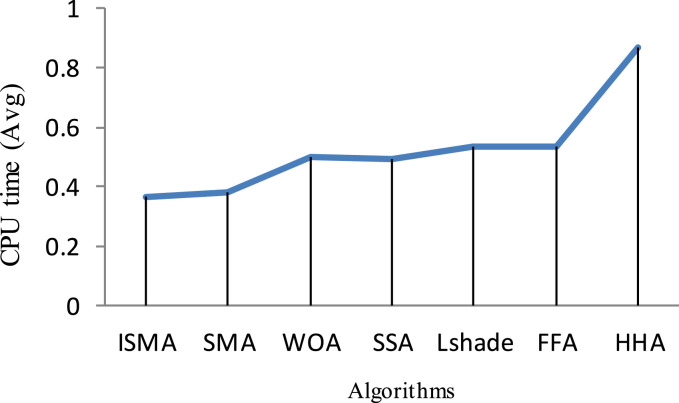
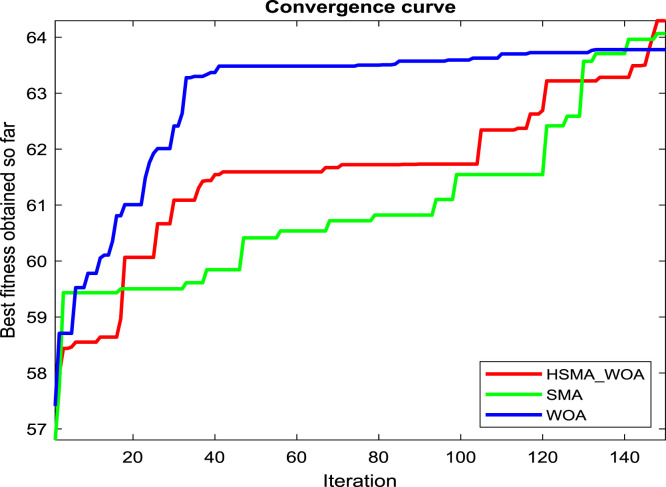
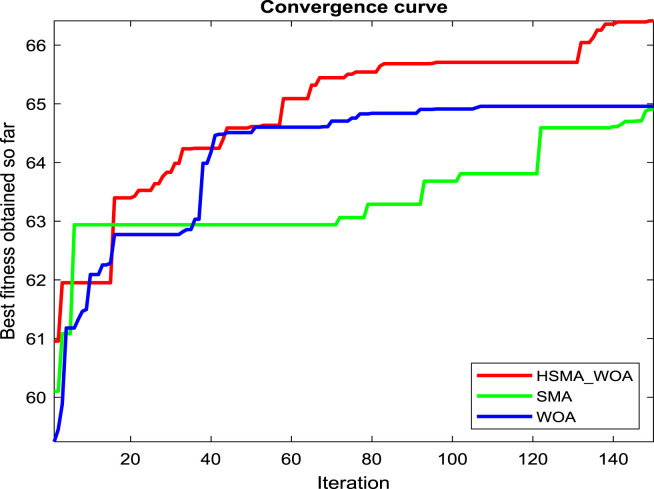
Under Kapur’s function, respectively, Fig. 3, Fig. 4 show the average of SD and CPU time values obtained by each algorithm within 20 independent runs. As a result of inspecting those figures, HSMA_WOA could reach less SD and CPU time values, while Lshade, and HHA achieve the worst value for both Std and CPU time.
Fig. 3.
The Std values obtained under Kapure’s function.
Fig. 4.
Comparison of the CPU time values obtained under Kapur.
7.2. Fitness values under Kapur
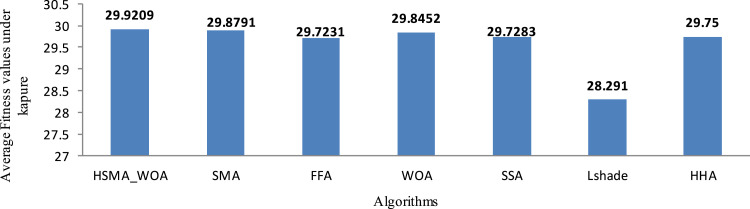
Regarding the fitness values of Kapur’s method, Table 3 shows the fitness values obtained by the compared algorithm and the proposed under this function. After calculating the average of the fitness values within 20 runs on each threshold level for each image, those values are recorded in Table 3 and displayed graphically in Fig. 5. Based on this table, the proposed could outperform the others in most cases. This is confirmed based on Fig. 5 that shows the superiority of the proposed algorithm with a value of 29.29 compared with the others with a difference of at least 0.0418.
Table 3.
Fitness values of each algorithm under Kapur’s entropy.
| img | T | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
Img | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 2 | 12.2074 | 12.2074 | 12.2074 | 12.2068 | 12.2074 | 12.2074 | 12.1556 | X7 | 12.2964 | 12.2967 | 12.2967 | 12.2964 | 12.2967 | 12.2967 | 12.2777 |
| 3 | 15.4120 | 15.4120 | 15.4120 | 15.4119 | 15.4120 | 15.4119 | 15.2913 | 15.5549 | 15.5549 | 15.5548 | 15.5548 | 15.5548 | 15.5547 | 15.3888 | ||
| 4 | 18.3112 | 18.3112 | 18.3108 | 18.3102 | 18.3104 | 18.3108 | 18.0011 | 18.4683 | 18.4683 | 18.4681 | 18.4682 | 18.4681 | 18.4680 | 18.1718 | ||
| 5 | 20.9774 | 20.9776 | 20.9758 | 20.9751 | 20.9760 | 20.9753 | 20.5394 | 21.1420 | 21.1417 | 21.1395 | 21.1418 | 21.1398 | 21.1410 | 20.6861 | ||
| 6 | 23.4434 | 23.4440 | 23.4375 | 23.4412 | 23.4358 | 23.4416 | 22.8031 | 23.6338 | 23.6324 | 23.6265 | 23.6337 | 23.6297 | 23.6326 | 22.9432 | ||
| 7 | 25.7537 | 25.7343 | 25.7294 | 25.7547 | 25.7436 | 25.7337 | 24.9663 | 25.9929 | 25.9718 | 25.9499 | 25.9919 | 25.9322 | 25.9826 | 25.2158 | ||
| 8 | 27.9823 | 27.9577 | 27.9280 | 27.9621 | 27.9293 | 27.9527 | 26.9708 | 28.3005 | 28.2498 | 28.1752 | 28.2776 | 28.1857 | 28.2527 | 27.2256 | ||
| 9 | 30.1637 | 30.1407 | 30.0533 | 30.1534 | 30.0713 | 30.1281 | 29.1068 | 30.4908 | 30.4411 | 30.3546 | 30.4587 | 30.3330 | 30.4322 | 29.2097 | ||
| 10 | 32.2340 | 32.2322 | 32.0841 | 32.2147 | 32.1798 | 32.1957 | 30.8905 | 32.6062 | 32.5833 | 32.5143 | 32.5549 | 32.5056 | 32.5387 | 31.1228 | ||
| 15 | 41.5906 | 41.5320 | 41.3379 | 41.5832 | 41.4564 | 41.4961 | 39.3727 | 42.3377 | 42.3673 | 41.8330 | 42.1271 | 41.8258 | 41.8732 | 39.5835 | ||
| 20 | 50.1159 | 50.0046 | 49.7143 | 50.1298 | 49.9001 | 49.6968 | 46.7057 | 50.3917 | 50.4087 | 49.6449 | 50.1529 | 49.5730 | 49.7524 | 46.6173 | ||
| 30 | 63.8093 | 63.7036 | 63.2656 | 63.8746 | 63.4349 | 62.7237 | 58.4513 | 63.8513 | 63.2789 | 62.8727 | 62.7227 | 62.5030 | 62.6031 | 58.4957 | ||
| X2 | 2 | 12.6324 | 12.6324 | 12.6324 | 12.6324 | 12.6324 | 12.6324 | 12.6044 | X8 | 12.3441 | 12.3441 | 12.3441 | 12.3441 | 12.3441 | 12.3441 | 12.3095 |
| 3 | 15.7263 | 15.7263 | 15.7263 | 15.7263 | 15.7263 | 15.7263 | 15.6539 | 15.4573 | 15.4573 | 15.4573 | 15.4573 | 15.4573 | 15.4572 | 15.3512 | ||
| 4 | 18.7055 | 18.7054 | 18.7052 | 18.7055 | 18.7053 | 18.7054 | 18.4603 | 18.1902 | 18.1884 | 18.1867 | 18.1887 | 18.1945 | 18.1959 | 18.0256 | ||
| 5 | 21.4534 | 21.4532 | 21.4522 | 21.4533 | 21.4528 | 21.4531 | 21.0459 | 20.8900 | 20.8896 | 20.8809 | 20.8895 | 20.8880 | 20.8898 | 20.6162 | ||
| 6 | 24.0311 | 24.0238 | 24.0237 | 24.0295 | 24.0248 | 24.0304 | 23.4316 | 23.4203 | 23.4146 | 23.4043 | 23.4177 | 23.4019 | 23.4168 | 23.0338 | ||
| 7 | 26.4825 | 26.4711 | 26.4763 | 26.4821 | 26.4789 | 26.4805 | 25.5994 | 25.8917 | 25.8778 | 25.8747 | 25.8904 | 25.8771 | 25.8906 | 25.3007 | ||
| 8 | 28.8380 | 28.8289 | 28.7895 | 28.8381 | 28.7971 | 28.8337 | 27.7372 | 28.2040 | 28.1926 | 28.1680 | 28.1957 | 28.1705 | 28.1858 | 27.4058 | ||
| 9 | 31.0405 | 31.0292 | 31.0151 | 31.0395 | 31.0096 | 31.0283 | 29.5524 | 30.4411 | 30.4344 | 30.3963 | 30.4455 | 30.3813 | 30.4329 | 29.6020 | ||
| 10 | 33.1868 | 33.1659 | 33.1504 | 33.1946 | 33.1522 | 33.1614 | 31.5542 | 32.6168 | 32.5619 | 32.4833 | 32.5955 | 32.4729 | 32.5696 | 31.5018 | ||
| 15 | 42.6820 | 42.6037 | 42.5246 | 42.7080 | 42.5106 | 42.5746 | 38.9055 | 42.7217 | 42.5800 | 42.4650 | 42.6246 | 42.5328 | 42.5093 | 40.8442 | ||
| 20 | 50.7079 | 50.5412 | 50.4158 | 50.7806 | 50.2943 | 50.3530 | 45.7687 | 51.5077 | 51.3147 | 51.0380 | 51.2673 | 51.0484 | 51.0233 | 48.3724 | ||
| 30 | 63.8566 | 63.3631 | 63.0311 | 63.8308 | 63.0813 | 62.6600 | 56.8894 | 65.7863 | 65.4368 | 65.1388 | 65.3790 | 65.0701 | 64.6126 | 60.6688 | ||
| X3 | 2 | 11.7581 | 11.7581 | 11.7581 | 11.7581 | 11.7581 | 11.7581 | 11.7534 | X9 | 12.6276 | 12.6276 | 12.6276 | 12.6276 | 12.6276 | 12.6276 | 12.6022 |
| 3 | 14.5988 | 14.5988 | 14.5988 | 14.5988 | 14.5988 | 14.5988 | 14.4816 | 15.8423 | 15.8423 | 15.8423 | 15.8423 | 15.8423 | 15.8423 | 15.7972 | ||
| 4 | 17.1833 | 17.1832 | 17.1832 | 17.1832 | 17.1832 | 17.1833 | 16.9445 | 18.7937 | 18.7936 | 18.7936 | 18.7938 | 18.7936 | 18.7935 | 18.6185 | ||
| 5 | 19.6124 | 19.6116 | 19.6108 | 19.6124 | 19.6109 | 19.6125 | 19.1511 | 21.5610 | 21.5605 | 21.5613 | 21.5602 | 21.5585 | 21.5634 | 21.3423 | ||
| 6 | 21.9391 | 21.9349 | 21.9307 | 21.9388 | 21.9325 | 21.9388 | 21.0710 | 24.2487 | 24.2489 | 24.2449 | 24.2489 | 24.2438 | 24.2466 | 23.8325 | ||
| 7 | 24.1795 | 24.1732 | 24.1435 | 24.1743 | 24.1512 | 24.1742 | 22.8515 | 26.7337 | 26.7297 | 26.7176 | 26.7325 | 26.7149 | 26.7305 | 26.1619 | ||
| 8 | 26.2990 | 26.2891 | 26.2626 | 26.2988 | 26.2664 | 26.2935 | 24.6100 | 29.1067 | 29.1013 | 29.0893 | 29.1069 | 29.0719 | 29.1027 | 28.4645 | ||
| 9 | 28.3243 | 28.3033 | 28.2610 | 28.3266 | 28.2817 | 28.3108 | 26.3513 | 31.4107 | 31.3829 | 31.3743 | 31.4094 | 31.3314 | 31.3819 | 30.3883 | ||
| 10 | 30.2695 | 30.2522 | 30.1717 | 30.2758 | 30.1624 | 30.2327 | 27.9424 | 33.6113 | 33.5793 | 33.5479 | 33.5034 | 33.5391 | 33.5901 | 32.4441 | ||
| 15 | 38.7253 | 38.7204 | 38.4560 | 38.6548 | 38.4627 | 38.5182 | 34.0568 | 43.6111 | 43.4979 | 43.3693 | 43.4066 | 43.3396 | 43.3413 | 41.2879 | ||
| 20 | 45.7534 | 45.8173 | 45.1861 | 45.3783 | 45.2480 | 45.2328 | 39.6107 | 52.1459 | 52.1104 | 51.6784 | 51.7949 | 51.6493 | 51.4513 | 48.8682 | ||
| 30 | 56.8804 | 57.0820 | 55.9473 | 55.9056 | 56.1606 | 56.0479 | 48.6062 | 66.1320 | 65.9175 | 65.2294 | 65.6912 | 65.7141 | 65.1745 | 61.3303 | ||
| X4 | 2 | 11.5969 | 11.5969 | 11.5969 | 11.5922 | 11.5969 | 11.5969 | 11.5018 | X10 | 11.4659 | 11.4659 | 11.4659 | 11.4659 | 11.4659 | 11.4658 | 11.4416 |
| 3 | 14.6869 | 14.6869 | 14.6869 | 14.6869 | 14.6869 | 14.6865 | 14.3767 | 14.4734 | 14.4734 | 14.4734 | 14.4734 | 14.4734 | 14.4734 | 14.3120 | ||
| 4 | 17.5072 | 17.5072 | 17.5057 | 17.5072 | 17.5000 | 17.5021 | 17.0861 | 17.1998 | 17.1997 | 17.1993 | 17.1991 | 17.1994 | 17.1994 | 16.9438 | ||
| 5 | 20.1209 | 20.1205 | 20.1129 | 20.1199 | 20.1137 | 20.1110 | 19.3430 | 19.7327 | 19.7314 | 19.7288 | 19.7322 | 19.7272 | 19.7314 | 19.1657 | ||
| 6 | 22.5707 | 22.5680 | 22.5443 | 22.5601 | 22.5491 | 22.5594 | 21.6035 | 22.1103 | 22.1136 | 22.1041 | 22.1126 | 22.0954 | 22.1114 | 21.2619 | ||
| 7 | 24.8598 | 24.8493 | 24.7909 | 24.8597 | 24.7693 | 24.8236 | 23.5827 | 24.3413 | 24.3347 | 24.3276 | 24.3410 | 24.3121 | 24.3337 | 23.2309 | ||
| 8 | 27.0702 | 27.0339 | 26.9016 | 27.0394 | 26.8738 | 26.9829 | 25.4259 | 26.5355 | 26.5175 | 26.5121 | 26.5258 | 26.5101 | 26.5241 | 25.0055 | ||
| 9 | 29.2080 | 29.2076 | 28.9102 | 29.1391 | 28.9810 | 29.1070 | 27.2155 | 28.6495 | 28.6020 | 28.5441 | 28.6429 | 28.5219 | 28.5987 | 26.8410 | ||
| 10 | 31.2598 | 31.1961 | 30.9021 | 31.1877 | 30.8910 | 31.1434 | 29.0150 | 30.6022 | 30.5700 | 30.4296 | 30.5823 | 30.4392 | 30.5532 | 28.1181 | ||
| 15 | 40.3413 | 40.3433 | 39.5598 | 40.1708 | 39.3364 | 40.0304 | 36.4513 | 39.3277 | 39.2510 | 38.8889 | 39.2983 | 38.9420 | 39.0566 | 34.8619 | ||
| 20 | 47.9266 | 47.8417 | 46.5941 | 47.6547 | 46.6598 | 47.2432 | 42.4565 | 46.6662 | 46.5212 | 46.0319 | 46.6636 | 46.0741 | 46.2364 | 40.8092 | ||
| 30 | 60.0793 | 59.6827 | 58.0592 | 59.6088 | 58.2804 | 59.1605 | 52.8618 | 57.9616 | 57.9755 | 57.1485 | 57.6431 | 56.8034 | 57.3010 | 50.4033 | ||
| X5 | 2 | 12.2716 | 12.2716 | 12.2716 | 12.2716 | 12.2716 | 12.2716 | 12.2343 | X11 | 12.5867 | 12.5867 | 12.5867 | 12.5867 | 12.5867 | 12.5867 | 12.5640 |
| 3 | 15.1753 | 15.1753 | 15.1753 | 15.1753 | 15.1753 | 15.1753 | 15.0662 | 15.8311 | 15.8311 | 15.8311 | 15.8310 | 15.8311 | 15.8311 | 15.7465 | ||
| 4 | 17.9995 | 17.9995 | 17.9993 | 17.9995 | 17.9993 | 17.9991 | 17.7654 | 18.7378 | 18.7377 | 18.7376 | 18.7378 | 18.7375 | 18.7376 | 18.6008 | ||
| 5 | 20.8227 | 20.8232 | 20.7797 | 20.8005 | 20.7691 | 20.8018 | 20.2735 | 21.4981 | 21.4977 | 21.4958 | 21.4977 | 21.4952 | 21.4969 | 21.2420 | ||
| 6 | 23.3704 | 23.3589 | 23.3467 | 23.3463 | 23.3381 | 23.3406 | 22.6542 | 24.0897 | 24.0837 | 24.0810 | 24.0833 | 24.0753 | 24.0854 | 23.6556 | ||
| 7 | 25.8073 | 25.8326 | 25.7707 | 25.7956 | 25.8197 | 25.7531 | 24.8665 | 26.5695 | 26.5703 | 26.5640 | 26.5760 | 26.5627 | 26.5638 | 26.0417 | ||
| 8 | 28.1356 | 28.1180 | 28.0283 | 28.1002 | 28.0606 | 28.0664 | 26.9687 | 28.9554 | 28.9516 | 28.9416 | 28.9590 | 28.9469 | 28.9529 | 28.1990 | ||
| 9 | 30.2882 | 30.2694 | 30.2412 | 30.2119 | 30.2515 | 30.1984 | 29.1365 | 31.2528 | 31.2362 | 31.1760 | 31.2486 | 31.1696 | 31.2182 | 30.4522 | ||
| 10 | 32.5805 | 32.5036 | 32.4395 | 32.3911 | 32.4113 | 32.3871 | 31.1720 | 33.4313 | 33.4086 | 33.3633 | 33.4224 | 33.3296 | 33.4041 | 32.2970 | ||
| 15 | 42.5845 | 42.5995 | 42.2694 | 42.2985 | 42.3155 | 42.2362 | 40.3625 | 43.2185 | 43.1243 | 43.0157 | 43.1955 | 43.0276 | 43.0623 | 41.0752 | ||
| 20 | 51.2666 | 51.2620 | 50.6443 | 50.8380 | 50.7128 | 50.6155 | 47.9260 | 51.9702 | 51.7279 | 51.4212 | 51.7075 | 51.3078 | 51.4473 | 48.6555 | ||
| 30 | 65.4349 | 65.0206 | 64.2166 | 64.8382 | 64.3390 | 64.2387 | 60.5143 | 65.8829 | 65.4744 | 64.8427 | 65.3291 | 64.8827 | 64.5217 | 61.0966 | ||
| X6 | 2 | 12.3680 | 12.3680 | 12.3680 | 12.3680 | 12.3680 | 12.3680 | 12.3459 | X12 | 11.5270 | 11.5270 | 11.5270 | 11.5270 | 11.5270 | 11.5270 | 11.5051 |
| 3 | 15.5171 | 15.5171 | 15.5171 | 15.5171 | 15.5170 | 15.5170 | 15.4254 | 14.3421 | 14.3421 | 14.3421 | 14.3421 | 14.3421 | 14.3421 | 14.1520 | ||
| 4 | 18.3767 | 18.3767 | 18.3763 | 18.3766 | 18.3766 | 18.3766 | 18.1390 | 16.9039 | 16.9038 | 16.9039 | 16.9039 | 16.9038 | 16.9038 | 16.4324 | ||
| 5 | 21.0194 | 21.0192 | 21.0135 | 21.0170 | 21.0150 | 21.0207 | 20.6942 | 19.2474 | 19.2462 | 19.2425 | 19.2474 | 19.2436 | 19.2467 | 18.5003 | ||
| 6 | 23.5388 | 23.5188 | 23.5184 | 23.5308 | 23.5222 | 23.5305 | 22.9603 | 21.4496 | 21.4303 | 21.3734 | 21.4494 | 21.3800 | 21.4478 | 20.6131 | ||
| 7 | 26.2273 | 26.0760 | 26.0680 | 26.1715 | 26.0603 | 26.1610 | 25.3283 | 23.4149 | 23.4171 | 23.3540 | 23.4218 | 23.4021 | 23.4578 | 22.6905 | ||
| 8 | 28.7099 | 28.6659 | 28.6314 | 28.6177 | 28.5135 | 28.6417 | 27.6532 | 25.5494 | 25.5592 | 25.5187 | 25.5551 | 25.5211 | 25.5676 | 24.7982 | ||
| 9 | 31.1027 | 31.0934 | 30.8702 | 31.0039 | 30.9502 | 30.9094 | 29.9045 | 27.7060 | 27.7039 | 27.6170 | 27.7009 | 27.6496 | 27.6898 | 26.6235 | ||
| 10 | 33.3305 | 33.3115 | 33.2345 | 33.2451 | 33.1824 | 33.0647 | 31.8420 | 29.7960 | 29.7688 | 29.6837 | 29.7730 | 29.6457 | 29.7596 | 28.5756 | ||
| 15 | 43.2567 | 43.2632 | 43.0468 | 42.9601 | 42.8639 | 42.8860 | 41.0070 | 39.2299 | 39.2056 | 38.6952 | 39.0824 | 38.7402 | 38.8831 | 36.3898 | ||
| 20 | 51.8206 | 51.9327 | 51.5385 | 51.5309 | 51.4507 | 51.2959 | 48.2590 | 47.0948 | 46.9360 | 46.4421 | 46.9399 | 46.4491 | 46.6039 | 42.7844 | ||
| 30 | 66.0900 | 65.7362 | 64.7226 | 65.4600 | 64.9066 | 65.0200 | 61.3966 | 59.7040 | 59.4203 | 58.0159 | 59.4729 | 58.1772 | 58.5367 | 53.0049 |
Bold value expresses the best outcome.
Fig. 5.
Average fitness values obtained under Kapur’s method.
7.3. Peak signal to noise ratio (PSNR)
In this section, another metric called PSNR has been used to measure the segmented image’s quality compared with the original image. PSNR determines the ratio between the square of the maximum gray level, , and the mean square error (MSE) between the original and separated one and it is calculated using as follows:
| (25) |
And is calculated as shown in the following equation:
| (26) |
Where is the gray level of the segmented image and is the gray level of the row th and column th in the original image matrix. M, and N are the number of columns and rows within the image. PSNR must be maximized to get to better quality.
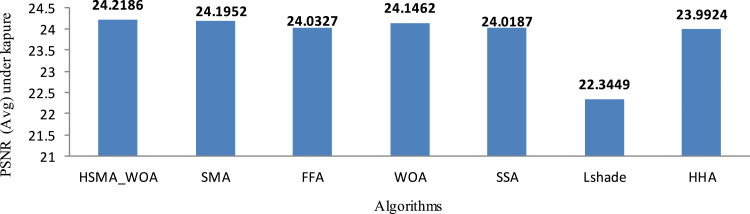
Based on the segmented images under Kapure’s function, the average PSNR value within 20 runs is calculated and introduced in Table 4. By observing this table, it is obvious that HSMA_WOA could be superior in 59 cases and equal in 14 out of 144, while SMA could be the best for 26 cases and equal in 14 out of 144. Generally, the proposed algorithms could be superior and equal in 104 out of 144. As a result, both SMA and HSMA_WOA could reach better-segmented images in all the superior cases compared with the other algorithms. In order to illustrate the results in Table 4 graphically, Fig. 6 is given to show the average of the PSNR values obtained by each algorithm. Based on this figure, the proposed algorithms: SMA, HSMA_WOA is considered superior compared with the others and HSMA_WOA is superior in comparison with SMA.
Fig. 6.
Average PSNR values under Kapure’s entropy.
Table 4.
PSNR values under Kapur’s entropy.
| img | T | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
Img | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 2 | 13.1162 | 13.1162 | 13.1143 | 13.1134 | 13.1162 | 13.1162 | 12.8150 | X7 | 15.2050 | 15.3933 | 15.3933 | 15.2050 | 15.3933 | 15.3933 | 15.1889 |
| 3 | 16.4252 | 16.4252 | 16.4272 | 16.4224 | 16.4260 | 16.4342 | 16.0049 | 17.2119 | 17.2119 | 17.2103 | 17.2126 | 17.2103 | 17.2138 | 16.6914 | ||
| 4 | 18.9556 | 18.9487 | 18.9706 | 18.9472 | 18.9729 | 18.9282 | 18.0015 | 19.4480 | 19.4630 | 19.4441 | 19.4513 | 19.4407 | 19.4623 | 18.5221 | ||
| 5 | 21.2097 | 21.2093 | 21.3252 | 21.2233 | 21.3038 | 21.2017 | 19.5347 | 21.4352 | 21.4649 | 21.3603 | 21.4409 | 21.3665 | 21.4431 | 20.4637 | ||
| 6 | 22.8398 | 22.8121 | 22.9398 | 22.8181 | 22.9310 | 22.7924 | 20.3662 | 22.8084 | 22.7867 | 22.6449 | 22.8054 | 22.6897 | 22.7897 | 20.5910 | ||
| 7 | 24.1734 | 23.8189 | 23.9626 | 24.2318 | 24.1870 | 23.9846 | 21.6186 | 23.1957 | 23.7250 | 23.3627 | 23.0896 | 23.3614 | 23.2624 | 21.9508 | ||
| 8 | 24.2804 | 24.7267 | 25.0769 | 24.4745 | 25.0152 | 24.3947 | 22.4469 | 23.8709 | 23.9958 | 23.7704 | 23.9287 | 23.9326 | 23.7384 | 22.3479 | ||
| 9 | 25.3263 | 25.2232 | 25.9481 | 25.2295 | 25.8470 | 25.0828 | 23.3580 | 24.5680 | 24.3410 | 24.2142 | 24.5100 | 24.3554 | 24.5018 | 22.9391 | ||
| 10 | 25.9865 | 26.1360 | 26.8390 | 26.0330 | 26.5743 | 25.8618 | 24.3433 | 25.1472 | 25.0194 | 24.5543 | 24.9923 | 24.5985 | 24.9951 | 23.0372 | ||
| 15 | 29.4277 | 29.4927 | 29.8138 | 29.4908 | 29.8449 | 29.2103 | 26.5681 | 27.1336 | 27.1160 | 26.4416 | 27.1190 | 26.4248 | 26.4378 | 25.0565 | ||
| 20 | 31.6407 | 31.5051 | 31.8526 | 31.5302 | 32.0161 | 30.8344 | 29.0766 | 28.3797 | 28.3409 | 27.8586 | 28.2522 | 27.3527 | 27.6881 | 26.5497 | ||
| 30 | 34.2147 | 34.7117 | 34.4426 | 34.2688 | 34.8958 | 33.4774 | 31.6066 | 29.5656 | 29.3375 | 29.1227 | 29.2851 | 28.9762 | 29.1881 | 28.4078 | ||
| X2 | 2 | 15.4339 | 15.4339 | 15.4339 | 15.4339 | 15.4339 | 15.4339 | 15.0664 | X8 | 15.0584 | 15.0584 | 15.0584 | 15.0581 | 15.0584 | 15.0584 | 15.0231 |
| 3 | 19.0614 | 19.0614 | 19.0598 | 19.0614 | 19.0598 | 19.0593 | 17.5684 | 18.5399 | 18.5397 | 18.5300 | 18.5398 | 18.5397 | 18.5384 | 18.3247 | ||
| 4 | 19.5687 | 19.5676 | 19.5460 | 19.5845 | 19.5473 | 19.5785 | 19.0799 | 20.4752 | 20.4396 | 20.2559 | 20.3902 | 20.3021 | 20.3089 | 19.3735 | ||
| 5 | 21.8944 | 21.9055 | 21.8064 | 21.9103 | 21.8351 | 21.8833 | 19.9896 | 21.7622 | 21.7326 | 21.4727 | 21.6882 | 21.3617 | 21.7624 | 20.7030 | ||
| 6 | 23.3280 | 23.2037 | 23.1561 | 23.3193 | 23.1632 | 23.3404 | 21.1292 | 23.2417 | 23.0551 | 22.7673 | 23.1817 | 22.6722 | 23.1439 | 21.3987 | ||
| 7 | 23.6048 | 23.7391 | 23.4373 | 23.6147 | 23.4716 | 23.6404 | 22.3326 | 23.8725 | 23.7568 | 23.6656 | 23.8724 | 23.7051 | 23.8228 | 22.1885 | ||
| 8 | 25.2772 | 25.2649 | 24.7597 | 25.2939 | 24.8453 | 25.2088 | 22.7135 | 25.1533 | 25.1050 | 24.3448 | 24.9353 | 24.4041 | 24.8915 | 23.3818 | ||
| 9 | 26.1459 | 26.0982 | 25.7633 | 26.2206 | 25.7351 | 26.0065 | 24.1776 | 26.0072 | 25.8164 | 25.1265 | 25.8631 | 25.1310 | 25.9092 | 24.3065 | ||
| 10 | 26.8214 | 26.7884 | 26.3162 | 26.6867 | 26.3212 | 26.5252 | 24.6270 | 27.0580 | 26.6239 | 25.7109 | 26.8672 | 25.5503 | 26.6832 | 23.3187 | ||
| 15 | 30.2230 | 30.2786 | 29.0026 | 30.3224 | 28.8439 | 29.7970 | 26.6702 | 28.4823 | 28.6101 | 27.4389 | 28.2749 | 27.9789 | 28.5384 | 26.9208 | ||
| 20 | 32.5178 | 32.2824 | 31.1105 | 32.6471 | 30.7657 | 31.6089 | 29.3500 | 31.0909 | 30.2209 | 29.5583 | 30.8247 | 29.2329 | 30.0101 | 28.1920 | ||
| 30 | 35.6553 | 35.7611 | 33.5503 | 35.7363 | 33.8251 | 34.0759 | 31.9949 | 34.4386 | 33.9666 | 32.9237 | 34.4272 | 32.7464 | 33.1187 | 31.0745 | ||
| X3 | 2 | 13.5597 | 13.5597 | 13.5597 | 13.5597 | 13.5597 | 13.5597 | 13.5856 | X9 | 13.9264 | 13.9264 | 13.9264 | 13.9264 | 13.9264 | 13.9264 | 13.9408 |
| 3 | 15.4668 | 15.4608 | 15.4653 | 15.4668 | 15.4659 | 15.4668 | 15.8627 | 17.4209 | 17.4217 | 17.4209 | 17.4209 | 17.4200 | 17.4217 | 17.0266 | ||
| 4 | 18.6812 | 18.6322 | 18.7060 | 18.6334 | 18.7064 | 18.6933 | 17.7343 | 19.7395 | 19.7373 | 19.7204 | 19.7387 | 19.7242 | 19.7436 | 18.6316 | ||
| 5 | 20.5014 | 20.5286 | 20.9156 | 20.4033 | 20.8693 | 20.3339 | 18.6695 | 20.6141 | 20.6085 | 20.4564 | 20.5715 | 20.5183 | 20.5629 | 20.1364 | ||
| 6 | 23.7724 | 23.5477 | 23.9135 | 23.7670 | 23.7958 | 23.7620 | 20.6607 | 22.2588 | 22.2602 | 22.2333 | 22.2654 | 22.2294 | 22.2429 | 21.0136 | ||
| 7 | 24.5192 | 24.4967 | 25.1493 | 24.5074 | 25.0146 | 24.4681 | 21.0312 | 23.6050 | 23.5830 | 23.3621 | 23.5882 | 23.3540 | 23.5769 | 22.2219 | ||
| 8 | 26.3355 | 25.9230 | 26.5196 | 26.2487 | 26.6897 | 26.1332 | 22.3935 | 24.4299 | 24.5225 | 24.2443 | 24.4996 | 24.1444 | 24.5016 | 22.8170 | ||
| 9 | 27.5838 | 27.2210 | 27.7576 | 27.5861 | 27.8061 | 27.5820 | 22.8420 | 25.2991 | 25.2872 | 25.0545 | 25.2862 | 24.9055 | 25.1897 | 23.3581 | ||
| 10 | 28.3308 | 28.2626 | 28.6363 | 28.2831 | 28.7330 | 28.2442 | 24.4468 | 26.1767 | 26.2434 | 25.8457 | 26.1998 | 25.8211 | 26.1591 | 23.7645 | ||
| 15 | 30.9231 | 31.3151 | 31.9472 | 30.5238 | 31.9835 | 30.8741 | 27.0095 | 29.0098 | 29.2177 | 28.8906 | 28.6140 | 28.6985 | 28.2695 | 26.2449 | ||
| 20 | 32.7470 | 33.3867 | 34.4622 | 32.3973 | 34.4528 | 32.4652 | 28.4250 | 31.4450 | 31.3282 | 30.6876 | 30.8601 | 30.6150 | 30.0195 | 28.5902 | ||
| 30 | 36.0843 | 36.9800 | 37.9711 | 35.5183 | 37.9570 | 35.8354 | 31.7538 | 34.7220 | 34.5881 | 33.3637 | 34.1399 | 33.7642 | 33.4018 | 31.5622 | ||
| X4 | 2 | 14.0817 | 14.0817 | 14.0817 | 14.1187 | 14.0817 | 14.0817 | 13.9607 | X10 | 16.0138 | 16.0138 | 16.0138 | 16.0219 | 16.0138 | 16.0299 | 15.4414 |
| 3 | 18.3927 | 18.3927 | 18.3927 | 18.3927 | 18.3927 | 18.3874 | 16.5780 | 19.4769 | 19.4769 | 19.4769 | 19.4801 | 19.4774 | 19.4774 | 18.4177 | ||
| 4 | 20.8446 | 20.8528 | 20.8181 | 20.8524 | 20.7754 | 20.8269 | 18.6470 | 21.6089 | 21.6270 | 21.6471 | 21.6303 | 21.6809 | 21.6223 | 20.2690 | ||
| 5 | 22.7884 | 22.7420 | 22.4952 | 22.7890 | 22.5426 | 22.7888 | 20.7013 | 23.5025 | 23.4975 | 23.4472 | 23.5018 | 23.4589 | 23.4938 | 20.9350 | ||
| 6 | 24.3006 | 24.3038 | 24.0282 | 24.2793 | 24.0370 | 24.2615 | 21.2844 | 24.9480 | 24.9837 | 24.7865 | 25.0199 | 24.7514 | 24.9710 | 22.1587 | ||
| 7 | 25.3571 | 25.4504 | 25.2328 | 25.4069 | 25.0215 | 25.1716 | 21.9359 | 25.8710 | 25.9455 | 25.5210 | 25.8056 | 25.3843 | 25.8204 | 22.9135 | ||
| 8 | 26.0496 | 26.1674 | 25.8153 | 26.0798 | 25.6611 | 26.0980 | 22.6437 | 26.5926 | 26.7707 | 26.4238 | 26.5759 | 26.5108 | 26.4779 | 23.9432 | ||
| 9 | 26.6098 | 26.5313 | 26.1939 | 26.1744 | 26.4447 | 26.6716 | 23.5580 | 27.7314 | 27.8226 | 27.5119 | 27.7398 | 27.3700 | 27.5431 | 24.5070 | ||
| 10 | 27.3563 | 27.2461 | 26.8866 | 27.3559 | 26.8032 | 27.2050 | 24.3201 | 28.8519 | 28.7088 | 28.0721 | 28.8094 | 28.0597 | 28.5790 | 25.1122 | ||
| 15 | 30.2457 | 29.8135 | 29.1392 | 30.2096 | 29.0109 | 30.1001 | 26.9848 | 31.6919 | 31.5349 | 31.0770 | 31.6099 | 31.2207 | 30.8728 | 26.8402 | ||
| 20 | 32.2000 | 31.5708 | 30.9785 | 31.9510 | 30.2745 | 31.4728 | 28.1634 | 34.3762 | 33.6492 | 33.3989 | 34.0633 | 33.4870 | 33.1391 | 29.2939 | ||
| 30 | 34.2907 | 33.3357 | 32.9391 | 33.8974 | 32.9951 | 33.6508 | 30.8160 | 36.6847 | 36.4906 | 36.1726 | 36.2996 | 35.5768 | 35.7522 | 32.5480 | ||
| X5 | 2 | 16.8558 | 16.8558 | 16.8558 | 16.8558 | 16.8558 | 16.8558 | 16.5945 | X11 | 14.2717 | 14.2717 | 14.2717 | 14.2717 | 14.2717 | 14.2717 | 14.2243 |
| 3 | 19.9997 | 19.9997 | 19.9966 | 19.9987 | 19.9967 | 19.9975 | 18.5084 | 17.2552 | 17.2552 | 17.2540 | 17.2551 | 17.2540 | 17.2551 | 17.1190 | ||
| 4 | 20.4189 | 20.3982 | 20.3662 | 20.4464 | 20.3874 | 20.4801 | 18.9831 | 19.9315 | 19.9244 | 19.9145 | 19.9315 | 19.9040 | 19.9273 | 19.1704 | ||
| 5 | 20.6283 | 20.6116 | 20.7390 | 20.6807 | 20.8800 | 20.4794 | 20.1040 | 20.9527 | 20.9345 | 20.8917 | 20.9406 | 20.8786 | 20.9346 | 20.0765 | ||
| 6 | 22.5190 | 22.2922 | 22.4222 | 22.4383 | 22.2021 | 22.3436 | 21.1247 | 22.2043 | 22.1748 | 22.0959 | 22.1603 | 22.0270 | 22.2015 | 20.9618 | ||
| 7 | 23.4453 | 23.2175 | 22.9219 | 23.2131 | 22.8777 | 23.1368 | 21.8744 | 23.2544 | 23.2099 | 23.0703 | 23.2271 | 23.0977 | 23.2535 | 22.1135 | ||
| 8 | 24.6961 | 24.5548 | 23.7161 | 24.6919 | 24.0570 | 24.2918 | 22.3592 | 24.2597 | 24.3125 | 24.0775 | 24.2580 | 24.1121 | 24.2203 | 22.7172 | ||
| 9 | 25.2118 | 25.2193 | 24.3273 | 25.3126 | 24.2135 | 24.8847 | 22.8288 | 25.2773 | 25.2904 | 24.8579 | 25.2501 | 24.8420 | 25.0545 | 23.6391 | ||
| 10 | 24.9566 | 25.0411 | 24.3275 | 24.8350 | 24.4260 | 24.9272 | 23.8191 | 26.1130 | 26.1173 | 25.7950 | 26.0308 | 25.6674 | 25.9849 | 24.1108 | ||
| 15 | 27.5008 | 27.7911 | 27.1203 | 27.2337 | 26.8370 | 26.9085 | 25.6230 | 28.7869 | 28.7463 | 28.2373 | 28.6988 | 28.4623 | 28.5285 | 26.3509 | ||
| 20 | 29.1286 | 29.1651 | 29.0824 | 28.6639 | 29.0095 | 28.4533 | 27.2341 | 30.8302 | 31.4031 | 30.6196 | 30.3909 | 30.5756 | 30.2222 | 28.2633 | ||
| 30 | 30.7165 | 30.6026 | 30.5441 | 30.2876 | 30.7036 | 30.0646 | 29.4905 | 33.5412 | 33.3217 | 32.9252 | 32.9138 | 32.9945 | 32.0790 | 30.4614 | ||
| X6 | 2 | 14.5488 | 14.5488 | 14.5488 | 14.5488 | 14.5488 | 14.5488 | 14.5558 | X12 | 11.7366 | 11.7366 | 11.7366 | 11.7366 | 11.7366 | 11.7366 | 12.4388 |
| 3 | 17.8770 | 17.8770 | 17.8753 | 17.8770 | 17.8671 | 17.8702 | 17.5791 | 14.7809 | 14.7809 | 14.7815 | 14.7797 | 14.7809 | 14.7782 | 11.1844 | ||
| 4 | 19.8781 | 19.8781 | 19.8623 | 19.8749 | 19.8699 | 19.8702 | 18.9017 | 17.1519 | 17.0353 | 17.1667 | 17.1374 | 17.1667 | 17.1084 | 17.1003 | ||
| 5 | 21.2166 | 21.2187 | 21.0808 | 21.1654 | 21.1375 | 21.2583 | 19.5376 | 18.0776 | 18.1041 | 18.4005 | 18.0776 | 18.3146 | 18.0667 | 18.0707 | ||
| 6 | 21.5448 | 21.9494 | 21.8046 | 21.4509 | 21.5674 | 21.7895 | 20.0646 | 19.4659 | 19.6111 | 20.7148 | 19.4475 | 20.6380 | 19.4496 | 19.4717 | ||
| 7 | 21.2614 | 21.9631 | 21.7077 | 21.1139 | 21.6558 | 20.9267 | 19.9842 | 24.1208 | 23.2142 | 24.0832 | 23.4850 | 23.8491 | 22.3931 | 22.3033 | ||
| 8 | 22.1957 | 22.2642 | 21.7215 | 21.9257 | 22.1219 | 21.7240 | 21.3627 | 24.6843 | 25.7926 | 25.9087 | 25.6349 | 25.9052 | 25.8755 | 23.6704 | ||
| 9 | 22.8453 | 22.7665 | 22.4835 | 22.6769 | 22.5525 | 22.5510 | 21.4795 | 26.8606 | 26.6221 | 26.6835 | 26.8531 | 26.7703 | 26.7230 | 24.2734 | ||
| 10 | 23.6546 | 23.5141 | 23.2509 | 23.4438 | 22.8786 | 22.9563 | 22.0010 | 27.5479 | 27.5171 | 27.5659 | 27.7848 | 27.3789 | 27.8282 | 24.9804 | ||
| 15 | 25.1382 | 25.1011 | 24.8791 | 24.9874 | 24.3782 | 24.7988 | 23.9355 | 30.6922 | 30.5015 | 30.4197 | 30.4398 | 30.6144 | 29.7160 | 26.9165 | ||
| 20 | 25.9393 | 25.9809 | 25.6561 | 25.7365 | 25.6036 | 25.5312 | 24.9332 | 33.0374 | 33.0790 | 32.8630 | 32.9186 | 32.8577 | 32.3296 | 29.6352 | ||
| 30 | 26.6336 | 26.6257 | 26.3605 | 26.5272 | 26.4522 | 26.3838 | 25.9521 | 36.5517 | 36.0368 | 35.5624 | 36.0258 | 36.1598 | 34.9519 | 31.0913 |
The bold value indicates the best value.
7.4. Structured similarity index metric (SSIM)
Unfortunately, PSNR calculates only the ratio of the error between the segmented and the source image without taking into consideration the structure of the image. Therefore, SSIM [61] is proposed to measure the similarity, contrast distortion and brightness between the original and the segmented one using the following formula:
| (27) |
Where is the average intensities of the original image, while indicates the average intensities of the segmented image. , are the SD of the original and segmented images, respectively. are the covariance between the two images. And is equal to 0.001 and 0.003, respectively. SSIM must also be maximized to get better results.
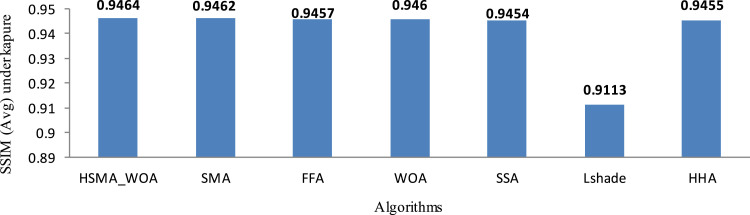
In order to inspect the results under using Kapur’s entropy as a fitness function, the average SSIM values obtained within 20 runs under Kapur’s are calculated and given in Table 5. This table shows that HSMA_WOA could get to the best in 57 cases and equal in 24 while its performance on the other cases is converged with the other algorithms. Meanwhile, SMA could outperform in 24 and equal in 22. Fig. 7 shows the superiority of HSMA_WOA in comparison with SMA that is superior to the others.
Table 5.
SSIM values under Kapur’s method.
| img | T | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
Img | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 2 | 0.7439 | 0.7439 | 0.7439 | 0.7441 | 0.7439 | 0.7439 | 0.7250 | X7 | 0.8638 | 0.8727 | 0.8727 | 0.8638 | 0.8727 | 0.8727 | 0.8637 |
| 3 | 0.8745 | 0.8745 | 0.8746 | 0.8746 | 0.8746 | 0.8748 | 0.8577 | 0.9038 | 0.9038 | 0.9036 | 0.9038 | 0.9036 | 0.9036 | 0.8833 | ||
| 4 | 0.9243 | 0.9246 | 0.9248 | 0.9243 | 0.9246 | 0.9240 | 0.8993 | 0.9368 | 0.9370 | 0.9367 | 0.9368 | 0.9367 | 0.9370 | 0.9114 | ||
| 5 | 0.9524 | 0.9524 | 0.9537 | 0.9525 | 0.9535 | 0.9523 | 0.9271 | 0.9576 | 0.9578 | 0.9570 | 0.9577 | 0.9571 | 0.9577 | 0.9427 | ||
| 6 | 0.9654 | 0.9651 | 0.9669 | 0.9653 | 0.9667 | 0.9650 | 0.9364 | 0.9659 | 0.9658 | 0.9650 | 0.9660 | 0.9652 | 0.9657 | 0.9387 | ||
| 7 | 0.9741 | 0.9715 | 0.9730 | 0.9744 | 0.9714 | 0.9727 | 0.9498 | 0.9688 | 0.9706 | 0.9686 | 0.9685 | 0.9680 | 0.9689 | 0.9559 | ||
| 8 | 0.9746 | 0.9763 | 0.9782 | 0.9751 | 0.9781 | 0.9747 | 0.9570 | 0.9722 | 0.9721 | 0.9701 | 0.9723 | 0.9709 | 0.9710 | 0.9571 | ||
| 9 | 0.9791 | 0.9782 | 0.9818 | 0.9786 | 0.9815 | 0.9778 | 0.9658 | 0.9745 | 0.9733 | 0.9715 | 0.9744 | 0.9722 | 0.9740 | 0.9598 | ||
| 10 | 0.9816 | 0.9822 | 0.9849 | 0.9818 | 0.9840 | 0.9808 | 0.9720 | 0.9763 | 0.9759 | 0.9733 | 0.9758 | 0.9733 | 0.9755 | 0.9607 | ||
| 15 | 0.9910 | 0.9912 | 0.9916 | 0.9912 | 0.9918 | 0.9904 | 0.9825 | 0.9812 | 0.9811 | 0.9785 | 0.9812 | 0.9781 | 0.9785 | 0.9712 | ||
| 20 | 0.9939 | 0.9937 | 0.9940 | 0.9938 | 0.9943 | 0.9926 | 0.9893 | 0.9833 | 0.9833 | 0.9820 | 0.9829 | 0.9806 | 0.9814 | 0.9776 | ||
| 30 | 0.9956 | 0.9959 | 0.9957 | 0.9956 | 0.9960 | 0.9949 | 0.9930 | 0.9854 | 0.9848 | 0.9841 | 0.9848 | 0.9838 | 0.9845 | 0.9828 | ||
| X2 | 2 | 0.8255 | 0.8255 | 0.8255 | 0.8255 | 0.8255 | 0.8255 | 0.7973 | X8 | 0.7400 | 0.7400 | 0.7400 | 0.7400 | 0.7401 | 0.7400 | 0.7498 |
| 3 | 0.9162 | 0.9162 | 0.9161 | 0.9162 | 0.9161 | 0.9161 | 0.8683 | 0.9058 | 0.9058 | 0.9058 | 0.9058 | 0.9058 | 0.9060 | 0.8904 | ||
| 4 | 0.9238 | 0.9238 | 0.9234 | 0.9240 | 0.9235 | 0.9239 | 0.8953 | 0.9329 | 0.9328 | 0.9304 | 0.9321 | 0.9353 | 0.9364 | 0.9099 | ||
| 5 | 0.9524 | 0.9525 | 0.9512 | 0.9526 | 0.9516 | 0.9522 | 0.9124 | 0.9533 | 0.9529 | 0.9482 | 0.9522 | 0.9469 | 0.9532 | 0.9299 | ||
| 6 | 0.9628 | 0.9621 | 0.9613 | 0.9627 | 0.9613 | 0.9620 | 0.9231 | 0.9656 | 0.9641 | 0.9613 | 0.9653 | 0.9604 | 0.9649 | 0.9366 | ||
| 7 | 0.9642 | 0.9655 | 0.9630 | 0.9642 | 0.9633 | 0.9645 | 0.8546 | 0.9706 | 0.9695 | 0.9686 | 0.9705 | 0.9690 | 0.9705 | 0.9449 | ||
| 8 | 0.9767 | 0.9768 | 0.9725 | 0.9770 | 0.9734 | 0.9765 | 0.9415 | 0.9775 | 0.9770 | 0.9721 | 0.9763 | 0.9727 | 0.9759 | 0.9579 | ||
| 9 | 0.9808 | 0.9805 | 0.9786 | 0.9811 | 0.9781 | 0.9801 | 0.9608 | 0.9811 | 0.9802 | 0.9763 | 0.9807 | 0.9761 | 0.9806 | 0.9635 | ||
| 10 | 0.9833 | 0.9831 | 0.9806 | 0.9827 | 0.9807 | 0.9821 | 0.8743 | 0.9845 | 0.9829 | 0.9788 | 0.9839 | 0.9777 | 0.9833 | 0.9563 | ||
| 15 | 0.9915 | 0.9912 | 0.9877 | 0.9912 | 0.9874 | 0.9902 | 0.9722 | 0.9884 | 0.9885 | 0.9835 | 0.9877 | 0.9857 | 0.9875 | 0.9787 | ||
| 20 | 0.9943 | 0.9937 | 0.9914 | 0.9944 | 0.9901 | 0.9927 | 0.9851 | 0.9927 | 0.9909 | 0.9882 | 0.9923 | 0.9871 | 0.9901 | 0.9825 | ||
| 30 | 0.9965 | 0.9963 | 0.9935 | 0.9964 | 0.9936 | 0.9948 | 0.9906 | 0.9957 | 0.9951 | 0.9934 | 0.9957 | 0.9927 | 0.9940 | 0.9898 | ||
| X3 | 2 | 0.7356 | 0.7356 | 0.7356 | 0.7356 | 0.7356 | 0.7356 | 0.5969 | X9 | 0.8256 | 0.8256 | 0.8256 | 0.8256 | 0.8256 | 0.8256 | 0.8213 |
| 3 | 0.8023 | 0.8020 | 0.8026 | 0.8023 | 0.8022 | 0.8023 | 0.5878 | 0.9151 | 0.9151 | 0.9151 | 0.9151 | 0.9151 | 0.9151 | 0.9090 | ||
| 4 | 0.8804 | 0.8791 | 0.8802 | 0.8790 | 0.8810 | 0.8802 | 0.7837 | 0.9518 | 0.9518 | 0.9516 | 0.9518 | 0.9516 | 0.9518 | 0.9344 | ||
| 5 | 0.9120 | 0.9127 | 0.9199 | 0.9102 | 0.9189 | 0.9090 | 0.6624 | 0.9590 | 0.9589 | 0.9577 | 0.9588 | 0.9581 | 0.9587 | 0.9489 | ||
| 6 | 0.9596 | 0.9569 | 0.9608 | 0.9596 | 0.9595 | 0.9595 | 0.9099 | 0.9724 | 0.9724 | 0.9719 | 0.9724 | 0.9719 | 0.9721 | 0.9557 | ||
| 7 | 0.9648 | 0.9643 | 0.9700 | 0.9649 | 0.9689 | 0.9641 | 0.9148 | 0.9782 | 0.9782 | 0.9772 | 0.9782 | 0.9771 | 0.9781 | 0.9667 | ||
| 8 | 0.9776 | 0.9740 | 0.9802 | 0.9768 | 0.9799 | 0.9758 | 0.9348 | 0.9819 | 0.9824 | 0.9809 | 0.9822 | 0.9803 | 0.9823 | 0.9695 | ||
| 9 | 0.9838 | 0.9809 | 0.9842 | 0.9838 | 0.9844 | 0.9836 | 0.9398 | 0.9855 | 0.9850 | 0.9837 | 0.9854 | 0.9831 | 0.9847 | 0.9728 | ||
| 10 | 0.9859 | 0.9852 | 0.9867 | 0.9856 | 0.9869 | 0.9853 | 0.9572 | 0.9878 | 0.9879 | 0.9861 | 0.9878 | 0.9860 | 0.9876 | 0.9726 | ||
| 15 | 0.9908 | 0.9912 | 0.9926 | 0.9899 | 0.9927 | 0.9904 | 0.9753 | 0.9928 | 0.9930 | 0.9923 | 0.9919 | 0.9918 | 0.9910 | 0.9833 | ||
| 20 | 0.9931 | 0.9941 | 0.9954 | 0.9927 | 0.9954 | 0.9925 | 0.9811 | 0.9952 | 0.9952 | 0.9942 | 0.9945 | 0.9938 | 0.9932 | 0.9899 | ||
| 30 | 0.9962 | 0.9969 | 0.9973 | 0.9957 | 0.9974 | 0.9958 | 0.9903 | 0.9971 | 0.9969 | 0.9959 | 0.9967 | 0.9963 | 0.9961 | 0.9939 | ||
| X4 | 2 | 0.7787 | 0.7787 | 0.7787 | 0.7764 | 0.7787 | 0.7787 | 0.5612 | X10 | 0.8216 | 0.8216 | 0.8216 | 0.8217 | 0.8216 | 0.8217 | 0.7915 |
| 3 | 0.8813 | 0.8813 | 0.8813 | 0.8813 | 0.8813 | 0.8813 | 0.8058 | 0.9115 | 0.9115 | 0.9115 | 0.9115 | 0.9115 | 0.9115 | 0.8726 | ||
| 4 | 0.9368 | 0.9369 | 0.9368 | 0.9369 | 0.9359 | 0.9361 | 0.8656 | 0.9411 | 0.9414 | 0.9414 | 0.9417 | 0.9418 | 0.9413 | 0.9071 | ||
| 5 | 0.9542 | 0.9539 | 0.9518 | 0.9542 | 0.9522 | 0.9542 | 0.9091 | 0.9603 | 0.9603 | 0.9595 | 0.9603 | 0.9595 | 0.9602 | 0.9130 | ||
| 6 | 0.9662 | 0.9662 | 0.9634 | 0.9661 | 0.9637 | 0.9657 | 0.9155 | 0.9705 | 0.9707 | 0.9693 | 0.9710 | 0.9691 | 0.9705 | 0.9291 | ||
| 7 | 0.9725 | 0.9727 | 0.9706 | 0.9726 | 0.9691 | 0.9703 | 0.9276 | 0.9757 | 0.9761 | 0.9739 | 0.9754 | 0.9732 | 0.9753 | 0.9345 | ||
| 8 | 0.9756 | 0.9758 | 0.9731 | 0.9755 | 0.9720 | 0.9748 | 0.9368 | 0.9796 | 0.9803 | 0.9785 | 0.9799 | 0.9788 | 0.9789 | 0.9524 | ||
| 9 | 0.9781 | 0.9773 | 0.9747 | 0.9753 | 0.9758 | 0.9771 | 0.9468 | 0.9839 | 0.9842 | 0.9827 | 0.9839 | 0.9820 | 0.9828 | 0.9544 | ||
| 10 | 0.9804 | 0.9800 | 0.9771 | 0.9800 | 0.9773 | 0.9788 | 0.9523 | 0.9876 | 0.9870 | 0.9842 | 0.9874 | 0.9845 | 0.9864 | 0.9621 | ||
| 15 | 0.9874 | 0.9864 | 0.9836 | 0.9872 | 0.9815 | 0.9865 | 0.9675 | 0.9925 | 0.9922 | 0.9910 | 0.9923 | 0.9913 | 0.9903 | 0.9685 | ||
| 20 | 0.9903 | 0.9892 | 0.9875 | 0.9896 | 0.9845 | 0.9885 | 0.9735 | 0.9953 | 0.9944 | 0.9934 | 0.9950 | 0.9939 | 0.9935 | 0.9829 | ||
| 30 | 0.9922 | 0.9909 | 0.9899 | 0.9918 | 0.9898 | 0.9912 | 0.9849 | 0.9961 | 0.9961 | 0.9956 | 0.9961 | 0.9942 | 0.9954 | 0.9909 | ||
| X5 | 2 | 0.8627 | 0.8627 | 0.8627 | 0.8627 | 0.8627 | 0.8627 | 0.8491 | X11 | 0.8247 | 0.8247 | 0.8247 | 0.8247 | 0.8247 | 0.8247 | 0.8201 |
| 3 | 0.9311 | 0.9311 | 0.9311 | 0.9311 | 0.9311 | 0.9311 | 0.8950 | 0.8994 | 0.8994 | 0.8995 | 0.8994 | 0.8994 | 0.8994 | 0.8929 | ||
| 4 | 0.9368 | 0.9366 | 0.9363 | 0.9370 | 0.9363 | 0.9374 | 0.7296 | 0.9381 | 0.9379 | 0.9377 | 0.9381 | 0.9375 | 0.9380 | 0.9237 | ||
| 5 | 0.9404 | 0.9402 | 0.9403 | 0.9410 | 0.9417 | 0.9368 | 0.8291 | 0.9542 | 0.9539 | 0.9533 | 0.9539 | 0.9532 | 0.9538 | 0.9362 | ||
| 6 | 0.9589 | 0.9565 | 0.9575 | 0.9581 | 0.9548 | 0.9569 | 0.9327 | 0.9638 | 0.9635 | 0.9631 | 0.9636 | 0.9628 | 0.9636 | 0.9444 | ||
| 7 | 0.9652 | 0.9636 | 0.9611 | 0.9635 | 0.9600 | 0.9617 | 0.9418 | 0.9708 | 0.9706 | 0.9694 | 0.9708 | 0.9697 | 0.9707 | 0.9572 | ||
| 8 | 0.9723 | 0.9713 | 0.9657 | 0.9719 | 0.9678 | 0.9691 | 0.9481 | 0.9766 | 0.9764 | 0.9748 | 0.9763 | 0.9751 | 0.9764 | 0.9613 | ||
| 9 | 0.9737 | 0.9740 | 0.9687 | 0.9739 | 0.9682 | 0.9714 | 0.7643 | 0.9809 | 0.9808 | 0.9781 | 0.9808 | 0.9777 | 0.9798 | 0.9669 | ||
| 10 | 0.9739 | 0.9733 | 0.9699 | 0.9712 | 0.9684 | 0.9713 | 0.9614 | 0.9834 | 0.9834 | 0.9817 | 0.9831 | 0.9811 | 0.9828 | 0.9700 | ||
| 15 | 0.9815 | 0.9822 | 0.9798 | 0.9797 | 0.9788 | 0.9785 | 0.9708 | 0.9906 | 0.9897 | 0.9875 | 0.9905 | 0.9877 | 0.9893 | 0.9802 | ||
| 20 | 0.9849 | 0.9850 | 0.9847 | 0.9835 | 0.9845 | 0.9828 | 0.9772 | 0.9931 | 0.9936 | 0.9921 | 0.9923 | 0.9916 | 0.9916 | 0.9860 | ||
| 30 | 0.9872 | 0.9868 | 0.9866 | 0.9863 | 0.9870 | 0.9856 | 0.9841 | 0.9951 | 0.9949 | 0.9941 | 0.9944 | 0.9941 | 0.9932 | 0.9900 | ||
| X6 | 2 | 0.7549 | 0.7549 | 0.7549 | 0.7549 | 0.7549 | 0.7549 | 0.7461 | X12 | 0.6720 | 0.6720 | 0.6720 | 0.6720 | 0.6720 | 0.6720 | 0.3302 |
| 3 | 0.8863 | 0.8863 | 0.8863 | 0.8863 | 0.8862 | 0.8863 | 0.8712 | 0.7837 | 0.7837 | 0.7837 | 0.7837 | 0.7837 | 0.7837 | 0.4418 | ||
| 4 | 0.9131 | 0.9131 | 0.9129 | 0.9131 | 0.9130 | 0.9131 | 0.8925 | 0.8514 | 0.8482 | 0.8518 | 0.8510 | 0.8518 | 0.8502 | 0.7148 | ||
| 5 | 0.9281 | 0.9282 | 0.9263 | 0.9275 | 0.9269 | 0.9288 | 0.8965 | 0.8710 | 0.8713 | 0.8777 | 0.8710 | 0.8757 | 0.8705 | 0.8963 | ||
| 6 | 0.9318 | 0.9354 | 0.9333 | 0.9305 | 0.9302 | 0.9343 | 0.9061 | 0.8975 | 0.8994 | 0.9190 | 0.8972 | 0.9180 | 0.8972 | 0.9418 | ||
| 7 | 0.9303 | 0.9359 | 0.9320 | 0.9282 | 0.9318 | 0.9251 | 0.9006 | 0.9661 | 0.9524 | 0.9708 | 0.9575 | 0.9627 | 0.9423 | 0.8765 | ||
| 8 | 0.9399 | 0.9397 | 0.9323 | 0.9357 | 0.9357 | 0.9331 | 0.9260 | 0.9688 | 0.9824 | 0.9837 | 0.9804 | 0.9837 | 0.9828 | 0.9672 | ||
| 9 | 0.9441 | 0.9429 | 0.9370 | 0.9422 | 0.9394 | 0.9395 | 0.9219 | 0.9864 | 0.9853 | 0.9863 | 0.9864 | 0.9864 | 0.9858 | 0.9724 | ||
| 10 | 0.9493 | 0.9482 | 0.9454 | 0.9467 | 0.9420 | 0.9425 | 0.9311 | 0.9881 | 0.9879 | 0.9886 | 0.9893 | 0.9882 | 0.9894 | 0.9758 | ||
| 15 | 0.9560 | 0.9554 | 0.9538 | 0.9547 | 0.9481 | 0.9532 | 0.9462 | 0.9939 | 0.9935 | 0.9934 | 0.9936 | 0.9936 | 0.9920 | 0.9824 | ||
| 20 | 0.9587 | 0.9588 | 0.9566 | 0.9575 | 0.9566 | 0.9564 | 0.9523 | 0.9959 | 0.9960 | 0.9957 | 0.9957 | 0.9956 | 0.9950 | 0.9903 | ||
| 30 | 0.9607 | 0.9604 | 0.9589 | 0.9602 | 0.9590 | 0.9594 | 0.9571 | 0.9975 | 0.9972 | 0.9968 | 0.9972 | 0.9971 | 0.9964 | 0.9918 |
Bold value indicates the best value.
Fig. 7.
Average SSIM values obtained under Kapure’s entropy.
7.5. Universal quality index (UQI)
UQI [62] is an indicator similar to SSIM in measuring the quality of the segmented image based on the similarity structure between the two images rather than the error rate and mathematically formulated as in Eq. (24).
| (28) |
where refers to the original image, is the segmented image, are the mean intensities of the original image are the mean intensities of the and segmented image. and are the standard deviations for both the source and predicted image; is the covariance between the separated and source image. A higher value of UQI indicates better results.
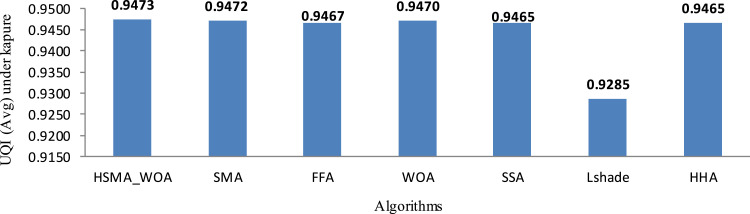
After executing each algorithm, 20 runs and calculated the average UQI within them obtained by each one under Kapure’s entropy, it is introduced in Table 5. By observing outcomes in this table, we notify that HSMA_WOA could overcome the others in 58 cases and equal in 20 others. In the same context, SMA could achieve the best in 18 and equal in 19. Specifically, the proposed algorithms could be superior and equal in 101 out of 144 test cases. Based on that, the proposed algorithms are competitive with others for generating a better-segmented image. In order to illustrate the data in Table 6, Fig. 8 is taken to show the average UQI obtained by the algorithms within 20 runs and all the test images and threshold levels. This figure shows the superiority of the comparison of the proposed algorithms with the others under Kapur’s method.
Table 6.
UQI values under Kapur’s entropy.
| img | T | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
Img | HSMA_WOA | SMA | FFA [39] |
WOA [33] |
SSA [60] |
HHA [38] |
LShade [59] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 2 | 0.7479 | 0.7479 | 0.7478 | 0.7477 | 0.7479 | 0.7479 | 0.7262 | X7 | 0.8641 | 0.8729 | 0.8729 | 0.8641 | 0.8729 | 0.8729 | 0.8647 |
| 3 | 0.8760 | 0.8760 | 0.8761 | 0.8760 | 0.8760 | 0.8764 | 0.8590 | 0.9042 | 0.9042 | 0.9042 | 0.9042 | 0.9042 | 0.9042 | 0.8844 | ||
| 4 | 0.9260 | 0.9259 | 0.9263 | 0.9258 | 0.9264 | 0.9255 | 0.9004 | 0.9380 | 0.9383 | 0.9379 | 0.9380 | 0.9379 | 0.9383 | 0.9126 | ||
| 5 | 0.9538 | 0.9537 | 0.9553 | 0.9539 | 0.9550 | 0.9536 | 0.9285 | 0.9590 | 0.9593 | 0.9582 | 0.9590 | 0.9583 | 0.9590 | 0.9438 | ||
| 6 | 0.9671 | 0.9668 | 0.9681 | 0.9669 | 0.9661 | 0.9666 | 0.9378 | 0.9673 | 0.9672 | 0.9662 | 0.9675 | 0.9665 | 0.9671 | 0.9398 | ||
| 7 | 0.9752 | 0.9727 | 0.9742 | 0.9755 | 0.9755 | 0.9738 | 0.9512 | 0.9700 | 0.9718 | 0.9698 | 0.9697 | 0.9692 | 0.9701 | 0.9571 | ||
| 8 | 0.9758 | 0.9777 | 0.9796 | 0.9765 | 0.9794 | 0.9760 | 0.9583 | 0.9734 | 0.9732 | 0.9713 | 0.9734 | 0.9721 | 0.9722 | 0.9583 | ||
| 9 | 0.9804 | 0.9796 | 0.9831 | 0.9800 | 0.9827 | 0.9792 | 0.9670 | 0.9757 | 0.9745 | 0.9727 | 0.9756 | 0.9734 | 0.9752 | 0.9610 | ||
| 10 | 0.9830 | 0.9836 | 0.9862 | 0.9832 | 0.9853 | 0.9821 | 0.9734 | 0.9776 | 0.9771 | 0.9745 | 0.9769 | 0.9745 | 0.9767 | 0.9619 | ||
| 15 | 0.9925 | 0.9926 | 0.9931 | 0.9926 | 0.9933 | 0.9918 | 0.9838 | 0.9825 | 0.9824 | 0.9797 | 0.9824 | 0.9793 | 0.9798 | 0.9723 | ||
| 20 | 0.9954 | 0.9952 | 0.9955 | 0.9953 | 0.9958 | 0.9941 | 0.9908 | 0.9845 | 0.9845 | 0.9832 | 0.9842 | 0.9818 | 0.9827 | 0.9788 | ||
| 30 | 0.9971 | 0.9974 | 0.9972 | 0.9971 | 0.9975 | 0.9964 | 0.9944 | 0.9867 | 0.9861 | 0.9854 | 0.9861 | 0.9850 | 0.9858 | 0.9841 | ||
| X2 | 2 | 0.8263 | 0.8263 | 0.8263 | 0.8263 | 0.8263 | 0.8263 | 0.7989 | X8 | 0.7406 | 0.7406 | 0.7406 | 0.7406 | 0.7406 | 0.7406 | 0.7506 |
| 3 | 0.9181 | 0.9181 | 0.9180 | 0.9181 | 0.9180 | 0.9180 | 0.8696 | 0.9064 | 0.9063 | 0.9065 | 0.9064 | 0.9063 | 0.9066 | 0.8912 | ||
| 4 | 0.9248 | 0.9248 | 0.9244 | 0.9251 | 0.9244 | 0.9250 | 0.8966 | 0.9338 | 0.9337 | 0.9312 | 0.9329 | 0.9361 | 0.9372 | 0.9108 | ||
| 5 | 0.9532 | 0.9533 | 0.9524 | 0.9534 | 0.9527 | 0.9531 | 0.9137 | 0.9541 | 0.9537 | 0.9491 | 0.9529 | 0.9478 | 0.9543 | 0.9308 | ||
| 6 | 0.9639 | 0.9631 | 0.9627 | 0.9639 | 0.9627 | 0.9640 | 0.9243 | 0.9666 | 0.9650 | 0.9622 | 0.9662 | 0.9614 | 0.9659 | 0.9375 | ||
| 7 | 0.9653 | 0.9666 | 0.9640 | 0.9654 | 0.9643 | 0.9656 | 0.9438 | 0.9713 | 0.9704 | 0.9695 | 0.9714 | 0.9699 | 0.9714 | 0.9457 | ||
| 8 | 0.9781 | 0.9779 | 0.9737 | 0.9782 | 0.9746 | 0.9778 | 0.9427 | 0.9783 | 0.9779 | 0.9730 | 0.9771 | 0.9735 | 0.9767 | 0.9588 | ||
| 9 | 0.9819 | 0.9815 | 0.9798 | 0.9822 | 0.9792 | 0.9812 | 0.9618 | 0.9820 | 0.9811 | 0.9772 | 0.9815 | 0.9770 | 0.9815 | 0.9643 | ||
| 10 | 0.9845 | 0.9842 | 0.9817 | 0.9840 | 0.9818 | 0.9831 | 0.9647 | 0.9854 | 0.9838 | 0.9797 | 0.9848 | 0.9786 | 0.9841 | 0.9572 | ||
| 15 | 0.9924 | 0.9923 | 0.9887 | 0.9922 | 0.9884 | 0.9913 | 0.9732 | 0.9893 | 0.9893 | 0.9844 | 0.9885 | 0.9865 | 0.9884 | 0.9796 | ||
| 20 | 0.9952 | 0.9947 | 0.9924 | 0.9954 | 0.9912 | 0.9936 | 0.9861 | 0.9935 | 0.9918 | 0.9890 | 0.9932 | 0.9880 | 0.9910 | 0.9834 | ||
| 30 | 0.9975 | 0.9973 | 0.9945 | 0.9976 | 0.9946 | 0.9958 | 0.9916 | 0.9966 | 0.9959 | 0.9943 | 0.9965 | 0.9935 | 0.9949 | 0.9907 | ||
| X3 | 2 | 0.7345 | 0.7345 | 0.7345 | 0.7345 | 0.7345 | 0.7345 | 0.7353 | X9 | 0.8269 | 0.8269 | 0.8269 | 0.8269 | 0.8269 | 0.8269 | 0.8227 |
| 3 | 0.8029 | 0.8027 | 0.8032 | 0.8029 | 0.8029 | 0.8029 | 0.8111 | 0.9160 | 0.9160 | 0.9160 | 0.9160 | 0.9160 | 0.9160 | 0.9103 | ||
| 4 | 0.8801 | 0.8790 | 0.8806 | 0.8790 | 0.8806 | 0.8804 | 0.8546 | 0.9528 | 0.9527 | 0.9525 | 0.9527 | 0.9525 | 0.9527 | 0.9358 | ||
| 5 | 0.9125 | 0.9130 | 0.9202 | 0.9106 | 0.9193 | 0.9093 | 0.8676 | 0.9608 | 0.9607 | 0.9593 | 0.9605 | 0.9598 | 0.9604 | 0.9503 | ||
| 6 | 0.9605 | 0.9576 | 0.9604 | 0.9605 | 0.9600 | 0.9603 | 0.9105 | 0.9732 | 0.9733 | 0.9730 | 0.9733 | 0.9729 | 0.9731 | 0.9569 | ||
| 7 | 0.9653 | 0.9649 | 0.9706 | 0.9654 | 0.9695 | 0.9646 | 0.9153 | 0.9795 | 0.9794 | 0.9783 | 0.9794 | 0.9781 | 0.9794 | 0.9679 | ||
| 8 | 0.9783 | 0.9747 | 0.9809 | 0.9775 | 0.9806 | 0.9765 | 0.9354 | 0.9833 | 0.9836 | 0.9821 | 0.9835 | 0.9815 | 0.9835 | 0.9706 | ||
| 9 | 0.9849 | 0.9816 | 0.9849 | 0.9844 | 0.9851 | 0.9843 | 0.9404 | 0.9864 | 0.9861 | 0.9848 | 0.9864 | 0.9841 | 0.9857 | 0.9739 | ||
| 10 | 0.9867 | 0.9860 | 0.9874 | 0.9863 | 0.9877 | 0.9861 | 0.9579 | 0.9888 | 0.9890 | 0.9871 | 0.9889 | 0.9871 | 0.9887 | 0.9738 | ||
| 15 | 0.9916 | 0.9921 | 0.9935 | 0.9907 | 0.9936 | 0.9912 | 0.9760 | 0.9939 | 0.9941 | 0.9934 | 0.9929 | 0.9929 | 0.9921 | 0.9844 | ||
| 20 | 0.9940 | 0.9950 | 0.9964 | 0.9936 | 0.9963 | 0.9934 | 0.9819 | 0.9963 | 0.9962 | 0.9952 | 0.9955 | 0.9949 | 0.9942 | 0.9909 | ||
| 30 | 0.9971 | 0.9978 | 0.9983 | 0.9967 | 0.9983 | 0.9968 | 0.9912 | 0.9981 | 0.9979 | 0.9970 | 0.9977 | 0.9973 | 0.9971 | 0.9949 | ||
| X4 | 2 | 0.7793 | 0.7793 | 0.7793 | 0.7770 | 0.7793 | 0.7793 | 0.7374 | X10 | 0.8214 | 0.8214 | 0.8214 | 0.8216 | 0.8214 | 0.8217 | 0.7919 |
| 3 | 0.8818 | 0.8818 | 0.8818 | 0.8818 | 0.8818 | 0.8819 | 0.8067 | 0.9120 | 0.9120 | 0.9120 | 0.9121 | 0.9120 | 0.9120 | 0.8731 | ||
| 4 | 0.9376 | 0.9377 | 0.9376 | 0.9377 | 0.9367 | 0.9369 | 0.8665 | 0.9419 | 0.9422 | 0.9422 | 0.9425 | 0.9426 | 0.9421 | 0.9078 | ||
| 5 | 0.9552 | 0.9548 | 0.9527 | 0.9551 | 0.9531 | 0.9551 | 0.9100 | 0.9610 | 0.9610 | 0.9602 | 0.9611 | 0.9602 | 0.9610 | 0.9137 | ||
| 6 | 0.9670 | 0.9670 | 0.9643 | 0.9668 | 0.9646 | 0.9665 | 0.9163 | 0.9714 | 0.9715 | 0.9701 | 0.9719 | 0.9699 | 0.9714 | 0.9298 | ||
| 7 | 0.9733 | 0.9735 | 0.9714 | 0.9734 | 0.9700 | 0.9712 | 0.9284 | 0.9766 | 0.9769 | 0.9748 | 0.9763 | 0.9741 | 0.9762 | 0.9352 | ||
| 8 | 0.9764 | 0.9767 | 0.9740 | 0.9764 | 0.9729 | 0.9757 | 0.9377 | 0.9805 | 0.9812 | 0.9794 | 0.9808 | 0.9797 | 0.9798 | 0.9533 | ||
| 9 | 0.9789 | 0.9782 | 0.9756 | 0.9762 | 0.9767 | 0.9780 | 0.9477 | 0.9849 | 0.9852 | 0.9836 | 0.9849 | 0.9829 | 0.9837 | 0.9552 | ||
| 10 | 0.9813 | 0.9808 | 0.9780 | 0.9809 | 0.9782 | 0.9797 | 0.9532 | 0.9886 | 0.9879 | 0.9852 | 0.9884 | 0.9854 | 0.9873 | 0.9629 | ||
| 15 | 0.9883 | 0.9873 | 0.9845 | 0.9881 | 0.9824 | 0.9874 | 0.9684 | 0.9935 | 0.9932 | 0.9920 | 0.9933 | 0.9923 | 0.9913 | 0.9694 | ||
| 20 | 0.9912 | 0.9901 | 0.9884 | 0.9905 | 0.9854 | 0.9894 | 0.9744 | 0.9963 | 0.9954 | 0.9945 | 0.9960 | 0.9949 | 0.9945 | 0.9838 | ||
| 30 | 0.9931 | 0.9918 | 0.9908 | 0.9926 | 0.9907 | 0.9921 | 0.9857 | 0.9972 | 0.9972 | 0.9967 | 0.9971 | 0.9953 | 0.9964 | 0.9919 | ||
| X5 | 2 | 0.8640 | 0.8640 | 0.8640 | 0.8640 | 0.8640 | 0.8640 | 0.8496 | X11 | 0.8261 | 0.8261 | 0.8261 | 0.8261 | 0.8261 | 0.8261 | 0.8213 |
| 3 | 0.9314 | 0.9314 | 0.9314 | 0.9314 | 0.9314 | 0.9314 | 0.8955 | 0.9010 | 0.9010 | 0.9010 | 0.9010 | 0.9010 | 0.9010 | 0.8939 | ||
| 4 | 0.9371 | 0.9369 | 0.9366 | 0.9374 | 0.9368 | 0.9378 | 0.9051 | 0.9392 | 0.9391 | 0.9388 | 0.9392 | 0.9386 | 0.9391 | 0.9246 | ||
| 5 | 0.9410 | 0.9407 | 0.9409 | 0.9416 | 0.9424 | 0.9374 | 0.9225 | 0.9550 | 0.9548 | 0.9545 | 0.9549 | 0.9543 | 0.9547 | 0.9370 | ||
| 6 | 0.9595 | 0.9570 | 0.9584 | 0.9587 | 0.9556 | 0.9576 | 0.9335 | 0.9649 | 0.9646 | 0.9641 | 0.9647 | 0.9637 | 0.9647 | 0.9453 | ||
| 7 | 0.9659 | 0.9644 | 0.9618 | 0.9642 | 0.9608 | 0.9625 | 0.9426 | 0.9717 | 0.9715 | 0.9703 | 0.9716 | 0.9705 | 0.9716 | 0.9582 | ||
| 8 | 0.9731 | 0.9721 | 0.9664 | 0.9727 | 0.9687 | 0.9698 | 0.9489 | 0.9775 | 0.9774 | 0.9757 | 0.9772 | 0.9760 | 0.9773 | 0.9623 | ||
| 9 | 0.9745 | 0.9748 | 0.9695 | 0.9746 | 0.9690 | 0.9722 | 0.9539 | 0.9819 | 0.9817 | 0.9790 | 0.9818 | 0.9787 | 0.9807 | 0.9679 | ||
| 10 | 0.9746 | 0.9741 | 0.9706 | 0.9720 | 0.9692 | 0.9721 | 0.9622 | 0.9843 | 0.9843 | 0.9828 | 0.9841 | 0.9821 | 0.9838 | 0.9709 | ||
| 15 | 0.9824 | 0.9831 | 0.9806 | 0.9805 | 0.9797 | 0.9794 | 0.9716 | 0.9913 | 0.9907 | 0.9884 | 0.9915 | 0.9887 | 0.9903 | 0.9811 | ||
| 20 | 0.9858 | 0.9859 | 0.9856 | 0.9844 | 0.9854 | 0.9837 | 0.9780 | 0.9940 | 0.9945 | 0.9930 | 0.9933 | 0.9926 | 0.9925 | 0.9870 | ||
| 30 | 0.9881 | 0.9877 | 0.9875 | 0.9872 | 0.9879 | 0.9865 | 0.9850 | 0.9960 | 0.9958 | 0.9950 | 0.9954 | 0.9950 | 0.9941 | 0.9910 | ||
| X6 | 2 | 0.7571 | 0.7571 | 0.7571 | 0.7571 | 0.7571 | 0.7571 | 0.7472 | X12 | 0.6728 | 0.6728 | 0.6728 | 0.6728 | 0.6728 | 0.6728 | 0.6992 |
| 3 | 0.8880 | 0.8880 | 0.8880 | 0.8880 | 0.8878 | 0.8879 | 0.8724 | 0.7842 | 0.7842 | 0.7842 | 0.7842 | 0.7842 | 0.7842 | 0.7617 | ||
| 4 | 0.9142 | 0.9142 | 0.9140 | 0.9142 | 0.9141 | 0.9143 | 0.8934 | 0.8524 | 0.8490 | 0.8528 | 0.8520 | 0.8528 | 0.8511 | 0.8471 | ||
| 5 | 0.9292 | 0.9293 | 0.9274 | 0.9287 | 0.9280 | 0.9299 | 0.8977 | 0.8715 | 0.8719 | 0.8785 | 0.8715 | 0.8764 | 0.8711 | 0.8971 | ||
| 6 | 0.9329 | 0.9365 | 0.9344 | 0.9316 | 0.9313 | 0.9354 | 0.9071 | 0.8984 | 0.9002 | 0.9198 | 0.8980 | 0.9189 | 0.8980 | 0.9027 | ||
| 7 | 0.9315 | 0.9369 | 0.9330 | 0.9294 | 0.9330 | 0.9262 | 0.9017 | 0.9670 | 0.9533 | 0.9717 | 0.9584 | 0.9635 | 0.9432 | 0.9511 | ||
| 8 | 0.9410 | 0.9408 | 0.9335 | 0.9368 | 0.9368 | 0.9342 | 0.9271 | 0.9697 | 0.9833 | 0.9846 | 0.9813 | 0.9846 | 0.9837 | 0.9681 | ||
| 9 | 0.9452 | 0.9440 | 0.9381 | 0.9433 | 0.9405 | 0.9406 | 0.9230 | 0.9874 | 0.9863 | 0.9873 | 0.9874 | 0.9873 | 0.9868 | 0.9733 | ||
| 10 | 0.9503 | 0.9493 | 0.9464 | 0.9479 | 0.9431 | 0.9436 | 0.9321 | 0.9891 | 0.9888 | 0.9895 | 0.9902 | 0.9892 | 0.9904 | 0.9767 | ||
| 15 | 0.9570 | 0.9565 | 0.9548 | 0.9558 | 0.9491 | 0.9543 | 0.9472 | 0.9948 | 0.9945 | 0.9944 | 0.9945 | 0.9946 | 0.9930 | 0.9834 | ||
| 20 | 0.9597 | 0.9598 | 0.9577 | 0.9586 | 0.9576 | 0.9574 | 0.9534 | 0.9969 | 0.9969 | 0.9966 | 0.9967 | 0.9966 | 0.9959 | 0.9913 | ||
| 30 | 0.9617 | 0.9614 | 0.9599 | 0.9612 | 0.9600 | 0.9604 | 0.9581 | 0.9985 | 0.9982 | 0.9978 | 0.9982 | 0.9981 | 0.9974 | 0.9927 |
The bold value indicates the best value.
Fig. 8.
Average UQI values obtained under Kapur’s entropy.
Fig. 9 shows the segmented images obtained by the proposed algorithm on X1, X2, X3, and X3 under both Kapur’s for the threshold levels 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, and 30.
Fig. 9.
Segmented images by proposed algorithm under Kapure’s entropy.
7.6. Comparison of convergence curve among SMA, HSMA_WOA, and WOA
In this part, the convergence rate by SMA, HSMA_WOA, and WOA will be observed to illustrate the effectiveness of our approach. Generally speaking, X1, X2, X3, X4, X5, and X6 test images with 30 threshold levels are used to check the convergence rate of each algorithm. After running each algorithm, the output in each iteration on each test image from X1 to X6 is plotted in Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, respectively. Inspecting these figures show that within the first CI=100 iteration, the convergence is accelerated as possible, but at the end of CI, the outcomes have no change and the possibility of reaching a better solution is so hard because the algorithm may be gotten stuck into local minima. As a result, it is time to integrate SMA with WOA to refresh its performance to get out of local optima, find better solutions and use the significant exploitation capability of SMA.
Fig. 10.
Convergence curve on X1.
Fig. 11.
Convergence curve on X2.
Fig. 12.
Convergence curve on X3.
Fig. 13.
Convergence curve on X4.
Fig. 14.
Convergence curve on X5.
Fig. 15.
Convergence curve on X6.
8. Conclusion and future work
According to the ongoing outbreaks of COVID-19 worldwide since December 2019, the entire world has moved to rely on technology to find tools and techniques to help identify the infected persons out of the normal ones. After many attempts and confirmed by the medical scientists, chest CT images could significantly identify whether the suspected patients have been infected. COVID-19 infection could be identified by the bilateral pulmonary parenchymal ground-glass and consolidative pulmonary opacities. Sometimes a rounded morphology and a peripheral lung distribution could be spotted. However, CT scan is so expensive compared to X-ray, and unfortunately, the specification of the infection under X-ray is so hard. The reason was that the X-ray images were considered normal images, so it could be processed using a machine learning technique to specify if this person infected or not. But when machine learning focused on the whole image, their accuracy reduced significantly. Therefore, it was necessary to find a tool to extract similar regions within the image until managing to improve the accuracy of the machine learning technique when classifying the CT images.
The process of separating or extracting the similar regions into an image was called image segmentation problem. According to that, in this paper, our techniques were based on extracting the similar small regions into chest images as an attempt to extract the regions that may contain COVID-19, and this process was known as image segmentation problem (ISP). Several techniques were proposed for tackling ISP. A technique called threshold-based segmentation was distinguished from involving those techniques with its simplicity, speed, and accuracy when segmenting an image. Hence, a new hybrid multi-thresholding approach based on the SMA behavior with WOA for overcoming ISP was proposed in this paper. Its effectiveness was observed with five state-of-art algorithms such as WOA, SSA, Lshade, HHA, and FFA. The comparison was performed by applying the algorithms on a set of chest X-ray images with threshold levels between 2 and 30. Based on the results obtained by each algorithm, the performance of the proposed algorithm was verified to outperform all other algorithms in the fitness values, SSIM, PSNR, UQI, CPU time and (Std).
With rapidly-increased reported cases worldwide and the need to verify our algorithm with new images, the future work will involve validating the performance of the proposed algorithm on a set of the test images taken from The Berkeley Segmentation Dataset and Benchmark. The aim will be focused on checking whether its performance is stable on the other images. Furthermore, the improved Slime mold algorithm will be applied to solve flow shop scheduling problems, DNA fragment assembly problems, and parameter estimation of the photovoltaic solar cell.
CRediT authorship contribution statement
Mohamed Abdel-Basset: Investigation, Methodology, Resources, Supervision, Visualization, Writing - original draft, Writing - review & editing. Victor Chang: Formal analysis, Investigation, Project administration, Validation, Writing - review & editing. Reda Mohamed: Conceptualization, Formal analysis, Methodology, Writing review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This research is partly supported by VC Research, UK (VCR 0000075) for Prof Chang.
References
- 1.Bai Y. Presumed asymptomatic carrier transmission of COVID-19. JAMA. 2020;323(14):1406–1407. doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Guan C.S. Imaging features of coronavirus disease 2019 (COVID-19): Evaluation on thin-section CT. Acad. Radiol. 2020 doi: 10.1016/j.acra.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kuruvilla J. 2016 International Conference on Data Mining and Advanced Computing, SAPIENCE. IEEE; 2016. A review on image processing and image segmentation. [Google Scholar]
- 4.Hu R. 2016. Utilizing large scale vision and text datasets for image segmentation from referring expressions. arXiv preprint arXiv:1608.08305. [Google Scholar]
- 5.Mittal M. Advancement of Machine Intelligence in Interactive Medical Image Analysis. Springer; 2020. Image segmentation using deep learning techniques in medical images; pp. 41–63.. [Google Scholar]
- 6.Zhang Z. DENSE-INception U-net for medical image segmentation. Comput. Methods Programs Biomed. 2020 doi: 10.1016/j.cmpb.2020.105395. [DOI] [PubMed] [Google Scholar]
- 7.Wang X., Wang X., Wilkes D.M. Machine Learning-Based Natural Scene Recognition for Mobile Robot Localization in an Unknown Environment. Springer; 2020. An efficient image segmentation algorithm for object recognition using spectral clustering; pp. 215–234. [Google Scholar]
- 8.Karydas C.G. Optimization of multi-scale segmentation of satellite imagery using fractal geometry. Int. J. Remote Sens. 2020;41(8):2905–2933. [Google Scholar]
- 9.Su T., Zhang S. Local and global evaluation for remote sensing image segmentation. ISPRS J. Photogramm. Remote Sens. 2017;130:256–276. [Google Scholar]
- 10.M. Alberti, et al. Historical document image segmentation with LDA-initialized deep neural networks, in: Proceedings of the 4th International Workshop on Historical Document Imaging and Processing, 2017.
- 11.Naoum A., Nothman J., Curran J. 2019 International Conference on Document Analysis and RecognitionI, ICDAR. IEEE; 2019. Article segmentation in digitised newspapers with a 2D Markov model. [Google Scholar]
- 12.Barman R. 2020. Combining visual and textual features for semantic segmentation of historical newspapers. arXiv preprint arXiv:2002.06144. [Google Scholar]
- 13.Aksac A., Ozyer T., Alhajj R. Complex networks driven salient region detection based on superpixel segmentation. Pattern Recognit. 2017;66:268–279. [Google Scholar]
- 14.Prathusha P., Jyothi S. Data Engineering and Intelligent Computing. Springer; 2018. A novel edge detection algorithm for fast and efficient image segmentation; pp. 283–291. [Google Scholar]
- 15.Narayanan B.N. Optimized feature selection-based clustering approach for computer-aided detection of lung nodules in different modalities. Pattern Anal. Appl. 2019;22(2):559–571. [Google Scholar]
- 16.Han J. A new multi-threshold image segmentation approach using state transition algorithm. Appl. Math. Model. 2017;44:588–601. [Google Scholar]
- 17.Oliva D. A multilevel thresholding algorithm using electromagnetism optimization. Neurocomputing. 2014;139:357–381. [Google Scholar]
- 18.Arora S. Multilevel thresholding for image segmentation through a fast statistical recursive algorithm. Pattern Recognit. Lett. 2008;29(2):119–125. [Google Scholar]
- 19.Dirami A. Fast multilevel thresholding for image segmentation through a multiphase level set method. Signal Process. 2013;93(1):139–153. [Google Scholar]
- 20.Kapur J.N., Sahoo P.K., Wong A.K. A new method for gray-level picture thresholding using the entropy of the histogram. Comput Vis. Graph. Image Process. 1985;29(3):273–285. [Google Scholar]
- 21.Oliva D., Elaziz M.A., Hinojosa S. Metaheuristic Algorithms for Image Segmentation: Theory and Applications. Springer; 2019. Fuzzy entropy approaches for image segmentation; pp. 141–147. [Google Scholar]
- 22.Abdel-Basset M. A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem. Future Gener. Comput. Syst. 2018;85:129–145. [Google Scholar]
- 23.Sayed G.I., Hassanien A.E., Azar A.T. Feature selection via a novel chaotic crow search algorithm. Neural Comput. Appl. 2019;31(1):171–188. [Google Scholar]
- 24.Rizk-Allah R.M. A new binary salp swarm algorithm: development and application for optimization tasks. Neural Comput. Appl. 2019;31(5):1641–1663. [Google Scholar]
- 25.Cuevas E., Gálvez J., Avalos O. Recent Metaheuristics Algorithms for Parameter Identification. Springer; 2020. An enhanced crow search algorithm applied to energy approaches; pp. 27–49. [Google Scholar]
- 26.Cuevas E., Fausto F., González A. New Advancements in Swarm Algorithms: Operators and Applications. Springer; 2020. The locust swarm optimization algorithm; pp. 139–159. [Google Scholar]
- 27.Ibrahim R.A. An opposition-based social spider optimization for feature selection. Soft Comput. 2019;23(24):13547–13567. [Google Scholar]
- 28.Guo C., Li H. Australasian Joint Conference on Artificial Intelligence. Springer; 2007. Multilevel thresholding method for image segmentation based on an adaptive particle swarm optimization algorithm. [Google Scholar]
- 29.Xiong L. Color disease spot image segmentation algorithm based on chaotic particle swarm optimization and FCM. J. Supercomput. 2020:1–15. [Google Scholar]
- 30.Di Martino F., Sessa S. PSO Image thresholding on images compressed via fuzzy transforms. Inform. Sci. 2020;506:308–324. [Google Scholar]
- 31.Kaveh A., Talatahari S. An improved ant colony optimization for constrained engineering design problems. Eng. Comput. 2010;27(1):155–182. [Google Scholar]
- 32.Huo F., Sun X., Ren W. Multilevel image threshold segmentation using an improved bloch quantum artificial bee colony algorithm. Multimedia Tools Appl. 2020;79(3):2447–2471. [Google Scholar]
- 33.El Aziz M.A., Ewees A.A., Hassanien A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017;83:242–256. [Google Scholar]
- 34.Elsayed S.M., Sarker R.A., Essam D.L. A new genetic algorithm for solving optimization problems. Eng. Appl. Artif. Intell. 2014;27:57–69. [Google Scholar]
- 35.Kandhway P., Bhandari A.K. Spatial context cross entropy function based multilevel image segmentation using multi-verse optimizer. Multimedia Tools Appl. 2019;78(16):22613–22641. [Google Scholar]
- 36.Agrawal S. Tsallis entropy based optimal multilevel thresholding using cuckoo search algorithm. Swarm Evol. Comput. 2013;11:16–30. [Google Scholar]
- 37.Chakraborty F., Nandi D., Roy P.K. Oppositional symbiotic organisms search optimization for multilevel thresholding of color image. Appl. Soft Comput. 2019 [Google Scholar]
- 38.Bao X., Jia H., Lang C. A novel hybrid harris hawks optimization for color image multilevel thresholding segmentation. IEEE Access. 2019;7:76529–76546. [Google Scholar]
- 39.Erdmann H. Developments in Medical Image Processing and Computational Vision. Springer; 2015. A study of a firefly meta-heuristics for multithreshold image segmentation; pp. 279–295. [Google Scholar]
- 40.Wang R. A hybrid flower pollination algorithm based modified randomized location for multi-threshold medical image segmentation. Biomed. Mater. Eng. 2015;26(s1):S1345–S1351. doi: 10.3233/BME-151432. [DOI] [PubMed] [Google Scholar]
- 41.Oliva D. Cross entropy based thresholding for magnetic resonance brain images using crow search algorithm. Expert Syst. Appl. 2017;79:164–180. [Google Scholar]
- 42.Yao X. IOP Publishing; 2019. Multi-threshold image segmentation based on improved grey wolf optimization algorithm. (IOP Conference Series: Earth and Environmental Science). [Google Scholar]
- 43.Horng M.-H. Multilevel minimum cross entropy threshold selection based on the honey bee mating optimization. Expert Syst. Appl. 2010;37(6):4580–4592. [Google Scholar]
- 44.Cuevas E., Fausto F., González A. Locust search algorithm applied to multi-threshold segmentation. In: Cuevas E., Fausto A., editors. New Advancements in Swarm Algorithms: Operators and Applications. Springer International Publishing; Cham: 2020. pp. 211–240.. [Google Scholar]
- 45.Singla A., Patra S. A fast automatic optimal threshold selection technique for image segmentation. Signal Image Video Process. 2016;11:1–8. [Google Scholar]
- 46.Manikandan S. Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm. Measurement. 2014;47:558–568. [Google Scholar]
- 47.Maitra M., Chatterjee A. A hybrid cooperative–comprehensive learning based PSO algorithm for image segmentation using multilevel thresholding. Expert Syst. Appl. 2008;34(2):1341–1350. [Google Scholar]
- 48.Liu Y. Modified particle swarm optimization-based multilevel thresholding for image segmentation. Soft Comput. 2015;19(5):1311–1327. [Google Scholar]
- 49.Ghamisi P. Multilevel image segmentation based on fractional-order darwinian particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2013;52(5):2382–2394. [Google Scholar]
- 50.Chen K. Multilevel image segmentation based on an improved firefly algorithm. Math. Probl. Eng. 2016;2016 [Google Scholar]
- 51.Bhandari A.K., Kumar A., Singh G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015;42(3):1573–1601. [Google Scholar]
- 52.Sanyal N., Chatterjee A., Munshi S. An adaptive bacterial foraging algorithm for fuzzy entropy based image segmentation. Expert Syst. Appl. 2011;38(12):15489–15498. [Google Scholar]
- 53.Sathya P., Kayalvizhi R. Modified bacterial foraging algorithm based multilevel thresholding for image segmentation. Eng. Appl. Artif. Intell. 2011;24(4):595–615. [Google Scholar]
- 54.Abdel-Basset M., Chang V., Mohamed R. A novel equilibrium optimization algorithm for multi-thresholding image segmentation problems. Neural Comput. Appl. 2020:1–34. [Google Scholar]
- 55.Abdel-Basset M. A hybrid COVID-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE Access. 2020 [Google Scholar]
- 56.Chouksey M., Jha R.K., Sharma R. A fast technique for image segmentation based on two meta-heuristic algorithms. Multimedia Tools Appl. 2020:1–53. [Google Scholar]
- 57.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]
- 58.Nakagaki T., Yamada H., Ueda T. Interaction between cell shape and contraction pattern in the physarum plasmodium. Biophys. Chem. 2000;84(3):195–204. doi: 10.1016/s0301-4622(00)00108-3. [DOI] [PubMed] [Google Scholar]
- 59.Brest J., Maučec M.S., Bošković B. 2016 IEEE Congress on Evolutionary Computation, CEC. IEEE; 2016. Il-SHADE: Improved l-SHADE algorithm for single objective real-parameter optimization. [Google Scholar]
- 60.Wang S., Jia H., Peng X. Modified salp swarm algorithm based multilevel thresholding for color image segmentation. Math. Biosci. Eng.: MBE. 2019;17(1):700–724. doi: 10.3934/mbe.2020036. [DOI] [PubMed] [Google Scholar]
- 61.Hore A., Ziou D. 2010 20th International Conference on Pattern Recognition. IEEE; 2010. Image quality metrics: PSNR vs. SSIM. [Google Scholar]
- 62.K. Egiazarian, et al. New full-reference quality metrics based on HVS, in: Proceedings of the Second International Workshop on Video Processing and Quality Metrics, 2006.