A Multitype Birth–Death Model for Bayesian Inference of Lineage-Specific Birth and Death Rates

Abstract

Heterogeneous populations can lead to important differences in birth and death rates across a phylogeny. Taking this heterogeneity into account is necessary to obtain accurate estimates of the underlying population dynamics. We present a new multitype birth–death model (MTBD) that can estimate lineage-specific birth and death rates. This corresponds to estimating lineage-dependent speciation and extinction rates for species phylogenies, and lineage-dependent transmission and recovery rates for pathogen transmission trees. In contrast with previous models, we do not presume to know the trait driving the rate differences, nor do we prohibit the same rates from appearing in different parts of the phylogeny. Using simulated data sets, we show that the MTBD model can reliably infer the presence of multiple evolutionary regimes, their positions in the tree, and the birth and death rates associated with each. We also present a reanalysis of two empirical data sets and compare the results obtained by MTBD and by the existing software BAMM. We compare two implementations of the model, one exact and one approximate (assuming that no rate changes occur in the extinct parts of the tree), and show that the approximation only slightly affects results. The MTBD model is implemented as a package in the Bayesian inference software BEAST 2 and allows joint inference of the phylogeny and the model parameters.[Birth–death; lineage specific rates, multi-type model.]

The deep connection between phylogenies and the populations in which they are embedded enables genetic sequence data, in combination with other heritable trait data, to inform a wide array of scientific investigations in fields as diverse as macroevolution, ecology, and epidemiology. Such methods often assume that the data has evolved in a neutral fashion, meaning that the birth and death rates of the underlying population model (corresponding to speciation and extinction rates in the macroevolutionary setting, or infection and recovery rates in the epidemiological setting) were unaffected by changes in the ancestral type. However, for many traits this is unreasonable, and the presence of such traits is known to be a source of bias in estimates of diversification (Maddison 2006).

Multitype birth–death (MTBD) models have been widely used to model population structure and analyze phylogenies built from individuals in a structured population (Maddison et al. 2007; FitzJohn 2012; Stadler and Bonhoeffer 2013; Kühnert et al. 2016), both in epidemiological and macroevolutionary applications. These models contain a series of discrete types with type-specific birth and death rates, such that each type corresponds to a specific evolutionary regime. Based on a phylogeny where each tip is associated with a type, the type-dependent birth and death rates are estimated. Birth events correspond to transmission events in epidemiology and speciation events in macroevolution, while death events correspond to becoming-noninfectious events in epidemiology and extinction events in macroevolution. A type might be for example an ecological niche or the presence of a particular trait.

The Binary State Speciation and Extinction (BiSSE, Maddison et al. (2007)) and its extension to multiple states MuSSE, included in the package Diversitree (FitzJohn 2012), provided the first means of explicit model-based inference of type-specific birth and death rates from complete ultrametric phylogenies, that is, trees with all tips sampled at the same point in time, where each tip is assigned to a type. (The earlier method of sister clade contrasts (Mitter et al. 1988) provided a hypothesis testing framework enabling detection of type-specific diversification rates, but no explicit model for the correlation between diversification rate and type.)

BiSSE was later extended to incomplete trees (FitzJohn et al. 2009). In Stadler and Bonhoeffer (2013), these approaches were extended to nonultrametric trees. More recently, the BEAST 2 package BDMM (Kühnert et al. 2016) allowed the joint reconstruction of a phylogeny and quantification of the parameters of an underlying MTBD model. These approaches all have in common that the model is conditioned on a particular total number of types and the type at each tip in the phylogeny. This necessitates the formulation of a hypothesis as to which underlying feature drives the pattern of evolutionary rates. The BiSSE models in particular have been criticized for their approach being biased towards inferring trait-dependent rates regardless of the chosen trait (Rabosky and Goldberg 2015). Although this was addressed by the introduction of the HiSSE model (Beaulieu and O’Meara 2016) which uses a more appropriate null hypothesis, in the current implementation testing multiple different traits or combinations of traits would still require a different run of the inference for each. Thus, there is a clear need for models which do not make such strong prior assumptions on the process driving the changes in evolutionary rates.

The method Bayesian Analysis of Macroevolutionary Mixtures (BAMM, Rabosky et al. (2013)) addresses these issues and is able to infer the number of types, assign each lineage of the tree to a type and estimate the birth- and death-rate parameters associated with each type. However, its results have been called into question, as Moore et al. (2016) identified issues regarding the calculation of its likelihood function and a strong dependency on the prior when inferring the number of types, as well as inaccurate diversification rates estimates. Some of those criticisms were addressed by Rabosky et al. (2017), who showed that the simulation used in Moore et al. (2016) contained a large number of shifts which only affected small clades of the phylogeny, making them difficult to detect. Rabosky et al. (2017) also pointed out that the sensitivity to the prior decreased sharply when using the default settings of BAMM rather than the setting used by Moore et al. (2016). However, issues regarding the calculation of the extinction probability in the likelihood function used by BAMM have to our knowledge not been addressed. Moreover, the process of moving between types is not explicitly modeled by BAMM, which may be a contributing factor to the prior sensitivity observed in some situations. Additionally, BAMM assumes that each type emerges only once along the tree. It thus implicitly links the changes in birth and death rates to lineage-specific innovations with no innovation occurring more than once, which may not adequately represent situations where the rates are driven by environmental or geographic conditions, for instance.

Two other methods have been developed in parallel with our approach, addressing shortcomings of BAMM. ClaDS (Maliet et al. 2019) models the changes in birth and death rates by assuming that upon speciation, the two offspring species obtain new rate values following a distribution which is fixed across the tree but can be dependent on the ancestral rate values. During the inference, the rates at the start of branches in the tree are inferred, and potential rate changes on a branch or extinct parts in the tree are integrated out analytically. This approach essentially models many small rate changes—that is, a rate change upon each speciation event—whereby most speciation events give rise to offspring species with the same rates as their mother species, while BAMM models a few large rate changes. Another proposed method, implemented in RevBayes (Hoehna et al. 2019), discretizes a prior distribution on rates into a fixed number of categories. The rates are then estimated through the hyperparameters of the chosen prior. The method, like BAMM, models few large rate changes. However, it further takes into account rate changes in extinct parts of the tree. As of yet it cannot estimate the number of rate categories.

In this article, we present a new Bayesian method for inferring lineage-specific birth and death rates jointly with a phylogeny, using a MTBD model assuming few large rate changes. This method infers the number and position of evolutionary regimes as well as the type change rate, and requires no strong assumption with respect to the features driving the variation in birth and death rates. We provide two distinct implementations of this method: (i) a computationally fast implementation, which ignores rate shifts in extinct parts of the tree and (ii) a computationally slow implementation which explicitly accounts for these rate shifts. We validate both implementations of this new method and evaluate their performance on simulated data sets. In particular, we assess the impact of ignoring rate shifts in the extinct part of the tree. We then use our method to reanalyze two empirical phylogenies and compare the results to those obtained by BAMM on those trees. Finally, we discuss the limitations of the method and planned future work.

1 Materials and Methods

1.1 Multitype Birth–Death Model

We use a MTBD model with contemporaneous and noncontemporaneous sampling. This model contains types, each associated with a specific birth rate and death rate , . The process starts with one individual in a type picked uniformly at random from the possible types, at time in the past. Through time, each individual in type undergoes birth events giving rise to an additional individual in type with rate , and dies with rate . Additionally, each individual in any type undergoes a change in birth and death rates to any different type with rate . Thus, the overall rate of change for any individual to another type is . Note that for . Throughout this article, we consider (and not ) as a parameter.

The process stops at present time . The model includes both extinct and extant sampling: individuals are sampled upon death with a probability and individuals at the present are sampled with a probability .

The process gives rise to complete trees, displaying all birth, death, type change, and sampling events (Fig. 1, left). The reconstructed tree is obtained by pruning all lineages of the complete tree without sampled descendants (Fig. 1, right). By analogy with the figure, we will call the attribution of types to lineages and the position of type changes on the tree the coloring of the reconstructed tree.

Figure 1.

Visual representation of the MTBD model on a complete tree (left) with sampling events indicated in orange, and on the corresponding reconstructed tree (right). Each type is represented by a color: the ancestral type, in black, starts at the root. The other types, in blue, red, and green, start at change points along the tree. The same type can be present in multiple clades along the tree, such as the blue type in the complete tree.

1.2 Probability Density of a Reconstructed Tree

We derive the likelihood of the MTBD model on a given phylogeny, that is, the probability density of the reconstructed tree with the coloring , given the vector , which contains the values of the birth and death rates for each type: .

In the following, we will split the phylogeny into edge segments, where each branching event or type change event marks the start of a new segment. Thus, the edge segments of correspond to the edges of subdivided at type change events, and any edge segment belongs to only one type.

Following Kühnert et al. (2016), we define as the probability of a lineage in type at time not appearing in the reconstructed tree, that is, the probability of this lineage not being sampled before or at the present. We also define as the probability density of a given edge segment in type at time evolving according to the tree and types between time and the present.

Note that , with being the root type, and being the probability of the first individual being in type . Since the types of the MTBD model are not tied to specific tips or specific character types in the model, their order and numbering is arbitrary. We thus assume here a uniform distribution, that is, .

We obtain the ordinary differential equations Eq. 1 for and Eq. 2 for where with and respectively, the end and start times of edge segment :

(1)

and

(2)

The derivations of these equations follow the procedure initially described in Maddison et al. (2007), and can be found in full in Kühnert et al. (2016). These ordinary differential equations do not have an analytical solution. Numerical integration is computationally expensive and can be unstable for certain parameters. Thus, in our implementation, we make the assumption that no type changes happen in the unsampled parts of the tree, meaning we observe all type changes in the reconstructed tree. In the Supplementary Section 2 available on Dryad at http://dx.doi.org/10.5061/dryad.zpc866t5n, we also present the method and all analysis results without this approximation (referred to as BDMM). With this assumption, the differential equation for simplifies to Eq. 3.

(3)

With this approximation, we can derive an analytical solution for :

(4)

Using Equation (4) in the differential equation for (Equation 2) allows us to derive analytically:

(5)

For an edge in type which starts at time and ends at time (), is the likelihood of the full subtree descending from edge segment . The likelihood of edge segment can be obtained as .

Following the tree decomposition described in Nee et al. (1994), this allows us to write the probability density of the phylogeny and the type changes assigned to the lineages , with being the set of edge segments in type , being the set of birth events in type (and for each event , the time of this event), being the set of extinct tips in type , being the number of extant tips, and being the number of type change events:

(6)

Note that the transition term contains only the contribution of the instantaneous type change events, as the contribution of the waiting times between events is already included in the edge segment likelihood . If , then and this transition term becomes and is thus removed from Equation 6. Note also that if the tree starts with 2 lineages at time instead of 1 lineage at time , the likelihood becomes .

Surface plots showing how and change in function of the model parameters can be found in Supplementary Figure S13 available on Dryad.

1.3 Bayesian Inference

We implemented our model in a Bayesian framework as an add-on to the popular Markov chain Monte-Carlo (MCMC) inference software BEAST 2 (Bouckaert et al. 2014), which allows to estimate (the type history) and (the rates , and ) from a phylogeny based on Equation 6. The inference can be performed on a fixed tree , or directly on sequences, in which case is inferred jointly with the other parameters using the substitution and clock models provided by BEAST 2. In a joint inference, we sample from the following distribution:

with the data being the sequence alignment, being the parameters of the sequence evolution model, being the prior distributions for the model parameters, and being Felsenstein’s phylogenetic likelihood (Felsenstein 1981) for the sequencing data. If we condition on a fixed tree , we use .

While we infer for our data, the number of types assigned to the reconstructed phylogeny, , may be smaller than , that is, . To reduce the complexity of the computation, we do not sample the birth and death rates associated with the types which are not currently assigned to the tree, and instead marginalize over those rates. This marginalization introduces an additional term to the probability density to account for the sampling of unassigned types.

It has been shown that in unstructured models, the three parameters and are not identifiable (Stadler et al. 2013). In order to avoid potential parameter correlations in the structured model, we require the sampling probabilities and to be provided as inputs.

More details on the implementation can be found in the Supplementary material available on Dryad.

1.4 Simulation Study

To study the behavior of our method, we simulated trees under our model. We used a stochastic forward in time simulation process which takes the following inputs:

• a stopping condition: the process is stopped upon reaching a certain number of tips or after a certain time had passed

• a rate of type change

• the total number of types in the process

• a function to sample birth rates and death rates for all types

• sampling rates or sampling numbers for the extant tips and extinct tips

The specific parameter values were chosen in function of the purpose of the data set and are detailed in the following sections. The birth–death process is started with either one or two lineages and is simulated using the Gillespie algorithm (Gillespie 1976), which consists in randomly drawing the waiting times between events and the nature of these events (in this case, speciation, extinction, or type change events). The process continues until the stopping condition is met or all lineages descending from one of the starting lineages have gone extinct, in which case the resulting tree is discarded. At the end of the process, lineages are discarded based on the sampling settings to obtain the reconstructed tree. If the sampling settings lead to no lineages being sampled, the resulting tree is also discarded.

1.4.1 Validation: sampling from prior

To ensure that the implementation of our model is correct, we performed a comparison of the distribution of trees obtained from forward in time simulations of the process to the distribution obtained from running an MCMC inference without sequence data under our model with the same priors. This “sampling from the prior” procedure has been described in Vaughan et al. (2014).

We performed two sets of simulations, one with death (i.e., ) and one without death (i.e., ). The distributions obtained without death should match if the model is correctly implemented; however, we expect a discrepancy when simulating with death, due to the approximation of no type changes on unsampled lineages made in the probability density function used by the MCMC.

The number of tips was fixed to 50, and was fixed to . The priors used were the following: LogNormal(1.5,1.0) for the birth rates and LogNormal(1.0,1.0) for the type change rate . The prior for the death rates was the Dirac function in simulations without death and LogNormal(1.0,0.5) in simulations with death. The prior on was set to Poisson().

The forward in time simulation was performed as follows. Parameters for five different types were drawn from the prior distributions, then a tree was simulated starting with two lineages in the same type, with this initial type being chosen uniformly at random. The simulation was stopped after a time , or when all lineages had gone extinct, whichever came first. The simulated tree was kept in the data set if the following two conditions were met: the number of extant tips was and the time of the most recent common ancestor , that is, neither of the original two lineages had gone fully extinct. New parameters were drawn from the priors for the next simulation, independent of the previous draw having resulted in a tree which was kept or not.

We assessed the match between the two distributions of trees on two measures: the gamma statistic, which measures the balance of recent branching events in a tree against older events, and the Colless statistic, which measures the left–right balance of lineages in a tree. We also assessed the match between the distributions of type positions on the trees on two measures: the number of tips in the largest type (i.e., the type with the maximum number of tips) and the total number of sampled types.

1.4.2 Accuracy of the inference

We assessed the quality of the MTBD inference on simulated data sets covering a range of possible configurations: constant birth and death rates, multiple types with different birth rates, multiple types with different death rates, and multiple types with different birth and death rates. Some of these data sets were simulated using the forward in time process described previously. Our parameter choices for and are displayed in Figure 3. In short, we performed one set of simulations with . Then, we performed a set of simulations with two different birth rates (). Next, we performed a set of simulations with two death rates, where the net diversification (birth–death) matched the simulation with the birth rate variation (). The rationale for keeping the net diversification the same was to investigate the difference of performance of the method when varying birth versus death rates in the light of as few changes as possible across the simulations. Finally, we did a set of simulations with five birth rates and one death rate. We chose “low” and “high” values of such that the resulting trees would contain respectively between and type changes and between and type changes on average, excluding the changes on edges leading to tips. The “low” value was thus set to for data sets with 2 types, and for the data set with 5 types, while the “high” value was set to .

Figure 3.

Performance of the birth, death, and type change rates inference on different data sets, measured by the relative error (absolute difference between the estimate and the true value, divided by the true value) and the coverage (proportion of 95% HPDs which contain the true value). All measures are averages over 100 trees, with 200 tips for the data sets with 1 or 2 types and 500 tips for the data set with 5 types. Tip errors are averaged over all tips, while tree errors are averaged over all edges, weighted by the edge lengths.

This process often led to trees where one of the types only covered a small portion of the tree, and so there was little signal for the presence of two types. Previous research showed that using trees with inadequate signal for multiple diversification regimes could lead to misleading conclusions about the accuracy of the inferences (Rabosky et al. 2017). To address this issue, we also simulated so-called joined trees, which were made of two trees simulated separately under a constant birth–death process. The root of the smaller tree was then attached to the bigger tree such that the resulting tree was ultrametric. These joined data sets were thus characterized by the proportion of tips in type rather than by a change rate .

No sequences were simulated, and all analyses were performed with fixed tree topologies. Thus, we estimated and for a fixed tree . We measured the accuracy of the parameter estimates as well as the coloring .

2 Results

We developed and implemented the MTBD model as a package within the BEAST 2 framework. It takes genetic sequences or fixed phylogenetic trees as an input. The output is the inferred trees (in the case of sequences) and an assignment of lineage-specific birth and death rates to all lineages in the tree. Changes of these rates may happen anywhere along a branch. The standard MTBD implementation assumes that there are no type changes in the extinct parts of the tree (referred to as “approximate MTBD” or simply MTBD). We have a second, much slower implementation referred to as the “exact MTBD,” which takes into account type changes in extinct parts, that is, it does not make any approximation. In what follows, we will first show evidence for the correctness of our approximate MTBD implementation in the absence of extinction in a simulation study. Then, based on simulations, we investigate the accuracy of the approximate MTBD when estimating the rates and change times. In the Supplementary Section 3 available on Dryad, we validate the exact MTBD and compare the approximate MTBD to the exact MTBD, revealing that the approximation has no major effect towards our simulation results. We also explore the impact of high or zero death rates in the Supplementary Section 4 available on Dryad, and the impact of asymmetric type change rates in Supplementary Section 5. Finally, we will present the results of an analysis of a lizard and a hummingbird phylogeny using both approximate and exact implementations of the method.

2.1 Validation: Sampling from Prior

The results of the simulations without extinction are shown in Figure 2. The distributions obtained by forward simulation and by sampling from the prior match perfectly for all statistics, which provides strong evidence that the MCMC method is implemented correctly.

Figure 2.

Comparison of the distributions of multiple summary statistics on trees obtained from forward simulation (in green) and MCMC sampling from the prior (in red) under a pure-birth MTBD process.

As expected, the simulations with extinction do not fully match between the two methods, as the forward simulation allows for type changes in the extinct parts of the tree whereas our method assumes there were none. As shown in Supplementary Figure S14 available on Dryad, there is a slight discrepancy in the statistics linked to the tree topology, and a stronger discrepancy in the statistics linked to the type distribution.

The validation of the exact MTBD is shown in the Supplementary Section 3.1 available on Dryad.

2.2 Accuracy of the Inference

We use simulated phylogenies to assess the accuracy of the inference. Some data sets were simulated under the model, using a fixed set of types and a change rate . Other data sets were created by simulating two different trees under constant birth–death processes and attaching them. These joined data sets were thus characterized by the proportion of tips in type rather than .

2.2.1 Parameter estimates

We evaluated the accuracy of the parameter estimates for the birth rates, death rates, and type change rates in simulated data sets by estimating the relative error of the median estimate and the coverage, that is, the proportion of inferences where the true value appeared in the 95% Highest posterior density (HPD) interval. The error on the birth and death rates was evaluated both as an average across all tips and as an average across the entire tree, weighted by the edge lengths.

The results are shown in Figure 3. Estimates for the parameter are accurate for values around , corresponding to between 1 and 3 type changes in the tree on average. However, the estimates are much worse when is high, that is, . This is likely partly due to the approximation of no type changes in the unsampled parts of the tree being more violated when is high, but also to the presence of undetected type changes, as detailed below.

Estimates of the birth rates are very accurate, except for the estimates at the tips under high . Since the estimates averaged over the whole tree do not suffer in a similar way, this exception is likely due to misattributing tips to the wrong regime rather than increased error on the regimes themselves: type changes affecting edges leading to tips, which are more likely when is high, have a very weak to nonexistent signal and so cannot be detected by the inference. This in turn leads to tips being assigned a different type in the inference than the one recorded in the simulation, and also to underestimating , particularly when is high. Estimates of the death rates are generally less accurate, although the true value is still in the 95% HPD interval in at least 75% of the trees in all data sets.

In conclusion, the MTBD method is able to recover the correct birth and death rates from simulated phylogeny, and is able to estimate the type change rate when it is small. However, the type change rate is frequently underestimated when the true value is high.

2.2.2 Type number and positions

We measure the accuracy of the inference regarding the number of types and the partition of tips into the different types. We use the variation of information (VI) criterion (Meilă 2003) to measure the distance between the inferred type placement and the truth: a measure of 0 indicates perfect concordance between the two. The upper bound of the VI distance depends on the number of types in the coloring and varies between for 2 types and for 5 types; however, in this article, we have rescaled all VI distances so they range from to , in order to make comparisons easier. VI distances were calculated for each sample of the posterior separately and on a “consensus” coloring built from the parameter values inferred for each edge. This consensus coloring put tips in the same type if the median estimates of their birth and death rates over the entire posterior were less than apart, and is designed to represent a summary of the coloring over the posterior. Finally, we also estimated the posterior support for tips to be in the same type, analyzed for both pairs in and pairs not in the same type in the true coloring.

Results are shown in Figures 4 and 5. The first finding is that the number of types inferred by MTBD is not a reliable estimate of the underlying process (Fig. 4, right). In particular, the median estimate is similar for all data sets. Thus the precise number of inferred types should not be considered a good indicator of how many diversification regimes are in the process. This is unsurprising, as this number counts regimes that may be extremely similar as being distinct, and in such cases is likely to suffer from unidentifiability. This indicates that instead, one should use the actual rate variation inferred by MTBD. The VI distance also shows discrepancies between the sampled clusterings and the truth on all data sets, in particular on the data set with high , the data set with 5 types and data sets with identical birth rate and different death rates (Fig. 4, left). The consensus clustering however is closer to the truth on all data sets, which confirms that birth and death rate estimates are reliable. Since type changes happen at a constant rate throughout the process and most of the length of a tree is concentrated towards the tips, the simulation process will naturally create trees which contain small clades of one type nested within another type. We expect these clades to be difficult to detect, as they cause small differences in the probability density. To test this hypothesis, we recolored all clades which contained less than six nodes (internal nodes included) in the true coloring, by attributing the tips of that clade to the ancestor type instead. Thus, the tips belonging to small clades are not removed but simply recolored (indicated as “With recoloring” in Figs 4 and 5). We observe a marked improvement in similarity, as measured by the VI distance, when using this method, confirming that those small clades are unlikely to be detected by the MTBD inference. As seen earlier, the death rate estimates are less accurate than the birth rate estimates, and this is reflected by these results as well: the inference cannot easily distinguish between two types when the death rates are different but the birth rates are identical even when those two types are clearly delimited in the tree (see row of Fig. 4). In conclusion, when types differ by their birth rates, the consensus coloring represents an accurate estimate of the original coloring, especially when excluding smaller clades. The quality of the inference is however much worse on types which only differ by their death rates.

Figure 4.

Performance of the type number and coloring inference on different data sets, measured by the VI distance (difference between the true and estimated type partitions of tips) and the difference between true and estimated number of types. Measures are shown for the original true tree, and for the true tree recolored to remove small clades. All measures are averages over 100 trees, with 200 tips for the data sets with 1 or 2 types and 500 tips for the data set with 5 types.

Figure 5.

Posterior support for pairs of tips being inferred in the same type over different data sets. Measures are shown for the original true tree, and for the true tree recolored to remove small clades. All measures are averages over 100 trees, with 200 tips for the data sets with 1 or 2 types and 500 tips for the data set with 5 types.

We also looked at the posterior support for pairs of tips being in the same type, shown in Figure 5: if the inferred coloring is accurate, we expect pairs which are in the same type in the true coloring (in red in the figure) to have much higher support than pairs in different true types (in green in the figure). The results are consistent with the previous findings, showing that the posterior support reflects the true type partition if small clades are “excluded” (by recoloring as described above) and types have different birth rates.

2.2.3 Tip type inference

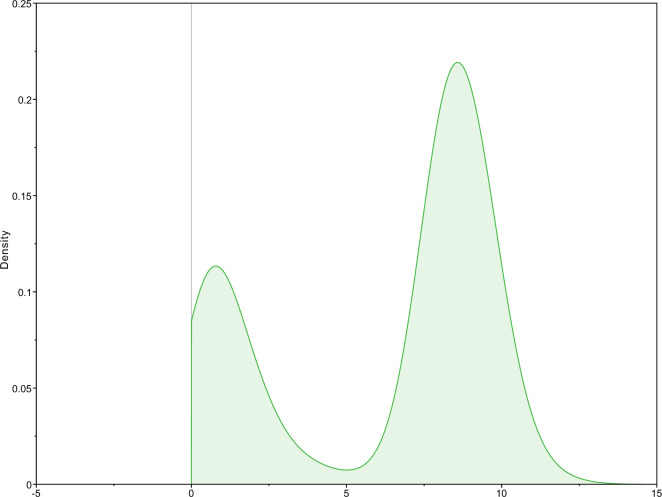
Figure 6 shows an example of the posterior distribution on the birth rate for one tip of a tree. The tree was originally simulated with parameters , , and . The figure shows a clear bimodal distribution, which is indicative that the inference has identified (at least) two separate diversification regimes across the tree, but that there is uncertainty on which regime this specific tip belongs to. The two modes identified are at and , close to the true parameter values.

Figure 6.

Kernel density estimation of a bimodal posterior distribution of the birth rate on one tip of the tree, as inferred by the MTBD method.

This figure illustrates both the power of the MTBD inference, which is able to infer complex and nuanced evolutionary dynamics, and the complexity involved in interpreting the results. The median of the posterior is here , which corresponds to the most sampled mode for this tip, but entirely misses the mode with lower . The 95% HPD interval is , which covers both identified modes but gives no indication that the distribution is bimodal. Finally, the mean estimate is , which is a misleading summary of the distribution.

In this work, we have used the median estimates to measure the accuracy of the inference, as it is the most representative of the configuration with the most posterior support. However, one should keep in mind that commonly used summary statistics can be flawed when summarizing distributions which are strongly multimodal. Other measures such as the highest density region (HDR) (Hyndman 1996) are more appropriate for these distributions. The HDR can be composed of multiple disjoint intervals and is thus a better representation of multimodal distributions than HPD intervals. As an example, the 90% HDR for the posterior density shown in Figure 6, calculated using the R package hdrcde, is , and shows the two modes clearly.

2.2.4 Comparison with the exact method

For the exact MTBD where rate changes in extinct parts of the tree are properly taken into account, the accuracy is shown in Supplementary Figures S3–S5 available on Dryad.

Regarding parameter estimates, using the exact MTBD method results in more accurate estimates of when the true value is high (), but also less accurate estimates of in some data sets. The inferred number of types is increased; however, this is expected due to the inclusion of all types in the exact MTBD, as opposed to the (approximate) MTBD model which only samples types observed in the tree. The VI scores are similar to the results obtained from the approximate MTBD method, although they are lower for data sets containing joined trees simulated using two separate trees. As explained above, these data sets were designed specifically to have no extinct type changes and thus represent a violation of the exact MTBD model, which explains the lower performance. Finally, the measures of posterior support for pairs of tips show little difference between the two methods.

2.3 Empirical Data Sets

We reanalyzed two empirical trees which were originally analyzed using BAMM: a phylogeny of hummingbird species obtained from McGuire et al. (2014) and a phylogeny of scincid lizards obtained from Rabosky et al. (2014). Both trees contain only extant species, with sampling proportions respectively and . In both analyses, the sampling proportions were fixed to the truth and the priors for the birth and death rates were set to LogNormal(,). The tree topology was fixed and the prior on the number of types in the birth–death process was set to Poisson(). The prior on was set to LogNormal(,). We also performed a second analysis on the lizards phylogeny using the priors on birth rate and death rate which were originally used with BAMM, that is, Exponential() for both rates. Priors for and were set to the same value as the previous analysis. The BAMM settings used on the hummingbirds phylogeny are not publicly available, so a similar analysis was not possible.

Average diversification rates per edge, weighted by the edge length, were logged for each edge. Figure 7a,b, shows the results of the MTBD inference with lognormal priors on both empirical phylogenies, summarized as the median of the average diversification rate for each edge.

Figure 7.

Empirical hummingbirds phylogeny (a, c) and lizards phylogeny (b, d) colored by the median diversification rate inferred by MTBD for each edge. Inferences were run with a prior favoring low values of (a, b) or higher values of (c, d).

The hummingbirds inference (Fig. 7a) shows some similarities with the original analysis by BAMM, but also differences. The diversification rates inferred by BAMM were between and , consistent with our results. BAMM also found strong posterior support for between and types with elevated diversification in the clade that includes Bees, Mountain Gems, and Emeralds, with particularly strong support for the Bees clade having a distinct diversification regime. In accordance with those results, the MTBD inference identifies three clades with elevated diversification rate, the Bees clade and two subclades of the Emeralds family. The main difference between the two inferences is that our method finds no evidence for time dependency in the diversification rates, contrary to BAMM which infers an average speciation decay of to over myr, corresponding to an exponential decay rate of across the tree.

On the lizard phylogeny (Fig. 7b), the results are quite different from the original analysis performed using BAMM. BAMM found strong support for two distinct configurations: one configuration with two separate diversification regimes, one in the Lerista and Ctenotus clades and one in the rest of the tree, and one configuration with three separate diversification regimes, one in the Lerista clade, one in the Ctetonus clade, and one in the rest of the tree. MTBD on the other hand shows no evidence of separate diversification regimes in the tree and infers a median speciation rate of and a median extinction rate of across the entire phylogeny. Similarly to the hummingbirds data set, our method also detects no time dependency in the diversification rate, although BAMM infers an average speciation decay rate of .

As time dependency is not explicitly modeled in the MTBD inference, detecting it requires inferring widespread type changes across the tree. Thus the absence of time dependency in our original inference could be due to the prior on being too low, and thus moving the inference away from this configuration. To test this hypothesis, we also ran an analysis with a much higher prior on , set to LogNormal(,). The results are shown in Figure 7c,d. With the larger prior mean on , we can indeed recover signal for time dependency in the lizards phylogeny, with edges close to the tips inferred to have a lower diversification rate than edges closer to the backbone of the tree. On the other hand, the hummingbirds phylogeny still shows no strong evidence for time dependency, and no longer detects the clades identified as under different diversification regimes by the previous analysis. Thus it appears that the results are sensitive to the prior in , and that the higher diversification rate identified in some hummingbirds clades by the original analysis is not robust to changes in the inference settings. In conclusion, it is not possible to conclude whether this data set contains evidence for changes in diversification rates.

However, this also illustrates the necessity of being careful when summarizing results from the MTBD inference, as a more in-depth analysis shows that edges in the hummingbirds phylogeny actually show a strong bimodal distribution which is very similar from edge to edge. The strong differences apparent in Figure 7c are in fact due to small variations in this bimodal distribution which lead the median to switch from one mode to the other. The posterior distributions on selected tips of this phylogeny are shown in Supplementary Figure S15 available on Dryad.

Similar results were obtained when summarizing based on the median speciation and extinction rate, as well as when using the same priors as the original BAMM analysis. They are shown in Supplementary Figures S16–S19 available on Dryad.

In summary, the empirical analyses show two very different situations when using the default priors: on the hummingbirds data set, our method and BAMM reach similar conclusions both regarding the presence and positions of separate diversification regimes and the parameter estimates. On the lizards phylogeny however, BAMM and MTBD obtain very different results, with MTBD finding no evidence of either rate changes or time-dependent rates. Further analyses on the empirical data sets show that MTBD is able to infer a pattern of time-dependent rates in a piecewise manner, however this requires the prior for to have a much higher mean than for detecting single clades with different diversification regimes. Additionally, clades with elevated diversification rates are no longer detected in the hummingbirds data set when using the higher prior, indicating that they may be spurious and the product of specific model settings. The results obtained with the higher prior are consistent with the results obtained with the exact MTBD method, indicating that the hummingbirds clades detected by BAMM and the default MTBD may be spurious. On the other hand, the time dependency shown by the lizards data set is also detected by the exact MTBD. Overall, the MTBD results are quite sensitive to the prior set on , implying that there is little signal for the number of type changes in these two data sets.

It is not clear what is the source of the difference between MTBD and BAMM. The two methods model the type change process in different ways, as BAMM does not include a type change rate. The results obtained with BAMM were postprocessed using the recommended BAMMtools package, which filters out some of the inferred type changes. Some of the differences may also be due to stochastic variation and a low amount of signal in the data. Finally, it is to be noted that our comparison was done using the published BAMM results for both empirical data sets, which were obtained using BAMM v1.0.0. BAMM has undergone significant changes since, including several bugfixes and modifications of the likelihood function, thus it is possible that the original results do not reflect the results which would be obtained with the latest version of the method.

2.3.1 Comparison with the exact MTBD

The diversification rate estimates using the exact MTBD method on the empirical data sets are shown in Supplementary Figure S6 available on Dryad. One thing to note is that the results are less sensitive to the prior on , although the results obtained with a prior placing an emphasis on higher values show more variation in estimates between edges, as expected.

On the hummingbirds data set, the clades with higher diversification rate identified by BAMM are not identified by the exact MTBD method with either prior settings, confirming that these clades may be spurious results and the product of specific inference settings. On the lizards data set, the results show a pattern of interedge variation, with edges closer to the root having a higher diversification rate than edges at the tips, supporting the time dependency inferred by the original BAMM analysis on this data set.

On both empirical data sets, the range of values obtained with BAMM for the diversification rates matches the estimates obtained with both versions of MTBD.

For both data sets, MTBD estimates of the edge speciation and extinction rates are strongly bimodal, thus the median estimate shown in Supplementary Figure S6 available on Dryad is only a partial representation of the results. However, the results obtained using the exact MTBD method are consistent with the estimates from the approximate MTBD with the high- prior.

2.4 The Consequences of Assuming No Type Changes in Extinct Parts of the Tree

The approximation of no type changes in the extinct parts of the tree does not affect strongly the accuracy of the results on the simulated data sets. For the empirical analysis, the exact MTBD is less sensitive than the approximate MTBD to the prior on , and the results obtained are consistent with the results obtained by the approximate MTBD with the high- prior.

This test confirmed that the performance impact of using numerical integration instead of an analytical approximation is important: runs were between 6 and 10 times slower for the same number of iterations when using the exact MTBD inference as opposed to the approximate method.

In conclusion, our approximation improves the performance of the inference with respect to computational time without strongly affecting the results. One caveat of this conclusion is that our current model uses symmetric transition rates between all types. It is possible that the impact of the approximation would increase in the presence of strongly asymmetrical transitions, for instance if the types correspond to the “exposed” and “infected” phases of an infection.

3 Discussion

In this manuscript, we present an MCMC sampler for colored trees where the tip types and the number of types are unknown. This contrasts with previous approaches like the State Speciation and Extinction models (BiSSE, MuSSE, etc.) or BDMM, where the types at the tips are fixed. We associate this sampler with a new MTBD for Bayesian inference of lineage-specific birth and death rates. The model is composed of multiple types, each associated with a specific birth and death rate, as well as a type change rate. The positions and times of type changes on the phylogeny then define the type to which each lineage belongs. The MTBD model thus represents a discretization of the underlying evolutionary process as a series of separate evolutionary regimes. We provide the likelihood function for this model and combine it with the MCMC sampler to perform phylodynamic inference.

The two components, sampler and MTBD model, can be used independently, as the sampler is not dependent on the particular likelihood function used. We demonstrate this in our work by testing both the exact MTBD likelihood and an approximate version of this likelihood. Thus the sampler could easily be reused in association with other multitype phylodynamic models, such as those based on the structured coalescent (Notohara 1990). Further, the sampler could be combined with models for gradual phenotypic evolution (Mitov et al. 2019).

Regarding our new MTBD model, we have shown using simulated data sets that the MTBD inference can accurately estimate birth and death rates, and that those estimates can be used to build an accurate partition of the tree into types. However, our results also show that the MTBD inference cannot detect clades with different rates if the clades consist of very few tips. This is expected, as the method relies on the pattern of relative edge lengths to infer rates, thus small clades will not contain enough signal for type changes to be detected. Additionally, death rate estimates are less accurate than birth rate estimates in all simulation conditions. This in turn leads to lower accuracy when partitioning the tree into types in data sets where types only differ by the death rate. In this case, many trees are inferred as containing only one type. Finally, the estimated number of types is not a reliable representation of the true number of distinct regimes in the underlying process.

One challenge of performing inference under the MTBD model, also shared by other complex inference models, is the computational complexity of calculating the likelihood. To minimize the impact of this issue, we make several approximations in the likelihood calculation, including the assumption that there are no type changes in the extinct parts of the tree. The method BAMM (Rabosky et al. 2013) uses a similar assumption, which has been criticized previously (Moore et al. 2016). Thus, we tested our approximate likelihood against the exact version. As we found no major differences in the accuracy of our estimates between the two methods, this approximation has no major drawbacks for the investigated parameter choices, while ensuring much faster run times (about 6- to 10-fold).

Our MTBD model differs from the model used by BAMM in several key ways. First, the MTBD model includes an explicit type change process, controlled by the type change rate , which is not present in BAMM. Second, BAMM assumes that each type change is the start of an entirely new evolutionary regime, while the MTBD model allows the same type to be present in multiple distinct parts of the tree. Although these differences may seem minor, the results of the comparison on the empirical data sets demonstrate that those differences and assumptions can have an important impact on the results. Thus, our work in validating and testing MTBD under a variety of different conditions, including an explicit test of the main approximation allowing for no type changes in extinct parts, improves on the foundational understanding of multitype models in phylogenetics.

A unique and powerful feature of our approach is that the MTBD model can be used in combination with the rest of the BEAST2 framework to infer both the tree topology and evolutionary parameters from genetic sequences. It allows users to model the phylogenetic tree distribution and in particular take into account the phylogenetic uncertainty, compared to an approach such as BAMM which enforces a fixed tree topology.

One should be aware that interpreting the results of the MTBD inference requires more care than for other models. This is primarily for two reasons, with the first being that the types are not linked to specific tips. If two MCMC samples contain types, we cannot determine a precise correspondence between the types in the first sample and the types in the second. This problem is compounded by the variation in the number of types between different samples across the chain. Considering different sampled types in the MCMC reveals a large amount of uncertainty as shown in Figure 4. However, the introduced consensus clustering obtained from the rate estimates approximates the true clustering well.

The second reason is that the MTBD inference will frequently produce multimodal posterior distributions on the rates associated with specific nodes or edges. This multimodality reflects the uncertainty of assigning a node or edge to a particular type. For multimodal distributions, the usual metrics used to describe Bayesian parameter estimates, that is, the median and HPD interval, give an incomplete picture of the output by failing to distinguish between uncertainty around the rate estimate and uncertainty on regime (i.e., type) attribution. We suggest that the HDR is a more adequate summary statistic for multimodal distributions, however analyzing the output of the MTBD inference should be tailored to the research question being considered, and may require different metrics than the ones we have used in this article.

Concerns about a more general form of unidentifiability in complex birth–death processes have recently been discussed (Louca and Pennell 2019). In our work, we explicitly tested the identifiability of the type change rate parameter . Our results show that is identifiable, despite the variability we observe in the empirical results depending on the prior on . However, more complex identifiability problems (i.e., affecting a combination of parameters rather than a single one) may still exist. Models containing lineage-specific changes in birth and death rates were not the focus of Louca and Pennell (2019), thus it is currently unknown whether the MTBD model suffers from similar issues. One way to avoid potential problems would be to avoid a focus on point estimates such as the median estimate. Instead, we should always consider the full posterior distribution as the output, which should continue to properly represent uncertainty in inference results even in the face of unidentifiability. However, due to its high-dimension, the full posterior distribution is hard to deal with.

Future work will focus on implementing explicitly time-dependent birth and death rates in the MTBD model to better accommodate situations where diversity-dependent or environment-dependent diversification is present. Additionally, the available inference options should be generalized, in particular regarding sampling schemes. Currently only type-independent extinct and extant sampling are supported, and the associated parameters are assumed to have known (fixed) values. Similarly, the current implementation of the MTBD model assumes that all transitions are symmetric. Our simulations show that parameter estimates remain reliable in the presence of strongly asymmetric transition rates; however, the inferred type partition becomes less accurate. Including asymmetric transition rates would expand the applicability of our model to real-world data, for instance epidemiology data sets where the types could correspond to “exposed” and “infectious” phases. Moreover, it will be interesting to use our colored tree sampler in association with other tree generating processes. In particular, phenotype evolution models as presented in Mitov et al. (2019) would be great models to be linked with our sampler. Such a linkage would allow to determine distinct regimes of phenotypic evolution processes. In summary, we expect that our sampler for colored trees will become a standard sampler within BEAST2 for a range of models. Our analysis of the MTBD model, using this sampler, provides a deeper understanding of the MTBD models.

Data availability

All simulations and analyses were done using custom R scripts (available in the Supplementary Materials). The method is publicly available as the BEAST 2 package MSBD.

Supplementary Material

The code and data are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.zpc866t5n.

Funding

This work was supported in part by the European Research Council under the Seventh Framework Programme of the European Commission (PhyPD: grant agreement number 335529) and the Swiss National Science Foundation (407240_167060) as part of the National Research Programme (NRP72) to J.B.S. and T.S.