The Conjugation Window in an Escherichia coli K-12 Strain with an IncFII Plasmid

There has been growing interest in horizontal gene transfer of antibiotic resistance plasmids as the antibiotic resistance crisis has worsened over the years. Most studies examining conjugation of bacterial plasmids focus on growing cultures of bacteria for short periods, but in the environment, most bacteria grow episodically and at much lower rates than in the laboratory. We examined conjugation of an IncFII antibiotic resistance plasmid in E. coli under growing and nongrowing conditions to understand the dynamics of conjugation under which the plasmid is transferred. We found that conjugation occurs in a narrow time frame when E. coli is transitioning from a growing to nongrowing phase and that the conjugation plateau develops because of a lack of capable donor cells in growing cultures. From an environmental aspect, our results suggest that episodic growth in nutrient-depleted environments could result in more conjugation than sustained growth in a nutrient rich environment.

ABSTRACT

Many studies have examined the role that conjugation plays in disseminating antibiotic resistance genes in bacteria. However, relatively little research has quantitively examined and modeled the dynamics of conjugation under growing and nongrowing conditions beyond a couple of hours. We therefore examined growing and nongrowing cultures of Escherichia coli over a 24-h period to understand the dynamics of bacterial conjugation in the presence and absence of antibiotics with pUUH239.2, an IncFII plasmid containing multiantibiotic- and metal-resistant genes. Our data indicate that conjugation occurs after E. coli cells divide and before they have transitioned to a nongrowing phase. The result is that there is only a small window of opportunity for E. coli to conjugate with pUUH239.2 under both growing and nongrowing conditions. Only a very small percentage of the donor cells likely are capable of even undergoing conjugation, and not all transconjugants can become donor cells due to molecular regulatory controls and not being in the correct growth phase. Once a growing culture enters stationary phase, the number of capable donor cells decreases rapidly and conjugation slows to produce a plateau. Published models did not provide accurate descriptions of conjugation under nongrowing conditions. We present here a modified modeling approach that accurately describes observed conjugation behavior under growing and nongrowing conditions.

IMPORTANCE There has been growing interest in horizontal gene transfer of antibiotic resistance plasmids as the antibiotic resistance crisis has worsened over the years. Most studies examining conjugation of bacterial plasmids focus on growing cultures of bacteria for short periods, but in the environment, most bacteria grow episodically and at much lower rates than in the laboratory. We examined conjugation of an IncFII antibiotic resistance plasmid in E. coli under growing and nongrowing conditions to understand the dynamics of conjugation under which the plasmid is transferred. We found that conjugation occurs in a narrow time frame when E. coli is transitioning from a growing to nongrowing phase and that the conjugation plateau develops because of a lack of capable donor cells in growing cultures. From an environmental aspect, our results suggest that episodic growth in nutrient-depleted environments could result in more conjugation than sustained growth in a nutrient rich environment.

INTRODUCTION

In recent years, the role of horizontal gene transfer (HGT) in the dissemination of antibiotic resistance genes (ARG) in the environment has become a serious concern to scientists and public health officials (1, 2). The vast majority of conjugation studies have examined conjugation in growing bacteria, and there is a strong correlation with bacterial growth and conjugation (3–6). Studies have found that conjugation frequency curves strongly resemble bacterial growth curves, with a lag phase occurring after initial mixing of donor and recipient cells, followed by a period of increasing conjugation (e.g., an exponential phase) that typically ends in a plateau (e.g., a stationary phase) (7–12). The conjugation plateau has been attributed to saturation of donor cells (8, 12) and changes in growth stage (7, 12). The significance of this is that conjugation under growing conditions appears to occur in a finite time span after initial mixing of donor and recipient cells and then stops (12, 13).

Previous studies have noted a decrease in conjugation with starvation (14, 15), in nutrient-depleted environments (3), and upon entry into stationary phase (16). A limited number of studies have shown that conjugation can still occur in nutrient-depleted natural and artificially created environments (17–24). Recently, it was demonstrated that the conjugation frequency can even be higher under nongrowing rather than growing conditions (25). The underlying factors that control the dynamics of conjugation under nongrowing conditions and their relationship to growing conditions remain unresolved. This knowledge gap has important implications for conjugation in natural environments that experience episodic conditions that are favorable for bacterial growth.

Many scientists and engineers have turned to computer modeling to better understand and predict the spread of ARGs in the environment. Most computer models simulating bacterial conjugation assume that it is equal to the product of a conjugation rate coefficient and the concentrations of donor and recipient cells (see, e.g., references 6, 7, and 26). The conjugation rate coefficient has been modeled as a constant rate (see, e.g., references 6, 7, and 26) or in a manner similar to that for the growth rate coefficient (see, e.g., references 8, 9, and 11). In the absence of bacterial growth and death, a constant conjugation rate predicts a linear increase in transconjugants over time. This model formulation is not consistent with observed dynamics of conjugation in growing cultures with a lag phase, an increase in conjugation, and then a plateau region (7–12). However, these trends can be captured when the conjugation rate is described in a manner similar to that of the Monod growth rate coefficient (8, 9, 11). Note that such growth expressions are not appropriate for nongrowing conditions. Model descriptions for conjugation under nongrowing condition are unknown because of the paucity of experimental information.

Models for conjugation also implicitly treat the bacteria as clonal populations. For example, they assume that transconjugants will become donor cells (and often with equal conjugation rates as the donor cells) (7, 12, 27, 28). In addition, they frequently consider the same growth rates for all donor and recipient cells (7, 12, 27–31). Microbiologists have long noted that single-species bacterial cultures are not necessarily genetically or phenotypically clonal (32–35), particularly when it comes to growth (36–38). Within any given bacterial culture, subpopulations exist that are not in sync with other subpopulations (39–41). The net effect is that the entirety of a growing bacterial culture is not in exponential growth phase at the same time (37, 42). From a conjugation standpoint, this is a very important distinction. Studies have shown that conjugation frequencies are highest in exponential phase (6, 43), but there is still a gap in knowledge as to exactly when conjugation occurs in growing bacteria and how the dynamics of conjugation produce a conjugation plateau.

This research examined conjugation dynamics of E. coli over a 24-h period in growing and nongrowing cultures to better understand and simulate factors controlling this behavior. We found that nongrowing cultures of E. coli exhibited the same pattern of conjugation as growing cultures (i.e., a lag phase, a conjugation phase, and a plateau) and that both nongrowing and growing cultures ceased conjugation after about 4 to 8 h after mixing of donor and recipient cells. Our data suggest that conjugation takes place after cells divide and before they enter a nongrowing phase. Thus, there is only a finite time span in which E. coli organisms are capable of conjugating with the IncFII group plasmid examined in this study. In growing cultures, the number of capable donor cells decreases rapidly after the first couple of hours, and this produces a conjugation plateau. Our data also shows that not all transconjugants become donors cells. We present a computer model that takes these factors into account.

RESULTS

Growth characteristics in growing cultures.

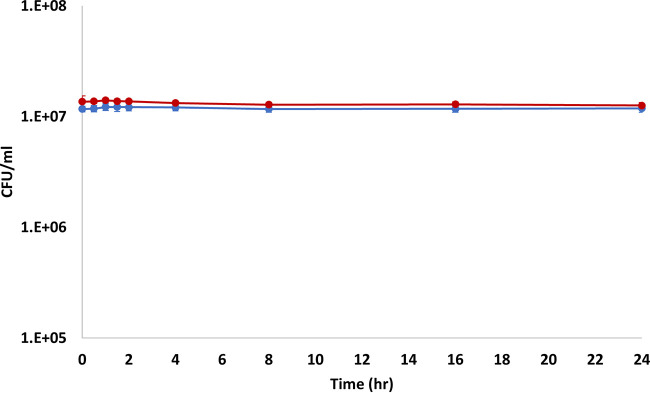
In LB cultures without antibiotics, both the donor and recipient bacteria exhibited a short lag phase of between 0.5 and 1 h and then began to grow. Between 1.5 and 4 h, the cultures were in exponential phase, and then at around 4 h, the cultures entered stationary phase, with modest growth for the remainder of the experiment (Fig. 1A, Fig. S1A and C to E, and Table S2A). In LB cultures supplemented with cefotaxime sodium salt (CFX; 25 μg/ml) (LB+CFX cultures), there was a short lag period of between 0.5 and 1 h followed by growth of donor cells and death among the recipient population. Between 1.5 and 4 h the donors exhibited exponential phase and entered stationary phase after 4 h, with modest growth for the remainder of the experiment. The recipient population continued to decrease in concentration until about 2 h, after which there was modest growth for the remainder of the experiment (Fig. 1B, Fig. S1B, D, F, and G, and Table S2A).

FIG 1.

Growth curves of growing cultures. (A) Average growth curve of LB cultures (no antibiotics). (B) Average growth curve of LB+CFX (25 μg/ml) cultures. The solid lines with circles represent experimental data. The dotted lines with no symbols represent computer modeling. Blue lines represent donor bacteria, and red lines represent recipient bacteria. Error bars represent standard deviations.

Conjugation in growing cultures.

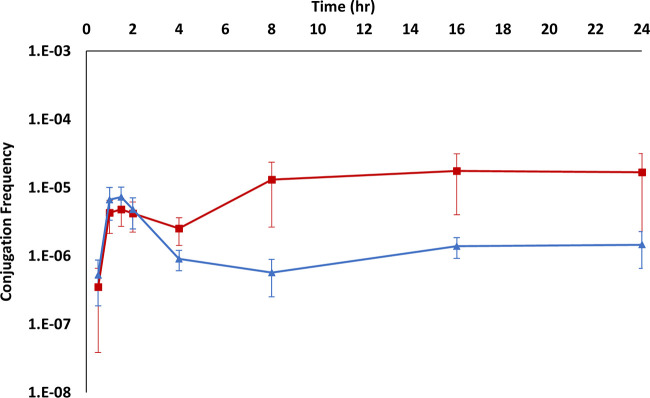
In LB cultures without antibiotics at 37°C, the conjugation frequency increased for the first 1.5 h before decreasing between 1.5 and 4 h. Between h 4 and 8 there was a large increase in the conjugation frequency. The frequency plateaued at h 8 and continued this trajectory for the remainder of the experiment (Fig. 2, Fig. S2A to C, and Table S2B). The decrease in conjugation frequency between 1.5 and 4 h coincided with exponential-phase growth, and the large increase between 4 and 8 h coincided with stationary phase. The decrease in conjugation frequency between 1.5 and 4 h was statistically significant for all cultures (P ≤ 0.0001 to 0.0215) (Table S3). The large error bars associated with the LB (no antibiotics) cultures were due to large differences in the magnitude of conjugation between the three different experiments (at the peak, the total numbers of transconjugants were close to 1,300, 17,000, and 30,000 per milliliter in experiments 1, 2, and 3, respectively). In the presence of CFX, the conjugation frequency increased for the first 1.5 h and then decreased between 1.5 h and 4 h, after which it leveled off well below the peak at 1.5 h (Fig. 2, Fig. S2A and D, and Table S2B). Interestingly, the raw number of transconjugants increased in the CFX-supplemented culture for the first 2 h and then declined between 2 and 8 h before increasing again at 16 h. The decrease in the raw number of transconjugants coincided with exponential growth for donor cells and modest growth for the recipient cells.

FIG 2.

Average conjugation frequency in growing cultures. The red line represents LB cultures (no antibiotics), and the blue line represents LB+CFX (25 μg/ml) cultures. Error bars represent standard deviations. The major increases and decreases in conjugation are statistically significant (i.e., 0.5 h versus 1 h, 2 h versus 4 h, and 4 h versus 8 h) for both cultures. P values for comparisons of adjacent time points on the same line and different time points between lines can be found in Table S1.

Survival characteristics in nongrowing cultures.

The numbers of donor and recipient cells remained fairly constant throughout the duration of the experiment (there was some variation which we attribute to sampling and instrument error), and changes in concentrations were generally not statistically significant from one time point to the next (Fig. 3, Fig. S3A to G, and Table S4A). Overall, there was a slight decrease in the concentrations at 0 h compared to those at 24 h in most cultures.

FIG 3.

Average donor and recipient concentrations of all cultures (with and without antibiotics) in 9.1 mM NaCl. The blue line represents donor cells, and the red line represents recipient cells. Error bars represent standard deviations.

Conjugation in nongrowing cultures.

All cultures in 9.1 mM NaCl (with and without antibiotics) exhibited a lag phase that lasted for approximately 0.5 to 1.5 h, and then the conjugation frequencies increased until approximately 4 to 8 h, when the frequency began to level off and a plateau formed (Fig. 4, Fig. S4A to D, and Table S4B). The large error bars associated with the conjugation frequencies can be attributed to the difference in the magnitude of the conjugation among the three experiments conducted on different days (the first experiment had ∼11,500 total transconjugants/ml, the second experiment had ∼5,500 total transconjugants/ml, and the third experiment had ∼9,500 total transconjugants/ml). The highest conjugation frequencies were observed in 9.1 mM NaCl supplemented with 25 μg/ml of CFX, with the nonantibiotic control having lower conjugation frequencies. These trends are consistent with our earlier findings (25).

FIG 4.

Average conjugation frequency in 9.1 mM NaCl. The red line represents 9.1 mM NaCl (no antibiotics), and the blue line represents 9.1 mM NaCl plus CFX (25 μg/ml). Error bars represent standard deviations. The increases in conjugation frequency for adjacent time points are statistically significant until 8 h and beyond. P values for comparisons of adjacent time points on the same line and different time points between lines can be found in Table S1.

Harvesting time versus conjugation.

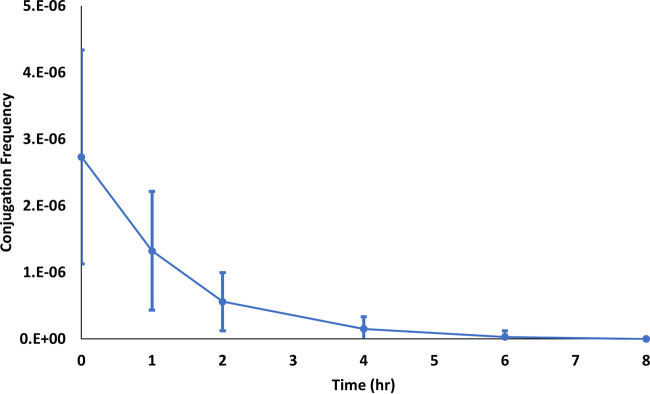
Transferring exponentially growing bacteria to a nongrowth medium will undoubtedly induce the bacteria into a nongrowing phase. We hypothesized that during the time in which the bacteria were transitioning from growing to nongrowing they were able to undergo conjugation, but after that transition was completed, they would no longer undergo conjugation. Thus, we conducted an experiment in which we prepared the donor and recipient bacteria as described above, placed them in separate flasks of 9.1 mM NaCl without antibiotics at 37°C and ∼200 rpm, and mixed donor and recipients at 0, 1, 2, 4, 6, and 8 h postharvest (donor and recipient cells were mixed at the same times, i.e., 0-h donor with 0-h recipient, etc.). The number of transconjugants decreased rapidly in the first 2 h, and by 6 h there were no transconjugants formed (Fig. 5).

FIG 5.

Conjugation frequency versus mixing time of donor and recipients in 9.1 mM NaCl (donor and recipient cells mixed at same times for each). Error bars represent standard deviations. The difference in conjugation frequency between adjacent time points is statistically significant (P ≤ 0.0001 to P = 0.0406) except between 6 h and 8 h (P = 0.1881).

Mixing exponential- and stationary-phase cultures.

We next conducted an experiment in which we harvested exponentially growing donor cells, placed them in a nongrowth medium (9.1 mM NaCl without antibiotics), and mixed them with recipient cells that had been harvested and left on the countertop for 8 h in a nongrowth medium and vice versa. The highest conjugation frequencies occurred when we mixed donor cells and recipient cells immediately after harvesting exponential-phase cultures. When freshly harvested donor cells were mixed with recipient cells that had been in a nongrowth medium for 8 h, the number of transconjugants was nearly 6 times less. When freshly harvested recipients were mixed with donor cells that had been in a nongrowth medium for 8 h, the number of transconjugants was nearly 20 times less than when freshly harvested donor and recipient cells were mixed. When donor and recipient cells that had been in nongrowth medium for 8 h postharvesting were mixed, the number of transconjugants was nearly 20 times less than when freshly harvested donor and recipient cultures were mixed (Fig. 6).

FIG 6.

Conjugation frequency versus growth phase of donor and recipients in 9.1 mM NaCl. D0, donor cells immediately after harvesting; R0, recipient cells immediately after harvesting; D8, donor cells 8 h after harvesting; R8, recipient cells 8 h after harvesting. Error bars represent standard deviations. The magnitude of conjugation between the D8R0 and D8R8 cultures was not statistically significant (P = 1.0000). For all other comparisons, the difference was statistically significant (P ≤ 0.0001 to P = 0.0338).

Computer modeling.

The logistic model provided a reasonable description of growth for donor cells in LB and LB+CFX cultures, with a Pearson coefficient of linear correlation (R²) of >0.98 (Fig. 1A and Table 1). In this case, values for donor cell growth rate (μ_D) and maximum concentration of donor cells (C_DMAX) were similar in the presence and absence of antibiotics. The logistic model also provided a reasonable description of the concentration of recipient cells in the absence of antibiotics (R² = 0.98) and, to a lesser extent, in the presence of CFX (R² = 0.74) (Table 1). In the LB+CFX culture, the recipient cells initially exhibited a rapid die-off for the first 2 h and then a gradual increase in concentration thereafter (Fig. 1B). The logistic model approximates this behavior, with a die-off phase when the concentration of recipient cells (C_R) exceeds the maximum concentration of recipient cells (C_RMAX) for the first 2 h and then a constant concentration plateau at C_RMAX. Note that the value of C_RMAX for the LB+CFX culture was about 2 orders of magnitude smaller than for the other cultures (donor and recipient in LB and the donor in LB+CFX). Concentrations of donor and recipient cells during nongrowing conditions tended to slowly decrease over time but exhibited some scatter (Fig. 3). This behavior was adequately modeled using a first-order decay expression (Fig. S5A and B). However, the scatter in the concentration values sometimes produced relatively low values of R², ranging from 0.2 to 0.79 (Table 1).

TABLE 1.

Fitted survival and conjugation parameters, along with the Pearson correlation^a

Culture	CDi (N cm−3)	CDMAX (N cm−3)	CRi (h−1)	CRMAX (N cm−3)	μD (h−1)	μR (h−1)	R2		μC (h−1)	kc (cm3 N−1 h−1)	m (h)	σ (h)	R2, TC
							Donor	Recipient
9.1 mM	1.21E+07	NA	1.39E+07	NA	−2.88E−03	−6.12E−03	0.584	0.792	−0.015	2.70E−09	2	4	0.964
9.1 mM+CFX	1.19E+07	NA	1.36E+07	NA	1.11E−03	−2.30E−03	0.201	0.728	−0.022	4.57E−09	2	3.7	0.920
LB	1.12E+07	3.52E+08	1.20E+07	4.75E+08	1.97E+00	1.12E+00	0.980	0.981	0	7.80E−10	2	6.5	0.997
LB+CFX	1.13E+07	4.16E+08	1.39E+07	5.66E+06	1.20E+00	1.11E+00	0.996	0.735
With decayb									−0.9b	1.50E−08	0.1	4.72	0.588
Without decay									0	1.57E−08	0.1	1	0.475

^aTC, transconjugants; NA, not applicable.

^bDecay was active only for the first 8.8 h and then set to zero.

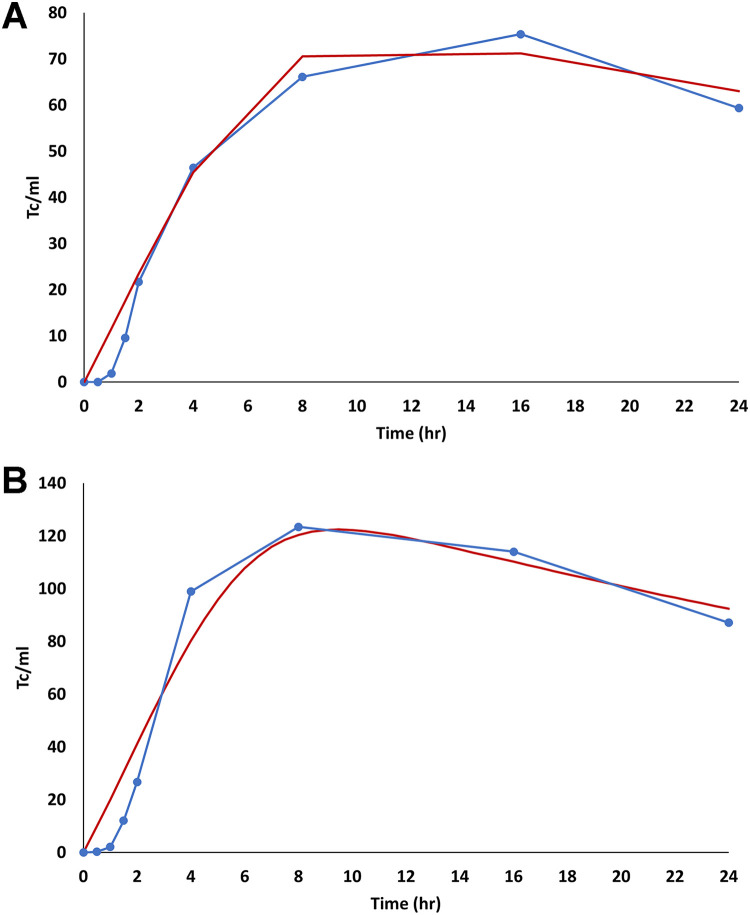
Figure S6 presents simulated transconjugant concentrations as a function of time in 9.1 mM NaCl solution when applying the M1 model. The optimized conjugation efficiency rate (k_c) for the M1 model was 2.92E−14 cm³/(N h). The M1 model does not accurately capture the lag phase, the rapid increase in conjugation, or the plateau phase and will therefore not be considered further. The M2 model was subsequently employed to simulate the conjugation data sets (LB, LB+CFX, 9.1 mM, and 9.1 mM+CFX) (Fig. 7 and 8). Table 1 presents a summary of fitted conjugation parameters, decay coefficients, and R² values when using the M2 model. The M2 model provided a very good description of the LB, 9.1 mM, and 9.1 mM+CFX conjugation data set (R² > 0.92), which exhibited a lag phase, a rapid increase in conjugation, a plateau phase, and then a constant rate of die-off in the nongrowing cultures. The mean conjugation time (m) was equal to 2 h in these systems, and this reflects a similar lag time. The standard deviations of conjugation times (σ) were similar in nongrowing cultures (4 h in 9.1 mM and 3.7 h in 9.1 mM+CFX) but was somewhat larger in the LB culture (6.5 h). The k_c followed the same order as the peak transconjugant concentration in the nongrowing experiments (9.1 mM+CFX > 9.1 mM).

FIG 7.

Computer modeling of transconjugant (Tc) concentrations over time in growing cultures. (A) Observed and optimized M2 model simulations of transconjugants in the LB culture without antibiotics. (B) Observed and optimized M2 model simulations of transconjugants in the LB+CFX (25 μg/ml) culture. The blue lines with circles are the experimental data. The red and orange lines are optimized M2 model simulations with and without die-off transconjugants for the first 8.8 h, respectively. Table 1 includes a summary of fitted conjugation parameters.

FIG 8.

Computer modeling of nongrowing cultures. (A) Transconjugants with 9.1 mM NaCl (no antibiotics). (B) Transconjugants with 9.1 mM NaCl plus CFX (25 μg/ml). The blue lines with circles are the experimental data. The red lines are optimized M2 model simulation results. Table 1 includes a summary of fitted conjugation parameters.

The LB+CFX conjugation data set was less adequately described by the M2 model (R² = 0.59) (Fig. 7B). Transconjugants exhibited complex dynamics that included a very short lag phase, a high rate of conjugation, fast decay, and then a rebound in the transconjugant concentration to the plateau level. In this case, the k_c in the LB+CFX culture was more than 2 orders of magnitude higher than in the LB culture. The general shape of the conjugation dynamics was captured by the M2 model when a more-negative transconjugant decay rate (μ_C; −0.9 h⁻¹) was employed for the first 8.8 h and then set to zero. However, the M2 model predicted the arrival of the first transconjugant peak at a later time than was experimentally observed. The arrival time of this first peak could be captured by the M2 model if μ_C was 0 h⁻¹ and a smaller σ (1 h) was employed, but then the later-occurring dynamics of decay and rebound were not captured by the model (Fig. 7B).

DISCUSSION

The conjugation dynamics for growing and nongrowing E. coli cultures were studied over a 24-h period using an IncFII plasmid. Our experiments show that in E. coli containing pUUH239.2, a conjugation plateau occurs after approximately 4 to 8 h in growing and nongrowing cultures. There are a variety of scenarios that could cause a conjugation plateau. If the entire recipient population became transconjugants a plateau would form, but our data clearly show that this did not occur. If the growth rate equaled the conjugation rate, a plateau could form, but our data do not support this scenario, especially for the nongrowing cultures. If transconjugants lost the plasmid at a rate higher than new transconjugants formed, a plateau could form. We examined the plasmid stability and found that after 24 h, only 1 transconjugant colony out of 300 tested failed to grow on LB agar plates supplemented with 20 μg/ml of tetracycline hydrochloride (TET) and LB agar plates supplemented with 25 μg/ml of CFX (in all cases, the transconjugants that lost the plasmid failed to grow on both plates, not just one or the other). After 5 days less than 2% of the tested transconjugants had lost the plasmid (see Supplemental Methods and Table S1). The most likely explanation for the existence of the plateau is that conjugation has stopped due to a physiological change in the E. coli cultures associated with the transition from a growing to nongrowing phase.

Timing of conjugation.

A decrease in conjugation after entry into stationary phase, upon starvation, and/or under low-growth-rate conditions has been reported (7, 12, 14, 16, 44), and reintroduction into fresh media of cultures that have plateaued has been shown to increase conjugation again and result in another conjugation plateau (12). In Enterobacteriaceae, the cause of the decrease in conjugation could be the expression of nucleoid-associated host protein (H-NS) as bacteria enter stationary phase, which has been shown to repress expression of the tra genes on plasmids (45–47). In addition, other regulatory systems, such as FinOP, can further repress tra genes to such an extent that it has been estimated that between 99% and 99.9% of all potential donor cells cannot express the genes for conjugation and thus cannot conjugate (47–49). It is important to note that the default setting for tra genes is “off” and that even under optimal conditions, only a fraction of donor bacteria are actually capable of participating in conjugation (49). We did not specifically examine the role of H-NS and FinOP in our experiments, but if present, these regulatory components would be expected to have reduced the number of potential donor cells significantly from the onset and only become more restrictive over the time course of our experiments. Thus, the total number of donor cells in our bacterial cultures does not equal the actual number of donor cells that are capable of conjugating. The number of capable donor cells is much lower.

If conjugation occurred while the bacteria in our experiments were growing, then we would have expected the conjugation frequency to increase during exponential phase in our growing experiments, but we observed the opposite. Furthermore, we would have expected no transconjugants to form for our nongrowing cultures (which were forced into a nongrowing phase), as the window of opportunity to conjugate would have passed. If conjugation occurred only in a nongrowing phase (i.e., physiological stationary phase), then we would have expected an ever-increasing number of actual transconjugants in both our growing and nongrowing cultures, which we did not find. If conjugation could occur at any point during the bacterial life cycle (i.e., before, during, and/or after binary fission), then we would not have expected a plateau to form in our growing cultures; instead, we would expect ever-increasing numbers of transconjugants accumulating at a constant rate over the course of the experiments, which we did not observe. If conjugation occurred only during the transition from a growing to a nongrowing phase, then we would expect a spike in conjugation as the culture entered stationary phase followed by a plateau as the majority of the culture transitioned to a nongrowing phase. In a nongrowing culture (forced into a nongrowing phase), we would expect a more rapid (compared to the growing culture) increase in conjugation frequency followed by a plateau, which is what we observed.

In our growing cultures (no antibiotics) (Fig. 2), there was an increase in conjugation frequency for the first 1.5 h, which we attribute to subpopulations within the culture that were out of sync with the rest of the bacteria in the culture and transition to a nongrowing phase earlier than the majority of the culture (it is also possible that some subpopulations did not recover from the harvesting procedure). Once these bacteria conjugated, the conjugation frequency decreased for the next 2 h, as the majority of the culture was in exponential phase and very little conjugation occurred. Some conjugation still occurred during exponential phase (the actual number of transconjugants did increase in the LB culture without antibiotics) because even in an exponential-phase culture, not all the subpopulations of cells experience exponential growth simultaneously and some enter into a nongrowing phase earlier than others. As the culture approaches stationary phase, the majority of the culture begins to transition to a nongrowing phase and there is a spike in the conjugation frequency. In our CFX-supplemented culture (Fig. 2), there was a similar increase in conjugation frequency for the first 1.5 h which we likewise attribute to subpopulations transitioning to a nongrowing phase earlier than others. After this initial pulse of conjugation, the conjugation frequency remained low, even as the donor cells were in exponential phase, because the concentrations of the recipient cells was low. The recipient population never fully recovered (there was some modest growth after ∼2 h and for the remainder of the experiment), so the conjugation frequency was low for the remainder of the experiment. We interpret the modest growth of recipients after ∼2 h as the influence of CFX diminishing over time, presumably due to biosorption or degradation of CFX by donor cells. In our nongrowing culture, there was no opportunity to grow after the harvesting procedure (though one cannot completely rule out small amounts of growth as bacteria die and carbon sources become available) and thus no decrease in conjugation frequency similar to what was observed in the growing cultures (Fig. 4). Instead, all of the capable donor cells were forced into a nongrowing phase and there was only one pulse of conjugation, followed by a plateau, as there were no more cells capable of conjugating.

It is important to note that the raw number of transconjugants actually decreased in the LB+CFX cultures (in all three experiments) between 2 and 8 h (Table S2B). The most likely explanation for the decrease in transconjugants is cell death. Plasmid loss seems unlikely given the results of our plasmid stability tests (Table S1) and because the culture was supplemented with a selective agent that favored plasmid retention. It is possible that some of the recipients (and transconjugants produced) in the first 2 h of the experiment were not growing and thus were initially able to survive the effects of CFX. However, when (and if) they attempted to grow, even some transconjugants could have become susceptible to the effects of the CFX if there was a lag time for the protective effects of the plasmid to materialize. CFX is known to cause elongation in growing bacterial cells because it binds to a key protein involved in septum formation that prevents cell division, causing the cell to continue to grow into a filamentous morphology (50, 51). This would increase the surface area of the cell and could allow even more CFX to enter the cytoplasm. A delay between the time that the transconjugant receives pUUH239.2 and the actual β-lactamase is produced in sufficient quantities to counter the CFX could cause some transconjugants to be overwhelmed, causing death despite their possession of the resistance genes. Furthermore, this could have been a more important factor early during the experiment rather than later because the ability of CFX to kill recipients began to wane. The recipient population began to grow between 4 and 8 h in the first experiment and between 2 and 4 h in experiments 2 and 3 (Table S2A), suggesting that the CFX concentration was no longer sufficient to prevent growth. The differences in the average recipient concentrations of all three experiments between 2, 4, and 8 h were not statistically significant (P = 0.2930, 0.1849, and 0.1490) despite growth occurring but were statistically significant later in the experiment (P ≤ 0.0001 for recipient concentrations at 2 h versus 16 h and 4 h versus 16 h). Thus, later in the experiment, transconjugants might not have been as likely to be overwhelmed by the CFX and die as they would have been early in the experiment.

Conjugation plateau.

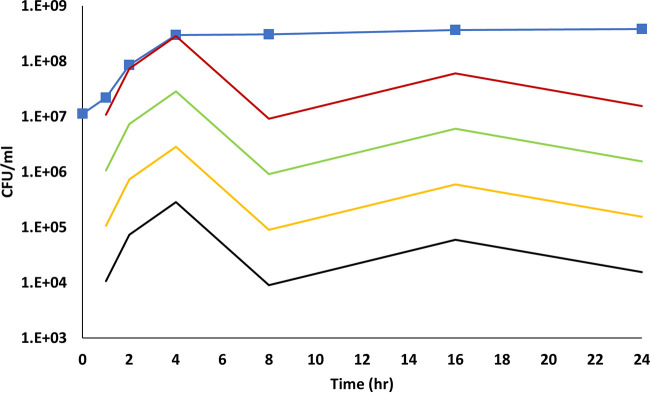
If one assumes that bacterial growth is clonal, then growing cultures could be perceived as an inexhaustible source of new donor and recipient cells. However, if bacterial growth is not clonal (at least as it relates to subpopulations within the culture) and if conjugation with pUUH239.2 occurs only while E. coli cells are transitioning from a growing to a nongrowing phase, then the number of capable donor cells will decrease rapidly after exponential phase in a growing culture and a conjugation plateau is inevitable. In the first hours after inoculation of a culture the vast majority of the cells are growing; however, within a couple of hours the growth rate slows and bacteria begin to transition to a nongrowing phase, even though the culture is still in “exponential phase.” We assume that in order for E. coli cells to have conjugated with pUUH239.2 in our experiment, they must first have been in a growing phase in order to transition to a nongrowing phase. In our LB (without antibiotics) experiment (Fig. 1A and 7A), by the time the culture entered stationary phase at approximately 4 h, there likely would have been as many as 2.8 × 10⁸ CFU/ml of donor cells capable of conjugating because at some point during the first 4 h they would have been growing, but by 8 h, this number would have decreased to approximately 9.6 × 10⁶ CFU/ml and by the end of the experiment to just 3.8 × 10⁶ CFU/ml. As a percentage of the total population, capable donor cells peaked at 4 h, with capable donor cells representing as much as 44% of the culture, and this proportion decreased to around 1% by 8 h. Recipient cells had a similar trajectory. If molecular regulatory restrictions were applied to these numbers, the proportions of capable donor cells could be reduced by up to a thousand times, depending on how strictly one wishes to apply the molecular controls (Fig. 9).

FIG 9.

Number of donor cells capable of conjugating. The blue line with squares represent the actual number of donor cells as measured by flow cytometry in our LB (no antibiotics) experiment. The red line represents the number of capable donor cells that would be present in the culture based on the assumption that bacteria must grow in order to enter a nongrowing phase and be capable of conjugating. The green line represents the number of bacteria that would be capable of conjugating if one were to apply the growth assumption and molecular regulatory controls that enable only 10% of donor cells to conjugate. The orange line represents the number of bacteria that would be capable of conjugating if one were to apply the growth assumption and molecular regulatory controls that enable only 1% of donor cells to conjugate, and the black line represents the number of capable donor cells if one were to apply the growth assumption and molecular regulatory controls that enable only 0.1% of donor cells to conjugate. The increase at 16 h is caused by an increase (6 × 10⁷ CFU/ml) in the donor population between 8 h and 16 h that is amplified in log scale.

Fate of transconjugants.

Many models assume that transconjugants will become active donor cells. Our data suggest that in both growing and nongrowing cultures this is not necessarily the case. Conjugation with donor cells that were harvested from a growing phase and mixed with recipient cells from a stationary-phase culture produced low conjugation frequencies (Fig. 6). This suggests that E. coli cells containing pUUH239.2 that are in their window of opportunity for conjugation to occur can conjugate with recipient cells that are not in their window of opportunity. However, these transconjugants would not be expected to become donors, as they would likely already be in a nongrowing phase. In a growing culture of E. coli, a potential donor cell is more likely to encounter a nongrowing recipient cell (or other nongrowing donor cell) rather than a recipient that is either growing or transitioning to a nongrowth phase after the culture enters into stationary phase. Thus, many transconjugants formed later in the experiment would not be expected to become donor cells unless the culture was supplied with fresh media. While some growth (and almost certainly conjugation) occurs during stationary phase, in our experiments, the numbers were not significant enough to overcome the plateau.

In addition, in our experiments with growing cultures, transconjugants did not appear to have grown in appreciable numbers. We attribute the lower concentrations of donor cells (relative to recipient cells) to the fitness costs associated with pUUH239.2, not transconjugants growing. During the periods with the largest increase in transconjugants (4 h to 16 h), the growing cultures were in stationary phase, and the generation times were approximately 26 h for donor cells and 28 h for recipient cells. While the number of recipient (and donor) cells did increase during this period, transconjugants would have had to grow faster than donor and recipient cells while the culture was in stationary phase to achieve the observed number of transconjugants (transconjugants at 4 h, 1,912/ml; at 8 h, 11,221/ml; and at 16 h, 20,622/ml). Growth experiments with transconjugants and donor cells showed that their growth curves were almost superimposable (data not shown), suggesting that transconjugant growth behavior is similar to donor cell behavior (the only differences between a transconjugant and a donor cell are the possession of either a blue or yellow fluorescent gene and that transconjugants are resistant to chloramphenicol [CAT]).

Environmental implications.

We examined conjugation in the laboratory under ideal conditions in order to generate quantitative data that provided information on the underlying dynamics of conjugation under growing and nongrowing conditions. Consequently, the full scope of the environmental relevance can be realized only with more studies examining different bacteria, plasmids, and experimental conditions (temperature, solution chemistry, etc.). From an environmental aspect, the results presented here suggest that E. coli possessing pUUH239.2 would have only a short time frame in which to conjugate, even within a suitable host. Given the temperatures at which E. coli is reported to be capable of growing (∼8°C to >42°C), nutrient availability might play a bigger role in regulating conjugation than temperature. Environments with episodic nutrient fluxes could contribute more to conjugation than environments with sustained nutrients over the long term, as the former could result in continued pulses of conjugation, whereas the latter might result in a more sustained plateau. In addition, there is always the possibility of the E. coli conjugating with an environmental bacterium (assuming that plasmid stability is not an issue) in a host or in the environment that might increase the range of growth conditions under which a plasmid such as pUUH239.2 could be passed horizontally (as well as vertically).

Modeling.

The M1 conjugation model (Ω = 1) dramatically overestimated conjugation at times >20 h and incorrectly predicted that all recipient cells would eventually become transconjugants (Fig. S6). The M1 model also greatly underestimated conjugation at times <20 h (Fig. S6). Consequently, the conventional M1 model is clearly not consistent with experimental observations. Furthermore, conjugation models that have been developed for growing conditions cannot readily be applied to nongrowing conditions because they simulate k_c in an analogous fashion to Monod growth and therefore predict a dependency on the substrate concentration (8, 11). Conversely, the M2 model provided a satisfactory description of the conjugation data under growing and nongrowing conditions and in the presence and absence of antibiotics (Fig. 7 and 8 and Table 1).

The M2 model reflects the time dependency of a nonclonal population as it transitions from exponential to stationary phases, and model parameters are physically meaningful. For example, m and σ reflect the mean and standard deviation of conjugation times for a nonclonal population due to differences in growth stage. In addition, the parameter m implicitly accounts for the observed lag time for conjugation. The larger value of σ in the LB cultures versus the 9.1 mM NaCl cultures suggest that conjugation occurred over a longer period in the growing than the nongrowing cultures, and the lower k_c values in growing versus nongrowing cultures suggest that conjugation was more rapid in nongrowing cultures. This is consistent with our hypothesis that in nongrowing cultures all of the cells are forced into a nongrowing phase at the same time and so conjugation occurs rapidly in one large pulse and once the capable donor cells conjugate, there is no longer any conjugation. In growing cultures there is much more variability in the growth stage of subpopulations in the cultures, and therefore, conjugation occurs over a longer period than in nongrowing cultures and conjugation does not occur as a single, rapid pulse.

A constant value of μ_C was needed to describe transconjugant concentrations in the nongrowing culture, and its magnitude was one order higher than either the μ_D or the recipient cell decay rate (μ_R) (Table 1). This suggests that transconjugants were dying more rapidly than either donor or recipient cells, but it is not clear why transconjugants would be more susceptible to death in nongrowing cultures than either donor or recipient cells (the only differences between transconjugants and donor cells are the color of the fluorescent gene and the fact that transconjugants are resistant to CAT). During the periods in which the raw number of transconjugants decreased in nongrowing cultures (∼16 h to 24 h), the standard deviation of the transconjugants was larger than the decrease in transconjugants (16 transconjugants/ml died per hour in 9.1 mM NaCl, but the standard deviation of total transconjugants during this time was 34/ml per hour). Thus, it is possible that the differences in μ represent greater uncertainty in the concentrations of transconjugants instead of transconjugants dying more rapidly than donors and recipients. The modeling of LB+CFX cultures was more problematic due to the complex interplay between conjugation dynamics and survival in the presence of antibiotics like CFX in growing cultures, but the M2 model shows promise for simulating conjugation behavior in natural environments where bacterial populations exhibit cycles of growing and nongrowing conditions. Additional research is warranted to study these effects at different concentrations and for various antibiotic types.

Conclusions.

We examined conjugation in growing and nongrowing cultures of E. coli with an IncFII plasmid and found that conjugation most likely occurs after the growing cells divide and before they transition into a nongrowing phase. This produces a short time span in which E. coli containing pUUH239.2 can conjugate and produces a conjugation plateau as the number of capable donor cells rapidly decreases as the culture enters stationary phase. As a result, many transconjugants cannot become donor cells themselves because they will not be in the correct growth phase in which to act as a donor cell when they receive pUUH239.2. We presented a conjugation model that takes into account conjugation in nonclonal E. coli populations under growing and nongrowing conditions.

MATERIALS AND METHODS

Bacterial strains and plasmids.

pUUH239.2 was provided by Linus Sandegren at Uppsala University, Sweden, in an E. coli K-12 strain (DA14833). The plasmid was originally isolated from a Klebsiella pneumoniae strain associated with a nosocomial outbreak in Uppsala. pUUH239.2 is a 220,884-bp conjugative plasmid belonging to the IncFII group that encodes resistance to multiple antibiotics (e.g., β-lactams, tetracycline, and kanamycin) and a variety of heavy metals (e.g., copper and silver) (52). The plasmid has been fully sequenced and characterized with respect to its ability to be transferred via conjugation, associated fitness costs, and antibiotic and metal concentrations necessary to select for it (52, 53).

E. coli K-12 ER1793 is a streptomycin-resistant and restriction enzyme-deficient strain obtained from New England BioLabs (Ipswich, MA) that was modified to produce a strain that contained a chromosomal blue fluorescent protein (mTagBFP2) and pUUH239.2 (herein referred to as ER1793_mTag/pUUH239.2) and a strain that contained a chromosomal yellow fluorescent protein gene (SYFP2) and a chromosomal chloramphenicol resistance gene (herein referred to as ER1793_SYFP2-Cat). Details on the strain modification have been previously described (25).

Antibiotics.

MIC assays of strains used in conjugation experiments were carried out previously (25) to establish selective concentrations of antibiotics for use in conjugation experiments. The following antibiotics were used to maintain strains and/or used in conjugation experiments: ampicillin sodium salt (AMP; Fisher Scientific, Waltham, MA), cefotaxime sodium salt (CFX; ACROS Organics, Thermo Fisher Scientific, Waltham, MA), kanamycin monosulfate (KAN; Fisher Scientific), gentamicin sulfate (GEN; Sigma-Aldrich, St. Louis, MO), tetracycline hydrochloride (TET; RPI, Mount Prospect, IL), and chloramphenicol (CAT; Fisher Scientific, Waltham, MA).

Conjugation experiments.

ER1793 mTag/pUUH239.2 and ER1793 SYFP2-Cat were grown overnight in separate cultures of 10 ml of LB broth (Fisher Scientific, Waltham, MA) supplemented with 150 μg/ml of CFX and 20 μg/ml of CAT, respectively, at 37°C and ∼200 rpm. Two milliliters of each overnight culture (∼16 h postinoculation) was then inoculated into separate cultures of 48 ml of LB broth (supplemented with 25 μg/ml of CFX for ER1793 mTag/pUUH239.2) and grown at 37°C for approximately 4 to 4.5 h to an optical density at 600 nm (OD₆₀₀) of 0.550, which corresponded to late exponential phase. Cultures were then centrifuged at 3,500 × g at 22°C for 15 min and pellets resuspended in 60 ml of 1 mM NaCl. The OD₆₀₀ was then adjusted with 1 mM NaCl to ensure that both cultures were within an OD₆₀₀ of 0.005 of one another.

Conjugation experiments were initiated by adding 5 ml of ER1793 mTag/pUUH239.2 and ER1793 SYFP2-Cat to 90 ml of LB or 10 mM NaCl (to generate a 9.1 mM NaCl solution) and incubated at 37°C for 24 h at ∼200 rpm with and without CFX. We chose 9.1 mM NaCl solution as the nongrowing medium because previous experiments had found that there was enhanced conjugation (compared to those at 1 mM and 100 mM NaCl) at this solution chemistry (25). Likewise, we chose CFX because previous experiments had shown that E. coli cells containing pUUH239.2 had more conjugation in the presence of CFX (under nongrowing conditions) than other antibiotics we tested (25). All experiments were carried out in triplicate and repeated three times. Cultures were sampled at 0, 0.5, 1, 1.5, 2, 4, 8, 16, and 24 h. After incubation at 37°C, 1 ml of each culture in 250-μl aliquots was plated onto four LB agar plates (Fisher Scientific, Waltham, MA) supplemented with TET (20 μg/ml) and CAT (20 μg/ml) and incubated for ∼40 h at 37°C. Dilutions (1:100 to 1:10,000) of each culture were read on an Attune NxT flow cytometer (Thermo Fisher, Waltham, MA) to obtain the concentrations of ER1793 mTag/pUUH239.2 and ER1793 SYFP2-Cat in each culture. Traditional plate counts were performed to verify flow cytometry bacterial concentrations. For experiments involving the mixing of cultures at different time intervals, cultures were harvested as described above and then allowed to sit on the countertop (∼22°C) for up to 8 h before inoculation into experimental cultures of 9.1 mM NaCl not supplemented with antibiotics. For logistical reasons, these experiments were only carried out in duplicate and were repeated twice. Potential transconjugants that grew on the LB agar plates supplemented with TET and CAT were confirmed by restreaking onto separate LB agar plates supplemented with AMP (100 μg/ml), KAN (50 μg/ml), CFX (25 μg/ml), TET (20 μg/ml), CAT (20 μg/ml), TET (20 μg/ml) plus CAT (20 μg/ml), and GEN (25 μg/ml). Successful transconjugants fluoresced yellow and were able to grow on all plates except the LB agar plates supplemented with GEN. Any potential transconjugant that failed to grow on all plates except GEN was regarded as not being a transconjugant. We examined our experimental protocol to determine if placing growing cultures of LB (∼171 mM NaCl) into 1 mM NaCl as per our harvesting procedure may have lysed cells and released pUUH239.2 into solution, causing unintended transformation to occur, or if the hypoosmotic shock induced a response (stress response, altering the surfaces of the bacteria, etc.) that may have enabled more (or less) conjugation to occur. We were unable to induce transformation using our experimental protocol or find any evidence that hypoosmotic shock significantly changed the amount of transconjugants produced.

Conjugation frequency (F_c) for all experiments was determined by dividing the average number of transconjugants by the total number of bacteria:

$$F_c=\frac{C_C}{C_D+C_R+C_C}$$ (1)

where C_C (N L⁻³; “N” and “L” indicate the number of microbes and length, respectively) is the concentration of transconjugants, C_D (N L⁻³) is the concentration of donor bacteria (ER1793 mTag/pUUH239.2), and C_R (N L⁻³) is the concentration of recipient bacteria (ER1793 SYFP2-Cat). The concentration of transconjugants (the numerator in equation 1) was determined by plating onto selective media as described above. The total concentration (donors, recipients, and transconjugants, the denominator in equation 1) was determined via flow cytometry. The flow cytometer could not differentiate recipient cells from transconjugants, and by default, recipient concentrations determined by flow cytometry included both recipient bacteria and transconjugants.

Plasmid stability tests were conducted to determine the stability of the plasmid in donor and transconjugants in LB and 9.1 mM NaCl. The detailed methodology and results can be found in the Supplemental Methods and Table S1.

Modeling.

Aqueous-phase concentrations of donor, recipient, and transconjugant bacteria as a function of time were simulated for our batch experiments by numerically solving the following mass balance equations:

$$\frac{d{C}_D}{\mathit{dt}}={\mu }_D{\psi }_D{C}_D$$ (2)

$$\frac{d{C}_R}{\mathit{dt}}={\mu }_R{\psi }_R{C}_R-k_c\Omega C_R{C}_D$$ (3)

$$\frac{d{C}_C}{\mathit{dt}}={\mu }_C{\psi }_C{C}_C+k_c\Omega C_R{C}_D$$ (4)

where k_c (L³ N⁻¹ T⁻¹) (where “T” indicates time) is the conjugation efficiency rate, μ (T⁻¹) is the survival rate coefficient, ψ determines the survival model (logistic growth or first-order decay), Ω determines the conjugation model, and subscripts D, R, and C on μ and ψ indicate expressions for donor, recipient, and transconjugant cells, respectively. The logistic model (see, e.g., references 54 and 55) was employed under growing conditions by setting ψ_i = (1 − C_i/C_iMAX), where C_iMAX (N L⁻³) is the maximum concentration in the aqueous phase of donor, recipient, or transconjugant cells (subscript i equals D, R, or C, respectively). The value of ψ_i equals −1 when first-order decay is accounted for during nongrowing conditions. The second term on the right-hand side of equations 3 and 4 account for conjugation using the mass-action kinetic model of Levin et al. (7). Equations 2 to 4 assume that transconjugants do not act as donors and the plasmid loss rate can be neglected over the experimental duration.

Several different functional forms for k_c have appeared in the literature (7, 8). In this work, two different formulations for conjugation were considered. The first approach (called the M1 model) assumed a constant conjugation rate at a maximum value (Ω = 1). The second approach (called the M2 model) assumed that there is a normal probability density function of donor cells in the proper state (e.g., growth phase and nonrepressed conjugation genes) to undergo conjugation as a function of time as

$$\Omega =\frac{1}{\sigma \sqrt{2\pi }}\exp \hspace{0.17em}\left(-\frac{{\left(t-m\right)}^2}{2{\sigma }^2}\right)$$ (5)

where m (T) and σ (T) are the mean and standard deviation of the normal distribution with respect to time. The value of m determines the average time when conjugation is initiated and accounts for a lag phase. The parameter σ determines the conjugation window or the duration that conjugation occurs. Note that values of m would need to be related to the growth conditions if multiple cycles of growth were considered in conjugation experiments.

Equations 2 to 5 were implemented and numerically solved using the COMSOL Multiphysics software (COMSOL, Inc., Palo Alto, CA). Growth parameters μ_D, μ_R, C_DMAX, and C_RMAX were inversely fitted to the analytic solution of the logistic growth model (ψ_i = 1 − C_i/C_iMAX) using a nonlinear least-squares optimization algorithm (56). Values of μ_D and μ_R under nongrowing conditions (ψ_i = −1) were determined from experimental values of C_D and C_R, respectively, by inverse optimization to the solution to the first-order decay equation using Microsoft Excel 2010 (Microsoft, Redmond, WA). The values of k_c, m, σ, and μ_C for the M2 model were estimated by visually fitting the COMSOL simulation results to the measured conjugation data by manually adjusting these parameters. Note that parameters m, σ, k_c, and μ_C reflect the average time when conjugation is initiated (e.g., time of maximum slope), the duration that conjugation occurs, the peak transconjugant concentration, and the exponential decay rate observed in the plateau phase, respectively. The value of k_c in the M1 model was similarly estimated when Ω was 1.

Statistics.

Two-sample t tests assuming unequal variances were carried out using Microsoft Excel 2010 (Microsoft, Redmond, WA). P values of <0.05 were considered significant.