Impacts of Heterogeneous Host Densities and Contact Rates on Pathogen Transmission in the Channel Island Fox (Urocyon littoralis)

Abstract

Diseases threaten wildlife populations worldwide and have caused severe declines resulting in host species being listed as threatened or endangered. The risk of a widespread epidemic is especially high when pathogens are introduced to naive host populations, often leading to high morbidity and mortality. Prevention and control of these epidemics is based on knowledge of what drives pathogen transmission among hosts. Previous disease outbreaks suggest the spread of directly transmitted pathogens is determined by host contact rates and local host density. While theoretical models of disease spread typically assume a constant host density, most wildlife populations occur at a variety of densities across the landscape. We explored how spatial heterogeneity in host density influences pathogen spread by simulating the introduction and spread of rabies and canine distemper in a spatially heterogeneous population of Channel Island foxes (Urocyon littoralis), coupling fox density and contact rates with probabilities of viral transmission. For both diseases, the outcome of pathogen introductions varied widely among simulation iterations and depended on the density of hosts at the site of pathogen introduction. Introductions into areas of higher fox densities resulted in more rapid pathogen transmission and greater impact on the host population than if the pathogen was introduced at lower densities. Both pathogens were extirpated in a substantial fraction of iterations. Rabies was over five times more likely to go locally extinct when introduced at low host density sites than at high host-density sites, leaving an average of >99% of foxes uninfected. Canine distemper went extinct in >98% of iterations regardless of introduction site, but only after >90% of foxes had become infected. Our results highlight the difficulty in predicting the course of an epidemic, in part due to complex interactions between pathogen biology and host behavior, exacerbated by the spatial variation of most host populations.

INTRODUCTION

The ecology of disease in wildlife populations is complicated and often unpredictable, making the management of dangerous health risks an ongoing and adaptive process. One of the primary determinants of infectious disease dynamics is the rate of pathogen transmission from infectious to susceptible hosts (McCallum et al. 2001). For pathogens that are passed directly between hosts, the rate of transmission is strongly affected by the frequency, duration, and type of contact between infected hosts and conspecifics. How frequently potentially disease spreading contacts occur varies with the number of neighboring conspecifics and the amount of contact those neighbors have with one another (Woodroffe 1999). Neighbor interactions in turn depend on the density of the population, home range sizes, and the amount of overlap between home ranges (McCallum et al. 2001, Sanchez and Hudgens 2015), all of which vary across space in wild populations.

Host densities and contact rates among neighbors are likely to vary spatially due to differences in the distribution of required habitats and resources. Vegetation and habitat types are often patchy in distribution, leading to areas that contain more favorable habitat types being used more frequently or supporting higher population densities than areas with less favorable habitat types (Lawes and Nanni 1993, Simcharoen et al. 2008, Turner 2009). Similarly, resources such as food and mates are rarely distributed uniformly. The size of home ranges and the degree of overlap individuals tolerate with their neighbors can vary with the density of resources within the home range (Dill et al. 1981, Erlinge et al. 1990, Marshall and Cooper 2004). Interspecific competition for resources also influences density (Vucetich and Creel 1999, Berger and Gese 2007) through changes in the number of neighboring home ranges an individual has (Woodroffe et al. 2006, Sanchez and Hudgens 2015) and the amount of contact among neighbors (Ramsey et al. 2002, Dantzer et al. 2012, Sanchez and Hudgens 2015).

Differences in host density and spatial distribution alter pathogen transmission rates by influencing how hosts move and interact with one another in their environment (Ramsey et al. 2002, Ji et al. 2005, Creech 2011). Hosts with spatially heterogeneous densities often have spatially heterogeneous interaction rates with conspecifics as well, leading to variable disease transmission rates in different areas of the host range (Böhm et al. 2009). Previous disease outbreaks and epidemiological modelling have demonstrated the important role that host behaviors play in disease spread (Dobson 1988, Loehle 1995, Woolhouse et al. 1997), and the heterogeneous transmission rates and spatially aggregated occurrences of infection that result from variation in host behavior (Deal et al. 2000, Bjørnstad et al. 2002, Keeling 2005, Hamede et al. 2009). Although studies of species living in large social groups have provided information on how group structure can determine transmission dynamics (Craft et al. 2008, Böhm et al. 2009, Almberg et al. 2012), it remains unclear how spatially variable host densities affect disease dynamics in species which are solitary or live primarily in small social groups, such as male-female dyads. Large social groups with a high degree of contact among hosts are conducive to continued pathogen transmission within a group, maintaining disease until a less frequent inter-group contact occurs to further spread the pathogen spatially through the larger host population (Craft et al. 2008, Böhm et al. 2009, Almberg et al. 2012). However, solitary individuals or small groups plausibly only ever encounter conspecifics at lower rates similar to the inter-group contacts of more social species, potentially increasing the risk of local pathogen extinction (“fadeout”), especially in populations with variable host densities.

Stochastic models show that the likelihood of disease persistence decreases as spatial heterogeneity of hosts increases, and environmental and demographic stochasticity can determine pathogen success when the number of infected hosts or the total susceptible host population size is small (Hagenaars et al. 2004, Lloyd-Smith et al. 2005). As an epidemic proceeds, some hosts will already be infected or immune, and this reduction in the local density of susceptible hosts may lead to pathogen fadeout. Vaccination and culling are two management methods employed to reduce the density of susceptible hosts with the goal of reducing contacts that could potentially transmit pathogens in order to prevent disease outbreaks and cause pathogen fadeout. However, models simulating these methods have demonstrated mixed effects on probability of disease fadeout, in part due to the increased contact of hosts that occurs after culling as hosts encounter new neighbors and establish new territories (Smith and Cheeseman 2002, Haydon et al. 2006, Hampson et al. 2009).

The history of the island fox (Urocyon littoralis) illustrates the significant impacts a disease outbreak can have on a host population, and the importance of host contact and spatial distribution in determining the outcome of an epidemic. The island fox is found on six of the eight Channel Islands off the coast of southern California. In 1999, the Santa Catalina Island subspecies suffered an ~85% decline in population size due to an epidemic of canine distemper virus (CDV), resulting in the subspecies being federally listed as critically endangered (Timm et al. 2009, Munson 2010). Santa Catalina Island is divided into two distinct land masses connected by a narrow isthmus that few foxes have been observed to cross (Timm et al. 2009). It was estimated that the fox population on the eastern section of the island declined by ~95% by the end of the epidemic, while the population estimates on the western section were comparable before and after the epidemic (Timm et al. 2009). The lack of reduction in population size west of the isthmus indicates that the epidemic ended when the density of foxes on the eastern side of the island became so low that CDV transmission could not continue due to a lack of susceptible hosts (Timm et al. 2009).

CDV and rabies are considered the primary disease threats to all six island fox populations (Coonan 2003, Vickers and Clifford 2009), and a subset of foxes on each of the Channel Islands are vaccinated against these diseases annually. Developing accurate predictions of how these high-risk pathogens would spread through a naive population of island foxes, and how best to implement management methods such as vaccination to prevent and control epidemics, has become the focus of island epidemic response plans (Hudgens et al. 2011) and a key component of the recent reclassification of the Catalina Island subspecies to “threatened” and the delisting of three subspecies formerly listed as “endangered” under the Endangered Species Act (U.S. Fish and Wildlife Service 2016).

To evaluate the impacts of spatial variation in host density on the spread of an introduced pathogen, we created a spatially explicit, individual-based, discrete-time, stochastic epidemiological model simulating the spread of rabies and CDV in island foxes. On San Clemente Island (SCI), there is substantial variation in fox density over short distances, with corresponding variation in home range size and contact rates (Sanchez and Hudgens 2015). Pair-wise contact rates are positively correlated with the amount of overlap between home ranges, and the total amount of contact each fox experiences with all of its neighbors is greater in areas of high fox density due to the positive relationship between density and the number of overlapping home ranges (Sanchez and Hudgens 2015). The model simulated the spread of disease initiated at two likely points of introduction that differed in local fox densities and predicted how quickly disease would across the island. Pathogen introduction to SCI is expected to be most likely on the northern tip of the island where fox density is high (Fig. 1). There are many potential routes of introduction to this region of the island (town, airport, and harbor) where humans and supplies are transported to and from the mainland on a regular basis (personal communication, M. Booker 2010. Naval Base Coronado Environmental Department, P. O. Box 357088, San Diego, CA 92135–7088). The southern end of the island is also considered at risk for pathogen introduction due to a large, unoccupied area with many beaches not regularly patrolled by the U. S. Navy and with access by land restricted (Fig. 1). This area has a low to medium-density of foxes and civilian boaters have been known to come ashore here with domestic dogs (Canis lupus familiaris), which may expose foxes to canine pathogens.

Figure 1.

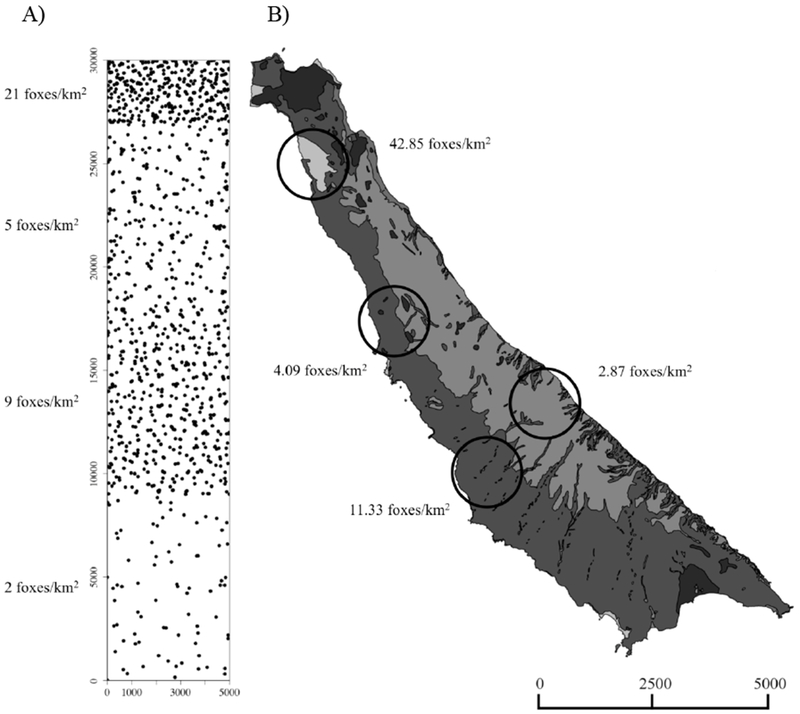
Maps of San Clemente Island (SCI) illustrating the distribution of fox densities. SCI depicted by the disease model (A), with dots representing the simulated home range center of each fox. Habitat map of SCI with circles marking study sites (B) where foxes were fitted with proximity collars to estimate model parameters (Sanchez and Hudgens 2015). Scales are in meters.

We used this model of rabies and CDV spread in island foxes to explore how host density at the site of pathogen introduction might affect the course of an epidemic. The large variation in island fox densities on SCI, coupled with the presence of fewer mammalian host species compared to mainland ecosystems, makes island foxes an excellent study system for exploring the effect of local host density and contact rates on the progression of an epidemic. In contrast to disease models which only infer contact among hosts, the model presented here was parameterized using empirical measurements of host density, home range size and distribution, and contact rates (Sanchez and Hudgens 2015).

Rabies and CDV were chosen as model pathogens because they were considered the pathogens most likely to be introduced to island foxes due to the continual exposure of foxes to mainland domestic dogs (both legally and illegally). While both pathogens are directly transmitted through close contact between hosts, they differ in their mode of transmission and duration of infectiveness. Rabies has a longer latency period and shorter infectious period relative to CDV, resulting in a shorter window of time for the virus to be transmitted to an uninfected host and potentially a lower risk of being transmitted before the infected host dies (Table 1).

Table 1.

Parameter values used to model the spread of rabies and canine distemper virus (CDV) in island foxes on San Clemente Island, California. MDS = maritime desert scrub. N ($\stackrel{‒}{x}$, variance) = normal distribution from which parameter value was sampled.

Parameter	Value		Source
Home range radius (meters; based on fox density)	High density: N (252.31, 2.28) Medium-high density: N (282.09, 1.56) Medium-low density: N (504.63, 2.02) Low density: N (713.65, 1.59)		Field data (Sanchez and Hudgens 2015)
Proportion of home range overlap	≤ 0.75		Maximum overlap between non-related pairs (Sanchez and Hudgens 2015)
Contact rate	Rabies (number of contacts/day): N (0.02+0.88m, 0+0.25m) CDV (seconds in contact/day): N (1.42+58.57m, 0+2594.03m) m = home range overlap		Field data (Sanchez and Hudgens 2015)
Transmissibility	Rabies: 0.49c c = contact rate	$CDV:N\left(\frac{1}{1+e^{-(0.12+0.02c)}},\frac{1}{e^{-(0.42c)}}\right)$	Farrell et al. 1955, Hampson et al. 2009
Transition probabilities1	Rabies: latent to infectious class: 1/42 (max 90 days)      infectious to dead class: 1/4 (max 14 days) CDV: latent to infectious class: 1/5 (max 14 days)     infectious to dead class (no recovery): 1/21 (max 60 days)     infectious to dead class (recovery): 1/60 (max 90 days)		Gorham and Brandly 1953, Gillespie 1962, Appel 1987, Blancou et al.1991, Kitala et al. 1997, Greene and Vandevelde 2012, Rhodes et al. 1998, Gorham 1999, Deem et al. 2000, Headley and Graça 2000, Hampson et al. 2009
Background transmission rate2	1 − (1 − f )(# of infectious foxes) f = 0.000001 = probability per time-step of pathogen transmission between two foxes with non-overlapping home ranges		Reed-Frost equation; Abbey 1952

¹Transition probabilities calculated as the average number of days a fox is in each disease class.

²During the 206-day study period (Sanchez 2012) only one fox out of 40 made a foray outside its study site. The probability of transmission between a focal fox and a fox on a foray was set to the arbitrarily low value of 1% because contact rates among foxes outside their home ranges are not known. The resulting daily risk each focal fox had of encountering a fox on a foray outside its home range and contracting a pathogen was approximately (1 ÷ 40 ÷ 206) × 0.01 ≈ 0.000001.

Modeling these two pathogens allowed us to ask the following: How does host density at the site of pathogen introduction influence the risk of an epidemic occurring and the epidemic outcome for each pathogen? Do pathogens with different transmission and infection patterns, such as different latency times and durations of infectivity, differ in the threat they pose to fox populations? We hypothesize that the larger amount of total contact per fox in high-density areas will result in faster rates of pathogen transmission, increased risk of an epidemic, and lower rates of disease fadeout than in areas with low fox density, and that host density at pathogen introduction site will have different effects on epidemic outcome between the two pathogens.

METHODS

Previously measured island fox densities, home ranges, and contact rates (Sanchez and Hudgens 2015) were used to inform a spatially explicit, individual-based, discrete-time, stochastic model of disease spread to address questions about how fox density might affect epidemic outcome under different conditions of disease introduction. A simplified island landscape was created using Program R (R Foundation for Statistical Computing, Vienna, Austria, <http://www.R-project.org>) to simulate the spread of infectious disease through the SCI fox population. To evaluate how fox density affects the spatial spread of disease, infection was introduced into one simulated home range located in either a high or low-density area of the island that was considered to have a high risk of pathogen introduction.

The model island approximated the dimensions of SCI (5 km × 30 km) and contained an average of 1,000 fox home ranges during each simulation, approximating the currently estimated fox population. The island was divided into four blocks, with each block reflecting the density of foxes observed at four study sites where fox contact rates had been previously measured (Sanchez and Hudgens 2015; Fig. 1). From north to south, the blocks were “high” density representing sand dune habitat and developed areas (simulated 21 foxes/km²), “medium-low” density representing maritime desert scrub vegetation on gently sloping marine terraces (simulated 5 foxes/km²), “medium-high” density representing maritime desert scrub vegetation with rugged canyons and drainages (simulated 9 foxes/km²), and “low” density representing the grasslands dominating the SCI’s central plateau (simulated 2 foxes/km²; Fig. 1A). The relative proportions of the different habitat types roughly matched the relative proportions of each habitat type on SCI. Each habitat block was a rectangular section of the simulated island, encompassing the entire island from east to west, and a subset of the island from north to south (Fig. 1A).

As described in Sanchez and Hudgens 2015, foxes were radio-transmittered with collars containing VHF transmitters and proximity loggers at four sites of differing fox densities across SCI (Fig. 1B), allowing for the simultaneous measurement of home range size, home range overlap, and the frequency and duration of contacts between neighbors. The relationships between these variables were used to parameterize the simulation model. Simulated fox home ranges were circular, with the center of the home range placed at a randomly selected xy-coordinate, and the radius selected from a normal distribution corresponding to the habitat block the center of the home range was located in (Table 1). The resulting average home range sizes were 0.20 km² for the high-density block, 0.25 km² for medium-high density, 0.80 km² for medium-low density, and 1.60 km² for low-density blocks. Although the target density of foxes changed abruptly from one habitat block to another, there was a minor density gradient at habitat borders created by the home ranges of foxes centered near the edges of blocks that extended into the neighboring block.

Simulated home ranges were restricted to overlap ≤75%, the maximum degree of overlap observed between non-related fox pairs on SCI (Sanchez and Hudgens 2015). Mates and family members (“related pairs”) are known to have greater home range overlap and orders of magnitude higher rates of contact than unrelated pairs (Crooks and van Vuren 1996, Roemer et al. 2001, Ralls et al. 2013, Sanchez and Hudgens 2015). However, for each fox, the proportion of neighboring home ranges that might belong to related animals is not known. Therefore, we simplified the simulated fox population by assuming all individuals were unrelated. The exclusion of related pairs should result in slower pathogen spread and a lower risk of an epidemic in our simulations than might occur in reality.

A daily contact rate between each pair of foxes was sampled from a normal distribution (Table 1) with a mean and variance generated from the regression of SCI fox home range overlap and contact rates among non-related pairs (Sanchez and Hudgens 2015). The mean of the contact rate distribution was determined by the regression line of home range overlap and contact rates. The variance of the distribution was determined by regressing the squared residual contact rates from the previous regression against home range overlap. The intercepts of both regressions were constrained to be nonnegative to reflect the impossibility of negative contact rates.

Rabies and CDV can present with variable neurological signs including increased activity, lethargy, restlessness, paralysis, altered activity cycles, or no change in behavior whatsoever (Andral et al. 1982, Appel 1987, Rupprecht et al. 2001, Williams 2001). We made the simplifying assumption that contact rates of infected foxes would, on average, be the same as uninfected foxes because it is unknown what proportion of infected animals will display any particular disease sign.

Foxes may come into contact with non-neighboring animals during juvenile dispersal, long distance forays outside their home ranges, or when home ranges shift as foxes die and home ranges are left unoccupied (JS and BH personal observations, Roemer et al. 2001). Although long distance forays are rare, even a low level of long-distance transmission risk could have dramatic effects on epidemic outcome by moving pathogens from areas with low local host density to areas with high local host density. In order to represent unpredictable long-distance movements, all simulated foxes were exposed to a low-level risk of infection even if they were not adjacent to an infected home range (Table 1). This background transmission rate was based on the number of long-distance forays observed in SCI foxes and scaled with the number of infectious foxes in the population. Similar techniques have been used in disease models when host contact behaviors and movements are not known or not adequately quantified (Daley and Gani 1999, Vynnycky and White 2010).

At each time-step, the infection risk for each susceptible fox was calculated based on the contact it had with adjacent infected foxes, the background transmission risk from all infected foxes across the island, and virus transmissibility (i.e., the probability of pathogen transmission during each adequate contact between a susceptible and infectious host; Table 1). The disease status of every fox was then updated to susceptible, latent, infectious, or dead. Susceptible animals were those that are capable of becoming infected with a pathogen and are not protected by native immunity or vaccination. Latent animals had been infected with a pathogen but were not yet capable of transmitting the pathogen to other hosts, whereas animals in the infectious class were capable of infecting susceptible animals.

Each simulation consisted of 365 daily time-steps, and 100 replicate iterations were performed for each of four treatments: introduction of rabies into the high fox density region of the island, introduction of rabies into the low fox density region of the island, introduction of CDV into the high fox density region of the island, and introduction of CDV into the low fox density region of the island. Once a fox was infected with a pathogen, it entered the latent class for an average of 42 days for rabies and 5 days for CDV (Table 1). The fox then entered the infectious class for an average of 5 days for rabies and 21 days for CDV. It is unrealistic that the latent and infectious periods of such virulent diseases in highly susceptible hosts last indefinitely (Deem et al. 2000, Rupprecht et al. 2001, Williams 2001), therefore, animals infected with rabies were constrained to be latent for a maximum of 90 days and infectious for a maximum of 14 days, and animals infected with CDV were latent for a maximum of 14 days and infectious for a maximum of 60 days (Table 1). All infected animals eventually died.

Transmission of rabies viruse depends on a susceptible host encountering an infectious host during a short period of infectivity before death, and transmission risk is assumed to increase with the frequency of contact because each new encounter carries the possibility that the infected fox will have entered the furious form of the disease (characterized by excitable, aggressive behavior; Rupprecht et al. 2001) and/or not recognize a previously well-established neighbor as they approach, leading to an aggressive territorial encounter. Therefore, contact rates between foxes were based on the regression of home range overlap with the observed number of contacts per day in SCI foxes for rabies simulations (Table 1). In contrast, CDV is transmitted via aerosol or contact with bodily fluids, and the duration of time that two foxes are in close contact will increase the likelihood of exchanging respiratory secretions. We reflect this mechanism of transmission in CDV simulations by basing transmission on the regression of home range overlap with the amount of time in contact per day (Table 1). Transmissibility and the length of latent and infectious periods were obtained from the literature describing rabies and CDV in mainland species such as gray fox (Urocyon cinereoargenteus), mink (Neovison vison), ferret (Mustelaputorius furo), and domestic dogs (Table 1).

Simulation output included the percentage of the original susceptible population that remained uninfected at the end of one year, the percentage of simulation iterations resulting in epidemic fadeout, the number of secondary infections caused by the first infected animal during each simulation (basic reproductive number, R₀), and the average number of new infections caused by an infectious animal over the course of the epidemic (effective reproductive number, R_e; calculated as the number of new infections per infectious fox per time step multiplied by the duration of the average infectious period). In order for an epidemic to occur, the first infected host must transmit a pathogen to at least one other host before it dies (R₀ ≥ 1). If subsequent infected hosts continue to transmit the pathogen to an average of ≥1 other host (R_e ≥ 1), the epidemic will persist (Heesterbeek and Roberts 1995, Keeling 2005). For each treatment, we calculated the median and 25% and 75% quartiles (Q1 and Q3, respectively) of each output variable using the results from all 100 iterations. Medians and quartiles were chosen to summarize the data because the distribution of output variables was often highly skewed. We used a Kolmogorov-Smirnov test to determine if the distribution of each output variable differed among treatments. When multiple Kolmogorov-Smirnov tests were compared, a Dunn-Šidák correction was performed to reduce the likelihood of Type 1 error. We used chi-squared tests to evaluate differences in the percentage of iterations resulting in epidemic fadeout between treatments.

Sensitivity (s) and elasticity values (e) were calculated to test the robustness of model predictions to uncertain parameters, evaluate assumptions made to simplify the model, and help interpret model results. Each model treatment was re-run with one parameter altered at a time, and the results were compared to the primary model to determine how sensitive model outcomes were to changes in these parameters (Table 2). We considered simulations to be sensitive to parameters if elasticity values had an absolute value ≥0.5.

Table 2.

Sensitivity and elasticity analyses for the simulated spread of rabies and canine distemper virus (CDV) in San Clemente Island foxes. Sensitivity (s) is the proportional difference in output between simulations with new parameter value and simulations with baseline parameter value. Elasticity (e) is the proportional difference in output value divided by the proportional difference in parameter value. Bolded values indicate parameters with |e| ≥ 0.5.

			Low density introduction				High density introduction
			Percent of original susceptible population uninfected at day 365		Percent of simulations resulting in epidemic fadeout		Percent of original susceptible population uninfected at day 365		Percent of simulations resulting in epidemic fadeout
	Parameter	Change in parameter value	s	e	s	e	s	e	s	e
Rabies	Contact	+ 50%	−3.3	−0.1	−36.8	−0.7	−14.7	−0.3	−14.3	−0.3
		− 50%	3.8	−0.1	121.1	−2.4	47.5	−1.0	385.7	−7.7
	Transmissibility	+ 50%	0.7	0.1	18.4	3.0	0.0	0.0	0.0	0.0
		− 50%	1.8	−0.2	31.6	−3.9	12.8	−1.6	157.1	−19.3
	Background	Double	0.4	0.0	−5.3	−0.1	12.6	0.1	142.9	1.4
	Transmission Reate	Remove	−1.1	0.0	2.6	0.0	17.2	−0.2	100.0	−1.0
	Latent Period	+ 50%	1.8	0.0	18.4	0.4	26.3	0.5	−14.3	−0.3
		− 50%	−1.6	0.0	52.6	−1.1	−24.2	0.5	100.0	−2.0
	Infectious Period	+ 50%	0.7	0.0	15.8	0.3	3.2	0.1	100.0	2.0
		− 50%	2.2	0.0	47.4	−0.9	37.3	−0.7	342.9	−6.9
CDV	Contact	+ 50%	−39.6	−0.8	2.0	0.0	−5.3	−0.1	1.0	0.0
		− 50%	8.9	−0.2	−3.1	0.1	17.4	−0.3	1.0	0.0
	Transmissibility	+ 50%	−40.5	−0.8	−1.0	0.0	−6.5	−0.1	0.0	0.0
		− 50%	−27.9	0.6	2.0	0.0	−6.7	0.1	1.0	0.0
	Background	Double	10.6	0.1	2.0	0.0	−14.2	−0.1	1.0	0.0
	Transmission Rate	Remove	1214.5	−12.1	−13.3	0.1	78.8	−0.8	−9.1	0.1
	Latent Period	+ 50%	−23.4	−0.5	−10.2	−0.2	−0.1	0.0	−4.0	−0.1
		− 50%	−7.0	0.1	1.0	0.0	−3.3	0.1	1.0	0.0
	Infectious Period	+ 50%	−53.5	−1.1	−20.4	−0.4	−4.9	−0.1	−10.1	−0.2
		− 50%	−1.6	0.0	2.0	0.0	67.4	−1.3	1.0	0.0
	Recovery Rate	50%	−20.1	0.0	−78.6	0.0	−21.2	0.0	−93.9	0.0
		10%	−26.9	0.0	−55.1	−0.1	−13.5	0.0	−44.4	0.0

Based on the high fox mortality observed during the Santa Catalina Island CDV epidemic, primary model treatments do not include CDV recovery, and all infected foxes eventually die. However, island foxes exhibit serologic evidence of exposure to a CDV strain that is suspected to be low pathogenicity and island-fox adapted (Clifford et al. 2006), and recovery from CDV infection and subsequent immunity has been reported in mainland canids (Reinhard and Rausch 1955, Appel 1987). In order to test the robustness of model predictions to our assumption of no recovery, we performed additional sensitivity analyses, running additional simulations of CDV including a recovered class of foxes. The recovered class consisted of animals that contracted the disease and survived, thereby developing life-long immunity. We tested two recovery rates, 10% and 50%, based on established recovery rates for mink (Gorham and Brandly 1953, Gorham et al. 1972) and domestic dogs (Reinhard and Rausch 1955, Appel 1987). Domestic dogs generally continue to shed CDV after they recover from clinical disease, and this longer infectious period for recovering animals was incorporated into treatments that included recovery ($\stackrel{‒}{x}=60$ days, max. = 90 days; Appel 1987, Greene and Vandevelde 2012). We did not model rabies recovery because rabies is almost always fatal to mammals, and in rare instances of apparent recovery the data is often incomplete (Rupprecht et al. 2001, Warell and Warell 2004).

RESULTS

Rabies

Rabies introduced into areas with low fox densities typically moved slowly through the population and left the majority of animals uninfected at the end of one year (median = 95.9%, Q1 = 90.9%, Q3 = 98.7%; Fig. 2A, B). In contrast, introductions in areas with high fox densities typically spread faster, resulting in fewer animals left uninfected (median = 56.4%, Q1 = 48.0%, Q3 = 63.2%; D = 0.87, P < 0.001; Fig. 2C, D). Introductions into low-density sites were more likely to experience epidemic fade-out than were introductions to high-density sites (38.0% ± 9.5% vs. 7.0% ± 5.0%, respectively; ${\chi }_1^2=16.3$, P < 0.001). For iterations in which fadeout occurred, the median percentage of foxes remaining uninfected was >99% regardless of introduction site.

Figure 2.

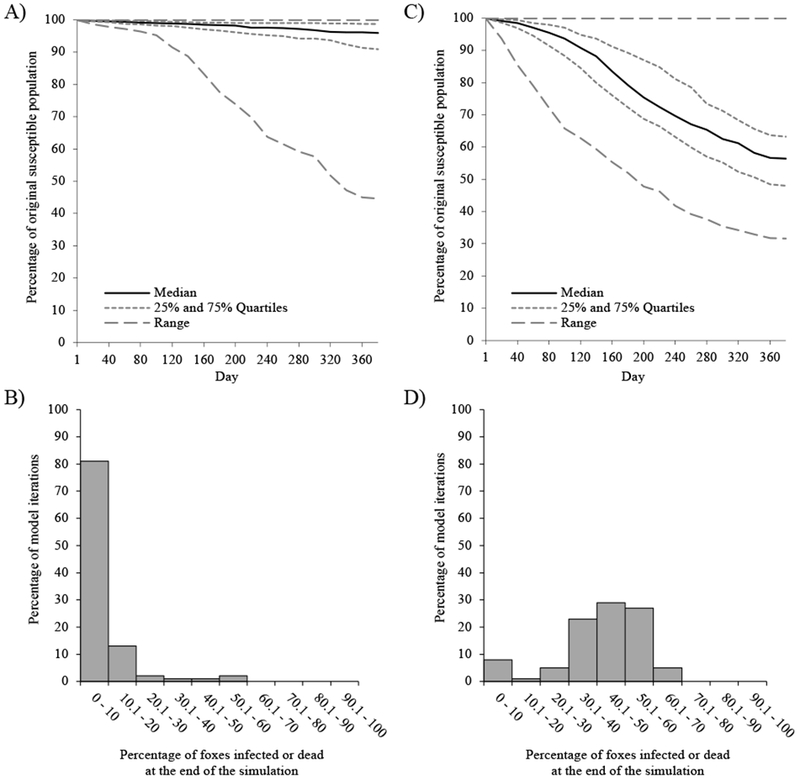
Model simulation results of rabies introduction to areas of San Clemente Island with low (A, B) or high (C, D) fox density. Line graphs show the percentage of the original susceptible fox population remaining uninfected during each day of the simulation after rabies was introduced into an area of the island with low (A) or high (C) fox density. Histograms show the percentage of model iterations that resulted in a given percentage of the original susceptible fox population being infected or dead at the end of the one-year simulation when rabies was introduced to an area of low (B) or high (D) fox density, demonstrating the variability of epidemic severity.

Initial rates of rabies spread (R₀) were similar for introductions at both low-density sites (median = 2.0, Q1 = 0.0, Q3 = 4.0) and high-density sites (median = 2.0, Q1 = 1.0, Q3 = 4.3; D = 0.09, P = 0.813). While introductions at both sites typically resulted in rabies successfully invading the population and causing at least one secondary infection (R₀ > 1), only outbreaks in high-density sites experienced sustained disease spread (R_e > 1). R_e at high-density pathogen introduction sites (median = 1.2, Q1 = 1.1, Q3 = 1.3) was higher (D = 0.80, P < 0.001) than at low-density sites (median = 0.4, Q1 = 0.3, Q3 = 0.7).

Simulation results were sensitive to different parameters depending on both the measured effect and point of introduction. When rabies was introduced to areas of low fox density, the percentage of the original susceptible population remaining uninfected at the end of one year was robust to changes in all parameters (Table 2). When rabies was introduced to areas of high fox density, the percentage of the original susceptible population remaining uninfected at the end of one year was sensitive to reductions in fox contact rates, transmissibility, and infectious period, and changes in the length of the latent period (Table 2). The percentage of iterations resulting in epidemic fadeout when rabies was introduced into low fox densities was sensitive to changes in contact rates and transmissibility, and reductions in the length of the latent and infectious periods (Table 2). The percentage of iterations resulting in epidemic fadeout when rabies was introduced into high fox densities was sensitive to reductions in fox contact rates, transmissibility, and latent period, and changes in the background transmission rate and the length of infectious period (Table 2).

Canine Distemper

CDV introduction at both low and high-density sites resulted in a rapid and drastic decline in the percentage of uninfected foxes. This decline continued until day 140-180, at which point the infection rate slowed and the percentage of susceptibles remaining plateaued (Fig. 3A, C). At the end of one year, slightly more of the original susceptible population remained uninfected when CDV was introduced in low-density areas (median = 6.3%, Q1 = 3.7%, Q3 = 94.2%) compared to high densities (median = 4.7%, Q1 = 3.8%, Q3 = 7.5%; D = 0.42, P < 0.001; Fig. 3). However, there was more variation in model outcome when CDV was introduced at low-density sites, with the percentage of susceptible foxes remaining after one year having a bimodal distribution with peaks at <10% and >90% (Fig. 3B). Simulations with CDV introduced to high-density sites also had a second peak at <10%, albeit much smaller (Fig. 3D).

Figure 3.

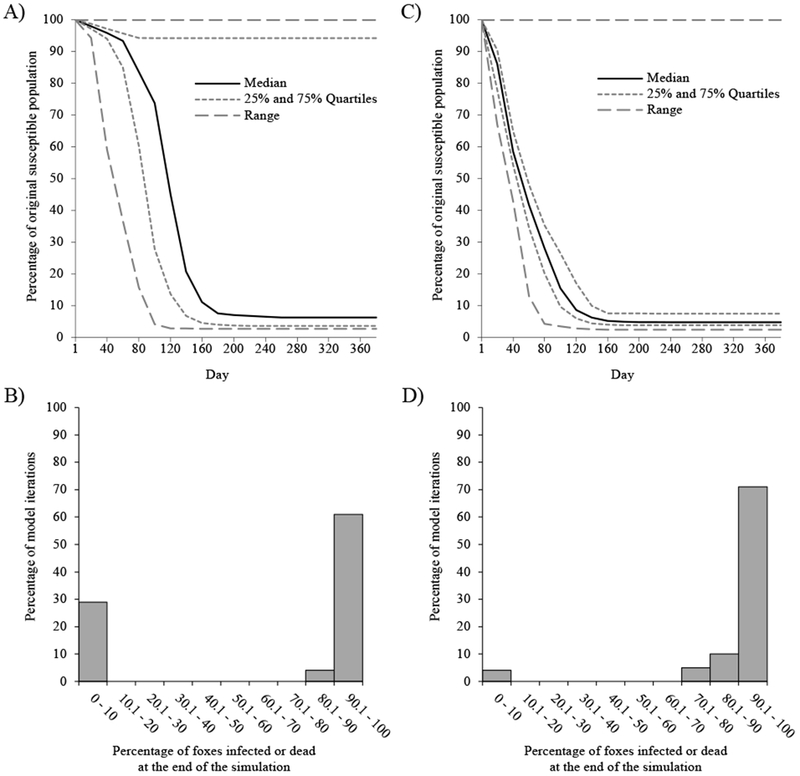
Model simulation results of canine distemper virus (CDV) introduction to areas of San Clemente Island with low (A, B) or high (C, D) fox density. Line graphs show the percentage of the original susceptible fox population remaining uninfected during each day of the simulation after CDV was introduced into an area of the island with low (A) or high (C) fox density. Histograms show the percentage of model iterations that resulted in a given percentage of the original susceptible fox population being infected or dead at the end of the one-year simulation when CDV was introduced to an area of low (B) or high (D) fox density, demonstrating the variability of epidemic severity.

Nearly all simulations resulted in epidemic fadeout, and the probability of fadeout did not differ between introduction sites (low-density = 98.0%, binomial SE = 2.74%; high-density = 99.0%, binomial SE = 1.95%; ${\chi }_1^2=0.003$, P = 0.960). Consequently, patterns in the percentage of foxes remaining uninfected after epidemic fadeout mirrored the overall patterns described above. The bimodal distribution of infected foxes at the end of one year (or after epidemic fadeout) reflects two possible progressions of the epidemic. In most cases, fadeout occurred after the island-wide population of foxes was reduced to densities too low to maintain transmission, with the second peak corresponding to cases where locally depressed fox densities resulted in fadeout early in the simulation.

R₀ at high-density pathogen introduction sites (median = 13.5, Q1 =5.8, Q3 = 23.3) did not differ (D = 0.12, P = 0.468) from low-density sites (median = 16.5, Q1 = 6.8, Q3 = 31.3), however, R_e at high-density pathogen introduction sites (median = 1.3, Q1 = 1.1, Q3 = 1.4) was higher (D = 0.71, P < 0.001) than at low-density sites (median = 1.0, Q1 = 0.6, Q3 = 1.1).

When CDV was introduced to areas of low fox density, the percentage of the original susceptible population remaining uninfected at the end of one year was sensitive to increases in contact rates and length of the latent and infectious periods, changes in transmissibility, and reductions in the background transmission rate (Table 2). When CDV was introduced to areas of high fox density, the percentage of the original susceptible population remaining uninfected at the end of one year was sensitive to reductions in the background transmission rate and the length of the infectious period (Table 2). The percentage of iterations resulting in epidemic fadeout was robust to changes in all parameters regardless of introduction site (Table 2).

When recovery was added to the model, the longer infective period of recovering foxes resulted in reduction in epidemic fadeouts at early time steps. For introductions to low-density habitats, a 10% recovery rate reduced the probability of epidemic fadeout from 98% to 44.0% (binomial SE = 9.7%; ${\chi }_1^2=20.5$, P < 0.001) and a 50% recovery rate reduced fadeout probability to 21.0% (binomial SE = 8.0%; ${\chi }_1^2=49.8$, P < 0.001). That the difference was due to reductions in early epidemic fadeouts is indicated by the negligible change in the first quartiles of the distribution of susceptibles remaining at the end of simulations (10% recovery: median = 4.6%, Q1 = 4.0%; 50% recovery: median = 5.1%, Q1 = 2.5%) but large reductions in the third quartile of susceptibles remaining at the end of simulations (10% recovery: Q3 = 25.4%; D = 0.23, P = 0.01; 50% recovery: Q3 = 7.8%; D = 0.30, P < 0.001). The percentage of foxes remaining uninfected after fadeout occurred showed a similar pattern, differing from simulations without recovery in the tail of this distribution (10% recovery: median = 4.6%, Q1 = 4.0%, Q3 = 86.9%; D = 0.23, P = 0.02; 50% recovery: median = 5.0%, Q1 = 2.5%, Q3 = 8.3%; D = 0.32, P < 0.001).

Similarly, when CDV was introduced at high-density sites, most simulations had very few susceptibles remaining at the end of one year when recovery was added (10% recovery rate: median = 4.1%, Q1 = 3.4%, Q3 = 5.4%; D = 0.24, P = 0.006; 50% recovery rate: median = 3.7%, Q1 = 3.2%, Q3 = 4.8%; D = 0.29, P < 0.001). This difference stems from the reduced chance of early epidemic fadeout; the probability of epidemic fadeout declined from 99% to 55% with 10% recovery rate (binomial SE = 9.8%; ${\chi }_1^2=12.6$, P < 0.001) and to 6% with a 50% recovery rate (binomial SE = 4.7%; ${\chi }_1^2=82.4$, P < 0.001). The percentage of foxes remaining uninfected after fadeout occurred was lower with 10% recovery (median = 4.1%, Q1 = 3.3%, Q3 = 5.5%; D = 0.23, P = 0.01) and 50% recovery (median = 3.8%, Q1 = 3.2%, Q3 = 4.9%; D = 0.28, P < 0.001) compared to simulations with no recovery.

DISCUSSION

This study utilizes empirically estimated host contact rates and host spatial distributions to parameterize a spatially explicit, individual-based simulation model of disease spread. Until recently, detailed measurements of host contact rates were difficult to obtain, and most models of disease dynamics had to infer contact from the degree of static spatial overlap among individuals, such as home range overlap obtained from VHF radio-transmitters. The model presented here is unique in its use of so many direct empirical measurements of host spatial and behavioral ecology, including density, home range size and distribution, and contact rates. These parameters were incorporated into a spatially explicit model that reflects the biology of two pathogens, heterogeneous distribution of hosts in the environment, and the uncertainty of where pathogen introduction might occur. The model clearly showed that CDV has the capacity to cause much greater declines in island fox populations than does rabies, and that spatial heterogeneity in both host density across the landscape and at the site of pathogen introduction influence epidemic outcomes.

A striking feature in our simulations was the large range of observed outcomes across individual iterations for both pathogens. Regardless of pathogen biology or entry point, outbreak size ranged from fadeout with <10% infected individuals to an epidemic with >50% of the population becoming infected within one year. The high potential for epidemic fadeout shortly after disease introduction highlights the likelihood that many wildlife disease outbreaks go undetected by the passive surveillance implemented by many monitoring systems. This may be especially true when the outbreak is small in size, short in duration, or only affects rare or cryptic species (MacInnes et al. 2001, Rupprecht et al. 2001, Lembo et al. 2008).

Previous studies examining the effect of landscape heterogeneity in host density or home-range size on the rate of pathogen spread have yielded mixed results. Smith and Harris (1991) concluded that spatial heterogeneity in fox densities did not affect the velocity of the rabies front across a landscape. In contrast, Bar-David et al. (2006) found that landscape heterogeneity created a spatially variable disease invasion front. They also found an interaction between disease transmissibility and landscape heterogeneity in determining the probability of disease extinction. Our results are in line with those of Bar-David et al. (2006), demonstrating that pathogen biology had a strong influence on both epidemic outcome and the importance of introduction site. Rabies introductions tended to move slowly across the island regardless of introduction site and often failed to establish in the population before fading out. In contrast, CDV introductions typically resulted in fast-spreading epidemics, with most foxes on the island infected within six months. The greater propensity for CDV to cause a more severe epidemic can be explained by the longer infectious period in CDV compared to rabies, leading to more opportunities for an infected fox to contact neighbors and transmit the disease to other foxes. As a consequence, the average initial CDV infection resulted in 6–8 times more secondary infections than the average initial rabies infection.

A similar pattern has been observed in wild epidemics. Initial rates of spread for rabies in wild populations are typically 1-3 secondary infections per initially infected animal (feral dogs: R₀ = 1.14 [95% CI = 1.03 – 1.25; Hampson et al. 2009], R₀ = 2.44 [95% CI = 1.52 – 3.36; Kitala et al. 2002], R₀ = 1.63 – 2.33 [Coleman and Dye 1996]; spotted hyenas [Crocuta crocuta] R₀ = 1.9 [range = 1.8 – 2.1; East et al. 2001]; Ethiopian wolves R₀ = 2.4 [95% CI = 1.7 – 3.4, Haydon et al. 2006]). In contrast, initial rates of spread in CDV outbreaks have been estimated to range from 3 – 12 for wolves (Canis lupus) and 2 – 6 for coyotes (Canis latrans) in Yellowstone National Park (Almberg et al. 2010). Both of these canids live at lower densities than island foxes (0.002 – 0.099 wolves/km² and 0.194 – 0.726 coyotes/km²; Almberg et al. 2010) which may correspond to lower contact and transmission rates.

In addition to being associated with higher infection rates, CDV has a shorter latency period than rabies, further increasing the speed at which an outbreak spreads through the population. Our simulations suggest that even for a severe outbreak infecting >95% of an island fox population, the entire epidemic could run its course within a span of six months. The potential for CDV to cause a rapid and near total extinction of an island fox host population as suggested in our simulations is consistent with the 1999 CDV epidemic on Santa Catalina Island, which resulted in a 95% decline in the foxes on the eastern side of the island in less than one year (Timm et al. 2009). The inclusion of CDV recovery in the model resulted in even greater losses to the fox population, primarily driven by the prolonged viral shedding of recovered animals. Experimental infection of captive ferrets with a genetically modified strain of CDV that inefficiently infected epithelial cells resulted in no detectable virus in throat swabs or urine, suggesting that recovery and subsequent clearance of CDV from epithelial cells may reduce viral shedding (Sawatsky et al. 2012). If recovered foxes do not shed CDV for as long as predicted, then we might see an epidemic outcome more similar to CDV simulations without the recovered class, in which epidemic fadeout was more likely and fewer foxes became infected over the course of a year.

Despite the differences in pathogen biology and resulting patterns of infection, spatial heterogeneity in host density had an overall similar effect on epidemic progression for both diseases: pathogen introductions into high host density areas were likely to cause an epidemic while introductions into low host density areas were more likely to fade out after infecting only a few individuals. Importantly, outbreaks starting in high-density areas are not confined to the high-density region but spread throughout the landscape. This is likely because there are multiple introductions into the neighboring lower density region after an epidemic has spread through the high-density region. Multiple introductions into low-density regions from high-density regions can cause high infection rates in the former through multiple mechanisms. First, each introduction is likely to result in at least a few infections, which, when summed up over numerous introductions can result in a high enough fraction of animals infected to sustain the spread of disease. Second, each introduction has the potential to cause an outbreak in the region, even if the probability of doing so is small. For example, even if a single introduction of rabies into the low-density region has 90% chance of fadeout with only a few animals being infected, multiple introductions from an outbreak spreading through neighboring high-density regions quickly leads to a high risk of a sustained outbreak in the low-density region. Third, multiple introduction points mean that infected animals are less likely to be restricted to areas with locally suppressed densities of susceptible individuals due to infection or mortality. Likewise, multiple introduction points mean it is more likely that the pathogen enters a low-density region in locations where landscape features creating barriers to dispersal (e.g., Real and Biek 2007) can be relatively easily circumvented. A similar effect is often built into disease models to represent long-distance transmission of pathogens through host dispersal or translocation, often resulting in more severe epidemics than would be expected if transmission was restricted to neighboring animals (Smith et al. 2002, Clifford et al. 2009). The effect of these recurrent introductions can be seen by comparing the slow spread of rabies predicted even at high fox densities in our spatially structured model compared to the rapid spread predicted in the relatively low-density populations of island foxes evaluated by Doak and Bakker’s (2013) non-spatial model. An important consequence of these last two mechanisms is that regions with low host densities may be resistant to the initial introduction of a pathogen into a naive population, but less effective at preventing the spread of an established epidemic across the landscape.

Conversely, pockets of high host densities can cause a fizzling outbreak to turn into a widespread epidemic. We observed this dynamic in a small number of rabies simulations, where the percentage of infected animals began to rise sharply around day 100 and continued to increase through the end of the year until approximately half of the foxes were infected. In these simulations, the fast rise in the number of infections was due to the virus entering an area of the island with higher fox densities, where the rate of pathogen spread increased dramatically due to the large number of newly available and susceptible neighbors. The ability of pockets of high host densities on the landscape to promote sustained epidemics may contribute to high rates of enzootic rabies in mainland populations where multiple species may circulate the pathogen (Kappus 1970, Carey 1982, Krebs et al. 2003). Not only does transmission between multiple species increase the mean density of potential hosts within a landscape (Craft et al. 2008, Böhm et al. 2009), but differences in habitat preference or avoidance of competitors and predators can create numerous pockets of high host densities where outbreaks can be sustained and spread.

The interaction between spatial heterogeneity in host density and pathogen introduction site is largely driven by variation across the landscape in the numbers of potential contacts an infected individual has. There is a rich literature examining how variation in host contact heterogeneity impacts disease spread (White et al. 2017 and references therein). However, there are important differences between the effects of spatial heterogeneity in host density and variation in contact networks arising from other mechanisms such as social structure. A key difference is that in socially structured networks, there is evidence for a negative correlation between the potential for an individual to be highly susceptible to infection and the potential for an individual to cause a disproportionately large number of subsequent infections; super-recipients are not necessarily super-spreaders (White et al. 2017). In contrast, the density of potential hosts is likely to be similar for neighboring animals, creating an inherent positive correlation between susceptibility and potential to cause secondary infections in heterogeneous landscapes.

While we did not include individual variation in contact rates in our simulation, the interaction between background transmission rates (which mimics the potential for some individuals to have contact networks extending well beyond their immediate neighbors), pathogen biology, and host density at the introduction site (Table 2) suggest a potentially complex relationship between spatial heterogeneity in host density and host social structure. There was a similarly complex interaction between transmissibility, pathogen biology, and host density (Table 2). If reducing transmissibility mimics (in a crude way) the effect of a vaccination program, this interaction suggests that the efficacy of vaccination programs may be influenced by spatial heterogeneity in host density. While many questions remain, it is clear that accounting for the influence of spatially variable host densities will improve both our understanding of, and ability to manage wildlife diseases.

Uncertainty about the source and location of novel pathogen introduction is a challenge for the conservation of many vulnerable species, and disease surveillance and vaccination campaigns are often limited by financial and logistical constraints. For conservationists and land managers with limited budgets and resources, predictions about how a pathogen will spread through a host population can advise the targeted distribution of control strategies such as the application of vaccinations, and guide risk assessment of which diseases should be of highest priority for prevention efforts. For example, on SCI this means that fox monitoring and biosecurity efforts should be focused on northern end of the island, where fox densities are highest, with a lower priority assigned to efforts on the southern end of the island, where fox densities are lowest. Similarly, it may be more effective to concentrate vaccination efforts in the northern region to create a second region of the island with a low density of susceptible foxes rather than spread vaccinations evenly throughout the island. How spatial heterogeneity in host density influences optimal vaccination strategies remains an open question deserving further investigation.