Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jul 15;7(8):2197–2203. doi: 10.1021/acsphotonics.0c00701

Nanoelectromechanical Position-Sensitive Detector with Picometer Resolution

Miao-Hsuan Chien 1, Johannes Steurer 1, Pedram Sadeghi 1, Nicolas Cazier 1, Silvan Schmid 1,*
PMCID: PMC7441496  PMID: 32851117

Abstract

graphic file with name ph0c00701_0005.jpg

Subnanometer displacement detection lays the solid foundation for critical applications in modern metrology. In-plane displacement sensing, however, is mainly dominated by the detection of differential photocurrent signals from photodiodes, with resolution in the nanometer range. Here, we present an integrated nanoelectromechanical in-plane displacement sensor based on a nanoelectromechanical trampoline resonator. With a position resolution of 4 pm/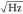Inline graphic for a low laser power of 85 μW and a repeatability of 2 nm after five cycles of operation as well as good long-term stability, this new detection principle provides a reliable alternative for overcoming the current position detection limit in a wide variety of research and application fields.

Keywords: in-plane displacement sensor, position-sensitive detector, nanoelectromechanical resonators, photothermal effect

High-performance position sensing is a substantial corner stone for challenging applications such as state-of-the-art atomic force microscopy for molecular- and mechano-biology,1,2 nanomechanical transduction and sensing,3−6 and experimental physics such as the tracking of single electron spins and trapped ions.7,8 Position-sensitive detectors (PSDs) that can measure the position of a light spot are an integral part of modern metrology. The two most common PSD designs are based on segmented or lateral effect sensors. The former PSDs consist of multiple sensor segments each giving its own photocurrent, while the latter is based on a single photodetector element. 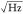Typical segmented-quadrant position-sensitive detectors have a good position resolution of the order of 10 nm/Inline graphic to 100 nm/Inline graphic for light powers of 10–100 μW.9 Due to their quick response time and large operation bandwidth, they are dominating the commercial atomic force microscope market. Each detector segment is separated by a gap. The intensity profile of a spot is in general very nonlinear, which directly results in a strong nonlinear position response if the spot is not perfectly centered. In contrast, lateral effect position-sensitive detectors have no gaps and give positional information independent of beam shape, size, and intensity profile. Lateral effect PSDs have a good lateral resolution in the range of a few nm/Inline graphic, however, typically have a slower response speed than quadrant detectors.9,10 For both PSDs, as a characteristic of semiconductor photodetectors, the dark-current noise can limit the detector sensitivity to one to two orders higher than the shot-noise-limit without any considerations of external artifacts, setting an upper limit for the sensitivity of photodiode-based PSDs.9,11

Besides the common photodiode-based PSDs, it has been shown that a spatial resolution of 25 pm/Inline graphic can be achieved by direct transmission of a Gaussian beam through a slit.12 This transmission-based experiment, however, requires a photodetector behind the slit, which renders it impractical for the use in more general applications. Recently, a fundamentally new approach based on the directional scattering of a laser spot on a silicon nanoantenna has been demonstrated.13,14 This nanophotonic displacement sensor has reached a position resolution in the nanometer range. A nano-optomechanical displacement sensor using a mechanical coupler has also been reported with a sensitivity of 45 fm/Inline graphic.

Here, we present a nanoelectromechanical position-sensitive detector (NEMS-PSD) with a position resolution in the picometer range. Recently, similar nanoelectromechanical resonators have demonstrated unprecedented sensitivity for radiation15 as well as single nanoparticle and molecule absorption detection.16−18 The NEMS-PSD principle is based on the highly beam-position-dependent photothermal heating of plasmonic Au nanoparticles that are placed on top of a silicon nitride trampoline resonator, as schematically depicted in Figure 1a. A scanning electron microscope image of the nanoelectromechanical trampoline resonator is shown in Figure 1b. The NEMS-PSD is transduced electrodynamically,19−21 as schematically depicted in Figure 1c. More details of the NEMS-PSD design can be found in the Supporting Information. During operation, due to the Gaussian power distribution of the beam, the displacement of the laser beam changes the power absorbed by the nanoparticles, resulting in a detectable frequency shift of the temperature-sensitive nanoelectromechanical resonator. In this way, the presented NEMS-PSD reached a position resolution of 4 pm/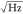Inline graphic for a laser power of 85 μW.

Figure 1.

Figure 1

Open in a new tab

(a) Working principle of the nanoelectromechanical position-sensitive detector (NEMS-PSD). Displacement of the light beam could be detected by the shift of the trampoline resonance frequency as a result of the change in absorption of gold nanoparticle. (b) SEM image of trampoline nanomechanical resonator with readout and actuation electrodes, with a close-up SEM image of the gold electrode in the marked area. Both electrodes are 1 μm wide and following the profile of the trampoline with approximately 1 μm spacing to the edge. The electrodes have a resistance of 150 Ω resulting in a Johnson noise of below 2 nV/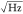Inline graphic. A total of 200 nm Au nanoparticles are distributed on the center area of the trampoline, as shown in the SEM image in the inset. (c) Detection scheme of the NEMS-PSD. The trampoline features two gold electrodes, one for inductive readout and the other for Lorentz force actuation. To obtain an optimal signal-to-noise ratio, an enhanced Halbach array is used to create a static magnetic field of approximately 1 T. The magnetomotive readout current is amplified by a homemade low-noise preamplifier. The resonance frequency is then tracked with a phase-locked loop (PLL).

Results and Discussion

Theoretical Model

The laser spot displacement Δx is measured in terms of the measured relative frequency shift δf = Δf/f0 of the trampoline resonator

graphic file with name ph0c00701_m008.jpg 1

with the relative responsivity δR of the nanoelectromechanical resonator.

The displacement responsivity δR of the nanomechanical resonator is defined as its relative frequency change per laser spot displacement. Since the laser displacement and the resonant frequency change are connected by the change in absorbed laser power P, δR can be written as

graphic file with name ph0c00701_m009.jpg 2

with the well-investigated relative power responsivity δRp18,22 and the beam displacement related power responsivity Rx.

δRp can be modeled as the responsivity of a nanomechanical cross resonator, which represents the most extreme case of a trampoline that features no central area. A cross resonator has half the responsivity of a nanomechanical string resonator and can be written as22

graphic file with name ph0c00701_m010.jpg 3

where α is the thermal expansion coefficient, E is the Young’s modulus, κ is the thermal conductivity, σ is the tensile stress, L is the tether length of the cross, w is the width, and h is the thickness of the cross resonator.

Since the dimension of the nanoparticle is around 10% of the laser beam diameter, the nanoparticle antenna can be approximated as a point absorber with an absorption cross-section σabs. Then, the power absorbed by the nanoparticle (P) at a position x, with respect to a Gaussian beam center, under different beam positions, which is the convolution of a point source and a Gaussian beam profile, can be expressed as

graphic file with name ph0c00701_m011.jpg 4

with the beam radius w0 and the laser power P0, and I(x) as the laser irradiance. According to eq 2, Rx can then be obtained by taking the first derivative of P(x) with respect to x. And since the gradient of a Gaussian beam profile is maximum at half of the beam radius 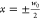Inline graphic, the maximum Rx value becomes

graphic file with name ph0c00701_m013.jpg 5

Combining eqs 3 and 5, an upper limit for the relative displacement responsivity (eq 2) becomes

graphic file with name ph0c00701_m014.jpg 6

As indicated by eq 6, first, the displacement responsivity limit is dependent on the resonator’s intrinsic material properties and geometry, and second, on the laser beam profile. In practice this means that for a given resonator material, the NEMS resonator geometry should produce a maximum thermal isolation, and the laser spot should be as small as possible with maximum power.

Displacement Responsivity and Resolution

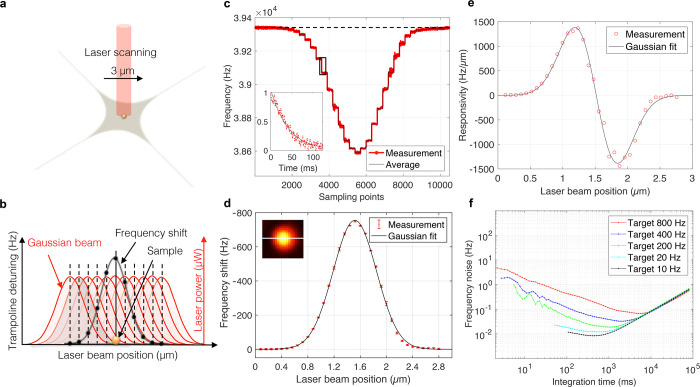
As has been shown in the derivation of eq 5, the displacement responsivity is dependent on the relative position of an absorbing particle with respect to the laser spot, following the first derivative of a Gaussian function. To examine this, a single Au nanoparticle that is well-isolated from other particles in the center area of the trampoline resonator is selected, and a 3 μm × 3 μm area scan is done with a step size of 80 nm and a dwell period of approximately 300 ms for each step, as schematically shown in Figure 2a. As mentioned, the formation of the Gaussian frequency shift profile is a result of the convolution between a single point absorber and the Gaussian power profile of the laser, as illustrated in Figure 2b. The raw frequency signal for a scan across the single Au particle is plotted in Figure 2c. The rise time of the NEMS-PSD can be extracted by fitting the step frequency response with a first order exponential function, as shown in the inset of Figure 2c, yielding a 10% to 90% rise time of 53 ms. Therefore, a delay time of around 50 ms is set for each scan point. More details on the calculation of the rise time is provided in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

(a) Schematic of the long-range scanning of the single nanoparticle absorber to investigate the position-dependent displacement responsivity. (b) Schematic of the formation of the Gaussian frequency shift profile from the Gaussian beam. As the beam scans through the nanoparticle, the Gaussian power distribution results in a Gaussian absorption profile and thus a Gaussian frequency shift. (c) Resonance frequency tracked by the PLL with a target bandwidth of 800 Hz. The reference frequency is indicated by the dashed line. The mean frequency of each scan step is marked by the solid line. The rise time is extracted from the fit indicated in the inset. (d) Extracted frequency shift of each scan point averaged over the dwell time. The error bars represent the respective standard deviation. The inset shows the full 2D scan. (e) The responsivity for the different beam positions assuming piece-wise linearity, with the first derivative of the Gaussian fit from (d) indicated with a solid line. (f) Allan deviation for different target bandwidths.

Figure 2d shows the NEMS-PSD frequency shift for a scan across the center of the nanoparticle, as indicated by the white line in the two-dimensional frequency shift mapping in the inset of Figure 2d. The data points are fitted with a Gaussian function. The extracted full width at half-maximum (fwhm) of the Gaussian fit is 1.1 μm, corresponding to a beam radius of 0.93 μm, which is close to the nominal fwhm of the laser objective (NA = 0.55) of around 0.9 μm (beam radius of 0.75 μm). For the 200 nm Au nanoparticle an absorption cross-section of σabs = 9 × 10–14 m2 for a wavelength of 633 nm can be calculated from Mie theory.18,23 With an input laser power of P0 = 85 μW, the expected peak frequency shift is calculated to be approximately 720 Hz, based on the finite element method (FEM) simulations, which fits with the peak frequency shift of 750 Hz in the measurement quite well.

Figure 2e shows the displacement responsivity, represented by the first derivative of the measured frequency shift profile shown in Figure 2d. A maximum responsivity of approximately 1400 Hz μm–1 is reached at half of the beam waist of the Gaussian profile. As expected from the theoretical model, the responsivity is maximal for a particle position at half of the beam radius.

Figure 2f shows the Allan deviation for different phase-locked loop (PLL) target bandwidths. It can be seen that the thermal drift, represented in the positive slope for the large integration times is consistent for all target bandwidths. In contrast, the negative slopes for short integration times varies for specific target bandwidths, which is because the inductive readout is not limited by thermomechanical noise.24 From Figure 2f it can be seen that a target bandwidth of 800 Hz and integration time of 250 ms results in a frequency noise of about 250 mHz. This matches with the standard error of around 253 mHz calculated from the integrated data for individual scan points shown in Figure 2d (the calculations are presented in more detail in the Supporting Information). Together with the previously extracted responsivity of 1400 Hz μm–1, a position resolution of 105 pm/Inline graphic can be calculated from the current measurement according to eq 1. Since smaller target bandwidths yield lower frequency noise, it is possible to improve the position resolution with the trade-off of longer minimal integration times, for example, using a target bandwidth of 10 Hz results in a minimum frequency noise of 8 mHz for an integration time of 450 ms, which ultimately results in a position resolution of 4 pm/Inline graphic.

Optimization of Trampoline Geometry

As discussed previously in eq 2, the maximum responsivity depends on the design of the trampoline geometry. Figure 3 presents the study of trampoline resonators with various sizes of the center area, both measured and simulated using FEM. The window size is kept constant at 1 mm for all designs. The width of the trampoline tethers were kept constant at 5 μm and a silicon nitride thickness of 50 nm. The curvatures of all trampoline geometries are optimized for an even stress distribution. Single 200 nm gold nanoparticles are used as absorber for all measurements, and the maximum displacement responsivity is extracted, as shown in Figure 2e. The measured responsivities share a similar trend with the FEM simulation, with decreasing responsivity for increasing center area from type A to type E trampoline. This can be explained by the resulting lower temperature profile for trampolines with larger center area, as shown in more detail in the Supporting Information, Figure S5. The most extreme design of type A trampoline has a responsivity close to the theoretical limit according to eq 6 of around 2100 Hz μm–1, representing a trampoline with no center area.

Figure 3.

Figure 3

Open in a new tab

Measured and simulated responsivity for trampoline resonators with different geometries, indicated as type A to type E with corresponding microscopic images. The center area is marked in percentage, which is a factor of the scaling, with type E representing maximum scaling of 100%. The FEM-simulated distance dependency of the responsivity is plotted in the inset. All values are normalized for better visualization. The direction of the distance is indicated with the red arrow in the image of the type C trampoline.

However, the small center area makes it challenging to distribute nanoparticles on the surface by means of spin-coating. Type C trampolines have a large enough center area and show a high responsivity, only 10% less compared to the most responsive type A trampoline. Therefore, type C trampolines were the devices of choice used for the present study. Furthermore, since the nanoparticles are distributed randomly on the trampoline resonator, the position-dependency of the power responsivity is worth discussing. As shown in the finite element simulation in the inset of Figure 3, the power responsivity remains constant over the entire center area. It is not until the tethers of the trampoline resonator are reached that the responsivity starts to drop. Hence, the displacement measurement can be operated optimally over the whole center area, which is a precondition for the displacement sensing with type C trampoline resonators.

Repetitive Displacement Measurements

After the characterization of the displacement responsivity and the optimization of the trampoline geometry, a repetitive displacement measurement within a small range of 15 nm and small step size of 3 nm is performed. Therefore, the laser spot was placed randomly on the center of the trampoline in order to demonstrate the possibility to operate the NEMS-PSD without any fine alignment and calibration process demonstrating the practicability. Furthermore, the repeatability and long-term stability of displacement sensing is studied, as illustrated in Figure 4a. The integration time for each step remains 250 ms. As in the schematics of Figure 4b, the frequency shift is no longer a Gaussian profile; instead, an approximated linear relation between the frequency shift of the trampoline resonator and the beam displacement with an almost constant displacement responsivity can be expected for such a small scan range. The frequency signal from the PLL is plotted in Figure 4c, where the individual displacement steps of 3 nm can be clearly identified. The averaged frequency and standard deviation of each displacement step is then calculated and plotted in Figure 4d with respect to the laser beam position. For generalization, a reference position is then defined as the center point of the repetitive movement, and the frequency shift is then subtracted according to this reference frequency, as shown in Figure 4e. A linear fit is subsequently performed to extract the displacement responsivity within this range. The averaged displacement responsivity obtained from the fit is 1.15 Hz nm–1. The target bandwidth of the PLL is reduced to 200 Hz in these measurements, resulting in a frequency noise of around 0.025 Hz. This gives a position resolution of 12 pm/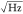Inline graphic, which is slightly worse than previous values, which were obtained for an optimized particle/beam position. With this measurement, NEMS-PSD demonstrates the feasibility of operation without fine optical alignment on a random absorber on the trampoline resonator.

Figure 4.

Figure 4

Open in a new tab

(a) Schematic of the 15 nm short-range fine and repetitive scanning of the single nanoparticle absorber. (b) Schematics of the partly linear behavior of a frequency shift within a small displacement region. (c) Raw frequency signal from the PLL, with the average frequency of each step marked as a black solid line. (d) The average and standard deviations of the frequency for each step. The trajectory of the beam movement is marked with a black line. (e) The subtracted frequency shift with respect to displacement, with a linear fit to identify responsivity.

The repeatability after 5 cycles of operation is within a maximum deviation of 2 nm. This deviation could also partly result from the accuracy of the nanopositioning stage that controls the position of the beam. With a drift below 500 nm within 4 h, as discussed in the Supporting Information, the long-term stability of NEMS-PSD is of the same order as of photodiode-based PSDs with 0.1 to 1 μm.9,12 The drift could be partly contributed by the whole optical system, including sample mounting. This high repeatability and long-term stability of NEMS-PSD can result from the localized absorption of nanoparticles, making the system less susceptible to background scattering and interference.

Conclusions

We presented a NEMS-PSD based on silicon nitride trampoline resonators with integrated electrodynamic readout and actuation. We demonstrated a sensitivity of 4 pm/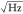Inline graphic with the potential of further optimization by using, for example, silicon nitride with lower stress. The stress can be engineered by the deposition condition in low-pressure chemical vapor deposition (LPCVD) process,25 by a post-treatment with the oxygen plasma,18,26 or by controlling the temperature of the samples.27 The NEMS-PSD demonstrated a repeatability of approximately 2 nm after 5 cycles of operation and showed a long-term stability better than 500 nm in 4 h. This position-sensitive detector design overcomes the issue of nonuniformity of multiple segments by measuring the direct absorption instead of differential current from photodiodes, which improves the sensitivity greatly and also requires minimum signal processing effort. Due to the localized nanoparticle absorber, the parasitic effect from the ambient is also minimized, which enables better long-term stability. It is also compatible with a small beam diameter and even irregular beams, since the artifact could be easily calibrated with a scan before operation to identify the beam profile. The presented NEMS-PSD is promising to provide a sensitive alternative to existing PSDs and could bring advances to a great variety of research and application fields.

Methods

Sample Fabrication

The samples are fabricated with a bulk micromachining process. A silicon wafer with a thickness of 370 μm is coated with a 50 nm silicon-rich silicon nitride (SiN) with low pressure chemical vapor deposition (LPCVD). The prestress is approximately 150 MPa, which is extracted from the resonance frequency by means of a finite element method-based analysis. The 190 nm thick gold electrodes together with a 10 nm chrome adhesion layer for magnetomotive transduction are first defined with photolithography on the front side of the SiN wafer, and the SiN trampoline structure is then defined with another step of photolithography after lift-off. The excess SiN is then removed with reactive ion etching (RIE) and protected with a layer of photoresist. A window is defined from the back side and etched with KOH to release the trampoline resonator. Reactant-free gold nanoparticles with a diameter of 200 nm in 0.1 mM PBS stabilized suspension solution (Sigma Aldrich) are first diluted in Micropur deionized water (18 MΩ·cm, Milli-Q) at a ratio of 1:100 at room temperature and then spin-coated on the trampoline resonator at 2000 rpm.

Finite Element Method Simulation

The finite element simulations are done with the thermal stress module of COMSOL multiphysics, including first the simulation of the temperature field of a point heat source and, subsequently, the stress distribution and the eigenfrequency. The responsivity could be extracted by simulating the eigenfrequency at different powers of the point heat source. The thermal expansion coefficient (α) used in the simulation is 2.2 × 10–6 K–1, the Young’s modulus (E) is 250 GPa, thermal conductivity (κ) is 3 W m–1 K–1, and the prestress (σ) is 150 MPa. All the constants are also consistent with the ones used for theoretical calculations.

Measurement Setup

The optical setup is shown in detail in the Supporting Information. In this experiment, a diode laser with a 633 nm wavelength (Toptica TopMode) is used. The beam passes through a beam expander and the power is reduced to approximately 85 μW before the vacuum chamber with a linear polarizer. A 50 times objective (0.55 N.A.; Mitutoyo) is mounted on the nanopositioning stage (PiMars, Physikinstrumente) for control of the beam position. All the measurements are done under a vacuum of 1 × 10–3 mbar. The magnetomotive transduction is done with an enhanced Halbach array with the layout shown in Figure S1. The magnetic field in the center 5 mm region is measured to be above 1 T. The electrical signal from the trampoline resonator is first amplified with a home-built low-noise preamplifier (LT1028, Analog Devices) with a gain of 200, and fed to the lock-in amplifier with a phase-locked loop (HF2LI, Zurich Instrument), with its output driving the actuation.

Acknowledgments

We gratefully acknowledge the assistance of Sophia Ewert and Patrick Meyer with the sample fabrication and preparation and the useful discussions with Markus Piller and Hendrik Kähler. This work is supported by the European Research Council under the European Unions Horizon 2020 Research and Innovation Program (Grant Agreement 716087-PLASMECS).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c00701.

  • Detailed measurement setup and calculations of rise time, frequency noise, temperature field and long-term stability (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ph0c00701_si_001.zip (1.3MB, zip)

References

  1. Dufrêne Y. F.; Ando T.; Garcia R.; Alsteens D.; Martinez-Martin D.; Engel A.; Gerber C.; Müller D. J. Imaging modes of atomic force microscopy for application in molecular and cell biology. Nat. Nanotechnol. 2017, 12, 295. 10.1038/nnano.2017.45. [DOI] [PubMed] [Google Scholar]
  2. Krieg M.; Fläschner G.; Alsteens D.; Gaub B. M.; Roos W. H.; Wuite G. J.; Gaub H. E.; Gerber C.; Dufrêne Y. F.; Müller D. J. Atomic force microscopy-based mechanobiology. Nature Reviews Physics 2019, 1, 41–57. 10.1038/s42254-018-0001-7. [DOI] [Google Scholar]
  3. Knobel R. G.; Cleland A. N. Nanometre-scale displacement sensing using a single electron transistor. Nature 2003, 424, 291–293. 10.1038/nature01773. [DOI] [PubMed] [Google Scholar]
  4. Naik A. K.; Hanay M.; Hiebert W.; Feng X.; Roukes M. L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. 10.1038/nnano.2009.152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Hanay M. S.; Kelber S.; Naik A.; Chi D.; Hentz S.; Bullard E.; Colinet E.; Duraffourg L.; Roukes M. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602. 10.1038/nnano.2012.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Sage E.; Brenac A.; Alava T.; Morel R.; Dupré C.; Hanay M. S.; Roukes M. L.; Duraffourg L.; Masselon C.; Hentz S. Neutral particle mass spectrometry with nanomechanical systems. Nat. Commun. 2015, 6, 1–5. 10.1038/ncomms7482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Biercuk M. J.; Uys H.; Britton J. W.; VanDevender A. P.; Bollinger J. J. Ultrasensitive detection of force and displacement using trapped ions. Nat. Nanotechnol. 2010, 5, 646. 10.1038/nnano.2010.165. [DOI] [PubMed] [Google Scholar]
  8. Grinolds M. S.; Hong S.; Maletinsky P.; Luan L.; Lukin M. D.; Walsworth R. L.; Yacoby A. Nanoscale magnetic imaging of a single electron spin under ambient conditions. Nat. Phys. 2013, 9, 215–219. 10.1038/nphys2543. [DOI] [Google Scholar]
  9. Mäkynen A.Position-sensitive devices and sensor systems for optical tracking and displacement sensing applications. Ph.D. Thesis, University of Oulu, Faculty of Technology, 2000. [Google Scholar]
  10. Andersson H.Position sensitive detectors: device technology and applications in spectroscopy. Ph.D. Thesis, Mid Sweden University, Department of Information Technology and Media, 2008. [Google Scholar]
  11. Azaryan N. S.; Budagov J. A.; Lyablin M.; Pluzhnikov A. A.; Di Girolamo B.; Gayde J.-C.; Mergelkuhl D. Position-Sensitive Photoreceivers: Sensitivity and Detectable Range of Displacements of a Focused Single-Mode Laser Beam. Physics of Particles and Nuclei Letters 2019, 16, 354–376. 10.1134/S1547477119040058. [DOI] [Google Scholar]
  12. Haddad D.; Juncar P.; Geneves G.; Wakim M. Gaussian beams and spatial modulation in nanopositioning. IEEE Trans. Instrum. Meas. 2009, 58, 1003–1009. 10.1109/TIM.2008.2008475. [DOI] [Google Scholar]
  13. Bag A.; Neugebauer M.; Woźniak P.; Leuchs G.; Banzer P. Transverse kerker scattering for angstrom localization of nanoparticles. Phys. Rev. Lett. 2018, 121, 193902. 10.1103/PhysRevLett.121.193902. [DOI] [PubMed] [Google Scholar]
  14. Bag A.; Neugebauer M.; Mick U.; Christiansen S.; Schulz S. A.; Banzer P. Towards fully integrated photonic displacement sensors. Nat. Commun. 2020, 11, 1–7. 10.1038/s41467-020-16739-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Piller M.; Luhmann N.; Chien M.-H.; Schmid S. Nanoelectromechanical infrared detector. Optical Sensing, Imaging, and Photon Counting: From X-Rays to THz 2019 2019, 1108802. 10.1117/12.2528416. [DOI] [Google Scholar]
  16. Schmid S.; Wu K.; Larsen P. E.; Rindzevicius T.; Boisen A. Low-power photothermal probing of single plasmonic nanostructures with nanomechanical string resonators. Nano Lett. 2014, 14, 2318–2321. 10.1021/nl4046679. [DOI] [PubMed] [Google Scholar]
  17. Larsen T.; Schmid S.; Villanueva L. G.; Boisen A. Photothermal analysis of individual nanoparticulate samples using micromechanical resonators. ACS Nano 2013, 7, 6188–6193. 10.1021/nn402057f. [DOI] [PubMed] [Google Scholar]
  18. Chien M.-H.; Brameshuber M.; Rossboth B. K.; Schütz G. J.; Schmid S. Single-molecule optical absorption imaging by nanomechanical photothermal sensing. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 11150–11155. 10.1073/pnas.1804174115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cleland A. N.; Roukes M. L. Fabrication of high frequency nanometer scale mechanical resonators from bulk Si crystals. Appl. Phys. Lett. 1996, 69, 2653–2655. 10.1063/1.117548. [DOI] [Google Scholar]
  20. Cleland A.; Roukes M. External control of dissipation in a nanometer-scale radiofrequency mechanical resonator. Sens. Actuators, A 1999, 72, 256–261. 10.1016/S0924-4247(98)00222-2. [DOI] [Google Scholar]
  21. Venstra W.; Westra H.; Gavan K. B.; Van der Zant H. Magnetomotive drive and detection of clamped-clamped mechanical resonators in water. Appl. Phys. Lett. 2009, 95, 263103. 10.1063/1.3275014. [DOI] [Google Scholar]
  22. Schmid S.; Villanueva L. G.; Roukes M. L.. Fundamentals of Nanomechanical Resonators; Springer, 2016; Vol. 49. [Google Scholar]
  23. Myroshnychenko V.; Rodriguez-Fernandez J.; Pastoriza-Santos I.; Funston A. M.; Novo C.; Mulvaney P.; Liz-Marzan L. M.; Garcia de Abajo F. J. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–1805. 10.1039/b711486a. [DOI] [PubMed] [Google Scholar]
  24. Demir A.; Hanay M. S. Fundamental Sensitivity Limitations of Nanomechanical Resonant Sensors due to Thermomechanical Noise. IEEE Sens. J. 2020, 20, 1947–1961. 10.1109/JSEN.2019.2948681. [DOI] [Google Scholar]
  25. Temple-Boyer P.; Rossi C.; Saint-Etienne E.; Scheid E. Residual stress in low pressure chemical vapor deposition SiN x films deposited from silane and ammonia. J. Vac. Sci. Technol., A 1998, 16, 2003–2007. 10.1116/1.581302. [DOI] [Google Scholar]
  26. Luhmann N.; Jachimowicz A.; Schalko J.; Sadeghi P.; Sauer M.; Foelske-Schmitz A.; Schmid S. Effect of oxygen plasma on nanomechanical silicon nitride resonators. Appl. Phys. Lett. 2017, 111, 063103. 10.1063/1.4989775. [DOI] [Google Scholar]
  27. Larsen T.; Schmid S.; Grönberg L.; Niskanen A.; Hassel J.; Dohn S.; Boisen A. Ultrasensitive string-based temperature sensors. Appl. Phys. Lett. 2011, 98, 121901. 10.1063/1.3567012. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph0c00701_si_001.zip (1.3MB, zip)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES