Technical Note: In silico and experimental evaluation of two leaf‐fitting algorithms for MLC tracking based on exposure error and plan complexity

Abstract

Purpose

Multileaf collimator (MLC) tracking is being clinically pioneered to continuously compensate for thoracic and pelvic motion during radiotherapy. The purpose of this work was to characterize the performance of two MLC leaf‐fitting algorithms, direct optimization and piecewise optimization, for real‐time motion compensation with different plan complexity and tumor trajectories.

Methods

To test the algorithms, both in silico and phantom experiments were performed. The phantom experiments were performed on a Trilogy Varian linac and a HexaMotion programmable motion platform. High and low modulation VMAT plans for lung and prostate cancer cases were used along with eight patient‐measured organ‐specific trajectories. For both MLC leaf‐fitting algorithms, the plans were run with their corresponding patient trajectories. To compare algorithms, the average exposure errors, i.e., the difference in shape between ideal and fitted MLC leaves by the algorithm, plan complexity and system latency of each experiment were calculated.

Results

Comparison of exposure errors for the in silico and phantom experiments showed minor differences between the two algorithms. The average exposure errors for in silico experiments with low/high plan complexity were 0.66/0.88 cm² for direct optimization and 0.66/0.88 cm² for piecewise optimization, respectively. The average exposure errors for the phantom experiments with low/high plan complexity were 0.73/1.02 cm² for direct and 0.73/1.02 cm² for piecewise optimization, respectively. The measured latency for the direct optimization was 226 ± 10 ms and for the piecewise algorithm was 228 ± 10 ms. In silico and phantom exposure errors quantified for each treatment plan demonstrated that the exposure errors from the high plan complexity (0.96 cm² mean, 2.88 cm² 95% percentile) were all significantly different from the low plan complexity (0.70 cm² mean, 2.18 cm² 95% percentile) (P < 0.001, two‐tailed, Mann–Whitney statistical test).

Conclusions

The comparison between the two leaf‐fitting algorithms demonstrated no significant differences in exposure errors, neither in silico nor with phantom experiments. This study revealed that plan complexity impacts the overall exposure errors significantly more than the difference between the algorithms.

1. Introduction

One of the main advantages of radiation therapy as opposed to other types of cancer treatment is that the treatment is noninvasive and highly targeted to the tumor. Despite strong evidence that the ITV‐based planning technique (Internal Target Volume planning, ICRU 62¹) provides safe radical treatment for stage I nonsmall cell lung carcinoma, there are no guarantees that the tumor will remain within the planned aperture throughout the entire treatment.^{2, 3}

New delivery approaches have been introduced to improve the targeting of the tumor during treatment. These techniques come in various forms, either by shifting the therapeutic beam to the tumor using a robotic arm CyberKnife,^{4, 5} a gimballed linear accelerator (Vero),^{6, 7} or the multileaf collimator (MLC)^{8, 9, 10} or by adjusting the patient couch (couch tracking).¹¹

Real‐time MLC tracking is a novel technique that optimizes the leaf positions within the head of the linear accelerator to shift the radiation beam multileaf collimator leaves according to tumor motion. It has been implemented preclinically in several institutions on commercial linear accelerators^{12, 13, 14} or developed into in‐house control software and leaf‐fitting algorithms.^{8, 10, 12, 15, 16, 17} Real‐time MLC tracking has been clinically pioneered with three clinical trials leading to the first MLC tracking treatment for prostate^{18, 19, 20} and stereotactic lung²¹ with results reported in previous publications.^{19, 21}

The current clinically used version of MLC tracking relies on a leaf‐fitting optimization algorithm (also known as “MLC tracking algorithm”) named “direct optimization” algorithm.²² A recent publication by Moore et al.¹⁷ introduced an alternative MLC tracking algorithm named “piecewise optimization algorithm”. With the current design of the piecewise algorithm, Moore et al. investigated its performances in silico using standard tumor motion (three patients) and intensity‐modulated radiation therapy (IMRT) plans. However, in silico tests do not always reflect the real‐life clinical situation. For that reason, their respective performances should be tested utilizing a linear accelerator with a broad range of tumor motions and MLC plan complexity.

To allow a thorough performance comparison between both algorithms in a clinical setting, the piecewise algorithm was implemented in the clinical version of the MLC tracking software. The aim of this work was to characterize the performance of two MLC leaf‐fitting algorithms used in real‐time motion compensation. This will be done both in silico and experimentally, spanning a range of tumor motions and treatment plans with varying degree of MLC modulation.

The significance of this paper is that it is the first to investigate and experimentally compare two MLC tracking algorithms in the identical clinical setting on a linear accelerator.

2. Method

2.A. Principle of multileaf collimator tracking algorithms

Multileaf collimator tracking is operated via an optimization algorithm tasked with finding the best‐fitted leaf positions given a set of various constraints (finite leaf width and speed), or constraints setup by the user prior to treatment delivery, such as prescribing various tolerances or radiobiological properties to the organs‐at‐risk to avoid excessive overdosing.

The mechanism for managing these setup constraints differs between the direct and piecewise optimization algorithm. The different components of the direct optimization algorithm can be found in Ruan et al.²², while more extensive explanations on the piecewise algorithm can be found in Moore et al.¹⁷ Although both algorithms allow the MLC leaf positions to be optimized according to the radio‐sensitivity factor attributed to different OAR (connoted as $\lambda$ and $\sigma$ constraints in the respective papers^{17, 22}), each algorithm deals with spatial variance differently. The optimization process is operated for the direct optimization on a pixel basis within the beam's eye view, therefore relying on a two‐dimensional map of the organs.

The main difference between the two algorithms is that the piecewise algorithm deals with spatial variance by having an arbitrary number of volumetric ROI (Regions of Interest), hence accounting for the radio‐sensitivity in three dimensions. In both cases, this implies that an a priori knowledge of the position and volume of OAR is available prior to treatment, or that each OAR is being localized in real‐time during the treatment delivery.

The second difference is the way each algorithm deals with the quantification of exposure area that is sought to be minimized. For the direct optimization, the cost function is integrated both along and perpendicular to the leaf motion, as opposed to the piecewise algorithm where the algorithm resolves the integration linearly in one direction, solely along the leaf motion direction. Linear integral implicates that the algorithm is expected to converge faster toward a solution with the piecewise algorithm given equivalent set of constraints.

2.B. Experiments to assess and compare the algorithm performances

To characterize the performances of the algorithms, a series of in silico simulations and phantom experiments were performed. Both algorithms were tested under identical conditions assuming homogenous dose conditions: the target is considered as a rigid, nondeformable body and the underdose and overdose weights are set to be equal. Variables included the tumor motion, treatment site, and plan complexity. Comparison of algorithm performance was based on exposure errors, plan complexity, and the system latency. Figure 1 provides an overview of the method to assess the performance of each algorithm both in silico and experimentally on a linear accelerator. Further details are provided below.

Figure 1.

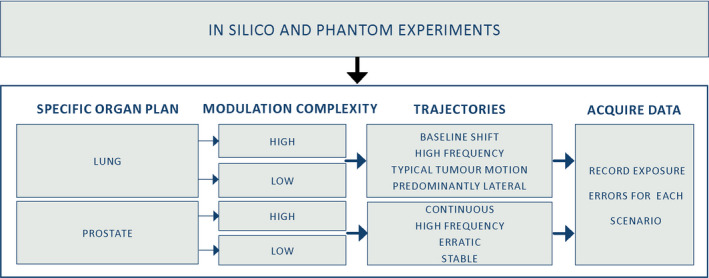
Performance of each algorithm was characterized by two sets of experiments, in silico and phantom, conducted for two specific target scenarios (lung and prostate) combining different sets of plan complexities (high and low) and trajectories (baseline shift, high frequency, etc.). The exposure errors were calculated for each scenario. [Color figure can be viewed at wileyonlinelibrary.com]

2.B.1. In silico and phantom experiments

The in silico experiments were performed on a Latitude E7450 i7 2.60 GHz Dell 16 Gb RAM using an MLC simulator.²³ The tumor motion traces were imported into the simulator as text files. The DICOM plan was read by the software and the treatment delivery was simulated. The simulator leaf speed was limited to 3.6 cm/s being the leaf speed of the actual linear accelerator.

The phantom experiments were performed on a Trilogy (Varian, Palo Alto, CA, USA) linear accelerator. Tumor motion traces were loaded into the HexaMotion programmable motion platform (Scandidos, Uppsala, Sweden) and triggered to start 10 s before the beginning of the beam delivery to allow training of the prediction algorithm. Calypso electromagnetic transponders (Varian Medical System, Palo Alto, CA, USA) were embedded into the HexaMotion platform, with a research version of the Calypso system sending the target position to the MLC tracking system. The kernel density estimation algorithm²⁴ currently used was clinically used for the lung trajectories.

2.B.2. Tumor motion

To span the type of tumor motion observed during radiation therapy, thoracic and pelvic tumor motion traces were selected from published databases to be characteristic three‐dimensional (3D) motion patterns for those sites. Four types of motion were chosen for the lung²⁵ from a CyberKnife study, and four motion patterns for the prostate²⁶ obtained from a study with patients implanted with Calypso electromagnetic transponders. These tumor motion traces were categorized and named according to their characteristic pattern in previous study. Thoracic motion patterns were categorized as typical tumor motion, high‐frequency breathing, a predominantly lateral motion, and characterized baseline shift. The represented prostate motion patterns were continuous drift, high‐frequency excursions, erratic tumor motion, and stable tumor position.

2.B.3. Treatment plans

For each clinical site (lung and prostate), a selection of treatment plans used for previous MLC tracking experiments²⁷ were delivered that differed in MLC modulation to span the plan complexity expected during clinical practice. Two plans, low and highly modulated VMAT plan, were selected for each site, by varying the set of competitive objectives on the target and OARs. All arcs spanned a 358° revolution with the collimator set at 90° (i.e., with the leaves parallel to longitudinal target motion). All plans were prescribed to deliver 2 Gy to 95% of the Planning Target Volume.

2.B.4. Evaluation of plan complexity

With MLC tracking, the plan complexity is known to complicate the task of the algorithm for the leaves to reach the desired positions.^{28, 29} Therefore, for each of the four plans lung/prostate and modulation high/low modulations, their complexity needed to be quantified. The plan complexity was evaluated based on four parameters:

1. MU weighted Average adjacent Leaf Distance (ALDw²⁹), previously shown to correlate with MLC tracking performance²⁸

2. The average leaf travel for each plan, considering solely the leaves that contribute to the open leaves aperture.²⁸

3. The average area over circumference $\mathit{AoC}$ ²⁸ with formula $AoC=\frac{\mathit{AreaofMLCaperture}}{\mathit{Circumference}}$

4. The VMAT modulation score (MCs) by Masi et al.³⁰

2.B.5. Measuring the system latency

Multileaf collimator tracking latency represents the inherent time delay between the tumor motion and the finished movement of the leaves to align the beam and the tumor. While execution of both MLC tracking algorithms possesses some inherent amount of latency, it is expected that a faster algorithm will be able to reduce the overall system latency.

The latency was evaluated using the setup described in Sawant et al.³¹ A ball bearing was moving in a superior–inferior direction along the parallel motion of a circular shape radiation field during which EPID images were acquired at 15 Hz operated on the computer console equipped with a 2.27 GHz Intel Xeon E5520 processor and 4 GB RAM. The ball bearing was placed onto the HexaMotion platform embedded with the Calypso electromagnetic beacons. For each optimization algorithm, EPID projections were obtained over 10 periods. Since both the ball bearing and the leaves move in a sinusoidal motion, the two structures were segmented from the EPID and a sinusoidal fit was used to calculate the temporal offset between the centroid of the ball and the MLC aperture. The latency was then calculated as the time delay between the ball position and the segmented MLC aperture.

2.C. Comparing MLC tracking algorithm performances based on leaf‐fitting exposure errors

To compare both performances, the exposure errors (overdose + underdose) were quantified in the beam's eye view using a framework developed by Poulsen et al.³²

The mismatched area between the actual and planned MLC aperture represents the total amount of exposure errors which can be separated into individual sources of errors, namely the exposure errors due to width of the leaves, their speed and prediction algorithm errors when in use.

For each experiment, the exposure errors were computed using the fitted MLC positions obtained from the MLC tracking software. The fitted MLC positions corresponded to the given MLC positions fitted by the algorithm, thereby accounting for the width of the leaves but regardless of their physical speed. Focusing solely on the fitted MLC position dismisses any potential source of uncertainties allowing for a more direct comparison between the algorithms.

For each paired experiment, the exposure errors throughout the treatment arc were compared between each other using the Pearson correlation coefficient and root‐mean‐square error to evaluate the differences in exposure errors for each control point. Figure 2 provides an example of the exposure errors for a “paired experiment”, representing identical experimental conditions (same plan and tumor). For each experiment, these exposure errors were computed using the resulting tumor tracking logs and fitted MLC position updated at 30 Hz into text files. Exposure error computation was achieved using MATLAB (R2017a, Math Works).

Figure 2.

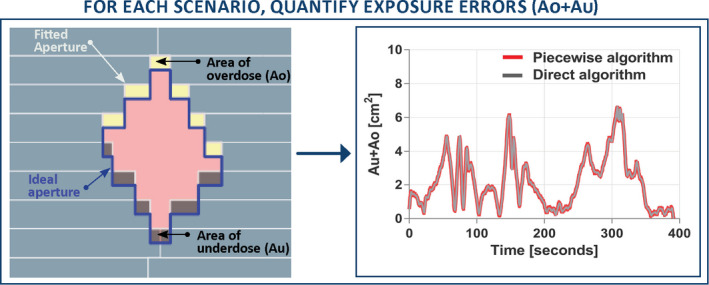
For each scenario, the exposure errors were compared for each set of paired experiments to compare the piecewise algorithm against the direct optimization.

3. Results

3.A. Quantification of exposure errors for each optimization algorithm

The average exposure errors for in silico low/high modulation were 0.66/0.88 cm² for direct optimization and 0.66/0.88 cm² for piecewise optimization. For the phantom experiment, it was 0.73/1.02 cm² for direct and 0.73/1.02 cm² for piecewise optimization. The side‐by‐side exposure errors displayed in Fig. 3 suggests that both algorithms performed equivalently spanning a large range of tumor motion, plan complexity, and treatment site.

Figure 3.

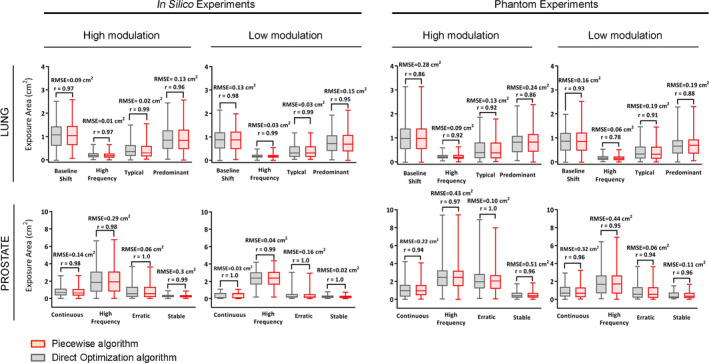
Leaf‐fitting exposure errors for the direct (gray) and piecewise (red) optimization for both in silico and phantom experiment (delivered). The Pearson correlation coefficient (r) and the root‐mean‐square error are provided for each paired experiment showing that the sum of exposure errors is equivalent given any tumor motion, organ, and plan complexity.

The analysis of the in silico experiments demonstrated that the Pearson correlation coefficient for both algorithms is higher than r = 0.96 for all sets of organs and trajectories. The similar data obtained during linac experiments also showed strong correlation (r > 0.9) in most cases. The mean root‐mean‐square errors (RMSE) between paired algorithms were 0.10 cm² for the in silico and 0.18 cm² for the phantom experiments. High correlation and small RMSE error suggest strong relationship between paired experiment results for all types of trajectory and plan complexity, indicating that both algorithms performed equivalently.

3.B. Relationship between plan complexity and exposure errors

The quantified simulated and phantom experiment exposure errors for each treatment plan established that the exposure errors from the high modulation plan (0.96 cm², 2.88 cm² 95% percentile) were all significantly different from the low modulation (0.70 cm², 2.18 cm² 95% percentile) (P < 0.001, two‐tailed, Mann–Whitney statistical test). The descriptive metrics used to quantify the plan complexity are summarized in Table 1.

Table 1.

Summary of the plan metric to assess the plan complexity of each of the four plans

	Lung		Prostate
	High modulation	Low modulation	High modulation	Low modulation
Field MU	596	342	737	422
ALDw	0.71 cm	0.20 cm	1.40 cm	0.70 cm
Leaf travel	0.19 cm	0.04 cm	0.30 cm	0.22 cm
AoC	0.34	0.75	0.49	0.92
MCS	0.07	0.17	0.15	0.28

AoC, Area over Circumference; ALD_w, Average adjacent Leaf Distance; MCs, modulation score; MU weighted.

The average distance to adjacent leaves and leaf travel distance was shown to increase with plan complexity while the modulation score (MCs) and relative area over circumference decreases with plan complexity. These results provide further evidence of the impact of treatment complexity on the exposure errors.

3.C. Latency

The latency for the direct optimization was 226 ± 10 ms and for the piecewise algorithm 228 ± 10 ms. These physical latencies can be compared with the fitting latency within the software. Across all the plans and tumor motion, the in silico fitting latency for the direct optimization algorithm was 12.2 ± 5 ms, compared with the piecewise algorithm computed as 3.1 ± 1 ms. Despite these differences, the fitting time between algorithms did not impact the overall latency of the experimental setup, only capable of detecting uncertainties within ±10 ms.

4. Discussion

The goal of this study was to characterize the performance of two MLC tracking algorithms for radiotherapy in a realistic simulated and clinical environment. Both algorithms were tested alternatively in silico and experimentally on a linear accelerator for the range of organ motion and plan complexity that may be expected during clinical practice.

This is the first time that two MLC tracking algorithms were experimentally compared in the identical clinical setting on a linear accelerator. Moore et al.¹ tested the performances of the piecewise algorithm in silico with IMRT plans as a proof of concept. However, leaf‐fitting is one part of the larger MLC tracking framework, and while in silico validation is a valuable tool to demonstrate proof of concept, the ultimate test is experimental investigation. Experimental investigation captures the impact of the leaf‐fitting algorithm with other software and hardware subsystems (e.g., compatibility issues with the Calypso tracking system, error catching, beam‐hold assertion, or constant rotating gantry during VMAT). For these reasons, this paper presents the first empirical comparison between the two algorithms.

We found that the plan complexity and tumor motion patterns have a much larger impact on dosimetric fidelity than the leaf‐fitting algorithms. The implication is that there are bigger gains to be made by improved planning than developing more complex or faster algorithms.

The implementation and development of faster MLC tracking algorithms is therefore potentially marginalized by the prerequisite to reduce plan complexity or improve the hardware capabilities. Hardware enhancement has been investigated under diverse forms. Pommer et al.²⁸ investigated the dosimetric impact of finer leaves by testing alternatively a Varian Novalis Tx with Millennium MLC (5 mm leaf with) and High‐Definition MLC (2.5 mm leaf width). Using reflective markers and the ExacTrac (Brainlab, Germany) to provide positional input to the tracking system, they found that finer leaves improved the tracking accuracy compared with 5 mm leaf width. The Varian TrueBeam system equipped with High‐Definition MLC also provides MLC tracking capabilities in developer mode, but no performance analysis or dosimetric comparisons with other systems have been published to date.

Falk et al.²⁹ found that leaf position constraints can be setup within the treatment planning system during planning optimization to limit the movement of the leaves during planning. Other hardware enhancement, such as dynamic alignment of the collimator angle,³³ hybrid couch‐MLC tracking strategies³⁴ improves MLC tracking accuracy by reducing the exposure errors for both prostate and lung.

Using a 2D time‐resolved framework for performance analysis provides a fast and reliable comparison of exposure errors. This method offers a point‐by‐point analysis that conceptually facilitates the search of exposure errors and allows a straightforward comparison between multiple plan parameters within a single fixed analysis framework. Also, the analysis of exposure errors for MLC tracking has been shown to be correlated with dosimetric errors for lung and prostate^{32, 35} using gamma failure and root‐mean‐square errors.

An application where MLC tracking is uniquely capable of motion compensation is tracking deforming targets and deforming systems, e.g., a primary tumor and regional nodes for locally advanced lung and prostate cancer radiotherapy. Preliminary studies using the direct optimization algorithm have investigated experimental target deformation and multitarget tracking.³⁶ These experiments have been carried out on a linear accelerator using phantoms by mapping the deformation field in the linear accelerator beam's eye view and optimizing the fitting process accordingly.

The treatment plans and the tumor motion traces are included as supplementary materials (Data S1) to allow other groups to benchmark their algorithms against the results shown here.

5. Conclusion

The performance of two MLC tracking algorithms was characterized and compared using a 2D time‐resolved framework in a clinical realistic scenario. The comparison was based on the quantification of fitted exposure errors attributed by the optimization algorithm solely, regardless of the speed of the leaves. Our results showed that the two algorithms performed similarly and provide equivalent quality‐of‐fit for the scenarios evaluated. The main source of error can be attributed to the complexity of the plan, quantified prior to plan delivery, which was shown to greatly impact on the MLC tracking accuracy.

Conflicts of interests

Paul J Keall and Jeremy Booth are investigators on one completed and two ongoing MLC tracking clinical trials that have been partially supported by Varian Medical Systems. Paul J Keall and Amit Sawant are inventors on one licensed patent and one unlicensed patent related to MLC tracking. Paul J Keall, Ricky O'Brien, and Vincent Caillet gratefully acknowledge funding from the Australian Cancer Research foundation. Paul J Keall acknowledges funding from an Australian Government NHMRC Senior Principal Research Fellowship.

Supporting information

Data S1: All the treatment plans and tumor motion traces used in this manuscript can be downloaded from the following link: https://cloudstor.aarnet.edu.au/plus/s/cC7Jy0LrfH2SiAz