Abstract
This paper describes a Bayesian method for learning causal Bayesian networks through networks that contain latent variables from an arbitrary mixture of observational and experimental data. The paper presents Bayesian methods (including a new method) for learning the causal structure and parameters of the underlying causal process that is generating the data, given that the data contain a mixture of observational and experimental cases. These learning methods were applied using as input various mixtures of experimental and observational data that were generated from the ALARM causal Bayesian network. The paper reports how these structure predictions and parameter estimates compare with the true causal structures and parameters as given by the ALARM network. The paper shows that (1) the new method for learning Bayesian network structure from a mixture of data that this paper introduce, Gibbs Volume method, best estimates the probability of the data given the latent variable model and (2) using large data (>10,000 cases), another model, the implicit latent variable method, is asymptotically correct and efficient.
Keywords: Bayesian Method, Bayesian Network, Causal Discovery, Latent Variable Modeling, Knowledge Discovery from Databases
1 Introduction
Causal knowledge makes up much of what we know and want to know in science and other areas of inquiry. Thus, causal modeling and discovery are central to science and many other areas. Experimental studies, such as randomized controlled trials (RCTs), provide the most trustworthy methods we have for establishing causal relationships. Typically, one or more variables are (randomly) manipulated and the effects on other variables are measured in experimental studies. Observational data are passively observed and can be used in cross-sectional, retrospective, or longitudinal study. In general, both observational and experimental data may exist on a set of variables of interest. For example, in public health, medicine, and biology, there is a growing abundance of case control studies (observational) and gene knock-out studies (experimental) using microarray gene expression data. In addition, for selected variables of high biological interest, there are data from experiments, such as the controlled alteration of the expression of a given gene. We need a coherent way of combining these two types of data to arrive at an overall assessment of the causal relationships among variables of interest.
Bayesian discovery of causal networks is an active field of research in which numerous advances have been—and continue to be—made in areas that include causal representation, model assessment and scoring, and model search [1, 2]. In prior work on Bayesian discovery of causal networks, researchers have focused primarily on methods for discovering causal relationships from observational data [2, 3]. A notable exception is a paper by Heckerman on learning influence diagrams as causal models. It contains key ideas for learning causal Bayesian networks from a combination of both experimental data under deterministic manipulation and observational data [4]. Bayesian discovery of causal networks with latent variables has been widely applied in systems biology research, especially in learning gene networks from various experiments [5–7].
The contribution of the current paper is to investigate explicitly and in detail the learning of causal models from an arbitrary mixture of observational and experimental data. It extends earlier work [8] by considering latent variables. First, this paper introduces several traditional and a new method, Gibbs Volume method, to approximate the Bayesian scoring of structures that include latent variable. Also we further specify necessary conditions to derive a close-form formula for a heuristic causal learning method that was introduced earlier, Implicit Latent Variable Scoring method (ILVS), and show with large (10,000 observational and 10,000 experimental) simulation cases that ILVS is asymptotically correct and efficient. Next, the paper describes Bayesian methods for learning Bayesian networks when variable manipulation is not necessarily deterministic, but rather stochastic. In the important special case in which manipulation is deterministic, there is a closed-form Bayesian scoring metric that is a simple variation on a previous scoring metric for Bayesian network learning [3, 9]. Finally, the paper investigates the learning performance of the best-performing method for scoring (approximately) a Bayesian network that contains latent variables. This evaluation is a simulation study in which cases were generated from the ALARM causal Bayesian network.
2 Modeling Methods
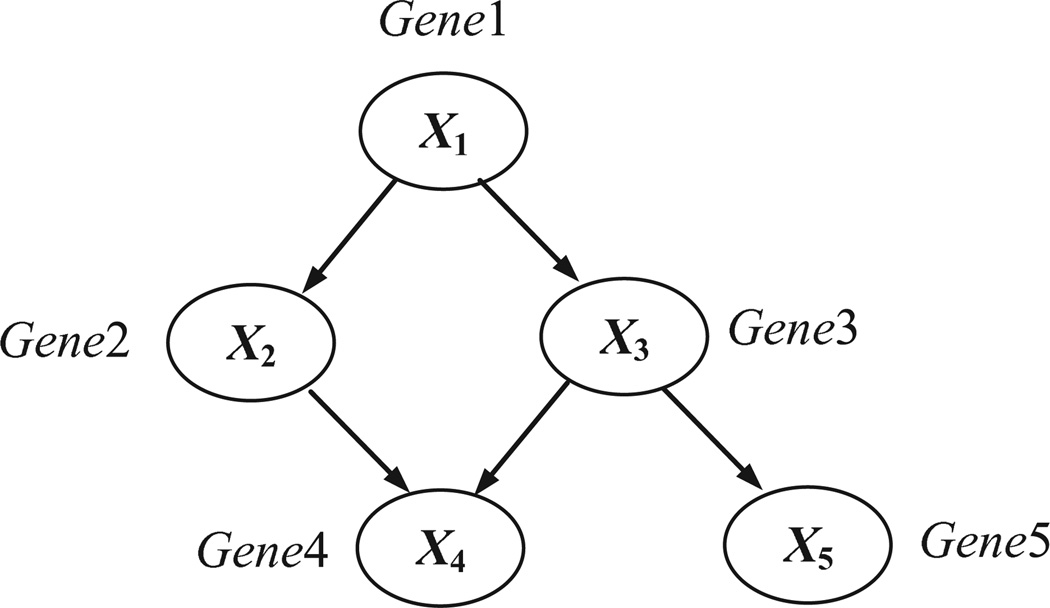
A causal Bayesian network (or causal network for short) is a Bayesian network in which each arc is interpreted as a direct causal influence between a parent node (variable) and a child node, relative to the other nodes in the network [10]. Figure 1 illustrates the structure of a hypothetical causal Bayesian network structure that contains five nodes. The probabilities associated with this causal network structure are not shown.
Figure 1.
A causal Bayesian network that represents a hypothetical gene-regulation pathway.
The causal network structure in Figure 1 indicates, for example, that the Gene1 can regulate (causally influence) the expression level of the Gene3 gene, which in turn can regulate the expression level of Gene5 gene.
A node is independent of its non-descendants (i.e., non-effects) given its parents (i.e., its direct causes).
The causal Markov condition permits the joint distribution of the n variables in a causal Bayesian network to be factored as follows [10]:
| (1) |
where xi denotes a state of variable Xi, πi denotes a joint state of the parents of Xi, and K denotes background knowledge that is discussed in the next section.
2.1 A General Bayesian Analysis
This section considers the posterior probability that variable1 X causes variable Y given database D on measured variables V. Let H denote an additional set of latent (hidden) variables. We use V+ to designate the union of V and H. Let S denote an arbitrary causal Bayesian network structure containing all of the variables in V+. Let K denote any background knowledge that may influence our beliefs about the causal relationships among the variables in V+ . Such background knowledge could come from scientific laws, common sense, expert opinion, or accumulated personal experience, as well as other sources. As we will see later in this section, K can also include knowledge of which cases (also known as records, instances, or samples) in D are experimental and which are observational. We can derive the posterior probability that X causes Y as:
| (2) |
where the sum is taken over all causal network structures that (1) contain just the nodes in V+, and (2) contain an arc from X to Y2. Based on the properties of probabilities, the term within the sum in Equation 2 may be rewritten as follows:
| (3) |
Since the probability P(D | K) is a constant relative to the entire set of causal structures being considered, Equation 2 shows that the posterior probability of causal structure S is proportional to P(S, D | K), which we can view as a score of S in the context of D. The probability terms on the right side of Equation 3 may be expanded as follows:
| (4) |
where (1) P(S | K) is a prior belief that network structure S correctly captures the qualitative causal relationships among the variables in V+; (2) θS are the probabilities (parameters) that relate the nodes in S quantitatively to their respective parents; (3) P(D | S, θS , K) is the likelihood of data D being produced, given that the causal process generating the data is a causal Bayesian network given by S and θS ; and (4) P(θS | S, K) expresses a prior belief about the probability distributions that serve to model the underlying causal process. The integral in Equation 4 integrates out the parameters θS in a causal Bayesian network with structure S to derive P(D | S, K), which is called the marginal likelihood. Combining Equations 2, 3, and 4, we obtain Equation 5:
| (5) |
The only assumption made in this equation is that causal relationships are represented using causal Bayesian networks.
The full Bayesian approach to causal discovery expressed by Equation 5 considers—at least in principle—all causal Bayesian networks that are a priori possible. Thus, for example, the sums in Equation 5 are over all possible causal Bayesian network structures on V+, and the integrals are over all possible parameters for each possible causal structure. The result of such a global analysis of causality is that the derived posterior probabilities summarize a comprehensive, normative belief about the causal relationships among a set of variables.
The Bayesian analysis given by Equation 5 presents three considerable challenges: (1) the assessment of prior probabilities on causal network structures and parameters; (2) the summation over a large set of causal network structures; and (3) the evaluation of the integral for each causal network structure. In this paper, we focus on the third task. In particular, we introduce a set of assumptions that simplify the evaluation of the integral, and we show that the solution corresponds closely to a previous solution for observational data only.
2.2 Modeling Manipulation
In the current section, we consider the situation in which manipulation of a variable may not be deterministic. A classic example from medicine is when a patient, who has volunteered to participate in a study, is randomized to receive a certain medication, but he or she decides not to take it. Let MXi be a variable that represents the value k (from 1 to ri) to which the experimenter wishes to manipulate Xi. Let MXi = o denote that the experimenter does not wish to manipulate Xi, but merely wants to observe its value. Augment the model variables V in Section 2.1 to include MXi. Finally, carry out the analysis in Section 2.1 assuming only observational data. The causal network hypotheses used in that analysis will include probabilities that specify prior beliefs about the causal influence of MXi on Xi. Those prior beliefs (on structure and parameters) will be updated by data on stated experimental intentions and observed variable value outcomes. For the special case of deterministic manipulation, we have that (1) with probability 1 variable MXi is a parent of Xi; and (2) , where are the parents of Xi other than MXi. When scoring Xi, this is equivalent to ignoring the cases in which Xi were manipulated [8]. In the remainder of this paper, we assume that manipulation is deterministic.
For example, Figure 2 shows a causal network structure that has an additional variable MX2 relative to the network structure in Figure 1. In Figure 2, variable X2 (Gene2) is modeled as being manipulated in some cases, such as, knocking out Gene2.
Figure 2.
A hypothetical causal Bayesian network structure with manipulation
To incorporate experimental data, we evaluate the following equation [3, 9]:
| (6) |
where ri is the number of states that Xi can have, qi denotes the number of joint states that the parents of Xi can have, Nijk is the number of cases in D in which node Xi is passively observed to have state k when its parents have states as given by j, Γ is the gamma function, αijk and αij express parameters of the Dirichlet prior distributions, and . We used the BDe metric [3] with which is a commonly used non-informative parameter prior for the BDe metric. Note that to incorporate experimental data, we evaluate Equation 6 not adding the cases to Nijk when Xi is manipulated [8]. It also follows from the results [3, 9] that when Xi is observed, we estimate its conditional distribution as follows:
| (7) |
2.3 Parameter Estimation
Since the probabilities given by Equation 6 define all the parameters for a causal Bayesian network B with structure S, we can use B to perform probabilistic inference. Let P(Xa | xb, D, S, K) designate a generic instance of using B to infer the distribution of the variables in Xa conditioned on the state of other variables as given by xb. We assume that Xa contains only variables that will be observed. The variable set xb may, however, contain both observed and manipulated variables.
In this paper we model latent variable H to be discrete. We define a fill-in as substituting missing values in the dataset. Let D be a dataset with a latent variable and D̂ be the set of all possible unique complete datasets that could be generated with fill-ins of D. The size of D̂ is exponential in the number of cases in D . We also define dimensionality to be the number of states of the latent variable H and denote it as Z. Since we do not know the actual dimensionality of H, it is reasonable to use a weighted sum among the possible dimensionalities of H. We can infer the distribution of Xa conditioned on xb by model averaging over all dataset fill-ins, over all possible network structures, and over all possible dimensionalities of H as follows:
| (8) |
where UB is an upper bound for the dimensionality and
| (9) |
Here, it would be ideal if we could make UB → ∞, but this is not computationally feasible. In this paper we seek a proper value for UB such that the sum for all j > UB in Equation 8 is relatively small compared to the sum for j=2,3,…,UB. Note that in Equation 8, we are assuming uniform priors for the dimensionalities Z=2,3,…,UB and P(S|Z=j,K)= P(S|Z=k,K) for all j and k.
Sampling all possible complete datasets in D̂ is not feasible, especially with large number of cases (>30). So we sample a fixed number of complete datasets from D̂. If we denote each sampled complete dataset as Di, then we use instead of D̂ in Equation 8, where Nd is the number of the complete datasets generated by the sampling method.
3 Scoring Methods of Structures with Latent Variable
Exact computation of scoring causal structures with a latent variable is not feasible because we have to calculate the following:
| (10) |
where each Cl represents one of m measured (observed or manipulated) cases and Hl is the l-th case of the latent variable H in data set D. In Equation 10, the term P(Cl, Hl | S,θS , K) denotes using the causal Bayesian network with structure S and parameters θS to infer the probability of the state of the variables as given by Cl and Hl. We define a configuration as a unique instantiation among the variables. For example, if we have binary node X and Y, possible configurations are (T,T), (T,F), (F,T), and (F,F), where T and F stand for “True” and “False” states, respectively. The number of configurations of H is exponential in m. Thus, in practice, we use approximation methods to evaluate Equation 10.
To investigate the performance of various methods for scoring causal structures with a latent variable, we (1) implemented a brute force method, a heuristic method, and five different sampling methods; and (2) evaluated them with simulated data. We selected the best-performing method and used it for the experiments described in Section 4.2.
In Section 3.2 we introduce six approximation methods, and in Section 4.1 we compare their performances. Among the six approximation methods, we introduce an heuristic method called the Implicit Latent Variable Scoring (ILVS) method to score efficiently, in closed form, a causal relationship that includes a latent variable. We also compare the performance of the ILVS method with the best-performing approximation method.
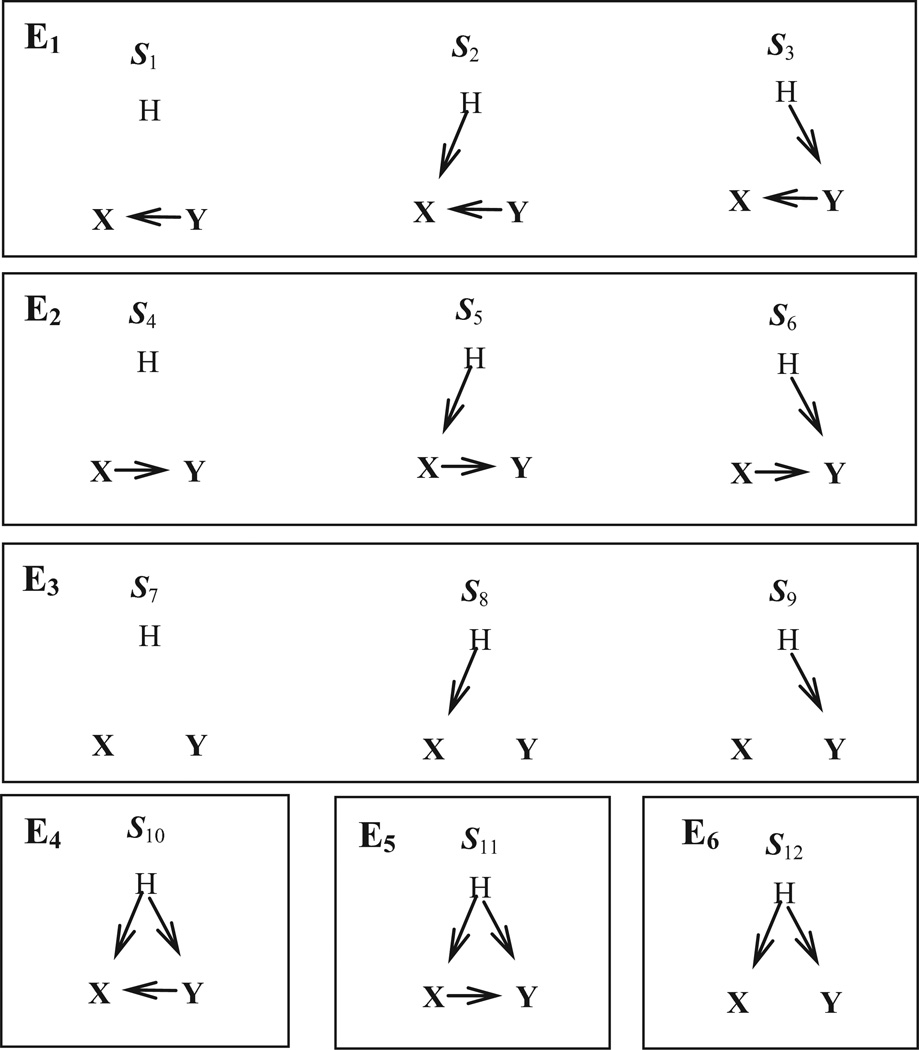
3.1 Latent Variable Model
We introduce 12 hypotheses of causal Bayesian network structures (S1 through S12) and 6 equivalence classes (E1 through E6) among the relationships between two variables (Figure 3). The causal networks in an equivalence class are statistically indistinguishable for any observational and experimental data on X and Y. We denote an arbitrary pair of nodes in a given Bayesian network B as (X, Y). If there is at least one directed causal path from X to Y or from Y to X, we say that X and Y are causally related in B. If X and Y share a common ancestor, we say that X and Y are confounded in B. We understand that modeling all nodes will decrease the structure and parameter prediction errors, but as the first step of modeling latent variable, we only look at pairwise relationships between two nodes (X and Y) and a latent variable H.
Figure 3.
Twelve hypotheses and six equivalence classes
3.2 Latent Variable Scoring Methods
In this section we introduce six different scoring methods. We denote D(X,Y) as a dataset where both node X and Y are observed. D(mX,Y) denotes a dataset where node X is manipulated and Y is observed in every case in that dataset. Similarly, D(X,mY) denotes a dataset where node X is observed and Y is manipulated.
3.2.1 Implicit Latent Variable Scoring (ILVS) Method
In this section we introduce the implicit latent variable scoring (ILVS) method that was first described in Yoo and Cooper [11] and referred by many others [12–15]. The focus in this section will be on modeling with a single latent variable.
Since the number of configurations of a latent variable is exponential in the number of cases in Equation 10, approximation methods have been used to evaluate the equation, including methods based on stochastic simulation and on expectation maximization [16–18]. However, with large number of cases (> 50), the approximation methods often fail in producing acceptable approximations even after a long computation time. These challenges motivated our development of the Implicit Latent Variable Scoring (ILVS) method [19].
The main idea behind ILVS is to assume parameters’ distributions of different experiments are independent. This enables us to effectively decompose the scoring of a latent variable model into scoring multiple non-latent variable models. Note that these non-latent variable models can be scored using Equation 6. Finally, we combine the scores of the non-latent variable models to derive an overall score (i.e., marginal likelihood or ILVS score). Note that this transformation (a latent variable model into non-latent variable models) enables us to calculate the ILVS score within the time that is linear to the number of cases.
In this section, we expand Equation 4 under the assumption of impendency of parameters’ distributions (of experiments) and derive how we calculate the ILVS score. After the derivation, as an example, we use a small dataset and show how the ILVS score is calculated. In the following sections, we use large (10,000 observational and 10,000 experimental) simulation cases to show ILVS is asymptotically correct and efficient.
We denote D(X, Y) as the set of cases (in dataset D) where both node X and Y are observed. D(mX, Y) denotes set of cases where node X is manipulated and Y is observed. Similarly, D(X, mY) denotes set where node X is observed and Y is manipulated. If the latent variable distribution is the same for D(X, Y) and D(mX, Y) and for D(X,Y) and D(X, mY) then we cannot distinguish between E1 and E4, E2 and E5, and E3 and E6. Therefore, the six equivalence classes collapse to three equivalence classes: ℵ1(E1 and E4), ℵ2(E2 and E5), and ℵ3(E3 and E6). However, in the remainder of this paper we will assume that the latent variable distribution is different for D(X, Y) and D(mX, Y) and for D(X,Y) and D(X, mY)..
The ILVS method scores the six equivalence classes shown in Figure 3 by using a heuristic Bayesian method. Since scoring E3 is straightforward, we will concentrate on other equivalence classes. Also it is easy to see that the scoring of E1 and E2 and of E4 and E5 are symmetric. Therefore we will only describe the scoring methods of E2, E5, and E6. ILVS does not explicitly model the latent variable as in Equation 10, nor does it use a sampling method. Instead, ILVS uses the method described in Section 3.1.3 to calculate the marginal likelihood, as is explained next.
To illustrate the ILVS method, we assume that we have a statistical method that can tell us whether X and Y are statistically dependent (e.g., correlated) above some specified threshold. Additionally, we assume that the faithfulness condition [2] holds between each equivalence-class causal structure and its parameters. This means that if the causal structure indicates no independence, then in fact there is dependence. For example, if E2 were the generating causal structure of a dataset, then according to the faithfulness assumption X and Y should be dependent. In Table 1, p(Y | X) denotes the conditional probability distribution of Y given X for the cases D(X,Y), p(Y | mX) denotes the conditional probability distribution of Y given X for the cases D(mX, Y), and p(X | mY) denotes the conditional probability distribution of X given Y for the cases D(X,mY). The function δ is defined as follows:
where p and p′ are any probability distributions. In Table 1, p(Y | X) and p(Y | mX) are different except for equivalence classes E2 and E3. This is because deterministic manipulation of X changes a structure in equivalence classes E1, E4, E5, and E6 into a structure in some other equivalence class. In general, we expect different structures to have different distributions. For example, for structure S11 in E5, deterministic manipulation of X removes the causal link from H to X, and consequently S11 (in E5) becomes S6 (in E2)). In contrast if a causal process has an E2 structure, then data generated by manipulating X and observing Y will have the same distribution for Y as data generated by passively observing X and Y. A parallel situation holds E3. Analogously, in the last column of Table 1, E1 and E3 are indistinguishable.
Table 1.
Equivalence classes and their patterns of statistical dependency
| Dataset & Function | ρ(X, Y) | ρ(mX, Y) | ρ(X, mY) | δ(p(Y|X), p(Y|mX)) |
δ(p(X|Y), p(X|mY)) |
|---|---|---|---|---|---|
| Equivalence Classes | |||||
| E1 | + | − | + | 0 | 1 |
| E2 | + | + | − | 1 | 0 |
| E3 | − | − | − | 1 | 1 |
| E4 | + | − | + | 0 | 0 |
| E5 | + | + | − | 0 | 0 |
| E6 | + | − | − | 0 | 0 |
The + and − symbols in Table 1 represent the output of the statistical method, where + and − represent statistically dependent and not statistically dependent respectively. It is easy to see that when X and Y are causally related or confounded, the statistical method outputs that X and Y are statistically dependent (+). For example, since X and Y are confounded in E6, the statistical method outputs that X and Y are statistically dependent (+) when X and Y are passively observed (D(X,Y)). When X is manipulated (D(mX,Y)) from Figure 3, we see that S12 (in E6) becomes S9 (in E3) and the statistical method outputs that X and Y are not statistically dependent (−).
Additionally, Table 1 shows that neither observational data nor experimental data alone can distinguish all six equivalence classes. Observational data alone (D(X,Y)) can distinguish E3 from the other five equivalence classes. Experimental data alone, which involves cases generated by manipulation of X and/or Y, cannot distinguish E1 from E4, E2 from E5, nor E3 from E6. Only when we combine the observational and experimental data can we distinguish all six equivalence classes. For example, to distinguish between E3 and E6, we can check the value of δ(p(X | Y), p(X | mY)). If it is 0, indicating that these two distributions differ, this result suggests E6; otherwise, it suggests E3.
In a previous simulation study with a large number of stochastically generated cases (>50,000), we show that the ILVS method scored the generating structure as the most probable structure with high posterior probability (>0.99) [11]. An open issue is to investigate theoretically the convergence properties of ILVS to the patterns in Table 1 in the large sample limit. We show that with additional assumptions, the ILVS method can be readily derived as an extension of Equation 6.
The ILVS method models the possible relationships between variables X and Y with the Bayesian networks X → Y , Y → X, and X → Y. So in terms of Bayesian networks, the ILVS method uses the same structure for E1 and E4, and E2 and E5. Structure E6 can be represented either as X → Y or Y → X. E1, E2, and E3 can be scored directly with the method discussed in Section 2.1, because the Bayesian network structures of these three classes correctly represent their distributions. For example, consider scoring a hypothesis that the generating structure is E1. In this situation we use a Bayesian network Y → X for scoring with the cases in D(X,Y). For scoring with the cases in D(mX, Y), the Bayesian network structure changes to Y → X, because the deterministic manipulation of X removes all of the arcs coming into X; we see a distribution change as expected, and thus, δ(p(Y | X), p(Y | mX))=0. For D(X, mY), the Bayesian network does not change in E1, and the distribution does not change, and thus δ(p(X | Y), p(X | mY)) =1.
Structure E4 must be handled differently from E1, E2, and E3, because of the presence of confounding in E4. When E4 is the data generating causal structure, the distribution of X obtained by passively observing X when Y is observed to be y will in general be different than the distribution of X that is obtained upon manipulating Y to the value y. These two distributions can be represented by the same network structure with an arc from Y to X, but the two Bayesian network models are different because the distributions on those network structures are different.
Hypotheses E5 and E6 also contain confounding, and they are handled in a way analogous to E4.
As previously stated, scoring E4, E5, and E6 needs a different method than that used in Section 2.1. The term P(D | S, θS, K) in Equation 4 can be expanded as follows, given the assumptions in Section 2.1:
| (11) |
Let D = D(X, Y) ∪ D(mX, Y) ∪ D(X ,mY). Let ξ, = {ED(X, Y), ED(mX, Y), ED(X, mY)} be the set of experiments that are performed to obtained data D3, where ED(X,Y) denotes passively observing X and Y, ED(mX,Y) denotes manipulating X and passively observing Y, and ED(X,mY) denotes manipulating Y and passively observing X If we assume that a distribution of parameters under an experiment ε∈ ξ, is independent of a distribution of parameters under an experiment ε′∈ ξ, where ε ≠ ε′ we may expand Equation 11 as follows4:
| (12) |
where is the parent of the node Xi under the experiment ε, Sε and θε are the overall structure and parameters under the experiment ε, and is the number of cases in D in which node Xi has state k when its parents have states as given by j under the experiment ε. Note that if for all experiments ε, then Equation 12 becomes Equation 11 for node Xi.
Using the same assumption of independence as used in Equation 12, P(θS | S, K) may be expanded as follows:
| (13) |
where represents under the experiment ε. Combining Equation 12 and Equation 13 and using Theorem 1 from Cooper and Herskovits [9], we derive:
| (14) |
where and express parameters of Dirichlet prior distributions under the experiment ε., and . Let ε0 denote an experimental condition where the experimenter passively observes all variables modeled in a Bayesian network B.
Equation 12, Equation 13, and Equation 14 state that if there is an experimental condition ε, where ε ≠ ε0 and ε modifies the Bayseain network B (either its structure or its parameter), separately consider the and terms and the and terms in deriving the overall score. This is consistent with how ILVS scores hypotheses E1, E2, and E3. Next, we will describe how ILVS score hypotheses E4, E5, and E6 and not surprisingly it is analogous to Equation 12, Equation 13, and Equation 14.
Based on Equation 14, we will show how to derive the marginal likelihood for a hypothesis E5. Since (just considering measured variables) for all experiments ε in class E5 (X → Y), we score node X with Equation 11 and dataset D = D(X,Y) ∪ D(X,mY). Since δ(p(Y | X), p(Y | mX))=0, indicating that the distributions (p(Y | X) and p(Y | mX)) are in general different, we score node Y with Equation 12, which expands to become:
| (15) |
In summary, for class E5, we score node X by pooling the cases in D(X,Y) with those in D(X, mY), because we expect there to be the same distribution over X in both these sets of datasets. We score node Y with two different Bayesian networks. One network scores the cases in D(X, Y). A second network scores the cases in D(mX, Y). Although both these networks have the same structure that contains an arc from X to Y, they have in general a different distribution for Y given X, because the first network models confounding and the second one does not.
The scoring of hypothesis E4 is directly analogous to the scoring of E5 just described. For class E6, there is no direct causal relationship between X and Y. Since there is confounding between X and Y, we can model the statistical dependency between X and Y with either Bayesian network X → Y or Y → X. We randomly choose one of these two structures by randomly mapping node X and Y to nodes PXY and CXY, which represent the parent and child nodes, respectively, in the Bayesian network that is used for scoring E6. The scoring method is now almost the same as that used for E5. Node PXY is scored just like the node X in E5, by pooling the cases in D(PXY, CXY) with those in D(PXY, mCXY). We score node CXY slightly differently than node Y in E5, expanding Equation 12 as follows:
| (16) |
where for brevity P and C denote PXY and CXY, respectively.
As shown in Equation 16 we score CXY with D(PXY, CXY) and D(mPXY , CXY) separately, as we scored node Y in E5. Note that node Y in E5 is scored as a child node in two Bayesian networks, whereas for node CXY with D(PXY, CXY), it is scored as a node with a parent PXY (Figure 4(a)), and with D(mPXY, CXY), it is scored as a node without a parent (Figure 4(b)).
Figure 4.
Scoring E6.
Note that for E6, we assigned X as PXY and Y as CXY.
Finally, we assume that P(Ei | K) = 1/6 for i=1,2,…,6. That is, we assume that each equivalence class is equally likely. Therefore, we can solve Equation 4 as P(Ei,D | K) = 1/6. P(D| Ei, K), which can then be used to solve Equation 3.
When n variables and m cases are given, the computational complexity of ILVS is O(mn2). ILVS has to consider pairs of variables and for each pair, it has to evaluate terms in Equation 14 with m cases.
We developed and investigated other latent variable approximation scoring methods, including Gibbs sampling methods [11]. We have shown that ILVS not only performs as well as these other sampling methods, but also runs much faster than the other methods
As an example, we derive the marginal likelihood P(D| E2, K) using the ILVS method with the hypothetical data in Table 2.
Table 2.
An Example Dataset
| case# | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| variable | ||||||||||||
| X | F | T | T | T | F | T | F | T | T | T | F | T |
| MX | o | o | o | o | F | T | F | T | o | o | o | o |
| Y | T | F | F | F | T | F | T | F | F | T | F | T |
| MY | o | o | o | o | o | o | o | o | F | T | F | T |
We assume that X and Y are binary variables. Note that in Table 2, cases 1 through 4 represent D(X,Y), cases 5 through 8 represent D(mX,Y), and cases 9 through 12 represent D(X,mY). Also, we assume that the manipulation is deterministic.
For E2, we apply Equation 6 to derive P(D | E2, K) as follows:
where we have assumed that the parameters α1jk equal 1/2 and the parameters α2jk equal 1/4.5 We use the convention that F is represented by k = 1 and T by k = 2. When i = 2, the parent state X = F of Y is represented by j = 1, and the parent state X = T of Y by j = 2. For example, consider the term N221, which corresponds to the frequency with which jointly Y has the state F and X (the parent of Y in the hypothesis being considered) has the state T. Following the analysis in Section 2.1, we derive N221 from Table 2 by considering only the cases in which Y was not manipulated; these correspond to the first eight cases in the table. Of those eight cases, five occur when Y has the state F and X has the state T. Thus, N221 = 5 in the equation of the example.
As another example, we derive P(D | E5, K) using the dataset given in Table 2 as follows:
Note that for E5 we have two separate counts for node Y: Nijk and . Nijk is the count from D(X,Y) and is the count from D(mX,Y).
Using the dataset from Table 2, we derive P(D | E6, K) as follows:
3.2.2 Gibbs Volume Method
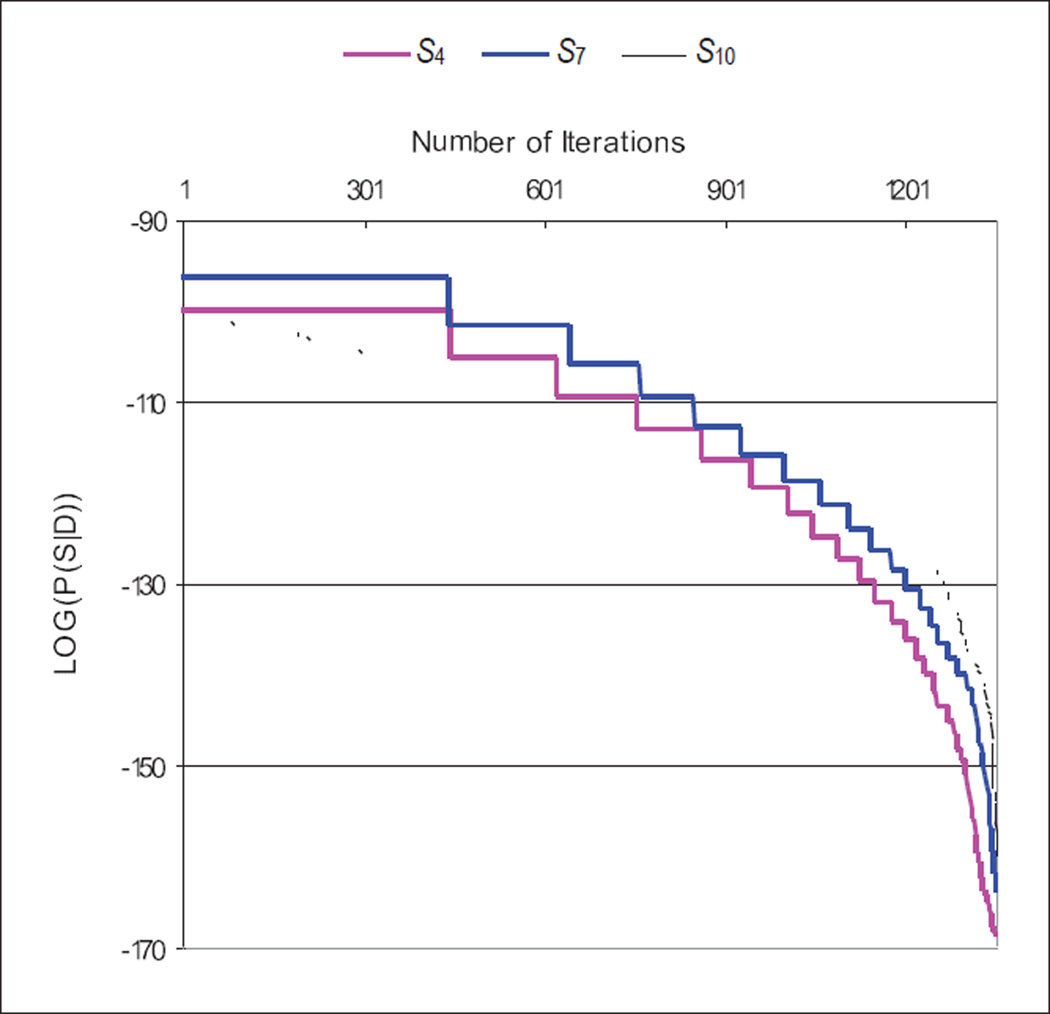
Figure 5 is generated by Gibbs Sampling (see Appendix A.2) on two variables from Alarm Bayesian network, namely: “error in heart rate reading due to low cardiac output” (ERRLOWOUTPUT, node 7) and “heart rate obtained from electrocardiogram” (HREKG, node 9). Their true equivalence class is E3. We used a binary latent variable with non-informative prior over its distribution. We generated 1,500 complete datasets Di in Gibbs Sampling and sorted by the log score of P(Di | S, K). In Figure 5, the X-axis represents the number of iterations and the Y-axis represents the log(P(Di| S, K)) for each of the structures S4 (in class E2), S7 (in class E3), and S10 (class E4) in Figure 3. The figure apparently shows that the curve decreases fairly smoothly, especially when the structure is confounded. We observed the same trend among all 12 structures.
Figure 5.
Gibbs Sampling score plot sort by P(Di | S, K) score
If the Y-axis of the plot in Figure 5 is plotted on a linear scale rather than a logarithmic one, then the area underneath the curve approximates Equation 10. If we choose the maximum score (the Gibbs Maximum method) from Figure 5, it is clear that the area underneath is underestimated. The Gibbs Maximum method assumes that the structure score space is a delta function. Figure 5 supports that the search space does not necessarily contain a delta function, at least not for a feasible number of iterations. So a better approximation may be a sampling method that estimates the area directly. The Laplace approximation method seeks to approximate the volume closely [20]. Since, however, this method depends on asymptotic normality (in the large sample limit), it may not be an accurate approximation for typical finite samples. The Gibbs Average method assumes that Gibbs Sampling samples the fill-ins of H uniformly. Figure 5 shows that Gibbs Sampling samples more of the fill-ins of H, where P(Di | S, K) is higher. We introduce a new method called the Gibbs Volume method (we simply refer it as Gibbs Volume).
This method estimates Equation 10 by using Gibbs Sampling (see Appendix A) and bookkeeping of the fill-ins that it has generated. The pseudo-code of the method is shown in Figure 6. There are two major steps in the Gibbs Volume method: First, the method randomly fills in the missing values in D and generates a complete dataset D0. Second, in the i-th iteration, the Gibbs Volume method applies Gibbs Sampling on Di−1 to generate Di. Gibbs Sampling does not guarantee that the complete dataset Di will be different from D0, …, Di−1. Thus, we need to store all the previous fill-ins of D0, …, Di−1 to check the uniqueness of Di. In the i-th iteration, let the previous set of unique fill-ins be denoted as Pi−1 (Pi−1 = {H0,H0,…,Hi−1}, where Hj denotes the fill-in in Dj). If Hi has different fill-ins from all Hj∈ Pi−1, we let Pi = Pi−1 ∪ Hi and continue to the (i+1)-th iteration. Otherwise, discard Di and repeat the i-th iteration. We repeat the second step (N−1) times to generate N unique complete datasets D0, …, DN−1.
Figure 6.
Pseudo-code of the Gibbs Volume method given dataset D and number of iterations N.
We perform the above two steps for all 12 structures (Figure 3). Let PN−1[Sk] be the unique fill-ins generated using structure Sk after the (N−1)-th iteration. We define ST = {PN−1[S1],PN−1[S2],…,PN−1[S12]}. The score for structure Si is calculated as follows:
| (17) |
where C denotes data on the measured variables.
3.2.3 Other Methods
Other methods are mentioned briefly in this section. The methods are described in detail in Appendix A.
Efficient Brute Force Method
By grouping configurations for observed variables in D, Cooper [21] provides a method for solving Equation 10 that is polynomial in the number of cases but exponential in the number of configurations.
Gibbs Sampling Method
Gibbs Sampling [22] is a Monte-Carlo method to approximate Equation 10. Initially, Gibbs Sampling fills in randomly the missing state of variables in the dataset D. Case by case, subsequent steps efficiently calculate the distribution of the latent variable given the observed cases and fill in the latent variable according to the calculated distribution.
Gibbs Sampling and EM Method (Candidate Method)
This approximation method combines Gibbs Sampling with an expectation maximization (EM) method [23]. Using the EM method with Gibbs Sampling is known as the Candidate Method [24].
Importance Sampling Method
Self-importance sampling samples more often where the dataset indicates that the configuration of the latent variable is more probable [25].
Importance Sampling with Gibbs Sampling
This method combines Gibbs Sampling with Importance Sampling. This combined method first performs the Gibbs Sampling to generate a complete dataset D*. Then it uses the Importance Sampling upon dataset D*.
4 Experimental Methods
In section 4.1, we compare ILVS and Gibbs Volume with other latent variable scoring methods. We show that ILVS and Gibbs Volume perform as good as (or even better than) other latent variable scoring methods. In section 4.2, we further compare how well ILVS and Gibbs Volume predict causal relationships.
4.1 Comparison of Latent Variable Scoring Methods
We compare ILVS and Gibbs Volume with other latent variable scoring methods that were introduced in Section 3.2.3. Simulation data from a well known Bayesian network were used for the comparisons. We describe the simulation data in the next section.
4.1.1 Data Generation
Since confident knowledge of underlying causal processes is relatively rare, for comparison of approximation methods and study of causal discovery from mixed data, we used as a gold standard a causal model constructed by an expert. In particular, we used the ALARM causal Bayesian network6, which contains 46 arcs and 37 nodes that can have from two to four possible states. Beinlich constructed ALARM as a research prototype to model potential anesthesia problems in the operating room [26]. In constructing ALARM, he used knowledge from the medical literature, as well as his personal experience as an anesthesiologist. The 37 nodes in ALARM may be paired in 666 unique ways. Table 3 summarizes the types of causal relationships among the 666 node pairs of ALARM. Recall from Section 3.1 that if there is at least one directed causal path from X to Y or from Y to X, we say that X and Y are causally related. If X and Y share a common ancestor, we say that X and Y are confounded. We randomly selected 100 of the 666 node pairs. Table 4 shows the frequencies of the types of pairs that were sampled. The frequencies in Table 4 closely match those in Table 3, supporting that this sample of 100 is not biased.
Table 3.
Types of Node Pairs in ALARM
| Confounded | Total | |||
|---|---|---|---|---|
| Yes | No | |||
| Causally Related |
Yes | 56 (8.4%) | 167 (25.1%) | 223 (33.5%) |
| No | 78(11.7%) | 365 (54.8%) | 443 (66.5%) | |
| Total | 134 (20.1%) | 532 (79.9%) | 666 (100%) | |
Table 4.
Types of Node Pairs Sampled from ALARM.
| Confounded | Total | |||
|---|---|---|---|---|
| Yes | No | |||
| Causally Related |
Yes | 8 (8.0%) | 29 (29.0%) | 37 (37.0%) |
| No | 11 (11.0%) | 52 (52.0%) | 63 (63.0%) | |
| Total | 19 (19.0%) | 81 (81.0%) | 100 (100%) | |
Let U denote these 100 pairs. For each pair (X, Y) in U, we used stochastic simulation [27] to generate three types of data from ALARM. In particular, we generated data in which (1) X is manipulated and Y is observed (D(mX,Y)); (2) Y is manipulated and X is observed (D(X,mY)); and (3) X and Y are both observed (D(X,Y)). For data that were generated under manipulation, we used a uniform prior over the states by which to manipulate the manipulated variable (e.g., if X is binary with states T and F, then P(MX = T) = P(MX = F) = 0.5). We generated (1) up to 250 cases for each of D(mX,Y) and D(X,mY); and (2) up to 500 cases for D(X,Y).
4.1.2 Comparison of Latent Variable Scoring Methods
To compare the performance of all the approximation methods, we should ideally give each approximation method the same number of operations to execute. However, this is not feasible because different approximation methods have different numbers of steps to generate the final scores for each structure. Therefore, we tried to equalize the number of iterations, or the number of complete datasets generated by fill-ins, of each approximation method. We selected 700 iterations of Gibbs Sampling and matched other methods to run with the same number of iterations. 700 iterations was selected based on the fact that the Gibbs Sampling score had significantly low variance than 600 iterations but not significantly larger variance than 800 iterations.
We performed two experiments with the 100 node pairs from ALARM network. For the first experiment (Small Case Experiment), we compared the performance of each method by counting how many highest scored structure compute by the method matches the highest scored structure compute by the Efficient Brute Force (EBF) method. The evaluation score of each method is defined as the number of instances where both the given method and the EBF method picked the same structure as the most probable relationship. As explained in Appendix A.1, the computational complexity of the EBF method depends on how many configurations we can get from the observed variables in the dataset. More cases in the dataset can be used to score the EBF method if the numbers of groups are relatively small. The number of cases we can score with the EBF method varies among the node pairs. In the Small Case Experiment, the EBF method could feasibly score structures with up to 29 cases (15 observational and 14 experimental) 7 for all the pairs in U.
As a second experiment (Large Case Experiment), we ran all the other methods, except the EBF method, with 100 cases (50 observational and 50 experimental). The evaluation score of each method is defined as the number of instances where the method outputs the true structure as the most probable structure.
In Gibbs Sampling, for each structure S, we used 700 iterations and discarded the first 70 iterations (burn-in phase). In the Candidate Method, for each structure S, we used 700 iterations (with 70 burn-in phase) of Gibbs Sampling and then EM with either 700 iterations or a difference of successive values of P(θ | D*, S, K) smaller than e−20, whichever came first. In the Importance Sampling method, we set the number of configurations N=700 (see Appendix A.4) for each structure. In the Gibbs Volume method, we restricted | ST | to 700.
4.2 Evaluation of ILVS and the Gibbs Volume Method
Ideally, in evaluating causal learning, we would know the real-world causal relationships (both the structure and parameters) among a set of variables of interest. With such knowledge, we could generate experimental and observational data. Using these datasets as input, a learning method could predict the causal structure and estimate the causal parameters that exist among the modeled variables. These predictions and estimates would then be compared to the true causal relationships. In Section 4.1.1 we described how we generated data from ALARM. The remainder of the current section describes how we used this data in evaluating the learning methods described in Section 2.1.
4.2.1 Methodological Details
For learning, a dataset D consisted of m/2 cases in which X was manipulated and Y was observed, m/2 cases in which Y was manipulated and X was observed, and n cases in which X and Y were both observed. Thus, D contains m + n cases. We varied m incrementally from 0 to 500. For each value of m, we varied n incrementally from 0 to 500. For each of the 100 pairs of nodes in U, we used the Gibbs Volume method in Section 3.2.2 to compute a posterior probability distribution over the 12 causal network structures in Figure 3. We assumed a uniform prior probability of 1/12 for each of the twelve structures. In applying Equation 6 to derive the marginal likelihood, we used the following parameter priors: aijk = 1/(qi·ri) for all i, j and k. This choice of priors has two properties (among others) [3]. First, the priors are weak in the sense that the marginal likelihood is influenced largely by the dataset D. Second, given only observational data, equivalence classes E1 and E2 will have equal posterior probabilities. These two properties provide a type of non-informative parameter prior. We chose to use a non-informative prior in the current evaluation in order to draw insights that are based mainly on the data and not on our own subjective beliefs.
4.2.2 Unique Fill-ins
The Gibbs Volume method is computationally intensive, and computation time is proportional to the number of possible fill-ins of the latent variable. To determine the number of unique fill-ins in the Gibbs Volume method, we picked two node pairs from each of equivalence classes E1, E3, E4, and E6. After reviewing the results of the experiment with the 8 node pairs, we determined that using 200 fill-ins for each of the 12 structure models yielded a good balance between score stability and computational time cost. Thus, we used this number of fill-ins in the experiments that follow.
4.2.3 Dimensionality Issues
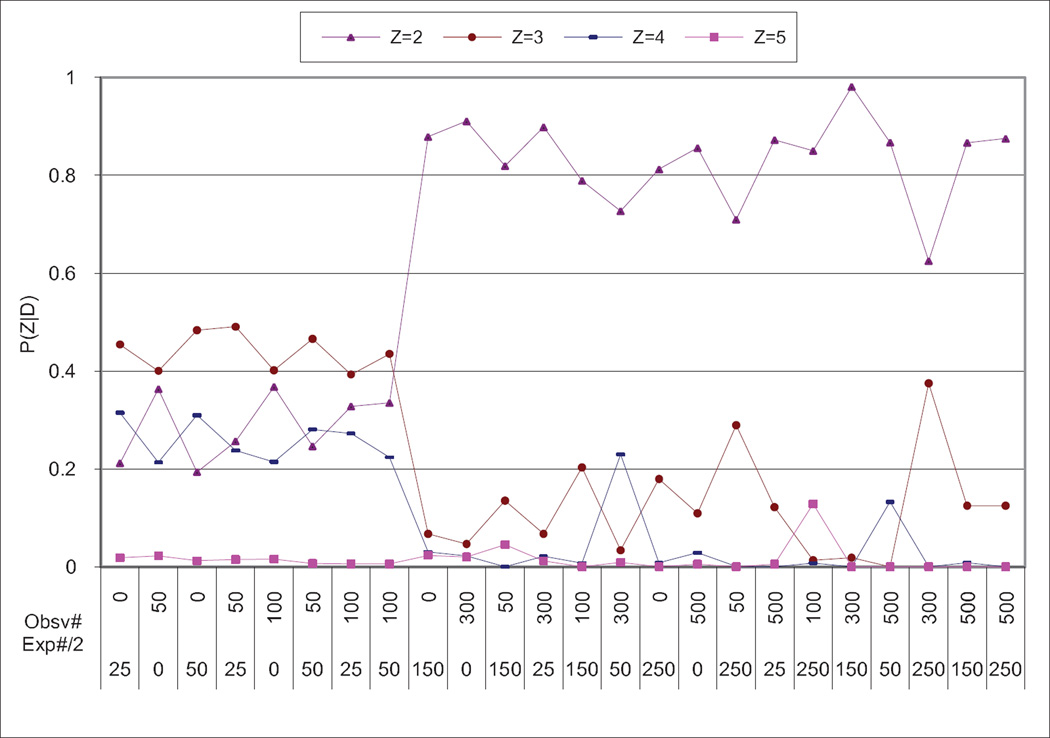
As mentioned in Section 2.3, we need to define a working upper bound on the dimensionality Z of the latent variable H. To explore this issue, we used the same 8 node pairs as in Section 4.2.2. Figure 7 shows that for datasets with more than 300 cases, the binary latent variable dominates. For fewer than 300 cases, dimensionalities 2, 3, and 4 are similar, and dimensionality 5 is distinctly inferior. This is because in the confounded node pairs, one or both nodes have a weak correlation with the real confounded variable. The generating structure may seem like unconfounded classes (E1, E2, and E3) by this weak correlation. Further experiments show that dimensionality 1 (not modeling latent variable) gets the highest score among the 8 node pairs.
Figure 7.
Average score of dimensionality of eight node pairs vs. number of cases. Obsv# stands for number of observational cases in dataset D(X,Y). Exp#/2 stands for number of experimental cases used each in dataset D(mX,Y) and D(X,mY).
Based on these observations, in the experiments that follow in Equation 8, we use UB = 4 when |D| < 300 and UB = 2 when |D|≥ 300.
4.2.4 Evaluation Metrics
For a given node pair (X, Y), let Etrue designate which of the six equivalence classes from Figure 3 is the actual structural relationship between X and Y in ALARM. For each pair (X, Y) and dataset D, we derived the following structural error metric:
| (18) |
where P(Etrue | D, K) is the posterior probability derived by using the method in Section 2. If that method always predicted the true relationship in ALARM with probability 1, then the error would be 0. We computed an overall structural error rate by averaging over all the pairwise error rates as follows:
| (19) |
where the sum is taken over b node pairs. In our analyses, b is either 29 (corresponding to unconfounded, causally related nodes, as shown in Table 4), 52 (corresponding to unconfounded, causally unrelated nodes), 11 (corresponding to confounded, causally unrelated nodes) or 8 (corresponding to confounded, causally related nodes). We were also interested in how accurately the learned models could predict the distribution of one variable (in a pair) given manipulation or observation of the other variable. In the remainder of these sections, we define an error of predicting the distribution of Y given that X is observed. We also define an error of predicting the distribution of Y given that X is manipulated. Let x denote an arbitrary state of X and y an arbitrary state of Y. Let PA(X = x) denote the marginal probability that X is observed to be x, according to the ALARM Bayesian network. Let PA(Y = y | X = x) designate a conditional probability as inferred using ALARM of observing Y to be y given that X is observed to be x. Let PE(Y = y | X = x) be an estimate of the same conditional probability that is obtained by applying model averaging using Equation 8. For a given (X, Y) we define the expected error of predicting the observation of Y given an observation of X as follows:
| (20) |
where the outer sum is taken over all the states of X, the inner sum is taken over all states of Y, and rY is the number of states that Y can have. For a given dataset D, OPErrX,Y (D) measures the expected absolute error of predicting an observed state of Y given an observed state of X The expectation is taken with respect to the observational distribution of the states of X. The overall observational prediction error (OPErr) is defined as follows:
| (21) |
Now consider the situation in which X is manipulated to a state and we observe the distribution of Y. We use the notation mX = x to represent that X is manipulated to the state x. We have no particular reason to assume that X would be manipulated to any one state more than another. Thus, for the purpose of deriving an error metric, we assume that X is equally likely to be manipulated to each of its rX possible states. Under these terms, we obtain the following manipulation error metrics:
| (22) |
| (23) |
4.2.5 Running Time
We used dual Pentium 1GHz processors running the Linux operating system to perform this experiment. It took 35 days to complete all 100 node pairs, each pair with 24 different numbers of observational and experimental datasets. We also used a Pentium 1GHz Windows XP computer that ran in parallel with the Linux machine for a small portion of the main experiment (most of the cases where Z=2 and |D|≤300).
5 Experimental Results and Discussion
ILVS and Gibbs Volume methods performed better than most of other latent variable scoring methods in predicting the generating structures. In terms of the computation time, ILVS was more than 100 times faster than all the latent variable scoring methods.
In general, the overall results showed that the Gibbs Volume method and the ILVS method agreed in predicting the correct structures. Especially for large number of cases (≥300), the ILVS method generated relatively more stable structure scores than those of the Gibbs Volume method. Also with experimental data alone, ILVS predicted the confounded structures (E4, E5, or E6) better than the Gibbs Volume method.
In terms of parameter predictions – OPErr(D) and MPErr(D) – all of the results show that observational data alone yield a lower OPErr(D) than the same number of experimental cases (also experimental data alone yield a lower MPErr(D) than the same number of observational cases.) In addition, we could make accurate observational predictions based just on a large amount of observational training data; adding experimental data to the large amount of observational data did not improve observational predictions much.
In the following sections, we show the detail results of the comparison of latent variable scoring methods (section 5.1) and the results of the evaluation of ILVS and Gibbs Volume (section 5.2).
5.1 Results of the Comparison of Latent Variable Scoring Methods
We compare the performance of ILVS and Gibbs Volume with other latent variable scoring methods by showing (1) how well they predict the generating structures (Section 5.1.1); and (2) how long do they run to analyze all the relationships of the100 node pairs (Section 5.1.2).
5.1.1 Experimental Scores
The Gibbs Volume method outperformed the other approximation methods when compared to the EBF method (Table 5). The Gibbs Volume method performed comparably to the other methods when evaluated against the generating structure (Table 6). Therefore we chose the Gibbs Volume method as the approximation method to use for further experimentation. Note that the performance of the ILVS method is equal to the Gibbs Volume method. In Table 5, to our surprise, the Importance Sampling outperformed the Importance Sampling with Gibbs Sampling. We believe that Gibbs Sampling tends to bias the Importance Sampling method unfavorably. For example, if the search plain is relatively flat and has many peaks, Gibbs Sampling may guide Importance Sampling to sample in only one peak.
Table 5. Result of the Small Case Experiment.
Score of each method represents the number of cases that agree with the EBF method. Abbreviations are T: True Structure; BF: Efficient Brute Force Method; IV: Implicit Latent Variable Scoring Method; GM: Gibbs Maximum Method; GA: Gibbs Average Method; GE: Gibbs & EM Method; IM: Importance Sampling Method; Gl: Gibbs Maximum with Importance Sampling Method; and GV: Gibbs Volume Method.
| Method | T | BF | IV | GM | GA | GE | IM | GI | GV |
|---|---|---|---|---|---|---|---|---|---|
| Score | 56 | 100 | 74 | 84 | 84 | 56 | 71 | 64 | 90 |
Table 6. Result of the Large Case Experiment.
Score of each method represents the number of incidents that agree with the generating structure.
| Method | T | IV | GM | GA | GE | IM | GI | GV |
|---|---|---|---|---|---|---|---|---|
| Score | 100 | 62 | 63 | 59 | 64 | 60 | 34 | 62 |
5.1.2 Running Time
Since the ILVS introduced in Section 3.2.1, does not use sampling, it is the fastest in the Large Case Experiment (Table 7). Other methods’ running times are based on equal numbers of iterations (N=700). Note that GE (the Gibbs and EM method) and GI (the Gibbs and Importance Sampling method) have extra phases in each iteration. For GE, there is an extra EM phase, for GI, there is an extra Importance Sampling phase.
Table 7.
Running Time in minutes of the Large Case Experiment.
| Method | IV | IM | GM | GA | GV | GE | GI |
|---|---|---|---|---|---|---|---|
| Running Time (minute) | 1.5 | 211 | 238.2 | 238.2 | 304 | 405 | 450 |
5.2 Results of Evaluation of ILVS and the Gibbs Volume Method
In this section we show the results of structure error [SErr(D)] of both the Gibbs Volume and ILVS method. We only show the observational and manipulation prediction errors [OPErr(D) and MPErr(D)] for the Gibbs Volume method because no significant differences were observed between the observational and manipulation prediction errors of ILVS and the same errors of Gibbs Volume method.
5.2.1 Structure Error
The structure errors [SErr(D)] of Gibbs Volume and ILVS that were computed using different number of mixture of observational and experimental data are shown in next two sections.
5.2.1.1 Gibbs Volume Method
Table 8 shows the SErr(D) of the Gibbs Volume method. In Table 8(a) and Table 8(b), for the most part, the more experimental data that D contains, the more probable is the prediction of the generating causal relationship. Although the experiment stopped at 500 experimental cases, we would expect the error rate to continue to decrease as more experimental cases were available. Observational data alone are not sufficient to determine whether X is causing Y or Y is causing X. Significantly, however, Table 8 (and later Table 9) indicates that observational data can augment experimental data in decreasing the error by helping determine whether X and Y are independent, which is class E3.
Table 8.
The Structural Error Metric SErr(D) for Pairs of Nodes Scored with Gibbs Volume Method for Different Combinations of Observational and Experimental Data.
| Obsv#\Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.833 | 0.613 | 0.586 | 0.434 | 0.368 |
| 50 | 0.753 | 0.539 | 0.483 | 0.356 | 0.320 |
| 100 | 0.741 | 0.544 | 0.478 | 0.350 | 0.300 |
| 300 | 0.721 | 0.488 | 0.451 | 0.312 | 0.305 |
| 500 | 0.744 | 0.491 | 0.404 | 0.304 | 0.274 |
| (a) E1 and E2 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.833 | 0.480 | 0.390 | 0.258 | 0.273 |
| 50 | 0.449 | 0.346 | 0.315 | 0.208 | 0.196 |
| 100 | 0.368 | 0.298 | 0.284 | 0.206 | 0.233 |
| 300 | 0.258 | 0.235 | 0.234 | 0.200 | 0.181 |
| 500 | 0.241 | 0.223 | 0.231 | 0.218 | 0.222 |
| (b) E3 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.833 | 0.957 | 0.950 | 0.993 | 0.893 |
| 50 | 0.961 | 0.975 | 0.942 | 0.994 | 0.992 |
| 100 | 0.967 | 0.985 | 0.984 | 0.993 | 0.994 |
| 300 | 0.987 | 0.985 | 0.971 | 0.995 | 0.995 |
| 500 | 0.988 | 0.991 | 0.995 | 0.990 | 0.800 |
| (c) E4 and E5 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.833 | 0.823 | 0.877 | 0.906 | 0.924 |
| 50 | 0.729 | 0.627 | 0.704 | 0.830 | 0.845 |
| 100 | 0.683 | 0.628 | 0.674 | 0.860 | 0.849 |
| 300 | 0.691 | 0.712 | 0.733 | 0.932 | 0.876 |
| 500 | 0.683 | 0.784 | 0.780 | 0.941 | 0.913 |
| (d) E6 | |||||
Table 9.
The Structural Error Metric SErr(D) for Pairs of Nodes Scored with the ILVS Method for Different Combinations of Observational Data and Data Resulting from Experimental Manipulation.
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.8333 | 0.7627 | 0.7592 | 0.6771 | 0.6579 |
| 50 | 0.8719 | 0.5120 | 0.4678 | 0.3671 | 0.3144 |
| 100 | 0.8809 | 0.5273 | 0.4816 | 0.3575 | 0.3074 |
| 300 | 0.8755 | 0.4684 | 0.4294 | 0.3342 | 0.2543 |
| 500 | 0.8734 | 0.4522 | 0.4116 | 0.3353 | 0.2384 |
| (a) E1 and E2 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.8333 | 0.6664 | 0.6284 | 0.5513 | 0.5442 |
| 50 | 0.4438 | 0.2844 | 0.2684 | 0.1263 | 0.1202 |
| 100 | 0.3469 | 0.2265 | 0.2204 | 0.1304 | 0.1183 |
| 300 | 0.1965 | 0.1340 | 0.1282 | 0.0905 | 0.0868 |
| 500 | 0.1703 | 0.1194 | 0.1210 | 0.0860 | 0.0812 |
| (b) E3 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.8333 | 0.9229 | 0.8939 | 0.8693 | 0.7609 |
| 50 | 0.9077 | 0.9978 | 0.9976 | 0.9988 | 0.9966 |
| 100 | 0.9054 | 0.9957 | 0.9962 | 0.9976 | 0.9981 |
| 300 | 0.8973 | 0.9981 | 0.9959 | 0.9988 | 0.9994 |
| 500 | 0.8494 | 0.9991 | 0.9992 | 0.9998 | 0.9999 |
| (c) E4 and E5 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.8333 | 0.5477 | 0.5073 | 0.5004 | 0.5002 |
| 50 | 0.8864 | 0.6138 | 0.6483 | 0.6301 | 0.6301 |
| 100 | 0.8715 | 0.5787 | 0.5850 | 0.5391 | 0.5420 |
| 300 | 0.8501 | 0.5788 | 0.5212 | 0.4463 | 0.4540 |
| 500 | 0.8210 | 0.5161 | 0.5140 | 0.2793 | 0.2747 |
| (d) E6 | |||||
Table 8(a) shows the results of the structure prediction error when X and Y are causally related but are not confounded (E1 and E2). Since the prior probability of each structure is 1/6, the error rate is 5/6, or approximately 0.833, when there is no data. With no experimental cases, when observational cases increase from 300 to 500, the error rate increases slightly, from 0.721 to 0.744. This is because in 11 of the 29 generating structures of type E1 or E2, X and Y are very weakly correlated; with samples on the order of 50 to 500 cases, these 11 structures are given relatively low posterior probabilities of being causally related. [8] reported that 10 out of the 11 structures converged to the expected error rate of 0.8 (because observational data can only eliminate class E3 and can not distinguish among the other 5 classes) by performing additional simulations with 50,000 cases of observational data. Since, with observational data, the same 11 node pairs are showing high error rates in Table 8(a) (and later Table 9(a)), we expect the overall error rate to converge to 0.8 as expected.
Table 8(b) shows the structure prediction error when X and Y are not causally related and are not confounded. As expected, both experimental and observational data are able to determine about equally well that X and Y are independent.
Table 8(c) shows the structure prediction error when X and Y are causally related and confounded (E4 and E5 in Figure 3). The table shows the highest error rate among all the results. Two distinct groups were discovered from the 8 node pairs in E4 or E5. The first group, denoted as G3, had three node pairs. Gibbs Volume scored E3 as the most probable class, with 1,000 cases (500 observational and 500 experimental) on all three pairs in E3. The second group, denoted as G5, consists of the remaining 5 node pairs. Gibbs Volume failed to predict E5 as the most probable class for them. However, Gibbs Volume scored all of the five node pairs with a consistent increase in the E5 score as more observational and experimental cases were added. Node pairs in G3 had relatively low absolute correlation (<0.25) given 500 observational cases alone. Also, they showed low correlation (<0.06) for 500 experimental cases in which the causal node was manipulated. This indicates that for the node pairs in G3, there exists a strong correlation between node X and H (or between node Y and H). Gibbs Volume scored E2 as the most probable structure, with 1,000 cases (500 observational and 500 experimental) on three node pairs in G5. Gibbs Volume scored E5 correctly as the most probable structure given the same number of cases on the other two node pairs in G5. These two node pairs are the only adjacent ones (direct causes or effects) among the 8 node pairs in E5.
Results of Table 8(d) show that for the dataset with a large number of cases (≥300), the Gibbs Volume method generates unstable results. For example, in Table 8(d), with 100 observational data and 100 experimental data, the SErr(D) is 0.674. Adding 200 observational data and 200 experimental data increases the SErr(D) to 0.932. This can be explained in several ways: First, as pointed out for Equation 10, the number of possible configurations of the latent variable H is exponential in the number of cases in the dataset. If we assume the dimensionality of H is z, the Gibbs Volume method has to search among z200 possible fill-ins of H in a dataset with 200 cases. Adding 400 cases to the dataset will increase the possible fill-ins of H to z600. In return, the scores of the Gibbs Volume method show higher variance when datasets have more cases. To overcome this problem, we can use the Gibbs Volume method along with the configuration used in the EBF method. Then the number of configurations of the latent variable H becomes polynomial in the number of cases but exponential in the number of configurations (see Appendix A.1 for more information). Second, since E4(E5) and E6 have a small number of node pairs (8 and 11, respectively), the SErr(D) is more sensitive to the possible noise in the structure scores than for the other equivalent classes (E1/E2 and E3).
Table 8(d) shows the structure prediction error when X and Y are not causally related and are confounded (E6 in Figure 3). Since Table 8(d) shows a possible noise on Gibbs Volume with large numbers of cases, to minimize the noise in the SErr(D) for each node pair, we calculated the average SErr(D) over cases fewer than 300. Six (out of 11) node pairs showed high average SErr(D) (between 0.83 and 0.91), while the other 5 node pairs showed relatively low average SErr(D) (between 0.34 and 0.63). The 6 node pairs that showed high average SErr(D) were the same 6 pairs with the average SErr(D) between 0.70 and 1.0 in the ILVS method. Further analyses on these 6 node pairs are given in the next section.
5.2.1.2 Implicit Latent Variable Scoring (ILVS) Method
Here we show the SErr(D) tables for the ILVS method that was introduced in 3.2.1. Comparing Table 9 with Table 8 in the Gibbs Volume method, the ILVS method shows similar SErr(D) with a small number of cases (<300). This is encouraging because we can further assume that the ILVS method can represent the SErr(D) for a large number of cases (≥300) in the Gibbs Volume method (especially the SErr(D) on the confounded structure E6).
Table 9(a) shows a high SErr(D) relative to Table 9(b). This is because of the node pairs with very low correlation in E1 or E2 [8]. Among 29 node pairs in class E1 or E2, with 1,000 cases (500 observational and 500 experimental), ILVS scored E3 as the most probable structure on six node pairs. With the same number of cases, ILVS predicted E5 on 8 node pairs, and E6 on one node pair, as the most probable structures. Further experimentation showed that ILVS correctly predicted E1 (E2) with 20,000 cases (10,000 observational and 10,000 experimental) on 28 out of 29 node pairs. The node pairs that ILVS predicted to be in E3 with these 20,000 cases were also predicted by ILVS to be in E3 with 50,000 observational cases and no experimental cases [8].
Table 9(b) shows that the ILVS method correctly predicts E3 with 1,000 (500 observational and 500 experimental) cases. ILVS predicted all 52 node pairs in E3, their generating class, with 20,000 cases (10,000 observational and 10,000 experimental). Most of the node pairs had SErr(D) lower than 0.1, except 4 node pairs that had SErr(D) between 0.12 and 0.28. These 4 node pairs showed relatively higher correlation than other node pairs in E3.
Table 9(c) shows that with 1,000 (500 observational and 500 experimental) cases, the ILVS method cannot predict E4 (E5) correctly. The same groups G3 and G5 were observed while analyzing the SErr(D) of E4 (E5) in the ILVS method. We further analyzed the 8 node pairs in E4 (E5) with more cases. ILVS predicted E4 (E5) as the most probable structure on 2 node pairs in G5, with 13,000 cases (6,500 observational and 6,500 experimental). These 2 node pairs were the only ones that gained high posterior probability (>0.5) on E4 (E5) in the Gibbs Volume method. For the other 3 node pairs in G5, the E4 (E5) score got closer to the E1 (E2) score as the number of cases increased to 20,000 (10,000 observational and 10,000 experimental). We believe these 3 node pairs will correctly pick E4 (E5) if enough cases are provided. ILVS predicted E6 and E3 as the most probable structures, with 20,000 cases (10,000 observational and 10,000 experimental) on node pairs in G3. As pointed out in the previous section, these 3 node pairs had low correlation between the node pair (<0.25), and the one ILVS predicted as the most probable structure with 20,000 cases, E3, had the lowest absolute correlation between the node pair (<0.1).
Table 9(d) shows that ILVS correctly predicts E6 with 1,000 cases (500 observational and 500 experimental). Comparing Table 9(d) with Table 8(d), ILVS performs better than Gibbs Volume with experimental cases alone but worse with observational cases alone. This is because Gibbs Volume prefers the model with fewer parameters. With observational data alone, ILVS cannot distinguish among E1, E2, E4, E5, and E6 (see Figure 3). So the error rate converges to 0.8 as expected in Table 9(d). Because Gibbs Volume prefers structure with fewer parameters, Gibbs Volume gives higher scores to E1, E2, and E6 than E4 and E5. Thus Gibbs Volume shows error relatively less than 0.8 with observational data alone in Table 8(d). With experimental data alone, ILVS cannot distinguish E3 from E6 (see Figure 3), so the error rate converges to 0.5 as expected. Gibbs Volume performs worse with experimental data alone because Gibbs Volume prefers E3 over E6.
The ILVS method correctly picked the generating structure of all 11 node pairs in E6 with 14,000 (7,000 observational and 7,000 experimental) cases. All of the SErr(D) values were lower than 0.01. The 6 node pairs in E6, which showed high SErr(D) in the Gibbs Volume method, were the only pairs with a SErr(D) greater than 0.01 with 1,000 cases (500 observational and 500 experimental cases) in the ILVS method.
5.2.2 Observational and Manipulation Predicted Error
Table 10 reports the OPErr(D) from the Gibbs Volume method given by Equation 21. We give the OPErr(D) using the Gibbs Volume method to report the result of Equation 8. All of the tables show that observational data alone yield a lower OPErr(D) than the same number of experimental cases. For example, in Table 10(c), with 500 observational cases, the OPErr(D) is 0.021, and with 500 experimental cases, the OPErr(D) almost triples to 0.061. The main reason for this result is that all observational data are relevant in parameter estimation for observational prediction, whereas only a subset of experimental data is relevant [8]. In particular, in the experiment, we are using m experimental cases as m/2 cases for each of D(mX,Y) and D(X,mY). Consequently, only half of the experimental data are relevant to observational prediction. In Table 10(d), with 300 observational cases, the OPErr(D) is 0.007; adding even 100 experimental cases will only decrease the OPErr(D) by 0.001. Similar trends can be seen for the other classes. This pattern of results shows that, regardless of the generating structure, given sufficient observational data and a relatively small amount of experimental data, adding more experimental data does not dramatically lower the OPErr(D). In other words, not surprisingly, we can make accurate observational predictions based just on a large amount of observational training data, without need for experimental data.
Table 10.
The Gibbs Volume Method Observational Prediction-Error Metric OPErr(D) for Pairs of Nodes for Different Combinations of Observational Data and Data Resulting from Experimental Manipulation.
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.264 | 0.081 | 0.037 | 0.020 | 0.021 |
| 50 | 0.026 | 0.024 | 0.024 | 0.017 | 0.017 |
| 100 | 0.019 | 0.019 | 0.018 | 0.014 | 0.014 |
| 300 | 0.015 | 0.014 | 0.014 | 0.012 | 0.012 |
| 500 | 0.010 | 0.011 | 0.010 | 0.009 | 0.010 |
| (a) E1 and E2 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.318 | 0.083 | 0.034 | 0.033 | 0.028 |
| 50 | 0.029 | 0.027 | 0.022 | 0.022 | 0.022 |
| 100 | 0.020 | 0.018 | 0.020 | 0.020 | 0.020 |
| 300 | 0.012 | 0.011 | 0.017 | 0.012 | 0.013 |
| 500 | 0.010 | 0.010 | 0.010 | 0.009 | 0.014 |
| (b) E3 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.239 | 0.116 | 0.037 | 0.037 | 0.062 |
| 50 | 0.045 | 0.033 | 0.037 | 0.038 | 0.032 |
| 100 | 0.027 | 0.028 | 0.028 | 0.032 | 0.032 |
| 300 | 0.030 | 0.027 | 0.024 | 0.028 | 0.034 |
| 500 | 0.021 | 0.022 | 0.022 | 0.020 | 0.023 |
| (c) E4 and E5 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.178 | 0.117 | 0.019 | 0.021 | 0.015 |
| 50 | 0.016 | 0.012 | 0.011 | 0.011 | 0.008 |
| 100 | 0.020 | 0.012 | 0.011 | 0.012 | 0.008 |
| 300 | 0.007 | 0.007 | 0.006 | 0.006 | 0.008 |
| 500 | 0.005 | 0.006 | 0.005 | 0.005 | 0.005 |
| (d) E6 | |||||
Table 11 reports the MPErr(D) given by Equation 23. All tables show that the experimental data contribute more toward lowering the MPErr(D) than observational data does. This is because experimental data can distinguish whether X is causing Y or Y is causing X. For example, for E1 and E2, experimental data decrease the MPErr(D) two times better than observational data, with 500 cases for each. Here we can also see the same trend we have noticed in the OPErr(D) tables. With few experimental and many observational data, we can make the MPErr(D) very low. In Table 11(a), 50 experimental data alone yield an MPErr(D) level of 0.084; adding 100 observational data will lower the error to 0.017. With 50 observational cases and 300 experimental data, the error decreases to 0.012, which is comparable to the error of 0.011 when using 500 experimental data alone.
Table 11.
The Gibbs Volume Method Manipulation Prediction-Error Metric MPErr(D) for Different Combinations of Observational Data and Data resulting from Experimental Manipulation.
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.240 | 0.084 | 0.029 | 0.014 | 0.011 |
| 50 | 0.031 | 0.022 | 0.020 | 0.013 | 0.011 |
| 100 | 0.028 | 0.017 | 0.015 | 0.011 | 0.010 |
| 300 | 0.021 | 0.012 | 0.008 | 0.008 | 0.007 |
| 500 | 0.023 | 0.009 | 0.007 | 0.007 | 0.006 |
| (a) E1 and E2 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.287 | 0.068 | 0.018 | 0.011 | 0.008 |
| 50 | 0.025 | 0.018 | 0.014 | 0.011 | 0.008 |
| 100 | 0.017 | 0.012 | 0.011 | 0.009 | 0.007 |
| 300 | 0.015 | 0.008 | 0.008 | 0.008 | 0.007 |
| 500 | 0.013 | 0.008 | 0.007 | 0.007 | 0.006 |
| (b) E3 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.247 | 0.114 | 0.031 | 0.023 | 0.022 |
| 50 | 0.034 | 0.023 | 0.026 | 0.020 | 0.020 |
| 100 | 0.029 | 0.023 | 0.022 | 0.018 | 0.019 |
| 300 | 0.021 | 0.019 | 0.017 | 0.015 | 0.021 |
| 500 | 0.029 | 0.022 | 0.020 | 0.015 | 0.016 |
| (c) E4 and E5 | |||||
| Obsv# \Exp# | 0 | 50 | 100 | 300 | 500 |
|---|---|---|---|---|---|
| 0 | 0.189 | 0.088 | 0.011 | 0.004 | 0.004 |
| 50 | 0.017 | 0.009 | 0.008 | 0.003 | 0.003 |
| 100 | 0.017 | 0.007 | 0.006 | 0.003 | 0.003 |
| 300 | 0.009 | 0.004 | 0.004 | 0.003 | 0.003 |
| 500 | 0.010 | 0.003 | 0.002 | 0.003 | 0.003 |
| (d) E6 | |||||
Table 11 shows that with only observational data, we can achieve the MPErr(D) close to the MPErr(D) with only experimental data. For example, in Table 11(a), with 300 observational cases and no experimental cases, the MPErr(D) is 0.021, whereas with 300 experimental cases and no observational cases, the MPErr(D) is 0.014. This is because with 300 observational cases, Gibbs Volume predicts E3 as the most probable structure on many node pairs of type E1 (E2) and E4 (E5). To see why this causes low MPErr(D) with only observational data, let us think of node pairs (X, Y) of type E1. For most of the node pairs (X, Y) of type E1, the Gibbs Volume method outputs higher scores on P(E3|D,Z=j,K) than P(E1|D,Z=j,K) when calculating Equation 8 with 300 observational cases and no experimental cases. Since with dataset D(mX,Y), E1 and E3 are equivalent classes and with 300 observational cases and no experimental cases, the dataset is showing X and Y are independent (E3), PE(Y|mX,Di,E3,K) and PE(X|mY,Di,E3,K) have similar distributions of PA(Y|mX,Di, E1,K) and PA(X|mY,Di, E1,K) in Equation 8 and Equation 22. This makes the MPErr(D) low with 300 observational cases and no experimental cases. But with 500 observational cases and no experimental cases, we see that the Gibbs Volume method scores E1 higher than E3 on most of the node pairs, and as a result, the MPErr(D) will increase. This can be observed in Table 11(c): with 300 observational cases and no experimental cases, the MPErr(D) is 0.021; but with 500 observational cases and no experimental cases, the MPErr(D) increases to 0.029. (The same trend can be observed in Table 11(a): the MPErr(D) increases from 0.021 to 0.023).
6 Conclusions
In this paper we introduced a general representation of manipulation in causal Bayesian networks. Based on this representation, we extended the Bayesian scoring method to score structures given a mixture of observational and experimental data. We also introduced a heuristic structure scoring method called ILVS. The method uses a mixture of observational and experimental data to score structures that include a latent variable. Since the ILVS method does not explicitly model the latent variable, it evaluates the structure with very low computational complexity when compared to the other approximation methods we investigated.
Beyond ILVS, we implemented six different latent variable scoring methods (one exact scoring method and five approximation methods). Among these approximation methods, we selected the Gibbs Volume method as a representative of the best-performing approximation methods tested. This was achieved using two experiments. First, we compared structure scores of the five approximation methods with the structure scores of the EBF method with a small amount of data. Second, we compared the number of cases in which the five approximation methods predicted the generating structure as the most probable structure with a large amount of data. The ILVS method showed comparable performance to the Gibbs Volume method on these two experiments. However, unlike the ILVS method, the Gibbs Volume method had to model the dimensionality of the latent variable, and consequently its computational complexity was much higher than that of ILVS.
Using the Gibbs Volume method and the ILVS method, we used a mixture of observational and experimental data to predict the generating structures of 100 randomly sampled node pairs from the ALARM network. The results showed that when the true generating structures were confounded, the Gibbs Volume method and the ILVS method agreed on the fewer number of cases (<300), and on greater number of cases (≥300), the ILVS method generated relatively more stable structure scores, especially for E6, than the Gibbs Volume method. This is because the ILVS method does not have to search the exponentially large space of possible configuration of the latent variable. With 20,000 cases (10,000 observational and 10,000 experimental), the ILVS method correctly predicted the generating structures of 93 out of the 100 node pairs in U. These results support that the ILVS method is making asymptotically correct predictions. Also with experimental data alone, ILVS predicted the confounded causal structures (E4 or E5) and confounded independence structures (E6) – especially confounded independence structures – better than the Gibbs Volume method.
In this paper we showed that a mixture of observational and experimental data is useful in learning causal structure and its parameters. Moreover, this paper quantified the synergy of synthetic observational and experimental data generated from the ALARM Bayesian network that was created by an expert.
Extensions of this work include examining the synergy of case control data in conjunction with observational and experimental data [28] and modeling latent variables beyond the pairwise relationship of nodes [29].
Acknowledgements
I wish to thank Drs. Gregory F. Cooper and Subramani Mani for their useful comments on an earlier draft of this paper. The research was supported by NIH grant P20RR017670 from NCRR and University Research Fund from Florida International University.
Appendix A
Here we describe the methods introduced in Section 3.2.3 in detail.
A.1 Efficient Brute Force Method
Since calculating exact likelihood score is an exponentially expensive procedure, it is not feasible, especially for a large number of cases. For a given causal Bayesian network structure S and dataset D, the exact score can be calculated from Equation 4. If D contains a latent variable H, then Equation 4 becomes Equation 10. Equation 10 is exponential in the number of cases. By grouping configurations for observed variables in D, Cooper [21] provides a method for solving Equation 10 that is polynomial in the number of cases but exponential in the number of configurations of the Markov Blanket8 of H.
For example, let |D | = 10, let H be a binary variable, and suppose there are two groups of the same configuration of {Cl} each of size 5. From Equation 10, we have to perform 210 = 1,024 operations, whereas considering that there are two groups each of size 5, we need only to perform operations.
A.2 Gibbs Sampling Method
Gibbs Sampling, introduced by Geman and Geman [22], is a common Monte-Carlo method to approximate Equation 10. Initially, Gibbs Sampling randomly fills in the missing state of variables in the dataset D. This will generate an initial complete dataset, which we will denote as D0. We will denote Di as a complete dataset generated after the i-th iteration of Gibbs Sampling. We define Gibbs Sampling iteration as follows:
Given any complete dataset Di (missing values filled in in a certain way), we generate a new complete dataset Di+1 by going through all missing values (in Di) one by one and reassigning them according to a new probability distribution calculated by the following equation:
| (24) |
where denotes the state of variable Xi in case l and denotes the new state to be assigned to variable Xi. Since is a complete dataset, we can use Equation 6 to calculate the numerator and denominator of Equation 24. We generate different {Di} for each structure Sk, for k=1, 2, …, 12.
In Gibbs Sampling, we usually discard the first few generated datasets, i.e., discard datasets D0, D1, … ,D10 with 1,000 generated complete datasets. This step is known as a burn-in phase. We also calculate P(D | S, K) in two different ways. In a method called Gibbs Maximum, we calculate P(D | S, K) by using dataset D, which maximizes the score of P(Di | S, K) for all Di. The score for structure Sk is calculated as follows:
| (25) |
where D̂ denotes all Di generated after the burn-in phase.
For Gibbs Average method, P(D | S, K) is an average of P(Di | S, K) over all Di in D̂. Formally, the score for structure Sk is calculated as:
| (26) |
A.3 Gibbs Sampling and EM Method (Candidate Method)
We have also implemented an approximation method that combines Gibbs Sampling with an expectation maximization (EM) method [30]. Using the EM method with Gibbs Sampling is known as the Candidate Method [24, 31]. In Chickering and Heckerman [16] EM is used to find the □□□ that maximizes P(□□□D*,S,K), where D* is the most frequently occurring dataset in D̂. They report that this method leads to a better estimation than the other known methods they tried. We pick D* as in the Gibbs Maximum method and run the EM method with D*.
Let θ* denote the parameter estimated from D*. Given a complete dataset D*, we can initialize θ* from D* and then perform EM starting with θ*. The EM method consists of two steps: the expectation step and the maximization step. In the expectation step, instead of collecting true counts, Nijk, we calculate the expectation of Nijk on the t-th step, denoted as Et(Nijk), from the following equation:
| (27) |
where Cl denotes the observed variables and Hl denotes the latent variables of the l-th case in D*. If Xi and the parents of Xi are all observed in the l-th case, then the addition is just a simple count. Otherwise, we perform Bayesian network inference to calculate the l-th term in the sum in Equation 27.
The next step is the maximization step, in which is updated as follows:
| (28) |
where θijk denotes P(Xi = k | ∏i = j, S, K).
After reaching a local maximum for θ*, we calculate P(D | S, K) as follows:
| (29) |
where we evaluate terms in the numerator exactly and approximate the denominator by averaging P(θ*|Di, S, K) for all Di.
A.4 Importance Sampling Method
We also implemented a sampling method called the self-importance sampling method. This method uses the following approximation for its sampling procedure:
| (30) |
where SN is a simulation set size of N that is sampled from all possible configurations of latent variable H and observed variables C. In Equation 30, we use an uniform prior for H, that is, P(Di | S, K) = c for normalization constant c. Also, . To generate each sample in SN , we first randomly set H to get complete dataset D′ and use Equation 24 to resample H.
A.5 Importance Sampling with Gibbs Sampling Method
This method combines Gibbs Sampling with Importance Sampling. This combined method first performs the Gibbs Maximum method and picks dataset D*. The next step is to use the dataset D* and perform Importance Sampling as follows: In the Importance Sampling initialization step, instead of randomly setting H, we initialize D as D*. The following steps are the same as in Importance Sampling.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
We use the terms variable and node interchangeably in this paper.
In Equation 1 and subsequent equations in this section, the substructure X → Y can be replaced by any other substructure containing a subset of the variables in V+ . For simplicity of exposition, however, we focus in this section on a pairwise causal relationship of the form X → Y.
For notational parsimony, let us consider passive observation of X and Y as a type of experiment. That is, we are using the term experiment in the broad sense of meaning to obtain data by some means.
Although this is a strong assumption, it allows efficient structure scoring. Furthermore, we conjecture that it still leads to the discovery of the generating causal structure in the large sample limit; proof of this conjecture is an open problem for future research.
Section 2.1 contains an explanation of these choices for the αijk parameters.
In particular, we used the version of ALARM that is publicly available for download as alarm.dsc from the Bayesian Network Repository at http://www.cs.huji.ac.il/labs/compbio/Repository/Datasets/alarm/alarm.htm.
When we say m experimental cases, we mean that D(mX, Y) contains m/2 cases and likewise for D(X,mY).
A Markov Blanket of a node Xi is given by the set of nodes consisting of πi, the parents of Xi, the children of Xi and all the parents of children of Xi, except Xi itself 10. Pearl, J., Probabilistic Reasoning in Intelligent Systems. Representation and Reasoning, ed. R.J. Brachman. 1988, San Mateo, CA: Morgan Kaufmann.
References
- 1.Cooper GF. An overview of the representation and discovery of causal relationships using Bayesian networks. In: Glymour C, Cooper GF, editors. Computation, Causation, and Discovery. Cambridge, MA: MIT Press; 1999. [Google Scholar]
- 2.Spirtes P, Glymour C, Scheines R. Causation, prediction, and search. 2 ed. Cambridge, MA: MIT Press; 2000. [Google Scholar]
- 3.Heckerman D, Geiger D, Chickering D. Learning Bayesian networks: The combination of knowledge and statistical data. Machine Learning. 1995;20:197–243. [Google Scholar]
- 4.Heckerman D. Proceedings of the Conference on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann; 1995. A Bayesian approach to learning causal networks. [Google Scholar]
- 5.Wille A, et al. Sparse graphical Gaussian modeling of the isoprenoid gene network in Arabidopsis thaliana. Genome Biology. 2004;5(11) doi: 10.1186/gb-2004-5-11-r92. R92.1-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Beal M, et al. A Bayesian approach to reconstructing genetic regulatory networks with hidden factors. Bioinformatics. 2005;21(3):349–356. doi: 10.1093/bioinformatics/bti014. [DOI] [PubMed] [Google Scholar]
- 7.Yoo C, Cooper G. An Evaluation of a System that Recommends Microarray Experiments to Perform to Discover Gene-Regulation Pathways. Journal of Artificial Intelligence in Medicine. 2004;31:169–182. doi: 10.1016/j.artmed.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 8.Cooper GF, Yoo C. Proceedings of the Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann; 1999. Causal discovery from a mixture of experimental and observational data. [Google Scholar]
- 9.Cooper GF, Herskovits E. A Bayesian method for the induction of probabilistic networks from data. Machine Learning. 1992;9:309–347. [Google Scholar]
- 10.Pearl J. Probabilistic Reasoning in Intelligent Systems. In: Brachman RJ, editor. Representation and Reasoning. San Mateo, CA: Morgan Kaufmann; 1988. [Google Scholar]
- 11.Yoo C, Cooper G. Center for Biomedical Informatics Research Report CBMI-173. Pittsburgh, PA: Center for Biomedical Informatics; 2001. Causal discovery of latent-variable models from a mixture of experimental and observational data. [Google Scholar]
- 12.Liang F, Zhang J. Learning Bayesian networks for discrete data. Computational Statistics & Data Analysis. 2009;53(4):865–876. [Google Scholar]
- 13.Chu T, et al. A statistical problem for inference to regulatory structure from associations of gene expression measurements with microarrays. Bioinformatics. 2003;19(9):1147–1152. doi: 10.1093/bioinformatics/btg011. [DOI] [PubMed] [Google Scholar]
- 14.Sebastiani P, et al. Statistical Challenges in Functional Genomics. Statistical Science. 2003;18(1):33–70. [Google Scholar]
- 15.Liu B, Fuente A, Hoeschele I. Gene Network Inference via Structural Equation Modeling in Genetical Genomics Experiments. Genetics. 2008;178:1763–1776. doi: 10.1534/genetics.107.080069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chickering DM, Heckerman D. Efficient approximation for the marginal likelihood of Bayesian networks with hidden variables. Machine Learning. 1997;29:181–212. [Google Scholar]
- 17.Friedman N. Learning belief networks in the presence of missing values and hidden variables; International Conference on Machine Learning; 1997. [Google Scholar]
- 18.Friedman N. Proceedings of the Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann; 1998. The Bayesian structural EM algorithm. [Google Scholar]
- 19.Yoo C, Thorsson V, Cooper GF. Pacific Symposium on Biocomputing. Maui, Hawaii: World Scientific; 2002. Discovery of a gene-regulation pathway from a mixture of experimental and observational DNA microarray data. [DOI] [PubMed] [Google Scholar]
- 20.Chickering D, Heckerman D. Efficient Approximations for the Marginal Likelihood of Bayesian Networks With Hidden Variables. In: Research M, editor. Technical Report MSR-TR-96-08. Seattle, WA: 1997. p. [Google Scholar]
- 21.Cooper GF. A method for learning belief networks that contain hidden variables. Journal of Intelligent Information Systems. 1995;4:1–18. [Google Scholar]
- 22.Geman S, Geman D. Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6:721–742. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- 23.Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via EM algorithm. Journal of the Royal Statistical Society. 1977;B39:1–38. [Google Scholar]
- 24.Chib S. Marginal likelihood from Gibbs output. Journal of the American Statistical Association. 1995;90:1313–1321. [Google Scholar]
- 25.Shachter RD, Peot MA. Simulation approaches to general probabilistic inference on belief networks. In: Henrion M, et al., editors. Uncertainty in Artificial Intelligence 5. North-Holland: Amsterdam: 1990. pp. 221–231. [Google Scholar]
- 26.Beinlich IA, et al. The ALARM monitoring system: A case study with two probabilistic inference techniques for belief networks. Proceedings of the Second European Conference on Artificial Intelligence in Medicine; London, England. 1989. [Google Scholar]
- 27.Henrion M. Propagating uncertainty in Bayesian networks by logic sampling. In: Lemmer JF, Kanal LN, editors. Uncertainty in Artificial Intelligence 2. North-Holland: Amsterdam: 1988. pp. 149–163. [Google Scholar]
- 28.Cooper GF. Proceedings of the Confernce on Uncertainty in Artificial Intelligence. San Franciso, CA: Morgan Kaufmann; 2000. A Bayesian method for causal modeling and discovery under selection. [Google Scholar]
- 29.Yoo C, Cooper G. AMIA. San Antonio, Texas: 2002. Discovery of gene-regulation pathways using local causal search. [PMC free article] [PubMed] [Google Scholar]
- 30.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. 1977;39:1–38. [Google Scholar]
- 31.Raftery A. Chapter 10. Hypothesis testing and model selection. In: Gilks WR, Richardson S, Spiegelhalter DJ, editors. Markov Chain Monte Carlo in Practice. Chapman and Hall; 1996. [Google Scholar]