What is optimal in optimal inference?

Abstract

Inferring hidden structure from noisy observations is a problem addressed by Bayesian statistical learning, which aims to identify optimal models of the process that generated the observations given assumptions that constrain the space of potential solutions. Animals and machines face similar “model-selection” problems to infer latent properties and predict future states of the world. Here we review recent attempts to explain how intelligent agents address these challenges and how their solutions relate to Bayesian principles. We focus on how constraints on available information and resources affect inference and propose a general framework that uses benefit(accuracy) and accuracy(cost) curves to assess optimality under these constraints.

Introduction

We continuously gather noisy and incomplete information to make inferences about past, present, and future states of the world. Classical Bayesian theory provides a probabilistic framework to identify optimal solutions to this problem [1]. However, Bayesian approaches to inference typically rely on immediate access to all available and appropriate sources of information and unlimited time and resources to carry out the necessary computations. These prerequisites can be met only partially for inference problems faced in the real world, leading to questions about the applicability of Bayesian principles for understanding how the brain and other intelligent agents solve these problems.

Here we discuss recent findings that are beginning to provide a more nuanced understanding of how optimality can be defined in conditions that are subject to real-world constraints, which include limits on the available information and the time and other resources needed to carry out the inference process. We focus on identifying the conditions under which inference strategies employed by animals and machines are consistent with Bayesian principles and those in which they deviate from them. We show that the effectiveness of strategies under real-world constraints could be assessed by maximizing benefit/cost, where realistic benefit(cost) curves can be defined by combining two separate components, corresponding to benefit(accuracy) and accuracy(cost) curves. We argue that this approach can, in principle, be used to explain: (1) the large variation in cost and complexity of inference strategies used for different tasks and conditions, and (2) why individuals sometimes choose inference strategies that are seemingly sub-optimal compared to the Bayesian solution.

Constraints on accessible information

Animals face the fundamental problem of inferring the model that best explains noisy observations, given information from a priori beliefs and ongoing observations. Both of these kinds of information can be limiting. For example, prior knowledge may or not specify the functional form of the process that generated the observations. Likewise, sampling of the environment may be constrained by how much and what kind of data can be gathered. Bayesian theory predicts how these constraints affect the speed of learning and the complexity the learned model. Below we explain these predictions and compare them with animal behavior in three scenarios: (1) the underlying generative process is known, leaving uncertainty only about its parameters; (2) the underlying process is unknown but lies within a specified hypothesis space of processes; (3) there is no prior knowledge of the hypothesis space for the generative process.

Uncertainty about model parameters

When the functional form of the model is known, Bayesian methods seek to infer the optimal parameter values by maximizing the posterior distribution of the parameters θ given the observed data x (where θ and x can be vectors). This distribution is obtained through Bayes’ rule: p(θ|x) α p(x|θ)p(θ), where p(x|θ) is the likelihood of the data x in the model parameterized by θ, and p(θ) reflects a priori expectations about the parameter values and further constrains the hypothesis space.

Strong sampling, weak sampling, and the “size principle”:

In general, as more data are observed, the Bayesian posterior converges to the likelihood (and departs from the prior). If sampling is “strong”, i.e., if samples are drawn independently at random from the model to infer, this convergence occurs exponentially fast in the number of samples. Consider a special case in which the different parameters θ index categories such that each θ describes a probability distribution, p(x|θ), that is nonzero in a subset x_θ of the sample space. The elements of x_θ are then examples of the category, and it is possible that the x_θ overlap or intersect. In this setting, if examples are drawn independently at random from a given underlying category (strong sampling), the likelihood of seeing examples under that category is inversely proportional to the number of items contained in that category. As a result, the Bayesian posterior concentrates exponentially quickly in the number of observed examples on the smallest and most specific category from which the examples could be drawn. This effect, known as the “size principle”, has been proposed to explain the striking human ability to learn categories from a few examples [2, 3, 4, 5]. In contrast, if sampling is “weak”, the relation between the sample distribution and the true distribution of items in the category is not known, because of which all categories compatible with observed samples will be equally likely. In this case, the posterior probability does not concentrate on the most specific category. Human categorization sharpens with increasing data but at variable speeds and generally not as fast as the size principle would prescribe. This result has been interpreted in terms of different assumptions that people make about how observations are generated, usually compatible with a mix of strong and weak sampling [3, 4, 5].

Hierarchical Bayesian Models:

Other sampling effects are evident in more complex problems addressed by Hierarchical Bayesian Models (HBMs) [6, 7]. HBMs solve inference problems in which the prior probability is split on multiple levels: typically, each level defines the probability of certain parameters conditional on other parameters, whose probability is defined at the immediately higher level. The distribution at the top level can be thought of as an “innate prior”. Thus, these models represent increasingly abstract knowledge, for example about classes of categories, along a hierarchy, and can learn at multiple levels of abstraction simultaneously [8]. This property has made HBMs successful as models of language learning [3, 8, 9, 10, 11, 12], conceptual learning [7, 13, 14], reinforcement learning [15], and adaptive inference of dynamic internal states [16, 17, 18, 19]. HBMs make quantitative predictions about how the speed of learning structure in the data at different levels of abstraction is determined by both the sampling process and the structure of the data. For example, abstract knowledge can be acquired faster than specific knowledge: (1) when sampling interleaves examples of different categories [6, 13]; (2) if independent, random sampling results in a skewed distribution of categories, because the incidence of low frequency categories supports inference of the existence of novel categories [13]; and (3) if the features defining a category have little variance among the items of the category [20]. These kinds of sampling constraints are also likely to play critical roles in inference problems in which there is hierarchical or complex structure in the temporal sequences of observations, for which both Bayesian and other solutions require sampling over potentially many different timescales that provide relevant information about volatility of the environment [16, 17, 21, 22, 23, 24, 25, 26, 27, 28].

Uncertainty about the model form in a constrained hypothesis space

When the functional form of the model generating the observed data is unknown, but the set of plausible models is constrained, Bayesian theory can again be used to select the appropriate model form. In this case, the posterior for a certain model form is defined by integrating over the manifold of all the model probability distributions that have the same functional form $f:p(f|x)\propto p(f)\int d\theta p(x\left|\theta ,f)p(\theta \right|f)$. Assuming a uniform prior over distributions (called Jeffreys’ prior), the log-posterior can be expressed asymptotically as a sum of terms of decreasing importance with increasing number N of data points: the leading-order term $(\mathcal{O}(N))$ is the log-likelihood of the data under the optimal model and represents fitting accuracy, and the lower-order terms $(\mathcal{O}(\text{log}N)$ and $\mathcal{O}(1))$ correspond to a measure of statistical simplicity of the model family, which is important to prevent overfitting [33, 34]. These competing quantities produce tradeoffs between the model complexity and fitting accuracy in Bayesian model selection as the number of sampled observations changes.

Bias-variance tradeoffs as a balance between fitting accuracy and complexity:

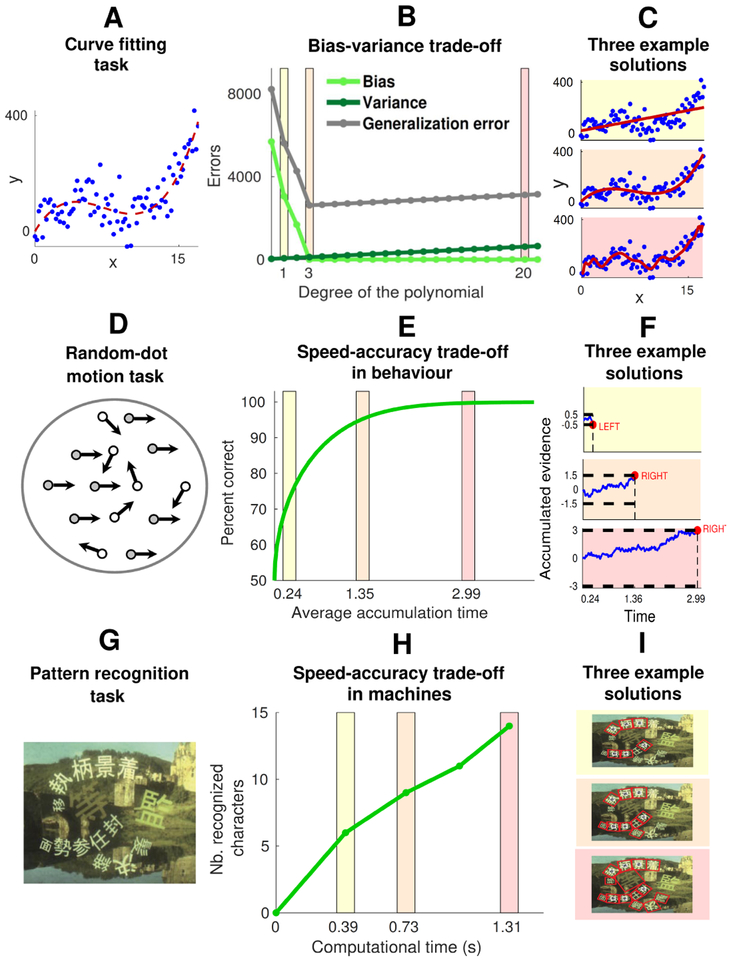
The asymptotic expansion of the Bayesian posterior formalizes the biasvariance trade-off, such that simple models tend to underfit the data and thus yield biased results with low variance across resamplings from the true model, whereas complex models tend to fit the data but overfit the noise and thus yield lower bias but higher variance (Fig.1A,B,C). The optimal model family, which can maximally generalize to new data sampled from the true generative process, typically has intermediate statistical complexity. The tradeoff between fitting accuracy and complexity is sensitive to amount of data. When the amount of data is small, complexity and accuracy compete on an equal basis in model selection. With increasing amounts of data, model accuracy dominates model selection, driving the inference of more complex models that better explain structure in the data. Recent studies on perception [35] and human inference in simple sensorimotor (curve-fitting) tasks [29, 30] have shown, among models of different complexities and equivalent fitting accuracy, people prefer the simplest option, which makes fewer assumptions about the generative process and generalizes better. However, as more data accumulate individuals tend to infer more complex models, as expected from principles of Bayesian inference [36].

Figure 1: Trade-offs in inference with limited information, time, and computational resources.

Top panels: The bias-variance trade-off. A A curve-fitting task that requires an inference about the hidden curve (red dashed line) that is most likely to generate the data points (blue dots) with Gaussian noise [29, 30]. B Under limited data, increasing the degree of the fitting polynomial (and hence the statistical complexity of the solution) decreases errors due to bias (underfitting) but increases errors due to variance (overfitting). The total generalization error is minimized at intermediate complexity. C Three example solutions of increasing statistical complexity (yellow to pink); intermediate is optimal in this case. Middle panels: An example of speed-accuracy trade-off in behaviour. D A random-dot motion task that requires an inference about the dominant direction of motion of stochastic visual dots [31]. E The percentage of correct responses can be increased by increasing the time to sequentially process information (accumulation time) about the direction of motion of the dots. F Example solutions showing increased accuracy but longer decision times as the pre-defined bound on the total evidence to integrate in the decision process (black dashed line) increases (yellow to pink). Bottom panels: An example of speed-accuracy trade-off in machines (adapted from [32]). G A pattern-recognition task that requires the identification of characters embedded in a scene image. H This task can be solved by an “anytime” algorithm that is governed by a trade-off between accuracy and computational time to process information in the image. I As the running time increases, the algorithm localizes (red rectangles) more and more characters (yellow to pink).

Complex model selection:

Even if the set of plausible models or hypothesis space is known, it can be highly complex, with many correlated hypotheses (i.e., partially overlapping model families in the parameter space) and non-uniform prior densities. Under these conditions, consistent Bayesian model selection requires that the different priors match over the shared structure of the models. However, this constraint can lead to an interference effect on model selection given by the particular hypothesis space that is considered: for a fixed generative process, if a model is preferred to another one within a given hypothesis space, this preference is not guaranteed to be preserved when the same models are embedded in a different hypothesis space [37]. It would be interesting to understand if and how these effects relate to interference, measurement-order, and other contextual effects found in psychology [38, 39, 40, 41, 42, 43].

Uncertainty about the hypothesis space

In real-world statistical-inference problems, there may be so much uncertainty about which hypotheses should be considered that identifying a set of options that is likely to contain the true generative model is not feasible [44]. Ideally, the goal of model selection in these cases is to find a model within a given hypothesis space that is as simple as possible and yet comes close to the true data-generating distribution, with closeness quantified in this tradeoff by the log-likelihood of the observed data [33]. In this setting, we are not looking for the “optimal” model but simply the best choice in the set that is feasible to consider.

Ecological rationality – simple though biased models work better:

Real-world problems in which the optimal model cannot be found because relevant information about the structure of the environment is lacking are the focus of “ecological rationality,” which aims to determine which models or strategies are better than others and in which environments [45, 46, 47, 48, 49, 50, 51, 52]. In general, these studies have highlighted a “less-is-more” effect, whereby simple fast-and-frugal heuristics or experience-based intuition, which may have evolved to meet recurrent needs in animal evolution, outperform complex statistical models that require more computations, evidence, and assumptions [48, 49, 52, 53, 47]. This effect is consistent with expectation from Bayesian theory [33] and can also be interpreted as a consequence of the bias-variance trade-off. Specifically, when uncertainty is high because of an underconstrained hypothesis space or because of excessive noise or instability of the environment, subjects often opt for simple strategies that are inflexible (high bias) but marginally affected by noise (low variance). These simple strategies can match, or in some cases surpass, the performance of more complex strategies that minimize bias at the expense of higher variance [54, 48]. The simple strategies may then form building blocks for more complex and adaptable strategies that are needed only under particular conditions, such as when the environment is moderately unstable [55, 46, 56].

Constraints on resources

Bayesian inference often involves complex manipulations of probabilities requiring a long time to perform, extensive memory, and/or substantial investment of computational resources [57, 58, 7, 59]. In practice, however, computational resources are limited and inferences must be made quickly to be useful. Thus, recent work has sought to understand Bayesian optimality in the presence of resource and time constraints.

Inference with limited time

Animals:

Even when sufficient information for optimal Bayesian inference is available in the environment or from memory, the brain needs time to extract and process this information, implying a speed-accuracy trade-off (Fig.1D,E,F) [60, 61, 62, 63, 64, 65, 66, 67]. For the kinds of two-alternative forced-choice (TAFC) tasks used commonly to study perception, memory, and value-based decision-making, the optimal trade-off that maximizes expected accuracy for a given processing time is implemented by the drift-diffusion model (DDM). The DDM selects the alternative with the highest Bayesian posterior given the portion of the evidence that can be processed or accumulated in the available time [68]. These computations can be thought of as Bayesian inference constrained by limited time for sequential information processing, and are consistent with both behavioural and neural responses in these tasks [62, 63, 64, 66, 69, 70]. The optimal speed-accuracy trade-off implemented by the DDM can also be seen, using a physics perspective, in terms of a variational principle that trades off a negative “energy” (representing performance gains) against an information-theoretic distance between the prior and the posterior probability distributions (representing information-processing costs) over the possible options. This interpretation is part of a new statistical theory of bounded, rational decision-making [71].

Machines:

Trade-offs between accuracy and computational speed are also prominent in machine-learning applications, as exemplified by “Anytime” algorithms that are designed to generate increasingly accurate solutions to specific problems the longer they run (Fig.1G,H,I) [58, 72]. Anytime algorithms can be interrupted at any time and still produce a valid solution, which gives them the flexibility to solve inference and other decision-making tasks under variable time constraints. They are also well suited to complex problems in which exact solutions are often hard to find and require substantial computational resources and time. Recent examples include the problem of real-time, efficient distribution of power [73]; large-scale optimal web service composition [74]; ranked information retrieval [75]; approximate resolution in limited time of NP-hard problems, such as the identification of common patterns in strings of data [76] and the problem of heterogeneous multirobot coordination [77, 78, 79]; the SLAM (simultaneous localization and mapping) problem for robot navigation [80]; the related motion-planning problem [81]; and pattern recognition [32] and classification [82]. It would be interesting to understand whether such algorithms have a neural or cognitive realization.

Inference with limited computation and memory

Animals:

Even without a constraint on processing time, the optimal Bayesian solution might be unachievable because of limitations of computational resources and memory capacity. This idea has led researchers to seek alternative algorithms that the brain might use to solve statistical inference tasks subject to resource constraints. This problem has been studied in some detail in the context of inference in dynamic environments, where latent states, like the source of an uncertain reward, change in time with unknown and possibly time-varying volatility. When the latent states drift continuously in time, they can be inferred with limited memory and computational costs using an algorithm that is derived from a variational-Bayesian approximation of the posterior distribution of the states in a hierarchical Bayesian model [16, 17]. This algorithm implements Markovian equations with dynamic learning rates that weigh prediction errors based on the amount of uncertainty in the observations [16, 17]. These equations closely resemble classical reinforcement-learning heuristics and might therefore be implementable in the brain [19, 18]. Several approximate Bayesian algorithms have also been proposed to explain how the brain might infer latent states that do not drift but undergo sudden change points. These algorithms include particle filters, which reduce the computational and memory costs by approximating the Bayesian posterior using a small set of Monte Carlo samples that is updated as new observations are made [22, 83, 84, 85, 86, 87, 88]; approximate Bayesian models in which the memory load is reduced by forgetting or exponentially discounting past information [55, 24, 89, 90, 91, 92]; low-dimensional approximations of Bayesian models that can infer dynamic discrete-valued states and could be implemented by neural networks with plausible plasticity rules [25]; integrate-and-fire neuron models [28] and leaky evidence-accumulation models [27] that can infer dynamic binary states. All of these models approximate optimal solutions with different levels of accuracy and different computational costs and, in many tasks and conditions, match human behaviour more closely than exact Bayesian models [89, 90, 91, 83, 84, 85, 87, 88]. Ongoing work is assessing how some of these solutions, and the cognitive operations that they represent, are related to one another, the quantitative form of the cost-accuracy trade-off that emerges from them, and how this trade-off can be optimized in different environments [55].

Machines:

Trade-offs between accuracy and computational costs are also studied in machine learning. For example, in the field of deep neural networks (DNNs), there is a growing demand for efficient machine learning in devices with limited memory and computational power [93, 94, 95, 96, 97, 98, 99, 100]. These trade-off have been characterized in terms of different performance metrics, including: (1) “information density,” or the accuracy-per-parameter ratio that takes into account architectural complexity (the parameters used) but not computational complexity (the operations performed) [101]; (2) “NetScore,” which gauges accuracy relative to both architectural and computational complexity [102]; and (3) predictive accuracy per input compression, and its distance to the “information-bottleneck” theoretical limit, which defines the maximum predictive accuracy that can be achieved for any given level of compression of the input [103, 104, 105]. These and other metrics are being used to compare DNNs and elucidate the specific cost-accuracy trade-off that they must navigate. Large scale comparisons of DNNs for object detection [106] and image classification [101, 93] have shown, for instance, that different DNNs lie at different points of a specific monotonic trade-off between accuracy and computational complexity: as the amount of computation increases, accuracy also increases but at progressively smaller rates. This phenomenon also applies to the theoretical information-bottleneck limit, which predicts diminishing returns in performance with increasing complexity of input encoding [104]. Identification of upper bounds on accuracy given different constraints on memory and computational costs and comparison of these bounds with current DNN performance can be useful to guide selection of the DNNs that best match the constraints of each application [101, 102, 107] and to develop better architectures and training algorithms [103].

What is optimal in optimal inference?

Classically, optimal Bayesian inference balances prior knowledge and ongoing observations to identify the model with maximum posterior probability. We have argued that inference in the real world is beset by constraints on available information and computational resources. In this context, optimality must be defined in terms of a tradeoff that balances the accuracy or benefit of the inference against an appropriate information or computational cost. Concretely, we might say that an inference procedure is optimal if it maximizes benefit per unit cost, in which the benefit is some monotonically increasing function of accuracy. An example of this kind of objective is benefit per unit time. In fact, in some cases optimization of this objective is straightforward to implement by adjusting the amount of evidence that is integrated in the decision process (the decision threshold in the DDM and similar models) and can help account for reward-driven decision-making behaviors [66, 67, 61, 62, 68, 70, 108].

We propose a generalization of this approach that decomposes the benefit/cost curve into two components (Fig. 2 and [55]). The first component describes the benefit, perhaps the reward obtained, as a function of accuracy. This function generally increases monotonically with accuracy but can take many different forms that reflect the goals or needs of the decision-maker, the task conditions, and other factors [109, 85]. The second component describes accuracy as a function of costs, which can include the time, memory, and computational resources needed to process information [55, 60]. This function is also generally monotonically increasing (e.g., investing more resources yields more accurate solutions in TAFC tasks, dynamic-state inference, and machine-learning applications). Optimizing benefit per cost in this setting will not generally lead to the solution that maximizes benefit, which is the target of classical optimization approaches. For example, consider scenarios in which benefit increases monotonically with accuracy of the inference procedure, and accuracy increases monotonically with the cost of carrying out the inference procedure. Also recall that a typical inference engine (whether a brain or computer) has a fixed resting-state cost to maintain the computational machinery. Below this threshold cost, accuracy will vanish. Here we analyze several scenarios of this kind.

Figure 2: Different Benefit vs. Accuracy (top) and Accuracy vs. Cost (middle) curves yield optimal solutions that vary widely in cost and accuracy.

The optimum is defined as the maximum of the Benefit/Cost ratio (red markers). We consider cases where Benefit increases monotonically as a function of the Accuracy, and Accuracy increases monotonically as a function of Cost. There is minimum operating cost, which means that Accuracy vanishes if Cost is less than this minimum. We consider four general scenarios for the two functions: (A) convex, (B) concave, (C) sigmoid, and (E), a common scenario in which there is little Benefit below a threshold Accuracy and maximal Benefit is quickly attained above this threshold, while Accuracy is a concave function of Cost. Concave functions encode a law of diminishing returns – e.g., if Accuracy is a concave function of Cost, then doubling the Cost gives less than double the return in Accuracy. In this scenario, different rates of diminishing returns (different blue lines) give optimal solutions with widely different costs (different red markers) [55].

First consider a setting in which benefit (B) is proportional to accuracy (A) so that B = αA, while accuracy is a linear function of cost (C) above a threshold (t) so that A = β(C–t), and vanishes when C < t. So if C < t, the ratio B/C vanishes. But for C > t, B/C = αβ(C – t)/C = αβ (1 – t/C) which is maximized at the largest cost, or equivalently at the highest benefit. Thus, if benefit grows linearly with accuracy, and accuracy grows linearly with cost over a threshold, benefit/cost is maximized by simply maximizing the benefit, as expected in traditional optimization approaches. Next consider a setting (Fig. 2, column A) in which benefit is a convex (super-linear) function of accuracy, while accuracy is a convex function of cost above a threshold. Here doubling the cost more than doubles the accuracy, which in turn more than doubles the benefit. These relationships imply that benefit/cost is again maximized when benefit is maximized, in this case at the highest cost.

More realistically, consider scenarios (Fig. 2, column B) in which benefit is a concave (sub-linear) function of accuracy, while accuracy is a concave function of cost above a threshold. Concavity here implies a law of diminishing returns [55, 101, 110]: doubling the cost over threshold yields less than double the accuracy, which in turn gives less than double the benefit. In this setting, the benefit/cost is maximized at an intermediate cost and thus at less than maximal accuracy and benefit (red dots in Fig. 2, column B). Columns C and D of Fig. 2 demonstrate the same result for a saturating (sigmoidal) benefit-accuracy curve with both sigmoidal and concave accuracy-cost curves. In fact, this tradeoff appears very generally in scenarios in which there is a threshold cost and a subsequent law of diminishing returns, for example in energy-efficient information transmission [110] in which information/energy is maximized at some intermediate information rate.

These results suggest that when animals use strategies that do not maximize accuracy or other benefits, they may actually be rationally trading off benefits against costs that reflect constraints on information and computation.