A single-index model with multiple-links

Abstract

In a regression model for treatment outcome in a randomized clinical trial, a treatment effect modifier is a covariate that has an interaction with the treatment variable, implying that the treatment efficacies vary across values of such a covariate. In this paper, we present a method for determining a composite variable from a set of baseline covariates, that can have a nonlinear association with the treatment outcome, and acts as a composite treatment effect modifier. We introduce a parsimonious generalization of the single-index models that targets the effect of the interaction between the treatment conditions and the vector of covariates on the outcome, a single-index model with multiple-links (SIMML) that estimates a single linear combination of the covariates (i.e., a single-index), with treatment-specific nonparametric link functions. The approach emphasizes a focus on the treatment-by-covariates interaction effects on the treatment outcome that are relevant for making optimal treatment decisions. Asymptotic results for estimator are obtained under possible model misspecification. A treatment decision rule based on the derived single-index is defined, and it is compared to other methods for estimating optimal treatment decision rules. An application to a clinical trial for the treatment of depression is presented.

1. Introduction

In precision medicine, a critical concern is to identify baseline measures that have distinct relationships with the outcome from different treatments so that patient-specific treatment decisions can be made [1, 2]. Such variables are called treatment effect modifiers, and these can be useful in determining a treatment decision rule that will select a treatment for a patient based on observations made at baseline. There is a growing need to extract treatment effect modifiers from (usually noisy) baseline patient data that, more and more commonly, consist of a large number of clinical and biological characteristics.

Typically, treatment effect modifiers (or, “moderators”) are identified either one by one, using one model for each potential predictor, or from a large model which includes all potential predictors and their (two-way) interactions with treatment, and then testing for significance of the interaction terms, almost exclusively using linear models. In the linear model context, [3] proposed a model using a linear combination (i.e., an index) of patients’ characteristics, termed a generated effect modifier (GEM) constructed to optimize the interaction with a treatment indicator. Such a composite variable approach is especially appealing for complex diseases such as psychiatric diseases, in which each baseline characteristic may only have a small treatment modifying effect. In such settings, it is not common to find variables that are individually strong moderators of treatment effects.

Here we present novel flexible methods for determining composite variables that permit non-linear association with the outcome. In particular, the proposed methods allow the conditional expectation of the outcomes to have a flexible treatment-specific link function with an index. We define the index to be a one-dimensional linear combination of the covariates. This approach is related to single-index models [4, 5, 6, 7, 8, 9, 10], as well as to single-index model generalizations such as projection pursuit regression [11] and multiple-index models [12, 13]. We employ a single projection of the covariates (i.e., an index) to summarize the variability of the baseline covariates, and multiple link functions to connect the derived single-index to the treatment-specific mean responses; we call these single-index models with multiple-links (SIMML). This single-index models with multiple-links provides a parsimonious extension of the single-index model in modeling the effect of the interaction between a categorical treatment variable and a vector-valued covariate. The dependence of treatment-specific outcomes on a common single-index improves the interpretability, and helps in determining treatment decision rules. This approach generalizes the notion of a composite “treatment effect modifier” from the linear model setting, to a nonparametric context, to define a nonparametric generated effect modifier.

2. A Single-index model with multiple-links (SIMML)

Let $X={\left(x_1,\dots ,x_p\right)}^{\top }\in {ℝ}^p$ denote the set of covariates. Let T denote the categorical (treatment assignment) variable of interest, taking values in {1, …, K} with nonzero probabilities (π₁, … π_K) that sum to one. Let $Y\in ℝ$ denote an outcome variable; without loss of generality, we assume that a higher value of Y is preferred. We focus on data arising from a randomized experiment, however, the method can be extended to observational studies.

A common approach to interrogate the effect of the interaction between X and the treatment indicator T on an outcome is to fit a regression model separately for each of the K treatment groups, as functions of X. For instance, a single-index model can be fitted separately for each treatment group t, resulting in K indices, ${\beta }_t^{\top }X,t\in \left\{1,\dots ,K\right\}$. We refer to this as a K-index model; it has the form

$$\mathbb{E}(Y|T=t,X=x)=g_t\left({\mathit{\beta }}_t^{\top }x\right)(t=1,\dots ,K),$$ (1)

where both the treatment-specific nonparametric link functions g_t(·), and the treatment-specific index vectors ${\beta }_t\in {ℝ}^p$, need to be estimated for each group t. (The vectors β_t need to satisfy some identifiability condition ([14]).) While this is a reasonable approach, the K indices of model (1) lack useful interpretation as effect modifiers and often lead to over-parametrization.

For parsimony and insight, the SIMML constrains the β_t in (1) to be equal, and it requires separate nonparametrically defined curves for each treatment t as a function of a single index α^⊤X common for all t:

$$\mathbb{E}(Y|T=t,X=x)=g_t\left({\alpha }^{\top }x\right)(t=1,\dots ,K),$$ (2)

where both the links g_t and the vector α need to be estimated. The SIMML (2) provides a single parsimonious biosignature, ${\alpha }^{\top }X\in ℝ$. Due to the nonparametric nature of g_t, the scale of α is not identifiable in (2) and to address this we restrict α to be in $\mathrm{\Theta }=\left\{\alpha ={\left({\alpha }_1,\dots ,{\alpha }_p\right)}^{\top }|{\sum }_{j=1}^p{\alpha }_j^2=1,{\alpha }_p>0\right\}$, i.e., to be in the upper hemisphere of the unit sphere.

If the true model for the treatment-specific outcome Y_t is not a SIMML, then the SIMML can be regarded as the L² projection of the treatment specific mean outcome $m_t(X)=\mathbb{E}\left(Y_t|X\right)$ on the single index u = α^⊤X,

$$g_t(u)=\mathbb{E}\left(m_t(X)|{\alpha }^{\top }X=u\right)(t=1,\dots ,K),$$ (3)

for each given α. Specifically, suppose the true treatment-specific model can be expressed as

$$Y_t=m_t(X)+{\sigma }_t(X)ϵ(t=1,\dots ,K),$$ (4)

in which $\mathbb{E}(ϵ|X)=0,\mathbb{E}\left({ϵ}^2|X\right)=1$. Let $R(\alpha )={\sum }_{t=1}^K{\pi }_t\mathbb{E}{\left(Y_t-g_t\left({\alpha }^{\top }X\right)\right)}^2$, where g_t is defined in (3) and let

$${\mathit{\alpha }}_0:=\underset{\mathit{\alpha }\in \mathrm{\Theta }}{\arg \min }R(\mathit{\alpha }).$$ (5)

Then α₀ can be shown to be the minimizer of the cross-entropy (e.g., [15]) between the SIMML (2) and the general model (4) under the Gaussian noise assumption. Here, the cross-entropy of an arbitrary distribution with probability density f, with respect to another reference distribution $\mathcal{P}$ is defined as ${\mathbb{E}}_{\mathcal{P}}(-\log f)$, where the expectation is take with respect to the distribution $\mathcal{P}$. Model (3) evaluated at α₀ can be viewed as the “projection” (in the sense of the closest point) of the true distribution $\mathcal{P}$ (4) onto the space Θ of the SIMML distribution, using the Kullback-Leibler divergence as a distance measure.

The SIMML (2) allows a visualization useful for characterizing differential treatment effects, varying with the single-index α^⊤X. As $X\in {ℝ}^p$ varies, the mean response of model (2) changes only in the specific direction α ∈ Θ, and the effect of varying X, described by the link functions g_t, is different for each treatment condition t ∈ {1, …, K}. Therefore, the single-index can be viewed as a useful biosignature for describing differential treatment effects, provided g_t ≠ g_t′ for at least one pair t, t′ ∈ {1, …, K}.

3. Estimation

While any smoothing technique can be used to approximate the unspecified smooth links g_t(·) in (2), in this paper, we will focus on cubic B-splines. Specifically, $g_t(u)\approx {\eta }_t^{\top }{Z}_t(u)$, for some coefficients ${\eta }_t\in {ℝ}^{d_t}$. Here, $Z_t(u)={\left[B_1(u),\dots ,B_{d_t}(u)\right]}^{\top }\in {ℝ}^{d_t}$ consists of a set of d_t normalized cubic B-spline basis functions [16]. Let n_t be the sample size for the tth treatment group and $n={\sum }_{t=1}^K{n}_t$ denote the total sample size. Note, d_t depends on n_t (see Assumption 5 and [17]). For a given α, let ${\mathbb{Z}}_{\alpha ,t}$ denote the B-spline evaluation matrix (n_t × d_t), so that the ith row is Z_t(α^⊤X_ti)^⊤, which is the B-spline evaluation of the ith individual from the tth treatment group. The subscript α in the matrix ${\mathbb{Z}}_{\alpha ,t}$ highlights its dependence on α. Without loss of generality we assume that the outcome and the covariates are all centered at zero for each treatment group t, so that the model does not involve any intercept terms.

For sample data, SIMML (2) can be represented by

$${[\mathit{Y}]}_{n\times 1}={\left[{\mathbb{Z}}_{\mathit{\alpha }}\right]}_{n\times \left({\sum }_{t=1}^K{d}_t\right)}{[\mathit{\eta }]}_{\left({\sum }_{t=1}^K{d}_t\right)\times 1}+{[\mathit{ϵ}]}_{n\times 1},$$ (6)

where $Y={\left[Y_1^{\top },\dots ,Y_K^{\top }\right]}^{\top }$ is the observed response vector with $Y_t\in {ℝ}^{n_t}$,${\mathbb{Z}}_{\alpha }$ is $n\times \left({\sum }_{t=1}^K{d}_t\right)$ block-diagonal B-spline design matrix of the ${\mathbb{Z}}_{\alpha ,t}{}^{\prime }\text{s}$, $\mathit{\eta }={\left[{\eta }_1^{\top },\dots ,{\eta }_K^{\top }\right]}^{\top }$ is the B-spline coefficient vector, and $\mathit{ϵ}={\left[{\mathit{ϵ}}_1^{\top },\dots ,{\mathit{ϵ}}_K^{\top }\right]}^{\top }$ is a mean zero noise vector with covariance matrix σ²I_n.

For a given α, we define the n × n single-index projection matrix to be ${\mathbb{S}}_{\alpha }={\mathbb{Z}}_{\alpha }{\left({\mathbb{Z}}_{\alpha }^{\top }{\mathbb{Z}}_{\alpha }\right)}^{-1}{\mathbb{Z}}_{\alpha }^{\top }$ . Assuming Gaussian noise and treating η as a nuisance parameter, the negative “profile” loglikelihood of α, up to a constant multiplier, is

$$Q(\alpha )=\Vert Y-{\mathbb{S}}_{\alpha }Y{\Vert }^2.$$ (7)

We define the profile likelihood estimator of the index parameter α as

$$\widehat{\mathit{\alpha }}=\underset{\mathit{\alpha }\in \Theta }{\arg \min }Q(\mathit{\alpha }).$$ (8)

Each link function g_t(·) in (2) can be estimated by

$${\widehat{g}}_t(u)=Z_t{(u)}^{\top }{\left({\mathbb{Z}}_{\widehat{\mathit{\alpha }},t}^{\top }{\mathbb{Z}}_{\widehat{\mathit{\alpha }},t}\right)}^{-1}{\mathbb{Z}}_{\widehat{\mathit{\alpha }},t}^{\top }{\mathit{Y}}_t(t=1,\dots ,K),$$ (9)

where ${\mathbb{Z}}_{\widehat{\mathit{\alpha }},t}$ is ${\mathbb{Z}}_{\mathit{\alpha },t}$ evaluated at $\mathit{\alpha }=\widehat{\mathit{\alpha }}$.

To solve (8), we can perform a procedure that alternates between the following two steps: first, for a fixed α, estimate each link functions g_t(·) in (2) by (9), where $\widehat{\mathit{\alpha }}$ is taken at α; second, for a fixed ${\widehat{g}}_t(u)$, perform an iteratively reweighted least squares (IRLS) to approximately solve (8) for α. These two steps can be iterated until convergence.

4. Asymptotic theory

In this section, we establish the asymptotic results of the profile estimator $\widehat{\alpha }$ in (8) under possible misspecification, when the true model is assumed to be(4). Let us denote the pth component of the vector α₀ in (5) by α_0,p(> 0, since α₀ ∈ Θ). By the completeness property of $ℝ$, we can always find some c > 0 such that α_0,p ≥ c, and therefore, without loss of generality, we may assume that α₀ is in a compact set ${\mathrm{\Theta }}_c=\left\{\alpha ={\left({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_p\right)}^{\top }\in {ℝ}^p|{\sum }_{j=1}^p{\mathit{\alpha }}_j^2=1,{\mathit{\alpha }}_p\ge c\right\}$, with an appropriate choice of small c > 0. Further, to avoid the complication from the restricted parameter space Θ_c, we can consider instead the “pth component removed” R(α) in (5), as follows:

$$R\left({\alpha }_{-p}\right)=R\left({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_{p-1},\sqrt{1-\left({\mathit{\alpha }}_1^2+\cdots +{\mathit{\alpha }}_{p-1}^2\right)}\right),$$ (10)

where a vector ${\alpha }_{-p}=\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{p-1}\right)\in {ℝ}^{p-1}$ lives inside the unit ball. Let the “pth component removed” value of α₀ in (5) be denoted by ${\mathit{\alpha }}_{0,-p}\in {ℝ}^{p-1}$.

Similarly, let the “pth component removed” value of the corresponding profile estimator $\widehat{\mathit{\alpha }}$ in (8) be denoted by ${\widehat{\mathit{\alpha }}}_{-p}\in {ℝ}^{p-1}$. The following conditions are assumed for the asymptotic results.

Assumption 1. The objective function R(α_−p) in (10) is locally convex at α_0,−p, and its Hessian function, H(α_−p) evaluated at α_−p = α_0,−p, is positive definite, with bounded eigenvalues.

Assumption 2. The underlying mean functions m_t(X) in (4) are in $C^{(4)}(B_a^p)$, t ∈ {1, …, K} for some finite a > 0, where $B_a^p$ is the p-dimensional ball with center 0 and radius a and $C^{(q)}\left(B_a^p\right)=\left\{f|theqthorderpartialderivativesoffarecontinuousin{B}_a^p\right\}$.

Assumption 3. The probability density function of X, $f_X(x)\in C^{(4)}\left(B_a^p\right)$, and there exist constants 0 < c_f < C_f such that $c_f/Vo{l}_p\left(B_a^p\right)\le f_X(x)\le C_f/Vo{l}_p\left(B_a^p\right)$, if $x\in B_a^p$ and f_X(x) = 0, if $x\notin B_a^p$.

Assumption 4. The underlying noise ϵ in (4) satisfies $\mathbb{E}(ϵ|X)=0$ with $\mathbb{E}\left({ϵ}^2|X\right)=1$, and there exists a constant C_ϵ > 0, such that ${\sup }_{x\in B_a^p}\mathbb{E}(|ϵ{|}^3|X=x)<C_{ϵ}$. For each group t ∈ {1, …, K}, the standard deviation function σ_t(x) is continuous in $B_a^p$, with $0<c_{{\sigma }_t}\le {\inf }_{x\in B_a^p}{\sigma }_t(x)\le {\inf }_{x\in B_a^p}{\sigma }_t(x)\le C_{{\sigma }_t}<\infty$, for some constants $0<c_{{\sigma }_t}<C_{{\sigma }_t}$.

Assumption 5. The number of interior knots, N_t(= d_t − 4), in the cubic B-spline approximation of the link function g_t(·) for the tth treatment group satisfies: $n_t^{1/6}\ll N_t\ll n_t^{1/5}{\left(\log \left(n_t\right)\right)}^{-(2/5)}$, t ∈ {1, …, K}.

The first theorem establishes consistency of the estimator (8) and the second theorem establishes asymptotic normality of the estimator ${\widehat{\alpha }}_{-p}$ for α_0,−p.

Theorem 1. (Consistency) Under Assumption 1 to 5, $\widehat{\alpha }\to {\alpha }_0$ almost surely, where α₀ is defined in (5).

Theorem 2. (Asymptotic Normality) Under Assumption 1 to 5, $\sqrt{n}({\widehat{\mathit{\alpha }}}_{-p}-{\mathit{\alpha }}_{0,-p})\to \mathcal{N}\left(0,{\Sigma }_{{\alpha }_{0,-p}}\right)$ in distribution, with asymptotic covariance matrix ${\Sigma }_{{\alpha }_0,-p}=H_{{\alpha }_{0,-p}}^{-1}{W}_{{\alpha }_{0,-p}}{H}_{{\alpha }_{0,-p}}^{-1}$, where the matrix $H_{{\alpha }_0,-p}$ is the Hessian matrix $H\left({\alpha }_{-p}\right)=\frac{{\partial }^2}{\partial {\alpha }_{-p}\partial {\alpha }_{-p}^T}R\left({\alpha }_{-p}\right)$ evaluated at α_−p = α_0,−p and the matrix $W_{{\alpha }_{0,-p}}$ is defined in the Appendix.

The proofs of the theorems are given in the Appendix.

5. Simulation illustrations

5.1. Performance on estimating treatment decision rules

A treatment decision function, $\mathcal{D}(X):{ℝ}^p\mapsto \left\{1,\dots ,K\right\}$, mapping a subject’s baseline characteristics $X\in {ℝ}^p$ to one of K available treatments, defines a treatment decision rule for the single decision time point [1, 2, 18, 19, 20]. Given covariates X, a treatment decision rule based on SIMML is $\mathcal{D}(X)=\arg {\max }_{t\in \left\{1,\dots ,K\right\}}{g}_t\left({\alpha }^{\top }X\right)$. We investigate the performance of the estimated treatment decision rules of the form $\mathcal{D}(X)=\arg {\max }_{t\in \left\{1,\dots ,K\right\}}\mathbb{E}(Y|X,T=t)$, where the conditional expectation is obtained from various modeling procedures.

In our simulation settings, the baseline covariate vector $X={\left(x_1,\dots ,x_p\right)}^{\top }~\mathcal{N}\left(0,{\mathrm{\Psi }}_X\right)$, with Ψ_X having 1′s on the diagonal and 0.1 everywhere else. We consider K = 2 with different noise levels for the two treatment groups: ${ϵ}_1~\mathcal{N}\left(0,{0.4}^2\right)$, ${ϵ}_2~\mathcal{N}\left(0,{0.2}^2\right)$ The outcome data are generated under the following fairly broad model

$$Y_t=\delta M\left({\mu }^{\top }X;\nu \right)+C_t\left({\alpha }^{\top }X;\omega \right)+{ϵ}_t(t=1,2).$$ (11)

As a function of the index μ^⊤X, M is referred to as the “main effect” of X. As functions of the other index α^⊤X, the C_t’s are referred to as the “contrast” functions that define the treatment-by-X interaction. Here, we will use the parameters ν and ω to control the degree of non-linearity of M and C_t’s, respectively.

An optimal treatment decision rule depends only on the C_t’s, not on M or the ϵ_t’s. The parameter δ in (11) controls the relative contribution of the “signal” component $C_t^{\prime }s$ to the variance in the outcomes, and is calibrated to obtain a relative contribution of 0.35. The contrast functions C_t’s in (11) are set to

$$C_t(u;\omega )=\{\begin{array}{l}{C}_1(u;\omega )=+1-\cos (0.5\pi \omega u)+0.5(u-\omega )\hfill \\ C_2(u;\omega )=-1+\cos (0.5\pi \omega u)-0.5(u-\omega ),\hfill \end{array}$$ (12)

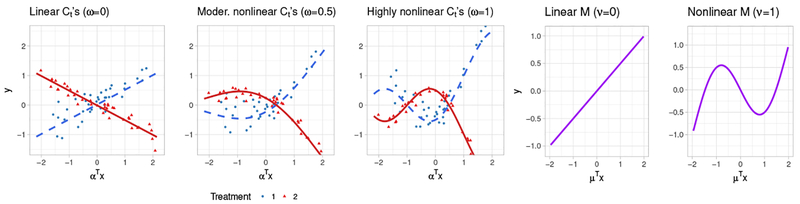
where, if ω = 0, then the C_t’s are linear functions; and they are more nonlinear for larger values of ω. We considered three cases, corresponding to linear (ω = 0), moderately nonlinear (ω = 0.5), and highly nonlinear (ω = 1) C_t’s, respectively, illustrated in the first three panels of Figure 1. We set the main effect function M in (11) to be

$$M(u;\nu )=0.5u-\sin (0.5\pi \nu u),$$

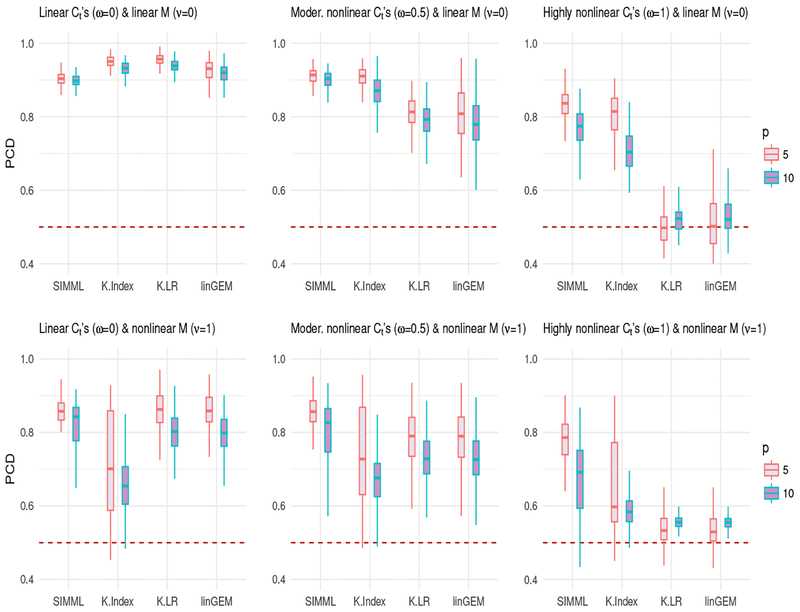
where, as ν increases, the degree of nonlinearity in the main effect function M increases. We considered two cases, ν = 0, corresponding to a linear M; and ν = 1, corresponding to a nonlinear M, illustrated in the fourth and the fifth panels of Figure 1. We set p = 5 and p = 10 with α = (1, …, 5)^⊤ and α = (1, …, 10)^⊤, respectively, each standardized to have norm one. We set μ to be proportional to a vector of 1’s, standardized to have norm one. Two treatment groups were considered, with equal sample sizes n₁ = n₂ = 40. We used d₁ = d₂ = 5 B-spline basis functions to approximate the link functions. The treatment decision rules were based on the following regression models: (i) SIMML (2) estimated from maximizing the profile likelihood; (ii) the K-Index model (1) fitted separately for each treatment group by the B-spline approach of [17], denoted as K-Index; (iii) the linear GEM model ([3]) estimated under the criterion of maximizing the difference in the treatment-specific slope, denoted as linGEM; and (iv) linear regression models fitted separately for each treatment group under the least squares criterion, denoted as K-LR. For each scenario, using the outcome Y from a simulated test set (of size 10⁵), we computed the proportion of correct decisions (PCD) of the treatment decision rules estimated from each method and the methods were compared in terms of PCD using boxplots from training datasets.

Figure 1:

The first panel shows the linear contrast C_t’s (ω = 0), the second panel the moderately nonlinear contrast C_t’s (ω = 0.5), and the third panel displays highly nonlinear contrast C_t’s (ω = 1). Data points are generated from model (11) with δ = 0 and p = 5. The fourth and the fifth panels show the linear (ν = 0) and the nonlinear main effect M (ν = 1), respectively.

Figure 2 shows that SIMML outperforms all other methods, except for the case under the linear M and C_t’s in which all 4 approaches perform well. The K-Index model is clearly second best, under the linear M (ν = 0) (the top panels) with the nonlinear C_t’s (ω = 0.5 and ω = 1). However, with a more complex M function (ν = 1) (the bottom panels), the performance of the K-index approach is considerably worse compared to SIMML. Given a relatively small sample size and under the complex main effect, the SIMML that emphasizes the treatment contrasts through the common single-index is more effective in estimating optimal treatment decisions than the K-Index model. As would be expected, additional complexity in the contrasts C_t’s (ω = 0.5 and ω = 1) has a greater effect on the performance of the more restrictive models (linGEM and K-LR) than it does on the flexible models (SIMML and K-index). The number of covariates, p, also has a clear impact on the performance of all methods. As p changes from 5 (red) to 10 (blue), the deterioration in performance is more pronounced for the K-Index model that requires separate fits for each treatment and thus involves estimation of more parameters (K(p − 1) + Kd), compared to the more parsimonious SIMML with a fewer number of parameters (p − 1 + Kd) to be estimated.

Figure 2:

Boxplots of the proportion of correct decisions (PCD) of the treatment decision rules obtained from 200 training datasets for each of the four methods. Each panel corresponds to one of the six combinations of ω ∈ {0, 0.5, 1} and ν ∈ {0, 1}: the shape of the contrast functions C_t’s controlled by ω; the shape of the main effect function M controlled by ν; the number of predictors p ∈ {5, 10}. The sample sizes are n₁ = n₂ = 40.

5.2. Coverage probability of asymptotic 95% confidence intervals

The next simulation experiment assesses the coverage probability of the asymptotic confidence intervals derived from Theorem 2. The data were generated under model (11) with δ = 0 (i.e., no main effect M) with p = 5 covariates. We set the SIMML index vector α(= α₀) to be stepwise increasing: (1, …, 5)^⊤, normalized to have unit L² norm. The associated contrast functions, C_t’s, are given by (12). As in Section 5.1, we consider three levels of the curvature of the contrasts, corresponding to linear (ω = 0), moderately nonlinear (ω = 0.5), and highly nonlinear (ω = 1) contrasts (see Figure 1). In (11), the standard deviations of the noise ϵ_t were set to 0.5. We set the sample size n = n₁ + n₂ with n₁ = n₂. With varying n ∈ {50, 100, 200, 400, 800, 1600, 3200}, the number of interior knots used in the B-spline approximation, N_t, was determined to be $N_t=\left[n_t^{1/5.5}\right]$, as recommended by [17] ([v] denotes the integer part of v). Two hundred datasets were generated for all combinations of n and ω. For each (i.e., the jth) component α_j of α, the proportion of times the 95% asymptotic confidence interval contains the true value of α_j was recorded in the Table C.2 in the Appendix. Notice that the 5th (i.e., the pth) element is estimated to satisfy the constraint α ∈ Θ in Theorem 2. To obtain the confidence intervals for the 5th component, we applied Theorem 2 with the 4th component removed (without loss of generality), and obtained the confidence intervals for the 5th component.

We note that the choice of $N_t=\left[n_t^{1/5.5}\right]$ is an approximation to the N_t of Assumption 5 which requires $n_t^{1/6}\ll N_t\ll n_t^{1/5}{\left(\log \left(n_t\right)\right)}^{-(2/5)}$, as such N_t can only be obtained for a very large n_t. Nevertheless, in Table C.2 in the Appendix, as the sample size n(= n₁+n₂) increases, the “actual” coverage probability gets closer to the “nominal” coverage probability, with better coverage results for the linear and the moderately nonlinear contrasts (ω ∈ {0, 0.5}) compared to the highly nonlinear contrasts (ω = 1).

6. Application to data from a randomized clinical trial

Major depressive disorder afflicts millions and, according to the World Health Organization, it is the leading cause of disability worldwide. It is a highly heterogeneous disorder, however, no individual biological or clinical marker has demonstrated sufficient ability to match individuals to efficacious treatment. Here we illustrate the utility of the proposed SIMML method for estimating a composite biomarker and treatment decision rules, with an application to data from a randomized clinical trial comparing an antidepressant and placebo for treating depression.

Of the 166 subjects, 88 were randomized to placebo and 78 to the antidepressant. In addition to standard clinical assessments, patients underwent neuropsychiatric testing prior to treatments. Table 1 summarizes the information on p = 9 baseline patient characteristics, X = (x₁, …, x₉)^⊤. These baseline covariates were considered as potential treatment effect modifiers, and standardized to have unit variance. The treatment outcome Y was the improvement in symptom severity from week 0 (baseline) to week 8 and thus larger values of the outcome were better.

Table 1: Depression randomized clinical trial:

Description of the p = 9 baseline covariates (means and SDs); the estimated values (“Indiv. Value”) of treatment decision rules from each individual covariate, using either the B-spline regression (“Nonpar.”, in the third column) or the linear regression (“Linear”, in the fourth column); the estimated single-index coefficients (in the last three columns), and the values of the associated treatment decision rules from the three methods (in the bottom row).

(Label) Baseline	Mean	Indiv. Value		Coefficients αj’s, j ∈ {1, …, 9}
patient characteristics	(SD)	Nonpar.	Linear	SIMML*	SIMML	linGEM
(xi) Age at evaluation	38.00 (13.84)	8.56	8.24	−0.53	−0.50	−0.43
(x2) Severity of depression	18.80 (4.29)	6.85	7.07	−0.07	−0.13	−0.37
(х3) Dur. MDD (month)	38.19 (53.17)	7.42	7.33	0.08	−0.18	0.20
(x4) Age at MDD	16.46 (6.09)	6.29	6.95	0.23	0.05	0.31
(x5) Axis II	3.92 (1.43)	7.16	7.11	0.23	0.20	0.17
(x6) Word Fluency	37.42 (11.68)	7.64	7.11	0.11	0.09	0.27
(x7) Flanker RT	59.51 (26.63)	8.19	8.39	0.12	0.23	−0.18
(x8) Post-conflict adjus.	0.07 (0.12)	6.73	7.23	−0.30	−0.29	−0.18
(x9) Flanker Accuracy	0.22 (0.15)	7.89	8.37	0.70	0.70	0.59
Value from single-index model				9.34	8.72	8.22

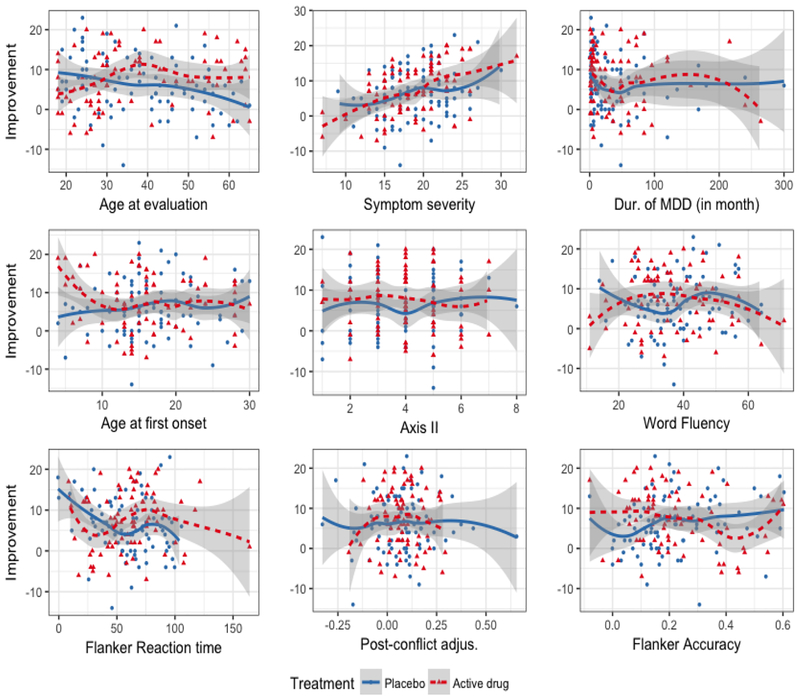
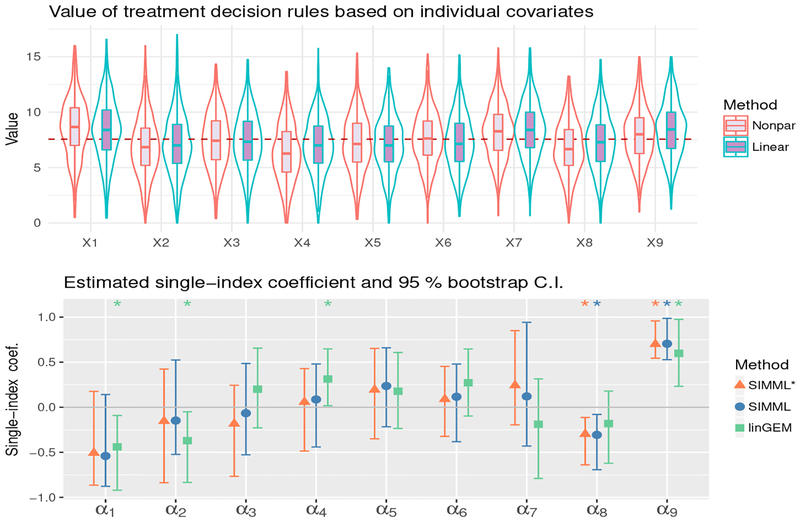
Figure 3 shows the treatment outcomes Y against each of the 9 baseline covariates, for the placebo group (blue) and the active drug group (red). The estimated B-spline approximated curves for each individual covariate are shown with the associated 95% confidence bands: the solid blue curves for the placebo group and the dotted red curves for the active drug group. In Figure 3, each individual covariate has at most a small treatment modifying effect, as its treatment-specific curves do not differ much.

Figure 3: Depression randomized clinical trial:

For each of the 9 baseline covariates individually, treatment-specific spline approximated regression curves with 5 basis functions are overlaid on to the data points; the placebo group is the blue solid curve and the active drug group is the red dotted curve. The associated 95% confidence bands of the regression curves were also plotted.

One natural measure for the effectiveness of a treatment decision rule $\mathcal{D}$ is called the “value” (V) of a treatment decision rule $\mathcal{D}$ [20], which is defined as the expected mean outcome if everyone in the population receives treatment according to that rule:

$$\text{V}(\mathcal{D})={\mathbb{E}}_X\left({\mathbb{E}}_{Y|X}(Y|X,T=\mathcal{D}(X))\right).$$ (13)

In the third and the fourth columns of Table 1, “Indiv. Value” refers to the estimated “value” of a decision rule $\mathcal{D}$ estimated from each of the 9 individual covariates, using the following two approaches for estimating $\mathcal{D}$: the B-spline regressions of the treatment-specific outcome on each individual covariate (“Nonpar.” in the third column of Table 1) as suggested by the overlaid curves in Figure 3, and the linear regressions of the treatment-specific outcome on each individual covariate (“Linear” in the fourth column of Table 1). The value (13) of $\mathcal{D}$ can be estimated by the inverse probability weighted estimator [21]:

$$\widehat{V}(\mathcal{D})=\sum _{i=1}^{\tilde{n}}{Y}_i{I}_{T_i=\mathcal{D}\left(X_i\right)}/\sum _{i=1}^{\tilde{n}}{I}_{T_i=\mathcal{D}\left(X_i\right)},$$ (14)

using a testing set, say, $\left\{\left(Y_i,X_i,T_i\right),i=1,\dots ,\tilde{n}\right\}$, where, if one uses only the jth covariate for estimating $\mathcal{D}$, then X_i = x_ij. The data were randomly split into a training set and a testing set with a ratio of 10 to 1. This splitting was performed 500 times, each time estimating $\mathcal{D}$ on the training set and computing (14) from the testing set. Values (14) are averaged over the 500 splits.

The SIMML can be made more efficient by incorporating a main effect component β^⊤D(X) in the model, i.e., we can consider $\mathbb{E}(Y|T=t,X=x)={\beta }^{T}D(x)+g_t\left({\alpha }^{\top }x\right)$, for an appropriate vector-valued function D(X). If the n × q matrix $\mathbb{D}$ denotes the evaluation of D(X) on the sample data, then for each α, the negative “profile” loglikelihood (7) under this extended model (with Gaussian outcome), up to constants, is $Q^{*}(\alpha )={\Vert \tilde{Y}-{\mathbb{S}}_{\alpha }\tilde{Y}\Vert }^2$, where $\tilde{Y}=\left(I_n-\left(I_n-{\mathbb{S}}_{\alpha }\right)\mathbb{D}{\left({\mathbb{D}}^T\mathbb{D}\right)}^{-1}{\mathbb{D}}^T\right)Y$. In this analysis, we took D(X) = X. We refer to this approach as “main effect adjusted” profile likelihood SIMML and denote it by SIMML*.

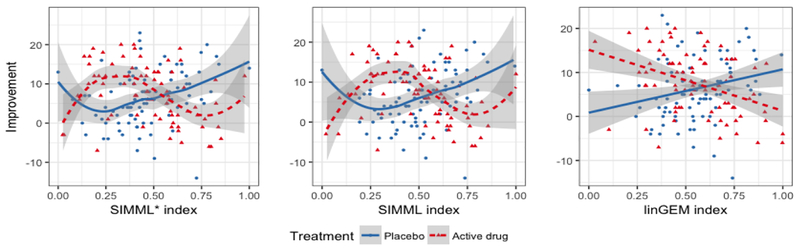
In Table 1, the last three columns show the estimated single-index coefficients α obtained by two different SIMMLs (SIMML* and SIMML) and the linear GEM (linGEM) which restricts the link g_t(·) to be a linear function. In Figure 4, the estimated pairs of link functions are plotted against the approach-specific single-index α^⊤X, obtained from applying the two SIMML approaches and the linear GEM approach. From Figures 3 and 4, it appears that the index α^⊤X exhibits a stronger moderating effect of treatment than the individual covariates. Also, the shapes of the regression curves from the SIMML approaches appear to capture a nonlinear treatment-by-index interaction effect, especially due to some non-monotone relationship between the index and the outcome in the active drug group.

Figure 4: Depression randomized clinical trial:

Pair of estimated link functions (g₁ and g₂) obtained from SIMML with the “main effect adjusted” profile likelihood (first panel), SIMML with the (main effect un-adjusted) profile likelihood (second panel), and the linear GEM model estimated under the criterion maximizing the difference in the linear regression slopes (third panel), respectively, for the placebo group (blue solid curves) and the active drug group (red dotted curves). The 95% confidence bands were constructed conditioning on the single-index coefficient α. For each treatment group, the observed outcomes are plotted against the estimated single-index.

In Figure 5, we illustrate the single-index coefficient estimates from each of the methods, and the associated 95% confidence intervals obtained from a bias-corrected and accelerated (BC_a, [22]) bootstrap with 500 replications. The coverage of the asymptotic-based confidence intervals for this sample size is not expected to be very good (based on the simulation results in Section 5.2) and thus instead we used bootstrap confidence intervals. The magnitude of the estimated coefficients α₁, …, α₉ reflects the relative importance of the covariates x₁, …, x₉ in determining a composite treatment effect modifier α^⊤X.

Figure 5: Depression randomized clinical trial:

Top panel: Violin plots of the estimated values of treatment decision rules based on each of the individual covariates x₁, …, x₉, determined from univariate nonparametric and linear regressions, respectively, obtained from 500 randomly split testing sets (with higher values preferred). Bottom panel: The estimated index coefficients α₁, …, α₉, associated with the covariates x₁, …, x₉, and the 95% confidence intervals for each of the three methods, obtained from BC_a bootstrap with 500 replications. An estimated significant coefficient is marked with * on top of each confidence interval.

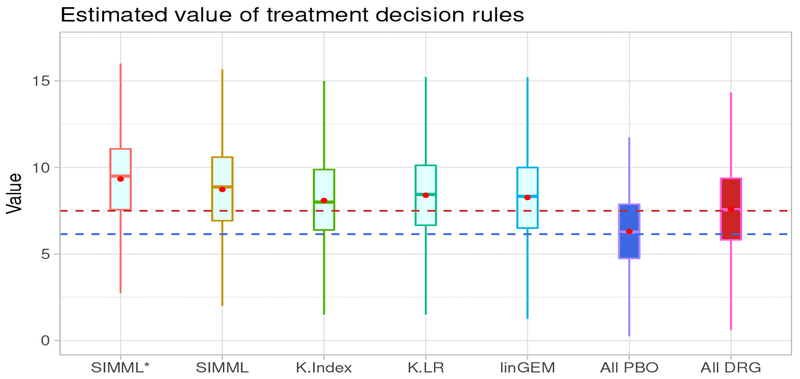
In this analysis, the incorporation of the “main effect” component improved the value of treatment decision rules determined from the proposed SIMML method, as illustrated in the boxplots in Figure 6; we compared the two SIMML approaches (SIMML* and SIMML); the linear GEM (linGEM) and the two approaches based on separate regression models for each treatment group (K-Index and K-LR), with respect to the estimated values (14) of the treatment decision rules. For comparison, we also included the decision to treat everyone with placebo (All PBO), and the decision to treat everyone with the active drug (All DRG). The results are summarized in Figure 6.

Figure 6: Depression randomized clinical trial:

Boxplots of the estimated values of treatment decision rules, obtained from the 500 randomly split testing sets (higher values are preferred). The estimated values (and the standard deviations) are given as follow. SIMML*: 9.34(2.68); SIMML: 8.72 (2.68); K-Index: 8.04 (2.69); K-LR: 8.36 (2.69); linear GEM (linGEM):8.22 (2.67); All placebo (PBO): 6.17 (2.63); All drug (DRG): 7.57 (2.67).

In Figure 6, in terms of the averaged estimated values (14) estimated from the aforementioned 500 randomly split testing sets, the proposed SIMML approaches outperform all other methods. The visualization (see Figure 4) indicates that the superiority of the active drug over placebo does not linearly decrease with the index, but rather, it appears to remain relatively constant to the left of the crossing point, exhibiting some nonlinear patterns. Finally, we note that the value of the treatment decision rule All PBO was lower than the value of the treatment decision rule All DRG, and that all treatment decision rules that took patient characteristics into account outperformed the decision of treating everyone with the drug (which is standard current clinical practice). In particular, the superiority the treatment decision rule SIMML* over treating everyone with the drug in terms of value was of similar magnitude of the superiority of the decision to treat everyone with the drug versus treating everyone with placebo. This is a clear indication that patient characteristics can help treatment decisions for patients with depression, and the more flexible SIMML methods are well suited for developing treatment decision rules. Particularly, the proposed methods show that combining patient characteristics with little moderating effects of a treatment can result in a strong treatment effect modifier which exhibits nonlinear association with the outcome that can help with making treatment decisions.

7. Discussion

The SIMML model (6) can be extended in various ways, for example, by allowing treatment-specific noise variances ${\sigma }_t^2$. Under a Gaussian noise assumption, the B-spline approximated profile log likelihood of α, that profiles out the nuisance parameters ${\sigma }_t^2$ and η_t, up to constants, is ${\sum }_{t=1}^K{n}_t\log Q_t(\alpha )$, in which $Q_t(\alpha )=\Vert Y_t-{\mathbb{S}}_{\alpha ,t}{Y}_t{\Vert }^2/n_t$. The corresponding profile estimator of α is $\underset{\alpha \in \mathrm{\Theta }}{\arg \min }{\sum }_{t=1}^K{n}_t\log Q_t(\alpha )$. The estimation can be performed similarly as in the estimation of $\widehat{\mathit{\alpha }}$ in (8), but the criterion function Q(α) will be replaced by ${\sum }_{t=1}^K{n}_t\log Q_t(\alpha )$.

The SIMML can also be extended to generalized linear models (GLM) in which the outcome variable is a member of the exponential family. The standard form of the density is f_Y(Y; θ, ϕ) = exp {(Y θ − b(ϕ))/a(ϕ) + c(Y, ϕ)}, with a canonical link function h(·). We can extend the SIMML approach to the GLM setting with treatment-specific natural parameters θ_t, t ∈ {1, …, K} by modeling the treatment-specific outcomes as a function of a single-index ${\alpha }^{\top }X:{\theta }_t(x)=h^{-1}(\mathbb{E}(Y|T=t,X=x))=g_t\left({\alpha }^{\top }x\right)$, t ∈ {1, …, K}; g_t(·), hence ${\theta }_t(x)\in ℝ$, can be approximated, for example, by B-splines. The approximates can be denoted by ${\tilde{\theta }}_t(x)={\mathit{\eta }}_t^{\top }{Z}_t\left({\alpha }^{\top }x\right)$ for some ${\mathit{\eta }}_t\in {ℝ}^{d_t}$. As in Section 3, the general strategy of nonlinear maximization of the “profile” likelihood over α ∈ Θ, where we profile out η_t for each value of α, can be employed. The dispersion parameter ϕ can also be profiled out. Other potential extensions involve incorporating variable selection in high-dimensional covariate settings using a regularization method and incorporating functional-valued data objects (such as images) as patient covariates.

An important extension to the SIMML model is to factor out baseline effects common to all treatment groups, by allowing an unspecified main-effect term μ(X) [e.g., 23] in the model. Generally, this can be handled by an “orthogonalization” approach, and the estimation can be performed under the framework of A-learning [1, 24, 25, 26, 27]. To elaborate, consider the following extension of model (2),

$$\mathbb{E}(Y|T=t,X=x)=\mu (x)+g_t\left({\alpha }^{\top }x\right)(t=1,\dots ,K),$$ (15)

where we impose a structural constraint, ${\mathbb{E}}_T\left(g_T\left({\alpha }^{\top }X\right)|X\right)={\sum }_{t=1}^K{\pi }_t{g}_t\left({\alpha }^{\top }X\right)=0$, which is a sufficient condition for orthogonality between the SIMML, g_T (α^⊤X), and the unspecified main effect, μ(X) in (15), as in [27]. Optimization of model (15) can be achieved by constrained least squares under this orthogonality constraint and A-learning can be employed for estimating an optimal treatment decision rule, focusing on estimating the interactions in the presence of the unspecified main effect μ(X). The technicalities of this adjustment are treated in a separate work.

Appendix A. The asymptotic covariance matrix in Theorem 2

Define $R_t(\alpha )={\mathbb{E}}_{Y,X|T=t}{\left(Y-g_t\left({\alpha }^{\top }X\right)\right)}^2$, t ∈ {1, …, K}. In Theorem 2, the asymptotic covariance matrix is given as ${\Sigma }_{{\alpha }_{0,-p}}=H_{{\alpha }_{0,-p}}^{-1}{W}_{{\alpha }_{0,-p}}{H}_{{\alpha }_{0,-p}}^{-1}$. Here, the Hessian matrix $H_{{\alpha }_0,-p}={\left[H_{j,q}\right]}_{j,q=1}^{p-1}$ evaluated at α_−p = α_0,−p has its (j, q)th element given by

$$H_{j,q}=\sum _{t=1}^K{\pi }_t[\frac{{\partial }^2}{\partial {\alpha }_j\partial {\alpha }_q}{R}_t(\alpha )-\frac{{\alpha }_j}{{\alpha }_p}\frac{{\partial }^2}{\partial {\alpha }_p\partial {\alpha }_q}{R}_t(\alpha )-\frac{{\alpha }_q}{{\alpha }_p}\frac{{\partial }^2}{\partial {\alpha }_p\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_j{\alpha }_q}{{\alpha }_p^3}\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )+\frac{{\alpha }_j{\alpha }_q}{{\alpha }_p^2}\frac{{\partial }^2}{\partial {\alpha }_p^2}{R}_t(\alpha ){]|}_{\alpha ={\alpha }_0}.$$ (A.1)

The matrix $H_{{\alpha }_0,-p}={\left[H_{j,q}\right]}_{j,q=1}^{p-1}$ evaluated at α_−p = α_0,−p has its (j, q)th element given by

$$W_{j,q}=\sum _{t=1}^K{\pi }_t{\mathbb{E}}_{Y,X|T=t}(\left\{2\left(g_t\left(u_{\mathit{\alpha }}\right)-Y\right)\left(\frac{\partial }{\partial {\alpha }_j}{g}_t\left(u_{\mathit{\alpha }}\right)-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{g}_t\left(u_{\mathit{\alpha }}\right)\right)+\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )\right\}\times \left\{2\left(g_t\left(u_{\alpha }\right)-Y\right)\left(\frac{\partial }{\partial {\alpha }_q}{g}_t\left(u_{\mathit{\alpha }}\right)-\frac{{\alpha }_q}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{g}_t\left(u_{\alpha }\right)\right)+\frac{\partial }{\partial {\alpha }_q}{R}_t(\mathit{\alpha })-\frac{{\alpha }_q}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )\right\}{)|}_{\alpha ={\alpha }_0}$$ (A.2)

where u_α = α^⊤X.

Appendix B. Proof

Appendix B.1. Proof of Theorem 1

Proof. Let us write $Q_t(\alpha )=\Vert Y_t-{\mathbb{S}}_{\alpha ,t}{Y}_t{\Vert }^2/n_t$ and $Q(\alpha )={\sum }_{t=1}^K{n}_t{Q}_t(\alpha )/n$. Under Assumptions 2–4, by the results from A.14 of [28], we have

$$\underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\left|Q_t(\alpha )-R_t(\alpha )\right|\le O\left({\left(n_t^{-1/2}{h}_t^{-1/2}\log n_t\right)}^2+{\left(h_t^4\right)}^2\right)+O\left(n_t^{-1/2}\log n_t{h}_t^{-1/2}+h^4\right)$$

almost surely, where $h_t=\frac{1}{N_t+1}$ is the distance between knot points, and N_t (note, N_t = d_t − 4) is the number of interior knots on [0, 1]. Since we choose N_t such that $n_t^{1/6}\ll N_t\ll n_t^{1/5}{\left(\log \left(n_t\right)\right)}^{-(2/5)}$ for all t ∈ {1, …, K}, under Assumption 5,

$$\underset{\alpha \in {\mathrm{\Theta }}_e}{\sup }|Q_t(\alpha )-R_t(\alpha )|\to 0t\in \left\{1,\dots ,K\right\},$$

almost surely. By the continuous mapping theorem,

$$\underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\left|\sum _{t=1}^K\frac{n_t}{n}{Q}_t(\alpha )-\sum _{t=1}^K{\pi }_t{R}_t(\alpha )\right|\le \underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\sum _{t=1}^K\left|\frac{n_t}{n}{Q}_t(\alpha )-{\pi }_t{R}_t(\alpha )\right|\to 0$$

almost surely, therefore, we have

$$\underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\left|Q(\alpha )-R(\alpha )\right|\to 0,$$ (B.1)

almost surely. Denote by (Ω, $\mathcal{F}$, $\mathcal{P}$) the probability space on which all ${\left\{Y_i,T_i,X_i^{\top }\right\}}_{i=1}^{\infty }$ are defined. By (B.1), for any δ > 0, ω ∈ Ω, there is an integer n*(ω), such that Q(α₀, ω) − R(α₀) < δ/2, whenever n > n*(ω). Since $\widehat{\alpha }(\omega )$ is the minimizer of Q(α, ω), we have $Q(\widehat{\alpha }(\omega ),\omega )-R\left({\alpha }_0\right)<\delta /2$. Also, by (B.1), there exists an integer n**(ω), such that $R(\widehat{\alpha }(\omega ),\omega )-Q(\widehat{\alpha }(\omega ),\omega )<\delta /2$, whenever n > n**(ω). Therefore, whenever n > max(n*(ω), n**(ω)), we have $R(\widehat{\alpha }(\omega ),\omega )-R\left({\alpha }_0\right)<\delta$. The strong consistency $\widehat{\alpha }\to {\alpha }_0$ follows from the local convexity of Assumption 1. □

Appendix B.2. Proof of Theorem 2

Proof. We first derive the expression (A.1) from the Appendix for the Hessian matrix. We can write $R\left({\alpha }_{-p}\right)={\sum }_{t=1}^K{\pi }_t{R}_t\left({\alpha }_{-p}\right)$, where the “pth component removed” function corresponding to the tth treatment is $R_t\left({\alpha }_{-p}\right)=R_t\left({\alpha }_1,\dots ,{\alpha }_{p-1},\sqrt{1-\left({\alpha }_1^2+\cdots +{\alpha }_{p-1}^2\right)}\right)$. Applying the chain rule for taking the derivative of R_t(α_−p) with respect to α_j, we obtain

$$\frac{\partial }{\partial {\alpha }_j}{R}_t\left({\alpha }_{-p}\right)=\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )$$ (B.2)

for each j ∈ {1, …, p – 1}. Taking another derivative of (B.2) with respect to α_q, for each q ∈ {1, …, p – 1}, again by applications of the chain rule,

$$\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_j}{R}_t\left({\alpha }_{-p}\right)=\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_q}{{\alpha }_p}\frac{{\partial }^2}{\partial {\alpha }_p\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_j}{{\alpha }_p}\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_p}{R}_t(\alpha )-\frac{\partial }{\partial {\alpha }_q}\left(\frac{{\alpha }_j}{{\alpha }_p}\right)\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )+\frac{{\alpha }_q{\alpha }_j}{{\alpha }_p^2}\frac{{\partial }^2}{\partial {\alpha }_p\partial {\alpha }_p}{R}_t(\alpha ).$$ (B.3)

After summing (B.3) over the groups t ∈ {1, …, K}, weighted by the group probabilities π₁, …, π_K, evaluated at α = α₀, we obtain (A.1).

Next, we examine the asymptotics of the profile estimator $\widehat{\alpha }$. From A.15 of [28] and under Assumptions 2–5, we have

$$\underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\underset{1\le j\le p}{\sup }\left|\frac{\partial }{\partial {\alpha }_j}\left\{Q_t(\alpha )-R_t(\alpha )\right\}-\frac{1}{n_t}\sum _{i=1}^{n_t}{\xi }_{\mathit{\alpha },i,j,t}\right|=o\left(n_t^{-1/2}\right)$$ (B.4)

almost surely, with ${\xi }_{\alpha ,i,j,t}=2\left\{g_t\left(u_{\alpha ,ti}\right)-Y_{ti}\right\}\frac{\partial }{\partial {\alpha }_j}{g}_t\left(u_{\alpha ,ti}\right)-\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )$, where u_α,ti = α^⊤X_ti and furthermore

$$\begin{gathered} \underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\underset{1\le j\le p}{\sup }\left|\frac{\partial }{\partial {\alpha }_j}\left\{Q_t(\alpha )-R_t(\alpha )\right\}\right|=o(1), \\ \underset{\alpha \in {\mathrm{\Theta }}_c}{\sup }\underset{1\le q,j\le p}{\sup }\left|\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_j}\left\{Q_t(\alpha )-R_t(\alpha )\right\}\right|=o(1), \end{gathered}$$ (B.5)

almost surely, for each group t ∈ {1, …, K}.

Now, we will prove that the estimated score of $Q\left({\alpha }_{-p}\right)={\sum }_{t=1}^K{\widehat{\pi }}_t{Q}_t\left({\alpha }_{-p}\right)$, where ${\widehat{\pi }}_t={\sum }_{i=1}^{n}I\left(T_i=t\right)/n$, evaluated at α_−p = α_0,−p, is represented up to o(n^−1/2) almost surely, by a sum of mean-zero independent random variables, which we denote by ${\eta }_i\in {ℝ}^{p-1},i\in \left\{1,\dots ,n\right\}$, i ∈ {1, …, n} where $n={\sum }_{t=1}^K{n}_t$. Let us denote the estimated score function by $\widehat{\mathrm{\Psi }}\left({\alpha }_{-p}\right)=\frac{\partial }{\partial {\alpha }_{-p}^{\top }}Q\left({\alpha }_{-p}\right)$, where ${\mathit{\alpha }}_{-p}\in {ℝ}^{p-1}$. We will show

$$\underset{1\le j\le p-1}{\sup }\left|{\widehat{\mathrm{\Psi }}}_j\left({\mathit{\alpha }}_{0,-p}\right)-\frac{1}{n}\sum _{i=1}^n{\eta }_{i,j}\right|=o\left(n^{-1/2}\right),$$ (B.6)

almost surely, where ${\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{-p}\right)\in ℝ$ is the jth component of the score function $\widehat{\mathrm{\Psi }}\left({\alpha }_{-p}\right)$ and ${\eta }_{i,j}\in ℝ$ is the jth component of the random variable η_i. In order to employ the result (B.4), we first consider the score function defined on the set Θ_c, i.e., the score function ${\widehat{\mathrm{\Psi }}}_j(\alpha )$, instead of the “pth component removed” score function defined on ${ℝ}^{p-1}$, i.e., ${\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{-p}\right)$. We will show that, for some mean-zero independent random variables, which we denote by ${\xi }_{\alpha ,i,j}^{*},i\in \left\{1,\dots ,n\right\}$, i ∈ {1, …, n}, j ∈ {1, …, p},

$$\underset{\alpha \in {\Theta }_{c}1\le j\le p}{\sup }\left|\frac{\partial }{\partial {\alpha }_j}\{Q(\alpha )-R(\alpha )\}-\frac{1}{n}\sum _{i=1}^n{\xi }_{\alpha ,i,j}^{*}\right|=o\left(n^{-1/2}\right)$$ (B.7)

is satisfied almost surely. Let us set the desired mean-zero independent random variable ${\xi }_{\alpha ,i,j}^{*}$ to be ${\xi }_{\alpha ,i,j}^{*}={\sum }_{t=1}^K{\xi }_{\alpha ,i,j,t}^{*}$, where

$${\xi }_{\alpha ,i,j,t}^{*}=\left[2\left\{g_t\left({\alpha }^{\top }{X}_i\right)-Y_i\right\}\frac{\partial }{\partial {\alpha }_j}{g}_t\left({\alpha }^{\top }{X}_i\right)-\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )\right]I\left(T_i=t\right),$$

which must satisfy the following:

$$\underset{\alpha \in {\Theta }_{c}1\le j\le p}{\sup }\left|\sum _{t=1}^K{\pi }_t\left[\frac{\partial }{\partial {\alpha }_j}{Q}_t(\alpha )-\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )\right]-\frac{1}{n}\sum _{i=1}^n\sum _{t=1}^K{\xi }_{\alpha ,i,j,t}^{*}\right|=o\left(n^{-1/2}\right).$$ (B.8)

We can write

$$\begin{gathered} \left|\sum _{t=1}^K{\pi }_t\left[\frac{\partial }{\partial {\alpha }_j}{Q}_t(\alpha )-\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )\right]-\frac{1}{n}\sum _{t=1}^K\sum _{i=1}^n{\xi }_{\alpha ,i,j,t}^{*}\right| \\ =\left|\sum _{t=1}^K{\pi }_t\left[\frac{\partial }{\partial {\alpha }_j}{Q}_t(\alpha )-\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )-\frac{1}{{\pi }_t}\frac{n_t}{n}\frac{1}{n_t}\sum _{i=1}^{n_t}{\xi }_{\alpha ,i,j,t}\right]\right|, \end{gathered}$$

where ξ_α,i,j,t is defined in (B.4). Therefore, applying the continuous mapping theorem and Slutsky’s theorem to (B.4) leads to the desired result (B.8).

Next, we will show (B.6), the result corresponding to the “pth component removed” estimated score function, $\widehat{\mathrm{\Psi }}\left({\alpha }_{-p}\right)$ on ${ℝ}^{p-1}$. Considering the linear operator $\frac{\partial }{\partial {\alpha }_j}-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}$, we note that by the chain rule,

$$\left(\frac{\partial }{\partial {\alpha }_j}-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}\right)\{Q(\alpha )-Q(\alpha )\}={\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{-p}\right)-{\mathrm{\Psi }}_j\left({\alpha }_{-p}\right),$$

for j ∈ {1, …, p−1}, where Ψ_j(α_−p) denotes the jth component of the gradient of R(α_−p). If we set the approximation variable η_i,j of (B.6) to be

$$\begin{gathered} {\eta }_{i,j}={\xi }_{\alpha ,i,j}^{*}-\frac{{\alpha }_j}{{\alpha }_p}{\xi }_{\alpha ,i,p}^{*} \\ =\sum _{t=1}^K[2\left\{g_t\left({\alpha }^{\top }{X}_i\right)-Y_i\right\}\left\{\frac{\partial }{\partial {\alpha }_j}{g}_t\left({\alpha }^{\top }{X}_i\right)-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{g}_t\left({\alpha }^{\top }{X}_i\right)\right\} \\ +\frac{\partial }{\partial {\alpha }_j}{R}_t(\alpha )-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}{R}_t(\alpha )]I\left(T_i=t\right), \end{gathered}$$ (B.9)

then we can show

$$\begin{gathered} \underset{\alpha \in {\Theta }_c}{\sup }\underset{1\le j\le p-1}{\sup }\left|\left(\frac{\partial }{\partial {\alpha }_j}-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}\right)\{Q(\alpha )-R(\alpha )\}-\frac{1}{n}\sum _{i=1}^n{\eta }_{i,j}\right| \\ \le \underset{\alpha \in {\Theta }_c}{\sup }\underset{1\le j\le p-1}{\sup }\left|\frac{\partial }{\partial {\alpha }_j}(Q(\alpha )-R(\alpha ))-\frac{1}{n}\sum _{i=1}^n{\xi }_{\alpha ,i,j}^{*}\right| \\ +\underset{\alpha \in {\Theta }_c}{\sup }\frac{{\alpha }_j}{{\alpha }_p}\left|\frac{\partial }{\partial {\alpha }_p}(Q(\alpha )-R(\alpha ))-\frac{1}{n}\sum _{i=1}^n{\xi }_{\alpha ,i,p}^{*}\right|=o\left(n^{-1/2}\right), \end{gathered}$$ (B.10)

by the triangle inequality and the result of (B.7). Since Ψ_j(α_−p) is evaluated at the minimum α_0,−p, we have

$${\mathrm{\Psi }}_j\left({\alpha }_{0,-p}\right)=\left(\frac{\partial }{\partial {\alpha }_j}-\frac{{\alpha }_j}{{\alpha }_p}\frac{\partial }{\partial {\alpha }_p}\right)\left\{Q(\alpha )\right\}{|}_{\alpha ={\alpha }_0}=0,$$ (B.11)

by the local convexity under Assumption 1. Then we obtain the desired result of (B.6), by (B.10) and (B.11).

The uniform consistency of the observed Hessian, $\widehat{\mathit{H}}(\alpha )=\frac{{\partial }^2}{\partial {\alpha }_{-p}\partial {\alpha }_{-n}^{\top }}Q\left({\alpha }_{-p}\right)$, to the population Hessian H(α_−p) of (A.1) follows directly from the results of (B.5) under Assumptions 2–5, with applications of the continuous mapping theorem.

Finally, we prove the main result. Consider the random variable ${\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{0,-p}\right)$ introduced in (B.6), and the following parametrization: for each component j ∈ {1, …, p – 1}

$$f_j(s)={\widehat{\mathrm{\Psi }}}_j\left(s{\widehat{\mathit{\alpha }}}_{-p}+(1-s){\mathit{\alpha }}_{0,-p}\right),s\in [0,1].$$

Taking the derivative with respect to t, we have by the chain rule

$$\frac{d}{dt}{f}_j(s)=\sum _{m=1}^{p-1}\frac{\partial }{\partial {\alpha }_m}{\widehat{\mathrm{\Psi }}}_j\left(s{\widehat{\mathit{\alpha }}}_{-p}+(1-s){\mathit{\alpha }}_{0,-p}\right)\left({\widehat{\alpha }}_m-{\alpha }_{0,m}\right).$$

Since ${\widehat{\mathrm{\Psi }}}_j\left({\widehat{\alpha }}_{-p}\right)=0$ by the definition of ${\widehat{\alpha }}_{-p}$, it follows that $f_j(1)-f_j(0)={\widehat{\mathrm{\Psi }}}_j\left({\widehat{\alpha }}_{-p}\right)-{\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{0,-p}\right)=-{\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{0,-p}\right)$. Therefore, for any particular j = 1, …, p−1, there exists $s_j^{*}\in [0,1]$ by the mean value theorem, such that

$$\begin{gathered} -{\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{0,-p}\right)=[\frac{\partial }{\partial {\alpha }_1}{\widehat{\mathrm{\Psi }}}_j\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right), \\ \dots ,\frac{\partial }{\partial {\alpha }_{p-1}}{\widehat{\mathrm{\Psi }}}_j\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right)]\left[{\widehat{\alpha }}_{-p}-{\alpha }_{0,-p}\right], \end{gathered}$$

which is just

$$\begin{gathered} [\frac{{\partial }^2}{\partial {\alpha }_1\partial {\alpha }_j}\widehat{Q}\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right), \\ \dots ,\frac{{\partial }^2}{\partial {\alpha }_{p-1}\partial {\alpha }_j}\widehat{Q}\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right)]\left[{\widehat{\alpha }}_{-p}-{\alpha }_{0,-p}\right], \end{gathered}$$ (B.12)

where $\left[{\widehat{\alpha }}_{-p}-{\alpha }_{0,-p}\right]$ is a p − 1 dimensional random vector. Writing (B.12) in matrix notation, we have

$$-\widehat{\mathrm{\Psi }}\left({\alpha }_{0,-p}\right)={\left[\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_j}\widehat{Q}\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right)\right]}_{j,q=1}^{p-1}\left[{\widehat{\alpha }}_{-p}-{\alpha }_{0,-p}\right].$$ (B.13)

Then, by (B.13) one can write

$$\sqrt{n}\left({\widehat{\alpha }}_{-p}-{\alpha }_{0,-p}\right)=-{\left\{{\left[\frac{{\partial }^2}{\partial {\alpha }_q\partial {\alpha }_j}\widehat{Q}\left(s_j^{*}{\widehat{\alpha }}_{-p}+\left(1-s_j^{*}\right){\alpha }_{0,-p}\right)\right]}_{j,q=1}^{p-1}\right\}}^{-1}\sqrt{n}\widehat{\mathrm{\Psi }}\left({\alpha }_{0,-p}\right).$$ (B.14)

Meanwhile, by (B.6), for each component j ∈ {1, …, p−1} of $\widehat{\mathrm{\Psi }}\left({\alpha }_{0,-p}\right)$, we can write

$${\widehat{\mathrm{\Psi }}}_j\left({\alpha }_{0,-p}\right)=\frac{1}{n}\sum _{i=1}^n{\eta }_{i,j}+o\left(n^{-1/2}\right),$$ (B.15)

almost surely with $\mathbb{E}\left({\eta }_{i,j}\right)=0$. The variance-covariance matrix of the random vector ${\eta }_i={\left[{\eta }_{i,1},\dots ,{\eta }_{i,p-1}\right]}^{\top }\in {ℝ}^{p-1}$ evaluated at α_−p = α_0,−p, where η_i,j are specified in (B.9), is given in (A.2), where it is denoted by W_α0,−p. From (B.15), the central limit theorem ensures that $\sqrt{n}\widehat{\mathrm{\Psi }}\left({\alpha }_{0,-p}\right)\to \mathcal{N}\left(0,W_{{\alpha }_{0,-p}}\right)$ in distribution. Now, by the representation of (B.14) together with an application of Slutsky’s theorem on the observed Hessian, we obtain $\sqrt{n}\left({\widehat{\alpha }}_{0,-p}-{\alpha }_{0,-p}\right)\to \mathcal{N}\left(0,{\Sigma }_{{\alpha }_{0,-p}}\right)$ in distribution, where ${\Sigma }_{{\alpha }_{0,-p}}=H_{{\alpha }_{0,-p}}^{-1}{W}_{{\alpha }_{0,-p}}{H}_{{\alpha }_{0,-p}}^{-1}$, which is the desired result of Theorem 2. □

Appendix C. Table for Section 5.2 Coverage probability of asymptotic 95% confidence intervals

Table C.2:

The proportion of time (“Coverage”) that the asymptotic 95% confidence interval contains the true value of α_j, j ∈ {1, …, 5}, for varying ω ∈ {0, 0.5, 1}, corresponding to linear, moderately nonlinear, and highly nonlinear contrasts, respectively, with varying n(= n₁ + n₂, where n₁ = n₂).

ω = 0 (linear)						ω = 0.5 (moderate nonlinear)					ω =1 (highly nonlinear)
n	α1	α2	α3	α4	α5	α1	α2	α3	α4	α5	α1	α2	α3	α4	α5
50	0.36	0.45	0.43	0.44	0.42	0.49	0.46	0.45	0.46	0.40	0.59	0.58	0.57	0.55	0.52
100	0.64	0.67	0.72	0.68	0.64	0.76	0.75	0.80	0.72	0.76	0.89	0.82	0.84	0.75	0.73
200	0.77	0.77	0.79	0.78	0.73	0.88	0.83	0.82	0.85	0.79	0.92	0.88	0.84	0.78	0.81
400	0.85	0.90	0.87	0.87	0.85	0.88	0.88	0.88	0.82	0.85	0.95	0.88	0.84	0.79	0.78
800	0.95	0.92	0.91	0.89	0.88	0.92	0.89	0.92	0.89	0.87	0.92	0.91	0.83	0.78	0.81
1600	0.93	0.93	0.92	0.93	0.92	0.94	0.94	0.91	0.93	0.91	0.93	0.90	0.87	0.84	0.81
3200	0.94	0.95	0.94	0.94	0.94	0.96	0.94	0.90	0.92	0.90	0.93	0.92	0.87	0.90	0.85