Abstract
The conventional method for developing health care plan payment systems uses observed data to study alternative algorithms and set incentives for the health care system. In this paper, we take a different approach and transform the input data rather than the algorithm, so that the data used reflect the desired spending levels rather than the observed spending levels. We present a general economic model that incorporates the previously overlooked two-way relationship between health plan payment and insurer actions. We then demonstrate our systematic approach for data transformations in two Medicare applications: underprovision of care for individuals with chronic illnesses and health care disparities by geographic income levels. Empirically comparing our method to two other common approaches shows that the “side effects” of these approaches vary by context, and that data transformation is an effective tool for addressing misallocations in individual health insurance markets.
Keywords: Health insurance, Managed competition, Risk adjustment
1. Introduction
Public and private regulators set prices in health care – to physicians, hospitals, health plans and other providers – with the purpose of improving economic efficiency of health care delivery. To implement a payment system, the regulator selects a methodology to establish prices for each of the thousands of procedures physicians perform, the hundreds of disease groups treated by hospitals, or per capita prices paid to plans for the nearly innumerable combinations of enrollees’ health conditions. In many health care settings, prices are set according to observed costs in the market. In the U.S. Medicare program, a hospital’s payment for a given inpatient admission is tied to the national average cost of admissions belonging to the same diagnosis-related group (DRG). In the Medicare Advantage program, the Affordable Care Act Marketplaces, most state Medicaid programs, and in Germany, the Netherlands, Switzerland, and other countries, a health plan’s payment for enrolling a given individual is tied to the average cost of individuals with similar demographics and histories of chronic conditions. This method for setting prices weakens incentives for inefficient “cream-skimming” behaviors by insurers (Geruso et al., 2016; Newhouse et al., 2015).
While acknowledging the benefits of setting prices in this way, this paper explores a previously unresolved deficiency: when the existing health care system is inefficient or unfair, setting payments based on observed costs may sustain those inefficiencies or inequities, which may be precisely the issues the payment system is meant to correct. Consider the following extreme example: suppose under the current health plan payment system individuals with cancer are highly unprofitable due to low revenues relative to costs, and insurers rationally respond by limiting access to care for individuals with cancer to deter those individuals from enrolling in their plans. Further, assume insurers are so effective at rationing access that individuals with cancer obtain only very low levels of spending, for example, $1000. Now suppose a regulator seeks to address the problem of insurers inefficiently limiting access to care for individuals with cancer by “risk adjusting” payments to health plans, and they use a standard risk adjustment system where plan payments are adjusted according to the observed $1000 of spending for individuals with cancer. Such a payment system will not solve the problem the regulator sought to fix, because individuals with cancer will appear relatively inexpensive due to the insurers’ actions limiting their access to care. Thus, this conventional approach to payment will sustain rather than correct the insurers’ incentive to inefficiently limit access to care for this group. While this example is extreme, a weaker version of this feedback loop between inefficiencies embedded in the health care system and the incentives embedded in the payments is likely to play out in many more realistic settings.1 The general point is that if regulated prices are intended to move the health care system to be more efficient and fair, using observed (inefficient/unfair) patterns of care for payment calibration will not fix the existing flaws.
The problem of basing risk adjusted payments on observed costs has been previously acknowledged (van de Ven and Ellis, 2000; Zweiful et al., 2009), but using data other than observed costs has been dismissed as being difficult to put into practice, and instead observed costs are often assumed to represent “acceptable” cost levels. Both Schokkaert and van de Voorde (2004) and Stam et al. (2010) propose methods for risk adjustment improvement that incorporate information on normative costs by leveraging risk factors that are desirable to subsidize and those that are not (e.g., inefficient practice styles or higher rates of smoking in some subpopulations). However, these approaches maintain the basic practice of correcting inefficient risk adjustment payments by modifying the risk factors included in the algorithm, rather than through transformations to the underlying data used to estimate the payments tied to those risk factors.
In this paper, we show that data modified to reflect the researcher’s or policymaker’s beliefs about efficient and fair levels of spending versus the observed spending levels can be used for calibrating health plan payments. We propose a systematic approach for transforming data in a pre-estimation step to break the feedback loop between plan payments and insurer actions. The intuition behind our proposed method follows from conditions of market equilibrium: set prices to buy the equilibrium you want, not the equilibrium you currently have. After introducing background material in Section 2, we lay out the theoretical basis of our approach in Section 3. The model in Section 3 characterizes the optimal input data (which leads to the desired health care system outcomes) at an abstract level, and then translates the ideas for our empirical applications of health plan payment in Medicare. In Section 4, we describe two data transformation examples. The first focuses on underpayment for individuals with chronic illnesses, and the second addresses disparities in health care spending by zip code-level income. We empirically compare our method to approaches based on modifying payment algorithms using existing data. This includes exploring the conventional approach of adding or removing risk adjustor variables from the pricing algorithm. In the chronic diseases example, we include additional risk adjustors for chronic illness groups, and in the disparities example we include a low-income neighborhood indicator. We also leave the set of risk adjustors in place but introduce constraints on the OLS regression that target spending for groups of interest (van Kleef et al., 2017).2
Both applications demonstrate that data transformation is a powerful approach for moving plan payments closer to the desired levels. In the chronic diseases application, data transformation is the most effective method for improving fit across all groups. Introducing constraints on the risk adjustment formula also performs well at the group level, while adding risk adjustors to the OLS regression is the least effective approach. The substantial improvements in group-level fit for both our method and constrained regression come at only a trivial decrease in statistical fit at the individual level (i.e., R2) compared to an unconstrained OLS regression. In the disparities application, adding a risk adjustor for neighborhood income is highly ineffective if the objective is to address health care spending disparities for that group. Such an action aggravates the disparity by income group. Data transformation improves incentives to serve a group, but combining data transformation with adding a risk adjustor is even more effective at altering incentives because it combines the strengths of both approaches.
2. Background
2.1. Medicare health plan payment and risk adjustment
Medicare adjusts per person payments to health plans according to age, sex, Medicaid status, reason for Medicare eligibility, and diagnostic information. The Medicare risk adjustment formula is calibrated on data from traditional fee-for-service Medicare but used to pay private Medicare Advantage plans (whose data are not used for calibration purposes). Most efforts to improve risk adjustment have centered on adding and refining the risk adjustor variables that indicate the presence of a diagnosis for a particular chronic disease (currently the Hierarchical Condition Categories, abbreviated HCCs), or on segmenting the population and estimating mutually exclusive subgroup formulas (e.g., separating community-dwelling and institutionalized beneficiaries). Medicare tracks regression fit at the individual level, updating the risk adjustment coefficients every few years by refitting the regression on more recent fee-for-service data. The most recently publicly evaluated Medicare risk adjustment formula is CMS HCC Version 21; the subgroup formula for the largest group, community-dwelling beneficiaries, has an R2 of 12.46%.3
Despite a risk adjustment scheme refined over many years, some groups remain vulnerable to selection-related incentives.4 For example, plans are underpaid for individuals with certain chronic conditions in that the revenue a plan receives for members of this group falls short of the expected costs. Research on Medicare Advantage plans shows plans react to such “underpayments” by cutting back on services to unprofitable illness groups (Han and Lavetti, 2017).
2.2. Related policy interventions
The most significant example in the U.S. of using normative inputs for setting provider payment is the Resource-Based Relative Value Scale (RBRVS) used by Medicare since the early 1990s to set physician procedure prices. Prior to the RBRVS reform, a policy consensus held that the prices set for “Evaluation and Management” (E&M) procedures (i.e., routine office visits) were too low and prices for some interventions (i.e., many surgical procedures) were too high. These payment levels resulted in too little physician time spent with patients and too high a volume of some procedures – patterns in the existing data policymakers wanted to change (Newhouse, 2002). Rather than accepting these patterns, Medicare incorporated information about normative time and effort – what doctors should be doing – and raised the prices of E&M procedures relative to surgery. In short, the RBRVS fee schedule was designed not to simply reflect the time spent by physicians for various procedures, it was meant to affect the time spent.5 While the RBRVS is similar in spirit to our approach, it differs substantially in terms of implementation and focus: the RBRVS sets physician fees, whereas our method transforms the input data for health plan risk adjustment, which is then estimated via an OLS regression that preserves individual and group-fit properties.
We also see limited forms of using modified data in regulated health insurance markets in the Netherlands and the ACA Marketplaces. The Dutch risk adjustment algorithm is estimated on data modified to incorporate benefit package changes over time (Layton et al., 2016). In the ACA Marketplaces, the risk adjustment algorithm is estimated on a pooled sample of data not subject to the selection incentives in the Marketplaces, and modified by an anticipated annual growth rate. The 2017 update of the formula additionally features separate specialty drug, traditional drug, and medical expenditure trends based on external actuary and industry reports. Similar to the Dutch approach, the goal of applying a trend modification to the data is to incorporate expected patterns of spending, not to alter those expected patterns (Centers for Medicare and Medicaid Services, 2016). The key difference between the actuarial approach to risk adjustment (which motivates these real-world examples of data modification) and the economic approach to risk adjustment is that actuaries typically set payments to cover predicted costs, while economists typically consider costs as endogenous to payments and set payments to produce optimal insurance contracts. Applying the economic lens to the question of data transformation thus motivates our key contribution, which is the application of data interventions to alter the allocation of services and patterns of care rather than just to account for changes in insurer costs due to exogenous forces.
3. Conceptual framework
Here, we develop a general model of plan actions in response to plan payment coupled with recognition that plan payments are endogenous to plan actions and vice versa. After formalizing our idea of data transformation, we describe how it can be used as a systematic approach to address spending allocation problems.
3.1. A data transformation model
Define the matrix X = {xis} , where i indexes individuals in the health insurance market and s indexes the services provided by health plans (Layton et al., 2016). A service could be a particular type of care for a particular condition or conditions, e.g., office-based care for depression. An element of X is xis, spending in dollars on service s for individual i. Also define R = {ri}, a vector of payments a health plan receives for enrolling each individual i. In essence, X is what consumers and the health care system do in response to the insurance contract offered by insurers, and R is how the regulator pays plans.
X and R are related in two ways. The vector of payments affects the contract offered by the insurer which, in turn, affects both the care produced by health care providers and the level of health care consumption chosen by consumers. And data from the health care system are inputs into the algorithm that generates the payment vector. For example, if insurers are paid high rates for individuals with mental illness (ri), insurers will design contracts offering generous coverage for behavioral health services and set high rates to providers to ensure sufficient supply of those services. These consumer and provider responses to the contract combine to generate realized spending xis. Realized spending, xis, is then used to determine payments to insurers, ri. We represent these two relations as:
| (1) |
| (2) |
The function f(·) represents the working of the health care system in response to payment incentives. Dependent on the payments set for each enrollee, plans set contracts with providers and engage in other actions, including selection, that lead to an allocation of spending on various services to each individual. The function g(·) is the algorithm specified by the regulator that takes as input the patterns of health care spending and determines a payment for each person. The empirical methodology used by Medicare to assign risk scores to individuals based on age, sex, and indicators of medical morbidity is an example of a g(·) function.6
In the conventional approach to economic analysis of health plan payment, the payment vector R is treated as an exogenous policy choice, and the health care system is characterized by f(·) only (Glazer and McGuire, 2002). This may not, however, constitute a full equilibrium. In general, the health care allocations that result from a given payment vector will not, given the payment algorithm g(·), generate the original payment vector. We broaden the concept of equilibrium by recognizing the second relationship between the health care system and payments, represented in g(·). We say that with a fixed algorithm g(·), relating data from the health care system to payment, the system is in full equilibrium when both conditions are satisfied. We thus define a full equilibrium in the health care system (Xe, Re) as:7
| (3) |
| (4) |
To motivate transforming the data, we assume another allocation, X*, is preferred to Xe. We refer to X* as the “desired” allocation; X* might be preferred to Xe for reasons of efficiency or fairness.
Conventional health policy analysis modifies the g(·) function (for example, by adding variables to the risk adjustment regression). With knowledge of the operation of the health care system (i.e., the g(·) function), one could solve for the vector of per person payments that would lead to the desired allocation.8 Call this desired vector of payments R*:
| (5) |
Eq. (5) represents the strand of the health plan payment literature referred to as “optimal risk adjustment,” with f−1 as the optimal risk adjustment formula.9 Note that (5) is consistent with a full equilibrium, in the sense that the optimal risk adjustment formula, f−1, when applied to the optimal health care system, X*, yields the optimal vector of per person payments R*.
In this work, we take a different approach and ask, what X matrix, used in Eq. (2) with a fixed algorithm g(·), would lead to the optimal set of per person payments, and thus to the efficient health care system. Define to be this optimal data input matrix:
| (6) |
Eq. (6) presents our main idea in abstract form. By disconnecting the data used as input to the plan payment algorithm from the spending in the current system, i.e., by transforming the data, we can induce an efficient health care system. We recognize the h(·) function is complex and we have little policy experience with its properties. Nonetheless, we believe (6) represents a novel and useful observation. Data used as input into payment system calibration, in (6), can be chosen by policy. And although the form of (6) is unknown, simple and intuitive transformations of the input data have foreseeable effects on incentives. A well-chosen intervention on the data that improves incentives should move the health care system in the right direction.10
3.2. A Medicare application
To address allocation problems in Medicare we operationalize (6) and illustrate the data transformation process. We specify the variables and some properties of how the health care system responds to price incentives (f(·)), and how the data from the health care system is used to construct payments to health plans (g(·)). In this section, we use the chronic diseases application to translate our model into practice. A parallel method is used in our disparities application; these examples are selected to illustrate our new method and are simplified versions of a systematic approach to improving the health plan payment system.11
3.2.1. The inefficiency
As with other systematic risk adjustment improvement approaches, such as constrained regression, our data transformation method requires an initial assessment of baseline risk adjustment performance to identify groups underserved in the current system. To demonstrate performing a data intervention for an inefficiency problem, we select our groups of interest and the target of our intervention based on prior research and a baseline assessment of the Medicare risk adjustment system: as shown by McGuire et al. (2014) in another context and as our data analysis confirms for Medicare, among four major chronic illnesses – cancer, diabetes, heart disease, and mental illness – the incentives are strongest to underspend on mental health care. We therefore intervene to address the incentives to underspend on persons with mental illness and track the incentives for groups defined by the other chronic illnesses.
3.2.2. The plan payment algorithm: R = g(X)
The function g(·) is the algorithm that determines the per person payments paid to health plans for enrollment of beneficiaries with various indicators for health status (which come from the data). We implement a slightly modified version of Medicare’s current algorithm, described in detail in Section 4 and the Appendix.
3.2.3. The health care system: X = f(R)
The f(R) function relates per person payments to the functioning of the health care system. This function encompasses not only plan spending and beneficiary enrollment, but also involves the relationships between providers, hospitals, insurers, and individual consumers. Rather than making strong assumptions about the form of f(·), we make a weaker assumption about its local properties, the signs of the derivatives of f(·). This assumption is sufficient to determine the sign of the local effect of a data intervention. Specifically, we assume plans respond positively to incentives in the sense that if the payment for an individual is increased (decreased), the plan spends more (less) on that person.12 The assumption implies that in response to an increase in the level of plan payment for a group of beneficiaries, plans will spend more on the services used by those beneficiaries in order to encourage more of that group to enroll.
4. Data and methods
We study methods for reducing underpayment (which we assume induces underservice) for the targeted group in the chronic diseases application, and methods to reduce underservice for the targeted group in the disparities application. In both the chronic diseases and disparities applications, we identify the target group using a classification system that is distinct from the CMS HCC risk adjustment system. We track the impact of alternative methods on regression fit at the group and individual levels. As a summary measure, we calculate Group Payment System Fit (GPSF), which captures how well a given risk adjustment formula matches payments and costs at the group, rather than the individual, level (Layton et al., 2018). Similar to other group-fit measures, such as Grouped R2, GPSF depends on partitioning the sample into mutually exclusive groups.
4.1. Data and baseline risk adjustment formula
In practice and in this paper, data from fee-for-service Medicare are used to estimate payment coefficients on the risk adjustment variables for setting capitation payments to Medicare Advantage plans. We follow CMS and include only individuals with 12 months of continuous Parts A and B coverage in the base year (2010) and those with at least one month of coverage in the prediction year (2011). We exclude beneficiaries with end-stage renal disease and those residing in an institution. After applying these exclusion criteria, we draw a random sample of 1.5 million individuals in order to approximate CMS’s practice of using a random 5% sample of Medicare beneficiaries for risk adjustment estimation. Our sample is predominately white (85%) and urban-dwelling (75%) (Table 1). Approximately two-thirds of our sample has at least one of four major chronic conditions: cancer, diabetes, heart disease, or mental illness. For our random sample we combine the Medicare Beneficiary Summary File on enrollment with Part A, Part B, home health, and durable medical equipment claims files for 2010 and 2011. We map ICD-9 diagnoses to 87 HCCs, combine age and sex into 24 age-sex cells, and create indicators for disabled enrollees and individuals enrolled in Medicaid. Our outcome measure, health care spending in 2011, is total Medicare spending on inpatient, outpatient, durable medical equipment, and home health, weighted to reflect each individual’s eligible fraction of the prediction year. To predict spending we use a similar specification as the Version 21 CMS HCC risk adjustment formula for the community-dwelling subgroup:
| (7) |
Table 1.
Sample Characteristics in 2010 (N = 1.5 million).
| Variable | Mean (%) |
|---|---|
| Sex | |
| Female | 55 |
| Age | |
| <65 | 17 |
| 65–69 | 21 |
| 70–74 | 17 |
| 75–79 | 16 |
| 80+ | 25 |
| Race/Ethnicity | |
| White | 85 |
| Black | 9 |
| Hispanic | 6 |
| Urban/Rural | |
| Rural | 25 |
| Region | |
| Northeast | 18 |
| Midwest | 24 |
| South | 40 |
| West | 17 |
| Chronic Conditions | |
| Mental illness | 22 |
| Cancer | 23 |
| Heart disease | 41 |
| Diabetes | 27 |
| At least one chronic condition | 68 |
| Insurance | |
| Medicaid | 18 |
Notes: Race/Ethnicity groups are mutually exclusive. Chronic conditions groups are defined using CCS categories. “At least one chronic condition” refers to having at least one of four listed major chronic conditions (cancer, diabetes, heart disease, or mental illness).
where Yi is observed spending for individual i, HCCik is the value of HCC indicator k for individual i (k = 1, …, 87), βk is the coefficient for HCC indicator k, age − sexil is the value of the age-sex cell indicator l for individual i (l = 88, …, 112), βl is the coefficient for age-sex cell l, Disabled − HCC6i indicates the combination of disability and an opportunistic infection for individual i, Disabled − HCC34i indicates disability and chronic pancreatitis for individual i, Disabled − HCC46i indicates disability and severe hematological disorders for individual i, Disabled − HCC54i indicates disability and drug/alcohol psychosis for individual i, Disabled − HCC55i indicates disability and drug/alcohol dependence for individual i, Disabled − HCC110i indicates disability and cystic fibrosis for individual i, Disabled − HCC176i indicates disability and complications of an implanted device or graft for individual i, and the remaining terms are indicators capturing interactions between Medicaid status, disability, original reason for Medicare enrollment, and sex.13 The principal differences between the formula in Eq. (7) and the Version 21 CMS HCC formula are that we omit interaction terms between diseases, which are sparsely populated, and we also do not modify coefficients post-estimation as CMS does (Pope et al., 2011). The goal of estimating Eq. (7), rather than using the CMS risk adjustor weights to calculate individual payments, is to fit the means of our particular data sample and illustrate the potential of the data transformation method.
We map ICD-9 diagnoses to Clinical Classification Software (CCS) groups and to Prescription Drug Hierarchical Condition Categories (RxHCCs) (AHRQ, 2016; DHHS, 2017). CCS groups are used to identify beneficiaries with a chronic condition because, unlike the HCCs included in the risk adjustment formula, all ICD-9 codes map to a condition group.14 RxHCCs are the categories used by the Medicare Part D risk adjustment formula and capture a greater number of mental illness diagnoses than HCCs (Montz et al., 2016). We use the RxHCCs to demonstrate the effect of including additional risk adjustor variables.15
4.2. Defining and measuring underpayment for a group with a chronic illness
In our first application we target the systematic underpayment of persons with a chronic illness. We divide our sample into seven mutually exclusive groups based on clinical diagnoses in 62 CCS categories: 1) mental illness only, 2) mental illness and at least one other major chronic condition (cancer, diabetes, or heart disease), 3) diabetes only, 4) heart disease only, 5) cancer only, 6) multiple chronic conditions, not including mental illness, and 7) no chronic conditions.
We define net compensation as the difference between average payments and average costs for a group.16 We assume an individual’s total Medicare spending is the cost the plan bears for that individual, and payments to a plan are the predicted values from estimating the risk adjustment regression; for example, net compensation at baseline is based on estimating the formula in Eq. (7). In general, individual payments are calculated from risk adjustment regression estimation: , where ri is the payment for individual i, is the estimated coefficient for risk adjuster j, and zij is the value of the risk adjuster j for individual i. We then calculate group-level net compensation for the average plan based on the predicted values:
| (8) |
Where , , ng is the number of individuals in the group of interest g, and Yi is the observed spending for individual i. Negative values of net compensation indicate under-payment, where the group-level revenues (predicted spending) are systematically less than group-level costs (observed spending). Positive values indicate overpayment, where group-level revenues exceed group-level costs.17
4.3. Defining and measuring a health care disparity
Our second application addresses a disparity between groups defined by a sociodemographic variable. We divide our sample into individuals residing in low-income zip codes (those with a zip code-level median income in the lower 60% of individuals in our sample) and high-income zip codes (upper 40%).18 We measure the disparity in health care between these two groups. Measuring and addressing disparities between groups does not require knowledge about the source(s) of the disparity – many factors contribute to disparities in care across neighborhood of residence. Rather than seeking to directly address these underlying causes, we rely on the responsiveness of the health care system to financial incentives to reduce disparities between low- and high-income neighborhoods: if health plans are paid more to enroll individuals in low-income neighborhoods, then the plans will act to attract these individuals by providing them with more care.
Disparity for a group is defined, following the Institute of Medicines (2002) Unequal Treatment report, as differences in health care not due to health status or preferences. Because of the difficulties in measuring preferences, the literature on disparities compares care for groups after adjusting for health status only,19 and we do the same. Specifically, we estimate a disparity in total health care spending between the group of interest and the reference group as the difference in estimated and observed price-adjusted spending, conditional on health status. We define disparity as:
| (9) |
where g is the group of interest, ref is the reference group, Yi,g is the observed spending for an individual in the group of interest, Yi,ref is the observed spending for an individual in the reference group, is predicted spending conditional on health status (as measured by CCS categories, age, and sex) for an individual in group g, and is predicted spending conditional on health status for an individual in the reference group. We follow common practice in the disparities literature and also adjust for age and sex, because differences related to these demographic factors could stem from differences in prevalence of illness correlated with age and sex, and thus would not constitute a disparity. The first term in Eq. (9), for group g (low-income), is expected to be negative, with actual services received less than predicted based on health status. The second term is expected to be positive, measuring the excess of services received by the reference group in relation to their health status. When the difference between these two terms, the disparity, is negative, it measures the underservice of group g, conditional on health status, in relation to the reference group.
The estimation of Dg,ref in Eq. (9) depends on accurate predicted values , where “accuracy” can be defined with respect to an underlying squared error loss function.20 Therefore, we employ ensemble statistical machine learning methods to obtain optimal predicted values in the calculation of the disparity. The Appendix contains additional details on implementation.
4.4. Data transformations
4.4.1. Targeting underpayment for a group with a chronic illness
In our demonstration applying the data transformation method to an inefficiency problem, we start by estimating the basic OLS specification in Eq. (7) to assess the status quo performance of the risk adjustment regression across patient groups. We then intervene on the group that is the most undercompensated on average under the basic OLS risk adjustment regression: in this example, that is the mental illness group. Specifically, the intervention consists of increasing the Y vector by 10% for each individual in the targeted group. The choice of 10% is arbitrary. Notably, we only need to transform the data once in order to project the effect of transforming the data by any amount because of the linear form of least-squares estimators.21 This linearity property does not, however, hold for the impact of data changes on a quadratic measure of fit.
After intervening to transform the Y vector, we estimate the risk adjustment regression, ensuring total payments remain constant by imposing a constraint on the coefficients:
| (10) |
where is the sample average of observed total Medicare spending and are the sample means for the j risk adjustor indicator variables. By constraining the coefficients to produce the observed sample mean spending, we guarantee that the total payments after the data intervention sum to total costs. Put differently, we implement the constraint Eq. (10) so that spending for individuals without a mental illness is reduced and counterbalances the increase for individuals with a mental illness.22 From the regression fit on the transformed Y we obtain a set of predicted revenues for each individual in the sample.
Using these predicted spending values, we can then calculate net compensation under the data transformation risk adjustment approach for each disease subgroup in the manner described above. Net compensation reveals how a given group fares under a particular risk adjustment formula, but does not summarize overall group fit across the entire sample. We use Group Payment System Fit (GPSF) (Layton et al., 2018) to summarize the overall impact of each risk adjustment approach on net compensation:
| (11) |
where rg comes from the estimated risk adjustment regression and cg is the observed, unmodified vector of spending; is the mean of the observed, unmodified vector of spending for the entire sample; and sg is the share of the sample in group g, with . GPSF is a measure of regression fit calculated at the group level (where groups are required to be mutually exclusive); we use a linear scale to maintain consistency with our net compensation measure.23 The denominator is the weighted sum of absolute differences between group-level costs and the overall sample average, and the numerator is the group-level sum of absolute residuals under a given payment system. GPSF falls between 0 (the risk adjustment formula is equivalent to paying sample average costs) and 1 (the risk adjustment formula perfectly matches payments and costs at the group level). We expect the denominator to be large relative to the numerator (and GPSF to be high) in cases where group-level costs vary widely from the average cost of the entire sample, and group-level payments are close to group-level costs. In our application, GPSF calculated using the baseline OLS risk adjustment regression is the floor we seek to improve on with alternative risk adjustment approaches, and 1 is the ceiling. Comparing GPSF allows us to rank our risk adjustment approaches based on how well they address discrepancies in net compensation for all of the defined groups, not just the targeted group of interest. Concerns about how other groups might be affected by transforming the data or imposing linear constraints should guide the selection of the mutually exclusive groups for calculating GPSF.
We also present Grouped R2, an earlier measure of group-level fit on the quadratic scale (Ash et al., 2005; Gruenberg et al., 1986):
| (12) |
Although both GPSF and Grouped R2 capture regression fit at the group level, we prefer GPSF because it enables greater differentiation between regression approaches when group-level costs vary widely from the average cost of the entire sample and group-level payments are close to group-level costs, whereas the Grouped R2 will tend to compress these differences in fit.
To compare fit at the individual level of the estimated alternative risk adjustment regression to the baseline OLS version, we calculate an R2 as follows:
| (13) |
where comes from the estimated risk adjustment regression Yi,obs is the observed, unmodified vector of spending; and is the mean of Yi,obs.
We examine the potential for creating unintended incentives to attract or deter certain observable groups by comparing the estimated coefficients of the baseline OLS regression to the alternative risk adjustment methods.
In addition to specifically targeting one chronic illness group, we perform another intervention, where we proportionally increase spending for a beneficiary with at least one of the chronic conditions. Here the goal is to provide an additional example to demonstrate how intervening based on a group categorization can affect subgroups within the broader classification. We estimate the effect of an initial 5% spending increase and show proportional increases in the range of 0–15% of spending.
4.4.2. Targeting a disparity
In the disparities application, we use the plan payment system to reduce incentives for the targeted underservice. Recall that the method is agnostic as to the cause of the disparity in the first place, but makes the simple assumption, discussed above, that increasing the profitability of the group suffering a disparity will encourage plans to provide that group with more services. Because we do not modify costs, tracking changes in group-level payments is sufficient to capture how well transforming the data addresses disparities. We calculate group-level payments, , by estimating the same CMS−HCC risk adjustment formula described above to obtain individual-level payments (ri). Groups that are underserved, like those living in low-income areas, will likely already have payments exceed costs, i.e., be profitable. Despite this, the disparity indicates that the incentives conveyed by the payment system are not strong enough to encourage health plans to compete for these individuals by providing them with more services, and thus reduce disparities.
To transform the data, we increase spending by 10% for all individuals in the low-income zip code group, and again reduce spending for the complementary group by imposing an overall budget constraint. We estimate the risk adjustment regression with the transformed Y vector and calculate group-level payments. It is then possible to characterize the tradeoffs between reducing incentives for disparities and traditional measures of statistical fit for the risk adjustment system, such as R2, described above in Eq. (13). We include an extension of this example in the Appendix: in an even more targeted intervention, we increase spending by 10% for the low-income group, but counterbalance the increase by only reducing spending for the upper half of the high-income group (the fifth quintile)
4.5. Comparison to alternative methods: adding risk adjustor variables and constrained regression
We compare data transformation with two changes to the risk adjustment algorithm used to define payments based on the existing data. First, in the mental illness application, we add RxHCCs from the Medicare Part D risk adjustment formula related to mental illness and not already included in the Medicare Advantage risk adjustment formula.24 In the disparities application, we add a low-income neighborhood indicator to the formula. When low-income neighborhoods are underserved, adding an indicator is a poor choice because it reinforces incentives to underserve; we add a low-income neighborhood indicator to illustrate that adding indicators related to socioeconomic status can often be counterproductive and to allow us to set up a combination approach. A related alternative, which we do not consider empirically, is to impose a positive coefficient on a variable such as low-income neighborhood. OLS fit properties are lost with a post-risk adjustment ad hoc modification.
Second, we impose linear constraints on the estimated coefficients from the risk adjustment regression to ensure that group-level payments for a chronic illness group hit targeted levels. Thus, to completely eliminate underpayment for the targeted chronic illness group we set . To compare constrained regression to data transformation, we also apply a constraint with the same reduction of underpayment as achieved by our data transformation approach. Again, we maintain aggregate spending levels by imposing a second constraint on spending for the entire sample: . We do not implement a constrained regression comparator for the disparities application because it is not possible to directly constrain the target (disparities) without making strong assumptions regarding how the health care system reacts to changes in payments.
5. Results
5.1. Increasing net compensation for beneficiaries with a chronic illness
Prior to transforming the data, we assess net compensation by chronic illness. In aggregate, net compensation for individuals with a mental illness is −$607 per person; separating this group into those with mental illness only and those with mental illness and another chronic condition shows the latter and larger group is subject to the greatest underpayment (Table 2). Individuals in the multiple chronic conditions with no mental illness group are the most accurately compensated of the chronic illness groups we examine, followed by the heart disease only group. Those with diabetes only, cancer only, and no chronic conditions are overpaid at $678, $217, and $273 per person.
Table 2.
Net Compensation and Average Spending (in U.S. Dollars, 2011) by Mutually Exclusive Chronic Condition Groups as Defined by CCS Categories.
| Group | Net Compensation | SE | Mean Spending | SE | N |
|---|---|---|---|---|---|
| Mental illness | −607 | 66 | 15,702 | 70 | 336,228 |
| Mental illness only | 415 | 65 | 7,540 | 66 | 97,746 |
| Multiple chronic conditions, mental illness | −1,026 | 88 | 19,047 | 94 | 238,482 |
| Multiple chronic conditions, no mental illness | −32 | 68 | 14,570 | 72 | 266,614 |
| Diabetes only | 678 | 53 | 6,674 | 54 | 117,014 |
| Heart disease only | −101 | 65 | 10,082 | 67 | 197,196 |
| Cancer only | 217 | 61 | 7,742 | 64 | 106,284 |
| No chronic condition | 273 | 24 | 4,384 | 25 | 476,664 |
Notes: Net Compensation is calculated using an OLS risk adjustment regression similar to the Version 21 CMS−HCC risk adjustment formula for the aged, community-dwelling subgroup. Chronic conditions refer to cancer, diabetes, heart disease, and mental illness, as defined by CCS categories; the groups are mutually exclusive. The total N = 1.5 million, drawn as a random sample of age-based Medicare beneficiaries with 12 months of continuous Parts A and B coverage in 2010 and at least one month of coverage in 2011; we exclude beneficiaries with ESRD or residing in an institution.
Transforming the data to increase spending by 10% for all individuals with a mental illness increases net compensation for individuals with a mental illness and at least one other chronic condition from −$1026 to only −$257 per person (Table 3, Columns (1) and (2)). Net compensation for individuals with only a mental illness increases from $415 to $748 per person. Notably, compensation for individuals with cancer only and no chronic conditions becomes much more accurate. Net compensation for the diabetes only group is reduced, and underpayment is aggravated slightly for the heart disease only group.
Table 3.
Comparison of Risk Adjustment Methods Targeting Mental Illness Group – Net Compensation by Mutually Exclusive Chronic Condition Groups (in U.S. Dollars, 2011).
| Group | Baseline OLS | Data Transformation | Adding RxHCC Risk Adjustors | Constrained Regression | N | ||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | ||
| GPSF | 92.81 | 97.85 | 96.06 | 94.07 | 96.96 | 97.22 | 1,500,000 |
| Grouped R2 | 99.34 | 99.90 | 99.78 | 99.62 | 99.85 | 99.86 | 1,500,000 |
| R2 | 11.38 | 11.32 | 11.36 | 11.39 | 11.35 | 11.35 | 1,500,000 |
| Mental illness only | 415 | 748 | 581 | 623 | 1021 | 1058 | 97,746 |
| Multiple chronic conditions, mental illness | −1026 | −257 | −641 | −789 | −468 | −434 | 238,482 |
| Multiple chronic conditions, no mental illness | −32 | 29 | −1 | −115 | −141 | −148 | 266,614 |
| Diabetes only | 677 | 426 | 552 | 608 | 492 | 481 | 117,014 |
| Heart disease only | −101 | −214 | −157 | −170 | −247 | −256 | 197,196 |
| Cancer only | 217 | −2 | 107 | 162 | 24 | 12 | 106,684 |
| No chronic conditions | 273 | −56 | 108 | 217 | 80 | 68 | 476,664 |
Notes: Column (1) contains the simplified CMS−HCC Version 21 risk adjustment regression. (2) contains the regression where we intervene to increase spending by 10% for all persons with a mental illness. (3) contains the regression where we intervene to increase spending by 5% for all persons with a mental illness. (4) is the baseline OLS regression with three additional RxHCC risk adjustor indicators. (5) is a constrained regression with a constraint of (targeting the average spending for the mental illness group achieved by the data transformation implementation in (2)). (6) is a constrained regression with a constraint of to achieve zero net compensation for the mental illness group. GPSF, Grouped R2 , and R2 have a maximum of 100. For GPSF and Grouped R2 , the data are partitioned into 6 groups (mental illness (combining “mental illness only” and “multiple chronic conditions, no mental illness”), diabetes only, heart disease only, cancer only, and no chronic conditions). Chronic conditions refer to cancer, diabetes, heart disease, and mental illness, as defined by CCS categories; the groups are mutually exclusive.
5.2. Comparison to alternative methods increasing net compensation for beneficiaries with a chronic illness
After adding three RxHCC risk adjustors to the baseline regression, average per person net compensation for the multiple chronic conditions with a mental illness group is increased to −$789. In the mental illness only group, net compensation is increased to $623 per person (Table 3, Column (4)).
Setting the constrained regression target to be equal to the average spending for the mental illness group achieved by data transformation (so that the two methods are directly comparable) does more than transforming the data to increase net compensation for the mental illness only group ($748 vs. $1021; Table 3, Columns (2) and (5)) and less to decrease net compensation for the multiple chronic conditions with a mental illness group (−$257 vs. −$468). The constrained regression targeting zero net compensation for all individuals with a mental illness extends these trends, yielding net compensation of $1058 per person in the mental illness only group, and −$434 per person in the multiple chronic conditions with a mental illness group (Table 3, Column (6)).
To calculate GPSF we combine the “mental illness only” and “multiple chronic conditions with a mental illness” group into a single category, which reflects the group targeted by the intervention. At baseline GPSF is 92.81, where a GPSF of 100 signals that average payment equals spending for each subgroup in the partition. Transforming the data by a 10% spending increase yields the largest improvement over the baseline (by 5 percentage points) with a GPSF of 97.85. The constrained regression approach leads to a 4 percentage point improvement over baseline, while adding in the risk adjustors generates only a 1 percentage point improvement. In contrast, adding the risk adjustors has the best individual fit, with an R2 of 11.39%, compared to 11.32% for data transformation and 11.38% for the base risk adjustment formula.25 The Grouped R2 measure is less able to distinguish between the risk adjustment methods: all fall between 99.34 and 99.90, with the baseline OLS regression yielding the lowest Grouped R2 and the 10% spending increase yielding the highest.
Overall, in this application, data transformation is the most effective method for addressing underpayment for individuals with a mental illness within a balanced budget. Adding in risk adjustors is the least effective method. By design, the data transformation regression and constrained regression are comparable in their results for the aggregate mental illness group, but transforming the data moves closer to eliminating under- and overpayment in all of the non-mental illness subgroups. Improvements in fit at the group level essentially come at no expense of fit at the individual level as measured by R2.
These approaches to addressing underpayment also affect subgroups of people with mental illness differently. Fig. 1 compares changes in net compensation by method, across mental illness subgroups occurring in at least 10% of individuals with a mental illness.26 The data transformation regression substantially increases net compensation compared to the baseline OLS regression for the screening history of mental health and substance use disorders, anxiety disorders, and mood disorders groups. The dementia/delirium and alcohol/substance disorder groups have the highest average spending ($21,802/person and $20,219/person) – thus receiving the largest increases – and become overpaid after we transform the data. The constrained regression performs similarly to the data transformation regression in terms of the impact on mental illness subgroups. The regression that includes the RxHCCs for bipolar, depression, and major depression yields similar results to the baseline regression, although compared to the constrained regression and data transformation it generates the largest increase in net compensation for individuals without a mental illness HCC. The formula with the added RxHCCs also substantially increases net compensation for the mood disorders subgroup, which includes depression and bipolar ICD-9 codes.
Fig. 1.

Comparing Changes to Net Compensation for Mental Illness Subgroups by Methodological Approach. Notes: The “Any Mental Illness” group includes all individuals in the mental illness group defined by CCS categories, and the mental illness subgroups are not mutually exclusive. The “Baseline OLS” bar shows the average undercompensation for each group under status quo conditions, while the remaining bars reflect average net compensation under alternative risk adjustment schemes.
Figs. 2 and 3 provide a side-by-side comparison of specifically targeted individuals with mental illness (Fig. 2) versus all individuals with at least one chronic condition (Fig. 3). Fig. 2 shows how increasing spending for individuals with a mental health illness and decreasing it for all others affects predicted spending – and thus net compensation – at the group level. Increasing spending by slightly less than 15% would eliminate underpayment for individuals with multiple chronic conditions and a mental illness, while the increase exacerbates the overpayment for the mental illness only group. Fig. 3 shows transforming the data to increase spending for individuals with multiple chronic conditions has a similar effect on the multiple chronic conditions groups with and without mental illness. Given the differing levels of initial net compensation, the multiple chronic conditions with mental illness group requires a spending increase of approximately 12% while the multiple chronic conditions with no mental illness group requires only about a 1% increase to eliminate underpayment.
Fig. 2.
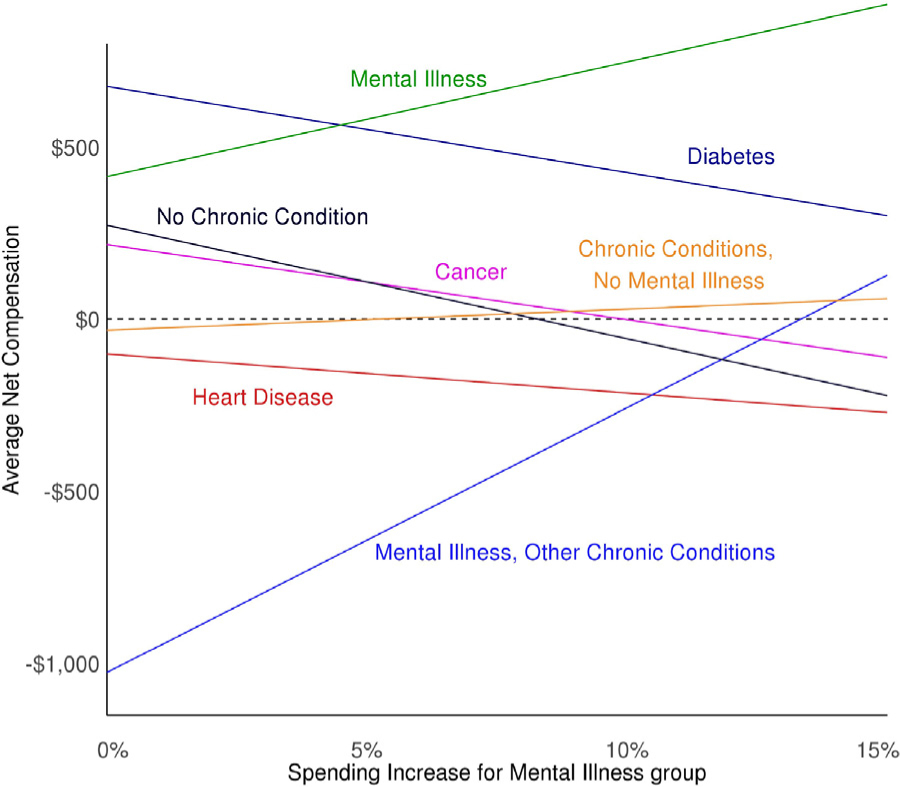
Relationship between Data Transformation Spending Increase for Mental Illness Group and Net Compensation, by Chronic Condition.
Fig. 3.
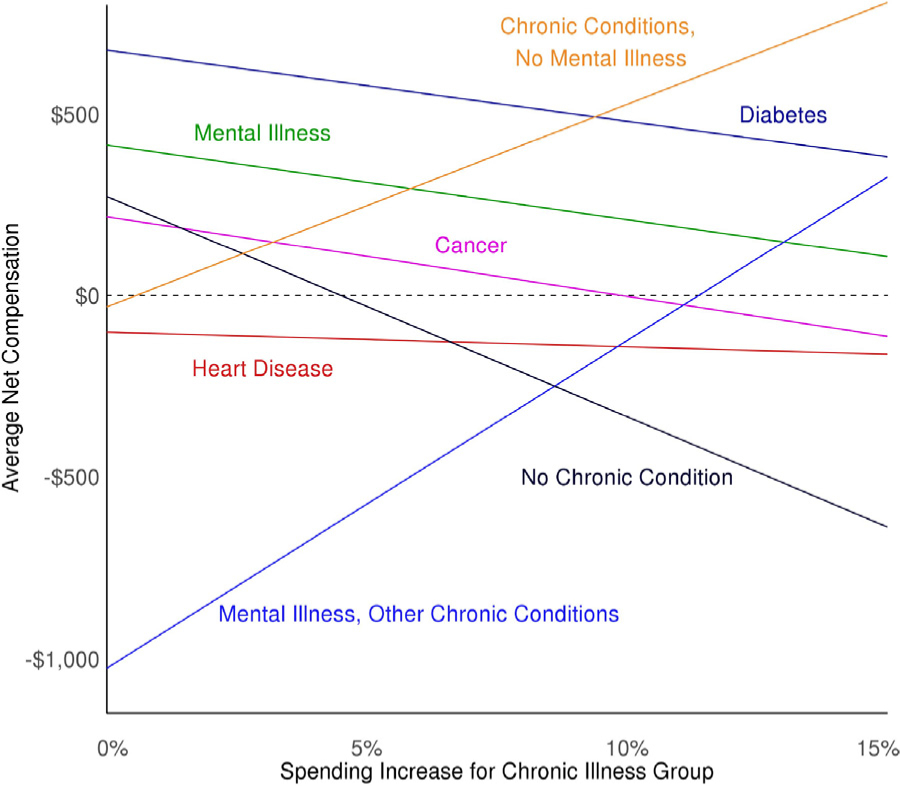
Relationship between Data Transformation Spending Increase for Any Chronic Condition Group and Net Compensation by Chronic Condition.
We also compare the estimated coefficients of the baseline OLS regression to the data transformation regression, constrained regression, and regression with additional risk adjustors for the mental health example. Appendix Fig. 1 presents the coefficients for the top ten most rare conditions, Appendix Fig. 2 shows the coefficients for the top ten most common conditions, and Appendix Fig. 3 includes the coefficients for the mental health condition risk adjustors. The risk adjustors exhibiting the largest shifts correspond to rare conditions or mental health conditions, while the more common conditions are relatively stable. Overall, the coefficient differences are relatively small in magnitude.
5.3. Reducing disparities for individuals in low-income neighborhoods
The low-income group faces a disparity of $162 compared to the high-income (reference) group (Table 4). Examined by subgroups (zip code income quintiles), we see the disparity primarily occurs in the second and third income quintiles, and largely in relation to use in the fifth income quintile. The goal is to increase the average payment for the low-income group in order to decrease the disparity. Transforming the data via a 10% spending increase to the low-income group raises payments by approximately $25 per person compared to the baseline OLS regression (Table 5). The overall fit of the regression is minimally reduced from 11.38% by a 10% spending increase: the data transformation regression yields an R2 of 11.33%. By contrast, adding in a risk adjustor for the low-income group has a large effect and makes average payments equal to average costs, as expected. The combination of adding a risk adjustor and data transformation leads to the most dramatic change in payments. The addition of the low-income group indicator means there is a risk adjustor in the formula that is perfectly imbalanced between the group of interest and the reference group. This risk adjustor provides a clear channel for the intervention to work through without greatly disturbing other coefficients in the risk adjustment formula. Appendix Table 4 presents deviations from mean spending by income groups across the risk adjustment alternatives.
Table 4.
Health Care Spending Disparity, Initial Mean Payments, and Mean Spending by Neighborhood Income Groups (in U.S. Dollars, 2011).
| Income Group | Disparity | Mean Payments | Mean Spending | N |
|---|---|---|---|---|
| Binary | ||||
| Low (Quintiles 1–3) | −162 | 10,055 | 9,928 | 900,000 |
| High (Quintiles 4–5) | 0 | 9,660 | 9,852 | 600,000 |
| Quintiles | ||||
| 1st | 40 | 10,195 | 10,235 | 300,000 |
| 2nd | −257 | 10,063 | 9,847 | 300,000 |
| 3rd | −268 | 9,908 | 9,702 | 300,000 |
| 4th | 0 | 9,773 | 9,726 | 300,000 |
| 5th | 0 | 9,548 | 9,977 | 300,000 |
Table 5.
Reducing Disparities by Neighborhood Income – Comparing Group Payments and Spending (in U.S. Dollars, 2011).
| Income Group | Base OLS | Data Transformation | Low-Income Indicator | Combination | Mean Spending |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| R2 | 11.38 | 11.33 | 11.38 | 11.27 | |
| Binary | |||||
| Low (Quintiles 1–3) | 10,055 | 10,080 | 9,928 | 10,922 | 9,928 |
| High (Quintiles 4–5) | 9,660 | 9,623 | 9,852 | 9,851 | 9,852 |
| Quintiles | |||||
| 1st | 10,195 | 10,250 | 10,075 | 11,080 | 10,235 |
| 2nd | 10,063 | 10,084 | 9,936 | 10,928 | 9,847 |
| 3rd | 9,908 | 9,906 | 9,777 | 10,758 | 9,702 |
| 4th | 9,773 | 9,751 | 9,964 | 9,975 | 9,726 |
| 5th | 9,548 | 9,496 | 9,735 | 9,727 | 9,977 |
Notes: Column (1) contains the simplified CMS−HCC v21 risk adjustment regression. (2) contains the regression where we intervene to increase spending by 10% for individuals in the low-income group. (3) is the baseline OLS regression with an indicator the low-income group. (4) contains the baseline OLS regression with an indicator for the low-income group, combined with transforming the data to increase spending by 10% for the low-income group. (5) shows mean group-level spending.
Similar to the inefficiency application, the changes in risk adjustor coefficients between the baseline regression and alternative methods are minor and we see the largest differences occur for rare conditions. Again, the sizes of the coefficient changes are relatively small.
6. Discussion
This paper contributes to the literature on health plan payment on both theoretical and practical levels. Our central theoretical insight is that there is a two-way relationship between the data describing the performance of the health care system and the level of payments that emerge from a risk adjustment methodology. Payments determine behavior, and behavior generates the data that feeds into payment algorithms. Our paper calls attention to the second link, and introduces a new mechanism for affecting payment and, thus, health system performance. The researcher/regulator need not accept the behavior from the flawed health care system as the input data for use in calibrating payment, and in general, they should not. The mechanism of data transformation is easy to implement in practice, and intuitive, and therefore may have ready practical application. Health care systems are complex and suffer from allocation problems related to efficiency and fairness. We show how the process of transforming the data is a systematic and transparent way to address both types of problems.
We present two simplified empirical applications, which assume the current health care system underspends on individuals with chronic illnesses and underprovides services for individuals living in low-income zip codes. In the context of net compensation by disease group, data transformation and constrained regression both outperform the approach of including additional risk adjustors. Both data transformation and constrained regression are effective methods, have little effect on R2, and improve group fit. If a group is currently underserved, adding in a risk adjustor for low-income status will exacerbate the health care disparity between low-income and high-income neighborhoods. Combining adding a risk adjustor with a spending increase is more effective at altering incentives than data transformation in isolation.
Our goal in this paper is to introduce a new idea for improving the performance of health plan payment methods. While the empirical applications show how our model might be implemented, this method requires further practical development in terms of how it would be deployed within an existing health plan payment system. For example, policy objectives, groups to be targeted, and outcome measures would all need to be specified in each year of implementation. Additionally, desired spending levels for subgroups must be specified. Subgroup performance across a wide variety of groups – including those based on predicted spending deciles, chronic conditions, number of HCCs, and demographic characteristics – are already routinely used to evaluate Medicare risk adjustment formulas and could help shape how the data transformation process is applied (Pope et al., 2004, 2011). Although we use the Medicare program as the setting for our empirical demonstration, in practice it may be more straightforward to transform the data in a health plan payment system where the data used for risk adjustment calibration is the same as the spending data in the current system the regulator seeks to affect.27 The Netherlands for example, has such a system, and would be an appropriate setting for further empirical work or policy applications.28
Regulators may choose from a variety of policy alternatives to achieve an efficiency or fairness goal via the risk adjustment system. Expanding the formula with additional risk adjustors is, as discussed earlier in this paper, a common approach. However, it not only is harmful in the case of the disparities example, but it also has potential costs in an efficiency setting, such as upcoding or other types of gaming, which are avoided by data transformation. Various forms of risk sharing, such as outlier payments, are another form of modification of health plan payment systems that may address some of the incentives of concern here. These policies are distinct, however, and have different effects. Outlier payments matter most to the groups with a few very high cost cases, and would have little effect on systematic underservice for a broad group of plan enrollees. There is also a large set of ad hoc, post-estimation adjustments regulators can implement – i.e., increasing the prices paid for certain groups after estimating the risk adjustment formula – but these modifications do not attempt to preserve OLS fit properties, rely on risk adjustors exactly identifying groups of interest, and do not take into account other subgroups, whose coefficients/payments remain untouched. These payment approaches also have problematic incentive properties, where insurers face weak incentives to limit spending for individuals likely to trigger ex-post payments. Our approach does not share these properties, in that we break the connection between insurer spending and insurer payment via a data transformation prior to risk adjustment estimation. We aim to expand the regulator’s toolkit in order to facilitate achieving objectives that may be more costly or difficult when implementing other approaches like ad hoc adjustments or including more risk adjustors.
“Big data” and machine learning methods have been explored as another potential policy option for risk adjustment improvement in smaller targeted studies that have shown particular promise in terms of producing more parsimonious algorithms that may be less vulnerable to insurer gaming (e.g., Rose, 2016; Shrestha et al., 2017; Park and Basu, 2018). Despite this promise, these machine learning methods have not been implemented in practice, are in need of further vetting, and there is currently no consensus on the extent to which data sources like electronic medical records and machine learning tools may ultimately improve risk adjustment performance (Ellis et al., 2018). Importantly, big data and machine learning methods will not solve the problem of using observed data to estimate risk adjustment formulas: although these methods may yield more accurate prediction, if the outcome is based on observed data then improved prediction will not address the inefficiencies or inequities in the market. Machine learning methods attempt to address the risk adjustment problem at the fitting stage rather than our data transformation approach, which targets the pre-processing phase.
An increasingly discussed component of using algorithms for social policy decision-making is examining the possibility of undesired outcomes or side effects (e.g., Diakopoulos et al., 2016). All of the risk adjustment approaches we compare demonstrate the potential for unintended consequences: in the mental health example, the heart disease group’s undercompensation is exacerbated by each of the risk adjustment approaches. In the case of data transformation and constrained regression, this is a result of explicitly imposing a total budget constraint; in the additional risk adjustor version the budget constraint is implicit. This negative side effect raises the issue of which groups to intervene on, which is possible and relatively transparent via data transformation or constrained regression, but less straightforward in the case of adding risk adjustors. Additionally, we often do not know the “right” level of spending for a group or service, so there is always the risk of pushing a service “too high” or “too low” when transforming the data. A related potential side effect is the shifts in estimated coefficients. Overall, the magnitude of the coefficient differences we observe combined with the prevalence of the conditions suggests data transformation does not create strong incentives to deter or attract certain groups via direct risk selection.
While the main objective of this paper has been to provide a new approach to payment system design, there is another important implication of the basic conceptual issue we explore here. It is not only problematic to use observed data to design payment systems, it is also problematic to use observed data to evaluate payment systems. R2, predictive ratios, and under/overpayment measures of payment system performance evaluate how well plan revenues match observed costs, which generally will not be efficient or fair. However, a more revealing measure of payment system performance would evaluate how well plan revenues track desired levels of spending. Estimation and evaluation methods are clearly linked, and if a different estimation approach is warranted, different measures of performance are also likely needed.
A strand of the European literature on risk adjustment proposes to address this problem of using observed costs to evaluate risk adjustment by instead using “acceptable costs” or “normative expenditures” for payment algorithm evaluation (Stam et al., 2010; van de Ven and Ellis, 2000). Acceptable costs are those that capture medically necessary care delivered in a cost-effective manner. Our approach is conceptually similar – to set targets for acceptable levels of spending that reflect a social policy choice. However, our goals are more general in that they allow for a variety of reasons why observed spending may differ from efficient spending and we explore a different implementation approach: rather than modifying the coefficients assigned to risk adjustment variables, we modify spending data based on our beliefs about what acceptable costs should be for the groups we are concerned about. An additional, more subtle difference between our approach and the European literature is that the existing normative cost approaches focus on removing certain (unacceptable) costs when estimating risk adjustment, whereas our method and examples involve adding costs that do not occur in the markets generating the observable data. Similar to other approaches that make explicit choices about risk factors to subsidize, transforming the data may spark political and social debate about which groups should be targeted and intervened upon; this debate may be particularly fierce in the U.S. context, where the solidarity principle is not well-established.
“Getting the prices right” will be a central problem of health plan payment in health insurance markets around the world for years to come. There are many improvements that can be made to current methods. Transforming the data itself should be part of any policymaker’s toolkit.
Supplementary Material
Acknowledgements
This research was supported by the National Institute of Aging (P01 AG032952) and the Laura and John Arnold Foundation. The views presented here are those of the author(s) and not necessarily those of the Laura and John Arnold Foundation, its directors, officers, or staff. Bergquist received additional support from the Harvard Data Science Initiative. We are grateful to Konstantin Beck, Michael Barnett, Ben Cook, Randy Ellis, Jacob Glazer, Sebastien Haneuse, Laura Hatfield, Joran Lokkerbol, Joseph Newhouse, Bryan Perry, Anna Sinaiko, Mark Shepard, Piet Stam, Ariel Dora Stern, Richard van Kleef, Alan Zaslavsky, and Wenjia Zhu for helpful comments and discussion.
Footnotes
Appendix A. Supplementary data
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.jhealeco.2019.05.005.
Algorithmic fairness with biased data is a growing area of study outside of health care. The theme of using a data- or algorithm-based intervention to break a feedback loop that reproduces or exacerbates biases in data runs through many, diverse applications. For example, Lum and Isaac (2016) discuss how using biased data in predictive policing algorithms can reproduce and amplify the biases in police data, and in some cases lead to a discriminatory feedback loop between policing practices and algorithm predictions. Hu and Chen (2017) show how a fairness constraint can be imposed on firms’ hiring practices to ensure both individual- and group-based fairness and address discrimination in the labor market.
Van Kleef et al. (2017) show that in the case where certain groups are undercompensated but it is problematic to include indicators of group membership in the risk adjustment formula, a constrained regression can be used to mitigate selection incentives while avoiding the introduction of perverse incentives.
The Medicare risk adjustment formula currently used in practice is CMS-HCC Version 22; it includes fewer HCCs than Version 21 and estimates a greater number of subgroup regressions.
Pope et al. (2004) outline ten principles to guide developing the first HCC system for Medicare Advantage, which include factors such as choice of diagnostic categories, approaches to mitigate insurer gaming, and properties of fairness and consistency. Ellis et al. (2018) propose two updates: risk adjustment design should anticipate the effects of the payment system on coding and risk adjusters, and should optimize given potential selection incentives set by the payment system. The data transformation approach is in the spirit of this second principle; our method explicitly acknowledges the relationship between the payment system and insurer actions and breaks this feedback loop.
This is an example of the well-accepted idea that, as Newhouse (2002) pointed out in the context of physician pricing, provider costs are endogenous to the payment method.
Relations (1) and (2) should be understood broadly and remain true even in a system like Medicare where the payment system calibration is based on data from fee-for-service Medicare. Medicare Advantage plan behavior in response to payment incentives affects how many and what type of beneficiaries remain in fee-for-service Medicare. The relations also remain in place even in the case in which the data used for calibration is entirely disconnected from system performance. In that case, the g(X) function is a set of payments unaffected by X. Such a system may be desirable in that it eliminates the feedback loop between payments and realized costs, but it is not necessarily the case that it will produce optimal insurance contracts without modifying data from the fee-for-service setting due to potential inefficiencies in that setting.
In practice, data from a previous period are typically used to set payments in the current period. If a system is in full equilibrium as we describe, such timing does not affect the equilibrium. Out of equilibrium, a system characterized by (1) and (2) would need to take account of timing and any iterative process leading to equilibrium.
Throughout, we assume that solutions exist, correspond to positive values of all spending, and are unique and stable. Our Medicare application only requires the assumptions to hold locally.
In Glazer and McGuire (2002), optimal coefficients are those that lead the plan, in profit maximization, to supply efficient health care. In both of these instances, the coefficients are found by inverting the function describing system response to the price incentives. Theoretical solutions to optimal risk adjustment are assumed to be applied to the optimal allocations and are not designed to move the system to optimal based upon some arbitrary inefficient/unfair initial allocation.
There are direct parallels in our proposed approach to the theory underlying structural causal modeling (Pearl, 2009). Specifically, we could formulate the two relationships in (1) and (2) as nonparametric structural equation models with unknown functional forms f(·) and g(·), although an explicit representation of equilibrium does not always apply. We can intervene on the system we have defined to set random variables (here, payments) to specific values.
We focus on a subset of features of Medicare payment and Medicare Advantage plan spending allocations. Our examples are concerned only with medical spending predicted by the Medicare Advantage risk adjustment formula – primarily Part A and B spending – not drug spending (which has its own plan payment system). The analyses we present focus on community-dwelling individuals, the largest set of Medicare beneficiaries. We ignore any joint cost issues introduced by the presence of other payers of health plan services.
This assumption is based on the model of health plan choice and plan design presented in Frank et al. (2000). Geruso et al. (2016), Carey (2017), Lavetti and Simon (2018), and Shepard (2016) present empirical evidence supporting this assumption.
Age-sex cells capture female and male with age groups 0–34, 35–44, 45–54, 55–59, 60–64, 65–69, 70–74, 75–79, 80–84, 85–89, 90–94, and 95+. Appendix Table 1 contains the full list of HCC indicators and descriptions, and omitted interaction terms.
In our sample, the mental illness HCCs capture only 44% of individuals in the mental illness group defined by CCS groups. The difference in how CCS groups are defined versus how the HCC-based risk adjustors are defined accounts for why some groups are underpaid in the current risk adjustment scheme, despite having HCC indicators in the formula.
It is sometimes an explicit choice on the part of the regulator to reduce predictive accuracy by blurring some medical distinctions between conditions (e.g., among mental health diagnoses) or excluding some conditions due to concerns about incentives for gaming; these concerns would likely to continue to affect any formulas used in payment.
Papers and government evaluations of underpayment by group in the U.S. commonly measure underpayment in ratio form (predictive ratios) rather than by a difference (e.g., McGuire et al., 2014; Pope et al., 2011). Here we work with the difference metric to keep net compensation on the dollar scale. Our approach is similar to the European literature, which uses the difference rather than the ratio (e.g., Van Kleef et al., 2013).
Note that net compensation is defined in relation to observed spending rather than the desired, efficient level of spending. We return to the matter of using observed vs. efficient levels for payment system evaluation in the Discussion.
We examined disparities across zip code median income quintiles and compared two different definitions for the reference group: the upper 60% and the upper 40%. We found the middle quintile aligned more closely with the bottom two quintiles, thus we defined the reference group (high-income) as the upper 40% and the group of interest (low-income) as the lower 60%.
For a review of methods for implementing the IOM definition of health care disparity, see Cook et al. (2012).
Other loss functions can be considered, including those for bounded continuous outcomes.
Intervening on Yi leads to a constant change in net compensation because revenues at the individual and group level are linear in Z′Y Transforming the data changes Y, while (Z′Z)−1 Z′ and cg are constant. Thus, any ΔY leads to the same Δβ, , and, ultimately, change in net compensation.
Another way to maintain the same aggregate budget would be to directly deduct the corresponding amount of spending from the complementary group. Using a constraint, however, is our preferred approach. First, using a constraint does not require calculating the addition to the targeted group before running the regression, allowing the analysis to proceed in one step rather than two. And second, if the data transformation is complex – for example, if there are multiple targeted groups – our approach of intervening on the Y vector to enact the desired changes for the targeted groups and then imposing an overall constraint is simple and easily implemented.
GPSF on a linear scale is a group-level version of Cumming’s Prediction Measure (CPM) (van Veen et al., 2015).
Details on selecting the additional risk adjustors can be found in the Appendix.
The baseline regression R2 is slightly lower than that reported for the CMS-HCC Version 21 regression (12.46%). However, the correlation between predicted values from our regression and those using the CMS-HCC coefficients is 98%, indicating our empirical formula is a good representation of the one used by CMS for plan payment.
We center Fig. 1 at “$0” to demonstrate that both positive and negative net compensation can be achieved by different methods across the subgroups; we do not intend to imply that zero is the appropriate level of net compensation.
Recall that the Medicare risk adjustment formula is calibrated on traditional fee-for-service Medicare data but used to pay private Medicare Advantage plans.
Although in Germany the risk adjustment formula is also calibrated with the spending data the regulator seeks to influence, in practice it is likely to be a less impactful setting for our method. Sickness funds (i.e., health plans) have little ability to influence the allocation of health care spending, because allocation decisions for nearly all health expenditures (95%) are taken at the collective level, leading to uniform prices for physicians and hospitals across sickness funds (Wasem et al., 2018). Thank you to an anonymous reviewer for pointing out this detail of the German health plan payment system.
References
- Agency for Healthcare Research and Quality, 2016. Clinical Classification Software (CCS) 2015. [Google Scholar]
- Ash Arlene, McCall Nancy, Fonda Jenn, Hanchate Amresh, Speckman Jeanne, 2005. Risk Assessment of Military Populations to Predict Health Care Cost and Utilization. RTI, project number 08490.006.
- Carey Colleen, 2017. Technological change and risk adjustment: benefit design in Medicare Part D. Am. Econ. J. Econ. Policy 9 (1), 38–73. [Google Scholar]
- Centers for Medicare and Medicaid Services, 2016. March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting: Discussion Paper.
- Cook Benjamin Le, McGuire Thomas G., Zaslavsky Alan M., 2012. Measuring Racial/Ethnic disparities in health care: methods and practical issues. Health Serv. Res. 47 (3.2), 1232–1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Department of Health and Human Services, 2017. Medicare Part D 2013 Model software/ICD-9 Mappings.
- Diakopoulos Nicholas, et al. , 2016. Principles for Accountable Algorithms and a Social Impact Statement for Algorithms. FATML.org., July (accessed December 4, 2018) http://www.fatml.org/resources/principles-for-accountable-algorithms.
- Ellis Randall P., Martins Bruno, Rose Sherri, 2018. Risk adjustment for health plan payment In: McGuire Thomas G., van Kleef Richard C. (Eds.), Risk Adjustment, Risk Sharing and Premium Regulation in Health Insurance Markets: Theory and Practice. Elsevier, London. [Google Scholar]
- Frank Richard G., Glazer Jacob, McGuire Thomas G., 2000. Measuring adverse selection in managed health care. J. Health Econ. 19 (6), 829–854. [DOI] [PubMed] [Google Scholar]
- Geruso Michael, Layton Timothy J., Prinz Daniel, NBER Working Paper No. 22832 2016. Screening in Contract Design: Evidence From the ACA Health Insurance Exchanges. [DOI] [PMC free article] [PubMed]
- Glazer Jacob, McGuire Thomas G., 2002. Setting health plan premiums to ensure efficient quality in health care: minimum variance optimal risk adjustment. J. Public Econ. 84 (2), 153–173. [Google Scholar]
- Gruenberg Leonard, Wallack Stanley S., Tompkins Christopher P., 1986. Pricing strategies for capitated delivery systems. Health Care Finance Review, pp.35–44, Spec No. [PMC free article] [PubMed]
- Han Tony, Lavetti Kurt, 2017. Does part d abet advantgeous selection in Medicare Advantage? J. Health Econ. 56, 368–382. [DOI] [PubMed] [Google Scholar]
- Hu Lily, Chen Yiling, 2017. Fairness at equilibrium in the labor market. Proceedings of Fairness, Accountability, and Transparency in Machine Learning, 5 pages.
- Institute of Medicine, 2002. Unequal Treament: Confronting Racial and Ethnic Disparities in Health Care. National Academies Press, Washington, DC. [PubMed] [Google Scholar]
- Lavetti Kurt J., Simon Kosali, 2018. Strategic formulary design in medicare part d plans. Am. Econ. J. Econ. Policy 10 (August 3), 154–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton Timothy J., McGuire Thomas G., Kleef Richard Cvan, NBER Working Paper No. 22642 2016. Deriving Risk Adjustment Payment Weights to Maximize Efficiency of Health Insurance Markets. [DOI] [PMC free article] [PubMed]
- Layton Timothy J., Ellis Randall P., McGuire Thomas G., van Kleef Richard C., 2018. Evaluating the performance of health plan payment systems In: McGuire Thomas G., van Kleef Richard C. (Eds.), Risk Adjustment, Risk Sharing and Premium Regulation in Health Insurance Markets: Theory and Practice. Elsevier, London. [Google Scholar]
- Lum Kristian, Isaac William, 2016. To predict and serve? Significance 13 (5), 14–19. [Google Scholar]
- McGuire Thomas G., Newhouse Joseph P., Normand Sharon-Lise, Shi Julie, Zuvekas Samuel, 2014. Assessing incentives for service-level selection in private health insurnace exchanges. J. Health Econ. 35, 47–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montz Ellen, Layton Tim, Busch Alisa B., Ellis Randall P., Rose Sherri, McGuire Thomas G., 2016. Risk-adjustment simulations: plans may have incentives to distort mental health and substance use coverage. Health Aff. 35 (6), 1022–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newhouse Joseph P., 2002. Pricing the Priceless. The MIT Press. [Google Scholar]
- Newhouse Joseph P., Price Mary, Hsu John, Michael McWilliams J, McGuire Thomas G., 2015. How much favorable selection is left in Medicare Advantage? Am. J. Health Econ. 1 (1), 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park Sungchul, Basu Anirban, 2018. Alternative evaluation metrics for risk adjustment methods. Health Econ. 27 (6), 984–1010. [DOI] [PubMed] [Google Scholar]
- Pearl Judea, 2009. Causality: Models, Reasoning and Inference. Cambridge University Press, New York. [Google Scholar]
- Pope Gregory C., et al. , 2004. Risk adjustment of Medicare capitation payments using the CMS-HCC model. Health care finance Rev. 25 (4). [PMC free article] [PubMed] [Google Scholar]
- Pope Gregory C., Kautter John, Ingber Melvin J., Freeman Sara, Sekar Rishi, Newhart Cordon, 2011. Evaluation of the CMS-HCC Risk Adjustment Model: Final Report. Centers for Medicare and Medicaid Services. [Google Scholar]
- Rose Sherri, 2016. A machine learning framework for plan payment risk adjustment. Health Serv. Res. 51 (6), 2358–2374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schokkaert Erik, van de Voorde Carine, 2004. Risk selection and the specification of the conventional risk adjustment formula. J. Health Econ. 23 (6), 1237–1259. [DOI] [PubMed] [Google Scholar]
- Shepard Mark, NBER Working Paper No. 22600 2016. Hospital Network Competition and Adverse Selection: Evidence Form the Massachusetts Health Insurance Exchange.
- Shrestha Akritee, Bergquist Savannah, Montz Ellen, Rose Sherri, 2017. Mental Health Risk Adjustment With Clinical Categories and Machine Learning. Health Services Research. [DOI] [PMC free article] [PubMed]
- Stam Pieter J.A., van Vliet RCJA, van de Ven Wynand P.M.M., 2010. A limited-sample benchmark approach to assess and improve the performance of risk equalization models. J. Health Econ. 29 (3), 426–437. [DOI] [PubMed] [Google Scholar]
- Van de Ven Wynand P.M.M., Ellis Randall P., Chapter 14 2000. Risk adjustment in competitive helath insurance plan markets In: Culyer Anthony J., Newhouse Joseph P. (Eds.), Handbook of Health Economics, Vol. 1 Elsevier, pp. 755–845. [Google Scholar]
- Van Kleef Richard C., van Vliet Rene C.J.A., van de Ven Wynand P.M.M., 2013. Risk equalization in the Netherlands: an empirical evaluation. Expert Reviews Pharacoeconomics Outcomes Research 13 (6), 829–839. [DOI] [PubMed] [Google Scholar]
- Van Kleef Richard, McGuire Thomas, Vliet Renevan, van de Ven Wynand, 2017. Improving risk equalization with constrained regression. Eur. J. Health Econ. 18 (9), 1137–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Veen SCHM, van Kleef RC, van de Ven WPMM, van Vliet RCJA, 2015. Is there one measure-of-fit that fits all? A taxonomy and review of measures-of-fit for risk-equalization models. Med. Care Res. Rev. 72 (2), 220–243. [DOI] [PubMed] [Google Scholar]
- Wasem Jugen, Buchner Florian, Lux Gerald, Schillo Sonja, 2018. Health plan payment in Germany In: McGuire Thomas G., van Kleef Richard C. (Eds.), Risk Adjustment, Risk Sharing and Premium Regulation in Health Insurance Markets: Theory and Practice. Elsevier, London. [Google Scholar]
- Zweiful Peter, Breyer Friederich, Kifmann Mathias, 2009. Health Economics, 2nd. Springer, Berlin. [Google Scholar]
Further reading
- Friedman Jerome, Hastie Trevor, Tibshirani Robert, 2010. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33 (1), 1–22. [PMC free article] [PubMed] [Google Scholar]
- Liaw Andy, Wiener Mattew, 2002. Classification and regression by randomForest. R News 2 (3), 18–22. [Google Scholar]
- Petersen Maya L., et al. , 2015. Super learner analysis of electronic adherence data improves viral prediction and may provide strategies for selective HIV RNA monitoring. J. Acquir. Immune Defic. Syndr. 69 (1), 109–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirracchio Romain, Petersen Maya L., Carone Marco, Rigon Matthieu Resche, Chevret Sylvie, van der Laan Mark J., 2015. Mortality prediction in intensive care units with the Super ICU Learner Algorithm (SICULA): a population-based study. Lancet Respir. Med. 3 (January 1), 42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose Sherri, Bergquist Savannah L., Layton Timothy J., 2017. Computational health economics for identifying unprofitable health care enrollees. Biostatistics 18 (4), 682–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Laan Mark J., Rose Sherri, 2011. Targeted Learning: Causal Inference for Observational and Experimental Data. Springer, New York. [Google Scholar]
- Van der Laan Mark, Polley Eric C., Hubbard Alan E., 2007. Super learner. Stat. Appl. Genet. Mol. Biol. 6 (1). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


