Taking the Relational Structure of Fractions Seriously: Relational Reasoning Predicts Fraction Knowledge in Elementary School Children

Abstract

Understanding and using symbolic fractions in mathematics is critical for access to advanced STEM concepts. However, children and adults consistently struggle with fractions. Here, we take a novel perspective on symbolic fractions, considering them within the framework of relational structures in cognitive psychology, such as those studied in analogy research. We tested the hypothesis that relational reasoning ability is important for reasoning about fractions by examining the relation between scores on a domain-general test of relational reasoning (TORR Jr.) and a test of fraction knowledge consisting of various types of fraction problems in 194 second grade and 145 fifth grade students. We found that relational reasoning was a significant predictor of fractions knowledge, even when controlling for non-verbal IQ and fractions magnitude processing for both grades. The effects of relational reasoning also remained significant when controlling for overall mathematics knowledge and skill for second graders but was attenuated for fifth graders. These findings suggest that this important subdomain of mathematical cognition is integrally tied to relational reasoning and opens the possibility that instruction targeting relational reasoning may prove to be a viable avenue for improving children’s fractions skills.

Introduction

Proficiency with symbolic fractions is critical for advanced learning in STEM disciplines (Kilpatrick, Swafford, & Findell, 2001; National Council of Teachers of Mathematics, 1989, 2000; National Mathematics Advisory Panel, 2008; Booth & Newton, 2012; Booth, Newton, & Twiss-Garrity, 2014; Siegler, Fazio, Bailey, & Zhou, 2013). However, decades of work demonstrate that both children and adults struggle when reasoning about symbolic fractions (e.g., Bright, Behr, Post, & Wachsmuth, 1988; Dufour-Janvier, Bednarz, & Belanger, 1987; Kerslake, 1986; Lesh, Behr, & Post, 1987; Mack, 1995; Ni, 2001; Novillis, 1979). Common errors in fraction reasoning are often attributed to a “whole-number bias,” the inclination to consider the components of a fraction separately rather than considering the fraction as determined by the holistic relations between its two components (Braithwaite & Siegler, 2017; Ni & Zhou, 2005). Several domain-specific explanations for these difficulties exist, ranging from interference from prior knowledge (e.g., Hartnett & Gelman, 1998; Streefland, 1978; Vamvakoussi & Vosniadou, 2004; see Pitkethly & Hunting, 1996, for a review) to the possible absence of necessary neurocognitive startup tools that would support intuitions of rational number constructs (Feigenson, Dehaene, & Spelke, 2004; Gelman, 2015; Gelman & Meck, 1983; Bonato, Fabbri, Umilta, & Zorzi, 2007). In this study, we explore another possible, more domain general factor: this tendency to focus on fraction components (and therefore the observed whole number bias) may reflect difficulties with relational reasoning more broadly.

There is a strong a priori case for that general relational reasoning might play a strong role in fractions understanding, as the bipartite structure of a symbolic fraction is inherently relational. Indeed, a fraction cannot be meaningfully understood without relating its two components (numerator and denominator) to each other. If the tendency to think about the components of a symbolic fraction separately reflects a general weakness in relational reasoning ability, then measures of general relational reasoning should be predictive of competence with symbolic fractions. Moreover, this should be true over and above other domain specific measures of numerical competence with whole numbers. The current study sought to test this hypothesis in two groups of elementary school children: 5^th-graders, who have received sustained formal instruction with fractions, and 2^nd-graders who have not.

Fractions as a special case of relational reasoning

The structure of symbolic fractions can be compared to the structure of general propositional relations frequently studied in cognitive psychological research on analogy. Viewed from this research perspective, relational reasoning allows us to make inferences and to generalize based on the roles that entities play, rather than the properties of the entities (Doumas, Hummel, & Sandhofer, 2008; Hummel & Holyoak, 2003). In an analogy, the relation or relational structure is the key quality shared by the source and the target (Alexander et al., 2016; Gentner & Smith, 2012). For example, in the verbal analogy “cat: mouse :: frog : fly” (cat is to mouse as frog is to fly), the implied relation is “preys on.” The entities cat and frog take the role “predator”, and the entities “mouse” and “fly” take the role “prey.” Cat and frog cannot be aligned based on surface features or properties – nor can mouse and fly. However, by recognizing the common relation in both sets, we can make inferences from one to the other. For example, if we know that bringing cats into an ecosystem can reduce the rodent population, it is reasonable to infer that introducing frogs (the cat analog) could reduce the fly population (rodent analog).

Symbolic fractions share several formal properties with propositional relations and acknowledging those relations may similarly help promote inferences and understanding of the fractions domain. In a common symbolic fraction of the form “a/b” (such as 3/4), the roles of the respective components are numerator and denominator. As with many of the relations studied in analogy and relational reasoning research, fractions are not commutative with respect to these roles (e.g., “cat preys on mouse” ≠ “mouse preys on cat” and 5/7 ≠ 7/5). Also in parallel with general propositional relations, the numerator-denominator relation can be represented independently of any particular component numerals (entities); for example “a/b” represents the numerator-denominator relationship without reference to any particular numerals or magnitudes. When relations are represented this way, without reference to particular exemplars, they are considered abstract; such abstract representations facilitate transfer (Gick & Holyoak 1980, 1983).

Although some previous research has highlighted the relational nature of symbolic fractions, a domain general object-role relational reasoning approach has not been widely applied to fractions. Mathematics education researchers have pointed out for some time that symbolic fractions have many possible interpretations (such as the part-whole, quotient, measure, or operator interpretations), many of which hinge on the relational nature of the fraction in some way (e.g., Behr, Lesh, Post, & Silver, 1983; Empson et al., 2010; Ohlsson, 1988). Despite this complexity, considerable recent work in psychology has emphasized the importance of a single interpretation: the unidimensional magnitude of a fraction (for example, its position on number line—See Figure 1) (Siegler, 2016). These studies demonstrate that understanding of fraction magnitudes (particularly with fraction number lines) is an important predictor of fraction knowledge and overall mathematics competence (Fazio, Bailey, Thompson, & Siegler, 2014a; Hansen et al., 2017; Hurst & Cordes, 2018a, 2018b; Yoshida & Shinmachi, 1999) and suggest that this interpretation should be emphasized in instruction (Fazio, Kennedy, & Siegler, 2016; Siegler, 2016). Whereas fraction magnitude understanding is clearly important, additional relation-based approaches to fractions could complement the work done on fraction magnitudes.

Figure 1.

Example number line demonstrating equivalent fractions and unusual part-whole relationships (improper fractions).

There are in fact two senses in which we are referring to fractions as relations. The first is a sort of formal relation, based only on the assignment of roles, and potentially applies to any fraction interpretation. For example, saying that “2/3 means 2 parts out of 3” is analogous to “4/7 means 4 parts out of 7” in the sense that each has a denominator, which can be interpreted as a whole or total, and each has a numerator, which can be interpreted as a subset of the whole. Understanding the entailments of 2/3—for example, that it has a complement which can be found by subtracting from the total in the form 3/3 (3/3-2/3 = 1/3)—allows us to make inferences about 4/7 (7/7-4/7 = 3/7). Although we have used the part-whole interpretation here, any interpretation of numerator and denominator could be considered in a similar relational framework. An understanding of this qualitative relation shared by all fractions facilitates transfer to examples or problems using numerators and denominators different from those used for training/teaching.

However, there is also a more specific type of quantitative relation that is shared by fractions that represent equivalent values. For example, the fractions 3/4 and 75/100 are not merely analogous in the sense described above for all fractions; they are in fact equivalent. As members of the same equivalence class, they represent the same quantitative relation (or relative quantity). Although the components may change across instantiations (e.g., 3/4, 75/100, 8/12), in each case, the denominator is multiplied by the same factor to yield the numerator. Understanding this multiplicative relation is widely seen as key to understanding fractions throughout the mathematics education literature (e.g. Behr, Lesh, Post & Silver, 1983; Hackenberg, 2007; Thompson & Saldhana, 2003; Vergnaud, 1983).

Relational reasoning and common fractions errors

Reframing common fraction errors studied in numerical cognition research as failures of relational reasoning may help to link these errors with broader domain general accounts of errors in relational reasoning. Two of the most common sources of error are attention to the numerator or denominator separately rather than attending to the holistic magnitude (for example, choosing 4/9 as larger than 3/4 because 4 > 3 or because 9 > 4) and treating equivalent fractions with larger components as being larger (treating 16/20 as larger than 4/5 even though they are equivalent)¹ (Braithwaite & Siegler, 2017; DeWolf & Vosniadou, 2015; Fazio et al., 2014a; Ganor-Stern, Karasik-Rivkin, & Tzelgov, 2011; Meert, Gregoire, & Noel, 2009; Zhang, Fang, Gabriel, & Szucs, 2014). These errors are attributed to a “whole number bias.” But what is the underlying source of this bias? This whole-number bias has sometimes been conceptualized in terms of issues specific to numerical cognition, such as difficulties in mapping number symbols to number concepts (Mix et al., 1999; Sophian et al., 1997), differences in the representations of discrete vs. continuous quantities (Boyer & Levine, 2015; Boyer, Levine, & Huttenlocher, 2008) or differences in the possibility of experiential or embodied grounding (Streefland, 1991; Gallistel & Gelman, 1992).

We suggest that these whole-number bias errors might be better characterized as failures to think relationally in a general sense, rather than failures of processes specific to numerical cognition. If students treat the components as separate entities to compare, rather than as role-fillers in a relation, students will make exactly these types of errors: for example selecting 2/3 > 3/4 because 2 > 3 or 3 > 4 could be a failure to recognize and engage with the role-based relation between 2 (numerator) and 3 (denominator) and between 3 (numerator) and 4 (denominator). That error could also be characterized as attention to the surface features (magnitude/identity) of the components rather than the roles they are assigned to. Turning to arithmetic operations with fractions, additional difficulties may stem from failures to consider and maintain these roles when carrying out operations. For example, attempts to add fractions by simply adding numerators and adding denominators could be viewed as a failure to respect the respective roles of numerator and denominator. On the other hand, identifying equivalent fractions requires the more specific, “quantitative” relational understanding of equivalence classes. Given this relational framing of fractions and fraction errors, it might be the case that reasoning about fractions often depends on the ability to reason about relations in a more general sense.

Previous studies of fractions and relational reasoning

Previous researchers have highlighted links between relational reasoning and human higher cognition in general (Halford, Wilson, & Phillips, 2010) and mathematics in particular (Alexander, 2017), even specifically implicating fractions. For example, Richland, Stigler, and Holyoak (2012) argued that conceptual understanding in mathematics depends on relational structure, and specifically point to previous research on learning by analogy. They illustrated their argument for the importance of relational concepts in mathematics with examples of poor reasoning about fractions among college students, such as their difficulty placing rational numbers (fractions and decimals) on a number line, or their failures to correctly answer the question “Which is greater? a/5 or a/8.” Several commentators have pointed out that placing a rational number on a number line requires an understanding of relative magnitudes (Newcombe, Levine, & Mix, 2015; Sidney, Thompson, Matthews, & Hubbard, 2017). Answering the “Which is greater” question, entails several steps that depend on the correct understanding an assignment of numerator and denominator roles: first, the students must correctly assign the unknown, ‘a’, to the role of ‘numerator;’ next, they must recognize that for a constant numerator, the holistic magnitude of the fraction is greater when the denominator is smaller; and finally, they must finally relate the two sets of unknown/denominator to each other.

These theoretical arguments have been bolstered by empirical results. Domain-general relational reasoning measures have been found to predict early mathematics performance in preschoolers (Collins & Laski, 2018) and calculation skill in 5-13 year olds (Fyfe, Evans, Matz, Hunt, & Alibali, 2017), as well as intervention effectiveness in engineering students (Dumas & Schmidt, 2015). Moreover, there is some precedent in cognitive psychology for connecting relational reasoning and symbolic fractions in particular. For example, DeWolf and colleagues (DeWolf, Grounds, Bassok, & Holyoak, 2014) observed greater reaction times for fractions than other types of compositional numbers (multidigit integers, decimals) in a magnitude comparison task. They attributed this difference to greater processing demands created by the greater relational complexity of symbolic fractions’ bipartite structure. However, the bipartite structure of fractions can also facilitate certain aspects of numerical reasoning because it makes the relational aspect visible. DeWolf, Bassok, and Holyoak (2015a) found that that symbolic fractions enabled relational problem solving more than decimals (a representation that privileges magnitude information over relational structure). In another study, DeWolf and colleagues demonstrated that priming with fraction problems facilitated judgements of related multiplication problems (with or without fractions) (DeWolf, Son, Bassok, & Holyoak, 2017).

However, most psychology research on fractions and relational reasoning to date has focused on fractions as a bridge to algebraic reasoning² and has used mathematics domain-specific measures (such as fraction arithmetic performance or relational fraction knowledge), rather than domain-general measures of relational reasoning as predictors. For example, Hurst and Cordes (2018a, 2018b) found that fraction arithmetic performance predicted algebraic reasoning above and beyond rational number magnitude knowledge and decimal arithmetic. DeWolf, Bassok, and Holyoak (2015b) also introduced the construct of relational fraction knowledge and tasks that tap relational fraction knowledge, such as non-calculation questions focused on part-part or part-whole relationships. They found that this relational fraction knowledge explained unique variance in middle-school students’ early algebraic reasoning. They also found that priming with a relational fraction task facilitates algebraic reasoning more than priming with a procedural fraction task in both pre-algebra students and adults (DeWolf, Bassok, & Holyoak, 2016).

The Current Study

However, there is currently no research on whether and to what extent domain-general relational reasoning ability, like that seen in analogy research, is related to fraction knowledge in itself. Given the structural similarity between common fractions and propositional relations, we hypothesized that a common cognitive process might support both domain-general relational reasoning and reasoning about fractions. To test this hypothesis, we used a domain-general assessment of relational reasoning with known psychometric properties, the Test of Relational Reasoning Jr. (TORR Jr.), and a paper-and-pencil test of fraction knowledge, the Fraction Knowledge Assessment (FKA), in two groups of school-age children: 2^nd graders, who have little or no formal instruction with symbolic fractions, and 5^th graders, who have received or are receiving formal instruction with symbolic fractions. Because we expected general mathematics ability, fraction magnitude understanding, and general non-verbal reasoning ability to be important predictors of fraction knowledge, we included measures of these abilities as controls to examine whether relational reasoning predicts unique variance in fraction knowledge above and beyond what is accounted for by these measures.

Methods

Participants

We recruited participants from multiple school districts near a moderate-sized Midwestern city in the United States, including a mix of urban and suburban districts with varying demographics. These data were collected as part of a larger longitudinal study of the development of children’s symbolic and non-symbolic fraction knowledge and how that development is related to a variety of cognitive and noncognitive factors. The data for the current study come from Year 1 of the longitudinal study. In total, 194 second-grade students (mean age = 8.03 years) and 145 fifth-grade students (mean age = 10.95 years) participated. Participation criteria included fluent English production and comprehension and lack of known developmental or learning atypicalities (by parental report). Two participants were excluded from the current analysis because the parents disclosed a learning disability diagnosis (1 ADHD, 1 dyslexia) after initial participation in the study. Not all scores were available for all participants due either to discontinuation due to participant fatigue/non-compliance, or experimenter error (see Tables 4 & 5 for details). Participants received $10 per hour of participation and a small toy per study visit. All study procedures were approved by the IRB (IRB #2016-0665).

Table 4.

Zero-order correlations between measures for 5^th graders

	FKA	Analogy	WJ-III WM	WJ-III SR	WISC BD	WISC Matrix	Non-verbal Factor	WJ-III Mathematics	WJ-III Calc	NLE PAE	Mag. Comp.
FKA	1
Analogy	0.41***	1
WJ-III WM	0.46***	0.4***	1
WJ-III SR	0.29***	0.45***	0.27***	1
WISC BD	0.39***	0.43***	0.50***	0.48***	1
WISC Matrix	0.21***	0.44***	0.41***	0.33***	0.56***	1
Non-verbal Factor	0.38***	0.54***	0.51**	0.73**	0.90***	0.77***	1
WJ-III Mathematics	0.32***	0.27**	0.47***	0.14***	0.29***	0.2***	0.27***	1
WJ-III Calc	0.46***	0.5***	0.53***	0.38***	0.53***	0.4***	0.55***	0.53***	1
NLE PAE	−0.45***	−0.45***	−0.50***	−0.27*	−0.51***	−0.35***	−0.49***	−0.38***	−0.5***	1
Mag. Comparison	0.3***	0.22*	0.30***	0.17**	0.28**	0.19*	0.28**	0.44***	0.41***	−0.3***	1

^*p<.05

^**p<.01

^***p<.001

Table 5.

Second grade regression models for domain-general variables.

	Model 1	Model 2
Age in months	0.223***	0.218***
Nonverbal component	0.356***	0.231**
Auditory Working Memory	0.347***	0.318***
TORR Jr. Analogy		0.252***
N	158	158
R-sq	0.448	0.491
adj. R-sq	0.437	0.477
ΔR2		0.043

The school districts that participants were drawn from met statewide Common Core standards (National Governors Association Center for Best Practices, 2010), and the sequence of math standards with regard to fractions is generally in keeping with most mainstream United States K-12 curricula. In this set of standards, there is no content related to fractions for second graders. Third graders are expected to “develop understanding of fractions as numbers,” fourth graders to “Extend understanding of fraction equivalence and ordering; build fractions from unit fractions; understand decimal notation for fractions, and compare decimal fractions.” The fifth graders in our sample would probably have traversed this content, as well as varying amounts of the content related to the fractions standards for fifth graders: “Use equivalent fractions as a strategy to add and subtract fractions; apply and extend previous understandings of multiplication and division” (National Governors Association Center for Best Practices, 2010).

Procedure

Participants completed assessments in two lab visits on separate days. At the first visit they completed standardized measures of cognitive capacities (WISC and WJ subtests, see below), and at the second visit they completed fraction magnitude comparison and fraction number line tasks, a Fraction Knowledge Assessment, and the TORR Jr. The duration of each visit was about 60 minutes.

Materials

Dependent variable—fraction knowledge.

Fraction Knowledge Assessment (FKA).

The FKA is a pencil-and-paper assessment designed to measure fraction knowledge broadly, including conceptual and procedural aspects of fraction knowledge. Some questions on the FKA also measure fraction magnitude understanding, but others address other interpretations of fractions, such as part-whole, or operator interpretations, which are related but not identical to fraction magnitude. We constructed this instrument using items taken from key national and international assessments, including the National Assessment of Educational Progress (NAEP) and the Trends in International Mathematics and Science Study (TIMSS), and from instruments developed by psychology and mathematics-education researchers (Carpenter, 1981; Hallett, Nunes, Bryant, & Thorpe, 2012). A separate FKA was constructed for each grade, featuring grade-appropriate items (i.e., there was a second grade version of the FKA and a fifth grade version of the FKA). Each version of the FKA contained 41 items, and each had strong internal consistency reliability (second grade FKA Cronbach’s α = .90; fifth grade FKA Cronbach’s α = .92. These estimates are based on the sample included in the current study). The fifth grade FKA included a set of fraction arithmetic problems; the second grade FKA included four fraction arithmetic problems. The difference in the specific items, and in the types of items, between the two versions of the FKA does raise potential issues for alignment. Although the current analysis does not assume vertical alignment, for future projects we are working with experts in item response theory (IRT) and test construction to examine the extent to which vertical alignment is possible between the versions of the FKA.

Relational reasoning measure.

Test of Relational Reasoning Jr. (TORR Jr.).

The TORR Jr. was developed by Alexander et al. (Alexander, Dumas, Grossnickle, List, & Firetto, 2015; Dumas & Alexander, 2016; Jablansky, Alexander, Dumas, & Compton, 2015) specifically to test relational reasoning among children. All items in the TORR are figural (i.e. non-verbal) and do not require any outside information to solve. The entire assessment consists of four subtests of eight items each (total 32 items) designed to test different forms of relational reasoning: analogy, anomaly, antinomy, and antithesis. For the present study, we used only the analogy subtest of the TORR Jr. for several reasons: First, as this study was part of a larger longitudinal study, time constraints prevented administration of the entire TORR Jr. Second, we initially piloted testing with the analogy and antithesis subtests based on their reported psychometric properties (Alexander et al., 2015; Jablansky et al., 2015), and for construct face-validity and consistency with previous research (analogical reasoning tasks are the most widely used measure of relational reasoning). We observed a problematic floor effect for the antithesis subtest in our pilot sample, so we proceeded with only the analogy subtest.

The reported internal consistency reliability for the TORR Jr. (from a sample of 455 children aged 8-14 years old) as a whole is high (Cronbach’s α=.834), and moderate for the analogy subtest alone (Cronbach’s α = .532). The authors suggest the relatively weaker internal consistency values for the subtests may be related to the small number of items (8) per subtest (Jablanksy et al., 2017). Test-retest reliability for the TORR Jr is not currently available (Jablansky, personal communication)³.

Domain-general predictors.

WJ-III subtests: Spatial Relations and Auditory Working Memory.

We used two subtests of the Woodcock-Johnson Tests of Abilities, 3^rd Edition (WJ-III, Woodcock et al., 2001) as domain-general predictors. In the Spatial Relations subtest, participants are shown a whole shape, then asked to select the component shapes necessary to construct the whole from a set of options. Spatial Relations items probe visual-spatial abilities such as visual segmentation and rotation. Scores on this subtest are understood to reflect non-verbal reasoning ability. During the Auditory Working Memory subtest, participants listen to a mixed series of words and digits and then must rearrange them by first saying the words in order and then the numbers. Working memory, and in particular verbal working memory, is known to be an important predictor of mathematics skills (e.g., Formoso et al., 2018). The reported split-half reliability for the auditory working memory subtest is r = .87; the reported reliability for spatial relations it is r=.81 (based on Rasch analysis) (Schrank & McGrew, 2001).

WISC-IV subtests: Matrix Reasoning and Block Design.

We also used two subtests of the Wechsler Intelligence Scale for Children, 4^th edition, (WISC-IV, Wechsler, 2004) to assess general cognitive abilities. In the Matrix Reasoning subtest, children are shown an array of pictures with one missing square and instructed to select the picture that fits the array from five options. Some late items in the Matrix Reasoning task could be solved by analogical reasoning, but many require only pattern recognition, such as recognizing sequences in object size, color, orientation, or identity. In the Block Design subtest, children put together red-and-white blocks in a pattern according to a displayed model. Block Design is timed, and some of the more difficult puzzles award bonuses for speed. These two subtests were chosen because they reflect non-verbal reasoning and spatial abilities, which have been previously found to predict mathematics abilities, and because they contribute to the Performance IQ (PIQ) sub-score of the WISC. The reported test-retest reliability for block design is r =.82 and its internal consistency reliability is r = .86; for matrix reasoning test-retest reliability is r = .83 and internal consistency reliability is r = .89 (Williams, Weiss, & Rolfhus, 2003).

Non-verbal Reasoning Component Scores.

Given the similarity in task demands and hypothesized constructs for Matrix Reasoning, Block Design, and Spatial Relations, we hypothesized that a composite measure could be effectively be used. Therefore, we performed a principal components analysis (PCA), which revealed that all three variables had strong, positive coefficients for the first component. In addition, the first component captured 71% of the variance. We used the resulting component scores as a predictor variable in our regression models. Details of the PCA, including eigenvectors and eigenvalues, can be found in the supplemental material.

Mathematics domain-specific predictors.

WJ-III Subtests: Mathematics Fluency and Calculation.

The Mathematics Fluency subtest is a timed assessment in which participants must correctly answer as many simple (single digit, two operand) written addition, subtraction and multiplication problems as possible within 3 minutes. In contrast, the Calculation subtest is untimed and therefore may provide more information about participants’ numerical reasoning skills than recall of arithmetic facts (which are reflected more in the Mathematics Fluency test). Items on this subtest range from number identification through arithmetic operations (addition, subtraction, multiplication, division), to geometric, trigonometric, and even calculus operations at the high end. Some items on the Calculation subtests may involve fraction arithmetic or other fraction operations (for example, simplifying algebraic expressions). The reported split-half reliability of math fluency is r = .90; calculation split-half r=.86 (Schrank & McGrew, 2001).

Fraction magnitude understanding predictors.

Fraction magnitude understanding is known to be an important component of overall fraction competence (Fazio, Bailey, Thompson, & Siegler, 2014b; Fazio et al., 2016; Hamdan & Gunderson, 2017; Liu, 2018). In order to assess whether relational reasoning predicts fraction knowledge above and beyond what is predicted by fraction magnitude understanding, we included two measures of fraction magnitude understanding as predictors.

Fraction number line estimation task.

The number-line estimation task was modeled on Siegler, Thompson, and Schneider (2011). Participants used a mouse to indicate the position of fraction stimuli on a number line with the end points 0 and 1 in the 0-1 condition, and between 02 and 0-5 in two other conditions. Performance was defined as each participants’ mean percentage of absolute error (PAE), where PAE = (|answer − correct answer|/numerical range), as is typical for these tasks. A smaller PAE indicates greater accuracy.

Fraction magnitude comparison task.

This task was adapted from the task used for adults in a previous study (Binzak et al., 2019). In each trial, participants viewed a screen on which two fractions appeared and were instructed to choose the larger of the two. The fractions included all the non-unit proper fractions with denominators of 2-9. Reaction time and accuracy were recorded on each trial, and a mean RT and accuracy rate were calculated for each participant.

Results

Overall performance

Table 2 displays the means and standard deviations for standardized test scores for both second and fifth graders. Mean performance was well above chance on all experimental tasks. As expected for raw scores, fifth graders scored significantly higher than second graders on all assessments except the FKA. Importantly, the second grade FKA and fifth grade FKA are different instruments, each with age-appropriate items as well as some overlapping (anchor) items. The current results suggest that for our sample, the second grade FKA was easier for the second graders than the fifth grade FKA was for the fifth graders.

Table 2.

Performance on all measures by grade, with independent sample-t-test by grade

	Possible Raw Score	2nd M (SD)	5th M (SD)	t	p
	Range	n = 200	n = 149	df = 348
Spatial Relations	0-81	64.33 (6.85)	69.26 (5.99)	7.03	<.001
Block Design	0-68	32.58 (12.04)	42.79 (11.81)	7.92	<.001
Matrix Reasoning	3-35	20.51 (4.87)	24.75 (4.29)	8.48	<.001
Spatial/Block/Matrix composite	NA	−0.34(0.80)	.45 (.72)	9.50	<.001
Auditory working memory	0-45	19.9 (5.28)	25.27 (5.26)	9.44	<.001
Mathematics Fluency	0-160	44.51 (15.91)	75.32 (21.62)	15.38	<.001
Calculation	0-45	13.43 (3.83)	23.15 (4.93)	20.80	<.001
Number Line PAE	0-1	0.27 (0.09)	0.11 (0.08)	15.50	<.001
Fraction Comparison Accuracy	0-1	0.84 (0.13)	0.93 (0.08)	7.00	<.001
FKA Score	0-1	0.63 (0.21)	0.56 (0.26)	2.58	0.01
TORR Jr. Analogy	0-8	3.7 (1.96)	5.37 (1.63)	7.82	<.001

In addition, examination of performance by item revealed that the second graders were at floor on the fraction arithmetic items (the arithmetic item on which second graders did best yielded only 6% correct responses, and the other items were at 2%, 3% and 0%) as well as items that required advanced procedural knowledge of symbolic fractions. The second graders’ performance on these items is consistent with the fact that they have not yet received formal instruction in fraction procedures. The fifth grade fraction knowledge assessment included many fraction arithmetic problems, and the fifth graders displayed a range of performance on these problems (fraction arithmetic median score = 58.8%) that did not suggest floor or ceiling effects (see also Kalra et al., 2020).

Although we observed a wide range of scores on the standardized assessments, the average scores for both second graders and fifth graders on all subtests were above the expected averages for their respective grades. This likely reflects the self-selection aspect of recruitment (i.e., families with higher income, parental education and familiarity with academic settings were more likely to respond to our recruitment methods).

Correlations

Pairwise correlations among the behavioral measures are presented in Tables 3 and 4. For both grades, all predictors were significantly positively correlated as might be expected due to positive manifold effects and the design of the WJ-III and WISC-IV. Visual inspection of the first column of each table confirms that the TORR Jr. Analogy (and all the other predictors) were significantly correlated with our outcome of interest, the Fraction Knowledge Assessment. Furthermore, as seen in bivariate scatterplots of Figure 2, there appears to be a positive linear relationship between TORR Jr. Analogy score and FKA score in both grades. However, this observed relationship could be due to other shared factors between the TORR Jr. and FKA. For example, if both scores are related to common underlying factors, including more general cognitive abilities, then those common factors would better explain the observed relationship. In the following regression analyses, we controlled for some of the most likely possible factors

Table 3.

Zero-order correlations between measures for 2^nd Graders

	FKA	Analogy	WJ-III WM	WJ-III SR	WISC BD	WISC Matrix	Non-verbal Factor	WJ-III Mathematics	WJ-III Calc	NLE PAE	Mag. Comp.
FKA	1
Analogy	0.49***	1
WJ-III WM	0.53***	0.36***	1
WJ-III SR	0.33***	0.41***	0.38***	1
WISC BD	0.49***	0.45***	0.4***	0.57***	1
WISC Matrix	0.48***	0.47***	0.45***	0.48***	0.52***	1
Non-verbal Factor	0.54***	0.54***	0.50***	0.81***	0.88***	0.79***	1
WJ-III Mathematics	0.46***	0.31***	0.34***	0.33***	0.37***	0.28***	0.41***	1
WJ-III Calc	0.58***	0.38***	0.44***	0.42***	0.44***	0.44***	0.53***	0.65***	1
NLE PAE	−0.54***	−0 29***	−0.33***	−0.10***	−0.28***	−0.24***	−0.26**	−0.31***	−0.47 ***	1
Mag. Comparison	0.49***	0.41***	0.26***	0.32***	0.33***	0.40***	0.43***	0.47***	0.42***	−0.20***	1

^*p<.05,

^**p<.01,

^***p<.001

Figure 2.

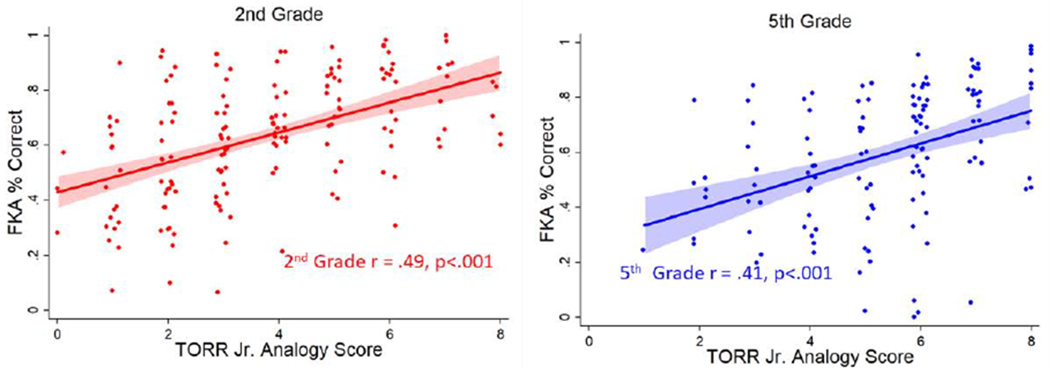
Scatterplot of FKA proportion correct against TORR Jr. Analogy score for second graders (left) and fifth graders (right) with OLS fitted regression lines. Shaded areas represent 95% confidence intervals.

Multiple regression analyses

We conducted a series of two-stage linear regressions to test whether individual differences in relational reasoning predicted fraction knowledge (FKA score) above and beyond individual differences in domain-general cognitive capacities and mathematics-specific facilities. In the first stage of each analysis, we entered the control variables (either domain-general or mathematics-specific). In the second stage, we added the TORR Jr. analogy score. Regression results are reported in Tables 4–8. We report standardized coefficients because they facilitate interpretation of effect sizes. We conducted these regressions separately for 2^nd graders and 5^th graders because 2^nd graders scored systematically lower on the TORR and the raw scores of the standardized assessments, and therefore combining 2^nd and 5^th graders in a regression model would introduce a confound based on grade. We also included age in months because developmental differences within a grade could be a potential confounding variable. Because of the potential overlap between general non-verbal reasoning ability and relational reasoning ability, we retained the non-verbal reasoning factor as a control predictor in all subsequent models.

Table 8.

Fifth grade regression models for mathematics predictors.

	Model 3	Model 4
Age in months	−0.112	−0.105
Nonverbal component	0.329***	0.268**
Math Fluency	0.185*	0.181*
Calculation	0.353***	0.310***
TORR Jr. Analogy		0.155*
N	127	127
R-sq	0.507	0.522
adj. R-sq	0.491	0.502
ΔR2		0.015

Controlling for domain-general cognitive abilities.

Of course, there is an obvious alternative hypothesis for the observed relation between TORR Jr. analogy scores and FKA scores: it could be that a common domain-general faculty (such as non-verbal reasoning ability or working memory) is in fact driving both. To test this hypothesis, we examined the relationship between TORR Jr. analogy and FKA scores while statistically controlling for domain-general predictors, specifically the non-verbal reasoning factor and a measure of auditory working memory. These results are shown in Model 1 and Model 2 of Tables 5 and 6. For both second graders and fifth graders, TORR analogy remained a significant predictor of FKA scores, contributing unique variance. Age in months was also an important predictor of FKA score for second graders but not for fifth graders.

Table 6.

Fifth grade regression models for domain-general variables.

	Model 1	Model 2
Age in months	−0.076	−0.072
Nonverbal component	0.368***	0.258**
Auditory Working Memory	0.374***	0.341***
TORR Jr. Analogy		0.230**
N	127	127
R-sq	0.435	0.471
adj. R-sq	0.421	0.454
ΔR2		0.036

Controlling for mathematics ability and knowledge.

Next, we considered the hypothesis that TORR Jr. analogy score might be accounted for by general mathematical ability. In previous studies with 5^th grade children, similar to our older cohort (Hansen et al., 2017; Ye et al., 2016) overall mathematics ability has been demonstrated to be an important predictor of fraction knowledge. It might therefore be the case that TORR predicts fraction knowledge because mathematics ability mediates the relationship between them. For both grades TORR Jr. analogy remained a significant predictor of FKA scores when controlling for WJ-III Mathematics Fluency and Calculation scores, and the additional variance explained by including TORR Jr. analogy made the fit of Model 3 better than that of Model 4 (Tables 7 & 8). However, we note that the effect size and variance explained by the TORR Jr. is attenuated in fifth graders compared to second graders.

Table 7.

Second grade regression models for mathematics predictors.

	Model 3	Model 4
Age in months	0.140*	0.142*
Nonverbal component	0.339***	0.222**
Math Fluency	0.137	0.123
Calculation	0.298***	0.275***
TORR Jr. Analogy		0.240***
N	158	158
R-sq	0.471	0.509
adj. R-sq	0.457	0.493
ΔR2		0.038

Controlling for fraction magnitude understanding.

Finally, we considered whether TORR Jr. analogy could explain performance on the FKA above and beyond fraction magnitude understanding (as measured by fraction number line estimation and fraction magnitude comparison). For both second and fifth graders, TORR Jr. analogy remained a significant predictor. Indeed, for 5^th graders, it had an effect as large as fraction comparison accuracy (see Models 5 and 6, Tables 9 and 10). However, for fifth graders, the additional variance explained by TORR Jr. was small compared to second graders.

Table 9.

Second grade regression models for fraction magnitude understanding.

	Model 5	Model 6
Age in months	0.107	0.112
Nonverbal component	0.296***	0.237**
Number Line PAE	−0.381***	−0.358***
Fraction Comparison Accuracy	0.270***	0.244***
TORR Jr. Analogy		0.145*
N	129	129
R-sq	0.546	0.56
adj. R-sq	0.531	0.542
ΔR2		0.014

Table 10.

Fifth grade regression models for fraction magnitude understanding.

	Model 5	Model 6
Age in months	−0.107	−0.112
Nonverbal component	0.300***	0.231**
Number Line PAE	−0 414***	−0.370***
Fraction Comparison Accuracy	0.155*	0.162*
TORR Jr. Analogy		0.169*
N	110	110
R-sq	0.491	0.51
adj. R-sq	0.471	0.486
ΔR2		0.019

Discussion

We have demonstrated that domain-general relational reasoning ability is related to children’s competence with symbolic fractions, suggesting that understanding the relational structure of fractions depends on—or at least can be addressed with—the ability to reason about relations more generally. Specifically, we found an association between a standardized measure of domain-general relational reasoning ability and performance on a paper-and-pencil test of fraction knowledge, in both second graders and fifth graders. For both age groups, the effect size of relational reasoning (as seen in the standardized beta coefficients) as a predictor of fraction knowledge was modest by Cohen’s guidelines (Cohen, 1988, 1992). The association between relational reasoning ability and fraction performance could not be explained by general non-verbal reasoning, demonstrating that relational reasoning, in particular, is important for fraction understanding, above and beyond other measures of other types of fluid reasoning. Relational reasoning ability remained a significant predictor even when we controlled for participants’ understanding of fraction magnitudes, suggesting that magnitude and relational conceptions of fractions may be complementary, both necessary for fraction mastery. In second graders, but not fifth graders, relational reasoning also explained variance in fraction knowledge above and beyond calculation ability and arithmetic fact knowledge. In contrast, arithmetic fact knowledge (mathematics fluency) contributed to fraction knowledge above and beyond relational reasoning and calculation ability for fifth graders, but not for second graders.

One compelling explanation for this difference between age groups is based on the difference in formal instruction with fractions between the groups. Within our sample, as in the U.S. more generally, fifth graders have usually received at least 2 years of instruction with symbolic fractions, whereas second graders have usually received little or no formal instruction with symbolic fractions. The first fraction standards that appear in the Common Core (for third graders) relate to a conceptual understanding of fractions. Fraction arithmetic is not mentioned in the standards until fifth grade.

Interpretation of Results

Why would (relative) expertise with symbolic fractions be associated with a weaker relation between domain-general relational reasoning ability and symbolic fraction knowledge? In general, experts’ performance in a domain is less strongly associated with domain-general cognitive abilities than novices’ performance in the same domain. This has been observed so often for general intelligence (conceptualized as Spearman’s g) that it referred to as “Spearman’s Law of Diminishing Returns (SLODR) (Blum & Holling, 2017). For example, less skilled players’ (~novices) performance is more strongly predicted by g than more skilled players’ (~experts) performance. In the domain of chess, expertise is known to be associated with not only increased domain knowledge, but also with more effective organization of that knowledge (Gobet & Simon, 1998, 2000; Schneider, Gruber, Gold, & Opwis, 1993). Presumably, as experts’ knowledge of the domain becomes crystallized, performance becomes more dependent on recall of stored knowledge than de novo reasoning in each situation.

Thus, fifth graders’ greater knowledge of mathematics generally, and of symbolic fractions in particular, may explain the difference in the role of relational reasoning between second and fifth graders. It may be that fifth graders are better able to leverage their mathematics fact knowledge to help them solve fraction arithmetic problems because they recognize symbolic fractions as a subset of the number system they are already familiar with (Siegler, Thompson, & Schneider, 2011). Similarly, since arithmetic knowledge predicts performance on fraction computation problems, it is likely that they have memorized certain arithmetic facts about symbolic fractions, particularly highly frequent/familiar fractions (Hecht, Close, & Santisi, 2003). As their FKA performance suggests, fifth graders have learned and are able to use procedures to solve fraction problems, consistent with the timing and sequence of Common Core standards. It is possible that once they learn these procedural strategies and arithmetic facts, they may be less dependent on relational consideration of the fractions than before learning them. In contrast, second graders, lacking fraction arithmetic fact fluency or fraction procedural strategies (as seen in their FKA performance), must grapple with the fraction problems using their general cognitive capacities; of these, relational reasoning may be particularly apt for the domain of symbolic fractions. However, this is speculation, and the results of the current study cannot confirm or refute these hypotheses. Future research, including structural equation modeling and other latent variable approaches, that attempts to measure and isolate the effect of procedural fraction knowledge as well as relational reasoning ability on overall fraction competence could clarify this issue.

Limitations

Our future work will aim to address some of the limitations of the current study. For example, we would like to confirm the direction of causality and rule out additional possible confounds in the relation between relational reasoning and fraction knowledge. The data from the current study were collected as part of the first wave of data in a longitudinal study. When coupled with later time points, we will be able to chart growth curves and compare forward and backward correlational models to see which better accounts for the relation we see in our data. Future experimental studies might further unpack these causal relations by assigning participants to relational reasoning training groups to be contrasted with controls. Previous studies have shown that it is possible to improve relational reasoning skills (Mackey, Hill, Stone, & Bunge, 2011; Mackey, Park, Robinson, & Gabrieli, 2017), but it is unclear how far these training effects would transfer. Examining construct validity would also be desirable, for example, by including additional subtests of the TORR Jr. or different (e.g. experimental) measures of relational reasoning, especially given the low reliability of the analogy subtest alone. (Indeed, the low reliability of this subtest attenuate correlations with other measures in the current study.) It would be informative to know whether it is analogy alone or relational reasoning more broadly construed that is most important for fraction competence. Finally, although the current study was not designed to address this question, future item-based analysis fraction knowledge assessments could clarify what types of fraction knowledge depends most on relational reasoning.

Broader Implications

We may now be able to translate basic cognitive science findings on improving relational reasoning in general into methods that specifically improve fraction learning, based on the understanding that relational reasoning plays a role in fraction understanding. For example, comparison, contrast, relational language, and structural alignment are known to improve relational learning (Christie & Gentner, 2010, 2014; Gentner, 2010; Kurtz, Boukrina, & Gentner, 2013), and instructional methods that use these techniques may prove beneficial if adapted for use with fractions. However, there is much work yet to be done to determine how best to translate the findings from the lab to the classroom; for example, although introducing fraction division by analogy to whole number division has shown some benefits, some adjustments may need to be made to this approach before it is more widely effective (Sidney & Alibali, 2015; Sidney & Alibali, 2017).

More broadly, these results suggest a role for considering relational complexity in curricular knowledge components for mathematics. Relational complexity can be defined in terms of the number of entities that must be represented simultaneously to define or solve a problem (Halford, Wilson, & Phillips, 1998; Livins & Doumas, 2015). For example, according to Halford et al.’s relational complexity metric, either of the constituent gas laws (Charles’ Law V/T = k or Boyle’s Law PV = k) would have a lower level of complexity than the combined ideal gas law (PV = nRT)⁴ because the ideal gas law requires the relations among four entities to be maintained in working memory rather than only three terms in each of the named laws ( Halford et al., 1998; Halford et al., 2010). From this perspective, reasoning about whole numbers or performing whole number arithmetic differs from reasoning about fractions or fraction arithmetic because fractions are more relationally complex than whole numbers: fractions have a bipartite form, therefore at least binary complexity; whole numbers have a simpler, unary form, therefore a lower level of relational complexity (assuming other aspects of the problem or concept to be the same). Note that this would be true regardless of whether we considered fractions from a part-whole perspective or from a magnitude perspective which requires thinking about the relative size that emerges from comparing the sizes of the components. Behavioral and neuroimaging findings confirm that, like other higher cognitive functions including executive function, relational reasoning ability increases across developmental time (Bazargani, Hillebrandt, Christoff, & Dumontheil, 2014; Crone et al., 2009; Dumontheil, 2014; Krawczyk, Holyoak, & Hummel, 2004; Rattermann & Gentner, 1998;) and that increasing relational complexity increases processing demands (Cocchi et al., 2014; Xiao et al., 2014).

However, to date no work has been done to apply or validate a measure of relational complexity specific to content in the in the mathematics curriculum. The items we refer to here could be labeled “knowledge components” as used in the Knowledge-Learning-Instruction framework (Koedinger, Corbett, & Perfetti, 2012). There are multiple ways to operationalize“knowledge components” in mathematics, but one simple and practical way would be to consider each standard detailed by the Common Core (National Governors Association Center for Best Practices, 2010) as a “knowledge component.” Given that there are multiple ways to look at different mathematical constructs, measuring relational complexity may not always be straightforward, but several general frameworks for measuring relational complexity exist (Feldman, 2000; Halford, Andrews, & Jensen, 2002; Halford, Wilson, & Phillips, 1998), and adapting them to mathematics does not seem to be an insurmountable challenge. Characterizing relational complexity stands to help guide choices in instructional strategy and curriculum design to make knowledge components developmentally appropriate in terms of the relational complexity typical students at a given age can handle. It can also help educational practitioners recognize the need for appropriate scaffolding (for example, reducing working memory load) when introducing more complex knowledge components.

Beyond quantifying relational complexity, systematic identification of the specific relational structures in curricular knowledge components could facilitate teaching and learning of these concepts. For example, if the relational structure of the knowledge component is known, then the instructor or curriculum designer can choose a familiar concept with a similar relational structure for learning by analogy. However, in cases where a familiar analog is not available—as when the relational structure is one the learner has not encountered before—basic research on induction of relational structures (Gick & Holyoak, 1983; Goldwater, Don, Krusche, & Livesey, 2018; Halford & Busby, 2007; Halford, Bain, Maybery, & Andrews, 1998) may provide insights for new instructional strategies.

The current results demonstrate the importance of relational reasoning for fraction understanding, and as a corollary, point to importance of recognizing relational complexity and relational structures in the mathematics curriculum. To some extent, these issues have been explored in the context of early (preschool) mathematics (Fyfe et al., 2017; Miller, Rittle-Johnson, Loehr, & Fyfe, 2016; Rittle-Johnson, Fyfe, Loehr, & Miller, 2015); the current study suggests that it would be appropriate to extend this trend to grade-school mathematics. Addressing relational structures and relational complexity in instructional strategies and curriculum designs could provide a new route to improving teaching and learning of these concepts. For fractions in particular, helping students engage with the relational interpretations could complement existing successful magnitude-based instructional methods and lead to greater overall mastery of fractions.

Table 1.

Demographic characteristics of sample

	Second grade	Fifth grade
Sex: Female	38%	42%
Ethnicity: Hispanic (vs. non-Hispanic)	9%	17%
Race:
Caucasian/White	68%	69%
African-American/Black	3%	5%
Asian	3%	1%
Multiracial	9%	13%
Not reported	17%	12%

Highlights.

• Relational reasoning ability, as measured by the Test of Relational Reasoning Jr. (TORR Jr.) was correlated with performance on a test of fraction knowledge in both second graders and fifth graders

• Relational reasoning remained a significant predictor of fraction knowledge even when controlling for general non-verbal IQ and measures of fraction magnitude understanding

• For second graders, relational reasoning remained a significant predictor when controlling for general calculation ability and arithmetic fact knowledge, but this was not the case for fifth graders.