Abstract
Tractions exerted by cells on their surroundings play an important role in many biological processes including stem cell differentiation, tumorigenesis, cell migration, cancer metastasis, and angiogenesis. The ability to quantify these tractions is important in understanding and manipulating these processes. Three-dimensional traction force microscopy (3DTFM) provides reliable means of evaluating cellular tractions by first measuring the displacement of fluorescent beads in response to these tractions in the surrounding matrix, and then using this measurement to compute the tractions. However, most applications of 3DTFM assume that the surrounding extra-cellular matrix (ECM) is non-fibrous, despite the fact that in many natural and synthetic environments the ECM contains a significant proportion of fibrous components. Motivated by this, we develop a computational approach for determining tractions, while accounting for the fibrous nature of the ECM. In particular, we make use of a fiber-based constitutive model in which the stress contains contributions from a distribution of nonlinear elastic fibers and a hyperelastic matrix. We solve an inverse problem with the nodal values of the traction vector as unknowns, and minimize the difference between a predicted displacement field, obtained by solving the equations of equilibrium in conjunction with the fiber-based constitutive model, and the measured displacement field at the bead locations. We employ a gradient-based minimization method to solve this problem and determine the gradient efficiently by solving for the appropriate adjoint field. We apply this algorithm to problems with experimentally observed cell geometries and synthetic, albeit realistic, traction fields to gauge its sensitivity to noise, and quantify the impact of using an incorrect constitutive model: the so-called model error. We conclude that the approach is robust to noise, yielding about 10% error in tractions for 5% displacement noise. We also conclude that the impact of model error is significant, where using a nonlinear exponential hyperelastic model instead of the fiber-based model, can lead to more than 100% error in the traction field. These results underline the importance of using appropriate constitutive models in 3DTFM, especially in fibrous ECM constructs.
Keywords: Traction force microscopy, Inverse problem, Fiber-based model, Model error
1. Introduction
Cells interact with their surroundings mechanically by exerting and sensing mechanical stimuli through the process of mechanotransduction [1, 2]. Mechanotransduction plays an important role in physiological and pathological processes like stem cell differentiation, tumorigenesis, cell migration, cancer metastasis, and angiogenesis [3, 4]. A fundamental component of mechanotransduction is the traction exerted by a cell on the extra-cellular matrix (ECM) that surrounds it. This traction can be used by the cell to sense the stiffness of the ECM and to migrate within the ECM [5, 6]. In order to understand how tractions influence these biological processes, it is crucial to quantify the spatial distribution of the traction with high resolution, and to correlate it either causally or statistically with a biological process of interest [7]. For example, the asymmetry in the traction field between the front and the rear of a migrating cell has been found to correlate with its speed and direction [8]; the anisotropy and polarity in the traction field plays an important role in cancer cell invasion [9].
Over the years, many innovative methods have been developed to estimate the tractions exerted by cells. The reader is referred to several excellent review articles written on this topic for a comprehensive description [10, 7, 11, 12]. Among these, three-dimensional traction force microscopy (3DTFM) has the advantage that it can be used to measure tractions exerted by cells in their natural state [13]. In 3DTFM, cells cultured in a synthetic ECM seeded with fluorescent beads are imaged using confocal microscopy. These images are used to determine the geometry of the cell and the locations of the beads. This data corresponds to the stressed state of the cell-matrix environment, since the cell has grown through the ECM, exerting tractions through focal adhesion complexes. The mechanical connection between cell and ECM is broken when the cell is chemically lysed and the ECM relaxes to an unstressed state. Another set of images of the ECM and the beads is acquired after this relaxation. Thereafter, the displacement of the beads is determined by applying image cross-correlation techniques to ECM images acquired in the stressed and the unstressed state.
Given the measurements of the cell geometry in the stressed state, the displacement of the beads, and a model for the stress-strain behavior (constitutive model) for the ECM, there are several ways in which cellular tractions may be recovered. The simplest approach is to extend the measured ECM displacements up to the surface of the cell, and use this field to compute strain, stress and tractions [14, 15, 16, 17]. This approach is simple, however, it involves extrapolating displacements from locations close to the cell surface to the surface itself, which may introduce errors, especially since the displacements tend to decay rapidly away from the cell surface. Another approach is to model cellular tractions as distributed volumetric forces confined to a small region outside the cell, and to determine these tractions such that the difference between the predicted and measured bead displacements is minimized [18]. The main drawback of this approach is that surface tractions are approximated by distributed volumetric forces, which may not be justified if those forces are distributed over a significant volume.
Another approach to determining cellular tractions, and the one considered in this paper, is to create a mechanical model for the ECM and apply tractions at the cell-ECM interface such that the predicted bead displacements are close to the measured displacements [13, 19, 20, 21, 22]. This approach circumvents the need to extrapolate measured displacements, and does not model tractions as diffuse body forces. It does, however, require an accurate measurement of the cell geometry and the solution of an inverse problem to determine tractions. Initially, this approach was applied while assuming infinitesimal strains and without accounting for the differences in the geometry of the cell in the stressed and unstressed states [13]. In [23], this approach was extended to finite deformations for a Neo-Hookean and a Blatz (exponential) constitutive model for the ECM, while assuming that the geometry of the cell in the reference state was known. (However, the cell geometry in the reference configuration is typically unknown, since it is difficult to locate the cell surface after cell lysis.) In [24] the requirement of knowing the cell geometry in the relaxed state was released as the finite deformation problem was reformulated in the current configuration. This method was then applied to compute the traction exerted by 3T3 fibroblast cells in a dextran-based hydrogel.
In this manuscript we further extend the approach described above by applying it in conjunction with a constitutive model for the ECM that specifically accounts for its fibrous microstructure. Our work is motivated by the fact that a large number of TFM studies are conducted in gels with a fibrous microstructure [15], such as collagenous gels and matrigels, and for these gels a simple phenomenological model may not suffice. Our constitutive model for the gel includes two components for the strain energy: one from a collection of fibers that are assumed to be distributed isotropically in the reference configuration, and another from a background matrix that is Neo-Hookean hyperelastic. Moreover, the fibers are assumed to display an exponential stress-stretch response, and the fibers and the matrix together are assumed to undergo affine deformations. That is, the strains in both the fibers and the matrix are equal to the macroscopic strain applied to the composite material. Note that it is common to make the affine assumption for fibrous materials [25, 26].
In addition to extending 3DTFM to fibrous gels, we also quantify the model error that could be introduced in this approach. In particular, we consider the following question: assuming that the true behavior of the ECM is represented with the fiber-based constitutive model, what is the error that is introduced if an incorrect model is used its place? In particular, if an exponential (e.g., Blatz model [27, 28]) or a linear (Neo-Hookean [29]) phenomenological model is used. In both cases we find that the errors are significant and can be explained by the inability of these models to capture changes in the ECM stiffness that are caused by the realignment of fibers along the direction of the principal stretch. For the Neo-Hookean model these errors can also be attributed to its inability to model nonlinear elastic response.
We are not aware of any other studies that account for the fibrous microstructure of the ECM while estimating cellular surface tractions. In [30], the authors used a simplified fiber-based model and demonstrate how cellular tractions could lead to fiber realignment. However, they do not develop techniques to solve the 3DTFM problem. In [18], the authors do solve the 3DTFM problem with a fiber-based model; however as discussed earlier, they model the tractions as a distributed volumetric force that is spread over a distance that is of the same order as the cell diameter. In contrast, we model cellular tractions for what they are.
The organization of the remainder of this manuscript is as follows. In Section 2, we present a mathematical formulation of the problem of determining cellular tractions for an ECM with fibrous microstructure, and develop efficient techniques for solving it. We also introduce two phenomenological hyperelastic models, which will be used to study the effect of model error. In Section 3, we present numerical results obtained using the computational methods developed in Section 2. In particular, using real cell geometries and synthetic traction fields, we estimate the sensitivity of our fibrous 3DTFM to noise. We also quantify the error introduced by not accounting for the fibrous microstructure of the ECM and explain the origins of this error. We end with conclusions in Section 4.
We conclude this section with the following note. In the field of biomechanics and mechanobiology, the techniques used to estimate cellular tractions have been referred to as “traction force microscopy (TFM).” We take exception to this nomenclature. We believe that “traction microscopy (TM)” alone is sufficient, and more importantly, accurate, since there is no “traction force” in mechanics. Given this, from here on in this manuscript we refer to “traction force microscopy” as “traction microscopy.”
2. Problem Formulation
We pose the problem as a non-linear source identification problem, where we minimize the difference between a predicted and a measured displacement field. The predicted displacement is driven by the unknown tractions, and is determined by solving the equations of equilibrium for the ECM posed in the current configuration. The stress-strain response of the ECM is dictated by the choice of the appropriate constitutive model. The choices include a fiber-based model [31], a phenomenological model with an exponential stress-strain response [27, 28, 32], and the Neo-Hookean model [29]. In particular, all the three models are assumed to be compressible, since water may filtrate in or out of the ECM thereby changing its volume [18].
2.1. Forward Problem and Constitutive Models
The strong form of the equations of equilibrium is given by
| (1) |
| (2) |
| (3) |
Here Ω is the volume occupied by the ECM in the current configuration, ∂Ωt is the boundary over which tractions are applied, that is the cell-ECM interface, ∂Ωg is the boundary over which displacement data is prescribed. Further, T is the Cauchy stress tensor, n is the unit outward normal on a given boundary, t is the traction field, and g is the prescribed Dirichlet data.
Fiber-based model.
The equations above need to be supplemented by constitutive models that link the Cauchy stress to appropriate measures of strain. We consider a constitutive model that is motivated by fibrous nature of the ECM. In particular, we assume that the ECM is comprised of a collection of elastic fibers embedded in a hyperlastic matrix. For simplicity, we assume that the orientations of these fibers are uniformly distributed in the reference configuration, although more general types of distribution can be accounted for [26, 33]. We further assume that the fibers and the matrix are firmly bonded and the composite material undergoes affine deformations.
Under these conditions, the strain energy density for the ECM is given by
| (4) |
| (5) |
| (6) |
In the above expressions, Wm is the strain energy density for the isotropic Neo-Hookean matrix, μ and λ are the two Lame constants at small strains, and Wf is the strain energy density for the fibers, where κ characterizes the product of the fiber density with the initial (small strain) stiffness of a fiber, and γ is a nonlinear parameter describing the exponential hardening rate of a fiber as it is stretched. Moreover, I1 = tr(B) = tr(C), where B = FFT and C = FTF are the left and right Green-Lagrange stretch tensors, respectively, J = det(F), and F is the deformation gradient tensor. Further, λf = ∣FM∣ denotes the stretch of the fiber, where M = [sinθcosϕ, sinθsinϕ, cosθ]T is the unit vector along the fiber orientation in the reference configuration. Note that the evaluation of the strain energy density (6) at each material point involves computing an integral over the surface of a unit sphere S (θ ϵ [0, π], ϕ ϵ [0, 2π]), where each point on S represents a unique fiber direction. More details on the derivation of equation (6) can be found in [31].
Then, the Cauchy stress for the ECM is given by
| (7) |
| (8) |
| (9) |
Note that the surface integrals involved in equation (6) and (9) are computed by discretizing the surface of S with 808 triangular elements and employing linear finite element interpolations. This number was found to be sufficient to guarantee convergence [31]. In particular, we assume that fibers are unable to sustain compressive loads [26, 33], and therefore in (6) and (9) we include contributions only from fibers for which λf ≥ 1. A few comments about the material response predicted by this model:
At small strains the distribution of the fibers is isotropic. As a consequence, the material response is isotropic and is determined by the parameters λ, μ and κ.
At finite strains, the distribution of the fibers is not isotropic. In general, in the current configuration the fibers rotate towards the direction of the maximum principal stretch, thereby increasing the fiber density along this direction and reducing it in other directions. As a consequence, it can lead to hardening or softening behavior of the material along different directions.
Given this, in a uniaxial tension test, we can anticipate a nonlinear elastic effect, that is an increasing tangent modulus, due to the reorientation of the fibers along the axis of stretch. Additionally, we can expect another contribution to this nonlinear effect from the exponential stress-stretch response of the fibers.
Since fibers only contribute to the overall mechanical response when they are stretched (λf > 1), the composite material is expected to exhibit distinct behaviors under tension and compression, being much stronger under the former than the latter.
Phenomenological models.
We consider two other constitutive models where the fibrous microstructure is not explicitly represented. These include the Blatz model (also referred to as the Veronda-Westmann or the Fung model [27, 28, 32]), where the strain energy density and the corresponding Cauchy stress are given by
| (10) |
| (11) |
This model contains three material parameters which include the two Lame parameters at small strain, λ and μ, and another parameter γ which describes the exponential hardening rate of the material response at large deformations. We remark that while this model is capable of exhibiting a nonlinear elastic behavior at large strains, it does not account for the effects of fiber reorientation.
Finally, we also consider the standard Neo-Hookean model, where the strain energy density function and the Cauchy stress are given by equation (5) and (8), respectively. Note that while this model uses measures of strain that are appropriate for finite or large strains, it does not include any type of material nonlinearity in the stress-strain response.
Weak form.
We solve the equations of equilibrium (1)-(3) using the finite element method. For this, we work with the weak form of these equations which is given by: find such that
| (12) |
where
| (13) |
| (14) |
The function spaces and in the above equations are defined as
| (15) |
| (16) |
and H1 is the Sobolov space of square-integrable functions with square-integrable derivatives.
In equation (13), the dependence of the Cauchy stress on the displacements (through F) and the set of material parameters β is made explicit through its arguments. In particular, we note that material points in the reference configuration, denoted by X, are related to material points in the current configuration, denoted by x, through the displacement field via,
| (17) |
| (18) |
| (19) |
| (20) |
This provides a simple expression linking the deformation gradient, which is used to define the Cauchy stress in (13), to the displacement vector in the current configuration u, which is the unknown field we solve for. A similar approach of solving finite-strain hyperelasticity problems in the current configuration is described in [34, 35].
We solve the weak form (12) numerically by approximating the infinite-dimensional functions space by their finite-dimensional counterparts. In particular, we make use of the finite element basis functions for linear tetrahedral finite elements. This leads us to a set of nonlinear equations that can be solved using the Newton-Raphson method after constructing the consistent tangent.
2.2. Inverse problem
Following the standard procedure in traction microscopy, we assume that the ECM is seeded by a dense collection of fluorescent beads and the displacement of these beads, denoted by , in response to the cellular tractions has been measured. From this noisy measurement we wish to recover the traction exerted by the cell. We do this by computing the tractions that will generate displacements that best match the measured displacements, under the constraint that the predicted displacements satisfy the equations of equilibrium for the ECM characterized by a specified constitutive model. The optimal traction field is given by
| (21) |
The first term in the equation above is the data mismatch term. It is a measure of the difference between the measured and predicted displacement field (denoted by uk) at the k-th bead location. This displacement is related to the traction field through (12). The second term is a smooth version of the total variation (TV) regularization, which penalizes large changes in the traction along the cell surface without regard to their spatial gradient. Since we expect the traction to vary significantly as we move from the center of the cell to one of its protrusions, this insensitivity of TV to spatial gradients is particularly useful in traction microscopy. The parameter α is the regularization parameter which determines the importance of the regularization term in relation to the data mismatch term, and c is a smoothness parameter that ensures that the derivative of the regularization term is continuous when ∇st = 0. Finally the ∇s operator is the surface gradient operator such that ∇st = ∇t(I−n⊗n), keeping in mind that n denotes the unit outward normal to the cell surface. We note that for a given value of the traction field, t, different choices for the constitutive relations lead to different expressions for the Cauchy stress in (13), and thus, different predicted displacement fields. Therefore, we expect the optimal traction field that is recovered to vary with the choice of the constitutive model.
Gradient-based approach.
We solve the optimization problem defined in (21) using a gradient-based approach, L-BFGS [36], where for a given traction field t and its variation δt, we require an efficient method for computing the variation of π. Following [23], we derive this expression through the use of a Lagrangian defined as,
| (22) |
Here is the Lagrange multiplier field that enforces the constraint of the equation of equilibrium in the ECM, that is, equation (12). When the displacement field u that appears in the definition of L satisfies this constraint, then from the definition of L we note that (a) , and (b) . These two results together imply that,
| (23) |
Here for a given function M that depends on the field v, DvM ∙ δv denotes the Gateaux derivative,
| (24) |
Setting the first term on the right hand side of (23) to zero yields an equation for λ:
| (25) |
where the operator on the left hand side of (25) is the linearization of the original operator in (13) about the solution u, that is,
| (26) |
It is evident from (25) that the equation for the Lagrange multiplier is driven by the data mismatch term.
Returning to (23), and with λ given by the solution of (25), we have
| (27) |
This leads us to the result that variation in π in the direction of δt can be determined by first solving (12) for u, then solving (25) for λ, and finally using λ, t and δt in (27). Since the expression for λ is independent of δt, this approach provides an efficient means to compute the variation along different directions, and hence to compute the gradient vector for the objective function. Similar strategies of computing the gradient vector have been used to solve the inverse problems for the spatial distribution of material parameters (e.g., [37, 38, 39]).
In practice, we work with finite-dimensional counterparts of these fields, and in this manuscript we have discretized all these fields using linear finite element basis functions. When initializing the inverse problem, we avoid biasing the solution by setting the initial guess for the traction field to be 0. The value of the objective function, π (see (21)), along with its gradient, equation (27), serve as the input for the L-BFGS optimization procedure, which returns an updated guess for the traction field and the entire process is repeated until convergence. Finally, note that the traction field and its variations are defined only on the interface between the cell and the ECM, while all the other functions are defined in the ECM volume.
3. Results
In this section we perform numerical tests to verify the computational methods for traction microscopy with a fiber-based model. We quantify the effects of both experimental noise and model error on our ability to accurately recover tractions, where model error refers to inaccuracy associated with the use of an incorrect material model.
More specifically, we assume that the true mechanical behavior of the ECM is represented by the fiber-based model. Given this, and a chosen traction field, we compute the true displacements at the bead locations. Then we add noise to these displacements to mimic the measured bead displacements in the experiment. These displacements are used to determine the traction field by solving the inverse problem, while using the three different constitutive models (fiber-based, Blatz and Neo-Hookean). The difference between the recovered and the true tractions contains useful information. In particular, for the traction determined using the fiber-based model, it represents an estimate of the effect of noise in traction microscopy. For the tractions determined using the Blatz and Neo-Hookean models, it provides an estimate of the error induced by an incorrect choice of the constitutive model - the so-called model error.
In this work, we perform numerical tests on two different cell geometries. The geometric models for these cells, seen in Fig. 3 and Fig. 6, are generated by meshing a series of Z-stack microscopy images using SimModeler software [40]. We have a set of chosen tractions for each cell, made to replicate typical experimental measurements, that are used in the creation of synthetic data and in the error analysis. In particular, the traction field is applied such that its magnitude is maximum at the cell protrusions, and decreases progressively towards the center of the cell [13, 24]. Moreover, the traction field is roughly pointed to the center of the cell, in order to simulate the typical behavior of a contractile cell.
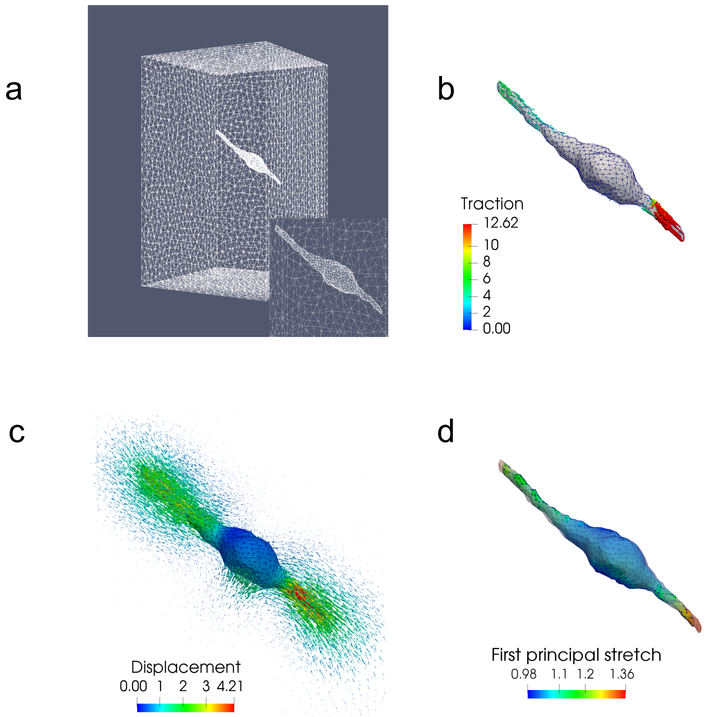
Figure 3:
Problem setup for a 3T3 cell. (a) Finite element mesh used for this problem, with the inset showing mesh refinement on the cell surface. (b) Simulated tractions applied to the cell, which are concentrated on the two long protrusions. (c) Displacement field generated by these tractions, using the fiber-based constitutive model. The magnitude of the displacement field on the cell surface is also color coded. (d) First principal stretch at every point on the cell surface. The surface of the cell in the reference configuration is displayed as a semi-transparent outline around the current configuration.
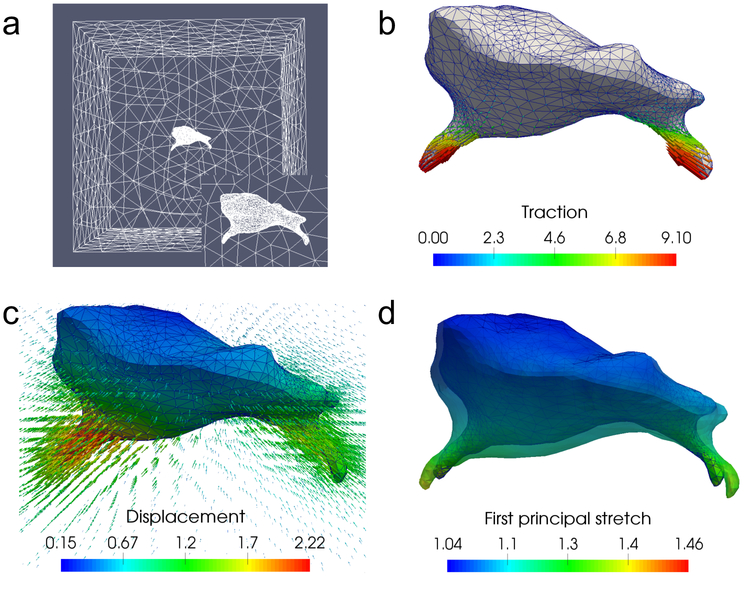
Figure 6:
Problem setup for a microglial cell. (a) Finite element mesh used for this problem, with the inset showing mesh refinement on the cell surface. (b) Simulated tractions applied to the cell, which are concentrated on the two long protrusions. (c) Displacement field generated by these tractions, using the fiber-based constitutive model. The magnitude of the displacement field on the cell surface is also color coded. (d) First principal stretch at every point on the cell surface. The surface of the cell in the reference configuration is displayed as a semi-transparent outline around the current configuration.
3.1. Problem Setup
Creating Synthetic Data.
We generate displacement data by using the given geometries and applying chosen traction fields to the cell surfaces; solving a forward problem using these tractions allows us to compute a displacement field throughout the ECM surrounding the cells. For both cell geometries, we use the fibrous model for the ECM when solving the forward problem.
We determine the values of the material parameters for the fibrous model, needed for the forward problem, through curve fitting. More specifically, we find the parameter values that produce a stress-stretch curve in uniaxial tension that best matches the experimental data of [41]. These parameters are assumed to be uniform throughout the ECM, and are used for both cell types. We repeat this process for the two phenomenological models, since we require the material parameters of these models to solve the inverse problem and quantify model error. The stress-stretch curves of best fit for all th. three models, as well as the associated material parameters, are shown in Fig. 1. For each of the three models, we choose the material parameters in such a way that the material has a Poisson’s ratio of 0.4 at small strains to enforce compressibility. Note that this choice is somewhat arbitrary, due to the lack of experimental data. For any future experimental work on 3D traction microscopy (TM) in fibrous gels, measurements should be made to adequately calibrate this parameter. In this study we use the same value of the initial Poisson’s ratio to guarantee meaningful comparisons among the three models. Further, as will become evident below, the differences we observe among the models can be attributed to the realignment of fibers. Since fiber realignment is expected to occur for any value of Poisson’s ratio, expect these differences to persist for different values of the initial Poisson’s ratio. Finally, note that we only make use of the data prior to fiber damage for the curve fitting, since none of our current models can capture this effect. It is possible to account for the damage of fibers following the work of [42]; however, this is beyond the scope of this work and will be pursued in future studies.
Figure 1:
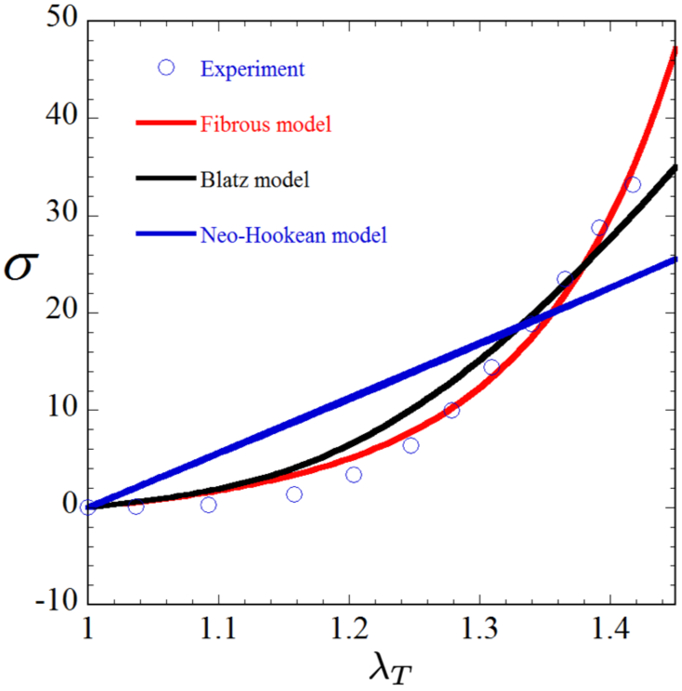
Stress vs. stretch for each of our three constitutive models alongside the experimental data of [41], showing that the fibrous model best captures the material behavior, followed by the Blatz model. Material parameters are as follows for each model: Fiber-based, λ = 3.79KPa, μ = 2.53KPa, κ = 3.61KPa, γ = 9.23; Blatz, λ = 21.97KPa, μ = 5.49KPa, γ = 11.92; Neo-Hookean, λ = 79.83KPa, μ = 19.96KPa.
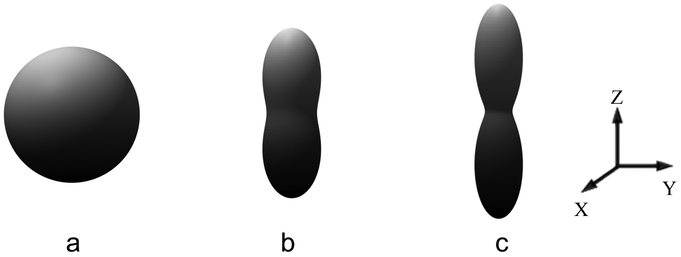
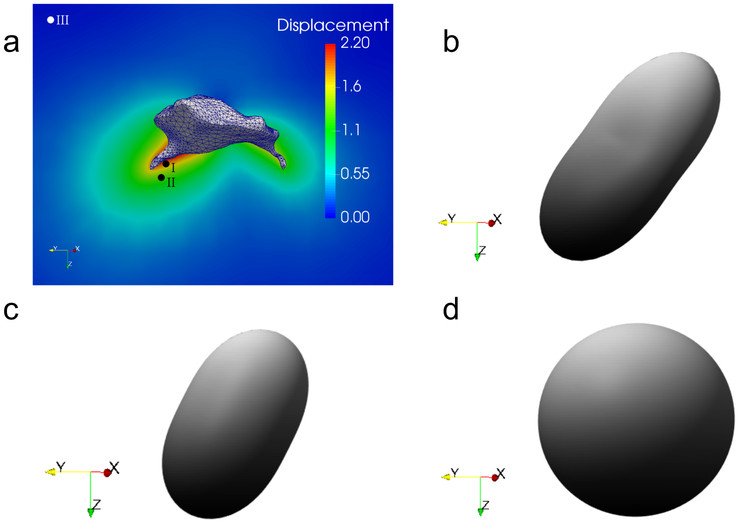
The results from the uniaxial test can also be used to understand and visualize the fiber realignment that takes place for the fiber-based model. When the material specimen is in its unstressed state, the distribution of the fibers is uniform with respect to fiber orientation. This distribution can be visualized in a plot, shown in Fig. 2a, using a surface whose locus is a set of points whose distance from the origin, along a given direction, is determined by the value of the fiber density along that direction in the current configuration. When the material is in the unstressed state, the fiber density is uniform, and the distance of all points from the origin is , and the surface assumes the shape of a sphere. When the material is stretched along a given direction and the fibers are subjected to this affine deformation, they rotate towards the direction of the maximum principal stretch. Since the total number of fibers at any material point is conserved, this implies that the density of the fibers along the direction of stretch increases, while the fiber density along orthogonal directions reduces. Therefore, the spherical shape of the original surface for the fiber density is transformed to a shape for which the distance from the origin along the direction of the maximum principal stretch is increased, as shown in Figs. 2b and c. Given the affine assumption, the transformation from the spherical shape to this prolate shape is completely determined by the deformation gradient F. In particular, the fiber density ρ in the direction m (where m is a unit vector) in the current configuration is given by (see Appendix A for the proof)
| (28) |
Figure 2:
Distribution of the fiber density in the current configuration for a specimen subject to uniaxial tension (along z direction). Results are shown for (a) λT = 1, (b) λT = 1.2, and (c) λT = 1.5, where λT denotes the principal stretch along z direction. The fiber orientations are assumed to be uniformly dispersed in the reference configuration corresponding to λT = 1.
Plotting the fiber density distribution for different points in the ECM provides a quick visualization of the amount of fiber realignment in the ECM. As a consequence of this realignment, the material effectively stiffens in the direction of the maximum principal stretch and weakens in the other directions.
We return now to the processes of generating synthetic data: upon solving the forward problem, we take a subset of the resultant displacement field to represent bad locations, and create a set of measured values for the inverse problem. To better mimic experimental data, we add noise to our synthetic measurements. We use two levels of noise, 1% and 5%, applied in accordance with the following expression for the noisy signal :
| (29) |
where is a random vector with its three components given by , and denotes the standard normal distribution. In addition, the parameter η controls the level of noise in the synthetic displacement field. In particular, we select η = 1% and 5% in this work.
Inverse problem setup.
We solve the inverse problem for all three constitutive models, using data at 1% and 5% noise levels as input. We also need to determine the appropriate boundary conditions and the regularization parameter α. These determinations are made on a case-by-case basis, and will be discussed further for each individual cell.
Error Analysis.
Solution of the inverse problem yields a reconstructed traction field t. Using the known traction , we can evaluate the relative error e(t):
| (30) |
where ∥ ∙ ∥2 denotes the L2 norm of a given quantity defined on the cell surface ∂Ωt. Since the “true” displacements are generated using the fiber-based constitutive model, for the traction recovered with that model, e(t) represents the effect of noise in recovering the tractions. That is, it can be used to quantify the sensitivity of traction microscopy to noise in the displacement measurement. However, for the tractions recovered using the Blatz and the Neo-Hookean models, this error also includes contributions from the model error, that is the error incurred by using an incorrect constitutive model for the material response.
We can also evaluate the ability of a model to capture the true ECM response by computing the value of the data mismatch term, which describes how closely the predicted displacement field uk matches the measured displacement . In particular, we define the normalized data mismatch as follows:
| (31) |
Note that e(u) in (31) is particularly useful for assessing the performance of traction microscopy with real experimental data, in which case the true traction field is unknown and (30) cannot be used.
Model error.
As discussed in the Introduction, in this manuscript we wish to demonstrate how traction microcopy can be performed using a constitutive model that assumes a fiber-laden microstructure, and to investigate the error incurred when this model is not used in estimating the tractions. For a given traction field, the choice of a constitutive model influences the displacements predicted at the bead locations, and therefore directly affects the data mismatch term. Thus, the tractions fields recovered by assuming two different constitutive relations will be different, and we propose to quantify this difference.
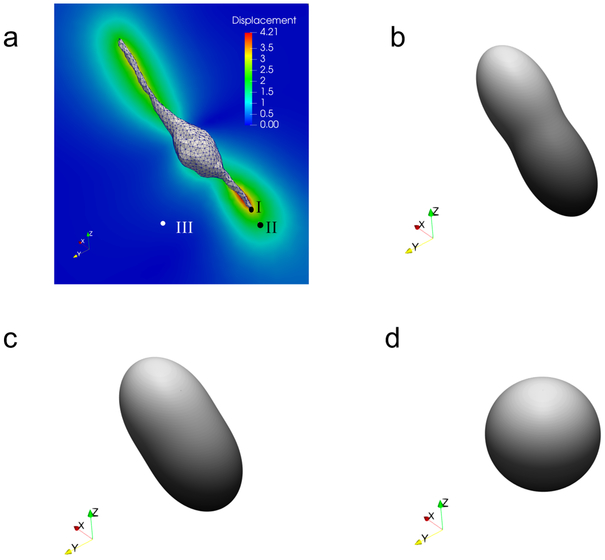
The 3T3 cell shown in Fig. 3 is comprised of a bulbous central section with a maximum diameter of approximately 17 micrometers and two long protrusions, with a tip-to-tip length of nearly 93 micrometers. The 3D model of the cell is reconstructed from a set of z-stack microscopy images obtained in an earlier 3D TM experiment [24], although in the context of non-fibrous (dextran) gels. The surface of the cell is embedded in the center of a 146 × 146 × 237 micrometer mesh, with refinement performed on the cell surface to capture the tractions on the spindle-like protrusions with appropriate fidelity. The applied traction field is very large at the tips of these protrusions and decreases towards the central bulb. Displacements are “measured” at selected nodes within 20 micrometers of the cell to produce the noisy measured displacement field for the inverse problem. These node locations correspond to the true locations of beads in a previous 3D TM experiment [24]. Displacement vectors far from the cell surface are not used for traction reconstructions. This is because the magnitude of the displacement at these points is very small, and there the “measurement” is dominated by noise. Finally, note that the cell-generated displacements are large enough to produce significant local strains on and near the cell surface, as seen in Fig. 3(d). As a consequence, there are noticeable differences between cell geometries in the relaxed and stressed states, especially at the tips of the cell protrusions, indicating that it is critical to account for the geometric disparity between states. The large strain field in the ECM leads to strong fiber realignment, visualized in Fig. 4. In particular, we observe significant fiber reorientation very close to the cell (Fig. 4b), and this effect is reduced as we move away from the cell surface (Figs. 4c and d).
Figure 4:
Displacement and fiber orientation distributions in the current configuration for the 3T3 cell using the fibrous model,illustrating how displacement induces fiber re-orientation. (a) Displacement field on a critical cross-section of the domain, (b) - (d) Fiber orientation distributions in the current configuration at point I, II, and III, respectively.
The outer boundaries of the domain are not very far from the cell, and the cell-generated displacement may not have completely vanished on the boundaries. Therefore, for each face of the box we set only the normal displacement to zero, while allowing free lateral motion (traction-free) of the outer boundaries.
To prepare for the inverse problem, we first determine the appropriate regularization parameters α for each of the constitutive models by means of the standard L-curve approach [43]. In particular, we solve the inverse problem for different values of α, and then plot the data mismatch between the recovered and measured displacements as a function of α. The optimal value of α is near the point of maximum curvature on the L curve. For instance, for the 1% noise data this procedure yields α values of 1 × 10−2, 8 × 10−3, and 1 × 10−3, respectively, for the fiber-based, Blatz, and Neo-Hookean models.
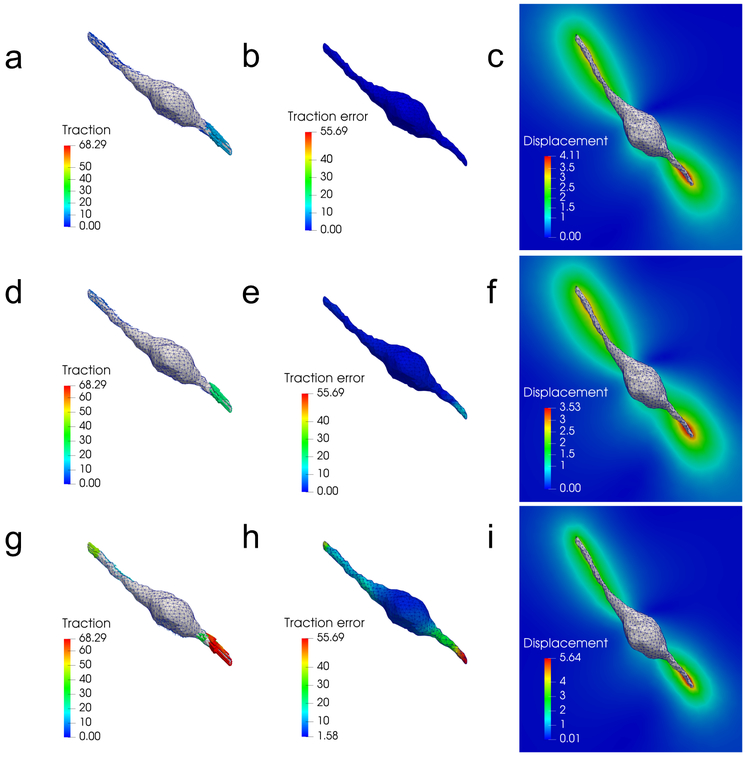
In Fig. 5, we present results for the reconstructed tractions, t, local traction error, , as well as the displacement field, u, for all the three models and for the 1% noise case. We can see that the fibrous model produces the lowest tractions and traction error. Conversely, the Neo-Hookean model produces the highest tractions, traction error, and displacements.
Figure 5:
A comparison of traction reconstructions for the 3T3 cell and 1% noise showing tractions (t), local traction errors , and displacement fields (u) recovered by each model. (a) - (c): results for the fiber-based model, (d) - (f): results for the Blatz model, and (g) - (i): results for the Neo-Hookean model. We observe that the Blatz and Neo-Hookean models overestimate the traction fields in order to match the measured displacement data.
The reason for the over-prediction of tractions for the Blatz and Neo-Hookean models can be understood as follows. The material parameters for all three constitutive models are chosen such that the material response is similar under uniaxial stretch (Fig. 1). In the case of the fiber-based model, the response under uniaxial stretch is very different from the response under other types of the loadings, such as compression or pure shear. This is because fiber reorientation is rather strong in uniaxial stretch, and its effect in other types of loadings may not be as pronounced. Consequently, the contribution to the increase in stiffness from fiber reorientation is smaller in these loadings. In contrast, the Blatz and Neo-Hookean models, which do not account for the fibrous microstructure, are unable to capture the drastically asymmetric behavior of the fibrous materials under different loadings. Therefore, these models could overestimate the material stiffness for loading conditions different from uniaxial tension (e.g., see Appendix B for results for simple shear loadings). As a consequence, larger tractions are required for the Blatz and Neo-Hookean models to generate displacements matching the measured data.
There is another source of error that leads to the overestimation of traction for the Neo-Hookean model. In particular, in fibrous ECM the displacement field decays slowly as we move away from the cell, due to fiber realignment. However, this phenomenon does not occur for the Neo-Hookean model, where the displacement decays more rapidly (compare Fig. 5i with Fig. 5c), and the model attempts to match the true decay by over-predicting the displacement near the cell and under-predicting them away from the cell. This leads to significantly higher strains, and therefore higher stresses and tractions at the cell surface.
Our predictions of the slow decay of the displacement field in fibrous ECMs (Fig. 5c) are in qualitative agreement with experimental observations (e.g., [18, 44, 45]). This phenomenon is induced, at least in part, by the realignment of fibers at large deformations [30], underscoring the necessity of accounting for the microstructure of fibrous ECMs. Failure to do so in a TM experiment could lead to the inability to reproduce, even qualitatively, the measured displacements, and therefore to significant errors in the estimation of cellular tractions.
By comparing the relative errors for the different models at 1% and 5% noise level (see Table 1) we conclude that the proposed algorithm is reasonably insensitive to noise in displacement yielding around 6% error for displacement noise of 5% with the fiber-based model. We also observe that the model error for this problem is significant. For the Blatz model, this error is around 69% and for the Neo-Hookean model it is around 457%. As explained above, these large errors are due to the inability of the Blatz and Neo-Hookean models to capture the realignment of fibers during the deformation. From the second row of Table 1 we observe that the fiber-based model also lead to much lower values of the data mismatch compared with the Blatz and Neo-Hookean model.
Table 1:
Relative errors and data mismatch, as defined by equations (30) and (31), respectively, for all tests with the 3T3 cell. Results are shown for each material model and level of noise (η = 1% and 5%).
| Fiber-based | Blatz | Neo-Hookean | ||||
|---|---|---|---|---|---|---|
| Error | η =1% | η =5% | η =1% | η =5% | η =1% | η =5% |
| e(t) | 0.047 | 0.059 | 0.69 | 0.68 | 4.57 | 4.57 |
| e(u) | 0.011 | 0.047 | 0.113 | 0.123 | 0.112 | 0.120 |
3.3. Microglial Cell
The microglial cell, seen in Fig. 6, is approximately 20 × 20 × 15 micrometers, and is centered within a cubic domain with sides of length 100 micrometers. The 3D model of the cell is reconstructed from a set of z-stack microscopy images courtesy of Sebastian Rhode at ZEISS Microscopy [46]. The traction field we apply for the forward problem is, as in the 3T3 case, characteristically high along the cell protrusions; most of the smooth cell body experiences uniformly low tractions. Out of the resulting displacement field, we take the values at all nodes within 50 micrometers of the cell surface (excluding the surface itself) and treat them as bead locations for measured displacements in the inverse problem. This yields a total of 7,023 bead locations, which is comparable to the number of beads in a typical TM experiment [13, 24]. We note that the distribution of the first principal stretch on the cell indicates local strains of above 100% in some regions, necessitating nonlinear modeling to successfully reconstruct the displacement field. This displacement field significantly affects the ECM, as illustrated in Fig. 7, where fibers near the protrusions are strongly realigned, and non-negligible realignment is seen in a region extending as much as 10 to 15 micrometers outside the cell.
Figure 7:
Displacement and fiber orientation distributions in the current configuration for the microglial cell using the fibrous model, illustrating how displacement induces fiber re-orientation. (a) Displacement field on a critical cross-section of the domain. (b) - (d) Fiber orientation distributions in the current configuration at point I, II, and III, respectively.
To solve the inverse problem, we determine the necessary α using the aforementioned L-curve method, yielding values of 3 × 10−3, 6 × 10−3, and 6 × 10−3 for the fiber-based, Blatz, and Neo-Hookean models, respectively, using the 1% noise data. Since the walls of the bounding box are very far from the cell, we assume that all displacements induced by cellular traction will decay to zero before reaching them. Thus, we set all three components of displacement to be zero on all faces of the boundary.
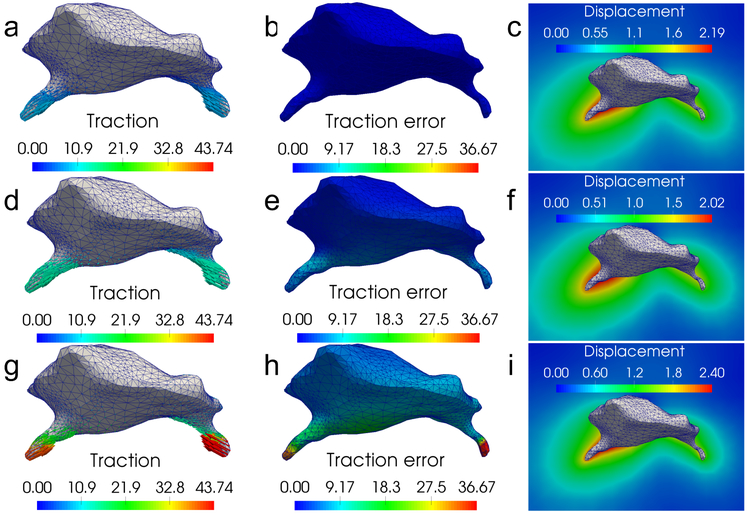
Figure 8 shows that the error in traction is the lowest for the fibrous model. Progressing through the Blatz and Neo-Hookean models, traction error increases as the models over-predict the traction, just as in the 3T3 cell case.
Figure 8:
A comparison of traction reconstructions for the microglial cell and 1% noise showing tractions (t), local traction errors , and displacement fields (u) recovered by each model. (a) - (c): results for the fiber-based model, (d) - (f): results for the Blatz model, and (g) - (i): results for the Neo-Hookean model. We observe that the Blatz and Neo-Hookean models overestimate the traction fields in order to match the measured displacement data.
Once again, we may attribute the large traction errors produced by the Blatz and Neo-Hookean models to their inability to account for the fiber realignment, which leads to a significantly different response from the fibrous materials under different loading conditions. For the Neo-Hookean model, error is also induced by its inability to account for the slow decay of displacements produced by fiber-realignment; it compensates for this by overestimating displacements close to the cell and underestimating them away from cell. This in turn leads to an over-estimation of strain, stress and traction.
Finally, we note that while noise in the displacement measurement leads to error in the reconstructed tractions, the error induced by the incorrect choice of the constitutive model is far greater (at least 10 times greater for the Blatz model and 30 times greater for the Neo-Hookean model). These values are recorded in Table 2. This confirms that, for traction microscopy in fibrous materials, the model error induced by an incorrect choice of constitutive behavior can be significant.
Table 2:
Relative errors and data mismatch, as defined by equations (30) and (31), respectively, for all tests with the microglial cell. Results are shown for each material model and level of noise (η = 1% and 5%).
| Fiber-based | Blatz | Neo-Hookean | ||||
|---|---|---|---|---|---|---|
| Error | η =1% | η =5% | η =1% | η =5% | η =1% | η =5% |
| e(t) | 0.06 | 0.11 | 1.22 | 1.16 | 3.62 | 3.54 |
| e(u) | 0.009 | 0.045 | 0.048 | 0.066 | 0.078 | 0.091 |
4. Summary
In this manuscript we have developed, implemented and verified algorithms for performing three-dimensional traction microscopy in ECMs with a fibrous microstructure. We have modeled the microstructure using a constitutive model that accounts for stress contributions from nonlinear elastic fibers embedded in a hyperelastic matrix. By solving forward problems with realistic cell shapes and traction distributions, we have demonstrated significant fiber re-alignment along the direction of principle stretch near the cell surface. Further, we have developed and implemented an efficient algorithm for solving the inverse 3D traction microscopy problem that uses as input the displacement of beads around the cell and the shape of the cell in the stressed configuration, which is often much easier to measure than its shape in the unstressed configuration. In solving this inverse problem we treat the nodal values of the traction vector as unknowns, and minimize the difference between a predicted displacement field (obtained by solving the equations of equilibrium) and the measured displacement field. We solve the minimization problem using a gradient-based method and determine the gradient efficiently by solving for an appropriate adjoint field.
We have used this method to quantify the sensitivity of the recovered traction to noise in the displacement measurement and to the choice of the constitutive model. We conclude that, for realistic measures of displacement noise (around 5 %), the error in the recovered tractions is around 10% when using an appropriate microstructural model to account for the fibrous nature of the ECM. Conversely, using an incorrect constitutive model leads to very large errors in the predicted tractions. This error, which is often referred to model error in the parlance of inverse problems, is around 70% for the Blatz model and around 300% for the Neo-Hookean model. These large errors are a result of the inability of the phenomenological models to capture behavior linked to fiber reorientation, and highlight the importance of using the correct constitutive model for traction microscopy in ECMs with fibrous microstructures.
A computational approach is proposed to recover cellular tractions in fibrous ECM.
Cellular tractions can induce strong fiber realignment.
Model error incurred by using incorrect constitutive models is significant.
Acknowledgments
This material is based upon work supported in part by the National Institute of Health under Grant Numer 1R41CA224898-01. The authors declare no conflict of interest.
Appendix A: Detailed expressions for the fiber distribution function
In this Appendix, we determine the fiber distribution function at a given point in the current configuration, given its values in the reference configuration.
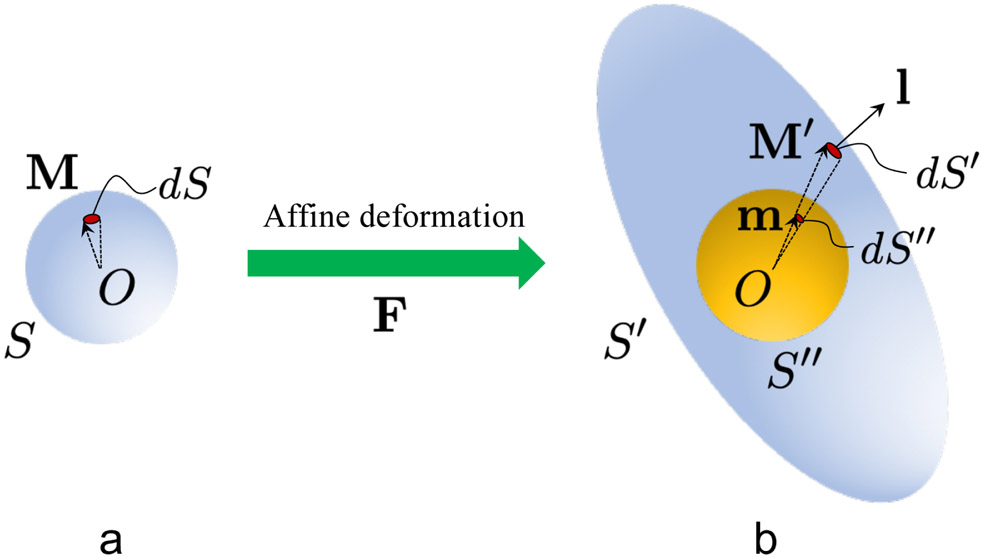
Let S : ∣M∣ = 1 be the surface of a unit sphere in the reference configuration (Fig. 9a), where each point on S represents a unique fiber orientation M. In addition, the fiber distribution function ρ0 in the reference configuration is known and satisfies the normalization condition
| (32) |
Figure 9:
Schematics linking the fiber orientation distribution in the (a) reference and (b) current configurations.
Here ρ0(M) is the fiber density in the direction M in the reference configuration, and dS is an incremental area representing fiber orientations in an infinitesimal neighborhood of M. For the special case where fibers are uniformly distributed in the reference configuration, ρ0(M) = 1/(4π), ∀M.
In this work, we assume that fibers undergo affine deformations, such that a fiber of unit length in the direction M in the reference configuration deforms into M′ = FM in the current configuration (Fig. 9b). Therefore, the unit spherical surface S is mapped into an ellipsoidal surface S′ : ∣F−1M′∣ = 1 in the current configuration (Fig. 9b). Making use of Nanson’s formula [47] to relate areas in the reference and current configurations, we have that
| (33) |
where l denotes the outward unit normal vector of S′ (Fig. 9b), dS′ is the deformed incremental area associated with dS, and J = det(F) is the Jacobian. Then, it is straightforward to show that
| (34) |
Given that the fiber distribution function ρ in the current configuration has to satisfy a normalization condition similar to (32), we project the ellipsoidal surface S′ onto a unit spherical surface S″ (Fig. 9b). In particular, the projected incremental area dS″ on S″ is related to dS′ via the relation
| (35) |
where m = M′/∣M′∣ = FM/∣FM∣ is the outward unit normal vector of S″. After some manipulations, (35) can be rewritten as
| (36) |
Given that the number of fibers is conserved during the deformation, we have the relation
| (37) |
| (38) |
| (39) |
| (40) |
In the expressions above, use has been made of equation (34) and (36), as well as the fact that M = F−1m/∣F−1m∣; ρ(m, F) denotes the fiber density in the direction m in the current configuration, with the deformation gradient given by F.
It can be easily verified that the fiber distribution function ρ satisfies the normalization condition
| (41) |
Note that ρ(m, F) is a homogeneous function of degree zero in F, such that ρ(m, pF) = ρ(m, F), ∀p > 0. Also note that for the special case where fibers are uniformly distributed in the reference configuration, equation (40) reduces to (28) in the main text of this manuscript.
Appendix B: Material response under simple shear deformations
In this Appendix, we compare the material response predicted by the three constitutive models (fiber-based, Blatz and Neo-Hookean) for simple shear loadings. Note that for each model, we use the same set of material parameters that are obtained through curve fitting in Fig. 1.
For a simple shear deformation, we have that
| (42) |
where F is the deformation gradient, and γs is the amount of shear. In Fig. 10 we plot the shear stress component τ = T12 = T21 as a function of γs. It can be seen that the Blatz and Neo-Hookean models predict arger shear stresses than the fiber-based model, especially for large values of γs.
Figure 10:
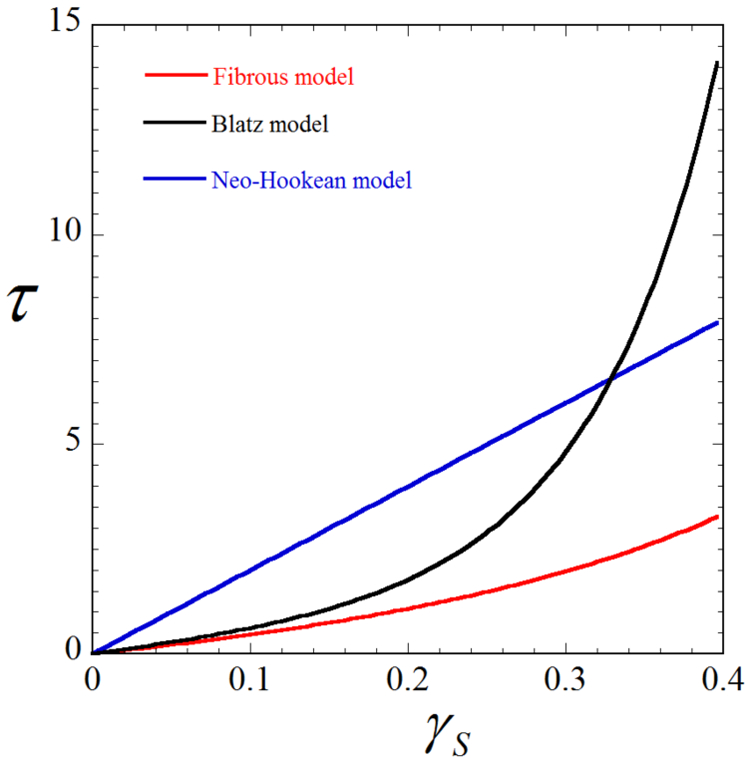
Shear stress vs. amount of shear for each of our three constitutive models, showing that the material response predicted by the three models are significantly different. In particular, the Blatz and Neo-Hookean models overestimate the shear stress compared to the fiber-based model. The material parameters are identical to that used in Fig. 10, and are listed as follows for each model: Fiber-based, λ = 3.79KPa, μ = 2.53KPa, κ = 3.61KPa, γ = 9.23; Blatz, λ = 21.97KPa, μ = 5.49KPa, γ = 11.92; Neo-Hookean, λ = 79.83KPa, μ = 19.96KPa.
These results suggest that while the three models exhibit fairly similar behavior under uniaxial tension Fig. 1), this may not be the case for other types of loadings, such as simple shear loading. This can lead to significant differences in the traction fields recovered using the three models, as seen in section 3. Thus, it is crucial to employ an accurate constitutive model that can faithfully characterize the ECM behavior under general loading conditions. Traction microscopy with a fiber-based model, like the one developed in this work, represents a step toward this goal.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Wang N, Butler JP, Ingber DE, Mechanotransduction across the cell surface and through the cytoskeleton, Science 260 (5111) (1993) 1124–1127. [DOI] [PubMed] [Google Scholar]
- [2].Iskratsch T, Wolfenson H, Sheetz MP, Appreciating force and shapethe rise of mechanotransduction in cell biology, Nature Reviews Molecular Cell Biology 15 (12) (2014) 825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Mui KL, Chen CS, Assoian RK, The mechanical regulation of integrin–cadherin crosstalk organizes cells, signaling and forces, J Cell Sci 129 (6) (2016) 1093–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Huang S, Chen CS, Ingber DE, Control of cyclin d1, p27kip1, and cell cycle progression in human capillary endothelial cells by cell shape and cytoskeletal tension, Molecular biology of the cell 9 (11) (1998) 3179–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, Fredberg JJ, Physical forces during collective cell migration, Nature physics 5 (6) (2009) 426. [Google Scholar]
- [6].Vogel V, Sheetz M, Local force and geometry sensing regulate cell functions, Nature reviews Molecular cell biology 7 (4) (2006) 265. [DOI] [PubMed] [Google Scholar]
- [7].Schwarz US, Soiné JR, Traction force microscopy on soft elastic substrates: A guide to recent computational advances, Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1853 (11) (2015) 3095–3104. [DOI] [PubMed] [Google Scholar]
- [8].Delanoë-Ayari H, Rieu J, Sano M, 4d traction force microscopy reveals asymmetric cortical forces in migrating dictyostelium cells, Physical Review Letters 105 (24) (2010) 248103. [DOI] [PubMed] [Google Scholar]
- [9].Koch TM, Münster S, Bonakdar N, Butler JP, Fabry B, 3d traction forces in cancer cell invasion, PloS one 7 (3) (2012) e33476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Style RW, Boltyanskiy R, German GK, Hyland C, MacMinn CW, Mertz AF, Wilen LA, Xu Y, Dufresne ER, Traction force microscopy in physics and biology, Soft matter 10 (23) (2014) 4047–4055. [DOI] [PubMed] [Google Scholar]
- [11].Polacheck WJ, Chen CS, Measuring cell-generated forces: a guide to the available tools, Nature methods 13 (5) (2016) 415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mulligan JA, Bordeleau F, Reinhart-King CA, Adie SG, Traction force microscopy for noninvasive imaging of cell forces, in: Biomechanics in Oncology, Springer, 2018, pp. 319–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Legant WR, Miller JS, Blakely BL, Cohen DM, Genin GM, Chen CS, Measurement of mechanical tractions exerted by cells in three-dimensional matrices, Nature methods 7 (12) (2010) 969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hall MS, Long R, Hui C-Y, Wu M, Mapping three-dimensional stress and strain fields within a soft hydrogel using a fluorescence microscope, Biophysical journal 102 (10) (2012) 2241–2250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hall MS, Long R, Feng X, Huang Y, Hui C-Y, Wu M, Toward single cell traction microscopy within 3d collagen matrices, Experimental cell research 319 (16) (2013) 2396–2408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Franck C, Maskarinec SA, Tirrell DA, Ravichandran G, Three-dimensional traction force microscopy: a new tool for quantifying cell-matrix interactions, PloS one 6 (3) (2011) e17833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Toyjanova J, Bar-Kochba E, López-Fagundo C, Reichner J, Hoffman-Kim D, Franck C, High resolution, large deformation 3d traction force microscopy, PloS one 9 (4) (2014) e90976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Steinwachs J, Metzner C, Skodzek K, Lang N, Thievessen I, Mark C, Münster S, Aifantis KE, Fabry B, Three-dimensional force microscopy of cells in biopolymer networks, Nature methods 13 (2) (2016) 171. [DOI] [PubMed] [Google Scholar]
- [19].Butler JP, Tolic-Nørrelykke IM, Fabry B, Fredberg JJ, Traction fields, moments, and strain energy that cells exert on their surroundings, American Journal of Physiology-Cell Physiology 282 (3) (2002) C595–C605. [DOI] [PubMed] [Google Scholar]
- [20].Schwarz US, Balaban NQ, Riveline D, Bershadsky A, Geiger B, Safran S, Calculation of forces at focal adhesions from elastic substrate data: the effect of localized force and the need for regularization, Biophysical journal 83 (3) (2002) 1380–1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Maskarinec SA, Franck C, Tirrell DA, Ravichandran G, Quantifying cellular traction forces in three dimensions, Proceedings of the National Academy of Sciences 106 (52) (2009) 22108–22113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Gjorevski N, Nelson CM, Mapping of mechanical strains and stresses around quiescent engineered three-dimensional epithelial tissues, Biophysical journal 103 (1) (2012) 152–162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Dong L, Oberai AA, Recovery of cellular traction in three-dimensional nonlinear hyperelastic matrices, Computer Methods in Applied Mechanics and Engineering 314 (2017) 296–313. [Google Scholar]
- [24].Song D, Dong L, Gupta M, Li L, Chen CS, Klaas O, Loghin A, Beall M, Oberai AA, Recovery of tractions exerted by single cells in 3d nonlinear matrices, Under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Lanir Y, Multi-scale structural modeling of soft tissues mechanics and mechanobiology, Journal of Elasticity 129 (1-2) (2017) 7–48. [Google Scholar]
- [26].Li K, Ogden RW, Holzapfel GA, Computational method for excluding fibers under compression in modeling soft fibrous solids, European Journal of Mechanics-A/Solids 57 (2016) 178–193. [Google Scholar]
- [27].Blatz PJ, Mae Chu B, Wayland H, On the mechanical behavior of elastic animal tissue, Transactions of the Society of Rheology 13 (1) (1969) 83–102. [Google Scholar]
- [28].Veronda D, Westmann R, Mechanical characterization of skinfinite deformations, Journal of biomechanics 3 (1) (1970) 111–124. [DOI] [PubMed] [Google Scholar]
- [29].Ogden RW, Non-linear elastic deformations, Courier Corporation, 1997. [Google Scholar]
- [30].Wang H, Abhilash A, Chen CS, Wells RG, Shenoy VB, Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers, Biophysical journal 107 (11) (2014) 2592–2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Liu T, Hall TJ, Barbone PE, Oberai AA, Inferring spatial variations of microstructural properties from macroscopic mechanical response, Biomechanics and modeling in mechanobiology 16 (2) (2017) 479–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Fung Y, Elasticity of soft tissues in simple elongation, American Journal of Physiology-Legacy Content 213 (6) (1967) 1532–1544. [DOI] [PubMed] [Google Scholar]
- [33].Li K, Ogden RW, Holzapfel GA, A discrete fibre dispersion method for excluding fibres under compression in the modelling of fibrous tissues, Journal of The Royal Society Interface 15 (138) (2018) 20170766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Govindjee S, Mihalic PA, Computational methods for inverse finite elastostatics, Computer Methods in Applied Mechanics and Engineering 136 (1-2) (1996) 47–57. [Google Scholar]
- [35].Govindjee S, Mihalic PA, Computational methods for inverse deformations in quasi-incompressible finite elasticity, International Journal for Numerical Methods in Engineering 43 (5) (1998) 821–838. [Google Scholar]
- [36].Byrd RH, Lu P, Nocedal J, Zhu C, A limited memory algorithm for bound constrained optimization, SIAM Journal on Scientific Computing 16 (5) (1995) 1190–1208. [Google Scholar]
- [37].Oberai AA, Gokhale NH, Feijóo GR, Solution of inverse problems in elasticity imaging using the adjoint method, Inverse problems 19 (2) (2003) 297. [Google Scholar]
- [38].Gokhale NH, Barbone PE, Oberai AA, Solution of the nonlinear elasticity imaging inverse problem: the compressible case, Inverse Problems 24 (4) (2008) 045010. [Google Scholar]
- [39].Goenezen S, Barbone P, Oberai AA, Solution of the nonlinear elasticity imaging inverse problem: The incompressible case, Computer methods in applied mechanics and engineering 200 (13-16) (2011) 1406–1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Simmetrix, inc., http://www.simmetrix.com/, 10 Halfmoon Executive Park Dr., Clifton Park, NY 12065. [Google Scholar]
- [41].Roeder BA, Kokini K, Sturgis JE, Robinson JP, Voytik-Harbin SL, Tensile mechanical properties of three-dimensional type i collagen extracellular matrices with varied microstructure, Journal of biomechanical engineering 124 (2) (2002) 214–222. [DOI] [PubMed] [Google Scholar]
- [42].Li K, Holzapfel GA, Multiscale modeling of fiber recruitment and damage with a discrete fiber dispersion method, Journal of the Mechanics and Physics of Solids 126 (2019) 226–244. [Google Scholar]
- [43].Hansen PC, Analysis of discrete ill-posed problems by means of the l-curve, SIAM review 34 (4) (1992) 561–580. [Google Scholar]
- [44].Ma X, Schickel ME, Stevenson MD, Sarang-Sieminski AL, Gooch KJ, Ghadiali SN, Hart RT, Fibers in the extracellular matrix enable long-range stress transmission between cells, Biophysical journal 104 (7) (2013) 1410–1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Hall MS, Alisafaei F, Ban E, Feng X, Hui C-Y, Shenoy VB, Wu M, Fibrous nonlinear elasticity enables positive mechanical feedback between cells and ecms, Proceedings of the National Academy of Sciences 113 (49) (2016) 14043–14048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Sebastian rhode, till photonics, sabine scheibe (2011), 10.7295/W9CIL27156, cIL:27156, Rattus, multipolar neuron, microglial cell. CIL. Dataset. [DOI] [Google Scholar]
- [47].Gurtin ME, Fried E, Anand L, The mechanics and thermodynamics of continua, Cambridge University Press, 2010. [Google Scholar]