Development and Validation of a Dynamic Risk Prediction Model to Forecast Psychosis Onset in Patients at Clinical High Risk

Abstract

The prediction of outcomes in patients at Clinical High Risk for Psychosis (CHR-P) almost exclusively relies on static data obtained at a single snapshot in time (ie, baseline data). Although the CHR-P symptoms are intrinsically evolving over time, available prediction models cannot be dynamically updated to reflect these changes. Hence, the aim of this study was to develop and internally validate a dynamic risk prediction model (joint model) and to implement this model in a user-friendly online risk calculator. Furthermore, we aimed to explore the prognostic performance of extended dynamic risk prediction models and to compare static with dynamic prediction. One hundred ninety-six CHR-P patients were recruited as part of the “Basel Früherkennung von Psychosen” (FePsy) study. Psychopathology and transition to psychosis was assessed at regular intervals for up to 5 years using the Brief Psychiatric Rating Scale-Expanded (BPRS-E). Various specifications of joint models were compared with regard to their cross-validated prognostic performance. We developed and internally validated a joint model that predicts psychosis onset from BPRS-E disorganization and years of education at baseline and BPRS-E positive symptoms during the follow-up with good prognostic performance. The model was implemented as online risk calculator (http://www.fepsy.ch/DPRP/). The use of extended joint models slightly increased the prognostic accuracy compared to basic joint models, and dynamic models showed a higher prognostic accuracy than static models. Our results confirm that extended joint modeling could improve the prediction of psychosis in CHR-P patients. We implemented the first online risk calculator that can dynamically update psychosis risk prediction.

Introduction

Preventive interventions in patients with a clinical high risk for psychosis (CHR-P)¹ offer a promising opportunity for ameliorating the course of psychotic disorders.^1,2 However, recent network meta-analyses^3,4 have indicated that one-size-fits-all preventive treatments are not effective, as the CHR-P group is heterogeneous,^5,6 with only about 20% developing frank psychosis⁷ and about one-third having a clinical remission within the first 2 years of the follow-up.⁸ Hence, an important line of research in recent years has been to develop multivariable risk prediction models to estimate the risk of psychosis on an individual level, thereby enabling more effective patient-tailored treatments.^9–11

Although several risk prediction models for CHR-P patients have been published,^12,13 the clinical application of these models remains challenging.¹⁰ The key obstacles are the use of small sample sizes and poor modeling strategies,^10,13 lack of internal or external validation,^10,13 and reliance on predictors that are hard to obtain in clinical practice.^10,14 To solve this problem, some studies have developed^15,16 and internally¹⁷ or externally^18–21 validated prediction models that are based on a priori clinical knowledge and easy to obtain predictors and have implemented them as online risk calculators (eg, http://riskcalc.org:3838/napls/, http://www.psychosis-risk.net, https://link.konsta.com.pl/psychosis, last accessed June 14, 2019). However, these risk calculators are all static because they exclusively rely on data obtained at the time of clinical service entry.²² Thus, they cannot take the dynamic psychopathological changes²³ of the CHR-P state into account and their risk prediction cannot be dynamically updated during the follow-up when new information becomes available. Models taking dynamic follow-up data into account could predict transition to psychosis with considerably higher prognostic accuracy.²²

Joint modeling methods²⁴ are a relatively recent statistical innovation that allow flexibly relating a longitudinal process (eg, change in CHR-P symptoms over time) to a time-to-event outcome (eg, time to transition to psychosis) and thus can dynamically update predictions over time. So far, only 3 studies have applied joint models to predict transition to psychosis,^25–27 with 2 of them^25,26 having largely overlapping samples. However, these studies were limited by the use of basic joint models in small effective samples (determined by the number of the transitions:¹⁰ 21,²⁵ 22,²⁶ and 40²⁷), relatively short follow-up durations (1 year), and lack of internal and external validation, which can lead to overoptimistic performance estimation.^10,13

We overcome these caveats by developing and internally validating the first robust dynamic prognostic model to forecast psychosis onset in CHR-P patients. We use a different and slightly larger effective sample, a considerably longer follow duration, and various extensions of joint models,²⁴ which would better allow incorporating the psychopathological changes over time. Our first hypothesis was that using extended model specifications of joint models,²⁴ such as modeling changes in symptoms over time with a nonlinear function, would have a better prognostic performance than basic joint models. Our second hypothesis was that joint models would forecast psychosis onset more accurately than a traditional model that only relies on baseline data.

Methods

Setting and Recruitment

CHR-P patients were recruited between March 1, 2000 and May 31, 2017 as part of the “Basel Früherkennung von Psychosen” (FePsy) study. The FePsy study is an open, prospective clinical study of all consecutive referrals to a specialized outpatient clinic for the early detection of psychosis at the Psychiatric University Hospital Basel. A detailed description of the study design can be found elsewhere.^28,29 The study was approved by the local ethics committee and conformed to the Declaration of Helsinki.

Patients were included in this study if they met CHR-P criteria (see below) and did not meet any of the following exclusion criteria: age <18 years, insufficient knowledge of German, IQ <70, treatment with antipsychotics for >3 weeks or exceeding lifetime cumulative chlorpromazine equivalent dose of 2500 mg,³⁰ psychotic symptoms clearly due to organic reasons or substance abuse, or psychotic symptomatology within a clearly diagnosed affective psychosis or borderline personality disorder.

Screening

Screening was performed with the Basel Screening Instrument for Psychosis (BSIP),^31,32 which has been specifically designed to identify patients with a CHR-P or first episode of psychosis and has been shown to have comparable prognostic accuracy to other CHR-P instruments³³ (see supplementary methods).

Follow-up

CHR-P patients who agreed to participate in the FePsy study were reassessed at regular intervals to examine whether transition to psychosis had occurred. At each follow-up visit, psychopathology was assessed with the Brief Psychiatric Rating Scale-Expanded (BPRS-E).³⁴ Transition to psychosis was assessed according to the original criteria of Yung et al.³⁵ During the first follow-up year, CHR-P patients were assessed monthly, during the second and third years 3 monthly, and thereafter annually. Follow-up assessments were terminated after transition to psychosis had occurred or—if no transition occurred—after 5 years. Some patients were followed-up for more than 5 years as part of other ongoing studies.³⁶ For this study, follow-up data were truncated at 5 years. Patients received treatment according to needs, case management, and supportive psychotherapy during the follow-up without any antipsychotic treatment.

Statistical Analysis

Model development and validation was conducted in accordance with the transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD) statement.³⁷ To predict transition to psychosis using both baseline (static) and follow-up (dynamic) data, we used joint models for longitudinal and time-to-event data (for an introduction to this model type, see ^24,38). Joint models are utilized where interest is in associating a longitudinal process (eg, repeatedly measured symptoms over time) with events (eg. transition to psychosis) and time-to-event outcomes (eg, time to transition).³⁹ Joint models are suitable when the time-dependent covariate (ie, longitudinal change in symptoms) is endogenous, ie, when it is (1) measured on the patients themselves at a regular or irregular sequence of time points, (2) its existence and/or future path is directly related to the event status, and (3) it is measured with error.²⁴ These assumptions are fully met in the case of CHR-P symptoms measured during the follow-up.

Model Development and Specification

Joint models consist of 2 linked submodels: a survival model and a longitudinal model (ie, mixed effects model). In a first step, we developed suitable submodels and then estimated these models jointly within the joint modeling framework using the R package JMbayes,³⁹ which fits joint models under a Bayesian approach using Markov chain Monte Carlo algorithms.

For the survival submodel, a relative risk model with penalized-spline-approximated baseline risk function was used. Suitable baseline predictor variables for the survival submodel were automatically selected among a priori predictors using the least absolute shrinkage and selection operator (LASSO) for the Cox model⁴⁰ (see supplementary methods).

The a priori predictors included 3 sociodemographic (ie, age, sex, and years of school education) and 6 clinical variables (ie, 5 BPRS-E subscales and the BPRS-E total score; see supplementary methods). These predictors were selected a priori because they are known to be associated with the risk of psychosis^41,42 and because they are easy to obtain in clinical practice (in fact, there were no missing values in these variables in our data set at baseline).

Longitudinal submodels were fitted for each of the 6 BPRS-E scales that were also collected over time. Additionally, for each BPRS-E scale, change over time was modeled both linearly (standard dynamic model) and nonlinearly (extended dynamic model; see supplementary methods).

Each of these 6 × 2 = 12 different longitudinal submodels was then jointly modeled with the survival submodel using 5 different association structures such that a total of 60 different joint models were fitted and compared. Specifically, the hazard for transition at any time t was assumed to be related to the

1. current level

2. current rate of change (ie, slope)

3. cumulative effect (ie, area under the curve [AUC])

4. current level + current rate of change

5. current level + cumulative effect

of the respective BPRS-E scale score at the same time point t. To avoid collinearity, the respective BPRS-E scale that was used in the longitudinal submodel was excluded from the survival submodel.

Model Performance and Internal Validation

For each of the 60 joint models, both discrimination and calibration were assessed. Discrimination at 1, 2, 3, 4, and 5 years after baseline and different amounts of follow-up information was assessed using time-dependent areas under the receiver-operating characteristics (ROC) curves (AUC). Additionally, we used the dynamic discrimination index (DDI),⁴³ which summarizes the discriminative ability over the whole follow-up period (see supplementary methods). We calculated DDIs with prognostic windows of 0.5, 1, 1.5, and 2 years because most transitions occur within these time frames.^44,45 For calibration assessment, we calculated the prediction error (PE) at 1, 2, 3, 4, and 5 years after baseline as well an integrated prediction error (IPE) for the whole follow-up period using a weighted average of PEs that corrects for censoring.

To protect against overoptimism, all models were internally validated. Specifically, all performance measures were calculated using 5-fold cross validation with 20 repetitions.

The joint model with the highest cross-validated discrimination (as determined by the highest average DDI across all 4 prognostic windows) was chosen as the final model. This also allowed testing the prognostic performance of standard vs extended definitions of models.

The prognostic performance of the final joint model was then compared to a Cox model with the same baseline predictors using cross-validated time-dependent AUC values (see supplementary methods). To facilitate external validation and clinical application, the final model was implemented as online risk calculator.

Results

Sociodemographic Sample Characteristics

Seven hundred and fifty-three individuals with a suspected CHR-P were screened, of whom 313 were identified as having a CHR-P. Of these, 196 provided written informed consent and had at least 1 BPRS-E assessment and thus were included in this study. The 117 excluded patients did not differ from the included patients with regard to sex and age but were significantly older (29.2 vs 25.0 years on average). Sociodemographic and clinical characteristics of the included patients are shown in table 1.

Table 1.

Sociodemographic and clinical sample characteristics

	CHR-P
	N = 196
Gender
Women	59 (30.1%)
Men	137 (69.9%)
Age	25.0 (6.9)
Years of education	11.7 (2.8)
Attenuated psychotic symptoms	133 (67.9%)
Brief limited intermittent psychotic symptoms	15 (7.7%)
Genetic risk and deterioration syndrome	47 (24.0%)
Unspecific risk category only	38 (19.4%)
BPRS-E activation	3.8 (1.8)
BPRS-E positive symptoms	5.4 (2.2)
BPRS-E negative symptoms	5.4 (2.7)
BPRS-E affect	6.7 (2.9)
BPRS-E disorganization	3.9 (1.4)
BPRS-E total	39.0 (9.6)

Note: CHR-P, Clinical high risk for psychosis; BPRS-E, Brief Psychiatric Rating Scale-Expanded. Continuous variables are described by means and standard deviation in parentheses.

Follow-up and Outcome

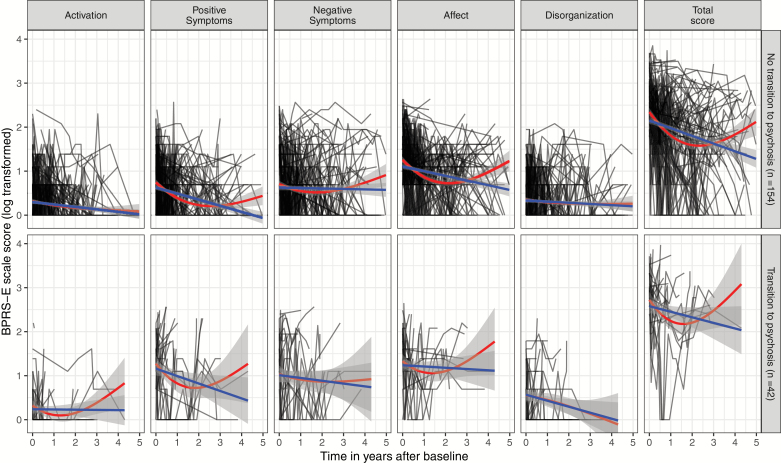
Forty-two CHR-P patients transitioned to psychosis within the 5-year follow-up period (CHR-P-T) and 154 did not (CHR-P-NT). The Kaplan–Meier transition risks were 16.3%, 19.2%, 22.5%, 24.8%, and 30.4% at 1, 2, 3, 4, and 5 years, respectively. Mean follow-up time was 2.7 years (median 2.8, range 0–5) for CHR-P-NT patients and 1.2 years (median 0.7, range 0–4.9) for CHR-P-T patients. Individual and averaged trajectories of BPRS-E scale scores are presented in figure 1.

Fig. 1.

Trajectories of log transformed Brief Psychiatric Rating Scale-Expanded scores in patients with a clinical high risk for psychosis with (above) and without (below) transition to psychosis during the follow-up. The black lines are the individual trajectories, the blue lines are the averaged trajectories using a linear function, and the red lines are the averaged trajectories using natural cubic splines with 2 degrees of freedom.

Selection of Baseline Predictors

BPRS-E positive symptoms, BPRS-E disorganization, and years of school education were selected by the LASSO Cox regression and used as baseline (ie, static) predictor variables.

Association between BPRS-E during the Follow-up and Psychosis Onset

The size of the associations between the longitudinal and event process for the 60 different joint models are shown in supplementary figure 1. The longitudinal processes of BPRS-E positive symptoms and the BPRS-E total tended to have the strongest positive association with transition to psychosis.

Influence of Joint Model Specifications on Prognostic Performance

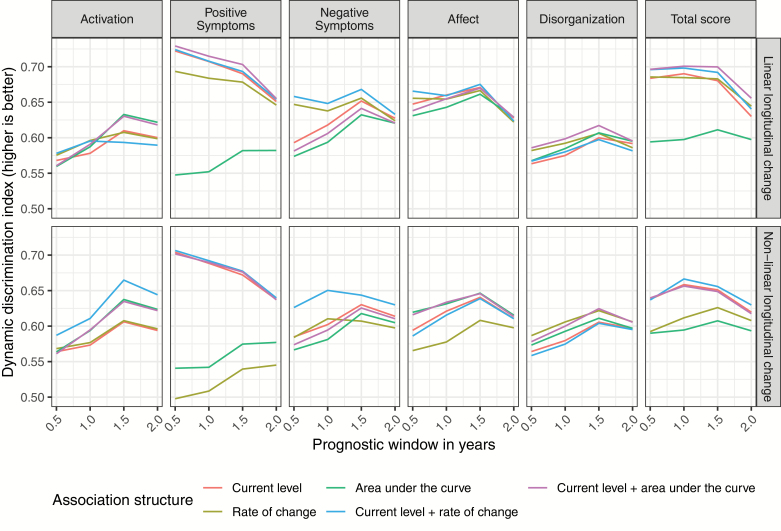
The cross-validated DDI values for the 60 different joint models are shown in figure 2 (for the IPE, see supplementary figure 2).

Fig. 2.

Cross-validated dynamic discrimination index values for the prognostic windows of 0.5, 1, 1.5, and 2 years for the 60 different joint survival models.

Regarding the choice of the time-dependent predictor, we found that the inclusion of BPRS-E total as time-dependent predictor led to the best average cross-validated discriminative performance (DDI = 0.645), followed by BPRS-E positive symptoms (DDI = 0.644), and affective symptoms (DDI = 0.632). In terms of calibration, the best performance was achieved by negative symptoms (IPE = 0.067), followed by affective symptoms (IPE = 0.068) and the total score (IPE = 0.069).

Discrimination on average was higher when change in symptoms over time was modeled linearly as compared to nonlinearly (average DDI = 0.631 vs 0.611), whereas calibration was very similar (IPE = 0.070 vs 0.069).

Regarding association structures, the current value (DDI = 0.627) on average discriminated better than the rate of change (DDI = 0.611) and AUC (DDI = 0.598), whereas calibration was very similar (average IPE: 0.070, 0.069, and 0.069, respectively). Combining the current value with the rate of change (DDI = 0.637) or the AUC (DDI = 0.633) led to a slightly better discriminative performance.

Final Joint Model

The best cross-validated discrimination for the prognostic time windows of 0.5, 1, and 1.5 years was achieved by the joint model that included the positive symptoms as dynamic predictor, modeled the change over time as linear, and used the current value and AUC as association parameters (DDI_{0.5 years} = 0.729; DDI_{1 year} = 0.715; DDI_{1.5 years} = 0.703). The best discrimination for the prognostic time windows of 2 years was achieved by a model that used the BPRS-E total as dynamic predictor and otherwise used the same specification (DDI_{2 year} = 0.656). Because the first model had a better average performance (mean DDI = 0.701 vs 0.688) and may be easier to use in clinical practice (ie, only 4 items instead of 24 need to be repeatedly assessed), we chose this model as our final model (table 2). This model was implemented in a web-based risk calculator (http://www.fepsy.ch/DPRP/, last accessed June 14, 2019).

Table 2.

Summary of final joint model

	Coef	P value	HR	CI
Longitudinal submodel
Intercept	0.40	<.001***
Time (years)	-0.15	.053
Survival submodel
BPRS-E disorganization	-0.04	.926	0.96	(0.59–1.43)
Years of school education	-0.22	.026*	0.80	(0.65–0.97)
Assoc. (current value) of positive symptoms	4.97	<.001***	144.08	(33.74–1004.08)
Assoc. (area under the curve) of positive symptoms	-1.12	.002**	0.33	(0.17–0.63)

Note: Coef, regression coefficient; HR, hazard ratio; CI, 95% confidence interval of HR; BPRS-E, Brief Psychiatric Rating Scale-Expanded; Assoc., association parameter.

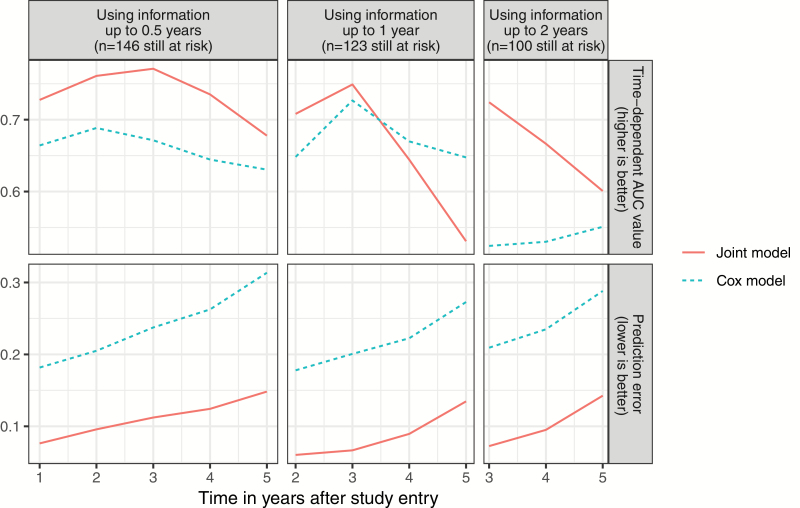
The cross-validated prognostic performance of the final joint model as compared to a traditional Cox model including only years of education, BPRS-E disorganization, and BPRS-E positive symptoms as static predictors is shown in figure 3. As can be seen from figure 3, the joint model achieved better discriminative and calibrative performance than the Cox model for most time points and lengths of follow-up.

Fig. 3.

Cross-validated time-dependent area under the receiver operating characteristic curves values and prediction errors for the best performing joint survival model (red, solid line) and a cox regression model predicting transition to psychosis from baseline variables only (blue, dotted line).

Because BPRS-E disorganization was not a significant baseline predictor in the final joint model, we also evaluated the prognostic performance when this predictor was removed from the final model. The performance did neither improve nor worsen when this predictor was eliminated (see supplementary table 1).

Discussion

This is the first study to develop and validate a dynamic prognostic model to predict psychosis onset in CHR-P individuals over a relatively long follow-up period of 5 years. Sixty different dynamic prognostic models were compared to each other and to a static prognostic model with regard to their internally validated prognostic performance. This study demonstrated that using extended specifications of joint models improved the prognostic performance and dynamic prediction fared better than static prediction.

Our first aim was to identify the most important time-dependent predictors of psychosis onset in CHR-P patients and to explore the prognostic performance of various extensions of joint models.²⁴ Our study revealed that (1) BPRS-E positive symptoms and the BPRS-E total score were the most important time-dependent predictors, (2) modeling the change in symptoms over time with a nonlinear function did not improve prediction, and (3) the hazard of transition was more strongly associated with the current severity of repeatedly assessed psychopathological symptoms over time than with their current rate of change or their cumulative effects since baseline. However, a slightly superior performance was achieved by combining the current severity with the cumulative effect or current rate of change. Hence, our primary hypothesis was confirmed.

Our finding that BPRS-E total and BPRS-E positive symptoms are the strongest time-dependent predictors is consistent with the results of Yuen et al,²⁷ who also found that these 2 variables had the strongest effect among all tested variables. However, while Yuen et al²⁷ evaluated the prognostic accuracy only at the 1-year follow-up, we calculated the cross-validated DDI over a follow-up period of 5 years using different prognostic windows and thereby could also disentangle the value of these variables for different scopes of prognostication. Our results suggest that positive symptoms during the follow-up tend to better predict the near future, whereas BPRS-E total tends to better predict the more distant future. This makes intuitive sense because BPRS-E positive symptoms consists of the 4 BPRS-E items that were also used to determine transition to psychosis. The BPRS-E total scale on the other hand is a measure of general psychopathology. It might therefore be that for the prediction of the far future, disease-unspecific factors are more important.

Although there is increasing recognition that psychopathological symptoms change dynamically rather than gradually before disease onset and that this could be exploited to improve the prediction of full-threshold disorders,²² nonlinear modeling of change in symptoms did not lead to improved prediction in this study. One possible explanation is that our effective sample size—although slightly larger than in previous studies^25–27—was not large enough and the signal-to-noise ratio was too small to reliably estimate such complex relationships and therefore a simpler model was preferred.

This study also explored 5 different association structures between the longitudinal and survival submodels and thereby could gain important insights into the specific relationships between psychopathological symptoms during the follow-up and psychosis onset. We found that for the most important predictors (ie, BPRS-E positive symptoms and total score), the current value in these variables at any time t was more strongly associated with the hazard of transition at the same time t than the current rate of change (ie, slope) or the cumulative effect (ie, AUC). However, it should be noted that all 3 showed a positive and significant relationship. Furthermore, current value models fared only slightly better than rate of change models and the best performance was achieved by models combining the current value with the cumulative effect or current rate of change.

Accordingly, the overall best performing model included BPRS-E disorganization and years of education as static predictors and the current and cumulative values of BPRS-E positive symptoms as dynamic predictors. This model was therefore implemented as an online risk calculator (Dynamic Psychosis-Risk Prediction, DPRP). Whereas the current value of BPRS-E positive symptoms was significantly positively associated with the hazard of transition, the cumulative effect was significantly negatively associated. Thus, the model predicts a particularly strong risk of transition if the patient currently experiences a high level of BPRS-E positive symptoms and at the same time had relatively few such symptoms during the previous follow-up period or, in other words, if the severity of BPRS-E positive symptoms is currently unusually high for that patient. Although BPRS-E disorganization was selected as important baseline predictor by the LASSO, it was no longer a significant baseline predictor in the final joint model and its omission did not change the prognostic performance, suggesting that its prognostic information becomes redundant when current and cumulative values of BPRS-E positive symptoms are included as dynamic predictors.

In accordance with our secondary hypothesis, we could demonstrate that the final joint model predicted psychosis with a considerably higher accuracy than a traditional Cox model using only the static predictors. For example, when using follow-up data up to 1 year, the joint model predicted psychosis at 2 years with a time-dependent cross-validated AUC value of 0.709, whereas the corresponding value of the Cox model was 0.648. According to Šimundić,⁴⁶ this indicates a “good” accuracy for the joint model and a “sufficient” accuracy for the Cox model. The joint model outperformed the Cox model particularly in terms of calibration.

Strengths and Limitations

Our study has the following strengths: First, compared to the existing studies applying joint models to CHR-P samples,^25–27 the follow-up duration was considerably longer. Second, whereas previous studies only applied basic joint models (ie, only considered the current value of a linear longitudinal process), this study explored various extensions of joint models. Third, while previous studies have only assessed the apparent prognostic performance, which can be overoptimistic due to overfitting,¹⁰ we calculated the internally validated prognostic performances. Fourth, in addition to discrimination, we also assessed calibration, which is an important aspect of predictive performance that is often neglected.^10,13,47 Fifth, our final model was implemented as web-based risk calculator.

One limitation is that the model implemented in our risk calculator has not yet been externally validated. Hence, it is unknown how well it predicts transition to psychosis when applied to data collected at different early detection centers. A further limitation is that the effective sample size, albeit slightly larger than in previous studies applying joint models to CHR-P data,^25–27 might not have been large enough to appropriately test more complex joint models. Future studies should therefore use larger samples to explore whether more complex joint models would improve prediction. Another potential limitation is that we also included patients fulfilling only the unspecific risk category (URC) of the BSIP, which has been shown to be associated with a lower transition risk compared to other CHR-P subgroups.³² Furthermore, the average age of our sample might be slightly higher than in other studies as we have excluded patients younger than 18 years and did not have an upper age restriction. However, because only 19.4% of the sample met the URC and because the overall transition risk was in accordance with the most updated meta-analytical estimate,⁷ we believe that our sample is still comparable to other CHR-P samples. It should also be noted that follow-up visit intervals increased with increasing follow-up duration in this study. Although this does not violate assumptions of the joint model, it might have led to a more reliable estimation of the longitudinal process at the beginning of the follow-up as compared to later time points. A further limitation is that to ease applicability in clinical routine and restrict overfitting, only a small set of sociodemographic and clinical baseline predictors were considered in this study. Future studies should also explore the potential prognostic advantage of using additional important sociodemographic and clinical variables that are likely to be associated with later transition and easy to obtain in clinical practice, such as functioning, urbanicity, immigration status, and race. The prognostic performance might also be improved by including baseline predictors from other domains, particularly neurocognition, electrophysiology, neuroimaging, and blood biomarkers.¹² At the same time, because these predictors are harder to obtain in clinical practice and the clinical utility for predicting the onset of psychosis in CHR-P is not completely clear, the ultimate added prognostic values of these measures must be carefully examined.^10,14

Conclusion

This study confirmed that the use of extended joint models can improve the prediction of psychosis onset in CHR-P patients. We developed the first online risk calculator predicting psychosis onset using joint modeling. The risk calculator can be easily applied in clinical practice as only few sociodemographic and clinical data are required and its predictions can be continuously updated during the follow-up.