Preprocessing, analysis and quantification in single-voxel magnetic resonance spectroscopy: Experts’ consensus recommendations

Abstract

Once a magnetic resonance spectroscopy (MRS) dataset has been acquired, several important steps must be taken to obtain the desired metabolite concentration measures. First, the data must be preprocessed to prepare them for analysis. Next, the intensity of the metabolite signal(s) of interest must be estimated. Finally, the measured metabolite signal intensities must be converted into scaled concentration units employing a quantitative reference signal to allow meaningful interpretation. In this paper, we will review these three main steps in the post-acquisition workflow of a single-voxel MRS experiment (preprocessing, analysis and quantification) and provide recommendations for best practices at each step.

Graphical Abstract

In this article, we summarize the three main stages in the post-acquisition workflow of an in vivo magnetic resonance spectroscopy (MRS) experiment: preprocessing, to prepare the acquired raw data; analysis, to estimate the signal intensities of the observed spectral peaks; and quantification to convert the estimated signal intensities into meaningful concentration units. We describe the most important and commonly used approaches in each stage, and we provide experts’ recommendations for best practices.

Introduction

The goal of an in vivo MRS experiment is to estimate the relative or absolute concentrations of tissue metabolites within a specific anatomical region of interest. Once the time domain MRS data have been acquired, several steps are needed in order to get meaningful and reliable concentration estimates. First a series of preprocessing steps should be applied to prepare the spectrum for analysis. Next, analysis of the processed dataset is performed, often by peak fitting, to estimate the metabolite signal intensities. Finally, the unitless signal intensity measures are converted into scaled concentration estimates, a process we refer to here as quantification, to enable meaningful interpretation and comparisons of tissue metabolite levels between subjects and groups, regardless of the site of acquisition or other measurement conditions. Each of these three steps is critically important; errors in any of them can reduce the reliability of, or completely invalidate, the obtained metabolite concentration measures.

In this article, we focus on these three important steps in the workflow of single-voxel ¹H-MRS following data acquisition: preprocessing, spectral analysis; and quantification. We describe some of the most important and commonly used approaches in each step, and provide recommendations for best practices (see Tables for all recommendations). Finally, we list common pitfalls in the post-acquisition workflow and suggest ways to avoid them. Though the emphasis in this article will be on single-voxel ¹H-MRS, with attention to the challenges of its application in the brain, many of the general principles of the post-acquisition workflow apply to MRS data obtained from other nuclei, other regions of the anatomy, and MR spectroscopic imaging (MRSI) data. For more information regarding MRSI specific processing and analysis methods, the reader is referred to the article on MRSI in this special issue by Maudsley et al¹.

Preprocessing

Preprocessing of MRS data, sometimes also simply called “processing”, describes any operation, or series of operations, that is applied to the acquired raw MRS data (free induction decays, FIDs) to prepare them for analysis. There are three main reasons for preprocessing in MRS. First, MRS data are unavoidably degraded by experimental imperfections (e.g. eddy currents, scanner drift, subject motion). Since spectral fitting models generally do not take all of these imperfections into account, some preprocessing operations are needed to remove the imperfections, to the extent possible, in advance. Second, raw data are almost always multi-dimensional, with multiple acquired signal averages by multiple coil channels from parallel receive array coils. Thus, some preprocessing is needed to combine these signals and reduce the data into a (usually) one-dimensional spectrum that can be analyzed. Finally, some other preprocessing operations, such as Fourier transformation, phasing, apodization and zero-filling, are not strictly related to data quality, but can be used to aid in visual interpretation or peak fitting performance.

Note that several of the preprocessing routines described below require access to the individual averages or transients, stored independently for each receiver channel. Accordingly, we strongly recommend the use of data formats in which the individual transients and individual receiver channels are preserved. At present, each MRI vendor has its own unique data formats, and each format differs in regards to which dimensions are preserved and which have been collapsed (implying some ‘online’ preprocessing, See Table 1 below). The lack of cross-vendor standardization in terms of MRS data formats and online preprocessing strategies can be a source of confusion, and represents a major unmet need in the MRS community².

Table 1.

Scanner vendor data formats

Vendor	Data Format	File naming convention	Dimensionality (Default)	Comments
GE	p-file	P01234.7	Np x Ntra/Npc	-By default, RF coil channels pre-combined online; and groups of Npc phase cycle steps pre-combined online. The resulting number of separately stored transients is Ntra/Npc. -However, the p-file can be customized to preserve or combine any/all dimensions. -Both water and metabolite data can may be stored within the same series.
Philips	data/list	filename.data filename.list	Np x Ntra	-Water and metabolite data are normally stored in separate files, but some pulse sequences may store both within the same series. -Depending on settings, water unsuppressed transients may be interleaved within groups of water suppressed transients, and frequency drift correction may have been applied. -Two files for each acquisition: .data file contains the acquired signal data; .list file contains header info.
	sdat/spar	filename.sdat filename.spar	Np x Ntra/Npc	-Separate files for water and metabolite data. -Two files for each acquisition: .sdat file contains the acquired signal data; .spar file contains header info.
Siemens	Twix	filename.dat	Np x NRF x Ntra	-All dimensions (RF channels, transients) are preserved without modification. - Water and metabolite data are normally stored in separate files, but some pulse sequences may store both within the same series.
	rda	filename.rda	Np	-By default, all dimensions (except time/spectral dimension) are pre-combined online. -However, .rda files can be customized to preserve or combine any/all dimensions. - Water and metabolite data are normally stored in separate files, but some pulse sequences may store both within the same series.
	.ima	filename.ima	Np	-By default all dimensions (except time/spectral dimension) are pre-combined online. -However, .ima files can be customized to preserve or combine any/all dimensions. In this case, each individual transient is stored in a separate .ima file. - Water and metabolite data are normally stored in separate files, but some pulse sequences may store both within the same series.
Bruker	fid-file	fid	Np	-All dimensions (except time/spectral dimension) are pre-combined online. -Separate files for water and metabolite data.
	fid.raw file	fid.raw (Up to PV 5)	Np x Ntra	-RF channels are pre-combined online. -All transients are preserved without modification. -Separate files for water and metabolite data.
	job0 file	rawdata.job0 (PV 6 and later)	Np x Ntra	-RF channels are pre-combined online. -All transients are preserved without modification. -Separate files for water and metabolite data.
Varian/Agilent	Fid file	Fid	Np x NRF x Ntra	-Full flexibility to preserve or collapse all dimensions. -Separate files for water and metabolite data.
DICOM (any vendor)	DICOM	Various e.g.: filename.dcm	Np	-By default, all dimensions are collapsed. -However, dicom files can be customized to preserve or combine any/all dimensions. In this case, each individual transient may be stored in a separate dicom file. -Separate files for water and metabolite data.

N_p = number of points in the FID

N_RF = number of RF channels

N_tra = number of transients

N_pc = number of phase encoding steps in one phase cycle

Preprocessing operations to remove/correct spectral imperfections

Correction of eddy current effects

Rapid gradient switching gives rise to unwanted short-lived fluctuation of the B₀-field, called eddy current effects, which can persist for hundreds of milliseconds after a gradient switching event. If the acquisition window occurs close to the end of a gradient pulse, a multi-exponential decaying B₀-field component may exist during the early part of the acquisition window, giving rise to a time-dependence in the resonance frequencies of the acquired FID. This unwanted effect distorts spectral line shapes and can severely impact the robustness of further spectral analysis.

The most common method of dealing with this issue involves collecting an unsuppressed water spectrum, centred on the water resonance, using identical gradient strengths and timings as in the water suppressed dataset³. Any time-dependence in the frequency of the water signal will be observed as a non-linearity in the phase of the FID signal. Since this phase function essentially describes the time-dependence of the field offset observed in both water-suppressed and water-unsuppressed scans, the correction involves simply subtracting this phase function from both the water-suppressed and water-unsuppressed FID signals. This simple approach is remarkably effective in most cases, and results in FID signals that are essentially free of residual eddy current effects. Related methods exist for correcting eddy current effects while simultaneously restoring purely Lorentzian line shapes by applying both phase and amplitude scaling to the acquired FID^4,5. An eddy current correction is illustrated in Figure 1.

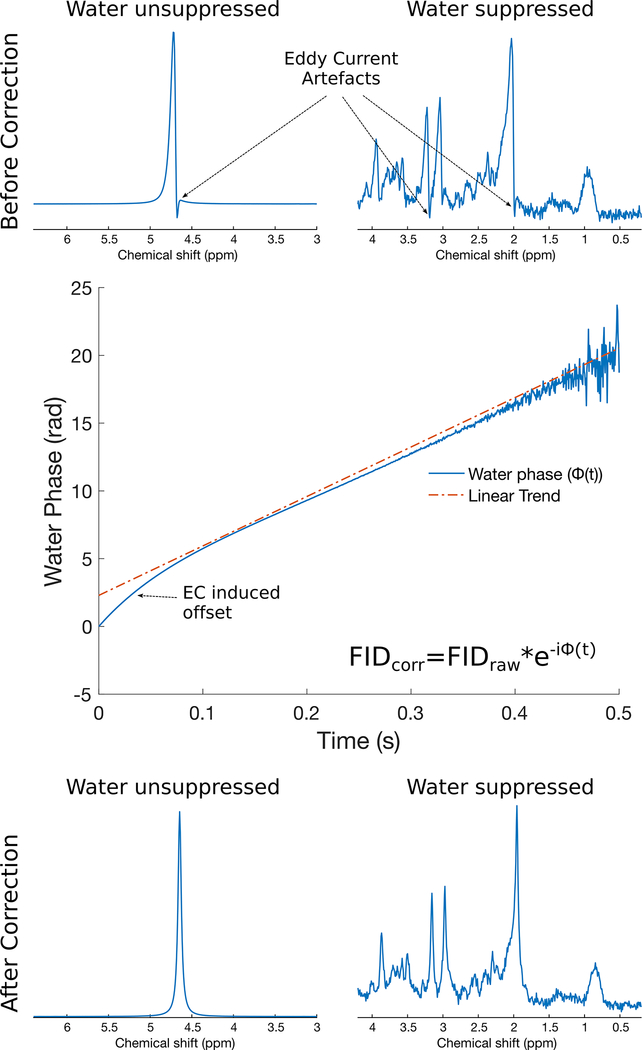
Figure 1.

Eddy current correction in synthetic 3T human brain PRESS spectra with TE=30 ms. In the top panel, water reference (left) and water suppressed (right) spectra with eddy current artefacts are shown. The central panel shows the phase evolution of the water reference FID before eddy current correction. Any deviation from linearity in this phase function is the result of the eddy current effect. The bottom panel shows the same water reference (left) and water suppressed (right) spectra following eddy current correction.

Motion correction

Subject motion has pronounced effects on spectral quality. Despite all efforts to control subject motion, some small amount of motion is practically inevitable in the timeframe of an MRS scan. One practical way to test for gross motion is to acquire a quick localizer image immediately before and after the MRS scan and compare the position of the anatomy of interest between those two scans. Better yet, the collection of rapid navigator images between each repetition^6–11, or optical tracking^12,13 can be used to precisely monitor subject motion, and even update the acquisition volume in real time to compensate. Although highly promising, these prospective motion correction strategies for ¹H-MRS are not yet in mainstream use, and thus retrospective correction methods are commonly employed.

Very small amounts of motion, for example due to normal physiological motion (breathing, cardiac pulsation, swallowing) or small bulk movements of less than a few millimetres, have a minor effect on spectral quality and are therefore relatively benign in most cases. These minute motions result in small changes in the frequency and phase of the individual transients which can easily be corrected by a retrospective frequency and phase drift correction (see below). In the case of large amounts of motion such as gross motion of the head or limbs, much larger spectral distortions are observed¹⁴. Moreover, severe gross motion can lead to unwanted sampling of tissue outside the region of interest. In this case, it may be necessary to either remove the transients that are most severely affected by motion¹⁵, or to discard the dataset altogether. To assess motion severity in a quantitative and unbiased way, signal reliability tests have been proposed¹⁶. An example of the removal of motion corrupted transients is illustrated in Figure 2a.

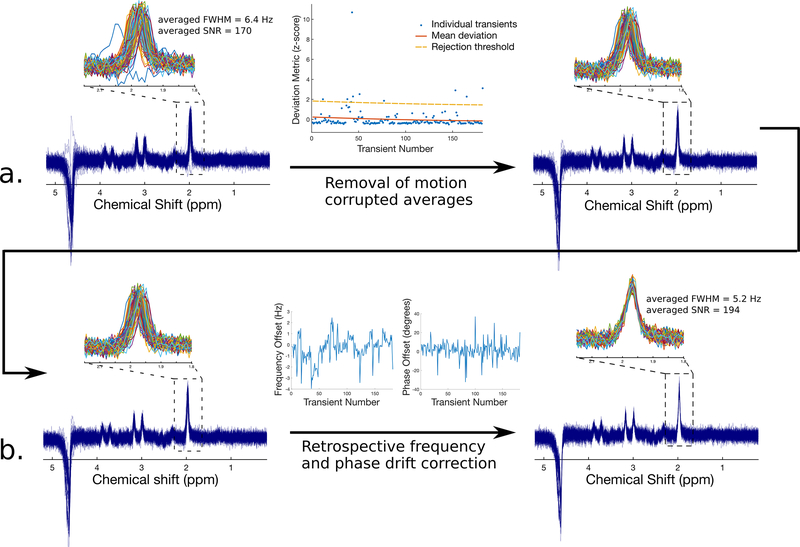
Figure 2.

Removal of corrupted transients and retrospective frequency and phase drift correction from a 3T human brain PRESS acquisition with TE=270 ms. Removal of motion corrupted transients is shown in the top panel (a). Corrupted transients stand out as noticeably different from the others, and are effectively removed using an unsupervised outlier removal procedure (see Ref. 15). Subsequent retrospective frequency and phase drift correction is shown in the bottom panel (b). Following drift correction using spectral registration, the individual transients have improved coherence and can now be averaged. These processing steps yield a marked improvement in both the FWHM and SNR of the final averaged spectrum.

Retrospective removal of frequency and phase drifts

The main magnetic field of an MRI scanner, B₀, is subject to subtle temporal drift (often called scanner drift), due to heating and cooling of the ferromagnetic passive shim elements, which are in thermal contact with the gradient coils¹⁷. As a result, frequency drifts are observed during the course of most MRS experiments. The magnitude of these drifts can vary greatly from scanner to scanner and is also affected by use of gradient-intensive pulse sequences before the MRS scan, but normally ranges between 1–10 Hz of total drift during the course of a typical MRS acquisition (i.e. 2–10 minutes). Moreover, as mentioned above, physiological motion or small bulk motion during the MRS scan leads to additional frequency and phase offsets, independent of scanner drift. If not corrected, these frequency and phase drifts will lead to broadening of spectral peaks, reduction in signal-to-noise ratio (SNR), and line shape distortion.

Several methods exist for retrospective correction of frequency and phase drifts. Some involve tracking the frequency and phase of the residual water peak to estimate and correct the frequency and phase drifts^11,18–21, while others make use of separately acquired navigator echoes²². If a residual water peak or navigator echoes are not available for frequency and phase estimation, individual metabolite peaks can also be used²³. More recently, methods such as spectral registration²⁴, RATS²⁵ or other variants^26,27 have been proposed and involve alignment of each transient, in either the frequency domain or the time domain, to a reference spectrum for estimation and correction of the frequency and phase offsets. The advantage of these latter methods is that they make use of the full spectrum to perform the correction, and do not rely on the presence of any one particular resonance. Most algorithms optimize the frequency and phase in a single step, rather than sequentially. An example of retrospective frequency and phase drift correction is illustrated in Figure 2b. In some cases, an online frequency drift correction may be employed by the scanner software. While the use of such online corrections is recommended, it may be advantageous to apply an additional retrospective drift correction offline, since online corrections may correct frequency, but not phase drifts.

Frequency and phase drift correction methods that rely on internal signals for alignment will inevitably fail if the SNR of the individual transients is low (for example if the voxel is very small). In such cases, one can average successive groups of 4–8 transients to improve SNR, and then apply a drift correction to the resulting series. Alternatively, a method called metabolite cycling^28–31 has been proposed in which the water peak is not suppressed, but the magnetization of the metabolites is inverted on every other acquisition. In this way, the high-SNR water peak can be used for drift correction, even if the metabolite SNR is low. When the averages are combined the water peak essentially vanishes due to its alternating phase from shot-to-shot.

Alignment and subtraction of sub-spectra

¹H-MRS pulse sequences involving subtraction are increasingly common. Some examples include J-difference editing sequences such as MEGA-PRESS³² and HERMES³³; or the SPECIAL sequence³⁴, which uses subtraction to achieve localization. If the sub-spectra in these acquisitions are not properly aligned prior to subtraction, the resulting difference spectrum may be corrupted by unwanted subtraction artefacts that can impact quantification.

Alignment of subtraction sub-spectra can be performed using the same techniques that are used for removal of frequency and phase drift in conventional spectra (e.g. spectral registration, etc.)^35,36. However, if subtraction sub-spectra are vastly different in appearance, conventional alignment procedures may not perform well, and dedicated routines may be required for optimal alignment. Dedicated alignment algorithms have previously been proposed for MEGA-PRESS^37,38, HERMES³⁹, and SPECIAL¹⁵.

Substantial frequency drift during J-difference edited acquisitions results in reduced editing efficiency, due to offsets in the frequency of the highly selective editing pulses. This effect is not corrected by retrospective alignment of the subtraction sub-spectra. Instead, drift-related reductions in editing efficiency must be addressed at the level of the acquisition (using real time frequency updating¹⁰), or in the analysis (by accounting for drift-related editing efficiency losses in the basis set⁴⁰). For more information on this topic, the reader is referred to the article on spectral editing in this special issue by Choi et al⁴¹.

Nuisance peak removal (residual water, lipids, spurious echoes)

In vivo ¹H-MRS acquisitions are specifically designed to suppress nuisance signals such as water and outer volume signal. However, perfect suppression is challenging, as the signals to be suppressed are usually orders of magnitude larger than the signals of interest. As a result, noticeable contamination of spectra is a relatively common occurrence, especially in challenging brain regions (regions very close to the scalp, or regions with poor B₀ homogeneity), and minimizing signal contamination is an important aspect of data preprocessing. Note that even though nuisance signals can sometimes be addressed via processing strategies, it is always preferable to remove these contaminating signals at the level of the acquisition.

Poor water suppression can be handled in two ways. Residual water signal can be removed prior to spectral analysis by fitting the peak to a line shape function – usually either Gaussian, Lorentzian, or Voigt (combination of Gaussian and Lorentzian) – or to a series of line shape components via singular value decomposition, and then subtracting the resulting fit from the spectrum^42,43. Another approach is to not remove the water peak, but to perform analysis using a fitting model that incorporates a water peak (or the sloping baseline that results from the residual water peak). Lipid contamination, like poor water suppression, can impact spectral quantification and can be dealt with in a similar manner, with the main difference being that contaminating lipid peaks are generally much broader than residual water peaks and often overlap with metabolites of interest, often making lipid contamination more difficult to correct.

Spurious echoes are another commonly observed nuisance signal in in vivo ¹H-MRS. These are typically caused by unwanted coherence pathways and often originate from tissues outside the region of interest. The issue of unspoiled coherences is best dealt with by modifications to the acquisition, such as changing the timing or amplitudes of the spoiler gradients, improving B₀ homogeneity, or improving the phase cycling scheme^14,44. A few preprocessing approaches have been proposed to identify and remove spurious echoes based on filtering, or deep learning⁴⁵, but these methods are still relatively new and may require further development before being deployed widely. Spurious echoes may occur near the end of an FID, in which case apodization can be used to greatly reduce their appearance; but users should analyze the resulting data with caution, since apodization is not recommended before spectral analysis (see Apodization section below). An example of commonly observed spurious echoes is shown in Figure 3.

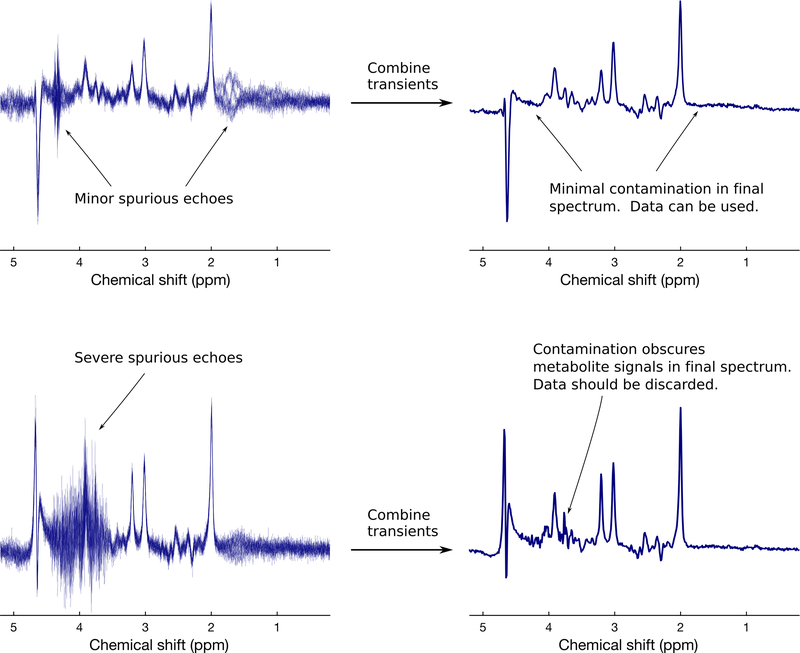
Figure 3.

Examples of spurious echoes in 3 T human brain MRS data (TE=68 ms). In the top panel, minor spurious echoes are observed in the individual transients around 1.8 ppm and 4.3 ppm. However, following averaging of the phase cycled scans, these are effectively removed, so that this spectrum can be safely analyzed. In the bottom panel, severe spurious echoes are observed in the individual transients between 3.5–4.6 ppm. Even after combining these phase cycled averages, visible contamination remains (e.g. overall jagged character of the spectrum between 3.6–4.4 ppm, distortion of the glutamate-H2 doublet at 3.75 ppm, and distortion of the myo-inositol peak at 4.1 ppm), and this spectrum should therefore be discarded.

Recommendations for the preprocessing operations to remove/correct spectral imperfections are listed in Table 2.

Table 2.

Recommendations for preprocessing operations to remove/correct spectral imperfections.

Name of operation	Recommendation
Eddy current correction	- An eddy current correction should be applied routinely during the preprocessing of any in vivo MRS dataset. - For accurate eddy current estimation, the unsuppressed water scan must be collected from the same voxel location and using the exact same gradient scheme as the water suppressed data (e.g. turn only water suppression RF pulses off for unsuppressed water acquisition.) - Some analysis software packages (LCModel54, Tarquin61, FiTAID62) perform an eddy current correction at the analysis stage, obviating the need to perform this step in advance.
Motion correction	- For small amounts of motion, correct the resulting frequency and phase jitter using a frequency and phase drift correction (see below). - More severe bulk motion is indicated by individual transients that stand out as significantly different from the rest. Identify these “corrupted” transients either by visual inspection or by unsupervised outlier detection, and remove them prior to analysis. - If more than ~30% of the acquired transients are corrupted by motion, we recommend discarding that particular dataset since a) the likelihood of significant unwanted sampling of tissue outside the region of interest is high, and b) the continued removal of transients has a detrimental effect on the final SNR.
Frequency and phase drift correction	- Frequency and phase drift correction should be applied routinely for in vivo MRS, provided that there is enough SNR in the individual (or a few summed) transients to achieve robust frequency and phase estimation. - There are many effective methods for retrospective frequency and phase drift correction. We recommend methods that make use of the full spectrum (unless a weakly suppressed water peak is used for alignment). -Where available, the use of vendor-provided online drift corrections is recommended, provided that their performance has been well-validated; but offline retrospective drift correction is still recommended.
Alignment of subtraction sub-spectra	- Subtraction-based MRS techniques should always be coupled with an appropriate alignment procedure to align sub-spectra prior to subtraction. The choice of alignment procedure depends on the acquisition method. - In J-difference edited MRS, retrospective alignment of subtraction sub-spectra does not restore drift-induced reductions in editing efficiency.
Nuisance peak removal	- It is always preferable to remove nuisance signals at the level of the acquisition, rather than via preprocessing. - If necessary, large water and lipid signals can either be removed prior to analysis, or accounted for in the analysis model. Alternatively, one can adjust the frequency range over which spectral analysis is performed, in order to avoid nuisance signals. - Spurious echoes should be identified by visual inspection. - Since processing methods to remove spurious echoes are not widely available, we recommend that spectra contaminated by large spurious echoes should be discarded from further analysis, particularly if the spurious echoes are obscuring the metabolite peaks of interest.

Preprocessing operations to reduce dimensionality

RF coil combination

Most modern MRI systems are equipped with highly parallel RF receiver arrays, sometimes with as many as 64 or even 128 elements in close proximity to the head. Each of the receiver elements will detect different signal and noise amplitudes as well as a different signal phase offset that will depend on the voxel location and head position relative to the coil element. Combining the signals from the various coil elements should be done in such a way that maximizes the SNR of the resulting spectrum. In all cases, this requires 1) adjusting the phase of each channel so that all elements are phase coherent; and 2) applying an amplitude weighting to each channel for optimal SNR combination. The RF channels with the strongest signals are given the highest weighting, while the RF channels with the weakest signals are given the lowest weighting^46,47. The amplitude, phase and noise terms necessary for coil combination can generally be determined from the high-SNR unsuppressed water data.

Signal averaging

Signal averaging is the process of taking the average of the acquired transients (the sum of all transients divided by the number of transients) to produce a resultant spectrum with increased SNR. The convention of averaging transients ensures that the signal remains constant, while noise is reduced (subjectively); thus, subsequent quantification of signal intensity in “averaged” spectra requires no consideration of the number of transients. Despite the fact that the arithmetic mean is by far the most common approach for combining transients, some authors have proposed taking the median of the acquired transients as an alternative approach, suggesting that the median is more robust against temporal instabilities in the signal¹⁶.

Recommendations for preprocessing operations to reduce dimensionality are listed in Table 3.

Table 3.

Recommendations for preprocessing operations to reduce dimensionality.

Name of operation	Recommendation
RF coil combination	- Most vendors provide a data output option in which an acceptable RF coil combination has already been performed. - However, if the raw data is provided with coils uncombined, the user must perform coil combination. - Coil combination should include appropriate complex weights (phase and amplitude). - Complex weights should be determined using an unsuppressed water scan. - The amplitude weighting should be generally determined by signal/noise2 as per Hall et al.46, although more sophisticated approaches may yield improved results for certain coil designs and voxel locations.
Signal averaging	- We recommend combining transients using the arithmetic mean (the sum of all transients divided by the number of transients). Although less robust to instabilities across transients than the median, we suggest dealing with these instabilities through removal of motion corrupted averages and frequency/phase drift correction prior to averaging. -If motion corrupted transients have been removed, divide only by the number of transients that were retained. - Avoid combining averages using the simple sum of the acquired transients (i.e., the sum should always be divided by the number of transients). - Likewise, subtraction operations used in difference spectroscopy should also be treated as an averaging operation, i.e., when subtracting sub-spectra of a MEGA-PRESS difference editing experiment or a SPECIAL localization experiment, the difference spectrum should always be divided by 2 (the number of transients involved in the subtraction) following subtraction.

Other preprocessing operations

Fourier transformation

Conversion of the discrete time-domain FID signal into a spectrum is performed using a discrete Fourier transformation such as the fast Fourier transform (FFT). Most software programming languages offer a built-in implementation of the FFT, and all MRS software packages will perform the Fourier transformation by default. To convert from the spectral domain back to the time domain, the discrete inverse Fourier transform should be used.

Phasing

Whereas MRI signal intensities are generally displayed as the magnitude of the complex signal intensity at each voxel, it is most common in MRS to display the real part of the complex signal, to avoid unwanted spectral broadening. As a result, the spectral appearance is greatly influenced by the phase of the complex spectral points, which depends on many factors including cable lengths, receiver phase, RF pulse phase, voxel position, pulse sequence timing, etc. In most cases, an “in-phase” spectrum is one in which the prominent singlet peaks display an absorption line shape, meaning that they are upright and symmetric (assuming minimal eddy current artefacts). Some spectral analyses may require that the spectrum first be “in-phase”, but many common analysis packages either perform an automatic phasing step prior to fitting, or include phase as a fitting parameter, so it is often not necessary for the user to perform this step in advance.

Phase correction involves either adding a constant phase to each point in the spectrum (zero-order phasing), or adding a linear phase shift as a function of frequency (first-order phasing), until the spectrum appears “in-phase”. Manual zero- and first-order phasing is a common approach, however, identifying a correctly phased spectrum takes practice and can be somewhat subjective. Therefore, automated phasing routines^48–50 can be useful.

Apodization

Apodization is a procedure aimed at attenuating the noise in an MR spectrum, while preserving the signals of interest. Conveniently, the signals of interest are strongest at the beginning of the FID signal in the time domain, whereas the later part of the FID is mostly noise. Thus, by applying an apodization function in the time domain which gives a higher weight to the early timepoints and a lower weight to the later timepoints, the desired effect is achieved. Apodization also minimizes truncation artefacts that occur due to incomplete FID decay during the acquisition window. Common apodization functions include an exponential or Gaussian decay. Although apodization reduces noise and generally improves SNR, it also has some unwanted consequences, such as broadening/distortion of spectral line shapes. As a result, apodization can have significant impact on analysis and quantification results, and is generally recommended for visual display purposes only.

Zero-filling

The digital resolution of an MR spectrum (frequency spacing between adjacent spectral samples) is given by 1/T_acq, where T_acq is the duration of the acquired FID signal. Thus, if the acquisition duration is especially short, the resulting spectrum may have limited digital resolution. This problem can be addressed by zero-filling (sometimes called zero-padding) whereby a train of zeros is added to the end of the FID signal. This artificially lengthens the FID (increases the value of T_acq) and therefore increases the digital resolution of the spectrum, without adding any additional noise. However, it’s important to realize that this operation amounts to an interpolation operation in the frequency domain and does not improve the actual resolution of the spectral peaks. For this reason, zero-filling before spectral analysis is not recommended. Nonetheless, zero-filling can be useful for visualization and display purposes, or for improving the stability of certain other operations such as evaluation of peak height, peak frequency, or linewidth.

Recommendations for other preprocessing operations are listed in Table 4.

Table 4.

Expert recommendations for other processing operations.

Name of operation	Recommendation
Fourier tansformation	- An implementation of a discrete Fourier transformation, such as the fast Fourier transform (FFT) should be used to convert the time-domain FID signal into a spectrum. - Conversion from the spectral domain back to the time domain should be performed using the inverse discrete Fourier transform.
Phasing	- Some common data analysis packages perform an automated phasing step prior to fitting, so it is often not necessary to perform a phasing step in advance of spectral analysis. - Phasing should generally be performed prior to displaying or inspecting a spectrum to enable easy visual interpretation. - Both manual and automated phasing routines are equally acceptable, but, visual verification of automatic phasing results is recommended.
Apodization	- Apodization can be useful for visualization purposes. - Not recommended to apodize data prior to spectral analysis – this can invalidate statistical assumptions associated with the fitting model.
Zero-filling	- Zero-filling before spectral analysis is not recommended. - May be helpful prior to some other processing routines such as peak fitting for linewidth estimation or center frequency estimation. - Use of zero-filling is recommended if increased digital resolution is required.

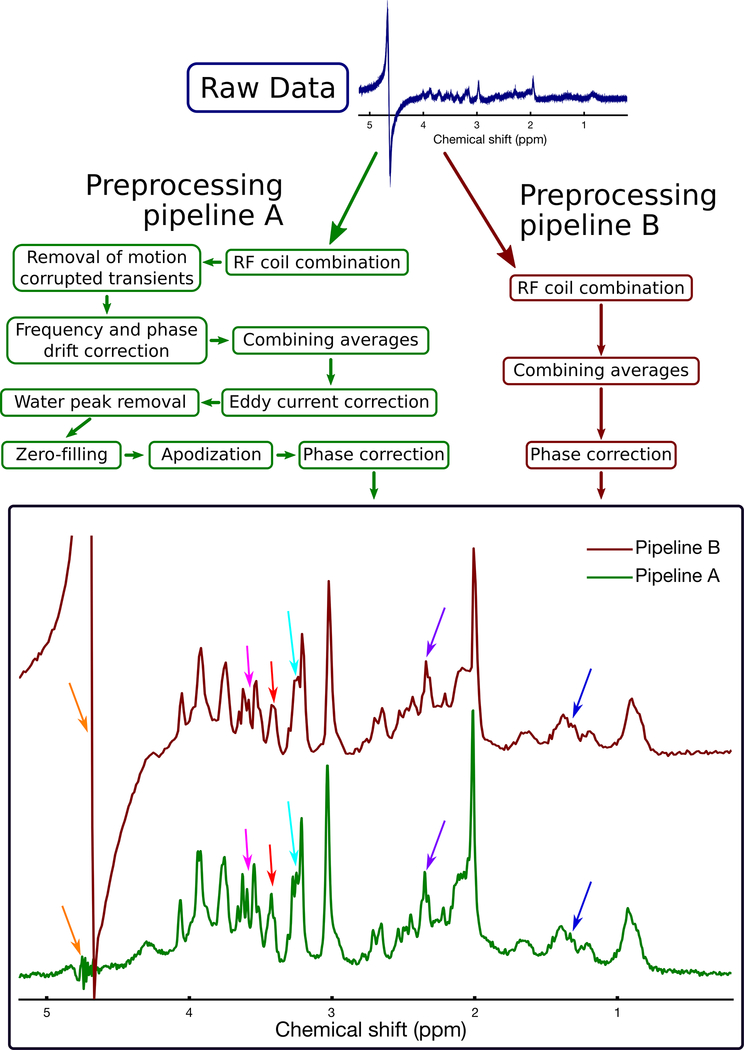
Figure 4 shows two preprocessing pipelines; one that includes only basic steps to combine the coils and transients (similar to the standard preprocessing pipelines provided by clinical scanner vendors), and a second involving additional steps to remove motion corrupted averages, to retrospectively correct frequency and phase drift, and to remove eddy current artefacts. When the same dataset is processed separately through these two pipelines, the resulting differences in spectral quality are apparent, highlighting the importance of removing motion corrupted scans and correcting frequency and phase drift.

Figure 4.

Illustration of two example processing pipelines, applied to the same raw data. The dataset was obtained from a rat brain using the PRESS sequence at 7 T with TE=11 ms. Processing pipeline B (dark red boxes, right side) includes only basic steps to combine the coils and transients (similar to the standard processing pipeline provided by clinical scanner vendors). Processing pipeline A (green boxes, left side) involves additional steps to remove motion corrupted averages, to retrospectively correct frequency and phase drift, and to remove eddy current artefacts. Pipeline A resulted in several noticeable improvements in spectral quality, including reduced water contamination (orange arrows), and improved visual definition of most spectral peaks, including lactate (1.3 ppm, dark blue arrows), glutamate-H4 (2.3 ppm, purple arrows), tCho (3.2 ppm, light blue arrows), taurine (3.4 ppm, red arrows), and myo-inositol (3.5 ppm, pink arrows). These improvements highlight the importance of using an appropriate processing pipeline. Note that as stated in the recommendations tables, zero-filling and apodization may be used to improve the visual appearance of the spectrum, but should not be performed prior to spectral analysis.

Following preprocessing, the user must judge whether the quality of the final processed spectrum is sufficient for meaningful analysis and quantification. This judgement should incorporate objective measures of spectral quality (linewidth and SNR), but may ultimately require consideration of factors that are difficult to quantify objectively, such as the presence of artefacts or nuisance signals. Recent advances in machine learning techniques have made it possible to objectively assess all of the above aspects of spectral quality in an automated fashion^51–53, thereby avoiding any potential user bias associated with visual inspection by human raters, but these approaches do not yet enjoy mainstream use.

Analysis

After preprocessing, the spectrum is ready for the next stage: spectral analysis. The goal of spectral analysis is to estimate the spectral peak areas (or equivalently, time-domain signal amplitudes) of the various metabolites of interest in the spectrum, as well as that of some reference signal. At this stage, the units of measurement are not important: only the relative raw signal intensities are needed. These will be converted to meaningful concentration units in the next stage (quantification). In this section, we will briefly summarize the process of spectral analysis and provide some basic recommendations.

The three most common ways of estimating MRS peak areas are 1) linear combination model fitting, 2) peak fitting, and 3) peak integration.

Linear combination model fitting

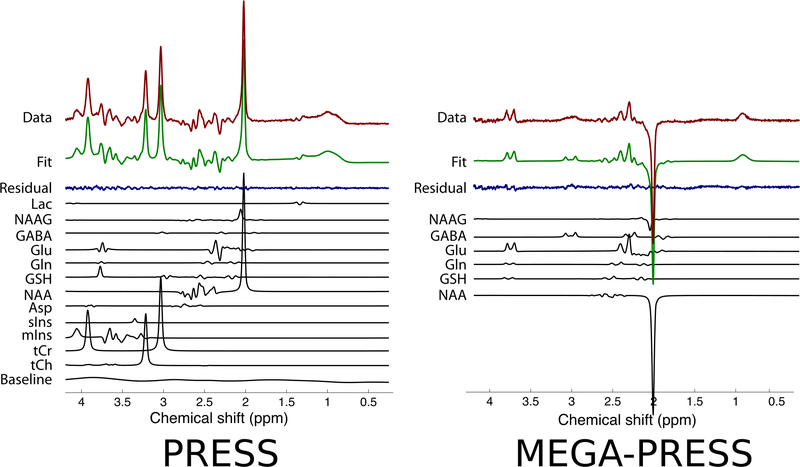
In linear combination model fitting, each metabolite’s contribution to the overall spectrum is modelled as a single response function called a ‘basis spectrum’. The basis spectrum describes an individual metabolite’s full spectral contribution, and can be obtained either by phantom experiment⁵⁴ or by numerical simulation^15,55–59. A major advantage of using basis spectra over individual peak components is that it greatly reduces the total number of model functions required to fully model the spectrum, resulting in fewer parameters to fit, and a corresponding reduction in the Cramér-Rao minimum variance bound (CRMVB) estimates (the most commonly used measure of the uncertainty of the model fit parameter estimates). Moreover, since basis spectra are generated directly from experiment or simulation, they are physically realistic, and can be highly accurate. Once the full set of metabolite basis spectra (the basis set) is produced, a constrained non-linear least-squares analysis can be used to fit a linear combination of the basis spectra to the acquired MR spectrum by adjusting their individual amplitudes and frequencies. Additional global terms such as spectral phase and linewidth are normally included to improve the fit, thus necessitating the non-linear least-squares approach. The relative amplitudes (or weights) of the various metabolite basis spectra in the best fit correspond to the estimated relative signal intensities. The fit residual – the difference between the fit and the data – provides an indicator of the goodness of fit, or the presence of unmodelled peaks in the spectrum. Quantitatively, this can be expressed using the fit quality number (FQN) which is the ratio of the variance in the fit residual divided by the variance in the pure spectral noise⁶⁰. For an ideal fit, the FQN should be close to 1.0, and the FQN/SNR ratio should be << 1. Some examples of linear combination model fitting are shown in Figure 6.

Figure 6.

Two examples of linear combination model fitting are shown. In both cases the acquired data are displayed at the top in dark red, the overall fit is displayed second from the top in green, and the fit residual is displayed third from the top in dark blue. Below the fit residual, the individual metabolite fit components are displayed in black. The example on the left is from a 3 T human brain PRESS spectrum with TE=68 ms. The example on the right is from a 3 T human brain MEGA-PRESS difference edited spectrum with TE=68 ms. Note the small peaks around 3.0 ppm in the MEGA-PRESS fit residual, indicating imperfect modelling of the GABA signal due to MM contamination.

Linear combination model fitting is the most popular method of analysis and is recommended for most in vivo MRS applications. Several software packages provide implementations of this approach, including LCModel⁵⁴, Tarquin⁶¹, Vespa⁵⁵, FiTAID⁶², INSPECTOR⁶³, and jMRUI⁶⁴. This approach is well-suited to analysis of crowded MRS data, such as short echo-time ¹H-MRS of the human brain, but can also be used to fit more sparse spectra, including long TE spectra and J-difference edited data. Linear combination model fitting allows for the inclusion of broad macromolecular components, as well as baseline components (often a “model-free” spline function) to account for any remaining broad, unmodeled background signal contributions as described below. Since the unmodeled baseline components are poorly characterized by definition, these baseline estimates often represent the greatest source of uncertainty in fitting models. For example, the knot spacing of the spline function can be chosen by the user, but the choice is fairly arbitrary and can have a significant impact on metabolite concentration estimates⁶⁵.

Peak fitting

Rather than using basis spectra to model each metabolite’s full spectral contribution, it is possible to select individual peaks of interest within a spectrum, and to fit each using a simple line shape model function. This involves choosing a line shape model that best describes the peaks of interest and fitting each spectral peak of interest to the model function. Common line shape functions include Gaussian, Lorentzian and Voigt. Fitting is achieved through adjustment of multiple model parameters including the amplitude, phase, frequency offset, linewidth, and baseline offset of each model function (or of all model functions, globally); however, the main parameter of interest is the amplitude, which scales in direct proportion to concentration. For metabolites with multiple resonances, prior knowledge of the fixed relative amplitudes, phases and frequencies of the various peaks can (and should) be used to constrain the fits and improve the results. This is the method employed by the AMARES⁶⁶ technique, which is built into the popular MRS software package jMRUI^64,67. However, in crowded spectra such as ¹H-MRS of the brain, the amount of prior knowledge quickly becomes overwhelming due to the large number of metabolites and the large number of peaks per metabolite. Therefore, like peak integration (see below), this method is most commonly used in applications involving relatively sparse MRS data such as long TE, or J-difference edited brain MRS^68,69, ³¹P MRS⁷⁰ or ¹³C MRS⁷¹. Compared with peak integration, peak fitting is less sensitive to baseline contamination, especially if a baseline offset parameter is included in the fit.

Modelling of macromolecule and baseline signal

Underlying the signals of the handful of detectable small molecules (metabolites) in tissue, are signals from many larger MR visible molecules (proteins, mobile lipids, etc). These larger molecules are often called macromolecules (MM), and are characterized by short T₂ relaxation, resulting in broad spectral components that underlie the signals of interest. Because the specific molecular origins of these signals are poorly characterized, modelling of MM signals is difficult, and necessarily empirical in nature. But if not accounted for, MM contamination will cause metabolite concentrations to be overestimated, particularly in short echo-time ¹H-MRS data. Because of their relatively rapid T₂ relaxation, MM components can be omitted from the model when fitting data acquired at very long echo times (see Table 5 for recommended TE thresholds for omitting MM).

Table 5.

Recommendations for spectral analysis.

Name of method	Recommendation
Linear combination model fitting	- Generally recommended due to its proven effectiveness, versatility and relative ease of use. - Ensure accuracy of the basis set:   a) for experimental basis sets derived from phantoms, the phantom temperature and pH, and the phantom acquisition parameters (pulse sequence, field strength, TE, etc.) should match the in vivo acquisition;   b) for simulated basis sets, the simulation parameters should match the in vivo acquisition (pulse sequence, field strength, echo time, and optionally the RF pulse shapes and durations).   c) simulations should use reliable estimates of chemical shifts and coupling constants of each metabolite spin system117–119. - Always visually inspect the quality of the fit. A good fit should have small fit residuals which mostly appears like noise. - Compute the Cramér-Rao minimum variance bounds (CRMVB), which are estimators of the minimum uncertainties in the estimated parameters (assuming that the model is complete and accurate. In particular the estimated errors would not apply if baseline estimation or phasing is done separately from actual modeling). - Metabolite measures of individual subjects should not be excluded based on high relative uncertainties (% CRMVB). Instead, individual subjects may be excluded on the basis of high absolute CRMVB values. - If the average %CRMVB for a metabolite is consistently high (>30%) across all subjects, consider excluding that metabolite from the reported results across the entire subject cohort. - Estimated baseline should be smooth, without fine structure or sharp peaks. - The number of protons per metabolite spin system is automatically encoded within the simulated or acquired basis set. Therefore, when using linear combination model fitting, the number of protons does NOT need to be considered in quantification (see quantification section).
Handling MM and baseline contributions	- MM fitting and baseline correction are generally required, but MM components can be omitted for long echo-time data (TE ≥ 150 ms at 3 T; TE ≥ 100 ms at 7 T; TE ≥ 100 ms at 9.4 T in rodent brain). - MM resonances should be removed or accounted for by including them as components in the analysis model. - Ideally, MM models should be based on an acquired MM spectrum. - Even with nuisance peak removal and MM modelling, an additional baseline correction should be performed. Use either time domain methods that assume rapid decay of baseline components, or frequency domain methods that assume a spline baseline.
Peak fitting and peak integration	- Recommended only in cases where   a) the spectrum is sparse (contains relatively few peaks), and   b) MM and baseline contribution are minimal, or have been removed in preprocessing. - Spectrum must be properly phased prior to peak integration. - Peak fitting requires that spectral peaks can be approximated by simple line shape functions. Peak integration does not have this requirement. - When using peak fitting or peak integration the number of protons per metabolite peak does need to be considered in quantification (see quantification section). - In case of peak fitting, always visually inspect the quality of the fit. A good fit should have small fit residuals and low uncertainties on peak area estimates.

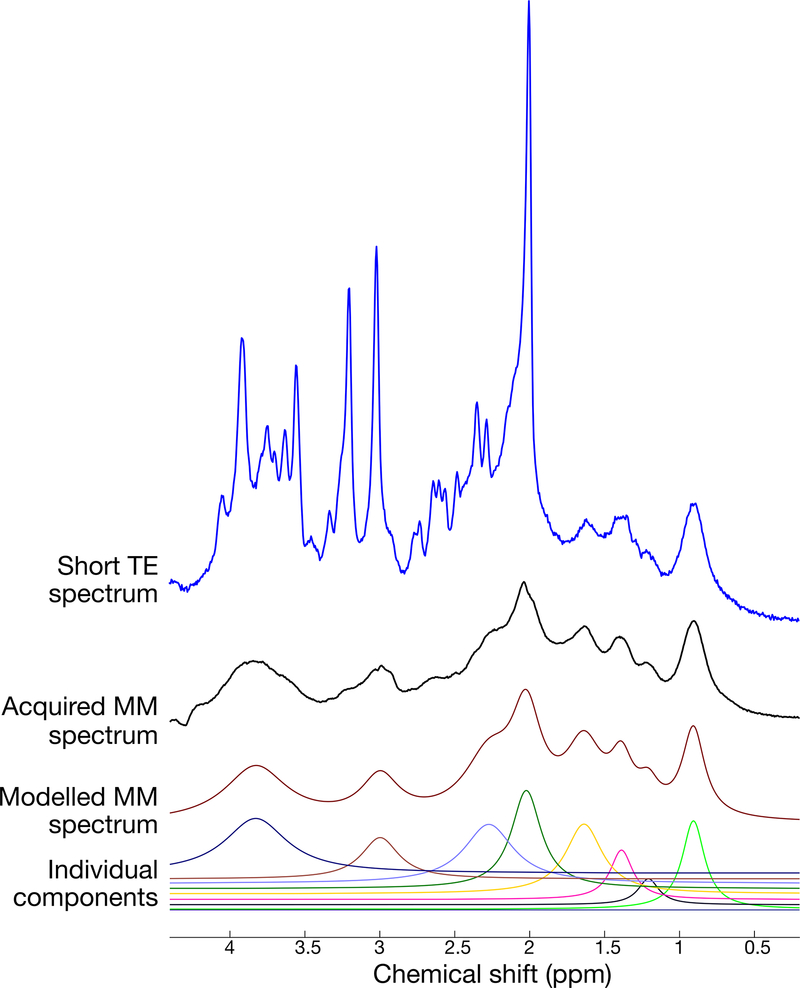
There are various ways to account for MM contributions. One common approach is to include parametrized models of the most prominent macromolecular signals as components in the spectral fitting model^72,73. Another common approach is to directly acquire the macromolecular signals using a metabolite-nulled (single or double) inversion recovery sequence^74,75. Once measured directly, this MM component can either be subtracted from the metabolite spectrum prior to analysis^76,77 or included as a component in the spectral fit⁷⁸. Figure 5 shows an example of the typical signal contribution from MM in short echo-time MRS, and its modeling via individual parametrized components.

Figure 5.

Macromolecule estimation in short-TE MRS. The top trace (blue) shows a 3 T MR spectrum from a human subject using the SPECIAL sequence with TE=8.5 ms. The second trace from the top (black) shows the metabolite-nulled MM spectrum from the same individual and voxel position, obtained using the same pulse sequence, but with an inversion recovery preparation. The third trace from top (dark red) illustrates a simple model fit of the above MM spectrum using 8 individual Lorentzian components. The 8 individual components of the modelled MM spectrum fit are shown in the bottom traces.

Even after nuisance signals and MM components have been removed from the spectrum as described above, the spectral baseline still may not appear perfectly flat. The remaining baseline arises from any unmodeled signal sources, including the long tail of an unsuppressed water peak, additional unmodeled macromolecular components, or outer volume contamination. These baseline signals should be removed prior to spectral analysis or included in the fitting model to avoid biasing metabolite concentration estimates. This baseline signal can be estimated directly from the acquired MRS data either using time domain approaches that assume very early decay⁷⁹, or by frequency domain methods which attempt to model the baseline as a spline function⁵⁴. In any case, it is difficult to separate the baseline from the metabolite signals; and as a result, this is one of the largest sources of uncertainty in in vivo MRS quantification. For further details on state-of-the-art of MM modeling and baseline signal correction, the reader is referred to the experts’ recommendations article on macromolecules in this special issue⁸⁰.

Peak integration

Peak integration estimates a metabolite’s signal intensity by calculating the area under its peak in the frequency domain⁸¹. This is done by choosing a frequency range around the centre of the (well-phased) peak of interest, and summing the discrete spectral points within that range. When quantifying multiple peaks in the same spectrum, it is important to ensure that the width of the integration range is the same for all peaks⁸². Although strictly speaking, spectral peaks have infinite extent in the frequency domain, it is generally sufficient to ensure that the integration range is at least twice the full-width at half maximum (FWHM) of the broadest peak. If a spectrum is sparse with few overlapping peaks, peak integration can be robust. However, if the spectrum contains multiple overlapping peaks, peak integration cannot effectively estimate their individual contributions. Similarly, peak integrals will be biased by the presence of baseline contributions, and are unreliable for multiplet groups whose net area is close to zero (e.g. anti-phase coherences). Therefore, peak integration is only recommended for MRS data with very sparse (non-overlapping), well-phased peaks and no baseline or macromolecule contribution (e.g. ¹H-MRS with TE>150 ms, or ¹³C spectra).

Recommendations for spectral analysis are listed in Table 5 below:

Quantification: From Signals to Concentrations

Converting ¹H-MRS signals from the brain into metabolite concentrations entails comparing the metabolite signals to either an internal or external chemical concentration reference or to an externally synthesized signal. The internal references used are either the tissue water signal or an individual signal (or combination of signals) within the metabolite spectrum. The most common external standard consists of water or a chemical of known concentration in a solution either positioned close to the subject’s head during the scan or scanned before or after the subject (‘phantom replacement’). Less commonly, an RF signal is artificially injected during the MRS sequence detection period, using either an external antenna or a scanner RF coil (ERETIC⁸³, although this method is not yet available from any of the major scanner vendors).

When referenced to other metabolite signals, metabolite levels are usually reported simply as a ratio to the reference metabolite (either an intensity ratio or a concentration ratio, the distinction being that the latter is corrected for the number of protons per peak, while the former is not) and not corrected for relaxation or partial volume effects. When referenced to a known concentration standard corrected for partial volume and relaxation effects, concentrations are reported in terms of “absolute” concentrations, using either molar (moles/L of tissue), or molal units (moles/kg of tissue water). Units of moles per kg of tissue are also sometimes used and are closely related to molar units, but are not further discussed here. Alternatively, “institutional units” are often used to report relative concentration levels, making limited corrections for relaxation or claims to be the actual concentrations. As described in more detail below, our main recommendation is to use molar or molal units over institutional units; and importantly, whatever concentration units are used, it should be explicitly stated in any publication of the findings.

Though a survey of the MRS literature may reveal that molarity is reported more often than molality, both are equally valid ways of reporting concentration. Regardless of which unit is used, the difference between them is important to understand when comparing results across studies.

In chemistry, molarity is the number of moles of solute (metabolite) per volume of solution (tissue). When comparing a metabolite signal from tissue to a water or chemical signal from an external solution of known molar concentration, the appropriate units are molarity. However, when using tissue water as a reference, either molarity or molality can be used. In the case of molarity, the tissue volume sampled (excluding cerebrospinal fluid (CSF)) is considered to be the volume of the “solution.” That is, the solution is the tissue water (the solvent) along with all the other components of the tissue, excluding CSF. To account for the fact that the water signal arises from only a fraction of the solution volume, the concentration of water in the tissue is estimated by scaling the concentration of pure water by the assumed tissue water density, which differs in grey matter (GM) and white matter (WM). Molality, on the other hand, is simply based on how much solute (metabolite) is present in a mass of solvent (the tissue water), and thus may relate more closely to the chemical concentration (i.e. intracellular concentration). As will be shown in the following section, if the MRS signals are not acquired under fully relaxed conditions, the tissue densities also need to be taken into account to properly scale for relaxation attenuation in different compartments when estimating either molarity or molality.

Internal references

Tissue water

The most commonly used reference for estimating metabolite concentrations is the tissue water signal^84–87. An advantage of using the water signal is that it arises from essentially the same volume of tissue as the metabolite when the same pulse sequence is used to acquire the metabolite signals. This ensures that the RF calibration and homogeneity, excitation profile and receiver sensitivity at the location of the metabolite and water acquisitions are identical. This is approximately the case for single-voxel ¹H-MRS if the chemical shift displacement is minimized.

The cellular environments of the metabolites are complex and varied, with different water, macromolecule and lipid densities, and other factors affecting signal relaxation and detection. To make the problem tractable, the first assumption generally made is that the various metabolite compartments can be approximated as gray matter (GM), white matter (WM), cerebrospinal fluid (CSF), and, possibly, pathological tissue (e.g. MRI-visible lesions), with uniform physical properties within each of these pools, including across cellular and extracellular sub-compartments. The different tissue and CSF fractions are determined by segmentation of an MR-image to which the MRS voxel has been registered. It is worth noting that different MRI segmentation methods generally give slightly different results, and there is no ‘gold standard’ to establish their relative accuracy⁸⁸.

In a simple solution, the ¹H-MRS signal from a solute (or from the solvent) is directly proportional to the number of moles of the solute (or of solvent) in the sampled voxel, scaled by any relaxation attenuation and instrumental factors (see Alger paper⁸⁹ for a comprehensive review). In the complex milieu of brain tissue, it is usually assumed that all of the molecules of a metabolite of interest are contributing to the measured signal. This implies that the molecules are mobile enough to have a relatively long transverse relaxation time (T₂), and hence relatively narrow spectral peak(s). When correcting a multi-peak metabolite signal for relaxation, it is often (but not always) assumed that the signals from distinct protons on the molecule, aside from any exchangeable ones, have the same T₂ and longitudinal relaxation time (T₁).

For the case of fully relaxed water and metabolite proton signals acquired identically from the same volume of pure tissue (i.e., no CSF), we can write:

$$\frac{S_M}{S_{H2O}}=\frac{\text{Moles}\text{of}\text{metabolite}\times N_M}{\text{Moles}\text{of}\text{water}\times 2}$$ [1]

where S_M and S_H2O are the metabolite and water proton signal intensities, respectively, N_M is the number of metabolite protons contributing to S_M and 2 is the number of water protons contributing to S_H2O. In the case of linear combination model fitting, the number of protons (N_M and the factor of 2 in the denominator) can safely be ignored here and in the equations that follow, since these values are encoded in the relative amplitudes of the peaks in the basis spectra.

To convert the signal ratio in Eq. [1] to units of concentration, we divide both mole factors by either the mass of the solvent (tissue water) for molal concentrations or liters of solution (total tissue) for molar concentrations and rearrange the equation. For molality, [M]_molal, this becomes:

$${[M]}_{\text{molal}}=\frac{S_M}{S_{H2O}}\times \frac{2}{N_M}\times {[H_{2}O]}_{\text{molal}}$$ [2]

where [H₂O]_molal is the molal concentration of pure water or 55.51 moles/Kg, the inverse of its molecular weight (18.015×10³ Kg/mole, https://pubchem.ncbi.nlm.nih.gov/compound/Water).

If molar concentration is to be estimated, the total volume of sampled tissue needs to be considered rather than just the volume of tissue water. In order to account for the fact that the water signal arises from only a fraction of the tissue volume, the molar concentration of tissue water is estimated by scaling the molar concentration of pure water by the tissue water density, which differs in GM and WM. Again assuming a voxel with pure tissue (no CSF), the molar concentration based on fully relaxed signals is calculated as

$${[M]}_{\text{molar}}=\frac{S_M}{S_{H2O}}\times (f_{GM}{d}_{GM}+f_{WM}{d}_{WM})\times \frac{2}{N_M}\times {[H_{2}O]}_{\text{molar}}$$ [3]

where d_GM and d_WM refer to the tissue-specific water content, defined as the MR visible water volume fraction in either GM or WM (see Appendix I, supplementary materials) and f_GM and f_WM are the volume fractions of GM and WM in the voxel, and [H2O]_molar is approximately 55.01 moles/L at 37 ⁰C and 1 bar of pressure. Values for water content in healthy human brain tissue have been drawn from various reports⁸⁵, but it is well to keep in mind that, regardless of the source, one set of water density values may not be appropriate for the entire brain nor for pathological tissue⁹⁰. In particular, in WM it should be considered whether and to what degree the short-T₂ pool of myelin water⁹¹ of up to 15% is contributing to the water reference signal⁸⁵.

If the voxel contains CSF, the water concentration in Eq. [2] is divided by the tissue water mole fraction in the voxel ($f_{G{M}_{H2O}}+f_{W{M}_{H2O}}$ or equivalently $1-f_{CS{F}_{H2O}}$, where $f_{CS{F}_{H2O}}$ is the CSF water mole fraction). Similarly, [M]_molar in Eq. [3] needs to be scaled by the volume fraction of tissue (f_GM + f_WM, or equivalently 1 – f_CSF, where f_CSF is the CSF volume fraction), and the term multiplying the signal ratio becomes (f_GMd_GM + f_WMd_WM + f_CSFd_CSF). CSF is generally devoid of detectable metabolites in healthy brain other than glucose (3–5 mM), lactate (~2 mM)^92,93 and glutamine (0.4–0.8 mM)^94,95, and the contributions of even these metabolites are usually assumed to be insignificant if care is taken to minimize the fraction of CSF in the voxel (e.g. f_CSF<0.2).

Taking into consideration the effect of signal relaxation leads to the final modifications of the fundamental equations [2] and [3]. If the data were not acquired under fully relaxed conditions, the observed signals, $S_{M_{obs}}$ and $S_{H2O_{obs}}$, need to be divided by appropriate relaxation factors. In the case of a typical double spin echo (e.g. PRESS) or stimulated echo experiment (e.g. STEAM) with TR >> TE, the form of the relaxation scaling factors is R = exp[−TE/T₂](1 − exp[−TR/T₁]), where the relaxation times are those of either the metabolite or the water protons. If TR is not much greater than TE, the factor is R = exp[−TE/T₂](1 − 2exp[−(TR − TE₁/2)/T₁] + 2exp[−(TR − TE₁ − TE₂/2)/T₁] − exp[−TR/T₁])^96,97 where TE₁ and TE₂ are the first and second echo times within the double-echo pulse sequence.

Water proton signals relax at different rates in GM, WM, and CSF, as do metabolite proton signals in GM and WM. The differences are large for water, spanning a factor of nearly 10 from WM to CSF. However, they are comparatively small for metabolites in GM and WM, such that the metabolite relaxation times can be approximated as the average of their GM and WM times without adding a large error to the concentration estimate⁹⁸. Accounting for tissue-specific water relaxation as well as a partial volume correction for CSF leads to the following expression for molal concentration⁸⁸:

$${[M]}_{\text{molal}}=\frac{S_{M_{obs}}\times \left(f_{G{M}_{H2O}}{R}_{H2O_{GM}}+f_{W{M}_{H2O}}{R}_{H2O_{WM}}+f_{CS{F}_{H2O}}{R}_{H2O_{CSF}}\right)}{S_{H2O_{obs}}\times \left(1-f_{CS{F}_{H2O}}\right)\times R_M}\times \frac{2}{N_M}\times {[H_{2}O]}_{\text{molal}}$$ [4]

where the relaxation scaling factors $R_{H2O_x}$ refer to the factors for water protons in GM, WM, or CSF, and the term R_M refers to the relaxation scaling factor for metabolite protons assuming average GM-WM relaxation times or, in the case of voxels with CSF and only GM or only WM, the metabolite relaxations times appropriate to either tissue.

As noted above, the fractions appearing in this equation are the tissue and CSF water mole fractions. They are related to the tissue volume fractions (obtained by image segmentation) according to the following equation:

$$f_{x_{H2O}}=\frac{f_x{d}_x}{f_{GM}{d}_{GM}+f_{WM}{d}_{WM}+f_{CSF}{d}_{CSF}}$$ [5]

where ‘x’ in the subscript refers to GM, WM or CSF. Converting from tissue volume to tissue water mole fractions using Eq. [5] relies on assumptions of water density, often assumed to be: d_GM = 0.78, d_WM = 0.65 and d_CSF = 0.97⁸⁵.

An equation similar to Eq. [4] can be derived for molar concentrations^98,99:

$${[M]}_{\text{molar}}=\frac{S_{M_{obs}}\times \left(f_{GM}{d}_{GM}{R}_{H2O_{GM}}+f_{WM}{d}_{WM}{R}_{H2O_{WM}}+f_{CSF}{d}_{CSF}{R}_{H2O_{CSF}}\right)}{S_{H2O_{obs}}\times \left(1-f_{CSF}\right)\times R_M}\times \frac{2}{N_M}\times {[H_{2}O]}_{\text{molal}}$$ [6]

Eqs. [4] and [6] can be further modified using Eq. 7 below to include tissue-specific (GM and WM) relaxation scaling factors for metabolites⁹⁸:

$$R_{M_{GM\_WM}}=\frac{f_{GM}{d}_{GM}\times ({\left[M\right]}_{GM}/{\left[M\right]}_{WM})\times R_{M_{GM}}+f_{WM}{d}_{WM}{R}_{M_{WM}}}{f_{GM}{d}_{GM}\times \left({\left[M\right]}_{GM}/{\left[M\right]}_{WM}\right)+f_{WM}{d}_{WM}}$$ [7]

This term introduces an extra unknown factor [M]_GM/[M]_WM, i.e., the ratio of the GM to the WM metabolite concentrations, which is not known a priori. The ratio arises from the need to know what fraction of the total metabolite signal is to be weighted by $R_{M_{GM}}$ and what fraction by $R_{M_{WM}}$. For a detailed derivation of the above quantification formulae, the reader is referred to Appendix I (supplementary materials).

Using Eqs. [4] and [7] with simulated 3 T data and assuming metabolite ratios from previous studies, it was shown that the errors that arise from not correcting for tissue-specific metabolite relaxation in mixed-tissue voxels will be less than 8% for NAA when assuming typical TRs and TEs, reported GM and WM metabolite relaxation times, and a hypothetical GM/WM NAA ratio of 1.2⁹⁸. For example, maximum errors of 7.8% in concentrations resulted when TR = 1.5 s and TE = 144 ms, but were reduced to 1.6% when TR =3 s and TE= 6 ms and to less than 0.5% when TR = 6 s and TE = 6 ms. The maximum errors occur when the tissue-averaged relaxation times are used instead of the tissue-specific relaxation times to “correct” the relaxation attenuation when the voxel actually contains only pure GM or pure WM. Eq.[7] can be used to examine the possible errors arising in any other scenario.

To minimize such errors, accurate estimates of tissue-specific metabolite relaxation times, when available, should be used to correct for relaxation attenuation in voxels with mixtures of GM and WM. It is worth noting, however, that metabolite relaxation times are very challenging to measure, even for metabolites with relatively high SNR, and are simply not practical to perform for all metabolites of interest, nor in every region of the brain or on a study-to-study basis. Furthermore, both water and tissue relaxation times are field-dependent and brain metabolite relaxation times have been reported to vary with age^100–102.

In lieu of accurate relaxation time estimates, long TR (TR>>T₁) and short TE (TE<<T₂) should be considered to reduce relaxation attenuation when possible, as illustrated in the case of NAA shown above. However, the TE used in a study is often determined by the specific pulse sequence applied, which depends on the goals of the study (e.g. spectral editing or otherwise optimizing detection of particular signals, reduction of high field artefacts with adiabatic pulses, etc.). Moreover, the TR needs to be short enough (usually ≤ 3 s) to be practical for human studies. If a long TR and short TE are not possible, ensuring that the MRS voxel contains mostly GM or mostly WM and using the metabolite relaxation times appropriate to that tissue will be the best option for reducing errors due to inaccurate relaxation times.

The recommendations for reducing errors related to inaccurate metabolite relaxation time estimates also apply to inaccuracies in the estimates of the water signal relaxation times. Long TRs and short TEs reduce the effect of these inaccuracies. A field-independent T₁ of approximately 4 s has been reported for CSF water protons¹⁰³, so the CSF water signal will still be appreciably attenuated even at a TR of 3 s. Therefore, care should be taken to minimize the fraction of CSF in the voxel to reduce the CSF water signal contribution. Additionally, it is worth noting that if molal concentrations are estimated, the impact of inaccurate assumptions about the tissue water densities are reduced at long TR and short TE, vanishing as the relaxation factors in Eq. [4] approach a value of 1.

Given the challenges for accurate ¹H-MRS concentration estimates in the brain, it is not surprising that some researchers opt for reporting “institutional units”, making no claim to be the actual concentration. Such units are fine when comparing different groups within a study, given the caveats on the interpretation of the results noted above. However, attempting to estimate the actual concentrations facilitates the comparison of results across studies and field strengths, essential for meta-analyses. Due to the challenges discussed above, particularly the unknown variation of water density and signal relaxation with pathology, this will be difficult to realize in practice. However, if MRS is ever to be used as a routine clinical exam, similar to a blood test, concentration estimates based on some standard protocol would be desirable.

Metabolite Ratios

In principle, using either the water signal or another metabolite signal within the spectrum as a concentration reference are both ‘ratio’ methods. The water signal is about 10⁴ times larger than the metabolite signals and is uncomplicated by overlap with other signals, whereas any metabolite reference is, by comparison, very weak and has to be resolved from its spectral neighbors. Furthermore, it is not possible to minimize the chemical shift displacement error inherent across the spectrum by changing the excitation frequency of the reference signal, as in tissue water referencing. However, a reference signal from within the metabolite spectrum (from either a single or a sum of metabolites), shares the other benefits of tissue water as a reference: it is inherently corrected for transmit RF field (B₁) and receiver inhomogeneity, magnetic field drift, and other instrumental factors. Additionally, a metabolite reference has two advantages over tissue water: 1) no extra scan is needed to obtain it and 2) it obviates the need to correct the results for CSF inclusion in the voxel, since, as noted previously, other than lactate and glucose, the metabolites in CSF are generally below the levels of detection by in vivo ¹H-MRS if care is taken to minimize its inclusion in the voxel.

An important factor to consider when using metabolite ratios is confidence in the stability of the reference across age, gender, pathology, or other factors. As noted earlier, while the concentration of pure water does not change (molarity does change with temperature and pressure, molality does not), the tissue water density, in fact, may change with pathology or other factors¹⁰⁴. Similarly, the metabolite signals typically used as references, such as those from the total creatine (tCr=Cr+PCr), total choline (tCho=GPC+PCh) or total NAA (tNAA=NAA+NAAG), are also subject to change with age^78,105–107 and pathology^108–111.

The majority of studies reporting metabolite ratios use the tCr signal as the reference, with the results given as the values of the ratio and not as concentrations. The latter option would require an assumption about the concentration of tCr which, in fact, would need to take into consideration its very different concentrations in GM and WM (GM [tCr] is nearly double WM [tCr]). Along these lines, generally no correction is made for GM and WM partial volume effects nor tissue-specific relaxation effects. Hence, metabolite ratios, while circumventing the needs for CSF partial volume correction and a separate acquisition to measure the reference (as is done for water referencing), are not concentration estimates, per se. They are conveniently acquired markers of metabolic differences, their interpretation subject to assumptions regarding which part of the ratio is changing, if not both, and in which direction.

External References

External solution

The most common approach to referencing the metabolites of the brain to an external reference involves scanning a spherical ‘phantom’ solution containing a particular concentration of the reference chemical after scanning the brain (phantom replacement or reciprocity principle)^112,113. Less commonly, a phantom solution is located next to the subject’s head during the scan. Either method requires correcting the signals for differences in RF power (coil loading and B₁ inhomogeneity) and/or receiver sensitivity between the phantom and brain voxel locations, introducing possible instrumental sources of error. Notably, variations in B₁ homogeneity are more likely at high B₀ field strength, largely limiting its use to 3 T and below. In addition to these, of course, one must still be concerned about partial volume and signal relaxation corrections, as discussed for internal standards, if accurate concentration estimates are desired.

ERETIC

Electric REference To access In vivo Concentrations (ERETIC) entails the synthesis of a calibrated RF signal close in frequency to the metabolite signals and detected either along with metabolite signals^83,114,115 or in a separate experiment¹¹⁶. The synthesized signal is broadcast either by a scanner coil or an external antenna^83,116 or it is directly inductively coupled to the receiver coil^114,115. The signal is calibrated with a water phantom with similar size and dielectric properties as the head. However, unlike using the phantom directly as a reference for the metabolite signal, the synthesized signal does not dielectrically load the ¹H receiver coil and, hence, does not need to be corrected for different loading. Transmit RF (B₁) inhomogeneity and receiver sensitivity differences between the brain and phantom acquisitions, however, still need to be measured and accounted for in the calculation of concentrations, as does the phase of the synthesized signal and the temperature difference between the phantom and brain¹¹⁵. Currently, the development of ERETIC has been limited to single-voxel studies. The need for accurate partial volume and relaxation corrections, as when using tissue water as an internal reference, remain. Three different studies have shown that ERETIC measurements of brain metabolites compare well with those based on tissue water as a concentration reference^114–116.

Recommendations for absolute quantification are listed in Table 6 below:

Table 6.

Recommendations for quantification referenced to water.

Method	Recommendations
Reference signal and quantification units	- Comparing metabolite signals to tissue water within the same region of interest, and calculating concentrations in either molarity or molality is the most robust and technically straightforward approach to ‘absolute’ quantification. - Whatever concentrations are used, it must be explicitly stated in any publication of the findings; preferably along with the specific quantification formulae that were used as well all assumed parameter values, so that the reader can fully reproduce the quantification method.
TE and TR	- While short TEs and long TRs are not an option for many pulse sequences, if absolute concentration estimates are a goal of the study, pulse sequences capable of very short TEs, such as STEAM120 or SPECIAL29, could be considered; - If short TE (<10 ms) and/or long TR (> 4 s) is not possible, measured or literature values of the metabolite and water relaxation constants (T1, T2) should be used in quantification. - All assumed values for relaxation constants, tissue water densities, etc. must be reported, so that others may compare results.
ERETIC	- The ERETIC method, while promising, is not yet widely available. We encourage scanner manufacturers to develop ERETIC referencing capabilities into their products, which we believe would be an important step towards reliable absolute quantification on clinical systems.

Conclusions

In conclusion, preprocessing, analysis and quantification are the three main steps in the post-acquisition MRS workflow. Each of these steps is challenging, and requires careful thought and planning in order to achieve the end goal of obtaining reliable quantitative measures of tissue chemistry. It is hoped that the guidelines and recommendations provided here will serve as a useful resource to inform on best practices and to warn of the pitfalls that are commonly encountered.

List of abbreviations

MRS

Magnetic resonance spectroscopy

¹H

Proton

MRSI

Magnetic resonance spectroscopic imaging

FID

Free induction decay

RF

Radiofrequency

N_P

Number of points in FID/spectrum

N_RF

Number of radiofrequency channels

N_tra

Number of transients

N_pc

Number of phase encoding steps in one phase cycle

B₀

The main magnetic field

ϕ(t)

Phase function of the water FID

SNR

Signal-to-noise ratio

MEGA-PRESS

Mescher-Garwood Point Resolved Spectroscopy

HERMES

Hadarmard Encoding and Reconstruction of Mega Edited Spectroscopy

SPECIAL

Spin Echo full Intensity Acquired Localized spectroscopy

MM

Macromolecules

T₂

Transverse (spin-spin) relaxation time constant

TE

Echo time

MRI

Magnetic resonance imaging

T_acq

Duration of the acquired free induction decay

FWHM

Full width at half maximum

¹³C

Carbon-13

CRMVB

Cramér-Rao minimum variance bounds

FQN

Fit quality number

ERETIC

Electric REference To access In vivo Concentrations

GM

Grey matter

WM

White matter

CSF

Cerebrospinal fluid

T₁

Longitudinal (spin-lattice) relaxation time constant

S_M

Metabolite signal intensity

S_H2O

Water signal intensity

N_M

Number of protons contributing to metabolite signal

[M]_molal

Metabolite concentration in moles of metabolite per kilogram of tissue water

[H₂O]_molal

Water concentration in moles of water per kilogram of tissue water == 55.49 moles/kg

[M]_molar

Metabolite concentration in moles of metabolite per litre of tissue water

[H₂O]_molar

Water concentration in moles of water per litre of tissue water

d_GM

Water density of grey matter

d_WM

Water density of white matter

f_GM

Volume fraction of gray matter inside the MRS voxel

f_WM

Volume fraction of white matter inside the MRS voxel

f_CSF

Volume fraction of cerebrospinal fluid inside the MRS voxel

$f_{G{M}_{H2O}}$

Water mole fraction in gray matter

$f_{W{M}_{H2O}}$

Water mole fraction in white matter

$f_{CS{F}_{H2O}}$

Water mole fraction incerebrospinal fluid

$S_{M_{obs}}$

Observed metabolite signal intensity in the presence of relaxation

$S_{{H2O}_{obs}}$

Observed water signal intensity in the presence of relaxation

TR

Repetition time

TE₁

First PRESS echo period

TE₂

Second PRESS echo period

$R_{H2O_{GM}}$

Relaxation scaling factor for water in gray matter

$R_{H2O_{WM}}$

Relaxation scaling factor for water in white matter

$R_{H2O_{CSF}}$

Relaxation scaling factor for water in cerebrospinal fluid

R_M

Relaxation scaling factor for tissue metabolite signal

[M]_GM/[M]_WM

Assumed ratio of grey matter to white matter metabolite concentrations

$R_{M_{GM}}$

Relaxation scaling factor for metabolite in grey matter

$R_{M_{WM}}$

Relaxation scaling factor for metabolite in white matter

B₁

Radiofrequency field

tCr

Total Creatine

Cr

Creatine

PCr

Phosphocreatine

tCho

Total Choline

GPC

Glycerophosphocholine

PCh

Phosphocholine

tNAA

Total N-acetylaspartate

NAA

N-acetylaspartate

NAAG

N-acetylaspartylglutamate