Cooling of medial septum reveals theta phase lag coordination of hippocampal cell assemblies

Summary

Hippocampal theta oscillations coordinate neuronal firing to support memory and spatial navigation. The medial septum (MS) is critical in theta generation by two possible mechanisms: either a unitary ‘pacemaker’ timing signal is imposed on the hippocampal system or it may assist in organizing target subcircuits within the phase space of theta oscillations. We used temperature manipulation of the MS to test these models. Cooling of the MS reduced both theta frequency and power, was associated with enhanced incidence of errors in a spatial navigation task but did not affect spatial correlates of neurons. MS cooling decreased theta frequency oscillations of place cells, reduced distance-time compression but preserved distance-phase compression of place field sequences within the theta cycle. Thus, the septum is critical for sustaining precise theta phase-coordination of cell assemblies in the hippocampal system, a mechanism needed for spatial memory.

Graphical Abstract

Introduction

Theta frequency oscillations coordinate neuronal activity in the hippocampus-subicular-entorhinal complex and entrain neurons in various neocortical areas (Buzsáki, 2002). Damage or inactivation of the medial septum–diagonal band (MS) abolishes theta oscillations in all these areas (Petsche et al., 1962; Vertes and Kocsis, 1997) and is associated with impairment of memory, spatial navigation and other cognitive functions (Bolding et al., 2020; Brandon et al., 2011; Chang and Gold, 2004; Chrobak et al., 1989; Givens and Olton, 1990; Jeffery et al., 1995; Leutgeb and Mizumori, 1999; Wang et al., 2015; Winson, 1978). However, whether the behavioral impairment is due to silencing or damaging important septal afferents or to the absence of theta phase-multiplexed coordination of activity of neurons (Harris et al., 2003; Kay et al., 2020) in the hippocampal system has remained an unsolved challenge. Such dissociation is not straightforward because manipulations that abolish theta also affect neurons and synapses which may exert their own, theta-independent effects.

Early experiments suggested that the MS acts as a ‘pacemaker’, sending out synchronous outputs, akin to a conductor of an orchestra (Borhegyi, 2004; Petsche et al., 1962; Stewart and Fox, 1990; Sweeney et al., 1992; Zutshi et al., 2018), followed by models in which cholinergic and GABAergic neurons of MS fire at distinct unique phases of the theta cycle (Borhegyi, 2004; Petsche et al., 1962; Stewart and Fox, 1990; Sweeney et al., 1992). However, a large body of observations that have accumulated over the past decades imply a more intricate involvement of the MS in coordinating activity patterns in the hippocampal-entorhinal system than being a simple rhythm generator. First, hippocampal neurons are not locked synchronously to a spatially coherent rhythm but show a systematic phase shift up to 270° in the CA1-CA3-dentate gyrus axis and in different layers of the entorhinal cortex (Buzsáki et al., 1986; Mizuseki et al., 2009). Second, theta is not synchronous over the entire septotemporal axis but, instead, shifts gradually as much as 180° from the septal to the temporal pole (Lubenov and Siapas, 2009; Patel et al., 2012). Third, all activated principal cells, such as neurons that fire at particular spatial positions (‘place cells’; O’Keefe and Nadel, 1978; O’Keefe and Recce, 1993) or in a given memory episode (Pastalkova et al., 2008), oscillate faster than the LFP theta. The oscillation frequency of place cells correlates inversely with the diverse sizes of place fields (Dragoi and Buzsáki, 2006) and vary systematically along the septotemporal axis (Kjelstrup et al., 2008; Maurer et al., 2006; Royer et al., 2010). Similarly, theta oscillation frequency of ‘grid cells’ in the entorhinal cortex decreases progressively in the dorsoventral direction (Giocomo et al., 2007), providing a frequency match between corresponding entorhinal and hippocampal neurons. Finally, as a result of the phase interference between population spiking behavior, as reflected by LFP theta, and the faster oscillatory spiking of individual neurons (Skaggs et al., 1996; Geisler et al., 2010) show a progressive backward phase shift of their spikes as their activity unfolds (‘phase precession’; O’Keefe and Recce, 1993). In summary, spikes of principal cells in the limbic system occur at all phases of the theta cycle and all active principal cells oscillate faster than the global LFP theta whose instantaneous frequency co-varies coherently across subregions and structures (Figure 1). These experiments suggest a more elaborate involvement of MS circuit in theta cycle phasing of hippocampal neuronal assemblies than the current models would imply (Borhegyi, 2004; Buzsáki, 2002; Hangya et al., 2009; Stewart and Fox, 1990).

Fig. 1. Theta phase dynamics and connectivity in the MS-hippocampal system.

a, Theta oscillation is a traveling wave and shows systematic phase shift in both the septo-temporal and CA1–CA3–dentate gyrus axes (color scale illustrates the phase offsets between regions). Hippocampal neurons are not locked synchronously to a global theta rhythm but show a systematic phase shift up to 270° in the CA1-CA3-dentate gyrus axis and a gradual 180° shift from the septal to the temporal pole (Lubenov and Siapas, 2009; Patel et al., 2012). b, Hypothetical effects of MS cooling on within-theta neuronal assembly organization. Top: Two spatially overlapping place fields along the track. Middle, Time lags between place cell assemblies (different color ticks) remain unchanged with theta cycle lengthening (gray). Bottom: Place cells assemblies expand in time but keep their theta phase relationships. c, Theta cycle relationship between overlapping place fields of the same size (L_PF) of two place cells (green and tangerine). The travel distance (L_tr) between the peaks of the two place fields is correlated with the time offset (τ) of spikes between the place neurons (Dragoi and Buzsáki, 2006). The ratio of travel distance and theta time scale time lag defines distance to time compression (c = L_tr / τ; Geisler et al., 2010). Middle and bottom, Hypothetical effects of MS cooling. Middle: Place field size changes but τ is preserved. Bottom: Fewer theta cycles occur within the same size place field and τ increases.

Damaging, silencing or pharmacological perturbation of MS circuit (Bolding et al., 2020) cannot effectively address temporal/theta phase coordination issues. Perturbation studies using synchronizing electrical (McNaughton et al., 2006) or optogenetic (Dannenberg et al., 2019; Vandecasteele et al., 2014; Zutshi et al., 2018) stimulation may not be effective either to fully examine this problem because strong pulses impose global synchrony on all neurons unlike the time-shifted patterns observed under physiological conditions (Lubenov and Siapas, 2009; Patel et al., 2012). Therefore, we used temperature manipulation, an approach that is applicable to localizing the origin of temporal coordination (Fee and Long, 2011). In contrast to unwanted synchronizing stimulation, cooling does not damage neurons or interrupt local interactions but alters multiple parameters of neurons from channel kinetics to transmitter release, resulting in temporal warping of circuit dynamic (Katz et al., 2004; Thompson et al., 1985; Volgushev et al., 2000). For example, reducing temperature in the vocal center of the zebra finch elongated the bird’s song by proportionally slowing its acoustic microstructure (Long and Fee, 2008).

By cooling the MS, we examined how slowing theta oscillations affect hippocampal network activity, physiological properties of neurons and their spatial correlates (O’Keefe and Nadel, 1978). Several models assume that the phase interference between MS theta oscillation (LFP theta) and the faster spike periodicity of place cells and grid cells, driven by a hypothetical ‘spatial input’, determines the slope of spike phase precession, and, consequently, place field size (Burgess et al., 2007; Chadwick et al., 2016; Harvey et al., 2009; Kamondi et al., 1998; O’Keefe and Recce, 1993; Zutshi et al., 2018). A prediction of these models, therefore, is that slowing MS-driven theta oscillation should affect the size of place fields by increasing the difference between the frequencies of the two oscillators. Each theta cycle contains a sequence of place cell assemblies that corresponds to the sequences of upcoming place cells on the maze (Dragoi and Buzsaki, 2006; Maurer et al., 2012). If the temporal lags within cell assemblies are preserved, more assemblies can be packaged in a wider theta cycle (‘temporal coding’). An alternative hypothesis is that the fundamental organization in the septo-hippocampal system is not time- but phase-based (‘phase coding’). Under the phase-model, theta phase assembly coordination should remain unaltered but at the expense of affecting timing between place cell assemblies (Figure 1). Our results favor the phase coding model of theta cycle coordination.

Results

MS cooling decreases hippocampal theta frequency and power

To achieve localized cooling of the medial septum, we constructed a cryoprobe, consisting of a silver wire (125μm in diameter), 25μm graphene sheet, air isolation and a polyimide tube (Fig. 2a; see Methods). The back end of the silver wire was coiled at the bottom of an insulated reservoir. Cooling was achieved by filling the reservoir with dry ice (−78.5° C). The protruding tip (1.5 mm) of the front-end wire was implanted into the medial septum-diagonal band area (MS; Fig. 2b). A temperature sensor (k-type thermocouple; two 80μm wires) was attached to the outer surface of the cryoprobe cannula to continuously monitor local temperature (Fig. 2a; Suppl. Fig. 1). Pilot experiments were performed to perfect the device so that hippocampal theta frequency could be reduced for 5 to 15 min (Suppl. Fig. 1).

Fig. 2. Cooling of MS affects theta oscillations.

a, Components of the cooling probe. b, Cooling probe and thermocouple are implanted in MS and silicon probes in the hippocampus. Dry ice is placed into the reservoir and MS is cooled by thermal conduction. c, Maze with left (blue) and right (green) run trajectories superimposed. d, top panel: Time-resolved spectrogram in a single session. Color scale is normalized. Middle panel: temperature; lower panel: running speed of animal. e, Frequency spectrum with power of theta and its 1^st–3^rd harmonics (arrows). f, Power spectra of the theta band and harmonics before (top) and after (bottom) cooling. Color scale is normalized. Same single session used in d,e,f. g, h, Effect of MS cooling on theta frequency (g) and power (h) Group data for all sessions and subjects (mean values with SE). i, Group data for theta frequency and power before, during and after MS cooling. g,h,i,j: 53 sessions in 5 rats. j, R and P values for theta frequency and power in individual rats (color coded).

In addition to the cooling probe, five rats were also implanted with multi-shank 64-site silicon probes bilaterally in the CA1 pyramidal layer of the dorsal hippocampus (Supplementary Material) and were trained in a figure-8 maze (spontaneous alternation task; Fig. 2b) to run for water reward. After a block of control trials (~ 40 trials), dry ice was placed into the reservoir, which reduced MS temperature for approximately 15 min (or corresponding to about 20 to 60 ‘cooling’ trials), followed by recovery trials (20 to 80). MS cooling induced fast and reversible change in the frequency and power of hippocampal theta oscillations (Figure 2d, e, f, i). Theta frequency decreased linearly with MS temperature (Figure 2g; down to 20° C; R = 0.81; P = 5.4 × 10⁻⁴⁸) and this relationship was more consistent across animals than the effect on theta power (R = 0.54; P = 1.2 × 10⁻¹⁶; Fig. 2g, h). The time course of theta frequency decrease, and less so its power, mirrored the temporal dynamic of MS cooling (see time course in Fig. 6).

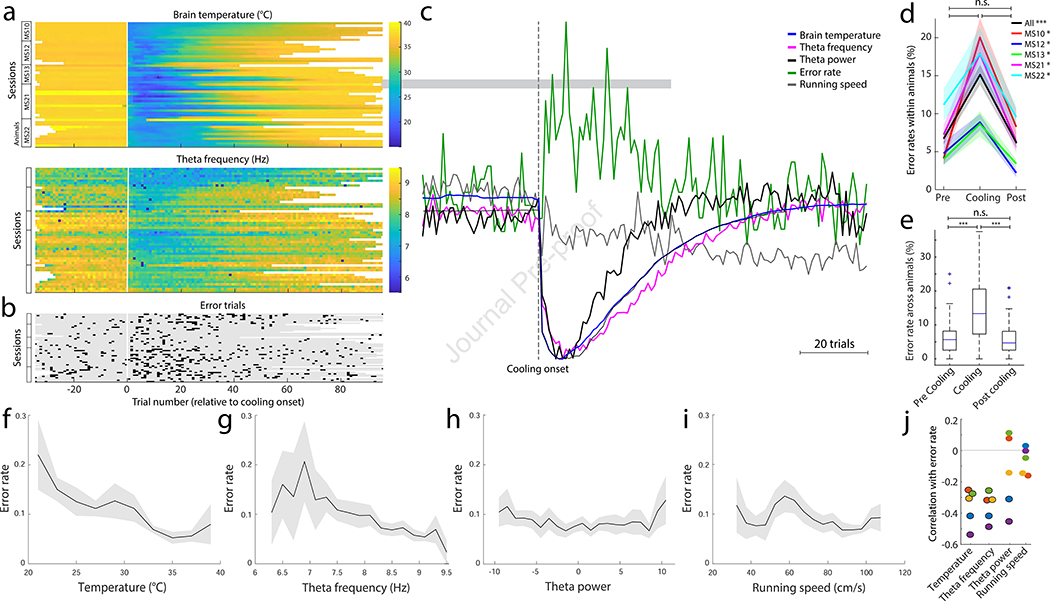
Figure 6. Effects of MS cooling on memory performance.

a, MS temperature (top) and theta frequency shift (bottom) as a function of trial number (x axis). Each line corresponds to a single session. Animal IDs are indicated on the left. Vertical line marks the onset of cooling. b, Incidence of error trials in the same sessions. c, Time courses of MS temperature, theta frequency, power and running speed (mean of all sessions). Note tight correlation between MS temperature, theta frequency and power. In contrast, speed shows a monotonic function across trials. d, Choice errors shown separately for each animal. Standard errors are shown in shaded colors. Black line, group means. * P < 0.05; *** p = 10⁻⁶. e, Choice errors shown as boxplots constructed from all sessions. ** P < 10⁻⁷ ns = nonsignificant. f-i, Relationship between memory errors and temperature (f), theta frequency (g), theta power (h) and running speed (i). Standard errors are shown in shaded colors (f-i). j, Correlation values between memory errors and parameters shown in f to i for each rat. Significant values indicated by black circles (P < 0.05). Same color indicates same animal.

In a control experiment, we measured temperature simultaneously in the MS and hippocampus, and found < 1.5° C decrease in the hippocampus at the time of the largest MS temperature decrease (16° C), that is within the physiological range of brain temperature (Suppl. Fig. 1h–k; Moser and Andersen, 1994). Critically, in contrast to the rapid onset of MS cooling (maximum effect at approximately 45 s; time constant: 11 s), the mild temperature decrease in the hippocampus was considerably delayed (peak at 115 s; time constant 48 s for the right hippocampus, and 72 s for the left). Furthermore, firing rates of both pyramidal cells and putative interneurons in the hippocampus decreased immediately after MS cooling and the changes correlated well with MS temperature change (see Suppl. Fig. 5g, h) rather than with the delayed minimal temperature decrease in the hippocampus. Finally, the waveforms of action potentials in the hippocampus, a sensitive measure of temperature change (Thompson et al., 1985; Volgushev et al., 2000), were not affected by MS cooling (Suppl. Fig. 1g). Overall, these findings show that MS cooling had an immediate and strong effect on LFP theta and suggest that these changes were not a consequence of the spread of cooling to the hippocampus.

Effect of MS cooling on place field features

Spatial parameters of place fields were largely left unaffected by MS cooling. Place field size (L_PF) remained highly correlated before and after MS cooling (Fig. 3a, b, c; see Suppl. Fig. 3 for other place field features). L_pf and f_p were negatively correlated (Dragoi and Buzsáki, 2006; O’Keefe and Recce, 1993), and this relationship was not altered by cooling, as illustrated by the similar slopes, even though the intercept of the regression line during cooling slightly decreased (Fig. 3c, d).

Fig. 3. Place field features are not affected by MS cooling.

a, Example of right arm runs in the T maze. b, Place fields in the right arm before (upward traces) and during MS cooling (downward traces) in a single session. Note preserved size, position and shape of place fields. c, Place field size does not change with MS cooling (R = 0.91). d, Place field size continues to be inversely correlated with f_p after MS cooling (R_pre = − 0.49; R_cooling = − 0.40; R_post = − 0.40. P < 10⁻⁹ all conditions). e, Correlation between measured (x) and model-predicted (y) size of place fields before, during and after MS cooling. Place field size in the model (Geisler et al., 2010) was derived from S_PF = v/(f_p -/lfp). v = speed. f, Information content of place cell spikes. None of the comparisons are significantly different (P > 0.26). g, Population vector cross-correlation matrices from a single session from baseline (pre-cooling) and MS cooling trials. The higher (yellow) values indicate that the correlation of population activity is relatively constant between neighboring positions. White lines mark the boundary between central arm, right and left arms. Normalized color scales are the same in the two panels. h) Population vector change as a function of distance. Superimposed decorrelation curves (cross-diagonal values in g) for trials before (red) and during MS cooling (blue). To quantify the scale of the spatial representation, the interval at which the correlation dropped to 0.5 was calculated for each session (dashed line). i) Decorrelation values for data from 21 sessions.

Next, we compared measured place field size with model-based calculations. Previous studies have demonstrated a quantitative relationship among theta frequency (f_LFP), oscillation frequency of pyramidal cells within their place fields (f_p), the duration it takes the rat to run across the place field (D_PF), place field size (S_PF) and the rat’s velocity (v) (Geisler et al., 2010). Since D_PF = 1/(f_p — f_LFP) (Geisler et al., 2010) and D_PF can be calculated by dividing place field size (S_PF) with locomotion velocity within the place field (S_PF = D_PF*v), place field size can be derived from S_PF = v/(f_p -f_LFP). We found a reliable and similar relationships between measured place field sizes and model-predicted sizes for trials before (R = 0.55), during (R = 0.54) and after (R = 0.11) MS cooling (Fig. 3e). Information content of place cell spikes was also left unaltered by MS cooling (P > 0.26; Fig. 3f).

We also investigated potential changes to the scale of distance representation at the population level resulting from MS cooling. We calculated the correlations between pairs of population vectors of unit firing constructed from binned rate maps (Gothard et al., 1996). The distance in maze corridor bins at which the spatial population vector correlation function dropped to 0.5 was used as a measure of the scale of the spatial representation, a measure independent of arbitrary definition of place field (Gothard et al., 1996). Population vector correlation of pyramidal cells was not affected by MS cooling (Fig. 3g, h). This analysis further suggested that spatial representation by place cell population was largely unaffected by MS cooling (Fig. 3i).

Effects of MS cooling on single neuron properties

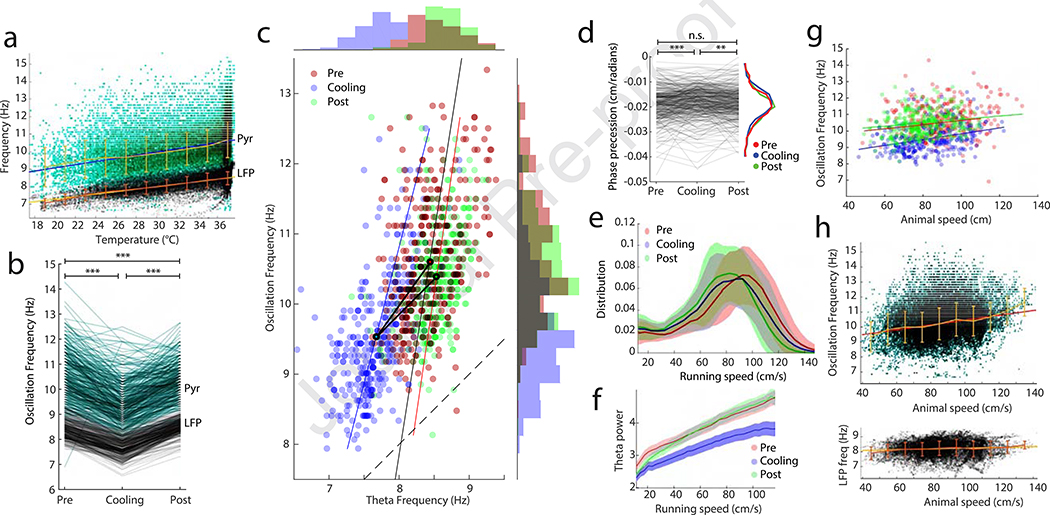
In contrast to the lack of changes of spatial features, MS cooling induced widespread but correlated physiological effects (Fig. 4). The theta oscillation frequency of pyramidal neurons decreased linearly and paralleled the downward frequency shift of LFP theta oscillation (Fig. 4a; f_LFP: R = 0.66, Slope = 0.071. f_p: R = 0.38, slope = 0.09). Theta frequency oscillation of putative fast spiking interneurons also decelerated (Suppl. Fig. 2d), commensurate with the downward frequency shift of LFP theta oscillation.

Figure 4. Effects of MS cooling on single unit parameters.

a, LFP theta frequency (f_LFP) and oscillation frequency of place cells (f_p) as a function of MS temperature. Each dot is a trial average measured within a single place field. Note parallel changes between f_p (green) and f_LFP (black). b, Oscillation frequency shown separately for all place cells (f_p; gray) and LFP theta frequency (f_LFP; black) measured in the corresponding place fields before, during and after MS cooling. *** P < 5.9e-8 c, Correlation between LFP theta frequency (f_LFP) and place cell oscillation frequency (f_p; R_pre = 0.61; R_cooling = 0.59; Rpost = 036; P < 10⁻⁶ each). Black lines connect the centers of mass of each cloud. Marginal histograms show the distribution of f_p of place cells and f_LFP in the corresponding place fields. Dashed line: diagonal. d, Theta phase precession slopes of place cell spikes before, during and after MS cooling. ** P < 0.007; *** P < 0.0003. e, Distribution of running speeds in all sessions (N = 53). f, Theta power as a function of running speed. g, Place cell oscillation frequency (f_p) as a function of running speed, measured in each place field. h, f_p and f_LFP as a function of running speed. As in g but trials before, during and after MS cooling are pooled to show that f_p depends more strongly on running speed than f_LFP.

The range of within-field oscillation frequency of place cells (f_p) was larger compared to the range of LFP theta frequency within place fields both before and during MS cooling (f_LFP; Fig. 4c), corresponding to the range of place field sizes. MS cooling decreased both f_p and f_LFP, measured within the place fields of neurons, by approximately the same degree (Fig. 3b,c; f_LFPpre = 8.4 ± 0.38, f_{LFP cooling} = 7.7 ± 0.36, f_{LFP post} = 8.5 ± 0.29; f_{p pre} = 10.6 ± 0.95, f_{p cooling} = 9.5 ± 0.84, f_{p post} = 10.4 ± 0.72, n = 365). Both values recovered after cooling. The y intercepts of regression lines of the f_p versus f_LFP relationship shifted from pre-cooling to cooling but remained parallel to each other in each condition. The lines connecting the centers of masses also remained largely parallel with the diagonal (Fig. 3 c), indicating preserved f_p – f_LFP differences. Both within-field and peak firing rates of place cells decreased moderately during MS cooling (Suppl. Fig. 2; 11% and 12%; P < 10⁻⁹ and P < 10⁻¹¹, respectively; see time course in Suppl. Fig. 5). Interneuron firing rates also decreased by approximately the same degree (Suppl. Fig. 2). The slope of the relationship between travel distance across the place field and phase advancement of spikes (‘phase precession’ index; O’Keefe and Recce, 1993) decreased slightly, but nevertheless significantly, during MS cooling (Fig. 4d).

Since previous studies showed that the running speed of the animal is correlated with several physiological parameters (Dannenberg et al., 2019; Diba and Buzsáki, 2008; Fuhrmann et al., 2015; Geisler et al., 2007; Maurer et al., 2012; McNaughton et al., 1983), we aimed to disambiguate the effect of MS cooling and running speed. Running speed decreased relatively monotonically within session (Fig. 4e; see also Fig. 5c). The animal’s speed correlated with both theta power and f_p (Fig. 4f, g). Yet, f_p changes during MS cooling could not be explained by decreased running velocity of the rat because f_p values during cooling were lower at all velocities (Fig. 4g). We examined the relationship between running speed and LFP theta frequency (f_LFP) in two different ways. The first comparison was done on a trial basis, comparing the mean theta frequency with the mean running speed in each trial. This comparison showed a positive correlation before, during and after MS cooling with the largest changes taking place at lower running speeds (10 to 40 cm/s; Suppl. Fig. 2e). However, this comparison cannot dissociate the effect of speed from the effect of maze environment (Montgomery et al., 2009). Therefore, we quantified speed – theta frequency relationship within each place field (f_LFP), together with the oscillation frequency of the corresponding place cell (f_p). This calculation revealed that while speed exerted a relatively linear effect on f_p, it had no or little effect on the frequency of f_LFP (Fig. 4h; Czurkó et al., 1999; Montgomery et al., 2009) within the dominant speed range of the rat. As a result, the f_p – f_LFP difference increased with running velocity. This is in contrast to the effect of MS cooling, after which the difference between f_p and f_LFP was preserved (Fig. 4a and c). Finally, we examined duration of theta cycles as function of the rat’s position on the track. While theta duration was consistently longer during MS cooling trials, duration distribution did not correlate with the speed distribution on the track (Suppl. Fig. 3). Overall, these findings indicate that the physiological effects of MS cooling are dissociable from running speed effects (Tsanov, 2017).

Figure 5. Distance-theta time scale compression is affected by MS cooling.

a, Selected place fields in the left arm of the maze before MS cooling in a single session. b, Within-theta cell assemblies. Each row of dots is a trial of the spiking activity of place cells (same color code as in a in successive theta cycles). 0 is the theta cycle in the middle of the left arm. Note shifting cell assemblies in successive theta cycles (from blue to red) and preserved phase preference of place cell spikes during and after MS cooling (right trace). c, Relationship between distances of place field peaks across neuron pairs (y axis) and their theta time-scale cross-correlogram lags (τ on x axis; as in Fig. 1c) during trials prior to MS cooling (2948 = pairs across 18 sessions, 5 rats). Green dashed line; compression index (slope), c = 0.54 cm/ms. Period of the CCG is highlighted (black solid line). d, Sum of the theta repeated spike cross-correlograms of place field pairs. The red line is the sum of all dots in c (NoCooling); blue line, sum of all dots of a similar graph during cooling. Vertical dashed line indicates that the oscillation frequency of the spike cross-correlation before cooling (~ 85 ms) is faster that f_LFP (~110 ms at 9 Hz). e, Similar to d but instead of time lags, within-theta phase lags between spikes were calculated. Vertical dashed line indicates that the oscillation frequency of the spike cross-correlation is faster than that of f_LFP (2π). f, Duration of the theta-repeated spike cross-correlograms (as in d), calculated for each session, significantly increased during MS cooling, compared to control (Pre and Post-cooling epochs combined) trials (** P = 0.002; two-sided signed rank test), whereas the spike phase-lag correlations remained unaffected (n.s., P = 0.32). Black disks and connected line, group means. g, Compression index, c (cm/ms; i.e., the slope in c), significantly decreased during MS cooling (* P = 0.02) but the distance/phase lag compression (cm/radian) remained unaffected (P = 0.92). h, Cumulative distributions of theta scale time lags (τ) between place cell pairs before (Pre), during and after (Post) MS cooling. MS cooling data are significantly different from both Pre- and Post-cooling trials (Pre vs cooling P = 8.0⁻⁵; Post vs cooling P = 0.00032; N = 10 sessions, 4 rats). Pre and post-cooling curves are strongly superimposed (Pre vs Post P = 0.79). i, Same as in h, but for phase lags (all comparisons are non-significant, P > 0.24). j, Cumulative plots of the fraction of all simultaneously recorded neurons active in the theta cycle (pre vs cooling P = 0.28; post vs cooling P = 0.006; pre vs post P = 0.0005). k, Distribution of spike counts within theta cycles (Pre and Post-cooling epochs are not different from MS cooling epochs or from each other; P > 0.058). y axis, probability.

MS temperature effects on theta time/phase compression of place cells sequences

Our findings so far revealed a contrast between consistent changes in physiological parameters of single neurons and the stability of their place field features by MS cooling. Because single neuron features do not inform us about their theta-organized assembly properties, we next examined the temporal sequences of place cell assemblies in the theta cycle (Fig. 5a, b). The distances between place cell peaks (L_tr) are known to correlate with their theta-scale time lags (τ) and phase lags, and the ratio of L_tr and τ is known as distance-time compression (c; figure 1a; Dragoi and Buzsáki, 2006; O’Keefe and Recce, 1993). To display the dynamics of ensemble compression of place cell distances as the animal passes through sequential positions on the maze, we plotted the sequence compression for the entire population of place cell pairs over several theta cycles within a 0.8-s period. In Fig. 5c, each dot corresponds to the time difference of spike occurrences of place neuron pairs (τ), averaged across all trials of a session (n = 18 sessions in 5 rats). This representation mimics the spatial-temporal evolution of spiking of all pyramidal neurons in the dorsal hippocampus as the rat traverses the place field center of a reference neuron (Dragoi and Buzsáki, 2006). The “clouds” are spaced by theta-scale intervals, relating to the joined oscillating frequency of place cell pairs, and the slope of the clouds corresponds to the distance-to-theta scale-time compression (c; Maurer et al., 2012). Several place cells are active together in each theta cycle, but the group composition varies from cycle to cycle (Fig. 5b; Dragoi and Buzsáki, 2006; Maurer et al., 2012).

Both the joined oscillating frequency of place cell pairs and c were affected by MS cooling (Fig. 5d, f, g). Because the compression index also depends on running speed (Maurer et al., 2012) and because running speed gradually decreased across the entire session (Fig. 3e; 6c), we combined trials before and after cooling into a single control group (mean running speed = 87.3±8.0). During MS cooling (mean running speed = 86.2±9.9), 1/f_p increased (i.e., f_p decreased) in each examined session relative to control runs (Fig. 5f, g; 0.002; Wilcoxon signed rank test), whereas distance-time compression decreased (Fig. 5g; P = 0.02). We also constructed analogous plots displaying L_tr versus theta phase lags of spike pairs, instead of time lags. Phase lags remained unchanged after MS cooling (Fig. 5f; P > 0.24 for all pairs; Wilcoxon signed rank test) and, as a consequence, the ratio (i.e., L_tr versus theta ‘phase compression’) between L_tr and phase lag did not change either (P < 0.92; Fig. 5g).

Because distances between place field peaks (L_tr) were not affected by MS cooling (Fig. 3 c and g–i) but distance-time compression decreased (Fig. 5g), time lags (τ) are expected to increase. To examine this effect directly, we plotted the distributions of both theta time lags (τ) and phase lags between all pairs of place cells in each session. During MS cooling, the time lags increased significantly (Fig. 5h; P < 10⁻⁴; sign rank test; n = 10 sessions), whereas they were not different from each other during precooling and post-cooling sessions (P = 0.79), despite slower running speed during Post compared to Pre-cooling trials. In contrast, phase lags between spikes of place cell pairs were not affected by MS cooling (Fig. 5i; P > 0.24 between all conditions). Thus, theta phase lags remained similar while time lags increased.

These findings suggested that the same number of place cell assemblies were compressed into theta cycles both before after MS cooling and the assemblies were proportionally dispersed within the lengthened cycle during cooling trials (Fig. 5c,d). In support of this hypothesis, we found that the fraction of place cells active in a given theta cycle was not significantly affected by MS cooling (Fig. 5j; P = 0.2). The number of spikes emitted by all neurons per theta cycle was also preserved after MS cooling (Fig. 5k), which might be explained by the similar magnitude of the within-field firing rate decrease of place cells (~12%; Suppl. Fig. 2) and theta frequency decrease (~12%; Fig. 4a and b; trial-wise correlations, see Suppl. Fig. 5).

MS cooling increases behavioral errors

The temperature decrease in the MS was immediately accompanied by increased choice errors in the maze (Fig. 6a–c). The worst memory performance occurred between trials 4 and 8 after MS cooling, when the MS temperature reached its minimum, accompanied by the largest decreases of theta frequency and power (Fig. 6c; see also Suppl. Fig. 5). Overall, the number of memory errors increased approximately 3-fold, assessed either within rats (P < 0.05 for all animals) or across all animals (P = 10⁻⁶; Fig. 6d, e). The incidence of errors negatively and significantly correlated with temperature change (R = − 0.35; P < 0.01; all animals), theta frequency (R = − 0.35; P < 0.01; all animals) and less so with theta power (only 2 of 5 animals had significant R > − 0.3; P < 0.01) and not with the running speed of the rat (R ~ 0.1; P > 0.05 for all animals; Figure 6f–j; see relationship to firing rates and number of spikes per theta cycle in Supp. Fig. 5).

Discussion

Cooling the MS reduced both LFP theta frequency and power in the hippocampus. It also resulted in more choice errors in a spatial navigation task but without affecting spatial attributes of individual place cells and the spatial map. The slowing of LFP theta oscillation was paralleled with a proportionate a) decrease of theta frequency oscillation of place cells, b) theta time cross-correlations of place cell pairs, c) reduced time compression but preserved phase compression of place field sequences within theta cycles and e) a decrease of firing rates of both pyramidal cells and interneurons, commensurate with the increased duration of theta cycles.

MS cooling may non-specifically affect several targets, including local neurons and their intraseptal interactions, transmitter release probability of subcortical neuromodulators terminating in MS and it can also alter spike propagation in axons passing through the MS (Fee and Long, 2011; Volgushev et al., 2000). Our goal was not to disclose the local physiological effects of temperature manipulations in MS but to bring about a reliable macroscopic phenotype, theta frequency, and examine the circuit mechanisms responsible for such change in the hippocampus. Since the cooling method affects circuit components relatively homogeneously, it is an alternative or complementary tool to neuron-specific perturbations (Fee and Long, 2011; Fuhrmann et al., 2015; Lee et al., 1994; Vandecasteele et al., 2014; Zutshi et al., 2018). Many of the subcortical neuromodulatory and supramammillary effects are likely mediated by affecting MS neurons (Vertes and Kocsis, 1997). They may be responsible for altering theta power but less so theta frequency. Selective damage to MS cholinergic neurons reduces theta power several-fold without affecting theta frequency (Lee et al., 1994). Furthermore, pharmacological blockade of muscarinic cholinergic receptors does not alter the cross-correlation structure of neuron pairs, spatial properties of place cells, the predictability of spiking in individual place cells from peer activity, or the decodability of patterns of simultaneously recoded place cell spikes (Venditto et al., 2019). Conversely, optogenetic activation of MS GABAergic, but not cholinergic, neurons can tune theta frequency (Zutshi et al., 2018; Fuhrmann et al., 2015), suggesting that MS cooling exerted its theta temporal/phase effects mainly via affecting MS GABAergic neurons (Borhegyi, 2004; Hangya et al., 2009; Simon et al., 2006; Stewart and Fox, 1990; Zutshi et al., 2018). Thus, even if MS cooling affects multiple mechanisms, the strongest correlation between MS temperature and theta frequency oscillation suggests that MS GABAergic neurons are likely involved.

Theta phase organization of hippocampal cell assemblies

Early experiments suggested that the MS acts as a ‘pacemaker’, sending out synchronous outputs, akin to a conductor of an orchestra (Borhegyi, 2004; Buzsáki, 2002; Chadwick et al., 2016; Petsche et al., 1962; Stewart and Fox, 1990; Sweeney et al., 1992; Zutshi et al., 2018). An alternative model is based on the reciprocal relationship between MS and the hippocampus (Hangya et al., 2009). In one arm of the loop, MS GABAergic neurons innervate hippocampal and entorhinal interneurons (Freund and Antal, 1988; Fuchs et al., 2016; Gonzalez-Sulser et al., 2014; Takács et al., 2008; Unal et al., 2015). In the return direction, long-range GABAergic neurons send axons to the MS (Gulyás et al., 2003; Toth et al., 1993). Our observations suggest that MS neurons work together with these long-range GABAergic hippocampo-septal, and likely entorhinal-septal, feedback neurons to provide theta phase-coordination in the entire entorhinal-hippocampal system (Supp. Fig. 6). Future experiments are needed to reveal whether MS cooling also affects theta phase delays along the septo-temporal axis of the hippocampus and whether there is a corresponding anatomical organization within the MS that may reflect such theta phase delays. Yet, the current findings provide important clues about how the MS contributes to theta phase space organization of hippocampal activity.

Interneurons, populations of pyramidal cells and MS neurons all fire at the frequency of hippocampal LFP (Buzsáki, 2010; Geisler et al., 2010; Gothard et al., 1996). In contrast, active individual pyramidal cells and granule cells oscillate faster (f_p) than the population activity (f_LFP), resulting in phase interference and measured experimentally by the ‘phase precession’ slope (O’Keefe and Recce, 1993). The difference between oscillation frequency of place cells and LFP theta is inversely correlated with place field size and affected by the running speed of the animal (L_PF = v/(f_p-f_LFP); Geisler et al., 2010). We found that at faster running velocities the difference between f_p and f_LFP increased, which may explain the place field size invariance (Geisler et al., 2007; Huxter et al., 2003). These relationships were preserved during MS cooling, which can account for the place field size invariance and other spatial features of place cells during MS cooling. In contrast, a unidirectional MS-hippocampus command mechanism cannot explain the observed place field size preservation.

The magnitude of phase precession is often explained by the interference between the MS-driven LFP theta and the faster oscillation of place neurons (O’Keefe and Burgess, 2005; Burgess et al., 2007). Under the unidirectional pacemaker model, the slowing the output MS theta frequency would result in a larger f_p –f_LFP difference and, consequently steeper phase precession and smaller place fields, as suggested by a computational model (Chadwick et al., 2016). However, during MS cooling f_p and f_LFP decreased proportionally (i.e., f_p–f_LFP difference remained constant) and the influence of the rat’s running velocity on f_p was preserved (Fig. 4a, c). These preserved relationships can explain why place field size was not affected by MS cooling. Proportional slowing of f_p and f_LFP was also observed in a virtual reality experiment (Aghajan et al., 2015; Ravassard et al., 2013). Overall, these distinct approaches support the hypothesis that theta phase preservation of spikes is a fundamental mechanism in the hippocampal system.

Further support for the primacy of phase, as opposed to time, comes from the time lag comparisons of place cell spikes. The travel distances between the peak positions of place cell sequences (L_tr) are correlated with their theta-scale time lags (τ) and phase lags, and the ratio of travel distance and theta-scale time lag (L_tr/τ) is known as distance-to-time compression (c; Dragoi and Buzsáki, 2006; Maurer et al., 2012). This distance-to-duration compression is believed to be the mechanism that chains together evolving place cell assemblies within theta cycles (Chadwick et al., 2016; Dragoi and Buzsáki, 2006; Harris et al., 2002; Lisman and Jensen, 2013; Mehta et al., 2002; O’Keefe and Burgess, 2005; Pastalkova et al., 2008; Samsonovich and McNaughton, 1997; Skaggs et al., 1996; Wang et al., 2015). Neither place field sizes (L_PF) nor the distances between place field peaks (L_tr) were affected by MS cooling. On the other hand, the theta-scale time lags (τ) between successive place cell assemblies increased. As a result, the compression index (c) decreased. In contrast, phase lags between successive place cells within the theta cycle were not affected.

Theta phase organization is also reflected by the observed firing rate changes. During MS cooling, LFP theta frequency decreased by 12 % and within-field firing rates of place cells decreased by a similar proportion (12%; interneurons 14%). This relationship can explain why the fraction of place cells and the number of spikes within theta cycles were largely unaffected by MS manipulation. MS cooling, therefore, exerted its main physiological effect by dispersing the same number of cell assemblies within the phase space of the prolonged theta cycles (Fig. 1b), as quantified by the longer t in the face of preserved phase differences between place field peaks. Overall, these findings suggest that the fundamental organization of cell assemblies in the hippocampus is based on theta phase-preservation mechanisms, even at the expense of longer temporal lags between assemblies. In general, our results imply that the physiological operations of the hippocampus can be described mechanistically by its cycle-based organization, and without reference to the concept of time (Buzsaki and Tingley, 2018).

Potential mechanisms

What are the mechanisms that keep the phase-organization within the MS-hippocampus loop when theta frequency changes? A previous experimental-computational model has shown that temporal lags between assemblies (τ) are correlated with the duration of the theta cycle (Geisler et al., 2010). It was hypothesized that the mechanism responsible for the delays between cells assemblies is inhibition in local hippocampal circuits (Geisler et al., 2010). However, the current findings demonstrate that the MS plays a critical role in adjusting the theta phase delays between neighboring place fields of pyramidal cells. In addition, previous finding indicate that following pharmacological inactivation of the MS, internally generated sequences disappear and theta-scale timing of place cells is impaired without affecting place cell positions in the maze (Wang et al., 2015). A putative mechanism may involve the reciprocal circuit between GABAergic neurons in MS and hippocampus (Suppl. Fig. 6). MS parvalbumin-expressing neurons innervate a variety of inhibitory neuron types in the hippocampus (Freund and Antal, 1988) and entorhinal cortex (Fuchs et al., 2016; Gonzalez-Sulser et al., 2014; Jeffery et al., 1995; Justus et al., 2017; Viney et al., 2018), while cholinergic neurons affect both principal cells and interneurons (Unal et al., 2015). In turn, long-range hippocampo-septal interneurons inhibit MS neurons (Gulyás et al., 2003; Takács et al., 2008; Toth et al., 1993). These hippocampo-septal inhibitory neurons are likely be of special importance because they are the best candidate for integrating the activity of multiple place cell assemblies and feedback population theta-oscillatory pulsing to subgroups of MS neurons.

MS cooling-induced memory impairment

MS cooling exerted a robust effect on spatial memory, comparable to damage or pharmacologic inactivation of MS (Bolding et al., 2020; Chang and Gold, 2004; Chrobak et al., 1989; Givens and Olton, 1990; Winson, 1978). Choice errors correlated best with the temporal dynamic of MS cooling. Whether memory impairment is due to the documented physiological changes in the hippocampus or other mechanisms remains an open question.

In addition to MS neurons, our manipulation may have affected septal afferents, fibers of passage and possibly its surrounding structures. Therefore, one possible interpretation of the behavioral effects is that moderate cooling of lateral septum, the n. accumbens and/or anterior end of the hippocampus is responsible for the behavioral deficit. However, lesion of lateral septum does not have an impact on spatial behavior (Fraser et al., 1991; Galey et al., 1985; Leutgeb and Mizumori, 1999; Winson, 1978). Electrolytic lesions (Thifault et al., 1998) or ibotenic acid-induced lesions (Annett et al., 1989) of the nucleus accumbens did not impair spatial behavior and, in fact, damaging catecholaminergic terminals selectively in the n. accumbens slightly improved spatial alternation (Taghzouti et al., 1985). Fibers of passage of subcortical neuromodulator neurons through the medial or lateral septum typically affect spontaneous alternation via the MS (Lalonde, 2002).

In our experiments, memory errors reached maximum tens of seconds before mild cooling was observed in the hippocampus, suggesting that this mild secondary effect cannot explain memory impairment. Importantly, previous studies have shown that decreasing brain temperature even down to 30° C was not sufficient to impair spatial navigation in rats (Andersen and Moser, 1995; Moser and Andersen, 1994). In humans, cognitive functions are not affected until the brain is cooled to about 33°C (Fay and Smith, 1941). Thus, while we cannot exclude impaired spike transmission of fibers of passage in MS as a contributing factor, moderate cooling of the structures surrounding MS may not fully account for the observed severe memory deficit. The moderate firing rate decrease of hippocampal neurons remains a candidate for the behavioral errors.

A remaining potential explanation is that the seemingly subtle but multiple changes of physiological parameters in the hippocampus (and expected but unobserved parallel changes in the entorhinal cortex) were responsible for the memory deficit. This possibility is supported by the observation that the temporal dynamic of choice errors correlated best with the time course of theta frequency decrease and that the maximum error rates occurred tens of seconds before a slight temperature decrease was detected in the hippocampus. Similarly, intra MS infusion of the tetracaine, muscimol and scopolamine suppressed theta oscillations and impaired performance in a spatial alternation task, and the choice errors best correlated with a change in theta oscillation frequency (Givens and Olton, 1990). During MS cooling, the same segment of the environment was ‘represented’ by the same number of neuronal assemblies but the time offsets between successive assemblies were longer in each theta cycle. Therefore, a possible explanation for the memory impairment, despite preserved spatial features of place cells, is that downstream reader structures, presumably not part of the MS-controlled theta system, failed to interpret the temporally altered hippocampal messages (Robbe and Buzsáki, 2009) but see (Venditto et al., 2019). Overall, our findings suggest that the fundamental organization scheme in the septo-hippocampal system is phase-based and that even minuscule temporal changes in large interconnected circuits may have behavioral consequences.

STAR Methods

Lead Contact

Further information and requests for resources and datasets should be directed to and will be fulfilled by György Buzsáki (gyorgy.Buzsaki@nyulangone.org).

Materials Availability

This study did not generate new unique reagents.

DATA AND CODE AVAILABILITY

The dataset will be available from our data share via our website buzsakilab.com/wp/public-data/ (Petersen et al., 2018) and will be uploaded to CRCNS.org. The code that support the findings of this study will be made available from the corresponding author upon reasonable request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Subjects and surgery

Rats (adult male Long-Evans, 250–450 g, 3–6 months old) were kept in a vivarium on a 12-hour light/dark cycle and were housed 2 per cage before surgery and individually after it. All experiments were approved by the Institutional Animal Care and Use Committee at New York University Medical Center.

Animals were anesthetized with isoflurane anesthesia and craniotomies were performed under stereotaxic guidance. A custom designed 3D printed cap (suppl. figure 1a) was attached to the skull with meta-bond, serving as a base for the probe implants and protection. A 12cm x 12cm sheet of copper mesh had beforehand been attached with dental cement to the base, from which a Faraday box/protector cap was later formed. Rats (Table 1) were implanted with silicon probes and tungsten wires to record local field potential (LFP) and spikes from the CA1 pyramidal layer (Vandecasteele et al., 2014). The tip of the cooling device was implanted at AP: +0.8mm, ML: 0.6mm (tilted 6° towards the midline), and lowered 6 mm below the brain surface, after which it was attached to the skull and base.

Silicon probes (NeuroNexus, Ann-Arbor, MI and Cambridge Neurotech, Cambridge, UK) were implanted in the dorsal hippocampus (antero-posterior (AP) −3.5mm from Bregma and 2.5 mm from the midline along the medial-lateral axis (ML)). The silicon probes consisted of three designs (table q): 4-shank with 16 sites per shank in a poly 3 staggered configuration, 5-shank with 12 sites each shank in a staggered configuration, and 6-shank probe with 10 sites per shank (Figure 2B). They were mounted on custom-made micro-drives (Suppl fig. 1e) to allow their precise vertical movement after implantation (Vandecasteele et al., 2012). Probes were implanted above the target region by attaching the micro-drives to the skull with dental cement (Suppl fig. 1e). Craniotomies were sealed with sterile wax or gel. Stainless steel screws or 100μm steel wires were bilaterally screwed or implanted above the cerebellum, serving as ground and reference electrodes, respectively, for electrophysiological recordings (Suppl fig. 1e). At the end of electrode implantation and cryoprobe implantation (see below), the copper mesh was folded upwards, connected to the ground screw, and painted with dental cement. The mesh acts as a Faraday cage, shielding the recordings from environmental electric noise and muscle artifacts, provides structural stability and keep debris away from the probe implants. After post-surgery recovery, probes were moved gradually in 50 μm to 150 μm steps until they reached the CA1 the pyramidal layer. The pyramidal layer of the CA1 region was identified by physiological markers: increased unit activity, strong theta oscillations and phase reversal of the sharp wave ripple oscillations (Mizuseki et al., 2011).

METHOD DETAILS

Cooling devices

Two different cooling techniques were used. A Peltier device and dry ice in Styrofoam chamber (‘dry ice cryoprobe’). Both cooling devices were attached to a silver wire that conducted the cooling to the medial septum (Fig. 2a).

Dry ice cryoprobe

A 15mm diameter 3D printed container with lid was constructed and a hollow cylinder made from Styrofoam (outer diameter: 18mm, inner diameter: 10mm; thermal conductivity: 0.03 W/m) was inserted into the container. A 20 mm silver wire (127 μm diameter, a-m systems, #781500; thermal conductivity: 406.0 W/mK), wrapped with graphene sheet (graphene-supermarket: Conductive Graphene Sheets, thickness: 25 μm; thermal conductivity: 1300–1500W/m in x-y plane and 13–15W/m in z plane), was inserted through the base of the Styrofoam container and attached to the inside of the chamber with thermal adhesive (Arctic Silver Thermal Adhesive, ASTA-7G; thermal conductivity: >7.5W/m-K). 10mm of the wire was protruding from the base of the chamber. The protruding silver wire was then inserted into an 8 mm long hollow polyimide tube (1.1 mm diameter, Cole-Parmer 95820–09), such that 1.5mm of the silver wire was exposed. The polyimide tube was further sealed with adhesive in both ends to create a contained air insulation around the silver wire (figure 2A). The air insulation served as a thermal insulation (thermal conductivity: 0.024), to minimize the cooling effects along the wire (Aronov and Fee, 2011). Finally, a thermocouple (a temperature sensor: Omega, 80pm wires, product number 5SC-TT-K-40–72) was attached with epoxy adhesive to the cooling implant with the tip of the probe aligned with the protruding silver wire (figure 2A, and suppl. figure 1A). Cooling with dry ice was achieved by placing a small amount of dry ice into the “cooling chamber”, which conducted the cooling to the exposed implanted silver wire.

Peltier cooling device

The hot side of a two-stage Peltier device (custom thermoelectric, 04812–5L31–04CFG 2 Stage Thermoelectric/Peltier Module) was attached to a copper heatsink (5mm x 5 mm, Enzotech MOS-C10 Forged Copper MOSFET Heatsinks) with heat-conductive adhesive (Arctic Silver, Arctic Silver Thermal Adhesive). The heatsink was shaped to fit the inner dimensions of a 25 mm x 25 mm electric fan (GDSTIME, 5 V DC Brushless fan). An 18 mm long silver wire (200μm diameter, a-m systems #782000) was attached to the cold side of the peltier device with heat conductive adhesive. An 8 mm long polyimide tube (1.1 mm diameter, Cole-Parmer 95820–09) was attached around the silver wire, sealed, and a thermocouple temperature sensor (Omega, 80pm wires, product number 5SC-TT-K-40–72) was attached to the tube. 1.5mm of the silver wire was exposed at the tip of the cooling device.

Electrophysiological Recordings

Animals were handled daily and accommodated to the experimenter before surgery. They were water restricted for 22 hours and trained to perform the behavioral task prior to surgery. After recovery from surgery, the animals were water restricted again to perform a spatial alternation task in a ‘theta’ (figure 8-shape) maze. The behavior session typically lasted 40 min, consisting of 40 control trials, after which the cooling was applied by manually placing a small amount of dry ice in the cooling chamber. The cooling typically peaked after about 60 sec after the cooling onset (suppl. fig. 1G) and lasted for about 10–12 minutes, corresponding to approximately 50 trials (figure 6C and suppl. Figure 2. The animal would continue the task for a total number of trials ranging from 80 to 200 (mean: 150 trials). The behavior was preceded and followed by 1–3 hours sleep sessions in the home cage of the rat.

Memory-demanding alternation task in a theta maze

In a ‘theta’ (figure 8-shape) maze (110 cm diameter, Fig. 2c), animals were trained to alternate between the left and the right arms to receive water drops at the reward locations (Figure 2C). The maze was placed on a platform 1 meter above the floor. The rat started from the reward location, ran along the central arm, after which it chose to run along the left or the right arm. If the animal performed the alternation correctly (visited the opposite arm than they visited in the previous trial), it received water reward. If it chose the wrong direction, the path to the reward location was blocked and the rat was forced to run back along the correct arm to collect reward.

The position of the animal was tracked with an OptiTrack 6-camera system (Natural Point Corp.). Calibration across cameras allowed for a three-dimensional reconstruction of the animal’s head position and orientation. A rigid body was created by mounting 6 reflective markers to a small 3D-printed holder, attached to the animal’s head-cap and tracked simultaneously by 6 infrared cameras (OptiTrack, Flex 3 cameras) at 120Hz.

QUANTIFICATION AND STATISTICAL ANALYSIS

Electrophysiological recordings were conducted using an Intan recording system: RHD2000 interface board with Intan 64 channel preamplifiers sampled at 20 kHz (Intan Inc).

Spike Sorting

Spike sorting was performed semi-automatically with KiloSort (Pachitariu et al., 2016) github.com/cortex-lab/KiloSort, using our own pipeline KilosortWrapper (a wrapper for KiloSort, github.com/petersenpeter/KilosortWrapper (Petersen et al., 2020), followed by a manual curation using the software Phy (github.com/kwikteam/phy) and our own designed plugins for phy (github.com/petersenpeter/phy-plugins).

Unit Classification

Well isolated units were classified into putative cell types using CellExplorer CellExplorer.org (Petersen and Buzsáki, 2020), see Supplementary figure 1l–o. Spiking characteristics, including the autocorrelograms, spike waveforms and putative monosynaptic connections derived from short-term cross-correlograms (English et al., 2017), were used to select and characterize well-isolated units. Three cell types were assigned: putative pyramidal cells, narrow and wide waveform interneurons.

Theta phase and phase precession

An LFP channel located in CA1 was filtered in the theta range (4–10Hz, third order butter filter, filt-filt), and translated into phase by the Hilbert transform. The phase precession slope of a place field, was determined by performing a circular-linear regression of the position vs theta phase for all spikes within the boundaries of the place field.

Oscillation Frequency of Neurons

For quantifying oscillation frequency of neurons, a 1ms-resolution spike raster was created and convoluted with an 80-point gaussian window. The auto-correlogram was calculated and the peak between 50ms and 150ms was determined and its reciprocal value was regarded as the oscillation frequency. For place field analysis (e.g. Fig. 3 B, C, F, H), only the spikes emitted as the animal passed through the field was included.

Place cell analysis

Spiking data were binned into 3–5 cm wide segments of the maze, generating the raw maps of spike number and occupancy probability. Place field boundaries were manually defined by the following criteria: a spatial tuned firing rate, phase precession, and peak firing rate above 10Hz. For figure 5, place fields were automatically defined by the following criteria: at least 4 bins, where the firing rate was above 10% of the peak rate in the maze, peak firing rate > 8 Hz and spatial coherence > 0.6 (Hafting et al., 2008; Muller and Kubie, 1989).

Spatial temporal compression

To determine the spatial-temporal compression, the distance between pairs of fields (determined as the spatial distance between the spatial peak firing rate) was plotted against the temporal delay inside theta cycles (either time or phase).

The temporal offset between individual overlapping fields was determined with a 1ms bin-sized cross correlogram, convoluted with a 60 bin-wide gaussian window. The phase offset was determined with a 0.01n bin-sized cross correlogram convoluted with a 60 bin-wide gaussian window. The compression and oscillation period were determined by fitting the surface equation below to the density of points (fig 5 c):

$$Z=\cos (x\frac{2\pi }{a\cdot b}+y\frac{2\pi }{b}+1)\cdot \mathit{exp}(-{(x+f\cdot y)}^{2/2c^2})\cdot \exp (-{(y-g)}^{2/2d^2})\cdot e$$

Where a is the compression (slope), b the CCG period (inverse of the oscillation frequency), c and d the widths of the two gaussian envelopes along the x and y dimensions, e the amplitude, f the x-y shift and g the y-offset.

Statistical Analyses

All statistical analyses were performed with MATLAB functions or custom-made scripts. For rank order calculation, the probability of participation and firing rate correlations, the unit of analysis was single cells. Unless otherwise noted, for all tests, non-parametric two-tailed Wilcoxon rank-sum (equivalent to Mann-Whitney U-test), Wilcoxon signed-rank or Kruskal-Wallis one-way analysis of variance were used. Due to experimental design constraints, the experimenter was not blind to the manipulation performed during the experiment.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Subjects: Long-Evans rats (9 male adults)	Charles River	Cat#: Crl:LE 006
Hippocampal data (Public data share with data from our lab)	Peter C. Petersen & Gyorgy Buzsaki	buzsakilab.com/wp/public-data/
CellExplorer (Cell classification pipeline and graphical interface)	Peter C. Petersen & Gyorgy Buzsaki	CellExplorer.org
KiloSort (Template based spike sorting Matlab software)	Pachitariu M & Cortex-lab	github.com/cortex-lab/KiloSort
KilosortWrapper (A wrapper for KiloSort written in Matlab)	Peter C. Petersen & Brendon Watson	github.com/petersenpeter/KilosortWrapper
Phy (Python GUI for manual spike curation)	Cyrille Rossant, Ken Harris et al.	github.com/cortex-lab/phy
Phy plugins	Peter C. Petersen	github.com/petersenpeter/phy-plugins
MATLAB	MathWorks	www.mathworks.com
Buzcode (MATLAB analysis tools)	Buzsaki Lab	github.com/buzsakilab/buzcode
FMA Toolbox (MATLAB toolbox for Freely Moving Animal (FMA))	Michaël Zugaro	fmatoolbox.sourceforge.net
Silicon probe (5×12, 6×10)	NeuroNexus	neuronexus.com
Silicon probe (4×16)	Cambridge Neurotech	www.cambridgeneurotech.com
Intan RHD2000 (recording equipment)	Intan technologies	intantech.com/RHD2000_evaluation_system.html

Highlights.

• Cooling the medial septum slowed down theta oscillations in the hippocampus

• The spatial representation in the hippocampus remained intact

• Choice errors increased in a spatial task

• Distance-time, but not distance-theta phase, compression was altered

Petersen et al. demonstrate that cooling of the medial septum slows theta oscillation and increases choice errors without affecting spatial features of pyramidal neurons. Cooling affects distance-time, but not distance-theta phase, compression. The findings reveal that cell assemblies are organized by theta phase and not by external (clock) time.