Fuzzy clustering method to compare the spread rate of Covid-19 in the high risks countries

Abstract

The numbers of confirmed cases of new coronavirus (Covid-19) are increased daily in different countries. To determine the policies and plans, the study of the relations between the distributions of the spread of this virus in other countries is critical. In this work, the distributions of the spread of Covid-19 in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran were compared and clustered using fuzzy clustering technique. At first, the time series of Covid-19 datasets in selected countries were considered. Then, the relation between spread of Covid-19 and population's size was studied using Pearson correlation. The effect of the population's size was eliminated by rescaling the Covid-19 datasets based on the population's size of USA. Finally, the rescaled Covid-19 datasets of the countries were clustered using fuzzy clustering. The results of Pearson correlation indicated that there were positive and significant between total confirmed cases, total dead cases and population's size of the countries. The clustering results indicated that the distribution of spreading in Spain and Italy was approximately similar and differed from other countries.

1. Background

Coronaviruses are a large group of viruses that trace respiratory and neurological systems [1], [2], [3]. In 2003 and 2012 two types of these viruses, called SARS coronavirus (SARS-CoV) and MERS coronavirus (MERS-CoV) were observed in some countries [4]. In last months of 2019, a new type of these viruses, called Covid-19 (2019-nCoV) was reported in Wuhan city in China [5], [6], [7], [8]. The reports show that Covid-19 has been observed in more than 220 countries (up to 18 April 2020). Since January to today 18 April 2020, the spread rate of Covid-19 has increased daily in different countries, specially in Unites States America [9], Spain [10], Italy [11], [12], [13], [14], Germany [15], United Kingdom [16], [17], [18], [19], France [11,[20], [21], [22]], Iran [23] and many others.

The spread rate of the Covid-19 has many dangers and consequently needs strict special policies and plans. Therefore, the study of the relations between the distributions of the spread of this virus in other countries is critical. In this work, the distributions of the spread of Covid-19 in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran are compared and clustered using fuzzy clustering technique. At first, we consider the time series of Covid-19 datasets in selected countries. Then, the correlations between these time series are computed. Finally, the observed time series are rescaled and categorized using fuzzy clustering technique. The main novelties of the current research can be summarized as following:

• 1The relation between spread of Covid-19 and population's size is studied.
• 2The Covid-19 datasets are rescaled based on the population's size of USA.
• 3The rescaled Covid-19 datasets of the countries with high spread risk are clustered using fuzzy clustering.

2. Material and method

This section discusses various topics such as data collection and data analysis techniques. The first subsection deals with the characteristics of research's dataset. Then the methods used to analyze the dataset are described.

2.1. Dataset

The dataset of this work contained the entire confirmed and dead Covid-19 cases in high risk countries including Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020 based on WHO statistics. Table 1 summarized descriptive statistics about the considered dataset.

Table 1.

Descriptive statistics for confirmed and dead Covid-19 cases in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020.

Cases	Country	Number	Minimum	Maximum	Mean	Standard deviation
Confirmed	Unites States America	59	0	35527	11900.8	13327.5
	Spain	59	0	9222	3187.6	3016.8
	Italy	59	0	6557	2922.6	2056.1
	Germany	59	0	6294	2329.2	2245.2
	United Kingdom	59	0	8719	1842.1	2207.7
	France	59	0	7578	1851.5	1876.0
	Iran	59	2	3186	1294.5	921.5
Dead	Unites States America	59	0	4928	628.0	1013.4
	Spain	59	0	950	330.1	340.5
	Italy	59	0	971	385.5	309.5
	Germany	59	0	315	69.7	94.9
	United Kingdom	59	0	980	247.1	342.0
	France	59	0	2004	316.6	447.3
	Iran	59	0	157	80.7	55.6

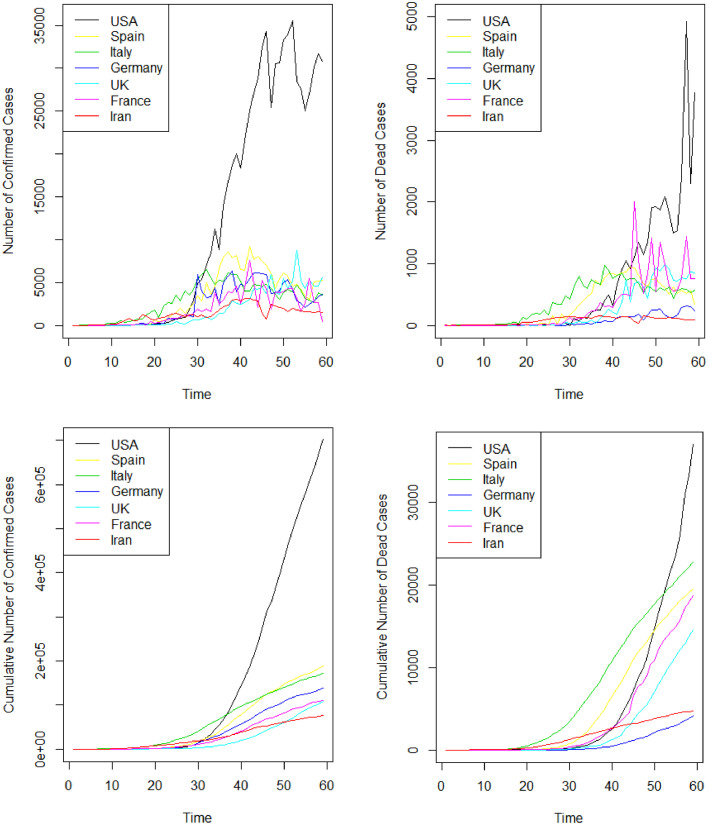
As it can be observed, Unites States America, Spain, Italy, Germany, France, United Kingdom, and Iran have the most means of daily confirmed cases, respectively. Also, Unites States America, Italy, Spain, France, United Kingdom, Iran, and Germany have the most means of daily dead cases, respectively. Fig. 1 also shows the plots of daily confirmed cases, dead cases, cumulative confirmed cases, and cumulative dead cases in in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020.

Fig. 1.

Daily confirmed cases (Top and Left), dead cases (Top and Right), cumulative confirmed cases (Bottom and Left), and cumulative dead cases (Bottom and Right), in in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020.

To study the relations between total confirmed cases, total dead cases and population's size of the countries, the Pearson coefficient of correlation is used. The results are reported in Table 2 .

Table 2.

Pearson coefficient of correlation test between confirmed and dead Covid-19 cases and population size up to 18 April 2020.

		Dead cases	Population's size
Confirmed cases	Pearson correlation	0.959	0.825
	p-value	<0.001	0.011
Dead cases	Pearson correlation		0.692
	p-value		0.042

The results indicated that there are positive and significant (p-value lower than 0.05) between total confirmed cases, total dead cases and population's size of the countries. Therefore, because the number of cases is dependent to the size of population, the comparison of the countries based on the number of confirmed cases or dead cases are not scientifically true. To solve this problem, the effect of the population's size should be eliminated. We used rescaled data as following:

$$\begin{array}{c}\hfill RescaleConfirmedCasesofCountry\\ \hfill =ConfirmedCasesofCountry\\ \hfill \times \frac{PopulationofUnitesStatesAmerica}{PopulationofCountry},\end{array}$$

and

$$\begin{array}{c}\hfill RescaleDeadCasesofCountry=DeadCasesofCountry\\ \hfill \times \frac{PopulationofUnitesStatesAmerica}{PopulationofCountry}.\end{array}$$

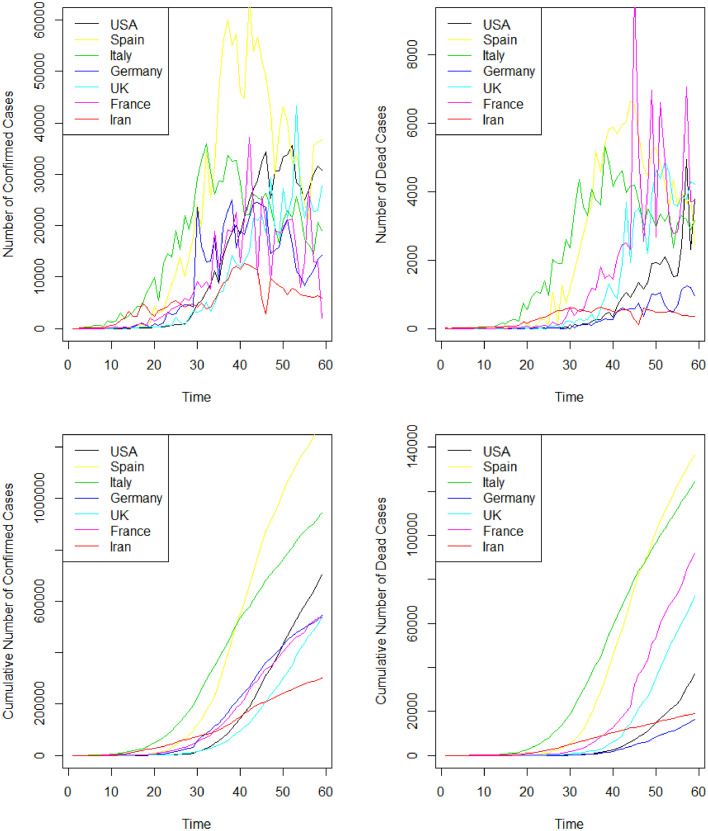
Fig. 2 shows the plots of rescaled data for daily confirmed cases, dead cases, cumulative confirmed cases, and cumulative dead cases in in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020. Table 3 summarized descriptive statistics about the rescaled dataset. As it can be observed, Spain, Italy, Unites States America, Germany, United Kingdom, France, and Iran have the most mean of rescaled daily confirmed cases, respectively. Also, Spain, Italy, France, United Kingdom, Unites States America, Iran, and Germany have the most mean of daily rescaled dead cases, respectively.

Fig. 2.

Daily rescaled confirmed cases (Top and Left), rescaled dead cases (Top and Right), rescaled cumulative confirmed cases (Bottom and Left), and rescaled cumulative dead cases (Bottom and Right), in in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020.

Table 3.

Descriptive statistics for rescaled confirmed and dead Covid-19 cases in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran from 22 February 2020 up to 18 April 2020.

Cases	Country	Number	Minimum	Maximum	Mean	Standard deviation
Confirmed	Unites States America	59	0.0	35527.0	11900.8	13327.5
	Spain	59	0.0	64505.5	22296.2	21101.4
	Italy	59	0.0	35861.4	15984.0	11245.3
	Germany	59	0.0	24938.2	9228.9	8896.1
	United Kingdom	59	0.0	43237.7	9134.9	10948.0
	France	59	0.0	37220.6	9094.1	9214.1
	Iran	59	7.9	12589.1	5115.0	3641.4
Dead	Unites States America	59	0.0	4928.0	628.0	1013.4
	Spain	59	0.0	6645.0	2309.2	2381.4
	Italy	59	0.0	5310.6	2108.6	1692.7
	Germany	59	0.0	1248.1	276.0	376.1
	United Kingdom	59	0.0	4859.8	1225.1	1695.9
	France	59	0.0	9843.0	1555.1	2196.9
	Iran	59	0.0	620.4	318.7	219.8

2.2. Fuzzy Clustering

Clustering [24] is a major task in data mining. It has many applications such as image processing, diagnosis systems, classification, missing value management and imputation, optimization, bioinformatics, machine learning [25]. Recently inspiring by classifier ensemble, the clustering ensemble [26] has emerged. But these methods use hard clustering as base clustering algorithm. Recently soft clustering algorithms [27] have been popular and it has been shown that these methods are superior to traditional hard clustering algorithms [28], [29], [30]. We can use soft clustering and fuzzy clustering interchangeably. Each data point belongs to all clusters (although the membership values are different) in soft clustering. It is worthy to be mention that the different membership values of a data point to all clusters should sum up to one. Fuzzy C-means (FCM) clustering algorithm [30] can be arguably considered to be the most popular soft clustering algorithm.

Given a set S of N records ${\overrightarrow{\mathit{x}}}_k=\left(x_{k1},x_{k2},\dots ,x_{kD}\right)$, a set of k fuzzy cluster defined by centroids ${\overrightarrow{\mathit{c}}}_i=\left(c_{i1},c_{i2},\dots ,c_{iD}\right)$, along with a membership matrix u, a soft clustering algorithm intends to divide S into k partitions $\left\{S_1,S_2,\dots ,S_k\right\}$, where S_j is achieved according to Eq. (1) (ties are broken randomly).

$$S_j=\left\{x\right|u_{jx}<u_{lx},\forall l\ne j\}$$ (1)

where c_ji is ith dimension of jth fuzzy cluster centroid.

All of centers and membership matrix are optimal, if they minimize the error function SSE presented in Eq. (2).

$$SSE\left(\mathit{c},\mathit{u}\right)=\sum _{j=1}^k\sum _{i=1}^D\sum _{x\in Data}{u}_{jx}^m{\left(x_i-c_{ji}\right)}^2,$$ (2)

subject to the constraints $\sum _{j=1}^k{u}_{jx}=1$. Matrix c is of size D × k whose column vectors are denoted by ${\overrightarrow{\mathit{c}}}_j$. To solve Eq. (11), we should employ a new set of Lagrange multipliers α_x for constraints $\sum _{j=1}^k{u}_{jx}=1$ , and then minimize the final (constraint-free) error function presented in Eq. (3).

$$SSE\left(\mathit{c},\mathit{u}\right)=\sum _{j=1}^k\sum _{i=1}^D\sum _{x\in Data}{u}_{jx}^m{\left(x_i-c_{ji}\right)}^2+\sum _{x\in Data}{\alpha }_x\left(1-\sum _{j=1}^k{u}_{jx}\right).$$ (3)

For a fix membership matrix u, the optimal $c_{ji}^{*}$ can be achieved by setting $\frac{\partial E}{\partial c_{ji}}=0$. Eq. (4) presents $\frac{\partial E}{\partial c_{ji}}=0$.

$$\frac{\partial E}{\partial c_{ji}}=2\sum _{x\in Data}{u}_{jx}^m\left(x_i-c_{ji}\right)=2\left(c_{ji}\sum _{x\in Data}{u}_{jx}^m-\sum _{x\in Data}{u}_{jx}^m{x}_i\right)=0.$$ (4)

Solving Eq. (4) with respect to c_ji gives Eq. (5).

$$c_{ji}^{*}=\frac{{\sum }_{x\in Data}{u}_{jx}^m{x}_i}{{\sum }_{x\in Data}{u}_{jx}^m}.$$ (5)

For a fixed cluster center matrix c, we compute the optimal $u_{jx}^{*}$ by setting $\frac{\partial E}{\partial u_{jx}}=0$ and $\frac{\partial E}{\partial {\alpha }_x}=0$. Eq. (6) represents $\frac{\partial E}{\partial u_{jx}}=0$.

$$\frac{\partial E}{\partial u_{jx}}=\sum _{i=1}^D\left(m{u}_{jx}^{m-1}{\left(x_i-c_{ji}\right)}^2\right)-{\alpha }_x=0.$$ (6)

Eq. (7) presents $\frac{\partial E}{\partial {\alpha }_x}=0$.

$$\frac{\partial E}{\partial {\alpha }_x}=1-\sum _{j=1}^k{u}_{jx}=0.$$ (7)

To solve Eq. (6) with respect to u_jx we can reach Eq. (8).

$$m{u}_{jx}^{m-1}\sum _{i=1}^D{\left(x_i-c_{ji}\right)}^2-{\alpha }_x=0.$$ (8)

Solving Eq. (8) with respect to u_jx we obtain Eq. (9).

$$u_{jx}={\left(\frac{{\alpha }_x}{m{\sum }_{i=1}^D\left(d_j{w}_{ji}{\left(x_i-c_{ji}\right)}^2\right)}\right)}^{\frac{1}{m-1}}$$ (9)

Substituting this expression in Eq. (7) results in a new equation and solving the resultant equation in terms of α_x yields to Eq. (10).

$${\alpha }_x={\frac{1}{\sum {\left(\frac{1}{{\sum }_{i=1}^{D}m{\left(x_i-c_{qi}\right)}^2}\right)}^{\frac{1}{m-1}}}}^{m-1}$$ (10)

If we substitute Eq. (10) in Eq. (9), we can reach a new $u_{jx}^{*}$ based on Eq. (11).

$$u_{jx}^{*}={\left(\frac{{\frac{1}{\sum {\left(\frac{1}{{\sum }_{i=1}^{D}m{\left(x_i-c_{qi}\right)}^2}\right)}^{\frac{1}{m-1}}}}^{m-1}}{{\sum }_{i=1}^{D}m{\left(x_i-c_{ji}\right)}^2}\right)}^{\frac{1}{m-1}}=\frac{\frac{1}{m^{\frac{1}{m-1}}{\sum }_{i=1}^D{{\left(x_i-c_{ji}\right)}^2}^{\frac{1}{m-1}}}}{m^{\frac{1}{m-1}}\sum {\left(\frac{1}{{\sum }_{i=1}^D{\left(x_i-c_{qi}\right)}^2}\right)}^{\frac{1}{m-1}}}=\frac{{\left(\frac{1}{{\sum }_{i=1}^D{\left(x_i-c_{ji}\right)}^2}\right)}^{\frac{1}{m-1}}}{\sum {\left(\frac{1}{{\sum }_{i=1}^D{\left(x_i-c_{qi}\right)}^2}\right)}^{\frac{1}{m-1}}}$$ (11)

To compare and classify the distributions of the spread of Covid-19 in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran, the fuzzy clustering technique is applied on rescaled Covid-19 datasets including confirmed cases, dead cases, cumulative confirmed cases, and cumulative dead cases.

3. Results

As it can be seen in Fig. 2 and Table 3, because of the effect of population's size, the rescaled datasets are different from main datasets and are scientifically good choices to compare different countries. In next subsections the results of fuzzy clustering are reported.

3.1. Rescaled number of confirmed cases

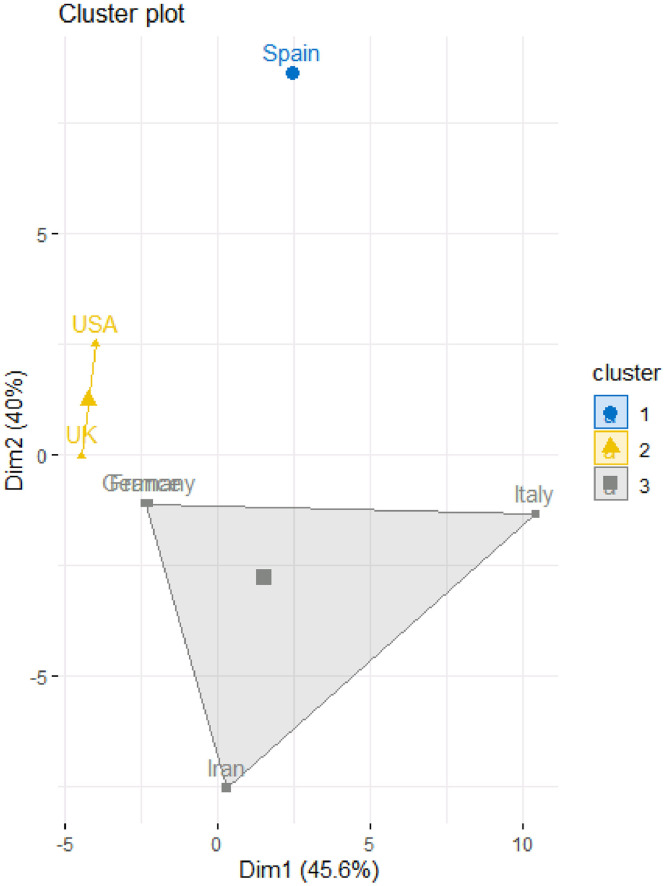
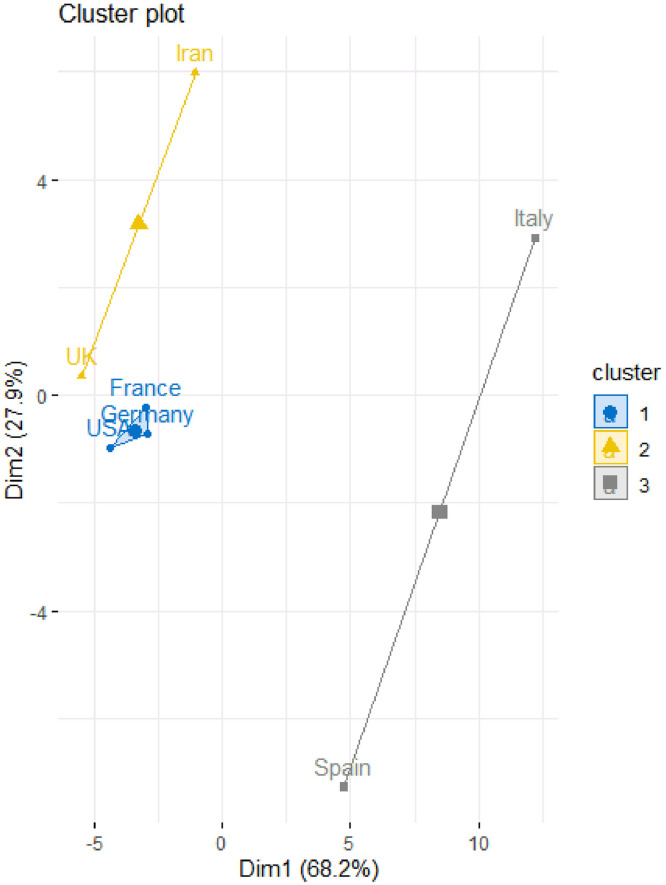
To determine the number of clusters Kaiser Index was used and the number was considered as the number of eigen-values of correlation matrix that are more than 1. Table 4 and Fig. 3, Fig. 4 provide the results of the fuzzy clustering technique. As it can be observed in Table 4 and Figs. 3 and 4, the rescaled numbers of confirmed cases in these considered countries can be divided in three clusters. Table 4 shows the probabilities of the membership of each country in each cluster. For each country, the maximum value of the probabilities of the membership to each cluster has been bolded. Based on these values, the first cluster consists of Spain (with probability 1.00). Also, the second cluster consists of Unites States America and United Kingdom (with probabilities 0.86 and 0.85, respectively). Moreover, the third cluster consists of Italy, Germany, France and Iran (with probabilities 0.46, 0.86, 0.78 and 0.73, respectively). In other words, Unites States America and United Kingdom are statistically similar; Italy, Germany, France and Iran are statistically similar; and Spain are significantly different form them.

Table 4.

The probabilities of membership in different clusters based on rescaled number of confirmed cases.

Country	Cluster 1	Cluster 2	Cluster 3
Unites States America	0.03	0.86	0.11
Spain	1.00	0.00	0.00
Italy	0.21	0.33	0.46
Germany	0.02	0.12	0.86
United Kingdom	0.02	0.85	0.13
France	0.03	0.20	0.78
Iran	0.04	0.23	0.73

Fig. 3.

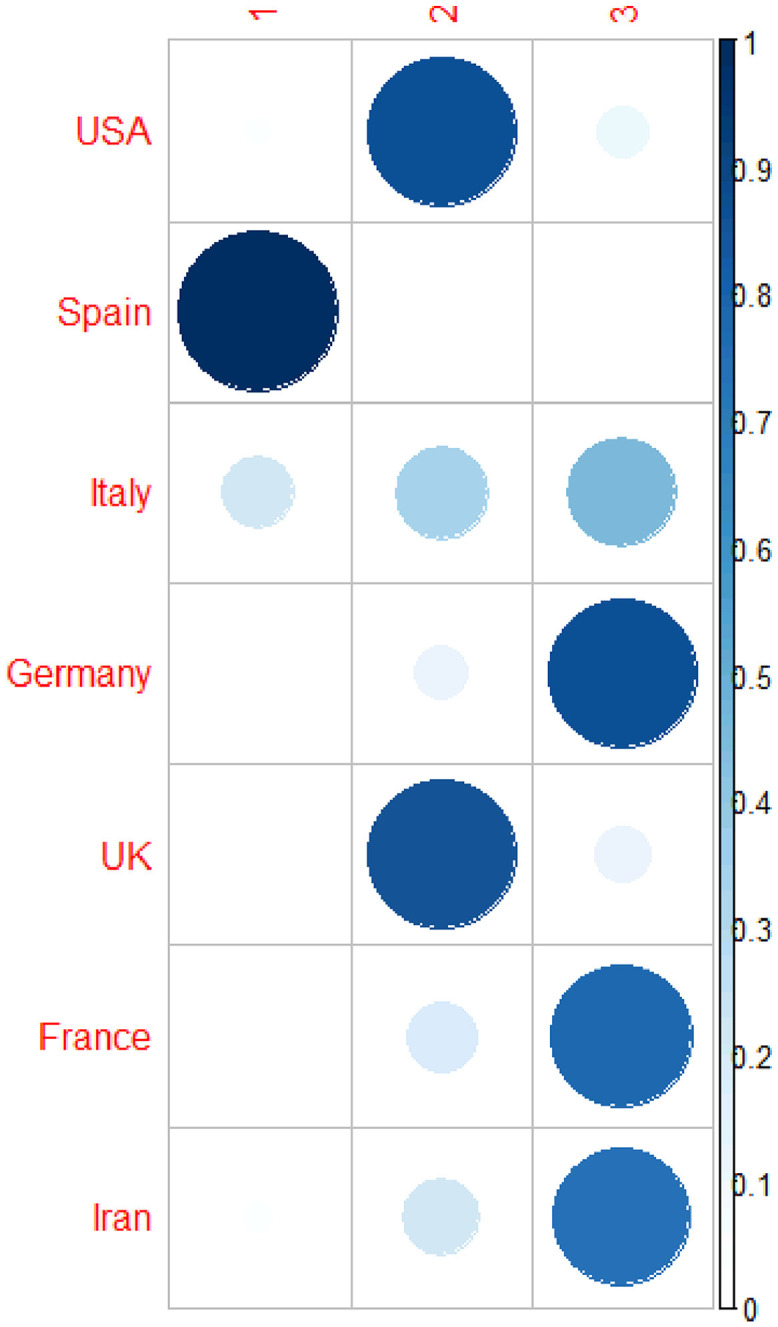
Fuzzy clustering method to classify the countries based on rescaled number of confirmed cases.

Fig. 4.

Fuzzy clustering plot to classify the countries based on rescaled number of confirmed cases.

3.2. Rescaled number of dead cases

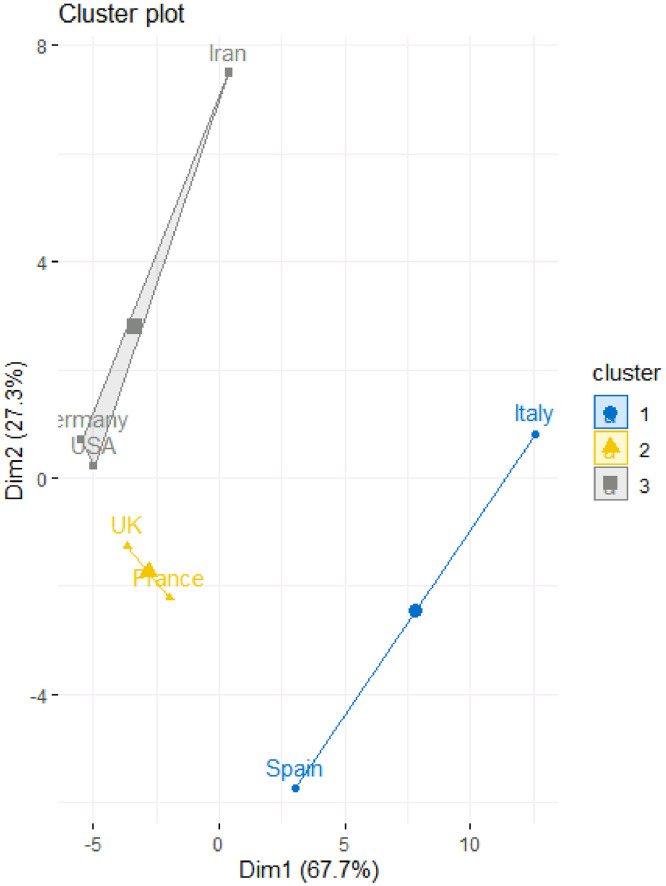
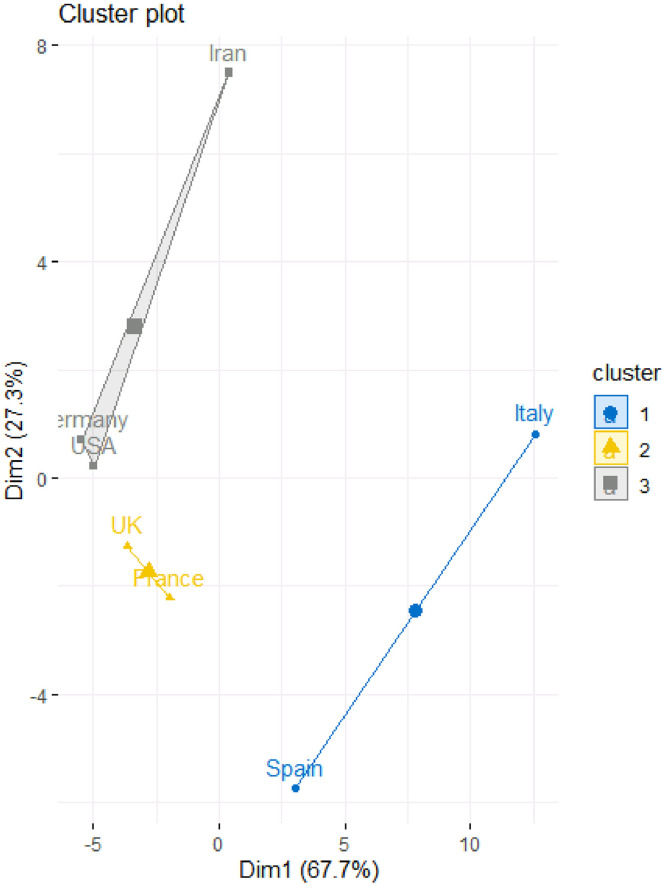
Table 5 and Fig. 5, Fig. 6 provide the results of the fuzzy clustering technique. As it can be observed in Table 5 and Figs. 5 and 6, the rescaled numbers of dead cases in these considered countries can be divided in three clusters. Table 5 shows the probabilities of the membership of each country in each cluster. For each country, the maximum value of the probabilities of the membership to each cluster has been bolded. Based on these values, the first cluster consists of United Kingdom and France (with probabilities 0.75 and 0.86, respectively). Also, the second cluster consists of Unites States America, Germany and Iran (with probabilities 0.77, 0.99 and 0.95, respectively). Moreover, the third cluster consists of Spain and Italy (with probabilities 0.89 and 0.73, respectively). In other words, United Kingdom and France are statistically similar; Unites States America, Germany and Iran are statistically similar; and Spain and Italy are statistically similar.

Table 5.

The probabilities of membership in different clusters based on rescaled number of dead cases.

Country	Cluster 1	Cluster 2	Cluster 3
Unites States America	0.17	0.77	0.06
Spain	0.08	0.03	0.89
Italy	0.10	0.06	0.84
Germany	0.01	0.99	0.00
United Kingdom	0.75	0.14	0.11
France	0.86	0.06	0.09
Iran	0.03	0.95	0.02

Fig. 5.

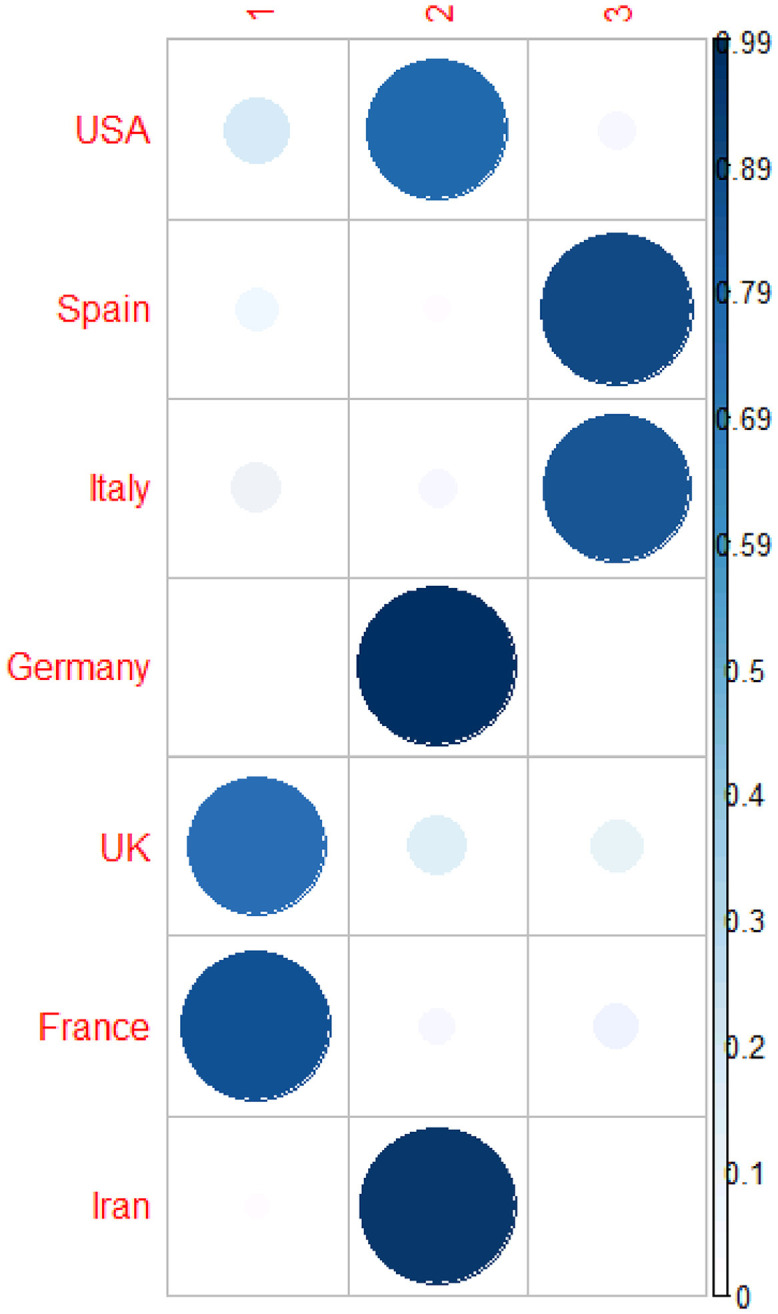
Fuzzy clustering method to classify the countries based on rescaled number of dead cases.

Fig. 6.

Fuzzy clustering plot to classify the countries based on rescaled number of dead cases.

3.3. Rescaled number of cumulative confirmed cases

Table 6 and Fig. 7, Fig. 8 provide the results of the fuzzy clustering technique. As it can be observed in Table 6 and Figs. 7 and 8, the rescaled numbers of cumulative confirmed cases in these considered countries can be divided in three clusters. Table 6 shows the probabilities of the membership of each country in each cluster. For each country, the maximum value of the probabilities of the membership to each cluster has been bolded. Based on these values, the first cluster consists of Unites States America, Germany and France (with probabilities 0.90, 0.95 and 0.97, respectively). Also, the second cluster consists of United Kingdom and Iran (with probabilities 0.58 and 0.96, respectively). Moreover, the third cluster consists of Spain and Italy (with probabilities 0.94 and 0.82, respectively). In other words, Unites States America, Germany and France are statistically similar; United Kingdom and Iran are statistically similar; and Spain and Italy are statistically similar.

Table 6.

The probabilities of membership in different clusters based on rescaled number of cumulative confirmed cases.

Country	Cluster 1	Cluster 2	Cluster 3
Unites States America	0.90	0.09	0.01
Spain	0.03	0.02	0.94
Italy	0.11	0.06	0.82
Germany	0.95	0.05	0.00
United Kingdom	0.41	0.58	0.01
France	0.97	0.03	0.00
Iran	0.04	0.96	0.00

Fig. 7.

Fuzzy clustering method to classify the countries based on rescaled number of cumulative confirmed cases.

Fig. 8.

Fuzzy clustering plot to classify the countries based on rescaled number of cumulative confirmed cases.

3.4. Rescaled number of cumulative dead cases

Table 7 and Fig. 9, Fig. 10 provide the results of the fuzzy clustering technique. As it can be observed in Table 7 and Figs. 9 and 10, the rescaled numbers of cumulative dead cases in these considered countries can be divided in three clusters. Table 7 shows the probabilities of the membership of each country in each cluster. For each country, the maximum value of the probabilities of the membership to each cluster has been bolded. Based on these values, the first cluster consists of Spain and Italy (with probabilities 0.97 and 0.97, respectively). Also, the second cluster consists of United Kingdom and France (with probabilities 0.89 and 0.94, respectively). Moreover, the third cluster consists of Unites States America, Germany and Iran (with probabilities 0.96, 0.98 and 0.98, respectively). In other words, Spain and Italy are statistically similar; United Kingdom and France are statistically similar; and Unites States America, Germany and Iran are statistically similar.

Table 7.

The probabilities of membership in different clusters based on rescaled number of cumulative dead cases.

Country	Cluster 1	Cluster 2	Cluster 3
Unites States America	0.00	0.03	0.96
Spain	0.97	0.02	0.01
Italy	0.97	0.02	0.01
Germany	0.00	0.02	0.98
United Kingdom	0.02	0.89	0.09
France	0.03	0.94	0.03
Iran	0.00	0.02	0.98

Fig. 9.

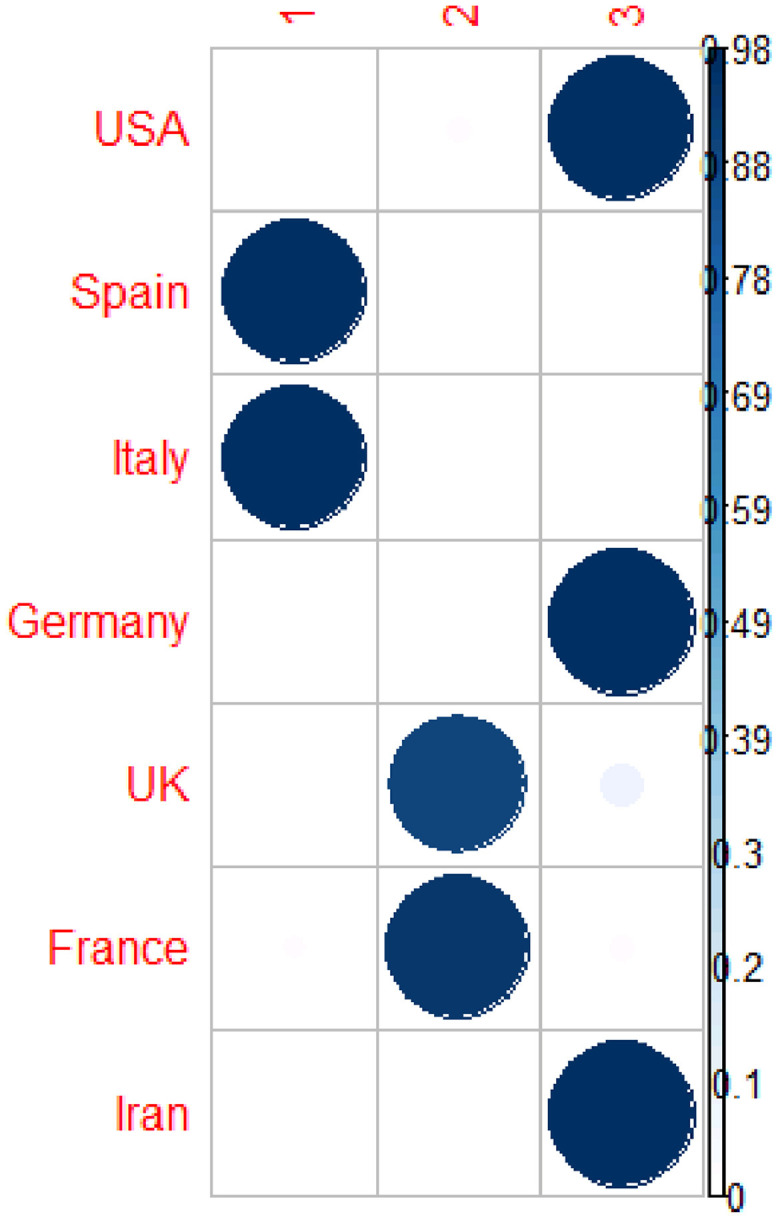
Fuzzy clustering method to classify the countries based on rescaled number of cumulative dead cases

Fig. 10.

Fuzzy clustering plot to classify the countries based on rescaled number of cumulative dead cases.

4. Conclusion

To consider the policies and plans to manage the spread of Covid-19, the study of the relations between the distributions of the spread of this virus in other countries is critical. In this work, the distributions of the spread of Covid-19 in Unites States America, Spain, Italy, Germany, United Kingdom, France, and Iran were compared and clustered using fuzzy clustering technique. In this research, the relation between spread of Covid-19 and population's size was firstly studied. The results indicated that there were positive and significant between total confirmed cases, total dead cases and population's size of the countries. Therefore, because the number of cases was dependent to the size of population, the comparison of the countries based on the number of confirmed cases or dead cases were not scientifically true. To solve this problem, the effect of the population's size has been eliminated by rescaling the Covid-19 datasets based on the population's size of USA. Finally, the rescaled Covid-19 datasets of the countries were clustered using fuzzy clustering. The clustering results indicated that the distribution of spreading in Spain and Italy was approximately similar and differed from other countries. For future works, the authors suggest the researchers categorize the statistical models including regression and time series models and artificial intelligence models that can be fitted on Covid-19 datasets [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59], [60], [61].

Funding

No fund.

CRediT authorship contribution statement

Mohammad Reza Mahmoudi: Data curation, Validation, Writing - original draft. Dumitru Baleanu: Conceptualization, Methodology, Software, Supervision. Zulkefli Mansor: Visualization, Investigation, Writing - review & editing. Bui Anh Tuan: Visualization, Investigation, Writing - review & editing. Kim-Hung Pho: Visualization, Investigation, Writing - review & editing.

Declaration of Competing Interest

The authors declare no conflict of interest.