Abstract
The current rise of protectionism has become the main uncertainty associated with global energy, economy, and the environment. Furthermore, the decoupling carbon emissions from economic growth is crucial for implementing Intended Nationally Determined Contributions (INDCs). These INDCs would be discounted if decreasing carbon emissions would require sacrificing economic growth. This study explored the effect of protectionism (by measuring trade openness based on available data) on the decoupling carbon emissions from economic growth. For this, the heterogenous effects of trade openness on carbon emissions were investigated using in data of 182 countries from 1990 to 2015. The results show that trade openness decreased carbon emissions in high-income and upper-middle-income countries, while having no significant impact on carbon emissions of lower-middle-income countries; even worse, for low-income countries, trade openness increased carbon emissions. The heterogeneous effects of trade openness on carbon emissions indicate that trade openness positively impacts the decoupling economic growth from carbon emission in rich countries, but negatively impacts poor countries. In addition, increasing individual incomes and population distort the decoupling economic growth from carbon emissions. Renewable energy and high oil prices contributed to the decoupling economic growth from carbon emissions. These effects are similar in all countries. Targeted policy implications are presented that enable the decoupling economic growth from carbon emissions for countries with different income levels.
Keywords: Decoupling, Trade openness, Oil price, Income level, Renewable energy, Carbon emissions
Graphical abstract
Highlights
-
•
Differences in the decoupling status of economic growth and carbon emissions in different income levels.
-
•
The effect of trade openness on the decoupling of economic growth and carbon emissions is heterogeneous.
-
•
Renewable energy and high oil prices contributed to decoupling economic growth from carbon emission.
-
•
Targeted policy implications are presented that enable the decoupling economic growth from carbon emission.
1. Introduction
The Kyoto Protocol relied on a top-down approach, while the Paris Agreement relied on a bottom-up approach. Under its new governance, the core of the Paris Agreement are the Intended Nationally Determined Contributions (INDCs), according to which, countries make their own commitments to decrease carbon emissions. However, one problematic issue is that if mitigating carbon emissions requires to sacrifice economic growth, the motivation and efforts of countries to commit to INDCs will greatly decrease. It is thus imperative to decouple economic growth from carbon emissions, so that more countries are stimulated to make every effort to curtail their carbon emissions.
Recently, to decrease Public Health Emergency of International Concern (PHEIC) COVID-19 transmission, numerous countries have implemented trade restrictions, which negatively impacted international trade. Undoubtedly, the current rise of protectionism has induced a new challenge for the carbon reduction for both developing and developed countries. Considering the strong inclination of countries to achieve the goals of the Paris Agreement, investigations regarding the impact of trade openness on the decoupling of economic growth and carbon emissions is necessary to develop more effective carbon reduction policies.
In this context, the present study is dedicated to solving three key issues based on panel data between the annual periods of 1990–2015 for 182 selected countries: (1) Is economic growth globally decoupled from carbon emissions? (2) What is the effect of trade openness on carbon emissions? (3) Is this effect heterogeneous for countries at different income levels?
To address these three issues, first, the Tapio decoupling model was applied to ascertain the decoupling between economic growth and carbon emissions. Then, the effect of trade openness on decoupling of economic growth and carbon emissions was investigated with the carbon functions. Unit root tests, cointegration tests, OLS and FMOLS estimates for panel models were adopted in carbon functions. This study established global panel and four income level panels, the results report the heterogeneous effect of trade openness on the decoupling of economic growth and carbon emissions. Effective policy implications can be drawn toward decoupling economic growth from carbon emissions, especially for countries with different income levels.
This article consists of five sections, which are organized as follows: Section 2 reviews and summarizes the relevant literature. Section 3 provides methods and data descriptions. Section 4 shows the results and discussion and Section 5 summarizes the main results and provides both conclusions and policy implications.
2. Literature review
2.1. Review of the decoupling process
The ideal state of decoupling indicates that economic growth does not depend on the growth of carbon emissions. To accurately understand the relationship between carbon emissions and economic growth, an indicator is required that reflects the relationship between both. The concept of decoupling was first proposed by Von in 1989 and was used to describe the relationship between carbon emissions and the economy. In 2002, the OECD first used the decoupling theory to study the relationship between economic growth and carbon emissions. Thus, the decoupling model gradually emerged. Subsequently, the concepts of primary decoupling and secondary decoupling were developed (Moldan et al., 2012). In 2005, the Tapio decoupling model began to use decoupling elasticity to describe the decoupling state (Tapio, 2005). In the following, for research level, the Tapio decoupling model was increasingly used in departmental and national research. At the departmental level, a deep understanding of the decoupling of industrial growth and carbon emissions was achieved (Wang and Jiang, 2019). In addition, decoupling process of soil erosion and human activities was investigated for the Loess Plateau of China using the concept of decoupling (Wei et al., 2006). In the tourism department, it has been suggested that China’s tourism economy experienced negative and weak decoupling (Tang et al., 2014). Moreover, many scholars also focused on the national level, and investigated relevant issues in specific countries, e.g., China (Yang et al., 2018), the United States (Datta, 2019), the OECD (Chen et al., 2018), Pakistan (Raza and Lin, 2020), and India (Wang et al., 2019). In short, the Tapio decoupling model has been widely used, which indicates the maturity and adaptability of this model. This study thus used the Tapio decoupling model to identify the decoupling status of economic growth and carbon emissions. Moreover, such a comparison between countries with different income levels can help to formulate targeted carbon emission reduction policies. Therefore, further empirical research is needed at the global level.
2.2. Review of trade openness and carbon emissions
The literature on factors affecting carbon emissions is quite rich (Al-mulali, 2011; Wang and Zhang, 2020; Zhang and Da, 2015). The linear econometric model is the most commonly used model to study the factors affecting carbon emissions (Jalil and Feridun, 2011), and has been applied to time series data and panel data (Bhattacharya et al., 2017). As research increases, the existing research in this field can be divided into three categories. The first category investigated the relationship between economic development and carbon emissions (Galeotti et al., 2009; Saboori et al., 2012; Selden and Song, 1994). The second category incorporated population and energy into the research framework of economic development and carbon emissions (Lehmann and Gawel, 2013; O’Neill and Chen, 2002; Weber and Perrels, 2000). Age structure (Fan et al., 2006), urbanization (Martínez-Zarzoso and Maruotti, 2011), the size of households (Poumanyvong and Kaneko, 2010), energy prices (Rout et al., 2008), and energy consumption (Fortes et al., 2008) were specifically investigated. The third category not only includes population and energy but also control variables such as trade and foreign direct investment (Dasgupta et al., 2001; Tamazian et al., 2009; Zhang, 2011).
The present research is part of the third category and presents in-depth research on the impact of trade openness on carbon emissions, including individual incomes, population, oil prices, and renewable energy. Free trade helps the global economy to grow faster by increasing the trade volume and income, both in developed and developing countries. However, this growth trend is accompanied by specific environmental consequences (Shahbaz et al., 2017b).
In general, the impact of trade openness can mainly be divided into two theories in the environmental field. The first theory assumes that the impact of trade openness on pollution is vague and can be divided into scale effect, technology effect and composition effect (Farhani et al., 2014a). The second theory is the Pollution Haven Hypothesis (Copeland and Taylor, 2004). Trade openness introduces foreign direct investment. Since different countries set different environmental standards, polluting enterprises will choose to produce in countries with comparatively low environmental standards, which thus become “pollution haven”. Therefore, the impact of trade openness on the environment needs to be considered for specific countries.
Based on these two theories, conclusions from the literature formed four hypotheses: (1) trade openness promotes carbon emissions; (2) carbon emissions promote trade openness; (3) feedback hypothesis: Trade openness and carbon emissions interact; (4) neutral hypothesis: Trade openness is independent of carbon emissions. In the evidence supporting hypothesis (1), at the national level, it has been found that trade openness positively affects carbon emissions in the long run for Pakistan by using the vector error correction model (VECM) (Nasir and Ur Rehman, 2011). Moreover, it has been observed that increased trade openness will increase pollution. This has been corroborated by applying the panel vector error correction model (PVECM), the fully modified ordinary least squares (PFMOLS) model, and the panel dynamic ordinary least squares (PDOLS) (Farhani et al., 2014b). With regard to hypothesis (2), China has been studied in the context of globalization using VECM causality as well as the ARDL bounds test (Shahbaz et al., 2017a). The causal test proved the unidirectional Granger causality of carbon emissions to trade openness. Besides, several international organizations also suggested that environmental regulations exert a serious impact on international trade. Hypothesis (3) refers to the bidirectional causality between trade openness and carbon emissions. At the transnational level, a study of 105 countries identified bidirectional causality between the global group and the middle-income group by using the panel regression model (Shahbaz et al., 2017b). While trade openness is affected by carbon emissions, it also affects carbon emissions. Hypothesis (4) does not support the link between trade openness and carbon emissions; however, relatively little literature supporting this hypothesis. At the national level, it has been argued that it is difficult to find a causal relationship between trade and the environment by using a linear econometric model (Frankel and Romer, 1999). At the transnational level, in the panel regression model, trade openness has been found to be not generally correlated with increased emissions when studying the effects of trade on environmental Kuznets curve (EKC) (Kearsley and Riddel, 2010). Clearly, the results of different studies support different hypotheses. Consequently, the relationship between trade openness and carbon emissions still merits further investigation.
Although the existing literature covers a similar scope than the present work, this study contributes to previous literature in a number of notable aspects. First, this study extends the literature by incorporating of trade openness into the existing economic growth-carbon emission research framework. Renewable energy and population are used as additional variables, and a systematic study was conducted. The conclusions also provide comprehensive policy recommendations toward the achieving decoupling of economic growth from carbon emissions. Second, this study not only includes a similarities analysis at the global level, but more importantly, investigates the differences of four income sub-panels (high-income, upper-middle-income, lower-middle-income, and low-income) on the effect of trade openness in the decoupling of economic growth from carbon emissions. Such an analysis of differences can help more countries to find effective ways to embark on the path of decoupling economic growth from carbon emissions.
3. Method and data
3.1. Decoupling index model
This study uses Tapio decoupling model, with the following equation:
| (1) |
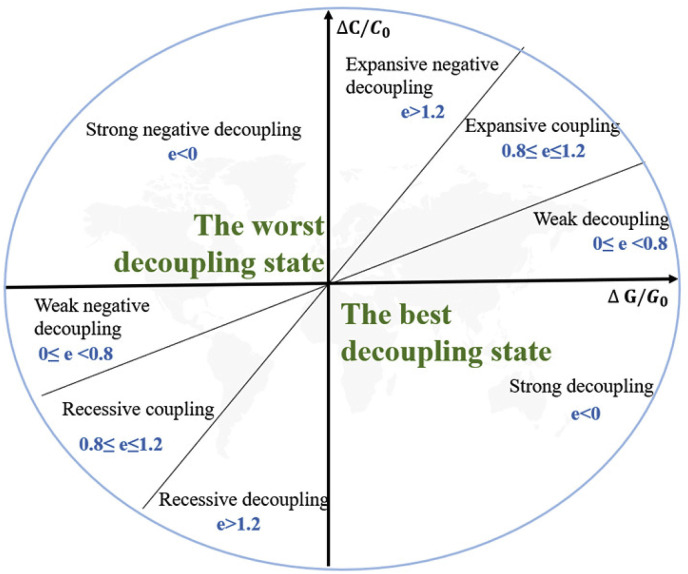
where e(C) represents the decoupling elasticity coefficient between economic activities and carbon emissions, ΔC represents the total carbon emission change from the base period to the end period, represents the carbon emissions at the base period. ΔG represents the total GDP change from the base period to the end, and represents the base period GDP. The Tapio model subdivides the decoupling state into eight states according to the decoupling elasticity value (Fig. 1 ).
Fig. 1.
Schematic diagram of decoupling states.
3.2. Empirical model
Based on previous research (Dong et al., 2018) (Dogan and Turkekul, 2016), the following models were established:
| (2) |
In Eq. (2), n (n = 1,2, …, 182) represents the sample country, t represents the year, OPEN represents trade openness, and C represents carbon emissions per capita. The estimation model is converted into a log linear econometric model:
| (3) |
In Eq. (3), X represents control variables, including oil prices, renewable energy consumption, individual incomes and population. Among these, and represent the intercept and error terms, respectively, and represent the estimated coefficients of different variables. In Model 1, the only independent variable is lnOPEN, and in Models 2 and 3, lnOP, lnGDP, lnRE, and lnPOP are added as control variables.
3.3. Estimation techniques
The study of the relationship between C, OPEN, OP, GDP, RE, and POP was divided into three steps. First, the panel unit root test was used to test the stability of each variable. Second, the panel cointegration test was used to determine the long-term cointegration relationship between variables. Next, the fixed-effect OLS and FMOLS cointegration estimates were used to analyze the long-term cointegration relationship between variables.
3.3.1. Panel unit root tests
This study used four panel unit root tests: LLC, IPS, Fisher-ADF and Fisher-PP. These four tests include the same root test and the different root test. The unit root test was used to test the stability of the variable (Wang and Su, 2019). The null hypothesis of this test is that the variable has a unit root. If the result shows that the null hypothesis can be accepted, then the variable is not stationary; otherwise, the variable is stationary.
The formula of LLC test is as follows (Levin et al., 2002):
| (4) |
where , represent the autoregression coefficients of the model, and the corresponding vectors of the regression parameters were p = 1,2,3.
The formula of the IPS test (Im et al., 2003) is similar to that of the LLC test. In addition, the unit root test of the Fisher-PP panel, as developed by Phillips and Perron is a different unit root test (Phillips and Perron, 1988), the expression of which is as follows:
| (5) |
| (6) |
where m, represents the reciprocal of the normal distribution function, and represents the P-value of the ADF unit root test. The null hypothesis is = 0, which indicates that there is a unit root; if < 0, there is no unit root.
3.3.2. Panel cointegration tests
The cointegration test can determine whether variables that are stable at a specific level or of the same order have a long-term stable cointegration relationship. In this study, the panel Kao test (Kao, 1999) and the panel Pedroni test (Pedroni, 2001) were used, both of which are part of the Engle-Granger method. The Pedroni cointegration test includes two alternative hypotheses: panel statistical hypotheses and outlier statistical hypotheses. The specific statistical formula is as follows:
A. Panel-ρ
| (7) |
B. Panel-
| (8) |
C. Group-ρ
| (9) |
D. Group-
| (10) |
where
| (11) |
3.3.3. Panel cointegration estimates
The second step of the long-term cointegration relationship is a cointegration estimation. This study used the ordinary least squares (OLS) method to perform regression on Model 2, and fully modified ordinary least squares (FMOLS) to perform regression on Models 1 and 3. FMOLS is widely used for regressions (Liu et al., 2019). Compared with OLS estimation, FMOLS estimation can correct sequence correlation and prevent pseudo regression, thus, it is a robust panel econometrics technology. In the FMOLS cointegration system, Pedroni (2000)proposed the following equation.
| (12) |
where , , is the long-term covariance. In Equation (12), x and have a cointegration relationship. The long-term covariance can be decomposed into , where represents the automatic covariance and represents the weighted sum of the covariance and The FMOLS criteria are as follows:
| (13) |
where
3.4. Data
Based data availability, unbalanced panel data was obtained for 182 countries from 1990 to 2015. Compared with many previous studies, this sample offers greater coverage in terms of country and year. First, a global panel composed of 182 countries was used. Second, the estimated sample was divided into four income sub-panels based on the 2020 World Bank’s country classification: low-income (LI), lower-middle-income (LMI), upper-middle-income (UMI) and high-income (HI). Among these, the LI group is composed of 27 countries, the LMI and UMI groups are composed of 45 and 56 countries respectively, and the HI group is composed of 54 countries (see Table A1 in Appendix A). The variable definitions are shown in Table 1 and Table 2 shows the descriptive statistics of variables.
Table 1.
Definitions and sources of data in the model.
| Symbol | Definition | Source |
|---|---|---|
| C | emissions (metric tons per capita) | World Bank |
| OP | Brent Spot crude prices (US dollars per barrel) | BP Statistical Review of World |
| RE | Renewable energy consumption (% of total final energy consumption) | World Bank |
| GDP | GDP per capita (constant 2010 US$) | World Bank |
| POP | Population, total (Ten thousand) | World Bank |
| OPEN | Trade (% of GDP) | World Bank |
Table 2.
Descriptive statistics of variables.
| Statistics | LNC | LNTRADE | LNOP | LNGDP | LNPOP | LNRE |
|---|---|---|---|---|---|---|
| Mean | 0.4927 | 4.2817 | 3.6128 | 8.3513 | 8.1262 | 2.7443 |
| Std. Dev | 1.6531 | 0.6276 | 0.7128 | 1.5074 | 4.4497 | 1.7258 |
| Max | 3.5812 | 6.0927 | 4.7155 | 11.6260 | 20.9934 | 4.5885 |
| Min | −4.5356 | −3.8633 | 2.5428 | 5.1019 | −0.0508 | −6.3399 |
4. Results and discussion
4.1. Analysis of decoupling status of carbon emissions and economic growth
4.1.1. Decoupling status of each income group
Five decoupling states were identified in HI countries over the investigated period (Fig. 2 ): recessive decoupling (4%), expansive coupling (17%), strong decoupling (25%), weak decoupling (50%), and expansive negative decoupling (4%). Strong decoupling and weak decoupling totaled 75% in HI countries, identifying these as the highest among the four income groups. This suggests that decoupling of economic growth and carbon emissions is relatively common in HI countries. In addition, strong decoupling was maintained over the last five years of this dataset (2010–2014). This indicates that HI countries have gradually acquired the ability to decrease their carbon emissions without sacrificing economic growth. However, the expansion coupling state and the negative expansion decoupling state still appeared in individual years. The economic crisis in 2008 caused negative growth of both carbon emissions and GDP in HI countries, which leads to the emergence of weak negative decoupling. Later, as the economy recovered, carbon emission reductions were successful. The decoupling state improved to strong decoupling (2010–2011) in HI countries.
Fig. 2.
Decoupling trend of economic growth and carbon emissions.
With regard to UMI countries, four decoupling states were identified: expansive coupling (29%), strong decoupling (12.5%), weak decoupling (37.5%), and expansive negative decoupling (21%). Overall, the year 2000 can be regarded as a turning point. Before 2000, strong and weak decoupling of economic growth from carbon emissions dominated. From 2000 to 2011, UMI countries entered a period of high-speed industrialization. The prevailing rapid economic development has caused excessive carbon emissions. In this context, expansion coupling has become the main performance of the relationship between economic growth and carbon emissions in 2000–2011. To overcome this dilemma, UMI countries strive to develop the tertiary industry and transform their economic development mode. In addition, many countries strive to increase the proportion of clean energy to adjust their energy structure (Wang and Wang, 2020). For example, China, which uses coal as its main energy source, showed a clear trend of improving its energy structure. Ultimately, the continuous weak decoupling appeared in 2011–2014, indicating that the efforts of the UMI countries have yielded results.
Four decoupling states were identified in LMI countries in 1990–2014, expansive coupling (25%), strong decoupling (17%), weak decoupling (33%), and expansive negative decoupling (25%). The decoupling of economic growth and carbon emissions has fluctuated state in LMI (1990–2014). The fluctuation was obvious compared with UMI over the same period. The reason may be that because of the desire to improve the economy, LMI countries focus more on economic development than environmental quality. However, the dependence of economic growth on energy will further stimulate carbon emissions, which is not conducive to their reduction (Wang and Su, 2020). In addition, developed countries export industrial production to LMI. The decrease of carbon emissions in HI countries is thus, in fact, paid for by developing countries (Schaltegger and Csutora, 2012). Hence, it is difficult for LMI countries to achieve a long-term decoupling of economic growth and carbon emissions.
The decoupling status of LI countries is quite rich, and the following six states were identified: expansive coupling (17%), strong decoupling (25%), weak decoupling (33%), expansive negative decoupling (17%), strong negative decoupling (4%), and weak negative decoupling (4%). This may be related to the ability of LI countries to resist risks. The economic development of LI countries was very difficult in 1991–1992. The negative economic growth and low carbon emissions led to the appearance of strong negative decoupling and weak negative decoupling. Overall, with improving economic conditions, the decoupling status gradually improves.
4.1.2. Global decoupling status
Five decoupling states appeared in the global sample over the considered period: strong decoupling (12%), weak decoupling (46%), expansive coupling (21%), expansive negative decoupling (17%), and weak negative decoupling (4%). Among these, weak decoupling occurred most frequently. Consequently, the world has been in a state where economic output and carbon emissions have simultaneously increased for most of the time. The lethargic economy of 2008 has decreased carbon emissions compared with the previous year. Therefore, weak negative decoupling occurred in 2008–2009. Judging from the overall decoupling evolution trend, the decoupling of global economic growth and carbon emissions was subject to an iterative process. First, weak decoupling was the dominant state of decoupling before 2000. Over the next decade, environmental protection was ignored as countries sought to accelerate their economic growth. This allowed decoupling to evolve into expansive coupling. Finally, climate change has induced countries to take practical action to control their carbon emissions. In fact, many practical actions were already taken before 2011, but only developed countries actively participated before 2011. With the participation of more developing countries, UMI (2011–2012) and LMI (2012–2013) gradually entered a weak decoupling state. This led to the emergence of weak decoupling at a global level in 2011–2014.
4.2. Unit root test results
All variables passed the four panel unit root tests, and the results are shown in Table 3, Table 4, Table 5, Table 6, Table 7 . Independent of the income group, the stationarity of the variables remains stable after the first-order difference. This prompted the next cointegration analysis. Specifically, since the test results of the four panel unit roots are sometimes inconsistent, the majority of the test results was selected.
Table 3.
Panel data unit root test results high-income (HI) countries.
| variable | Test method | At level |
At 1st difference |
||
|---|---|---|---|---|---|
| t-Statistic | Prob. | t-Statistic | Prob. | ||
| lnC | LLC | 0.3303 | 0.6294 | −25.3482∗∗∗ | 0.0000 |
| IPS | −0.5472 | 0.2921 | −24.7075∗∗∗ | 0.0000 | |
| ADF | 157.8240∗∗∗ | 0.0013 | 745.0330∗∗∗ | 0.0000 | |
| PP-Fisher | 119.4290 | 0.2128 | 945.6830∗∗∗ | 0.0000 | |
| lnOP | LLC | 0.0565 | 0.5225 | −14.4233∗∗∗ | 0.0000 |
| IPS | 4.7687 | 1.0000 | −18.5345∗∗∗ | 0.0000 | |
| ADF | 29.7437 | 1.0000 | 512.7750∗∗∗ | 0.0000 | |
| PP-Fisher | 30.0693 | 1.0000 | 472.4640∗∗∗ | 0.0000 | |
| lnRE | LLC | −0.1487 | 0.4409 | −26.5624∗∗∗ | 0.0000 |
| IPS | 2.9442 | 0.9984 | −25.5011∗∗∗ | 0.0000 | |
| ADF | 126.9620 | 0.1027 | 805.7770∗∗∗ | 0.0000 | |
| PP-Fisher | 142.2660∗∗ | 0.0151 | 829.9100∗∗∗ | 0.0000 | |
| lnGDP | LLC | −5.9370∗∗∗ | 0.0000 | −16.6356∗∗∗ | 0.0000 |
| IPS | 2.0601 | 0.9803 | −16.1460∗∗∗ | 0.0000 | |
| ADF | 81.7711 | 0.9612 | 456.0830∗∗∗ | 0.0000 | |
| PP-Fisher | 98.0067 | 0.6975 | 457.5450∗∗∗ | 0.0000 | |
| lnPOP | LLC | −2.5610∗∗∗ | 0.0052 | −0.9226 | 0.1781 |
| IPS | 5.2753 | 1.0000 | −5.4887∗∗∗ | 0.0000 | |
| ADF | 120.0550 | 0.1658 | 240.4860∗∗∗ | 0.0000 | |
| PP-Fisher | 229.1550∗∗∗ | 0.0000 | 227.2430∗∗∗ | 0.0000 | |
| lnOPEN | LLC | −3.2272∗∗∗ | 0.0006 | −27.3984∗∗∗ | 0.0000 |
| IPS | −0.7895 | 0.2149 | −25.1925∗∗∗ | 0.0000 | |
| ADF | 114.0190 | 0.3273 | 705.8020∗∗∗ | 0.0000 | |
| PP-Fisher | 116.7810 | 0.2653 | 789.7430∗∗∗ | 0.0000 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table 4.
Panel data unit root test results upper-middle-income (UMI) countries.
| variable | Test method | At level |
At 1st difference |
||
|---|---|---|---|---|---|
| t-Statistic | Prob. | t-Statistic | Prob. | ||
| lnC | LLC | −5.8321∗∗∗ | 0.0000 | −33.1267∗∗∗ | 0.0000 |
| IPS | −3.8975∗∗∗ | 0.0000 | −30.1645∗∗∗ | 0.0000 | |
| ADF | 200.2090∗∗∗ | 0.0000 | 1028.3200∗∗∗ | 0.0000 | |
| PP-Fisher | 239.9240∗∗∗ | 0.0000 | 1935.3500∗∗∗ | 0.0000 | |
| lnOP | LLC | 0.0575 | 0.5229 | −14.6880∗∗∗ | 0.0000 |
| IPS | 4.8562 | 1.0000 | −18.8746∗∗∗ | 0.0000 | |
| ADF | 30.8453 | 1.0000 | 531.7670∗∗∗ | 0.0000 | |
| PP-Fisher | 31.1830 | 1.0000 | 489.9630∗∗∗ | 0.0000 | |
| lnRE | LLC | −8.6057∗∗∗ | 0.0000 | −27.8186∗∗∗ | 0.0000 |
| IPS | −5.8853∗∗∗ | 0.0000 | −26.8433∗∗∗ | 0.0000 | |
| ADF | 265.1480∗∗∗ | 0.0000 | 798.1670∗∗∗ | 0.0000 | |
| PP-Fisher | 221.9790∗∗∗ | 0.0000 | 823.3950∗∗∗ | 0.0000 | |
| lnGDP | LLC | −2.0807∗∗ | 0.0187 | −21.7528∗∗∗ | 0.0000 |
| IPS | 4.4646 | 1.0000 | −20.5271∗∗∗ | 0.0000 | |
| ADF | 87.1641 | 0.9604 | 601.7010∗∗∗ | 0.0000 | |
| PP-Fisher | 90.8616 | 0.9288 | 620.9370∗∗∗ | 0.0000 | |
| lnPOP | LLC | −4.2406∗∗∗ | 0.0000 | −5.9177∗∗∗ | 0.0000 |
| IPS | −1.1059 | 0.1344 | −4.8509∗∗∗ | 0.0000 | |
| ADF | 244.5330∗∗∗ | 0.0000 | 231.6940∗∗∗ | 0.0000 | |
| PP-Fisher | 445.9320∗∗∗ | 0.0000 | 178.8140∗∗∗ | 0.0001 | |
| lnOPEN | LLC | −4.3522∗∗∗ | 0.0000 | −28.9283∗∗∗ | 0.0000 |
| IPS | −5.6305∗∗∗ | 0.0000 | −29.3186∗∗∗ | 0.0000 | |
| ADF | 213.7520∗∗∗ | 0.0000 | 810.5830∗∗∗ | 0.0000 | |
| PP-Fisher | 211.8550∗∗∗ | 0.0000 | 976.9980∗∗∗ | 0.0000 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table 5.
Panel data unit root test results lower-middle-income (LMI) countries.
| variable | Test method | At level |
At 1st difference |
|||
|---|---|---|---|---|---|---|
| t-Statistic | Prob. | t-Statistic | Prob. | |||
| lnC | LLC | −3.7109∗∗∗ | 0.0001 | −26.1813∗∗∗ | 0.0000 | |
| IPS | −1.6884∗∗ | 0.0457 | −24.0032∗∗∗ | 0.0000 | ||
| ADF | 147.4100∗∗∗ | 0.0001 | 644.9100∗∗∗ | 0.0000 | ||
| PP-Fisher | 124.3340∗∗∗ | 0.0097 | 857.0880∗∗∗ | 0.0000 | ||
| lnOP | LLC | 0.0515 | 0.5206 | −13.1666∗∗∗ | 0.0000 | |
| IPS | 4.3532 | 1.0000 | −16.9196∗∗∗ | 0.0000 | ||
| ADF | 24.7864 | 1.0000 | 427.3130∗∗∗ | 0.0000 | ||
| PP-Fisher | 25.0578 | 1.0000 | 393.7200∗∗∗ | 0.0000 | ||
| lnRE | LLC | 2.0742 | 0.9810 | −27.1339∗∗∗ | 0.0000 | |
| IPS | 4.9360 | 1.0000 | −26.2791∗∗∗ | 0.0000 | ||
| ADF | 62.5797 | 0.9877 | 693.2200∗∗∗ | 0.0000 | ||
| PP-Fisher | 61.3183 | 0.9911 | 688.8040∗∗∗ | 0.0000 | ||
| lnGDP | LLC | 5.2366 | 1.0000 | −19.2367∗∗∗ | 0.0000 | |
| IPS | 10.1081 | 1.0000 | −17.4271∗∗∗ | 0.0000 | ||
| ADF | 45.9966 | 1.0000 | 589.2890∗∗∗ | 0.0000 | ||
| PP-Fisher | 34.9186 | 1.0000 | 497.2910∗∗∗ | 0.0000 | ||
| lnPOP | LLC | −0.3006 | 0.3819 | −1.7484∗∗ | 0.0402 | |
| IPS | 4.0095 | 1.0000 | −4.5529∗∗∗ | 0.0000 | ||
| ADF | 79.3686 | 0.4989 | 183.4000∗∗∗ | 0.0000 | ||
| PP-Fisher | 415.3820∗∗∗ | 0.0000 | 109.4880∗ | 0.0795 | ||
| lnOPEN | LLC | −5.9406∗∗∗ | 0.0000 | −39.1776∗∗∗ | 0.0000 | |
| IPS | −4.0791∗∗∗ | 0.0000 | −31.4556∗∗∗ | 0.0000 | ||
| ADF | 166.7420∗∗∗ | 0.0000 | 662.1240∗∗∗ | 0.0000 | ||
| PP-Fisher | 140.6720∗∗∗ | 0.0005 | 729.1150∗∗∗ | 0.0000 | ||
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table 6.
Panel data unit root test results low-income (LI) countries.
| variable | Test method | At level |
At 1st difference |
||
|---|---|---|---|---|---|
| t-Statistic | Prob. | t-Statistic | Prob. | ||
| lnC | LLC | −1.7353∗∗ | 0.0413 | −15.2650∗∗∗ | 0.0000 |
| IPS | 0.8792 | 0.8103 | −15.2674∗∗∗ | 0.0000 | |
| ADF | 66.7183∗ | 0.0823 | 308.1050∗∗∗ | 0.0000 | |
| PP-Fisher | 41.5566 | 0.8498 | 357.0010∗∗∗ | 0.0000 | |
| lnOP | LLC | 0.0399 | 0.5159 | −10.1988∗∗∗ | 0.0000 |
| IPS | 3.3720 | 0.9996 | −13.1059∗∗∗ | 0.0000 | |
| ADF | 14.8718 | 1.0000 | 256.3880∗∗∗ | 0.0000 | |
| PP-Fisher | 15.0347 | 1.0000 | 236.2320∗∗∗ | 0.0000 | |
| lnRE | LLC | 2.4478 | 0.9928 | −15.8517∗∗∗ | 0.0000 |
| IPS | 2.6257 | 0.9957 | −15.6843∗∗∗ | 0.0000 | |
| ADF | 44.2898 | 0.8243 | 313.8250∗∗∗ | 0.0000 | |
| PP-Fisher | 48.4476 | 0.6876 | 346.8300∗∗∗ | 0.0000 | |
| lnGDP | LLC | 0.9599 | 0.8315 | −14.3983∗∗∗ | 0.0000 |
| IPS | 2.6465 | 0.9959 | −15.8866∗∗∗ | 0.0000 | |
| ADF | 51.3827 | 0.5760 | 337.3760∗∗∗ | 0.0000 | |
| PP-Fisher | 54.6054 | 0.4514 | 347.8860∗∗∗ | 0.0000 | |
| lnPOP | LLC | −0.5092 | 0.3053 | −2.0899∗∗ | 0.0183 |
| IPS | 1.5108 | 0.9346 | −6.7961∗∗∗ | 0.0000 | |
| ADF | 91.1887∗∗∗ | 0.0001 | 245.7320∗∗∗ | 0.0000 | |
| PP-Fisher | 96.2146∗∗∗ | 0.0000 | 75.3192∗∗ | 0.0292 | |
| lnOPEN | LLC | −3.4066∗∗∗ | 0.0003 | −20.3063∗∗∗ | 0.0000 |
| IPS | −2.2479∗∗ | 0.0123 | −19.9645∗∗∗ | 0.0000 | |
| ADF | 98.1022∗∗∗ | 0.0002 | 408.3280∗∗∗ | 0.0000 | |
| PP-Fisher | 95.6248∗∗∗ | 0.0004 | 492.3560∗∗∗ | 0.0000 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table 7.
Panel data unit root test results all countries (Global).
| variable | Test method | At level |
At 1st difference |
||
|---|---|---|---|---|---|
| t-Statistic | Prob. | t-Statistic | Prob. | ||
| lnC | LLC | −6.4189∗∗∗ | 0.0000 | −51.6412∗∗∗ | 0.0000 |
| IPS | −2.9896∗∗∗ | 0.0014 | −48.0612∗∗∗ | 0.0000 | |
| ADF | 572.1610∗∗∗ | 0.0000 | 2726.3700∗∗∗ | 0.0000 | |
| PP-Fisher | 525.2430∗∗∗ | 0.0000 | 4095.1200∗∗∗ | 0.0000 | |
| lnOP | LLC | 0.1037 | 0.5413 | −26.4791∗∗∗ | 0.0000 |
| IPS | 8.7546 | 1.0000 | −34.0267∗∗∗ | 0.0000 | |
| ADF | 100.2470 | 1.0000 | 1728.2400∗∗∗ | 0.0000 | |
| PP-Fisher | 101.3450 | 1.0000 | 1592.3800∗∗∗ | 0.0000 | |
| lnRE | LLC | −2.6812∗∗∗ | 0.0037 | −49.8834∗∗∗ | 0.0000 |
| IPS | 1.7832 | 0.9627 | −47.8708∗∗∗ | 0.0000 | |
| ADF | 498.9790∗∗∗ | 0.0000 | 2610.9900∗∗∗ | 0.0000 | |
| PP-Fisher | 474.0110∗∗∗ | 0.0001 | 2688.9400∗∗∗ | 0.0000 | |
| lnGDP | LLC | 0.4248 | 0.6645 | −36.7636∗∗∗ | 0.0000 |
| IPS | 9.6816 | 1.0000 | −35.0305∗∗∗ | 0.0000 | |
| ADF | 266.3150 | 1.0000 | 1984.4500∗∗∗ | 0.0000 | |
| PP-Fisher | 278.3920 | 0.9996 | 1923.6600∗∗∗ | 0.0000 | |
| lnPOP | LLC | −3.2912∗∗∗ | 0.0005 | −5.5718∗∗∗ | 0.0000 |
| IPS | 4.7683 | 1.0000 | −10.5915∗∗∗ | 0.0000 | |
| ADF | 535.1450∗∗∗ | 0.0000 | 901.3130∗∗∗ | 0.0000 | |
| PP-Fisher | 1186.6800∗∗∗ | 0.0000 | 590.8650∗∗∗ | 0.0000 | |
| lnOPEN | LLC | −8.2820∗∗∗ | 0.0000 | −59.3767∗∗∗ | 0.0000 |
| IPS | −6.4467∗∗∗ | 0.0000 | −53.3991∗∗∗ | 0.0000 | |
| ADF | 592.6160∗∗∗ | 0.0000 | 2586.8400∗∗∗ | 0.0000 | |
| PP-Fisher | 564.9330∗∗∗ | 0.0000 | 2988.2100∗∗∗ | 0.0000 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
4.3. Panel cointegration test results
The results of the panel cointegration test are shown in Table B1, Table B2, Table B3, Table B4, Table B5 (see Appendix B). To study the long-term relationship between trade openness, oil prices, individual incomes, population, renewable energy and carbon emissions, all variables were included in the panel cointegration test. The results of the Pedroni cointegration test and the Kao cointegration test were consistent. Independent of the income group results, the null hypothesis was rejected, i.e., a long-term co-integration relationship was identified between 182 countries and regions, trade openness, oil prices, individual incomes, population, renewable energy consumption and carbon emissions from 1990 to 2015. To further study this long-term stable relationship, OLS and FMOLS cointegration estimation were used in the next step.
4.4. Panel cointegration regression results
In light of the evidence of the long-term cointegration relationship among variables, regression estimates were calculated to identify reasonable environmental policies. This identification can be achieved by understanding the linear nexus between carbon emissions, trade openness, oil price, individual incomes, population and renewable energy. The OLS and FMOLS regression results are reported in Table B6 (see Appendix B). This analysis focuses on the FMOLS estimation results.
4.4.1. Regression results for the global group
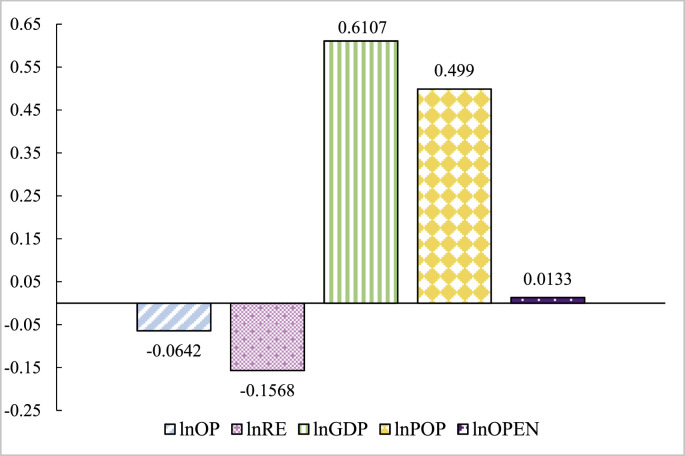
Fig. 3 shows the importance of each factor for 182 countries. The following section analyzes the results of the global group. In this study, Model 1 investigates the effect of trade openness on carbon emissions without interference of other factors. In Model 1, a 1% increase in trade openness leads to a 0.1279% increase of global carbon emissions in the long run. Additionally, Model 3 investigates the effect of trade openness on carbon emissions considering oil prices, individual incomes, population, and renewable energy. In Model 3, a 1% increase in trade openness leads to a 0.0133% increase of global carbon emission in the long run. The regression coefficient of trade openness is positive in all models. Therefore, regardless of have interference from other factors, trade openness significantly promotes global carbon emissions, which is in line with previous publications (Cole and Elliott, 2005; Grossman and Krueger, 1994; Jalil and Feridun, 2011).
Fig. 3.
Summary of regression coefficients on global carbon emissions influencing factors.
For individual incomes and population, this study traces that individual incomes and population positively affect carbon emissions in global group. In Model 3, a 1% increase in individual incomes and population leads to 0.6107% and 0.499% decrease of global carbon emission in the long run, respectively. These results match those reported by Mensah et al. (2019), who argued that carbon emissions are likely highly correlated with individual incomes because they are by-products of industrial processes, energy consumption (direct consumption of fossil fuels and electricity), and car use. Although a number of advanced economies have decoupled their economic growth from carbon emissions in recent years (Andreoni and Galmarini, 2012), this is not common.
The increasing population drives carbon emissions, however, this driving effect is less than that of individual incomes. This is desirable, as certain human behavior customs may directly trigger excessive energy consumption and subsequently influence environmental change. The ensuing increase of the number of private cars and construction operations has also increased energy consumption, which may be the main reason why increasing population leads to increased carbon emissions (Wong et al., 2015).
In contrast, higher oil prices and renewable energy hinder global carbon emission regardless of the income group, and the effect of renewable energy generation is stronger. Regarding renewable energy, a statistical inverse relationship exists with carbon emissions. In Model 3, a 1% increase in the proportion of renewable energy consumption yields a corresponding 0.1568% decrease in global carbon emissions over the considered period. These results confirm that the consumption of renewable energy effectively decreases carbon emissions (Cai et al., 2018).
A 1% increase in international crude oil prices leads to a 0.0642% decrease of global carbon emissions in the long run, which is supported in by previous research (Winchester and Ledvina, 2017). Changes in oil prices affect energy consumption since oil is an important component of the global energy consumption structure, and oil is also the main source of carbon dioxide. It should be noted that the turmoil in the financial market caused by the decline in oil prices has negatively impacted the economies of many crude oil producing countries. In the long run, this decline will accelerate the carbon dioxide emissions of these countries, which will undoubtedly bring difficulties to the global carbon emission reduction work.
4.4.2. Regression results for different income groups
This study also investigated four income groups. Comparative analysis of the results between different income groups has practical significance for many countries when formulating targeted emission reduction policies. Four carbon functions of different income groups were obtained from Model 3, as shown in Table 8 . Fig. 4 shows the distribution of the effects for different income levels. The effects of oil prices, individual incomes, population, and renewable energy on carbon emissions are consistent among all four income groups, however, the effect of trade openness is clearly inconsistent. Therefore, this section discusses the heterogeneous effects of trade openness on carbon emissions across four income groups.
Table 8.
Equations based on FMOLS regression results.
| Panel | Logarithmic panel model | R-squared |
|---|---|---|
| HI | 0.4291 | |
| UMI | 0.9812 | |
| LMI | 0.9561 | |
| LI | 0.9432 |
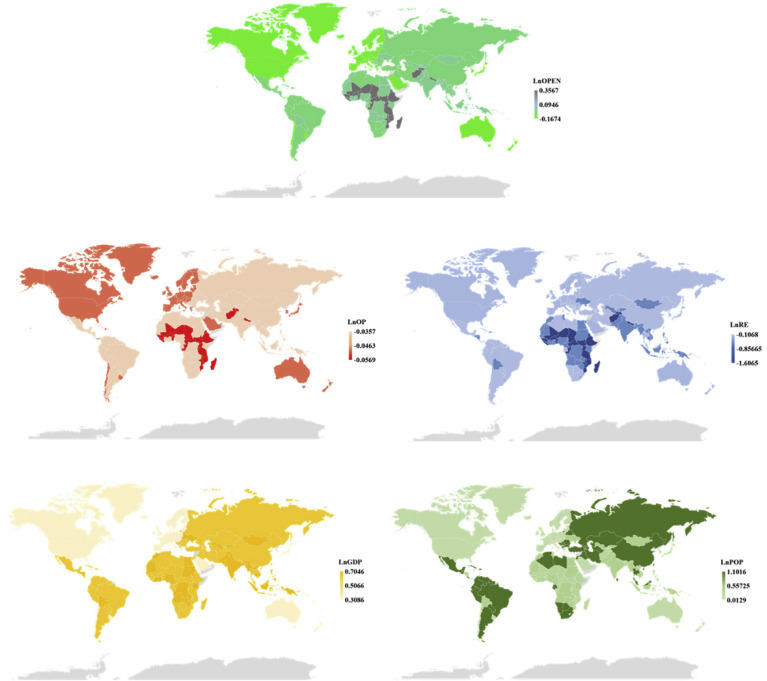
Fig. 4.
Spatial characteristics of elastic coefficients across the global.
Model 1 investigates the impact of trade openness on carbon emissions without interference from any other factors. For the HI group, the long-term coefficients of trade openness are negatively linked to carbon emission and the coefficients are also statistically significant at the 1% level. A 1% increase in trade openness will decrease carbon emission by 0.1276%. However, the result for the LI group is the complete opposite, showing that trade openness is positively linked to carbon emissions and the coefficients are also statistically significant at the 1% level. A 1% increase in trade openness will create 0.4942% additional carbon emissions. In addition, for UMI and LMI groups, the long-term coefficients of trade openness to carbon emissions are not statistically significant.
Importantly, Model 3 provides powerful evidence that trade openness exerts a heterogeneous effect on carbon emissions considering the roles of oil prices, individual incomes, population and renewable energy in the carbon function of the investigation of trade openness. Specifically, the outcome of Model 3 implies that the trade openness of HI and UMI groups increased by 1%, and carbon emissions decreased by 0.1674% and 0.0478% over in the long run, respectively. Regarding the LMI group, a linear positive relationship is indicated between trade openness and carbon emissions, however, this relationship is not significant. For the LI group, as a 1% increase in trade openness yields a corresponding 0.3567% increase in carbon emissions in the long run, which contrasts with the results of HI and UMI groups.
This is insightful, as it indicates that trade openness has a positive impact on carbon emission reduction in both the HI and UMI countries, but not significant on carbon emissions in LMI countries, and even a negative impact on LI countries. This indicates that with increasing income level, the impact of trade openness on carbon emissions also changes. This supports a previously reported the view (Shahbaz et al., 2017b), where trade openness contributes to carbon emissions at all income levels but exerts with varying influence on different panels. The heterogeneous effects of trade openness on carbon emission suggest that trade openness improves the environment of rich countries, but aggravates the environmental pollution of poor countries. This is in line with the recognized phenomenon of carbon transfer in the process of international trade (Essandoh et al., 2020). Environmental standards in LI countries are generally lower than in other countries with higher income levels, and the environmental management system is deficient. Therefore, with the formation of global supply chains, developed countries either transfer or outsource high-carbon emission industries to LI countries (Baumert et al., 2019). This supports the views of Grossman and Krueger (1994) who pointed out that dirty industries in developing countries tend to cause a heavy share of pollutants. Most developing countries are LI countries. The “Pollution Refuge Hypothesis” was verified (Zhang et al., 2017) and trade implied carbon emissions were also assumed as a key way to transfer pollution (Rafindadi et al., 2018). Hence, with decreasing income levels, the impact of trade openness on the environment changes from positive to negative.
5. Conclusions and policy implications
5.1. Conclusions
This study investigated the effect of trade openness on the decoupling of economic growth from carbon emissions. Combining the Tapio decoupling model with the log linear econometric model, differences of decoupling status and the heterogeneity effect of trade openness on carbon emissions were found in different income groups. The main findings are summarized in the following:
-
➢
Although global decoupling economic growth from carbon emissions converges on weak decoupling, obvious differences were found between countries with different income levels. Specifically, HI countries have the best decoupling status, followed by UMI and LI countries, which show a stable improvement trend. LMI countries are the worst because of their unstable decoupling status and lack of improvement trend.
-
➢
For the world as a whole, trade openness increases carbon emissions. For individual countries, trade openness decreases carbon emissions in HI and UMI countries, and does not significantly impact carbon emissions in LMI countries. However, for LI countries, trade openness increases carbon emissions. The heterogeneous effects of trade openness on carbon emissions indicates that trade openness has a positive impact on the decoupling of economic growth from carbon emissions in rich countries, but a negative impact in poor countries.
-
➢
Increasing individual incomes and population distort the decoupling of economic growth from carbon emissions, and the distortion of individual incomes is stronger than population growth. In contrast, renewable energy consumption and high oil prices contributed to the decoupling of economic growth from carbon emission, and the contribution of renewable energy is stronger than that of high oil prices. Moreover, these effects are similar in all countries independent of income levels.
5.2. Policy implications
Targeted policy implications are needed toward achieving a complete decoupling of economic growth from carbon emissions.
-
➢
HI countries already have the ability to decrease their carbon emissions without sacrificing economic growth. This is a sign for HI countries to strengthen their commitment to the Paris Agreement. Consequently, more developed countries should sign the Paris Agreement. Moreover, developed countries should consciously make more aggressive and efficient efforts with regard to INDCs.
-
➢
For LI countries, trade openness has led to more pollution because of the less stringent environmental regulations. Imposing environmental regulations on trade-related gas emissions and without hindering the improvement of production levels is difficult in these countries. Thus, developing countries should use clean and environmentally friendly technologies when producing trade goods. Furthermore, increasing the share of the tertiary industry in foreign direct investment is a feasible way to help decrease environmental pollution along the path of liberalizing of international trade.
-
➢
For the world, to contribute to the decoupling of economic growth from carbon emissions, increasing the share of renewable energy in the energy portfolio is a sensible option. This can also enhance the ability to resist energy risks, such as oil price fluctuations. Governments can attract further investors to explore and implement renewable energy technologies by developing further renewable energy policies and relevant institutions. This in turn, will promote the use of renewable energy.
CRediT authorship contribution statement
Qiang Wang: Conceptualization, Methodology, Software, Data curation, Writing - original draft, Supervision, Writing - review & editing. Fuyu Zhang: Methodology, Data curation, Investigation, Writing - original draft, Writing - review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to thank the editor and these anonymous reviewers for their helpful and constructive comments that greatly contributed to improving the final version of the manuscript. This work is supported by National Natural Science Foundation of China (Grant No. 71874203), Humanities and Social Science Fund of Ministry of Education of China (Grant No.18YJA790081), Natural Science Foundation of Shandong Province, China (Grant No. ZR2018MG016).
Handling editor: Cecilia Maria Villas Bôas de Almeida
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jclepro.2020.123838.
Appendix A.
Table A1.
List of sample countries.
| High-income | Upper-middle-income | Lower-middle-income | Low-income |
|---|---|---|---|
| Aruba | Albania | Angola | Afghanistan |
| United Arab Emirates | Argentina | Bangladesh | Burundi |
| Australia | Armenia | Bolivia | Benin |
| Austria | Azerbaijan | Bhutan | Burkina Faso |
| Belgium | Bulgaria | Cote d’Ivoire | Central African Republic |
| Bahamas, The | Bosnia and Herzegovina | Cameroon | Congo, Dem. Rep. |
| Bermuda | Belarus | Congo, Rep. | Eritrea |
| Barbados | Belize | Comoros | Ethiopia |
| Brunei Darussalam | Brazil | Cabo Verde | Guinea |
| Canada | Botswana | Egypt, Arab Rep. | Gambia, The |
| Switzerland | China | Micronesia, Fed. Sts. | Guinea-Bissau |
| Chile | Colombia | Ghana | Haiti |
| Cyprus | Costa Rica | Honduras | Liberia |
| Czech Republic | Cuba | Indonesia | Madagascar |
| Germany | Dominica | India | Mali |
| Denmark | Dominican Republic | Kenya | Mozambique |
| Spain | Algeria | Kyrgyz Republic | Malawi |
| Estonia | Ecuador | Cambodia | Niger |
| Finland | Gabon | Kiribati | Nepal |
| France | Georgia | Lao PDR | Rwanda |
| Faroe Islands | Equatorial Guinea | Lesotho | Sierra Leone |
| United Kingdom | Grenada | Morocco | South Sudan |
| Greece | Guatemala | Moldova | Chad |
| Greenland | Guyana | Myanmar | Togo |
| Hong Kong SAR, China | Iran, Islamic Rep. | Mongolia | Tajikistan |
| Croatia | Iraq | Mauritania | Tanzania |
| Hungary | Jamaica | Nigeria | Uganda |
| Ireland | Jordan | Nicaragua | |
| Iceland | Kazakhstan | Pakistan | |
| Israel | Lebanon | Philippines | |
| Italy | Libya | Papua New Guinea | |
| Japan | St. Lucia | West Bank and Gaza | |
| St. Kitts and Nevis | Sri Lanka | Sudan | |
| Korea, Rep. | Maldives | Senegal | |
| Kuwait | Mexico | Solomon Islands | |
| Lithuania | Marshall Islands | El Salvador | |
| Luxembourg | North Macedonia | Eswatini | |
| Latvia | Montenegro | Timor-Leste | |
| Macao SAR, China | Mauritius | Tunisia | |
| Malta | Malaysia | Ukraine | |
| Netherlands | Namibia | Uzbekistan | |
| Norway | Nauru | Vietnam | |
| New Zealand | Peru | Vanuatu | |
| Panama | Paraguay | Zambia | |
| Poland | Romania | Zimbabwe | |
| Portugal | Russian Federation | ||
| Saudi Arabia | Serbia | ||
| Singapore | Suriname | ||
| Slovak Republic | Thailand | ||
| Slovenia | Turkmenistan | ||
| Sweden | Tonga | ||
| Seychelles | Turkey | ||
| Uruguay | St. Vincent and the Grenadines | ||
| United States | Venezuela, RB | ||
| Samoa | |||
| South Africa |
Appendix B.
Table B1.
Cointegration Test results (HI)
| Pedroni Cointegration Test | Value | P-value |
|---|---|---|
| Panel v-Statistic | −2.6582 | 0.9961 |
| Panel rho-statistic | 4.4629 | 1.0000 |
| Panel PP-statistic | −8.6343∗∗∗ | 0.0000 |
| Panel ADF-statistic | −7.7463∗∗∗ | 0.0000 |
| Group rho-statistic | 6.0033 | 1.0000 |
| Group PP-statistic | −19.5805∗∗∗ | 0.0000 |
| Group ADF-Statistic | −12.8081∗∗∗ | 0.0000 |
| Kao Cointegration Test | ||
| Statistic | P-value | |
| ADF | −3.6300∗∗∗ | 0.0001 |
| Residual variance | 0.0086 | |
| HAC variance | 0.0079 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table B2.
Cointegration Test results (UMI)
| Pedroni Cointegration Test | Value | P-value |
|---|---|---|
| Panel v-Statistic | −4.6528 | 1.0000 |
| Panel rho-statistic | 3.2684 | 0.9995 |
| Panel PP-statistic | −13.5374∗∗∗ | 0.0000 |
| Panel ADF-statistic | −11.2282∗∗∗ | 0.0000 |
| Group rho-statistic | 6.0220 | 1.0000 |
| Group PP-statistic | −18.6456∗∗∗ | 0.0000 |
| Group ADF-Statistic | −13.3144∗∗∗ | 0.0000 |
| Kao Cointegration Test | ||
| Statistic | P-value | |
| ADF | −7.059443∗∗∗ | 0.0000 |
| Residual variance | 0.009924 | |
| HAC variance | 0.008044 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table B3.
Cointegration Test results (LMI)
| Pedroni Cointegration Test | Value | P-value |
|---|---|---|
| Panel v-Statistic | −3.7130 | 0.9999 |
| Panel rho-statistic | 2.7149 | 0.9967 |
| Panel PP-statistic | −8.8684∗∗∗ | 0.0000 |
| Panel ADF-statistic | −8.3578∗∗∗ | 0.0000 |
| Group rho-statistic | 5.4183 | 1.0000 |
| Group PP-statistic | −17.2533∗∗∗ | 0.0000 |
| Group ADF-Statistic | −11.3124∗∗∗ | 0.0000 |
| Kao Cointegration Test | ||
| Statistic | P-value | |
| ADF | −7.3790∗∗∗ | 0.0000 |
| Residual variance | 0.0206 | |
| HAC variance | 0.0172 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table B4.
Cointegration Test results (LI)
| Pedroni Cointegration Test | Value | P-value |
|---|---|---|
| Panel v-Statistic | −0.8150 | 0.7925 |
| Panel rho-statistic | 1.9785 | 0.9761 |
| Panel PP-statistic | −6.4175∗∗∗ | 0.0000 |
| Panel ADF-statistic | −6.5357∗∗∗ | 0.0000 |
| Group rho-statistic | 4.5462 | 1.0000 |
| Group PP-statistic | −5.3402∗∗∗ | 0.0000 |
| Group ADF-Statistic | −4.6913∗∗∗ | 0.0000 |
| Kao Cointegration Test | ||
| Statistic | P-value | |
| ADF | −4.9352∗∗∗ | 0.0000 |
| Residual variance | 0.0157 | |
| HAC variance | 0.0137 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table B5.
Cointegration Test results (Global)
| Pedroni Cointegration Test | Value | P-value |
|---|---|---|
| Panel v-Statistic | −6.2813 | 1.0000 |
| Panel rho-statistic | 5.9589 | 1.0000 |
| Panel PP-statistic | −18.3646∗∗∗ | 0.0000 |
| Panel ADF-statistic | −16.9298∗∗∗ | 0.0000 |
| Group rho-statistic | 11.0537 | 1.0000 |
| Group PP-statistic | −31.6636∗∗∗ | 0.0000 |
| Group ADF-Statistic | −21.8000∗∗∗ | 0.0000 |
| Kao Cointegration Test | ||
| Statistic | P-value | |
| ADF | −8.7903∗∗∗ | 0.0000 |
| Residual variance | 0.0147 | |
| HAC variance | 0.0133 | |
Note: ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Table B6.
Estimation results for carbon emissions
| Group | Model | LnOPEN | LnOP | LnGDP | LnPOP | lnRE | C |
|---|---|---|---|---|---|---|---|
| HI | Model 1 | −0.1276∗∗∗ (−10.4146) | |||||
| Model 2 | 0.1476∗∗∗ (4.9805) | −0.0722∗∗∗ (−6.8266) | 0.2938∗∗∗ (8.9418) | 0.0798 (1.4157) | −0.0974∗∗∗ (−15.9682) | −1.6808∗∗∗ (−3.4841) | |
| Model 3 | −0.1674∗∗∗ (−37.8510) | −0.0498∗∗∗ (−14.1915) | 0.3086∗∗∗ (122.8840) | 0.0129∗∗∗ (9.1165) | −0.1432∗∗∗ (−103.9827) | ||
| UMI | Model 1 | −0.0125 (−0.7720) | |||||
| Model 2 | −0.0231∗∗ (−2.0908) | −0.0031 (−0.2659) | 0.5349∗∗∗ (19.8765) | 0.0789 (1.3705) | −0.1889∗∗∗ (−14.3439) | −3.4723∗∗∗ (−7.9495) | |
| Model 3 | −0.0478∗∗∗ (−3.9945) | −0.0359∗∗ (−2.2256) | 0.6289∗∗∗ (12.4641) | 1.1016∗∗∗ (3.6288) | −0.1068∗∗∗ (−5.9398) | ||
| LMI | Model 1 | 0.0314 (0.9501) | |||||
| Model 2 | −0.0057 (−0.2852) | −0.0341∗∗ (−1.9789) | 0.6838∗∗∗ (16.8478) | 0.3248∗∗∗ (4.0718) | −0.5600∗∗∗ (−15.9217) | −7.8678∗∗∗ (−6.7930) | |
| Model 3 | −0.0126 (−1.1105) | −0.0357∗∗∗ (−3.4798) | 0.7046∗∗∗ (29.3625) | 0.3312∗∗∗ (6.6319) | −0.5378∗∗∗ (−26.4482) | ||
| LI | Model 1 | 0.4942∗∗∗ (8.3112) | |||||
| Model 2 | 0.3374∗∗∗ (10.5980) | −0.0615∗∗ (−2.4107) | 0.6426∗∗∗ (11.4468) | 0.1976∗ (1.9377) | −1.6291∗∗∗ (−18.8988) | −1.5394∗ | |
| Model 3 | 0.3567∗∗∗ (23.6731) | −0.0569∗∗∗ (−4.4696) | 0.6378∗∗∗ (23.6562) | 0.1834∗∗∗ (3.4174) | −1.6065∗∗∗ (−38.8503) | ||
| GLOBAL | Model 1 | 0.1279∗∗∗ (9.0018) | |||||
| Model 2 | 0.0154 (1.5672) | −0.0633∗∗∗ (−8.3419) | 0.6123∗∗∗ (31.2870) | 0.4834∗∗∗ (13.9385) | −0.1606∗∗∗ (−22.5117) | −8.0481∗∗∗ (−24.7188) | |
| Model 3 | 0.0133∗∗∗ (3.1040) | −0.0642∗∗∗ (−18.7342) | 0.6107∗∗∗ (67.8722) | 0.4990∗∗∗ (30.5800) | −0.1568∗∗∗ (−49.5702) |
Note: The data in brackets are the t-statistics. ∗∗∗, ∗∗, ∗ represent significant at 1%, 5%, and 10% inspection levels, respectively.
Appendix C. Supplementary data
The following is the Supplementary data to this article:
References
- Al-mulali U. Oil consumption, CO2 emission and economic growth in MENA countries. Energy. 2011;36(10):6165–6171. [Google Scholar]
- Andreoni V., Galmarini S. Decoupling economic growth from carbon dioxide emissions: a decomposition analysis of Italian energy consumption. Energy. 2012;44(1):682–691. [Google Scholar]
- Baumert N., Kander A., Jiborn M., Kulionis V., Nielsen T. Global outsourcing of carbon emissions 1995–2009: a reassessment. Environ. Sci. Pol. 2019;92:228–236. [Google Scholar]
- Bhattacharya M., Awaworyi Churchill S., Paramati S.R. The dynamic impact of renewable energy and institutions on economic output and CO2 emissions across regions. Renew. Energy. 2017;111:157–167. [Google Scholar]
- Cai Y., Sam C.Y., Chang T. Nexus between clean energy consumption, economic growth and CO2 emissions. J. Clean. Prod. 2018;182:1001–1011. [Google Scholar]
- Chen J., Wang P., Cui L., Huang S., Song M. Decomposition and decoupling analysis of CO2 emissions in OECD. Appl. Energy. 2018;231:937–950. [Google Scholar]
- Cole M.A., Elliott R.J.R. Wiley-Blackwell: Review of Development Economics; 2005. FDI and the Capital Intensity of ’Dirty’ Sectors: A Missing Piece of the Pollution Haven Puzzle. [Google Scholar]
- Copeland B.R., Taylor M.S. Trade, growth and the environment. J. Econ. Lit. 2004;42(1):7–71. [Google Scholar]
- Dasgupta S., Laplante B., Mamingi N. Pollution and capital markets in developing countries. J. Environ. Econ. Manag. 2001;42(3):310–335. [Google Scholar]
- Datta S. Decoupling and demand-side management: evidence from the US electric industry. Energy Pol. 2019;132:175–184. [Google Scholar]
- Dogan E., Turkekul B. CO 2 emissions, real output, energy consumption, trade, urbanization and financial development: testing the EKC hypothesis for the USA. Environ. Sci. Pollut. Control Ser. 2016;23(2):1203–1213. doi: 10.1007/s11356-015-5323-8. [DOI] [PubMed] [Google Scholar]
- Dong K., Sun R., Li H., Liao H. Does natural gas consumption mitigate CO2 emissions: testing the environmental Kuznets curve hypothesis for 14 Asia-Pacific countries. Renew. Sustain. Energy Rev. 2018;94:419–429. [Google Scholar]
- Essandoh O.K., Islam M., Kakinaka M. Linking international trade and foreign direct investment to CO2 emissions: any differences between developed and developing countries? Sci. Total Environ. 2020;712:136437. doi: 10.1016/j.scitotenv.2019.136437. [DOI] [PubMed] [Google Scholar]
- Fan Y., Liu L.-C., Wu G., Wei Y.-M. Analyzing impact factors of CO2 emissions using the STIRPAT model. Environ. Impact Assess. Rev. 2006;26(4):377–395. [Google Scholar]
- Farhani S., Chaibi A., Rault C. CO2 emissions, output, energy consumption, and trade in Tunisia. Econ. Modell. 2014;38:426–434. [Google Scholar]
- Farhani S., Shahbaz M., Sbia R., Chaibi A. What does MENA region initially need: grow output or mitigate CO2 emissions? Econ. Modell. 2014;38:270–281. [Google Scholar]
- Fortes P., Seixas J., Simoes S., Cleto J. 2008. Long Term Energy Scenarios under Uncertainty, International Conference on European Electricity Market; pp. 1–6. [Google Scholar]
- Frankel J.A., Romer D.H. Does trade cause growth. Am. Econ. Rev. 1999;89:379–399. [Google Scholar]
- Galeotti M., Manera M., Lanza A. On the robustness of robustness checks of the environmental Kuznets curve hypothesis. Environ. Resour. Econ. 2009;42(4):551–574. [Google Scholar]
- Grossman G.M., Krueger A.B. 1994. Economic Growth and the Environment. [Google Scholar]
- Im K.S., Pesaran M.H., Shin Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003;115(1):53–74. [Google Scholar]
- Jalil A., Feridun M. The impact of growth, energy and financial development on the environment in China: a cointegration analysis. Energy Econ. 2011;33(2):284–291. [Google Scholar]
- Kao C. Spurious regression and residual-based tests for cointegration in panel data. J. Econom. 1999;90(1):1–44. [Google Scholar]
- Kearsley A., Riddel M. A further inquiry into the pollution haven hypothesis and the environmental Kuznets curve. Ecol. Econ. 2010;69(4):905–919. [Google Scholar]
- Lehmann P., Gawel E. Why should support schemes for renewable electricity complement the EU emissions trading scheme? Energy Pol. 2013;52:597–607. [Google Scholar]
- Levin A., Lin C.-F., Chu C.-S.J. Unit root tests in panel data: asymptotic and finite-sample properties. J. Econom. 2002;108(1):1–24. [Google Scholar]
- Liu C., Jiang Y., Xie R. Does income inequality facilitate carbon emission reduction in the US? J. Clean. Prod. 2019;217:380–387. [Google Scholar]
- Martínez-Zarzoso I., Maruotti A. The impact of urbanization on CO2 emissions: evidence from developing countries. Ecol. Econ. 2011;70(7):1344–1353. [Google Scholar]
- Mensah I.A., Sun M., Gao C., Omari-Sasu A.Y., Zhu D., Ampimah B.C., Quarcoo A. Analysis on the nexus of economic growth, fossil fuel energy consumption, CO2 emissions and oil price in Africa based on a PMG panel ARDL approach. J. Clean. Prod. 2019;228:161–174. [Google Scholar]
- Moldan B., Janoušková S., Hák T. How to understand and measure environmental sustainability: indicators and targets. Ecol. Indicat. 2012;17:4–13. [Google Scholar]
- Nasir M., Ur Rehman F. Environmental Kuznets Curve for carbon emissions in Pakistan: an empirical investigation. Energy Pol. 2011;39(3):1857–1864. [Google Scholar]
- O’Neill B., Chen B. Demographic determinants of household energy use in the United States. Popul. Dev. Rev. 2002;28:53–88. [Google Scholar]
- Pedroni P. Fully modified OLS for heterogeneous cointegrated panels. Adv. Econom. 2000;15:93–130. [Google Scholar]
- Pedroni P. Emerald Group Publishing Limited; 2001. Fully Modified OLS for Heterogeneous Cointegrated Panels, Nonstationary Panels, Panel Cointegration, and Dynamic Panels; pp. 93–130. [Google Scholar]
- Phillips P.C., Perron P. Testing for a unit root in time series regression. Biometrika. 1988;75(2):335–346. [Google Scholar]
- Poumanyvong P., Kaneko S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010;70(2):434–444. [Google Scholar]
- Rafindadi A., Muhammad Muye I., Kaita R. The effects of FDI and energy consumption on environmental pollution in predominantly resource-based economies of the GCC. Sustainable Energy Technologies and Assessments. 2018;25:126–137. [Google Scholar]
- Raza M.Y., Lin B. Decoupling and mitigation potential analysis of CO2 emissions from Pakistan’s transport sector. Sci. Total Environ. 2020;730:139000. doi: 10.1016/j.scitotenv.2020.139000. [DOI] [PubMed] [Google Scholar]
- Rout U.K., Akimoto K., Sano F., Oda J., Homma T., Tomoda T. Impact assessment of the increase in fossil fuel prices on the global energy system, with and without CO2 concentration stabilization. Energy Pol. 2008;36(9):3477–3484. [Google Scholar]
- Saboori B., Sulaiman J., Mohd S. Economic growth and CO2 emissions in Malaysia: a cointegration analysis of the Environmental Kuznets Curve. Energy Pol. 2012;51:184–191. [Google Scholar]
- Schaltegger S., Csutora M. Carbon accounting for sustainability and management. Status quo and challenges. J. Clean. Prod. 2012;36:1–16. [Google Scholar]
- Selden T.M., Song D. Environmental quality and development: is there a Kuznets curve for air pollution emissions? J. Environ. Econ. Manag. 1994;27(2):147–162. [Google Scholar]
- Shahbaz M., Khan S., Ali A., Bhattacharya M. The impact of globalization on CO2 emissions in China. Singapore Econ. Rev. 2017;62:929–957. 04. [Google Scholar]
- Shahbaz M., Nasreen S., Ahmed K., Hammoudeh S. Trade openness–carbon emissions nexus: the importance of turning points of trade openness for country panels. Energy Econ. 2017;61:221–232. [Google Scholar]
- Tamazian A., Chousa J.P., Vadlamannati K.C. Does higher economic and financial development lead to environmental degradation: evidence from BRIC countries. Energy Pol. 2009;37(1):246–253. [Google Scholar]
- Tang Z., Shang J., Shi C., Liu Z., Bi K. Decoupling indicators of CO2 emissions from the tourism industry in China: 1990–2012. Ecol. Indicat. 2014;46:390–397. [Google Scholar]
- Tapio P. Towards a theory of decoupling: degrees of decoupling in the EU and the case of road traffic in Finland between 1970 and 2001. Transport Pol. 2005;12(2):137–151. [Google Scholar]
- Wang Q., Jiang R. Is China’s economic growth decoupled from carbon emissions? J. Clean. Prod. 2019;225:1194–1208. [Google Scholar]
- Wang Q., Jiang R., Zhan L. Is decoupling economic growth from fuel consumption possible in developing countries? – a comparison of China and India. J. Clean. Prod. 2019;229:806–817. [Google Scholar]
- Wang Q., Su M. The effects of urbanization and industrialization on decoupling economic growth from carbon emission – a case study of China. Sustainable Cities and Society. 2019;51:101758. [Google Scholar]
- Wang Q., Su M. Drivers of decoupling economic growth from carbon emission – an empirical analysis of 192 countries using decoupling model and decomposition method. Environ. Impact Assess. Rev. 2020;81:106356. [Google Scholar]
- Wang Q., Wang S. Is energy transition promoting the decoupling economic growth from emission growth? Evidence from the 186 countries. J. Clean. Prod. 2020;260:120768. [Google Scholar]
- Wang Q., Zhang F. Does increasing investment in research and development promote economic growth decoupling from carbon emission growth? An empirical analysis of BRICS countries. J. Clean. Prod. 2020;252:119853. [Google Scholar]
- Weber C., Perrels A. Modelling lifestyle effects on energy demand and related emissions. Energy Pol. 2000;28(8):549–566. [Google Scholar]
- Wei J., Zhou J., Tian J., He X., Tang K. Decoupling soil erosion and human activities on the Chinese Loess Plateau in the 20th century. Catena. 2006;68(1):10–15. [Google Scholar]
- Winchester N., Ledvina K. The impact of oil prices on bioenergy, emissions and land use. Energy Econ. 2017;65:219–227. [Google Scholar]
- Wong P.S.P., Lindsay A., Crameri L., Holdsworth S. Can energy efficiency rating and carbon accounting foster greener building design decision? An empirical study. Build. Environ. 2015;87:255–264. [Google Scholar]
- Yang L., Yang Y., Zhang X., Tang K. Whether China’s industrial sectors make efforts to reduce CO2 emissions from production? - a decomposed decoupling analysis. Energy. 2018;160:796–809. [Google Scholar]
- Zhang Y., Da Y. The decomposition of energy-related carbon emission and its decoupling with economic growth in China. Renew. Sustain. Energy Rev. 2015;41:1255–1266. [Google Scholar]
- Zhang Y.-J. The impact of financial development on carbon emissions: an empirical analysis in China. Energy Pol. 2011;39(4):2197–2203. [Google Scholar]
- Zhang Z., Zhu K., Hewings G.J.D. A multi-regional input–output analysis of the pollution haven hypothesis from the perspective of global production fragmentation. Energy Econ. 2017;64:13–23. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.