Abstract
The effect of air-borne nanoparticles (NPs) on human health is an active area of research, with clinical relevance evidenced by the current COVID-19 pandemic. As in vitro models for such studies, lung-on-a-chip (LOAC) devices can represent key physical and physiological aspects of alveolar tissues. However, widespread adoption of the LOAC device for NP testing has been hampered by low intra-laboratory and inter-laboratory reproducibility. To complement ongoing experimental work, we carried out finite-element simulations of the deposition of NPs on the epithelial layer of a well-established LOAC design. We solved the Navier–Stokes equations for the fluid flow in a three-dimensional domain and studied the particle transport using Eulerian advection–diffusion for fine NPs and Lagrangian particle tracking for coarse NPs. Using Langmuir and Frumkin kinetics for surface adsorption and desorption, we investigated NP adsorption under different exercise and breath-holding patterns. Conditions mimicking physical exercise, through changes in air-flow volume and breathing frequency, enhance particle deposition. Puff profiles typical of smoking, with breath-holding between inhalation and exhalation, also increase particle deposition per breathing cycle. Lagrangian particle tracking shows Brownian motion and gravitational settling to be two key factors, which may cooperate or compete with each other for different particle sizes. Comparisons are made with experimental data where possible and they show qualitative and semi-quantitative agreement. These results suggest that computer simulations can potentially inform and accelerate the design and application of LOAC devices for analyzing particulate– and microbe–alveolar interactions.
I. INTRODUCTION
The rapid development of nanotechnology is extending the use of nanoparticles (NPs) to ever-expanding new fields of applications (e.g., biomedicine, agriculture, food, renewable energy, electronics, and cosmetics) and is accelerating their release to the environment, posing serious risks to human health.1–3 The human body can interact with NPs via skin contact, inhalation, or ingestion.1,2 Although some defense mechanisms exist, the alveolar tissue is the most vulnerable contact site because it is not as well protected against environmental damages as the skin and gastrointestinal tract.1,3 In particular, the COVID-19 pandemic is caused by particles of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) being inhaled into the lower respiratory tract to initiate active infection.4 Other sources of air-borne NPs include cigarette and marijuana smoke, industrial and occupational exposure, and indoor and outdoor air pollution.5–7,1,8 Exposure to environmental NPs can lead to the development and progression of infectious diseases such as COVID-19, as well as other respiratory diseases such as asthma and chronic obstructive pulmonary disease.9–12,4 Hence, the study of air-borne NPs and their effects on human health continues to be an active area of research.
Much of our understanding of particle deposition in the airways and lungs stem from pharmacological studies.13 Apart from in vivo, ex vivo, and in vitro experimentation,14–16 there have also been numerous computer simulations of the deposition process, using simplified17,18 or CT-scanned geometries of the tracheobronchial system.19–21 The focus of such studies is the deposition of NPs in a certain portion of the airway or over the large-scale geometry of the whole lung. These studies have offered insights into how the flow of air affects the deposition in macroscopic geometric features of the lungs (e.g., recirculation zones and bifurcations).17 In contrast, there has been little study of NP deposition further downstream on alveolar epithelia, which happens at a much smaller length scale and in a more varied and complex geometry that cannot be easily captured by CT scan.22 A mechanistic understanding of particulate/microbe–alveolar interaction and its downstream inflammation reaction in lung diseases23 calls for a more detailed local model.
For this purpose, the microfluidic lung-on-a-chip (LOAC) device provides an ideal platform.24,25 The LOAC is among the first “organs-on-chips,” engineered micro-physiological systems that aim to recapitulate certain aspects of the real organ for disease modeling or drug development applications.26–30 A particularly successful LOAC design24,31 features an alveolar chamber separated from a microvascular chamber by a perforated elastic membrane. Different from the traditional monolayer cultures and co-culture systems with static air and fluid incubation, the LOAC design allows controlled air and liquid flow through the two chambers, and the membrane can be cyclically stretched to a strain comparable to physiological levels during normal breathing. This LOAC model reproduces closely in vivo conditions of the alveoli and allows well-controlled tests for NP deposition and transport. More recent LOAC designs have striven to capture other aspects of the human airways.32–34
Despite these advances, wide-spread adoption of the LOAC device (and other organ chips) has not occurred.25 For one, there has been a lack of communication between the device researchers and the end users to define the barriers to implementation. There has also been little quantitative data on the transport and deposition of NPs in LOAC. Most importantly, these devices have been designed mostly by trial and error, with little theoretical guidance and high failure rates.24,31 As a result, low intra-laboratory and inter-laboratory reproducibility has been a challenge for clinical translation of these devices.
Using LOAC as a surrogate for the human alveolus, we have developed computer simulations to examine the deposition and adsorption of NPs (a) under different exercise and breath-holding patterns and (b) for a range of particle sizes with varying relative importance of Brownian and gravitational forces. Our objective is to understand the transport of NPs in an LOAC device and show that in silico experiments can inform and potentially accelerate the design and application of such devices for analyzing particulate/microbe–alveolar interaction. We have based our simulations on the well-known design of Huh et al.,24 which features a relatively simple but physiologically relevant geometry. Compared with the existing literature of large-scale simulations of the human lung and airways, our work introduces the following novelties:
-
•
Adsorption–desorption kinetics. Previous work predicted the deposition efficiency, the ratio of particulates captured to the total amount released,18 solely based on the incidence of particle impingement, tacitly assuming instantaneous adsorption.35 We introduce adsorption–desorption kinetics by the Langmuir and Frumkin models to allow saturation on the solid surface and particle–particle interactions.
-
•
Physiologic breathing patterns. Earlier work distinguished the breath in resting and active states via the Reynolds numbers,18 with limited attention to the pulsatile nature of tidal breathing.36,17,22 We will study pulsatile flows corresponding to normal tidal breathing in a state of rest and intensified breathing—in terms of air volume per cycle and frequency—corresponding to physical exercising. Furthermore, we will examine the effect of “puff profiles” of tobacco and marijuana smoking.37–41
-
•
Effect of particle sizes and gravity. We represent finer particles by a continuum Eulerian model, where particle size is reflected by the diffusivity. For larger particles, we track them using a discrete Lagrangian model subject to gravitational settling and Brownian motion. Thus, we will be able to delineate the deposition of NPs across different sizes.
As main results of the study, our simulations predict enhanced NP adsorption during physical exercising, subject to opposing effects of elevated air volume and breathing frequency. Breath-holding during cigarette smoking is shown to increase particle deposition. Finally, the deposition efficiency varies non-monotonically with particle size, due to the distinct effects of gravitational settling and Brownian motion. These predictions are consistent with existing experimental data.
II. METHODS
Modeling of air-borne particles depends on the particle size and concentration. In most cases, the concentration of particulates is low such that the flow of air is minimally affected by the particles.42,43 This assumption results in the so-called one-way coupling in which the air flow affects the solid particles, but not vice versa. In the context of using LOAC for studying NPs (e.g., virus particles, ambient pollutants, and aerosols for drug delivery), the particle size can range from nanometers to micrometers. For example, the SARS-CoV-2 virus is 60–140 nm in diameter with 9–12 nm spikes.4 Cigarette smoke contains particulates with size ranging in the hundreds of nanometers, as well as some particles in the ultrafine region (diameter nm).44,45 Aerosols and vesicles can measure up to many micrometers.46,47 To cover a wide range of particle sizes, therefore, we will treat the particulate phase using two separate methods: Eulerian approach for fine nanoparticles and Lagrangian approach for coarse nanoparticles. The Eulerian model is used to investigate the effects of exercise and breath-holding patterns. The Lagrangian model is used to investigate the effects of Brownian motion, gravitational forces, and spatial orientation.
A. Modeling fine particles using Eulerian approach
The computational domain is schematically illustrated in Fig. 1. This study focuses on the air-particulate two-phase flow through the upper channel; blood flow in the lower channel is ignored. The particles can deposit and adsorb onto the membrane that forms the lower wall of the upper channel, representing the alveolar epithelial surface, according to a suitable adsorption kinetics. This surface will be called the “substrate” hereafter. The other walls do not carry epithelial cells and thus do not adsorb the particles.
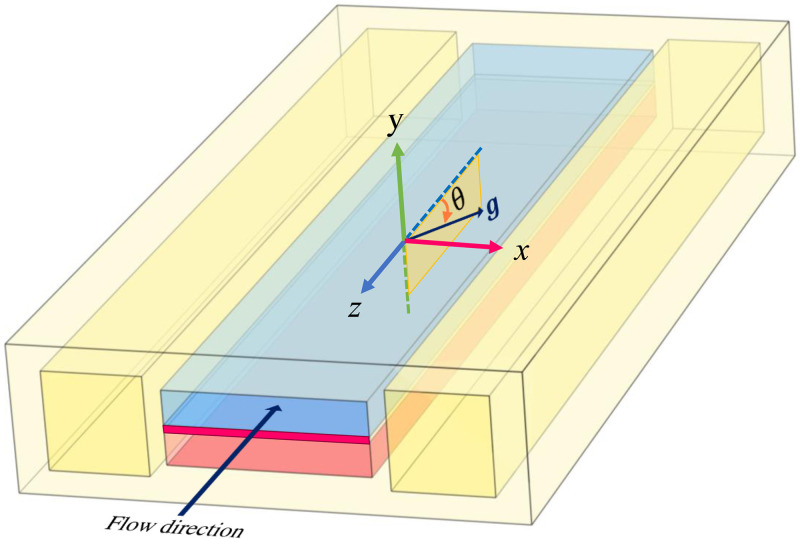
FIG. 1.
Schematic representation of the computational domain, modeled after the LOAC design of Huh et al.24 The upper channel (in blue) is separated from the bottom channel (in pink) by an elastic membrane (in magenta). The top mimics the alveolus through which air flows and the bottom mimics the blood vessel. The two side chambers are for the purpose of imposing vacuum to stretch the elastic membrane. The air flows along the direction, and denotes the angle between the air flow and gravity . Most of the computations have , but can be varied to allow different inclinations of the device relative to gravity.
Under physiologic conditions and typical designs and perfusion conditions of LOACs,24,18 the airflow is laminar with a Reynolds number up to several hundreds, governed by the standard Navier–Stokes equation,
| (1) |
| (2) |
where and are the velocity and pressure of the air flow, and and are the air density and viscosity, respectively. We have computed steady-state as well as pulsatile flows that reflect different breathing patterns (e.g., breathing at normal frequency, fast breathing typical of physical exercise, and breath-holding patterns that mimic cigarette and marijuana smoking). The frequency and pulsatile flow rate are tuned to physiological data and experimental designs in the literature.
For finer NPs of negligible inertia (diameter nm),35 we adopt an Eulerian approach that does not account for individual particles but represents the particulate phase by a concentration field that obeys a convection–diffusion equation to be solved together with the Navier–Stokes equation for the airflow,
| (3) |
where is the diffusivity of the particles. Typically the solid fraction is so low as not to affect the air flow (see Table I).
TABLE I.
Baseline values for the parameters used in our model, the evaluation of some being detailed in the supplementary material. For the channel length L, the experimental device of Huh et al.24 has L > 1 cm. In our model, L = 2 mm turns out to be sufficient for most of the simulations, with the exception of the breathing patterns of Sec. III C (see discussions therein).
| Symbol | Description | Value | Sources |
|---|---|---|---|
| H | Air channel height | 70 μm | 24 |
| W | Air channel width | 400 μm | 24 |
| L | Air channel length | 2 mm | 24 |
| d | Particle diameter | 100 nm | 6 and 44 |
| D | Diffusivity | 6.8 × 10−10 m2 s−1 | 20 |
| c0 | Volume concentration at inlet | 5.24 × 10−6 | Supplementary material |
| Γs | Maximum areal concentration | 52.4 nm | Supplementary material |
| kads | Adsorption rate | 12 600 s−1 | Supplementary material |
| kdes | Desorption rate | 40 s−1 | Supplementary material |
| V0 | Uniform air velocity at inlet | 0.337 mm s−1 | 20 |
| ρ | Air density (at 25 °C) | 1.18 kg m−3 | 52 |
| ρd | Solid density | 1180 kg m−3 | 45 |
| f | Normal breathing frequency | 15 min−1 | 53 |
| vs | Slip velocity on membrane | 1.37 μm s−1 | Supplementary material |
In our LOAC model, the membrane stretching amounts only to a periodic change in the substrate area, up to 7%. This strain is chosen as the mean of the range tested in the LOAC device of Huh et al.,24 which is in turn based on the physiologic level of alveolar stretching. The surface deposition changes accordingly, with a maximum variation of about 5.4%. In the supplementary material, Movie S1 shows the dynamic process of membrane deformation and Fig. S1 shows its effect on surface deposition. Since the effect is minor and the computational cost of fluid–structure interaction is high, we have omitted membrane stretching for most of the simulations, and assumed that all the solid walls are rigid in the LOAC.
B. Modeling coarser particles using Lagrangian approach
For larger particles, it becomes inaccurate to assume that they will follow the airflow perfectly, and an explicit particle-tracking scheme will be adopted following earlier studies.48,35,18,22 For each particle, a Langevin equation is written out that includes a drag force, the particle’s buoyant weight, and a Brownian force,
| (4) |
where is the mass of particle of density and diameter , is its velocity, and is the Schiller–Naumann drag coefficient49 as a function of the particle Reynolds number : . Following the literature,48,50 we treat the Brownian force as a Wiener process over a small discrete time step ,
| (5) |
with being a vector whose components are independent Gaussian random variables of zero mean and unit variance, is the Boltzmann constant, the absolute temperature, and the time step of the time integration. We have confirmed that the Lagrangian scheme predicts two-dimensional random walk of particles that are consistent with the continuum solution with a diffusivity given by the Stokes–Einstein relation: . In the Lagrangian simulations, we also assume that all the solid walls are rigid in the LOAC.
C. Adsorption models
In the Eulerian modeling for the particulate phase, we have tested three kinetic models for the surface adsorption and desorption. The simplest is a rapid uptake model, which assumes that once a particle contacts the substrate, it is instantaneously adsorbed, with no desorption or surface saturation. This amounts to posing as a boundary condition for the bulk air in contact with the substrate. To allow finite adsorption and desorption rates, we adopt the Langmuir and Frumkin models. The well-known Langmuir model relates adsorption to the bulk concentration as well as surface coverage,51
| (6) |
where and are the adsorption and desorption rate constants, respectively. is the bulk concentration of particles at the substrate (), is the areal concentration of deposited particles, and is the maximum areal concentration on the surface based on maximum available sites for deposition. The ratio is identified as the fraction of occupied sites. The Frumkin model generalizes the Langmuir model to account for attractive or repulsive interaction among adsorbed particles in a monolayer on the substrate,51
| (7) |
where is the interaction parameter, and a positive represents repulsive interaction among the absorbed particles. Setting to zero will recover the Langmuir model. The outcomes of different adsorption models will be compared and contrasted. For large particles using Lagrangian tracking, we follow previous studies in assuming rapid uptake on the substrate such that a particle is instantly adsorbed upon collision, with no desorption or saturation.35,18,22 This corresponds to the physical picture of larger particles being stuck on substrates on contact.
D. Boundary and initial conditions
To complete the statement of the mathematical problem, we pose the following boundary and initial conditions. On the four sidewalls of the air-flow channel, we impose the no-slip boundary condition, with the possible exception of a slip on the substrate due to a liquid lubricating film. The presence of a liquid film rich in surfactants atop the epithelium argues for a slip boundary condition for the airflow, and we will examine the effect of the slip velocity relative to the traditional no-slip boundary condition. We prescribe a uniform velocity at the inlet and the stress-free condition at the outlet. Note that for simulating tidal breathing, the flow reversal requires a periodic change in the designation of the inlet and outlet. More details will be given in Sec. III.
In the Eulerian treatment of the NPs, we typically impose a constant solid volume fraction at the inlet. An exception is in the exhalation phase of tidal breathing, when we impose at the inlet for reasons to be detailed in Sec. III. On the substrate (), we impose for the rapid uptake model. With an adsorption model, the following balance in NP transport is posed:
| (8) |
There is zero flux at the outlet and on the other walls.
For Lagrangian particle tracking, we release a large number of particles (typically 1000) at the inlet and trace out their trajectories. As the particles are treated as points with no spatial dimension or interactions among themselves, the trajectories do not interfere with each other, and the results are equivalent to the compilation of many individual simulations of single particles.
E. Parameters and numerics
The simulation requires a host of geometric and physical parameters, whose baseline values are tabulated in Table I, along with justifications and sources. For several of these, we have explored variations from the baseline over a range in parametric studies. We have evaluated these parameters from experimental measurements in the literature, or absent that, made estimations based on the most relevant information available. More details of parameter estimation are given in the supplementary material.
We have used COMSOL Multiphysics® to compute the air flow and the NP transport. We deploy cuboid elements for solving the Navier–Stokes equations in 3D, with finer elements in regions of sharper gradient to ensure adequate resolution. Typical finite-element meshes are shown in Fig. S2 of the supplementary material. For simulations with rigid walls, the CFD and particle-tracking modules of COMSOL are used, the latter incorporating the particle inertia and gravitational forces directly. To verify the accuracy of our numerical results, especially with respect to spatial and temporal resolution, we have conducted several validations of the flow field in the LOAC geometry and the solution of advection–diffusion problems. We have also examined how the discrete Brownian force representation [Eq. (5)] converges with decreasing time step. Two such results are shown in Figs. S3 and S4 in the supplementary material.
III. RESULTS AND DISCUSSION
A. Eulerian model: Particle deposition with constant unidirectional in-flow
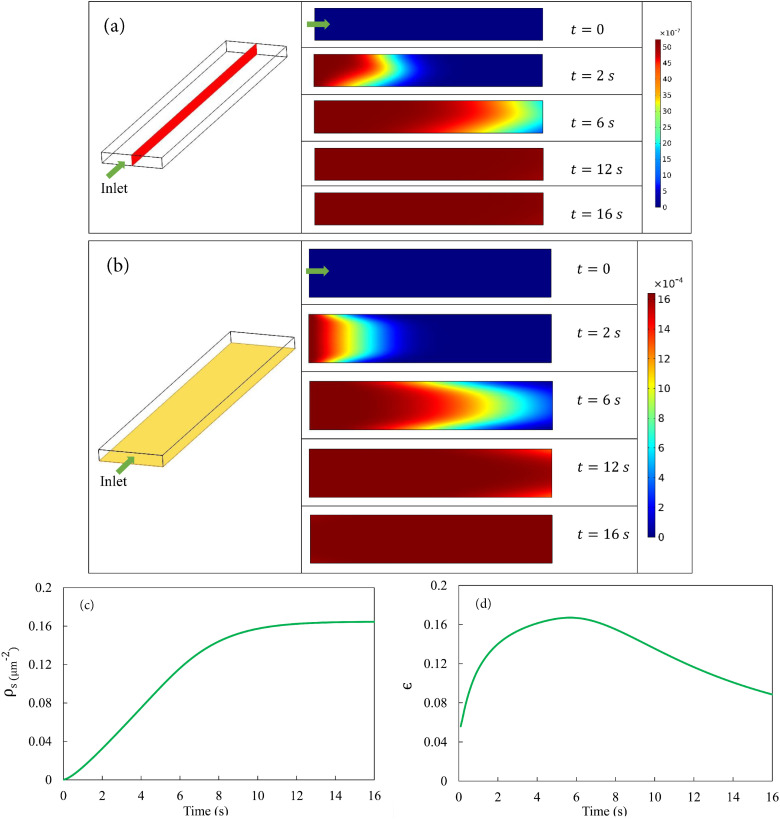
Figure 2 shows the results from Eulerian simulations for fine NPs using the Langmuir model. Before the simulation starts, the LOAC is filled with clean air. At , we impose a constant velocity mm/s at the inlet with a constant particulate volume concentration of (cf. Table I). Hereafter, “concentration” refers to the bulk volume concentration of the NPs unless otherwise stated. As the particle-laden air displaces the clean air inside the LOAC, adsorption of particles occurs on the substrate. Figure 2(a) shows five snapshots of the evolving concentration distribution on the midplane that cuts the air channel into symmetric halves. A profile develops with higher in the middle due to the higher air velocity and advection. The adsorption at the bottom generates an asymmetry in the profile at early times ( s). In time, surface adsorption and desorption reach an equilibrium, and the substrate can no longer take up more NPs. Thus, the profile becomes uniform at roughly around s. Figure 2(b) illustrates the same process by the fraction of occupied sites () on the substrate. First, the particles are deposited at the entrance of the channel until the fraction of occupied sites saturates locally. Note the relative deficit of adsorbed particles at the left and right edges of the plane. These are next to the sidewalls of the LOAC, with reduced air flow supplying fewer number of particles. The front of saturation propagates downstream until the fraction of occupied sites reaches saturation. Note that the saturation level corresponds to , or a mere 0.16% coverage of the area of the substrate. This percentage is determined by equilibrium between adsorption and desorption in the Langmuir kinetics and is consistent with experimental data.53,54
FIG. 2.
Deposition of NPs under constant in-flow with the Langmuir model. (a) Temporal evolution of volume concentration distribution in the air channel shown on the midplane highlighted in the left figure. The height of the rectangles has been stretched by four times to facilitate visualization. After about 12 s, the channel is full of smoky air at the constant particle volume concentration . (b) Temporal evolution of the distribution of the fraction of occupied sites on the substrate. (c) Temporal evolution of the averaged areal number density of deposited particles on the substrate. (d) Temporal evolution of the deposition efficiency .
The temporal evolution of surface coverage by deposited particles is depicted more explicitly in Figs. 2(c) and 2(d). Figure 2(c) shows the average number density of deposited particles on the substrate, while Fig. 2(d) plots the temporal variation of the “deposition efficiency” , defined as the ratio between the number of deposited particles and the number of particles that have entered the LOAC up to the present time.18 The areal number density of particles increases in time with a sigmoidal shape. Initially, the rate of increase is small since the particle-laden air has not reached much of the substrate. Upon equilibration, saturates at a level , which corresponds roughly to a sparse coverage of 16 NPs of diameter nm per 100 of the substrate. The deposition efficiency increases first, and then declines toward 0 as deposition saturates. Despite the sparse coverage on the substrate, reaches a peak value of 0.16, close to experimental data.53,54
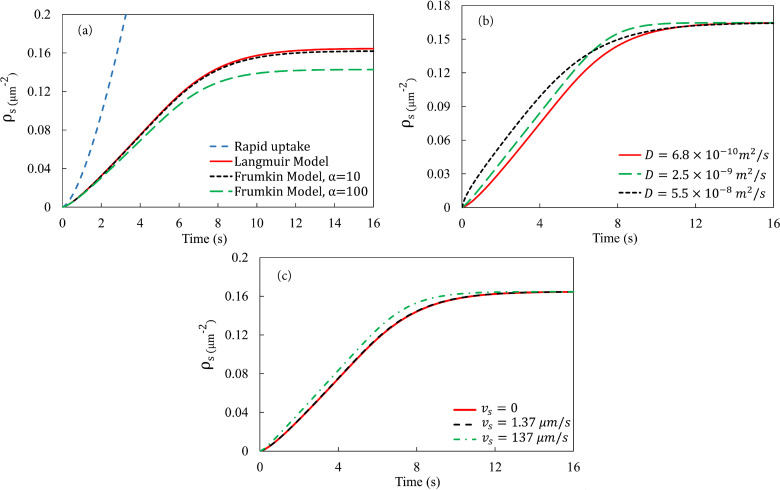
Having described the general features of the deposition process, we explore the effects of a few key factors and parameters next. The first is the three adsorption/desorption models of NPs. The model used in Fig. 2 is the Langmuir model of Eq. (6). Then, we consider a simpler “rapid-uptake” model that corresponds to as a boundary condition for the bulk concentration at the solid substrate. This resembles the “rapid reaction” limit in mass transfer55 and is a reasonable approximation in the limit of instantaneous adsorption of the particles followed by rapid transport through the epithelium so that no desorption occurs. Finally, we have the Frumkin model that allows interactions among adsorbed particles on the substrate.
Figure 3(a) compares the predictions of the three adsorption models for the amount of NP deposition. The average number density plateaus for the Langmuir and Frumkin models, but settles into an unbounded linear growth for the rapid uptake model. Interestingly, for a “reasonable” interaction parameter suggested in the literature,56–58 the Frumkin adsorption kinetics only results in a slight reduction in relative to the Langmuir model, which is recovered with in the Frumkin model. Due to the sparse surface coverage of NPs, their repulsive interaction will only have an observable effect at higher values. For example, if we raise by tenfold to 100, the steady-state decreases by 13%.
FIG. 3.
(a) Effect of the surface adsorption models on , the averaged areal particle number density on the substrate. (b) Effect of diffusivity on the number density of deposited particles. (c) Effect of slip velocity on the particle deposition on the substrate.
The second parameter to be varied is the diffusivity of the particulates in air. This directly affects the particle flux toward the substrate through Fickian diffusion. Figure 3(b) shows that with larger diffusivity , the deposition on the substrate is initially faster, but falls below that of a lower as time passes. This crossover is more obvious for the larger values, but is a general feature of the surface deposition that stems from the spatial heterogeneity of particle deposition. A larger produces faster initial deposition because of rapid diffusion in all three dimensions. First, the surface adsorption creates a deficit of particles in the air layer next to the substrate, and a larger delivers particles more efficiently to that layer in the direction normal to the substrate. Second, streamwise diffusion also delivers particles farther downstream, thus activating adsorption over longer sections of the substrate. Finally, spanwise diffusion also drives the particles toward the sidewalls, thus shrinking the low-deposition edges that would otherwise arise from ineffective advection [see Fig. 2(b)]. A natural consequence of the faster initial adsorption is more rapid attainment of saturation over a wider area of the substrate. Thus, the saturation front travels more rapidly downstream for the higher , shrinking the downstream portion of the substrate that is available for continued adsorption. This explains the earlier saturation of for higher and the crossover between different curves in Fig. 3(b).
Finally, we consider the effect of a slip velocity on the surface of the substrate that may arise from the presence of a thin film of lubricating liquid. The airway surface is covered by a surfactant solution, ranging in thickness from 1.8 m in bronchioles to 0.1 m in alveoli.59,60 Its viscosity is close to that of water.60 The slip velocity is calculated by considering the shear flow of air atop the liquid layer and turns out to be m/s under physiologic conditions (see Table I and supplementary material). The presence of the slip facilitates the air flow near the substrate, which in turn enhances the convection transport of the NPs to the near-wall region to be adsorbed. But for m/s, the increase in deposition is minuscule and hardly visible in Fig. 3(c). In order to see a considerable difference, we tested a much larger slip velocity m/s, 100 times the value estimated above. This does enhance particle deposition initially. But as the saturated steady state is approached, the bulk solid concentration becomes uniform everywhere in the air. Therefore, the slip-enhanced advection ceases to play any role and does not affect the saturated surface density of deposited particles on the substrate, which is entirely determined by the Langmuir kinetics.
B. Eulerian model: Particle deposition in bidirectional pulsatile flow
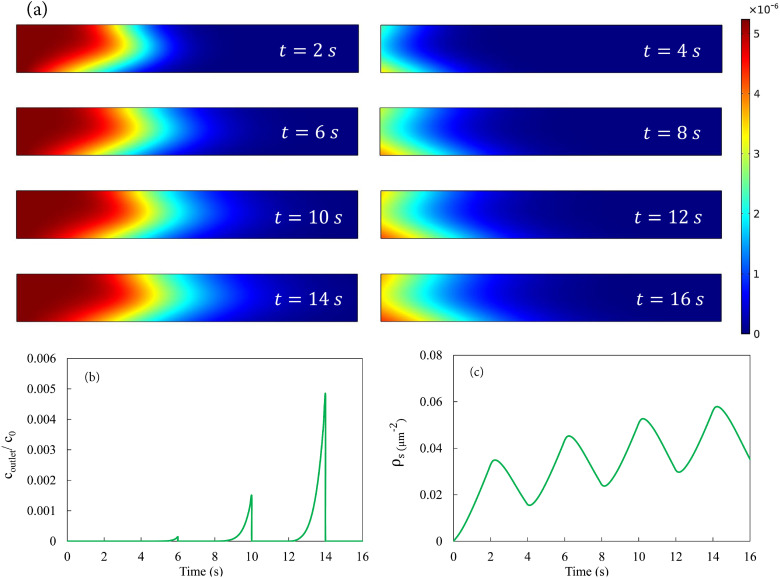
Having established a baseline using constant in-flow, we now explore how tidal breathing affects the deposition of NPs on the substrate. For normal breathing in a resting state, we assume equal duration of 2 s for inhalation and exhalation.49 We start the simulation with the air channel filled with clean air. At , particle-laden air flows into the chamber with a fixed velocity and solid volume concentration at the inlet. At s, we instantaneously reverse the flow direction by prescribing on the original outlet as well as a “clean air” condition , to be explained below. As a result, the original inlet is now an outlet with the stress-free boundary condition for the air flow and no-flux for the advection–diffusion of the solid phase. At s, we revert to the inhalation setup with and at the original inlet, and the cycle repeats itself. We have typically simulated four cycles as these seem sufficient to reveal all the key physics. Experimental measurements are usually for a similar number of cycles.53,54
For the exhalation phase, the boundary condition for the solid concentration at the new inlet, i.e., the original outlet, requires special attention. Numerical experimentation shows that for the and values used for the inhalation, hardly any solid particles will have passed the exit during the first four breathing cycles. Figure 4(a) shows the bulk NP concentration profiles on the midplane at the end of the first four inhalations and exhalations. At the end of the first inhalation ( s), essentially no particle has reached the exit of the LOAC. Note that the midplane enjoys the greatest flow velocity inside the channel, and advection should be weaker along other parallel planes. The same conclusion is borne out by averaging the solid concentration at the exit, which amounts to a negligible at s [Fig. 4(b)]. Each subsequent inhalation advances the solids further toward the exit, but even at the end of the fourth inhalation ( s), the average solid concentration at the exit is a mere 0.5% of [Fig. 4(b)]. Therefore, if we limit ourselves to the first few breathing cycles, posing an “inlet” condition of for the exhalation phase is reasonable, as the air downstream of the LOAC (or deeper inside the alveolar sac) will contain essentially no solids. This assumption becomes questionable for faster breathing during physical exercise or for longer simulations involving many cycles. We will adopt an extended channel for such cases in Sec. III C.
FIG. 4.
Deposition in bidirectional pulsatile flow. (a) Particle volume concentration in the midplane [cf. Fig. 2(a)] at the end of the first four inhalations (left) and four exhalations (right). The height of the rectangles has been stretched by four times to facilitate visualization. (b) Averaged bulk concentration at the outlet, scaled by the inlet concentration , as a function of time during the first four cycles. (c) Variation of the average particle number density adsorbed onto the substrate over the first four cycles of breathing.
Figure 4(c) shows the temporal evolution of the adsorbed particle number density over four breathing cycles. The initial inhalation produces a rapid increase in surface adsorption, following the same portion of the curve in Fig. 3(a) for constant-inflow with the Langmuir adsorption model, resulting in the bulk distribution at s in Fig. 4(a). Upon the start of the exhalation phase, clean air invades the LOAC channel in reverse direction. The Langmuir kinetics on the substrate is such that desorption occurs over the entire area of the substrate, causing the decline in . At the end of the exhalation ( s), the substrate retains about of the particles that have been deposited during the inhalation phase. In the bulk, the clean air has not displaced all the particle-laden air inside the LOAC [Fig. 4(a), s]. The remaining adsorbed particles on the substrate and particles in the bulk ensure that in the second cycle of inhalation, the surface deposition will exceed that of the first cycle, and the same trend continues for later cycles [Fig. 4(c)]. Eventually, the assumption of “clean-air exhalation” () becomes untenable, as the particle-laden air encroaches on the clean air over time and eventually exits the LOAC channel. In a physical experiment, continued cycles will lead to a limit with the channel fully filled with particle-laden air at and a substrate at the saturated number density . With our artificial condition , the curve in Fig. 4(c) will settle into a perfectly periodic oscillation.
C. Eulerian model: Breathing patterns during exercising and smoking
With the bidirectional pulsatile flow model established, we examine next how changes in breathing pattern during physical exercise and cigarette and marijuana smoking affect the deposition of NPs. Ongoing research indicates a two- to eightfold increase in inhalation dosage of ultrafine particles during exercise.61–65 The breathing pattern shows two prominent changes during physical activity: increased air speed and tidal volume per inhalation and elevated breathing frequency. Compared with the resting state, air volume of each inhalation increases from 7 to 40 l/min during moderate to strenuous exercise, which corresponds to an increase in averaged air speed from 0.337 to 1.91 mm/s. In addition, the breathing frequency increases from 15 to 20 cycles per minute.62,66,67 Experimentally, it is challenging to determine the individual and combined effect of these two factors on alveolar deposition of air-borne particulates. Limited evidence suggests that particle deposition increases with the tidal volume but decreases with the breathing frequency.61,62 We will examine each factor separately for its effect on particle deposition in our LOAC model.
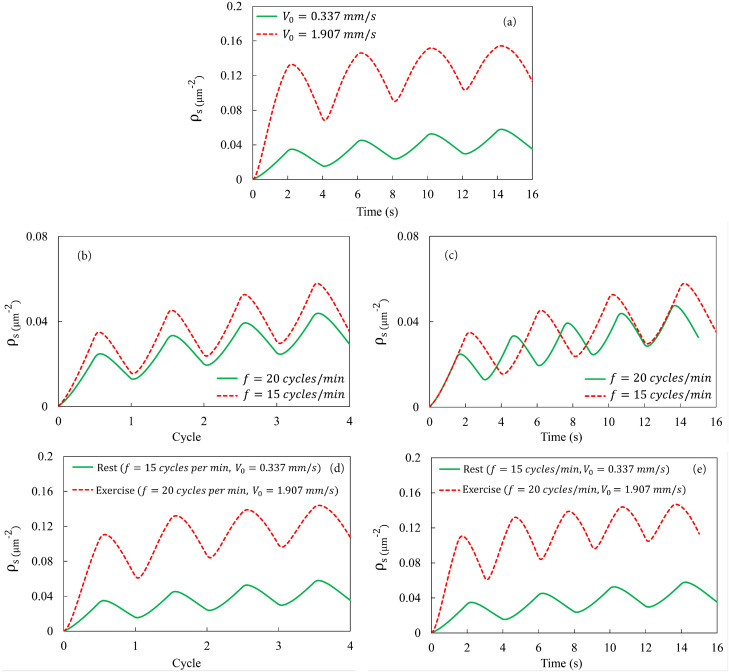
Figure 5(a) shows the particle deposition at the elevated velocity mm/s, characteristic of moderate exercising, compared with at mm/s for the resting state.66,67 At the higher , the “clean-air exhalation” boundary condition of , used in Fig. 4, becomes inaccurate as the faster flow does carry some particles outside the LOAC channel during the inhalation phase. To resolve this complication, we have added an auxiliary segment downstream of the LOAC that has thrice its length, extending the length from 2 to 8 mm. Now, again holds at the exit at the end of the inhalation, and we impose and at the new inlet for the exhalation phase. To measure the particle deposition, we collect data from the original segment ( mm) only. All the simulations on the effect of exercising are carried out in this extended LOAC device. As expected, the faster air flow delivers more NPs into the LOAC and produces a higher deposition, by a factor of about 3 in Fig. 5(a).
FIG. 5.
(a) Effect of the airflow velocity on NP deposition, with the frequency kept at the rest-state 15 cycles per minute or 4 s per cycle. (b) Effect of the breathing frequency on NP deposition, with the airflow velocity kept at the rest-state mm/s. The number density of deposited particles is plotted against the number of breathing cycles. (c) Same as the above, with plotted against real time. (d) Effect of exercise on NP deposition, with the faster airflow ( mm/s) and higher breathing frequency (20 cycles/min or 3 s per cycle). is plotted against the number of breathing cycles. (e) Same as the above, with plotted against real time.
Now we turn to the effect of a higher breathing frequency while keeping the airflow speed at the same mm/s. Figure 5(b) shows that per breathing cycle, the higher frequency produces a lower amount of deposited particles. This is easily understood since at the higher frequency, inhalation and exhalation each lasts 75% of the duration of the baseline case. Therefore, on average, only 75% of the NPs enter the LOAC for each inhalation, and there is also a shorter time for the adsorption on the substrate. If we plot the adsorption not against the cycles but against real time, the shorter breath at higher frequency still produces a lower particle deposition if averaged over time [Fig. 5(c)]. This is because the shorter breath draws in fewer NPs in each inhalation before expelling them by the clean air during exhalation. Effectively, a shorter initial segment of the substrate is exposed to the particulates in the air.
These results indicate opposite effects of the two factors that accompany physical exercise: faster airflow increases NP deposition whereas higher breathing frequency decreases it. Both predictions are consistent with in vivo measurements.61,62 Putting both factors together in Figs. 5(d), and 5(e), we see that the former dominates the latter, and overall physical exercising increases the amount of particulates deposited in the LOAC by a factor of about 3 relative to the resting state. This conclusion is consistent with prior experimental observations. Measurements done on running in urban areas have consistently shown increased inhalation of particulates, with the amount of increases ranging from 1.8 to about 8 times.63–65,68
Finally, we investigate the effect of breathing patterns relevant to smoking. Tobacco and marijuana smokers often adopt characteristic “puff profiles” that differ from the natural breathing pattern.41 One that has been widely studied clinically is the inhale-hold-exhale pattern, in which the smoker holds the breath for a period between inhalation and exhalation. The holding time ranges from 1 to a few seconds for tobacco smoking and can be as long as 20 s for marijuana smoking.37–40 To investigate this factor, we adopt the Langmuir kinetics along with the baseline parameters in the LOAC channel of regular length (i.e., mm of Sec. III B, without the extension used in Fig. 5). At the start of the exhalation, we impose at the inlet as done previously.
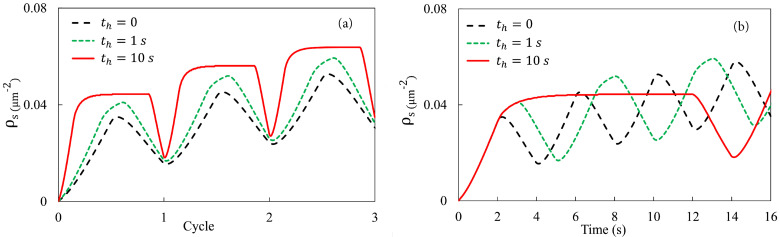
Figure 6 explores the effect of breath-holding, with and 10 s, in comparison with the default breathing pattern without pause (). Plotted against breathing cycles [Fig. 6(a)], our results show that a longer hold gives the air-borne particles extra time to adsorb onto the substrate per cycle. Averaged over the three cycles simulated, the amount of deposition per unit substrate area per cycle increases from 0.0307 m (for ) to 0.0358 m ( s) and 0.0483 m ( s). This can be compared with experimental measurement of the plasma concentration of -tetrahydrocannabinol after ten puffs of marijuana smoking,40 which increases by a factor of about 2 as the pause increases from to s. Assuming the same bioavailability in both cases, the increased drug intake is qualitatively consistent with our model prediction, but quantitatively underestimated. Figure 6(b) plots the deposition in real time. If averaged over a relatively short time, say, the first s, the rate of deposition is lower for longer holding periods.
FIG. 6.
Effect of breath-holding on particle deposition during smoking. For holding time s, 1 s, and 10 s, the number density of deposited particles is plotted against the number of breathing cycles in (a) and against real time in (b).
Our model uses the geometric design of the LOAC device of Huh et al.,24,31 and the original experiments involved only steady-state flows corresponding to the unidirectional simulations of Sec. III A. The bidirectional simulations of various breathing patterns typical of a resting state, physical exercise, and smoking have predicted interesting trends that are consistent with in vivo observations. Newer LOAC designs have started to incorporate bidirectional flows69 but we have found no directly comparable data in the literature. Our bidirectional numerical results in Secs. III B and III C may serve as guidelines for designing future devices.
D. Lagrangian model: Particle tracking
While the effective continuum description of the particulate phase is reasonable for fine NPs, larger particles will require a more detailed discrete description as drag and gravity forces on individual particles become important factors. Meanwhile, Brownian force must be explicitly accounted for through the Langevin equation [Eq. (4)]. We have carried out Lagrangian particle tracking for particles in the 50 nm range. For this subsection, we ignore desorption of the Lagrangian particles, effectively adopting the simplest “rapid uptake” kinetics on the substrate. Experiments have shown that irreversible adsorption may arise from the so-called adhesion hysteresis, with a greater energy barrier against desorption than the energy initially gained through adsorption.70 Given the no-slip boundary condition on the substrate, the hydrodynamic forces will be ineffectual for dislodging an adsorbed particle. So will be the Brownian force for relatively large particles.
Without desorption and surface saturation, both inhalation and exhalation will continually deposit particles on the substrate, and it becomes less meaningful to study the inhalation and exhalation phases separately. Thus, we have limited the following discussion to a constant-flow condition similar to Sec. III A. At , we release 1000 particles at the inlet and track their trajectories downstream. The particles are initially randomly distributed across the entry plane, with an initial velocity of . In the simulations, we treat the particles as points with no spatial dimension; they do not interact hydrodynamically or occupy an excluded volume spatially. Thus, the results are equivalent to the superposition of 1000 simulations of single particles. Whenever a particle comes into contact with the substrate, it is immobilized and adsorbed. On the top and sidewalls, the particles do not adhere but bounce back with a reflected velocity. The deposition efficiency is defined as the fraction of the deposited particles among the total released. The simulations are carried out until all particles have either settled onto the substrate or passed through the LOAC. The duration ranges from 2 s to 50 s, with smaller particles taking longer time.
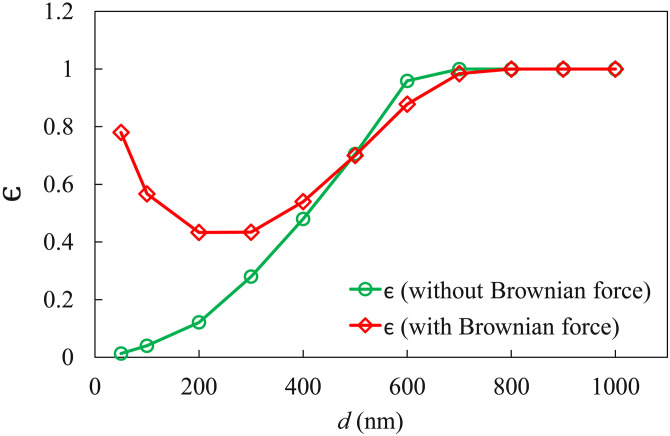
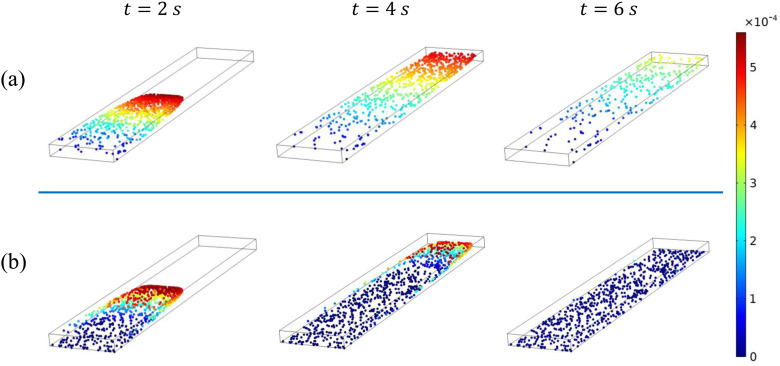
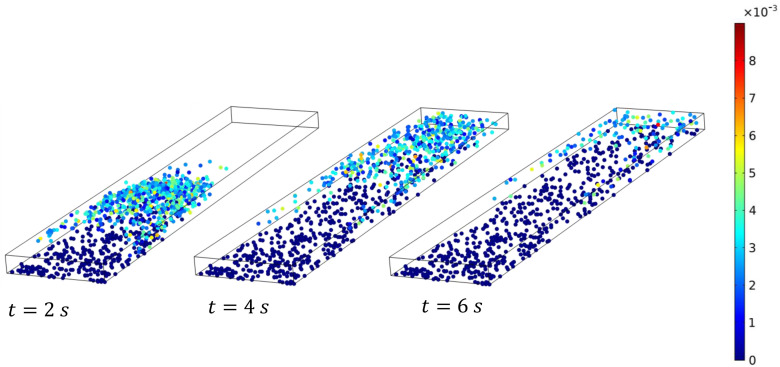
The main results of the Lagrangian simulations are shown in Fig. 7. The deposition efficiency depends strongly on the particle size. For clarity, we have plotted separate curves with and without Brownian forces. Without Brownian force, the fate of the particles is determined by the competition between the drag force and gravity. Larger particles are increasingly dominated by gravity and thus exhibit a greater in Fig. 7. Figure 8 shows three snapshots of non-Brownian particles of diameter nm and 500 nm. The corresponding movies can be viewed as Movies S2 and S3 in the supplementary material. At the start, the particles are carried downstream by the air flow. For nm, gravitational settling is slow and only particles initially near the substrate and the sidewalls have a long enough residence time to settle onto the substrate. The rest are afloat in air and being advected downstream, eventually producing a very low . The settling is more prominent for the larger particles ( nm). By s, most particles that remain inside the LOAC have settled onto the substrate. This explains the increasing with in Fig. 7. For nm, all the particles released settle in the LOAC and approaches unity.
FIG. 7.
Deposition efficiency for non-Brownian and Brownian particles of different sizes. is calculated by dividing the number of absorbed particles by the total number of particles released.
FIG. 8.
Snapshots of the distribution of non-Brownian particles at , 4, and 6 s, for particle diameter (a) nm and (b) nm. The color indicates the instantaneous particle speed, with blue particles () being stationary and adsorbed onto the substrate.
Brownian motion modifies the deposition behavior of the relatively fine particles and causes to vary non-monotonically with . For the finer particles (e.g., nm), gravitational settling is slow and surface adsorption is dominated by Brownian motion. The Brownian force gives the particles a stochastic movement normal to the substrate and, with a certain probability, drives particles into the substrate for adsorption. Figure 9 shows three snapshots of Brownian particles of size nm, and the whole process is shown in Movie S4 in the supplementary material. Comparing these with their counterparts in Fig. 8(a), we first note that Brownian motion randomly perturbs the instantaneous speed of the particles against the clear stratification of non-Brownian particles. In fact, the particles are moving in various directions at any instant. This directionality is not obvious from the magnitude of the speed in Fig. 9 but can be appreciated from Movie S4 in the supplementary material. The strong Brownian motion causes a streamwise spreading of the particles that blurs the traveling front clearly seen for the non-Brownian particles (see s plot of Fig. 8). Simultaneously, the Brownian motion agitates the particle motion in the direction normal to the substrate, and greatly enhances the adsorption relative to the non-Brownian particles. For the finer particles, therefore, Brownian motion and gravity both promote surface adsorption, with the former being dominant.
FIG. 9.
Snapshots of the distribution of Brownian particles of diameter nm at , 4, and 6 s. The color indicates the instantaneous particle speed, with blue particles () being stationary and adsorbed onto the substrate. Note the marked enhancement in deposition relative to the non-Brownian particles of Fig. 8(a).
With increasing particle size, the effect of Brownian motion declines and so does . In the meantime, gravitational settling starts to play an increasing role in enhancing deposition. Eventually, levels off and starts to increase for larger particles ( nm). Note that the Brownian motion is directionally isotropic; it drives the particles toward and away from the substrate with equal probability. As a result, for an intermediate size range (500 nm nm), the Brownian motion hinders gravitational settling more than it drives the particles to the substrate, and so the Brownian particles exhibit a lower desorption ratio than the non-Brownian particles (Fig. 7). For the largest particles ( nm), Brownian motion becomes negligible, and the two curves merge. It is interesting to note that in vivo experimental measurements also show to vary with non-monotonically (Figs. 16 and 17 in Ref. 20), consistent with our prediction for Brownian particles.
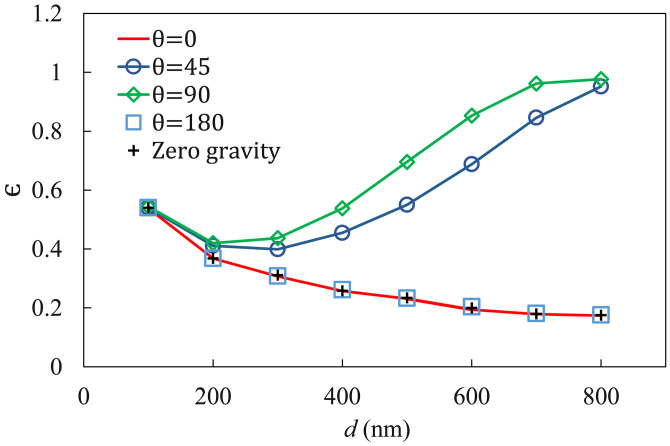
So far, we have only considered gravity acting toward the substrate. In view of the macroscopic structure of the lungs, however, gravity may act in a range of directions relative to the alveolar surface and air flow. For example, it may be parallel to the epithelium and along the flow direction in the lower lobes and against the flow in the upper lobes. Supine or prone postures will place more bronchiolar and alveolar surfaces perpendicular to gravity than an upright one. The LOAC can be inclined to test such effects. We have carried out simulations with gravity acting in co-flow () and counter-flow () directions as well as along a 45 angle with the flow direction (Fig. 10). For the finer particles ( nm), gravitational settling is small relative to Brownian motion, and so essentially the same prevails regardless of the direction of gravity. For larger , gravity parallel to the substrate ( and ) yields lower than gravity pointing toward the substrate () for the lack of gravitational settling. Curiously, there is essentially no difference between the two cases with gravity along () or against () the air flow and both agree with the curve of no gravity at all. Counter-flow gravity should prolong the residence time of the particles within the LOAC relative to co-flow gravity. But a quick estimation shows that for nm, for example, the Stokes drag is about three orders of magnitude greater than the buoyant weight of the particle. Thus, the difference in the residence time is negligibly small. The 45-inclined gravity has a component toward the substrate and produces an intermediate between the perpendicular and parallel cases discussed above. For the largest particles, even this partial gravity results in nearly perfect settling as approaches unity. Therefore, for the parameter values tested here, gravitational settling plays a significant role only if it has a non-zero component directed toward the substrate. One may infer that more particulates are deposited with the body horizontal than upright (e.g., during night vs day times), and more in the middle sections of the lungs than in the upper and lower lobes. These inferences remain to be tested experimentally.
FIG. 10.
Effect of the orientation of gravity on the deposition efficiency for Brownian particles of different sizes. The angle is between the directions of air flow and gravity (see Fig. 1). Gravity is along the flow direction at , perpendicular to the flow at and against the flow at .
IV. CONCLUDING REMARKS
The main motivation for this work is to understand the transport of nanoparticles (NPs) in a lung-on-a-chip (LOAC) device and show that computer simulations can inform and potentially accelerate the design and application of these devices for analyzing particulate– and microbe–alveolar interaction. We have presented two computational models: an Eulerian model for fine NPs and a Lagrangian model for coarser NPs. Using LOAC as a surrogate for the human alveolus, these models were applied to examine the deposition and adsorption of NPs (a) under different exercise and breath-holding patterns and (b) for a range of particle sizes with varying relative importance of Brownian motion and gravitational settling. The first set of results are for fine NPs for which gravitational settling is negligible and an Eulerian continuum approach is suitable, with Brownian motion represented by a diffusivity parameter. For larger particles, we employ Lagrangian particle tracking to probe how gravitational settling and Brownian effect cooperate or counter-act each other. Special attention is given to elucidating the underlying physical mechanisms by adopting parameter values relevant to human breathing and LOAC experiments. The key findings are summarized below.
-
(a)
Using physiologically relevant values for the bulk NP concentration and the adsorption and desorption coefficients in the Langmuir and Frumkin models, we find that the surface coverage by adsorbed particles saturates at a low level of 0.16%.
-
(b)
Tidal breathing produces a cyclic change in the amount of surface deposition, with a gradual increase over the cycles. The exhalation phase typically features a reduction in deposited NPs as a result of desorption.
-
(c)
Physical exercise, characterized by increased air-flow volume in each breath and higher breathing frequency, increases the amount of particulate deposition by a factor of about 3 relative to the state of rest. This is thanks to the deeper breath with greater air-flow volume, as higher breathing frequency causes a moderate decrease in deposition.
-
(d)
Breath-holding between inhalation and exhalation, characteristic of cigarette and marijuana smoking, increases the deposition by an amount that increases with the duration of the holding period.
-
(e)
Lagrangian particle tracking finds the deposition efficiency first to decrease with particle size for diminishing effects of Brownian motion and then to increase for more pronounced gravitational settling. Thus, the deposition varies with particle size non-monotonically. Spatial orientation of the epithelium relative to gravity also affects the deposition efficiency.
-
(f)
Where comparisons can be made with experimental data in the literature, the above results are in qualitative and sometimes semi-quantitative agreement.
These findings may have several clinical implications. First, because physical exercise leads to increased particle deposition in the airways, it is advisable for individuals to avoid or curtail outdoor exercise on days with poor air quality. Second, smokers should be warned against prolonged breath-holds during puffs. In contrast, for individuals with asthma or chronic obstructive pulmonary disease who use inhalers for a clinical indication, prolonged breath-holding should be encouraged.
We must note that as in any modeling work, certain simplifications and assumptions have to be made to make the problem tractable. One such assumption is the Langmuir and Frumkin kinetics for surface adsorption and desorption, which are both valid for a monolayer of adsorbed particles. In the current parameter range, where the surface areal coverage is sparse [0.16% in Fig. 2(b)], the monolayer models are suitable. For greater amount of deposition, a multilayer adsorption model such as the Brunauer–Emmett–Teller (BET) model may be more appropriate.71 In addition, the estimation of parameter values is subject to a degree of uncertainty, as discussed in the supplementary material. Finally, in Lagrangian particle tracking, we are unable to include sufficient number of particles to reach the appropriate bulk concentration. This is just a matter of linearly increasing the amount of computations, since the particles do not interact, and should not have affected the qualitative trend in the results.
The significance of the results lies mainly in identifying the principal factors that determine deposition in an LOAC device and delineating their effects individually and collectively on the outcome. These factors include surface adsorption and desorption kinetics, breathing patterns and puff profiles in smoking, Brownian force on fine particles and gravity on larger ones. Besides, our results provide guidelines for designing future LOAC devices and measurement protocols in terms of the pattern of depositions to anticipate and the key data to record. Current efforts are underway to extend the model to incorporate more complex biological processes, e.g., transport of the deposited NPs through the mucus layer atop the epithelium, and migration of particles and leukocytes between the air and blood chambers in LOACs.
V. SUPPLEMENTARY MATERIAL
The supplementary material contains a detailed description of the evaluation of the model parameters, as well as Figs. S1–S4 and Movies S1–S4.
ACKNOWLEDGMENTS
The authors acknowledge financial support by the Natural Sciences and Engineering Research Council of Canada (Discovery Grant No. 2019-04162), the MITACS (Accelerate Program), and the Providence Airway Centre at the Centre for Heart Lung Innovation, St. Paul’s Hospital. The computations were carried out at WestGrid (www.westgrid.ca) and Compute Canada (www.computecanada.ca), with software licensing through CMC Microsystems (www.cmc.ca). The authors would like to thank Mr. Irving Ding and Mrs. Chun Hong Tao for their financial support of the SPF COVID-19 Response Fund, Mohammad Ali Bijarchi for help with software setup, and Karen Cheung, Tanya Bennet and Tillie Hackett for discussions.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Biswas P. and Wu C.-Y., “Nanoparticles and the environment,” J. Air Waste Manage. Assoc. 55, 708–746 (2005). 10.1080/10473289.2005.10464656 [DOI] [PubMed] [Google Scholar]
- 2.Sajid M., Ilyas M., Basheer C., Tariq M., Daud M., Baig N., and Shehzad F., “Impact of nanoparticles on human and environment: Review of toxicity factors, exposures, control strategies, and future prospects,” Environ. Sci. Pollut. Res. 22, 4122–4143 (2015). 10.1007/s11356-014-3994-1 [DOI] [PubMed] [Google Scholar]
- 3.Garcia-Mouton C., Hidalgo A., Cruz A., and Pérez-Gil J., “The lord of the lungs: The essential role of pulmonary surfactant upon inhalation of nanoparticles,” Eur. J. Pharm. Biopharm. 144, 230–243 (2019). 10.1016/j.ejpb.2019.09.020 [DOI] [PubMed] [Google Scholar]
- 4.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., Zhao X., Huang B., Shi W., Lu R., Niu P., Zhan F., Ma X., Wang D., Xu W., Wu G., Gao G. F., and Tan W., “A novel coronavirus from patients with pneumonia in China, 2019,” N. Engl. J. Med. 382, 727–733 (2020). 10.1056/NEJMoa2001017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hiller F. C., Wilson F. J., Mazumder Jr. M. K., Wilson J. D., and Bone R. C., “Concentration and particle size distribution in smoke from marijuana cigarettes with different delta 9-tetrahydrocannabinol content,” Fundam. Appl. Toxicol. 4, 451–454 (1984). 10.1016/0272-0590(84)90202-1 [DOI] [PubMed] [Google Scholar]
- 6.Anderson P. J., Wilson J. D., and Hiller F. C., “Particle size distribution of mainstream tobacco and marijuana smoke. Analysis using the electrical aerosol analyzer,” Am. Rev. Respir. Dis. 140, 202–205 (1989). 10.1164/ajrccm/140.1.202 [DOI] [PubMed] [Google Scholar]
- 7.Bernstein D. M., “A review of the influence of particle size, puff volume, and inhalation pattern on the deposition of cigarette smoke particles in the respiratory tract,” Inhal. Toxicol. 16, 675–689 (2004). 10.1080/08958370490476587 [DOI] [PubMed] [Google Scholar]
- 8.van Dijk W. D., Gopal S., and Scheepers P. T., “Nanoparticles in cigarette smoke; real-time undiluted measurements by a scanning mobility particle sizer,” Anal. Bioanal. Chem. 399, 3573–3578 (2011). 10.1007/s00216-011-4701-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vogelmeier C. F., Criner G. J., Martinez F. J., Anzueto A., Barnes P. J., Bourbeau J., Celli B. R., Chen R., Decramer M., Fabbri L. M., Frith P., Halpin D. M., López Varela M. V., Nishimura M., Roche N., Rodriguez-Roisin R., Sin D. D., Singh D., Stockley R., Vestbo J., Wedzicha J. A., and Agustí A., “Global strategy for the diagnosis, management, and prevention of chronic obstructive lung disease 2017 report. GOLD executive summary,” Am. J. Respir. Crit. Care Med. 195, 557–582 (2017). 10.1164/rccm.201701-0218PP [DOI] [PubMed] [Google Scholar]
- 10.Kim W. J. and Lee C. Y., “Environmental exposures and chronic obstructive pulmonary disease,” Mol. Cell. Toxicol. 13, 251–255 (2017). 10.1007/s13273-017-0027-4 [DOI] [Google Scholar]
- 11.Nardone A., Neophytou A. M., Balmes J., and Thakur N., “Ambient air pollution and asthma-related outcomes in children of color of the USA: A scoping review of literature published between 2013 and 2017,” Curr. Allergy Asthma Rep. 18, 29 (2018). 10.1007/s11882-018-0782-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sun Z. and Zhu D., “Exposure to outdoor air pollution and its human health outcomes: A scoping review,” PLoS One 14, e0216550 (2019). 10.1371/journal.pone.0216550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fröhlich E., Mercuri A., Wu S., and Salar-Behzadi S., “Measurements of deposition, lung surface area and lung fluid for simulation of inhaled compounds,” Front. Pharmacol. 7, 181 (2016). 10.3389/fphar.2016.00181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Card J. W., Zeldin D. C., Bonner J. C., and Nestmann E. R., “Pulmonary applications and toxicity of engineered nanoparticles,” Am. J. Physiol. Lung Cell. Mol. Physiol. 295, L400–L411 (2008). 10.1152/ajplung.00041.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Geiser M. and Kreyling W. G., “Deposition and biokinetics of inhaled nanoparticles,” Part. Fibre Toxicol. 7, 2 (2010). 10.1186/1743-8977-7-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fröhlich E. and Salar-Behzadi S., “Toxicological assessment of inhaled nanoparticles: Role of in vivo, ex vivo, in vitro, and in silico studies,” Int. J. Mol. Sci. 15, 4795–4822 (2014). 10.3390/ijms15034795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nowak N., Kakade P. P., and Annapragada A. V., “Computational fluid dynamics simulation of airflow and aerosol deposition in human lungs,” Ann. Biomed. Eng. 31, 374–390 (2003). 10.1114/1.1560632 [DOI] [PubMed] [Google Scholar]
- 18.Augusto L. L. X., Gonçalves J. A. S., and Lopes G. C., “CFD evaluation of the influence of physical mechanisms, particle size, and breathing condition on the deposition of particulates in a triple bifurcation airway,” Water Air Soil Pollut. 227, 56 (2016). 10.1007/s11270-016-2753-y [DOI] [Google Scholar]
- 19.Choi L. T., Tu J. Y., Li H. F., and Thien F., “Flow and particle deposition patterns in a realistic human double bifurcation airway model,” Inhal. Toxicol. 19, 117–131 (2007). 10.1080/08958370601051719 [DOI] [PubMed] [Google Scholar]
- 20.Rostami A. A., “Computational modeling of aerosol deposition in respiratory tract: A review,” Inhal. Toxicol. 21, 262–290 (2009). 10.1080/08958370802448987 [DOI] [PubMed] [Google Scholar]
- 21.Ghalati P. F., Keshavarzian E., Abouali O., Faramarzi A., Tu J., and Shakibafard A., “Numerical analysis of micro- and nano-particle deposition in a realistic human upper airway,” Comput. Biol. Med. 42, 39–49 (2012). 10.1016/j.compbiomed.2011.10.005 [DOI] [PubMed] [Google Scholar]
- 22.Monjezi M., Saidi M. S., and Ahmadi G., “Submicron particle deposition in pulmonary alveoli during cyclic breathing,” Sci. Iran. B 24, 1975–1984 (2017). 10.24200/SCI.2017.4292 [DOI] [Google Scholar]
- 23.Geiser M., Wigge C., Conrad M. L., Eigeldinger-Berthou S., Künzi L., Garn H., Renz H., and Mall M. A., “Nanoparticle uptake by airway phagocytes after fungal spore challenge in murine allergic asthma and chronic bronchitis,” BMC Pulm. Med. 14, 116 (2014). 10.1186/1471-2466-14-116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huh D., Matthews B. D., Mammoto A., Montoya-Zavala M., Hsin H. Y., and Ingber D. E., “Reconstituting organ-level lung functions on a chip,” Science 328, 1662–1668 (2010). 10.1126/science.1188302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ewart L. and Roth A., “Opportunities and challenges with microphysiological systems: A pharma end-user perspective,” Nat. Rev. Drug Discovery (2020). 10.1038/d41573-020-00030-2 [DOI] [PubMed] [Google Scholar]
- 26.Esch E. W., Bahinski A., and Huh D., “Organs-on-chips at the frontiers of drug discovery,” Nat. Rev. Drug Discovery 14, 248–260 (2015). 10.1038/nrd4539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Konar D., Devarasetty M., Yildiz D. V., Atala A., and Murphy S. V., “Lung-on-a-chip technologies for disease modeling and drug development,” Biomed. Eng. Comput. Biol. 7, 17–27 (2016). 10.4137/BECB.S34252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Takayama S., White J. B., and Zhang C., “Lungs-on-a-chip,” in Inhalation Toxicol., 3rd ed., edited by H. Salem and S. A. Katz (CRC Press, 2016), Chap. 3, pp. 57–69.
- 29.Ronaldson-Bouchard K. and Vunjak-Novakovic G., “Organs-on-a-chip: A fast track for engineered human tissues in drug development,” Cell Stem Cell 22, 310–324 (2018). 10.1016/j.stem.2018.02.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Isoherranen N., Madabushi R., and Huang S.-M., “Emerging role of organ-on-a-chip technologies in quantitative clinical pharmacology evaluation,” Clin. Transl. Sci. 12, 113–121 (2019). 10.1111/cts.12627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huh D., Kim H. J., Fraser J. P., Shea D. E., Khan M., Bahinski A., Hamilton G. A., and Ingber D. E., “Microfabrication of human organs-on-chips,” Nat. Protoc. 8, 2135–2157 (2013). 10.1038/nprot.2013.137 [DOI] [PubMed] [Google Scholar]
- 32.Zhang M., Xu C., Jiang L., and Qin J., “A 3D human lung-on-a-chip model for nanotoxicity testing,” Toxicol. Res. 7, 1048–1060 (2018). 10.1039/C8TX00156A [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li K., Yang X., Xue C., Zhao L., Zhang Y., and Gao X., “Biomimetic human lung-on-a-chip for modeling disease investigation,” Biomicrofluidics 13, 031501 (2019). 10.1063/1.5100070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shrestha J., Bazaz S. R., Es H. A., Azari D. Y., Thierry B., Warkiani M. E., and Ghadiri M., “Lung-on-a-chip: The future of respiratory disease models and pharmacological studies,” Crit. Rev. Biotechnol. 40, 213–230 (2020). 10.1080/07388551.2019.1710458 [DOI] [PubMed] [Google Scholar]
- 35.Longest P. W. and Xi J., “Computational investigation of particle inertia effects on submicron aerosol deposition in the respiratory tract,” J. Aerosol Sci. 38, 111–130 (2007). 10.1016/j.jaerosci.2006.09.007 [DOI] [Google Scholar]
- 36.Gurman J. L., Lippmann M., and Schlesinger R. B., “Particle deposition in replicate casts of the human upper tracheobronchial tree under constant and cyclic inspiratory flow. I. Experimental,” Aerosol Sci. Technol. 3, 245–252 (1984). 10.1080/02786828408959012 [DOI] [Google Scholar]
- 37.Nemeth-Coslett R., Henningfield J. E., O’Keeffe M. K., and Griffiths R. R., “Effects of marijuana smoking on subjective ratings and tobacco smoking,” Pharmacol. Biochem. Behav. 25, 659–665 (1986). 10.1016/0091-3057(86)90156-5 [DOI] [PubMed] [Google Scholar]
- 38.Zacny J. P. and Chait L., “Breathhold duration and response to marijuana smoke,” Pharmacol. Biochem. Behav. 33, 481–484 (1989). 10.1016/0091-3057(89)90534-0 [DOI] [PubMed] [Google Scholar]
- 39.Simmons M. S. and Tashkin D. P., “The relationship of tobacco and marijuana smoking characteristics,” Life Sci. 56, 2185–2191 (1995). 10.1016/0024-3205(95)00206-L [DOI] [PubMed] [Google Scholar]
- 40.Azorlosa J. L., Greenwald M. K., and Stitzer M. L., “Marijuana smoking: Effects of varying puff volume and breathhold duration,” J. Pharmacol. Exp. Ther. 272, 560–569 (1995). [PubMed] [Google Scholar]
- 41.Brinkman M. C., Kim H., Chuang J. C., Kroeger R. R., Deojay D., Clark P. I., and Gordon S. M., “Comparison of true and smoothed puff profile replication on smoking behavior and mainstream smoke emissions,” Chem. Res. Toxicol. 28, 182–190 (2015). 10.1021/tx500318h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Alletto M. and Breuer M., “One-way, two-way and four-way coupled LES predictions of a particle-laden turbulent flow at high mass loading downstream of a confined bluff body,” Int. J. Multiphase Flow 45, 70–90 (2012). 10.1016/j.ijmultiphaseflow.2012.05.005 [DOI] [Google Scholar]
- 43.comsol Multiphysics, Particle Tracing Module User’s Guide, v. 5.4, COMSOL AB, Stockholm, Sweden, 2018.
- 44.Sahu S. K., Tiwari M., Bhangare R. C., and Pandit G. G., “Particle size distribution of mainstream and exhaled cigarette smoke and predictive deposition in human respiratory tract,” Aerosol Air Qual. Res. 13, 324–332 (2013). 10.4209/aaqr.2012.02.0041 [DOI] [Google Scholar]
- 45.Johnson T. J., Olfert J. S., Cabot R., Treacy C., Yurteri C. U., Dickens C., McAughey J., and Symonds J. P. R., “Steady-state measurement of the effective particle density of cigarette smoke,” J. Aerosol Sci. 75, 9–16 (2014). 10.1016/j.jaerosci.2014.04.006 [DOI] [Google Scholar]
- 46.Tsuda A., Henry F. S., and Butler J. P., “Particle transport and deposition: Basic physics of particle kinetics,” in Comprehensive Physiology, edited by R. Terjung (American Cancer Society, 2013), Vol. 3, pp. 1437–1471. [DOI] [PMC free article] [PubMed]
- 47.van Doremalen N., Bushmaker T., Morris D. H., Holbrook M. G., Gamble A., Williamson B. N., Tamin A., Harcourt J. L., Thornburg N. J., Gerber S. I., Lloyd-Smith J. O., de Wit E., and Munster V. J., “Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1,” N. Engl. J. Med. 382, 1564–1567 (2020). 10.1056/NEJMc2004973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li A. and Ahmadi G., “Dispersion and deposition of spherical particles from point sources in a turbulent channel flow,” Aerosol Sci. Tech. 16, 209–226 (1992). 10.1080/02786829208959550 [DOI] [Google Scholar]
- 49.Kolanjiyil A. V. and Kleinstreuer C., “Computational analysis of aerosol-dynamics in a human whole-lung airway model,” J. Aerosol Sci. 114, 301–316 (2017). 10.1016/j.jaerosci.2017.10.001 [DOI] [Google Scholar]
- 50.Allen M. P. and Tildesley D. J., Computer Simulation of Liquids, 2nd ed. (Oxford, 2017). [Google Scholar]
- 51.Adamczyk Z. and Petlicki J., “Adsorption and desorption kinetics of molecules and colloidal particles,” J. Colloid Interface Sci. 118, 20–49 (1987). 10.1016/0021-9797(87)90433-4 [DOI] [Google Scholar]
- 52.Engineering ToolBox, “Air–density, specific weight and thermal expansion coefficient at varying temperature and constant pressures,” 2003, see https://www.engineeringtoolbox.com/air-density-specific-weight-d˙600.html.
- 53.Heyder J., Gebhart J., Heigwer G., Roth C., and Stahlhofen W., “Experimental studies of the total deposition of aerosol particles in the human respiratory tract,” J. Aerosol Sci. 4, 191–208 (1973). 10.1016/0021-8502(73)90002-5 [DOI] [Google Scholar]
- 54.Heyder J., Gebhart J., Rudolf G., Schiller C. F., and Stahlhofen W., “Deposition of particles in the human respiratory tract in the size range 0.005–15 m,” J. Aerosol Sci. 17, 811–825 (1986). 10.1016/0021-8502(86)90035-2 [DOI] [Google Scholar]
- 55.Bird R. B., Stewart W. E., and Lightfoot E. N., Transport Phenomena (John Wiley & Sons, 2007). [Google Scholar]
- 56.Chun J. H., Ra K. H., and Kim N. Y., “Qualitative analysis of the Frumkin adsorption isotherm of the over-potentially deposited hydrogen at the poly-ni/KOH aqueous electrolyte interface using the phase-shift method,” J. Electrochem. Soc. 149, E325–E330 (2002). 10.1149/1.1497402 [DOI] [Google Scholar]
- 57.Chun J. and Chun J. H., “Review on the determination of Frumkin, Langmuir, and Temkin adsorption isotherms at electrode/solution interfaces using the phase-shift method and correlation constants,” Korean Chem. Eng. Res. 54, 734–745 (2016). 10.9713/kcer.2016.54.6.734 [DOI] [Google Scholar]
- 58.Yang C. W. T., “Adsorption of a carboxylated silane on gold: Characterization and application to PDMS-based electrochemical cells,” Ph.D. thesis (School University of British Columbia, Vancouver, 2016). [Google Scholar]
- 59.Widdicombe J. G., “Airway surface liquid: concepts and measurements,” in Airway Mucus: Basic Mechanisms and Clinical Perspectives (Springer, 1997), pp. 1–17.
- 60.Siebert T. A. and Rugonyi S., “Influence of liquid-layer thickness on pulmonary surfactant spreading and collapse,” Biophys. J. 95, 4549–4559 (2008). 10.1529/biophysj.107.127654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kim C. S. and Jaques P. A., “Analysis of total respiratory deposition of inhaled ultrafine particles in adult subjects at various breathing patterns,” Aerosol Sci. Technol. 38, 525–540 (2004). 10.1080/02786820490465513 [DOI] [Google Scholar]
- 62.Löndahl J., Massling A., Pagels J., Swietlicki E., Vaclavik E., and Loft S., “Size-resolved respiratory-tract deposition of fine and ultrafine hydrophobic and hygroscopic aerosol particles during rest and exercise,” Inhalation Toxicol. 19, 109–116 (2007). 10.1080/08958370601051677 [DOI] [PubMed] [Google Scholar]
- 63.Kantipudi N., Patel V., Jones G., Kamath M. V., and Upton A. R. M., “Air pollution’s effects on the human respiratory system,” Crit. Rev. Biomed. Eng. 44, 383–395 (2016). 10.1615/CritRevBiomedEng.2017019757 [DOI] [PubMed] [Google Scholar]
- 64.Dong J., Zhang S., Xia L., Yu Y., Hu S., Sun J., Zhou P., and Chen P., “Physical activity, a critical exposure factor of environmental pollution in children and adolescents health risk assessment,” Int. J. Environ. Res. Public Health 15, 176 (2018). 10.3390/ijerph15020176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.C. Peixoto K. S. K., Pereira M. D. C., and Morais S., “(Ultra)fine particle concentrations and exposure in different indoor and outdoor microenvironments during physical exercising,” J. Toxicol. Environ. Health A 82, 591–602 (2019). 10.1080/15287394.2019.1636494 [DOI] [PubMed] [Google Scholar]
- 66.Phalen R., Cuddihy R., Fisher G., Moss O., Schlesinger R., Swift D., and Yeh H., “Main features of the proposed NCRP respiratory tract model,” Radiat. Prot. Dosim. 38, 179–184 (1991). 10.1093/oxfordjournals.rpd.a081088 [DOI] [Google Scholar]
- 67.Harding E. M. and Robinson Jr. R. J., “Flow in a terminal alveolar sac model with expanding walls using computational fluid dynamics,” Inhal. Toxicol. 22, 669–678 (2010). 10.3109/08958371003749939 [DOI] [PubMed] [Google Scholar]
- 68.Slezakova K., Pereira M. C., and Morais S., “Ultrafine particles: Levels in ambient air during outdoor sport activities,” Environ. Pollut. 258, 113648 (2020). 10.1016/j.envpol.2019.113648 [DOI] [PubMed] [Google Scholar]
- 69.Miller P. G., Chen C.-Y., Wang Y. I., Gao E., and Shuler M. L., “Multiorgan microfluidic platform with breathable lung chamber for inhalation or intravenous drug screening and development,” Biotechnol. Bioeng. 117, 486–497 (2020). 10.1002/bit.27188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zhang M. and Akbulut M., “Adsorption, desorption, and removal of polymeric nanomedicine on and from cellulose surfaces: Effect of size,” Langmuir 27, 12550–12559 (2011). 10.1021/la202287k [DOI] [PubMed] [Google Scholar]
- 71.Foo K. Y. and Hameed B. H., “Insights into the modeling of adsorption isotherm systems,” Chem. Eng. J. 156, 2–10 (2010). 10.1016/j.cej.2009.09.013 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.