Abstract
Patterns of transmission of drug-resistant tuberculosis (TB) remain poorly understood, despite over half a million incident cases worldwide in 2017. Modeling TB transmission networks can provide insight into drivers of transmission, but incomplete sampling of TB cases can pose challenges for inference from individual epidemiologic and molecular data. We assessed the effect of missing cases on a transmission network inferred from Mycobacterium tuberculosis sequencing data on extensively drug-resistant TB cases in KwaZulu-Natal, South Africa, diagnosed in 2011–2014. We tested scenarios in which cases were missing at random, missing differentially by clinical characteristics, or missing differentially by transmission (i.e., cases with many links were under- or oversampled). Under the assumption that cases were missing randomly, the mean number of transmissions per case in the complete network needed to be larger than 20, far higher than expected, to reproduce the observed network. Instead, the most likely scenario involved undersampling of high-transmitting cases, and models provided evidence for super-spreading. To our knowledge, this is the first analysis to have assessed support for different mechanisms of missingness in a TB transmission study, but our results are subject to the distributional assumptions of the network models we used. Transmission studies should consider the potential biases introduced by incomplete sampling and identify host, pathogen, or environmental factors driving super-spreading.
Keywords: bias analysis, drug-resistant tuberculosis, missing data, network modeling, tuberculosis, tuberculosis transmission, whole genome sequencing
Abbreviations
- ERGM
exponential random graph model
- SNP
single nucleotide polymorphism
- TB
tuberculosis
- TRAX Study
Transmission Study of XDR TB
- XDR
extensively drug-resistant
Tuberculosis (TB) is the leading infectious cause of death worldwide (1). The ongoing transmission of extensively drug-resistant (XDR) TB, which is resistant to both first- and second-line antibiotics, is a severe threat to public health. South Africa has among the highest rates of TB and human immunodeficiency virus infection globally, and KwaZulu-Natal Province has the highest XDR TB incidence in South Africa (3 per 100,000 population) (2–5). In South Africa and elsewhere, the majority of drug-resistant TB cases are due to transmission of already-resistant strains, rather than inadequate treatment (6, 7). This underscores the importance of locating where and between whom TB transmission occurs to develop interventions targeting key transmission locations and at-risk groups (8).
Identifying transmission events is a challenge given the airborne transmission route of TB and the dramatic variability in the duration of latent TB infection. However, bacterial whole genome sequencing allows for high-resolution characterization of Mycobacterium tuberculosis sequences at the level of individual base pairs. Cases with similar M. tuberculosis sequences are likely to be linked through recent transmission; collectively, such links can be used to infer networks of transmission events (9). Previous studies have inferred transmission events using social-contact or molecular data, but a key limitation of these studies in high-incidence settings is that it is virtually impossible to identify all TB cases. Half of TB cases are estimated to be undiagnosed (10–12). Among diagnosed cases, epidemiologic or sequencing information may be missing, either because a clinical sample could not be collected or because a case died prior to diagnosis or study enrollment—a particular concern with XDR TB, given its low survival rate (though survival continues to improve) (13, 14). Thus, a major challenge of characterizing TB transmission networks is inferring a complete, or at least representative, set of transmission links from incomplete data. If an empirical network constructed from incomplete data poorly resembles the true transmission network, inferences about transmission may be biased.
A modeling approach to the problem of missing network data could provide insight into what the structure of the complete transmission network, had it been measured, would have looked like. Missing network data are different from missing data in traditional epidemiologic studies, because the dependence among cases in a network violates the assumption that data are independent and identically distributed. Even if cases are missing at random, inference from a partially sampled transmission network could be biased. However, we can still make inferences about the complete network if certain conditions are met (15). Most importantly, sampled cases must not differ systematically from unsampled cases with respect to their transmission potential (15). This may occur if, for example, undiagnosed cases have longer infectious periods and therefore contribute disproportionately to transmission as compared with diagnosed cases who receive prompt treatment. Failing to sample these highly connected cases could have a pronounced effect on network structure and, as a result, bias conclusions made from the empirical network (16).
We may be able to mitigate bias if we can quantify it, by identifying characteristics of cases that are undersampled and using this information to infer the structure of the true network. For example, TB cases without detectable mycobacteria in sputum (“smear-negative”) are both less infectious and more difficult to diagnose than smear-positive cases, leading to a scenario in which diagnosed cases may be responsible for more transmission than undiagnosed and unsampled cases (17). Conversely, transmission studies may tend to capture cases among people who present promptly to a health-care provider upon experiencing symptoms, resulting in shorter infectious periods among cases enrolled in the study than among unsampled cases. Cases diagnosed late in their disease course may be less likely to participate in a transmission study, either because they are very ill by the time they are diagnosed or because they have generally lower engagement with the health-care system. Understanding the effects of biased sampling is a first step in evaluating the robustness of empirical transmission networks of TB cases in different settings. Lastly, understanding the structure of complete networks can permit testing of hypotheses about drivers of TB transmission. Super-spreading, defined by the existence of cases that cause a disproportionate number of secondary infections, is increasingly being recognized as an important phenomenon shaping transmission dynamics but is difficult to measure empirically (18, 19). Detecting signatures of this phenomenon in transmission networks will improve our understanding of its role in TB epidemiology.
In this analysis, we used data from the Transmission Study of XDR TB (TRAX Study), which enrolled culture-confirmed XDR TB cases diagnosed from 2011 to 2014 in KwaZulu-Natal Province, South Africa. We constructed an empirical transmission network based on M. tuberculosis sequence data and used network models to infer “complete” transmission networks based on different assumptions about how data were missing from the empirical network. We tested models including a “super-spreading” factor to understand its impact on network structure. Our goal was to identify the typology of missingness most consistent with the empirical network in order to assess the extent to which our transmission study reflected true XDR TB transmission patterns.
METHODS
Study design and procedures
The TRAX Study investigators identified 1,027 XDR TB cases through the single referral laboratory that conducts drug-susceptibility testing for all public health-care facilities in KwaZulu-Natal Province and selected a convenience sample of 404 cases (6, 20). All participants provided written informed consent; for deceased or severely ill participants, consent was obtained from next-of-kin. We interviewed participants and performed medical record review to collect demographic and clinical information. The diagnostic XDR TB isolate was obtained for all enrolled participants. Raw paired-end sequencing reads were generated on the Illumina MiSeq platform (Illumina, Inc., San Diego, California) and aligned to the H37Rv reference genome (NC_000962.3). Single nucleotide polymorphisms (SNPs) were detected using standard pairwise resequencing techniques (Samtools, version 0.1.19) against the reference (21). A total of 344 cases had M. tuberculosis sequences that passed all quality filters (see Web Appendix 1 and Web Figure 1, available at https://academic.oup.com/aje). Sequencing data are available in the National Center for Biotechnology Information’s Sequence Read Archive (https://www.ncbi.nlm.nih.gov/sra; BioProject: PRJNA476470).
Constructing the empirical network using M. tuberculosis sequence data
We defined a genomic link as a pair of XDR TB cases with 5 or fewer SNP differences between their M. tuberculosis sequences (9). We constructed genomic transmission networks of TRAX cases, in which each node in the network represents a case and each edge represents a transmission event. The degree of each node is the number of edges per case (or the sum of the source and forward transmission links); the degree distribution represents the edge count across all nodes in the network. We considered this empirical genomic network a subset of the cases and links in the true, complete transmission network that includes all XDR TB cases and transmission events in KwaZulu-Natal during the study period.
Exponential random graph models
Conventional statistical models assume that the characteristics of each individual are independent from others’—an assumption that is not met in disease transmission networks. In a transmission network, the unit of interest is a transmission link, comprising 2 cases whose attributes may be correlated. Exponential random graph models (ERGMs) are a tool for statistically modeling the propensity of links to form between nodes (cases) in a network, accounting for correlation among attributes of cases. We used ERGMs to express the probability that a transmission link will occur between 2 cases as a function of their demographic and clinical characteristics (Web Appendix 2).
We used infectiousness estimates from the literature to define target statistics for the degree of a case based on their attributes (e.g., smear-negative cases had, on average, 25% fewer edges than smear-positive cases) (12, 22). If there was limited information in the literature for a given attribute, we used data from TRAX to define target statistics. We specified models under each missing-data scenario. Since the mean degree (number of links per case) in the complete network was unknown, we tested each scenario across a range of mean degrees (Web Appendices 2–5, Web Tables 1–7).
To model complete transmission networks, we estimated the total number of diagnosed and undiagnosed XDR TB cases in KwaZulu-Natal during the study period (2011–2014). We used data from the South African Tuberculosis Drug Resistance Survey to estimate the number of diagnosed XDR TB cases and active case-finding studies to estimate the number of additional, undiagnosed cases (23). We assumed a complete transmission network size of 2,000 cases for our primary analyses (Web Appendix 6).
From each scenario, we simulated 1,000 complete transmission networks (Figure 1). ERGMs were constructed using the ergm R package (24, 25). The software code is available at https://github.com/kbratnelson/tb-ergms.
Figure 1.
Modeling approach for assessment of the effect of missing cases on a transmission network inferred from Mycobacterium tuberculosis sequencing data on extensively drug-resistant tuberculosis, KwaZulu-Natal, South Africa, 2011–2014. HIV, human immunodeficiency virus.
Missing-data scenarios
We modeled 4 different scenarios in which information was missing from the empirical network (Table 1). First, we assumed that cases were missing at random (scenario 1). Second, we assumed systematic oversampling of cases involved in either many transmission events (“high transmitters”) or few transmission events (“low transmitters”) (scenario 2). Third, we hypothesized that cases were sampled differentially on the basis of smear status (scenario 3). Smear-negative cases are more difficult to diagnose and may therefore be underrepresented in empirical transmission networks (22). The final scenario modeled an unmeasured factor strongly related to the likelihood of transmission (scenario 4). We modeled this factor in a subset of cases (varying its prevalence from 10% to 40%) with varying strengths (the number of links among cases with this factor ranges from 10–40 times the network mean degree). This tested the hypothesis that an unmeasured characteristic in a minority of cases, representing super-spreading, could explain the structure of the empirical transmission network (Web Appendix 7).
Table 1.
Hypothetical Scenarios for Assessment of the Effect of Missing Cases on a Transmission Network Inferred From Mycobacterium tuberculosis Sequencing Data on Extensively Drug-Resistant Tuberculosis, KwaZulu-Natal, South Africa, 2011–2014
| Scenario | Changes to Complete Transmission Network Model or Sampling Procedures |
|---|---|
| 1. Cases missing at random | No changes to model terms. |
| 2. Cases missing by transmission | No changes to model terms. Sample from complete network nonrandomly using degree to define sampling weights. |
| I. Highly connected cases (“high transmitters”) more likely to be sampled: sampling weighted by degree | |
| II. Poorly connected cases (“low transmitters”) more likely to be sampled: sampling weighted by inverse degree | |
| 3. Cases missing by smear status | No changes to model terms. Increase proportion of smear-positive cases in complete network relative to sampled network. |
| 4. Latent, unmeasured (super-spreading) factor | Add model term corresponding to unmeasured factor strongly related to transmission in a minority of cases. Vary strength and prevalence of factor. |
| I. Unmeasured factor that increases transmission by a factor of 10 (prevalence: 10%) | |
| II. Unmeasured factor that increases transmission by a factor of 20 (prevalence: 10%) | |
| III. Unmeasured factor that increases transmission by a factor of 40 (prevalence: 10%) |
Sampling modeled networks and statistical analysis
From each modeled, complete network, we sampled a similar number of cases (n = 350) as in our empirical network (Web Appendix 8). We aimed to determine which scenario produced sampled networks that most closely matched the degree distribution of the empirical network. To compare the empirical network with the modeled and sampled networks, we compared locations of the quantiles (10%, 25%, 50%, 100%) of the degree distribution (median and interquartile range) and assessed 2-sided P values from a modified Kolmogorov-Smirnov test calculated using bootstrapping techniques (26–28).
Additional sensitivity analyses
Because there is considerable uncertainty about the genomic threshold that should be used to define a direct TB transmission event, we assessed the effect of using a more stringent SNP threshold (3 SNPs). We also tested the sensitivity of our results to assumptions about the size of the complete transmission network (Web Appendix 6).
RESULTS
The empirical genomic network comprised 344 TRAX cases with 1,084 genomic links, or edges. Each case had an average of 6.3 links (the overall network mean degree), and 182 (53%) cases in the network had at least 1 link. The 25th percentile of the degree distribution was located at 0, the 50th percentile (median) at 1, and the 75th percentile at 7 (Web Table 8). The most highly linked case had a degree of 62; 62 (18%) cases had 10 or more links.
The hypothesis that cases were randomly sampled from the complete network was inconsistent with the empirical TRAX network (Figure 2, parts A and D; scenario 1). Models implemented under this scenario with a high mean degree could reproduce the median of the empirical degree distribution (for mean degree 20, the median was 2; Table 2). However, a mean degree greater than 20 in the complete network was required to reproduce the highly connected cases in our transmission study (Table 2; Web Figure 2). P values suggested that none of these models were consistent with the empirical network.
Figure 2.
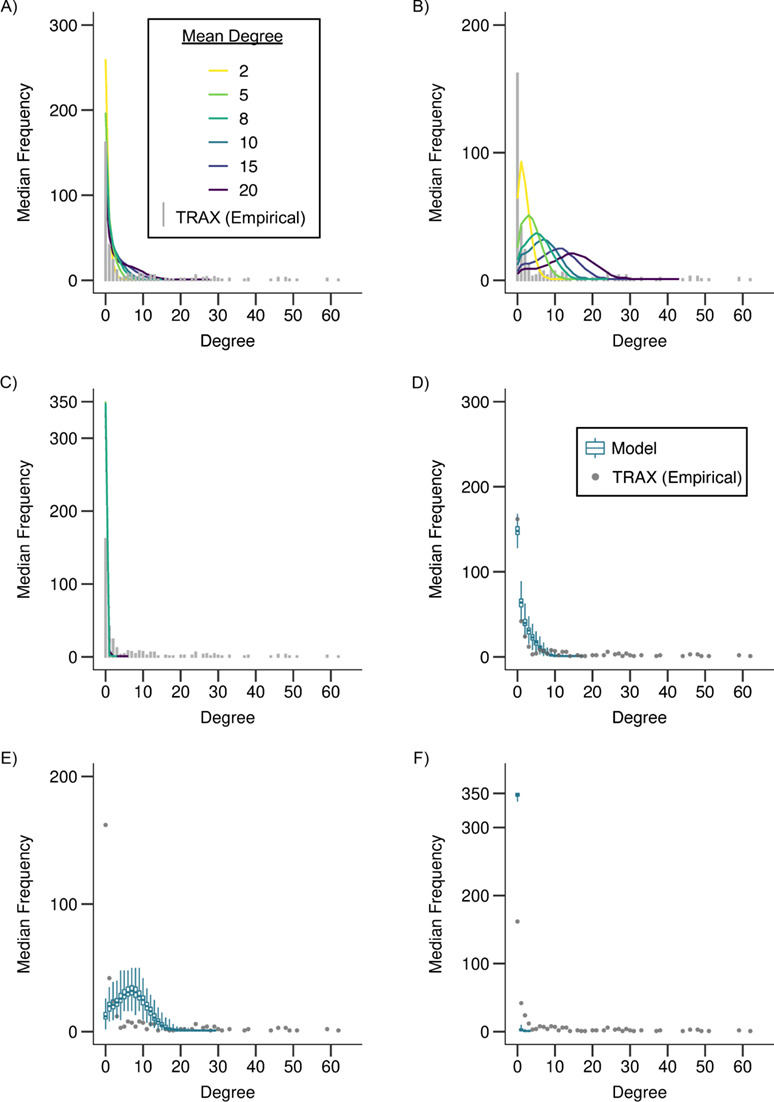
Degree distributions of empirical (≤5 single nucleotide polymorphisms (SNPs)) and modeled, sampled networks under scenario 1 (random sampling (panels A and D)) and scenario 2 (oversampling of high (panels B and E) and low (panels C and F) transmitters) as compared with an empirical network of extensively drug-resistant (XDR) tuberculosis (TB) cases, KwaZulu-Natal, South Africa, 2011–2014. In panels A–C, the gray bars show the distribution of the number of links per case, or the degree distribution, of the empirical network (≤5 SNPs) from the Transmission Study of XDR TB (TRAX Study). Each colored line shows the median degree distribution across 1,000 modeled, sampled networks for the corresponding model. Line color indicates the mean degree, or the average number of transmissions per case, assumed in the complete, modeled network. Panels D–F show the range of the degree distributions of the modeled, sampled networks for 1 model (mean degree = 10). The gray dots show the degree distribution of the empirical network (≤5 SNPs) from the TRAX Study and are equivalent to the distribution shown by the gray bars in panel A. Colored box plots show the median, interquartile range, minimum, and maximum frequencies for each degree in the distribution across 1,000 modeled, sampled networks. See Web Figure 3 for more detail on panel C.
Table 2.
Target Statistics (Median (Interquartile Range)) for Modeled, Sampled Networksa Under Scenarios 1 and 2 As Compared With an Empirical Network of Extensively Drug-Resistant Tuberculosis Cases, KwaZulu-Natal, South Africa, 2011–2014
| Degree and Percentile of Degree Distribution | P Value b | |||||
|---|---|---|---|---|---|---|
| Type of Sampling and Mean Degree | 10th Percentile c | 25th Percentile | Median | 75th Percentile | Maximum | |
| Target statistics for empirical network | ||||||
| 5-SNP threshold | 0 | 0 | 1 | 7 | 62 | |
| 3-SNP thresholdd | 0 | 0 | 0 | 1 | 21 | |
| Random sampling (scenario 1) | ||||||
| 2 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–1) | 4 (4–5) | 0 (0–0) |
| 5 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1.(1–0) | 7 (6–8) | 0 (0–0) |
| 10 | 0 (0–0) | 0 (0,0) | 1 (1–1) | 3 (3–3) | 11 (10–12) | 0 (0–0) |
| 20 | 0 (0–0) | 0 (0–0) | 2 (2–3) | 6 (6–6) | 21 (19–22) | 0 (0–0.00001) |
| Oversampling of high transmitters (scenario 2) | ||||||
| 2 | 0 (0–0) | 1 (1–1) | 2 (2–2) | 3 (3–3) | 9 (8–9) | 0 (0–0) |
| 5 | 1 (1–1) | 2 (2–2) | 4 (3–4) | 6 (5–6) | 13 (12–15) | 0 (0–0) |
| 10 | 2 (1–2) | 4 (4–4) | 7 (7–7) | 10 (9–10) | 20 (19–21) | 0 (0–0) |
| 20 | 4 (4–4) | 9 (8–9) | 14 (13–14) | 18 (18–19) | 32 (30–33) | 0 (0–0) |
| Oversampling of low transmitters (scenario 2) | ||||||
| 2 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–1) | 0 (0–0) |
| 5 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–1) | 0 (0–0) |
| 10 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (0–0) | 0 (0–0) |
| 20 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–0) | 2 (1–2) | 0 (0–0) |
Abbreviation: SNP, single nucleotide polymorphism.
a 1,000 networks were simulated from each model; each modeled network was sampled once.
b P values from a Kolmogorov-Smirnov test with a 2-sided alternative hypothesis, calculated using 1,000 bootstrap samples. P values shown as 0 were less than 2.2e−16.
c Median of the 10th percentile of the degree distribution from 1,000 modeled, sampled networks.
d Note that target statistics for both the 5-SNP and 3-SNP empirical networks are shown. These are independent of the results from the modeled networks under scenarios 1 and 2, which are shown in the body of the table.
Scenarios oversampling high- or low-transmitting cases (scenario 2) significantly changed the structure of modeled networks but did not produce networks fully consistent with the empirical network. If high transmitters were oversampled, the degree distributions of modeled networks were shifted to the right relative to the empirical network (Figure 2, parts B and E; Web Figure 3). The 25th percentile (range, 1–9), median (range, 2–14), and 75th percentile (range, 3–18) were close to those of the empirical network (0, 1, and 7, respectively). However, the maximum degree in modeled networks (range, 9–32) could not reproduce the highly connected cases in the empirical network (degree: 62), and all modeled networks under this scenario were statistically different from the empirical network (Table 2). When we assumed that low transmitters were oversampled, the degree distribution was shifted left relative to the empirical network (Figure 2 parts C and F), but the overall shape of the degree distribution was similar to the empirical network, with its median and mode at 0 (Table 2).
Sampling cases differentially by smear status (scenario 3) yielded few changes in the degree distributions of modeled networks (Table 3; Figure 3, parts A and C). Results from these models were similar to those from scenario 1.
Table 3.
Target Statistics (Median (Interquartile Range)) for Modeled, Sampled Networksa Under Scenarios 3 and 4 As Compared With an Empirical Network of Extensively Drug-Resistant Tuberculosis Cases, KwaZulu-Natal, South Africa, 2011–2014
| Degree and Percentile of Degree Distribution | ||||||
|---|---|---|---|---|---|---|
| Type of Sampling and Mean Degree | 10th Percentile c | 25th Percentile | Median | 75th Percentile | Maximum | P Value b |
| Target statistics for empirical network | ||||||
| 5-SNP threshold | 0 | 0 | 1 | 7 | 62 | |
| 3-SNP threshold | 0 | 0 | 0 | 1 | 22 | |
| Cases sampled preferentially by smear status (scenario 3)d | ||||||
| 50/50 smear−/+ (empirical network: 30/70 smear−/+) | ||||||
| 2 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–1) | 4 (4–5) | 0 (0–0) |
| 5 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–2) | 7 (7–8) | 0 (0–0) |
| 10 | 0 (0–0) | 0 (0–0) | 1 (1–1) | 3 (3–3) | 11 (10–12) | 0 (0–0) |
| 20 | 0 (0–0) | 1 (1–1) | 3 (2–3) | 6 (6–6) | 18 (17–19) | 0 (0–0) |
| 70/30 smear−/+ (empirical network: 30/70 smear−/+) | ||||||
| 2 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–1) | 4 (4–5) | 0 (0–0) |
| 5 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–1) | 7 (6–7) | 0 (0–0) |
| 10 | 0 (0–0) | 0 (0–0) | 1 (1–1) | 2 (2–3) | 11 (10–12) | 0 (0–0) |
| 20 | 0 (0–0) | 0 (0–1) | 2 (2–2) | 5 (5–5) | 19 (18–21) | 0 (0–0) |
| Unmeasured factor (scenario 4) (40×, P = 0.10) | ||||||
| 2 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 0 (0–0) | 7 (6–8) | 0 (0–0) |
| 5 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–1) | 14 (12–15) | 0 (0–0) |
| 8 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–1) | 30 (28–32) | 0 (0–0) |
| 10 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 1 (1–1) | 36 (34–38) | 0 (0–0) |
| 20 | 0 (0–0) | 0 (0–0) | 0 (0–0) | 2 (2–3) | 62 (60–63) | 0 (0–0.002) |
Abbreviations: SNP, single nucleotide polymorphism; TB, tuberculosis; TRAX Study, Transmission Study of XDR TB; XDR, extensively drug-resistant.
a 1,000 networks were simulated from each model; each modeled network was sampled once.
b P values from a Kolmogorov-Smirnov test with a 2-sided alternative hypothesis, calculated using 1,000 bootstrap samples. P values shown as 0 were less than 2.2e-16.
c Median of the 10th percentile of the degree distribution from 1,000 modeled, sampled networks.
d Smear distribution among TRAX cases (in empirical network): 32% smear-negative, 68% smear-positive.
Figure 3.

Degree distributions of empirical (≤5 single nucleotide polymorphisms (SNPs)) and modeled, sampled networks under scenario 3 (sampling biased by smear status (panels A and C)) and scenario 4 (inclusion of an unmeasured “super-spreading” factor (panels B and D)) as compared with an empirical network of extensively drug-resistant (XDR) tuberculosis (TB) cases, KwaZulu-Natal, South Africa, 2011–2014. For all results shown, the models assumed an average mean degree in the complete network of 10. In scenario 4, unmeasured (“super-spreading”) factors are shown at a range of strengths (×10 indicates that super-spreaders are responsible for 10 times more secondary cases than other cases). We assumed that this unmeasured factor had a population prevalence of 0.10. In panels A and B, bars show the distribution of the number of links per case, or the degree distribution, of the empirical network (≤5 SNPs) from the Transmission Study of XDR TB (TRAX Study). Each line shows the median degree distribution across 1,000 modeled, sampled networks for the corresponding model. Line type indicates the distribution of smear status (scenario 3) or the strength and prevalence of the unmeasured factor (scenario 4) assumed in the complete, modeled network. Panels C and D show the range of the degree distributions of the modeled, sampled networks for an individual model. Dots show the degree distribution of the empirical network (≤5 SNPs) from the TRAX Study and are equivalent to the distribution shown by the gray bars in panel A. Box plots show the median, interquartile range, minimum, and maximum frequencies for each degree in the distribution across 1,000 modeled, sampled networks.
In the scenario including a latent factor representing super-spreading that increased transmission risk 40-fold in 10% of cases (scenario 4), we could not reproduce the full empirical degree distribution, in which the 75th percentile was higher (degree: 7) than the modeled networks (range, 0–2); all P values suggested that the degree distributions of the modeled and empirical networks were dissimilar (Figure 3, parts B and D). However, we could reproduce the target statistics for the maximum of the degree distribution (range (7–62) vs. empirical maximum (62)) (Table 3).
When we assumed smaller complete transmission networks (n = 1,500), modeled networks more closely resembled the empirical network, with a higher median degree (range, 0–3) and more highly linked cases (75th percentile: 1–8; maximum: 5–23) than in our primary analysis (Web Figure 4 and Web Table 9). Thus, the empirical network was more consistent with assumptions of fewer XDR TB cases, rather than more, in the complete network.
We assessed the robustness of our results to the SNP threshold used to define a genomic link. Since a threshold of 3 SNPs requires cases’ TB strains to be more closely related to define an edge, the empirical degree distribution is shifted to the left relative to that of the network defined by a 5-SNP threshold (Web Table 10 and Web Figure 5). Under random sampling, the model with a mean degree of 20 (maximum degree: 21) could reproduce the maximum of the empirical 3-SNP network (maximum: 22), but not the median (2 in the modeled network, 0 in the empirical network) (Table 2).
When we accounted for a “super-spreading” factor (scenario 4), modeled networks could indeed reproduce a degree distribution similar to that of the 3-SNP empirical network. At a mean degree of 8, the modeled network closely matched the empirical network, with the median at 0 (empirical network: 0), the 75th percentile at 1 (empirical network: 1), and the maximum at 30 (empirical network: 22). However, the degree distributions were still statistically different (Table 3).
DISCUSSION
In this study, we explored whether partial and nonrandom sampling of TB transmission events may bias inferences we aim to make from transmission networks constructed using incomplete molecular and epidemiologic data. The methodological framework outlined in this study sheds light on the key assumptions required to make inferences from incomplete sampling of TB cases. On the basis of our models, missingness in our transmission study was unlikely to be random; rather, we more likely oversampled low-transmitting cases. Although super-spreading behavior may partially account for the structure of the empirical transmission network, it could not completely explain the transmission heterogeneity we observed. Our results advise caution when interpreting transmission networks measured from incomplete data in TB-endemic settings without a clear understanding of the sampling frame and factors potentially contributing to bias.
The fact that none of our models fully explained the empirical network is unsatisfying but itself informative. It suggests that factors traditionally thought to be among the most important determinants of transmission risk, including the key clinical and demographic characteristics included in our models, do not explain the structure of transmission networks measured in real-world settings and heterogeneity in the number of transmission links attributed to cases. However, our models suggested several potential factors contributing to this mismatch. First, we found that the scenario in which cases were missing completely at random from our transmission study was unlikely based on our models, and that this finding was robust to our choice of SNP threshold to define transmission. Instead, we found that low-transmitting cases were more likely to be sampled than high-transmitting cases. This may be due to preferential inclusion of symptomatic TB cases who present promptly to health-care providers: While these patients rapidly become noninfectious after initiating treatment, cases with mild symptoms may be infectious but relatively healthy and able to maintain their daily routines for an extended period of time, possibly resulting in many transmission events. Indeed, there is mounting epidemiologic and immunological evidence for a period of “subclinical” TB infection; understanding the potential for transmission at this stage of infection may be critical for explaining TB transmission heterogeneity (29–35). This explanation is also consistent with our finding that super-spreading may partially explain the network we observed, if a subclinical disease state accounts for more transmission than previously appreciated. Alternatively, or in addition to the potential role of subclinical disease, important sociobehavioral factors may also drive the transmission heterogeneity that we were unable to explain in our study. For example, the common practice in South Africa of traveling to urban centers for seasonal employment, which could lead to both higher contact rates and a lower likelihood of diagnosis due to lower engagement with the health-care system, could be driving XDR TB transmission in KwaZulu-Natal (36–41).
Our results were sensitive to factors about which there is substantial uncertainty in TB, including key natural history features and the SNP threshold defining a direct transmission event. Our primary models varied the mean degree in the complete network from 2 to 20. This range was selected after considering previous estimates of the effective reproduction number (Rf) of TB, which is not well-characterized (42). Interestingly, the models most consistent with the empirical network had a mean degree of 10 and above, which is substantially higher than previous estimates of Rf. This suggests either that Rf is truly higher in this setting because of a particularly high risk of XDR TB or, more likely, that our definition of a transmission event—5 SNPs—was too lenient (9). When we examined networks defined using a 3-SNP threshold, the empirical network was consistent with a wider range of models than the network based on a 5-SNP threshold. This result emphasizes the challenges of relying on pairwise genomic distances to define transmission events: Conclusions regarding transmission can be different based on the threshold being used.
Lastly, our results were sensitive to assumptions about the total number of XDR TB cases comprising the complete network. Underdiagnosis of TB is a persistent challenge in low-resource settings and is even more difficult for XDR TB, which requires culture-based drug susceptibility testing. In our primary analysis, we assumed that approximately half of all XDR TB cases are diagnosed. We found that larger complete networks were less likely to match the empirical network, suggesting it is unlikely that we greatly underestimated the number of XDR TB cases in KwaZulu-Natal. However, the results from this sensitivity analysis underscore the broader challenge of understanding the true magnitude of TB disease burden in low-resource settings and using this information to accurately model population-level transmission dynamics.
Limitations
We did not distinguish the direction of transmission in modeled or empirical networks to avoid fitting of our models with uncertain parameter data, but this prevented us from being able to distinguish between individual attributes that increased the risk of transmission and those that increased risk of acquisition of infection and progression to TB disease. More sophisticated probabilistic methods to define genomic transmission links between cases that account for directionality are warranted in future analyses (43). Second, ERGMs utilize mixed Poisson distributions (conditional on nodal attributes and other network features) to model the number of edges per node, but there is evidence that this distribution may fail to capture fundamental properties of TB transmission or the phenomenon of super-spreading (18). Although our results could be attributed to the failure of these distributional assumptions to hold, ERGMs are powerful tools precisely because they are formulated with this constraint, as it allows for investigation of the fundamental processes driving transmission network formation. However, our findings on “super-spreading” should be interpreted in light of these limitations.
Conclusions
While a clearer understanding of transmission is critical in settings with a high burden of disease, sparse data pose serious challenges for interpretation of transmission studies. Our analysis suggests that super-spreading behavior and biased sampling may partially explain the observed network. However, we also found that none of our network models could fully explain the observed network, which should motivate further inquiry into what is missing from our current understanding of TB transmission in order to better target interventions aiming to interrupt TB spread in endemic settings. Our conclusions are likely to be generalizable to transmission studies of drug-susceptible TB, but we note that this study of XDR TB may have been especially susceptible to biases resulting from underdiagnosis and survival, given the complexity of diagnostics and poor survival from XDR TB. Future research should focus on identifying host, pathogen, or environmental factors contributing to super-spreading. Transmission studies in high-incidence settings should aim to understand the impact of incomplete and potentially biased sampling and identify key assumptions about missingness on which inferences are based. These efforts will allow more accurate mapping of TB transmission patterns in endemic settings, where the need to design interventions tailored to local epidemics is greatest.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Rollins School of Public Health, Emory University, Atlanta, Georgia (Kristin N. Nelson, Neel R. Gandhi, Benjamin A. Lopman, Sara C. Auld, Salim Allana, Angie Campbell, Samuel M. Jenness); Department of Epidemiology, Mailman School of Public Health, Columbia University, New York, New York (Barun Mathema); School of Medicine, Emory University, Atlanta, Georgia (Neel R. Gandhi, Sara C. Auld); Albert Einstein College of Medicine and Montefiore Medical Center, New York, New York (James C. M. Brust); National Institute for Communicable Diseases, Johannesburg, South Africa (Nazir Ismail, Shaheed Vally Omar); Department of Medical Microbiology, School of Medicine, University of Pretoria, Pretoria, South Africa (Nazir Ismail); Infectious Diseases Division, Massachusetts General Hospital, Boston, Massachusetts (Tyler S. Brown); National Health Laboratory Service, Johannesburg, South Africa (Pravi Moodley, Koleka Mlisana); School of Laboratory Medicine and Medical Sciences, University of KwaZulu-Natal, Durban, South Africa (Pravi Moodley, Koleka Mlisana); and Centers for Disease Control and Prevention, Atlanta, Georgia (N. Sarita Shah).
This study was primarily funded by the National Institute of Allergy and Infectious Diseases, US National Institutes of Health (grants R01AI138783 (Principal Investigator (PI): S.M.J.), R01AI089349 (PI: N.R.G.), R01AI087465 (PI: N.R.G.), and R01AI138646 (PI: N.R.G.)). It was also supported in part by the National Institute of Allergy and Infectious Diseases (grants R01AI114304 (PI: J.C.M.B.), K24AI114444 (PI: N.R.G.), and K23AI134182 (PI: S.C.A.)), the Emory Center for AIDS Research (grant P30AI050409 (PI: James Curran)), the Einstein Center for AIDS Research (grant P30AI124414 (PI: Harris Goldstein)), and the Einstein/Montefiore Institute for Clinical and Translational Research (grant UL1 TR001073 (PI: Harry Shamoon)).
This work was presented at the Seventh International Conference on Infectious Disease Dynamics (Epidemics7), Charleston, South Carolina, December 3–6, 2019.
The findings and conclusions presented in this article are those of the authors and do not necessarily represent the official position of the funding agencies. The funders played no role in study design, data collection and analysis, the decision to publish, or the preparation of the manuscript.
B.A.L. reports receiving personal fees from Takeda Pharmaceutical Company Ltd. (Tokyo, Japan), the CDC Foundation (Atlanta, Georgia), and Hall Booth Smith, P.C. (Atlanta, Georgia) outside of this work. None of the other authors have any conflicts of interest to declare.
REFERENCES
- 1. World Health Organization Global Tuberculosis Report 2018. Geneva, Switzerland: World Health Organization; 2018. [Google Scholar]
- 2. National Institute for Communicable Diseases South African Tuberculosis Drug Resistance Survey 2012–2014. Johannesburg, South Africa: National Institute for Communicable Diseases; 2016. [Google Scholar]
- 3. Lim JR, Gandhi NR, Mthiyane T, et al. Incidence and geographic distribution of extensively drug-resistant tuberculosis in KwaZulu-Natal Province, South Africa. PloS One. 2015;10(7):e0132076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Shisana O, Rehle T, Simbayi LC, et al. South African National HIV Prevalence, Incidence, and Behaviour Survey, 2012. Cape Town, South Africa: HSRC Press; 2014. [Google Scholar]
- 5. Statistics South Africa Census 2011: Census in Brief. Pretoria, South Africa: Statistics South Africa; 2011. [Google Scholar]
- 6. Shah NS, Auld SC, Brust JCM, et al. Transmission of extensively drug-resistant tuberculosis in South Africa. N Engl J Med. 2017;376:243–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Yang C, Luo T, Shen X, et al. Transmission of multidrug-resistant Mycobacterium tuberculosis in Shanghai, China: a retrospective observational study using whole-genome sequencing and epidemiological investigation. Lancet Infect Dis. 2017;17(3):275–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Dowdy DW, Grant AD, Dheda K, et al. Designing and evaluating interventions to halt the transmission of tuberculosis. J Infect Dis. 2017;216(suppl 6):S654–S661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hatherell H-A, Colijn C, Stagg HR, et al. Interpreting whole genome sequencing for investigating tuberculosis transmission: a systematic review. BMC Med. 2016;14: Article 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gardy JL, Johnston JC, Ho Sui SJ, et al. Whole-genome sequencing and social-network analysis of a tuberculosis outbreak. N Engl J Med. 2011;364(8):730–739. [DOI] [PubMed] [Google Scholar]
- 11. Casali N, Broda A, Harris SR, et al. Whole genome sequence analysis of a large isoniazid-resistant tuberculosis outbreak in London: a retrospective observational study. PLoS Med. 2016;13(10):e1002137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Wood R, Middelkoop K, Myer L, et al. Undiagnosed tuberculosis in a community with high HIV prevalence: implications for tuberculosis control. Am J Respir Crit Care Med. 2007;175(1):87–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Shean K, Streicher E, Pieterson E, et al. Drug-associated adverse events and their relationship with outcomes in patients receiving treatment for extensively drug-resistant tuberculosis in South Africa. PloS One. 2013;8(5):e63057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Conradie F, Diacon A, Howell P, et al. Sustained high rate of successful treatment outcomes: interim results of 75 patients in the Nix-TB clinical study of pretomanid, bedaquiline and linezolid Presented at the 49th Union World Conference on Lung Health and Tuberculosis, The Hague, Netherlands, October 24–27, 2018. [Google Scholar]
- 15. Bliss CA, Danforth CM, Dodds PS, et al. Estimation of global network statistics from incomplete data. PloS One. 2014;9(10):e108471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Smith JA, Moody J, Morgan JH. Network sampling coverage II: the effect of non-random missing data on network measurement. Soc Networks. 2017;48:78–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Beck-Sagué C, Dooley SW, Hutton MD, et al. Hospital outbreak of multidrug-resistant Mycobacterium tuberculosis infections: factors in transmission to staff and HIV-infected patients. JAMA. 1992;268(10):1280–1286. [DOI] [PubMed] [Google Scholar]
- 18. Melsew YA, Gambhir M, Cheng AC, et al. The role of super-spreading events in Mycobacterium tuberculosis transmission: evidence from contact tracing. BMC Infect Dis. 2019;19(1):Article 244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. McCreesh N, White RG. An explanation for the low proportion of tuberculosis that results from transmission between household and known social contacts. Sci Rep. 2018;8(1):Article 5382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Nelson KN, Shah NS, Mathema B, et al. Spatial patterns of extensively drug-resistant tuberculosis transmission in KwaZulu-Natal, South Africa. J Infect Dis. 2018;218(12):1964–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Eldholm V, Monteserin J, Rieux A, et al. Four decades of transmission of a multidrug-resistant outbreak strain. Nat Commun. 2015;6: Article 7119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Abu-Raddad LJ, Sabatelli L, Achterberg JT, et al. Epidemiological benefits of more-effective tuberculosis vaccines, drugs, and diagnostics. Proc Natl Acad Sci. 2009;106(33):13980–13985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Ismail NA, Mvusi L, Nanoo A, et al. Prevalence of drug-resistant tuberculosis and imputed burden in South Africa: a national and sub-national cross-sectional survey. Lancet Infect Dis. 2018;18(7):779–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Handcock M, Hunter D, Butts C, et al. ergm: Fit, simulate and diagnose exponential-family models for networks (Version 3.9.4).Vienna, Austria: R Foundation for Statistical Computing; 2018. https://CRAN.R-project.org/package=ergm. Accessed February 20, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Hunter DR, Handcock MS, Butts CT, et al. ergm: A package to fit, simulate and diagnose exponential-family models for networks. J Stat Softw. 2008;24(3):nihpah54860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Hall P, Härdle W, Simar L. On the inconsistency of bootstrap distribution estimators. Comput Stat Data Anal. 1993;16(1):11–18. [Google Scholar]
- 27. Janssen A. Two-sample goodness-of-fit tests when ties are present. J Stat Plan Inference. 1994;39(3):399–424. [Google Scholar]
- 28. Abadie A. Bootstrap tests for distributional treatment effects in instrumental variable models. J Am Stat Assoc. 2002;97(457):284–292. [Google Scholar]
- 29. Dowdy DW, Basu S, Andrews JR. Is passive diagnosis enough? The impact of subclinical disease on diagnostic strategies for tuberculosis. Am J Respir Crit Care Med. 2013;187(5):543–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Bajema KL, Bassett IV, Coleman SM, et al. Subclinical tuberculosis among adults with HIV: clinical features and outcomes in a South African cohort. BMC Infect Dis. 2019;19(1):Article 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Drain PK, Bajema KL, Dowdy D, et al. Incipient and subclinical tuberculosis: a clinical review of early stages and progression of infection. Clin Microbiol Rev. 2018;31(4):e00021–e00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Achkar JM, Jenny-Avital ER. Incipient and subclinical tuberculosis: defining early disease states in the context of host immune response. J Infect Dis. 2011;204(suppl 4):S1179–S1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Mtei L, Matee M, Herfort O, et al. High rates of clinical and subclinical tuberculosis among HIV-infected ambulatory subjects in Tanzania. Clin Infect Dis. 2005;40(10):1500–1507. [DOI] [PubMed] [Google Scholar]
- 34. Oni T, Burke R, Tsekela R, et al. High prevalence of subclinical tuberculosis in HIV-1-infected persons without advanced immunodeficiency: implications for TB screening. Thorax. 2011;66(8):669–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Patterson B, Wood R. Is cough really necessary for TB transmission? Tuberculosis (Edinb). 2019;117:31–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Andrews JR, Morrow C, Wood R. Modeling the role of public transportation in sustaining tuberculosis transmission in South Africa. Am J Epidemiol. 2013;177(6):556–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Nelson KN, Shah NS, Mathema B, et al. Spatial patterns of extensively drug-resistant tuberculosis transmission in KwaZulu-Natal, South Africa. J Infect Dis. 2018;218(12):1964–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Lurie M, Harrison A, Wilkinson D, et al. Circular migration and sexual networking in rural KwaZulu/Natal: implications for the spread of HIV and other sexually transmitted diseases. Health Transit Rev. 1997;7(suppl 3):17–27. [PubMed] [Google Scholar]
- 39. Lurie MN, Williams BG. Migration and health in southern Africa: 100 years and still circulating. Health Psychol Behav Med. 2014;2(1):34–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lurie MN, Williams BG, Zuma K, et al. The impact of migration on HIV-1 transmission in South Africa: a study of migrant and nonmigrant men and their partners. Sex Transm Dis. 2003;30(2):149–156. [DOI] [PubMed] [Google Scholar]
- 41. Stuckler D, Basu S, McKee M, et al. Mining and risk of tuberculosis in sub-Saharan Africa. Am J Public Health. 2011;101(3):524–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Ma Y, Horsburgh CR, White LF, et al. Quantifying TB transmission: a systematic review of reproduction number and serial interval estimates for tuberculosis. Epidemiol Infect. 2018;146(12):1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Stimson J, Gardy JL, Mathema B, et al. Beyond the SNP threshold: identifying outbreak clusters using inferred transmissions. Mol Biol Evol. 2019;36(3):587–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


