Abstract
The world is in the midst of a pandemic caused by a novel coronavirus and is desperately searching for possible treatments. The antiviral remdesivir has shown some effectiveness against SARS-CoV-2 in vitro and in a recent animal study. We use data from a study of remdesivir in rhesus macaques to fit a viral kinetics model in an effort to determine the most appropriate mathematical descripton of the effect of remdesivir. We find statistically significant differences in the viral decay rate and use this to inform a possible mathematical formulation of the effect of remdesivir. Unfortunately, this model formulation suggests that the application of remdesivir will lengthen SARS-CoV-2 infections, putting into question its potential clinical benefit.
Keywords: COVID-19, Coronavirus, Antiviral, Treatment, Mathematical model
1. Introduction
A novel coronavirus, (SARS-CoV-2) has recently begun transmitting at a rapid pace around the world (Lippi et al., 2020). While many patients experience mild symptoms, the virus can lead to severe pneumonia and death (Goyal et al., 2020; Jiang et al., 2020). The rapid emergence of this virus has led to an urgent need to quickly find treatments that can improve patient outcomes for those who are severely ill (Martinez, 2020; Dhama et al., 2020).
Several broad spectrum antivirals are being investigated for treatment of SARS-CoV-2 (Yao et al., 2020; Elfiky, 2020; Du and Chen, 2019; Favalli et al., 2020), but one of the most promising to date is remdesivir (Ko et al., 2020), which was recently given emergency use authorization for treatment of SARS-CoV-2 by the FDA (Eastman et al., 2020). Remdesivir (GS-5734) was first developed as a possible treatment for Ebola (Warren et al., 2016), but was soon found to have broad antiviral effects on a number of different virus families (Lo et al., 2017), including coronaviruses (Sheahan et al., 2017; Brown et al., 2019; Parang et al., 2020). The mechanism of action of remdesivir in coronaviruses is interference with RNA-dependent RNA polymerase (RdRp) (Gordon et al., 2020a), specifically nsp12 polymerase in murine hepatitis virus (Agostini et al., 2018), nsp8 and nsp12 in Middle East Respiratory Syndrome virus (Gordon et al., 2020b), and nsp7 in the novel SARS-CoV-2 (Yin et al., 2020). The drug has shown some efficacy against SARS-CoV-2 in vitro (Choy et al., 2020; Wang et al., 2019; Pruijssers et al., 1101), as well as in animal studies (Williamson et al., 2020). There is some evidence of clinical benefit in patients (Holshue et al., 2020; Grein et al., 2020; Durante-Mangoni et al., 2020; Hillaker et al., 2020), although some adverse events have been noted (Durante-Mangoni et al., 2020). A number of clinical trials are underway (Eastman et al., 2020; chen Cao et al., 1016). One small observational study found clinical improvement of 68% of remdesivir-treated patients (Grein et al., 2020). Unfortunately, one completed clinical trial showed little benefit of remdesivir treatment in severely ill COVID patients, with an increase in adverse events (Wang et al., 2020), so there is still uncertainty about the benefit of remdesivir.
While in vitro, pre-clinical, and clinical studies are needed to definitively determine the effectiveness of remdesivir in treating COVID-19, mathematical modeling and computer simulations can help provide additional insight into how remdesivir interacts with the SARS-CoV-2 virus (Elfiky, 2020; Shannon et al., 2020; Zhang et al., 2020; Khan et al., 2020) and how that alters the viral kinetics (Goyal et al., 2020; Goyal et al., 2020). Mathematical modeling has been used to give guidance on timing of treatment of SARS-CoV-2 with other drugs (Gonçalves et al., 2020; Kim et al., 2020; Abuin et al., 2020; Chatterjee and Basir, 2020). Viral kinetics modeling has also previously been used to study treatment of other acute infectious diseases such as influenza (Dobrovolny et al., 2011; Melville et al., 2018; de Mello et al., 2018a), respiratory syncytial virus (RSV) (González-Parra and Dobrovolny, 2018), Ebola (Madelain et al., 2018), and Zika (de Mello et al., 2018b). This modeling has helped elucidate antiviral mechanisms (González-Parra and Dobrovolny, 2018; Cao and McCaw, 2015), quantify antiviral efficacy (Koizumi et al., 2017; Beggs and Dobrovolny, 2015), and investigate treatment timing (Gonçalves et al., 2020; Zhang et al., 2015), so this methodology might prove useful in helping develop tools to fight this pandemic. Two recent studies have used mathematical models to help explain why remdesivir seems to have different effects on nasal and lung titers (Goyal et al., 2020) and to assess the effect of different treatment timings on viral time course (Goyal et al., 2020).
In this paper, we use data from rhesus macaques infected with SARS-CoV-2 and treated with remdesivir to fit a viral kinetics model and determine the effect of remdesivir on the viral time course of SARS-CoV-2. We then used our results to investigate potential mathematical models for the effect of remdesivir. Our analysis finds that the only statistically significant difference between treated and control groups is slower viral decay caused by slower infected cell death in the remdesivir-treated group. This leads to a mathematical model of drug effect that predicts longer infection durations with remdesivir treatment.
2. Material and methods
2.1. Mathematical models
We use two models to help characterize the infection in untreated macaques as well as macaques treated with remdesivir. The first model is an empirical description of the viral time course, first presented in (Holder and Beauchemin, 2011). This model allows us to quantify different aspects of the viral titer curve although it does not provide any insight into the biological processes that might be affected by application of antiviral treatment. The model is given by the equation
| (1) |
where and are the exponential growth and decay rates, respectively; is the peak viral titer; and is the time of viral titer peak.
The second model we will use is a viral kinetics model consisting of ordinary differential equations (ODE). This model was originally used to describe influenza virus infections (Baccam et al., 2006),
| (2) |
In the model, target cells, T, become infected, I, at rate β when they encounter virus, V. Infected cells produce virus at rate p and die at rate δ. Virus loses infectivity at a rate c. We have chosen not to include eclipse cells, which are cells that have been infected but are not yet producing virus, since the duration of the eclipse phase cannot be uniquely identified from viral titer measurements alone (Smith et al., 2010).
In addition to estimating model parameters through fitting of the model to data, we examine two additional quantities derived from model parameters. The basic reproduction number,
represents the number of secondary infections caused by a single infected cell in a fully susceptible population. The infecting time,
Represents the average time between the virus being released from one cell and infecting the next.
2.2. Experimental data
Experimental data is taken from Williamson et al. (Williamson et al., 2020) who performed a study of the effectiveness of remdesivir treatment of SARS-CoV-2 in rhesus macaques. Briefly, 12 rhesus macaques were inoculated with a total dose of 2.6 of the nCoV-WA1-2020 strain of SARS-CoV-2 via intranasal, oral, ocular and intratracheal routes. Nasal swabs were taken daily for seven days. 6 of the animals were treated with remdesivir initiated at 12 h post infection. These animals were given a loading dose of 10 mg/kg of remdesivir, followed by a daily maintenance dose of 5 mg/kg. The other six animals served as infected controls and were given an equal dose volume of a placebo solution on the same schedule. Two animals, one from each treatment group, were excluded from this study since we could not get accurate estimates for the decay rate of the viral load. We extracted the nasal swab data from Fig. 3A of (Williamson et al., 2020) using WebPlotDigitizer.
Fig. 3.
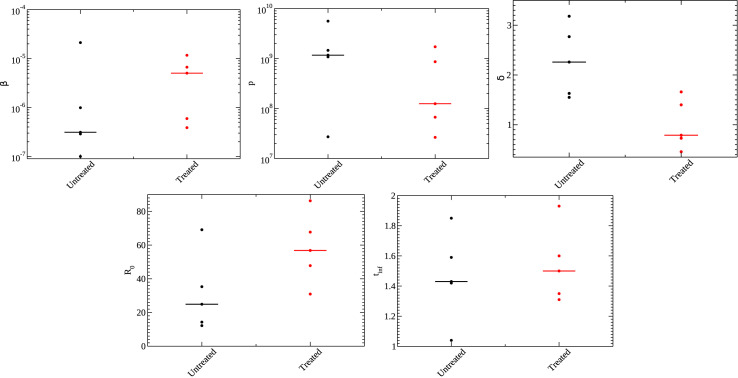
Parameters for the ODE model for untreated (black) and treated (red) animals. Shown are the infection rate (top right), production rate (top center), infected cell death rate (top right), (bottom right), and infecting time (bottom left). Median values are indicated by the line.
2.3. Data fitting
The models were fit to data by minimizing the sum of squared residuals (SSR),
| (3) |
where n is the number of experimental data points, are the values of the experimental data points, and are the model predictions at the times when experimental data were measured. A small SSR indicates a tight fit of the model to the experimental data. We used the nelder_mead_min algorithm in Octave to find the minimum SSR. We fixed the initial number of target cells to 1, meaning that cells are measured relative to the total number of cells. The initial amount of virus is also set to 1 copies/mL. While the macaques were given an initial inoculum of 2.6 , nasal swab measurement on day 0 returned values below the level of detection and was set to 1 copies/mL. We further set , as in (Gonçalves et al., 2020), since δ and c cannot be differentiated using viral titer data alone (Smith et al., 2010). To estimate the 95% confidence intervals for parameters, we perform 1000 bootstrapping replicates using the residuals from the best fit to generate new data sets, as described in (Efron and Tibshirani, 1986).
2.4. Statistical analysis
The goal of this study is to determine how remdesivir affects the viral kinetics of SARS-CoV-2. In order to identify statistically significant differences in parameter values between treated and untreated groups, we performed a Mann-Whitney (Wilcoxon rank-sum) test. We use the Mann-Whitney test since we cannot assume normal distributions for the parameters as is required for other statistical tests. When distributions are continuous, as they are in our case, the Mann-Whitney test can be interpreted as determining whether there is a significant difference in the medians of the two distributions. We consider p values less than 0.05 to be statistically significant.
3. Results
3.1. Effect of remdesivir on viral kinetics
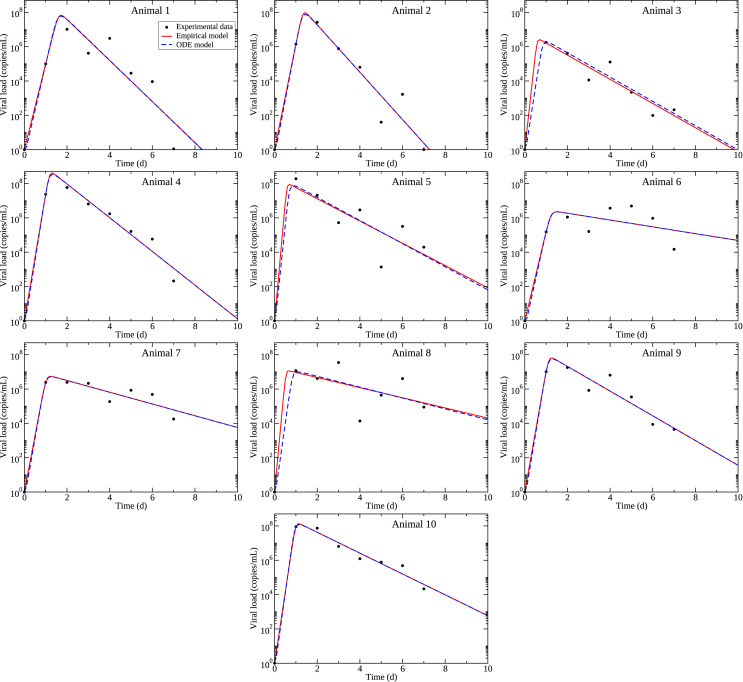
The experimental data, along with model fits to the data are shown in Fig. 1 . The best fit parameters are given in Table 1 for the empirical model and Table 2 for the viral kinetics model. Comparisons of the estimated parameter values for treated and control animals are shown in Fig. 2 for the empirical model, and in Fig. 3 for the viral kinetics model. Parameter correlation and distribution plots derived from bootstrapping are included in the supplemental material. While parameter distributions generally have a well-defined maximum, the parameter correlation plots show correlation among some of the parameters. In particular, for the empirical model, the time of peak and the growth rate are correlated in many animals and show an over-arching correlation when all animal bootstrapping results are plotted together (Fig. S11). For the viral kinetics model, we see correlations amongst all parameters that become more apparent when all animals are plotted together (Fig. S22). These correlations indicate that the parameters might not be uniquely identifiable.
Fig. 1.
Model fits to experimental data from (Williamson et al., 2020). Experimental data is indicated by the circles, empirical model best fits are given by the solid red lines, and viral kinetics (ODE) model best fits and given by dashed blue lines. Animals 1–5 are untreated; animals 6–10 are treated.
Table 1.
Best fit parameter estimates for the empirical model.
| Untreated animals | |||||
|---|---|---|---|---|---|
| Parameter | Animal 1 | Animal 2 | Animal 3 | Animal 4 | Animal 5 |
| (copies/mL) | |||||
| 95% confidence interval | |||||
| (d) | 1.61 | 1.33 | 0.578 | 1.19 | 0.582 |
| 95% confidence interval | 1.23–2.30 | 1.07–1.68 | 0.374–1.14 | 1.06–1.31 | 0.190–1.02 |
| (/d) | 11.5 | 14.2 | 25.9 | 17.0 | 31.8 |
| 95% confidence interval | 7.13–16.13 | 10.3–18.2 | 12.3–39.9 | 14.9–19.3 | 19.0–94.2 |
| (/d) | 2.75 | 3.18 | 1.62 | 2.26 | 1.49 |
| 95% confidence interval | 1.97–3.78 | 2.50–3.90 | 1.28–2.07 | 1.92–2.62 | 0.807–2.15 |
| SSR | 6.58 | 4.76 | 2.19 | 1.22 | 6.55 |
| 95% confidence interval | 0.718–6.60 | 0.0700–6.18 | 0.256–2.85 | 0.0710–1.55 | 0.364–9.07 |
| Treated animals | |||||
| Animal 6 | Animal 7 | Animal 8 | Animal 9 | Animal 10 | |
| (copies/mL) | |||||
| 95% confidence interval | |||||
| (d) | 1.23 | 1.04 | 0.533 | 1.13 | 0.999 |
| 95% confidence interval | 0.460–1.63 | 0.493–1.19 | 0.110–1.19 | 0.573–1.31 | 0.563–1.10 |
| (/d) | 12.0 | 15.1 | 30.7 | 16.2 | 19.0 |
| 95% confidence interval | 8.03–30.8 | 13.1–31.5 | 13.2–166 | 13.9–30.5 | 17.3–34.0 |
| (/d) | 0.457 | 0.789 | 0.680 | 1.66 | 1.40 |
| 95% confidence interval | 0.0128–1.08 | 0.479–1.13 | 0.0772–1.41 | 1.25–2.09 | 1.19–1.62 |
| SSR | 3.78 | 1.15 | 6.43 | 1.72 | 0.520 |
| 95% confidence interval | 0.423–4.71 | 0.144–1.20 | 0.506–9.55 | 0.123–1.91 | 0.0579–0.564 |
Table 2.
Best fit parameter estimates for the ODE model.
| Untreated animals | ||||||
|---|---|---|---|---|---|---|
| Parameter | Animal 1 | Animal 2 | Animal 3 | Animal 4 | Animal 5 | |
| β ((copies/mL)-1(d)-1) | ||||||
| 95% confidence interval | ||||||
| p (copies/mL(d)-1) | ||||||
| 95% confidence interval | ||||||
| δ (/d) | 2.77 | 3.18 | 1.63 | 2.26 | 1.55 | |
| 95% confidence interval | 1.92–3.81 | 2.49–3.89 | 1.39–1.98 | 1.92–2.61 | 1.16–2.16 | |
| 12.2 | 14.3 | 35.3 | 24.9 | 69.1 | ||
| 95% confidence interval | 6.77–19.8 | 9.92–21.4 | 3.19–466 | 20.7–31.0 | 2.52–631 | |
| (h) | 1.85 | 1.59 | 1.42 | 1.43 | 1.04 | |
| 95% confidence interval | 1.54–2.27 | 1.34–1.90 | 0.389–4.51 | 1.32–1.54 | 0.353–5.08 | |
| SSR | 6.56 | 4.76 | 2.19 | 1.22 | 6.59 | |
| 95% confidence interval |
1.10–7.85 |
0.159–6.76 |
0.530–3.19 |
0.107–1.66 |
0.766–10.4 |
|
| Treated animals | ||||||
| Animal 6 | Animal 7 | Animal 8 | Animal 9 | Animal 10 | ||
| β ((copies/mL)-1(d)-1) | ||||||
| 95% confidence interval | ||||||
| p (copies/mL(d)-1) | ||||||
| 95% confidence interval | ||||||
| δ (/d) | 0.457 | 0.789 | 0.729 | 1.66 | 1.40 | |
| 95% confidence interval | 0.0679–1.10 | 0.480–1.16 | 0.358–1.36 | 1.25–2.07 | 1.21–1.66 | |
| 67.7 | 56.8 | 86.3 | 30.94 | 47.8 | ||
| 95% confidence interval | 27.3–1230 | 36.6–533 | 2.69–116 | 23.4–570 | 36.8–494 | |
| (h) | 1.93 | 1.60 | 1.35 | 1.50 | 1.31 | |
| 95% confidence interval | 0.00316–2.25 | 0.0180–1.75 | 0.400–6.16 | 0.397–1.67 | 0.0132–1.43 | |
| SSR | 3.78 | 1.15 | 6.51 | 1.72 | 0.520 | |
| 95% confidence interval | 0.741–4.56 | 0.193–1.35 | 0.981–10.6 | 0.194–2.30 | 0.0910–0.673 | |
Fig. 2.
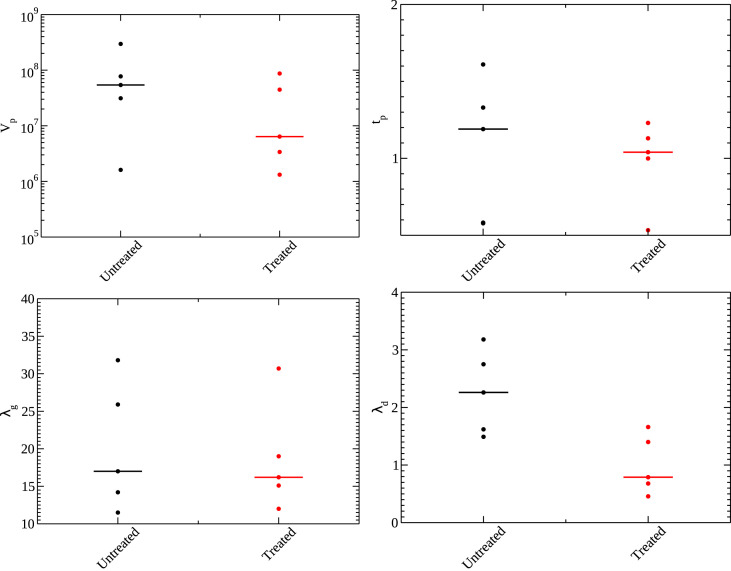
Parameters for the empirical model for untreated (black) and treated (red) animals. Shown are the viral peak (top left), time of peak (top right), growth rate (bottom left), and decay rate (bottom right). Median values are indicated by the line.
For the empirical model, we find that the peak viral load () is slightly lower for treated animals than for untreated animals, although the difference is not statistically significant (). There also appears to be a slight decrease in the time of viral peak for treated animals, but this is also not statistically significant (). There is little change in the growth rate between the two groups (), so the shorter time to viral peak is caused by the lower peak viral load of the treated group. The one statistically significant difference () we see between the groups is a difference in decay rates. Oddly, our results indicate a lower decay rate for the treated group meaning that the virus tends to linger for a longer period of time in treated animals than in untreated animals.
For the viral kinetics model, we see an increase in the infection rate in the treated animals, although this is not statistically significant (). We also see a decrease in the production rate, although this is also not statistically significant (). Interestingly, the increase in the infection rate is roughly the same as the decrease in the production rate such that the infecting time remains largely the same between the two groups (). The basic reproduction number, , increases for the treated group, although this is not statistically significant (). This difference is caused by the statistically significant () difference in infected cell death rates between the two groups. Here, we again find that the death rate is lower in treated animals, consistent with the decreased viral decay rate found for the empirical model, but suggesting that infected cells live longer in treated animals than in untreated animals.
3.2. Mathematical modeling of remdesivir
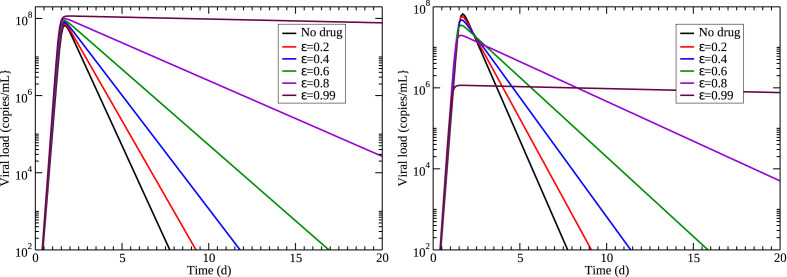
The effect of a drug is added to viral kinetics models through the use of drug efficacy, ε, which is a number between 0 and 1 that represents the reduction in the value of particular parameter due to the drug. For example, the effect of oseltamivir on influenza infections is modeled by multiplying production rate by ) (Dobrovolny et al., 2011; Baccam et al., 2006; HandelI et al., 2007; Palmer et al., 2017) so that a 100% effective drug () yields no viral production. Our analysis of the application of remdesivir in rhesus macaques indicates that remdesivir decreases the infected cell death rate, which suggests that we apply the drug effect to δ. Fig. 4 (left) shows the predicted results of this assumption on viral load when different drug efficacies are applied to the model. We see that the peak viral load rises slightly as the drug efficacy increases, contrary to the findings of the previous section. The viral load also decays more slowly, consistent with the results of the previous section. This, however, seems like an ineffective drug — as more drug is applied (efficacy increases), the infection lasts longer.
Fig. 4.
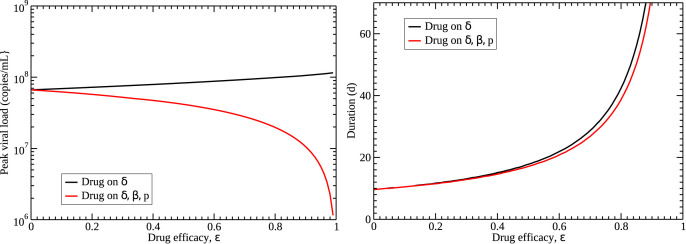
Predicted effect of a drug that only decreases infected cell death rate (left) or a drug that decreases infected cell death rate, increases infection rate, and decreases production rate (right). Median values of estimated parameters for the control group were used for the simulation.
An alternative possibility, suggested by our analysis of the previous section, is that remdesivir might have effects on multiple parameters. While not statistically significant, remdesivir appears to increase the infection rate and decrease the production rate. For simplicity, we assume that a particular dose of drug affects all three parameters equally, i.e. they are all changed by the same amount. In the case of the infection rate, we divide β by since we want the infection rate to increase as drug is applied. The effect of this assumption on viral load when different amounts of drug are applied is shown in Fig. 4 (right). In this case, increasing the amount of drug decreases the viral peak, consistent with results from the previous section. There is still a decrease in the decay rate of the viral titer with application of the drug.
The differences in predictions between the two drug models are shown in Fig. 5 . The starkest difference is in how drug affects the viral peak, where one model assumption has the peak increasing as drug effect increases, while the other has viral peak decreasing as drug effect increases. The latter assumption is consistent with the decrease in viral peak noted in rhesus macaques. Unfortunately, both models predict that duration of the infection (defined as the time the viral titer is above the detection threshold of 100 copies/mL) will increase with application of drug. While the model where drug affects all three parameters predicts a slightly lower duration, both models are not suggestive of a clinically beneficial drug.
Fig. 5.
Predicted effects of different drug models on features of the viral titer. (left) Viral peak increases slightly if the drug affects only the cell death rate (black), while it decreases if it affects cell death rate, infection rate, and production rate (red). (right) Duration of the infection is similar for both drug models, although a drug that affects three parameters has a slightly lower duration. Median values of estimated parameters for the control group were used for the simulation.
Another possibility is that the effect of remdesivir is modeled best by changing a parameter that is not included in our simple model. Infectious disease models typically include an eclipse phase after the virus has entered the cell, but before it starts actively producing virus. A previous study examining possible mathematical models for the effect of an RSV fusion inhibitor showed that modeling a drug by lengthening of the eclipse phase decreases the decay rate of virus (González-Parra and Dobrovolny, 2018). We explore this possibility by adding the eclipse phase into the viral kinetics model,
| (4) |
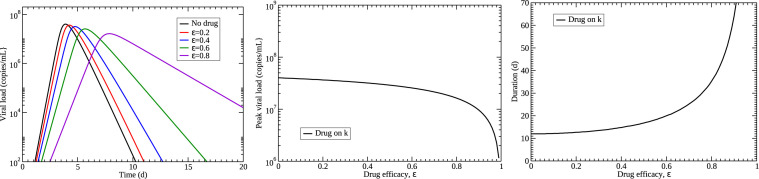
where E denotes cells in the eclipse phase and a new parameter k is the transition rate from eclipse to infectious. We set from the median value of k used in (Gonçalves et al., 2020). We model the effect of remdesivir as lengthening the eclipse duration, so we multiply k by . Results of this assumption are shown in Fig. 6 . The predicted viral titer curves give the expected decrease in viral decay rate as well as a decreasing peak viral load as the amount of drug increases. Unfortunately, the time of viral peak is also delayed with increasing amount of drug, an effect not observed in our analysis.
Fig. 6.
Predicted effects of a drug lengthening the eclipse phase. (left) The time course of viral load for different drug efficacies. (center) Viral peak decreases with increasing drug effect. (right) Duration of the infection increases with increasing drug effect. Median values of estimated parameters for the control group were used for the simulation and k was set to 3/d.
4. Discussion
In this paper, we analyzed remdesivir treatment of rhesus macaques using an empirical description of the viral titer curve as well as a viral kinetics model. We found a decrease in peak viral load, a decrease in time of peak, an increase in infection rate, and a decrease in production rate in remdesivir-treated macaques as compared to control, although none of these were statistically significant. We found two statistically significant differences: the empirical model indicated that the viral curves of remdesivir-treated macaques decayed more slowly than the control group, which was consistent with the viral kinetics model finding that infected cell death rate was lower in remdesivir-treated macaques than in control. This is not consistent with results of a clinical trial that show similar viral decay rates in remdesivir-treated and untreated human patients (Wang et al., 2020). However, another mathematical modeling analysis noted that remdesivir potency was lower in the nasal passages than in the lungs and that this leads to increased viral titer in the nasal passages (Goyal et al., 2020).
It should be noted that since we did not include an eclipse phase, and we fixed the viral decay rate, the only parameter in the viral kinetics model that could capture the decreased viral decay rate is cell death rate (Smith et al., 2010). Nonetheless, we used this result to explore a viral kinetics model that decreased the infected cell death rate, finding that it predicted both an increase in the peak viral load and lengthening of the duration of the infection. The increased peak viral load was inconsistent with our own analysis of remdesivir-treated macaques, as well as in vitro studies that show a decrease in the viral load (Choy et al., 2020; Wang et al., 2019; Pruijssers et al., 1101), although not necessarily measured at the peak. A mathematical model that incorporated a drug effect on infection rate and production rate, as well as cell death rate, fixed the problem of increasing viral load with application of drug, although it still predicted longer infections with application of drug. We explored the possibility of a drug that lengthens the eclipse phase, a parameter not originally included in the model, and found that it could capture the decreased decay rate as well as the decrease in viral peak. Unfortunately, this drug model suggested that remdesivir should also delay the time of peak, an effect we did not observe.
The mechanism of action of remdesivir can help in the formulation of appropriate mathematical models. Remdesivir interferes with replication of viral RNA (Gordon et al., 2020a; Yin et al., 2020). The virus originally enters the cell unimpeded, suggesting no change in the viral infection rate, but blocking viral RNA will impede production, so this is mechanistically the parameter that one would choose to apply the drug effect, and this is how other remdesivir modeling studies have modeled the effect of the drug (Goyal et al., 2020; Goyal et al., 2020). This is the parameter typically used to model the effect of oseltamivir in influenza (Dobrovolny et al., 2011; Baccam et al., 2006; HandelI et al., 2007; Palmer et al., 2017), so we know that this model predicts a decrease in the peak viral load and a lengthening of the infection duration as the time of peak is moved further out (Dobrovolny et al., 2011). It does not, however, change the viral decay rate. By hindering RNA replication, remdesivir could also be modeled by delaying the transition from the eclipse to the infectious phase. Applying the drug effect to the transition rate between phases does lead to a decrease in the decay rate as well as a slight decrease in viral peak, so this seems to be the most likely candidate for mathematically modeling the effect of remdesivir. It is also possible to construct even more detailed mathematical models that include intracellular processes (Zitzmann et al., 2020; Heldt et al., 2013) in order to apply the drug effect in a manner that more closely reflects the biological reality. Unfortunately, in order to properly parameterize a model that includes all these extra details, we need more than just viral titer measurements (Heldt et al., 2013; Miao et al., 2011), so it is not possible to test such models with the current data set.
We can compare the parameter values found here with other estimates of these parameters for SARS-CoV-2. There are two studies that have used modeling to estimate viral kinetics parameters in humans (Gonçalves et al., 2020; Kim et al., 2020; Hernandez-Vargas and Velasco-Hernandez, 2020). While it is impossible to compare any parameters that include viral units since they are not standardized, we can compare dimensionless parameters () and parameters that assess time scales ( ). Hernandez-Vargas et al. found values in human SARS-CoV-2 infections from 2–11, Goncalves et al. found values of 8–27, and Kim et al. found for humans, which are all somewhat lower than the 12–69 found for our untreated group. The infecting time estimated for humans (16–60 h) is much larger than the infecting time found here for untreated macaques (1.0–2.0 h). Hernandez-Vargas et al. also found viral growth and decay rates where possible, finding growth rates of 3.16/d and 5.01/d for the two patients that had growth data available. These are both quite a bit smaller than our estimates that range between 11 and 32/d. The decay rates they found ranged from 0.39/d to 2.51/d; this trends lower than the 1.5/d–3.2/d found here for the untreated group, although there is some overlap. Some of the differences found in viral kinetics could be due to differences in how the virus affects different species, but both studies are based on small numbers, so we cannot yet definitively draw that conclusion. Some of the estimated differences, however, are large enough that there should be caution in extrapolating results from this animal model to humans.
This study was largely limited by the data available for parameterizing the model. Viral titer measurements alone are not sufficient to uniquely determine the parameters of even our simple viral kinetics model (Smith et al., 2010; Miao et al., 2011). This means that we are not able to assess differences between treated and untreated groups for all the parameters — in this study we fixed the viral decay rate (c), so could not look for possible differences in viral decay rate. It also means that we cannot extend our model to include an eclipse phase and test a possible mathematical formulation of the effect of remdesivir that affects the transition rate from eclipse to infected. The number of animals used in the study is small, which means there is low power to detect statistically significant differences. We noted differences in the infection rate and the production rate between treated and control animals, but they were not statistically significant.
CRediT authorship contribution statement
Hana M. Dobrovolny: Data curation, Formal analysis, Conceptualization, Visualization, Writing - original draft.
Declaration of competing interest
The authors whose names are listed immediately below certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.virol.2020.07.015.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
Multimedia component 1
References
- Abuin P., Anderson A., Ferramosca A., Hernandez-Vargas E.A., Gonzalez A.H. arXiv; 2020. Characterization of SARS-CoV-2 Dynamics in the Host. 08447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agostini M.L., Andres E.L., Sims A.C., Graham R.L., Sheahan T.P., Lu X., Smith E.C., Case J.B., Feng J.Y., Jordan R., Ray A.S., Cihlar T., Siegel D., Mackman R.L., Clarke M.O., Baric R.S., Denison M.R. Coronavirus susceptibility to the antiviral remdesivir (GS-5734) is mediated by the viral polymerase and the proofreading exoribonuclease. mBio. 2018;9(2) doi: 10.1128/mBio.00221-18. e00221–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baccam P., Beauchemin C., Macken C.A., Hayden F.G., Perelson A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006;80(15):7590–7599. doi: 10.1128/JVI.01623-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beggs N.F., Dobrovolny H.M. Determining drug efficacy parameters for mathematical models of influenza. J. Biol. Dynam. 2015;9(S1):332–346. doi: 10.1080/17513758.2015.1052764. [DOI] [PubMed] [Google Scholar]
- Brown A.J., Won J.J., Graham R.L., Dinnon K.H., Sims A.C., Feng J.Y., Cihlar T., Denison M.R., Baric R.S., Sheahan T.P. Broad spectrum antiviral remdesivir inhibits human endemic and zoonotic deltacoronaviruses with a highly divergent RNA dependent RNA polymerase. Antivir. Res. 2019;169 doi: 10.1016/j.antiviral.2019.104541. UNSP 104541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao P., McCaw J.M. The mechanisms for within-host influenza virus control affect model-based assessment and prediction of antiviral treatment. Viruses - Basel. 2015;9(8):197. doi: 10.3390/v9080197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Y. chen Cao, Q. xin Deng, S. xue Dai, Remdesivir for severe acute respiratory syndrome coronavirus 2 causing COVID-19: an evaluation of the evidence, Trav. Med. Infect. Dis.doi:10.1016/j.tmaid.2020.101647. [DOI] [PMC free article] [PubMed]
- Chatterjee A.N., Basir F.A. A model for 2019-nCoV infection with treatment. medRxiv. 2020 doi: 10.1101/2020.04.24.20077958. [DOI] [Google Scholar]
- Choy K.-T., Wong A.Y.-L., Kaewpreedee P., Sia S.F., Chen D., Hui K.P.Y., Chu D.K.W., Chan M.C.W., Cheung P.P.-H., Huang X., Peiris M., Yen H.-L. Remdesivir, lopinavir, emetine, and homoharringtonine inhibit SARS-CoV-2 replication in vitro. Antivir. Res. 2020;178:104786. doi: 10.1016/j.antiviral.2020.104786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Mello C.P., Drusano G.L., Adams J.R., Shudt M., Kulawy R., Brown A.N. Oseltamivir-zanamivir combination therapy suppresses drug-resistant H1N1 influenza A viruses in the hollow fiber infection model (HFIM) system. Eur. J. Pharmaceut. Sci. 2018;111:443–449. doi: 10.1016/j.ejps.2017.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Mello C.P., Tao X., Kim T.H., Vicchiarelli M., Bulitta J.B., Kaushik A., Brown A.N. Clinical regimens of favipiravir inhibit zika virus replication in the hollow-fiber infection model. Antimicrob. Agents Chemother. 2018;62(9) doi: 10.1128/AAC.00967-18. e00967–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhama K., Sharun K., Tiwari R., Dadar M., Malik Y.S., Singh K.P., Chaicumpa W. COVID-19, an emerging coronavirus infection: advances and prospects in designing and developing vaccines, immunotherapeutics, and therapeutics. Hum. Vaccines Immunother. 2020;16(6):1232–1238. doi: 10.1080/21645515.2020.1735227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrovolny H.M., Gieschke R., Davies B.E., Jumbe N.L., Beauchemin C.A.A. Neuraminidase inhibitors for treatment of human and avian strain influenza: a comparative study. J. Theor. Biol. 2011;269(1):234–244. doi: 10.1016/j.jtbi.2010.10.017. [DOI] [PubMed] [Google Scholar]
- Y.-X. Du, X.-P. Chen, Favipiravir: pharmacokinetics and concerns about clinical trials for 2019-nCov infection, Clin. Pharmacol. Therapeut.doi:10.1002/cpt.1844. [DOI] [PubMed]
- Durante-Mangoni E., Andini R., Bertolino L., Mele F., Florio L.L., Murino P., Corcione A., Zampino R. Early experience with remdesivir in SARS-CoV-2 pneumonia. Infection. 2020 doi: 10.1007/s15010-020-01448-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eastman R.T., Roth J.S., Brimacombe K.R., Simeonov A., Shen M., Patnaik S., Hall M.D. Remdesivir: a review of its discovery and development leading to emergency use authorization for treatment of COVID-19. ACS Cent. Sci. 2020;6(5):672–683. doi: 10.1021/acscentsci.0c00489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B., Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986;1(1):54–75. [Google Scholar]
- Elfiky A.A. Anti-HCV, nucleotide inhibitors, repurposing against COVID-19. Life Sci. 2020;248:117477. doi: 10.1016/j.lfs.2020.117477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Favalli E.G., Biggioggero M., Maioli G., Caporali R. Baricitinib for COVID-19: a suitable treatment? Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30262-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonçalves A., Bertrand J., Ke R., Comets E., de Lamballerie X., Malvy D., Pizzorno A., Terrier O., Calatrava M.R., Mentré F., Smith P., Perelson A.S., Guedj J. Timing of antiviral treatment initiation is critical to reduce SARS-CoV-2 viral load. CPT Pharmacometrics Syst Pharmacol. 2020 doi: 10.1002/psp4.12543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Parra G., Dobrovolny H.M. Modeling of fusion inhibitor treatment of RSV in African green monkeys. J. Theor. Biol. 2018;456:62–73. doi: 10.1016/j.jtbi.2018.07.029. [DOI] [PubMed] [Google Scholar]
- Gordon C.J., Tchesnokov E.P., Woolner E., Perry J.K., Feng J.Y., Porter D.P., otte M.G. Remdesivir is a direct-acting antiviral that inhibits RNA-dependent RNA polymerase from severe acute respiratory syndrome coronavirus 2 with high potency. J. Biol. Chem. 2020;295(20):6785–6797. doi: 10.1074/jbc.RA120.013679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon C.J., Tchesnokov E.P., Feng J.Y., Porter D.P., Gotte M. The antiviral compound remdesivir potently inhibits RNA-dependent RNA polymerase from Middle East respiratory syndrome coronavirus. J. Biol. Chem. 2020;295(15):4773–4779. doi: 10.1074/jbc.AC120.013056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A. Goyal, E. F. Cardozo-Ojeda, J. T. Schiffer, 2020. Potency and timing of antiviral therapy as determinants of duration of SARS CoV-2 shedding and intensity of inflammatory response, medRxiv. doi:10.1101/2020.04.10.20061325. [DOI] [PMC free article] [PubMed]
- Goyal P., Choi J.J., Pinheiro L.C., Schenck E.J., Chen R., Jabri A., Satlin M.J., Campion T.R., Nahid M., Ringel J.B., Hoffman K.L., Alshak M.N., Li H.A., Wehmeyer G.T., Rajan M., Reshetnyak E., Hupert N., Horn E.M., Martinez FJ., Gulick R.M., Safford M.M. Clinical characteristics of covid-19 in New York city. N. Engl. J. Med. 2020;382:2372–2374. doi: 10.1128/JVI.00689-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goyal A., Duke E.R., Cardozo-Ojeda E.F., Schiffer J.T. Mathematical modeling explains differential SARS CoV-2 kinetics in lung and nasal passages in remdesivir treated rhesus macaques. bioRxiv. 2020 doi: 10.1101/2020.06.21.163550. [DOI] [Google Scholar]
- Grein J., Ohmagari N., Shin D., Diaz G., Asperges E., Castagna A., Feldt T., Green G., Green M., Lescure F.-X., Nicastri E., Oda R., Yo K., Quiros-Roldan E., Studemeister A., Redinski J., Ahmed S., Bernett J., Chelliah D., Chen D., Chihara S., Cohen S., Cunningham J., Monforte A.D., Ismail S., Kato H., Lapadula G., L’Her E., Maeno T., Majumder S., Massari M., Mora-Rillo M., Mutoh Y., Nguyen D., Verweij E., Zoufaly A., Osinusi A., DeZure A., Zhao Y., Zhong L., Chokkalingam A., Elboudwarej E., Telep L., Timbs L., Henne I., Sellers S., Cao H., Tan S., Winterbourne L., Desai P., Mera R., Gaggar A., Myers R., Brainard D., Childs R., Flanigan T. Compassionate use of remdesivir for patients with severe Covid-19. N. Engl. J. Med. 2020;382(24):2327–2336. doi: 10.1056/NEJMoa2007016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel A., M L I., Jr., Antia R. Neuraminidase inhibitor resistance in influenza: assessing the danger of its generation and spread. PLoS Comput. Biol. 2007;3(12):2456–2464. doi: 10.1371/journal.pcbi.0030240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heldt F.S., Frensing T., Pflugmacher A., Gropler R., Peschel B., Reichl U. Multiscale modeling of influenza A virus infection supports the development of direct-acting antivirals. PLoS Comput. Biol. 2013;9(11) doi: 10.1371/journal.pcbi.1003372. e1003372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillaker E., Belfer J.J., Bondici A., Murad H., Dumkow L.E. Delayed initiation of remdesivir in a COVID-19-positive patient. Pharma. 2020;40(6):592–598. doi: 10.1002/phar.2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holder B.P., Beauchemin C.A. Exploring the effect of biological delays in kinetic models of influenza within a host or cell culture. BMC Publ. Health. 2011;11(S1) doi: 10.1186/1471-2458-11-S1-S10. S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holshue M.L., DeBolt C., Lindquist S., Lofy K.H., Wiesman J., Bruce H., Spitters C., Ericson K., Wilkerson S., Tural A., Diaz G., Cohn A., Fox L., Patel A., Gerber S.I., Kim L., Tong S., Lu X., Lindstrom S., Pallansch M.A., Weldon W.C., Biggs H.M., Uyeki T.M., Pillai S.K. First case of 2019 novel coronavirus in the United States. N. Engl. J. Med. 2020;382(8):929–936. doi: 10.1056/NEJMoa2001191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- E. A. Hernandez-Vargas, J. X. Velasco-Hernandez, 2020. In-host modelling of COVID-19 kinetics in humans, medRxiv. doi:10.1101/2020.03.26.20044487. [DOI] [PMC free article] [PubMed]
- Jiang F., Deng L., Zhang L., Cai Y., Cheung C.W., Xia Z. Review of the clinical characteristics of coronavirus disease 2019 (COVID-19) J. Gen. Intern. Med. 2020;35:1545–1549. doi: 10.1007/s11606-020-05762-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan S.A., Zia K., Ashraf S., Uddin R., Ul-Haq Z. Identification of chymotrypsin-like proteaseinhibitors of SARS-CoV-2 via integratedcomputational approach. J. Biomol. Struct. Dyn. 2020 doi: 10.1080/07391102.2020.1751298. [DOI] [PubMed] [Google Scholar]
- Kim K.S., Ejima K., Ito Y., Iwanami S., Ohashi H., Koizumi Y., Asai Y., Nakaoka S., Watashi K., Thompson R.N., Iwami S. Modelling SARS-CoV-2 dynamics: implications for therapy. MedRxiv. 2020 doi: 10.1101/2020.03.23.20040493. [DOI] [Google Scholar]
- Ko W.-C., Rolain J.-M., Lee N.-Y., Chen P.-L., Huang C.-T., Lee P.-I., Hsueh P.-R. Arguments in favour of remdesivir for treating SARS-CoV-2 infections. Int. J. Antimicrob. Agents. 2020;55(4) doi: 10.1016/j.ijantimicag.2020.105933. UNSP 105933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koizumi Y., Ohashi H., Nakajima S., Tanaka Y., Wakita T., Perelson A.S., Iwami S., Watashi K. Quantifying antiviral activity optimizes drug combinations against hepatitis C virus infection. Proc. Natl. Acad. Sci. U.S.A. 2017;114(8) doi: 10.1073/pnas.1610197114. 1922–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippi G., Sanchis-Gomar F., Henry B.M. Coronavirus disease 2019 (COVID-19): the portrait of a perfect storm. Ann. Transl. Med. 2020;8(7):497. doi: 10.21037/atm.2020.03.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo M.K., Jordan R., Arvey A., Sudhamsu J., Shrivastava-Ranjan P., Hotard A.L., Flint M., McMullan L.K., Siegel D., Clarke M.O., Mackman R.L., Hui H.C., Perron M., Ray A.S., Cihlar T., Nichol S.T., Spiropoulou C.F. GS-5734 and its parent nucleoside analog inhibit filo-, pneumo-, and paramyxoviruses. Sci. Rep. 2017;7:43395. doi: 10.1038/srep43395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madelain V., Baize S., Jacquot F., Reynard S., Fizet A., Barron S., Solas C., Lacarelle B., Carbonnelle C., Mentre F., Raoul H., de Lamballerie X., Guedj J. Ebola viral dynamics in nonhuman primates provides insights into virus immuno-pathogenesis and antiviral strategies. Nat. Commun. 2018;9:4013. doi: 10.1038/s41467-018-06215-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez M.A. Compounds with therapeutic potential against novel respiratory 2019 coronavirus. Antimicrob. Agents Chemother. 2020;64(5) doi: 10.1128/AAC.00399-20. e00399–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melville K., Rodriguez T., Dobrovolny H.M. Investigating different mechanisms of action in combination therapy for influenza. Front. Pharmacol. 2018;9:1207. doi: 10.3389/fphar.2018.01207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao H., Xia X., Perelson A.S., Wu H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev. 2011;53(1):3–39. doi: 10.1137/090757009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer J., Dobrovolny H.M., Beauchemin C.A. The in vivo efficacy of neuraminidase inhibitors cannot be determined from the decay rates of influenza viral titers observed in treated patients. Sci. Rep. 2017;7:40210. doi: 10.1038/srep40210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- A. J. Pruijssers, A. S. George, A. Schäfer, S. R. Leist, L. E. Gralinksi, K. H. Dinnon, B. L. Yount, M. L. Agostini, L. J. Stevens, J. D. Chappell, X. Lu, T. M. Hughes, K. Gully, D. R. Martinez, A. J. Brown, R. L. Graham, J. K. Perry, V. Du Pont, J. Pitts, B. Ma, D. Babusis, E. Murakami, J. Y. Feng, J. P. Bilello, D. P. Porter, T. Cihlar, R. S. Baric, M. R. Denison, T. P. Sheahan, Remdesivir potently inhibits SARS-CoV-2 in human lung cells and chimeric SARS-CoV expressing the SARS-CoV-2 rna polymerase in mice, bioRxivdoi:10.1101/2020.04.27.064279. [DOI] [PMC free article] [PubMed]
- Parang K., El-Sayed N.S., Kazeminy A.J., Tiwari R.K. Comparative antiviral activity of remdesivir and anti-HIV nucleoside analogs against human coronavirus 229E (HCoV-229E) Molecules. 2020;25(10) doi: 10.3390/molecules25102343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon A., Le N.T.-T., Selisko B., Eydoux C., Alvarez K., Guillemot J.-C., Decroly E., Peersen O., Ferron F., Canard B. Remdesivir and SARS-CoV-2: structural requirements at both nsp12 RdRp and nsp14 exonuclease active-sites. Antivir. Res. 2020;178:104793. doi: 10.1016/j.antiviral.2020.104793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheahan T.P., Sims A.C., Graham R.L., Menachery V.D., Gralinski L.E., Case J.B., Leist S.R., Pyrc K., Feng J.Y., Trantcheva I., Bannister R., Park Y., Babusis D., Clarke M.O., Mackman R.L., Spahn J.E., Palmiotti C.A., Siegel D., Ray A.S., Cihlar T., Jordan R., Denison M.R., Baric R.S. The next wave of influenza drugs. Sci. Transl. Med. 2017;9(396) doi: 10.1126/scitranslmed.aal3653. eaal3653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith A.M., Adler F.R., Perelson A.S. An accurate two-phase approximate solution to an acute viral infection model. J. Math. Biol. 2010;60(5):711–726. doi: 10.1007/s00285-009-0281-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Y. Wang, Y. Wang, Y. Chen, Q. Qin, Unique epidemiological and clinical features of the emerging 2019 novel coronavirus pneumonia (COVID-19) implicate special control measures, J. Med. Virol.doi:10.1002/jmv.25748. [DOI] [PMC free article] [PubMed]
- Wang Y., Zhang D., Du G., Du R., Zhao J., Jin Y., Fu S., Gao L., Cheng Z., Lu Q., Hu Y., Luo G., Wang K., Lu Y., Li H., Wang S., Ruan S., Yang C., Mei C., Wang Y., Ding D., Wu F., Tang X., Ye X., Ye Y., Liu B., Yang J., Yin W., Wang A., Fan G., Zhou F., Liu Z., Gu X., Xu J., Shang L., Zhang Y., Cao L., Guo T., Wan Y., Qin H., Jiang Y., Jaki T., Hayden F.G., Horby P.W., Cao B., Wang C. Remdesivir in adults with severe COVID-19: a randomised, double-blind, placebo-controlled, multicentre trial. Lancet. 2020;395(10236):1569–1578. doi: 10.1016/S0140-6736(20)31022-31029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren T.K., Jordan R., Lo M.K., Ray A.S., Mackman R.L., Soloveva V., Siegel D., Perron M., Bannister R., Hui H.C., Larson N., Strickley R., Wells J., Stuthman K.S., Van Tongeren S.A., Garza N.L., Donnelly G., Shurtleff A.C., Retterer C.J., Gharaibeh D., Zamani R., Kenny T., Eaton B.P., Grimes E., Welch L.S., Gomba L., Wilhelmsen C.L., Nichols D.K., Nuss J.E., Nagle E.R., Kugelman J.R., Palacios G., Doerffler E., Neville S., Carra E., Clarke M.O., Zhang L., Lew W., Ross B., Wang Q., Chun K., Wolfe L., Babusis D., Park Y., Stray K.M., Trancheva I., Feng J.Y., Barauskas O., Xu Y., Wong P., Braun M.R., Flint M., McMullan L.K., Chen S.-S., Fearns R., Swaminathan S., Mayers D.L., Spiropoulou C.F., Lee W.A., Nichol S.T., Cihlar T., Bavari S. Therapeutic efficacy of the small molecule GS-5734 against Ebola virus in rhesus monkeys. Nature. 2016;531(7594):381–385. doi: 10.1038/nature17180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao T.-T., Qian J.-D., Zhu W.-Y., Wang Y., Wang G.-Q. A systematic review of lopinavir therapy for SARS coronavirus and MERS coronavirus-a possible reference for coronavirus disease-19 treatment option. J. Med. Virol. 2020;92(6):556–563. doi: 10.1002/jmv.25729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- B. N. Williamson, F. Feldmann, B. Schwarz, K. Meade-White, D. P. Porter, J. Schulz, N. van Doremalen, I. Leighton, C. K. Yinda, L. Pérez-Pérez, A. Okumura, J. Lovaglio, P. W. Hanley, G. Saturday, C. M. Bosio, S. Anzick, K. Barbian, T. Cihlar, C. Martens, D. P. Scott, V. J. Munster, E. de Wit, 2020. Clinical benefit of remdesivir in rhesus macaques infected with SARS-CoV-2, bioRxiv. doi:10.1101/2020.04.15.043166. [DOI] [PMC free article] [PubMed]
- Yin W., Mao C., Luan X., Shen D.-D., Shen Q., Su H., Wang X., Zhou F., Zhao W., Gao M., Chang S., Xie Y.-C., Tian G., Jiang H.-W., Tao S.-C., Shen J., Jiang Y., Jiang H., Xu Y., Zhang S., Zhang Y., Xu H.E. Structural basis for inhibition of the RNA-dependent RNA polymerase from SARS-CoV-2 by remdesivir. Science. 2020;368(6498):1499–1504. doi: 10.1126/science.abc1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B.-G., Tanaka G., Aihara K., Honda M., Kaneko S., Chen L. Dynamics of an HBV model with drug resistance under intermittent antiviral therapy. Intl. J. Bifur. Chaos. 2015;25(7):1540011. doi: 10.1142/S0218127415400118. [DOI] [Google Scholar]
- Zhang J., Tian S., Lou J., Chen Y. Familial cluster of COVID-19 infection from an asymptomatic. Crit. Care. 2020;24(1):119. doi: 10.1186/s13054-020-2817-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zitzmann C., Schmid B., Ruggieri A., Perelson A.S., Binder M., Bartenschlager R., Kaderali L. A coupled mathematical model of the intracellular replication of dengue virus and the host cell immune response to infection. Front. Microbiol. 2020;11:725. doi: 10.3389/fmicb.2020.00725. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Multimedia component 1