Composition-Dependent Hydrogen-Bonding Motifs and Dynamics in Brønsted Acid–Base Mixtures

Abstract

In recent years the interaction of organophosphates and imines, which is at the core of Brønsted acid organocatalysis, has been established to be based on strong ionic hydrogen bonds. Yet, besides the formation of homodimers consisting of two acid molecules and heterodimers consisting of one acid and one base, also multimeric molecular aggregates are formed in solution. These multimeric aggregates consist of one base and several acid molecules. The details of the intermolecular bonding in such aggregates, however, have remained elusive. To characterize composition-dependent bonding and bonding dynamics in these aggregates, we use linear and nonlinear infrared (IR) spectroscopy at varying molar ratios of diphenyl phosphoric acid and quinaldine. We identify the individual aggregate species, giving rise to the structured, strong, and very broad infrared absorptions, which span more than 1000 cm^–1. Linear infrared spectra and density functional theory calculations of the proton transfer potential show that doubly ionic intermolecular hydrogen bonds between the acid and the base lead to absorptions which peak at ∼2040 cm^–1. The contribution of singly ionic hydrogen bonds between an acid anion and an acid molecule is observed at higher frequencies. As common to such strong hydrogen bonds, ultrafast IR spectroscopy reveals rapid, ∼ 100 fs, dissipation of energy from the proton transfer coordinate. Yet, the full dissipation of the excess energy occurs on a ∼0.8–1.1 ps time scale, which becomes longer when multimers dominate. Our results thus demonstrate the coupling and collectivity of the hydrogen bonds within these complexes, which enable efficient energy transfer.

Introduction

Aggregates formed via association of a Brønsted acid and a Brønsted base are often considered as prototypes of strong hydrogen bonds.¹ The relevance of strong hydrogen bonds to, e.g., photochemical transfer cascades in biological systems,^2,3 enzyme function,⁴ or catalysis⁵⁻⁷ has triggered intense interest in the understanding of their fundamental physical and chemical characteristics.⁸⁻¹⁷ Of particular interest are such strong hydrogen bonds for fast (photo-) chemical reactions, as proton transfer along the hydrogen bond has been suggested to be an important part of the reaction coordinate.^3,18 In asymmetric catalysis, such strong bonds can restrict the number of thermally accessible conformations of the base.^19,20 Conversely, the bonding geometry has to be sufficiently flexible in order to allow the Brønsted acid catalyst to reversibly bind a wide range of substrates.²¹ As such, the location and bonding dynamics of the proton, which report on the bond strength and geometry, affect the catalytic efficiency.¹⁸ However, most of the current understanding of such strong hydrogen bonds stems from studies of carboxylic acids.^13,22−24 Hydrogen bonding involving phosphoric acid groups, as they occur in enzymatic transition⁴ states or in asymmetric catalysis,⁵ are less well studied.²⁵

Two limiting cases are usually considered for the aggregation of a Brønsted acid with a Brønsted base: a neutral hydrogen bond with the acidic proton remaining located at the acid or a doubly ionic hydrogen bond (a strongly hydrogen-bonded ion-pair), which is formed by transfer of the proton from the acid to the base.^12,26−28 For example, the interaction between organophosphoric acids and imines was initially described as the coexistence of these two limiting cases.²⁹ However, in recent years there has been evidence that proton transfer and subsequent ion-pair formation (doubly ionic hydrogen bond) dominate.^20,30,31 Yet, our previous studies have revealed an even more complex association behavior in the dipolar aprotic solvent dichloromethane: even for equimolar mixtures of phosphoric acids with imine bases, not only bimolecular aggregates (ion-pairs, Figure 1a) between the acid and the base but also multimers are formed. In the multimers a phosphoric acid donates a hydrogen bond to the deprotonated phosphoric acid anion of an ion-pair (Figure 1b).^30,31 Conceptually, this multimer formation can be interpreted as an acid homodimer (Figure 1c), which are commonly observed for such mixtures,³²⁻³⁴ protonating the imine base. Our earlier studies were, however, largely based on rather “slow” experimental methods (nuclear magnetic resonance (NMR) and dielectric relaxation spectroscopies (DRS)), which typically provide information on the average charge and/or proton distribution within the aggregates. As such, the different hydrogen-bonding motifs and their respective bond strengths and dynamics have remained elusive.

Figure 1.

(a) Structure of an ion-pair consisting of one Qu and one DPP molecule. (b) For the simplest multimeric structure, i.e., a trimer, an additional DPP molecule donates a hydrogen bond to the acid anion. In panel (c) a DPP homodimer is schematically shown.

Linear (and nonlinear) infrared (IR) spectroscopies provide insight into the nature and strength of strong hydrogen bonds because the hydrogen-bond potential is directly reflected in the IR absorption bands. For catalytically active phosphoric acids, the vibrational frequencies have in fact been suggested to be a powerful quantity to predict catalytic activity.^35,36 For strong hydrogen bonds, the anharmonic and flat potential along the proton transfer coordinate (e.g., as compared to a water–water hydrogen bond) lead, however, to rather complex infrared spectra^13,22,26,37 with the absorption bands spanning more than 1000 cm^–1. The width of these bands has been attributed to strong anharmonic coupling.^16,25,38,39 With increasing hydrogen-bonding strength, a Fermi resonance between the proton stretching mode and the overtone of the hydrogen-bond bending vibration(s) even results in heavily mixed vibrations and an apparent splitting of the band into two main absorbances (where the absorption dip is often referred to as an Evans hole^37,39−42). As a result of these strongly coupled vibrational modes, vibrational energy relaxation, as measured using ultrafast infrared spectroscopies, is very rapid (tens to hundreds of femtoseconds),^13,32,39,43 and population of lower-frequency modes in the course of energy relaxation results in a modulation of virtually the entire infrared spectrum.¹³ Yet, the energy released in the course of vibrational relaxation has been suggested to be insufficient to weaken or dissociate the aggregates.^13,22,44 Overall, the vibrational structure and dynamics of such acid–base pairs appear somewhat reminiscent of the structure and dynamics of the proton in aqueous solutions of Brønsted acids.⁴⁵⁻⁴⁷

To elucidate hydrogen bonding of catalytically relevant phosphoric acids,^48,49 we study vibrational signatures of intermolecular bonding in acid–base mixtures consisting of diphenyl phosphoric acid and the base quinaldine dissolved in dichloromethane. We find the broad infrared absorption of the phosphoric acid homodimers to red-shift upon addition of the base. Density functional theory calculations suggest that the red-shift can be explained by a flatter potential along the proton transfer coordinate for hydrogen bonds in the presence of the base, as compared to the acid homodimer. To study the composition-dependent bonding dynamics, we performed IR pump–probe spectroscopy and two-dimensional IR (2D-IR) spectroscopy⁵⁰⁻⁵⁴ experiments at different acid/base molar ratios. These experiments indicate—similar to other strong hydrogen bonds—extremely fast (∼100 fs) vibrational relaxation. Yet, full equilibration of the excess energy depends on the acid–base ratio, indicative of different relaxation channels in dimers and multimers. These relaxation pathways also result in a somewhat delayed appearance of a rather uncommon off-diagonal peak in the 2D-IR spectra, most apparent for an excess of acid. We ascribe this off-diagonal signal to the population of lower energy states during vibrational relaxation, which—via strong anharmonic coupling—transiently modulate all hydrogen bonds within the molecular complexes. As such, our results highlight the collective nature of hydrogen bonding in these aggregates, which affects both hydrogen-bond strengths and energy redistribution in such acid base mixtures.

Materials and Methods

Diphenyl phosphoric acid (diphenyl phosphate, DPP, 99%) and quinaldine (Qu, 95%), were purchased from Sigma-Aldrich. Dichloromethane (DCM, 99.9%) was purchased from Fisher Scientific. To remove residual water from DCM and Qu, both liquids were dried over molecular sieves (4 Å). Prior to use, the liquids were filtered with a 0.2 mm Omnipore membrane filter (Merck) to remove solid residues from the molecular sieves. All samples were prepared by weight in volumetric glass equipment and subsequently sonicated for ∼5 s. The samples were contained between two CaF₂ windows (4 mm thick) separated by a 25 μm PTFE spacer, except for infrared pump probe experiments, where we used 2 mm thick CaF₂ windows separated by a 50 μm PTFE spacer. For infrared pump–probe and 2D-IR spectroscopies the temperature was controlled to 22.0 ± 0.5 °C.

Fourier transform infrared spectra (FTIR) were measured using a Bruker VERTEX 70 spectrometer with 4 cm^–1 resolution in transmission geometry. To obtain information on vibrational dynamics, we used broadband infrared pump–probe experiments. In these experiments a broadband infrared pulse (centered at ∼2000 cm^–1, full width at half-maximum (fwhm) ∼ 300 cm^–1) excites infrared modes in the sample. The pump-induced modulation of the infrared absorption, Δα, is detected with a weak, variably delayed infrared probe pulse as a function of delay time, t. The detected modulation of the spectra is recorded for both parallel (Δα_||) and perpendicular (Δα_⊥) polarization of the probe pulse relative to the pump pulse polarization. The isotropic (rotation-free) modulation (i.e., at the magic angle), which reflects vibrational population dynamics, is calculated as Δα_iso = (Δα_|| + 2Δα_⊥)/3. The experimental setup is described in detail elsewhere.⁵⁵ Briefly, pulses centered at 800 nm (∼50 fs duration, 1.5 mJ pulse energy, 1 kHz repetition rate) from a Ti:sapphire regenerative amplifier (Spitfire Ace, Spectra-Physics) are used to generate infrared pulses using an optical parametric amplifier (OPA) together with a noncollinear difference frequency generation stage (TOPAS prime & NDFG, Light Conversion). The IR pulses (∼12 μJ pulse energy and ∼100 fs fwhm duration) are split into pump, probe, and reference beams, with the pump and the probe beams being focused into the sample. The probe beam is recollimated after the sample and, together with the reference beam, spectrally dispersed (Triax 180 spectrograph, Horiba, 100 l/mm grating) onto a 2 × 32 pixel mercury cadmium telluride (MCT) detector.

To resolve the spectral modulation for different pump frequencies, we perform two-dimensional infrared (2D-IR) spectroscopy experiments.⁵⁶ Here the sample is excited using two temporally separated pump pulses. Variation of the coherence time (t₁) between the two pump pulses and subsequent Fourier transformation of the transient signals at different probing frequencies provide spectral resolution along the pump axis.^50,57−60 The 2D-IR experiment is based on a regenerative amplifier (Astrella, Coherent) providing 800 nm pulses (35 fs pulse duration) at a 1 kHz repetition rate. Pulses with an energy of 2.7 mJ are used to pump an OPA with difference frequency generation to generate IR pulses (pulse energy ∼30 μJ) centered at 2000 cm^–1 with a ∼150 fs pulse duration. The infrared pulses are guided to a commercial 2D-IR spectrometer (2DQuick-IR, Phasetech Spectroscopy Inc.). Pump pulse pairs are generated using an infrared pulse-shaper, based on spectrally dispersed diffraction from a Ge-based acousto-optic modulator.⁶¹⁻⁶³ The pump and the probe beams are focused and overlapped in the sample. The probe beam is then detected together with a reference beam, by dispersing both beams (using a SP2156 spectrograph, Princeton Instruments, 30 l/mm grating) onto a 128 × 128 pixel MCT array detector. Two-dimensional-IR spectra are recorded for different values of the waiting time.

Results and Discussion

FTIR Spectra of DPP–Qu Mixtures

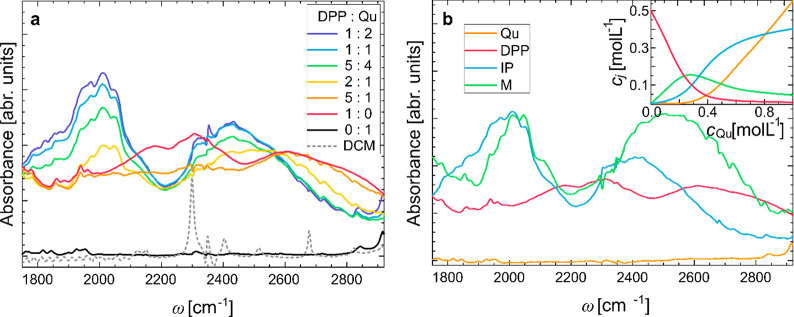
To study the interaction between the acid and the base at different compositions, we measure FTIR spectra of DPP–Qu mixtures in DCM at a constant concentration of DPP (0.5 mol L^–1) and varying concentrations of Qu (0–1 mol L^–1). The infrared absorption spectrum of Qu in the 1700–2800 cm^–1 spectral range (black line in Figure 2a) shows no vibrational features in this spectral range. Solutions of only DPP (solid red line) exhibit a rather broad absorption spanning the full ∼1000 cm^–1 spectral range of Figure 2a. This very broad absorption band is due to DPP homodimers, similar to what has been reported for solutions of other Brønsted acids in aprotic solvents.^32,33 The remarkable width of such homodimer absorptions has already earlier been—besides different molecular conformations—related to strong coupling (anharmonic and excitonic) as well as Fermi resonances.^23,25,32,64 Upon addition of the base Qu to the mixtures, we observe the emergence of two broad (more than 400 cm^–1 wide), yet structured absorption features at ∼2040 and ∼2500 cm^–1 (Figure 2a, for full spectral range see Figure S1 in the Supporting Information). Thus, the doubly ionic (O^–···H–N⁺) hydrogen bonds,²⁸ which are the predominant intermolecular interaction motif for an excess of Qu (blue solid line in Figure 2a), give rise to similarly broad absorptions in the infrared spectra.¹ The two spectral features are separated by a minimum in the absorbance at ∼2200 cm^–1, which has been explained by a Fermi resonance with the hydrogen-bond bending overtone.^16,25 The marked structuring of the absorbance in the presence of the base quinaldine, as opposed to the spectra in the absence of the base, shows that this Fermi resonance is most significant for ionic (O^–···H–N⁺) hydrogen bonds.

Figure 2.

(a) FTIR spectra for mixtures of DPP (0.5 mol L^–1) with varying concentrations of Qu in DCM. The spectrum of Qu in DCM (solid black line) shows essentially no spectral features in this frequency region. A solution of DPP in DCM (red solid line) exhibits a very broad band spanning more than 1000 cm^–1 due to DPP–DPP homodimers. In mixtures of DPP and Qu two structured spectral features at ∼2040 and ∼2500 cm^–1 are present. Contributions of the solvent (dotted gray line) have been subtracted from the mixture spectra. (b) Component spectra of Qu, DPP homodimers (DPP), ion-pairs (IP), and multimers (M). The decomposition is based on the variation of the different species concentrations based on the equilibria reported in ref (30) (inset).

Close inspection of the two absorbances at ∼2040 and ∼2500 cm^–1 reveals that the amplitudes of both spectral features depend on the acid:base molar ratio. Upon increasing concentration of Qu the absorbance overall red-shifts (see also Figure S1, Supporting Information): While the absorbance at blue-shifted frequencies decreases (see 2810 cm^–1 in Figure S1b), the absorption at 2460 cm^–1 increases by ∼40%, and at very red-shifted frequencies by ∼90% (2040 cm^–1 in Figure S1b) with increasing Qu concentration. These qualitative considerations suggest a redistribution of the spectral intensity between the two main absorption features at ∼2040 and ∼2500 cm^–1 depending on molar composition.

The isosbestic point at ∼2550 cm^–1 (Figure 1a) shows that at least two molecular species give rise to observed spectra. The spectral variation at ∼2040 and ∼2500 cm^–1 for high concentrations of Qu suggests the presence of a third molecular species. Previous results on the molecular complexes in solution^30,31 suggested the simultaneous presence of DPP homodimers, Qu–DPP dimers (ion-pairs with a doubly ionic O^–···H–N⁺ hydrogen bond), and (DPP)₂–Qu multimers containing both doubly ionic O^–···H–N⁺ and singly ionic P–O^–···H–O–P hydrogen bonds (see Figure 1). Taking additionally the presence of free Qu into account, we decompose the spectra of Figure 1a into the contributions of these species. We determine the spectral contributions of Qu, DPP homodimers, ion-pairs (IP), and multimers (M) (Figure 1) to the spectra in Figure 2a, using least-squares decomposition with the composition-dependent concentrations of all molecular aggregates as known covariances (see the inset of Figure 2b). The thus-extracted component spectra of Qu, DPP, IP, and M are shown in Figure 2b (for details see the Supporting Information, Figure S2). We note that using this decomposition based on molar concentrations of the species, the component spectrum for the multimers does not intersect the isosbestic point at 2550 cm^–1, since (DPP)₂–Qu complexes contain two acidic protons as opposed to IP and DPP. The decomposition suggests that the absorbances of the ion-pairs and multimers markedly differ from the spectral contributions of the DPP homodimers. Both the ion-pairs and the multimers show a marked absorbance at ∼2040 cm^–1, consistent with doubly ionic hydrogen bond O^–···H–N⁺ underlying this peak. Yet, this peak is red-shifted for the ion-pairs, as compared to the multimers, suggesting that association of a DPP molecule to an ion-pair to form a multimer also affects the O^–···H–N⁺ bond. The ion-pairs and the multimers show some additional absorption at ∼2500 cm^–1, yet for the multimers this band is more intense and broader.

Proton Transfer Potentials

The rather low (as, e.g., compared to the ∼3000–3500 cm^–1 range for weaker hydrogen-bonded O–H and N–H stretching bands) resonance frequency for the proton stretching band has been explained by the proton residing in a rather shallow and anharmonic potential.³⁹ Despite that the experimentally observed broad and structured absorbance cannot be explained by considering only a single vibrational coordinate,^25,64,65 the displacement of the proton along the proton transfer coordinate has been shown to be a good estimate for the overall position of the absorbance of the hydrogen bond in the vibrational spectra.⁴⁵⁻⁴⁷ Thus, to further support the assignment to the different bonding motifs, we calculate the potential energy landscapes for the proton transfer between the O (or N) atoms of DPP and Qu. To determine the potential of doubly ionic hydrogen bonds as in the ion-pairs and multimers (N–H⁺···^–O, Figure 1a and b), of neutral hydrogen bonds as in the DPP homodimers (P–O···H–O–P, Figure 1c), and of singly ionic hydrogen bonds (P–O^–···H–O–P, Figure 1b), we perform density functional theory (DFT) calculations.

The DFT calculations⁶⁶⁻⁶⁸ were performed for a Qu–DPP pair (IP) and an electroneutral DPP–DPP pair. For the “singly ionic” P–O^–···H–O–P hydrogen bonds in multimers we use an anionic DPP^––DPP pair with lithium as counterion, as a computationally feasible model system. To this end, we used the B3LYP-D3(BJ)/6-31G(d) level of theory⁶⁹⁻⁷¹ using Grimme’s D3 dispersion with Becke–Johnson damping.⁷² We use a polarizable continuum model for DCM,⁷³ as implemented in Gaussian 16.⁷⁴ Starting from an optimized geometry (Figure S3, Supporting Information), a nonrelaxed surface scan indeed indicates a very anharmonic potential upon translating the protons along the N–O (or O–O) axes (for details see Figure 3 and the Supporting Information). For the doubly ionic hydrogen bond, the global minimum of the potential corresponds to the proton located close to the nitrogen (r(N–H) ≈ 1.1 Å in Figure 3a) and is separated by ∼3000 cm^–1 from the plateau close to DPP’s oxygen (r(N–H) ≈ 1.5 Å in Figure 3a). The overall shape of the potential with a pronounced minimum located close to the nitrogen atom of Qu is similar to what has been previously reported for strong hydrogen bonds^{12,25,26,45,53,75−77} and agrees well with the notion of the ionic nature of DPP–Qu dimers.^30,31

Figure 3.

Potential energy profile along the proton transfer coordinate for hydrogen bonds between (a) Qu and DPP, (b) between two DPP molecules within a homodimer, and (c) between DPP and a DPP^– anion with lithium as counterion. The potentials and estimated transition energies are sensitive to the O–O or O–N distance (molecular separation).^16,25,65 Yet, calculations with fixed intermolecular distance allow for assessing the effect of variation of the hydrogen-bond acceptor. Schematic molecular structures together with the proton transfer coordinate (shaded red lines) are shown on the top of each panel. Symbols correspond to relative energies as obtained from a nonrelaxed energy scan for the hydrogen-bonding proton displaced along the N–O (or O–O coordinate). Black solid lines show quartic fits to the potential (see text and the Supporting Information for details). For better comparison, the potential shown in (a) is shown as dotted line in panels (b) and (c). Energy levels of the three lowest eigenstates |0>, |1>, and |2> obtained by numerically solving the one-dimensional Schrödinger equation are shown as dashed lines. The associated wave functions are depicted as solid lines and were vertically offset by the corresponding energies for clarity. Transition frequencies are highlighted with double-headed arrows.

To relate this potential to the vibrational transitions, we fit the potential with a quartic asymmetric double-well function as described in ref (47) (Figure 3). The corresponding one-dimensional nuclear Schrödinger equation for the fitted potential was numerically solved, using the discrete variable representation method⁷⁵ (see the Supporting Information for details). The thus-obtained wave functions of the three lowest lying eigenstates together with their energies are shown in Figure 3. The first vibrational excited state for the ion-pair is energetically very close to the plateau, which corresponds to the proton back transfer to the oxygen atom of DPP. As such, the proton is significantly delocalized between the acid and the base in the first vibrational excited state. The strong anharmonicity of the potential also results in a very large difference in transition energies between the lowest lying states: |0>−|1> ∼ 2040 cm^–1 vs |1>−|2> ∼ 1100 cm^–1, with the fundamental transition in qualitative agreement with the experimentally observed bands for an excess of Qu in Figure 2a.

For the electroneutral hydrogen bond in DPP homodimers (Figure 3b), we find the proton transfer potential to be steeper, resulting in the vibrational transitions to be located at ∼2310 cm^–1 (|0>−|1>) and at ∼1620 cm^–1 (|1>−|2>). We note that for the slightly nonlinear O–H–O bond of the DPP homodimers, the results are sensitive to the exact choice of the coordinate: translating the proton along the O–H axis results in an increase of the transition frequencies by up to 160 cm^–1 (see Figure S4, Supporting Information). The potential of a singly ionic hydrogen bond, which we model using a Li⁺ DPP^– DPP complex (Figure 3c), is comparable to the potential of the doubly ionic hydrogen bond and only differs for large proton displacements. Thus, the calculated transition frequencies are similar to those of the doubly ionic hydrogen bond and markedly lower than those of the electroneutral hydrogen bonds in DPP homodimers.

Overall, the thus-calculated transition energies are in broad agreement with the experimentally observed overall red-shift of the absorbance upon the addition of Qu (Figure 2a) and the spectral decomposition in Figure 2b. In the absence of Qu, the DPP homodimers give rise to spectral contributions at higher frequencies (see Figure 2b), in line with the transition energy of the DPP–DPP homodimers (Figure 3b). For an excess of Qu, ion-pairs dominate, for which the proton transfer is suggested to give rise to spectral contributions as low as 2000 cm^–1 (Figure 3a). Also the formation of singly ionic hydrogen bonds contributes to the gradual shift of the spectrum as shown in Figure 2a.

Composition-Dependent Vibrational Couplings

We use 2D-IR spectroscopy to elucidate the effect of these different hydrogen-bonding motifs on the vibrational dynamics of solutions of Qu and DPP. In 2D-IR spectroscopy the modulation of the infrared absorbance of the sample is probed (probe frequency, ω_Probe) as a function of (excitation) pump frequency, ω_Pump. Vibrational dynamics are detected by varying the delay time, t, between the pump and the probe pulses. Commonly, for each vibrational mode a pair of peaks is observed in the 2D-IR spectra: a negative peak on the diagonal (ω_Pump= ω_Probe) and a positive peak at red-shifted probe frequencies (ω_Pump > ω_Probe). The former results from ground state depletion and stimulated emission, while the positive peak is due to excited state absorption of the anharmonic vibrational mode. Vibrational coupling (and/or chemical exchange/energy transfer) between distinct vibrational modes typically gives rise to two instantaneous (or delayed) off-diagonal peaks. The position of such off-diagonal peaks is symmetric with respect to the diagonal.^{50,51,54,57,78}

In Figure 4 we show the absorptive 2D-IR spectra for mixtures of DPP and Qu with varying molar ratios at t = 50 fs (see Figure 4a). For all spectra we observe a bleaching signal on the diagonal, centered at 2040 cm^–1. Even at this early delay time (50 fs) the signal is already fairly round, and we find no significant elongation along the diagonal. This round shape indicates that no inhomogeneous broadening is detectable within our time resolution (∼150 fs). Thus, either the peak at 2040 cm^–1 is homogeneously broadened or—if also inhomogeneously broadened—spectral diffusion is very fast. Spectral diffusion due to breaking and reformation of these strong hydrogen bonds is unlikely to occur on such a fast time scale, given the size of the hydrogen-bonded molecules. Yet, coupling to or mixing with lower frequency modes, like, e.g., hydrogen-bond bending vibrations¹⁶ or librations of the solvent,⁷⁹ can explain the decay of frequency–frequency correlation on a subpicosecond time scale. Despite the round shape of the on-diagonal peak at 2040 cm^–1, the overall transient signal is somewhat structured, with two minima on the diagonal at ∼2010 and ∼2040 cm^–1 (see the diagonal cut in Figure S5, Supporting Information). As this structure is also present in the FTIR spectra (Figure 2), the clear structuring in the nonlinear infrared spectra may point toward vibrational progression with a (∼30 cm^–1) lower frequency vibration, similar to what has been observed for acid homodimers.⁸⁰ Remarkably, at all time delays we do not detect an excited state absorption adjacent to the bleaching signal at red-shifted probe frequencies. The absence of such detectable positive signals is consistent with our DFT calculations, which predict the excited state absorptions at ∼1000 cm^–1 (Figure 3), well outside our detection range. Additionally, rapid relaxation of the first vibrational excited state, which will be discussed below, can result in a significant attenuation of the excited state absorption.

Figure 4.

2D-IR spectra at t = 50 fs for solutions of 0.5 mol L^–1 DPP and (a) 0.75, (b) 0.5, and (c) 0.25 mol L^–1 Qu in DCM. All spectra show a bleach at 2040 cm^–1/2040 cm^–1, which is related to ionic hydrogen bonds. With increasing DPP concentration an off-diagonal bleaching signal at 2040 cm^–1/2100 cm^–1 appears.

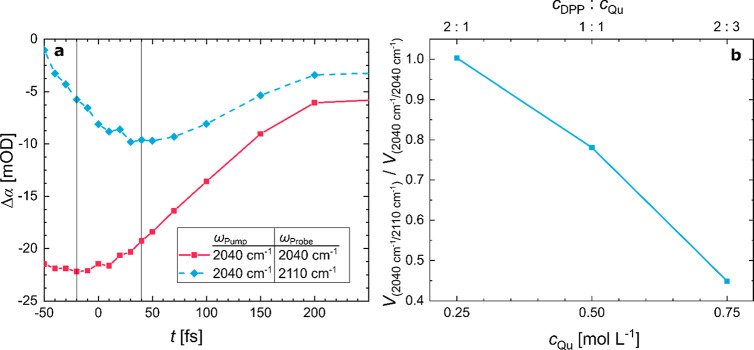
In contrast to the absence of a detectable off-diagonal peak due to the excited state absorption, we find at all molar ratios the predominant bleaching signal to be elongated toward higher probe frequencies: depending on molar composition a more or less intense blue-shifted bleaching signal at ω_Pump/ω_Probe = 2040 cm^–1/2100 cm^–1 adjacent to the transient signal at the diagonal is present. The fact that we do not detect corresponding spectral intensity on the diagonal (2100 cm^–1/2100 cm^–1) suggests that the transition dipole moment of the modes giving rise to the signal at ω_Probe = 2100 cm^–1 is too low to be directly excited in the 2D-IR experiment. Also the absence of a corresponding transient signal above the diagonal (symmetric with respect to the diagonal at 2100 cm^–1/2040 cm^–1) renders coupling, chemical exchange, or resonant energy transfer as the origin of this feature unlikely as these mechanisms would lead to a second peak above the diagonal. Thus, the signal must have different origins. A possible explanation for the appearance of such transient bleaching signals only below the diagonal is transient modulation of vibrational modes in the course of vibrational relaxation: vibrational relaxation of initially excited modes (transiently) populates lower-frequency modes. If some of these lower frequency modes are strongly coupled—similar to other strong hydrogen bonds^13,22,23,81 — to the modes that give rise to the weak, yet detectable, absorbance in the FTIR spectra at ∼2100 cm^–1 (Figure 2a), an off-diagonal peak appears.

Since this scenario results in off-diagonal contributions to the spectra only after vibrational relaxation, one may expect a delayed appearance of the transient signal below the diagonal. Despite our pulse duration being ∼150 fs and the contribution of different “artifacts”⁵⁰ at such early time delays, the time traces in Figure 5a may indeed indicate that the signal below the diagonal appears delayed relative to the signal on the diagonal. The observed 60 fs delay is in fact similar to the vibrational relaxation time of the on-diagonal peak (see discussion below). As such, also the temporal evolution of the signals supports the above-described scenario: After vibrational relaxation on a ∼100 fs time scale, a manifold of lower frequency vibrational states is transiently populated, which modulates the spectral signatures^23,32,82 of both the initially excited modes underlying the peak at 2040 cm^–1 and the modes giving rise to the absorbance at ∼2100 cm^–1 (Figure 2). It is important to note that in the studied concentration range, where molecular aggregates between the base and acid molecule(s) are separated from each other by solvent molecules, the vibrational energy is initially (within ∼100 fs) distributed over lower energy modes of molecules in spatial proximity. Conversely, relaxation and dissipation of the energy to low-frequency modes of more distant molecules typically occur on much longer time scales.^55,83,84 As such, the delayed, though very fast, appearance of the bleaching signal at ω_Probe ∼ 2100 cm^–1 suggests that after excitation of the vibrations at 2040 cm^–1 the transiently populated lower frequency modes are localized within the same molecular aggregate.

Figure 5.

(a) Time traces of selected 2D-IR peaks (2040 cm^–1/2040 cm^–1) and (2040 cm^–1/2110 cm^–1) for an equimolar mixture of DPP and Qu in DCM. A ∼60 fs delayed appearance of the maximum bleach for the 2040 cm^–1/2110 cm^–1 trace, relative to the 2040 cm^–1/2040 cm^–1 trace, can be observed. The two vertical solid gray lines mark the maximum bleaching of both signals. (b) Ratio of the volume integrals of the off-diagonal peak to the on-diagonal peak vs concentration of Qu at t = 50 fs. The integrals taken at pump frequencies from 1980 to 2083 cm^–1 and probe frequencies 1980–2083 cm^–1 or 2083–2230 cm^–1 evidence the increase of the 2040 cm^–1/2100 cm^–1 peak with increasing DPP to Qu ratio. Lines connecting the symbols are to a guide the eye.

The decomposed FTIR spectra, which indicate a shoulder at 2100 cm^–1 for the multimers (see Figure 2b), suggest the multimers being related to the off-diagonal peak in the 2D-IR spectra. In line with this notion, the negative signal at 2040 cm^–1/2100 cm^–1 in the 2D-IR spectra in Figure 4 is weak for an excess of base, where multimers are the minor species, and becomes more pronounced for an excess of acid, at which more multimers are formed. To quantify the intensity of this off-diagonal, we determine the volume integrals of both signals at (∼2040 cm^–1/∼2100 cm^–1) and (∼2040 cm^–1/∼2040 cm^–1). The ratios of the integrated intensities (over ω_Pump = 1980–2083 cm^–1 and ω_Probe = 1980–2083 or 2083–2230 cm^–1) in Figure 5b show a marked correlation with the concentration of base, indicating that the spectral signature below the diagonal correlates with the excess of acid. We note that for an excess of acid also DPP homodimers are present (Figure 2a), yet for solutions of only DPP, we find no detectable signals (see Figure S6, Supporting Information). This renders the signal below the diagonal in Figure 4 to be due to acid homodimers unlikely. Conversely, the singly ionic P–O^–···H–O–P hydrogen bonds in the multimers are in spatial proximity to the doubly ionic O^–···H–N⁺ hydrogen bonds (see also Figure 1), and our DFT calculations indicate that their transition frequencies are rather similar (Figure 3a and 3c). Hence, the appearance of the signal at ∼2040 cm^–1/∼2100 cm^–1 can be explained by excitation and relaxation of the O^–···H–N⁺ hydrogen bond at ∼2040 cm^–1 after which the dissipated excess energy gives rise to a transient modulation of the P–O^–···H–O–P hydrogen bonds (and the O^–···H–N⁺ hydrogen bonds) within multimers. As such, our results provide evidence for the frequently inferred strong coupling^23,25,32,64 for acid–base hydrogen bonds, also modulating hydrogen bonds in the direct proximity; i.e., the hydrogen bonds are highly collective.

Effect of Composition on Vibrational Relaxation Pathways

To explore the consequences of these composition-dependent couplings on vibrational energy relaxation pathways, we investigate the vibrational dynamics of Qu–DPP mixtures in more detail. As the 2D-IR spectra exhibit very little dependence on the pump frequency, we explore the vibrational dynamics based on broadband IR pump–probe experiments at 1880–2135 cm^–1 (for experiments centered at ∼2500 cm^–1 see Figures S7 and S8, Supporting Information). In an IR pump–probe experiment the transient signals are recorded as a function of delay time; in contrast to a 2D-IR experiment, the sample’s response is integrated over all pump frequencies. The thus-obtained transient spectra at early time delays (Figure 6a) resemble the spectral signatures (dominant bleach at ∼2040 cm^–1 and a shoulder above ∼2100 cm^–1) as seen in the 2D-IR experiments. Similar to the 2D-IR experiments, also in the pump–probe experiments the maximum bleaching signal shows a double-peak structure, and the maximum bleaching signal at ∼2100 cm^–1 is somewhat delayed (Figure 6a).

Figure 6.

(a) Transient infrared spectra of an equimolar mixture of Qu and DPP showing a structured peak at ∼2040 cm^–1 and a shoulder at ∼2100 cm^–1, which appears ∼100 fs delayed. (b) Delay traces at selected probing frequencies for an equimolar mixture of DPP and Qu in DCM. Symbols in panels (a) and (b) show experimental data, and solid lines show the fits with the three-state kinetic model (see also the Supporting Information). The dashed red line in panel (b) shows the fit with a two-state model at ω_Probe = 2040 cm^–1. (c) Relaxation times as a function of concentration of Qu, as extracted from fitting the kinetic model (see the inset of panel c) to the transient data.

As can be seen from the delay traces in Figure 6b and Figure S9, the transient signals rapidly decay with increasing time delay, indicative of fast vibrational energy relaxation. At t > 5 ps the signals plateau, and a persistent, weak modulation arises from a heated ground state, for which the spectral modulation results from a slight local rise in temperature. To quantitatively extract the vibrational relaxation dynamics, we fit a kinetic relaxation model (see the Supporting Information for more details) to the transient signals (Figure 6c):⁸⁵ In this model, infrared excitation populates a vibrationally excited state, 1*. Upon relaxation with a relaxation time τ_A an intermediate state, 0′, is transiently populated, which further relaxes with a relaxation time τ_B to a heated ground state, 0″. We note that in this model, the states 0′ and 0″ subsume the manifold of states over which the vibrational energy is distributed. For instance, the thermal state 0″ contains all states that are populated upon increase of the temperature after reaching a local thermal equilibrium. We assume the same population dynamics at all probe frequencies, with different transient spectra for the three states (i.e., different spectral contributions of the three states, see Figure S10). Similar to previous reports on the relaxation of strongly hydrogen-bonded complexes,^13,51 this three-state model can describe the experimental data with the least number of adjustable parameters: As can be seen from the solid lines in Figure 6a and b, the model excellently describes the experimental data for the DPP–Qu mixtures at t > 0.1 ps, while a two-state model cannot fully capture the dynamics at 0.1 ≤ t/ps <5 (see the red dashed line in Figure 6b). From this model, we find the initial relaxation time τ_A to be very fast, ∼100 fs (Figure 6c). Such short relaxation time is common to strongly hydrogen-bonded complexes^13,51 and is again indicative of strong (anharmonic) coupling to lower-frequency modes, as the coupling provides efficient transfer paths for the excess vibrational energy. Yet, we find that the acid–base composition hardly affects these dynamics (Figure 6c).

In contrast to the composition-independent values of τ_A, we find that τ_B—the relaxation from the intermediate state 0′—depends on the molar ratio of acid and base (Figure 6c). With increasing concentration of Qu, τ_B becomes shorter (τ_B ≈ 0.8 ps at c_Qu = 0.75 mol L^–1), whereas the relaxation is slower for an excess of the acid (τ_B ≈ 1.1 ps at c_Qu = 0.25 mol L^–1). This variation of the relaxation rate suggests that the formation of multimers affects vibrational energy relaxation pathways: With increasing acid concentration the vibrational energy is contained within the excited molecular complex for a longer time. This is again in broad concordance with vibrational coupling within multimers being markedly different than in dimers as concluded from the 2D-IR experiments.

Concluding Remarks

We report on the composition-dependent vibrational structure and dynamics of hydrogen-bonded complexes consisting of the base quinaldine and diphenyl phosphoric acid. At all compositions we find broad absorption features in the infrared absorption spectra spanning more than 1000 cm^–1—common to strongly hydrogen-bonded complexes. Upon addition of quinaldine to a solution of diphenyl phosphoric acid, the infrared absorption gradually red-shifts to lower frequencies, and for an excess of base the observed absorbance peaks at ∼2040 cm^–1. Spectral decomposition and DFT calculations show that the formation of doubly ionic hydrogen bonds between DPP and Qu and singly ionic hydrogen bond between DPP and DPP^– give rise to this red-shift. The associated proton potentials of these bonds are very anharmonic: within the doubly ionic hydrogen bonds the proton is localized near the base in its vibrational ground state but becomes more delocalized in the first excited state. Thus, the width of the absorption spectrum can be attributed to anharmonic coupling of the proton vibrations to other modes together with thermally induced fluctuations.

Ultrafast infrared experiments reveal very fast vibrational relaxation on a ∼100 fs time scale after excitation at ∼2000 cm^–1. This fast vibrational relaxation goes along with (transient) population of lower-frequency vibrational modes, which give rise to longer-lived (0.8–1.1 ps) spectral modulations. A delayed off-diagonal peak in the 2D-IR spectra, which is most pronounced for an excess of acid, suggests that some of these lower-frequency vibrational modes are strongly coupled to both the ⁺N–H···^–O–P hydrogen bond and the P–O^–···H–O–P hydrogen bond in multimers. The composition-dependent coupling also affects energy relaxation pathways, and our results suggest that the vibrational energy remains more localized within the multimers over longer times, as compared to the hydrogen-bonded dimers/ion-pairs, as evidenced by the longer equilibration time τ_B for an excess of DPP.

As such, our results indicate that the acid:base ratio affects the vibrational structure and dynamics. Even for equimolar mixtures, where one could intuitively assume solely 1:1 aggregation, formation of trimers and/or larger multimers results in additional vibrational couplings and dynamics that differ from those of isolated acid–base dimers. More generally, our results indicate a composition dependence of the very fast proton dynamics in strong, doubly ionic hydrogen-bonded aggregates of DPP and quinaldine, which are relevant to Brønsted acid organocatalysis. Fast vibrational relaxation and strong coupling of the studied vibrational modes show that the doubly ionic hydrogen bond can efficiently dissipate excess energy from Qu into lower-frequency modes. Coordination of an additional DPP molecule to form a trimer alters hydrogen-bond strengths, energy transfer paths, and transfer rates. These altered properties of the acidic site may be also relevant to substrate activation and transport of energy upon chemical conversion for catalyses involving two acidic groups, where the combination of two acidic moieties can enhance catalytic efficiency.⁸⁶ Overall, our findings highlight a high degree of collectivity of the hydrogen bonds in such multimeric aggregates.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c04714.

• Full spectral range infrared absorption spectra and details of the component decomposition; details of the DFT calculations and calculations of the vibrational transitions; additional pump–probe experiments together with details of the kinetic modeling of the infrared pump–probe data (PDF)

The authors declare no competing financial interest.