Optimizing immunization protocols to elicit broadly neutralizing antibodies

Significance

The global health burden could be substantially alleviated by the creation of universal vaccines against highly mutable pathogens like HIV and influenza. Broadly neutralizing antibodies (bnAbs) are encouraging targets for such vaccines, because they can bind to diverse strains of these pathogens. BnAbs typically develop only after the immune system has been exposed to many mutated versions of a pathogen, and then too in few people and low numbers. Thus, sequentially administering multiple different pathogen-like proteins is a promising strategy to elicit bnAbs through vaccination. However, it remains unclear how best to design/administer these proteins. We explore this using physics-based simulations and provide mechanistic insights into antibody evolution that could guide creation of universal vaccines against highly mutable pathogens.

Abstract

Natural infections and vaccination with a pathogen typically stimulate the production of potent antibodies specific for the pathogen through a Darwinian evolutionary process known as affinity maturation. Such antibodies provide protection against reinfection by the same strain of a pathogen. A highly mutable virus, like HIV or influenza, evades recognition by these strain-specific antibodies via the emergence of new mutant strains. A vaccine that elicits antibodies that can bind to many diverse strains of the virus—known as broadly neutralizing antibodies (bnAbs)—could protect against highly mutable pathogens. Despite much work, the mechanisms by which bnAbs emerge remain uncertain. Using a computational model of affinity maturation, we studied a wide variety of vaccination strategies. Our results suggest that an effective strategy to maximize bnAb evolution is through a sequential immunization protocol, wherein each new immunization optimally increases the pressure on the immune system to target conserved antigenic sites, thus conferring breadth. We describe the mechanisms underlying why sequentially driving the immune system increasingly further from steady state, in an optimal fashion, is effective. The optimal protocol allows many evolving B cells to become bnAbs via diverse evolutionary paths.

Successful vaccines stimulate immune responses that can protect the host from infection by a specific pathogen. Such a vaccine is usually unable to protect against the diverse circulating strains of highly mutable pathogens. Examples include viruses like HIV and the hepatitis C virus (HCV) (1). Such a vaccine can also not serve as a universal vaccine against variant strains of the influenza virus that arise annually. Creating an effective universal vaccine against highly mutable pathogens will likely require a novel approach to vaccine design.

Successful prophylactic vaccines induce the immune system to generate antibodies (Abs) that can bind to and neutralize the pathogen. The process that governs Ab production upon pathogen (or antigen, Ag) encounter/vaccine stimulation is a stochastic Darwinian evolutionary process called affinity maturation (AM) (2, 3). First, a few B cells become activated upon binding of their B cell receptors (BCRs) to the Ag with sufficient affinity. Activated B cells can then seed microstructures called germinal centers (GCs) in the spleen and lymph nodes. During AM, B cells proliferate, and upon induction of the activation-induced cytidine deaminase (AID) gene mutations are introduced into the BCR at a high rate via a process known as somatic hypermutation (SHM). The B cells with mutated receptors then interact with the Ag displayed on the surface of GC-resident follicular dendritic cells (FDCs) and attempt to bind and internalize the Ag. B cells with BCRs that bind to the Ag with higher affinity are more likely to internalize Ag. The internalized Ag is then processed and displayed on the surface of B cells as peptide-major histocompatibility complex (MHC) molecules. B cells that display peptide-MHC molecules then compete with each other to interact with T helper cells, productive binding of whose T cell receptors to peptide-MHC molecules delivers a survival signal. B cells that bind more strongly to the Ag on FDCs are likely to internalize more Ag and thus likely to display more peptide-MHC molecules on their surface, and are therefore more likely to be positively selected (4). B cells that do not bind the Ag strongly enough or do not receive T cell help undergo apoptosis (5, 6). A few positively selected B cells exit the GC and differentiate into Ab-producing plasma cells and memory B cells, while the majority are recycled for further rounds of mutation and selection (3, 7). Upon immunization with a single Ag, as cycles of diversification and selection ensue, Abs with increasingly higher affinity for the Ag are thus produced (8).

One promising strategy for the development of an effective vaccine against HIV is to induce the immune system to generate broadly neutralizing antibodies (bnAbs) that can neutralize diverse strains of mutable pathogens. bnAbs that can neutralize most HIV strains in vitro (9–12) and diverse influenza strains have been isolated (13, 14). These Abs target regions or epitopes on the surface of pathogenic proteins that contain amino acid residues that are relatively conserved because they are key to the virus’ ability to propagate infection in human cells. One possible strategy to generate bnAbs is to vaccinate with an immunogen (an immune response-eliciting Ag) containing only these conserved residues. This tempting solution is impractical, however, because the Abs thus generated cannot learn how to bind to the conserved residues in the molecular context in which they are presented on the pathogen’s surface. For example, an important target of bnAbs against HIV is the CD4 binding site (CD4bs) on the virus’ spike, and the conserved residues therein are surrounded by glycans and variable residues that, due to the three-dimensional (3D) nature of the HIV spike proteins, partially shield BCRs from binding to the conserved residues. In fact, mutations in variable antigenic residues can insert loops that further hinder access to conserved residues (15). Similarly, for influenza, the receptor binding site on the head of its spike is surrounded by variable residues (13), and another conserved region in the stem of the spike is sterically difficult to access because of the high density of spikes on the influenza virus’ surface (16). A potentially promising vaccination strategy that may elicit bnAbs is to first administer an Ag that can stimulate germline (GL) B cells that can target the pertinent conserved residues, followed by immunization with variant Ags that share the same amino acids at conserved positions but diverse amino acids at the surrounding variable positions presented in the same molecular context as in the real pathogen’s spike. A deep understanding of how Abs evolve in such a vaccination setting is required to be able to guide the design of optimal vaccination strategies that can efficiently stimulate the production of bnAbs (17–21) against different highly mutable pathogens in diverse individuals. Developing this knowledge also presents an interesting challenge at the intersection of immunology, evolutionary biology, and biophysics.

In cases where bnAbs develop in HIV-infected individuals, their emergence typically occurs only after several years of infection. During this time, the immune system of the infected individual has been exposed to many different antigenic strains of the rapidly mutating virus (22–24). BnAbs against influenza have similarly been observed to emerge in individuals upon exposure to antigenically distinct strains of the virus (13, 14). However, there are differences and similarities between the reasons that underlie the rarity of bnAbs upon natural infection with influenza and HIV. One similarity is that there are many epitopes on the spikes of both viruses that are highly variable, and these are usually targeted in an immunodominant fashion. The conserved stem epitope on influenza’s hemagglutinin (HA) spike protein is subdominant largely because of the high spike density of influenza, as mentioned earlier, which imposes a strong steric barrier to the evolution of bnAbs that target this conserved epitope. This is the principal reason for the rarity of such bnAbs, not because many mutations have to evolve. For the CD4bs epitope on the HIV spike, which is a target of potent bnAbs, acquiring several mutations seems to be necessary for evolving bnAbs. Several lines of evidence suggest that this is true. First, studies wherein the GL B cells that evolved to bnAbs have been identified show that they can bind weakly to the target epitope (25–27). Second, bnAbs acquire many mutations compared to the corresponding GL B cells to acquire breadth, and some of these mutations are critical for breadth (28). The importance of evolving multiple mutations for anti-CD4bs bnAbs is most likely because the conserved residues of this epitope occupy a region smaller than the footprint of a typical Ab.

Despite the differences and similarities mentioned above, the data suggest that in the case of both HIV and influenza, being selected by different, but somewhat related, Ags promotes the evolution of bnAbs. The diverse infecting Ags serve as selection forces that shape Ab evolution during AM. Can properly designed vaccination protocols using variant Ags that share conserved residues but differ in the variable regions result in AM that elicits bnAbs efficiently in diverse individuals? If so, a strategy for developing vaccines against highly mutable pathogens would be available. This tantalizing possibility has led to a great deal of research directed toward achieving this goal. Here, we note just a few advances in this regard that have resulted from work focused on eliciting bnAbs against HIV. Strategies and immunogens have been designed to activate the correct GL B cells that can target conserved residues on the HIV viral spike, which have the potential for developing into bnAbs upon subsequent immunization with variant Ags (29–31). Computational studies have explored how variant Ags impact the process and outcomes of AM (32–34). The variant Ags have been described as serving as conflicting selection forces because a BCR/Ab that binds well to one of the variant Ags is unlikely to bind well to another variant Ag unless relatively strong interactions with the shared conserved residues evolve. The presence of such conflicting selection forces has been termed “frustration,” too much of which has been shown to result in substantial B cell death/GC extinction (33, 34). Studies have suggested that, in some instances, sequential immunization with variant Ags may elicit bnAbs more efficiently than a mixture of the same Ags (30, 33–39). These studies also highlight the importance of separating the conflicting selection forces (or sources of frustration) over time to minimize significant B cell death and of using multiple immunizations to help the developing Abs acquire mutations that focus their binding on the conserved residues, and thus confer breadth. It has also been suggested that mixtures can potentially be optimally designed to promote bnAb formation while minimizing cell death by manipulating the vaccine dose and mutational distance between Ags (34), thus identifying these variables as two further sources of frustration that can influence the outcome of AM.

Despite this progress, several questions remain to be answered to devise immunogens and vaccination protocols that can efficiently induce bnAbs. In particular, 1) which Ags should be used as immunogens (number of Ags and their sequences/compositions) and 2) how should they be administered in time? Given the high diversity of the variable residues as well as the broad range of possible BCR–Ag binding sites, the number of Ags that share conserved residues and the number of different immunization protocols are too great to test all possible combinations of these Ags and protocols with experiments in animal models. It is, however, possible for computational/theoretical studies to elucidate the effect of these variables and evaluate the outcomes in terms of both the quality (mean breadth) and quantity (titers) of the produced Abs. These models could provide new insights into how immunogens and vaccination protocols influence bnAb evolution and thus help to guide the design of an Ab-based vaccine against highly mutable pathogens. Such studies can also shed light on fundamental questions in immunology and biophysics.

In this study, we used a computational model to explore how different sets of variant Ags administered sequentially at different concentrations influence the evolution of bnAbs by AM. We assume that a GL-targeting scheme has already taken place prior to vaccination to activate the correct bnAb precursors (29–31). This is why we consider only the effects of mutation on bnAb evolution, rather than the effects of competition with GL B cells that target immunodominant, variable epitopes. In support of this approach, GL targeting has been successfully employed to activate bnAb precursors against the CD4bs of HIV (29–31), allowing for subsequent vaccination steps to focus primarily on evolving bnAb-like mutations.

By quantifying frustration and characterizing its impact on AM, we predict that Ags and vaccination protocols that result in a temporally increasing level of frustration on GC reactions promote optimal bnAb responses. This can be realized, for example, by decreasing the Ag concentration for each new immunization, or by immunizing with increasingly dissimilar Ags. Our results further indicate that an intermediate amount of frustration during each new immunization is optimal. The optimum is defined by the highest level of frustration allowed that does not result in extensive GC collapse/cell death. We describe the mechanisms underlying these results, which highlight that an appropriate level of diversity among B cells needs to evolve early on. This optimal level of diversity allows B cells to subsequently acquire mutations that confer breadth by diverse evolutionary trajectories.

Results

Description of the Computational Model of AM.

Overview.

We built a simple computational AM model of B cells in the presence of different Ags that can be introduced at several time points. We simulate the processes that occur during AM using a stochastic model, as is appropriate for an evolutionary process. The set of rules that define AM are derived from experimental studies of AM with a single Ag (3, 40–42), and these serve as instructions that are executed by the computer. The goal of this model is not the quantitative reproduction of existing experiments but rather to provide mechanistic insights into how the nature of variant Ags and immunization protocols influence the development of Ab breadth and bnAb titers. While our model represents the steps of AM, it does not explicitly account for B cell migration within a GC or employ an atomistically detailed representation to compute the free energy of binding of a BCR to Ags. The model is based on those of previous works (26, 33, 34), but there are a number of new features that are described below. All parameters that will be discussed are listed in SI Appendix, Table S1.

Binding free energy.

As in the models described by Wang et al. (33) and Luo and Perelson (43), the BCR paratope and the Ag epitope of interest, which we will from here on refer to as BCR and Ag, respectively, are both represented by a string of residues. The BCR and the Ag have identical lengths (46 residues total; 28 variable and 18 conserved residues), so the BCR residue at position k binds to the antigenic residue located at the same position k. For the BCR, the identity of each residue is designated by a number, whose value was sampled from a continuous and bounded uniform distribution; variable residue values were bounded between −0.18 and 0.90, and conserved residue values were bounded between 0.3 and 0.6 (see the following section for more details). Note that these specific bounds only apply to the seeding B cell residues, and that the bounds for both variable and conserved residues change after the AID gene turns on and AM begins (SI Appendix, Table S1); after mutation, if the BCR residue value is outside of these bounds, the residue value is set to be equal to the closest bounded value. Similarly, each Ag residue is designated by a number. The value of this number corresponding to a conserved Ag residue is always +1, while the value of a variable residue can be either +1 (nonmutated) or −1 (mutated). The binding free energy depends on the strength of the interactions between the BCR and the Ag. We model this binding free energy as a sum of all pairwise interactions between the BCR and the Ag, estimated as the product of the values that describe the identity of each BCR residue and its analogous antigenic residue. Thus, the binding free energy is

$$E=\sum _{all\hspace{1em}residues\hspace{1em}k}BCR\left(k\right)\cdot Ag\left(k\right).$$ [1]

More positive binding free energies correspond to stronger affinities. This simple expression for the binding free energy is further embellished to account for the effects of 3D conformations of the BCR and Ag as described in context below. The absolute value of the binding free energy is arbitrary as it is determined only up to an additive constant. All binding free energies in our model are expressed in units of the thermal energy (k_BT). We assume that a binding free energy of 9 k_BT is the minimum requirement for Ag binding and therefore only B cells that bind to an Ag with a binding free energy above this threshold can seed a GC. The value of this threshold binding free energy sets the scale for our calculations, and we do not expect qualitative results to depend upon this particular choice.

GL targeting and activation of a GC.

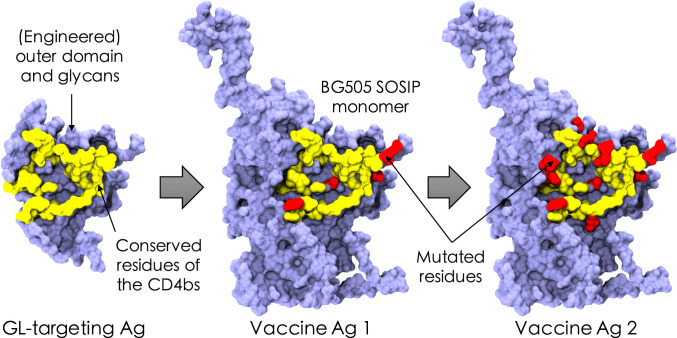
Immunizing with Ags designed to target specific GL BCRs is a key first step to eliciting bnAbs (29, 31, 38, 44). This is because the number of potential BCR/Ab binding sites on the HIV envelope that do not contain conserved residues far exceeds those that could be bnAb epitopes (45). In the repertoire of naïve B cells, bnAb precursors are rare (31), and thus the precursor frequency of GL B cells that target epitopes that do not contain conserved residues is much higher. Thus, it is unlikely that bnAb precursors will be activated during a natural infection (46). Similar considerations apply to influenza bnAbs, where there are many more highly variable HA head epitopes than those that can potentially be epitopes for bnAbs. Immunization experiments for HIV try to remedy this challenge by priming with an Ag that focuses immune responses on conserved residues (Fig. 1, Left). Upon performing binding assays with the GL-targeting Ag eOD-GT8, it was found that the Ag bound with considerable affinity and breadth to all Abs on a panel of 14 GL-reverted Abs from VRC01-class bnAbs (31). This implies that Ab binding was achieved primarily through binding to conserved antigenic sites (16/58 residues at the eOD-GT8/Ab interface were relatively conserved across this panel), rather than through variable-site binding. Thus, the GL-targeting Ag imposed a selection force only on the residues of the BCRs that bound to conserved antigenic residues.

Fig. 1.

Schematic of the in silico immunization scheme, which consists of an assumed GL-targeting scheme (Left), followed by two immunizations with variant Ags that mimic the viral spike of HIV (Middle and Right). The GL-targeting Ag was inspired by the eOD-GT8 construct designed to target precursor naïve B cells against the CD4bs of HIV (31). Conserved residues of the CD4bs are schematically depicted in yellow, example mutated variable residues are shown in red, and the surrounding residues are shown in blue. Visual Molecular Dynamics (VMD) (47) was used to construct the images from Protein Data Bank ID code 5fyj (48).

Our model mimics the priming to activate the appropriate GL BCRs by seeding the first GCs, upon immunization with variant Ags, with a pool of B cells that we assume has been generated by a prior GL-activating immunization and thus bind to epitopes containing conserved residues (e.g., the CD4bs of HIV). Mimicking the BCRs produced through GL-targeting experiments (29), we chose the residues of the BCRs that bind to the conserved residues of the Ag to be slightly biased toward positive values, reflecting that they favor these residues because they were activated initially by the GL-targeting immunogen. Since no specific selection force was imposed on the residues of these BCRs that bind to the variable residues of the Ags, these were chosen to be highly variable among the seeding B cells. Experiments have shown that the number of seeding B cells varies between a few to a hundred cells (42). We chose to seed GCs with 10 cells; changing this number did not affect our qualitative results. We assume that the GL-targeting immunogen residues are all +1s. This is just a reference sequence, and a different choice would lead to a linear shift in the mutational distances that we calculate for the variant Ags used for subsequent immunizations, and thus would have no effect on the qualitative results we report.

B cell expansion and SHM in the dark zone.

The B cells expand in the dark zone of the GC without mutation or selection for just over a week, reaching a population size of exactly 5,120 cells (2⁹ for each of the 10 seeding B cells and constant for all GC reactions prior to B cell division/mutation). After the initial expansion of the B cell population, the AID gene turns on and mutations are introduced into the BCRs with a probability determined by experiments: Each B cell of the dark zone divides twice per GC cycle (four divisions per day) (49), and mutations appear at a high rate (0.14 per sequence per division) (41). These mutations are known as SHMs and can have various effects on the fate of a B cell (50, 51). Recent evidence suggests that B cells that internalize more Ag divide more times (4), but this effect is not included in our simulations. Experiments have shown that SHMs are lethal 50% of the time (for example, by making the BCR unable to fold properly), are silent 30% of the time (due to redundancy of the genetic code, that is, synonymous mutations), and modify the binding free energy 20% of the time (41). The energy-affecting mutations are more likely to be detrimental; experiments have determined that across all protein–protein interactions, only ∼5 to 10% of energy-affecting mutations strengthen the binding free energy (52).

For mutations that affect the binding free energy, a particular residue on the BCR is randomly picked to undergo mutation. The change in the strength of binding between this BCR residue and the complementary antigenic residue is sampled from a bounded lognormal distribution whose parameters are chosen to approximate the empirical distribution of changes in binding free energies of protein–protein interfaces upon single-residue mutation (49). Thus, the random change in binding free energy ΔE is drawn from the following probability distribution:

$$\mathrm{\Delta }E=\epsilon -\exp \left(\mu +\sigma r\right)\hspace{1em}\text{and\hspace{1em}}-\delta <\mathrm{\Delta }E<\delta ,$$ [2]

where r is a standard normal variable with mean zero and SD equal to one. Here $\epsilon$ is a shift parameter, which is needed to center the lognormal distribution properly with respect to zero, and μ and σ are the mean and SD of the lognormal distribution, respectively. The parameters of the lognormal distribution ($\epsilon$, μ, σ, and r) are set so that only 5% of mutations increase the binding free energy and so that the tail of harmful mutations fits the distribution obtained by experiments. The additional parameter δ limits the effect of a single-residue mutation, chosen to prevent the B cell population from succeeding too fast and exceeding the average time for the GC population to reach its initial size after vaccination or infection with a single Ag (Parameters).

Steric and conformational effects on BCR–Ag interactions.

The effects of Ag residues that shield the conserved residues from being accessed easily by the BCR are incorporated into the model to account for the 3D nature of BCR-Ag interactions. Mutations in variable residues can insert loops that hinder access to conserved residues (15): Greater binding to loop residues reduces access to conserved residues, and vice versa. The insertion or deletion of a loop can drastically change the binding free energy (53). In particular, a new interaction with a loop residue can completely prevent BCR binding to nonloop residues and greatly lower the binding free energy. We mimic this effect as follows. If mutation of a BCR residue results in a stronger interaction with a variable antigenic residue, the interaction between a randomly chosen BCR residue that binds to a conserved antigenic residue is proportionally decreased by a factor α (Eq. 3). Similarly, a weaker interaction with a variable residue leads to a proportional increase in the binding to a conserved residue. The boundary for the free energy change due to a loop δ_L is chosen to be the same as that for a single-residue mutation (δ). This feature in our model favors the emergence of mutations that alleviate steric effects because it strengthens binding to conserved residues, and this aids binding to multiple variant Ags. Mathematically, this effect is described in Eq. 3 (see SI Appendix for an explanation of the choice of the parameter, $\alpha$):

$$\mathrm{\Delta }{E}_L=-\alpha \mathrm{\Delta }E\hspace{1em}\text{and\hspace{1em}}-{\delta }_L<\mathrm{\Delta }{E}_L<{\delta }_L.$$ [3]

Selection in the light zone.

After SHM, the mutated B cells migrate to the light zone of the GC, where selection takes place through competition for binding to Ag and receiving T cell help (4). B cells with the greatest binding free energy for the Ag presented on FDCs have a better chance to bind to that Ag and present its peptides on their MHC molecules to receive T cell help. Productive interactions with T helper cells results in positive selection, and otherwise B cells undergo apoptosis (54–56). We model this biology with a two-step selection process. First, each B cell successfully internalizes the Ag it encounters with a probability that grows with the binding free energy and then saturates, following a Langmuir form (Eq. 4). Only the B cells that successfully internalize Ag can then go on to the second step. The surviving B cells are ranked according to their binding free energy, a proxy for the concentration of peptide-MHC molecules that they display, and only the top 70% are selected (F_help,cutoff = 0.70). This selection probability, as well as the parameter e_scale in Eq. 4 below (pseudo inverse temperature, chosen to be 0.08 k_BT⁻¹), were manually adjusted to fit with experimental observations of GC dynamics upon single-Ag administration (see Parameters for more details) (42). The probability of B cell j internalizing Ag i depends on the binding free energy $E_i^j$ and the concentration c_i of that Ag, as well as the energy scale e_scale and the activation threshold E_act:

$$P_{internalize}=\frac{c_i\cdot e^{e_{scale}\left(E_i^j-E_{act}\right)}}{1+c_i\cdot e^{e_{scale}\left(E_i^j-E_{act}\right)}}.$$ [4]

Recycling to the dark zone, exit for differentiation, and termination of the GC reaction.

Most B cells that are positively selected are recycled for further rounds of mutation and selection (P_recycle = 0.70), while a few randomly selected B cells exit the GC to mimic differentiation into memory and Ab-producing plasma cells (7). As a proxy for the fact that all of the Ag will be consumed by internalization if a sufficient number of B cells successfully mature, the GC reaction is terminated if the number of B cells exceeds the initial GC population size of 5,120 cells (termed a successful GC reaction). Due to the stochastic nature of the simulations, the final B cell population size can exceed 5,120 cells (average of ∼5,400 ± 200 cells). In addition, to reflect Ag degradation over time, termination occurs when the number of cycles before the GC recovers its initial size exceeds 250 (125 d). The GC reaction also ends if all B cells die.

Seeding a new GC with previously produced memory B cells after a new immunization.

Every memory B cell that exits a GC is in circulation and could be reactivated by a second exposure to the Ag that initially triggered its development. Memory B cells can also then seed a new GC upon immunization with a second Ag that is different from the first Ag but shares conserved residues. The new GCs could also be seeded by naïve B cells that target the epitope of interest, as has been described in a recent study (57). The fraction of such naïve B cells that seed a new GC likely depends on the precursor frequencies of naïve B cells compared to the memory B cells, and the affinity advantage of the latter population. Here we consider that only memory B cells undergo AM upon the second immunization. This assumption is valid if 1) memory B cells outnumber the naïve precursor B cells and/or have a significant advantage in affinity for the target bnAb epitope and/or 2) the second Ag is given sufficiently soon after the first immunization such that it joins ongoing GCs with the first Ag almost depleted. Naïve B cells that target a different epitope without conserved residues can also seed the second GC. We assume that this does not happen because the second vaccine Ag has been designed to minimize off-target binding (e.g., by glycan shielding). For instance, Briney et al. (38) recently demonstrated that changing the exposed antigenic surface area in each subsequent immunization (via altered surface glycosylation patterns) reduces off-target responses, promoting the response of memory cells. In our model, 10 memory cells are randomly chosen to seed a new GC.

Parameters.

Our model depends on several parameters (SI Appendix, Table S1). Many of these parameters represent specific biological quantities, while the remaining parameters arise because of the coarse-grained nature of the model. The biological quantities can be split into those that have already been assessed by experiments—such as the SHM rate and the fate of mutations—and those that have yet to be measured experimentally. We estimated the latter type of biological quantities by making reasonable guesses. Experiments have so far focused on AM in the case where only one Ag is present, and thus we fit the parameters so that the simulation results are in qualitative agreement with experiments with a single Ag. Using this methodology, we fit the following parameters that control both the growth of the B cell population and the properties of the produced Abs: 1) F_help,cutoff, the fraction of B cells that receive T cell help after binding Ag; 2) e_scale, the factor multiplying k_BT in the equation for P_internalize (Eq. 4); 3) P_recycle, the probability to be recycled from the light zone to the dark zone; and 4) δ, the maximum value of a single-residue mutation. F_help,cutoff, e_scale, P_recycle, and δ are adjusted so that the population decreases sharply at the beginning of AM until a few beneficial mutations appear and allow for survival of a few B cells. Then the population plateaus for about 20 d until enough good mutations accumulate to increase the binding free energy dramatically. The population then rises quickly until it reaches and exceeds the initial size of 5,120 cells, ∼60 d postimmunization. The affinity of the Abs produced during AM with a single Ag accumulate about 10 mutations and see their binding affinity grow by at least 1,000-fold (42). With our chosen parameters (SI Appendix, Table S1), our model reproduces these features well.

Output/analysis.

For each GC reaction we record the total number of B cells over time, their binding affinities to a test panel of Ags to define the breadth of each Ab (discussed below), the number of energy-affecting mutations acquired by each BCR, the value of each residue (identity of pseudo amino acid) of every BCR, and the binding free energy of the BCR and the Ag it interacted with in the light zone during the GC reaction. Due to the stochastic nature of AM, we executed many simulations under identical conditions (discussed below) and aggregated the results to obtain meaningful statistics. As in the AM model described by Ovchinnikov et al. (26), we group B cells into sets of functionally identical B cells, called B cell clones. All cells of a clone have the same properties, including binding free energies, number of mutations, and breadth. The size of a clone varies with time and its evolutionary trajectory.

In order to determine the breadth of coverage of each Ab, we compute the binding free energy of each clone against an artificial panel of 100 Ags different from those that the clone matured against. We found that increasing the size of the panel to 1,000 Ags produced little to no change in our breadth estimates. These panel Ags share the conserved residues but the value of the variable residues has equal chance to be +1 or −1. We compute the binding free energies of the clone for each panel Ag and the breadth is calculated as the fraction of panel Ags for which the clone binds with a binding free energy above a certain threshold E_th (Eq. 5). The threshold was set to 12 k_BT so that B cells produced by single-Ag immunization had a breadth of 0. This criterion reflects the fact that the mutations required to confer breadth are unlikely to evolve in appreciable numbers in a single immunization, as implied by the fact that naturally evolving bnAbs usually emerge several years after infection, and sequential immunizations with variant Ags results in the evolution of bnAb-like Abs in mice (33, 35).

$$breadth\left(clone\hspace{0.17em}j\right)=\frac{1}{N_{panel\hspace{1em}Ags}}\sum _{all\hspace{1em}panel\hspace{1em}Ags\hspace{1em}i}{E}_{ij}>E_{th\text{.}}$$ [5]

A lower threshold would define Abs generated from immunization with a single Ag as “broad,” while a higher threshold would result in few or no Abs that would ever be defined as broad. In fact, the affinity of B cells for a single Ag can increase during AM by up to a few thousandfold but above a certain value the affinity saturates. The goal of this boundary may be to safeguard against potential autoimmune responses (58). We ran 1,000 GC trials per vaccination setting and calculated a mean breadth of all clones produced across all 1,000 GC trials (Eq. 6). We then averaged this mean clonal breadth across multiple simulations for each vaccination protocol studied.

$$mean\hspace{0.17em}clonal\hspace{0.17em}breadth=\frac{1}{N_{clones\hspace{1em}in\hspace{1em}all\hspace{1em}GCs}}\sum _{\begin{array}{c}all\hspace{0.17em}clones\hspace{0.17em}j\\ in\hspace{0.17em}all\hspace{0.17em}GCs\end{array}}breadth\left(j\right)\text{.}$$ [6]

Apart from breadth, the quantity of high-breadth Abs produced (bnAb titers; clonal breadth >0.8) by a vaccination protocol is a key metric of success. This is because low titers of bnAbs are unlikely to confer protection. A universal and efficient vaccine would likely need to elicit sufficiently high titers of high-breadth Abs. Thus, apart from the mean clonal breadth for a given vaccination setting, we also compute the average bnAb titers/GC (referred to simply as the bnAb titers/GC). We ran 1,000 GC trials per vaccination protocol and combined the outcome of all 1,000 trials in our calculations (Eq. 7). As with the mean clonal breadth, we then averaged this value across multiple simulations for each vaccination protocol.

$$bnAb\hspace{1em}titers/GC=\frac{1}{N_{GCs}}\sum _{\begin{array}{c}all\hspace{0.17em}clones\hspace{0.17em}j\\ in\hspace{0.17em}all\hspace{0.17em}GCs\end{array}}breadth\left(j\right)>0.8\text{.}$$ [7]

Due to the large number of GCs we analyzed (1,000) for each vaccination setting, our statistical results are robust (SI Appendix, Fig. S1).

An Optimal Level of Frustration Maximizes bnAb Titers.

We studied the situation where there are two sequential immunizations following the consequences of an assumed GL-targeting immunization (Fig. 1; see the previous section on GL targeting). Past work has shown that variant Ags subject B cells undergoing AM to conflicting selection forces, an effect referred to as frustration because these forces can, under some circumstances, frustrate the evolutionary process and lead to GC collapse (33, 34). In other words, variant Ags have the effect of throwing the B cell population further off of steady state. The degree to which this occurs depends on how different the Ags are, and we refer to the extent to which the B cell population is thrown off of steady state as the level of frustration imposed on GC reactions. Past work has also shown that the extent of frustration can be modulated by changing the concentration of the Ags and the mutational distances between them (34). We first performed simulations of a single immunization with one Ag. In the results described below, we study the effects of the Ag concentration (c1) and the mutational distance (d1) between the vaccine Ag and previously administered GL-targeting Ag (sequence of all +1s).

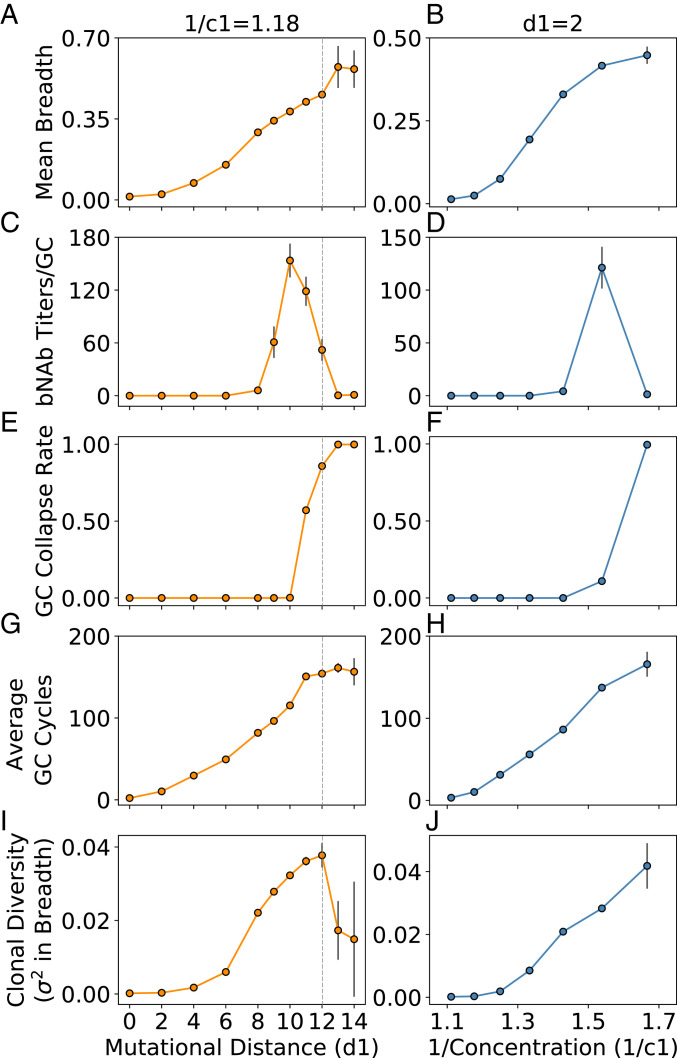
We find that the mean clonal breadth increases with increasing frustration (Fig. 2 A and B), arising from changes in sequence (as d1 is increased) and concentration (as 1/c1 is increased). The bnAb titers/GC goes through a maximum with changes in frustration (Fig. 2 C and D). The origins of these results can be understood as follows. At low frustration (Fig. 2, d1 ≤ 6, Left; 1/c1 ≤ 1.25, Right), the GC success rate—defined as the fraction of GCs (n = 1,000) for which the reaction terminates successfully, that is, for which the B cell population recovers/exceeds its initial size—is high (Fig. 2 E and F; n.b.: GC collapse rate = 1 – GC success rate). However, due to the ease with which the GC B cells can succeed at being positively selected, there is too little time to acquire mutations before the successful B cells consume all of the Ag and the GC reaction ends (Fig. 2 G and H), which results in a low diversity of clonal breadth (Fig. 2 I and J). As a consequence, essentially none of the B cell clones can acquire much breadth. This is illustrated by graphs showing the variation in breadth among the resultant clones (Fig. 3 A–D). Thus, the bnAb titers/GC are essentially zero.

Fig. 2.

The outcomes of AM after a single vaccine immunization (second overall immunization after GL targeting) are presented above after changing mutational distance d1 at constant concentration 1/c1 (Left) and concentration 1/c1 at constant d1 (Right). The measured parameters from the simulations are mean clonal breadth (A and B), bnAb titers/GC (C and D), fraction of collapsed GCs (E and F), average number of GC cycles (G and H), and clonal diversity (variance in breadth; I and J). Gray dotted lines indicate the point beyond which GCs are unlikely to be seeded due to a low Ag–BCR binding affinity. Error bars represent the SD of the mean across multiple simulations (n = 1,000 GCs). Note that some error bars are too small to be visible but are included on all points and are largest where some GC collapse occurs (introducing much stochasticity into the data), or at the highest levels of frustration where few statistics could be obtained altogether.

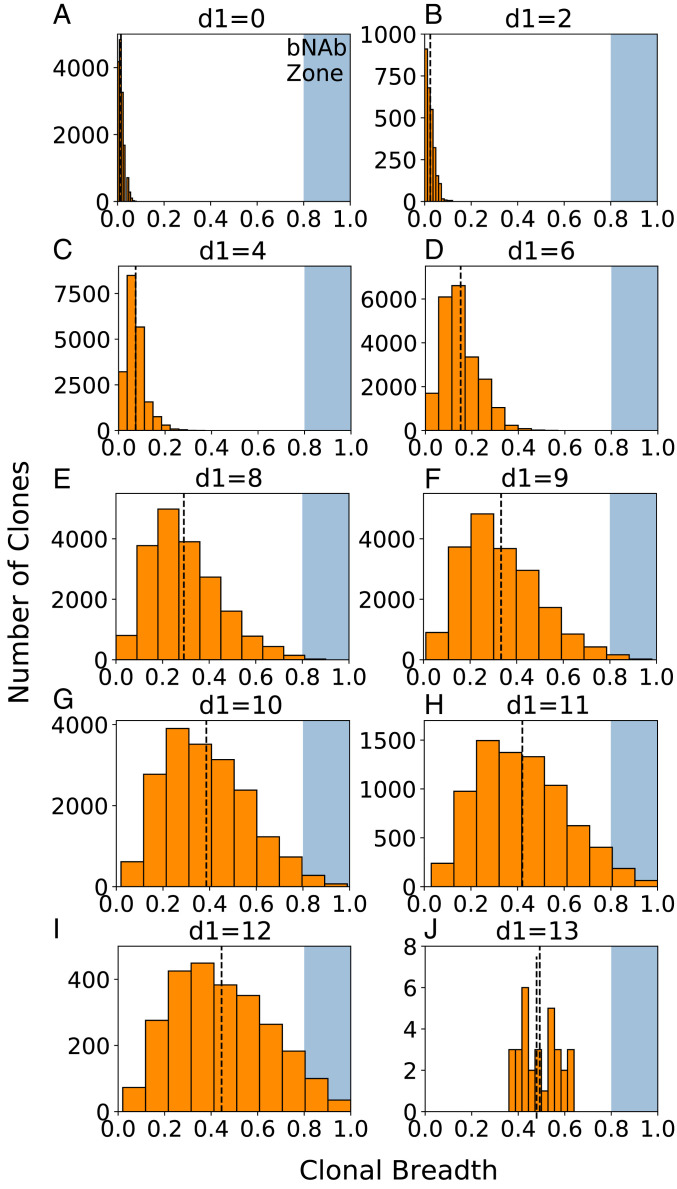
Fig. 3.

(A–J) Clonal breadth distributions characterize the diversity among clones across different GCs, corresponding to the points in Fig. 2 A, C, E, G, and I. A shaded blue region in each plot indicates the threshold above which BCRs are considered to have acquired breadth equivalent to a bnAb (breadth >0.8). The amount of overlap with this region (the “bnAb zone”) is indicative of the overall bnAb titers produced at the given vaccination condition indicated above each plot. A black dashed line indicates the mean clonal breadth at that particular vaccination setting. Results are plotted for all clones produced in 1,000 GC reactions at each vaccination setting.

As the level of frustration increases, the mean breadth and bnAb titers/GC begin to increase (Fig. 2: 6 < d1 ≤ 10, Left; 1.25 < 1/c1 ≤ 1.54, Right). This is because positive selection of B cells is less likely and so the GC reaction can continue longer without Ag depletion, enabling BCRs to acquire more mutations and increase their breadth. Thus, a more diverse population of B cells evolves with some BCRs acquiring reasonable breadth (Fig. 3 E–G). As the frustration increases further, a point is eventually reached (d1 = 10, 1/c1 = 1.54 in Fig. 2 C and D, respectively) beyond which the likelihood of B cells being positively selected decreases sharply, resulting in extensive GC extinction. Any additional increase in frustration results in a decline in the bnAb titers/GC. At the level of frustration corresponding to the peak in the bnAb titers/GC, the number of GC cycles is as high as possible to allow for the most time to make affinity-increasing mutations without incurring major GC extinction. In other words, more time for AM to take place—enabled by more frustration—is beneficial for increasing the mean breadth, but ultimately hurts bnAb titers because of decreased GC success rates. Thus, an intermediate level of frustration optimizes the time for AM to take place, creating the best balance between the resultant mean breadth and bnAb titers/GC. Note that as bnAb titers decline, breadth can still increase, up to a point, because diverse clones can still evolve (Fig. 3).

Ultimately, when frustration becomes very high, all that happens is GC extinction. For example, beyond a mutational distance of 12, the binding free energy between the seeding B cells and the administered Ag would likely be too weak to seed an actual GC. Yet, such high frustration settings might still be achievable in an experimental setting by manipulating concentration, and so we proceeded to simulate this regime (Fig. 2, 1/c1 > 1.54, Right). The results for mutational distances beyond 12 were included purely for completeness (Fig. 2, d1 > 12, Left) and were achieved by simply not setting a threshold Ag–BCR binding affinity for starting the GC reaction. At these high levels of frustration, we find that the changes in the number of cycles and mean breadth stall, almost all GCs collapse rapidly, and the very small population of B cells that survives contains no bnAbs (requires lower concentrations than explored/presented to see in Fig. 2J). Under these conditions, there are only rare evolutionary pathways to success (explored later in more detail).

A Single Metric for Predicting Ab Properties after Multiple Immunizations.

Our results thus far show that properties of the clonal population vary in similar ways with the level of frustration (Fig. 2), either through modulating the mutational distance between Ags (d1) or concentration (c1). Additionally, our results suggest a trade-off in frustration exists between these two variables in the determination of mean breadth. For example, a mean breadth of 0.42 can be achieved with either (d1, 1/c1) = (11, 1.18) in Fig. 2A or with a decreased mutational distance but increased inverse concentration of (d1, 1/c1) = (2, 1.54) in Fig. 2B. We thus hypothesized that these sources of frustration could be combined into a single metric for predicting breadth, allowing for a simpler comparison of different temporal patterns of immunization. To test this hypothesis, we chose a simple linear combination of the two individual sources of frustration (Eq. 8):

$$TF{L}_1=SF{L}_1+w_1\cdot CF{L}_1=d1+w_1\cdot \frac{1}{c1}.$$ [8]

TFL refers to the total frustration level (subscript refers to the first vaccine immunization), due to the combined effects of the frustration originating from the mutational distance of the variant Ag from the GL-targeting Ag (SFL, sequence frustration level) and Ag concentration (CFL, concentration frustration level). Note that the CFL has been written as 1/c1 because administering less Ag results in a higher level of frustration during the GC reaction. The parameter w describes the relative weight of the two contributions to the total level of frustration. With a random initial guess for w, we calculated the value of TFL₁ for each simulation, and then graphed this value against the resultant mean clonal breadth for the simulation (Fig. 4A). The data were fit to a third-order polynomial, where a refined value of w₁ = 24.6 was obtained by maximizing the R² correlation value for the data. This value is in part determined by the relative impacts of the two individual sources of frustration on P_internalize (Eq. 4), which is described in more detail in the SI Appendix. We note that our formulation of TFL₁ is entirely empirical, and while we used a third-order polynomial to fit the data in this case, other functional forms may also have been appropriate (e.g., a sigmoidal fit). Furthermore, TFL₁ refers to the frustration experienced by the memory B cell population upon immunization with a new Ag. As B cells evolve by AM dynamics, the frustration level can decrease. The frustration can also change during AM because Ag is depleted from GCs as AM proceeds. We do not account for the latter effect.

Fig. 4.

TFL of the first single-Ag vaccine immunization (A and B) and two sequential single-Ag immunizations (C and D), versus the mean clonal breadth (A and C) and bnAb titers/GC (B and D). Black dashed lines in A and C indicate the polynomial and linear fits used to collapse the data, respectively (A: 512 points; C: 331 points, due to some cases of complete GC collapse after immunization 1). Each dot represents the average output from n = 1,000 GCs and is colored in D according to the corresponding value of TFL₁. Ten points were identified as outliers from each dataset due to a lack of statistics (<10/1,000 successful GCs) and removed before fitting.

With this approach, we find that the data collapses onto a single curve that is highly predictive of the mean breadth after immunization with a single Ag (Fig. 4A). Furthermore, with the same value of w_1, the bnAb titers/GC exhibits a maximum at an intermediate TFL₁ (Fig. 4B), thus encapsulating the results in Fig. 2. We note that while Fig. 4B indicates small changes in TFL₁ away from the optimal value will result in low bnAb titers/GC (e.g., a decrease of ∼2.6% from 39 to 38, or an increase of ∼7.7% to 42), the operating range widens when the bnAb titers/GC are instead graphed against the manipulated variable d1, as was shown in Fig. 2C (see also SI Appendix, Fig. S2). For example, Fig. 2C shows that at an Ag concentration of 1/c1 = 1.18, d1 can be decreased by ∼20% or increased by ∼30% beyond the optimal distance of 10 before the bnAb titers/GC approach 0. Additionally, SI Appendix, Fig. S2 shows that this range widens as 1/c1 is increased (i.e., at 1/c1 = 1.34, bnAb titers/GC are ∼0 at $\pm 43\%$ from d1 = 7).

We next wanted to determine if the TFL concept could be used as a metric to predict Ab properties after multiple immunizations, enabling us to determine the optimal way in which to manipulate frustration with time. As such, we simulated a second sequential single-Ag immunization (third immunization overall; Fig. 4 C and D), following the first single-Ag vaccine immunization. Here, we manipulated frustration by changing concentration (c2) and the average mutational distance (d2) between the current Ag and both previously administered Ags (GL-targeting Ag and first vaccine Ag). We hypothesized that the TFL after multiple immunizations is the product of the TFL of each individual immunization. This history-dependent formulation is based on the idea that each new immunization operates on the memory B cells that resulted from the previous immunizations. This more general form of Eq. 8 is shown in Eq. 9 for N immunizations, where ${\displaystyle \sum _{j\ne k}{d}_{jk}}$ indicates a summation over the mutational distances between the sequences of all pairs $\left(N_{pairs}\right)$ of Ags j and k administered across all immunizations. Here, b is a weight that renormalizes differences in the simulated ranges of the CFL and SFL values, discussed below. Terms with a subscript i in Eq. 9 refer to each individual immunization (e.g., TFL₁), and TFL{N} refers to the TFL after N non-GL-targeting immunizations:

$$TFL\left\{N\right\}={\displaystyle \prod _{i=1}^{N}TF{L}_i}={\displaystyle \prod _{i=1}^N{\left[SFL+w\cdot CFL\right]}_i}={\displaystyle \prod _{i=1}^N{\left[\frac{b}{N_{pairs}}{\displaystyle \sum _{j\ne k}{d}_{jk}+w\cdot \frac{1}{c}}\right]}_i}.$$ [9]

In this case, we fit the curve of TFL{2} versus mean breadth to a linear form, because the minimum energy needed to achieve breadth was easily exceeded for all TFL{2} values, eliminating the lower end of the sigmoidal-like curve. We also set the value of $w_2$ equal to that of the first immunization (24.6), and maximized the R² correlation value for the data to obtain a value of 1.6 for the correction factor b. Due to how we designed the Ags to avoid overlapping mutations, the SFL for the second immunization was higher than that of the first immunization by close to the same value (∼1.75 on average). Thus, in the second immunization, the impact of the SFL on mean breadth appeared to increase, requiring the correction factor to account for such effects. We find that Eq. 9 is highly predictive of the mean breadth after multiple immunizations (Fig. 4C). As before, we also find that the bnAb titers/GC are maximized at intermediate levels of frustration, graphed in Fig. 4D as the net frustration after all immunizations (i.e., TFL{2}). However, note that different levels of TFL₁ lead to different peak positions and maximal values of the bnAb titers/GC when the results are graphed against TFL{2}. In the following section, we investigate this behavior to better understand how to manipulate frustration over time to maximize bnAb evolution.

Optimally Increasing Frustration with Successive Immunizations Maximizes bnAb Production via Diverse Evolutionary Paths.

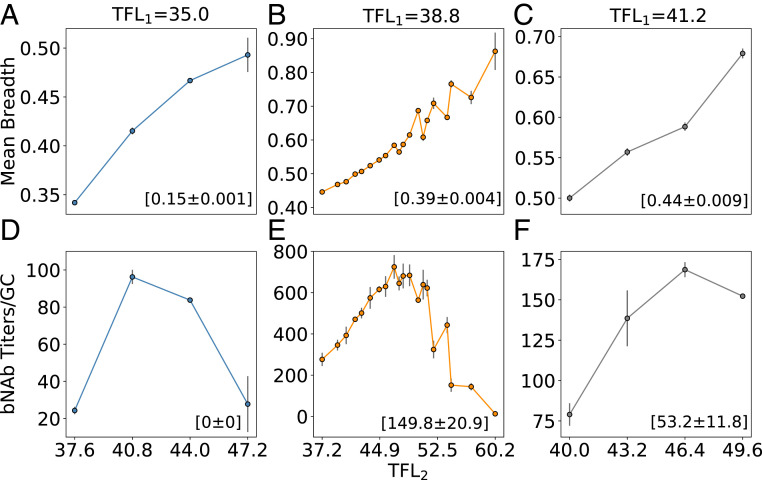
To determine the optimal way in which to manipulate frustration with successive immunizations (or time), simulations were performed that varied TFL₂ at constant values of TFL₁, namely at a low TFL₁ (Fig. 5 A and D), intermediate TFL₁ (Fig. 5 B and E), and high TFL₁ (Fig. 5 C and F). We find that regardless of the level of frustration imposed upon the immune system in the first immunization, an optimal level of frustration always exists for the second immunization that maximizes the bnAb titers/GC. The origin of the optimality in the bnAb titers/GC after the second immunization is the same as was described earlier for the first immunization. Notably, the optimal TFL₂ is always higher than the corresponding TFL₁. This result says that increasing the level of frustration in successive immunizations maximizes bnAb production. This is because after the first immunization some B cells are likely to have developed moderate to strong interactions with the conserved residues, and a stronger selection force is required for evolving additional mutations that can further focus their interactions on the conserved residues to acquire breadth. A higher level of frustration provides such a selection force to promote bnAb evolution. To shed more light on this finding, we calculated the fitness distributions of different B cells—which corresponds to their probability of internalizing Ag—and their associated selection coefficients (SI Appendix, Fig. S3). Given the selection probability $P_{internalize}$ of a sequence, the selection coefficient $s$ was calculated by normalizing $P_{internalize}$ with respect to the mean selection probability $\overline{P}$ of the population. We first performed a simulation of one single-Ag administration, where the Ag had a mutational distance of 9 from the GL-targeting Ag (case 1). Then, we performed a simulation of two sequential single-Ag administrations, where the mutational distances between the first and second vaccine Ags was 9 (case 2; TFL₂ > TFL₁). Concentration was kept constant across the two simulations and immunizations. The fitness distributions and selection coefficients of the B cells were calculated at the beginning of the first immunization for case 1, and at the beginning of the second immunization for case 2. The results show that in case 2, the B cells were better poised to successfully evolve into bnAbs during AM with the second Ag. This demonstrates that a higher level of frustration can be imposed fruitfully after B cells have evolved by AM induced by the first Ag.

Fig. 5.

Effect of changing the TFL administered in the second immunization (TFL₂), conditioned on (A, D) a low TFL administered in the first immunization (TFL₁), (B, E) an intermediate TFL₁, and (C, F) a high TFL₁, on the mean clonal breadth (A–C) and bnAb titers/GC (D–F) after the second vaccine immunization. Values in parentheses indicate the mean clonal breadth and bnAb titers/GC after the first immunization.

Comparing the maximum bnAb titer values in Fig. 5 D–F, we find that the highest titers are not only produced at intermediate values of TFL₂ but also at an intermediate value of TFL₁, which can also be observed in Fig. 4D. SI Appendix, Fig. S4 shows the validity of this finding across a wider range of TFL₁. Taken together, our results imply that each new immunization should be administered at an intermediate level of frustration above the optimum level in the previous immunization to maximize bnAb production. In light of likely deviations from optimality in any real immunization procedure, it is important to consider how large deviations from optimality can be while still achieving high bnAb titers. Fig. 5 D–F suggest that if the first immunization is performed below or above the optimum TFL₁, achieving high titers in the second immunization is not possible. However, if one does perform the first immunization below the optimum TFL₁, a route to moderate bnAb titers may be to perform the second immunization also at a suboptimal frustration, followed by a third immunization at an intermediate, optimal level of frustration. Performing the second immunization at suboptimal frustration will serve to keep the overall B cell titers high, while still allowing for some beneficial mutations to be acquired. We explored this strategy by performing simulations at a suboptimal TFL₁ of 35, followed by a second immunization at a suboptimal TFL₂ of 39, and finally by a third immunization spanning a TFL₃ of 41 to 51 (SI Appendix, Fig. S5). The results show that bnAb titers/GC of ∼360 can be achieved with this strategy, approximately half that of the maximum bnAb titers/GC in Fig. 5E. We note that this strategy will not suffice if the first immunization is performed at an above-optimal frustration level, due to extremely low GC success rates after the first immunization.

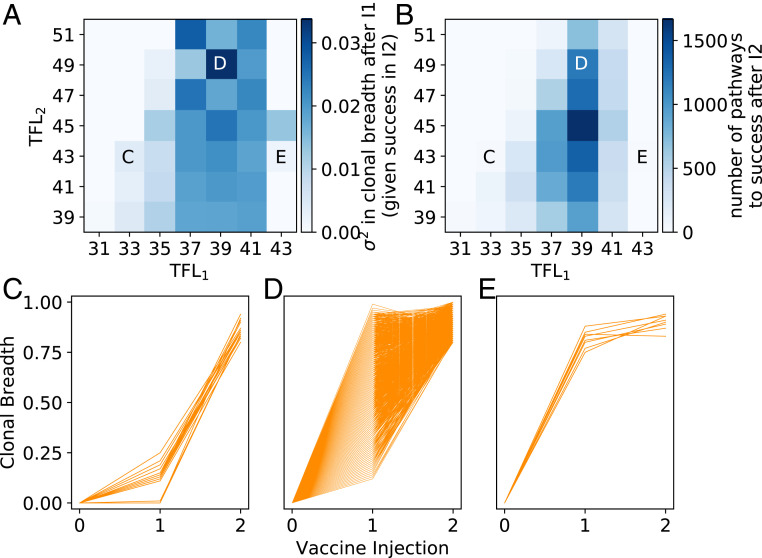
To determine the mechanism underlying the need for an intermediate TFL₁, we hypothesized that an intermediate TFL₁ resulted in an optimal clonal diversity of memory B cells that provided many potential evolutionary pathways to “success” (i.e., becoming a bnAb; breadth >0.8) upon the second immunization. To test this hypothesis, we performed a more comprehensive set of simulations that varied TFL₂ at constant TFL₁, recording the mutational trajectories of all clones. Considering only the clonal trajectories that achieved success after the second vaccine immunization, we find that the clonal diversity after the first vaccine immunization was high between a TFL₁ of 37 and 41 (Fig. 6A). Consistent with our hypothesis above, an intermediate value of TFL₁ equal to 39 resulted in the most successful trajectories (i.e., most bnAbs) after the second vaccine immunization (Fig. 6 B and D). Similar to our earlier discussion of Fig. 2, this is because at this particular value of TFL₁, the number of GC cycles—or equivalently, frustration—is as high as possible to allow for the most time to make affinity-increasing mutations and thus diversify the clonal population, without incurring major cell death. A lower TFL₁ resulted in either 1) low clonal diversity due to too little time to make mutations before the GC reaction ended, providing few pathways for achieving success in the next immunization (TFL₁ < 37; Fig. 6C), or 2) high clonal diversity but many of the resulting memory B cells are likely to lead to dead-end evolutionary trajectories that do not evolve bnAbs upon subsequent immunizations at suboptimal levels of frustration (e.g., TFL₁ = 37). Values of TFL₁ higher than the optimum resulted in extensive GC extinction, which restricted the number of successful evolutionary trajectories that could be generated upon the subsequent immunization (TFL₁ > 39; Fig. 6E).

Fig. 6.

(A) Clonal diversity after the first vaccine immunization (variance in clonal breadth across all n = 1,000 GCs), conditioned on “success” in the second immunization (becoming a bnAb; clonal breadth >0.8). (B) Number of successful trajectories after the second immunization. (C–E) Mutational trajectories of individual clones across multiple vaccine immunizations and n = 1,000 GCs, for (C) a low TFL₁, (D) an intermediate TFL₁, and (E) a high TFL₁. Corresponding points in frustration space are indicated on the top plots.

Finally, in all three scenarios in Fig. 6 C–E, we analyzed the mutational trajectories of individual clones from different GCs. We observe many instances where the mean breadth of a given clone is below that of another clone after the first immunization but surpasses the other clone in breadth after the second immunization (SI Appendix, Fig. S6). This result further emphasizes the importance of ensuring that multiple evolutionary pathways exist for achieving success, as promoted at intermediate frustration levels.

Discussion

Universal vaccines currently do not exist for diseases like HIV, HCV, influenza, and malaria, in large part because of the high genetic variability of the pathogens that cause these diseases. BnAbs, which target conserved regions of the pathogenic machinery, offer an exciting route to overcome this challenge. While bnAbs have been isolated from a number of patients (59–67), despite progress, vaccination protocols to elicit them are not available. Recent work identified that varying Ag sequence, concentration, or the pattern of administration can modulate bnAb formation by impacting AM (33–39, 68, 69). Efforts to develop systematic strategies to design vaccines against highly mutable pathogens would be greatly aided if a deep mechanistic understanding of the pertinent immunological processes was available. Toward this end, in this study we employed computational models to investigate the effect of sequential immunization with variant Ags with diverse Ag sequences and concentration on the evolution of bnAbs by AM. Changing these variables (Ag sequence and concentration) has the effect of throwing the current B cell population further off of steady state, and we define the degree to which this happens as the level of “frustration” imposed upon the immune system due to vaccination.

A large number of immunization protocols are made possible by changing both Ag sequence and concentration. Our results show that a simple lower-dimensional representation of this high-dimensional design space is likely predictive of outcome vis-à-vis bnAb production. Specifically, the total level of frustration (TFL) imposed on the immune system upon a single immunization could be formulated as a linear combination of the frustration due to changing Ag sequence and concentration. Then, this level of frustration was multiplied across immunizations to provide the TFL after multiple immunizations. We found this metric to be highly predictive of the resultant mean Ab breadth and bnAb titers. However, it remains puzzling why such a simple model works for our computational results, and we note that this governing scaling phenomena may not quantitatively translate in an experimental setting. For example, it is possible that when Ag concentrations deviate further away from those tested herein (e.g., experimental settings in which the concentration may vary logarithmically) this particular form of the TFL may no longer be applicable. However, we predict that some combination of the imposed sequence and concentration frustrations will still likely be predictive of the resultant Ab properties. For instance, rather than use mutational distance between Ags as a metric of frustration, it may instead be better to employ the difference in their ability to bind different GC B cells as a metric (if such calculations or experiments can be performed accurately).

Our model predicts that an optimal level of frustration imposed on GC reactions upon the first immunization followed by a temporally increasing level of frustration with each subsequent immunization promotes optimal bnAb responses. An initial optimal level of frustration results in a population of B cells that has the appropriate diversity to subsequently evolve into bnAbs via diverse evolutionary pathways when a stronger selection force to evolve breadth is imposed in subsequent immunizations. Too low or too high a level of initial B cell diversity leads to either extensive GC extinction or dead-end evolutionary paths. Recent advances in controlled Ag release platforms, such as osmotic pumps (68) or gene delivery vectors (70), may enable quantitative validation of the role of temporally increasing frustration on bnAb formation. We suggest immunizing with increasingly dissimilar Ags while holding concentration constant, modulating sequence frustration by inserting increasingly diverse amino acids at variable positions adjacent to conserved Ag residues. Additionally, advances in high-throughput mutagenesis, deep sequencing, and in vitro evolution methods (e.g., phage, yeast, bacterial, or ribosomal display) (21) may enable validation of our finding that diverse evolutionary trajectories optimize bnAb responses.

Like the CD4 binding site on HIV’s envelope spike protein, the conserved region of the receptor binding site on influenza’s hemagglutinin spike protein is smaller in size than the binding footprint of an Ab (71). Thus, similar to the epitope of CD4 binding site-directed Abs, the epitope of receptor binding site-directed Abs contains peripheral variable sites in addition to the core conserved sites (71). Our proposed vaccination approach may therefore be relevant to eliciting bnAbs to the receptor binding site of influenza’s hemagglutinin spike protein. Additionally, in the case of influenza, an intermediate level of frustration in the first immunization may be optimal for another reason, which is accounting for the effects of immunological memory in different individuals. For example, if the vaccine Ag is too different from what a person has been exposed to in the past (i.e., a high level of frustration), then naïve, strain-specific B cells may be more favorably recruited to GCs over cross-reactive memory B cells (72). After administering the first immunization at an intermediate level of frustration, increasing the frustration in subsequent immunizations (via differential Ag design, in a similar manner as discussed above for HIV) may transform B cells into true receptor binding site-directed bnAbs (73).

Our results exhibit an interesting analogy to cognitive learning models (74), where foundational material is introduced first, followed by more complex material later on. These models, as does our approach, present increasingly difficult material (frustration) over time, allowing many students (B cells) of varying initial skill (breadth) to succeed at each step along the way and eventually pass the test (become a bnAb). This is in contrast to providing complex material first and asking students to take the test right away (akin to a high level of frustration initially), resulting in the success of only a few very bright or lucky students. The idea of increasing frustration with time, particularly sequence frustration, is also similar to how highly mutable pathogens diversify their sequences over time, imposing ever-greater amounts of frustration upon the immune system and creating an evolutionary arms race.

Data Availability.

Data have been deposited at https://github.com/vanouk/Affinity-Maturation-PNAS.