Heuristics and optimal solutions to the breadth–depth dilemma

Significance

From choosing among the many courses offered in graduate school to dividing budget into research programs, the breadth–depth is a commonplace dilemma that arises when finite resources (e.g., time, money, cognitive capabilities) need to be allocated among a large range of alternatives. For such problems, decision makers need to trade off breadth—allocating little capacity to each of many alternatives—and depth—focusing capacity on a few options. We found that little available capacity (less than 10 samples for search) promotes allocating resources broadly, and thus breadth search is favored. Increased capacity results in an abrupt transition toward favoring a balance between breadth and depth. We finally describe a rich casuistic and heuristics for metareasoning with finite resources.

Abstract

In multialternative risky choice, we are often faced with the opportunity to allocate our limited information-gathering capacity between several options before receiving feedback. In such cases, we face a natural trade-off between breadth—spreading our capacity across many options—and depth—gaining more information about a smaller number of options. Despite its broad relevance to daily life, including in many naturalistic foraging situations, the optimal strategy in the breadth–depth trade-off has not been delineated. Here, we formalize the breadth–depth dilemma through a finite-sample capacity model. We find that, if capacity is small (∼10 samples), it is optimal to draw one sample per alternative, favoring breadth. However, for larger capacities, a sharp transition is observed, and it becomes best to deeply sample a very small fraction of alternatives, which roughly decreases with the square root of capacity. Thus, ignoring most options, even when capacity is large enough to shallowly sample all of them, is a signature of optimal behavior. Our results also provide a rich casuistic for metareasoning in multialternative decisions with bounded capacity using close-to-optimal heuristics.

The breadth–depth (BD) dilemma is a ubiquitous problem in decision making. Consider the example of going to graduate school, where one can enroll in many courses in many topics. Let us assume that the goal is to determine the single area of research that is most likely to result in an important discovery. One cannot know, even in a few weeks of enrollment, whether a course is the most exciting one. Should I enroll in few courses in many topics—breadth search—at the risk of not learning enough about any topic to tell which one is the best? Or should I enroll in many courses in very few topics—depth search—at the risk of not even taking the course with the really exciting topic for the future? One crucial element of this type of decision is that the resources (time, in this case) need to be allocated in advance, before feedback is received (before classes start). Also, once decided, the strategy cannot be changed on the fly, as doing so would be very costly.

The BD dilemma is important in tree search algorithms (1, 2) and in optimizing menu designs (3). It is also one faced by humans and other foragers in many situations, such as when we plan, schedule, or invest with finite resources while lacking immediate feedback. Furthermore, it is a dilemma that a large number of distributed decision-making systems have to tackle. These include, for example, ant scouts searching for a new colony settlement (4), stock market investors, or soldiers in an army during battle. Evidence suggests that distributed processing with limited resources is also a valid model of brain computations (5, 6). In face of this, it is remarkable that the bulk of research on the BD has been in fields outside of psychology and neuroscience (e.g., refs. 7–9). We believe that one reason for this is the lack of models and formal tools for thinking about the BD dilemma and separating it from other dilemmas.

Many features of the BD dilemma warrant its study in isolation. First, BD decisions are about how to divide finite resources, with the possibility of oversampling specific options and ignoring others, e.g., one can select several courses on the same topic while ignoring other topics. Second, the BD dilemma is about making strategic decisions, that is, decisions that need to be planned in advance and cannot be changed on the fly once initiated, e.g., it is very costly to change courses once they have started, at least during the first semester. Finally, BD decisions need to be made before the relevant feedback is received, e.g., enrollment happens before courses start, and thus before knowing the true relevance of the courses and topics. One can easily imagine replacing courses by ant scouts or neurons, and topics by potential new settlements or sensory functions, and so on, in the above example to reveal new relevant BD dilemmas pertaining to distributed decision making or brain anatomy, respectively.

The identifying features of the BD dilemma are distinct from those of the well-known exploitation–exploration (EE) dilemma (10–14) and its associated formalization in multiarmed bandits (15–17). Specifically, whereas in the EE dilemma samples are allocated sequentially, one by one, to gather information and reward after each sample, in the BD dilemma multiple samples can be allocated in parallel at once to multiple options (possibly allocating multiple samples to some) without immediate feedback to gather information and maximize future reward. It is worth pointing out that EE and BD are not mutually exclusive aspects of decision making, and therefore they are expected to appear hand-in-hand in many realistic situations.

Past work in multialternative choice has revealed that humans appear to carefully trade off the benefits of examining many options broadly and examining a smaller number of options deeply. For example, when faced with a large number of options, we often focus—even if arbitrarily—on a subset of them (18–21) with the presumable benefit that we can more precisely evaluate them. Likewise, we may consider all options, but arbitrarily reject value-relevant dimensions (22, 23), as if contemplating them all is too costly. Option narrowing appears to be a very general pattern, one that is shared with both human and nonhuman animals, despite the fact that rejecting options can reduce experienced utility (18, 21). It is often proposed that such heuristics reflect bounded rationality (24), which is likely correct in principle, but the exact processes underlying that boundedness remain to be identified. Why do we so often consider a very small number of options when considering more would a priori improve our choice? One possibility is that this pattern reflects an evolved response to an empirical fact: that when capacity is constrained, optimal search favors consideration of a small number of options.

Because cognitive capacity is limited in many ways, the BD dilemma has direct relevance to many aspects of cognition as well. For example, executive control is thought to be limited in capacity, such that control needs to be allocated strategically (25–28). Likewise, attentional focus and working memory capacity are limited, such that, during search, we often foveate only a single target or hold a few items in memory (29). Although the effective numbers are low, each contemplated option is encoded with great detail (30–32). Furthermore, it seems clear that recollection of information from memory can be thought of as a search-like process (33–35). That is, to retrieve a memory we must attend to a recollection processes, with its associated limited capacity. Thus memory-guided decisions presumably involve BD trade-offs too.

Although the relevance of the BD dilemma is clear, tractable models are lacking, and thus, optimal strategies for BD decisions are largely unknown. Here, we develop and solve a model for multialternative decision making endowed with the prototypical ingredients of the BD dilemma. Our model consists of a reward-optimizing yet bounded decision maker (24, 36, 37) confronted with multiple alternatives with unknown subjective values. The first critical element of the model is “finite-sample capacity,” which enforces a trade-off between sampling many options with few samples each (breadth) and sampling few options with many samples each (depth). The second critical element is that samples need to be allocated across alternatives before sampling starts and, thus, before feedback is available. This strategic decision with the finite-sample capacity constraint implies a metareasoning problem (37, 38) where deliberation about the multiple possible allocations of resources (meta-actions) need to be made in advance to optimize expected utility of a future choice.

Despite the simplicity of the model, it features nontrivial behaviors, which are characterized analytically. When capacity is low (less than 4 to 10 samples can be probed), it is best to sample as many alternatives as possible, but only once each; that is, breadth search is favored. At larger capacities, there is a qualitative and sharp change of behavior (a “phase transition”) and the optimal number of sampled alternatives roughly grows with the square root of sample capacity (“square root sampling law”), balancing breadth and depth. Therefore, in the high-capacity regime, it is best to ignore the vast majority of potentially accessible options. We considered globally optimal allocations in comparison to even allocation of samples across sampled alternatives and found that the square root sampling law, obtained for the latter, provides a close-to-optimal heuristic that is simpler to implement. We also study limit cases where the above rules break down, as well as generalizations to dynamic allocation of finite resources with feedback that illustrate the generality of the results. Our results are also robust to strong variations of the environments where the probability of finding good options widely varies.

Results

Finite-Sample Capacity Model.

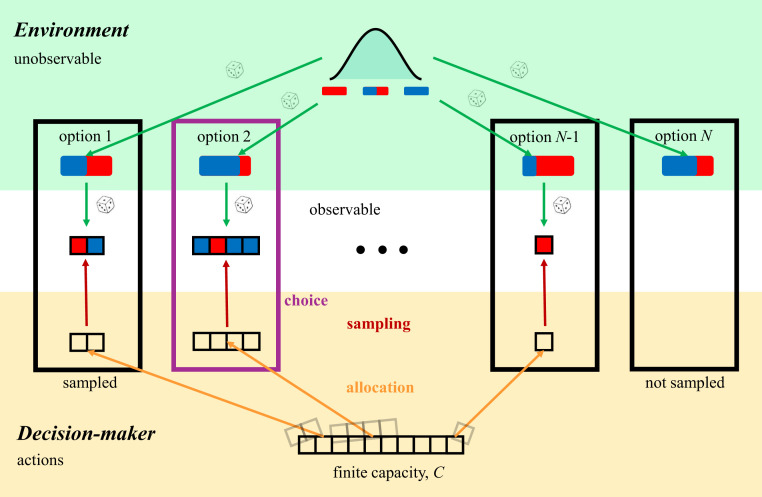
We assume that a decision maker can choose how to allocate a finite resource among options of unknown status to determine the best option (Fig. 1). The environment generates a large number of options, each characterized by the probability of delivering a successful outcome. The success probabilities, unknown to the decision maker, determine the quality of each of the options, with better options having higher success probabilities (e.g., options with a higher probability of delivering a large reward if they are sampled). The goal of the decision maker is to infer which of the options has the highest success probability (and, thus, highest expected value). The success probabilities of the options are generated randomly from an underlying prior probability distribution, modeled as a beta distribution with parameters $\left(\alpha ,\beta \right)$. We assume that this distribution is known by the decision maker, due, for example, to previous experience with the environment. The prior distribution determines the overall difficulty of finding successful options in the environment.

Fig. 1.

Finite-sample capacity model. The environment (Top, green) contains a large number N of options, and choosing any of them might lead to a successful outcome (e.g., a large vs. a small reward). For each option, the probability of success (blue fraction of red/blue bar) is a priori unknown to the decision maker and is drawn independently across options from an underlying prior probability distribution, modeled as a beta distribution (top distribution). The prior distribution defines the overall difficulty of finding successful options in the environment. Options are characterized by the probability of delivering a successful outcome (e.g., a large reward), and the outcomes are modeled as Bernoulli variables. The decision maker (Bottom, orange) has a finite capacity C, i.e., a finite number of samples (bar of squares) that can be allocated to any option in any possible way. The decision maker can decide to oversample options by allocating more than one sample to them (e.g., options on the left), and also ignore some options by not sampling them at all (e.g., rightmost option). All samples need to be allocated in advance, and allocation cannot be changed thereafter. Therefore, feedback is not provided at this stage. After allocation, sampling starts (Center, white), in which the decision maker observes a number of successes and failures for each of the sampled options (colored squares; blue: success, large reward, red: failure, small reward). Once this evidence is collected, the decision maker chooses the option that is deemed to have the highest probability of success (in this case, option 2; purple box).

The decision maker is endowed with a finite-sample capacity, $C$, i.e., a finite number of samples that she can allocate to any option and to as many options as desired. Within the allowed flexibility, it is possible that the decision maker decides to oversample some options by allocating more than one sample to them, and it is also possible that she decides to ignore some options by not sampling them at all. Feedback is not provided at the allocation stage, so this decision is based purely on the expected quality of options in the environment. After allocation has been determined, the outcomes of the samples are revealed, constituting the only feedback that the decision maker receives about the fitness of her sample allocation. Outcomes for each of the sampled alternatives are modeled as a Bernoulli variable, where a successful outcome (corresponding to a large reward) has probability equal to the success probability of that option (see below for a generalization in which we consider Gaussian outcomes). The inferred best alternative is the one with the largest inferred success probability based on the observed outcomes from the allocated samples to each of the options (39–41). Choosing this alternative maximizes expected utility (see below and SI Appendix).

While making a choice based on the observed outcomes is a trivial problem, deciding how to allocate samples over the options to maximize expected future reward is a hard combinatorial problem. There are many ways a finite number of samples can be allocated among a very large number of alternatives. At the breadth extreme, one can split capacity to over as many alternatives as possible, sampling each just once. In this case, the decision maker will likely identify a few promising options, but will lack the information for choosing well between them. At the depth extreme, the search could allocate all samples only to a couple of alternatives. The decision maker’s estimate of the success probability of those options will be accurate, but that of the other alternatives will remain unknown. It would seem that an intermediate strategy is better than either extreme. Specifically, the optimal allocation of samples should balance the diminishing marginal gains of sampling a new alternative and those of drawing an additional sample from an already sampled alternative.

To formalize the above model, let us assume that the decision maker can sample and choose from $N=C$ alternatives. That is, we consider scenarios where the number of alternatives $N$ is as large as the decision maker’s sampling capacity—if the number of alternatives is larger than capacity, the only difference is that there would be a larger number of ignored alternatives. The allocation of samples over the alternatives is described by the vector $\overrightarrow{L}$, with components $L_i$ representing the number of samples allocated to alternative $i=1,\dots ,N$. The finite-sample capacity of the decision maker imposes the constraint ${\displaystyle \sum _i{L}_i=C}$. Upon drawing $L_i$ samples from each alternative $i$, the decision maker observes the number of successes (1’s), denoted $n_i$, of each of the Bernoulli variables. The best option is then the one with the highest posterior mean probability $E\left(p_i\text{|}{n}_i,\alpha ,\beta \right)=\left(n_i+\alpha \right)/\left(L_i+\alpha +\beta \right)$ after observing these successes, such that the utility for a given allocation $\overrightarrow{L}$ and associated outcomes $\overrightarrow{n}$ becomes $U(\overrightarrow{n},\overrightarrow{L})=\underset{i}{\max }\hspace{0.17em}\left[\left(n_i+\alpha \right)/\left(L_i+\alpha +\beta \right)\right]$. Because the number of successes is only revealed after selecting the sample allocation strategy $\overrightarrow{L}$, the decision maker’s utility for using that strategy, $U\left(\overrightarrow{L}\right)$, is an average of $U\left(\overrightarrow{n},\overrightarrow{L}\right)$ over all possible outcomes given $\overrightarrow{L}$,

$$\begin{array}{c}U\left(\overrightarrow{L}\right)=\sum _{\to n}p\left(\overrightarrow{n},\text{|},\overrightarrow{L},,,\alpha ,,,\beta \right)\underset{i}{\max }\frac{n_i+\alpha }{L_i+\alpha +\beta },\end{array}$$ [1]

where $p\left(\overrightarrow{n}\text{|}\overrightarrow{L},\alpha ,\beta \right)$ is the joint probability distribution of the outcomes $\overrightarrow{n}$ given the allocation $\overrightarrow{L}$ and the prior distribution parameters. As each alternative is sampled independently, the distribution of success counts factorizes as $p\left(\overrightarrow{n}\text{|}\overrightarrow{L},\alpha ,\beta \right)={\displaystyle \prod _{i}p\left(n_i|L_i,\alpha ,\beta \right)}$, where $p\left(n_i|L_i,\alpha ,\beta \right)$ is a beta-binomial distribution (42). This distribution specifies the probability of observing exactly $n_i$ successes from a Bernoulli variable that is drawn $L_i$ times, and whose success probability $p_i$ follows a beta distribution with parameters $\alpha$ and $\beta$. These two parameters control the skewness of the distribution: If both parameters are equal, the distribution is symmetric around one-half, while for $\alpha$ larger (smaller) than $\beta$ the distribution is negatively (positively) skewed.

Finally, the optimal allocation of samples across options ${\overrightarrow{L}}^{\ast }$ is the one that maximizes the decision maker’s expected utility $U\left(\overrightarrow{L}\right)$ in Eq. 1 over all allocations of samples $\overrightarrow{L}$,

$$\begin{array}{c}{\overrightarrow{L}}^{\ast }=\arg \underset{\overrightarrow{L}}{\max }U\left(\overrightarrow{L}\right),\end{array}$$ [2]

with the above finite-sample capacity constraint (see SI Appendix for details). The optimal expected utility then becomes $U^{\ast }=\underset{\overrightarrow{L}}{\max }\hspace{0.17em}U\left(\overrightarrow{L}\right)$, which involves a double maximization over the expected success probabilities of the sampled alternatives and the allocation of samples over the alternatives, effectively solving the two-stage decision process (i.e., first allocate samples, then observe outcomes, and then choose) in reverse order (i.e., first optimize choices given outcomes and allocation, then optimize allocation).

This maximization allows total flexibility over how many samples to allocate to each alternative. However, for the sake of tractability, let us first consider the best even allocation of samples, that is, a subfamily of allocation strategies where the same number of samples $L$ are allocated to each of $M$ sampled alternatives, while the remaining alternatives $\left(C-M\right)$ are not sampled, subject to the standard capacity constraint $M\times L=C$. Indeed, finding the optimal even allocation of samples is easier than finding the globally optimal allocation, which might be uneven in general (see below). As we show in SI Appendix, a particularly simple expression for the optimal even sample allocation, $L^{\ast }$, arises when the prior distribution over success probabilities is uniform $\left(\alpha =\beta =1\right)$,

$$\begin{array}{c}{L}^{\ast }=\arg \underset{L}{\min }\frac{{\displaystyle {\sum }_{s=0}^L{\left(s+1\right)}^M}}{{\left(L+1\right)}^M\left(L+2\right)},\end{array}$$ [3]

where the right-hand side is related to utility by

$$\begin{array}{c}U\left(M=C/L\right)=1-\frac{{\displaystyle {\sum }_{s=0}^L{\left(s+1\right)}^M}}{{\left(L+1\right)}^M\left(L+2\right)}.\end{array}$$ [4]

Note that only $M^{\ast }=C/L^{\ast }\le C$ alternatives are sampled in the optimal allocation, while the remaining options are given zero samples, thus effectively being ignored. The sampled alternatives can be chosen randomly, as they are indistinguishable before sampling. Using extreme value theory (SI Appendix), we show that the optimal number of sampled alternatives $M^{\ast }$ and optimal number of samples per alternative $L^{\ast }$ both follow a power law with exponent 1/2 for large capacity $C$:

$$\begin{array}{c}\underset{C\to \infty }{\lim }{M}^{\ast }=\sqrt{C},\underset{C\to \infty }{\lim }{L}^{\ast }=\sqrt{C},\end{array}$$ [5]

which corresponds to perfectly balancing breadth and depth.

In the next section, we analyze this case in detail. After that, we consider optimal even allocations of samples for arbitrary prior distributions, and finally we provide results for the globally optimal allocations, not necessarily even.

Sharp Transition of Optimal Sampling Strategy at Low Capacity.

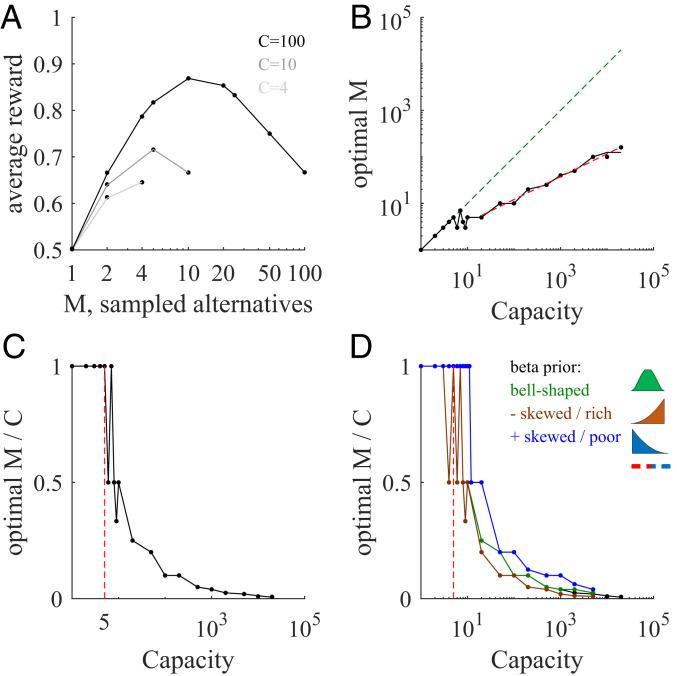
We first analyze the expected utility $U\left(M\right)$ as a function of the number of evenly sampled alternatives $M$, each sampled $L$ times (such that $M\times L=C$) (Fig. 2A). At low capacity ($C=4$, lighter gray line), the utility increases monotonically from sampling just one alternative $\left(M=1\right)$ four times, to sampling four alternatives $\left(M=4\right)$ one time each. Thus, a pure breadth strategy is favored. At intermediate capacity ($C=10$, medium gray line), the maximum occurs at an intermediate number of alternatives (specifically, $M=5$), reflecting an increasing emphasis on depth. At large capacity ($C=100$, black line), the maximum expected utility occurs when sampling few different alternatives ($M=10$ sampled alternatives with $L=10$ samples each), reflecting a tight balance between breadth and depth. For such large capacities, a breadth search that samples most of the alternatives (rightmost point of the black line) would lead to a reward that approaches 2/3, which is the lowest expected reward one would obtain if at least one sampled alternative has a positive outcome (SI Appendix).

Fig. 2.

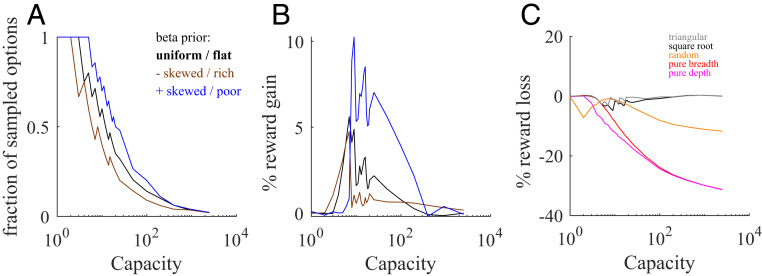
Sharp transitions in optimal number of sampled alternatives at low capacity, and power law behavior at large capacity. (A) Average reward (points, simulations; lines, theoretical expressions; Eq. 4) as a function of the number of sampled alternatives $M$ for three different capacities ($C=4,10,100$; light, intermediate, and dark lines, respectively) for the flat environment (uniform prior). The maximum occurs at the large extreme for low capacity but at a relatively low value for large capacity. Note log horizontal scale. (B) Optimal number of sampled alternatives as a function of capacity. When capacity is smaller than around 5, a linear trend of unit slope is observed (dashed green line), but when capacity is above 7, a sublinear behavior is observed (dashed red line corresponds to the best power law fit, with exponent close to 1/2). The black line corresponds to analytical predictions. The jagged nature of this prediction and simulation lines in this and other panels is due to the discrete values that the optimal $M$ can only take, not due to numerical undersampling. (C) The sharp transition is clearer when plotting the optimal number of sampled alternatives to capacity ratio as a function of capacity. For low capacity, the ratio is 1, but for large capacity the ratio decreases very rapidly. The last point below which the optimal ratio is always 1 (critical capacity) corresponds to capacity equal to 5 (indicated with a vertical red line). (D) Number of sampled alternatives to capacity ratios for different prior distributions ($\alpha =\beta =3,$ bell-shaped, green line; $\alpha =3,\beta =1$, negatively skewed prior modeling a “rich” environment, brown line; $\alpha =1,\beta =3$, positively skewed distribution modeling looking for a “needle in a haystack,” that is, a “poor” environment, blue line). Lines correspond to analytical predictions from SI Appendix, Eq. 9; points correspond to numerical simulations; error bars are smaller than data points in all panels.

The model displays a sharp transition when capacity crosses the critical value of 5 (Fig. 2B). Below this critical capacity, the optimal number of sampled alternatives equals capacity. That is, one should follow a breadth strategy and distribute one sample to each alternative. Above 5, the optimal number of sampled alternatives is much smaller than the capacity, with the temporary exception of capacity equal to 7. That is, one should balance the number of sampled alternatives with the depth of sampling each of them. Specifically, the optimal number of sampled alternatives follows a power law with exponent 1/2 (log-log linear regression, power = slope = 0.49, 95% CI = [0.48, 0.50]), as predicted by Eq. 5, which implies that the fraction of sampled alternatives decreases with the square root of capacity. This means that breadth and depth are tightly balanced in the optimal strategy. The sharp transition at around 5 becomes clearer when plotting the ratio between the optimal number of sampled alternatives and capacity as a function of capacity (Fig. 2C).

In summary, if the capacity of a decision maker increases by a factor of 100, the decision maker will roughly increase the number of samples alternatives just by a factor of 10, one order of magnitude smaller than the capacity increase. Because the optimal number of sampled alternatives increases with capacity with an exponent 1/2, we call this the “square root sampling law.” A remarkable implication of this law is that the vast majority of potentially accessible alternatives should be ignored (e.g., for $C=100$, $C-M=90$ options are “rationally” ignored).

Generalizing to Variations in Beta Prior Distributions.

The above critical capacity for optimal even sample allocation changes when, instead of using a uniform prior of success probabilities, we allow for variations of the prior distribution (Fig. 2D). However, the critical capacity consistently lies again at around low values (∼10) with the specific value depending on the environment. By changing the prior’s parameters, we can vary the difficulty of finding a good extreme alternative, and thus can compare different scenarios. For the uniform prior that we have used previously (a “flat” environment), a decision maker is equally likely to find an alternative with any success probability. Consider a prior distribution that is concentrated and symmetric around a success probability of 0.5 (approximately as a Gaussian, corresponding to the beta prior parameters $\alpha =\beta =3$). In this environment, unusually good (high success probability) and unusually bad (low success probability) options are rarer than medium ones (Fig. 2D, green line). In this case, the BD trade-off as a function of $C$ is remarkably similar to the uniform prior case, with a transition at $C=5$.

We also consider a negatively skewed prior distribution $\left(\alpha =3,\beta =1\right)$. This distribution refers to environments with rare bad options, as, for example, a tree whose fruits are mostly ripe but that has a few unripe ones. In this “rich” environment, one can afford sampling a smaller number of options, and as they are sampled more deeply, it is possible to better detect the really excellent ones. A sharp transition occurs even in this condition, exactly when the critical capacity equals 3 (brown line). As expected in this environment, the decay of the ratio between the optimal number of sampled alternatives and capacity after this transition is (slightly) faster than that of the symmetric prior. Therefore, negative skews engender a modest bias toward depth over breadth.

Finally, consider the opposite scenario, in which the prior distribution is concentrated at low success probability values ($\alpha =1,\beta =3$, positively skewed beta distribution), which corresponds to looking for a “needle in a haystack” or a “poor” environment. In this scenario, one ought to sample more alternatives less deeply to allow for the possibility of finding the rare good alternatives, and thus breadth should be emphasized over depth (Fig. 2D, blue line). In this scenario, the sharp transition occurs at capacities around 10 (blue line).

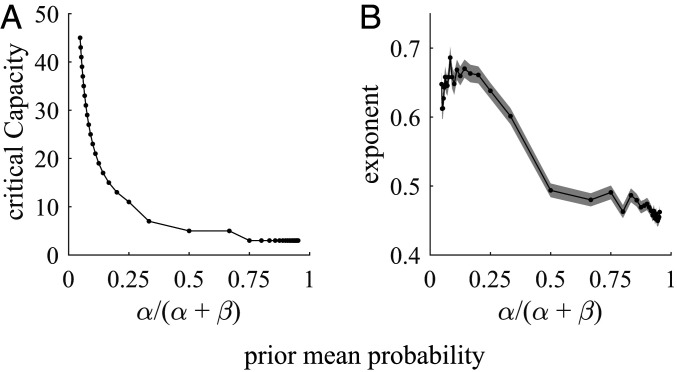
Despite the large variations of prior distributions, a fast transition occurs in all conditions at around a small capacity value, like in the uniform prior case. In addition, a power law behavior is observed at larger values of capacity regardless of skew, with exponents close to 1/2 in all cases (uniform prior, exponent = 0.49; negatively skewed prior, 0.49; positively skewed prior, 0.64; SEM = 0.01). These behaviors are observed over a larger range of parameters of the prior distribution (Fig. 3).

Fig. 3.

Sharp transitions at relatively low-capacity values and close to square root sampling behavior for large capacity are observed for a broad range of parameters of the prior distribution. (A) Critical capacity decreases very steeply to low values (∼10) as a function of the prior mean probability $\alpha /\left(\alpha +\beta \right)$. (B) Exponents decrease as a function of the prior mean probability and cluster around 1/2. The exponents are obtained from log-log linear regression fits of the optimal number of alternatives samples vs. capacity $\left(M\propto C^{exponent}\right)$ for $C$ values ranging from 1,000 to 2,000 in steps of 1. Shaded areas correspond to 95% CIs. In both panels, points are obtained by theoretical predictions from SI Appendix, Eq. 9. For prior mean probabilities smaller than or equal to 1/2, we fix $\alpha =1$ while $\beta$ varies from 1 to 20 in steps of 1, and for values larger than 1/2, we fix $\beta =1$ while $\alpha$ varies from 1 to 20.

One interesting limit scenario arises for strongly positively skewed prior distributions, e.g., by taking $\beta$ to infinity while fixing $\alpha =1$. In this limit, the prior mean probability $\alpha /\left(\alpha +\beta \right)$ decreases to zero, and the critical capacity rises very steeply to infinity (Fig. 3A as one moves leftward). Increasing the prior’s skewness makes finding good options less likely, as most of the options are very likely to be very bad, akin to an extreme case of the haystack environment considered before. As expected, this makes breadth search optimal for increasingly larger values of capacity, as indicated by the increasing values of critical capacity. However, for large enough capacities, a transition is still observed above which a roughly balanced mix between breadth and depth becomes optimal. More precisely, in this regime the optimal number of sampled alternatives features a power behavior with exponents close but above 1/2, indicating a bias toward breadth (leftmost points in Fig. 3B). When the prior mean probability exceeds values as low as 0.1, the critical capacity plateaus to low values below 10, and the exponent drops to values smaller but close to 1/2, indicating a weak preference toward depth.

To test how robust the behaviors we explored are, we furthermore considered Gaussian rather than Bernoulli samples (SI Appendix, Fig. S1). Strikingly, for a large range of the samples’ noisiness, we again observed a sharp transition occurring at low critical capacities $\left(\sim 10\right)$. Below the critical capacity, breadth search is preferred, while above it a mix between breadth and depth is optimal, characterized by a power law behavior ($\mathrm{exponent}=0.35$, $95\%\hspace{0.17em}\mathrm{CI}=\left[0.30,0.41\right]$). Thus, the resulting strategy was qualitatively identical, and numerically similar, to the Bernoulli samples case.

Optimal Choice Sets and Sample Allocations.

So far, we have focused on optimal even sample allocation. Let us now consider the payoffs for decision makers willing to consider all possible allocation strategies. The number of all possible allocations equals the number of partitions of integers in number theory, which grows exponentially with the square root of capacity (43). This makes finding the globally optimal sample allocation a problem that is intractable in general. For small capacity values $C\le 7$ and uniform prior distributions, we compute the exact optimal sample allocation by exhaustive search and rely on a stochastic hill climbing method for larger capacities and other priors. The latter finds a local maximum for the utility, which is likely to be a global maximum, as we found it to coincide with the one provided by exhaustive search for small capacities $C\le 7$, and the optimal utility did not significantly change across different initializations and random seeds for larger capacity values.

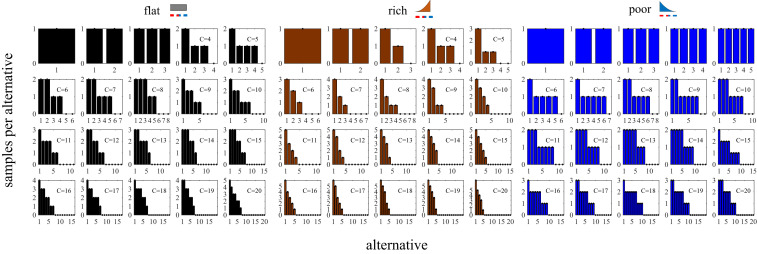
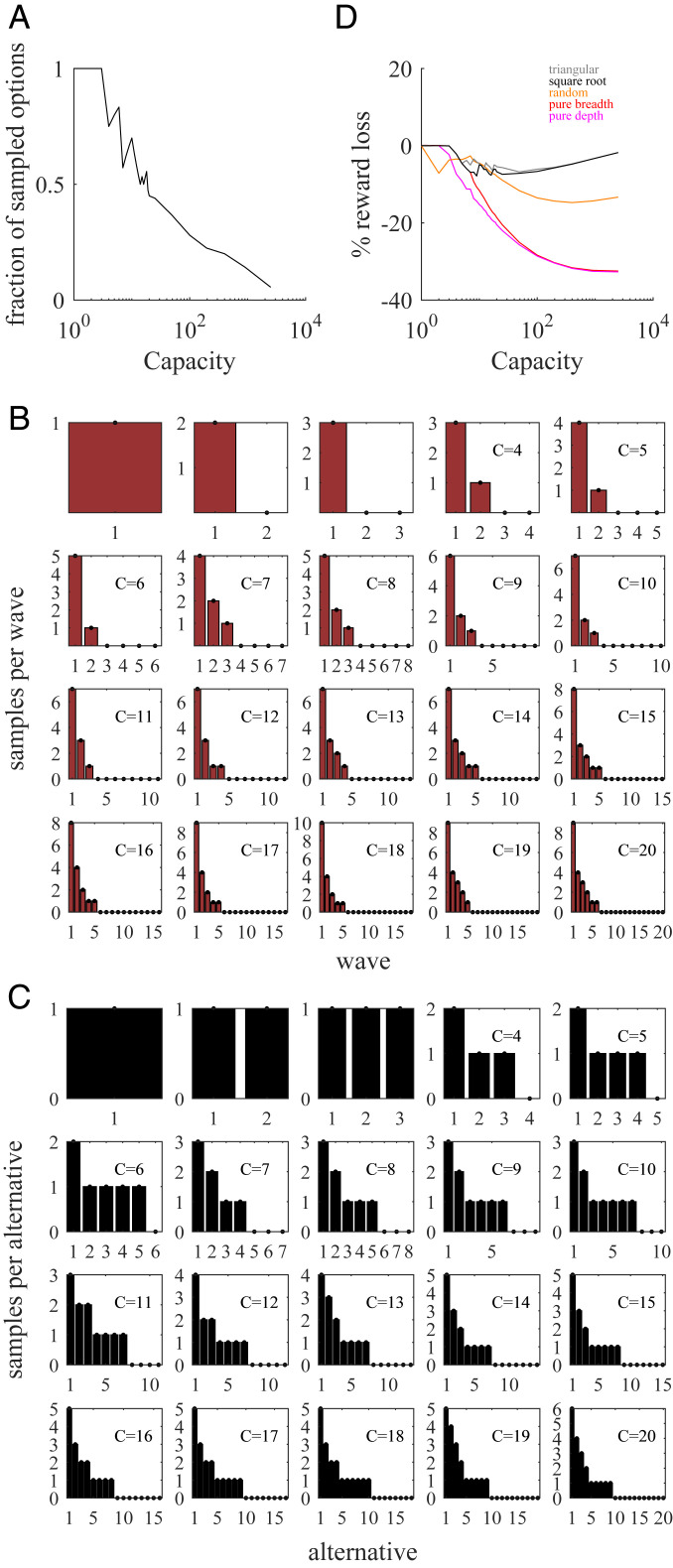
Globally optimal sample allocation (which defines optimal choice sets) for a uniform prior beta distribution tends to sample all or most of the alternatives when the capacity is small, but as capacity increases the number of sampled alternatives decrease (Fig. 4, Left). For instance, for capacity equal to 5 samples, the optimal sample allocation is (2, 1, 1, 1, 0). In general, in optimal allocations, the decision maker adopts a local balance between oversampling a few alternatives and sparsely sampling others—a local compromise between breadth and depth—even though all options are initially indistinguishable. This further level of specialization and distinction between alternatives might be able to better break ties between similar alternatives when compared to an even sampling strategy.

Fig. 4.

Optimal sample allocations and choice sets. Optimal sample allocation for flat, rich, and poor environments from capacity $C=1$ up to $C=20$. The environments correspond, respectively, to uniform, negatively and positively skewed prior distributions (top icons). Optimal sample allocations are represented as bar plots, indicating the number of samples allocated to each alternative ordered from the most to the least sampled alternative.

We also studied optimal sample allocation for positively and negatively skewed prior distributions. In a rich environment (center panel), the optimal sample allocation is uneven for capacities as low as $C=3$. In contrast, in a poor environment (right), the optimal sample allocation remains even up to capacity $C=5$, which was not the case for the flat environment (compare with left panel). For higher capacities, decision makers in rich environments ought to sample less broadly but more deeply. For instance, for capacity $C=20$, only around 5 alternatives are sampled, while the remaining 15 potentially accessible alternatives are neglected. In the poor environment, in contrast, about half of the alternatives are sampled, but not very deeply (only a maximum of 3 samples are allocated to the most sampled alternatives).

Even Sample Allocation Is Close to Optimal.

Three principles stand out. First, globally optimal sample allocation almost never coincides with optimal even allocation. Second, at low capacity optimal allocation favors breadth, while at large capacity a BD balance is preferred (Fig. 5A). Third, a fast transition is observed between the two regimes happening at a relatively small capacity value. The last two features are shared by the optimal even allocations as well (cf. Fig. 2C).

Fig. 5.

Globally optimal and optimal even sample allocations share similar features and have similar performances. (A) Fraction of sampled options (compared to the maximum number of potentially accessible alternatives, equal to $C$) as a function of capacity $C$. The fraction is close to 1 for small values for all environments (flat, black line; rich, brown; and poor, blue). The fraction decays rapidly to zero from a critical value that depends on the prior. The jagged nature of the lines is due to the discrete nature of capacity. (B) Percentage increase (gain) in averaged reward by using globally optimal sample allocation compared to even allocation (see SI Appendix). Color code as in the previous panel. (C) Percentage loss in averaged reward by using triangular (gray), square root sampling law (black), random (orange), pure breadth (red), and pure depth (pink) heuristics compared to optimal allocation, in a flat environment. For the square root and triangular heuristics, we used pure breadth search when C ≤ 5.

Optimal even and globally optimal sample allocations share some important features, but are they equally good in terms of average reward obtained? We compared the average reward from globally optimal and even optimal sample allocations. For comparison, we always used even sampling based on a uniform prior over each alternatives’ success probabilities, that is, we sample $M=C$ alternatives with one sample each if capacity is $C\le 7$ and $M=\sqrt{C}$ alternatives with $L=\sqrt{C}$ samples each if capacity is larger (square root sampling law; see SI Appendix for details). This heuristic produced comparable performances to the optimal ones (Fig. 5B). The worst-case scenario occurred in the poor environment (blue line) when capacity is close to 10, which led to a drop in reward by close to 10%, but the maximum discrepancy value was even smaller for the flat and rich environments. Indeed, for the flat environment, the maximum drop in reward was only around 5%.

For large capacity $C>100$, the square root sampling law produced results that were very close to the performance of the optimal solutions (as found by stochastic hill climbing). Therefore, the gain of globally optimal sample allocation over optimal even sampling at low capacity, and over the square root sampling law for high capacity, is at most marginal.

We also compared the merits of the square root sampling law to other sensible heuristics: pure breadth, pure depth, random sampling of options, and a triangular approximation. Pure breadth search allocates just one sample per alterative, such that the number of sampled alternatives equals capacity. The pure depth heuristic randomly chooses two alternatives that are each allocated half of the sampling capacity. Random search randomly assigns each of the $C$ samples to any alternative with replacement. A final heuristic, called “triangular,” is inspired by the seemingly isosceles right triangle shape of the optimal allocations (Fig. 4). It splits capacity by sampling the first alternative with $\lfloor 2\sqrt{C}-1\rfloor$ samples and any further alternative with one sample less than the previous one until capacity is exhausted ($\lfloor x\rfloor$ is the floor function). All heuristics finally choose the alternative with the highest posterior mean probability. While the loss relative to optimal allocation is smallest for triangular allocation, the square root sampling law performs similarly, and much better than random, pure breadth and pure depth heuristics (Fig. 5C).

Dynamic Allocation of Capacity.

Thus far, we have considered “static” allocations whereby no feedback is provided before all samples are allocated. In a less rigid “dynamic” sample allocation strategy, some basic form of interim feedback might be available, based upon which further alternatives can be sampled. To model such a scenario, assume that the capacity can be divided into a sequence of a maximum of $C$ waves $k=1,\dots ,C$, such that in each wave a number of alternatives $M_k$, no larger than in the previous wave, is sampled just once. The number of alternatives sampled at each wave can be chosen freely, but has to be allocated before sampling starts, that is, the decision maker has to determine the policy at the start knowing she will receive feedback in the future. However, to dynamically react to past sampling outcomes, the kth wave allocates its $M_k$ samples to only those $M_k$ alternatives with the largest number of successes so far (with random allocation in case of ties). This implies that, in wave $k+1$, one can only sample a subset of the alternatives sampled in wave $k$. Once sampling has been completed across all waves, the alternative with the highest posterior mean probability is chosen among the $M_1$ sampled alternatives in the first wave. We restricted the final choice to this initial set of alternatives sampled in the first wave to handle the unlikely case that the lastly sampled alternatives turned out to be worse than (our a priori belief about) the initially sampled ones. In that case, the dynamic strategy could lead to worse performance than the static one. We call the above flexible allocation of the predefined sample waves dynamic sample allocations. As for static allocations, we find the best-performing $M_1,M_2,\dots$sequence by stochastic hill climbing.

Optimal dynamic sample allocations share many features with optimal static sample allocations (Fig. 6). At low capacity, pure breadth search is again optimal. That is, it is best to allocate all samples in the first wave, assigning just one sample per alternative (Fig. 6A). For capacities larger than the critical capacity $C=3$, it is best to mix breadth with depth search, and for very large capacity most accessible alternatives are again ignored. The optimal dynamic and static sample allocations have, however, important differences (Fig. 6B and cf. Fig. 4). Specifically, the initial wave tends to sample many alternatives to identify good ones, and follow-up waves narrow down the search to the potentially best ones. This results in broader sample allocations (Fig. 6C) that, overall, sample more alternatives than for static allocations (cf. Fig. 4). Finally, we test how the static square root sampling law performs against the optimal dynamic allocations, finding that the former is worse by less than 9% for all capacity values (Fig. 6D). We also confirm that static random, pure breadth, and pure depth strategies are substantially worse than the square root sampling law, while the triangular strategy is similar to the simple square root sampling heuristic.

Fig. 6.

Optimal dynamic sample allocations display a sharp transition at low capacity, distribute samples unevenly across alternatives, and ignore a vast number of alternatives at high capacity. (A) Fraction of sampled alternatives (compared to the maximum number of potentially accessible alternatives, equal to $C$) as a function of capacity $C$ for the flat environment (uniform prior). The fraction is 1 for small-capacity values and decays rapidly to zero at large capacity. (B) Optimal sample waves, indicating the number of samples allocated in each wave. The number of samples allocated in each wave lies between 1 and $C$, and they sum up to the total available capacity $C$. The maximum allowed number of waves is $C$. (C) Optimal dynamic sample allocations and choice sets after the whole capacity has been allocated through the sample waves. The alternatives with largest number of successes are allocated a higher number of samples compared to static allocations (cf. Fig. 4). Many alternatives are given just one sample, typically arising from the first wave, which produces broader sample allocations compared to static allocations. (D) Percentage loss in averaged reward by using triangular (gray), square root sampling law (black), random (orange), pure breadth (red), and pure depth (pink) static heuristics compared to optimal dynamic allocation.

Discussion

We delineate a formal mathematical framework for thinking about a commonplace decision-making problem. The BD dilemma occurs when a decision maker is faced with a large set of possible alternatives, can query multiple alternatives simultaneously with arbitrary intensities, and has overall a limited search capacity. In such situations, the decision maker will often have to balance between allocating search capacity to more (breadth) or to fewer (depth) alternatives. We develop and use a finite-sample capacity model to analyze optimal allocation of samples as a function of capacity. The model displays a sharp transition of behavior at a critical capacity corresponding to just a small set of available samples (∼10). Below this capacity, the optimal strategy is to allocate one sample per alternative to access as many alternatives as possible (i.e., breadth is favored). Above this capacity, BD balance is emphasized, and the square root sampling law, a close-to-optimal heuristic, applies. That is, capacity should be split into a number of alternatives equal to the square root of the capacity. This heuristic provides average rewards that are close to those from the optimal allocation of samples. As it is easy to implement, it can become a general rule of thumb for strategic allocation of resources in multialternative choices. The same results roughly apply to a wide variety of environments, including flat, rich, and poor ones, characterized by very different difficulties of finding good alternatives.

Despite the billions of neurons in the brain, our processing capacity seems quite limited. This strict limit applies to attention, where it is sometimes called the attentional bottleneck (44–46), including spatial attention, where the limit is best characterized (47), over working memory (29, 31, 32, 48–50), to executive control (28, 51, 52), and to motor preparation (53). These narrow limits, which often number only a handful of items (although see ref. 32), suggest some sort of bottleneck. However, another interpretation is that capacity is much larger than it appears, and instead, observed capacity reflects the strategic allocation of resources according to the compromises that our model identifies as optimal. The square root sampling law, in other words, suggests that the apparently narrow bandwidth of cognition may reflect the optimal allocation across very few alternatives of a relatively large capacity.

This is particularly likely to be true for economic choice. We are especially interested in the apparent strict capacity limits of prospective evaluation (54–58). Indeed, the failures of choice with choices sets over a few items are striking and have been a major part of the heuristic literature (59, 60). These strict limits are ostensibly difficult to explain. They do not appear to derive, for example, from the basic computational or biophysical properties of the nervous system, as is evident from the fact that our visual systems are an exception to the general pattern and can process much information in parallel. Nor do these limits appear to relate to any desire to reduce the extent of computation, as large numbers of brain regions coordinate to implement these cognitive processes (61–64). Our results presented above offer an appealing explanation for this problem: Economic choice can be construed as BD search problems, and even when capacity is large, the optimal strategy is to focus on a very small region of the search space. Thus, our results can also help to understand why many cognitive systems operate in a regime of low sampling size, thus resolving the paradox of why low breadth sampling and large brain resources can coexist.

We believe that these results are particularly relevant to behavioral economics. Research has shown that consumers often consider just a small number of brands from where to purchase a specific product out of the many brands that exist in the market (65, 66). The prevailing notion is that decision makers hold a consideration choice set from where to make a final choice rather than contemplating all possibilities. Several reasons for this behavior have been provided. First, choice overload has been shown to produce suboptimal choices in certain conditions (60, 67). Second, selecting a small number of options from where to choose can be actually optimal if there is uncertainty about the value of the options and there is cost for exploring and sampling further options (68–70). Estimating the overall benefits of considering larger sets has to be balanced with the associated cost of exploring further options.

This research has provided a relevant line of thought for understanding low sampling behavior within the context of bounded rationality by formally assuming the presence of linear costs of time for searching for new options. Time costs come in their models at the expense of unknown parameters, which often are difficult to fit (68, 69). Furthermore, linear time costs always permit unlimited number of sampled options, as they do not impose a strict limit in the number of options that can be sampled. In our approach, in contrast, allocating finite resources imposes a strict limit to the number of options that can be sampled and, as resources are limited, there is a trade-off between sampling more options with less resources or sampling fewer options with more resources, directly addressing the BD dilemma. This difference could be the main reason why the consideration set literature has not reported sharp transitions of behavior as a function of model parameters (costs) nor power sampling laws, which are the main features of our finite-sample capacity model.

A number of extensions would be required to fully address more realistic problems associated to the BD dilemma. So far, we have considered a two-stage decision process, where the first metareasoning decision is about optimally distributing limited sampling capacity. We have also considered a sequential problem where some basic form of feedback can be used, but the allocation strategy needs to be chosen before the gathering of information and remains fixed thereafter. By construction, these optimal dynamic allocations at large capacity sample more deeply those alternatives that have largest values, in line with experimental work (55, 71). Perhaps a more relevant observation is that the depth of processing of the best alternatives increases with capacity and that more samples are allocated to the top alternatives than for optimal static sample allocations (cf. Fig. 6). Furthermore, if capacity increases, relatively more samples are allocated to the most-sampled than the second-most–sampled alternative. Both predictions are currently untested.

It would be interesting to extend these results to truly sequential processes where the decision of how many samples to allocate per wave is flexible and depends on intermediate feedback. An advantage of this more general setup (72) is that a full-fledged interaction between the BD and EE dilemmas could be studied. In particular, a relevant direction is relating our square root sampling law with Hick’s law (73) for multialternative choices. The two approaches touch different aspects of multialternative decision making: While Hick’s law refers to the problem of how long options should be sampled in a multialternative setting, it does so by sampling all available options; the square root sampling law, by contrast, applies to situations where there are many alternatives and a large fraction of them are to be ignored due to limited capacity, directly facing the BD dilemma. It will be interesting to integrate the two sets of results within a general framework of multialternative sequential sampling (74–76) under limited resources.

A second possible extension of our work is reconsidering the nature of capacity. For instance, “rate distortion theory” defines a natural capacity constraint over the mutual information between the inputs and the outputs in a system (77, 78). This capacity constraint might more naturally enforce a finite capacity than fixing the total number of samples that a system can draw from (externally or internally). A third relevant direction would be extending our study to cases where the capacity is continuous rather than discrete, and to cases where the observations are continuous variables. Showing that Gaussian rather than Bernoulli outcomes yield qualitatively similar strategies is a first step in this direction. Although it remains a topic for future research, we do not expect qualitative differences in behavior in other continuous settings, as for large capacity the continuous limit approximation applies, and for low capacities the optimality of low number of sampled alternatives is expected.

While we do not know of direct tests of BD capacities in humans, indirect measurements suggest that the square root sampling law can be at work in some realistic conditions, such as chess. It has been argued that chess players can image around 100 moves before deciding their next move (79). Assuming that their capacity is 100, then the square root sampling law would predict that players should sample 10 immediate moves followed by around 10 continuations. Indeed, estimates indicate that chess players mentally contemplate roughly between 6 and 12 immediate moves followed by their continuations (79) before capacity is exhausted due to time pressure. Although decisions in trees like this surely involve other types of search heuristics beyond balancing breadth and depth, the quantitative similarity between predictions and observations is intriguing.

Finally, our work potentially opens ways to understand confirmation biases. Confirmation biases happen when people extensively sample too few alternatives, thus effectively seeking information for the same source. We have demonstrated that oversampling some alternatives and completely ignoring others is optimal in certain conditions. It remains to be seen, however, whether this is actually the optimal strategy under more general conditions or whether the oversampling strategy induces severely harmful biases in certain niches.

It is important to note that we have described the phenomenology of the BD dilemma in conditions where all alternatives are, a priori, equally good. Thus, ignoring a large fraction of options and the associated square root sampling law can only be the worst-case scenario, in the sense that if there are biases or knowledge that a subset of alternatives is initially better than the rest, then fewer number of alternatives should be sampled. This consideration reassures us in the conclusion that the number of alternatives that ought to be sampled is much smaller than sampling capacity, an observation that might turn out to be of general validity in both decision-making setups as well as in terms of brain organization for cognition.

Methods

A detailed description of the finite-capacity model, a derivation of Eqs. 1–5, and a description of the numerical methods used to generate the figures can be found in SI Appendix.

Data Availability.

The data that support the findings of this study, as well as the codes used for analysis and to generate figures, are publicly available in GitHub at https://github.com/rmorenobote/breadth-depth-dilemma.