Significance
Alzheimer’s disease (AD) is caused by the accumulation of pathological aggregates, primarily composed of the A40 and A42 isoforms. Experiments have shown that A42 is more aggregation prone compared to A40. However, the molecular origin of this apparent anomaly remains elusive. Here, we provide a microscopic basis for the different aggregation rates in terms of the distinct populations of high free energy excited fibril-like states () that are encoded in the monomer spectra. The theory explains the emergence of fibril polymorphs and predicts the relative kinetic stabilities of A42 fibrils using Ostwald’s rule of stages. Our work shows that sequence-specific conformational heterogeneity of the monomer ensembles provides important cues for understanding protein aggregation.
Keywords: protein aggregation, Alzheimer’s disease, free energy gap, Ostwald’s rule, polymorphism
Abstract
The early events in the aggregation of the intrinsically disordered peptide, amyloid- (A), involve transitions from the disordered free energy ground state to assembly-competent states. Are the fingerprints of order found in the amyloid fibrils encoded in the conformations that the monomers access at equilibrium? If so, could the enhanced aggregation rate of A42 compared to A40 be rationalized from the sparsely populated high free energy states of the monomers? Here, we answer these questions in the affirmative using coarse-grained simulations of the self-organized polymer–intrinsically disordered protein (SOP-IDP) model of A40 and A42. Although both the peptides have practically identical ensemble-averaged properties, characteristic of random coils (RCs), the conformational ensembles of the two monomers exhibit sequence-specific heterogeneity. Hierarchical clustering of conformations reveals that both the peptides populate high free energy aggregation-prone () states, which resemble the monomers in the fibril structure. The free energy gap between the ground (RC) and the states of A42 peptide is smaller than that for A40. By relating the populations of excited states of the two peptides to the fibril formation time scales using an empirical formula, we explain nearly quantitatively the faster aggregation rate of A42 relative to A40. The concept accounts for fibril polymorphs, leading to the prediction that the less stable state of A42, encoding for the U-bend fibril, should form earlier than the structure with the S-bend topology, which is in accord with Ostwald’s rule rationalizing crystal polymorph formation.
Alzheimer’s disease (AD), a neurodegenerative disorder affecting a large proportion of the world population, is associated with the gradual accumulation of insoluble plaques in various parts of the brain (1–5). The fibrillar structures of the amyloid- (A) peptides, like other amyloid aggregates, have a characteristic cross- architecture (6–8). The fibrils form as a result of aggregation of the 39- to 43-residue-long A peptides. In vivo, A is produced by the proteolytic cleavage of the amyloid precursor protein (APP) by -secretases, with A40 and A42 being the major products (9, 10). The fibrils exhibit a high degree of polymorphism, even though globally they all have the characteristic -sheet architecture. The link between polymorphic structures, which could depend on the way they are generated, and the extent of neurotoxicity is a topic of continuing interest (1, 11). In addition to AD, several other neurodegenerative diseases, such as Parkinson’s and Huntington’s disease, are also the result of abnormal in vivo protein aggregation. Various studies (12, 13) have proposed that these diseases could share several common themes with AD, including similar fibril morphologies, mechanism of fibril formation, and the association of toxicity with oligomers. To obtain a more quantitative understanding of these general principles, it is crucial to understand the key steps involved in amyloid aggregation at the molecular level.
The cascade of events that describe the conversion of monomers to fibrils is complex (14–16). Because of the transient nature of species that form during the early stages (before a critical size nucleus), it is difficult to describe their structural details using experiments alone. A complete understanding requires describing the conformational changes that occur during the aggregation process starting from the monomer. Toward this end, conformational dynamics of A monomers have been extensively studied, using both experiments (17–19) and computer simulations (15, 20–25). The structural details of the predicted ensembles vary widely among the different studies. Some of the differences in the experiments could be due to differing external conditions, such as variations in pH, temperature, or salt concentration. Molecular dynamics simulations reveal that the populations of different secondary and tertiary structural elements are strongly dependent on the details of the force field and sampling strategies (26–29). However, based on recent NMR (17, 18) and Förster resonance energy transfer (FRET) experiments (30), a general consensus seems to be emerging that A monomers behave like many other intrinsically disordered proteins (IDPs) that are highly disordered, adopting random coil (RC) structures at room temperature and neutral pH. The structures are devoid of any persistent secondary structures (-helices and -sheets). In other words, it appears that the propensity to form amyloid fibrils cannot be discerned when only the average properties of the monomer ensemble are examined.
The natural question is whether there are any connections between the conformational heterogeneity of the monomer ensemble in solution and the eventual structures adopted in the fibril state. More precisely, at what stage of A aggregation does one observe a transition from the RC conformation to structures with considerable content? In a series of papers, we (31–33) showed that the structures that have a high propensity to aggregate are encoded as excitations in the monomer free energy spectrum. Subsequent studies (34–36) have confirmed our findings. More importantly, such conformations have some of the structural features of the monomers in the fibril. We first elucidated this concept using atomically detailed simulations of a 26-residue fragment of the A peptide using molecular dynamics simulations (31). Subsequently, we illustrated the consequences quantitatively using lattice models (32), for which precise computations could be carried out by exploring the entire sequence space. Simulations based on the lattice models also showed empirically that the time scales of fibril formation () could be linked to the population () of the aggregation-prone species (referred to from now on as states) (32, 36). The structures in the ensembles (there are more than one) are difficult to characterize using standard experimental techniques because they are high free energy states that are only sparsely populated. In this context computations are useful.
For A40 and A42, the two most prevalent isoforms in vivo, the question of whether there is a link between the underlying heterogeneity (and by inference, ) of the monomeric ensembles and their aggregation propensities is pertinent. This is because A42 aggregates faster and is the major constituent of amyloid plaques (37–39), despite being present in relatively lower abundance than A40 (40). Several studies have attributed the elevated pathogenicity of A42 to the pronounced structuring near the C terminus, which is mediated by the two extra residues (ILE41 and ALA42) (41–43). Recent A42 fibril structures determined using solution-state NMR (44, 45) and cryo-electron microscopy (EM) (46) seem to corroborate this viewpoint. Previous work based on all-atom studies (29, 30, 42, 47, 48), and simulations using coarse-grained models (49–51) further predict that the two isoforms could be associated with different populations of the metastable states and allude to a sequence-specific conformational heterogeneity that could be a key determinant of the contrasting aggregation propensities.
Here, we report results from simulations using a modified version of a recently developed highly accurate coarse-grained (CG) model for intrinsically disordered proteins (termed as self-organized polymer-intrinsically disordered protein [SOP-IDP] model) (52) to characterize the conformational ensembles of A40 and A42. The major purpose is to illustrate the theory that the differences in the extent of population of the sparsely populated states in the monomeric ensembles of the A peptides quantitatively explain the relative fibril formation rates of A42 and A40. We show that despite having practically identical ensemble-averaged values of several experimental observables under physiological conditions, the underlying conformational heterogeneities of the two peptides are distinct. In particular, the termini display a different extent of residual structuring in the two peptides. Most importantly, A42 has a higher population () of aggregation-prone (excited) states that display many of the characteristic structural features found in fibrils. The difference in the equilibrium populations of states between A42 and A40 when linked to kinetics rationalizes the nearly one order of magnitude faster fibril formation rate of A42 relative to A40. Our study, therefore, provides a crucial link between aggregation propensity and sequence-specific conformational heterogeneity in the monomer. In other words, the spectrum of excited, but sparsely populated states sampled at equilibrium is a harbinger of protein aggregation.
Results
Sizes and Polymeric Features of A Peptides Are Nearly Identical.
The distributions of the radius of gyration, , and end-to-end distance, , both of which describe the global dimensions of the A monomers, are similar (Fig. 1 and Table 1). The small differences are likely due the longer length of A42. Our estimates for and are in good agreement with the values reported in two recent studies (28, 30). The distributions of the scaled end-to-end distance, (), shown in Fig. 1C, for both the A monomers deviate from the well-established theoretical results for a Gaussian chain and a self-avoiding random walk (SAW) (see SI Appendix for further details). The departure from standard homopolymer theories is the first hint that sequence-specific effects as well as the inherent polyampholyte-like characteristic of the A peptides need to be accounted for when describing their conformational ensembles.
Fig. 1.
The sequences of A40 and A42 using one-letter code are displayed at Top. Ensemble characteristics of A40 and A42 are depicted as red and blue curves, respectively. (A) Distribution of the radius of gyration, . (B) Distribution of hydrodynamic radius, . (C) Distribution of end-to-end distance, , scaled by . To compare with the results for a Gaussian chain and a SAW, we show where . (D) Distribution of FRET efficiencies. The corresponding mean values are given in Table 1.
Table 1.
The ensemble-averaged values of different observables for A40 and A42
| Sequence | , nm | , nm | , nm | |
| A40 | 1.65 0.012 | 3.83 0.065 | 1.47 0.01 (1.6)* | 0.65 0.014 (0.6)† |
| A42 | 1.69 0.013 | 3.93 0.066 | 1.51 0.01 (1.7) | 0.63 0.015 (0.6)† |
The errors are reported in terms of standard deviations estimated using block averaging.
The experimental value of Rh is from FCS experiments of Wennmalm et al. (54).
The FRET efficiency values are from Meng et al. (30). The numbers in parentheses are taken from the quoted experiments
The experimental value of Rh is from the diffusion NMR experiments of Vendruscolo and coworkers (53).
Besides and , the hydrodynamic radius is another measure of polymer size, which can be estimated using dynamic light scattering (DLS), NMR, and fluorescence correlation spectroscopy (FCS) experiments (53, 54). The distributions of for the A40 and A42 also overlap to a large extent (Fig. 1B) and yield similar ensemble averages (Table 1). For both the sequences, the values are in excellent agreement with those (1.5 to 1.7 nm) measured in NMR (53) and FCS experiments (54). The ratio for both A40 and A42 is 0.9, which implies that neither peptide behaves as an RC or a Gaussian chain, for which the ratios should be 0.640 and 0.665, respectively (55).
A recent study (30) reported the global dimensions and conformational dynamics of A monomers using single-molecule experiments, thus complementing previous findings from NMR and circular dichroism (CD) experiments. The FRET histograms computed from our simulations, using Eq. 7 (see SI Appendix), are shown in Fig. 1D. The average FRET efficiencies, for both the peptides (Table 1) are in excellent agreement with the experimental estimates (0.6) at zero denaturant concentration (30). Unlike in the FRET experiment, however, we also observe a peak at . This discrepancy is not unexpected and could be attributed to the small size of the peptides, as well as the large Förster radius (5.2 nm) of the Alexa 488 and 647 dye pair, which according to Eq. 7 (see SI Appendix), would result in 1 for less than 4.0 nm. Similar observations have been made in two previous studies (28, 30). From all-atom simulations, Meng et al. (30) noted that although the A monomers were characterized by largely overlapping distributions for , , and , the distribution of A42 exhibited a minor peak at low end-to-end distances, corresponding to a subpopulation of conformations with long-range contacts. However, no such feature is discernible from our computed probability distributions (Fig. 1). The good agreement between our simulations and experiment for the observables in Table 1 attests to the accuracy of the SOP-IDP model in predicting the values of measurable quantities.
A Ensembles Are Disordered.
For both the sequences, the interresidue distances, , as a function of sequence separation, , adhere to the Flory scaling law: , with = 0.47 nm, and the scaling exponent, = 0.58 (Fig. 2; see SI Appendix for further details). The free energy landscapes projected onto the first and second principal components, based on the Cα–Cα distances and and coordinates (SI Appendix, Figs. S3 and S4), are featureless, further exemplifying the intrinsically disordered nature, as well as the underlying conformational heterogeneity of the A monomer ensembles.
Fig. 2.
(Left) The variation of interresidue distances () with sequence separation, for the A40 and A42 sequences, are shown as red circles and blue triangles, respectively. The solid lines are fits to the Flory scaling law expected for homopolymers in good solvents: , with = 0.47 nm and = 0.58 for both the peptides. Although scaling, an ensemble-averaged quantity, is consistent with polymer theory, the distribution of deviates from the expected universal behavior for self-avoiding walks (Fig. 1). (Right) Variation in the ensemble-averaged side-chain contacts for the A40 and A42 shown as a difference map, color coded (scale on the right) in terms of . Here, and are the ensemble-averaged contact probability maps for A40 and A42, respectively.
There are no discernible long-range contacts in the ensemble-averaged contact maps for A40 and A42 (SI Appendix, Fig. S5). However, from a zoomed-in view of the difference map, , it is apparent that a small but detectable population of substates (masked in the ensemble-averaged contact map), which have a tendency to form residual structure at the C terminus, is present in the conformational ensemble of A42 (Fig. 2). Taken together these results show that A monomers do not adopt stable well-defined secondary or tertiary structures at equilibrium, but rather dynamically interconvert among a menagerie of conformations.
A Monomers Have Negligible Residual Secondary Structure.
The secondary structure profiles associated with the A40 and A42 monomers are shown in Fig. 3. Both the peptides have very low preferences for structural elements, such as -strand or helices. All of the residues display a very high propensity (97%) to form turns or irregular coils. Our observations are consistent with NMR experiments (17, 18), as well as all-atom simulations (28, 30), which predict that A monomers populate mostly RC-like structures in equilibrium. Overall, we observe a large overlap between the turn profiles for A40 and A42. In particular, the elevated turn propensities near residues 7 to 11, as well as 23 to 27 (which include the well-known valine-glycine-serine-asparagine [VGSN] turn), are consistent with the NMR experiment (18). Nonetheless, there are some subtle differences in the propensity of forming residual structure in some parts of the sequence, which are worth noting.
Fig. 3.
Percentages of different secondary structure elements in the conformational ensembles of A40 (red) and A42 (blue). (Top) Ensemble-averaged percentages for forming turn/irregular coils. (Middle) Residue-wise percentages for forming helices. (Bottom) Residue-wise percentages for forming -sheets. The secondary structures were assigned based on the positions of the atoms using the protein C-alpha secondary structure output (PCASSO) algorithm.
A40 has a more structured N terminus (residues 4 to 6), as indicated by the marginally higher propensity to form -sheets and -helices in this region. In contrast, A42 has a slightly more ordered C terminus (38 to 42), with the residues in this region displaying a somewhat higher probability of forming both helices and -sheets and a pronounced bend near residues 36 to 37. The contrasting structural preferences at the two termini, particularly the enhanced ordering at the C terminus of A42, have also been noted in previous all-atom (26–28, 42, 56) and coarse-grained simulations (49, 57). Interestingly, in both the peptides, residues near 13 to 20, which include the central hydrophobic core (CHC), show an enhanced probability to form helical domains. As argued in previous experimental (58) and simulation studies (23, 59, 60), such residual structure near the CHC could play a key role in mediating the early events in amyloid fibrillogenesis. We also find that in both the monomers, residues 29 to 36 tend to form secondary structures with higher probability compared to the rest of the sequence. This feature is also consistent with previous work (18, 27, 48). It is worth emphasizing that the probabilities to adopt -sheet or -helix are really small relative to coil-like states. Our simulations suggest that detecting them using experiments is likely to be difficult.
Chemical Shifts.
The residue-wise chemical shifts for A40 and A42 are shown in Fig. 4. Given the coarse-grained nature of our model, and the higher errors associated with the estimation of chemical shifts of other nuclei with the LARMOR- formalism (SI Appendix) (61), we report only the ensemble-averaged values of the chemical shifts. As illustrated in Fig. 4, our predictions are in reasonable agreement with NMR experiments (17, 18). We note that the qualitative agreement was obtained (SI Appendix, Fig. S6) without adjusting any parameter to fit the experiments. To further validate the SOP-IDP model, we carried out a systematic comparison between our predictions for the chemical shifts and those from all-atom simulations based on different force fields (48, 62). The relative errors with respect to experimental data show that the predictions of the SOP-IDP model are on par and in some cases better than the all-atom force fields (see SI Appendix, SI Text, Table S3, and Figs. S7 and S8 for details).
Fig. 4.
Residue-wise chemical shifts for A40 (Left) and A42 (Right). The predicted shifts for A40 are shown in red, and those for A42 are shown in blue. The chemical shifts from the experiment of Bax and coworkers (17) are shown in light green, and those from Zagorski and coworkers (18) are shown in black. The predicted values are in qualitative (the trends are comparable) agreement with experiment. The weighted-root-mean-square error () for A40 between predicted shifts and those measured by Bax and coworkers (17) is 0.53. The error is smaller (0.47) relative to the measured values of Zagorski and coworkers (18). For A42, the trend is reversed, and corresponding values are 0.48 and 0.66.
The chemical shifts for the first 35 residues are nearly identical for both the peptides (Fig. 4 and SI Appendix, Fig. S9), mirroring the observed trend for the secondary structure profiles. Most residues show only minimal departures from the RC references, further demonstrating the completely disordered nature of the ensembles and the lack of substantially populated (metastable) structural elements. Nonetheless, the chemical shifts for some valines (Vs) and histidines (Hs) deviate from the RC values. In particular, the upshifted shifts for V18 (also visible in the experimental profiles) and V12-H14 for both A monomers imply that this region could adopt a residual structure, albeit only transiently. Similar observations have been made previously (63) using electron paramagnetic resonance (EPR) spectroscopy and all-atom simulations (34, 48). The chemical shifts for H6, V24, and V36 are also shifted upfield by 1 ppm, indicating that these residues could form fleeting structures. Although similar signatures are not present in the experimental profiles shown in Fig. 4, a previous study (48) does suggest that these residues could be involved in hydrogen-bonding interactions with V18, resulting in upshifted chemical shifts. Interestingly, the modest departure from the RC values for H6 and H14 hints at a possible role of these residues in mediating A self-assembly (18, 64) via formation of transient structures, as well as being a template for molecular recognition (65).
Given that all of the measurable and computable values are virtually identical for both the peptides, is it possible to explain the enhanced aggregation rate of A42 relative to A40 using equilibrium monomer properties? We show below that the answer lies in the differences in the conformational heterogeneities between the two peptides, which result in an enhanced population of states in A42 compared to A40.
Sequence-Dependent Conformational Heterogeneities.
The ensemble-averaged properties, as well as features of the free energy landscapes, although commensurate with the prevailing consensus regarding the intrinsically disordered nature of the A monomeric ensembles, do not reveal significant alloform-specific differences. Structural details of aggregation-prone conformers having extremely low equilibrium weights are masked in such averages, although subtle differences in the secondary structure profiles allude to sequence-specific conformational heterogeneity. To glean further insights into the fine structure of the free energy landscape of A40 and A42, we carried out hierarchical clustering of the conformational ensembles based on a robust distance metric (SI Appendix, Fig. S10). Our previous study (52) showed that this scheme provides an efficient means to quantify the contrasting conformational heterogeneities of many IDPs.
At a coarse level, the conformational ensembles of both the peptides can be partitioned into three major clusters: compact, semicompact, and extended. Even when such a simplistic classification is used, sequence-specific conformational preferences become apparent (SI Appendix, Fig. S10). For both the sequences, the equilibrium weights of the fully extended structures are relatively low, being 19.9 and 20.9% for the A40 and A42 sequences, respectively. Compact structures dominate the conformational ensemble of A40 (53.7%), and semicompact structures constitute the second-largest cluster (26.4%). This trend is reversed for A42; the population of semicompact structures is enhanced to 41%, and that of compact structures is diminished to 38.1%. The relative weights of the different cluster families, even at such a coarse resolution, hint at evident deviations from standard polymer models, even though ensemble-averaged contact maps and scaling behavior suggest otherwise.
To ascertain the arrangement of the local structural segments we performed more refined analyses using a smaller distance cutoff for (see Eq. 11 in SI Appendix). This splits the dendrogram further and divides the major clusters into additional subfamilies. A cutoff of 5.0 seems appropriate for both the A40 and A42 ensembles as it not only provides sufficient resolution to determine the key differences in the contact maps of the subclusters, but also keeps their number tractable. Using this scheme, we obtained 12 clusters for A40 and 11 clusters for A42 (SI Appendix, Fig. S10). The populations of the different clusters are tabulated in SI Appendix, Table S4. In Fig. 5 we show the most important cluster families that are related to the states, and the rest are included in SI Appendix, Figs. S12 and S13. The proper segregation of the various families in the two-dimensional surfaces defined by and implies that our clustering scheme is robust (SI Appendix, Fig. S11). The structural details of the different subfamilies are described below.
Fig. 5.
(A) The free energy ground state of the A40 and A42 ensembles consisting of RC-like conformations devoid of fibril-like contacts. The contact map averaged over the corresponding subensemble is featureless. B–D show the contact maps and representative snapshots of clusters identified for A40, which consist of aggregation-prone () conformations. These conformations exhibit many of the structural elements found in the A40 fibril. The E22, D23, and K28 residues, which form the key salt bridges, are explicitly shown. (B) Cluster 9: The VGSN turn is formed and is stabilized by the D23-K28 salt bridge. However, the N-terminal and C-terminal segments are quite flexible and do not form contacts. (C) Cluster 10: A SLS-like structure stabilized by the formation of a VGSN turn and the D23-K28 salt bridge. (D) Cluster 11: SLS-like structure stabilized by a turn formed near the VGSN region and the E22-K28 salt bridge. E–H show the contact maps and representative snapshots of clusters identified for A42, which consist of conformations, in some of which the structural elements found in the different A42 fibril polymorphs are visible. These structures are members of the ensemble. In E and F the K28 and A42 residues are shown as spheres. (E) Cluster 4: S-bend type motif, exhibiting close contact between K28 and A42, similar to that found in an A42 fibril structure. (F) Cluster 5: S-bend type structures, with enhanced ordering near the C terminus, including a close contact between the K28 and A42 residues. G and H denote clusters which bear resemblance to the monomer unit of a different A42 polymorph, which has a classical -strand–loop–-strand topology consisting of a U-bend. (G) Cluster 6: SLS-like structure consisting of a U-bend near the VGSN turn region, stabilized by the D23-K28 salt bridge (shown as spheres). (H) Cluster 7: SLS-like structures formed via the association of the two terminii. The D23-K28 salt bridge (shown as spheres) stabilizes the turn region in these structures.
A40.
The contact maps associated with clusters 1, 2, 3, and 7 (SI Appendix, Fig. S12) are devoid of short- or long-range contacts. Other clusters are also rich in RC-like conformations, but also contain some fingerprints in the contact map, which is suggestive of local structuring near the N terminus. Approximately 50% of the conformations in clusters 5 and 8 show enhanced structural contacts between the N terminus (residues 1 to 8) and those near the CHC (SI Appendix, Table S4). Specifically, residues 12 to 21 in cluster 5 and 10 to 20 in cluster 8 engage in interactions with the N terminus. The contact maps of clusters 4 and 6 (SI Appendix, Fig. S12) also indicate enhanced ordering near the N terminus of A40. However, these features are less prominent than those in clusters 5 and 8, and the contacts tend to be more short ranged (between residues and ). Cluster 12 consists of a nearly equal population of RC-like conformations and those that have a number of long-range contacts between the N terminus and residues 15 to 28 (SI Appendix, Fig. S12 and Table S4). Both simulations (22, 23, 66) and experiments (59, 60, 67, 68) have previously underscored the importance of residual structure in this region (particularly, LVFFA, residues 17 to 21) and its potential role in dictating aggregation kinetics. Overall, clusters containing exclusively RC-like states account for 32% of the equilibrium population. The cumulative population of clusters having a mixture of RC-like conformations and those having residual structuring near the N terminus is 47.3%. Taken together, 80% of the conformational ensemble is predominantly RC-like.
Fingerprints of the fibril structure.
Despite the dominance of RC-like conformations in the equilibrium ensemble, the essential fingerprints of the fibril state can be found in a few conformational clusters. Importantly, at the distance cutoff used for structural clustering, none of the constituent structures in these clusters resemble random coils. Previous studies have shown that the D23-K28 salt bridge, which is a key structural element of mature A40 fibrils, modulates the early events of amyloid aggregation (20, 21, 31). We find clear-cut signatures of these contacts in the structures in cluster 9 (Fig. 5B), which is associated with an equilibrium population of 7.7%. In addition to the presence of E22/D23-K28 salt bridges, a majority of structures also have hydrophobic contacts between V24 and N27, which stabilize the VGSN turn. However, the N-terminal and C-terminal segments remain mobile and do not form the complete strand–loop–strand (SLS) structure, which forms the repeating unit in the fibril. The conformations in cluster 11 (population 10%) are compact (SI Appendix, Fig. S11) with prominent off-diagonal elements in the contact map, which are reflected in the tendency to form SLS-like structures (see SI Appendix for details) via association of the two ends (Fig. 5D). The SLS structure, often thought to be a putative intermediate in fibril elongation (69), essentially has a hairpin-like topology and engages in hydrogen-bonding interactions with neighboring monomers to stabilize the fibril structure. Many of the conformations within cluster 10 (population 3.2%) are ordered and exhibit signatures of the fibril state (Fig. 5C). In these structures, contacts are formed between the CHC and residues 28 to 40.
A42.
Conformations belonging to clusters 2, 3, 8, and 9 consist of exclusively RC-like structures. Some clusters identified for A42 consist of an admixture of RC-like conformations and ones with different extent of local structuring (SI Appendix, Table S4). In cluster 1, nearly two-thirds of the constituent structures feature contacts between the central region (residues 22 to 29) and the C terminus (SI Appendix, Fig. S13). Structures within cluster 10 are mostly semicompact, and around 20% of these exhibit some tendency of structuring near the N terminus by forming contacts with residues 20 to 30 (SI Appendix, Fig. S13 and Table S4). Conformations within cluster 11 are mostly disordered and are typically RC-like, although a few of them exhibit structuring near the central region (SI Appendix, Fig. S13). Together, clusters having predominantly RC-like features (albeit with some degree of local structuring) contribute around 62.1% to the equilibrium population (Fig. 5A). In addition to those having RC-like features, there are other clusters in the conformational ensemble of A42, which exhibit structural features of different experimentally characterized fibril morphologies. We describe them below.
Fingerprints of the S-bend fibril structure.
Recently, NMR (44, 46) and cryo-EM (70) experiments have identified the “S-bend” motif as a building block of the A42 fibril structure. The S-bend structure, which apparently is not found in A40, results from enhanced ordering near the C terminus of A42 and is characterized by a close contact between residues K28 and A42. Although not immediately discernible from the contact maps, many of the conformations within clusters 4 and 5 exhibit the characteristic S-bend motif, stabilized by a close contact between residues K28 and A42 (Fig. 5). These clusters exhibit enhanced ordering near the C terminus, but differ somewhat in the specific residues involved in contact formation. In cluster 4 (Fig. 5E) the contacts are formed between the C terminus and residues 18 to 24, while in cluster 5 (Fig. 5F) residues 15 to 22 form contacts with the C terminus. Conformations similar to these have been previously identified by Garcia and coworkers (56) using all-atom simulations in conjunction with spectral clustering algorithms.
Fingerprints of the U-bend fibril structure.
Besides the S-bend topology, A42 also forms fibril structures in which the peptide adopts the canonical U-bend (71) (similar to the repeating unit of A40 fibrils). Clusters 6 (Fig. 5G) and 7 (Fig. 5H) exhibit SLS-like structures (see SI Appendix for details) and consist of the E22/D23-K28 salt bridges, as well as the VGSN turn in a large fraction of the constituent structures. These clusters contribute 9.7 and 10.2% to the equilibrium population. In cluster 6, the -strand–loop–-strand structures are formed via the association between residues 9 to 16 and the C terminus, whereas SLS conformations within cluster 7 involve contacts between the two terminii.
From our clustering analyses we draw important insights regarding the sequence-specific heterogeneities of A40 and A42 monomers: 1) For both the sequences, clusters that are predominantly RC-like or have RC-like structures in an admixture with conformations having some degree of residual structuring dominate the equilibrium population. Notably, these clusters do not exhibit any of the characteristic structural features found in the fibril. 2) Interestingly, despite having identical sequence for the first 40 residues, the structural features near the termini are distinct for the two A monomers. A40 has a structured N terminus, while A42 exhibits enhanced structuring near the C terminus, which is consistent with previous studies (19, 42, 48, 72, 73). As argued in a previous work (42), in A monomers, there is a tug of war between the C terminus and the N terminus for making contacts with the CHC. In the case of A40, the N terminus wins, because unlike A42, it does not contain an extra hydrophobic patch formed by I41 and A42 to induce structuring near the C terminus. Structuring near the N terminus of A40 could also have implications in the subsequent assembly process and in determining the fibril morphology. As shown in a recent study (74), a cryo-EM A40 fibril structure derived from a meningeal Alzheimer’s tissue is characterized by pronounced arches at the two ends (most notably at the N terminus). 3) Although masked in ensemble averages, clustering analyses reveal that the aggregation-prone structures ( states) are present in the spectrum of conformations populating the ensemble, in agreement with previous studies (21, 32, 34, 36). For A40, we find evidence of formation of E22/D23-K28 salt bridges, as well as SLS topologies, and within the A42 ensemble, we find signatures of SLS structures characterized both by U-bends and by the S-bend motifs.
Linking the Population of States to Aggregation Propensity.
The analyses based on hierarchical clustering show that fibril-like or aggregation-prone conformations () are populated in the monomer ensemble of the A peptides. However, to quantify their population, , a stringent order parameter, comparing the putative conformations identified using the cluster analysis with the fibril structure, is required. In other words, only a subset of conformations belonging to the basin of attraction has the propensity to aggregate. We estimate based on a geometric criterion. Because the conformations belonging to the state should be similar to the structure in the fibril, we use the fibril structures as reference states. We used the structural overlap parameter, , between a monomer conformation generated in the simulations at time and the monomer in the experimental fibril structure to characterize the states for both the peptides (see SI Appendix for further details). For A40, we used the striated fibril structure determined by Tycko and coworkers (75) as the reference. For A42, we used the two structures reported by Riek and coworkers: the U-bend topology (71), which is very much similar to the repeating unit found in A40 fibrils, and the S-bend motif (44).
The distributions of are shown in Fig. 6. The distributions for A40 and A42 nearly overlap when the U-bend (or striated) structure is chosen as a reference. This suggests that the population of fibril-prone structures exhibiting the canonical SLS motif is approximately similar between the two sequences. In contrast, the conformational ensemble of A42 seems to bear a higher overall resemblance to the S-bend motif.
Fig. 6.
(A) Distribution of for A40 (shown in red). The overlap parameter is computed with respect to the monomers in the experimental fibril structure. For A40, the reference state is the monomer unit from the striated (U-bend) fibril structure (75) (Protein Data Bank [PDB] ID: 2M4J) (75). The shaded area under the curve, which corresponds to the state is in red. Inset shows an enlarged view of this section of the curve. (B) Distribution of for A42 (shown in blue) using the monomer from the U-bend fibril structure (PDB ID: 2BEG) (71) as a reference. The shaded area under the curve (Inset) corresponds to the population of states with U-bend topology. (C) Same as B except that the overlap parameter, , is calculated using the S-bend fibril structure (PDB ID: 2NAO) (44). The shaded area under the curve (Inset) corresponds to the population of states having S-bend topology. In A–C the purple curves correspond to computed from the restrained simulations (see SI Appendix for details) starting from the monomer present in the fibril structure. (A) A40 fibril structure (PDB ID: 2M4J). (B) A U-bend fibril structure (PDB ID: 2BEG). (C) A42 S-bend fibril structure (PDB ID: 2NAO). In all cases, the center of the distribution is approximately at = 0.28. This value corresponds to and is marked in the plots.
The state is hidden in the tail of these distributions (Fig. 6). To identify the approximate location of the basin consisting of the aggregation-prone conformations, we carried out restrained simulations (see SI Appendix for details) starting from the monomer structure present in the experimental fibril morphologies of A40 and A42. The distributions are calculated from the restrained simulations and reflect the conformations within the basins of attraction that could readily aggregate (purple curves in Fig. 6 A–C). We find that the basin of aggregation-prone structures is approximately centered at = 0.28 for both A40 and A42. Hence, for both the sequences, we collectively define states as the ensemble of conformations with . Therefore, we calculated using
| [1] |
where is the structural overlap for the th snapshot in the th trajectory, denotes the number of snapshots in each trajectory, denotes the number of independent trajectories, and is the Heaviside function. Using Eq. 1, we estimated that is 0.45% for A40. For A42, is estimated to be 1.45% when the U-bend topology is used as a reference and 2.17% when the S-bend motif is used as a reference. These numbers fall within the same range as previous estimates of at physiological conditions for the src SH3 (33) domain, which is a globular protein.
As indicated by the presence of a minor peak near , only a subpopulation of conformations within the clusters (SI Appendix, Fig. S17), which exhibit structural signatures of the fibril state, meets the strict geometric definition (Eq. 1) for the conformations within the state that are likely to aggregate. This observation implies that although contact maps corresponding to various subensembles could be useful in discerning the presence of aggregation-prone species, they are probably too coarse as metrics for quantitatively measuring .
Previously (32), we proposed that the time scale of fibril formation, which should be thought of as an approximate estimate of the mean first passage time for the monomer to reach the structure in the fibril (U-bend or S-bend), is related to as
| [2] |
where the population of the state is expressed as a percentage. The expression in Eq.2 does not account for the multiplicity of events that are involved in fibril formation. Using = 1 for both the peptides and the estimated values of , we predict that for A42 is approximately 24 times smaller than for A40. Our prediction is in accord with recent experiments (39), which show that the fibril formation rate of A42 is about one order of magnitude greater than that of A40. Interestingly, the one order of magnitude difference cannot be rationalized if only the U-bend or striated conformations are identified with the state. In this case, the aggregation of A42 is only twice as fast. This implies that the enhanced ordering near the C terminus, which stabilizes the S-bend motif, provides an alternate route for fibril formation in A42 and could possibly explain why it is more aggregation prone despite being present in a much lower concentration than A40 in the plasma of cells.
N* States Spontaneously Assemble into Dimers.
To determine whether the monomer excited states are harbingers of aggregation we simulated the dynamics two N* states oriented randomly with respect to one another. The nematic order parameter, , was used to quantify dimer formation. For both A40 and A42, two N* conformations readily coalesce to form dimers upon collision, on the time scale of microseconds (Fig. 7). Melting and reformation of some of the dimer conformations hint at fluid-like behavior, which suggests that the critical nucleus is larger than two.
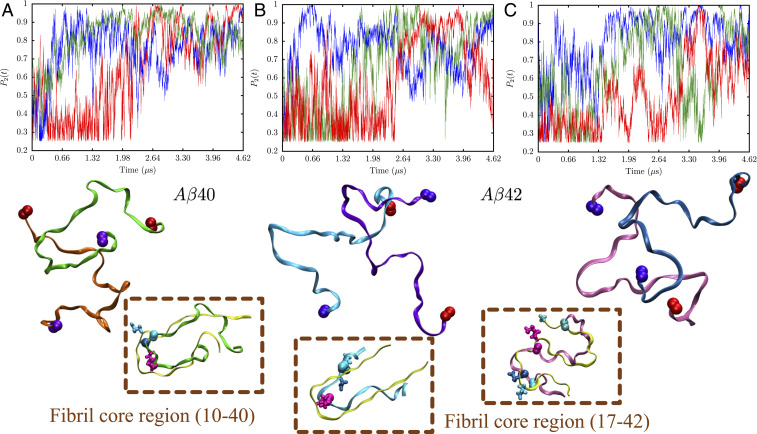
Fig. 7.
Kinetics of dimerization observed for A40 and A42 when two N* states are allowed to coalesce. (A) A40. Top shows the time evolution of the nematic order parameter, (high implies fibrillar order). Three representative trajectories associated with different first passage times of dimer formation are shown. Bottom shows a representative snapshot of the A40 dimer. (B) Top shows the time evolution of for three trajectories initiated from two N* conformations of A42 having the U-bend topology. Bottom shows a representative snapshot of the corresponding dimer. (C) Top shows the time evolution of for three trajectories initiated from two N* conformations of A42 having the S-bend topology. Bottom shows a representative snapshot of the corresponding dimer. In all of the snapshots, the red spheres denote the N terminus and the violet spheres denote the C terminus of the two chains. For all of the dimer snapshots shown in A–C, Insets, a zoomed-in view of the fibril core region is also shown. For both A40 and A42, one of the chains in the dimer overlaps appreciably with the monomer unit of the fibril structure (shown in yellow), while the other chain fluctuates to maintain fluidity. The E22, D23, and K28 residues which participate in salt bridge formation are shown in cyan, blue, and magenta colors, respectively. In case of the S-bend motif of A42, residue A42 is also shown.
We also carried out simulations where two N* states were aligned nearly perfectly relative to one another. These form dimers rapidly and mostly retain their fibril-like order. Some configurations exhibit only minor orientational melting (SI Appendix, Fig. S18). These exploratory simulations provide a sneak peek into the diverse range of dimer conformations explored by the A peptides. For both the peptides, the dimer interface is heterogeneous (SI Appendix, Fig. S19), involving interactions between different segments of the monomer chains. Specifically, for A42, the C terminus seems to play a key role in mediating monomer–monomer interactions.
When the simulations were initiated from monomer conformations, which do not exhibit fibril-like characteristics (non-N*), no appreciable fibril-like order was found on the time scale of microseconds (SI Appendix, Fig. S18). In a few trajectories, we observed only transitions to a state with intermediate order (characterized by ). Therefore, the free energy barrier for dimerization is likely to be much higher for these states.
Discussion
We used the SOP-IDP model to characterize the conformational ensembles of A40 and A42 monomers to quantify the role their excited states play in controlling fibril formation. The ensemble averages of many properties are practically identical for the two sequences. Clustering analyses revealed the details of sequence-specific heterogeneity. The interresidue contact maps for individual clusters show that both the peptides access an array of different structures. Specifically, the A40 monomer has a measurable probability of being structured at the N terminus, while the C terminus of A42 is ordered to some extent. For both the sequences, we find prominent fingerprints of the existence of aggregation-prone (excited) conformations ( states), which are only sparsely populated. The states share a number of features in common with the monomer structures in the fibrils (Fig. 8). By using the differences in the population of states between the two peptides in Eq. 2, we rationalize the higher value of in A40 relative to A42. We find that two N* states coalesce rapidly to form dimers. Thus, N* states may be templates for self-assembly.
Fig. 8.
(A–C, Top) Contact maps for the ensemble identified from simulations (lower triangle) and the monomer unit of the experimental fibril structure (upper triangle). (A) ensemble of A40, consisting of SLS-like configurations, stabilized by the VGSN turn, and D23-K28 salt bridge. As is evident, these structural features are also found in the A40 fibril structure. At least two structurally distinct states exist for A42, as shown in B and C. (B) SLS-like structure consisting of a U-bend near the VGSN region, stabilized by the D23-K28 salt bridge. The positions of the D23-K28 salt bridge in the simulated ensembles overlap to a great extent with the experimental structures in A and B. (C) S-bend motif stabilized by a contact between K28 and A42. (A–C, Bottom) Below the contact maps, a representative structure from the ensemble is shown superimposed on the monomer unit from the fibril structure (shown in yellow). The E22, D23, and K28 residues are shown in cyan, blue, and magenta colors, respectively. For the S-bend motif, residue A42 is also shown. For clarity, we only show residues that are part of the fibril core (10 to 40 for A40 and 17 to 42 for A42).
The propensity to form structures in the spectrum of monomers could be used as a marker for protein aggregation. Indeed, the slightly upshifted values of the chemical shifts for some residues relative to the ensemble averages (SI Appendix, Fig. S20) do imply that the overall propensity is somewhat enhanced in the ensemble. Nonetheless, the state retains some degree of disorder, which is essential for the rapid switching between the different structures. Ordered -sheet formation is expected only at the later stages in the aggregation cascade (formation of critical nuclei or protofibrils).
Free Energy Gap between and Ground States Determines Aggregation Propensities.
The concept has important implications: 1) Because the state is separated from the ground state by a free energy gap, , it follows that is vanishingly small if . In this scenario, aggregation is unlikely. 2) The value of is slave to external conditions because can be modulated by varying the temperature, pH, or crowder concentration (14). This implies that the full sequence-dependent folding landscape of the monomer has to be determined to estimate . 3) Many proteins aggregate under conditions such that the is not too large, which tidily explains why even the helical protein myoglobin can form fibrils under certain conditions (76). Sequences associated with higher values of are therefore likely to have higher rates of aggregation. For instance, it is known that introduction of a lactam bridge near the VGSN turn region of A enhances the kinetics of fibril formation in A40 by a factor of 1,000 (77), which was explained by substantial increase in the population of aggregation-prone states (21).
Generality of the Theory.
If the lowest free energy state is ordered, aggregation to a fibril is possible only if the state is populated. This was illustrated by analyzing the experiments on the aggregation of the SH3 domain, a small globular protein. By using relaxation dispersion NMR experiments (78), it was shown that under ambient conditions a very low percentage of excited states are populated. Using simulations we showed that 2%, which allowed us to estimate the fibril elongation rate nearly quantitatively (33) using Eq. 2. Significantly, the state determined in simulations was structurally identical to the one determined using NMR (see figure S7 in ref. 33 in which the two structures are superimposed). The earlier study (33) affirmed that even for globular proteins provides a good estimate of fibril formation times and that the aggregation-prone structures have similarities to the monomer in the fibril.
This study expands the scope of the N* concept, from synthetic polymeric sequences and globular proteins to two assembly-competent biological sequences, namely A40 and A42, which are inherently disordered in nature. The results show that the N* theory provides a molecular basis for the contrasting aggregation behavior of A40 and A42. Thus, the concept might be general and could provide important cues to the quantitative understanding of other aggregation-prone IDPs.
Polymorphism and Ostwald’s Rule.
The multiplicity of states (Fig. 8) implies that there should be several polymorphic fibril structures whose fingerprints should also be encoded in the excitation spectra of the monomer. The concepts underlying fibril polymorphism are illustrated using a schematic free energy landscape (Fig. 9). It is likely that the formation of distinct polymorphs follows Ostwald’s rule. A recent study demonstrated how Ostwald’s rule, well known in the formation of crystal polymorphs, is manifested during the supramolecular assembly of synthetic polymers (79). Ostwald’s rule affirms that the least stable polymorph would form first, followed by a subsequent rollover to the more stable form. We predict that for A42, transition from the disordered ground state to the U-bend topology is likely to be faster, with the S-bend topology appearing only on longer observation time scales. This prediction, which follows from the inequality ( and denoting the free energy difference of the U-bend and the S-bend motifs with respect to the disordered ground state), could be tested using kinetic simulations. It follows (Fig. 9) that formation of various polymorphic structures, which would not interconvert directly from one to another, could be under kinetic control (80).
Fig. 9.
A schematic free energy landscape illustrating the aggregation cascade that leads to the formation of fibrils, starting with the transition from the disordered ground state to the ensemble at the monomer level and ultimately the formation of fibril structures from an oligomeric assembly of states via different growth mechanisms. For A42, the seeds of polymorphism are encoded in the structurally diverse states. Furthermore, the aggregation cascade seems to be in harmony with Ostwald’s rule. For A42, this would imply that , and hence transition to the U-bend conformation is likely to be faster.
Materials and Methods
The A40 and A42 peptides are modeled using a modification of the recently introduced SOP-IDP model, which quantitatively and in unprecedented detail reproduces the scattering profiles of a diverse range of IDP sequences of varying lengths, sequence composition, and charge densities (52). We calculated the thermodynamic quantities using trajectories generated in low-friction Langevin dynamics simulations, which enhances conformational sampling (81). The simulations were used to calculate a number of observables for the A40 and A42 peptides, which were directly compared to experiments to validate the SOP-IDP model. Details of the simulations and analyses of the simulations may be found in SI Appendix.
Supplementary Material
Acknowledgments
We are grateful to Upayan Baul for assistance in the initial stages of this work. The comments of Robert Tycko and the encouragement of Tuomas Knowles are greatly appreciated. We also acknowledge Mauro Mugnai and Abhinav Kumar for several fruitful discussions. We acknowledge the Texas Advanced Computing Center for providing the necessary computing resources. This work was supported by a grant from the National Institutes of Health (GM-107703) and the Welch Foundation Grant F-0019 through the Collie-Welch chair.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: The dataset and the analysis scripts for this paper are hosted by Zenodo (https://zenodo.org/record/3891924#.XwxyqJNKgY0).
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2002570117/-/DCSupplemental.
Data Availability.
The dataset and the analysis scripts are hosted by Zenodo (https://zenodo.org/record/3891924#.XwxyqJNKgY0). The parameters of the SOP-IDP force field used in this study are included in SI Appendix.
References
- 1.Tycko R., Amyloid polymorphism: Structural basis and neurobiological relevance. Neuron 86, 632–645 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Aguzzi A., Haass C., Games played by rogue proteins in prion disorders and Alzheimer’s disease. Science 302, 814–818 (2003). [DOI] [PubMed] [Google Scholar]
- 3.Qiang W., Yau W., Lu J. X., Collinge J., Tycko R., Structural variation in amyloid- fibrils from Alzheimer’s disease clinical subtypes. Nature 541, 217–221 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Finder V. H., Glockshuber R., Amyloid-beta aggregation. Neurodegener. Dis. 4, 13–27 (2007). [DOI] [PubMed] [Google Scholar]
- 5.Maltsev A. V., Bystryak S., Galzitkskaya O. V., The role of -amyloid peptide in neurodegenerative diseases. Ageing Res. Rev. 10, 440–452 (2011). [DOI] [PubMed] [Google Scholar]
- 6.Eanes E. D., Glenner G. G., Physical and chemical properties of amyloid fibers I. X-ray diffraction studies on amyloid filaments. J. Histochem. Cytochem. 16, 673–677 (1968). [DOI] [PubMed] [Google Scholar]
- 7.Nelson R., et al. , Structure of the cross- spine of amyloid-like fibrils. Nature 435, 773–778 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kirschner D. A., Abraham C., Selkoe D. J., X-ray diffraction from intraneuronal paired helical filaments and extraneuronal amyloid fibers in Alzheimer disease indicates cross-beta conformation. Proc. Natl. Acad. Sci. U.S.A. 1, 503–507 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Glenner G. G., Wong C. W., Alzheimer’s disease: Initial report of the purification and characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Commun. 120, 885–890 (1984). [DOI] [PubMed] [Google Scholar]
- 10.Masters C. L., et al. , Amyloid plaque core protein in Alzheimer disease and down syndrome. Proc. Natl. Acad. Sci. U.S.A. 82, 4245–4249 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Qiang W., Yau W. M., Lu J. X., Collinge J., Tycko R., Structural variation in amyloid- fibrils from Alzheimer’s disease clinical subtypes. Nature 541, 217–221 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Prusiner S. B., Prions. Proc. Natl. Acad. Sci. U.S.A. 95, 13363–13383 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Flavin W. P., et al. , Endocytic vesicle rupture is a conserved mechanism of cellular invasion by amyloid proteins. Acta Neuropathol. 134, 629–653 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Straub J. E., Thirumalai D., Toward a molecular theory of early and late events in monomer to amyloid fibril formation. Annu. Rev. Phys. Chem. 62, 437–463 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nasica-Labouze J., et al. , Amyloid protein and Alzheimer’s disease: When computer simulations complement experimental studies. Chem. Rev. 115, 3518–3563 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ilie I. M., Caflisch A., Simulation studies of amyloidogenic polypeptides and their aggregates. Chem. Rev. 119, 6956–6993 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Roche J., Shen Y., Lee J. H., Ying J., Bax A., Monomeric A1–40 and A1–42 peptides in solution adopt very similar Ramachandran map distributions that closely resemble random coil. Biochemistry 55, 762–775 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hou L., et al. , Solution NMR studies of the A40 and A42 peptides establish that the Met35 oxidation state affects the mechanism of amyloid formation. J. Am. Chem. Soc. 126, 1992–2005 (2004). [DOI] [PubMed] [Google Scholar]
- 19.Yan Y., Wang C., A42 is more rigid than A40 at the C terminus: Implications for Abeta aggregation and toxicity. J. Mol. Biol. 364, 853–862 (2006). [DOI] [PubMed] [Google Scholar]
- 20.Tarus B., Straub J. E., Thirumalai D., Structures and free-energy landscapes of the wild type and mutants of the A21-30 peptide are determined by an interplay between intrapeptide electrostatic and hydrophobic interactions. J. Mol. Biol. 379, 815–829 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Reddy G., Straub J. E., Thirumalai D., Influence of preformed Asp23-Lys28 salt bridge on the conformational fluctuations of monomers and dimers of A peptides with implications for rates of fibril formation. J. Phys. Chem. B 113, 1162–1172 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Massi F., Klimov D. K., Thirumalai D., Straub J. E., Charge states rather than propensity for -structure determine enhanced fibrillogenesis in wild-type Alzheimer’s -amyloid peptide compared to E22Q Dutch mutant. Prot. Sci. 11, 1639–1647 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klimov D. K., Thirumalai D., Dissecting the assembly of A amyloid peptides into antiparallel sheets. Structure 11, 295–307 (2003). [DOI] [PubMed] [Google Scholar]
- 24.Bernstein S. L., et al. , Amyloid -protein: Monomer structure and early aggregation states of A42 and its Pro19 alloform. J. Am. Chem. Soc. 127, 2075–2084 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Baumketner A., et al. , Structure of the 21-30 fragment of amyloid -protein. Protein Sci. 15, 1239–1247 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ball K. A., et al. , Homogeneous and heterogeneous tertiary structure ensembles of amyloid- peptides. Biochemistry 50, 7612–7628 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rosenman D. J., Wang C., García A. E., Characterization of A monomers through the convergence of ensemble properties among simulations with multiple force fields. J. Phys. Chem. B 120, 259–277 (2016). [DOI] [PubMed] [Google Scholar]
- 28.Lincoff J., Sasmal S., Head-Gordon T., The combined force field-sampling problem in simulations of disordered amyloid- peptides. J. Chem. Phys. 150, 104108 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lin Y. S., Bowman G. R., Beauchamp K. A., Pande V. S., Investigating how peptide length and a pathogenic mutation modify the structural ensemble of amyloid beta monomer. Biophys. J. 102, 315–324 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Meng F., et al. , Highly disordered amyloid- monomer probed by single-molecule FRET and MD simulation. Biophys. J. 114, 870–884 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tarus B., Straub J. E., Thirumalai D., Dynamics of Asp23-Lys28 salt-bridge formation in A10-35 monomers. J. Am. Chem. Soc. 128, 16159–16168 (2006). [DOI] [PubMed] [Google Scholar]
- 32.Li M. S., et al. , Factors governing fibrillogenesis of polypeptide chains revealed by lattice models. Phys. Rev. Lett. 105, 218101 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhurvalev P., Reddy G., Straub J. E., Thirumalai D., Propensity to form amyloid fibrils is encoded as excitations in the free energy landscape of monomeric proteins. J. Mol. Biol. 426, 2653–2666 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rosenman D. J., Connors C. R., Chen W., Wang C., García A. E., A monomers transiently sample oligomer and fibril-like configurations: Ensemble characterization using a combined MD/NMR approach. J. Mol. Biol. 425, 3338–3359 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Eschmann N. A., et al. , Tau aggregation propensity engrained in its solution state. J. Phys. Chem. B 119, 14421–14432 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nam H. B., Kouza M., Zung H., Li M. S., Relationship between population of fibril-prone conformation in the monomeric state and oligomer formation times of peptides: Insights from all-atom simulations. J. Chem. Phys. 132, 165104 (2010). [DOI] [PubMed] [Google Scholar]
- 37.Kuperstein I., et al. , Neurotoxicity of Alzheimer’s disease A peptides is induced by small changes in the A42 to A40 ratio. EMBO J. 29, 3408–3420 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Finder V. H., Vodopivec I., Nitsch R. M., Glockshuber R., The recombinant amyloid-beta peptide A1-42 aggregates faster and is more neurotoxic than synthetic A1-42. J. Mol. Biol. 396, 9–18 (2010). [DOI] [PubMed] [Google Scholar]
- 39.Meisi G., et al. , Differences in nucleation behavior underlie the contrasting aggregation kinetics of the A40 and A42 peptides. Proc. Natl. Acad. Sci. U.S.A. 111, 9384–9389 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Harper J. D., Lansbury P. T., Models of amyloid seeding in Alzheimer’s disease and scrapie: Mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Annu. Rev. Biochem. 66, 385–407 (1997). [DOI] [PubMed] [Google Scholar]
- 41.Lazo N. D., Grant M. A., Condron M. C., Rigby A. C., Teplow D. B., On the nucleation of amyloid -protein monomer folding. Protein Sci. 14, 1581–1596 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yang M., Teplow D. B., Amyloid -protein monomer folding: Free-energy surfaces reveal alloform-specific differences. J. Mol. Biol. 384, 450–464 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Roychaudhuri R., et al. , C-terminal turn stability determines assembly differences between A40 and A42. J. Mol. Biol. 425, 292–308 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Walti W. A., et al. , Atomic-resolution structure of a disease-relevant A amyloid fibril. Proc. Natl. Acad. Sci. U.S.A. 1, E4976–E4984 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Colvin M. T., et al. , Atomic resolution structure of monomorphic A42 amyloid fibrils. J. Am. Chem. Soc. 138, 9663–9674 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Xiao Y., et al. , A (1-42) fibril structure illuminates self-recognition and replication of amyloid in Alzheimer’s disease. Nat. Struct. Mol. Biol. 22, 499–505 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sgourakis N., Yan Y., McCallum S., Wang C., Garcia A. E., The Alzheimer’s peptides A40 and 42 adopt distinct conformations in water: A combined MD/NMR study. J. Mol. Biol. 368, 1448–1457 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ball K. A., Phillips A. H., Wemmer D. E., Head-Gordon T., Differences in -strand populations of monomeric A40 and A42. Biophys. J. 104, 2714–2724 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Côté S., Derreumaux P., Mousseau N., Distinct morphologies for amyloid beta protein monomer: A1-40, A1-42, and A1-40(D23N). J. Chem. Theory Comput. 7, 2584–2592 (2011). [DOI] [PubMed] [Google Scholar]
- 50.Urbanc B., et al. , Molecular dynamics simulation of amyloid dimer formation. Biophys. J. 87, 2310–2321 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zheng W., Tsai M. Y., Wolynes P. G., Comparing the aggregation free energy landscapes of amyloid beta(1-42) and amyloid beta(1-40). J. Am. Chem. Soc. 139, 16666–16676 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Baul U., Chakraborty D., Mugnai M. L., Straub J. E., Thirumalai D., Sequence effects on size, shape, and structural heterogeneity in intrinsically disordered proteins. J. Phys. Chem. B 123, 3462–3474 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Granata D., et al. , The inverted free energy landscape of an intrinsically disordered peptide by simulations and experiments. Sci. Rep. 5, 15449 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wennmalm S., Chmyrov V., Widengren J., Tjernberg L., Highly sensitive FRET-FCS detects amyloid -peptide oligomers in solution at physiological concentrations. Anal. Chem. 87, 11700–11705 (2015). [DOI] [PubMed] [Google Scholar]
- 55.Doi M., Edwards S. F., The Theory of Polymer Dynamic (Oxford University Press, 1988), vol. 73. [Google Scholar]
- 56.Sgourakis N. G., et al. , Atomic-level characterization of the ensemble of the A (1-42) monomer in water using unbiased molecular dynamics simulations and spectral algorithms. J. Mol. Biol. 405, 570–583 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lam A. R., Teplow D. B., Stanley H. E., Urbanc B., Effects of the arctic (E 22G) mutation on amyloid -protein folding: Discrete molecular dynamics study. J. Am. Chem. Soc. 130, 17413–17422 (2008). [DOI] [PubMed] [Google Scholar]
- 58.Vivekanandan S., Brender J. R., Lee S. Y., Ramamoorthy A., A partially folded structure of amyloid-beta(1-40) in an aqueous environment. Biochem. Biophys. Res. Commun. 411, 312–316 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fezoui Y., Teplow D. B., Kinetic studies of amyloid-protein fibril assembly. J. Biol. Chem. 277, 36948–36954 (2002). [DOI] [PubMed] [Google Scholar]
- 60.Kirkitadze M. D., Condron M. M., Teplow D. B., Identification and characterization of key kinetic intermediates in amyloid -protein fibrillogenesis. J. Mol. Biol. 312, 1103–1119 (2001). [DOI] [PubMed] [Google Scholar]
- 61.Frank A. T., Law S. M., Ahlstrom L. S., Brooks C. L., Predicting protein backbone chemical shifts from coordinates: Extracting high resolution experimental observables from low resolution models. J. Chem. Theory Comput. 11, 325–331 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Olubiyi O. O., Strodel B., Structures of amyloid -peptides A (1-40) and A (1-42) as influenced by pH and a D-peptide. J. Phys. Chem. B 116, 3280–3291 (2012). [DOI] [PubMed] [Google Scholar]
- 63.Gu L., Ngo S., Guo Z., Solid-support Electron Paramagnetic Resonance (EPR) studies of A40 monomers reveal a structured state with three ordered segments. J. Biol. Chem. 287, 9081–9089 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Brannstrom K., Islam T., Sandblad L., Olofsson A., The role of histidines in amyloid fibril assembly. FEBS Lett. 591, 1167–1175 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.McLaurin J., Fraser P. E., Effect of amino-acid substitutions on Alzheimer’s amyloid-beta peptide-glycosaminoglycan interactions. Eur. J. Biochem. 267, 6353–6361 (2000). [DOI] [PubMed] [Google Scholar]
- 66.Baumketner A., Shea J. E., The structure of the Alzheimer amyloid 10-35 peptide probed through replica-exchange molecular dynamics simulations in explicit solvent. J. Mol. Biol. 366, 275–285 (2007). [DOI] [PubMed] [Google Scholar]
- 67.Cukalevski R., et al. , Role of aromatic side chains in amyloid -protein aggregation. ACS Chem. Neurosci. 3, 1008–1016 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Esler W. P., et al. , Point substitution in the central hydrophobic cluster of a human -amyloid congener disrupts peptide folding and abolishes plaque competence. Biochemistry 35, 13914–13921 (1996). [DOI] [PubMed] [Google Scholar]
- 69.Han W., Wu Y. D., A strand-loop-strand structure is a possible intermediate in fibril elongation: Long time simulations of amyloid-beta peptide (10-35). J. Am. Chem. Soc. 127, 15408–15416 (2005). [DOI] [PubMed] [Google Scholar]
- 70.Gremer L., et al. , Fibril structure of amyloid- by cryo–electron microscopy. Science 358, 116–119 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Luhrs T., et al. , 3D structure of Alzheimer’s amyloid- fibrils. Proc. Natl. Acad. Sci. U.S.A. 102, 17342–17347 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Maji S. K., Amsden J. J., Rothschild K. J., Condron M. M., Teplow D. B., Conformational dynamics of amyloid -protein assembly probed using intrinsic fluorescence. Biochemistry 44, 13365–13376 (2005). [DOI] [PubMed] [Google Scholar]
- 73.Fawzi N. L., et al. , Structure and dynamics of the Abeta(21-30) peptide from the interplay of NMR experiments and molecular simulations. J. Am. Chem. Soc. 130, 6145–6158 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kollmer M., et al. , Cryo-EM structure and polymorphism of A amyloid fibrils purified from Alzheimer’s brain tissue. Nat. Commun. 10, 4760 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lu J. X., et al. , Molecular structure of -amyloid fibrils in Alzheimer’s disease brain tissue. Cell 154, 1257–1268 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Fandrich M., Fletcher M. A., Dobson C. M., Amyloid fibrils from muscle myoglobin. Nature 410, 165–166 (2001). [DOI] [PubMed] [Google Scholar]
- 77.Sciaretta K. L., Gordon D. J., Petkova A. T., Tycko R., Meredith S. C., A40-Lactam(D23/K28) models a conformation highly favorable for nucleation of amyloid. Biochemistry 44, 6003–6014 (2005). [DOI] [PubMed] [Google Scholar]
- 78.Neudecker P., et al. , Structure of an intermediate state in protein folding and aggregation. Science 20, 362–366 (2012). [DOI] [PubMed] [Google Scholar]
- 79.Levin A., et al. , Ostwald’s rule of stages governs structural transitions and morphology of dipeptide supramolecular polymers. Nat. Commun. 5, 5219 (2014). [DOI] [PubMed] [Google Scholar]
- 80.Pellarin R., Schuetz P., Guarnera E., Calfisch A., Amyloid fibril polymorphism is under kinetic control. J. Am. Chem. Soc. 132, 14960–14970 (2010). [DOI] [PubMed] [Google Scholar]
- 81.Honeycutt J. D., Thirumalai D., The nature of folded states of globular proteins. Biopolymers 32, 695–709 (1992). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The dataset and the analysis scripts are hosted by Zenodo (https://zenodo.org/record/3891924#.XwxyqJNKgY0). The parameters of the SOP-IDP force field used in this study are included in SI Appendix.