Modeling of the Transmission of Coronaviruses, Measles Virus, Influenza Virus, Mycobacterium tuberculosis, and Legionella pneumophila in Dental Clinics

Abstract

Dental health care workers are in close contact to their patients and are therefore at higher risk for contracting airborne infectious diseases. The transmission rates of airborne pathogens from patient to dental health care workers are unknown. With the outbreaks of infectious diseases, such as seasonal influenza, occasional outbreaks of measles and tuberculosis, and the current pandemic of the coronavirus disease COVID-19, it is important to estimate the risks for dental health care workers. Therefore, the transmission probability of these airborne infectious diseases was estimated via mathematical modeling. The transmission probability was modeled for Mycobacterium tuberculosis, Legionella pneumophila, measles virus, influenza virus, and coronaviruses per a modified version of the Wells-Riley equation. This equation incorporated the indoor air quality by using carbon dioxide as a proxy and added the respiratory protection rate from medical face masks and N95 respirators. Scenario-specific analyses, uncertainty analyses, and sensitivity analyses were run to produce probability rates. A high transmission probability was characterized by high patient infectiousness, the absence of respiratory protection, and poor indoor air quality. The highest transmission probabilities were estimated for measles virus (100%), coronaviruses (99.4%), influenza virus (89.4%), and M. tuberculosis (84.0%). The low-risk scenario leads to transmission probabilities of 4.5% for measles virus and 0% for the other pathogens. From the sensitivity analysis, it shows that the transmission probability is strongly driven by indoor air quality, followed by patient infectiousness, and the least by respiratory protection from medical face mask use. Airborne infection transmission of pathogens such as measles virus and coronaviruses is likely to occur in the dental practice. The risk magnitude, however, is highly dependent on specific conditions in each dental clinic. Improved indoor air quality by ventilation, which reduces carbon dioxide, is the most important factor that will either strongly increase or decrease the probability of the transmission of a pathogen.

Introduction

The epidemic of the coronavirus disease (COVID-19) caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has a global impact on public health and health care workers (Wang et al. 2020). Pandemics are unique, but seasonal regional outbreaks of highly contagious airborne pathogens have occurred in previous years. Most frequently reported infectious agents causing airborne infections are influenza virus, Mycobacterium tuberculosis, and measles virus.

Dental health care workers (DHWs) are frequently in close contact with a large number of patients. These patients may unknowingly carry airborne transmitted infectious diseases, so they may infect DHWs during dental treatment. This may lead to the transmission of infectious diseases to the DHWs during dental treatment (Feller et al. 2009; Petti 2016). Sneezing, coughing, talking, and breathing induce the production of spatters and aerosols. Especially during seasonal epidemics or disease outbreaks, airborne pathogens are likely to reach the dental practice and contaminate DHWs. In addition to exposure to potentially infected patients, DHWs are at risk of acquiring infections from dental unit waterlines, which can harbor pathogens such as nontuberculous Mycobacterium spp., Pseudomonas aeruginosa, and Legionella pneumophila (Dutil et al. 2007). These pathogens can be transmitted through aerosols and splatters produced by dental instruments (Leggat and Kedjarune 2001).

The transmission of airborne pathogens to DHWs can be prevented by applying infection control strategies. A face mask, for instance, functions as a physical barrier against splatters arising from dental unit water and blood and saliva from patients (Coia et al. 2013). A face mask prevents the inhalation of part of the aerosols. The proportion of filtered pathogens, however, depends on the filter efficiency of the face mask and its face fit. Additionally, the microbial contamination of air can be reduced by improving ventilation or by removing the infectious source, meaning to postpone the treatment of patients with respiratory symptoms that may be associated with an infectious disease. The transmission probability of airborne pathogens in health care and non–health care settings was the subject of previous studies (Aliabadi et al. 2011).

One way of estimating this probability is to build a mathematical model with the use of relevant parameters and available data that provide an estimation of the probability for transmitting specific pathogens under different scenarios. The latter is currently of relevance concerning the COVID-19 outbreak. Airborne infection transmission can be modeled with the aid of the Wells-Riley equation as proposed by Rudnick and Milton (2003). This equation has been used to understand the dynamics of the transmission of airborne pathogens and to estimate the probability of the transmission of these airborne pathogens in a confined setting (Rudnick and Milton 2003; Sze To and Chao 2010). The equation allows one to estimate the probability based on differences in indoor CO₂ values, number of infectious particles, and different levels of respiratory protection, among others. DHWs are exposed to air- and waterborne pathogens. Even though the risk of catching an infectious disease for DHWs seems to be low, the risk of transmission of airborne or waterborne pathogens in the dental practice is unknown. Therefore, the aim of this study was to model the probability of the transmission of coronaviruses, measles virus, M. tuberculosis, influenza virus, and L. pneumophila with a modified version of the Wells-Riley equation.

Methods

Model

We adopted the Wells-Riley equation (see equation 1; Rudnick and Milton 2003). We extended the model by adding a respiratory protection factor (Sze To and Chao 2010):

$$P=1-\exp \left(-\frac{Itqf}{n}\right)R.$$ (1)

Here, P represents the transmission probability of a specific microorganism for 1 person per hour; I is the number of infectious sources in 1 space; t is the time of exposure to a certain microorganism in hours; q is the quanta generated per hour; f is the equivalent of the fraction of indoor air that is exhaled breath, which is also called the rebreathed fraction; and n is the number of people exposed to the infectious source. R represents the filtration capacity (i.e., the fraction of airborne particles that do not penetrate a device for respiratory protection). Parameter f is calculated with equation 2:

$$f=\frac{C-C_o}{C_a}.$$ (1)

Here, C is the carbon dioxide (CO₂) concentration in indoor air; C_o is the CO₂ concentration in outdoor air; and C_a is the CO₂ concentration in exhaled breath—all in parts per million.

The adopted Wells-Riley equation is based on several assumptions:

• Well-mixed airspace: meaning that once the infectious particle is generated, it can be anywhere within the room’s airspace.

• Steady state condition: meaning that the quantum concentration and the CO₂ concentration in outdoor air remain constant within the observed time.

• The elimination of infectious particles caused by loss of viability, filtration, or other mechanisms is small when compared with removal by ventilation (Rudnick and Milton 2003).

Parameterization

Selected Pathogens

The risk of transmission was assessed for 4 person-to-person transmitted airborne pathogens: M. tuberculosis, SARS virus, influenza virus, and measles virus. The choice for these pathogens was based on the severity of the associated infectious disease and the plausibility of exposure of DHWs to a patient who is positive for any of the aforementioned pathogens. From environmentally acquired airborne pathogens, we chose L. pneumophila, based on clinical relevance.

Quanta Estimation

The input values for q were extracted from studies that estimated quanta from outbreaks (Appendix Box 1). In the model, it is assumed that a quantum (infectious dose) is randomly distributed throughout the air of confined spaces and that each quantum has an equal chance of being anywhere within the space (Wells 1955; Chen et al. 2006). It is also assumed that the quantum concentration remains constant over time (Chen and Liao 2008).

Currently, quanta for SARS-CoV-2 cannot be estimated. Although definite evidence has yet to be established, the current causative agent of COVID-19 is expected to be transmitted in a similar way as other coronaviruses (van Doremalen et al. 2020). Moreover, epidemiologic data of SARS-CoV-1 and SARS-CoV-2 are similar (see Appendix), so with the best available evidence, we used the quanta data from the SARS-CoV-1 virus as a proxy for the current SARS-CoV-2. The quanta for L. pneumophila are unavailable and were calculated per the assumed ID₅₀ and the number of Legionella colonies sampled in the air of dental clinics (Appendix Box 1).

Rebreathed Fraction of Air That Is Exhaled Breath

The equation assumes a non–steady state condition of airborne pathogens (Sze To and Chao 2010). Rudnick and Milton (2003) incorporated the concentration of CO₂ in the room that is exhaled breath as parameter f in the equation to estimate the probability of transmission, in which all subparameters are steady over time (Sze To and Chao 2010). The input values of f are adapted from literature. The outdoor CO₂ concentration (C_o) is set at 400 ppm (ASHRAE 2016). The fraction of CO₂ in exhaled breath (C_a) is adapted from Rudnick and Milton (see Table 1). The measured range and average indoor CO₂ (C) values were adapted from a study conducted in a dental clinic and categorized according to the ASHRAE standard (Helmis et al. 2007).

Table 1.

Overview of the Parameter Values.

		Input Parameter Values			Sensitivity Analysis Values
Parameter	Description	Low Risk	Intermediate Risk	High Risk	Lower Limit (–75%)	Upper Limit (+75%)	Sources
R	Mask protection factor, %	85	24	0	6	42	Skaria and Smaldone 2014
t	Time in hour	1	1	1	0.25	1.75
C	Indoor CO2, ppm	774	1,135	2,375	283.75	1,986	Helmis et al. 2007
Co	Outdoor CO2, ppm	400	400	400			ASHRAE 2016
Ca	Fraction of CO2 in exhaled breath, ppm	37,500	37,500	37,500			Rudnick and Milton 2003
f	Fraction of indoor air that is exhaled breath	0.009973	0.0196	0.05264			Rudnick and Milton 2003
qm	Quanta for measles virus	106	124	480	31	217	Riley et al. 1978; Chen et al. 2006; Liao et al. 2008
qs	Quanta for SARS coronavirus	11.4	28.94	295.5	7.23	50.65	Liao et al. 2008; Qian et al. 2009
qi	Quanta for influenza virus	15	76.18	128	19	133.32	Rudnick and Milton 2003; Chen and Liao 2008; Liao et al. 2008
qt	Quanta for Mycobacterium tuberculosis	1.27	8.2	12.7	2.05	14.35	Escombe et al. 2007; Nardell 2015
ql	Quanta for Legionella pneumophila	5.45	8.39	11.32	2.1	14.68	Armstrong and Haas 2007; Dutil et al. 2007

CO₂, carbon dioxide; ppm, parts per million; SARS, severe acute respiratory syndrome.

Respiratory Protection

We modeled the transmission prevention effect of a face mask by incorporating the respiratory efficiency from different masks. In case of no respiratory protection (no mask or a mask not perfectly fitting the face), R = 0. From literature, it is known that a regular surgical medical face mask has an efficacy of 24%—meaning that 24% of the airborne particles <2.0 μm are prevented from inhalation by the user of the mask (Skaria and Smaldone 2014). For an FFP2 mask, it was reported that 85% of the airborne particles are prevented from inhalation (Skaria and Smaldone 2014). In the model, it is assumed that the face mask respiratory efficiency remains stable over time (i.e., is replaced before its efficacy decreases).

Number of Susceptible Persons and Infectious Sources

We based the number of infectors and susceptible persons on an average general dental clinic in the Netherlands, in which on average between 20 and 30 patient visits occur every day. We assumed that the number of susceptible persons in a closed single-chair room would be the dentist and dental nurse. We added 1 infectious source that was either the patient, for the human-transmitted pathogens, or the dental unit, for the transmission of environmental pathogens.

The parameter t (time) was set to 1 h and kept constant to calculate the risk per hour.

Plan of Analyses

Modeled Scenarios

We created 3 scenarios to assess the probability of pathogen transmission. The input values per scenario are presented in Table 1, and the description of the scenarios is found in Box 2 (Appendix).

Uncertainty and Sensitivity Analyses

The mean transmission probability and its 95% uncertainty interval were estimated by conducting a multivariate uncertainty analysis. The analysis was performed with the Monte Carlo simulation, which calculates possible probabilities of transmission within the range of input parameter values (see Table 1). The simulation uses different random combinations of input parameter values, a total of 5,000 combinations, from a triangular distribution. The triangular distribution was chosen because it allows for the definition of the minimum, the maximum, and the most likely values. A triangular distribution ensures that the most likely values have the highest frequency in the simulation.

A sensitivity analysis was conducted to reveal which parameter mainly drove variations in the estimated transmission probability. The sensitivity analysis was conducted by individually varying 1 of the parameters from the model over the sensitivity interval. The sensitivity interval was calculated as ±75% for each scenario value input.

Results

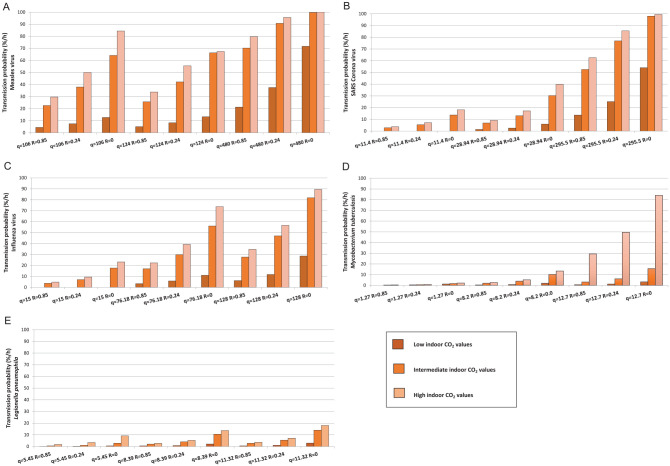
The transmission probability for each scenario and the estimated mean transmission rates with the corresponding 95% uncertainty interval are reported in Table 2. The highest transmission probability was found in the high-risk scenarios for measles virus (100%), SARS-CoV (99.4%), influenza virus (89.4%), and M. tuberculosis (84.0%). The probability of the transmission of all modeled pathogens was low in the low-risk scenario; there was only a small risk for transmitting measles virus (4.5%). The transmission probabilities were higher for viral airborne pathogens as compared with the bacterial pathogens. The transmission probabilities were higher in the intermediate- and high-risk scenarios (Figure).

Table 2.

Pathogen Transmission Probability for Each Modeled Pathogen Presented in Mean (95% UI) and for Each Scenario.

	Infection Transmission Probability, %
Pathogen	Mean (95% UI)a	Low Risk	Intermediate Risk	High Risk
Measles virus	41 (5.9 to 46.6)	4.5	42.2	99.98
SARS coronavirus	28.6 (1.3 to 45.2)	0.0	13.1	99.44
Influenza virus	27.8 (1.8 to 36.0)	0.0	29.8	89.4
Mycobacterium tuberculosis	3.8 (0 to 6.7)	0.0	4.0	84.0
Legionella pneumophila	4.1 (0 to 6.8)	0.1	4.08	18.0

SARS, severe acute respiratory syndrome; UI, uncertainty interval.

^aEstimated from uncertainty analysis.

Figure 1.

The probability of infection transmission of measles virus (A), severe acute respiratory syndrome (SARS) coronavirus (B), influenza virus (C), Mycobacterium tuberculosis (D), and Legionella pneumophila (E). The bars represent the indoor carbon dioxide concentrations, indicative for the level of ventilation. The values for q represent the 3 levels of patient infectivity, while the R values stand for the 3 levels of personal protection.

There is an increased risk of acquiring measles virus as soon as the patient infectivity and indoor CO₂ value increased. The transmission probability remained >20% once the indoor CO₂ reached intermediate values, regardless of respiratory protection and patient infectivity. In certain situations, the transmission risk was as high as 90% (Figure). When a DHW was exposed to a patient who generates low influenza virus quanta, the transmission risk remained 0% when the room had low indoor CO₂ concentration, regardless of respiratory protection. A high transmission probability of 89.4% at most for influenza virus occurred in case of intermediate to high quanta generation and high indoor CO₂ concentration. The transmission of coronaviruses remained <20% when the DHW was exposed to a patient with low infectivity, regardless of the mask protection and indoor air CO₂. However, once the infectivity of a pathogen and the indoor CO₂ concentration increased, the transmission risk increased to 52.6% and 99.4%, respectively.

The transmission probability for M. tuberculosis was as high as 84.0% when DHWs were exposed to a patient with high quanta production (q = 12.7) in a space with high indoor CO₂. However, in case of exposure to a patient with low quanta generation, the transmission risk remained <3.0% regardless of respiratory protection. Moreover, if the indoor CO₂ concentration remained low, the probability of M. tuberculosis transmission would be <3.5% regardless of the quanta and respiratory protection used. The highest infection transmission probability of L. pneumophila was 18.0% in a high-risk scenario. As long as the indoor air quality was good, the risk remained <3% regardless of quanta and respiratory protection.

The sensitivity analysis estimated that changes in indoor air quality had the strongest influence on the probability of pathogen transmission. Improved indoor air quality resulted in 0% probability of transmission if all other parameters remained fixed at intermediate-risk values. A decrease of the indoor air quality led to the highest probability of transmission for all pathogens (Table 3).

Table 3.

Sensitivity Analysis for the Transmission Probability If Only 1 Parameter Was Changed at the Time.

		Mask Protection Factor, R		Quanta, q		Indoor CO2, f		Time, t
Pathogen	Mean Probability, P	Lower Limit	Upper Limit	Lower Limit	Upper Limit	Lower Limit	Upper Limit	Lower Limit	Upper Limit
Low-risk scenario
Measles virus	4.5	0.0	0.0	1.3	6.9	0.0	8.9	1.3	6.9
SARS coronavirus	0.6	9.9	16.2	0.1	1.0	0.0	1.4	0.0	1.0
Influenza virus	0.7	0.0	0.0	0.2	1.3	0.0	1.8	0.0	1.3
M. tuberculosis	0.0	3.0	4.9	0.0	0.0	0.0	0.2	0.0	0.1
L. pneumophila	0.2	0.0	0.0	0.0	0.4	0.0	0.5	0.0	0.4
Intermediate-risk scenario
Measles virus	41.0	32.2	52.2	13.9	57.6	0.0	62.8	13.9	57.6
SARS coronavirus	13.1	9.9	16.2	3.5	21.4	0.0	25.4	3.5	21.4
Influenza virus	27.8	17.3	31.4	8.9	44.2	0.0	50.0	22.7	44.2
M. tuberculosis	3.8	3.1	4.1	0.96	6.6	0.0	8.0	1.0	6.7
L. pneumophila	4.1	1.1	1.5	0.4	2.6	0.0	3.2	0.4	2.6
High-risk scenario
Measles virus	99.99	32.2	52.20	87.8	100	0.0	100	87.8	100
SARS coronavirus	99.4	9.9	16.2	72.7	100	0.0	100	72.7	100
Influenza virus	89.43	22.7	36.7	43.0	98.0	0.0	98.9	43.0	98.8
M. tuberculosis	19.98	3.0	4.9	5.4	32.3	0.0	34.6	5.4	32.3
L. pneumophila	13.85	1.1	13.9	3.7	23.0	0.0	24.7	4.0	23.0

Based on lower and upper limits (±75%). Values are presented as percentages.

CO₂, carbon dioxide; L. pneumophila, Legionella pneumophila; M. tuberculosis, Mycobacterium tuberculosis; SARS, severe acute respiratory syndrome.

Discussion

In the dental clinic, spatters and aerosols are generated by patients when coughing, sneezing, and talking and with high-speed dental equipment. About 20 to 30 patients visit a dental room every day, making the transmission of pathogens plausible. However, the relative risk of the transmission of several airborne pathogens in the dental clinic is not known. Our study shows that the probability of transmission was low for M. tuberculosis and L. pneumophila, while the probability was high for the measles virus. The CO₂ concentration of the air in the dental practice had the highest influence on the transmission risk.

The CO₂ concentration of indoor air acts as an indicator for poor air quality and ventilation. Improved ventilation, leading to a decreased concentration of CO₂, will therefore reduce the transmission probability. The importance of the indoor air quality in the prevention of airborne pathogen transmission is supported by a previous study that associated a low ventilation rate to an increased transmission rate of M. tuberculosis (Menzies et al. 2000). The importance of continuous air changes was stressed in health care and non–health care settings (Nardell et al. 1991; Li et al. 2007; Hobday and Dancer 2013; Escombe et al. 2019). Nevertheless, the transmission of the measles virus is very likely to occur in case of high quanta, even when the indoor air quality is good.

The level of respiratory protection had a minor influence on the probability of transmission because the protection level is fairly low. Regular medical face masks filter about 24% of particles <2.0 μm. This protection rate is applicable only for closely fitting masks, while face seal leakage leads to reduced respiratory protection (Pankhurst et al. 2005; Grinshpun et al. 2009). A mask that is saturated with moist, what occurs usually after 20 to 30 min of use, provides no protection against bacteria or viruses. If the transmission probability was modeled with an FFP2 mask (N95 mask), a decrease of transmission probability was visible. However, using FFP2 masks in the dental clinic is not regularly practiced because of the low average risk for pathogen transmission and the difficulty breathing while wearing such a mask. Virus particles <2.0 μm are able to penetrate different types of mask and be inhaled by the wearer, although an FFP2/N95 mask reduces the risk for viral transmission to a factor of 1.5 to 2. However, a proportion of released viruses can be trapped in large aerosol particles and be prevented for inhalation through a medical face mask (Makison Booth et al. 2013).

The transmission probability is reported per hour, although the sensitivity analysis includes different exposure times. In dental practice, not every patient is in the treatment room for a whole hour. Regular check-ups may last about 10 to 15 min, and regular treatment may take about 30 to 40 min. So, the transmission probability is substantially lower if the contact time is less. However, if the treatment time is extended, for instance in the case of endodontic treatment, extended restorative treatment, or surgical treatment, the transmission probability becomes higher. A similar argument can be used for the number of patients per day in the clinic: the more patients are treated, the higher the risk.

The transmission probability was modeled on the basis of direct available or estimated quanta. These quanta were derived from disease transmission rates from studies in different environments, such as hospitals, public markets, and aircrafts. The specific circumstances in these environments had an influence on the derived quanta and are the best currently available. The same applies to quanta estimation of SARS-CoV-1, which was used as a proxy for SARS-CoV-2. Although the latter is similar in many ways, there are differences. The transmissibility, the infectious period, and the fatality rate seem to differ slightly; however, exact data are not available yet (Chen 2020; van Doremalen et al. 2020; Wilder-Smith et al. 2020). Extrapolation of the data generated for the SARS-CoV-1 into assumption for SARS-CoV-2 should thus be performed with caution. The results regarding L. pneumophila must also be interpreted with caution because the ID₅₀ in humans is still unknown. L. pneumophila is a clinically relevant pathogen; as such, we decided to use the best available data for our study.

We assessed the transmission probability in case that a DHW is exposed to an infectious patient, regardless of the local disease prevalence rates. However, the risk of meeting an infected person is higher in disease-endemic areas. So, the actual risk of contracting an infectious disease for DHWs is higher in disease-endemic areas. Moreover, the virulence of each pathogen varies among strains, influencing the infection risk for DHWs. Asymptomatic or presymptomatic carriers may still excrete viral particles or bacteria via aerosolized saliva. They may be contagious, but the microbial load is usually lower; consequently, the risk of transmission is possibly also lower.

Besides the transmission risk, virulence differences, and number of contagious persons in the direct environment, the risk of acquiring an infectious disease depends on the individual immune status. Immune-compromised people, such as people with HIV or cancer, are more susceptible to acquiring an infectious disease. There is currently not sufficient data available to include these confounders in the calculation of transmission probabilities.

The applied Wells-Riley equation comes with some limitations (Sze To and Chao 2010). The equation assumes that the infectious dose (quanta) is constant over time and has a homogenous spatial distribution. Yet, the number of infectious particles is higher in close proximity to the patient and dilutes in time and farther away from the source. Additionally, each pathogen has its own survival time depending on the indoor humidity and temperature (Phin et al. 2014). This influences the average produced quanta over time and results in an under- or overestimation of the transmission probability. Another assumption of the model is that not only droplets but also exhaled breath is infectious. The latter is not the case for patients carrying SARS-CoV-2 or influenza virus (Leung et al. 2020). Only patients who sneeze or cough may be infectious and contribute to the risk of transmission. However, during a treatment, aerosol will be produced that may contain a similar number of pathogens as compared with coughing or sneezing, so it is assumed that this transmission route is included in the equation. Although exact numbers of viral pathogens in aerosols from infectious patients are not known yet, we assume that this model applies to the situation of SARS-CoV-2- or influenza-infectious patients in the dental clinic. Other pathogens, such as nontuberculous Mycobacterium and P. aeruginosa, may be transmitted in the dental clinic. Unfortunately, quanta values are not available for these airborne pathogens.

We conclude that the risk for the transmission of the bacteria M. tuberculosis and L. pneumophila in the dental clinic was low, while the risk for the measles virus was high. Risk for transmission of coronaviruses was comparable to that of influenza. The CO₂ level in the dental clinic had the strongest influence on the transmission probability.

Author Contributions

C. Zemouri, contributed to conception, design, data analysis, and interpretation, drafted the manuscript; S.F. Awad, contributed to conception, design, data analysis, and interpretation, critically revised the manuscript; C.M.C. Volgenant, W. Crielaard, A.M.G.A. Laheij, contributed to conception and design, critically revised the manuscript; J.J. de Soet, contributed to conception, design, and data analysis, drafted and critically revised the manuscript. All authors gave final approval and agree to be accountable for all aspects of the work.