Modeling the binding and diffusion of receptor-targeted nanoparticles topically applied on fresh tissue specimens

Abstract

Nanoparticle (NP) contrast agents targeted to cancer biomarkers are increasingly being engineered for the early detection of cancer, guidance of therapy, and monitoring of response. There have been recent efforts to topically apply biomarker-targeted NPs on tissue surfaces to image the expression of cell-surface receptors over large surface areas as a means of evaluating tumor margins to guide wide local excision surgeries. However, diffusion and nonspecific binding of the NPs present challenges for relating NP retention on the tissue surface with the expression of cancer cell receptors. Paired-agent methods that employ a secondary “control” NP to account for these nonspecific effects can improve cancer detection. Yet these paired-agent methods introduce multidimensional complexity (with tissue staining, rinsing, imaging, and data analysis protocols all being subject to alteration), and could be greatly simplified with accurate, predictive in silico models of NP binding and diffusion. Here, we outline and validate such a model to predict the diffusion, as well as specific and nonspecific binding, of targeted and control NPs topically applied on tissue surfaces. In order to inform the model, in vitro experiments were performed to determine relevant NP diffusion and binding rate constants in tissues. The predictive capacity of the model was validated by comparing simulated distributions of various sizes of NPs in comparison with experimental results. The regression of predicted and experimentally measured concentration-depth profiles yielded <15% error (compared to ~70% error obtained using a previous model of NP diffusion and binding).

1. Introduction

Wide local excision is commonly used for the surgical treatment of sarcoma, skin, breast, pancreatic, gastrointestinal and other cancers, in which removal of a small margin of healthy tissue surrounding the cancerous tissue would not significantly affect the quality-of-life of the patient. For example, in the treatment of breast cancer, wide local excision (lumpectomy) followed by radiation provides equal survival rates to full breast removal (radical mastectomy) so long as the lumpectomy surgical margins are negative (i.e., the surfaces of the resected tissue specimens are absent of cancerous tissue) [1]. Unfortunately, excised surgical specimens from 6–8% of patients with skin cancer [2,3], 20–50% with breast cancer [4–6], 20–35% of patients with sarcoma [7], 14–76% of patients with pancreatic cancer [8,9], and approximately 7% of patients with head and neck cancer [10] exhibit positive margins when assessed in post-operative pathology, typically necessitating a callback surgery to remove the residual tumor. The development of intraoperative methods capable of accurately assessing surgical margins could help to eliminate the morbidity, psychological trauma, and financial burden of these callback surgeries. Approaches that have been tested include frozen section pathology [11,12], intraoperative cytology [13,14], RF spectroscopy [15,16], ultrasound [17,18], specimen radiography [12,19], molecular endoscopy [20–22], optical coherence tomography [23], nonlinear microscopy [24,25], structured illumination microscopy [26–29], photoacoustics [30], light-sheet microscopy [31], and molecular imaging with topically applied agents [20,32–39]. Of these methods, frozen section pathology and intraoperative cytology have been investigated most extensively to date; yet both methods only provide limited sampling of the surgical margin (<1% of the specimen surface). In addition, the high fat content in breast tissue negatively impacts the quality of frozen sections [40,41].

The topical application of agents targeted to cancer biomarkers has recently been explored to rapidly assess surgical margins [33,35,42–45]. Key advantages of topical application, for eventual clinical translation, include reduced toxicity and regulatory issues. However, nonspecific accumulation and off-target binding of imaging agents in tissue specimens often confound the interpretation of imaging results [46]. One way to normalize for nonspecific effects is to utilize a paired-agent method in which a control agent is co-administered with a cancer-targeted agent. Compared to the conventional approach where only targeted agents are used, such a paired-agent method has been shown to improve biomarker quantification when using various types of agents such as fluorescent dyes [32,39,46–49] and nanoparticles (NPs) [20,21,33–35,37,38,44,50,51]. Note that NPs can have functional and structural advantages over small molecules for topical application on tissue surfaces. As an example, for applications in which rapid molecular imaging of a tissue surface is desired (i.e. surgical margins), NPs in the size range of 10- to 100-nm in diameter diffuse into tissue much more slowly than small molecules, which confines their interactions to superficial cell layers. As a result, these larger NPs are also less likely to be nonspecificaly trapped within deep tissue layers. Minimizing this nonspecific background helps to improve image contrast and sensitivity at the tissue surface. Finally, in terms of their functionalization, NPs have a large surface area for conjugation with biomolecular targeting ligands (e.g., monoclonal antibodies, peptides, affibodies, etc.) to target malignant tumors with high specificity and multivalent affinity/avidity [52–55].

Despite the strengths of a paired-agent imaging approach, as described in the previous paragraph, tumor-to-benign tissue contrast with paired-agent topical staining is still affected by multiple factors, such as the staining and rinsing protocol (e.g., method, duration), diffusion rates of the imaging agents in the tissue, nonspecific binding of the agents, on- and off-rates of specific binding of the targeted imaging agent, and the method of data analysis [20,33,47–49,56]. Preliminary studies using NP-based imaging agents have sought to optimize staining, rinsing and imaging protocols through exhaustive trial-and-error experiments in tissues [20,33,51]. However, as the number of different NPs available for cancer-targeted imaging continues to grow, in which their diffusion and binding properties are unique [57–59], selecting the optimal staining/rinsing/imaging/analysis protocols for each new imaging agent will be prohibitive in terms of time and resources.

Here, we present and validate a mathematical model that can accurately simulate tumor-to-benign tissue contrast with paired-agent topical staining. The model requires the following inputs: the diffusion coefficient of the agents in tissue, the association rate constant governing the specific binding of targeted agents (k₃), the dissociation rate constant governing specific binding (k₄), the association rate constant governing non-specific tissue-surface binding (k₅), the dissociation rate constant governing non-specific binding (k₆), the free fluid volume fraction of the tissue (v_f), as well as the conditions of the staining and rinsing protocol (i.e. concentrations and times). Given these inputs, the model can be used in multiple ways to improve cancer margin molecular imaging protocols using topically applied NPs, such as: 1) guiding development of NPs (i.e., helping to identify ideal diffusion and binding properties when developing the agents), 2) optimizing staining and rinsing protocols to achieve sufficient tumor-to-benign tissue contrast within intraoperative time frames, and 3) helping to compare and select data analysis approaches for more quantitative estimates of cancer receptor expression (which could be used in the future for improving tumor staging and/or guiding adjuvant chemotherapy).

Previous models describing the binding and diffusion of targeted agents (e.g., antibodies, targeted NPs, etc.) within tissue are not ideal for simulating the behavior of topically applied NPs in thick tissues [60–63]. For example, the internalization diffusion model that describes the internalization of agents over hours [60] is not relevant for the large NPs (120-nm in diameter) used in our studies in which we stain and image tissues over a much shorter time scale of minutes. The cylindrical diffusion model is tailored for systemically delivered antibodies [61,62], and the fluorescence recovery after photobleaching (FRAP) model is an analytical solution to diffusion, binding, and FRAP [63]. These models were not developed for topical staining of thick tissue, nor do they take into account nonspecific binding/accumulation of targeted agents. Recently, our group published a preliminary model to simulate the topical staining of thick tissues with NPs [34]. This model was based on a model of drug diffusion and binding in tumor spheroids [64], and consisted of a system of partial and ordinary differential equations, combining Fick’s second law of diffusion with first-order binding kinetics. Here, we build on this previous model with new boundary conditions based on experimental observations and present the optimization and validation of this improved model. For example, to improve the regression of simulated concentration-depth profiles to experimentally measured profiles, and to expand the application of the model to larger NPs, the updated model assumes: 1) the possibility of nonspecific binding at the tissue surface; and 2) inclusion of a volume fraction parameter (v_f), which is the fraction of the tissue volume that is accessible to agents delivered within a staining/rinsing solution. This optimized model was evaluated and validated experimentally with epidermal growth factor receptor (EGFR)-targeted and control (untargeted) NPs of different diameters (120, 200, and 300 nm) used to stain human tumor xenografts implanted subcutaneously in athymic nude mice. The model exhibited 55% less error in comparison to a previous model for predicting the concentration-depth profile of larger NPs.

2. Theory

A model of NP binding and diffusion was derived based on a previously published mathematical model describing drug penetration and binding in tumor spheroids in which Fick’s second law of diffusion was combined with first-order binding kinetics [64]. The tissue was modeled to be a 1-dimensional vector in depth, perpendicular to the tissue surface, assuming negligible changes caused by lateral diffusion.

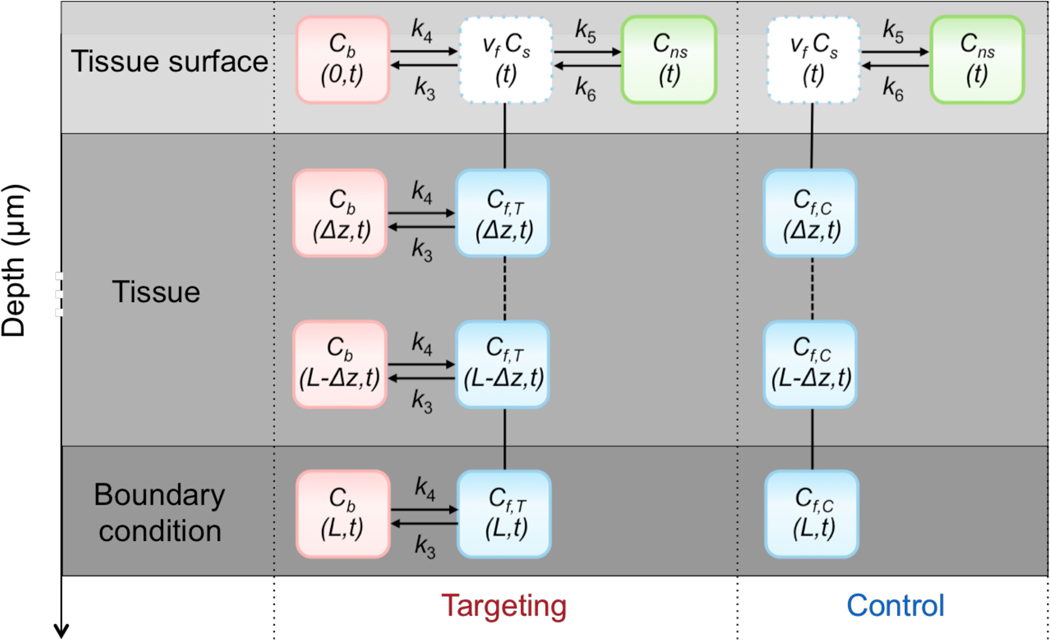
A direct modification of the drug penetration model for paired-agent imaging in a rectangular tissue geometry was described in detail in a previous study [34]; however, it failed to reliably predict NP diffusion and binding of NPs of different sizes. The updated model, which is based on homogeneous, 1-dimensional (in depth, z) diffusion and reversible binding in the tissue, is represented by the following system of differential equations and is illustrated in Fig. 1 as a compartmental model:

$$\begin{gathered} \frac{\partial c_{f,T}(z,t)}{\partial t}=D\frac{{\partial }^2{C}_{f,T}(z,t)}{\partial z^2}-k_3{C}_{f,T}(z,t)+k_4{C}_b(z,t) \\ \frac{\partial c_b(z,t)}{\partial t}=k_3{C}_{f,T}(z,t)-k_4{C}_b(z,t) \\ \frac{\partial C_{f,C}(z,t)}{\partial t}=D\frac{{\partial }^2{C}_{f,C}(z,t)}{\partial z^2} \end{gathered}$$ (1.1)

where C_f,T and C_f,C represent the concentrations of the targeted and control NPs, respectively, that can freely diffuse in the interstitial tissue volume; C_b represents the concentration of the targeted NPs that are bound to the cell-surface target biomolecules; D represents the diffusion coefficient (assumed to be the same for the targeted and control NPs); k₃ represents the rate constant governing the likelihood of the targeted NP binding to its target biomolecule (e.g., cell-surface receptor); and k₄ represents the rate constant governing the likelihood of bound NPs becoming dissociated from their targets. This representation of binding assumes that the concentration of target biomolecules is equal at all depths (z). It also assumes that the concentration of bound (targeted) NPs is always much lower than the concentration of target biomolecules, such that binding site saturation effects that would lower k3 are negligible, though the model could easily be modified to incorporate saturation by replacing k₃ with:

$$k_3(z,t)=k_{on}\left(B_{max,T}-C_b(z,t)\right)$$ (1.2)

where B_max,T is the total concentration of target biomolecules and k_on is the ex vivo association rate constant of binding.

Figure 1.

Illustration of the diffusion and binding model of targeted and control NPs topically applied on fresh tissue specimens. At the tissue surface, C_f is assumed to be in equilibrium with the staining solution according to a scaling factor, v_f (the tissue volume fraction of the free space). In addition, at the surface, the model includes a compartment for nonspecific retention of both the targeted and control NPs (C_ns). At all tissue layers, the targeted NP is able to bind specifically to the target biomolecule (C_b). Transport of both NPs between layers is assumed to be governed by Fick’s Law of Diffusion. Arrows were used to represent kinetic association and dissociation. Solid and dashed lines were used to represent diffusion between 2 and more layers.

The boundary condition at a distance of L = 30 μm was assumed to be impermeable (no-flux) and defined by setting the spatial gradient of the free concentrations equal to zero. This boundary condition was motivated by the fact that no appreciable NP signal has ever been observed at tissue depths greater than ~20 μm:

$$\frac{\partial c_{f,T}(L,t)}{\partial z}=\frac{\partial c_{f,C}(L,t)}{\partial z}=0$$ (1.3)

and the initial conditions were set to:

$$\begin{array}{l}{C}_{f,T}(z,0)=C_{f,C}(z,0)=0;z\ne 0\\ C_{f,T}(0,0)=C_{f,C}(0,0)=\text{const}.\end{array}$$ (1.4)

Here, we assume that some equal fraction of both the targeted and control NPs are able to “stick” nonspecifically to the surface of the tissue (perhaps owing to surface tension forces, or off-target chemical binding). The addition of the nonspecific compartment at the surface was based on experimental observations of NP retention at the tissue surface that could not be accounted for by our earlier model. Note that the addition of a nonspecific binding compartment below the tissue surface provided no additional improvements in the accuracy of the mathematical model, and therefore was omitted in order to minimize complexity and to improve the convergence of our model to a unique solution. A “volume fraction” correction factor has also been included to account for the fact that many structures (e.g., cells, extra-cellular matrix) in the tissue can limit the volume that the NP can access (depending on the chemical properties of the NP). The volume fraction (0 < v_f < 1) is incorporated into the model at the surface layer, (z = 0), by assuming an instantaneous equilibrium between the staining solution concentration of the agent, C_s, and the concentration of the agent in the accessible volume fraction of the tissue, v_fC_f(z = 0). The complete surface boundary condition can be represented as:

$$\begin{gathered} C_{f,T}(0,t)=C_{f,C}(0,t)=v_f{C}_s(t) \\ \frac{\partial c_{ns}(t)}{\partial t}=k_5{C}_{f,T}(0,t)-k_6{C}_{ns}(t) \end{gathered}$$ (1.5)

where C_ns represents the concentration of NPs that have nonspecifically bound to the surface of the tissue, k₅ is the rate constant governing the likelihood of nonspecific binding at the surface, and k₆ is the rate constant governing NP dissociation from the nonspecific sites. Note: the fraction of the tissue volume accessible to the NP, v_f, is assumed to be equivalent at all layers of the tissue; however, it only needs to be incorporated into the model at the surface, as all deeper layers are driven by the v_fC_s concentration at the surface.

3. Materials and methods

3.1. NP functionalization

The functionalization of surface-enhanced Raman scattering (SERS) NPs has previously been described [20,33,45,65]. These NPs were purchased from BD (Becton, Dickinson and Company), and consist of a 60-nm diameter gold core, a layer of Raman reporters adsorbed onto the surface of the gold cores, surrounded by a 30-nm thick silica coating, resulting in an overall diameter of ~120 nm. Note that based on the specific Raman reporter used, each “variety” of SERS NP emits a unique Raman fingerprint spectrum, which enables multiplexed detection of a mixture of NP varieties. In practice, each NP variety may be targeted to a different biomolecule (or none at all in the case of a control NP) for multiplexed molecular imaging. In this study, one variety of SERS NP was reacted with a reactive fluorophore (for fluorescence microscopy studies), DyLight 650–4xPEG Maleimide (Thermo Scientific, Product No. 62294, Rockford, IL), and functionalized with monoclonal antibodies (mAb) to target the epidermal growth factor receptor (EGFR; Thermo Scientific MS-378-PABX, Fremont, CA). A negative control was prepared by reacting a different variety of NP with another reactive fluorophore, DyLight 550–2xPEG Maleimide (Thermo Scientific, Product No. 62292, Rockford, IL), and conjugating the NP to isotype control mAbs (mouse IgG1; Thermo Scientific, MA110407, Rockford, IL). Previous studies have shown that the isotype NP is a highly accurate control for the nonspecific behavior of the targeted NPs [33]. UV-VIS spectrophotometry (Agilent 8453) was used to measure the concentration of the NP conjugates. Previous flow cytometry experiments [20,33,45,65] demonstrated robust binding of the EGFR-targeted NPs to A431 cells (human epidermoid, ATCC, Manassas, VA), which highly overexpress EGFR.

For studies with larger NPs, silica NPs (SiNPs) with diameters of 200-nm and 300-nm were purchased from NanoComposix (SISN200–10M and SISN300–10M, San Diego, CA) and conjugated to fluorescent dyes and antibodies in a similar manner to the SERS NPs, and as previously described [34]. Note that SiNPs were used due to the lack of commercial SERS NPs available in different sizes, and that since the SERS NPs are encapsulated in a silica shell, the behavior of these NPs (SERS NPs and SiNPs) are similar in terms of diffusion and chemical binding (both specific and nonspecific) when functionalized in a similar manner. The SiNPs were first PEGylated, to enable conjugations comparable to those with the SERS NPs, by introducing sulfhydryl groups on the SiNP surfaces by heating the SiNPs for 1 h at 72°C in ethanol containing 1% (v/v) (3-Mercaptopropyl) trimethoxysilane (Sigma Aldrich) according to a protocol described previously [66]. The surface-modified SiNPs were functionalized in the same manner as the SERS NPs—all NP sizes were subjected to two different sets of conjugation reactions: 1) DyLight 650–4xPEG Maleimide and an anti-EGFR mAb or 2) DyLight 550–2xPEG Maleimide and an IgG1 isotype control mAb. UV-VIS spectrophotometry was then used to measure the concentration of the SiNP conjugates. We have previously shown that the relative brightness of the fluorescence from each of the NP sizes was well-matched when tuning the NP concentrations used in the conjugation reactions such that the total surface area of the NPs (total sum within the mixture) was identical to that of the 120-nm SERS NPs used in previous experiments (and reacted with the same concentration of fluorophores) [34]. We have also previously verified with flow cytometry experiments that the binding of targeted NPs to EGFR-positive cell lines was comparable in magnitude for all NP sizes when staining cells with NP concentrations that were matched in terms of total NP surface area [34].

3.2. In vitro experiments to estimate NP binding and diffusion parameters

Due to the large number of parameters (6) used in the model compared to the number of input signals (targeted and control curves), the initial parameter values can play a role in model fitting. To more accurately estimate the range of some of the most-important binding and diffusion parameters described in Section 2 (specifically, k₃, k₄, and D), in vitro experiments were carried out based on previously published protocols [67,68].

3.2.1. Estimating binding rate constants.

A 96-well plate with a 200-μm-thick glass bottom was used to culture EGFR-positive cancer cells (A431) into monolayers. Cells were counted and seeded into wells (1×10⁵ A431 cells in 200 μL of media per well). After incubation for 24 h, confluent cell monolayers were observed in all wells. An equimolar mixture of EGFR-targeted and isotype-control NPs was added for staining the confluent monolayers. The staining procedure was followed by 3 rounds of rinsing with saline solution. Spectral measurements were collected after the final rinse step using the Raman-encoded molecular imaging (REMI) system described in Supplementary Figure S1. Prior to staining the cell monolayer, Raman spectra were first collected in the absence of NPs for background measurement. A direct classical least-squares (DCLS) demultiplexing method was used to compute the relative NP weights and the weights of all broadband background components, as previously described [21,33,69].

An approximate model based on single-cell binding and internalization [60] was used to obtain direct estimates of specific binding rate constants from the in vitro experiments. In this study, we assumed that the NPs were too large (120-nm in diameter) to be internalized by the cell within the short staining durations (<1 h), so the internalization component was excluded from the model. Instead, we assumed there was nonspecific binding of the control NPs, and both specific and nonspecific binding of the targeted NPs. The model equations to approximate single-cell interactions with NPs were then simplified to:

$$\begin{gathered} \frac{d{N}_s(t)}{dt}=k_{on,S}{C}_0\left(B_s-N_s(t)\right)-k_{off,S}{N}_s(t) \\ \frac{d{N}_{NS}(t)}{dt}=k_{on,NS}{C}_0\left(B_{NS}-N_{NS}(t)\right)-k_{off,NS}{N}_{NS}(t) \end{gathered}$$ (2.1)

where N_S(t) represents the number of NPs specifically bound at the cell surface as a function of time, t; N_NS(t) represents the number of NPs nonspecifically bound at the cell surface as a function of t; B_S and B_NS represent the number of specific and nonspecific binding sites, respectively; k_on,S, k_off,S, k_on,NS and k_off,NS represent the association (binding) and dissociation rate constant for specific and nonspecific binding, respectively; and C₀ represents the concentration of NP in the staining solution (assumed not to change over time; “infinite reservoir”). The system of equations in (2.1) can be solved for total number of control NPs bound at the cell surface (N_C), by setting B_S = 0:

$$N_{NS,C}(t)=\frac{k_{on,NS}{C}_0{B}_{NS}}{K_{on,NS}{C}_0+k_{off,NS}}\left(1-e^{-\left(k_{on,NS}{C}_0+k_{off,NS}\right)t}\right)$$ (2.2)

The total number of targeted NPs bound at the cell surface (N_T) is the summation of NPs bound specifically (N_S,T) and nonspecifically (N_NS,T). If we assume that N_S,C(t) = N_S,T(t):

$$N_T(t)-N_c(t)=\frac{k_{on,S}{C}_0{B}_S}{K_{on,S}{C}_0+k_{off,S}}\left(1-e^{\cdot \left(k_{on,S}{C}_0+k_{off.S}\right)t}\right)$$ (2.3)

Nonlinear curve fitting is used to determine the available number of specific and nonspecific binding sites, B_S and B_NS; nonspecific binding rates, k_on,NS and k_off,NS; and the specific binding rates, k_on,S and k_off,S. In this case, Eqs. (2.2)–(2.3) are fit to NP concentration measurements from confluent cell monolayers.

With confluent monolayers, it was assumed that the total exposed surface area of the cell membranes was equal to the area of the well, which allowed for the calculation of the number of NPs bound per unit cell membrane area. The average surface area per cell (assumed to be 2800 μm² for A431 cells based on past work [70,71]) was used to convert the number of NPs bound per unit cell area to the number of NPs bound per cell. The total number of nonspecific binding sites, B_NS, was estimated by staining cell monolayers with various concentrations of NPs (20–600 pM) for 1 h (sufficient staining time to assume equilibrium was reached) prior to rinsing the monolayer with a saline solution in triplicate and imaging the monolayer with the REMI system. Under these conditions, Eq. (2.3) simplifies to N_NS = B_NS. The total number of specific binding sites, B_S, used in the calculation was obtained from previous work [48].

The fitted association and dissociation rate constants were then determined by fitting Eqs. (2.2)–(2.3) to data collected by exposing confluent monolayers to an equimolar mixture of targeted and control NPs (150 pM) and measuring the number of NPs bound per cell as a function of time (15–120 min). The resulting rate constants, k₃ and k₄, were used in mathematical model simulations and compared to data as:

$$\begin{gathered} k_3=k_{on,S}{B}_{max,T} \\ {k}_4=k_{off,S} \end{gathered}$$ (2.4)

where B_max,T is the concentration of target receptors in the tissue converted from B_S, the number of specific binding sites per cell. The equation for k₃ is simplified from Eq. (1.2), assuming C_b << B_max,T. Note: it is assumed that the level of nonspecific binding is very different between ex vivo tissue studies and the in vitro experiments performed here, so k5 and k6 cannot similarly be estimated.

3.2.2. Estimation of diffusion coefficient.

The effective diffusion coefficient for 120-nm NPs topically applied on tissues, D, was calculated using a hydrogel drug release model [68] that represents the concentration of NPs released into the wash solution. The hydrogel drug release model, F_D, was updated to include a term that takes into account the release of nonspecifically bound NPs, F_N. The updated model was written as:

$$\begin{gathered} F_D=\left(1-{\sum }_{n=0}^{\infty }\frac{8}{{(2n+1)}^2{\pi }^2}\exp \left[-D{(2n+1)}^2\frac{{\pi }^{2}t}{l^2}\right]\right) \\ \begin{array}{l}{F}_N=\left(\frac{k_5}{k_6+k_5}\right)\left[1-\exp \left(-k_{6}t\right)\right]\hfill \\ F=f{F}_D+(1-f)F_N\hfill \end{array} \end{gathered}$$ (2.5)

where F represents the fraction of NPs rinsed out into the wash solution in comparison to concentration of NPs within the maximally stained tissue. This fraction, F, includes NPs released into the wash solution as a result of diffusion, F_D, and as a result of the dissociation of nonspecifically bound NPs, F_N. F_D and F_N are multipled by f and (1-f), respectively, where f describes the fraction of NPs released as a result of diffusion.

Experimental data for the release model was obtained by staining porcine muscle tissues (cut into 40 mm × 40 mm × 0.4 mm pieces to emulate 1D diffusion; n=3 pieces) overnight with 120 nm SiNPs (NanoComposix, San Diego, CA) that were conjugated with IRDye 700DX-labeled-NP (LI-COR Bioscience, Lincoln, NE). Specimens were imaged with a Pearl imager (LI-COR) at room temperature prior to staining, immediately after staining, and thereafter as a function of time as the specimen was rinsed in PBS, to calculate the fractional release value, F.

3.3. Ex vivo experiments to validate the mathematical model

3.3.1. Animal experiments.

All animal experiments were performed in accordance with guidelines approved by the Institutional Animal Care and Use Committee (IACUC) at the University of Washington. Nude mice (Taconic Farms Inc, model NCRNU-F, Rensselaer, NY) were used to develop tumor xenografts. 1×10⁶ A431 cancer cells were suspended in Matrigel (BD biosciences, 354234, San Jose, CA) in a 1:1 volume ratio to form a 200-μL mixture. At 7–9 weeks of age, nude mice were subcutaneously implanted with a cell mixture on their flanks. After 2–4 weeks, when the tumors reached a diameter of 8–10 mm, the mice were euthanized by CO₂ inhalation, followed by the surgical removal of the implanted tumors.

3.3.2. Concentration-depth profiles obtained from microscopic imaging of sectioned tissues.

Experimental concentration-depth profiles used to validate the mathematical model were obtained using a previously described method [34]. Briefly, fresh tissues obtained from tumor xenografts were stained with a NP mixture (150 pM each of 120, 200 and 300 nm EGFR-targeted and control NPs) for 6 min, briefly rinsed (~2 s) in 20 mL of PBS, snap-frozen, and cryosectioned into 10-μm-thick sections. The sectioned tissues were then mounted onto slides, fixed with formalin and imaged as illustrated in Fig. 2A with fluorescence microscopy (Leica DMIRB microscope with a CoolSnap CCD camera) to obtain depth-resolved microscopic images of the penetration of the targeted and control NPs within the tissues.

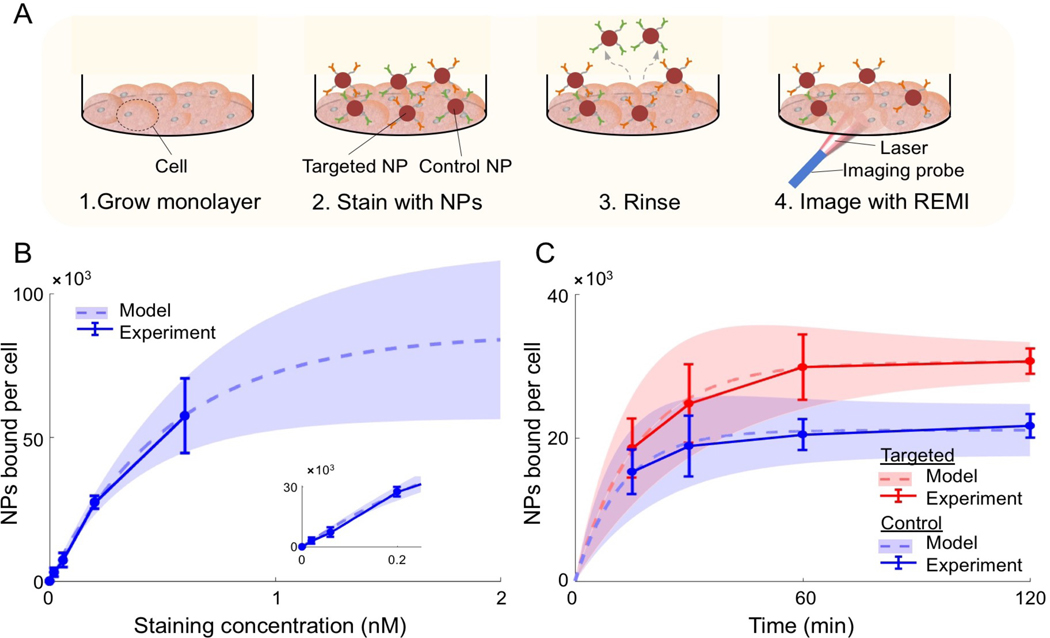
Figure 2. In vitro experiments to estimate key model parameters.

(A) For each well in a 96-well plate, A431 cells were (1) grown to a confluent monolayer (~24 h), (2) then the cell monolayer was stained with NPs, (3) the cell monolayer was rinsed three times to wash away unbound NPs, and (4) spectral measurements were collected with a Raman-encoded molecular imaging (REMI) system described in Supplementary Figure S1. The measured SERS signals were converted to NPs bound per cell using the calculations described in the Methods section. Note that the figure is not to scale. (B-C) Experimental data (error bars based on n = 3 repeated experiments) and fitted curves (dashed lines) for determining: (B) the available number of nonspecific binding sites, B, and (C) the association and dissociation rate constants for targeted (red) and control (blue) NPs. The shaded regions indicate the uncertainty in the fitted curves based on the error (standard deviation) in the experimental data. Curve fits were based on Eqs. (2.2)–(2.3). The staining time for the data in panel (B) was 1 h and the staining concentration for the data in panel (C) was 150 pM.

3.4. Numerical methods.

The methodology for solving Eqs. (1.1)–(1.5) are detailed in the supplemental information. Briefly, the system of equations are 2^nd-order parabolic partial differential equations that are solved implicitly by a Crank-Nicholson method where stability is maintained by ensuring:

$$\frac{D\left(t_s+t_r\right)N_z^2}{N_t{L}^2}<0.5$$ (2.6)

where t_s and t_r are the staining and rinsing times, respectively. Eq. (2.3) was maintained by adjusting the number of time point evaluations, N_t. The number of spatial point evaluations, N_z, was selected such that the spatial resolution ((N_z-1)/L = 0.1 μm) of the solution was one tenth of the resolution of the microscope used in the tissue imaging experiments. The motivation for this is provided in the next section (accurate convolution with the microscope’s point spread function to model the effects of diffraction).

3.5. Point-spread-function correction of simulation results for comparison with microscopy data.

To compare the model output (numerical simulations of NP diffusion and binding) with experimentally measured concentration profiles, each simulated concentration profile was convolved with a numerical point-spread-function (PSF) based on published software [72] along with the specifications of the fluorescence microscope (Leica DMIRB microscope with a CoolSnap CCD camera) that was used to obtain the experimental concentration profiles: numerical aperture = 0.7, objective magnification = 20, refractive index of the objective immersion medium = 1 (air), and refractive index of the specimen medium = 1.41. Note that for this convolution, a numerical integration (Riemann sum) step size of 0.5 μm was utilized. The excitation and emission wavelengths were 555 nm and 605 nm, respectively, for the control NP and 645 nm and 705 nm, respectively, for the targeted NP.

4. Results

4.1. Estimating the initial range of k₃ and k₄

Nonlinear least squares fitting of Eq. (2.2) to the in vitro data shown in Fig. 2B produced estimates of B_NS = 85×10³ ± 30×10³, which is the number of nonspecific binding sites available for NP binding per cell. The total number of specific binding sites, BS, was estimated to be 1.2×10⁶ based on previous work [48]. The resulting B_max,T was 7.6 ± 1.5 nM (number of nonspecific binding sites available for NP binding per liter of tissue in A431 tumor), assuming a cell density in A431 xenografts of 3.8×10⁴ cells/mm³ [48] and a xenograft EGFR expression of ~10% of in vitro EGFR expression for the A431 tumor line [73]. According to Eq. 2.4, k₃ and k₄ were estimated to be between 0.021 to 2.1 min⁻¹, and 0.015 to 0.6 min⁻¹, respectively. Note that the in vitro experiments are not exact representations of how NPs bind within thick tissues, which is why the parameter estimates were allowed to vary within 1-to-2 orders of magnitude.

The fractional release data (Section 3.2.2) was fitted with Eq. 2.5 to obtain an estimated diffusion coefficient. The estimated diffusion coefficient for 120-nm NPs in thin tissue was D = 1.18 ± 0.14 μm² s⁻¹ and this parameter was therefore allowed to vary between 0.118 and 11.8 μm² s^-1.

4.2. Model fitting to concentration-depth profiles

Both the optimized model of paired agent diffusion and binding (Section 2) and the previous model [24] were fitted to concentration-depth profiles of targeted and control NP obtained from excised A431 xenografts following 6 min of topical staining with the NPs. Fig. 3A shows a simple illustration of the process for obtaining depth-resolved microscopic images of sectioned tissues, which was used to fit the model. The concentration-depth profiles of the experimental data are shown in Fig. 3B–C in solid lines for the targeted (red) and control (blue) NPs. The fitted curves for the previous (simple) and newly optimized models are shown as dashed lines in Fig. 3B and Fig. 3C, respectively. Table 3 lists the final fitted parameter values from the optimized model as well as the initial parameter ranges that were determined from in vitro experiments (section 3.2). Figure 3D shows that the percent error in concentration-depth profiles increased as a function of depth for both models, with the previous model exhibiting a greater error compared to the newly optimized model. The average R-squared regression values for the targeted and control imaging agent was 0.32 for the previous model and 0.97 for the optimized model.

Figure 3. Fitting the simple model and the optimized model to depth-resolved microscopic images of NP distributions in tissues.

(A) A brief illustration of the experimental method used to fit the simple model and the optimized model. (1) Targeted and control NPs were prepared by conjugating NPs to monoclonal antibodies and different fluorophores. (2) Fresh tissue specimens were stained for 6 min with an equimolar NP mixture, rinsed and snap-frozen. (3) The specimens were then cryosectioned into 10 μm-thick slices and (4) imaged with fluorescence microscopy using different channels for the targeted and control NPs. Images were analyzed to obtain concentration-depth profiles of both NPs as a function of depth, z. (B-C) Experimental NP concentration profiles are shown in solid lines for targeted (red) and control (blue) NPs, which were used to fit all of the model parameters for: (B) the simple model and (C) the optimized model. As described in the manuscript, certain parameter ranges were determined based on in vitro experiments, as shown in Fig. 2. (D) The percent error (fitting error) in the concentration-depth profile is shown, in which there is increasing error as a function of depth for both models, and greater overall error seen with the simple model.

Table 3.

Comparison of initial parameter ranges from in vitro experiments and final parameter values from the optimized model.

	Initial ranges from in vitro experiments	Final values from optimized model
D (μm2.s−1)	0.118–11.8	0.23
k3 (min−1)	0.021–2.1	0.38
k4 (min−1)	0.015–0.6	0.34
BP	0.675–60.75	1.12
k5 (min−1)	N/A	0.74
k6 (min−1)	N/A	0.29
vf	N/A	0.68

4.3. Model prediction of larger NPs

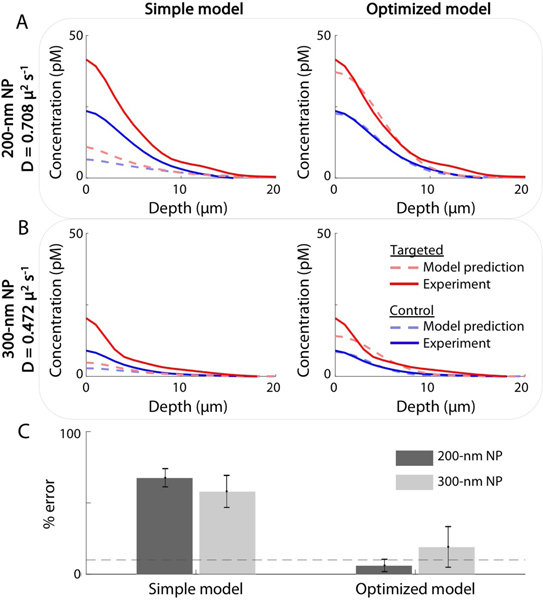
We further demonstrated the value of the optimized model by simulating the concentration-depth profiles of larger NPs. This was done by modifying the diffusion coefficient, D, according to the Stokes-Einstein generalized equation (in which D scales inversely with the radius of the NP) while fixing all other model parameters to the same values as determined from previous experiments with the 120-nm NPs. To verify the accuracy of model simulations for larger NPs, 200-nm and 300-nm NPs were prepared in an identical manner as the 120-nm NPs used in previous studies, according to a previously published protocol [34], and concentration-depth profiles were obtained for A431 tumor xenografts stained for 6-min. Figure 4 shows model predictions (dashed lines) and experimental results (solid lines) for both the targeted (red) and control (blue) NPs with diameters of: (A) 200-nm and (B) 300-nm. The percent errors in the area under the curves are shown for the simple and optimized models in Fig. 4C, where the simple model shows ~70% error and the optimized model shows ~15% error. This demonstrates the power of the optimized model for predicting the behavior of biomarker-targeted NPs topically applied on fresh tissue specimens.

Figure 4. Predicting the concentration-depth profiles of (A) 200-nm and (B) 300-nm NPs using the simple model (left) and the optimized model (right).

The models were run with identical parameters to those derived from the curve fits shown in Fig. 3, with the exception of the diffusion coefficient, D, which was modified according to the Stokes- Einstein generalized equation (in which D scales inversely with the radius of the NP). Model predictions are shown in dashed lines for the targeted (red) and control (blue) NPs. Experimental data are shown in solid lines and were obtained from A431 tumor xenografts stained for 6 min with NPs of varying sizes. In (C), the percent errors in the area under the curves are shown for the simple and optimized models. The dashed grey line indicates 10% error.

4. Discussion

Previous models for the binding and diffusion of targeted agents (e.g., antibodies, targeted NPs, etc.) within tissue have not been developed to describe the topical application of NPs on thick tissue surfaces, and have not taken into account the nonspecific accumulation of agents. In this paper, we developed and validated an optimized model for topical staining of receptor-targeted and control NPs in thick tissue (Fig. 1), in which the model was initialized with key parameter values (rough order-of-magnitude ranges) derived from in vitro experiments (Fig. 2). This allowed a final set of model parameters to be obtained by fitting the model to data from ex vivo experiments with NPs topically applied on fresh tissue specimens (Fig. 3). By accurately simulating the concentration-depth profile of topically applied NPs (Fig. 4), this model can potentially be used to establish optimized protocols for paired-agent molecular imaging of fresh tissue surfaces.

Several factors were considered in the development of this model, including diffusion, optical diffraction, and nonspecific retention. The model presented here accurately predicted the diffusion and binding of NPs in thick tumor tissues while retaining as much simplicity as possible. The key novelties in this model over a simpler model that accounted only for diffusion and specific binding [24] were: 1) inclusion of a volume fraction parameter (v_f), which is the fraction of the tissue volume that is accessible to agents delivered within a staining/rinsing solution, and 2) taking into account nonspecific retention of NPs at the tissue surface. Significant nonspecific binding/accumulation of the NPs has been observed in previous studies [20,21,33,34,37], including in cell-monolayer experiments (Fig. 2C). Introducing a nonspecific compartment below the surface of the tissue did not improve model accuracy. Therefore, a nonspecific binding compartment was only introduced at the surface layer of the tissue to reduce the complexity of the model and to improve the speed and convergence of the model to a unique solution.

We note that this model is highly simplified and does not include such complexities as NP trapping in fresh tissue and heterogeneities in tissue structure (e.g., due to vessels, glands, and other microstructures). However, the agreement of the model to experimentally obtained concentration-depth profiles, coupled with the predictive value of the model for simulating the behavior of NPs of differing sizes, highlights the potential of this model to “test out” various topical staining protocols rapidly in silico rather than via time-consuming and expensive experiments. These models will also be of value for developing and optimizing various NP-based imaging strategies and image-processing algorithms for the ultimate goal of achieving quantitative imaging of biomarker expression levels at tissue surfaces, including surgical margins.

Table 1.

List of the parameters used in the mathematical model that describes the binding and diffusion of NPs topically applied on fresh tissue specimens.

Name	Description
k3, k4	Association and dissociation rate constants, respectively, of a targeted NP binding to its target
k5, k6	Association and dissociation rate constants, respectively, of nonspecific binding
D	Diffusion coefficient
vf	Fraction of tissue volume accessible to NPs
Cf,T, Cf,C	Concentration of targeted and control (untargeted) NPs, respectively, that can freely diffuse in the interstitial tissue volume
Cns	Concentration of NPs nonspecifically bound to the surface of the tissue
Cb	Concentration of targeted NPs that are bound to the cell-surface target biomolecules
Cs	Concentration of NPs in the staining mixture
Bmax,T	Total concentration of target biomolecules

Table 2.

List of the parameters used in in vitro models/experiments to estimate some of the key parameters identified in Table 1.

Name	Description
NS, NNS	Number of NPs specifically and nonspecifically bound at the cell surface, respectively
kon,S, koff,S	Association and dissociation rate constants for specific binding, respectively
kon,NS, koff,NS	Association and dissociation rate constants for nonspecific binding, respectively
NT , NC	Total number of targeted and control NPs at the cell surface, respectively
C0	Concentration of NPs in the staining solution
BS, BNS	Number of specific and nonspecific binding sites, respectively
F	Fraction of total NPs rinsed out into the wash solution
FD	Fraction of targeted NPs rinsed out into the wash solution
FN	Fraction of nonspecifically bound NPs rinsed out into the wash solution
f	Fraction of NPs released as a result of nonspecific diffusion